Świąteczne



Testy T-Studenta





Ciąg dalszy





Problem badawczy:

Czy dzieci pochodzące z rodzin

zgodnych inaczej oceniają bajki niż
dzieci z rodzin skonfliktowanych?

Hipoteza badawcza 1:

Dzieci z rodzin skonfliktowanych wyżej ocenią

bajkę o wiewiórce niż bajkę o jeżykach.

Hipoteza badawcza 2:

Dzieci z rodzin zgodnych wyżej ocenią bajkę o

jeżykach niż bajkę o wiewiórce.

Kilka wersji zastosowanych procedur

statystycznych:

1.    Test „t” dla prób zależnych, dwukierunkowy,
poziom istotności p < 0,05
2.    Test „t” dla prób zależnych, dwukierunkowy,

poziom istotności p < 0,01

3.    Test „t” dla prób zależnych, jednokierunkowy
poziom istotności p < 0, 05

Hipoteza badawcza 3:

Dzieci z rodzin skonfliktowanych wyżej ocenią

bajkę o wiewiórce niż dzieci z rodzin zgodnych.

Hipoteza badawcza 4:

Dzieci z rodzin zgodnych wyżej ocenią bajkę o

jeżykach niż dzieci z rodzin skonfliktowanych 

Kilka wersji zastosowanych procedur

statystycznych:

1.    Test „t” dla prób niezależnych,

dwukierunkowy, poziom istotności p < 0,05

2.    Test „t” dla prób niezależnych,

dwukierunkowy, poziom istotności p < 0,01

3.    Test „t” dla prób niezależnych,

jednokierunkowy poziom istotności p < 0, 05

Wyniki analiz statystycznych:

Uwaga: uzyskane poziomy istotności dla wykonanych

analiz statystycznych zaokrąglamy w górę do

poziomu (p<0.05; p<0.01; lub p<0.001)

Hipoteza 1:

Wyniki analizy statystycznej dla odpowiednich wersji:
1.    Hipoteza badawcza została potwierdzona – hipoteza zerowa

odrzucona na poziomie istotności mniejszym niż 0.05

(dokładnie – mniejszym niż 0.006), t(9) = 3.60; p<0.01

2.    Hipoteza badawcza została potwierdzona – hipoteza zerowa

odrzucona na poziomie istotności mniejszym niż 0.01

(dokładnie – mniejszym niż 0.006), t(9) = 3.60; p<0.01

3.    Hipoteza badawcza została potwierdzona – hipoteza zerowa

odrzucona na poziomie istotności mniejszym niż 0.05

(dokładnie – mniejszym niż 0.003), t(9) = 3.60; p<0.01, test

jednostronny

Hipoteza 2

Wyniki analizy statystycznej dla odpowiednich wersji: 
1.    Hipoteza badawcza nie została potwierdzona, nie

można odrzucić hipotezy zerowej (dokładny poziom

istotności p<0.20 jest większy niż założone 0.05) t

(9) = 1.81; p<0.20 (prawidłowy zapis)

2.    Hipoteza badawcza nie została potwierdzona, nie

można odrzucić hipotezy zerowej (dokładny poziom

istotności p<0.20 jest większy niż założone 0.01)

3.    Hipoteza badawcza nie została potwierdzona, nie

można odrzucić hipotezy zerowej (dokładny poziom

istotności p<0.10 jest dalej większy niż założone

0.05)

Hipoteza 3

Wyniki analizy statystycznej dla odpowiednich

wersji:

1.    Hipoteza badawcza została potwierdzona –

hipoteza zerowa odrzucona na poziomie istotności

mniejszym niż 0.05 (dokładnie – mniejszym niż

0.002), t(18) = 3.64; p < 0.01

2.   Hipoteza badawcza została potwierdzona –

hipoteza zerowa odrzucona na poziomie istotności

mniejszym niż 0.01 (dokładnie – mniejszym niż

0.002), t(18) = 3.64; p < 0.01

3.   Hipoteza badawcza została potwierdzona –

hipoteza zerowa odrzucona na poziomie istotności

mniejszym niż 0.05 (dokładnie – mniejszym niż

0.001), t(9) = 364; p < 0.001, test jednostronny

Hipoteza 4

Wyniki analizy statystycznej dla odpowiednich wersji:
 
1.    Hipoteza badawcza została potwierdzona – hipoteza

zerowa odrzucona na poziomie istotności mniejszym niż
0.05 (dokładnie – mniejszym niż 0.04), t(18) = 2.25; p <
0.05

2.    Hipoteza badawcza nie została potwierdzona – hipoteza

zerowa odrzucona na poziomie istotności mniejszym niż
0,01 (dokładnie – mniejszym niż 0.04), t(18) = 2.25; p <
0.05

3.    Hipoteza badawcza została potwierdzona – hipoteza

zerowa odrzucona na poziomie istotności mniejszym niż
0.05 (dokładnie – mniejszym niż 0.02), t(18) = 2.25; p <
0.05, test jednostronny

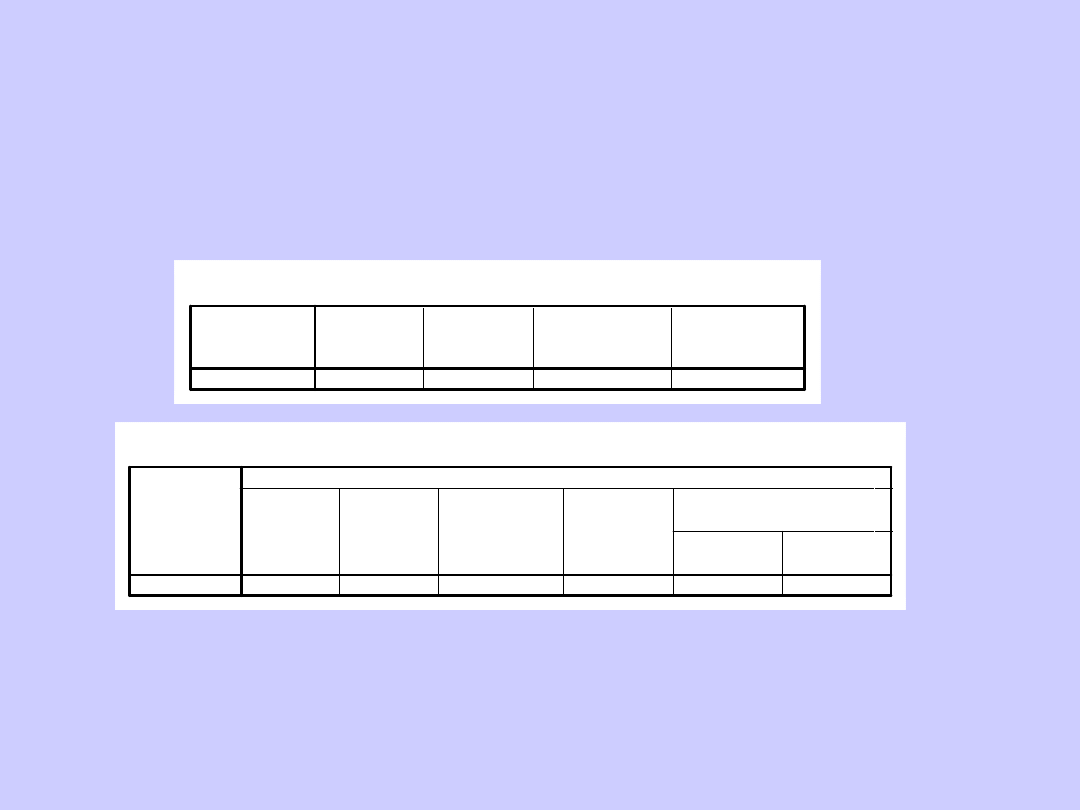
H1: Średnia długość kocich pazurów jest większa niż 1 cm.
H0: Średnia długość kocich pazurów jest mniejsza lub równa 1

cm

(test jednostronny). Założony poziom istotności: p<0,05

Statystyki dla jednej próby

10

1,3500

,3536

,1118

DL_PAZUR

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

3,130

9

,012

,3500

9,708E-02

,6029

DL_PAZUR

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 1

Wynik:
t(9) = 3,13; p< 0,01

(istotność dwustronną dzielimy przez 2)

Interpretacja:
Odrzucamy H0 i przyjmujemy H1. Średnia długość kocich pazurów
jest większa
niż jeden centymetr

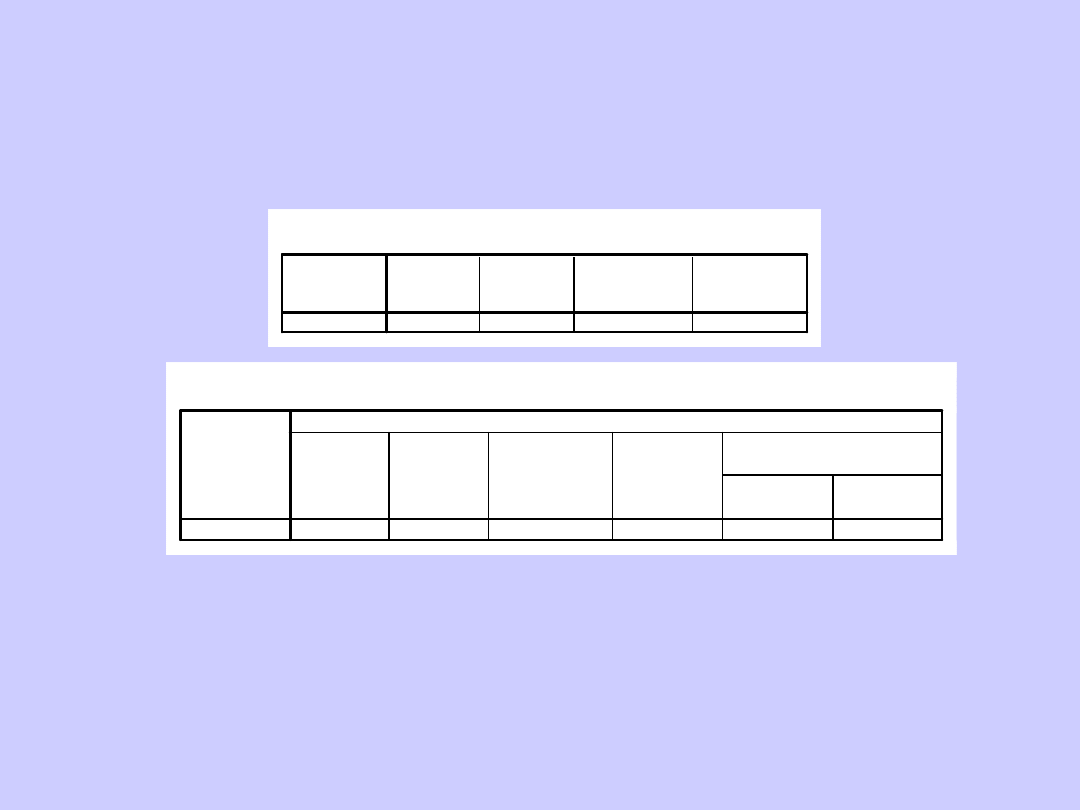
H1: Kocia sierść średnio jest dłuższa niż 4 cm
H0: Sierść kota jest równa 4 cm, lub krótsza (testujemy testem

jednostronnym)

Założony poziom istotności: p<0,05

Wynik:
t(9) = 6,5; p<0,001
Interpretacja:
Pomimo tego, że wynik jest wysoce istotny statystycznie nie możemy

odrzucić hipotezy zerowej, ponieważ postawiona przez nas

hipoteza alternatywna była hipotezą kierunkową, a wyniki

potwierdziły hipotezę o kierunku przeciwnym do H1.

Statystyki dla jednej próby

10

2,0100

,9689

,3064

DL_SIERS

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

-6,495

9

,000

-1,9900

-2,6831

-1,2969

DL_SIERS

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 4

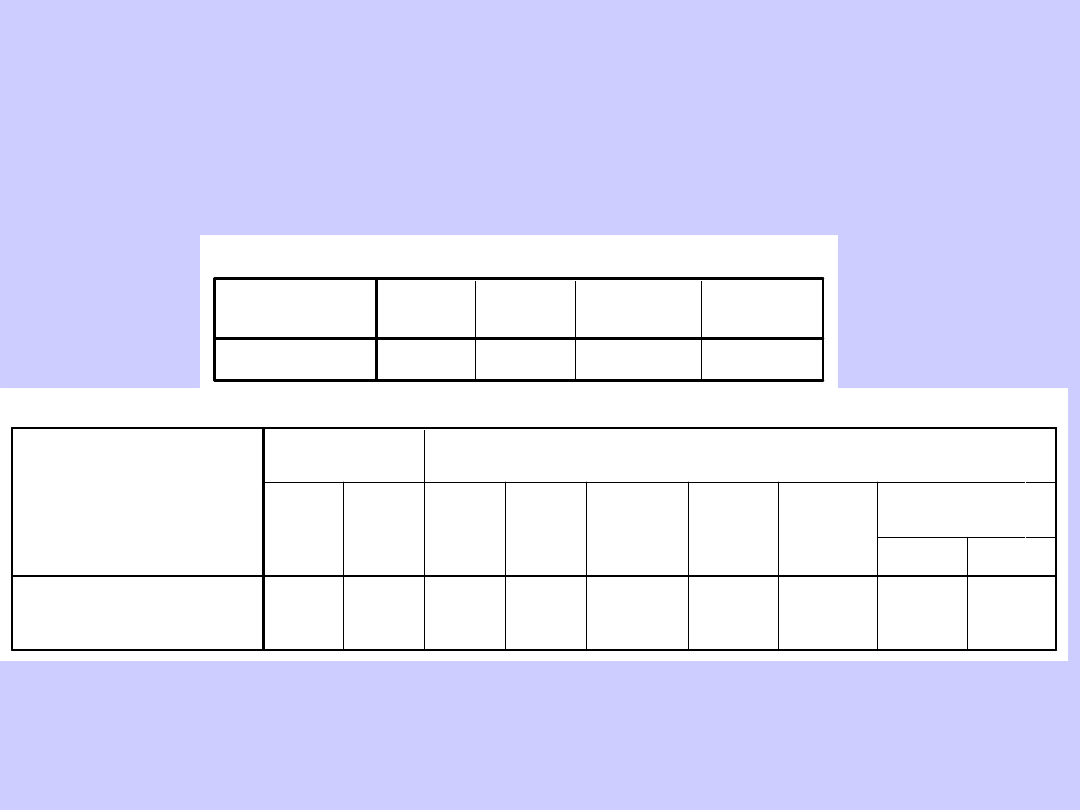
H1: Kocury mają maja dłuższe pazury niż kotki
H0: Kocury i kotki nie różnią się od siebie pod względem długości

pazurów (testujemy testem dwustronnym),

założony poziom

istotności: p<0,05

Statystyki dla grup

4

1,0250

,2217

,1109

4

1,7250

,2217

,1109

plec
kotki
kocury

DL_PAZ

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla prób niezależnych

,000

1,000

-4,465

6

,004

-,7000

,1568

-1,0837

-,3163

-4,465

6,000

,004

-,7000

,1568

-1,0837

-,3163

Założono równość
wariancji
Nie założono równości
wariancji

DL_PAZ

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

Wynik:
t(6) = 4,47;
p<0,01

Interpretacja (patrzymy do statystyk
opisowych):
Kocury maja dłuższe pazury niż kotki.
Odrzucamy H0, przyjmujemy H1.

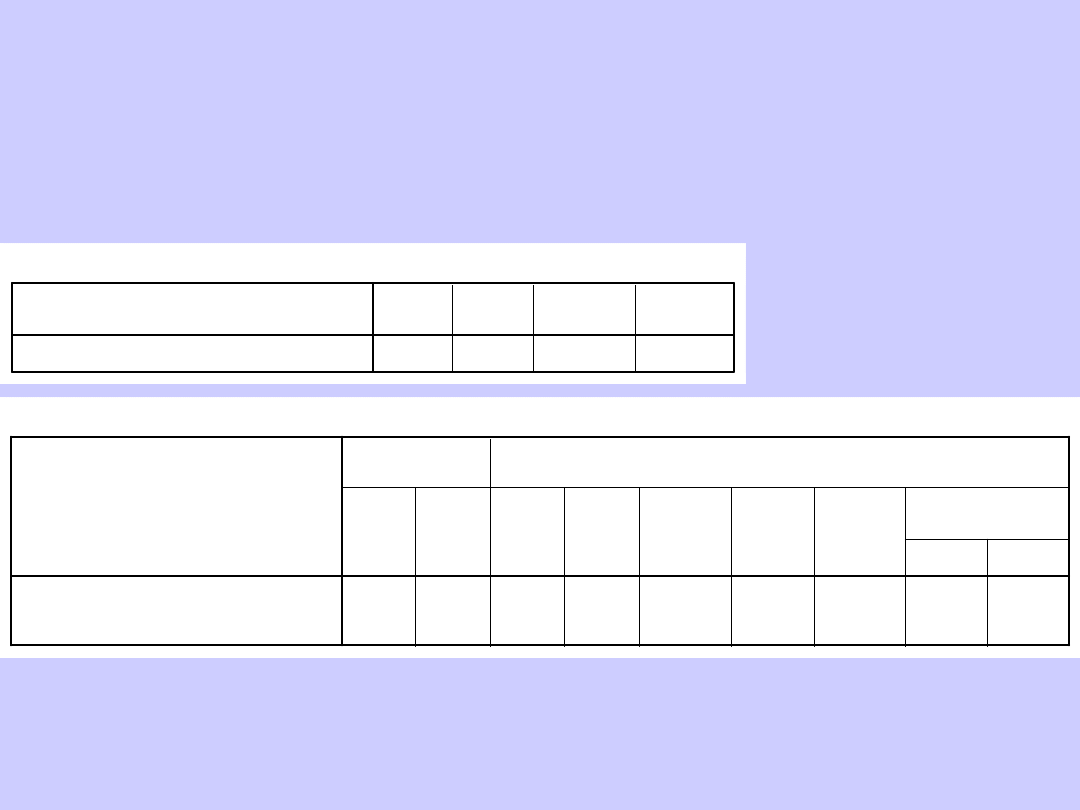
H1: Ogony kocurów maści białej są innej długości niż u kocurów czarnych
H0: Ogony kocurów białych są średnio tej samej długości co kocurów

czarnych, założony poziom istotności: p<0,05

Statystyki dla grup

6

10,5000

1,6432

,6708

6

11,5000

1,8708

,7638

kolor kociej siersci:

1-bialy, 2-czarny
1,00
2,00

dlugosc kocurzego ogona

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla prób niezależnych

,357

,563

-,984

10

,348

-1,0000

1,0165

-3,2650

1,2650

-,984

9,836

,349

-1,0000

1,0165

-3,2701

1,2701

Założono równość

wariancji
Nie założono równości

wariancji

dlugosc kocurzego ogona

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

Wynik:
t(10) < 1; n. i.
(p=0,35)

Interpretacja:
Nie mamy podstaw do odrzucenia hipotezy
zerowej. Wyniki testu pokazują, że ogony
kocurów białych i czarnych nie różnią się
długością

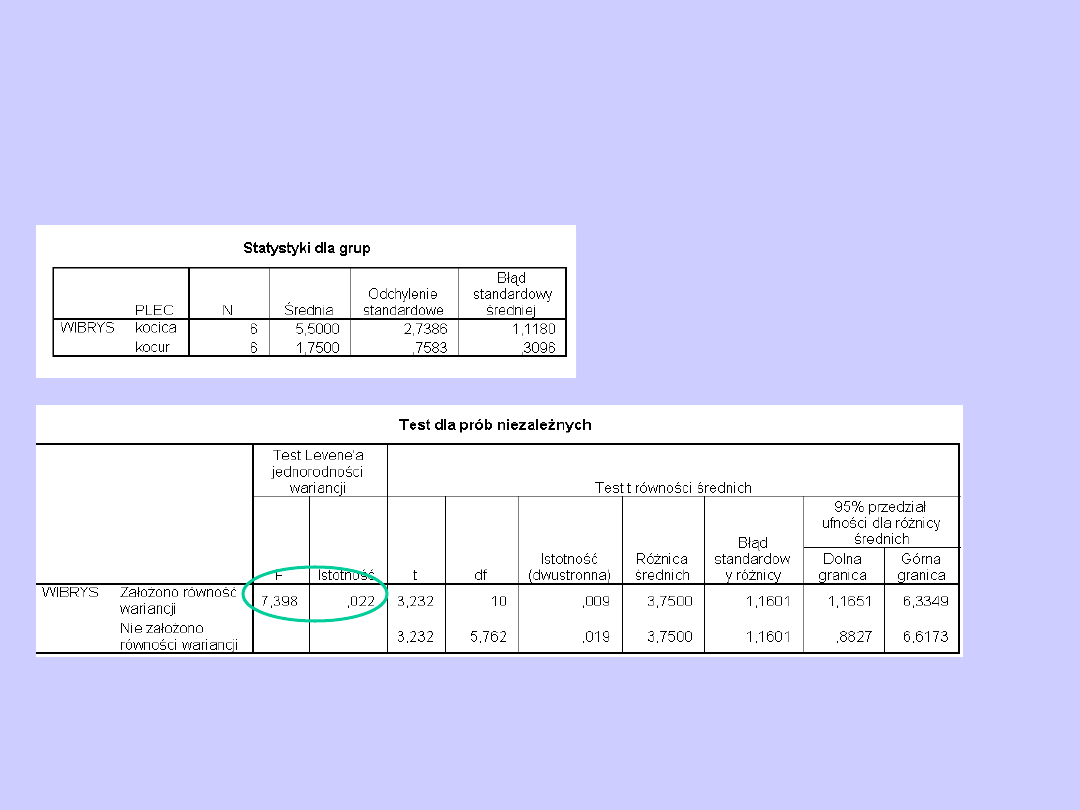
H1: Kotki są posiadaczkami dłuższych wibrysów niż kocury
H0: Długość wibrysów kotek nie różni się istotnie od

wibrysów kocurów

założony poziom istotności: p<0,05

Wynik:
t(5,5) = 3,44;
p<0,05

Interpretacja:
Odrzucamy hipotezę zerową. Kotki mają
dłuższe wibrysy niż kocury.

H1: Długość kocich pazurów zwiększa się się po wizycie u
weterynarza

H0: Długość kocich pazurów po wizycie u weterynarza pozostaje
bez zmian (test dwustronny) Założony poziom istotności: p<0,05

Statystyki dla prób zależnych

1,7625

8

,3815

,1349

1,2375

8

,3249

,1149

PRZED_WI
PO_WIZY

Para
1

Średnia

N

Odchylenie

standardowe

Błąd

standardowy

średniej

Korelacje dla prób zależnych

8

,993

,000

PRZED_WI & PO_WIZY

Para 1

N

Korelacja

Istotność

Test dla prób zależnych

,5250

7,071E-02

2,500E-02

,4659

,5841

21,000

7

,000

PRZED_WI - PO_WIZY

Para 1

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Różnice w próbach zależnych

t

df

Istotność

(dwustronna)

Wynik:
t(7) = 21;
p<0,001;
r = 0,99;
p<0,001

Interpretacja:
Kocie pazury są przed wizytą u weterynarza krótsze
niż po wizycie (statystyki opisowe). Co więcej, im
były krótsze przed wizytą tym są krótsze po wizycie
(korelacja). Odrzucamy H0, przyjmujemy H1.

H1: Uszy kota stają się większe po zjedzeniu myszy

H0: Uszy kota po zjedzeniu myszy, pozostają bez zmian lub
stają się mniejsze Założony poziom istotności: p<0,05

Statystyki dla prób zależnych

3,7000

10

1,3375

,4230

4,2500

10

1,4386

,4549

uszy kota przed
zjedzeniem myszy
uszy kota po zjedzeniu
myszy

Para
1

Średnia

N

Odchylenie

standardowe

Błąd

standardowy

średniej

Korelacje dla prób zależnych

10

,823

,003

uszy kota przed

zjedzeniem myszy & uszy

kota po zjedzeniu myszy

Para

1

N

Korelacja

Istotność

Test dla prób zależnych

-,5500

,8317

,2630

-1,1449

4,494E-02

-2,091

9

,066

uszy kota przed

zjedzeniem myszy - uszy

kota po zjedzeniu myszy

Para

1

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Dolna

granica

Górna

granica

95% przedział ufności dla

różnicy średnich

Różnice w próbach zależnych

t

df

Istotność

(dwustronna)

Wynik:
t(9) = 2,09; p<0,05 (istotność dwustronna podzielona przez 2 –
0,066/2=0,033)
Interpretacja:
Odrzucamy H0, przyjmujemy H1. Uszy kotów stają się większe po
zjedzeniu myszy.

H1: Istnieje pozytywny związek pomiędzy długością kocich pazurów i ilością
ran na rękach ich właścicieli

H0: Nie ma związku pomiędzy długością kocich pazurów a ilością ran na
rękach ich właścicieli (test dwustronny)

założony poziom istotności: p<0,05

Korelacje

,998**
,000

8

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

DL_PAZ

IL_RAN

DL_PAZ

IL_RAN

Korelacja jest istotna na poziomie 0.01
(dwustronnie).

**.

Wynik:
R(6) = 0,99; p<0,001
Interpretacja:
Istnieje bardzo silny, dodatni związek pomiędzy długością kocich
pazurów a liczbą ran na rękach ich właścicieli. Im kot ma
dłuższe pazury tym jego właściciel ma więcej ran na rękach

H1: Im starszy kot tym więcej ma zębów

H0 (test jednostronny): Z wiekiem kotu nie przybywa zębów, może
jedynie ubyć

założony poziom istotności: p<0,05

Wynik:
R(8) = -0,99; p<0,001
Interpretacja:
Nie odrzucamy hipotezy zerowej, ponieważ wyniki przedstawiają
zależność odwrotną od założonej w H1.

Korelacje

-,986**

,000

10

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

wiek koci

ilosc zebow

wiek koci

ilosc

zebow

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

• Chcemy porównać, czy ekstrawertycy

częściej niż introwertycy robią zakupy:

• Przebadano 20 osób pytając jak często

robią zakupy (rzadko, często, b. często)

• Jednocześnie mierzono poziom

ekstrawersji – okazało się, że 13 osób
to ekstrawertycy, a tylko siedem to
introwertycy

• Jakiego testu użyć, aby odpowiedzieć

na pytanie, kto częściej robi zakupy?

• Złamane założenia

– O liczebności
– O pomiarze zmiennej zależnej na

skali ilościowej

• Używamy nieparametrycznego

odpowiednika testu T dla prób
niezależnych, czyli U-Mann-
Whitney’a

Rangi

7

7,29

51,00

13

12,23

159,00

20

EKSTRAWE
introwertyk
ekstrawertyk
Ogółem

jak często robi zakupy

N

Średnia ranga Suma rang

Statystyki testu

b

23,000
51,000

-1,939

,053

,081

a

U Manna-Whitneya
W Wilcoxona
Z
Istotność asymptotyczna
(dwustronna)
Istotność dokładna
[2*(jednostronna)]

jak często

robi zakupy

Nieskorygowane ze względu na wiązania.

a.

Zmienna grupująca: EKSTRAWE

b.

Przy założonym
poziomie istotności
p<0,05:

-Test dwustronny: nie
odrzucamy H0 –
p=0,08 jest większe
niż założóny 0,05

-Test jednostronny:
odrzucamy H0 –
p=0,08/2=0,04, czyli
mniejsze niż 0,05

Czy samoutrudnianie
jest efektywne?

Czy istnieje różnica w
poziomie stresu
między osobami
stosującymi strategie
samoutrudniania a
tymi, które
przeciwdziałają
stresowi na inne
sposoby.

Zmienna niezależna

Zmienna zależna

Sposoby radzenia sobie ze

stresem

Wyniki

Uzyskano istotne statystycznie różnice
między średnim poziomem stresu między
grupą osób stosujących samoutrudnianie a
grupą wykorzystującą inne strategie T
(38)=6,420; p<0,001

0

5

10

15

20

stres

samoutrudnianie
inne

Średnia w grupie osób
samoutrudniających jest wyższa niż u
osób stosujących inne strategie

Wniosek: Samoutrudnianie nie jest
skuteczną strategią radzenia sobie ze
stresem

Relacja między uległą żoną
a dominującym mężem

Pytanie 1

Czy dominujący mężowie są
dominujący zarówno w
pracy jak i w domu?

Pytanie 2

Czy uległe żony nie
wyzwalają u swoich mężów
dominującej postawy?

Test T-Studenta dla prób

zależnych

Powtarzane pomiary
Wybieramy tylko żony, które są

uległe

Pytanie:
Czy mężowie, którzy mają uległe

żony są bardziej dominujący w
domu niż w pracy?

Dwie zmienne ilościowe:

Wyniki

• Średni poziom dominacji w domu u

mężów uległych żon różni się od
poziomu w pracy T (19)=9,56;
p<0,001

• Średni poziom dominacji w domu

jest wyższy niż w pracy

• Średnia w pracy 10,3, Średnia w

domu 19,3



Ocena atrakcyjności kartek

świątecznych – kartki jakiego

kształtu sprzedają się lepiej?



Osoby oceniające atrakcyjność

kartki prostokątnej

4, 3, 2, 2, 2, 2, 2, 2, 4, 1, 1, 4, 3



Osoby oceniające kartkę

kwadratową

6, 6, 7, 7, 8, 8, 7, 9, 5, 6, 4, 1, 1
Czy rozkład zmiennej ocena kartki

jest normalny?

Test Kołmogorowa-Smirnowa dla jednej próby

15

15

6,9333

6,9333

,96115

1,62422

,234

,216

,234

,216

-,166

-,211

,907

,838

,383

,484

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

CIEM_D

JASN_D

Testowana jest zgodność z rozkładem normalnym.

a.

Obliczono na podstawie danych.

b.



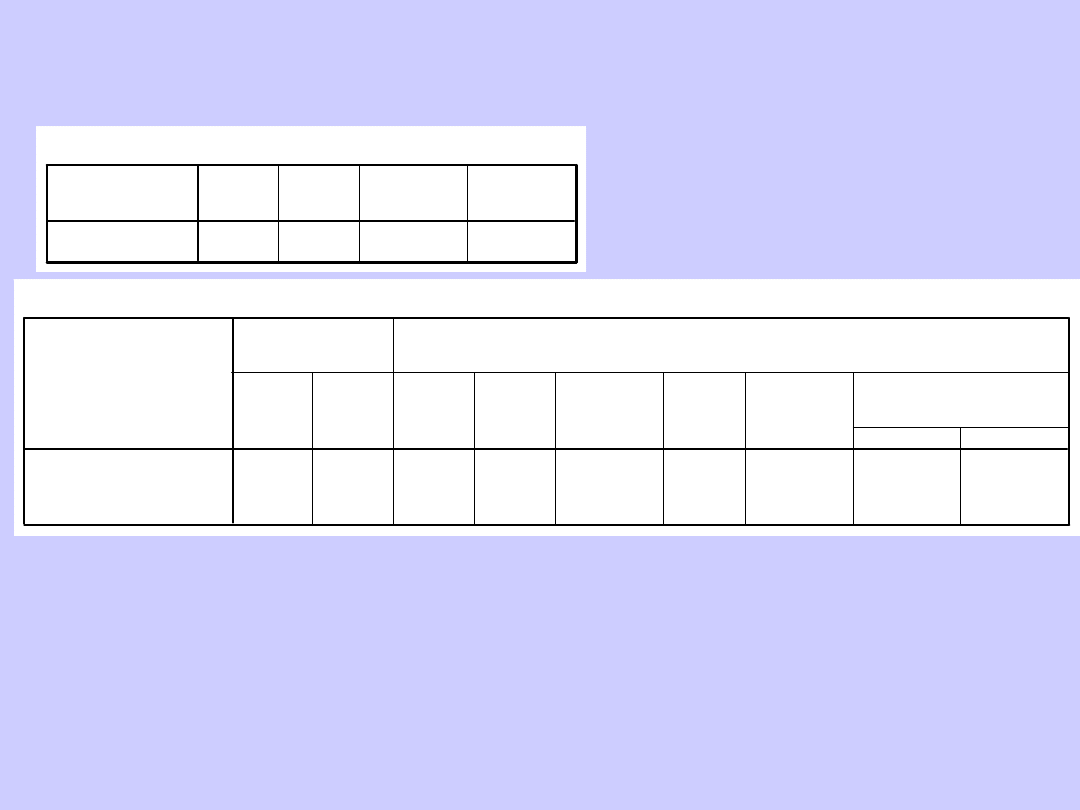
Wyniki



Wniosek: Ludzie wolą kartki świąteczne o

bardziej fantazyjnych kształtach

Statystyki dla grup

13

2,4615

1,05003

,29123

13

5,6923

2,39390

,66395

KSZTALT
1,00
2,00

KARTKA

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla prób niezależnych

4,636

,042

-4,456

24

,000

-3,2308

,72501

-4,72712

-1,73442

-4,456

16,453

,000

-3,2308

,72501

-4,76429

-1,69724

Założono równość
wariancji
Nie założono
równości wariancji

KARTKA

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich



Czy doświadczenie modyfikuje

zdolność oceny wieku małych

dzieci?

Ile miesięcy mają dzieci na

prezentowanym zdjęciu?

Hipoteza: Studentki będą
błędnie szacować wiek dzieci
(ale nie wiemy, czy będą go
przeszacowywać, czy też
niedoszacowywać)



Oszacowania wieku dzieci

dokonane przez studentki bezdzietne

(w miesiącach)
12, 7, 8, 9, 23, 12, 14, 15, 13, 14, 15,
14, 8, 9, 8, 7, 8, 9, 7, 5, 5, 5, 6, 6, 8
Właściwy wiek dzieci: 6 miesięcy

Wyniki testu Kołmogorowa Smirnowa

wskazują, że rozkład jest normalny

Z=1,1; p>0,05

Test Kołmogorowa-Smirnowa dla jednej próby

25

9,8800

4,28486

,221
,221

-,127

1,107

,172

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

DZIECI

Testowana jest zgodność z rozkładem normalnym.

a.

Obliczono na podstawie danych.

b.



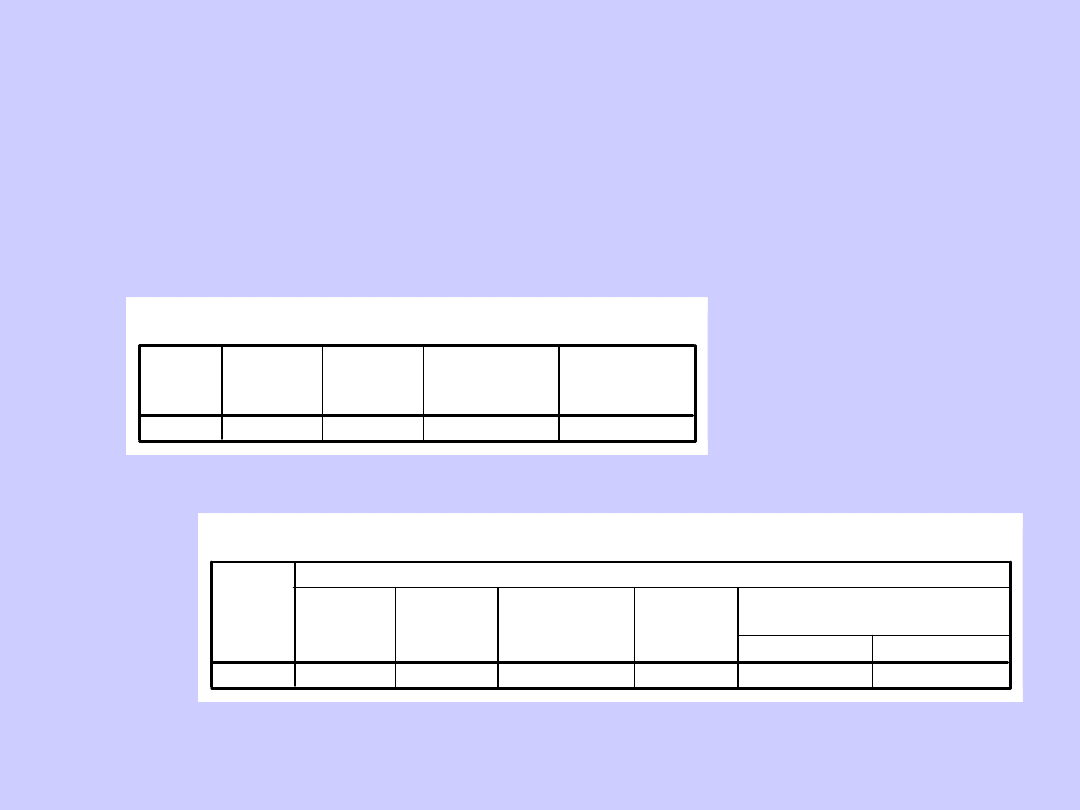
Test T-Studenta dla jednej próby

Testujemy, czy średnia badanej grupie jest

równa wartości testowanej (wartości którą
znamy z innych badań lub z innych źródeł)

T (24)=4,528; p<0,001

Statystyki dla jednej próby

25

9,8800

4,28486

,85697

DZIECI

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

4,528

24

,000

3,8800

2,1113

5,6487

DZIECI

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 6



Czy stereotypy wpływają na

percepcję kartek świątecznych?



Wyniki

Ocena pierwszej kartki
7, 6, 7, 6, 8, 7, 6, 8, 9, 8, 7, 6,

6, 6, 7

Ocena drugiej kartki:
6, 5, 7, 7, 8, 8, 5, 5, 8, 5, 5, 9,

9, 9,

8

Test Kołmogorowa-Smirnowa dla jednej próby

15

15

6,9333

6,9333

,96115

1,62422

,234

,216

,234

,216

-,166

-,211

,907

,838

,383

,484

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

CIEM_D

JASN_D

Testowana jest zgodność z rozkładem normalnym.

a.

Obliczono na podstawie danych.

b.

Rozkłady obu zmiennych
są normalne (dla
zmiennej ocena
pierwszego zdjęcia
Z=0,907; p>0,05 dla
oceny drugiego zdjęcia
Z=0,838; p>0,05)



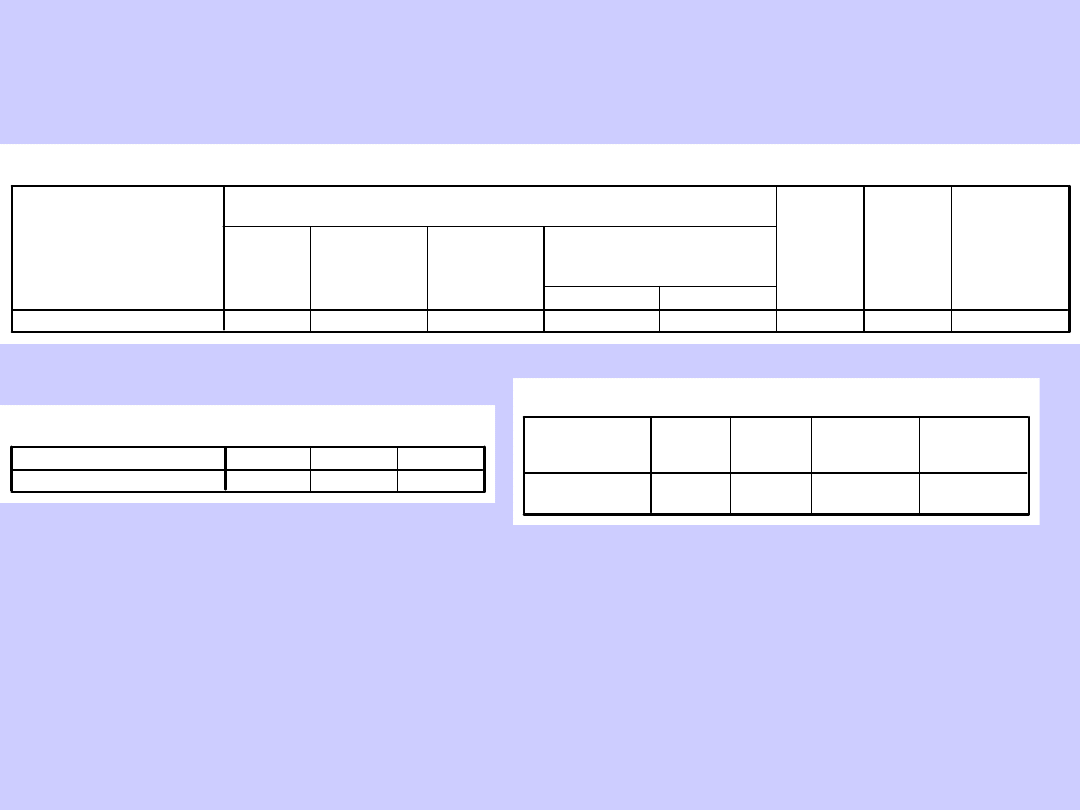
Test T-Studenta dla prób

zależnych

Czy stereotypy wpływają na ocenę kartek
świątecznych? Nie. Stereotypy nie mają wpływu na
ocenę kartek świątecznych T(14)=0; p>0,05

Statystyki dla prób zależnych

6,9333

15

,96115

,24817

6,9333

15

1,62422

,41937

CIEM_D
JASN_D

Para
1

Średnia

N

Odchylenie

standardowe

Błąd

standardowy

średniej

Korelacje dla prób zależnych

15

-,140

,618

CIEM_D & JASN_D

Para 1

N

Korelacja

Istotność

Test dla prób zależnych

,0000

2,00000

,51640

-1,1076

1,1076

,000

14

1,000

CIEM_D - JASN_D

Para 1

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Różnice w próbach zależnych

t

df

Istotność

(dwustronna)

Wesołych Świąt !!!