Dwuczynnikowa analiza

Dwuczynnikowa analiza

wariancji

wariancji

Wykład 5

Materiały do wykładu Izabela Krejtz

Pytanie z terminu A

Pytanie z terminu A



Pewien socjolog interesował się wpływem
światła i hałasu na efektywność pracy
kominiarzy. Tabela 3 przedstawia średnią
efektywność pracy w porównywanych
grupach. Wybierz prawidłową odpowiedź.



Jest efekt główny światła



Jest efekt główny hałasu



Nie ma efektów głównych



Są oba efekty główne

Materiały do wykładu Izabela Krejtz

Tabela 3

Tabela 3

Zmienne

niezależne

hałas

nisk

i

wyso

ki

światł

o

silne 50

20

słab

e

30

60

Materiały do wykładu Izabela Krejtz



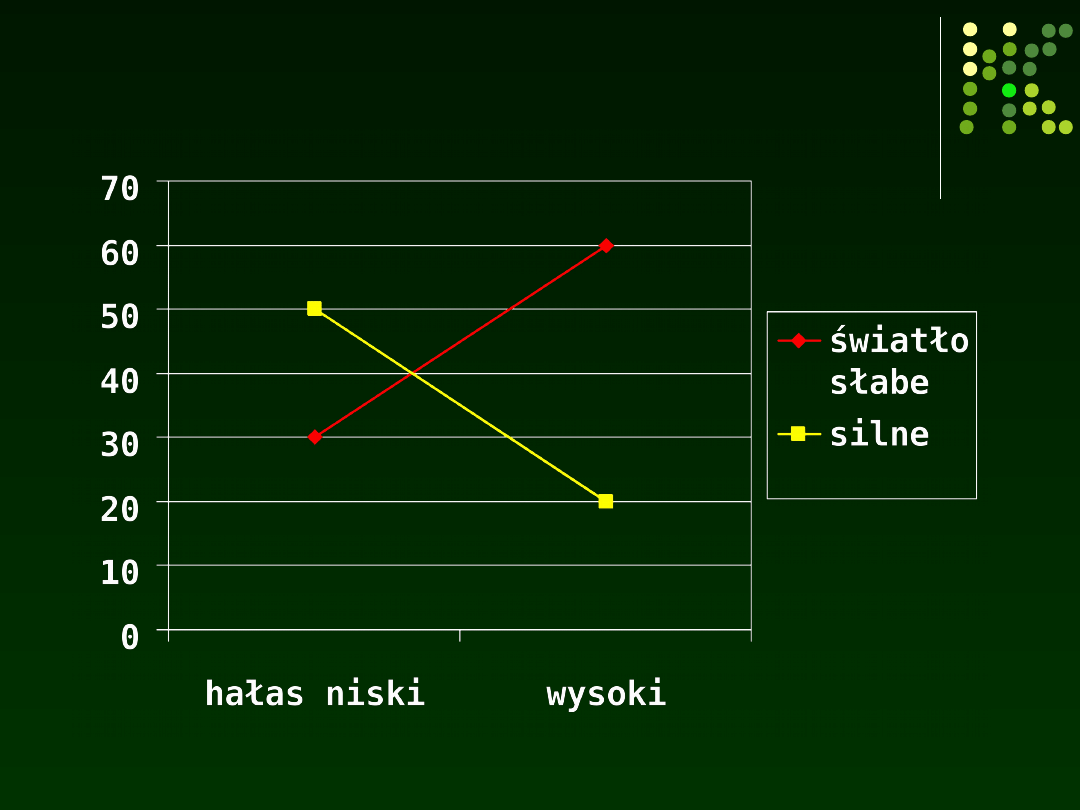
Pewien socjolog interesował się wpływem

światła i hałasu na efektywność pracy

kominiarzy. Tabela 3 przedstawia średnią

efektywność pracy w porównywanych

grupach. Sprawdź czy jest efekt interakcji

między tymi zmiennymi.



Brak efektu interakcji



Jest efekt interakcji



Są oba efekty interakcji



Jest interakcja nieskrzyżowana

Materiały do wykładu Izabela Krejtz

Można sporządzić wykres

Można sporządzić wykres

Procesy uwagi

Procesy uwagi

Przykład w oparciu o

procedurę DIVA

Analiza efektów prostych

Materiały do wykładu Izabela Krejtz

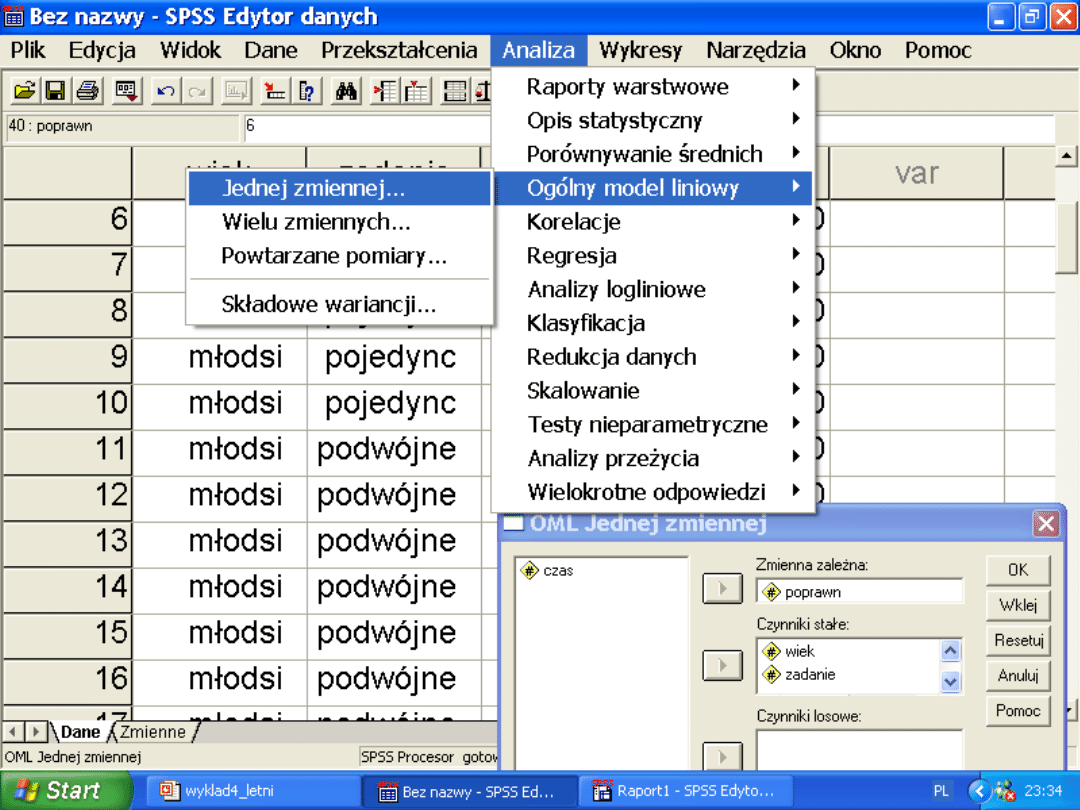
Procesy selektywnej uwagi a wiek

Procesy selektywnej uwagi a wiek

Zmienne niezależne

WIEK

MŁODSI

STARSI

ZADANI

E

Pojedyncz
e

Podwójne

Materiały do wykładu Izabela Krejtz

Materiały do wykładu Izabela Krejtz

Uproszczona tabelka

Uproszczona tabelka

Testy efektów międzyobiektowych

Zmienna zależna: POPRAWN

,900

1 ,900 1,227 ,275

656,10

1 656,1 894,7 ,000

2,500

1 2,500 3,409 ,073

26,400

36 ,733

685,90

39

Źródło zmienności
WIEK

ZADANIE

WIEK * ZADANIE

Błąd

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Wariancja nie wyjaśniona – błędu wykorzystywana w mianowniku każdej
statystyki F

Materiały do wykładu Izabela Krejtz

Testy F w dwuczynnikowej ANOVie

Testy F w dwuczynnikowej ANOVie



W dwuczynnikowej analizie wariancji mamy do czynienia

z trzema testami F:



1) dla efektu głównego pierwszego czynnika



2) dla efektu głównego drugiego czynnika



3) dla efektu interakcyjnego



W liczniku każdego z tych stosunków znajdzie się

wariancja międzygrupowa, która odnosi się do porównań

między średnimi dla danego efektu głównego lub

interakcyjnego



Natomiast wariancja wewnątrzgrupowa we wszystkich

trzech testach F będzie taka sama - jest to zawsze

średnia oszacowań wariancji w populacji utworzona z

wyników wewnątrz każdej z celek (wariancja błędu)

Materiały do wykładu Izabela Krejtz

Stopnie

Stopnie

swobody

swobody

ZN

2

poziomow

liczba

-

ZN

1

poziomow

liczba

-

)

1

(

)

1

(

interakcji

efekt

1

1

glowne

efekty

2

1

2

1

12

2

2

1

1

k

k

k

k

df

k

df

k

df

















Materiały do wykładu Izabela Krejtz

Stopnie

Stopnie

swobody cd.

swobody cd.

ZN

1

poziomow

liczba

-

celce

w

osób

liczba

-

badaniu

w

osób

liczba

-

1

)

1

(

bledu

1

2

1

2

1

k

n

N

N

df

ogolem

n

k

k

df

k

k

N

df

o

bledu

bledu













Materiały do wykładu Izabela Krejtz

Testy efektów międzyobiektowych

Zmienna zależna: POPRAWN

659,50

a

3 219,8 299,8 ,000

4040,1

1 4040 5509 ,000

,900

1 ,900 1,227 ,275

656,10

1 656,1 894,7 ,000

2,500

1 2,500 3,409 ,073

26,400

36 ,733

4726,0

40

685,90

39

Źródło zmienności
Model skorygowany

Stała

WIEK

ZADANIE

WIEK * ZADANIE

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,962 (Skorygowane R kwadrat = ,958)

a.

Pełna tabelka

Pełna tabelka

Istotny efekt główny zmiennej Zadanie F(1,36)=894,7; p<0,001

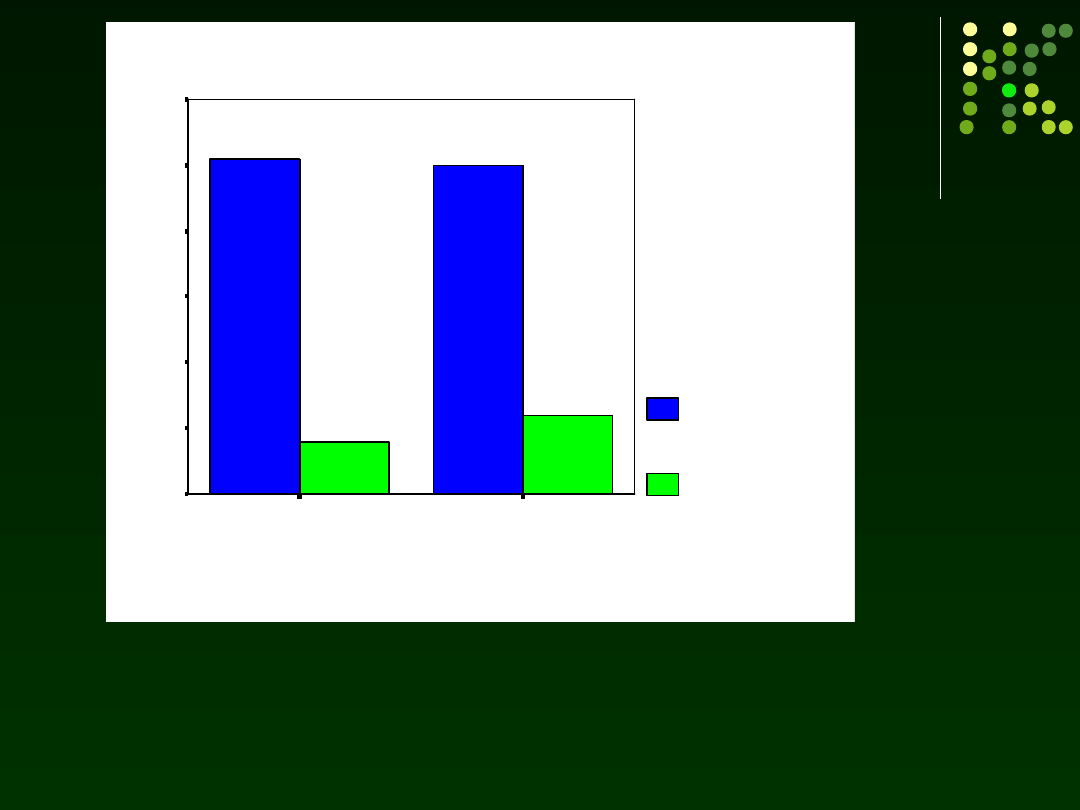
Materiały do wykładu Izabela Krejtz

Oszacowane średnie brzegowe - POPRAWN

WIEK

starsi

młodsi

16

14

12

10

8

6
4

ZADANIE

pojedyncze

podwójne

Niezależnie od wieku badani, lepiej wykonywali zadanie pojedyncze.
Poprawność wykonania zadania spadała przy wprowadzeniu obciążenia poznawczego

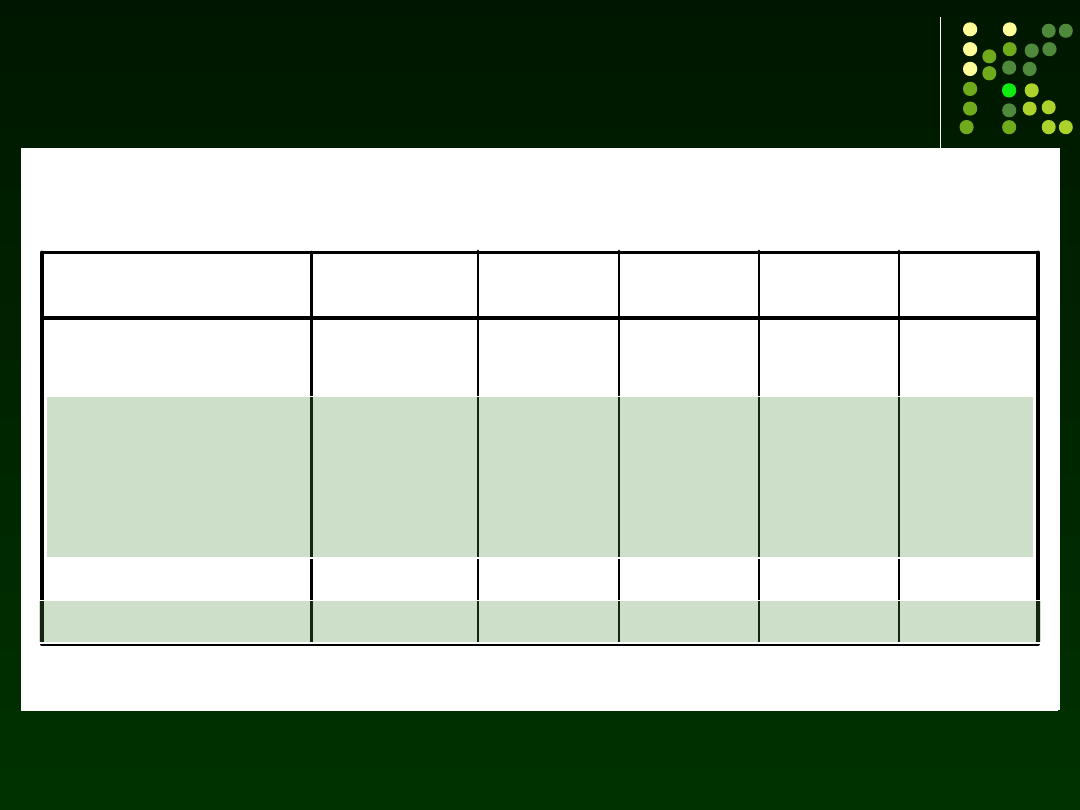
Materiały do wykładu Izabela Krejtz

Testy efektów międzyobiektowych

Zmienna zależna: CZAS

453500,0

a

3 151167 60,133

,000

1,8E+07

1 2,E+07 7142,7

,000

342250,0

1 342250 136,144

,000

81000,00

1

81000 32,221

,000

30250,00

1

30250 12,033

,001

90500,00

36 2513,9

1,9E+07

40

544000,0

39

Źródło zmienności
Model skorygowany
Stała
WIEK
ZADANIE
WIEK * ZADANIE
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,834 (Skorygowane R kwadrat = ,820)

a.

Czas wykonania głównego zadania

Czas wykonania głównego zadania

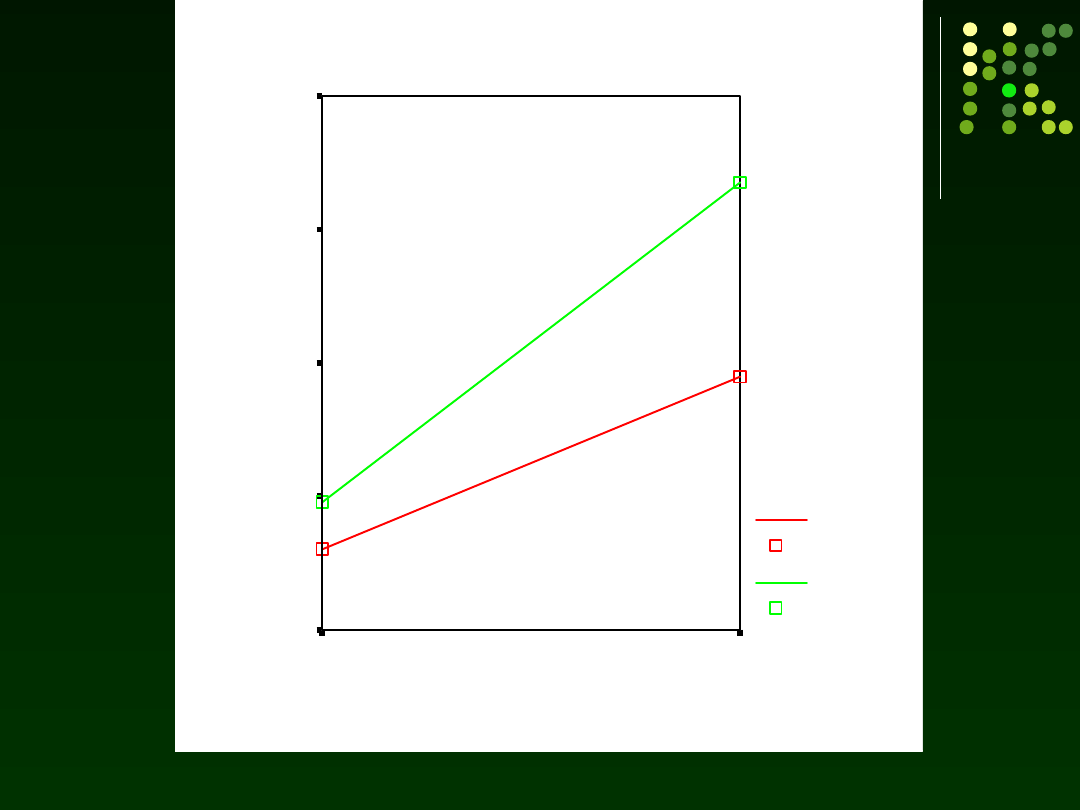
Materiały do wykładu Izabela Krejtz

Oszacowane średnie brzegowe - CZAS

WIEK

starsi

młodsi

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

ZADANIE

pojedyncze

podwójne

Materiały do wykładu Izabela Krejtz

Jeśli efekt interakcji jest istotny

Jeśli efekt interakcji jest istotny



Patrzymy na efekty proste,
szukamy, które grupy różnią się
między sobą istotnie



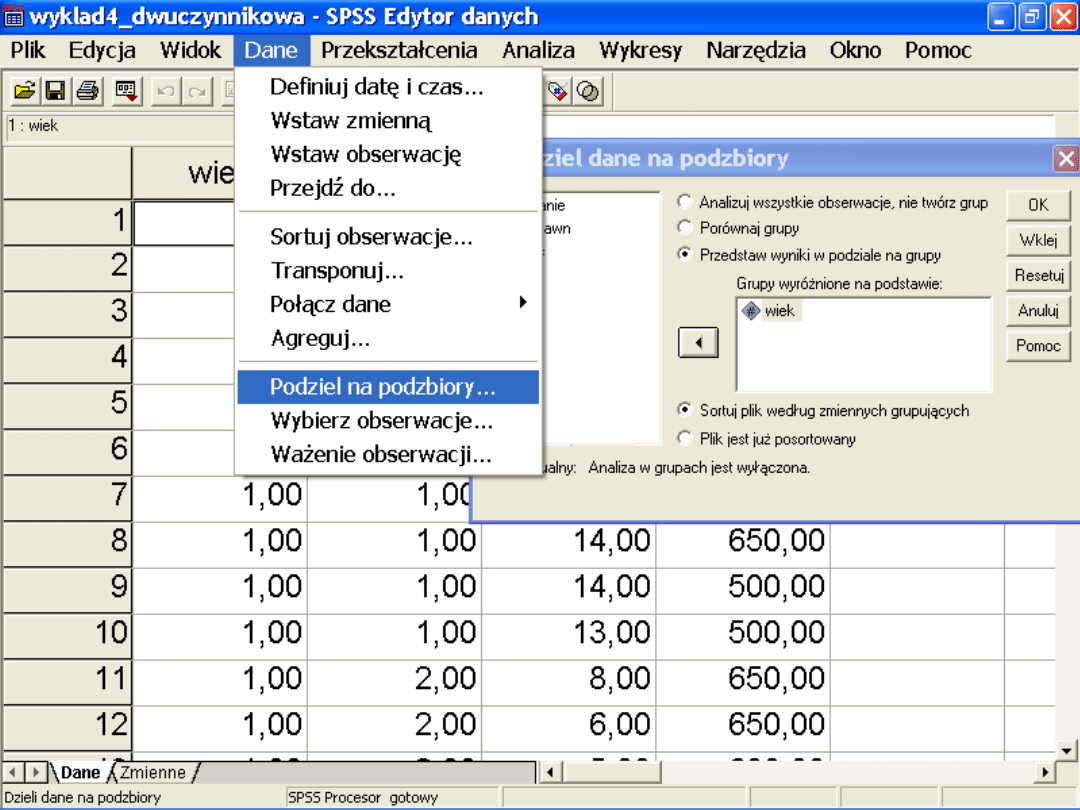
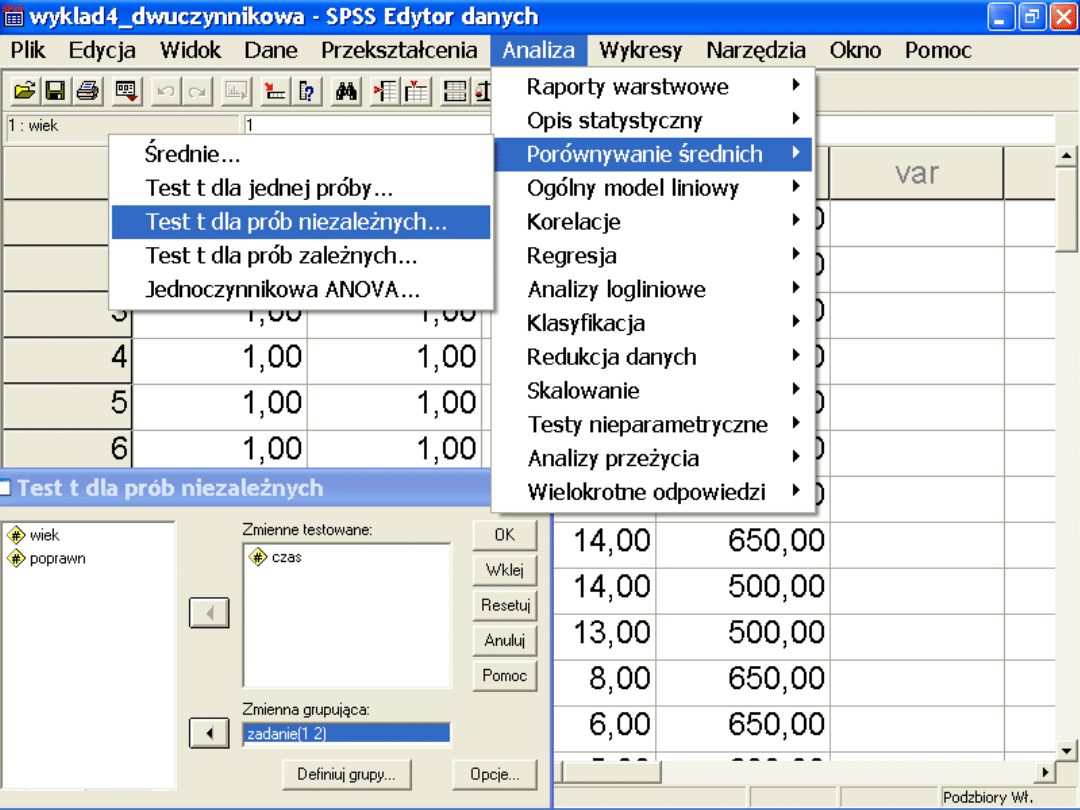
Możemy przeprowadzić analizy testami
t dla grup niezależnych wykorzystując
opcję podziel na podzbiory.



Lub spojrzeć na wykresy słupków błędu

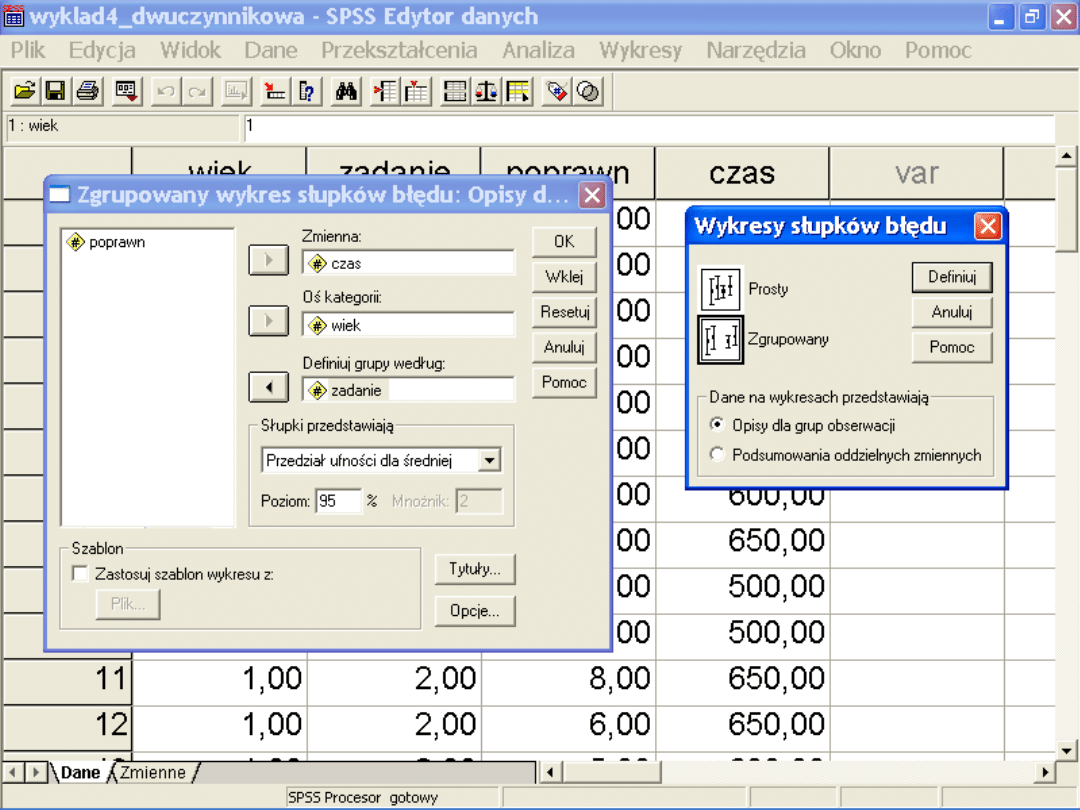
Materiały do wykładu Izabela Krejtz

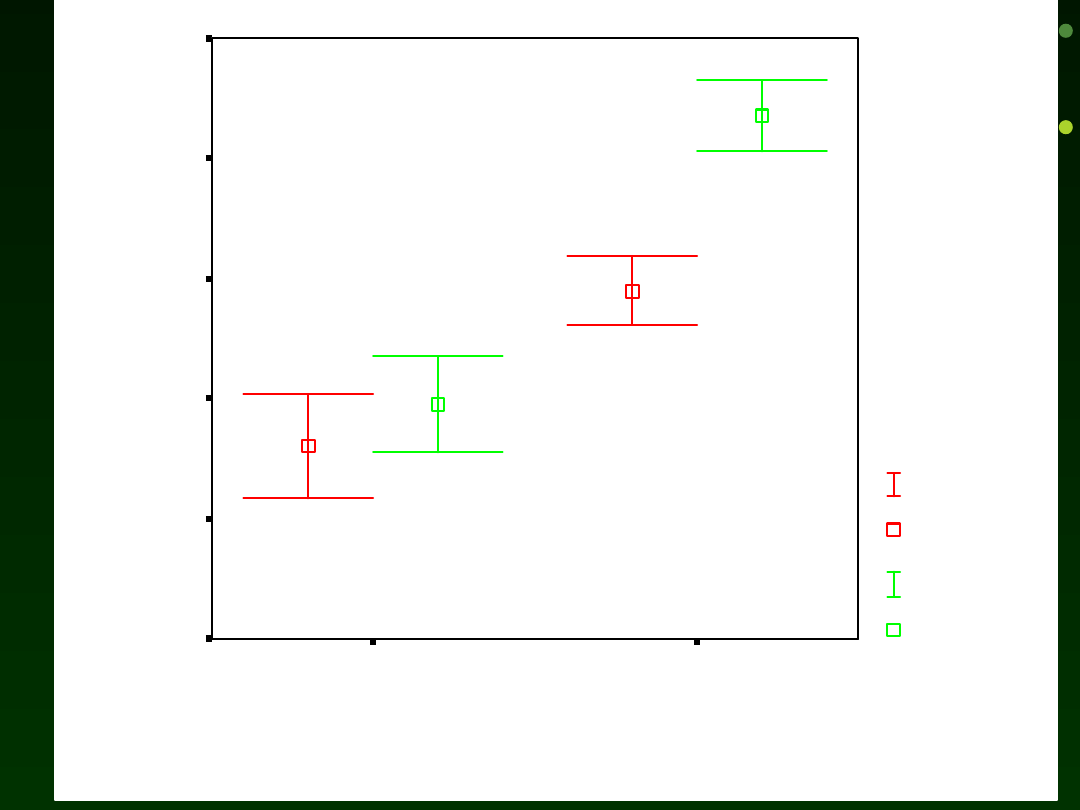
Materiały do wykładu Izabela Krejtz

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

Materiały do wykładu Izabela Krejtz

Materiały do wykładu Izabela Krejtz

Materiały do wykładu Izabela Krejtz

Test dla prób niezależnych

a

,892

,357 -1,34

18

,196 -35,0 26,0875 -89,808 19,8077

-1,34 17,78

,197 -35,0 26,0875 -89,855 19,8555

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

WIEK = młodsi

a.

Test dla prób niezależnych

a

,120

,733 -8,043

18

,000 -145,0 18,0278-182,8749 -107,1251

-8,043 17,967

,000 -145,0 18,0278-182,8799 -107,1201

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

WIEK = starsi

a.

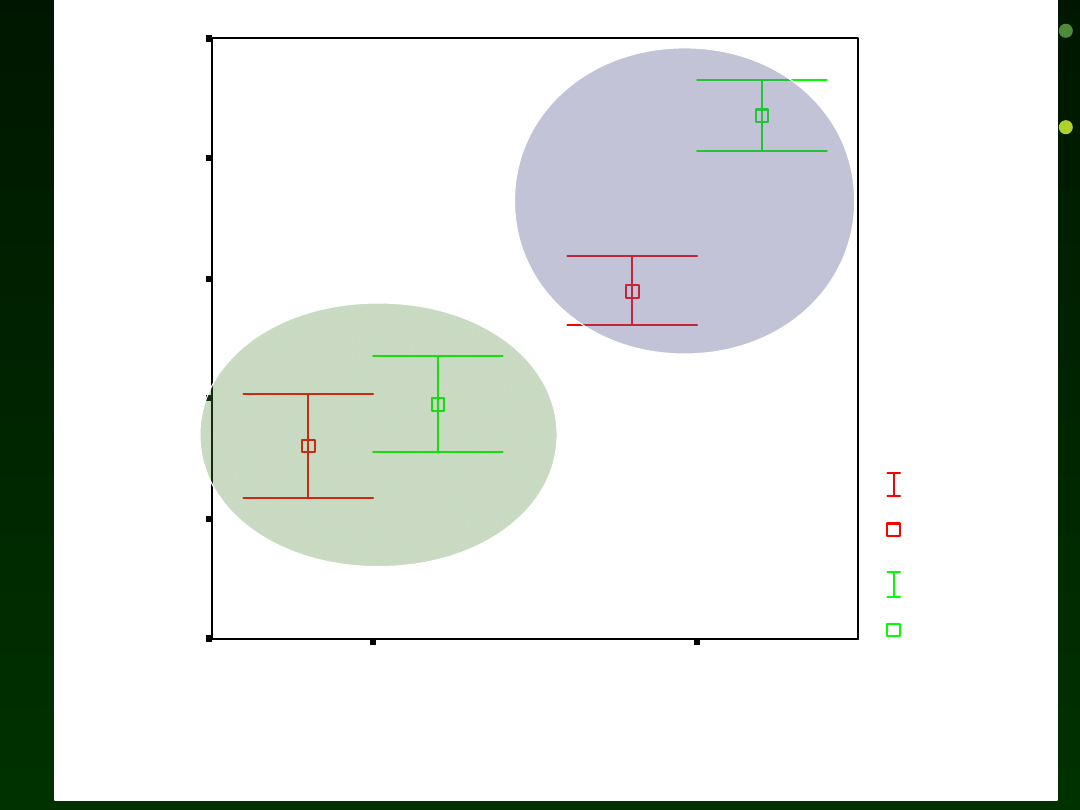
Materiały do wykładu Izabela Krejtz

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

Materiały do wykładu Izabela Krejtz

Test dla prób niezależnych

a

3,358

,083 -5,629

18

,000 -130,0 23,0940-178,5187 -81,4813

-5,629 15,337

,000 -130,0 23,0940-179,1296 -80,8704

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

ZADANIE = pojedyncze

a.

Test dla prób niezależnych

a

,051

,823 -11,04

18

,000 -240,0 21,7307-285,6545 -194,3455

-11,04 16,671

,000 -240,0 21,7307-285,9168 -194,0832

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

ZADANIE = podwójne

a.

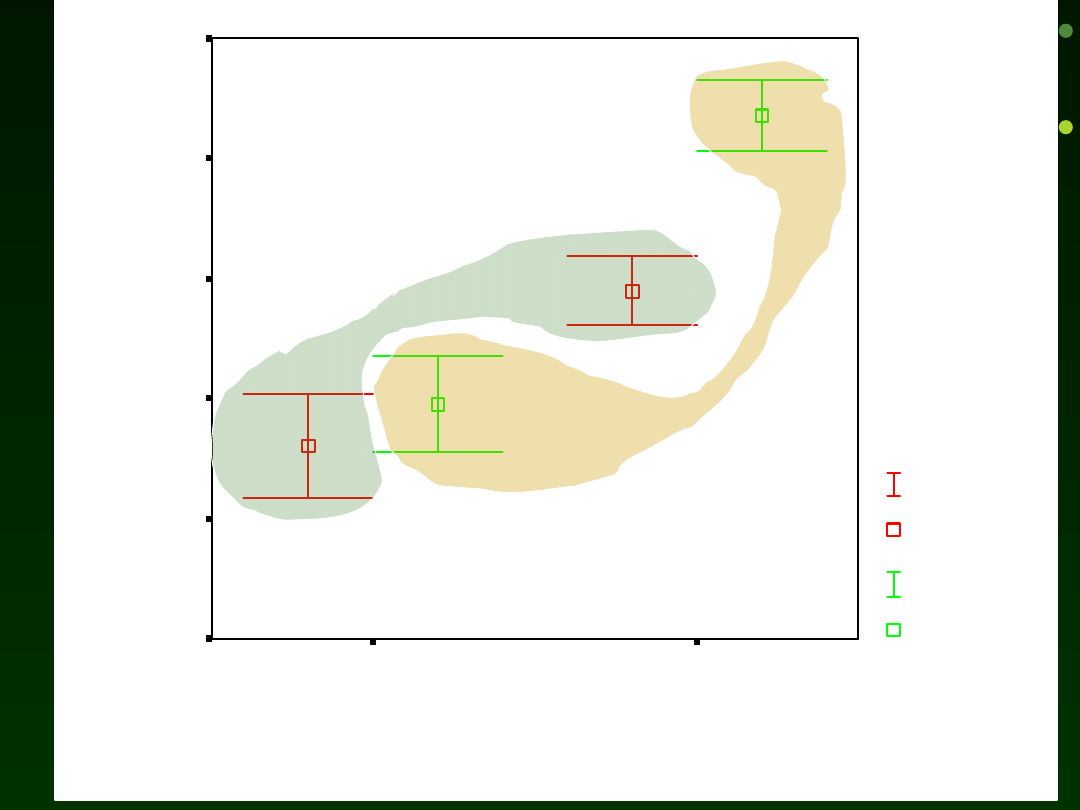
Materiały do wykładu Izabela Krejtz

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

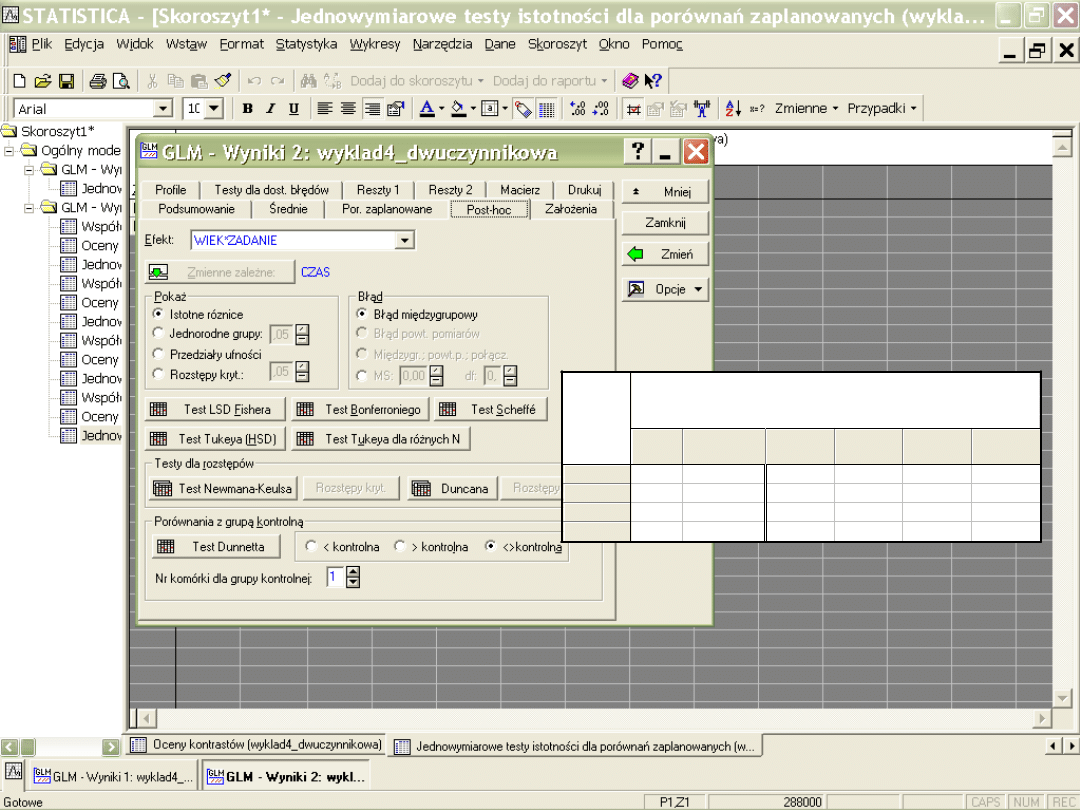
Materiały do wykładu Izabela Krejtz

Te st B o nfe ro ni e go ; z m ie nna C ZAS ( wykla d4_ dwuc z ynniko wa )
Pra wdo po do bi e ńst wa dl a t e stó w po st -ho c
B łą d: M S m ię dz ygrupo we = 2513,9, df = 36,000

Nr po dkl.

WIEKZADANIE{1}

560,00

{2}

595,00

{3}

690,00

{4}

835,00

1
2
3
4

młodsi

po je dync z e 0,763753

0,000008

0,000000

młodsi

po dwó j ne

0,763753

0,000901

0,000000

st a rsi

po je dync z e

0,000008

0,000901

0,000001

st a rsi

po dwó j ne

0,000000

0,000000

0,000001

Materiały do wykładu Izabela Krejtz

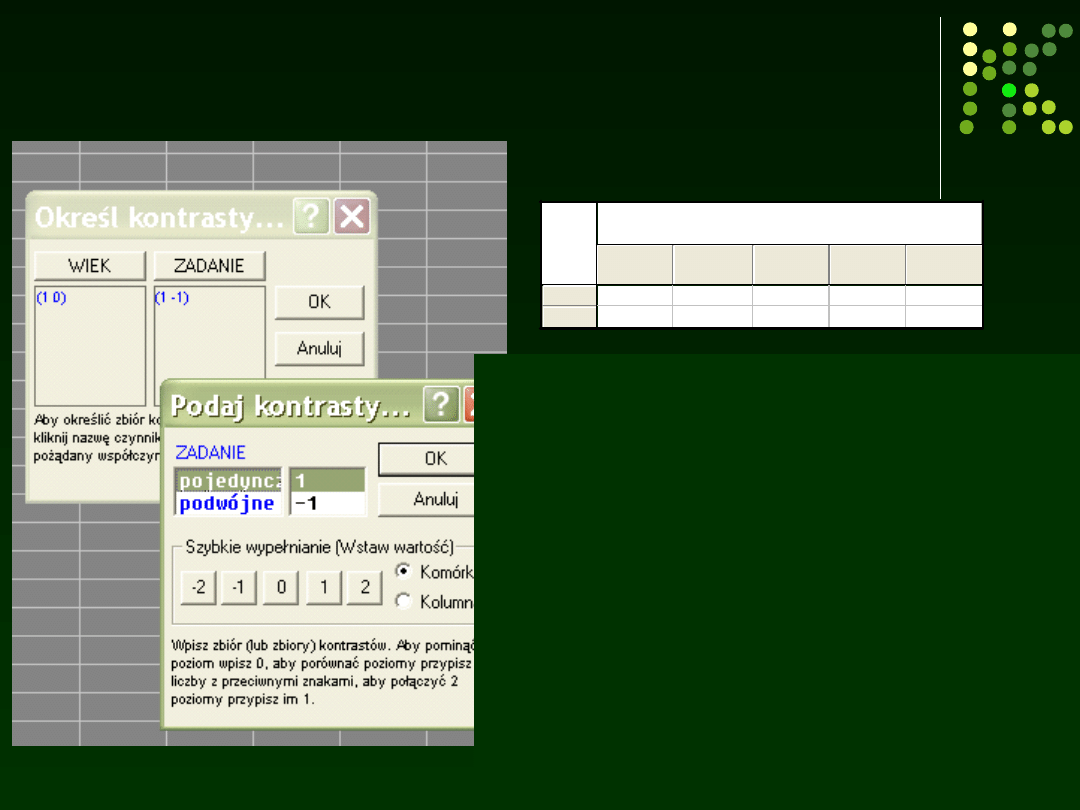
Kontrasty dla efektu interakcyjnego w

Kontrasty dla efektu interakcyjnego w

Statistice

Statistice

Je dno wymia ro we te st y isto t no śc i dla po ró wna ń z a pla no wa nyc h ( wykl a d4_ dwuc z ynni ko wa )
Zmie nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S t o pnie

swo bo dy

Ś rednie

kwa dr.

F

p

Efe kt
B łą d

6125,00 1 6125,000

2,436464

0,127292

90500,00362513,889

Czy wykonanie zadania
pojedynczego i podwójnego różni się
w grupie młodszych?

Wykluczamy z porównań grupę starszych (0),
młodsi dostają współczynnik (1)
i dla tej grupy przeprowadzamy kontrast
między zadaniem pojedynczym (1) i
podwójnym (-1)

Różnica jest nieistotne statystycznie

Materiały do wykładu Izabela Krejtz

Je dno wymia ro we te st y isto t no śc i dla po ró wna ń z a pla no wa nyc h (wykla d4_ dwuc z ynniko wa )
Zmie nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś re dnie

kwa dr.

F

p

Efe kt
B łą d

105125,0 1 105125,0

41,81768

0,000000

90500,0 36 2513,9

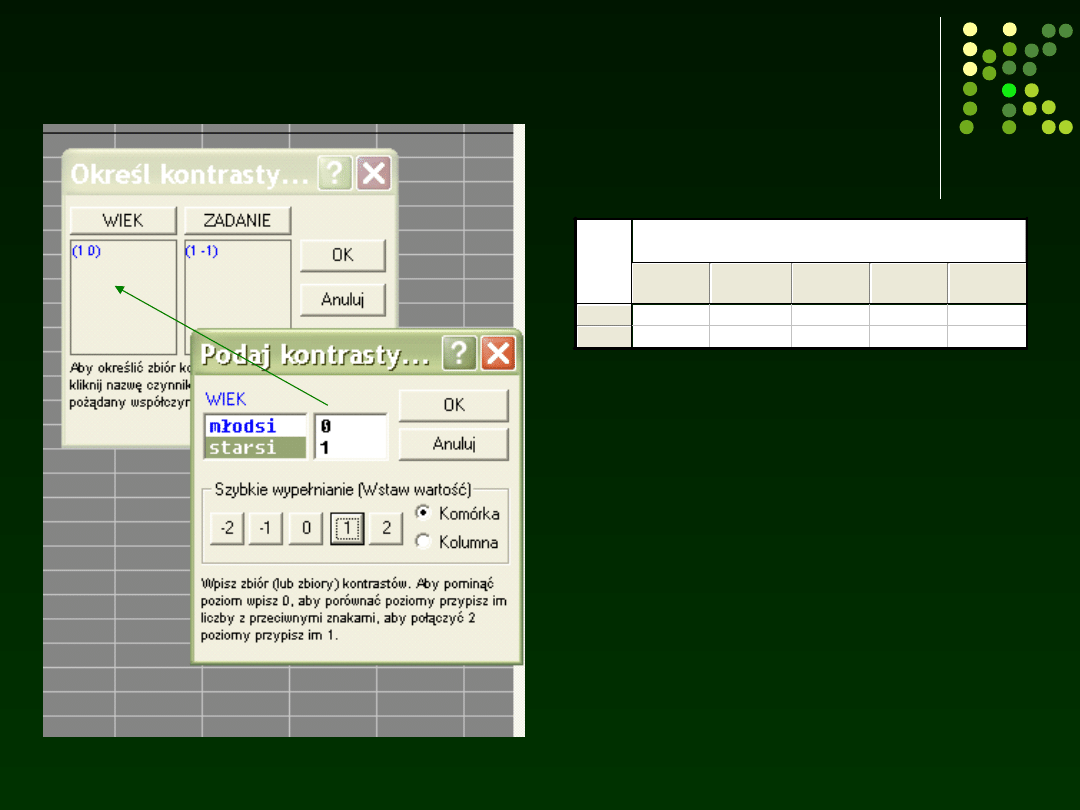
Zmieniamy współczynniki
kontrastu przy zmiennej wiek

Starsze osoby istotnie różnią się
wykonaniem zadania podwójnego i
pojedynczego

Materiały do wykładu Izabela Krejtz

Je dno wymi a ro we te sty isto tno śc i dla po ró wna ń z a pla no wa nyc h (wykla d4_ dwuc z ynniko wa )
Zmi e nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś re dnie

kwa dr.

F

p

Efekt
B łą d

84500,00 1 84500,00

33,61326

0,000001

90500,0036 2513,89

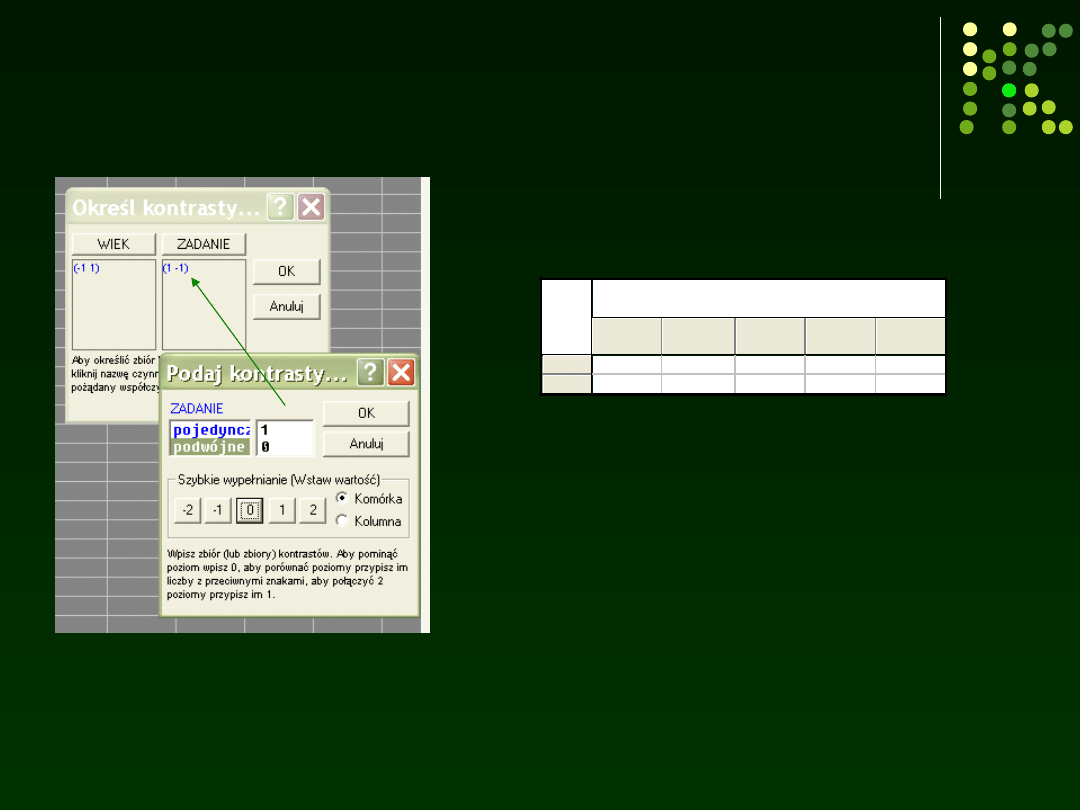
Tym razem chcemy porównać starszych i
młodszych w zadaniu pojedynczym,

Wynik kontrastu wskazuje na istotny efekt prosty

Materiały do wykładu Izabela Krejtz

Jedno wymia ro we te sty isto tno śc i dla po ró wna ń z a pla no wa nyc h ( wykla d4_ dwuc z ynniko wa )
Zmi e nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś rednie

kwa dr.

F

p

Efekt
B łą d

288000,0 1 288000,0

114,5635

0,000000

90500,0 36 2513,9

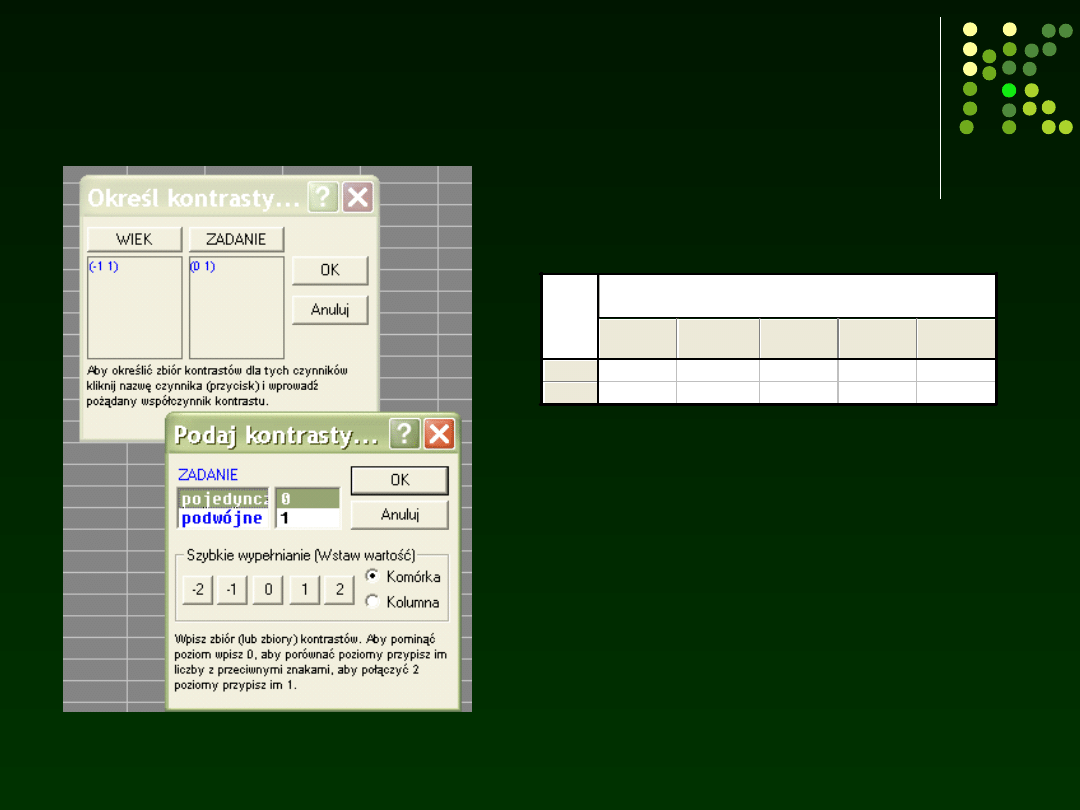
Czy są różnice między
starszymi i młodszymi w zadaniu podwójnym?

Materiały do wykładu Izabela Krejtz

Liczba efektów prostych

Liczba efektów prostych



Liczba efektów prostych jest równa
sumie poziomów obu zmiennych
niezależnych.



w planie 2x2 są 4 efekty proste;



w planie 2 x 3 jest 5 efektów
prostych

Materiały do wykładu Izabela Krejtz

Zalety zaawansowanych planów

Zalety zaawansowanych planów

eksperymentalnych

eksperymentalnych



Możliwość większej generalizacji
wyników



Patrzymy jednocześnie na wpływ dwóch
lub więcej zmiennych niezależnych na
interesującą nas zmienną zależną



Możemy analizować efekty interakcyjne



Ekonomia – za jednym razem
przeprowadzamy 4 eksperymenty w 1

Wprowadzenie do

Wprowadzenie do

analizy wariancji z

analizy wariancji z

powtarzanym pomiarem

powtarzanym pomiarem

Zmienna niezależna

wewnątrz osób

Ta sama grupa

kilkakrotnie badana

Materiały do wykładu Izabela Krejtz

Plan dla grup zależnych, z

Plan dla grup zależnych, z

powtarzanym pomiarem

powtarzanym pomiarem



Główne zalety: mniejsza liczba

uczestników badania, mniej czasu do

przeprowadzenia badania,



Odchodzi problem różnic indywidualnych

– redukcja niesystematycznej zmienności



Większa moc



Nie jest to prawdziwy eksperyment

Materiały do wykładu Izabela Krejtz

Nobody’s perfect = wady

Nobody’s perfect = wady



Nie da się już cofnąć wpływu manipulacji

eksperymentalnej



Może to zmienić nastawienie do badania



Uczestnicy nabywają wprawy w radzeniu sobie z

kolejnymi wymaganiami badania, uczą się

materiału eksperymentalnego



Wielokrotne uczestniczenie w badaniu prowadzi

również do zmęczenia a w związku z tym do

pogorszenia wykonywania zadania



Zmiany uczestników związane z dojrzewaniem



Efekt kolejności



Wyrównywanie kolejności warunków

Efekt twarzy w tłumie

Efekt twarzy w tłumie

Przykład eksperymentu z

powtarzanym pomiarem

Materiały do wykładu Izabela Krejtz

Opis badania

Opis badania



Grupa 20 osób została poproszona o
wyszukiwanie wśród tłumu twarzy tej,
która nie pasowała do innych



Wśród twarzy neutralnych – zagrażającej



Wśród twarzy neutralnych – przyjaznej



Wśród twarzy zagrażających – neutralnej

Materiały do wykładu Izabela Krejtz

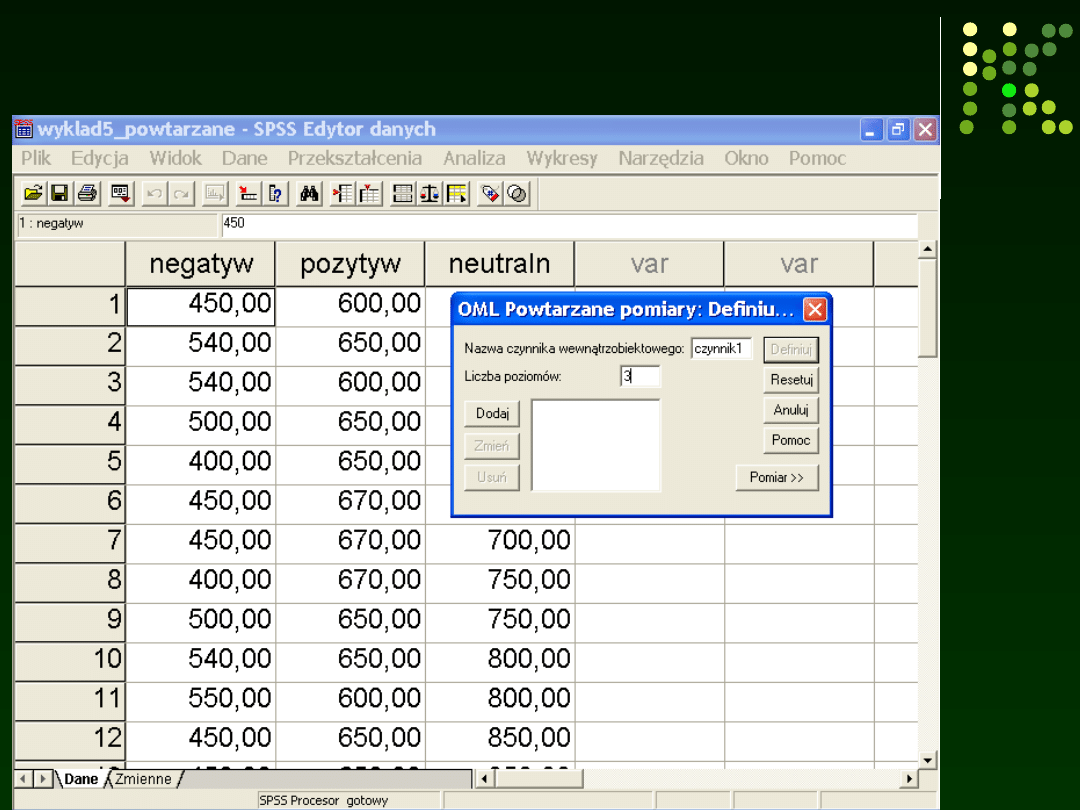
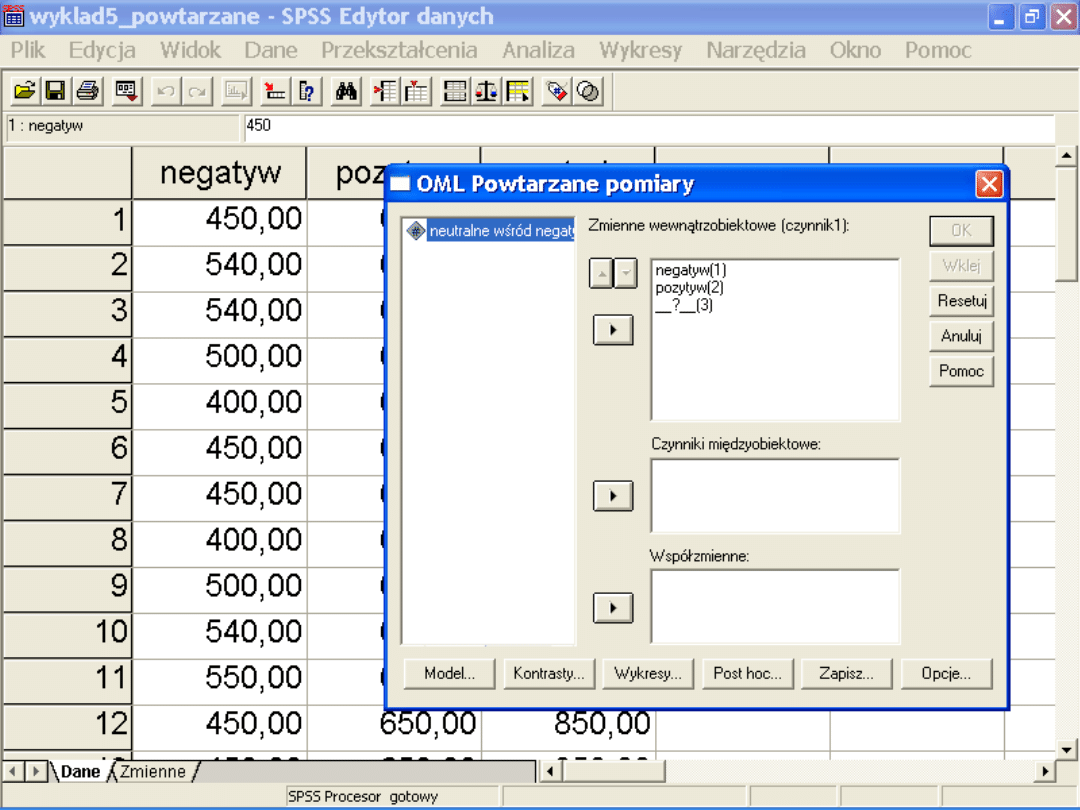
Definiujemy na ilu poziomach jest

Definiujemy na ilu poziomach jest

zmienna niezależna (czynnik)

zmienna niezależna (czynnik)

Materiały do wykładu Izabela Krejtz

Materiały do wykładu Izabela Krejtz

Kolejne elementy wydruku

Kolejne elementy wydruku

Czynniki wewnątrzobiektowe

Miara: MIARA_1

NEGATYW
POZYTYW
NEUTRALN

CZYNNIK1
1
2
3

Zmienna

zależna

Statystyki opisowe

494,50 49,4682

20

645,50 29,9956

20

794,50 53,5552

20

negatywne wśród
neutralnych
pozytywne wśród
neutralnych
neutralne wśród
negatywnych

Średnia

Odchylenie

standardowe

N

Materiały do wykładu Izabela Krejtz

Założenie sferyczności

Założenie sferyczności

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,981

,353

2

,838

,981

1,000

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: CZYNNIK1

b.

Założenie sferyczności – związki między parami
warunków badawczych są podobne, że zależności między
poszczególnymi warunkami są podobne – czy też inaczej
wariancje różnic między poszczególnymi warunkami
są podobne
W naszym przykładzie spełnione jest to założenie.
Gdyby był istotny, nie spełnione założenie – mniejsze zaufanie do wyników F -
poprawki

Materiały do wykładu Izabela Krejtz

Ważna tabelka

Ważna tabelka

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

900013,3

2 450007196,887

,000

900013,3

1,962 458751196,887

,000

900013,3

2,000 450007196,887

,000

900013,3

1,000 900013196,887

,000

86853,33

38 2285,6

86853,33 37,276 2330,0
86853,33 38,000 2285,6
86853,33 19,000 4571,2

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Df dla efektu zmiennej niezależnej k-1
Df dla błędu (N-1)(k-1)
N – liczba osób w badaniu

Prawidłowy zapis wyniku analizy:

F(2, 38)=196,89; p<0,001

Materiały do wykładu Izabela Krejtz

Testy kontrastów wewnątrzobiektowych

Miara: MIARA_1

900000,0

1 900000 346,154

,000

13,333

1 13,333

,007

,935

49400,00

19 2600,0

37453,33

19 1971,2

CZYNNIK1
Liniowy
Kwadratowy
Liniowy
Kwadratowy

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Oszacowane średnie brzegowe - MIARA_1

CZYNNIK1

3

2

1

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

400