Jednoczynnikowa

analiza wariancji c.d.

Porównania post hoc i kontrasty

Wykład 2

Analiza wariancji –

jednoczynnikowa analiza

wariancji

• Uogólniony test różnic między

średnimi.

– Jedna zmienna zależna
– Jedna zmienna niezależna (czynnik) na

dwóch lub więcej poziomach

• w przybliżeniu rozwinięcie testu-t

– porównuje średnie między różnymi

poziomami zmiennej niezależnej

• dla dwóch grup F=t

2

Wpływ spożycia alkoholu na

zdolność do prowadzenia

pojazdu

Opis badania

• 12 osób zostało losowo przypisanych

do 3 warunków eksperymentalnych:

– Placebo (taki sam smak jak inne napoje

wyskokowe)

– Mała dawka alkoholu
– Duża dawka alkoholu

• Proporcjonalnie do wagi
• Po godzinie przez dziesięć minut na

symulatorze prowadzili samochód –
rejestrowano liczbę błędów

Obliczenia dla wariancji

międzygrupowej

Grupa

1

Grupa 2

Grupa 3

3
4
4
5

8
6
6
4

9
8
8
7

M

1

= 4

M

2

= 6

M

3

= 8

M

ogólna

= 6

Tworzymy miarę zmienności dotyczącą
średnich w grupach (wariancja
międzygrupowa> patrz kolejne kroki)

Obliczenia dla wariancji

międzygrupowej 2 krok - SS

Grupa 1 Grupa 2

Grupa 3

3
4
4
5

8
6
6
4

9
8
8
7

M

1

= 4

M

2

= 6

M

3

= 8

M

ogólna

= 6

(4-6)

2

+

4+

(6-6)

2

+

0+

(8-6)

2

=

4=

SS =

8

x

n=8

x

4=32

Wariancja międzygrupowa,

krok 2 – wynik manipulacji

16

2

32







MG

MG

MG

df

SS

MS

grup

liczba

-

1

k

k

df

MG





Obliczenia dla wariancji

wewnątrzgrupowej

Grupa 1 Grupa 2

Grupa 3

3
4
4
5

8
6
6
4

9
8
8
7

M

1

= 4

M

2

= 6

M

3

= 8

Tworzymy miarę zmienności dotyczącą
zmienności w grupach (wariancja
wewnątrzgrupowa lub wariancja błędu -
wariancja niewyjaśniona> patrz kolejne kroki)

Różnice między poszczególnymi wynikami w danej
grupie a daną średnią grupową

Obliczenia dla wariancji

wewnątrzgrupowej 1 krok - SS

Grupa 1

Grupa 2

Grupa 3

(3 -4)

2

(4-4)

2

(4-4)

2

(5-4)

2

(8-6)

2

(6-6)

2

(6-6)

2

(4-6)

2

(9-8)

2

(8-8)

2

(8-8)

2

(7-8)

2

M

1

= 4

M

2

= 6

M

3

= 8

1+0+0+1

+

4+0+0+4

+

1+0+0+1

=

SS

WG

=12

Wariancja wewnątrzgrupowa,

wariancja błędu –

niewyjaśniona

3

,

1

9

12







WG

WG

WG

df

SS

MS

badania

w

uczestnikó

liczba

-

grup

liczba

-

N

k

k

N

df

WG





Statystyka F

• statystyka F - stosunek wariancji

międzygrupowej do wewnątrzgrupowej

– stosunek wariancji między średnimi do

wariancji niewyjaśnionej

• bliska 1 wtedy małe zróżnicowanie

międzygrupowe, bliskie wewnątrzgrupowemu -
Ho prawdziwa

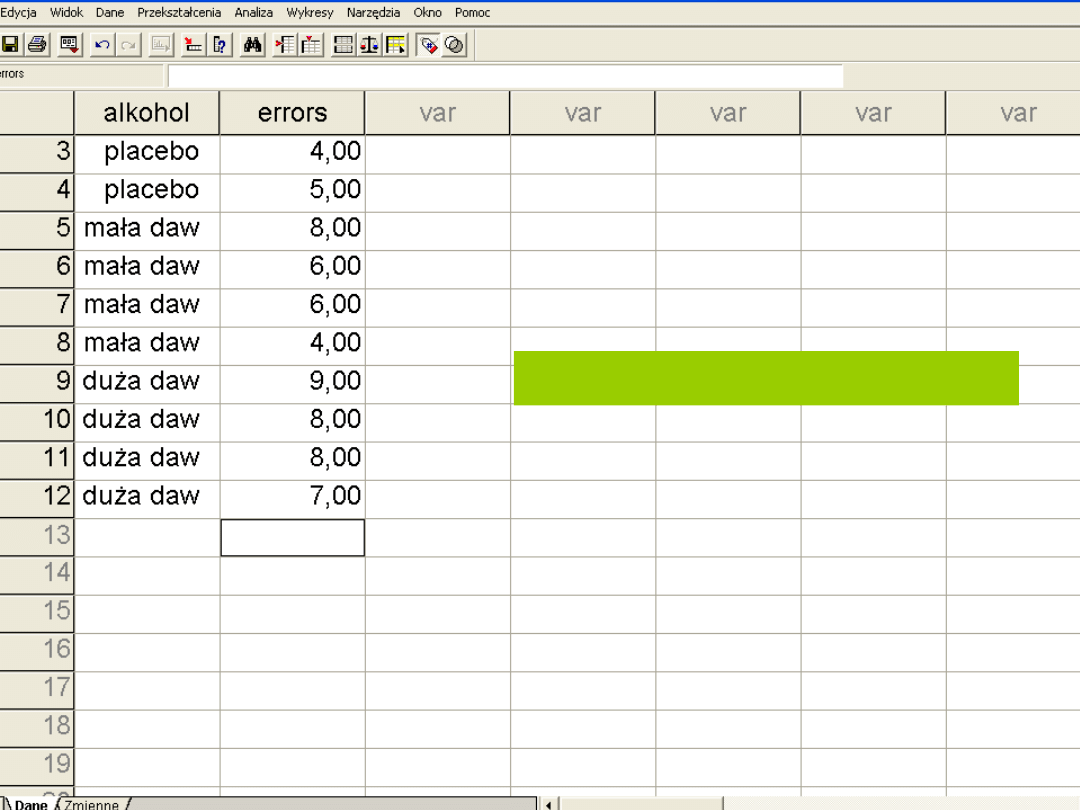
Plan dla grup niezależnych

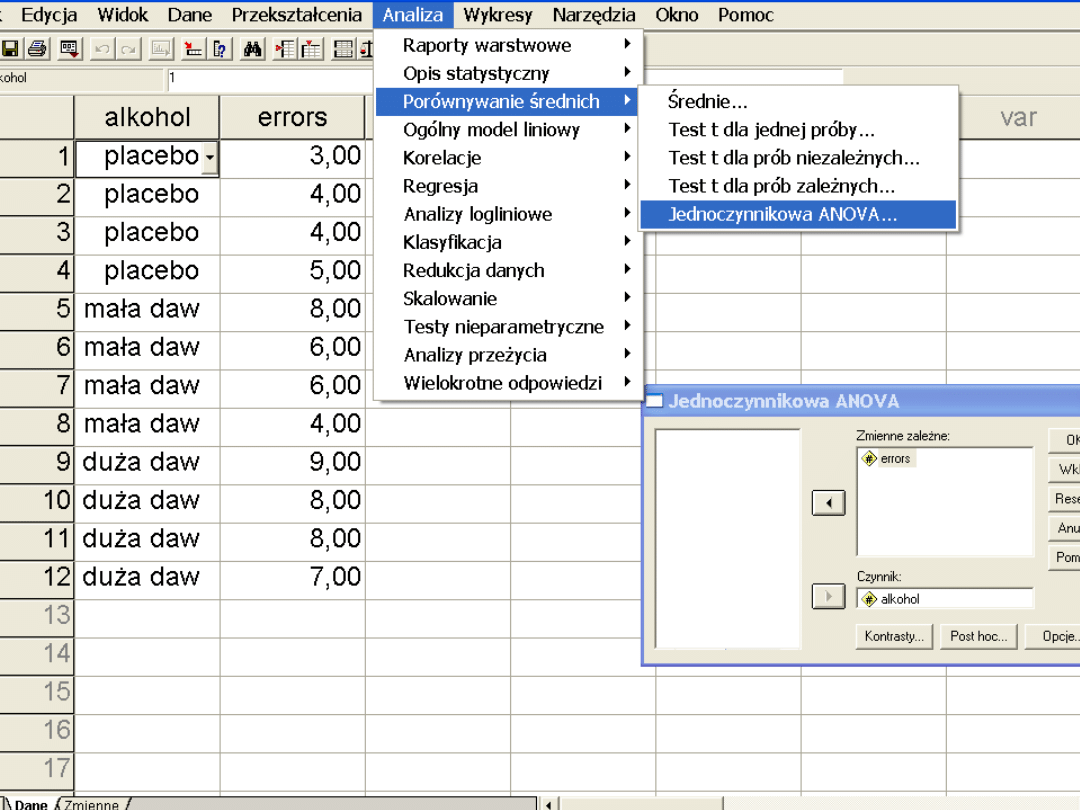
Analiza wariancji

ERRORS

32,000

2 16,00 12,00 ,003

12,000

9 1,333

44,000

11

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Analiza wydruku

• F

(2,9)

=12,00; p<0,01

• są istotne różnice między średnimi
• Jak silny jest efekt naszej zmiennej niezależnej?

Miara siły efektu

• Ogólna wielkość różnic między

grupami

– Czy efekt zmiennej niezależnej jest duży

czy mały, jeśli spojrzymy na

• procent wariancji wyjaśnionej przez zmienną

niezależną

– Eta

2

, ŋ

2

wariancji

72%

72

,

0

44

32

2







O

MG

SS

SS



Efekt jest silny, ale które

grupy różnią się od siebie?

Wykres słupków błędu i testy

post hoc

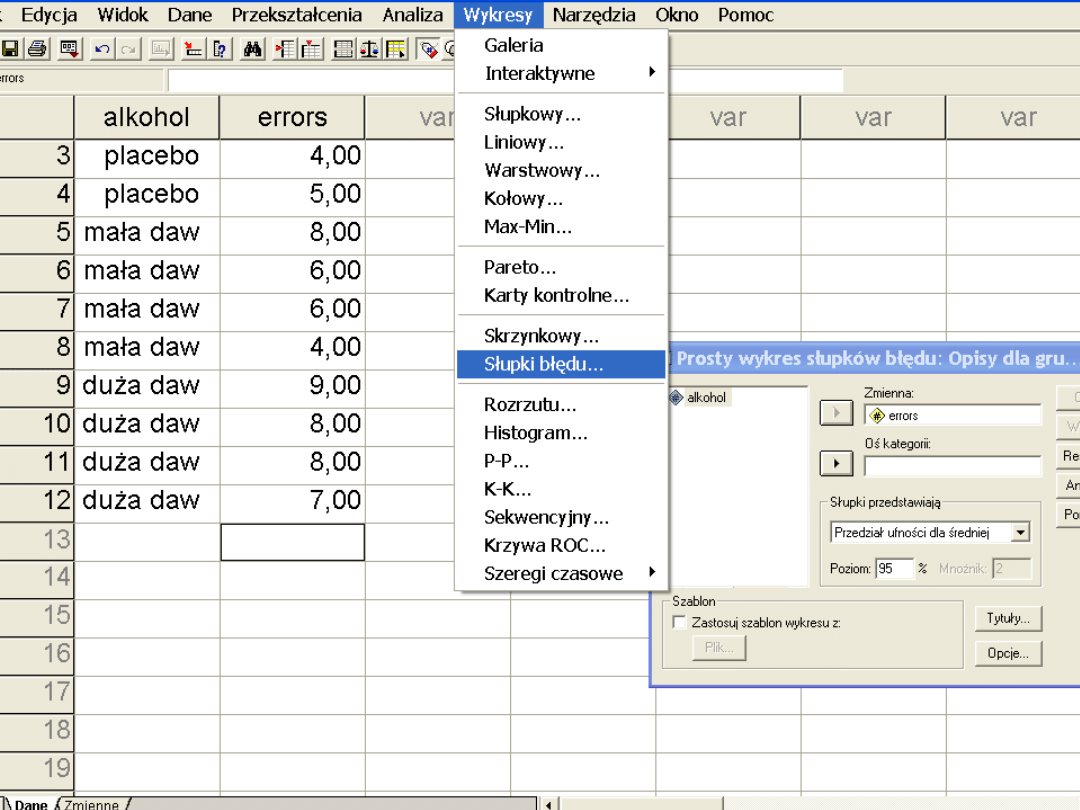
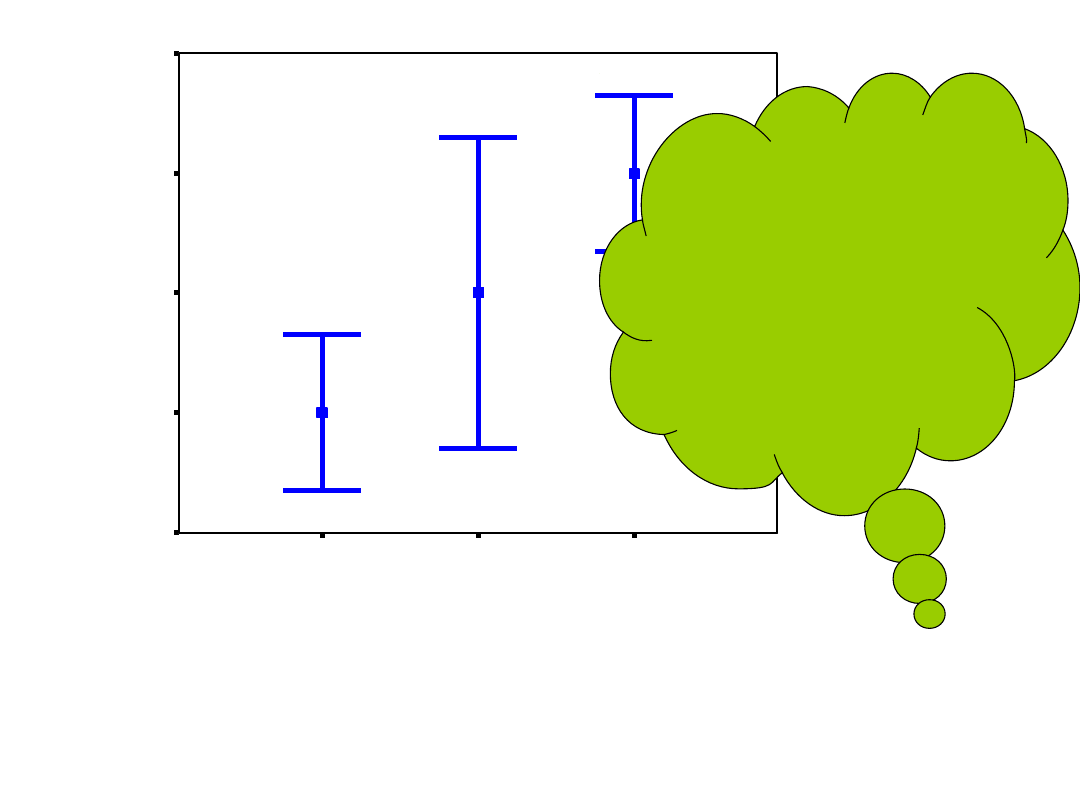
ALKOHOL

duża_d

mała_d

placebo

95

%

P

U

E

R

R

O

R

S

10

8

6

4

2

Grupa 1 i 3

najprawdopodobniej

różnią się od siebie,

przedziały ufności

dla średnich nie

nakładają się.

Natomiast grupa 2

najprawdopodobniej

nie różni się od

pozostałych

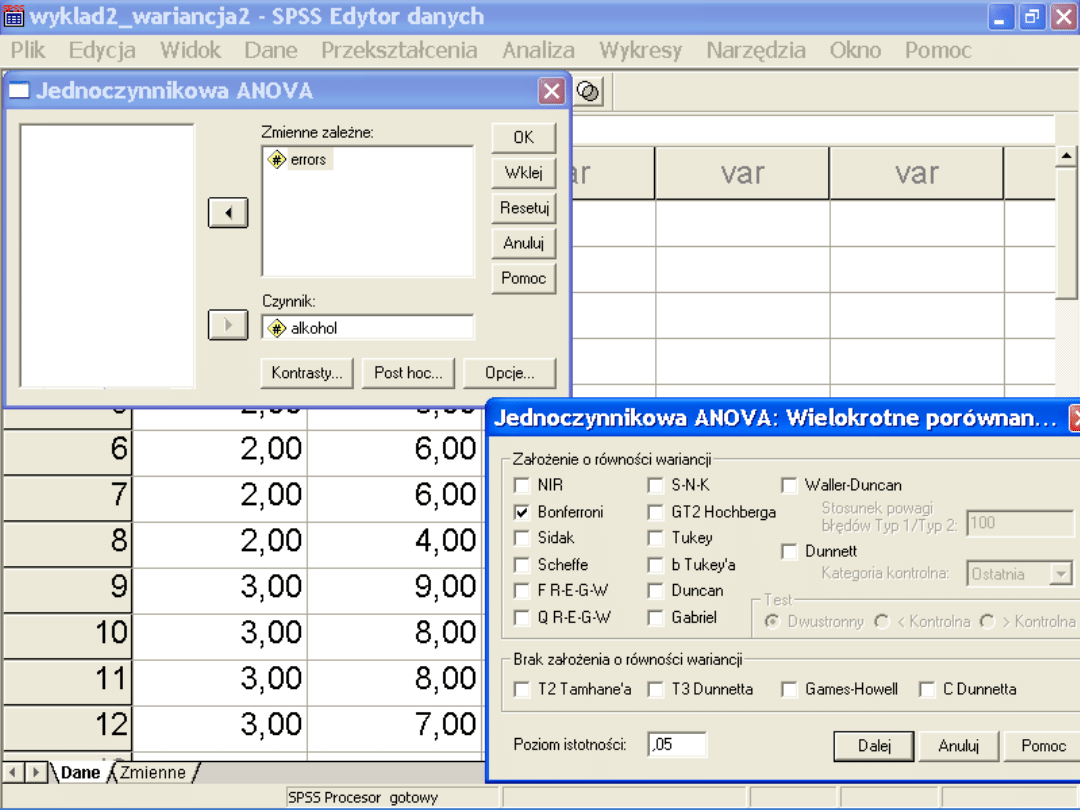
Porównania wielokrotne

Zmienna zależna: ERRORS
Test Bonferroniego

-2,0000

,8165 ,110 -4,3950

,3950

-4,0000* ,8165 ,003 -6,3950 -1,6050

2,0000

,8165 ,110 -,3950 4,3950

-2,0000

,8165 ,110 -4,3950

,3950

4,0000* ,8165 ,003 1,6050 6,3950
2,0000

,8165 ,110 -,3950 4,3950

(J) ALKOHOL
mała dawka

duża dawka

placebo

duża dawka

placebo

mała dawka

(I) ALKOHOL
placebo

mała dawka

duża dawka

Różnica

średnich (I-J)

Błąd

standardowy

Istotność Dolna granica Górna granica

95% przedział ufności

Różnica średnich jest istotna na poziomie .05.

*.

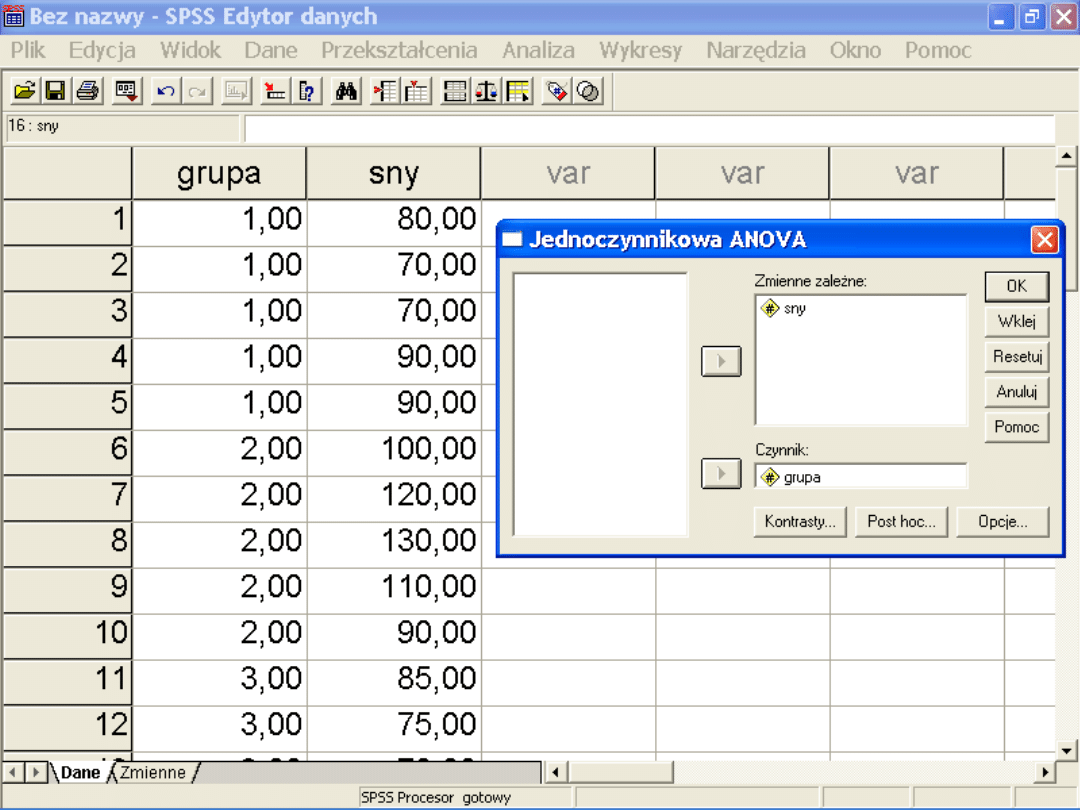
Efekt deprywacji snu -

Czy każdy każdej nocy śni? Czy

można odespać stracone sny?

Dement, W. (1960) -

adaptacja

Przybliżone wyniki w

minutach

Grupa 1

Kontrolna

Grupa 2

budzenie w

trakcie snu

Grupa 3

budzenie po

śnie

80
70
70
90
90

100
120
130
110

90

85
75
70
95
85

M

1

=80

M

2

=110

M

3

= 82

Analiza wariancji

SNY

2813

2 1407 9,483

,003

1780

12 148,3

4593

14

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Statystyki opisowe

SNY

5 80,000

10,0000

4,4721 67,5834

92,4166 70,00

90,00

5 110,00

15,8114

7,0711 90,3676 129,6324 90,00 130,00

5 82,000

9,7468

4,3589 69,8978

94,1022 70,00

95,00

15 90,667

18,1134

4,6769 80,6358 100,6975 70,00 130,00

kontrolna

przed REM

po REM

Ogółem

N

Średnia

Odchylenie

standardowe

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności dla

średniej

Minimum

Maksimum

Test jednorodności wariancji

SNY

,787

2

12

,477

Test Levene'a

df1

df2

Istotność

Eta

2

=0,61%

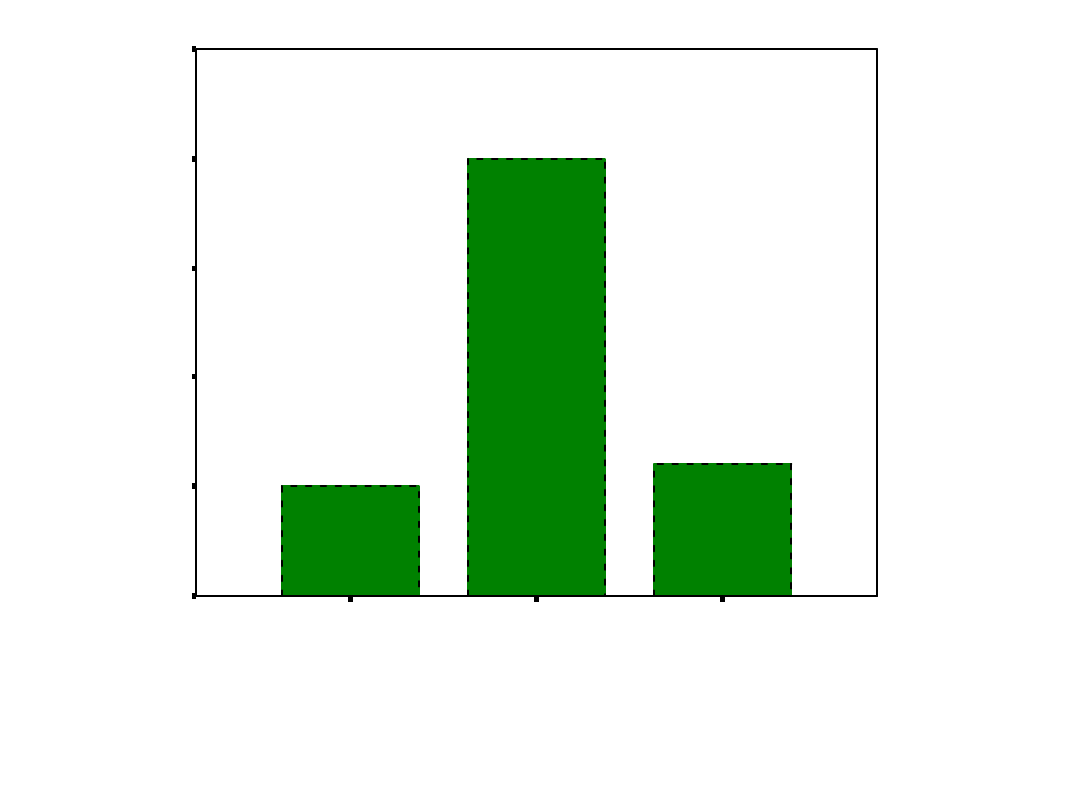
GRUPA

po REM

przed REM

kontrolna

Ś

re

dn

ia

-

S

N

Y

120

110

100

90

80

70

Porównania średnich testy post

hoc

• Istotna wartość testu F mówi tylko o

tym, że któreś średnie różnią się między

sobą, nie wiemy jednak które.

• Możemy sprawdzić, które grupy różnią

się od siebie przeprowadzając któryś z

testów a posteriori

– Porównania wielokrotne między parami

średnich

– Jest wiele testów, które różnią się siłą i

możliwością redukcji błędu I rodzaju

Dlaczego po prostu nie wybrać

testów t?

• Ze względu na zwiększone ryzyko

popełnienia błędu I rodzaju (0,05)

• Wzrasta ono wraz z liczbą

dokonywanych porównań

– Jeśli wykonalibyśmy 5 porównań, wtedy

• 0,05x5=0,25

– tyle wyniosłoby prawdopodobieństwo popełnienia

błędu I rodzaju, a na to nie chcemy się zgodzić

Rodzaje

• Scheffe

– najbardziej konserwatywny test (0.05) - jeżeli ogólne F nie będzie

istotne - na pewno żadne z porównań testem Scheffe też nie

będzie istotne.

• Tukey

– mniej konserwatywny niż Scheffe - łatwiej wychwycić istotną

różnicę między średnimi.

• Duncan

– przyjmuje różne wartości krytyczne w zależności od ile średnich

mieści się między porównywanymi średnimi. Im bardziej oddalone

od siebie średnie tym łatwiej uzyskać istotne wyniki.

• Boferroni

– robi testy t-Studenta z poprawką na ich liczbę

• NIR - Najmniejsza Istotna Różnica

– tak jak byśmy przeprowadzali wiele testów t (dla każdej

porównywanej pary średnich) - przekłamuje prawdopodobieństwa,

gdyż nie bierze poprawki na liczbę wykonywanych testów t (im

więcej tym łatwiej uzyskać istotny wynik, którego tak naprawdę nie

ma). UWAGA!!!

zastrzeżenia

• Kiedy grupki są nierównoliczne

– Gabriel

• Kiedy wariancje są różne

– Np. test Dunnetta C, Gamesa-Howella,

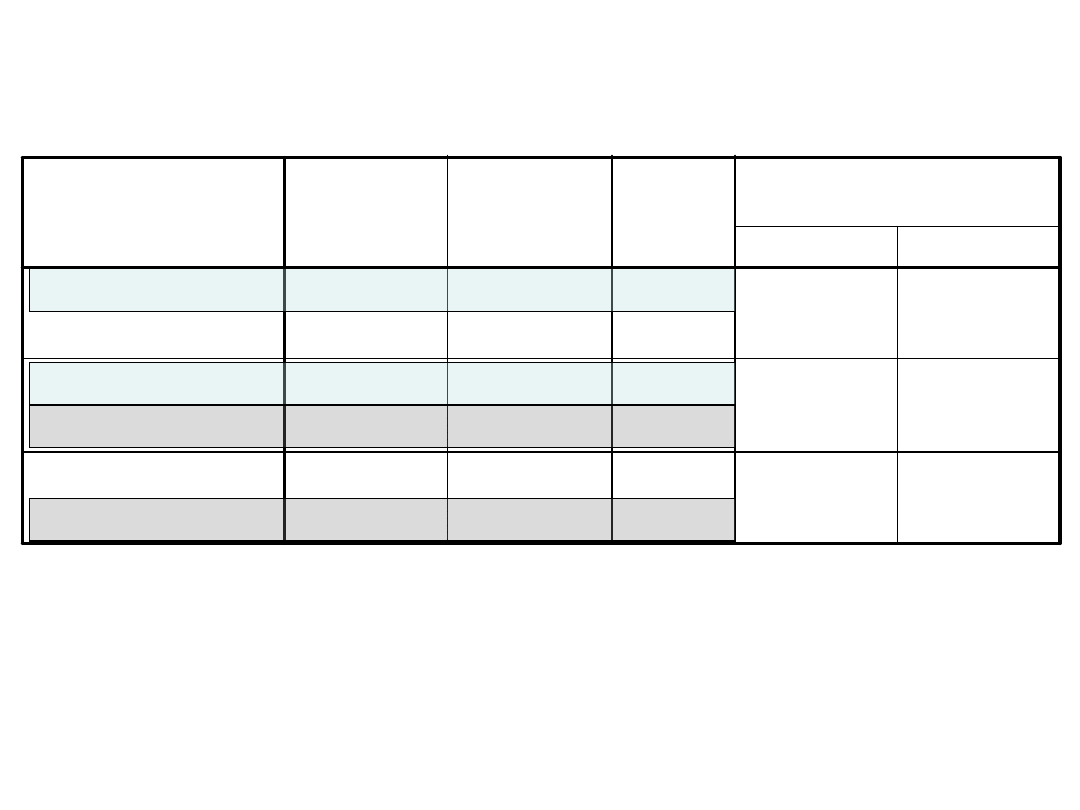
Porównania wielokrotne

Zmienna zależna: SNY
Test Bonferroniego

-30,0000*

7,7028

,006 -51,4098

-8,5902

-2,0000

7,7028 1,000 -23,4098 19,4098

30,0000*

7,7028

,006

8,5902 51,4098

28,0000*

7,7028

,010

6,5902 49,4098

2,0000

7,7028 1,000 -19,4098 23,4098

-28,0000*

7,7028

,010 -49,4098

-6,5902

(J) GRUPA
przed REM

po REM

kontrolna

po REM

kontrolna

przed REM

(I) GRUPA
kontrolna

przed REM

po REM

Różnica

średnich (I-J)

Błąd

standardowy Istotność Dolna granica Górna granica

95% przedział ufności

Różnica średnich jest istotna na poziomie .05.

*.

Zaznaczone są istotne różnice między średnimi,
Grupa budzona przez fazą REM różni się istotnie od pozostałych grup

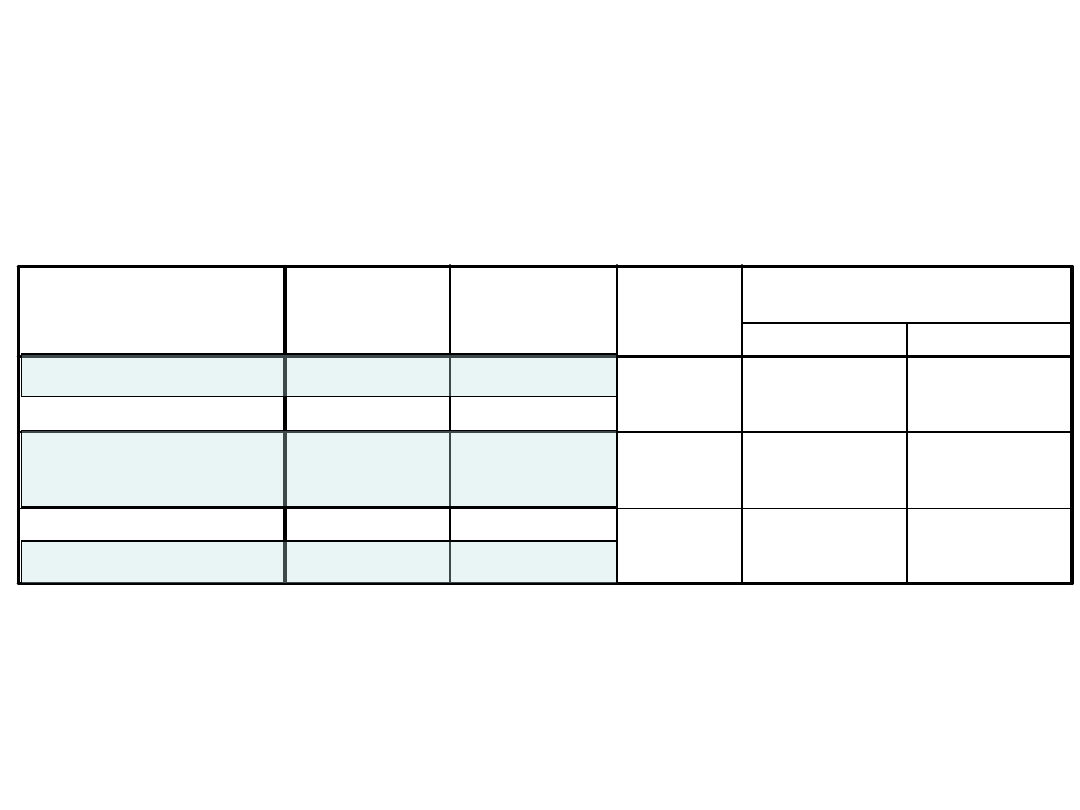
Porównania wielokrotne

Zmienna zależna: SNY
Test Scheffe

-30,0000*

7,7028

,007 -51,4722

-8,5278

-2,0000

7,7028

,967 -23,4722

19,4722

30,0000*

7,7028

,007

8,5278

51,4722

28,0000*

7,7028

,012

6,5278

49,4722

2,0000

7,7028

,967 -19,4722

23,4722

-28,0000*

7,7028

,012 -49,4722

-6,5278

(J) GRUPA
przed REM

po REM

kontrolna

po REM

kontrolna

przed REM

(I) GRUPA
kontrolna

przed REM

po REM

Różnica

średnich (I-J)

Błąd

standardowy

Istotność Dolna granica Górna granica

95% przedział ufności

Różnica średnich jest istotna na poziomie .05.

*.

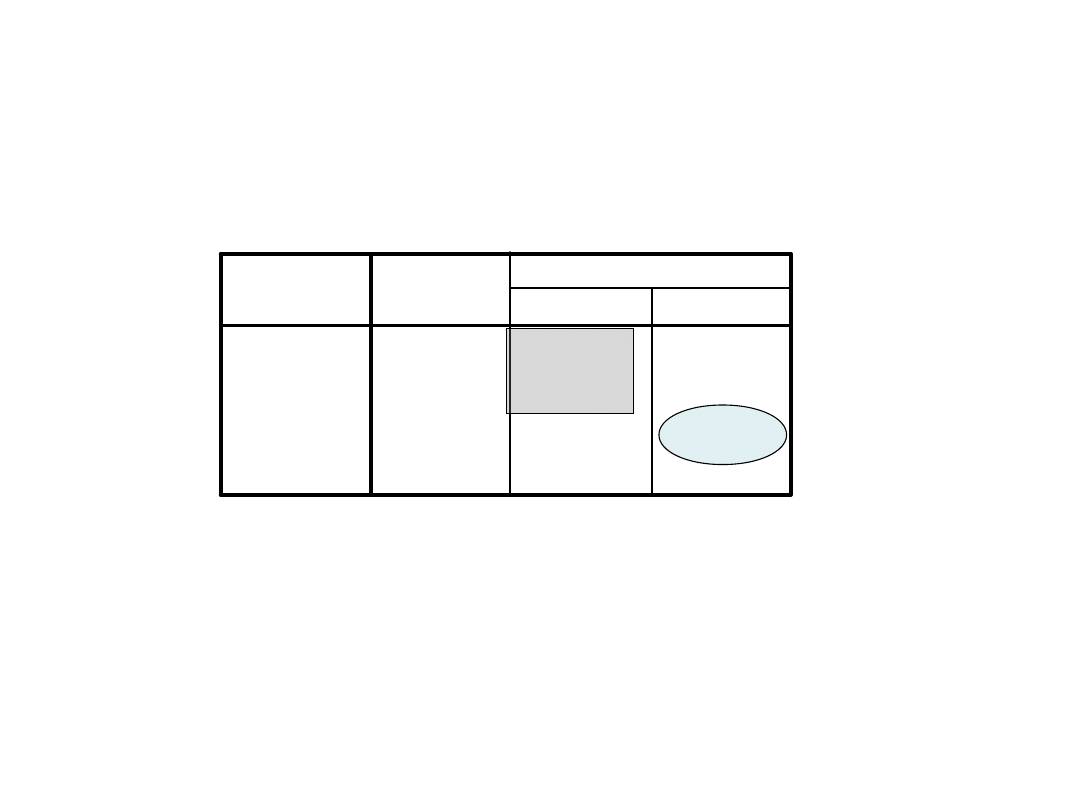
Grupy jednorodne

SNY

Test Scheffe

a

580,0000
582,0000
5

110,00

,967

1,000

GRUPA
kontrolna

po REM

przed REM

Istotność

N

1

2

Podzbiór dla alfa = .05

Wyświetlane są średnie dla grup jednorodnych.

Wykorzystywana jest średnia harmoniczna
wielkości próby = 5,000.

a.

80 a

83 a

83 b

88 b

Wpływ wiedzy o przeszłości

kryminalnej na wydanie

wyroku o winie oskarżonego.

Przykład

….gate

Opis badania

• 15 osób wybranych na sędziów przysięgłych, lecz nie

uczestniczących w prawdziwym procesie, ogląda video z 4-

godz. przesłuchania mężczyzny oskarżonego o korupcję.

• Wcześniej jednak dostają kartkę z informacjami (wiek, stan

cywilny itp.) taką samą dla wszystkich osób, z wyjątkiem

ostatniego akapitu.

– Dla jednej trzeciej osób mówi on, że był on wcześniej

trzykrotnie skazany za podobne przewinienie (grupa "karany"),

– dla jednej trzeciej, że nie był dotychczas karany (grupa

"niekarany"),

– dla jednej trzeciej - nie było żadnej informacji na ten temat

(grupa „kontrolna”).

• Badanych przydzielono losowo do jednej z trzech grup. Po

obejrzeniu taśmy podawali swoje oceny na skali od 1

(całkowicie pewny, że jest niewinny) do 10 (całkowicie

pewny, że jest winny).

Czy mamy przewidywania co

do różnic między grupami?

Które grupy powinny się

różnić?

Statystyki opisowe

WERDYKT

5 8,0000

1,0000

,4472

6,7583

9,2417

7,00

9,00

5 5,0000

,7071

,3162

4,1220

5,8780

4,00

6,00

5 5,0000

,7071

,3162

4,1220

5,8780

4,00

6,00

15 6,0000

1,6475

,4254

5,0876

6,9124

4,00

9,00

karany

niekarany

kontrolna

Ogółem

N

Średnia

Odchylenie

standardowe

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności dla

średniej

Minimum Maksimum

5

5

5

N =

GRUPA

kontrolna

niekarany

karany

95

%

P

U

W

E

R

D

Y

K

T

10

9

8

7

6

5

4

3

Porównania planowane (a

priori) kontrasty

• Kontrasty bezpośrednio testują z góry

założone hipotezy

– Jeśli mamy przewidywania co do tego, które

średnie powinny się różnic między sobą,

możemy przeprowadzić porównania a priori,

jako alternatywę dla testu F.

• Służą do porównywania kombinacji

średnich.

• Można je stosować również wtedy, gdy

ogólny test F nie jest istotny statystycznie

Kontrasty

• Porównując ze sobą grupy przypisujemy im

dla skontrastowania wartości dodatnie

jednym a ujemne drugim

• Suma dodanych wartości powinna być

równa zero

• Grupy, którym przypisaliśmy pozytywne

wartości, będą porównywane z grupami o

przypisanych negatywnych wartościach

• Jeśli daną grupę chcemy wykluczyć z

porównań, wtedy przypisujemy jej wartość

zero

Test jednorodności wariancji

WERDYKT

1,000

2

12

,397

Test Levene'a

df1

df2

Istotność

Współczynniki kontrastu

2

-1

-1

Kontrast
1

karany

niekarany kontrolna

GRUPA

Testy kontrastu

6,0000

,8944 6,708

12

,000

6,0000

1,0000 6,000 6,061

,001

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

WERDYKT

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

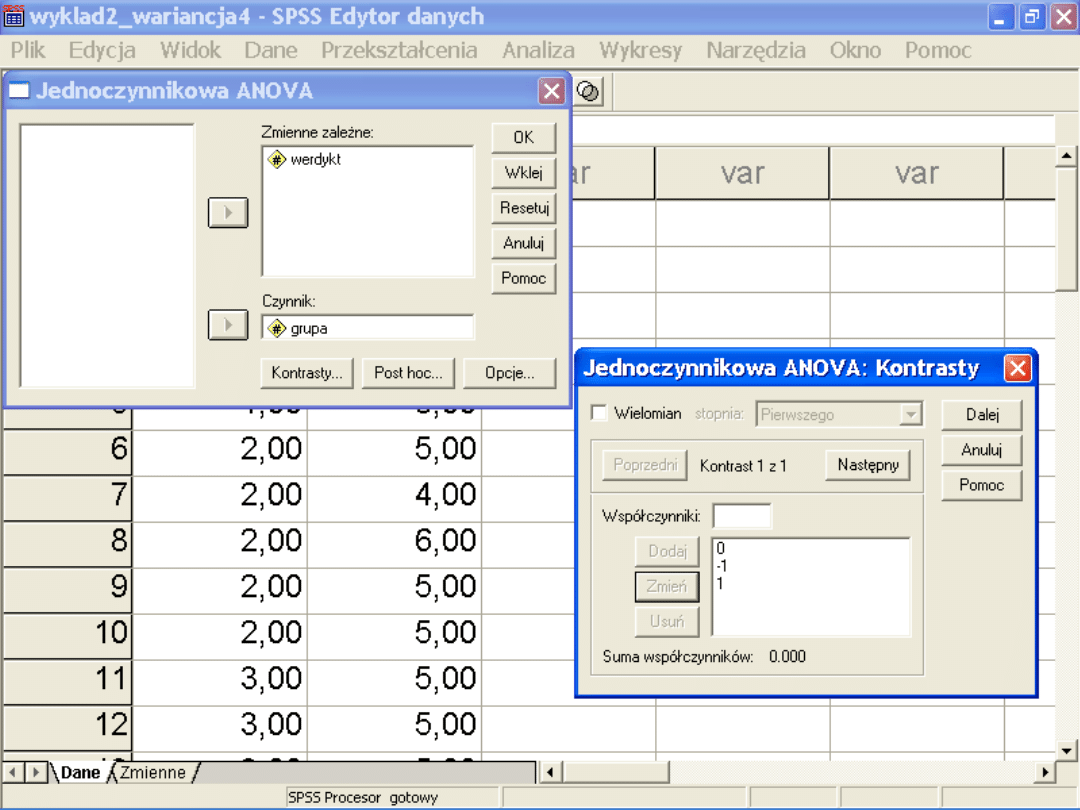
Współczynniki kontrastu

0

-1

1

Kontrast
1

karany

niekarany kontrolna

GRUPA

Testy kontrastu

,0000

,5164

,000

12

1,000

,0000

,4472

,000 8,000

1,000

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

WERDYKT

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Jeśli kontrasty są niezależne od

siebie:

1 kontrast

2 kontrast

1x2

2

0

0

-1

-1

1

-1

1

-1

Suma=0

0

0

Logika kontrastów

• Trochę jakbyśmy kroili ciasto, jak już

odkroiliśmy kawałek to, go nie

przyczepimy z powrotem do całości

• Kontrasty powinny być niezależne od

siebie

– (k-1) porównań

• Każdy kontrast porównuje tylko 2

porcje wariancji

Logika kontrastów

Całkowita zmienność

SS

MG

SS

WG

Grupa1

Grupa 2

+

kontrolna

Grupa 2

kontrolna