Analiza kowariancji i

Analiza kowariancji i

analiza czynnikowa

analiza czynnikowa

Wykład 11

Wykład 11

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Poruszane zagadnienia

Poruszane zagadnienia



Raport z

Raport z

wielozmiennowej

wielozmiennowej

analizy regresji

analizy regresji



Krótkie wprowadzenie

Krótkie wprowadzenie

do analizy kowariancji

do analizy kowariancji



Wprowadzenie do

Wprowadzenie do

analizy czynnikowej

analizy czynnikowej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Zmienne wprowadzone/usunięte

b

bud¿et w tysi¹cach

a

,

Wprowadzanie

atrakcyjnoϾ grupy, liczba

piosenek w tygodniu

a

,

Wprowadzanie

Model
1
2

Zmienne wprowadzone

Zmienne

usunięte

Metoda

Wszystkie wyspecyfikowane zmienne zostały wprowadzone.

a.

Zmienna zależna: sprzedaż w tysiącach

b.

Model - Podsumowanie

,578

a

,335

,331 65,9914

,335 99,587

1

198

,000

,815

b

,665

,660 47,0873

,330 96,447

2

196

,000

Model
1

2

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Zmiana

R-kwadrat

Zmiana F

df1

df2

Istotność

zmiany F

Statystyki zmiany

Predyktory: (Stała), budżet w tysiącach

a.

Predyktory: (Stała), budżet w tysiącach, atrakcyjność grupy, liczba piosenek w tygodniu

b.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynniki

a

134,14

7,537

17,799

,000

,096

,010

,578 9,979

,000

-26,61

17,350

-1,534

,127

,085

,007

,511 12,261

,000

3,367

,278

,512 12,123

,000

11,086

2,438

,192 4,548

,000

(Stała)

budżet w tysiącach

(Stała)

budżet w tysiącach

liczba piosenek w
tygodniu
atrakcyjność grupy

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: sprzedaż w tysiącach

a.





sc

atrakcyjno

09

,

11

radio)

37

,

3

(

reklama)

85

,

0

(

61

,

26

plyt

sprzedaz

















Statystyki t - pokazują, czy predyktor przyczynia się istotnie do predykcji zmiennej zależnej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Podsumowanie hierarchicznej

Podsumowanie hierarchicznej

analizy regresji

analizy regresji

R

R

2

2

Wzrost R

Wzrost R

2

2

F - wzrost

F - wzrost

Beta

Beta

Reklama

Reklama

0,33

0,33

0,33

0,33

99,58

99,58

* * *

* * *

0,51

0,51

* * *

* * *

Liczba

Liczba

piosenek

piosenek

Atrakcyjność

Atrakcyjność

0,66

0,66

0,33

0,33

96,45

96,45

* * *

* * *

0,51

0,51

* * *

* * *

0,19

0,19

* * *

* * *

* p < 0,05; * * p < 0,01;

* p < 0,05; * * p < 0,01;

* * * p < 0,001;

* * * p < 0,001;

Analiza kowariancji

Analiza kowariancji

podstawy

podstawy

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

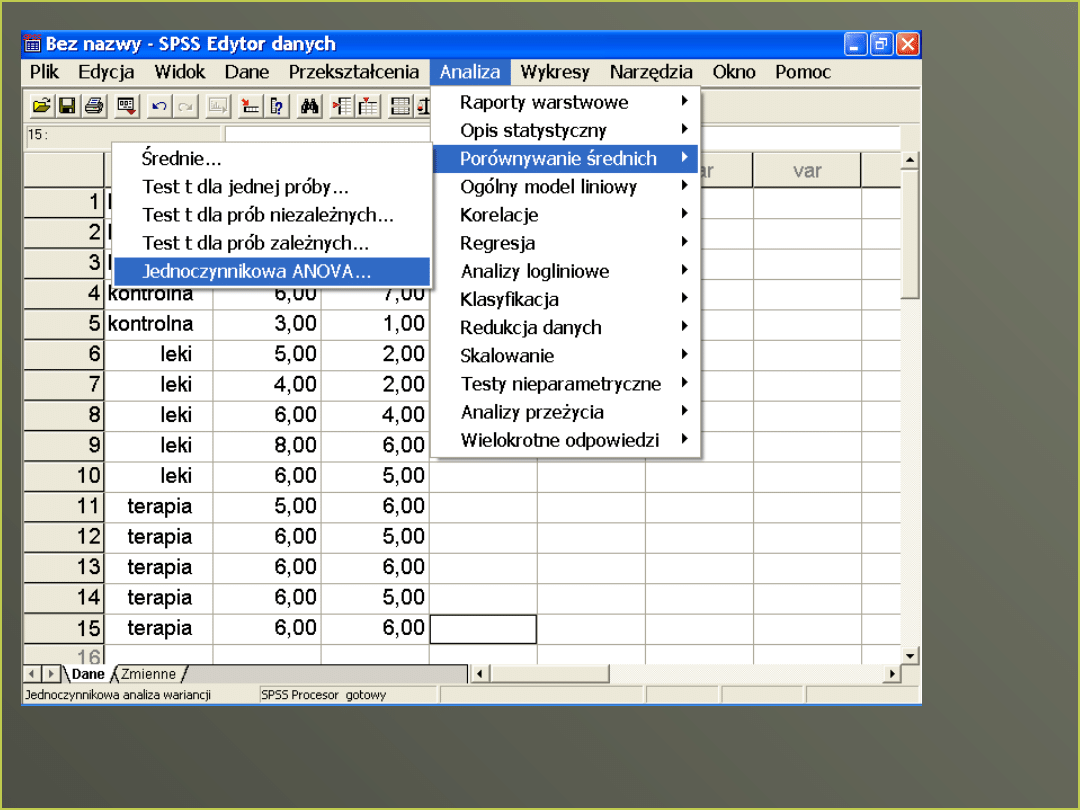
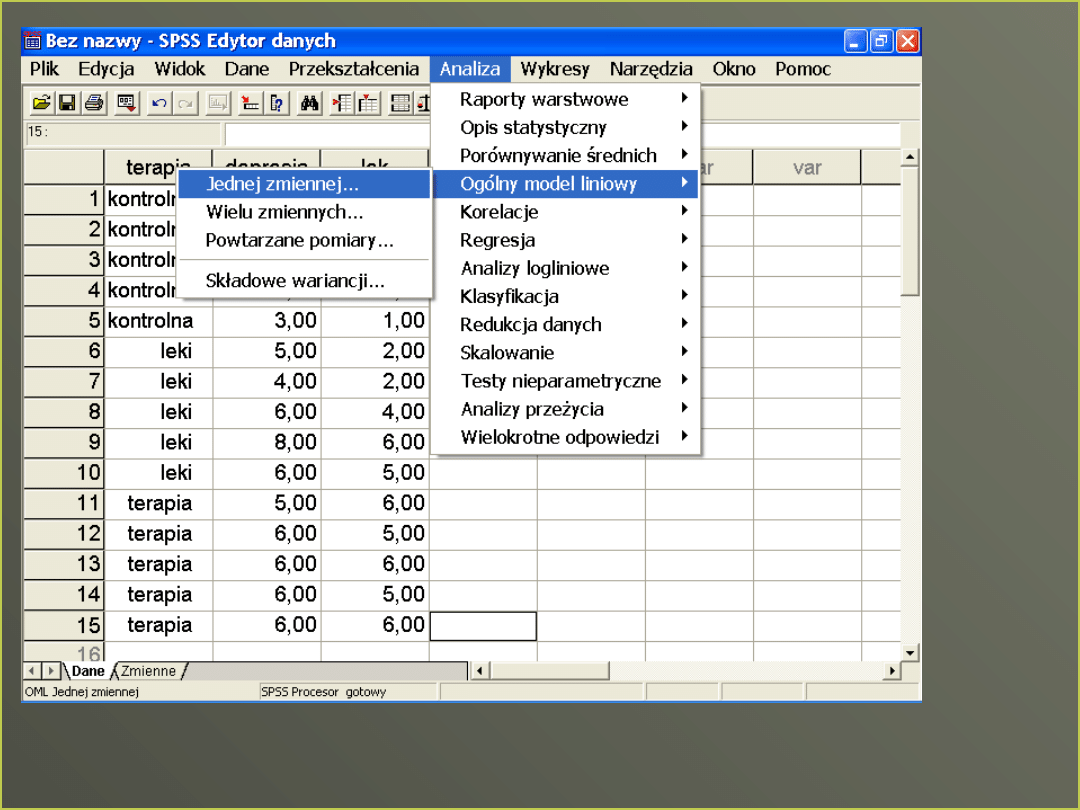
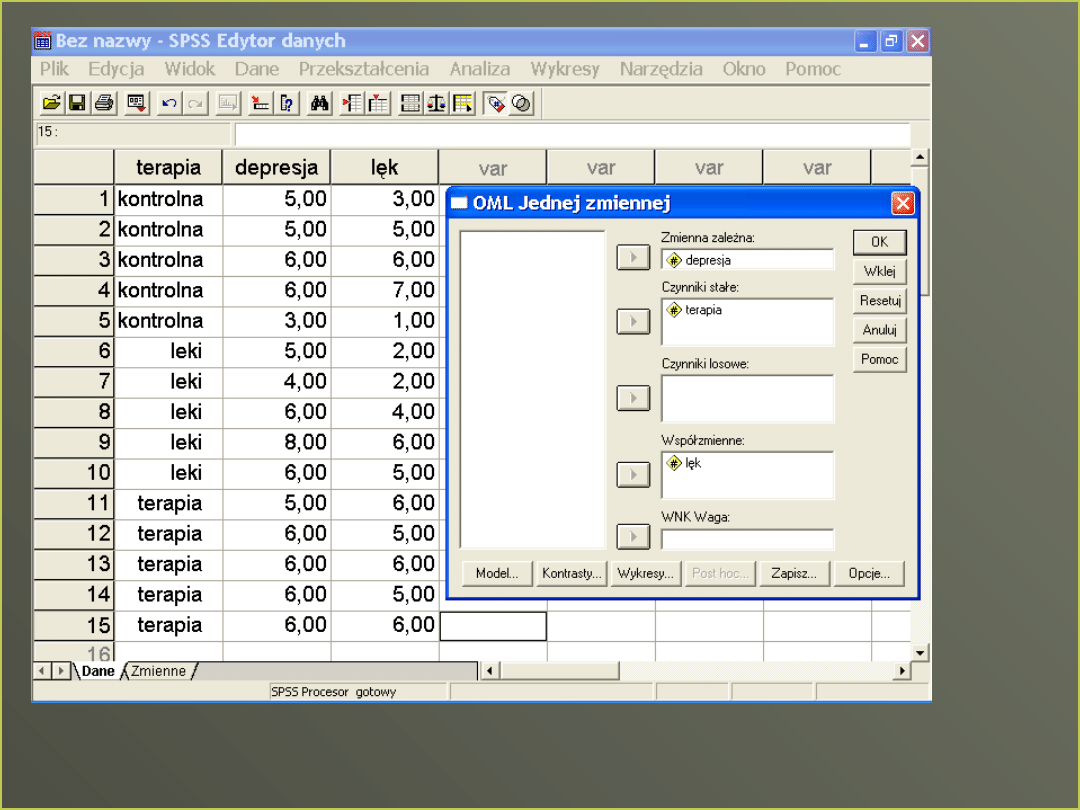
Jednoczynnikowa ANCOVA

Jednoczynnikowa ANCOVA



Czy średnie różnią się między sobą

Czy średnie różnią się między sobą

po uwzględnieniu współzmiennej

po uwzględnieniu współzmiennej

•

Czy średnie w populacji na różnych

Czy średnie w populacji na różnych

poziomach czynnika istotnie różnią się

poziomach czynnika istotnie różnią się

od siebie przy kontroli współzmiennej

od siebie przy kontroli współzmiennej

•

Dla każdej osoby mamy wyniki dla

Dla każdej osoby mamy wyniki dla

trzech zmiennych

trzech zmiennych



Niezależna – dzieli na grupy

Niezależna – dzieli na grupy



Współzmienna - ilościowa

Współzmienna - ilościowa



zmienna zależna - ilościowa

zmienna zależna - ilościowa

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

W jakich sytuacjach

W jakich sytuacjach

Badania z pretestem:

Badania z pretestem:
•

pretest,

pretest,

•

badani losowo przydzieleni do warunków

badani losowo przydzieleni do warunków

eksperymentalnych,

eksperymentalnych,

•

posttest (może być ta sama miara)

posttest (może być ta sama miara)



ANCOVA bierze poprawkę na początkowe

ANCOVA bierze poprawkę na początkowe

różnice ze względu kowariant w wynikach

różnice ze względu kowariant w wynikach

zmiennej zależnej

zmiennej zależnej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza kowariancji

Analiza kowariancji



Włączamy do analizy wariancji

Włączamy do analizy wariancji

zmienne, które nie były częścią

zmienne, które nie były częścią

manipulacji eksperymentalnej, ale

manipulacji eksperymentalnej, ale

wiemy, że mają wpływ na zmienną

wiemy, że mają wpływ na zmienną

zależną

zależną

•

Współzmienna - kowariant

Współzmienna - kowariant

•

Zmienna na skali ciągłej, koreluje z

Zmienna na skali ciągłej, koreluje z

zależną

zależną

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Założenia

Założenia



Rozkład normalny dla zmiennej

Rozkład normalny dla zmiennej

zależnej dla kowariantu i dla każdego

zależnej dla kowariantu i dla każdego

poziomu zmiennej niezależnej

poziomu zmiennej niezależnej



Wariancje są podobne w każdej

Wariancje są podobne w każdej

grupie

grupie



Kowariant jest w liniowym związku ze

Kowariant jest w liniowym związku ze

zmienną zależną (dla wszystkich

zmienną zależną (dla wszystkich

poziomów zmiennej niezależnej)

poziomów zmiennej niezależnej)



Pomiary są niezależne od siebie

Pomiary są niezależne od siebie

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

przykład

przykład



Zachorowanie na grypę a

Zachorowanie na grypę a

przyjmowanie witaminy c

przyjmowanie witaminy c

•

Placebo

Placebo

•

Mała dawka

Mała dawka

•

Duża dawka

Duża dawka

•

Liczba dni z objawami grypy w 1 roku

Liczba dni z objawami grypy w 1 roku

•

Liczba dni z ojawami w 2 roku

Liczba dni z ojawami w 2 roku

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

pytania

pytania



Czy liczba dni z objawami grypy jest

Czy liczba dni z objawami grypy jest

różna w zależności od dawki

różna w zależności od dawki

witaminy C, zakładając, że nie było

witaminy C, zakładając, że nie było

wcześniejszych różnic między

wcześniejszych różnic między

badanymi w liczbie dni z grypą

badanymi w liczbie dni z grypą

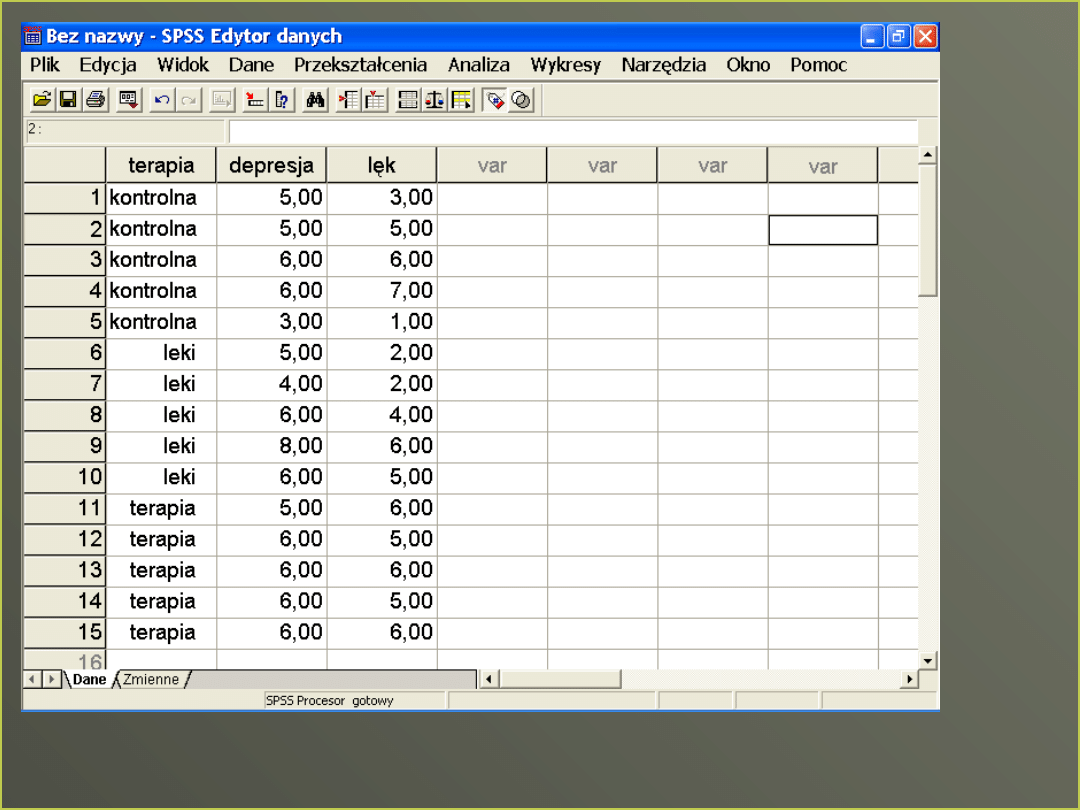
Efektywność terapii

Efektywność terapii

Przykład

Przykład

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Statystyki opisowe

Zmienna zależna: DEPRESJA

5,0000

1,2247

5

5,8000

1,4832

5

5,8000

,4472

5

5,5333

1,1255

15

TERAPIA
kontrolna

leki

terapia

Ogółem

Średnia

Odchylenie

standardowe

N

Analiza wariancji

DEPRESJA

2,133

2 1,067

,821

,463

15,600

12 1,300

17,733

14

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Po co wprowadzać

Po co wprowadzać

dodatkową zmienną?

dodatkową zmienną?



Redukujemy zmienność wewnątrzgrupową

Redukujemy zmienność wewnątrzgrupową

•

W analizie wariancji porównujemy wariancję

W analizie wariancji porównujemy wariancję

międzygrupową z wewnątrzgrupową (z tą,

międzygrupową z wewnątrzgrupową (z tą,

której nie wyjaśnia zmienna niezależna)

której nie wyjaśnia zmienna niezależna)



Możemy wyjaśnić cześć zmienności

Możemy wyjaśnić cześć zmienności

wewnątrzgrupowej wprowadzając dodatkową

wewnątrzgrupowej wprowadzając dodatkową

zmienną, która koreluje ze zmienną zależną

zmienną, która koreluje ze zmienną zależną

•

Uzyskujemy dokładniejsze oszacowanie

Uzyskujemy dokładniejsze oszacowanie

wpływu zmiennej niezależnej

wpływu zmiennej niezależnej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Co zyskujemy wprowadzając

Co zyskujemy wprowadzając

współzmienną?

współzmienną?



Możemy kontrolować wpływ tej

Możemy kontrolować wpływ tej

zmiennej na zmienną zależną

zmiennej na zmienną zależną



Patrzymy jak działa nasza

Patrzymy jak działa nasza

manipulacja eksperymentalna

manipulacja eksperymentalna

(zmienne niezależne) po wyłączeniu

(zmienne niezależne) po wyłączeniu

wpływu współzmiennej na zmienną

wpływu współzmiennej na zmienną

zależną (po wyrównaniu wyników

zależną (po wyrównaniu wyników

zmiennej zależnej pod jej względem)

zmiennej zależnej pod jej względem)

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Korelacje

1,000

,746**

,

,001

15

15

,746**1,000
,001

,

15

15

Korelacja Pearsona

Istotność (dwustronna)

N

Korelacja Pearsona

Istotność (dwustronna)

N

DEPRESJA

LĘK

DEPRESJA

LĘK

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza kowariancji a

Analiza kowariancji a

regresja

regresja



Idea podobna do regresji hierarchicznej

Idea podobna do regresji hierarchicznej

•

Najpierw do modelu włączamy zmienną, której

Najpierw do modelu włączamy zmienną, której

wpływ chcemy kontrolować – kowariant

wpływ chcemy kontrolować – kowariant



Patrzymy jak kowariant przewiduje zmienną zależną

Patrzymy jak kowariant przewiduje zmienną zależną

•

Następnie włączamy zmienną niezależną

Następnie włączamy zmienną niezależną



Patrzymy na oczyszczoną zależność między zależną i

Patrzymy na oczyszczoną zależność między zależną i

niezależną po wyłączeniu wpływu trzeciej zmiennej

niezależną po wyłączeniu wpływu trzeciej zmiennej



Idea korelacji semicząstkowej

Idea korelacji semicząstkowej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Testy efektów międzyobiektowych

Zmienna zależna: DEPRESJA

13,320

a

3 4,440 11,068

,001

14,264

1 14,264 35,556

,000

11,187

1 11,187 27,886

,000

3,464

2 1,732 4,318

,041

4,413

11

,401

477,000

15

17,733

14

Źródło zmienności
Model skorygowany

Stała

LĘK

TERAPIA

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,751 (Skorygowane R kwadrat = ,683)

a.

Wprowadzenie współzmiennej – poziomu lęku, istotnie zredukowało wariancję
wewnątrzgrupową



Uwzględnienie poziomu lęku dało czystszą miarę efektu zmiennej niezależnej

Istotny efekt współzmiennej – lęk istotnie przewiduje depresję
Przy kontroli wpływu tej zmiennej – efekt terapii staje się istotny

Analiza wydruku

Analiza wydruku

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Średnie grupowe obliczone

Średnie grupowe obliczone

przy uwzględnieniu

przy uwzględnieniu

współzmiennej

współzmiennej

Oszacowania

Zmienna zależna: DEPRESJA

5,110

a

,284

4,485

5,735

6,239

a

,295

5,589

6,888

5,252

a

,302

4,588

5,916

TERAPIA
kontrolna

leki

terapia

Średnia

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności

Obliczone przy współzmiennych występujących w modelu - LĘK =
4,6000.

a.

Widzimy inny układ średnich niż na początku, kiedy nie uwzględniliśmy współzmiennej.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

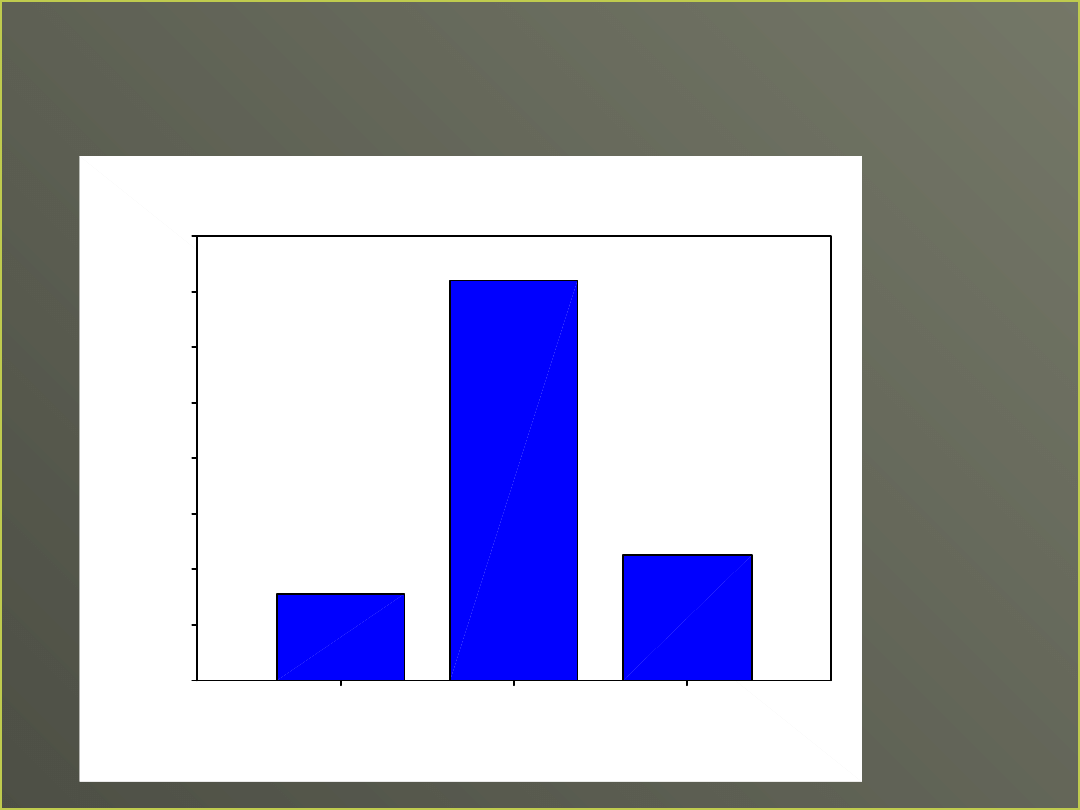
Inny układ średnich po

Inny układ średnich po

uwzględnieniu kowariantu

uwzględnieniu kowariantu

Oszacowane średnie brzegowe - DEPRESJA

TERAPIA

terapia

leki

kontrolna

O

sz

ac

o

w

an

e

ś

re

d

n

ie

b

rz

e

g

o

w

e

6,4

6,2

6,0

5,8

5,6

5,4

5,2

5,0

4,8

Analiza czynnikowa

Analiza czynnikowa

W badaniach nastawionych na

W badaniach nastawionych na

różnice indywidualne

różnice indywidualne

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza czynnikowa

Analiza czynnikowa



Metoda statystyczna stosowana do analizy

Metoda statystyczna stosowana do analizy

korelacji między wieloma zmiennymi

korelacji między wieloma zmiennymi

•

stosowana przy danych zbieranych z

stosowana przy danych zbieranych z

kwestionariuszy, testów psychologicznych

kwestionariuszy, testów psychologicznych



Szukamy powiązania między zmiennymi

Szukamy powiązania między zmiennymi

•

Ograniczamy wstępny zbiór zmiennych do kilku

Ograniczamy wstępny zbiór zmiennych do kilku

niepowiązanych ze sobą czynników

niepowiązanych ze sobą czynników



Czynników mniej niż wyjściowych zmiennych

Czynników mniej niż wyjściowych zmiennych



Za pomocą mniejszej ilości czynników, chcemy

Za pomocą mniejszej ilości czynników, chcemy

wyjaśnić zmienność wyników

wyjaśnić zmienność wyników

•

Nadajemy czynnikom znaczenie, zmienna, która

Nadajemy czynnikom znaczenie, zmienna, która

stoi za zbiorem powiązanych ze sobą zmiennych

stoi za zbiorem powiązanych ze sobą zmiennych

– wspólny mianownik, zmienne latentne

– wspólny mianownik, zmienne latentne

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

cel

cel



Celem analizy czynnikowej jest

Celem analizy czynnikowej jest

odkrycie wspólnego mianownika,

odkrycie wspólnego mianownika,

czynnika dla grupy powiązanych ze

czynnika dla grupy powiązanych ze

sobą zmiennych

sobą zmiennych



Patrzymy jak zmienne korelują ze

Patrzymy jak zmienne korelują ze

sobą, czy układają się wzdłuż

sobą, czy układają się wzdłuż

jakiegoś wymiaru

jakiegoś wymiaru



Co łączy te zmienne?

Co łączy te zmienne?

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Przykład 1

Przykład 1



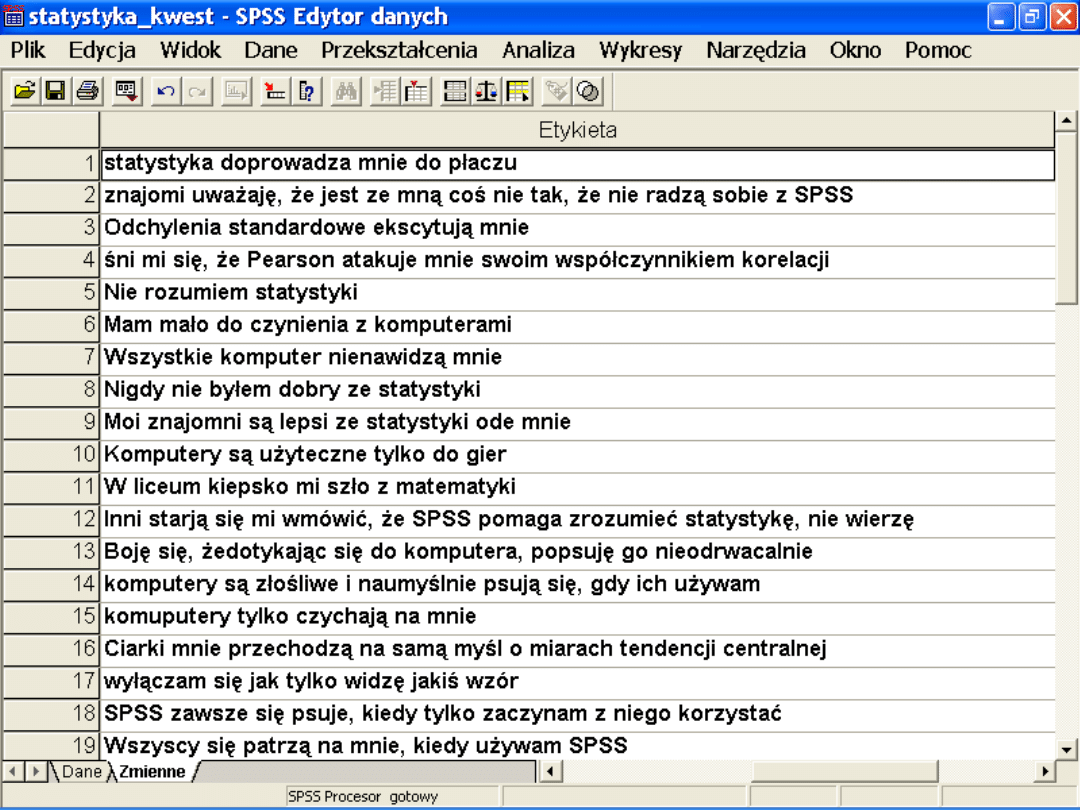
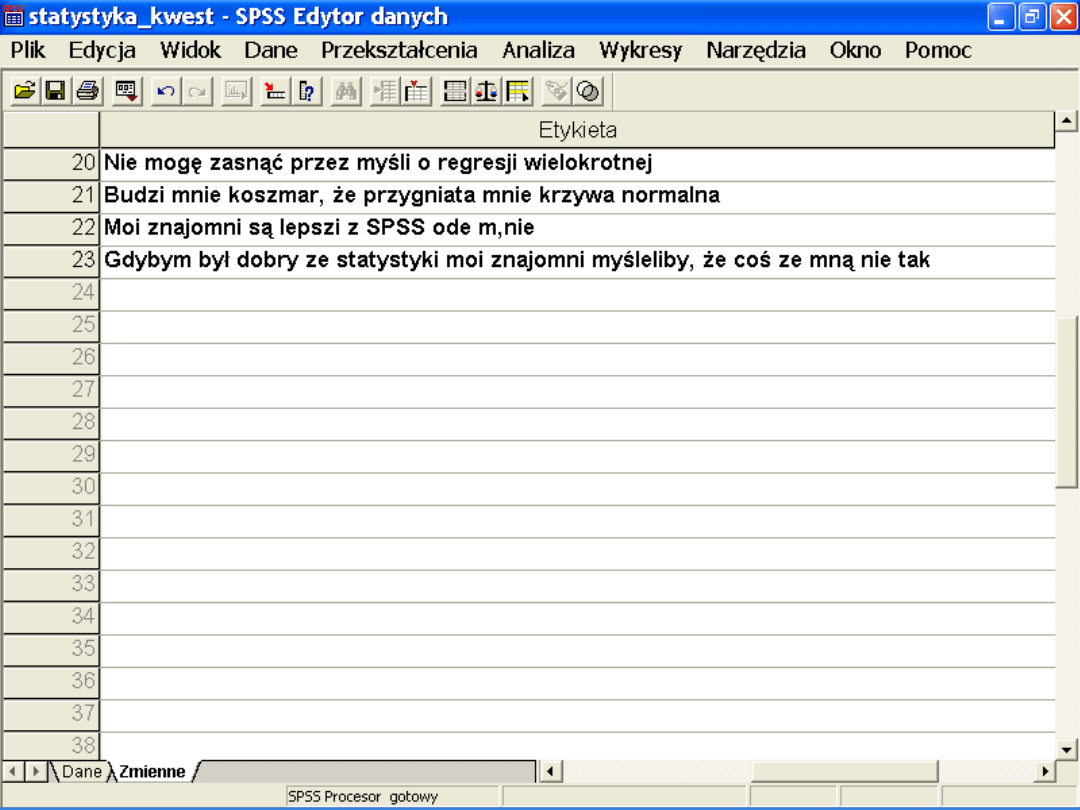
Zmienne wyjściowe: odpowiedzi na

Zmienne wyjściowe: odpowiedzi na

pytania kwestionariusza FCZ-KT

pytania kwestionariusza FCZ-KT

•

Czynniki (składowe): cechy

Czynniki (składowe): cechy

temperamentu (np. reaktywność,

temperamentu (np. reaktywność,

perseweratywność, aktywność....)

perseweratywność, aktywność....)

Andy Field „Discovering

Andy Field „Discovering

Statistics with SPSS”

Statistics with SPSS”

Męki przy nauce statystyki

Męki przy nauce statystyki

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

interkorelacje

interkorelacje



Szukamy takich zmiennych, które

Szukamy takich zmiennych, które

silnie korelują z grupą jednych

silnie korelują z grupą jednych

zmiennych a bardzo słabo z innymi

zmiennych a bardzo słabo z innymi

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza czynnikowa

Analiza czynnikowa



Celem tej analizy jest zastąpienie wielu

Celem tej analizy jest zastąpienie wielu

zmiennych wyjściowych przez kilka nowych

zmiennych wyjściowych przez kilka nowych

zmiennych (zwanych „czynnikami” lub

zmiennych (zwanych „czynnikami” lub

„składowymi”- „factors”)

„składowymi”- „factors”)

•

Czynniki są interpretowane (nazwane przez badacza) w

Czynniki są interpretowane (nazwane przez badacza) w

oparciu o to, które zmienne wyjściowe są z danym

oparciu o to, które zmienne wyjściowe są z danym

czynnikiem najsilniej skorelowane

czynnikiem najsilniej skorelowane



Następnie analizy wykonujemy na zredukowanej

Następnie analizy wykonujemy na zredukowanej

liczbie zmiennych, które nie są powiązane ze sobą

liczbie zmiennych, które nie są powiązane ze sobą

•

Odchodzi nam problem skorelowanych predyktorów w

Odchodzi nam problem skorelowanych predyktorów w

regresji

regresji

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Typy analizy czynnikowej

Typy analizy czynnikowej



Eksploracyjna

Eksploracyjna

•

Zaczynamy od korelacji między zmiennymi

Zaczynamy od korelacji między zmiennymi

i poszukujemy wspólnego czynnika

i poszukujemy wspólnego czynnika



Konfirmacyjna

Konfirmacyjna

•

Mamy model, teorię odnośnie czynników

Mamy model, teorię odnośnie czynników

wyjaśniających zmienność w

wyjaśniających zmienność w

odpowiedziach i sprawdzamy stopień na

odpowiedziach i sprawdzamy stopień na

ile wymiary te wyjaśniają korelacje między

ile wymiary te wyjaśniają korelacje między

zmiennymi

zmiennymi

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Najbardziej
popularna

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

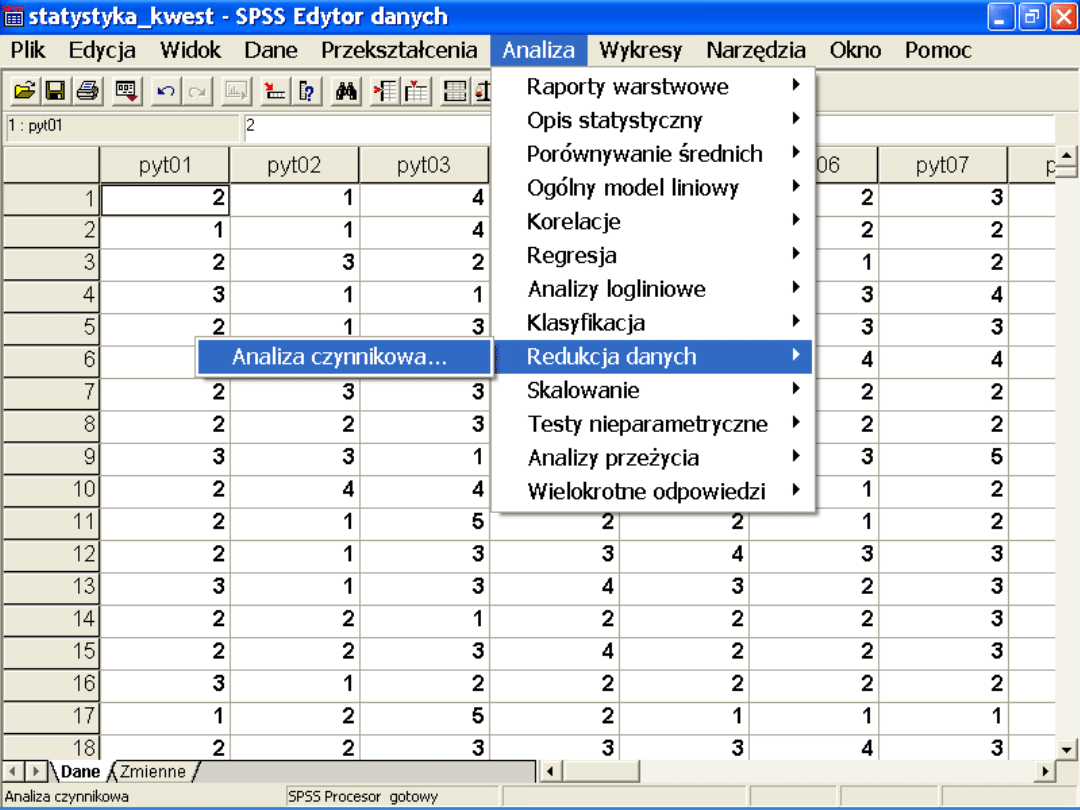
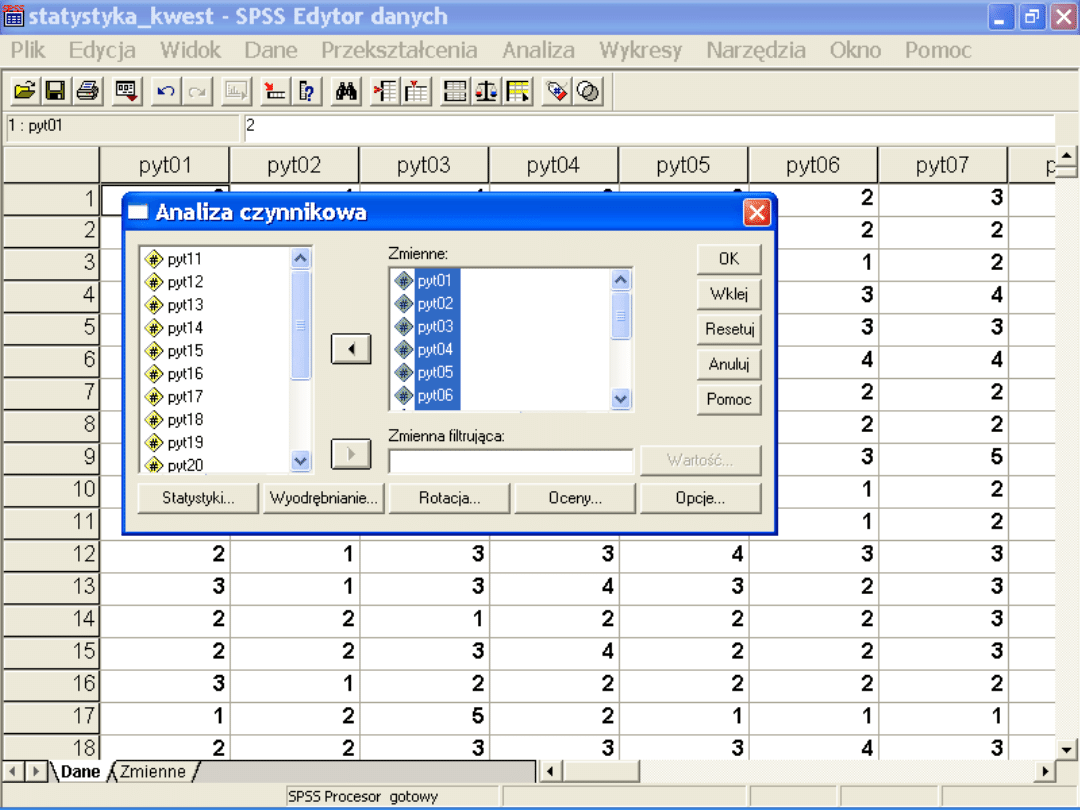
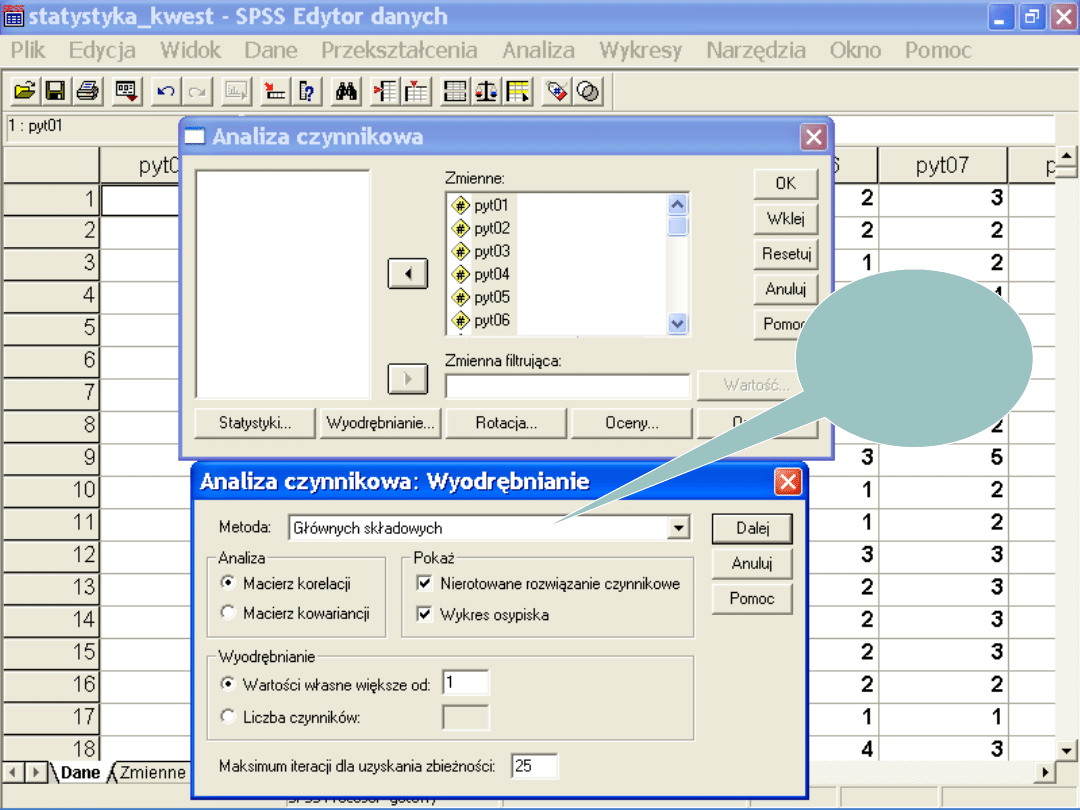
Techniki eksploracyjne

Techniki eksploracyjne



Analiza głównych składowych

Analiza głównych składowych



3 etapy:

3 etapy:

•

Obliczenie korelacji między zmiennymi (macierz

Obliczenie korelacji między zmiennymi (macierz

korelacji)

korelacji)

•

Wyodrębnienie czynników

Wyodrębnienie czynników



Wymiary, które opisują główne komponenty

Wymiary, które opisują główne komponenty

wariancji w matrycy korelacji

wariancji w matrycy korelacji



Matryca korelacji zmiennych z tymi czynnikami

Matryca korelacji zmiennych z tymi czynnikami

(nierotowane rozwiązanie czynnikowe)

(nierotowane rozwiązanie czynnikowe)

•

Identyfikacja czynników, które w najprostszy

Identyfikacja czynników, które w najprostszy

sposób opisują relacje między zmiennymi

sposób opisują relacje między zmiennymi

(rotowanie czynników w celu uzyskania bardziej

(rotowanie czynników w celu uzyskania bardziej

przejrzystej struktury, łatwiejszej do interpretacji)

przejrzystej struktury, łatwiejszej do interpretacji)

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Zasoby zmienności wspólnej

1,000

,435

1,000

,414

1,000

,530

1,000

,469

1,000

,343

1,000

,654

1,000

,545

1,000

,739

1,000

,484

1,000

,335

1,000

,690

1,000

,513

1,000

,536

1,000

,488

1,000

,378

1,000

,487

1,000

,683

1,000

,597

1,000

,343

1,000

,484

1,000

,550

1,000

,464

1,000

,412

PYT01
PYT02
PYT03
PYT04
PYT05
PYT06
PYT07
PYT08
PYT09
PYT10
PYT11
PYT12
PYT13
PYT14
PYT15
PYT16
PYT17
PYT18
PYT19
PYT20
PYT21
PYT22
PYT23

Początkowe

Po

wyodrębn

ieniu

Metoda wyodrębniania czynników - Głównych składowych.

% wspólnej zmienności

% wspólnej zmienności



Na początku, że =1,

Na początku, że =1,

wariancja zmiennej w

wariancja zmiennej w

jednostkach standardowych

jednostkach standardowych



Patrzymy po wyodrębnieniu

Patrzymy po wyodrębnieniu

czynników, zawsze mniejsza

czynników, zawsze mniejsza

niż 1. proporcja wariancji

niż 1. proporcja wariancji

danej zmiennej wyjaśniona

danej zmiennej wyjaśniona

przez wyodrębnione

przez wyodrębnione

czynniki

czynniki



Im bliższe 1 tym nasze

Im bliższe 1 tym nasze

czynniki lepiej wyjaśniają

czynniki lepiej wyjaśniają

oryginalne dane

oryginalne dane



Niskie oznaczają, że

Niskie oznaczają, że

zmienna ma niewiele

zmienna ma niewiele

wspólnego z innymi

wspólnego z innymi

zmiennymi

zmiennymi

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Całkowita wyjaśniona wariancja

7,290 31,696

31,696

7,290 31,696

31,696

3,730 16,219

16,219

1,739

7,560

39,256

1,739

7,560

39,256

3,340 14,523

30,742

1,317

5,725

44,981

1,317

5,725

44,981

2,553 11,099

41,842

1,227

5,336

50,317

1,227

5,336

50,317

1,949

8,475

50,317

,988

4,295

54,612

,895

3,893

58,504

,806

3,502

62,007

,783

3,404

65,410

,751

3,265

68,676

,717

3,117

71,793

,684

2,972

74,765

,670

2,911

77,676

,612

2,661

80,337

,578

2,512

82,849

,549

2,388

85,236

,523

2,275

87,511

,508

2,210

89,721

,456

1,982

91,704

,424

1,843

93,546

,408

1,773

95,319

,379

1,650

96,969

,364

1,583

98,552

,333

1,448

100,000

Składowa
1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

Ogółem

% wariancji

%

skumulowany

Ogółem

% wariancji

%

skumulowany

Ogółem

% wariancji

%

skumulowany

Początkowe wartości własne

Sumy kwadratów ładunków po

wyodrębnieniu

Sumy kwadratów ładunków po rotacji

Metoda wyodrębniania czynników - Głównych składowych.

Wartości własne –

jednostkach

standardowych –

wariancja 1 zmiennej=1,

jeśli czynnik wyjaśnia

zmienność więcej niż 1

zmiennej wtedy wartości

własne>1

Jeśli czynnik wyjaśnia

tylko zmienność 1

zmiennej, to nie redukuje

wyjściowej liczby

zmiennych

Wartości własne wskazują

ile zmiennych można

„zastąpić” danym

czynnikiem

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

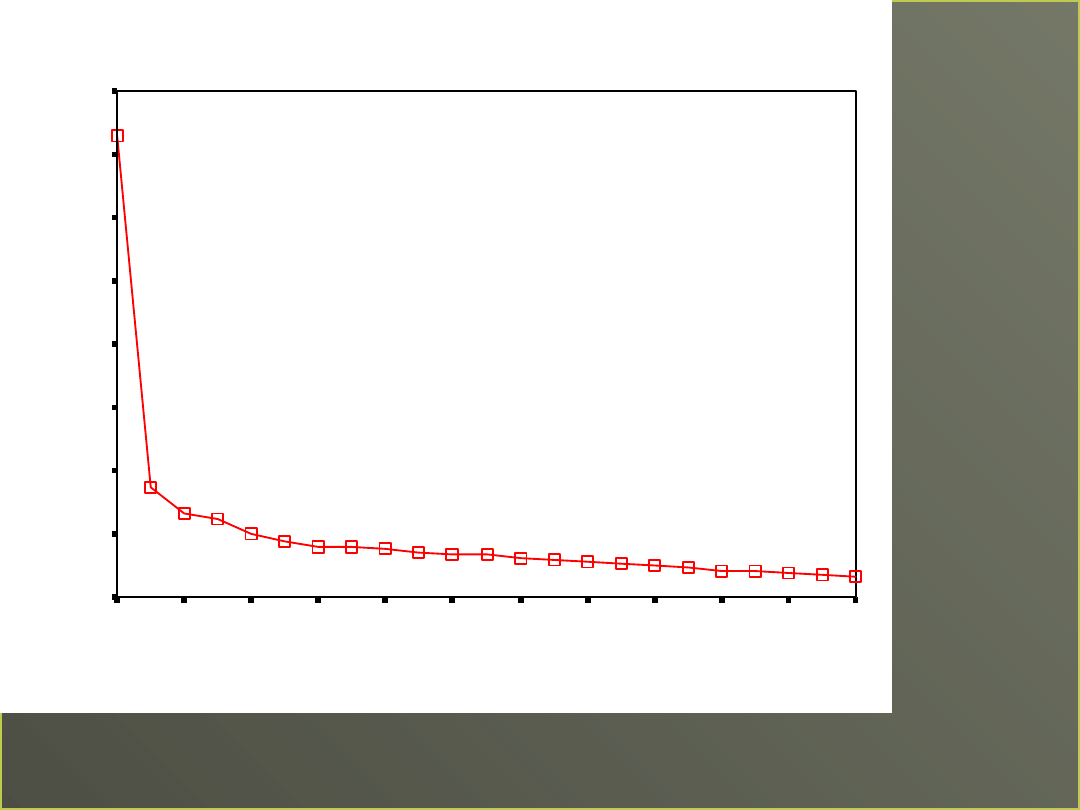
Jak zdecydować, który czynnik

Jak zdecydować, który czynnik

jest istotny

jest istotny



Patrzymy na „wartości własne” –

Patrzymy na „wartości własne” –

eigenvalues

eigenvalues



Bierzemy pod uwagę, tylko te, które mają

Bierzemy pod uwagę, tylko te, które mają

duże wartości własne

duże wartości własne

•

Wartości własne – odzwierciedlają procent

Wartości własne – odzwierciedlają procent

wariancji wyjaśnionej przez dany czynnik

wariancji wyjaśnionej przez dany czynnik



Wartość własna>1, uznaje się, że wyjaśnia sensowną

Wartość własna>1, uznaje się, że wyjaśnia sensowną

porcję wariancji

porcję wariancji



Stąd często kryterium wyodrębniania czynników –

Stąd często kryterium wyodrębniania czynników –

wartość własna

wartość własna

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Wykres osypiska

Numer składowej

23

21

19

17

15

13

11

9

7

5

3

1

W

ar

to

ść

w

ła

sn

a

8

7

6

5

4

3

2

1

0

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

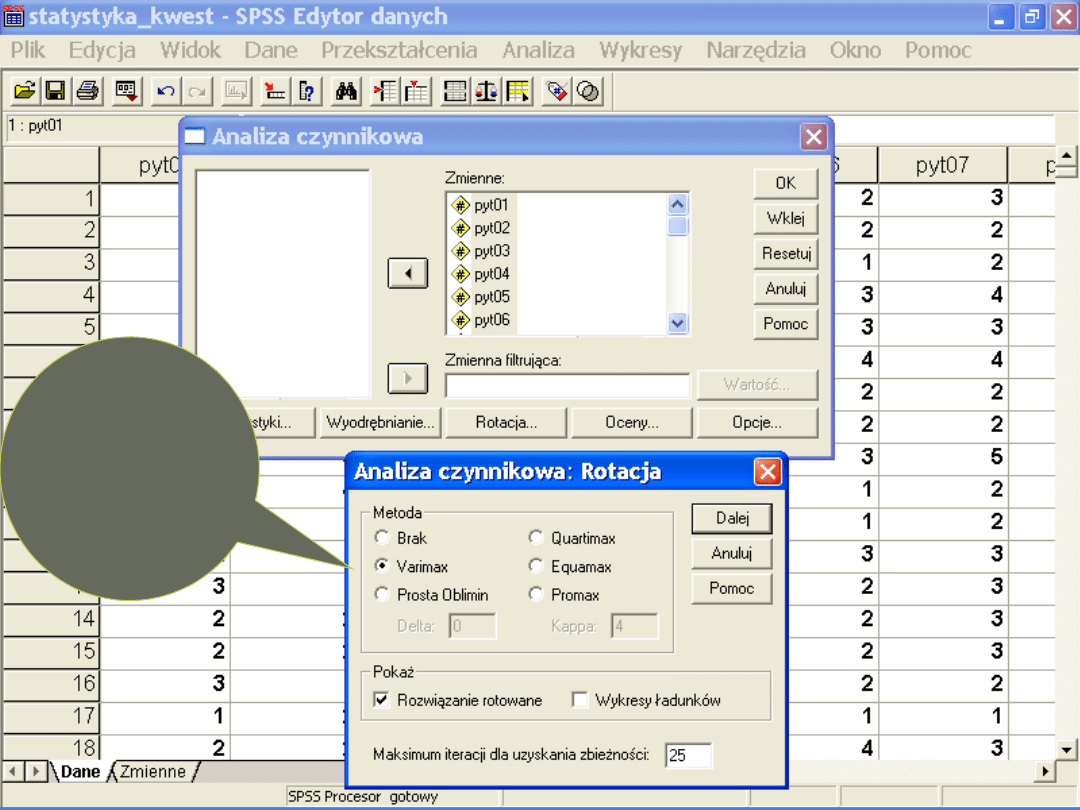
Rotacja

Rotacja



Jak już mamy wyodrębnione czynniki, możemy

Jak już mamy wyodrębnione czynniki, możemy

sprawdzić jak nasze zmienne „ładują” na

sprawdzić jak nasze zmienne „ładują” na

czynnikach

czynnikach

•

Zwykle zmienne korelują z jednym czynnikiem silniej, z

Zwykle zmienne korelują z jednym czynnikiem silniej, z

innymi zdecydowanie słabiej

innymi zdecydowanie słabiej



Rotacja pozwala na uzyskanie bardziej

Rotacja pozwala na uzyskanie bardziej

przejrzystej struktury czynnikowej, pokazuje

przejrzystej struktury czynnikowej, pokazuje

różnice między czynnikami, tak, aby

różnice między czynnikami, tak, aby

maksymalizować ładunki zmiennych z czynnikami

maksymalizować ładunki zmiennych z czynnikami

•

Opcja, dobrze ją wykonywać – uzyskujemy niezależne od

Opcja, dobrze ją wykonywać – uzyskujemy niezależne od

siebie czynniki

siebie czynniki

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Popularna –

w jej

wyniku

uzyskujemy

ortogonaln

e czynniki

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Macierz rotowanych składowych

a

,800
,684
,647
,638
,579
,550
,459

,677
,661

-,567

,473

,523
,516
,514
,496
,429

,833
,747
,747

,648
,645
,586
,543
,427

Mam mało do czynienia z komputerami
SPSS zawsze się psuje, kiedy tylko zaczynam z niego korzystać
Boję się, żedotykając się do komputera, popsuję go nieodrwacalnie
Wszystkie komputer nienawidzą mnie
komputery są złośliwe i naumyślnie psują się, gdy ich używam
Komputery są użyteczne tylko do gier
komuputery tylko czychają na mnie
Nie mogę zasnąć przez myśli o regresji wielokrotnej
Budzi mnie koszmar, że przygniata mnie krzywa normalna
Odchylenia standardowe ekscytują mnie
Inni starją się mi wmówić, że SPSS pomaga zrozumieć statystykę, nie
wierzę
śni mi się, że Pearson atakuje mnie swoim współczynnikiem korelacji
Ciarki mnie przechodzą na samą myśl o miarach tendencji centralnej
statystyka doprowadza mnie do płaczu
Nie rozumiem statystyki
Nigdy nie byłem dobry ze statystyki
wyłączam się jak tylko widzę jakiś wzór
W liceum kiepsko mi szło z matematyki
Moi znajomni są lepsi ze statystyki ode mnie
Moi znajomni są lepszi z SPSS ode m,nie
Gdybym był dobry ze statystyki moi znajomni myśleliby, że coś ze mną nie
tak
znajomi uważaję, że jest ze mną coś nie tak, że nie radzą sobie z SPSS
Wszyscy się patrzą na mnie, kiedy używam SPSS

1

2

3

4

Składowa

Metoda wyodrębniania czynników - Głównych składowych.
Metoda rotacji - Varimax z normalizacją Kaisera.

Rotacja osiągnęła zbieżność w 9 iteracjach.

a.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Końcowy etap analizy

Końcowy etap analizy

czynnikowej

czynnikowej



Po wyodrębnieniu grupy powiązanych

Po wyodrębnieniu grupy powiązanych

ze sobą zmiennych trzeba nadać im

ze sobą zmiennych trzeba nadać im

znaczenie – należy określić, jaki

znaczenie – należy określić, jaki

konstrukt psychologiczny łączy te

konstrukt psychologiczny łączy te

powiązane ze sobą pozycje skali.

powiązane ze sobą pozycje skali.