Testowanie hipotez

Testowanie hipotez

Na przykładzie testu t dla 1

Na przykładzie testu t dla 1

próby

próby

Proces analizy danych

Proces analizy danych



Statystyka opisowa – wstępny proces

Statystyka opisowa – wstępny proces

analizy danych

analizy danych



Statystyka inferencyjna

Statystyka inferencyjna

–

pozwala na wyciąganie wniosków z

pozwala na wyciąganie wniosków z

danych

danych

–

możemy na podstawie próby

możemy na podstawie próby

wnioskować o populacji

wnioskować o populacji

Statystyki i parametry

Statystyki i parametry

s

s

X

,

,

2







,

,

2

Statystyki na poziomie próby

Parametry w populacji

Statystyki w próbie są estymatorami odpowiednich parametrów w populacji

Etapy testowania hipotez

Etapy testowania hipotez



Stawiamy hipotezę badawczą

Stawiamy hipotezę badawczą



Zbieramy dane

Zbieramy dane



Stawiamy hipotezę zerową

Stawiamy hipotezę zerową



Konstruujemy rozkład prawdopodobieństwa

Konstruujemy rozkład prawdopodobieństwa

otrzymania takiego wyniku przy założeniu,

otrzymania takiego wyniku przy założeniu,

że hipoteza zerowa jest prawdziwa

że hipoteza zerowa jest prawdziwa



Porównujemy wynik uzyskany z rozkładem

Porównujemy wynik uzyskany z rozkładem



Znajdujemy prawdopodobieństwo

Znajdujemy prawdopodobieństwo

uzyskania takiego wyniku

uzyskania takiego wyniku



Podejmujemy decyzję o odrzuceniu bądź

Podejmujemy decyzję o odrzuceniu bądź

nie hipotezy zerowej.

nie hipotezy zerowej.

Testowanie hipotez i

Testowanie hipotez i

istotność statystyczna

istotność statystyczna



Stawiamy hipotezy

Stawiamy hipotezy

–

o różnicy między warunkami eksperymentalnymi.

o różnicy między warunkami eksperymentalnymi.

–

o związkach między zmiennymi.

o związkach między zmiennymi.



Zbieramy dane na ich poparcie

Zbieramy dane na ich poparcie



Jakie jest prawdopodobieństwo, że uzyskany przez nas

Jakie jest prawdopodobieństwo, że uzyskany przez nas

związek między zmiennymi, czy różnica jest dziełem

związek między zmiennymi, czy różnica jest dziełem

przypadku, błędu próbkowania?

przypadku, błędu próbkowania?



Im mniejsze to prawdopodobieństwo, tym bardziej

Im mniejsze to prawdopodobieństwo, tym bardziej

pewni jesteśmy, wniosku o występowaniu rzeczywistych

pewni jesteśmy, wniosku o występowaniu rzeczywistych

różnic na poziomie populacji

różnic na poziomie populacji

Prawdopodobieństwo

Prawdopodobieństwo



W procentach,

W procentach,

–

95%, że trafię w 10, > 5% że nie trafię

95%, że trafię w 10, > 5% że nie trafię

–

W rzutach kostkami 50% szans, że parzysta

W rzutach kostkami 50% szans, że parzysta



Ułamkach

Ułamkach

–

95/100 =0,95

95/100 =0,95

–

50% = 0,5

50% = 0,5

–

10% = 0,1

10% = 0,1

–

1% = 0,01

1% = 0,01

Testowanie hipotez

Testowanie hipotez



Testowanie naszych hipotez

Testowanie naszych hipotez

–

sprawdzamy, czy uzyskane przez nas wyniki

sprawdzamy, czy uzyskane przez nas wyniki

nie są czasem wynikiem przypadku

nie są czasem wynikiem przypadku

–

Poznamy narzędzia – testy statystyczne,

Poznamy narzędzia – testy statystyczne,

które pozwolą nam przetestować postawione

które pozwolą nam przetestować postawione

hipotezy

hipotezy



Ważne, żeby zrozumieć o co chodzi w procesie

Ważne, żeby zrozumieć o co chodzi w procesie

testowania hipotez

testowania hipotez

–

Inaczej nawet, jeśli będziemy umieć wykonywać

Inaczej nawet, jeśli będziemy umieć wykonywać

mechanicznie różne testy statystyczne, to będziemy mieć

mechanicznie różne testy statystyczne, to będziemy mieć

trudności w interpretowaniu wyników, wydruków z SPSS

trudności w interpretowaniu wyników, wydruków z SPSS

Podstawy testowania

Podstawy testowania

hipotez

hipotez



Ogólne założenia, kroki przy testowaniu

Ogólne założenia, kroki przy testowaniu

hipotez są takie same niezależnie od

hipotez są takie same niezależnie od

tego, jakie analizy statystyczne później

tego, jakie analizy statystyczne później

stosujemy

stosujemy



Logika wyciągania wniosków jest taka

Logika wyciągania wniosków jest taka

sama

sama

–

Szukamy sposobu na podjęcie decyzji czy

Szukamy sposobu na podjęcie decyzji czy

zaobserwowane przez nas prawidłowości są

zaobserwowane przez nas prawidłowości są

wynikiem przypadku czy też rzeczywiście

wynikiem przypadku czy też rzeczywiście

występują

występują

Hipoteza zerowa

Hipoteza zerowa



Podstawowy konstrukt przy testowaniu

Podstawowy konstrukt przy testowaniu

hipotez, przy podejmowaniu decyzji czy

hipotez, przy podejmowaniu decyzji czy

nasze różnice są istotne

nasze różnice są istotne



Dlaczego stawiamy hipotezę, która jest

Dlaczego stawiamy hipotezę, która jest

zaprzeczeniem tego, co chcemy udowodnić?

zaprzeczeniem tego, co chcemy udowodnić?

–

Ponieważ nigdy nie możemy udowodnić, że coś

Ponieważ nigdy nie możemy udowodnić, że coś

jest prawdą, ale możemy wykazać, że coś jest

jest prawdą, ale możemy wykazać, że coś jest

fałszem

fałszem



Wszystkie biedronki mają czarne kropki

Wszystkie biedronki mają czarne kropki



Wystarczy wskazać jeden przypadek sprzeczny z

Wystarczy wskazać jeden przypadek sprzeczny z

tym stwierdzeniem, aby je obalić

tym stwierdzeniem, aby je obalić

Czyli zaczynamy od

Czyli zaczynamy od

hipotezy zerowej –

hipotezy zerowej –

wnioskujemy nie wprost

wnioskujemy nie wprost



Zaczynamy od założenia, że nie ma

Zaczynamy od założenia, że nie ma

związku między zmiennymi lub nie ma

związku między zmiennymi lub nie ma

różnic między porównywanymi grupami

różnic między porównywanymi grupami

–

Hipoteza zerowa zawsze mówi o braku

Hipoteza zerowa zawsze mówi o braku

związku między zmiennymi/ o braku różnicy

związku między zmiennymi/ o braku różnicy

–

Jeśli chcemy sprawdzić związek między

Jeśli chcemy sprawdzić związek między

liczbą kłamstw polityków a czasem do

liczbą kłamstw polityków a czasem do

wyborów zakładamy najpierw:

wyborów zakładamy najpierw:



Brak związku między.......

Brak związku między.......

Poziom istotności, alfa, p

Poziom istotności, alfa, p



Jeśli, zakładając prawdziwość Ho, poziom

Jeśli, zakładając prawdziwość Ho, poziom

istotności uzyskaliśmy mniejszy niż 5%

istotności uzyskaliśmy mniejszy niż 5%

(0,05) – to nasz wynik jest istotny

(0,05) – to nasz wynik jest istotny

–

5% prawdopodobieństwo, że wyniki są

5% prawdopodobieństwo, że wyniki są

przypadkowe – jest wystarczające, żeby

przypadkowe – jest wystarczające, żeby

odrzucić Ho

odrzucić Ho

–

Alfa – prawdopodobieństwo, że uzyskalibyśmy

Alfa – prawdopodobieństwo, że uzyskalibyśmy

takie wyniki, przy założeniu, że Ho jest

takie wyniki, przy założeniu, że Ho jest

prawdziwa

prawdziwa



Nie jest to prawdopdobieństwo, że Ho jest prawdziwa

Nie jest to prawdopdobieństwo, że Ho jest prawdziwa

Jeśli poziom istotności:

Jeśli poziom istotności:

0,0

0,05

Odrzucamy Ho

Brak podstaw do odrzucenia Ho

Wnioskowanie statystyczne

Wnioskowanie statystyczne



Możemy wykorzystać

Możemy wykorzystać

testy statystyczne

testy statystyczne

do

do

oszacowania prawdopodobieństwa, że

oszacowania prawdopodobieństwa, że

uzyskane w badaniu wyniki są przypadkowe

uzyskane w badaniu wyniki są przypadkowe

–

(że np. różnica między grupą kontrolną a

(że np. różnica między grupą kontrolną a

eksperymentalną jest przypadkowa, czy też, że

eksperymentalną jest przypadkowa, czy też, że

związek między dwiema zmiennymi wynikiem

związek między dwiema zmiennymi wynikiem

błędu)

błędu)



Jeśli to prawdopodobieństwo jest małe,

Jeśli to prawdopodobieństwo jest małe,

można wnioskować, że różnica (czy też

można wnioskować, że różnica (czy też

związek) nie jest przypadkowa i rzeczywiście

związek) nie jest przypadkowa i rzeczywiście

występuje

występuje

Wnioski...

Wnioski...



Co to znaczy

Co to znaczy

istotna różnica (to samo

istotna różnica (to samo

odnosi się do korelacji)

odnosi się do korelacji)

–

Prawdopodobieństwo przypadkowego

Prawdopodobieństwo przypadkowego

uzyskania tych wyników było tak małe,

uzyskania tych wyników było tak małe,

że więcej sensu miało stwierdzenie, że

że więcej sensu miało stwierdzenie, że

wyniki pochodzą z różnych populacji,

wyniki pochodzą z różnych populacji,

czyli przyjęcie naszej hiptezy badawczej

czyli przyjęcie naszej hiptezy badawczej



Co to znaczy

Co to znaczy

brak podstaw do

brak podstaw do

odrzucenia hipotezy zerowej?.......

odrzucenia hipotezy zerowej?.......

witax

witax



Sprawdź, czy wzrost dzieci, które

Sprawdź, czy wzrost dzieci, które

regularnie łykały witaminy Witax są

regularnie łykały witaminy Witax są

istotnie wyższe od innych dzieci w

istotnie wyższe od innych dzieci w

tym wieku.

tym wieku.



Średni wzrost dzieci w tym wieku

Średni wzrost dzieci w tym wieku

wynosi 140 cm.

wynosi 140 cm.

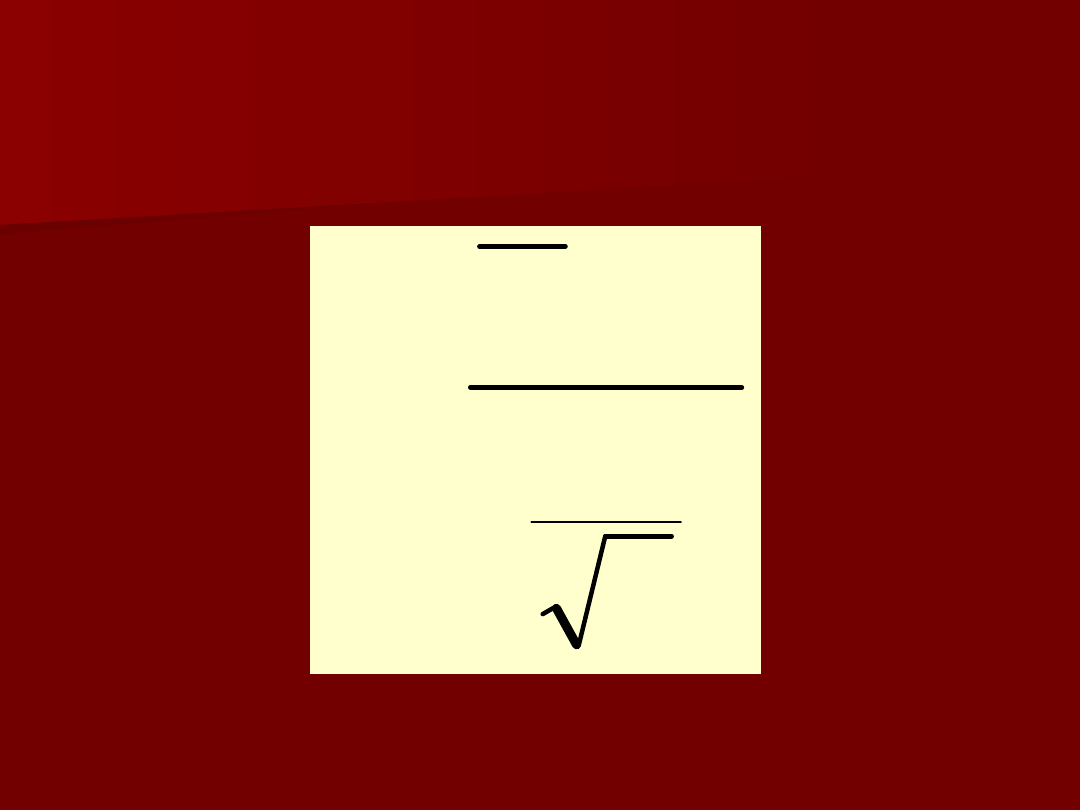
wzór

wzór

n

s

X

t







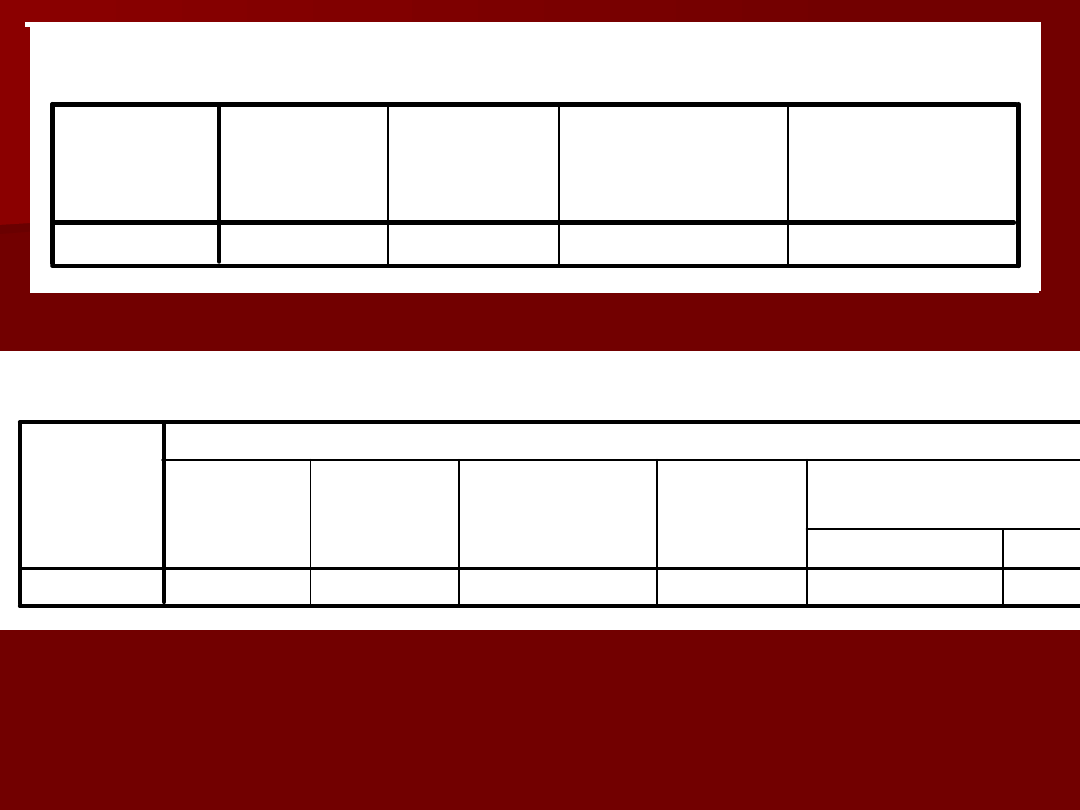
Statystyki dla jednej próby

15 133,4667

11,70999

3,02351

WZROST

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

-2,161

14

,049

-6,5333

-13,0181

-,0486

WZROST

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 140

Stopnie swobody

Stopnie swobody



Dla testu t dla 1 próby

Dla testu t dla 1 próby

df

df

=

=

n

n

- 1

- 1



Jest to związane z oszacowywaniem odchylenia

Jest to związane z oszacowywaniem odchylenia

standardowego w populacji na podstawie próby

standardowego w populacji na podstawie próby

t

t



Obliczamy odchylenie standardowe na

Obliczamy odchylenie standardowe na

podstawie średniej, wiemy, że suma odchyleń

podstawie średniej, wiemy, że suma odchyleń

od średniej zawsze = 0. Jak losujemy próbkę, to

od średniej zawsze = 0. Jak losujemy próbkę, to

wyniki mogą być dowolne, oprócz ostatniego,

wyniki mogą być dowolne, oprócz ostatniego,

aby to własność średniej została spełniona

aby to własność średniej została spełniona

Podejmując decyzję

Podejmując decyzję



Kiedy dochodzimy do wyciągania

Kiedy dochodzimy do wyciągania

wniosków przy testowaniu hipotez

wniosków przy testowaniu hipotez

możemy mieć rację, albo się mylić

możemy mieć rację, albo się mylić

–

Błąd I rodzaju

Błąd I rodzaju

α

α

(alfa)

(alfa)



Odrzucamy Ho wtedy, kiedy jest prawdziwa

Odrzucamy Ho wtedy, kiedy jest prawdziwa



Równy jest poziomowi istotności

Równy jest poziomowi istotności

–

Błąd II rodzaju

Błąd II rodzaju

β

β

(beta)

(beta)



Nie odrzucamy Ho wtedy kiedy jest fałszywa

Nie odrzucamy Ho wtedy kiedy jest fałszywa

Rodzaje błędów przy

Rodzaje błędów przy

wnioskowaniu

wnioskowaniu

Ho

prawdziwa

Ho

fałszywa

Nie odrzucamy Ho





Błąd II rodzaju

Odrzucamy Ho



Błąd I rodzaju



Hipotezy kierunkowe i

Hipotezy kierunkowe i

niekierunkowe

niekierunkowe



Kierunkowa hipoteza :

Kierunkowa hipoteza :

–

Przewidujemy nie tylko, że grupy (np.

Przewidujemy nie tylko, że grupy (np.

eksperymentalne i kontrolna) będą się

eksperymentalne i kontrolna) będą się

od siebie różniły, ale również kierunek

od siebie różniły, ale również kierunek

tej różnicy

tej różnicy



Niekierunkowa hipoteza

Niekierunkowa hipoteza

–

Przewidujemy tylko, że wystąpią różnice,

Przewidujemy tylko, że wystąpią różnice,

nic nie mówimy o kierunku zależności

nic nie mówimy o kierunku zależności

Testy jednostronne i

Testy jednostronne i

dwustronne

dwustronne



Przy hipotezie niekierunkowej

Przy hipotezie niekierunkowej

–

Test dwustronny

Test dwustronny



Przy hipotezie kierunkowej

Przy hipotezie kierunkowej

–

Test jednostronny

Test jednostronny

–

W praktyce, chociaż stawiamy hipotezy

W praktyce, chociaż stawiamy hipotezy

kierunkowe testujemy je dwustronnie,

kierunkowe testujemy je dwustronnie,

odchodzi się od testowania hipotez

odchodzi się od testowania hipotez

jednostronnie, ponieważ łatwiej wykazać w

jednostronnie, ponieważ łatwiej wykazać w

nich istotność

nich istotność

jedno i dwustronne testy

jedno i dwustronne testy



Dwustronny test pozwala na odrzucenie

Dwustronny test pozwala na odrzucenie

hipotezy zerowej, jeśli otrzymujemy

hipotezy zerowej, jeśli otrzymujemy

wartość, która jest zbyt skrajna

wartość, która jest zbyt skrajna

–

Niezależnie od znaku

Niezależnie od znaku



Test jednostronny odrzucamy hipotezę

Test jednostronny odrzucamy hipotezę

zerową jeśli nasza wartość jest zbyt

zerową jeśli nasza wartość jest zbyt

wysoka (zbyt niska)

wysoka (zbyt niska)

–

Obieramy sobie tylko jeden z krańców

Obieramy sobie tylko jeden z krańców

rozkładu do odrzucenia hipotezy zerowej

rozkładu do odrzucenia hipotezy zerowej

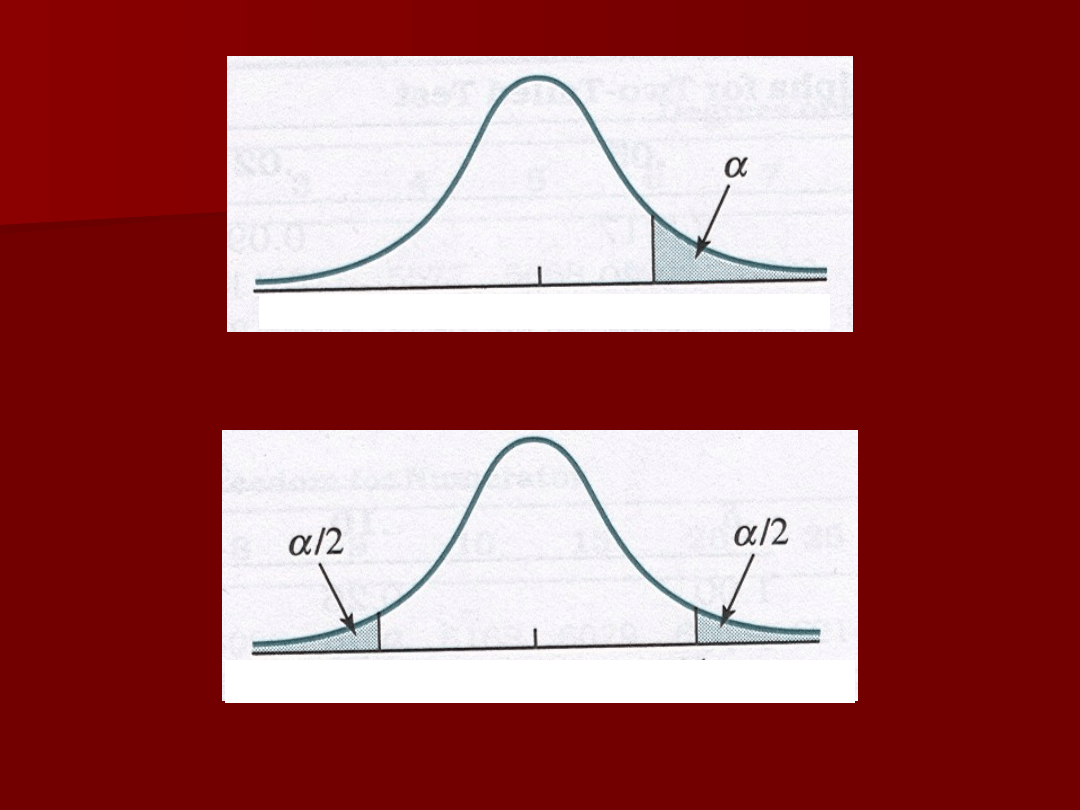
Obszary odrzucenia hipotezy zerowej



Jeśli otrzymaliśmy poziom istotności dla testu

Jeśli otrzymaliśmy poziom istotności dla testu

dwustronnego, a chcemy znać

dwustronnego, a chcemy znać

prawdopodobieństwo dla testu jednostronnego,

prawdopodobieństwo dla testu jednostronnego,

wystarczy podzielić wartość poziomu istotności

wystarczy podzielić wartość poziomu istotności

na pół

na pół

–

np. p=0,03 dla dwustronnego to dla jednostronnego

np. p=0,03 dla dwustronnego to dla jednostronnego

p=0,015

p=0,015



Wartość statystyki t nie zmienia się, jedynie

Wartość statystyki t nie zmienia się, jedynie

prawdopodobieństwo

prawdopodobieństwo

Błędy wnioskowania

Błędy wnioskowania

statystycznego

statystycznego



Błąd I rodzaju –

Błąd I rodzaju –

α

α

(alfa)

(alfa)

–

Odrzucenie hipotezy zerowej, gdy jest

Odrzucenie hipotezy zerowej, gdy jest

prawdziwa

prawdziwa

–

Równy poziomowi istotności

Równy poziomowi istotności



Błąd II rodzaju –

Błąd II rodzaju –

β

β

(beta)

(beta)

–

Nie odrzucenie hipotezy zerowej mimo,

Nie odrzucenie hipotezy zerowej mimo,

że jest fałszywa

że jest fałszywa