Dwuczynnikowa analiza

wariancji

cd.

Wykład 5

Pytanie z terminu A

• Pewien socjolog interesował się wpływem

światła i hałasu na efektywność pracy
kominiarzy. Tabela 3 przedstawia średnią
efektywność pracy w porównywanych
grupach. Wybierz prawidłową odpowiedź.

– Jest efekt główny światła
– Jest efekt główny hałasu
– Nie ma efektów głównych
– Są oba efekty główne

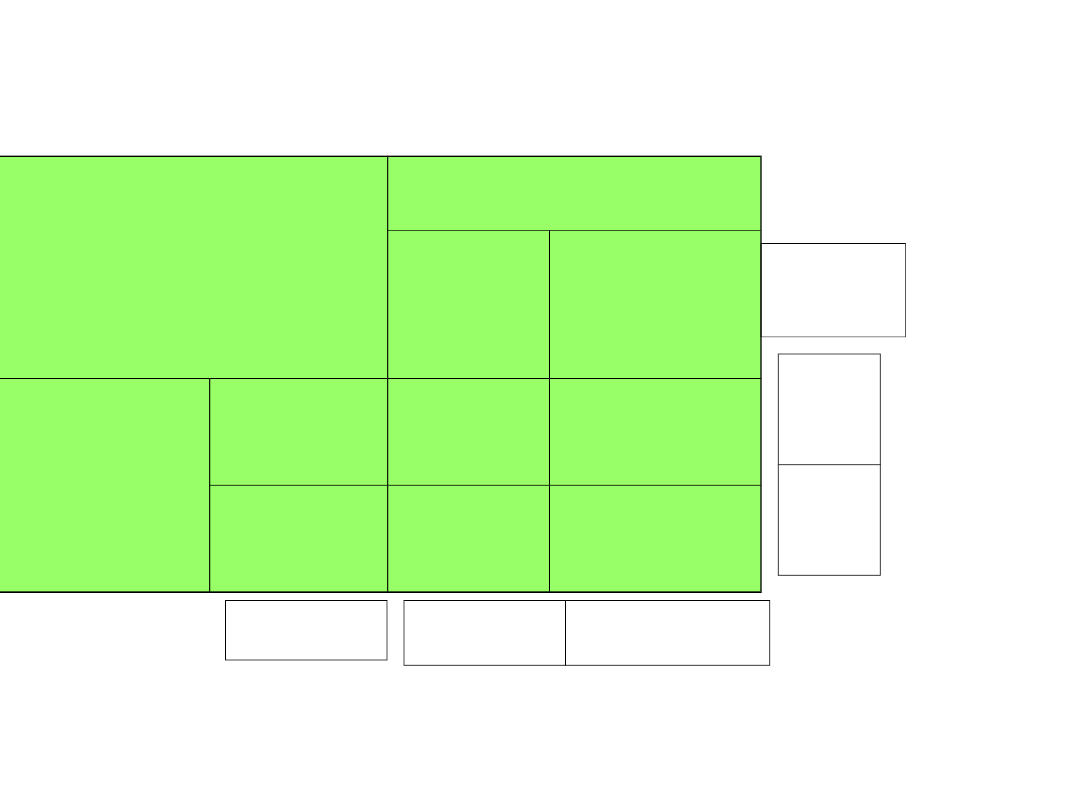
Tabela 3

Zmienne

niezależne

hałas

niski wysok

i

światł

o

silne 50

20

słabe 30

60

35

45

Średnia

40

40

Średnia

• Pewien socjolog interesował się wpływem

światła i hałasu na efektywność pracy

kominiarzy. Tabela 3 przedstawia średnią

efektywność pracy w porównywanych

grupach. Sprawdź czy jest efekt interakcji

między tymi zmiennymi.

– Brak efektu interakcji
– Jest efekt interakcji
– Są oba efekty interakcji
– Jest interakcja nieskrzyżowana

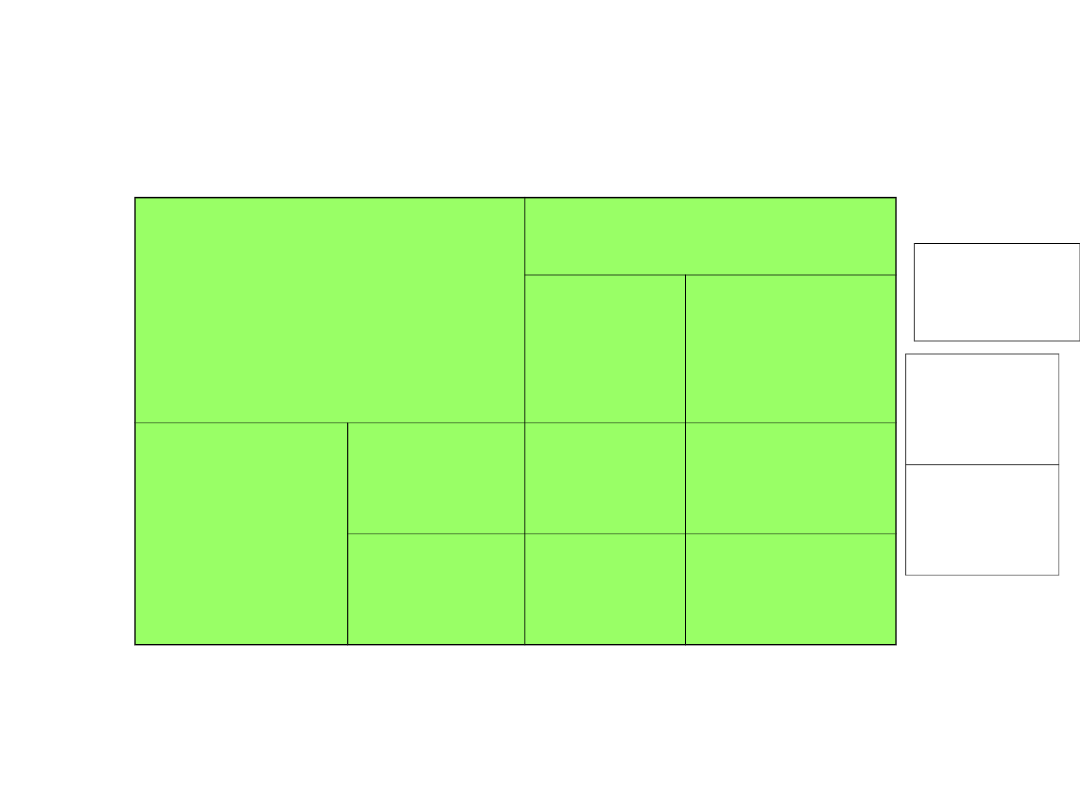
Tabela 3

Zmienne
niezależne

hałas

niski wysok

i

światł
o

silne 50

20

słabe 30

60

30

-30

Różnica
wierszy

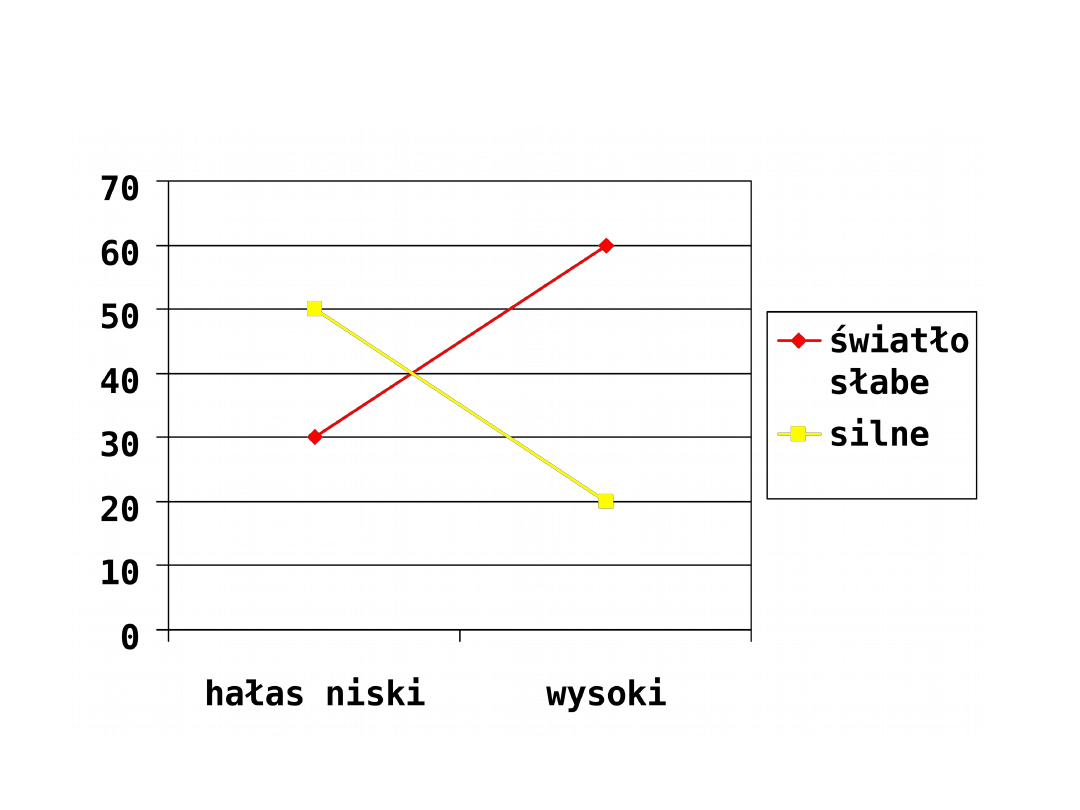
Można sporządzić wykres

Procesy uwagi

Analiza efektów prostych

Procesy selektywnej uwagi a

wiek

Zmienne niezależne

WIEK

MŁODSI

STARSI

ZADANI

E

Pojedyncze

Podwójne

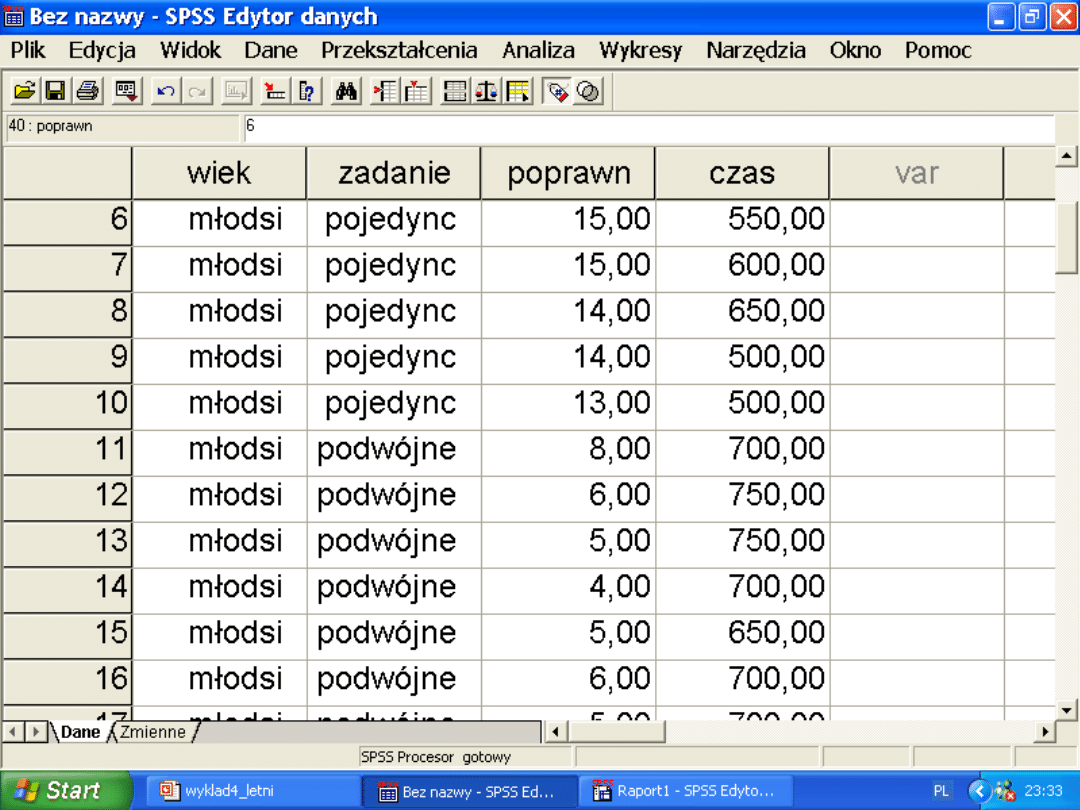
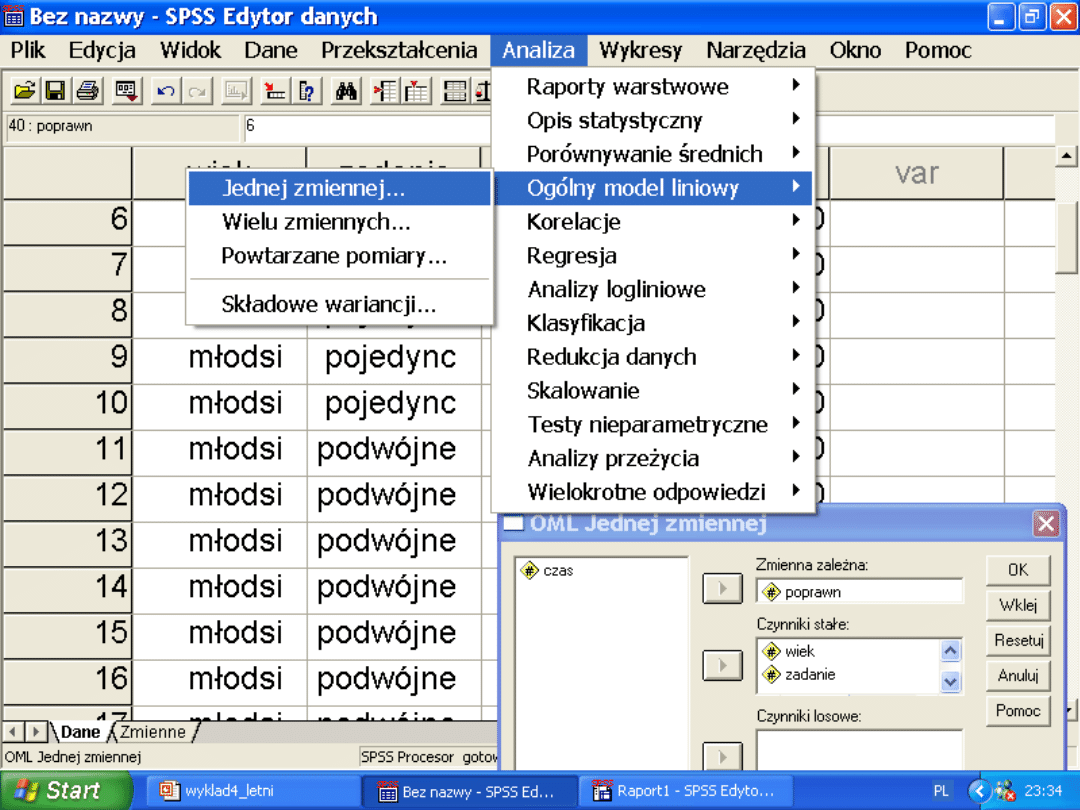
Uproszczona tabelka

Testy efektów międzyobiektowych

Zmienna zależna: POPRAWN

,900

1 ,900 1,227 ,275

656,10

1 656,1 894,7 ,000

2,500

1 2,500 3,409 ,073

26,400

36 ,733

685,90

39

Źródło zmienności
WIEK

ZADANIE

WIEK * ZADANIE

Błąd

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Wariancja nie wyjaśniona – błędu wykorzystywana w mianowniku każdej
statystyki F

Testy F w dwuczynnikowej

ANOVie

• W dwuczynnikowej analizie wariancji mamy do czynienia z

trzema testami F:

– 1) dla efektu głównego pierwszego czynnika

– 2) dla efektu głównego drugiego czynnika

– 3) dla efektu interakcyjnego

• W liczniku każdego z tych stosunków znajdzie się wariancja

międzygrupowa, która odnosi się do porównań między

średnimi dla danego efektu głównego lub interakcyjnego

• Natomiast wariancja wewnątrzgrupowa we wszystkich

trzech testach F będzie taka sama - jest to zawsze średnia

oszacowań wariancji w populacji utworzona z wyników

wewnątrz każdej z celek (wariancja błędu)

Stopnie

swobody

ZN

2

poziomow

liczba

-

ZN

1

poziomow

liczba

-

)

1

(

)

1

(

interakcji

efekt

1

1

glowne

efekty

2

1

2

1

12

2

2

1

1

k

k

k

k

df

k

df

k

df

















Stopnie

swobody cd.

ZN

1

poziomow

liczba

-

celce

w

osób

liczba

-

badaniu

w

osób

liczba

-

1

)

1

(

bledu

1

2

1

2

1

k

n

N

N

df

ogolem

n

k

k

df

k

k

N

df

o

bledu

bledu













Testy efektów międzyobiektowych

Zmienna zależna: POPRAWN

659,50

a

3 219,8 299,8 ,000

4040,1

1 4040 5509 ,000

,900

1 ,900 1,227 ,275

656,10

1 656,1 894,7 ,000

2,500

1 2,500 3,409 ,073

26,400

36 ,733

4726,0

40

685,90

39

Źródło zmienności
Model skorygowany

Stała

WIEK

ZADANIE

WIEK * ZADANIE

Błąd

Ogółem

Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,962 (Skorygowane R kwadrat = ,958)

a.

Pełna tabelka

Istotny efekt główny zmiennej Zadanie F(1,36)=894,7; p<0,001

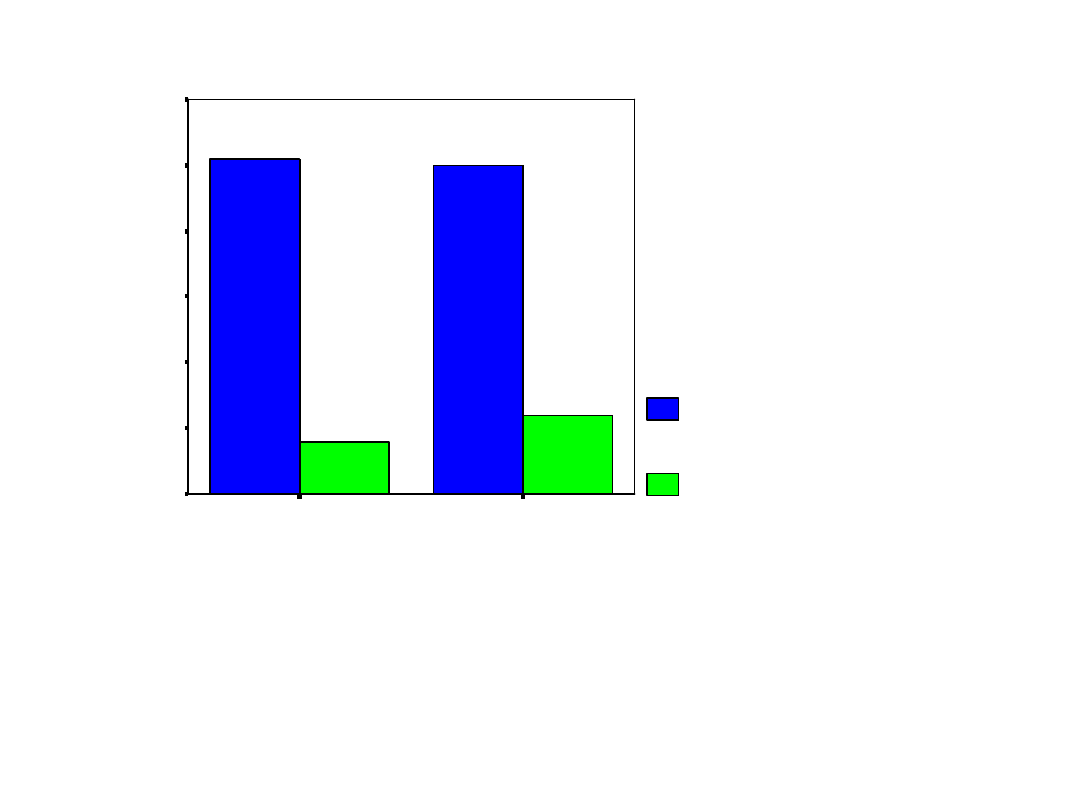
Oszacowane średnie brzegowe - POPRAWN

WIEK

starsi

młodsi

16

14

12

10

8

6
4

ZADANIE

pojedyncze

podwójne

Niezależnie od wieku badani, lepiej wykonywali zadanie pojedyncze.
Poprawność wykonania zadania spadała przy wprowadzeniu obciążenia poznawczego

Testy efektów międzyobiektowych

Zmienna zależna: CZAS

453500,0

a

3 151167 60,133

,000

1,8E+07

1 2,E+07 7142,7

,000

342250,0

1 342250 136,144

,000

81000,00

1

81000 32,221

,000

30250,00

1

30250 12,033

,001

90500,00

36 2513,9

1,9E+07

40

544000,0

39

Źródło zmienności
Model skorygowany
Stała
WIEK
ZADANIE
WIEK * ZADANIE
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,834 (Skorygowane R kwadrat = ,820)

a.

Czas wykonania głównego

zadania

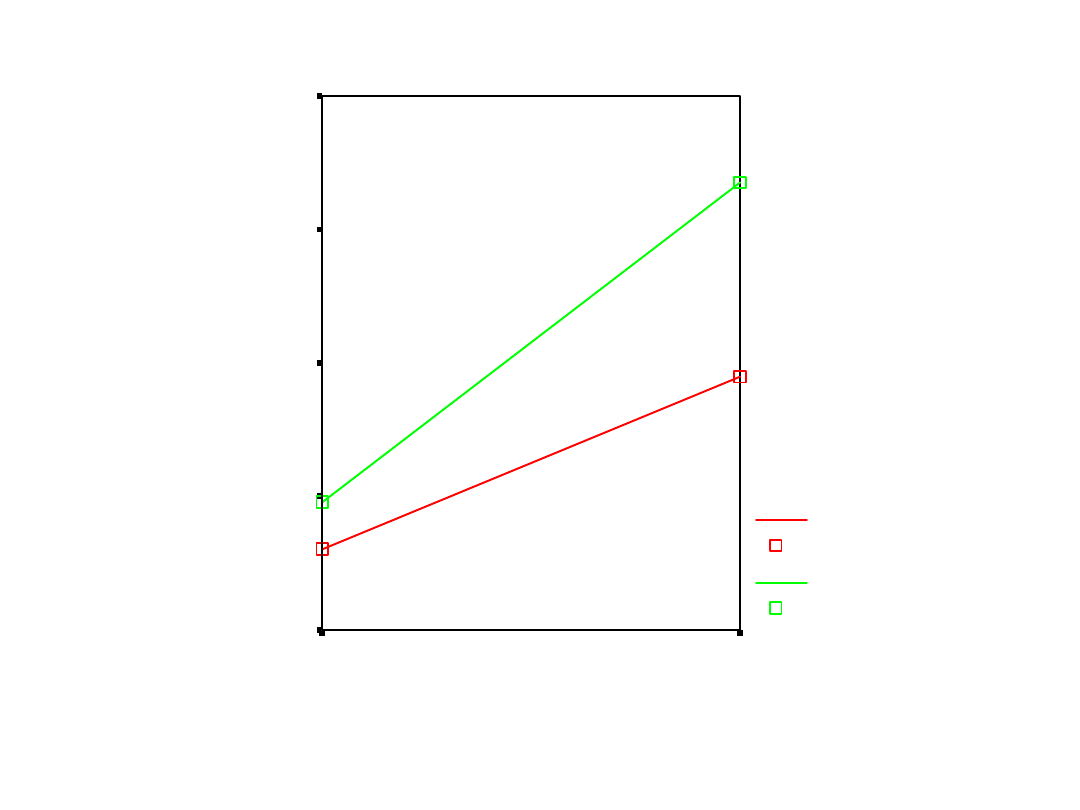
Oszacowane średnie brzegowe - CZAS

WIEK

starsi

młodsi

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

ZADANIE

pojedyncze

podwójne

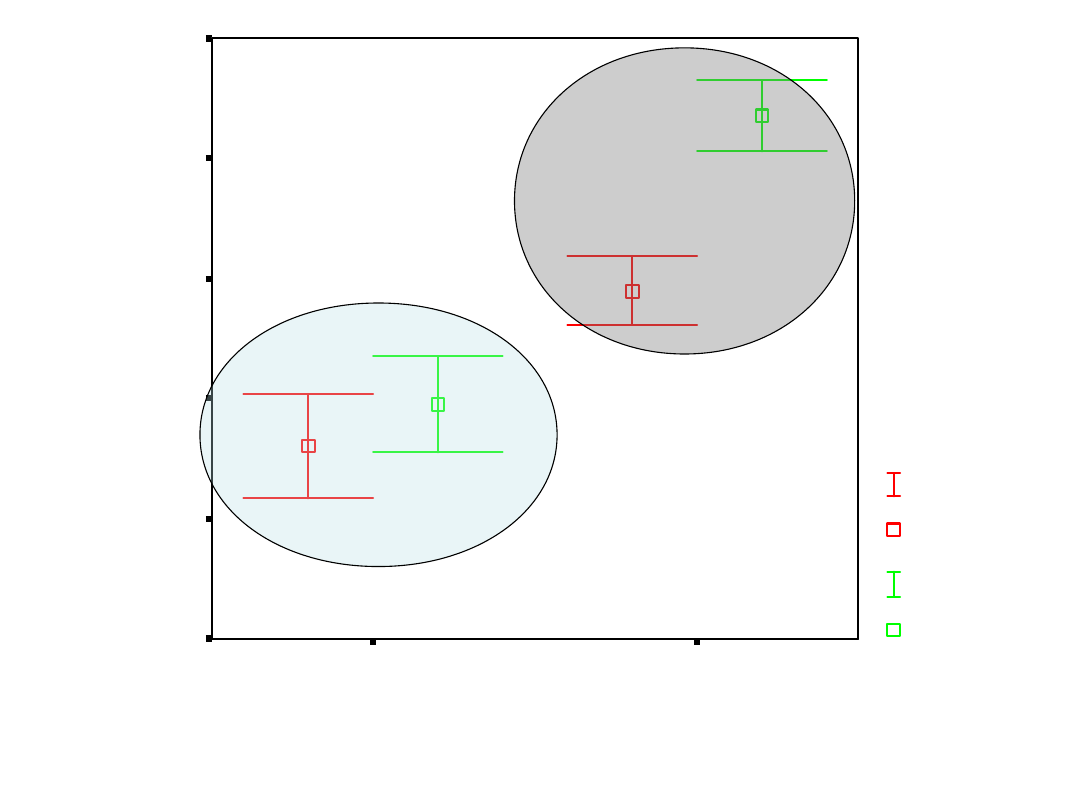
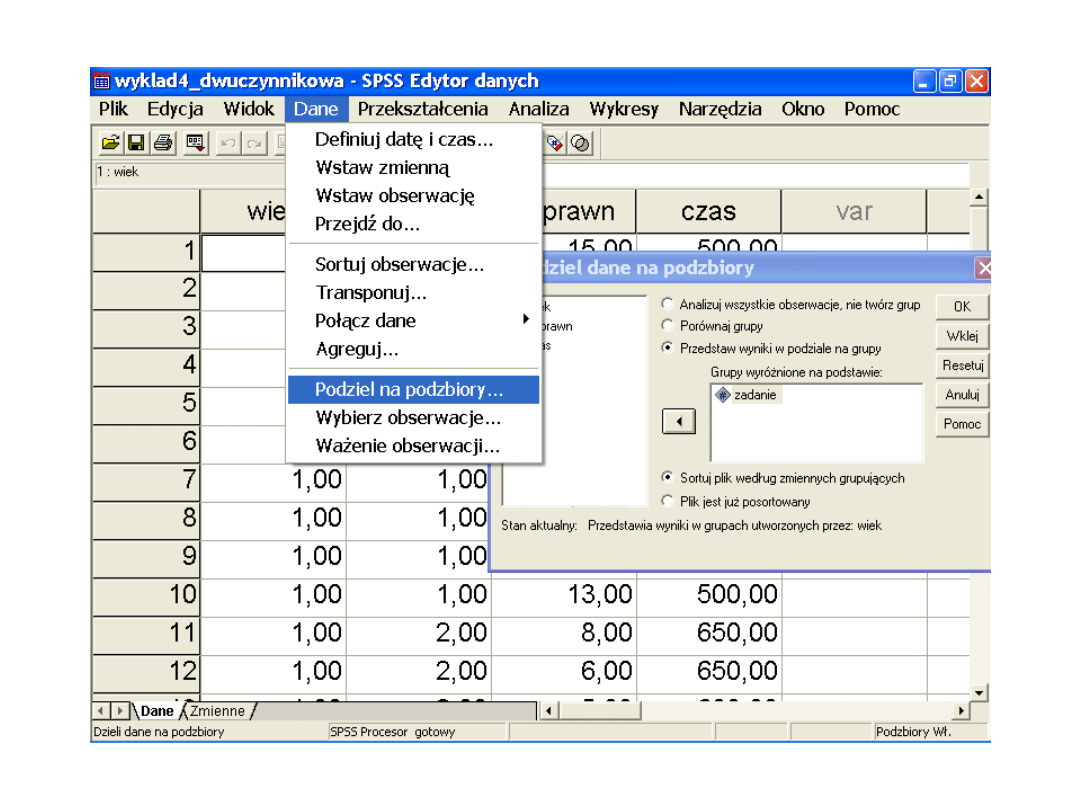
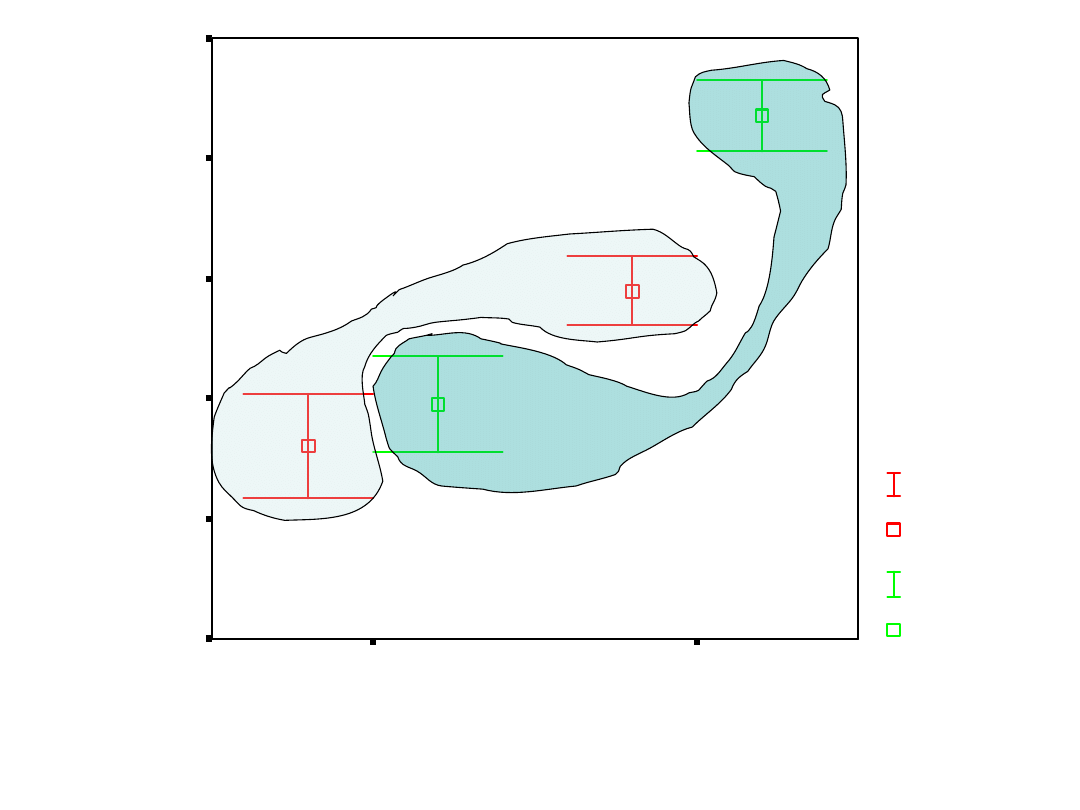
Jeśli efekt interakcji jest istotny

• Patrzymy na efekty proste, szukamy,

które grupy różnią się między sobą

istotnie

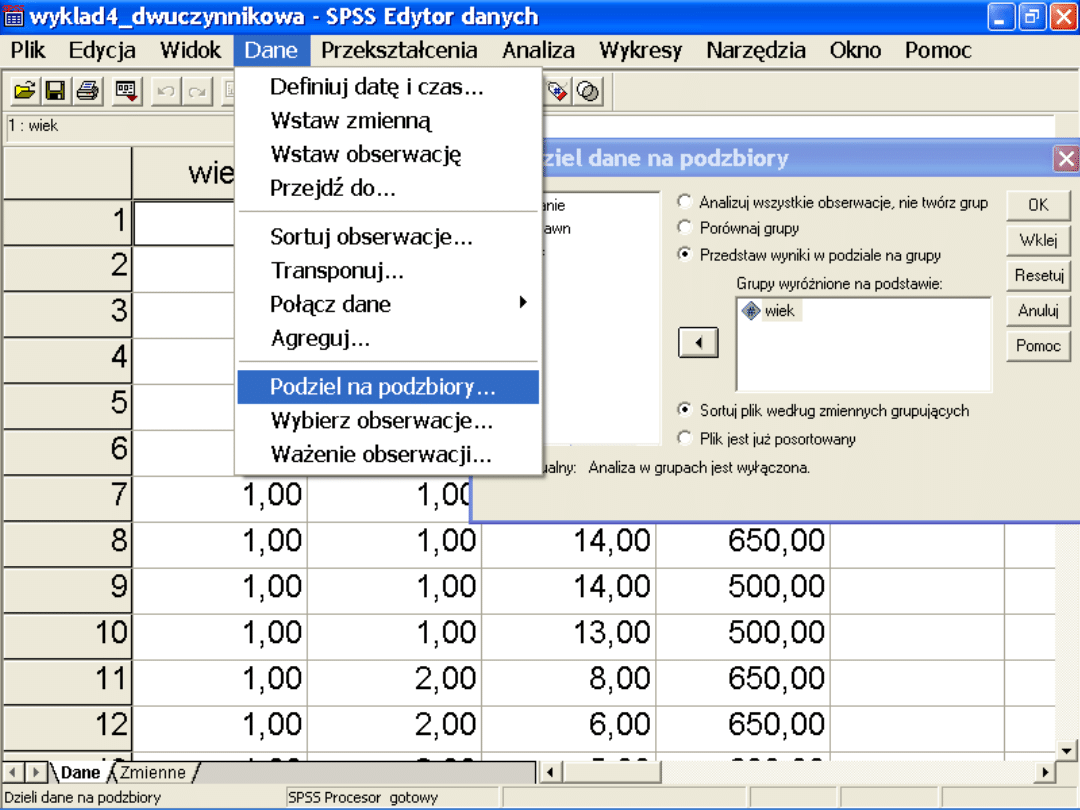
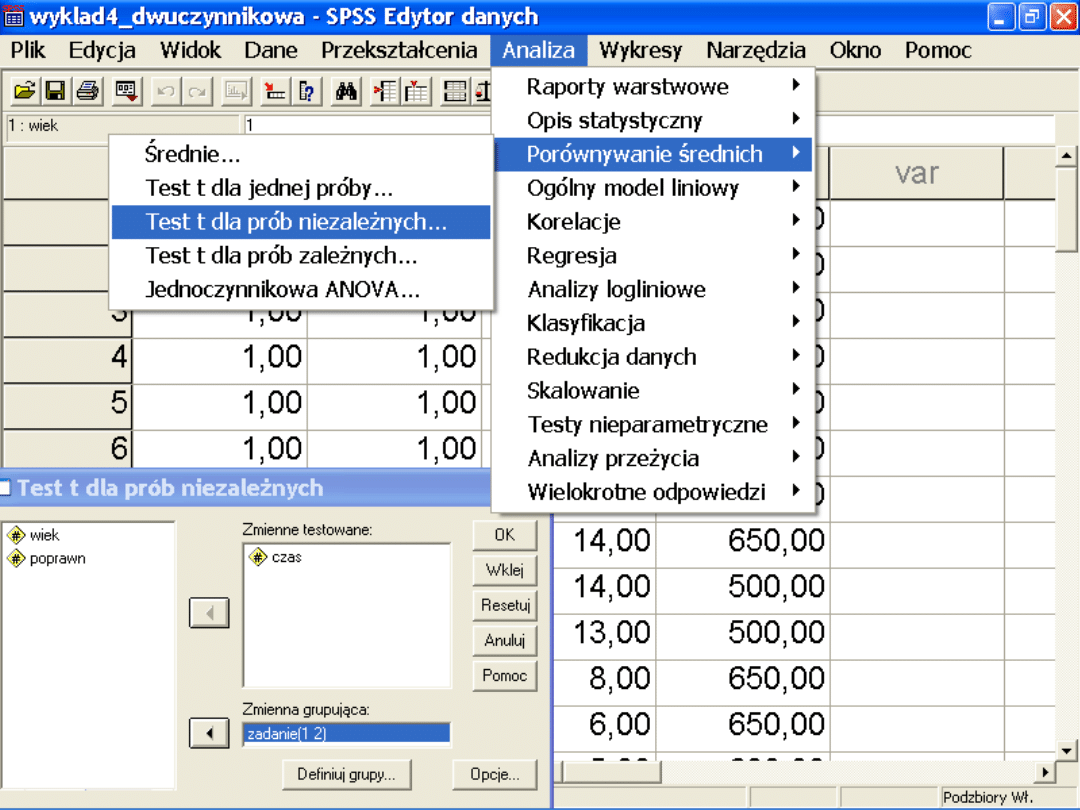
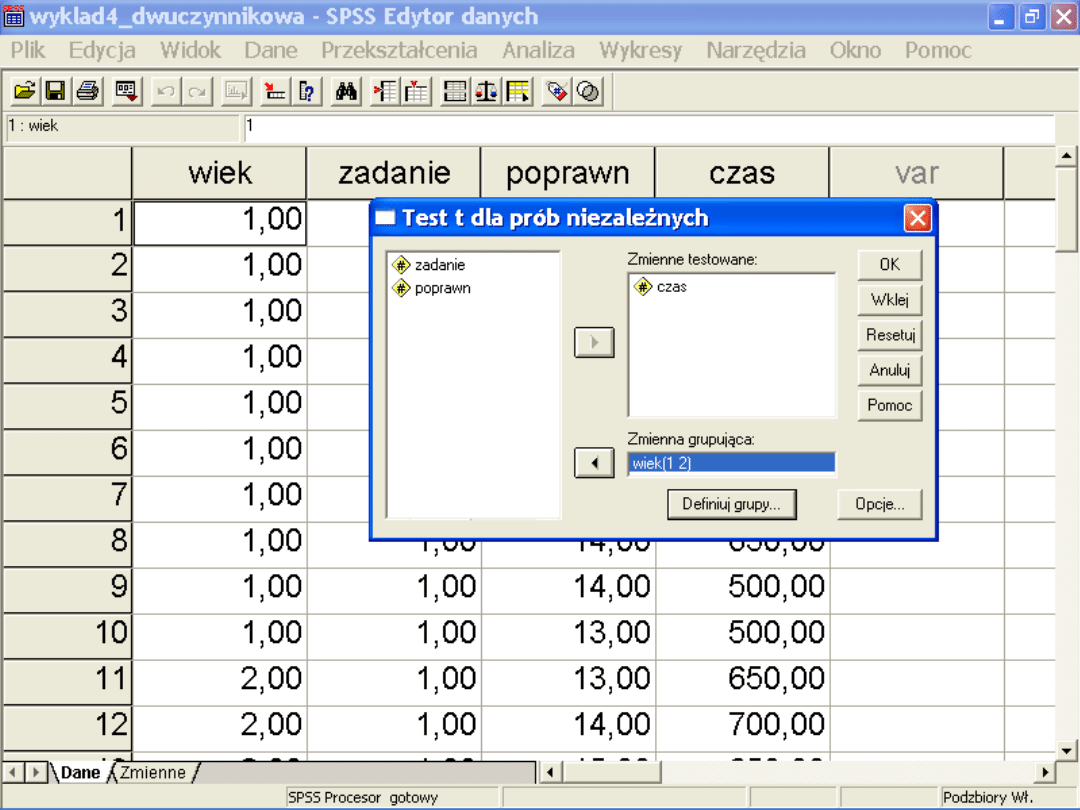
– Możemy przeprowadzić analizy testami t

dla grup niezależnych wykorzystując

opcję podziel na podzbiory.

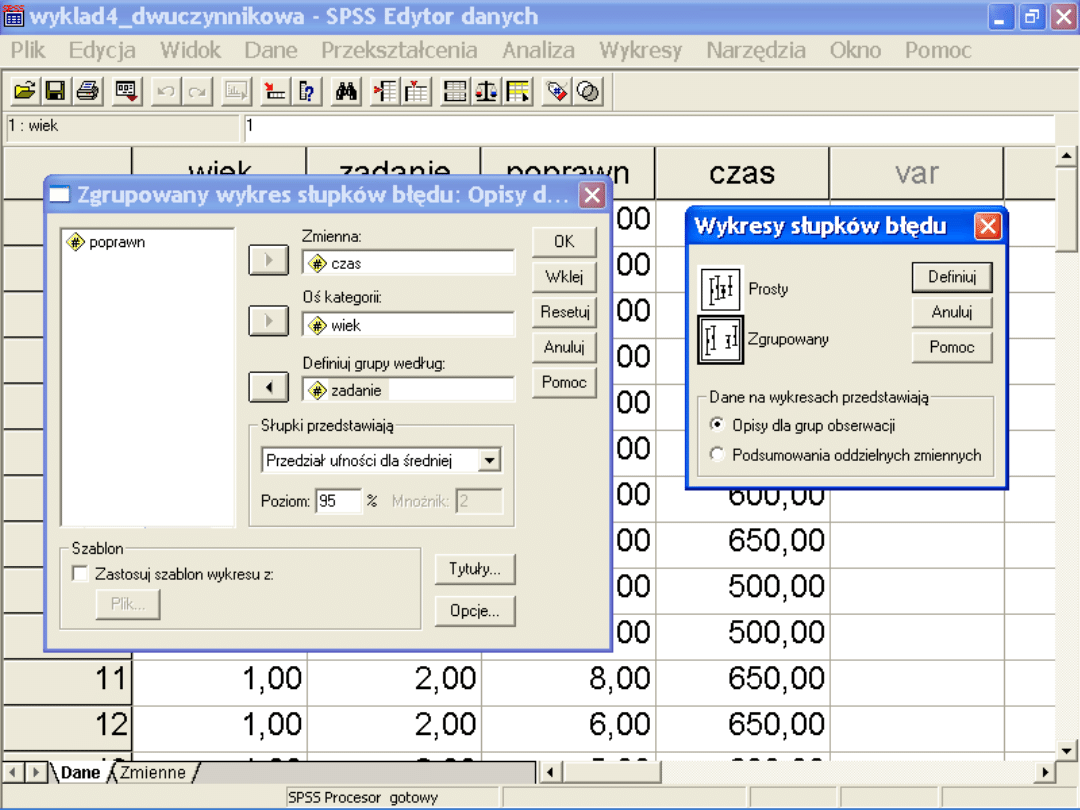
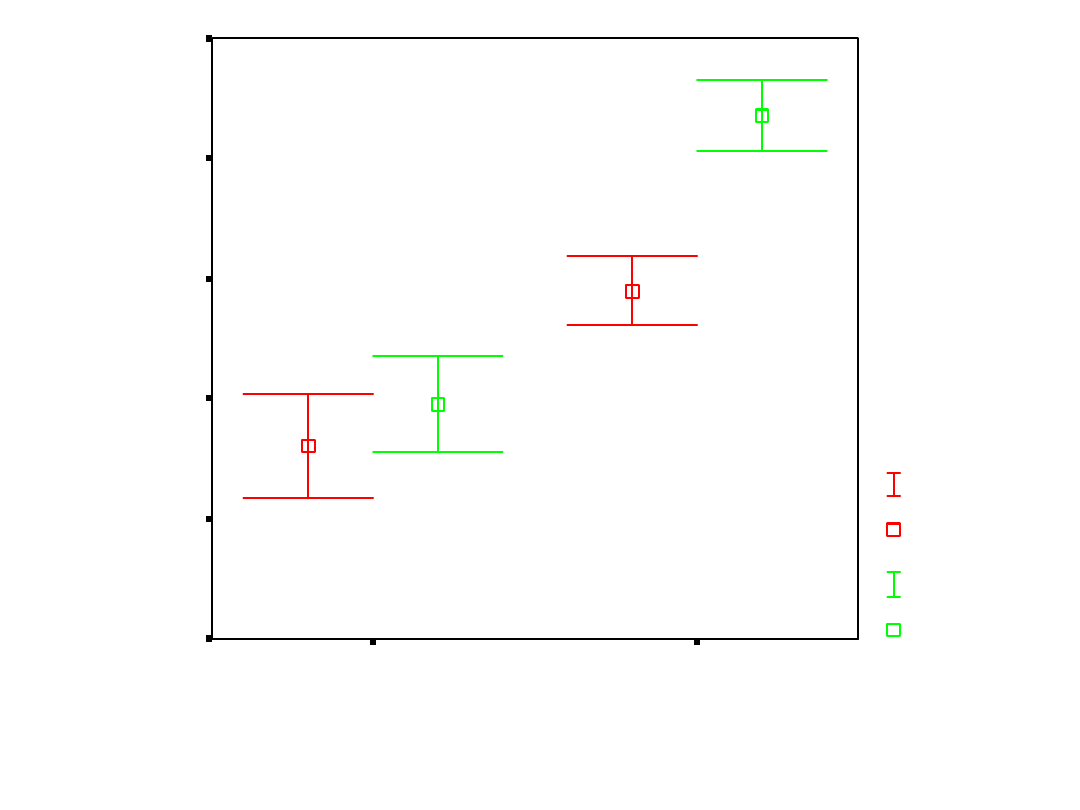
– Lub spojrzeć na wykresy słupków błędu
– Lub skorzystać z pakietu statystycznego

Statistica (pełna gama porównań)

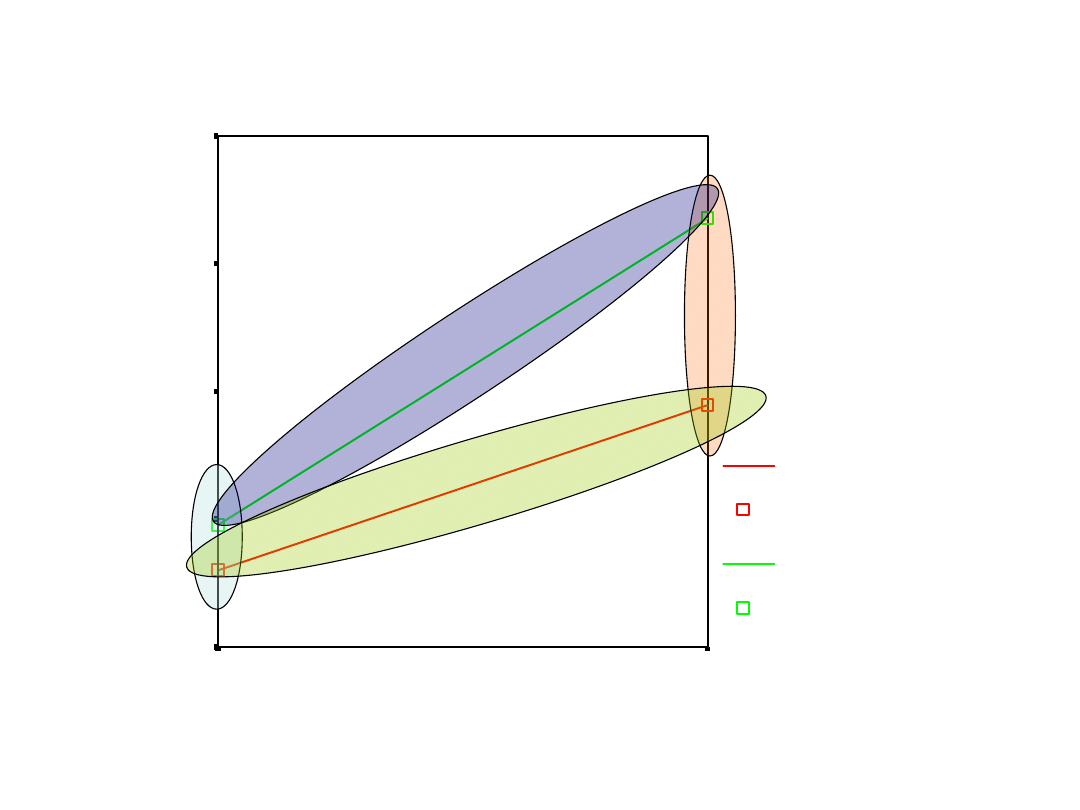
Oszacowane średnie brzegowe - CZAS

WIEK

starsi

młodsi

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

900

800

700

600

500

ZADANIE

pojedyncze

podwójne

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

Test dla prób niezależnych

a

,892

,357 -1,34

18

,196 -35,0 26,0875 -89,808 19,8077

-1,34 17,78

,197 -35,0 26,0875 -89,855 19,8555

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

WIEK = młodsi

a.

Test dla prób niezależnych

a

,120

,733 -8,043

18

,000 -145,0 18,0278-182,8749 -107,1251

-8,043 17,967

,000 -145,0 18,0278-182,8799 -107,1201

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

WIEK = starsi

a.

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

Test dla prób niezależnych

a

3,358

,083 -5,629

18

,000 -130,0 23,0940-178,5187 -81,4813

-5,629 15,337

,000 -130,0 23,0940-179,1296 -80,8704

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

ZADANIE = pojedyncze

a.

Test dla prób niezależnych

a

,051

,823 -11,04

18

,000 -240,0 21,7307-285,6545 -194,3455

-11,04 16,671

,000 -240,0 21,7307-285,9168 -194,0832

Założono równość
wariancji
Nie założono
równości wariancji

CZAS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

ZADANIE = podwójne

a.

10

10

10

10

N =

WIEK

starsi

młodsi

95

%

P

U

C

Z

A

S

900

800

700

600

500

400

ZADANIE

pojedyncze

podwójne

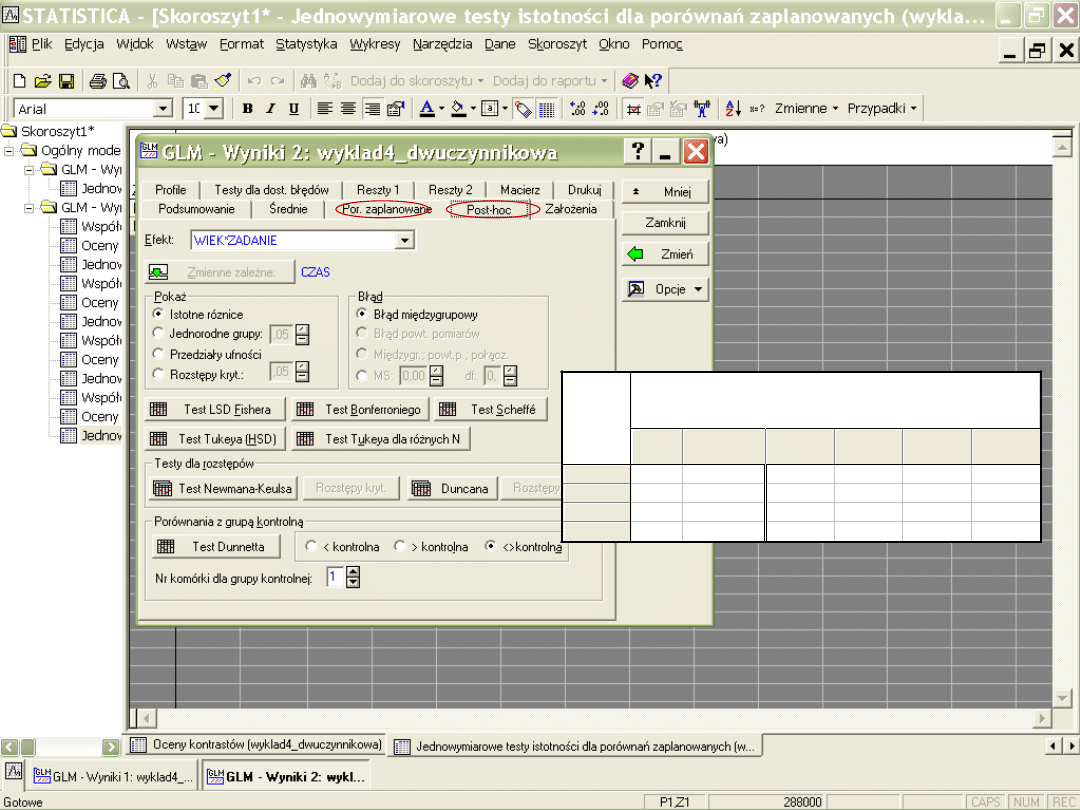
Te st B o nfe ro ni e go ; z m ie nna C ZAS ( wykla d4_ dwuc z ynniko wa )
Pra wdo po do bi e ńst wa dl a t e stó w po st -ho c
B łą d: M S m ię dz ygrupo we = 2513,9, df = 36,000

Nr po dkl.

WIEKZADANIE{1}

560,00

{2}

595,00

{3}

690,00

{4}

835,00

1
2
3
4

młodsi

po je dync z e 0,763753

0,000008

0,000000

młodsi

po dwó j ne

0,763753

0,000901

0,000000

st a rsi

po je dync z e

0,000008

0,000901

0,000001

st a rsi

po dwó j ne

0,000000

0,000000

0,000001

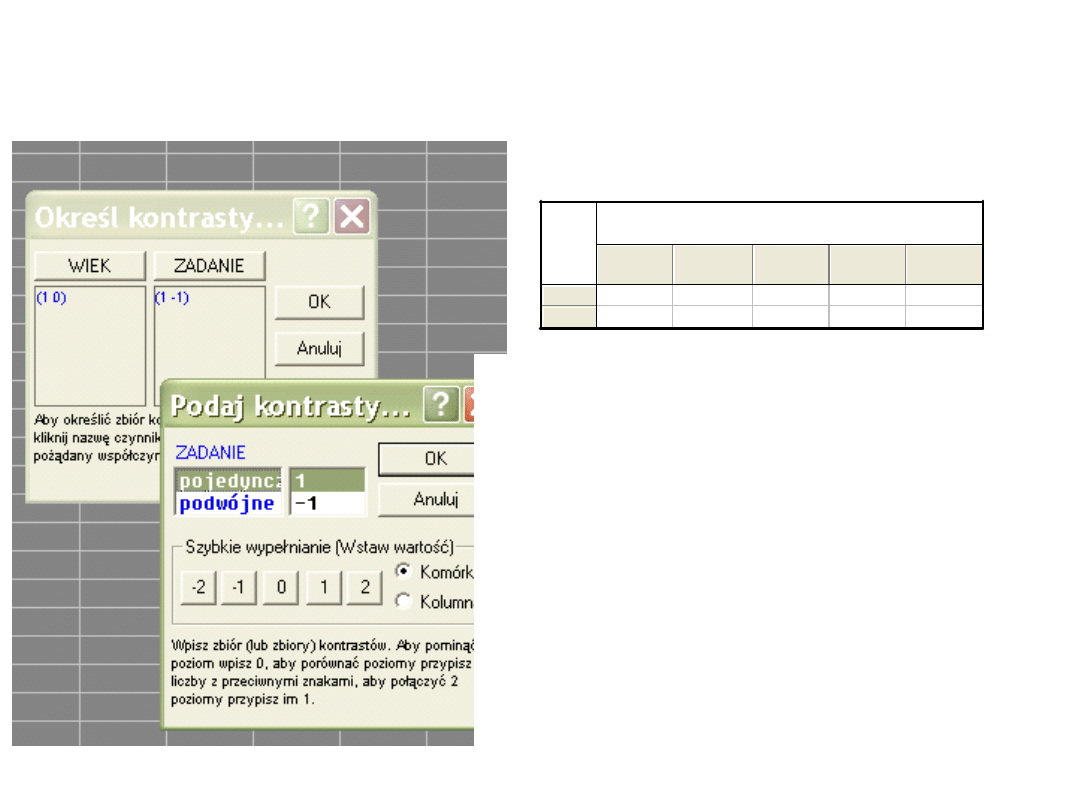
Kontrasty dla efektu

interakcyjnego w Statistice

Je dno wymia ro we te st y isto t no śc i dla po ró wna ń z a pla no wa nyc h ( wykl a d4_ dwuc z ynni ko wa )
Zmie nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S t o pnie

swo bo dy

Ś rednie

kwa dr.

F

p

Efe kt
B łą d

6125,00 1 6125,000

2,436464

0,127292

90500,00362513,889

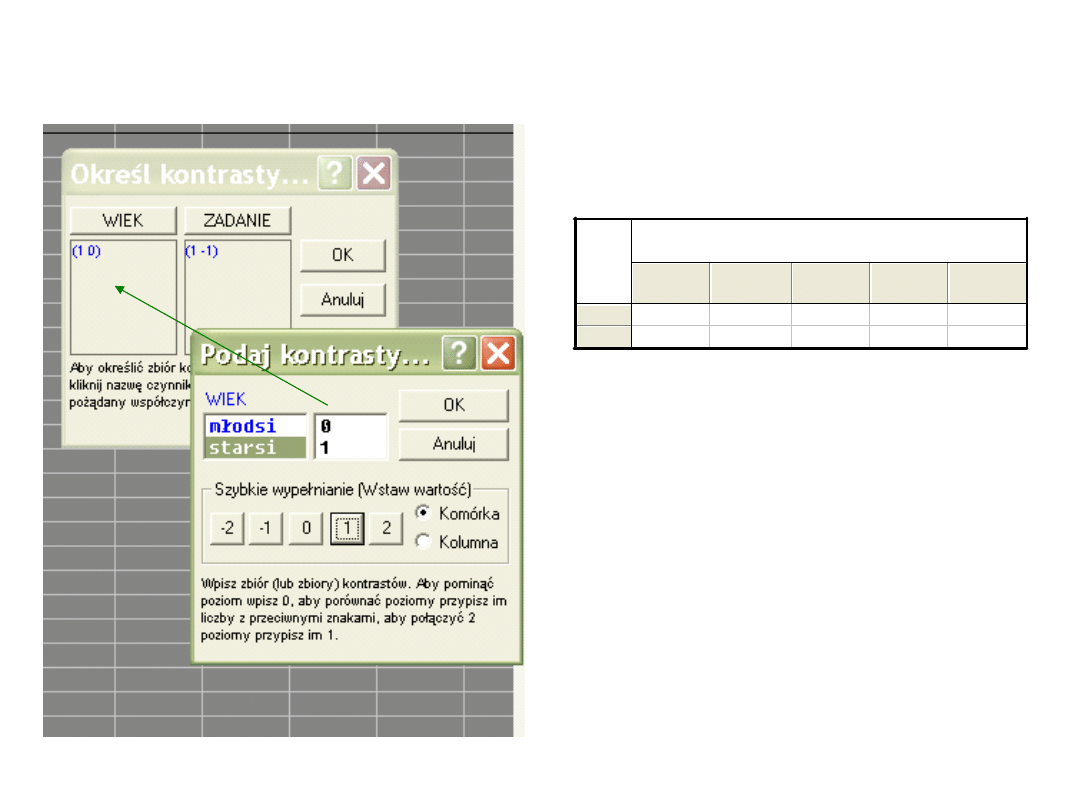
Czy wykonanie zadania
pojedynczego i podwójnego różni się
w grupie młodszych?

Wykluczamy z porównań grupę starszych (0),
młodsi dostają współczynnik (1)
i dla tej grupy przeprowadzamy kontrast
między zadaniem pojedynczym (1) i
podwójnym (-1)

Różnica jest nieistotne statystycznie

Je dno wymia ro we te st y isto t no śc i dla po ró wna ń z a pla no wa nyc h (wykla d4_ dwuc z ynniko wa )
Zmie nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś re dnie

kwa dr.

F

p

Efe kt
B łą d

105125,0 1 105125,0

41,81768

0,000000

90500,0 36 2513,9

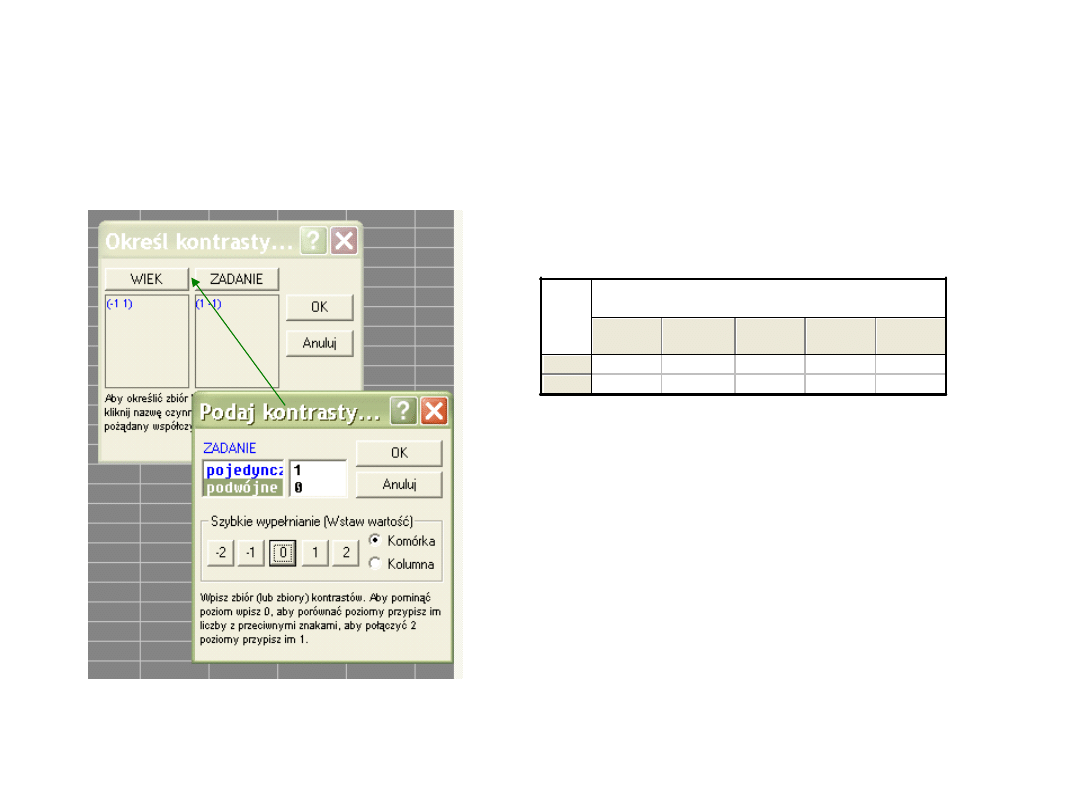
Zmieniamy współczynniki
kontrastu przy zmiennej wiek

Starsze osoby istotnie różnią się
wykonaniem zadania podwójnego i
pojedynczego

Je dno wymi a ro we te sty isto tno śc i dla po ró wna ń z a pla no wa nyc h (wykla d4_ dwuc z ynniko wa )
Zmi e nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś re dnie

kwa dr.

F

p

Efekt
B łą d

84500,00 1 84500,00

33,61326

0,000001

90500,0036 2513,89

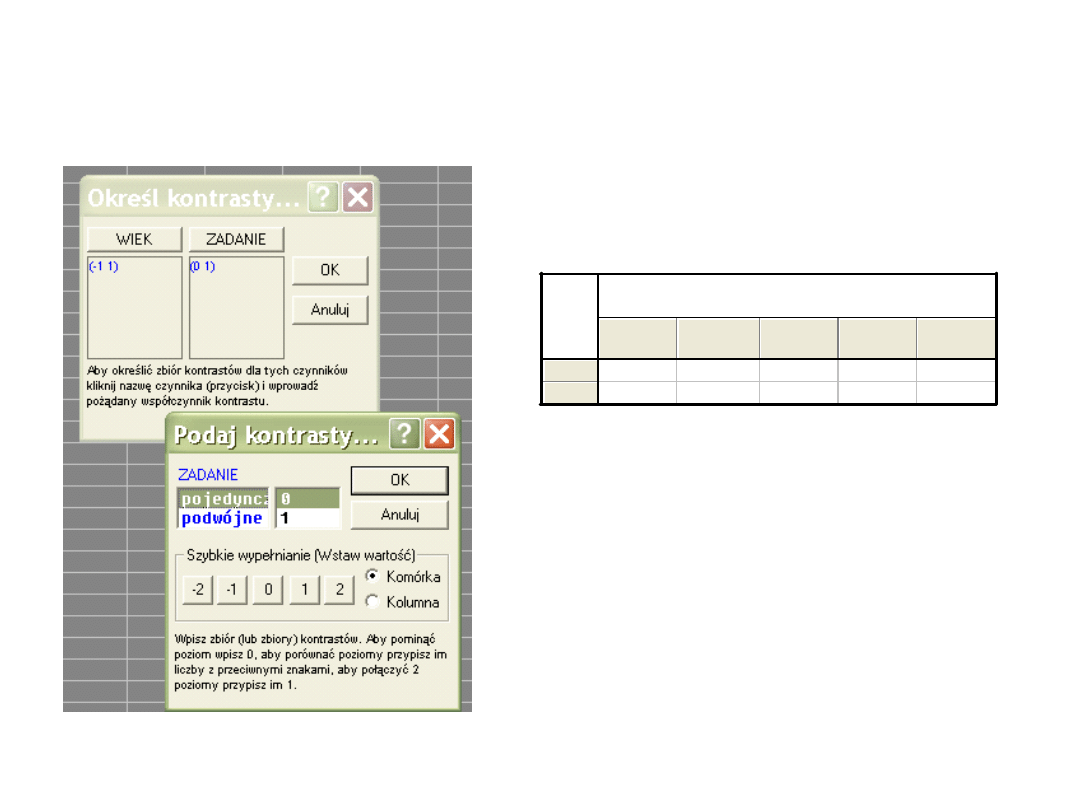
Tym razem chcemy porównać starszych i
młodszych w zadaniu pojedynczym,

Wynik kontrastu wskazuje na istotny efekt prosty

Jedno wymia ro we te sty isto tno śc i dla po ró wna ń z a pla no wa nyc h ( wykla d4_ dwuc z ynniko wa )
Zmi e nna z a le ż na : C ZAS

Źró dło

S uma

kwa dr.

S to pnie

swo bo dy

Ś rednie

kwa dr.

F

p

Efekt
B łą d

288000,0 1 288000,0

114,5635

0,000000

90500,0 36 2513,9

Czy są różnice między
starszymi i młodszymi w zadaniu podwójnym?

Liczba efektów prostych

• Liczba efektów prostych jest równa

sumie poziomów obu zmiennych
niezależnych.

– w planie 2x2 są 4 efekty proste;
– w planie 2 x 3 jest 5 efektów prostych

• Prof. Filutek analizował wyniki

eksperymentu dwuczynnikową

analizą wariancji w schemacie 3x3.

Ile efektów prostych będzie mógł

przeanalizować?

• 3
• 6
• 5
• 9

• Przy schemacie eksperymentalnym

2x3x3 z iloma zmiennymi
niezależnymi mamy do czynienia?

• 3
• 8
• 18
• 2

Zalety zaawansowanych

planów eksperymentalnych

• Możliwość większej generalizacji

wyników

– Patrzymy jednocześnie na wpływ dwóch

lub więcej zmiennych niezależnych na
interesującą nas zmienną zależną

– Możemy analizować efekty interakcyjne
– Ekonomia – za jednym razem

przeprowadzamy 4 eksperymenty w 1

Wprowadzenie do analizy

wariancji z powtarzanym

pomiarem

Zmienna niezależna wewnątrz

osób

Ta sama grupa kilkakrotnie

badana

Plan dla grup zależnych, z

powtarzanym pomiarem

• Główne zalety: mniejsza liczba

uczestników badania, mniej czasu do

przeprowadzenia badania,

– Odchodzi problem różnic indywidualnych

– redukcja niesystematycznej

zmienności

• Większa moc

• Nie jest to prawdziwy eksperyment

Nobody’s perfect = wady

• Nie da się już cofnąć wpływu manipulacji

eksperymentalnej

– Może to zmienić nastawienie do badania
– Uczestnicy nabywają wprawy w radzeniu sobie z

kolejnymi wymaganiami badania, uczą się

materiału eksperymentalnego

– Wielokrotne uczestniczenie w badaniu prowadzi

również do zmęczenia a w związku z tym do

pogorszenia wykonywania zadania

– Zmiany uczestników związane z dojrzewaniem

• Efekt kolejności

– Wyrównywanie kolejności warunków

Efekt twarzy w tłumie

Przykład eksperymentu z

powtarzanym pomiarem

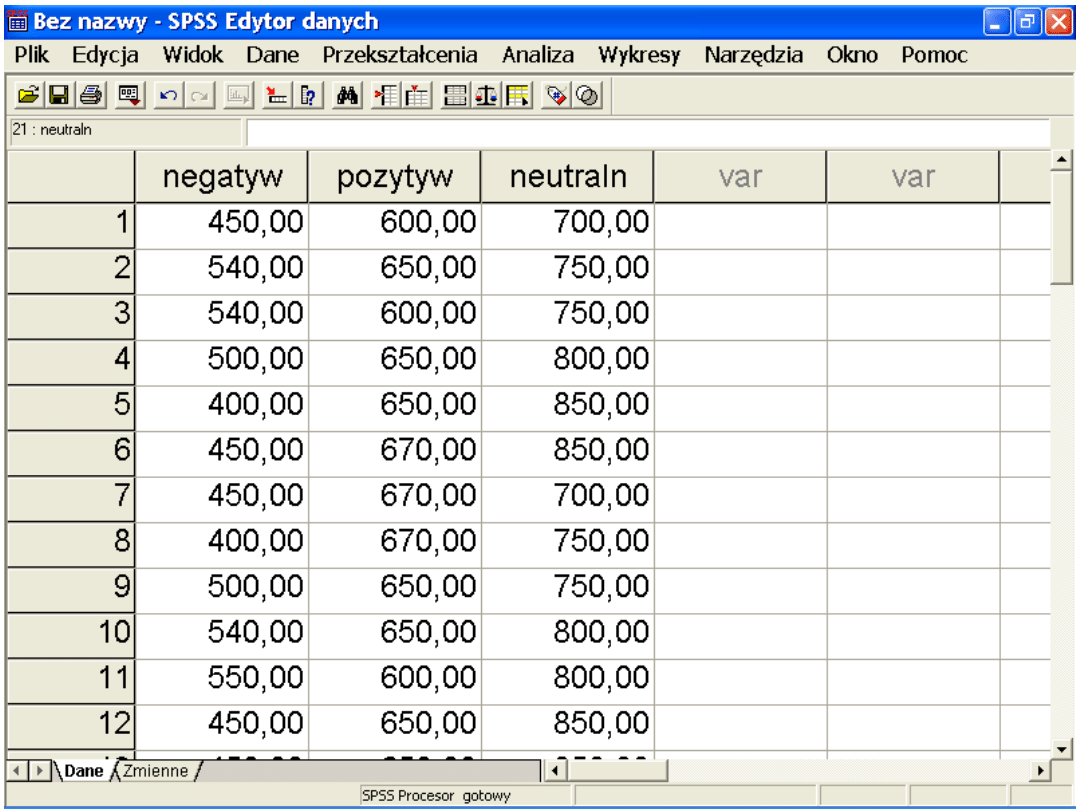
Opis badania

• Grupa 20 osób została poproszona o

wyszukiwanie wśród tłumu twarzy
tej, która nie pasowała do innych

– Wśród twarzy neutralnych – zagrażającej
– Wśród twarzy neutralnych – przyjaznej
– Wśród twarzy zagrażających – neutralnej

Założenia

• Zmienna zależna ma rozkład

normalny na każdym poziomie

czynnika

• Pomiary osób są niezależne od siebie,

losowa próbka z populacji

• Założenie o sferyczności

– Homogeniczność wariancji różnic

• Wariancje różnic obliczonych między 2

poziomami czynnika dla każdej z par są

podobne

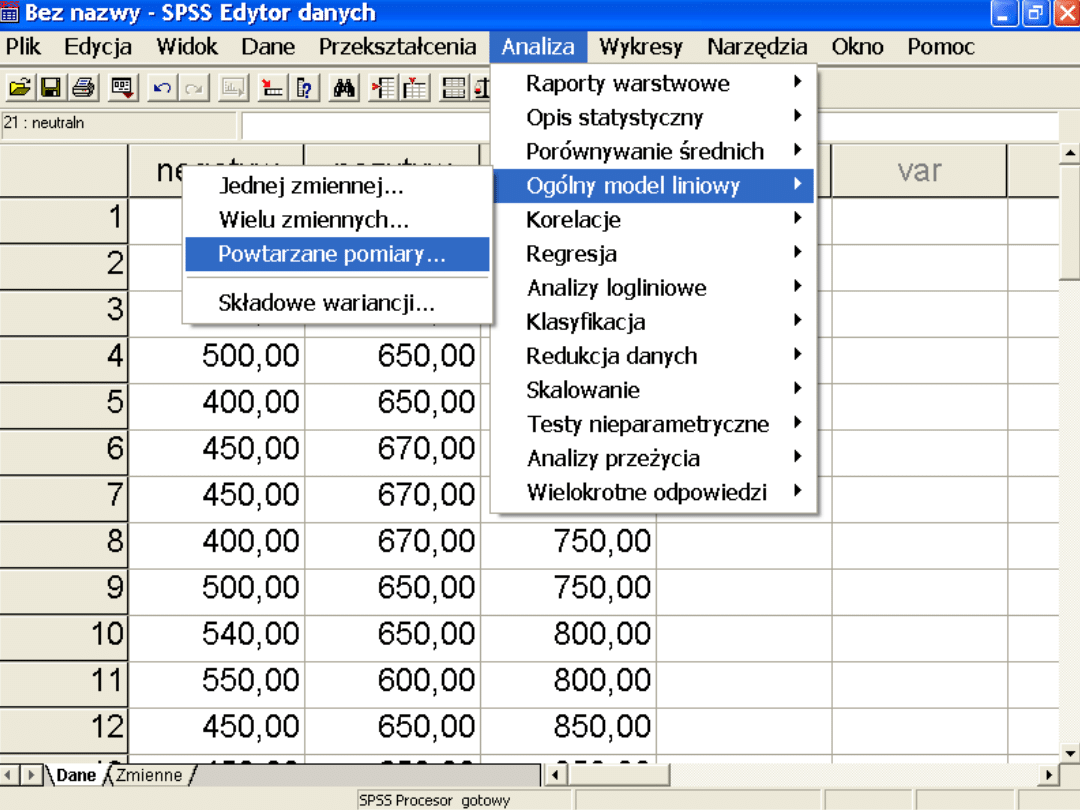
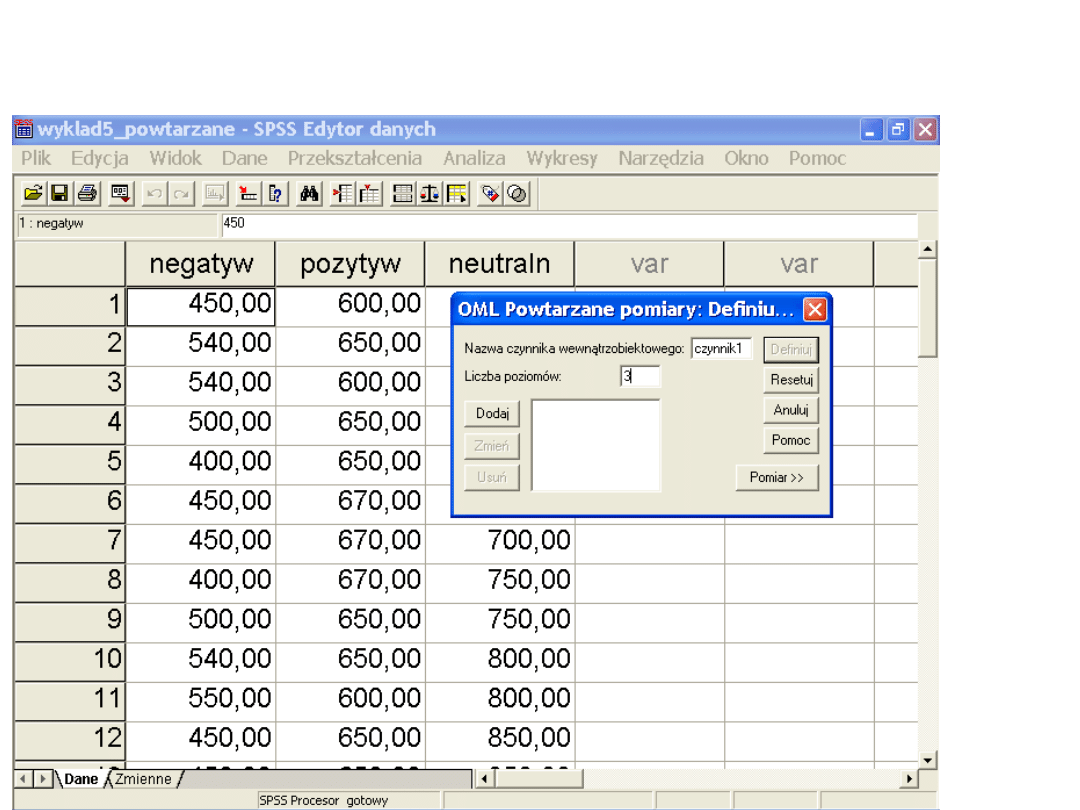
Definiujemy na ilu poziomach jest zmienna

niezależna (czynnik)

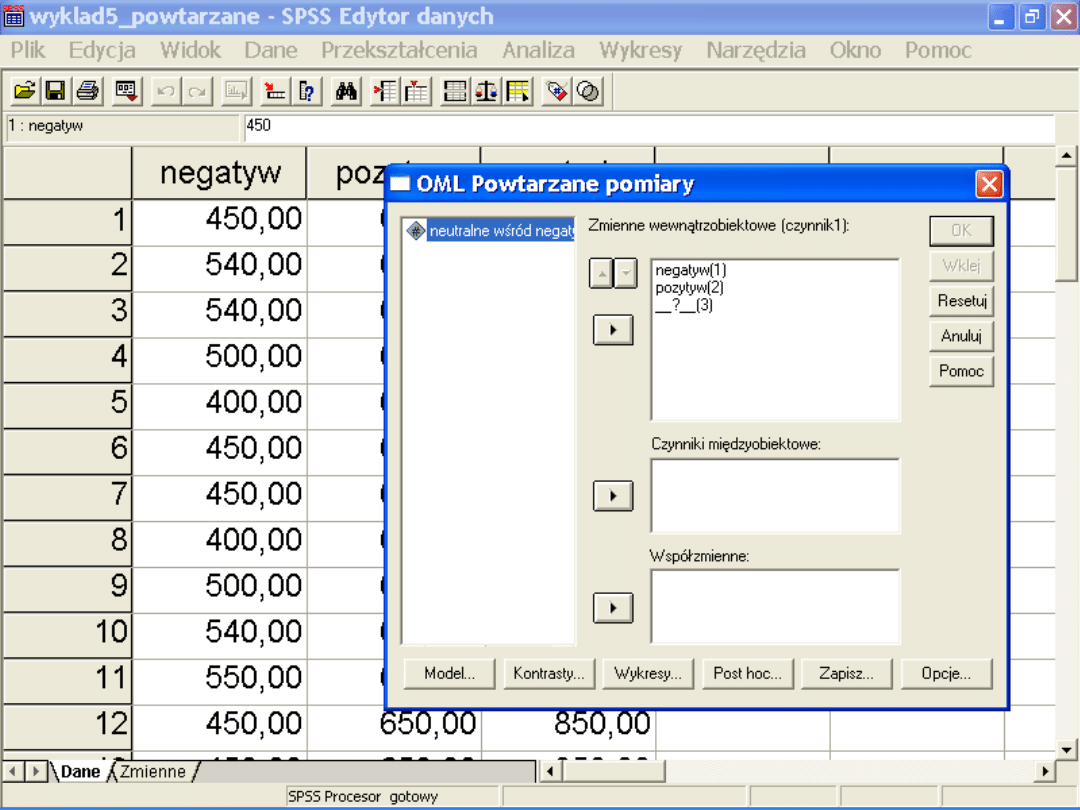
Kolejne elementy wydruku

Czynniki wewnątrzobiektowe

Miara: MIARA_1

NEGATYW
POZYTYW
NEUTRALN

CZYNNIK1
1
2
3

Zmienna

zależna

Statystyki opisowe

494,50 49,4682

20

645,50 29,9956

20

794,50 53,5552

20

negatywne wśród
neutralnych
pozytywne wśród
neutralnych
neutralne wśród
negatywnych

Średnia

Odchylenie

standardowe

N

Założenie sferyczności

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,981

,353

2

,838

,981

1,000

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: CZYNNIK1

b.

Założenie sferyczności – związki między parami
warunków badawczych są podobne, że zależności między
poszczególnymi warunkami są podobne – czy też inaczej
wariancje różnic między poszczególnymi warunkami
są podobne
W naszym przykładzie spełnione jest to założenie.
Gdyby test był istotny, nie spełnione założenie – mniejsze zaufanie do wyników F -
poprawki

Ważna tabelka

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

900013,3

2 450007196,887

,000

900013,3

1,962 458751196,887

,000

900013,3

2,000 450007196,887

,000

900013,3

1,000 900013196,887

,000

86853,33

38 2285,6

86853,33 37,276 2330,0
86853,33 38,000 2285,6
86853,33 19,000 4571,2

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Sferyczność założona

Greenhouse-Geisser

Huynh-Feldt

Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Df dla efektu zmiennej niezależnej k-1
Df dla błędu (N-1)(k-1)
N – liczba osób w badaniu

Prawidłowy zapis wyniku analizy:

F(2, 38)=196,89; p<0,001