Materiały do wykładu

Izabela Krejtz

Materiały do wykładu

Izabela Krejtz

Porównania planowane
cd.
Zaawansowane plany
eksperymentalne

Wykład 3

Materiały do wykładu

Izabela Krejtz

Porównanie jednoczynnikowej
analizy wariancji i testu t dla
grup niezależnych



Jednoczynnikowa analiza wariancji to
rozszerzenie testu t



Dla porównywania dwóch grup istnieje
między nimi ścisła zależność



F=t

2



W związku z tym nie jest możliwe uzyskanie
istotnego wyniku w teście t dla grup
niezależnych a nieistotnego przy
analizowaniu danych za pomocą analizy
wariancji

Materiały do wykładu

Izabela Krejtz

Kontekst a percepcja

Porównanie analizy wariancji i testu
t

Materiały do wykładu

Izabela Krejtz

A teraz

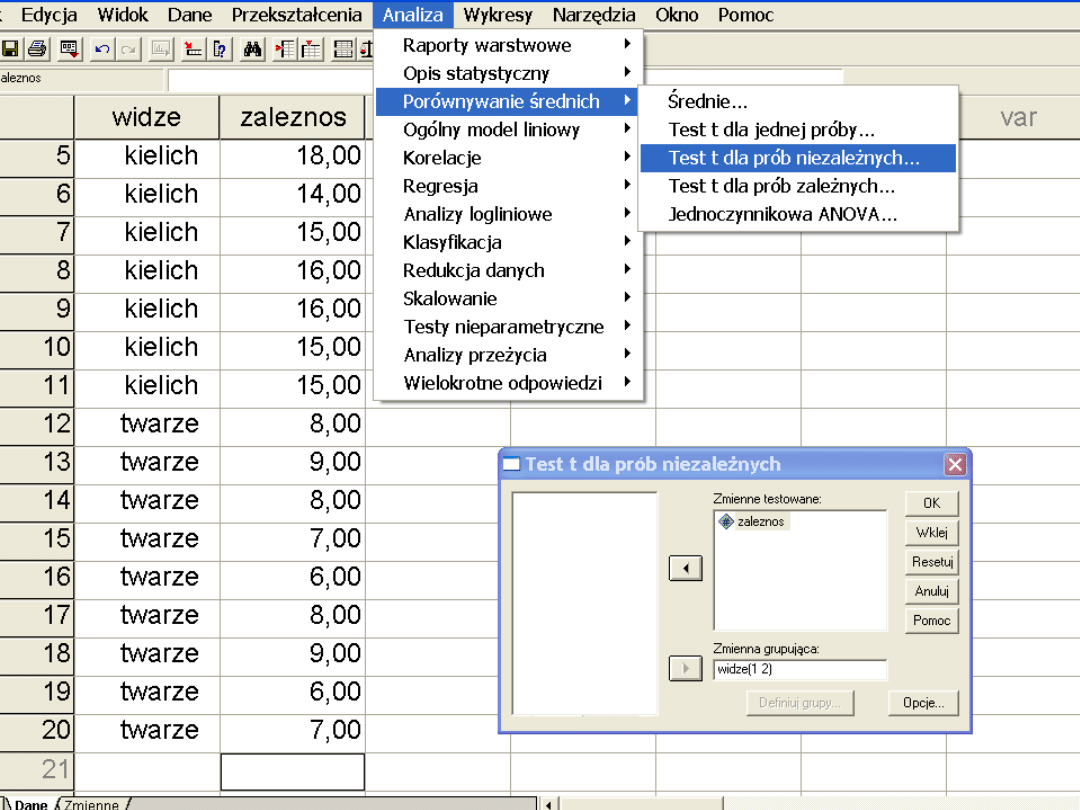
Tego typu zdjęcie pokazywano osobom w pubach, proszono o powiedzenie,
co widzą na obrazku. Mierzono wymiar zależność-niezależność od pola.
Interesowano się czy osoby, które zauważyły twarze były bardziej niezależne od pola

Materiały do wykładu

Izabela Krejtz

Materiały do wykładu

Izabela Krejtz

Statystyki dla grup

11 15,545

1,2136

,3659

9 7,5556

1,1304

,3768

WIDZE
kielich

twarze

ZALEZNOS

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla prób niezależnych

,005 ,942 15,10

18

,000 7,990

,5292 6,8782 9,1016

15,21 17,65

,000 7,990

,5252 6,8849 9,0949

Założono równość
wariancji
Nie założono
równości wariancji

ZALEZNOS

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

Analiza wariancji

ZALEZNOS

316,001

1 316,00 227,98

,000

24,949

18 1,386

340,950

19

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność



F=t

2

+

=

/

/

=

=

/

=

Materiały do wykładu

Izabela Krejtz

Porównywanie siły efektów z
różnych badań



Potrzebna jest miara
niezależna od liczby
osób



Im więcej osób, tym
bardziej istotne są
różnice



zapisu wyniku ANOVY
również można obliczyć
wielkość efektu



F(1,18)=227,98,
p<0,001

9268

,

0

18

1

98

,

227

1

98

,

227

)

(

)

(

)

(

2

2























WG

MG

MG

df

df

F

df

F

wariancji

93%

9268

,

0

950

,

340

001

,

316

2







O

MG

SS

SS



Materiały do wykładu

Izabela Krejtz

Porównywanie trzech
lub większej liczby
grup

Testy post hoc i kontrasty

Materiały do wykładu

Izabela Krejtz

Kiedy testy post hoc a kiedy
kontrasty?



Testy post hoc



Kontynuacja analizy wariancji w przypadku

istotnego wyniku, bez wcześniejszych hipotez



Uzyskujemy informacje, które grupy różnią się

istotnie od siebie



Kontrasty



Alternatywa wobec analizy wariancji



Możemy przeprowadzić wtedy, kiedy ogólny wynik

analizy wariancji jest nieistotny



Testują wcześniej postawione hipotezy, ścisły

związek z teorią

Materiały do wykładu

Izabela Krejtz



Wybór konkretnego testu post hoc
wiąże się z tym, czy zależy nam na
zmniejszeniu ryzyka popełnienia błędu I
rodzaju, czy też na większej mocy testu

Materiały do wykładu

Izabela Krejtz

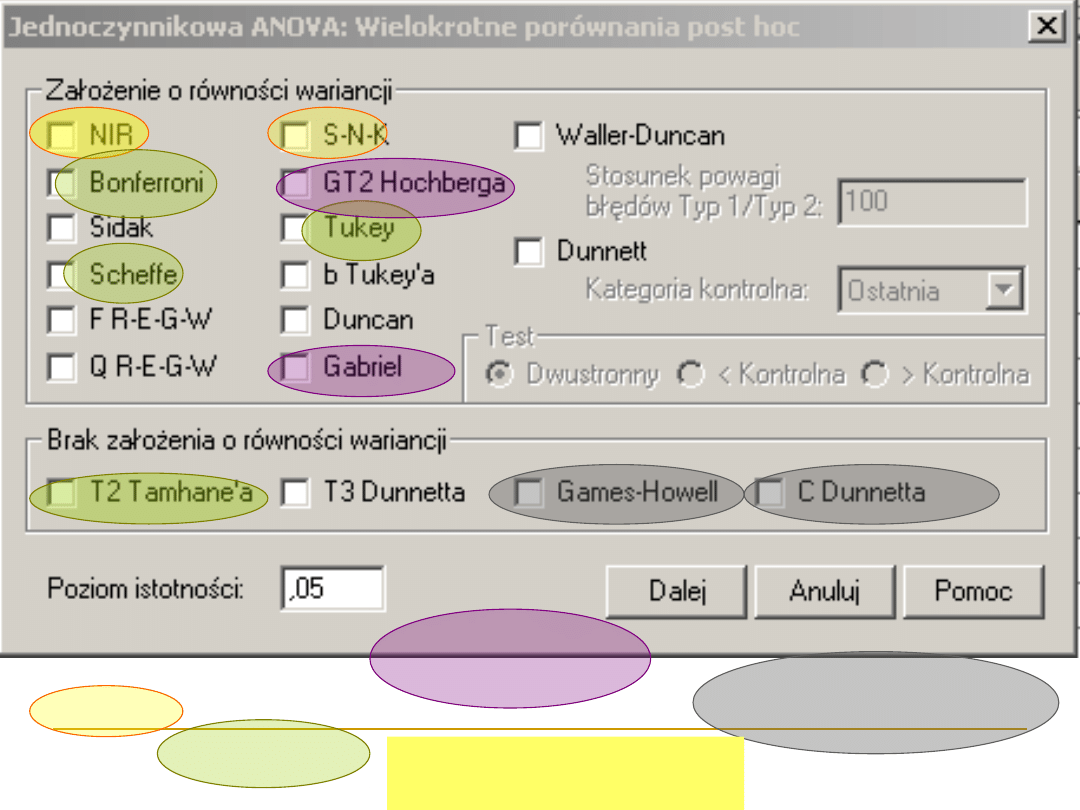
Jaki test post hoc wybrać do
analizy?



Bonferroni – większa moc przy małej liczbie

porównań



Bierze poprawkę na wielokrotne porównania między

parami średnich



Dzieląc poziom błędu I rodzaju przez liczbę porównań

tak, aby ogólny poziom alfa nie przekroczył 0,05



Tukey - większa moc przy większej liczbie

porównań



SNK – dość liberalny



Zaburzone założenia analizy wariancji – np.

Games-Howell – dosyć liberalny



Nierównoliczne grupki – Gabriel, jeśli bardzo

się różnią - Hochberg GT2

Materiały do wykładu

Izabela Krejtz

liberalne

konserwatywne

Polecane przy

nierównych grupach

Przy nierównych grupach

i zaburzonej wariancji

Autorka pięknego zestawienia:

dr Aneta Brzezicka-Rotkiewicz

Materiały do wykładu

Izabela Krejtz

Zalety porównań planowanych
(kiedy kontrasty są ostatnią
deską ratunku)



Porównujemy kombinacje (podzbiory) średnich



Zawsze porównujemy dwie porcje wariancji



Np. Kiedy mamy do porównania 3 grupy możemy

porównać dwie pierwsze z trzecią



(średnia_1 + średnia_2)/2 = Średnia_3



½ + ½ -1=0



Rozszerzenie analizy o sprawdzenie kształtu

zależności



Możemy również sprawdzać, czy średnie układają się

liniowo, czy też krzywoliniowo (analiza trendu -

wielomiany)

Materiały do wykładu

Izabela Krejtz

KTO BARDZIEJ DĄŻY
DO MAŁŻEŃSTWA?

Inspiracja za:
Aleksandra Olejnik

Kaja Ruszkowska

Kamila Sachanowska

Materiały do wykładu

Izabela Krejtz

Hipoteza i opis badania



Hipoteza: osoby z kobiecą płcią mózgu

wykazują większą chęć zawarcia małżeństwa

niż osoby z męską płcią mózgu



Koncepcja płci psychologicznej Sandry Bem:



Kobiece kobiety (kk)



Kobiecy mężczyźni (km)



Męskie kobiety (mk)



Męscy mężczyźni (mm)



Androgyniczne kobiety (ak)



Androgyniczni mężczyźni (am)



Zmienna niezależna: płeć psychologiczna,



Zmienna zależna: chęć zawarcia małżeństwa

Materiały do wykładu

Izabela Krejtz

Wyniki

Analiza wariancji

CHEC

209,2

5 41,83 56,90 ,000

39,700

54 ,735

248,9

59

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Test jednorodności wariancji

CHEC

1,316

5

54

,271

Test Levene'a

df1

df2

Istotność

Istotny efekt F (5,54)=56,90; p<0,001

Wariancje wyników w podgrupach są podobne, spełnione założenie o
homogeniczności wariancji

Materiały do wykładu

Izabela Krejtz

Porównania wielokrotne

Zmienna zależna: CHEC

4,8000*

,3835

,000

3,6223

5,9777

1,8000*

,3835

,000

,6223

2,9777

5,4000*

,3835

,000

4,2223

6,5777

4,1000*

,3835

,000

2,9223

5,2777

4,0000*

,3835

,000

2,8223

5,1777

-4,8000*

,3835

,000 -5,9777 -3,6223

-3,0000*

,3835

,000 -4,1777 -1,8223

,6000

,3835 1,000

-,5777

1,7777

-,7000

,3835 1,000 -1,8777

,4777

-,8000

,3835

,625 -1,9777

,3777

-1,8000*

,3835

,000 -2,9777

-,6223

3,0000*

,3835

,000

1,8223

4,1777

3,6000*

,3835

,000

2,4223

4,7777

2,3000*

,3835

,000

1,1223

3,4777

2,2000*

,3835

,000

1,0223

3,3777

-5,4000*

,3835

,000 -6,5777 -4,2223

-,6000

,3835 1,000 -1,7777

,5777

-3,6000*

,3835

,000 -4,7777 -2,4223

-1,3000*

,3835

,020 -2,4777

-,1223

-1,4000*

,3835

,009 -2,5777

-,2223

-4,1000*

,3835

,000 -5,2777 -2,9223

,7000

,3835 1,000

-,4777

1,8777

-2,3000*

,3835

,000 -3,4777 -1,1223

1,3000*

,3835

,020

,1223

2,4777

-,1000

,3835 1,000 -1,2777

1,0777

-4,0000*

,3835

,000 -5,1777 -2,8223

,8000

,3835

,625

-,3777

1,9777

-2,2000*

,3835

,000 -3,3777 -1,0223

1,4000*

,3835

,009

,2223

2,5777

,1000

,3835 1,000 -1,0777

1,2777

(J) PLEC
mk

km

mm

ak

am

kk

km

mm

ak

am

kk

mk

mm

ak

am

kk

mk

km

ak

am

kk

mk

km

mm

am

kk

mk

km

mm

ak

(I) PLEC
kk

mk

km

mm

ak

am

Test Bonferroniego

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

Dolna granica Górna granica

95% przedział ufności

Różnica średnich jest istotna na poziomie .05.

*.

KOBIECE_K

MĘSKIE_K

KOBIECY_M

MĘSCY_M

ANDROGY_K

MK
KM

MM

AK

AM

KK

KM

MM

AK

AM

KK

MK

MM

AK

AM

KK

MK
KM

AK

AM

KK

MK
KM

MM

AM

Materiały do wykładu

Izabela Krejtz

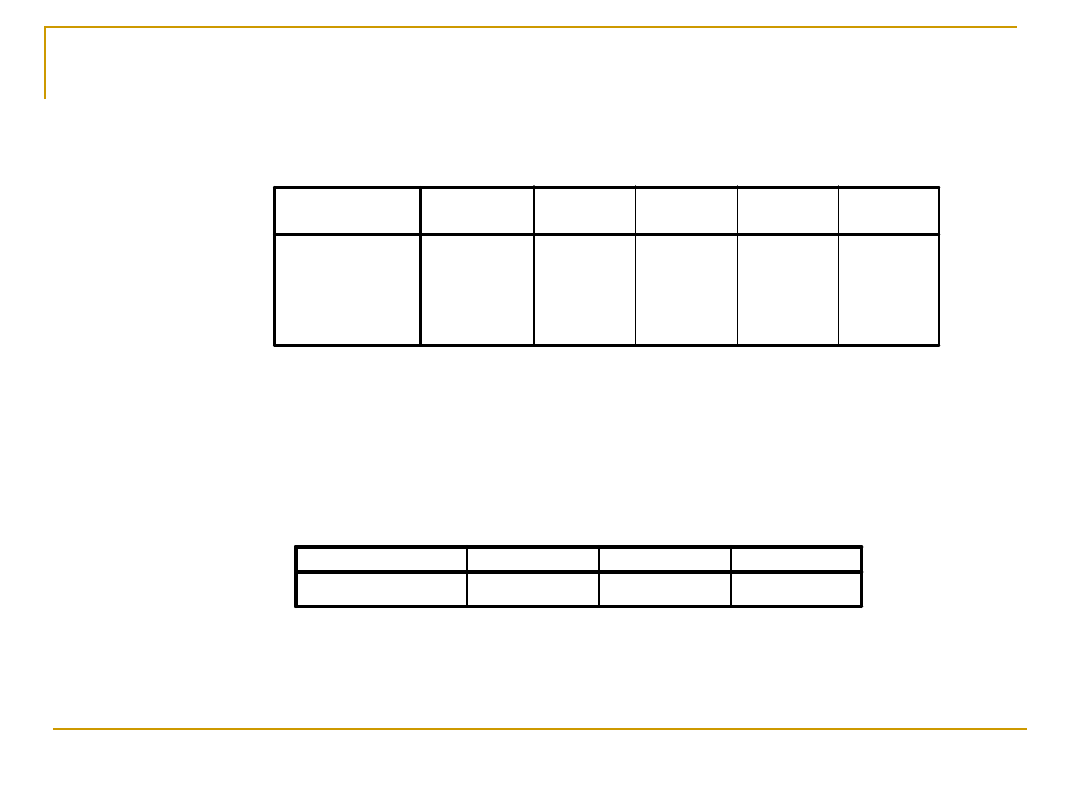
Grupy jednorodne

CHEC

10 3,000
10 3,600 3,600
10

4,300

10

4,400

10

6,600

10

8,400

,123

,102 1,000 1,000

PLEC
mm

mk

ak

am

km

kk

Istotność

Test
Studenta-New
mana-Keulsa

N

1

2

3

4

Podzbiór dla alfa = .05

Wyświetlane są średnie dla grup jednorodnych.

Męscy mężczyźni i męskie kobiety nie różnią się

Męskie kobiety (mk) nie różnią się od androgynicznych

Kobiecy mężczyźni różnią się od pozostałych grup, tak jak i kobiece kobiety

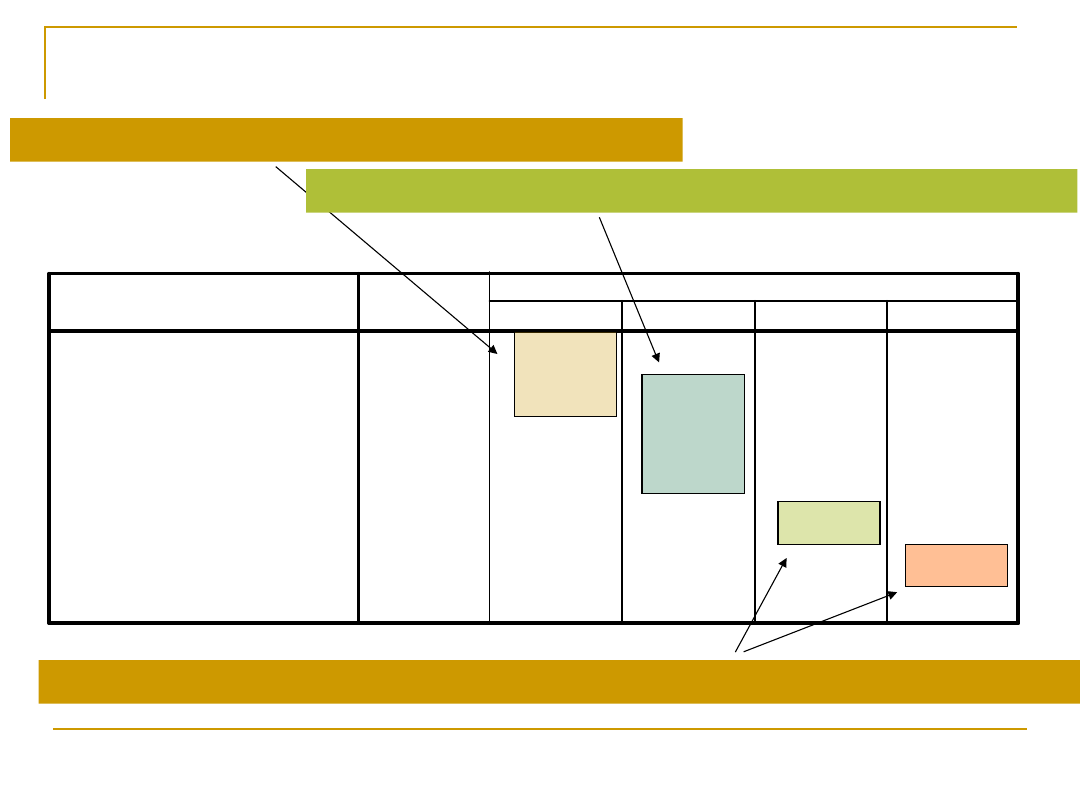
Materiały do wykładu

Izabela Krejtz

PLEC

am

ak

mm

km

mk

kk

Ś

re

dn

ia

-

C

H

E

C

9

8

7

6

5

4

3
2

Wykres średnich

a

b

b

b

c

c

d

Średnie oznaczone różnymi literkami różnią się od siebie

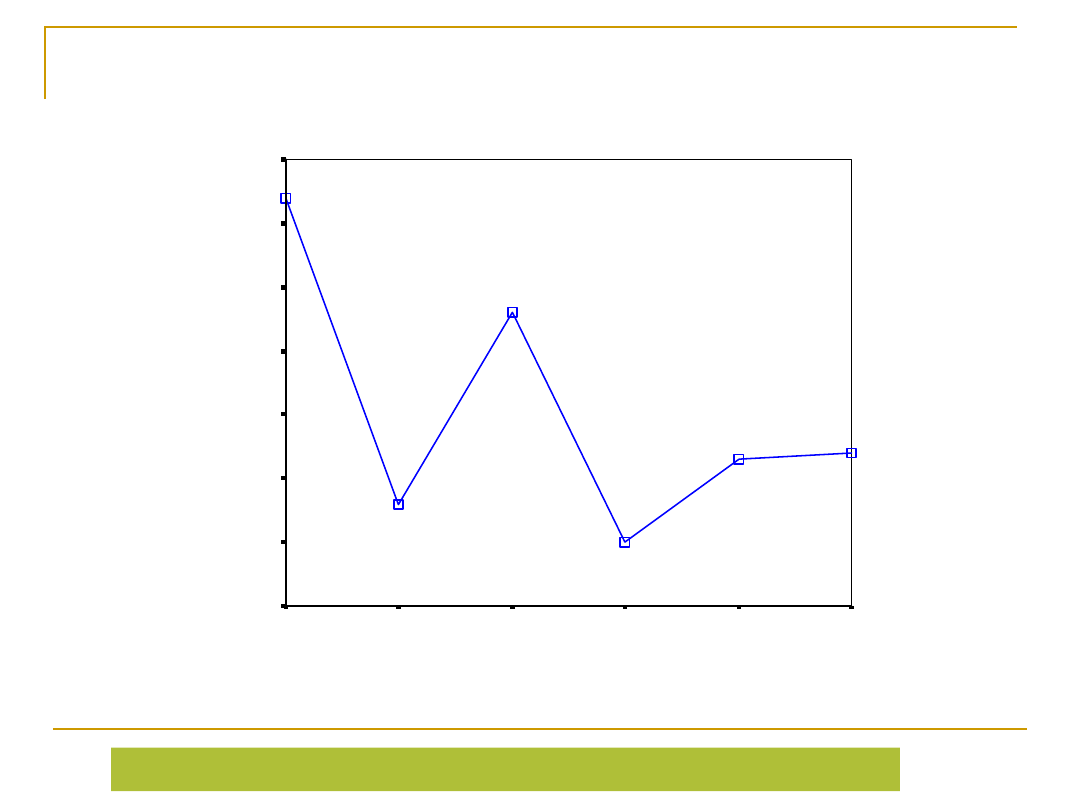
Materiały do wykładu

Izabela Krejtz

PLEC

am

ak

mm

km

mk

kk

Ś

re

dn

ia

-

C

H

E

C

9

8

7

6

5

4

3
2

Wykres średnich

a

b

b

b

c

c

d

Główna hipoteza mówiła o różnicy między osobami o kobiecych i męskich płciach psych.

Materiały do wykładu

Izabela Krejtz

osoby z kobiecą płcią mózgu
wykazują większą chęć zawarcia
małżeństwa niż osoby z męską
płcią mózgu - kontrasty



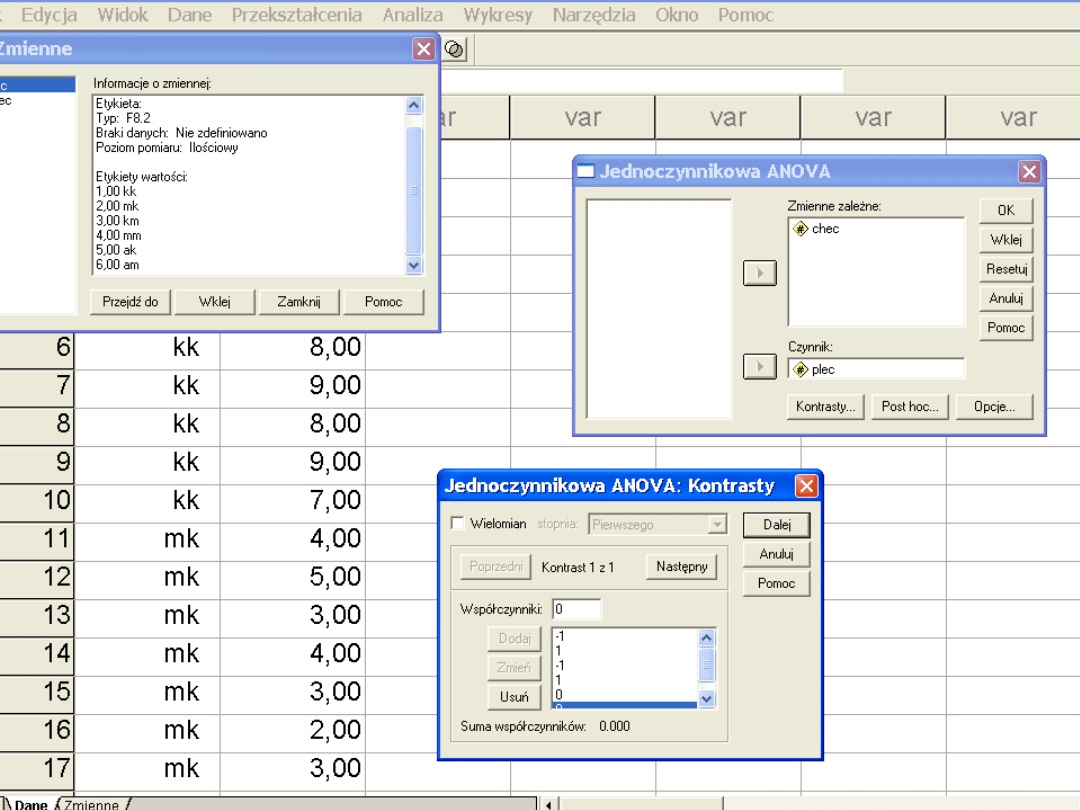
Jakie przypisać współczynniki poszczególnym grupom,

aby porównać osoby o kobiecej płci psychologicznej z

osobami o męskiej płci psychologicznej?

G1
KK

G2
MK

G3
KM

G4
MM

G5
AK

G6
AM

-1

1

-1

1

0

0

Materiały do wykładu

Izabela Krejtz

Materiały do wykładu

Izabela Krejtz

Wyniki

Współczynniki kontrastu

-1

1

-1

1

0

0

Kontrast
1

kk

mk

km

mm

ak

am

PLEC

Testy kontrastu

-8,40

,5423 -15,5

54

,000

-8,40

,5696 -14,7 33,70

,000

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

CHEC

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Materiały do wykładu

Izabela Krejtz

Analizy trendu
liniowego

wielomiany

Materiały do wykładu

Izabela Krejtz

Standardowe kontrasty



Większość kontrastów definiujemy sami



Są też gotowe kontrasty - wielomiany



Wielomian I stopnia



Testuje trend liniowy – czy nasze średnie w grupach

wzrastają na kolejnych poziomach zmiennej niezależnej



Czy linia prosta dobrze opisuje układ naszych średnich



Wielomian II stopnia – kwadratowy



Testuje zależność krzywoliniową



Czy np. średnie wzrastają na początku a potem maleją,

aby znów wzrosnąć – U lub odwrócone



Można je stosować, kiedy zmienną niezależną

można uporządkować (np. niski, średni i

wysoki poziom stresu)



Im więcej poziomów zmiennej niezależnej tym lepiej

przy analizie trendu

Materiały do wykładu

Izabela Krejtz

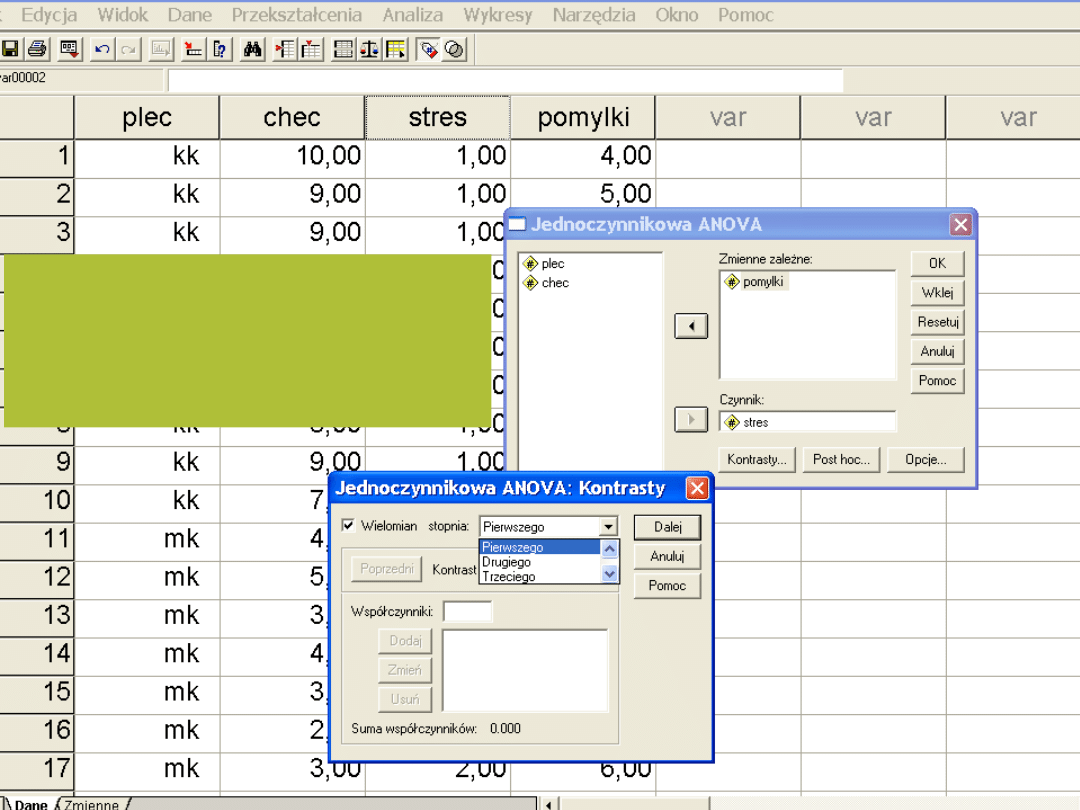
Stres a pomyłki na scenie –
uczniowie PWST



Im większy stres tym więcej pomyłek na
scenie i zmiany tekstu



Możemy sprawdzić zależność liniową

Materiały do wykładu

Izabela Krejtz

Wybierając wielomian, nie trzeba
przypisywać wartości w
kontrastach,
są one już automatycznie
przypisane – jest to duża zaleta

Materiały do wykładu

Izabela Krejtz

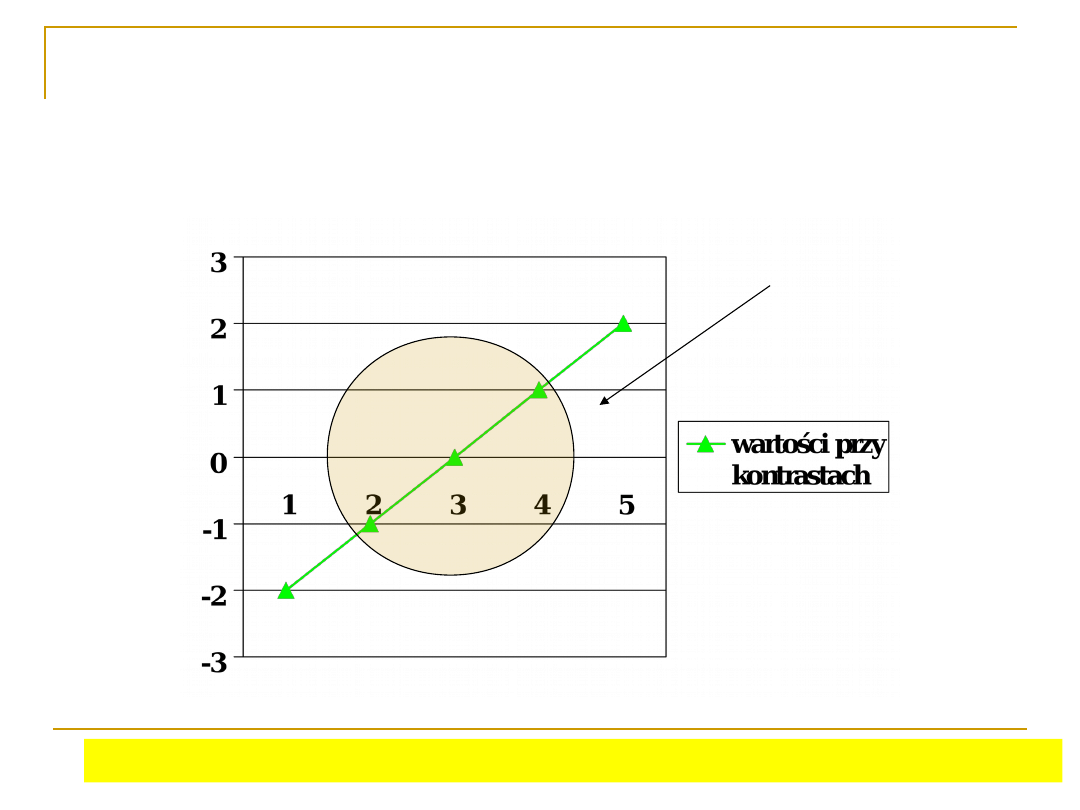
Przykładowe wartości
przypisane grupom w kontraście
testującym trend liniowy (dla 5
grup)

Sprawdzamy czy nasze średnie grupowe np. proporcjonalnie wzrastają

Przy trzech grupach

Liczba
grup

w

sp

ó

łc

zy

n

n

ik

i

Materiały do wykładu

Izabela Krejtz

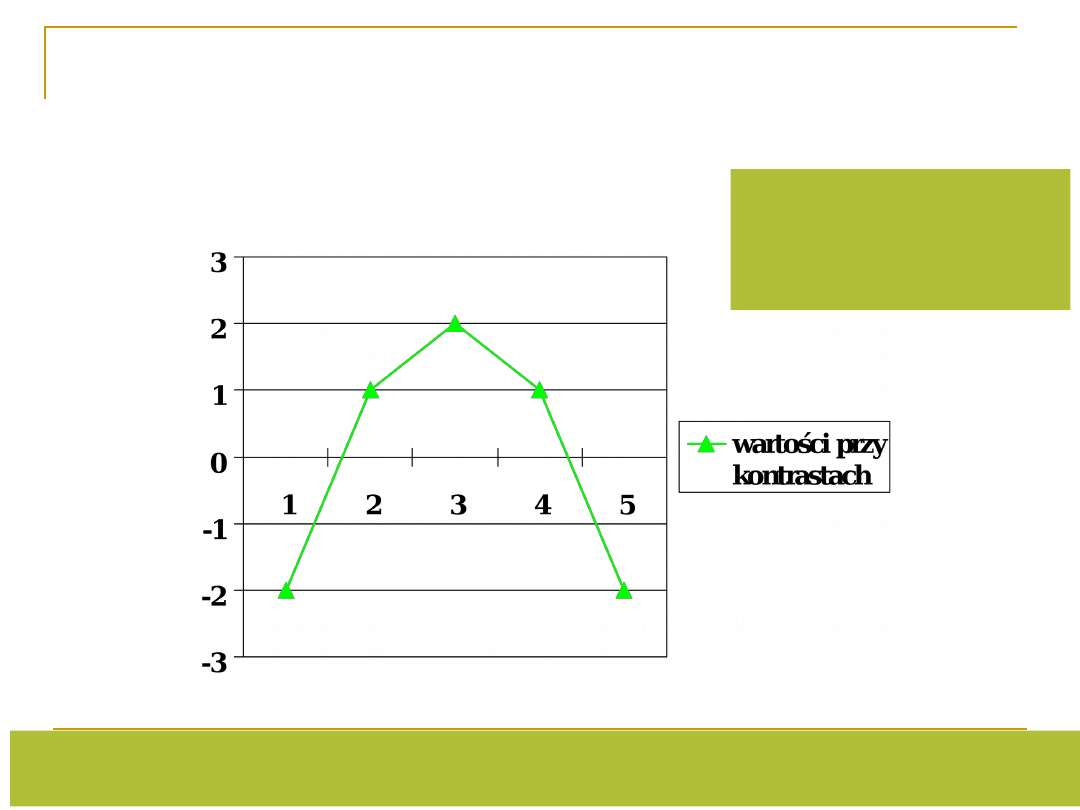
Zależność krzywoliniowa –
wielomian kwadratowy

Klasyczny przykład praw Yerkesa-Dodsona – poziom wykonania zadania a stres
Przy testowaniu tego trendu – przynajmniej 3 grupy, a najlepiej 4

Dla kształtu U przy 3 gr
wagi kontrastów:

1 -2 1

Materiały do wykładu

Izabela Krejtz

Przykłady zbiorów
współczynników dla 4 grup przy
analizach trendu



Liniowy -3 -1 1 3



Kwadratowy

1 -1 -1 1



Sześcienny -1 3 -3 1



Liczba zmian znaku określa stopień
wielomianu

Materiały do wykładu

Izabela Krejtz

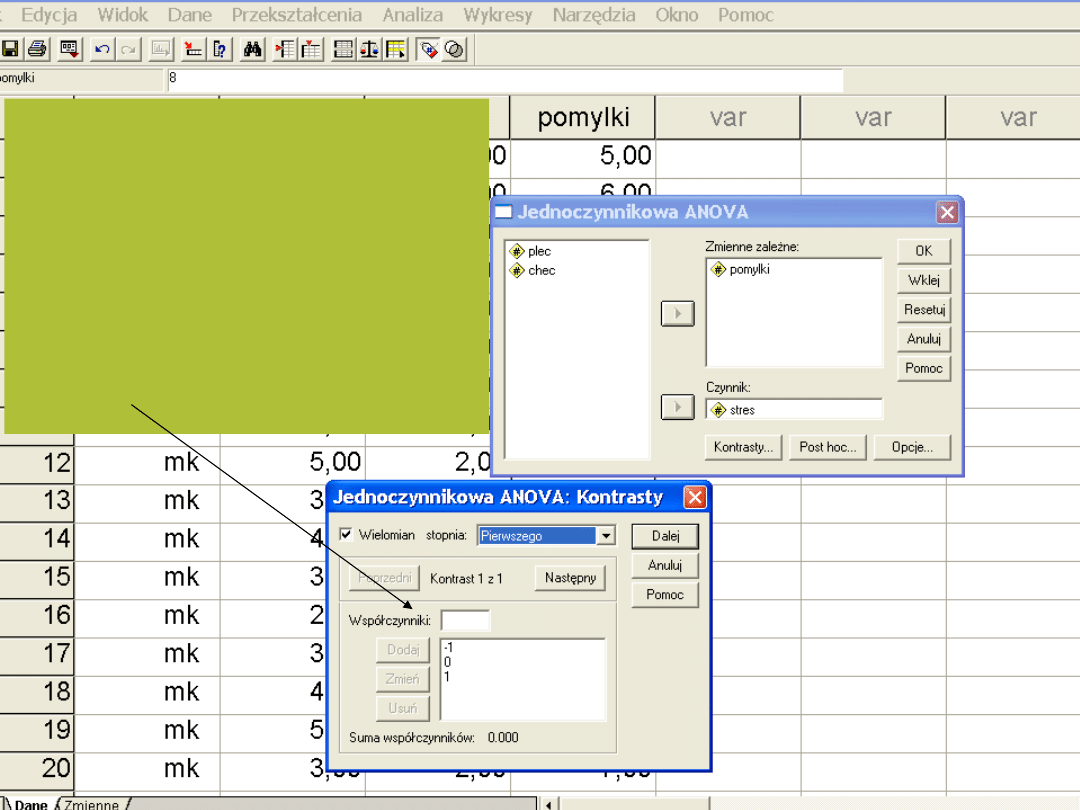
Dla porównania wyników
wielomianu i naszego kontrastu
możemy wpisać współczynniki:
-1, 0, 1
Równie dobrze możemy wpisać:
-5, 0, 5
Czy też
-10, 0, 10
Ważne aby suma współczynników
=0

Materiały do wykładu

Izabela Krejtz

Statystyki opisowe

POMYLKI

10 4,900

,7379

,2333 4,3722 5,4278 4,00

6,00

10 7,900

,5676

,1795 7,4939 8,3061 7,00

9,00

10 12,00 1,1547

,3651 11,1740 12,8260 10,00 14,00

30 8,267 3,0731

,5611 7,1192 9,4142 4,00 14,00

1,00

2,00

3,00

Ogółem

N

Średnia

Odchylenie

standardowe

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności dla

średniej

Minimum Maksimum

Test jednorodności wariancji

POMYLKI

1,438

2

27

,255

Test Levene'a

df1

df2

Istotność

Materiały do wykładu

Izabela Krejtz

Analiza wariancji

POMYLKI

254,067

2 127,03 173,23

,000

252,050

1 252,05 343,70

,000

2,017

1 2,017 2,750

,109

19,800

27

,733

273,867

29

(Połączone)

Kontrast

Odchylenie

Składnik
liniowy

Między grupami

Wewnątrz grup

Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Współczynniki kontrastu

-1

0

1

Kontrast
1

1,00

2,00

3,00

STRES

Testy kontrastu

7,1000

,3830 18,539

27

,000

7,1000

,4333 16,385 15,300

,000

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

POMYLKI

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

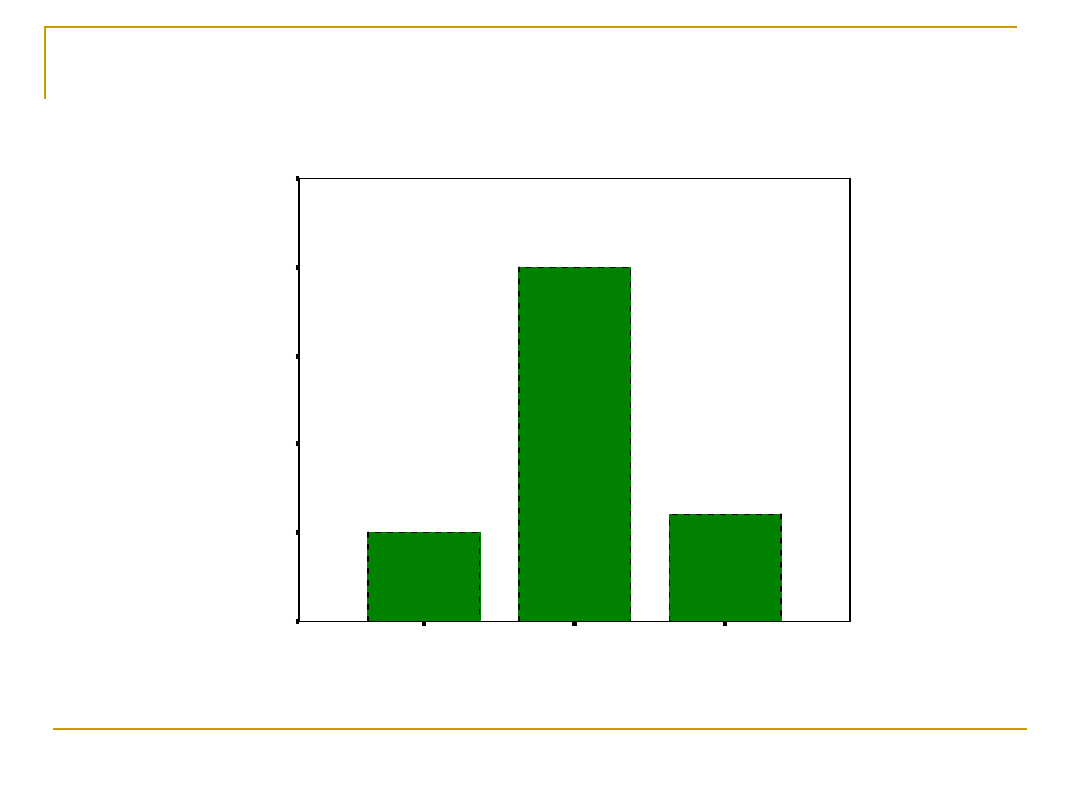
Zależność między F i t => dla dwóch grup F= t

2

= 343,70=(18,539)

2

Trend liniowy jest istotny
F(1,27)=343,70; p<0,001

Materiały do wykładu

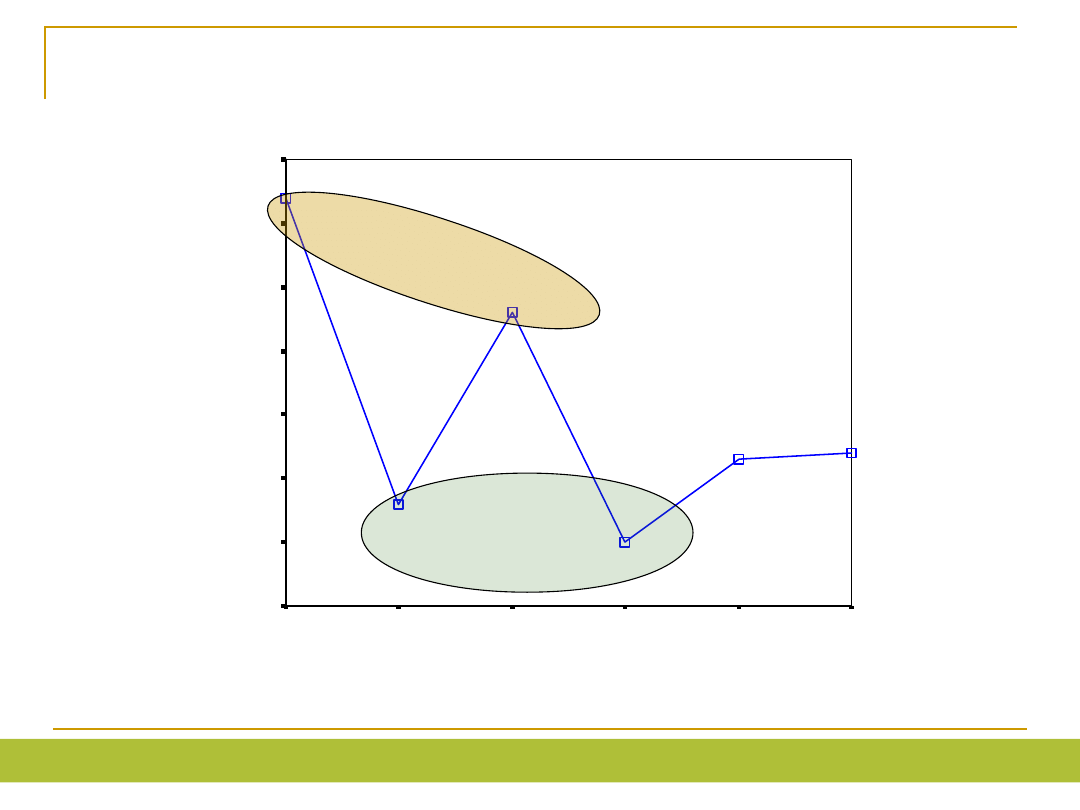
Izabela Krejtz

Z jakim kształtem zależności
mamy tu do czynienia ?

GRUPA

po REM

przed REM

kontrolna

Ś

re

dn

ia

-

S

N

Y

120

110

100

90

80

70

Materiały do wykładu

Izabela Krejtz

Jednoczynnikowa ANOVA

SNY

3095,000

2 1547,500

12,179

,001

13,333

1

13,333

,105

,750

36,818

1

36,818

,290

,597

3058,182

1 3058,182

24,069

,000

3058,182

1 3058,182

24,069

,000

3058,182

1 3058,182

24,069

,000

2160,000

17

127,059

5255,000

19

(Połączone)

Nieważone
Ważone
Odchylenie

Składnik liniowy

Nieważone
Ważone

Składnik kwadratowy

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Jednoczynnikowa ANOVA

SNY

2813,333

2 1406,667

9,483

,003

10,000

1

10,000

,067

,800

2803,333

1 2803,333

18,899

,001

2803,333

1 2803,333

18,899

,001

1780,000

12

148,333

4593,333

14

(Połączone)

Kontrast
Odchylenie

Składnik liniowy

Kontrast

Składnik kwadratowy

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Materiały do wykładu

Izabela Krejtz

Zaawansowane plany
eksperymentalne

Więcej niż 1 zmienna niezależna

Materiały do wykładu

Izabela Krejtz

Zaawansowane schematy
badawcze



Proste plany eksperymentalne, w

których manipuluje się



jedną zmienną niezależną,



a inne zmienne utrzymuje się na stałym

poziomie należą w psychologii do rzadkości,



Częściej w jednym eksperymencie



sprawdza się jednocześnie wpływ dwóch i

więcej zmiennych niezależnych na

interesujące nas zachowanie.

Materiały do wykładu

Izabela Krejtz

Jak wybrać odpowiedni plan
badawczy



Wprowadzając do eksperymentu kolejne
zmienne niezależne, musimy zastanowić się
czy będziemy wykorzystywać je jako zmienne



między osobami czy (dla grup niezależnych)



zmieniające się wewnątrz osób (dla grup zależnych)



Jeżeli wprowadzamy do badania zmienne
niezależne między grupami i wewnątrz grup
wtedy mówimy o planach mieszanych.

Materiały do wykładu

Izabela Krejtz

Plan 2x2



w najprostszej wersji zaawansowanego

planu eksperymentalnego



wprowadzamy do badania dwie zmienne

niezależne, każda na dwóch poziomach.



Opis planu podajemy mówiąc na ilu

poziomach są poszczególne zmienne

niezależne,



w najprostszym układzie mamy plan 2x2, co

czyta się „dwa na dwa”.

Materiały do wykładu

Izabela Krejtz

Przykład dla 2 zmiennych
niezależnych między osobami



Wyobraźmy sobie badanie, gdzie ilość
rozwiązanych łamigłówek będzie
zmienną zależną



Jeżeli w swojej szufladzie masz czarne i
brązowe skarpetki pomieszane w proporcji 4
do 5, ile skarpetek musisz wyjąć, aby mieć
pewność, że będziesz miał parę tego
samego koloru?

Materiały do wykładu

Izabela Krejtz

Przykład dla 2 zmiennych
niezależnych między osobami

Zmienne
niezależne

TYP PSYCHOLOGICZNY

SOWY

SKOWRONKI

PŁEĆ

K

M

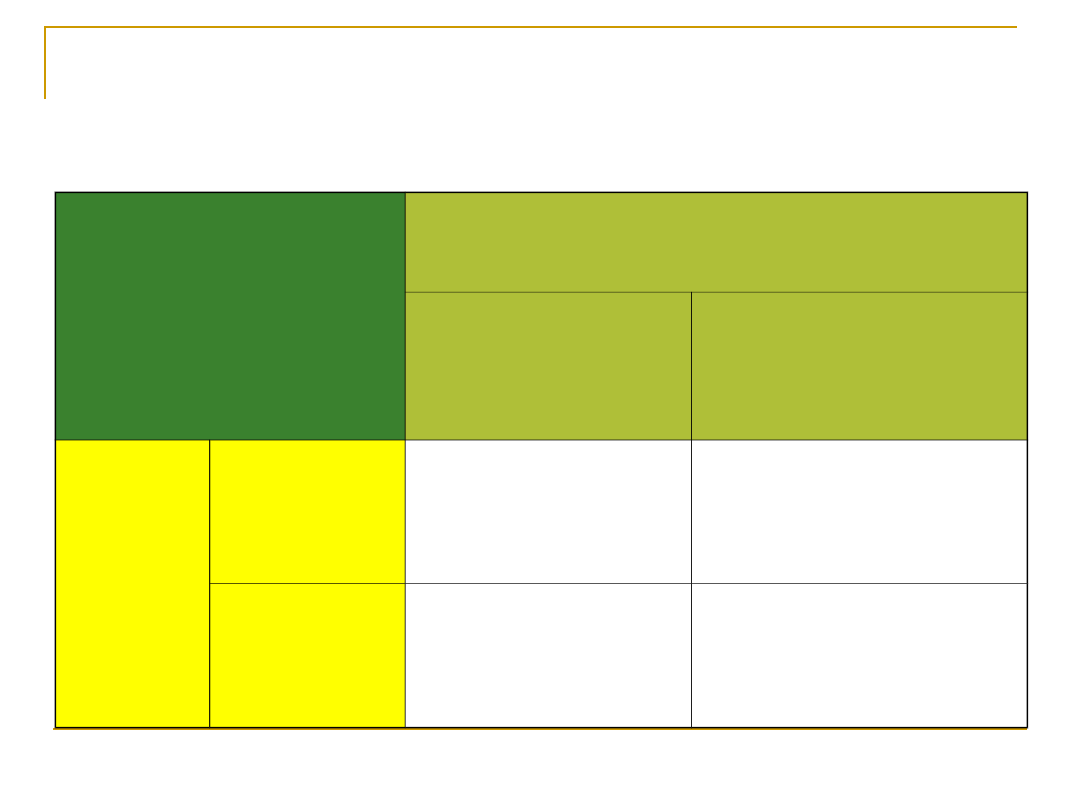
Materiały do wykładu

Izabela Krejtz

Przykład dla planu mieszanego:
1 zmienna niezależna między
osobami i 1 wewnątrz

Zmienne
niezależne

TYP PSYCHOLOGICZNY

SOWY

SKOWRONKI

PORA

BAD.

rano

wieczó
r