Prosta analiza regresji

Prosta analiza regresji

i

i

wprowadzenie do

wprowadzenie do

regresji wielokrotnej

regresji wielokrotnej

Wykład 8

Wykład 8

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Możliwości przewidywania średnich

Możliwości przewidywania średnich

zarobków, pogody w majowy

zarobków, pogody w majowy

weekend…

weekend…



Zdanie się na wróżkę – nie polecamy

Zdanie się na wróżkę – nie polecamy



Spojrzenie na średni wynik

Spojrzenie na średni wynik



Jeśli mamy zmienną, która jest

Jeśli mamy zmienną, która jest

skorelowana ze zmienną, którą chcemy

skorelowana ze zmienną, którą chcemy

przewidzieć, możemy sprawdzić,

przewidzieć, możemy sprawdzić,

•

czy przewidywanie będzie lepsze, gdy

czy przewidywanie będzie lepsze, gdy

uwzględnimy predyktor,

uwzględnimy predyktor,



na ile przewidywany wynik będzie różnił się od

na ile przewidywany wynik będzie różnił się od

wyniku, jaki przewidzielibyśmy na podstawie średniej

wyniku, jaki przewidzielibyśmy na podstawie średniej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

.

.

.

.

.

.

.

.

.

.

.

.

.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Założenia do liniowej analizy

Założenia do liniowej analizy

regresji

regresji



Odpowiednia liczba badanych (co najmniej

Odpowiednia liczba badanych (co najmniej

po 15 osób na 1 predyktor)

po 15 osób na 1 predyktor)



Zmienne z populacji o rozkładzie

Zmienne z populacji o rozkładzie

normalnym (patrzymy na histogramy)

normalnym (patrzymy na histogramy)



Zmienne w liniowym związku z zależną

Zmienne w liniowym związku z zależną

•

Czasem trzeba wyrzucić outlierów (dewiantów)

Czasem trzeba wyrzucić outlierów (dewiantów)



Najlepiej, jeśli zmienne niezależne

Najlepiej, jeśli zmienne niezależne

(predyktory) są związane tylko z zależną,

(predyktory) są związane tylko z zależną,

a nie ma związku między predyktorami

a nie ma związku między predyktorami

•

(jeśli jest to oznacza, że tak naprawdę mierzą

(jeśli jest to oznacza, że tak naprawdę mierzą

to samo)

to samo)

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza regresji

Analiza regresji



Pozwala na przewidywanie poziomu

Pozwala na przewidywanie poziomu

jednej zmiennej na podstawie

jednej zmiennej na podstawie

poziomu drugiej zmiennej.

poziomu drugiej zmiennej.



Nie ma sensu przeprowadzać prostej

Nie ma sensu przeprowadzać prostej

analizy regresji, kiedy nie ma

analizy regresji, kiedy nie ma

korelacji między zmiennymi

korelacji między zmiennymi

•

Im silniejsza korelacja między

Im silniejsza korelacja między

zmiennymi, tym lepsza możliwość

zmiennymi, tym lepsza możliwość

przewidywania

przewidywania

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

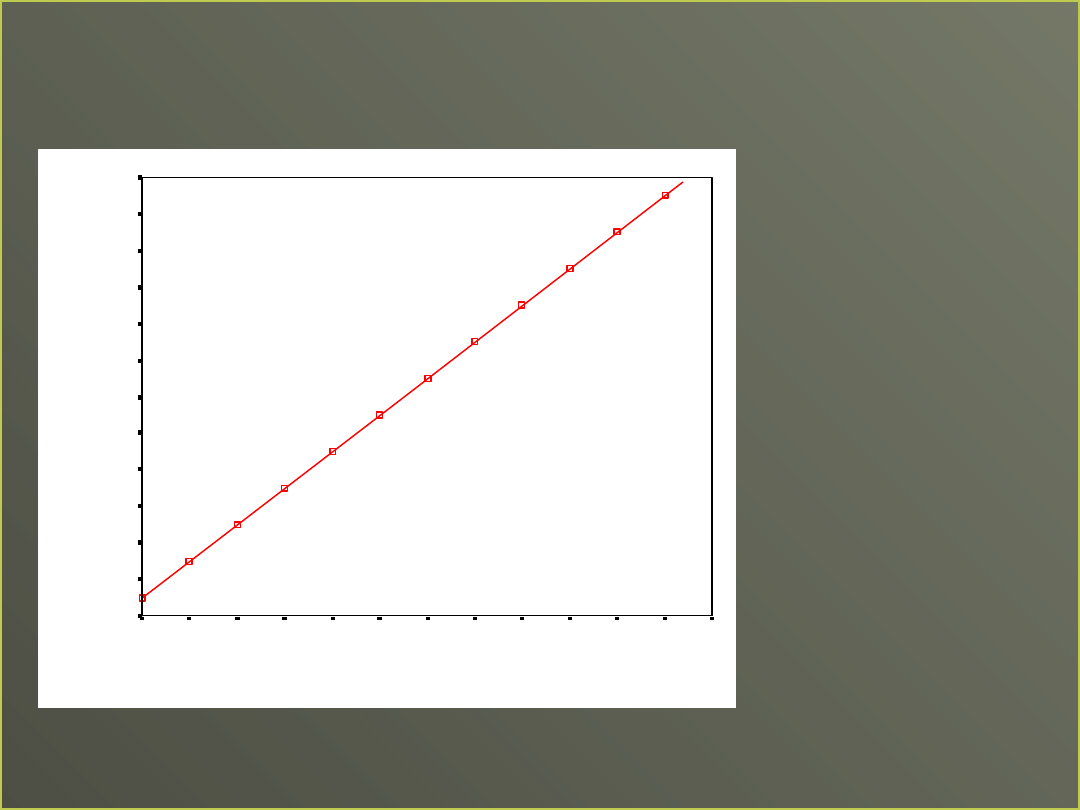
Y=2x+1

Y=2x+1

•

Jak wzrasta

Jak wzrasta

wartość X o 1,

wartość X o 1,

wartość Y

wartość Y

wzrasta o 2

wzrasta o 2

•

Idealna

Idealna

predykcja, w

predykcja, w

większości

większości

przypadków

przypadków

mamy do

mamy do

czynienia z

czynienia z

błędem

błędem

predykcji

predykcji

X

12

11

10

9

8

7

6

5

4

3

2

1

0

Y

24

22

20

18

16

14

12

10

8

6

4

2
0

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

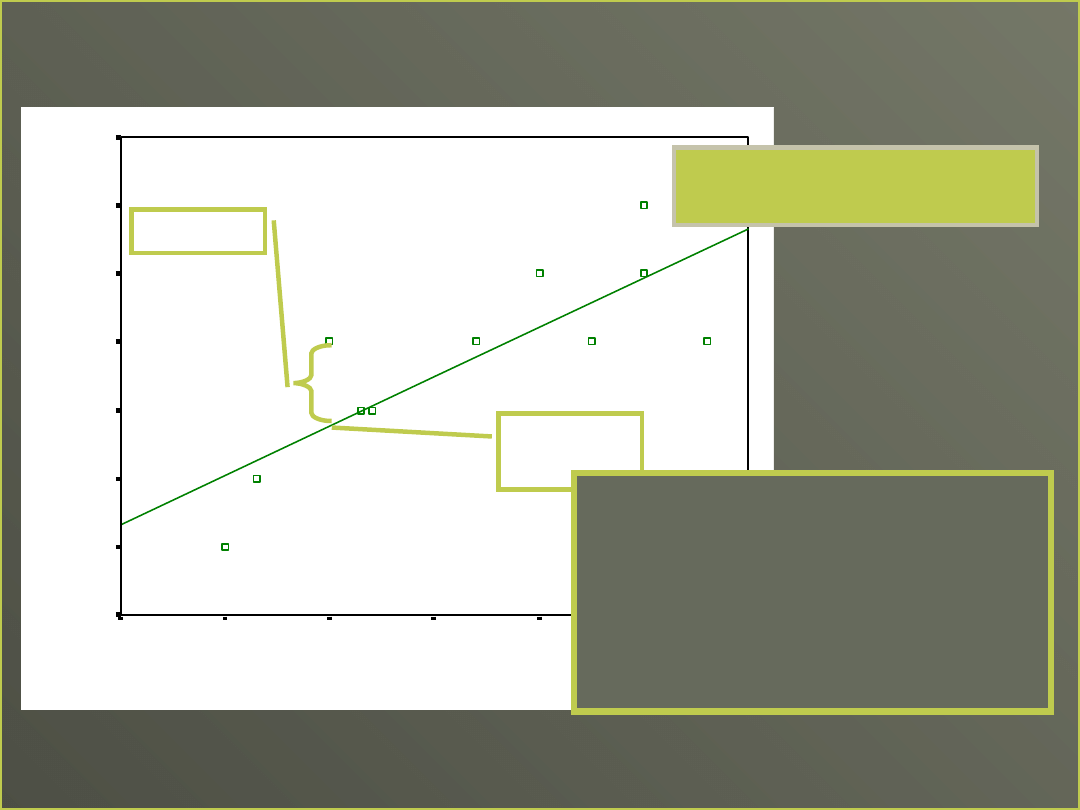
Staramy się minimalizować błąd

Staramy się minimalizować błąd

oszacowania

oszacowania

STRES

60

50

40

30

20

10

0

S

Y

M

P

T

O

M

Y

7

6

5

4

3

2

1

0

Reszta

Predykcj
a

stala

nachylenia

ˆ

B

X

B

Y







Chcemy aby Y’ było jak najbliższe

otrzymanym Y



(Y-Y’) błąd oszacowania (reszty)



Szukamy współczynników b i b

0

,

tak, aby linia minimalizowała błąd

oszacowania

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Linia prosta w regresji

Linia prosta w regresji



W analizie regresji poszukujemy

W analizie regresji poszukujemy

takiej linii, która najlepiej pasuje do

takiej linii, która najlepiej pasuje do

naszych danych

naszych danych



Szacujemy współczynniki regresji:

Szacujemy współczynniki regresji:

•

Współczynnik b – nachylenie tej

Współczynnik b – nachylenie tej

prostej, wielkość zmiany Y, gdy X

prostej, wielkość zmiany Y, gdy X

zmieni się o jednostkę

zmieni się o jednostkę



Standaryzowany współczynnik beta

Standaryzowany współczynnik beta

•

Stałą

Stałą b

0

– punkt przecięcia z osią y,

– punkt przecięcia z osią y,

sytuacja, gdy osoba nie odczuwa

sytuacja, gdy osoba nie odczuwa

stresu (x=0)

stresu (x=0)



Znając te wartości możemy

Znając te wartości możemy

przewidywać w oparciu o

przewidywać w oparciu o

konkretne wartości predyktora, ile

konkretne wartości predyktora, ile

wyniesie wartość zmiennej

wyniesie wartość zmiennej

zależnej

zależnej



Zmienna wynikowa Y jest

Zmienna wynikowa Y jest

przewidywana na podstawie

przewidywana na podstawie

równania prostej

równania prostej

X

b

Y

b





0

x

y

s

s

r

b

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Dokładność przewidywania

Dokładność przewidywania



Nie wiedząc nic o poziomie stresu,

Nie wiedząc nic o poziomie stresu,

wnioskowalibyśmy na podstawie średniej liczby

wnioskowalibyśmy na podstawie średniej liczby

odczuwanych symptomów

odczuwanych symptomów

•

(odchylenie wyników od średniej)

(odchylenie wyników od średniej)



Mając informację o poziomie stresu możemy

Mając informację o poziomie stresu możemy

przewidywać na podstawie tej zmiennej, ile będzie

przewidywać na podstawie tej zmiennej, ile będzie

dana osoba odczuwać symptomów

dana osoba odczuwać symptomów

•

Błąd standardowy oszacowania – uśredniona suma

Błąd standardowy oszacowania – uśredniona suma

kwadratów Y-Y’, SK reszt

kwadratów Y-Y’, SK reszt

•

Na ile nasza predykcja jest lepsza od przewidywania w

Na ile nasza predykcja jest lepsza od przewidywania w

oparciu tylko o średnią

oparciu tylko o średnią



SK regresji – suma kwadratów odchyleń wyników

SK regresji – suma kwadratów odchyleń wyników

przewidywanych od średniej

przewidywanych od średniej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Wspólna zmienność, istotność

Wspólna zmienność, istotność

modelu

modelu

Model - Podsumowanie

,818

a

,668

,632

,8623

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), STRES

a.

Analiza wariancji

b

13,490

1 13,49 18,14

,002

a

6,692

9

,744

20,182

10

Regresja

Reszta

Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), STRES

a.

Zmienna zależna: SYMPTOMY

b.

ogolem

regresja

SK

SK

R 

2

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

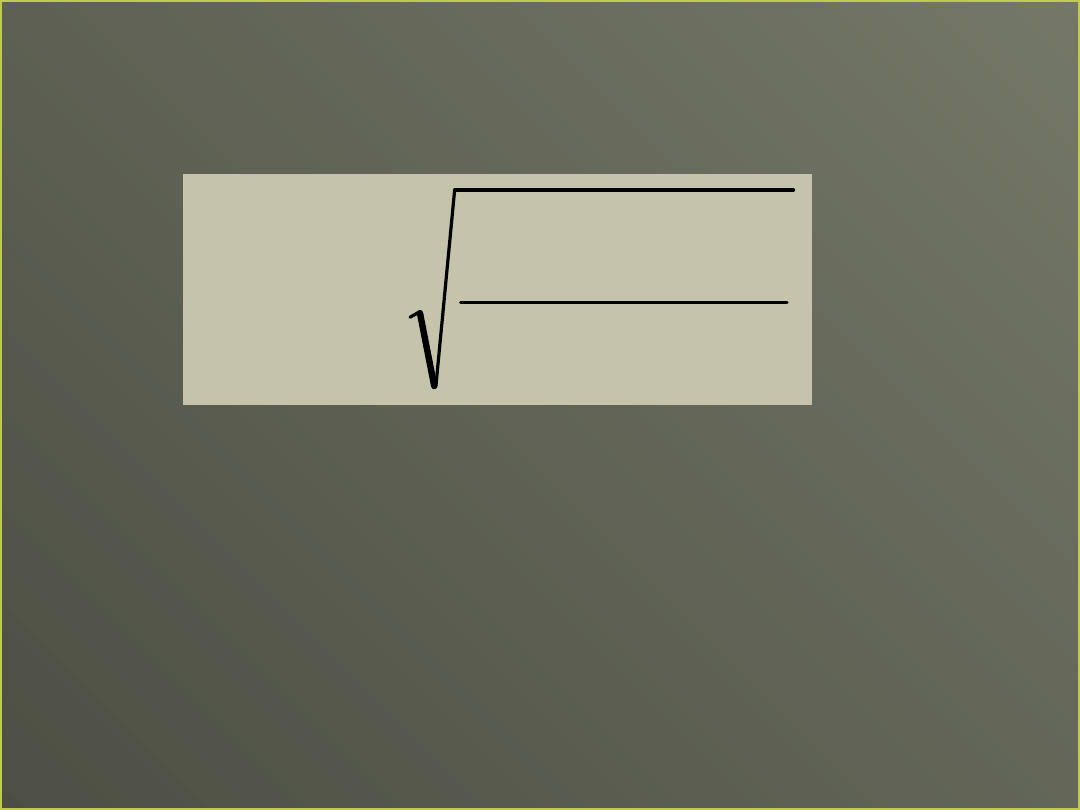
Błąd przewidywania

Błąd przewidywania



Wariancja reszty

Wariancja reszty

•

Zmienność przewidywanych wartości

Zmienność przewidywanych wartości



Błąd standardowy oszacowania

Błąd standardowy oszacowania

•

Odchylenie standardowe

Odchylenie standardowe

przewidywanych wartości od

przewidywanych wartości od

rzeczywistych

rzeczywistych

2

)

'

(

2

2

'











N

Y

Y

s

Y

Y

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

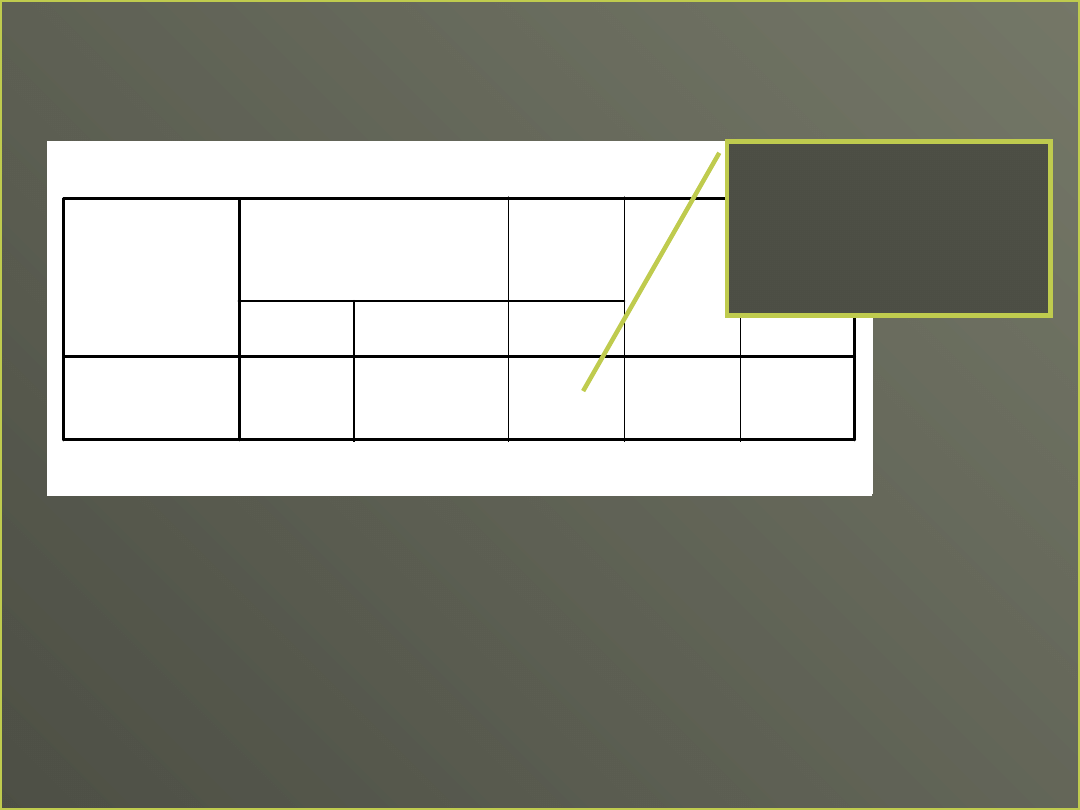
Błąd standardowy

Błąd standardowy

oszacowania

oszacowania



Miara dokładności naszego

Miara dokładności naszego

oszacowania

oszacowania

•

Chcemy, żeby był jak najmniejszy

Chcemy, żeby był jak najmniejszy

2

)

'

(

2

'











N

Y

Y

s

Y

Y

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynniki regresji

Współczynniki regresji



Testujemy hipotezę, że współczynnik regresji b

Testujemy hipotezę, że współczynnik regresji b

jest istotnie różny od zera

jest istotnie różny od zera



Ho: b=0

Ho: b=0



Ho: b

Ho: b

0

0

=0

=0

Współczynniki

a

1,328

,620

2,140

,061

,072

,017

,818 4,259

,002

(Stała)

STRES

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: SYMPTOMY

a.

Wyrażona zmiana w

jednostkach

odchylenia

standardowego,

w przypadku prostej

regresji = r,

Predykcja zmiennej zależnej w

Predykcja zmiennej zależnej w

oparciu o wiele predyktorów

oparciu o wiele predyktorów

(2 i więcej)

(2 i więcej)

Regresja

wielokrotna

Multiple

Regression

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Regresja wielokrotna

Regresja wielokrotna



Znalezienie miary ogólnego

Znalezienie miary ogólnego

dopasowania naszego modelu

dopasowania naszego modelu



Oszacowanie współczynników dla

Oszacowanie współczynników dla

każdego predyktora

każdego predyktora

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

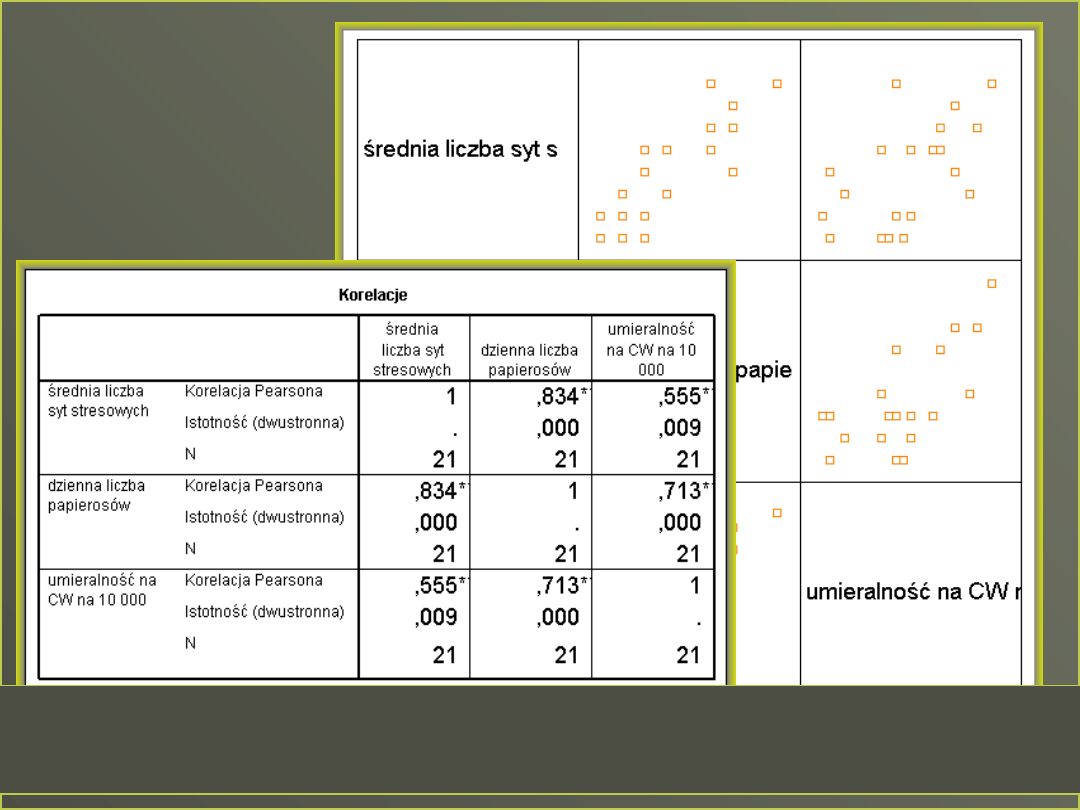
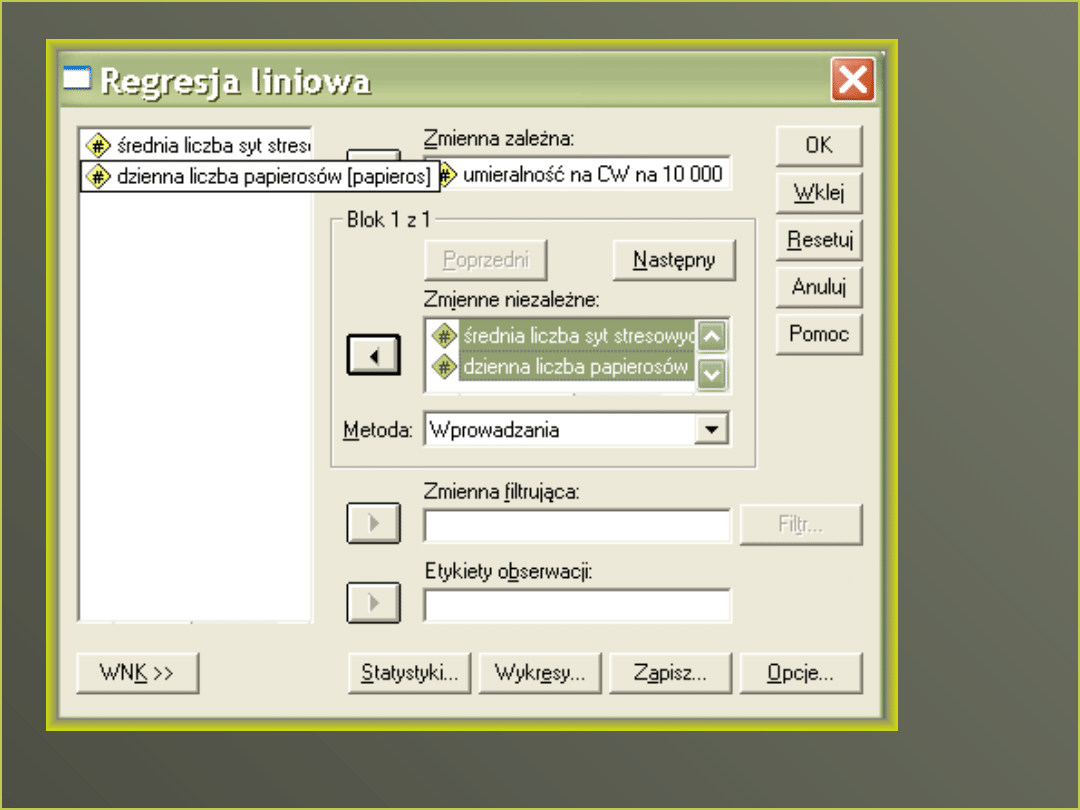
Obie zmienne sytuacje stresowe i liczba wypalanych papierosów są istotnie związane

Obie zmienne sytuacje stresowe i liczba wypalanych papierosów są istotnie związane

z umieralnością na CW, ale również predyktory są ze sobą związane

z umieralnością na CW, ale również predyktory są ze sobą związane

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynnik korelacji

Współczynnik korelacji

wielokrotnej

wielokrotnej



Współczynnik analogiczny do

Współczynnik analogiczny do

r

r



Zawsze oznaczany przez

Zawsze oznaczany przez

R

R



Zawsze pozytywny

Zawsze pozytywny

• Korelacja konstruktu stworzonego ze

wszystkich predyktorów łącznie ze
zmienna zależną

• Często zamiast R podaje się R

2

, które

łatwiej zinterpretować

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

R

R

2

2

R

2

has tak samo się interpretuje jak R

2

przy prostej

regresji
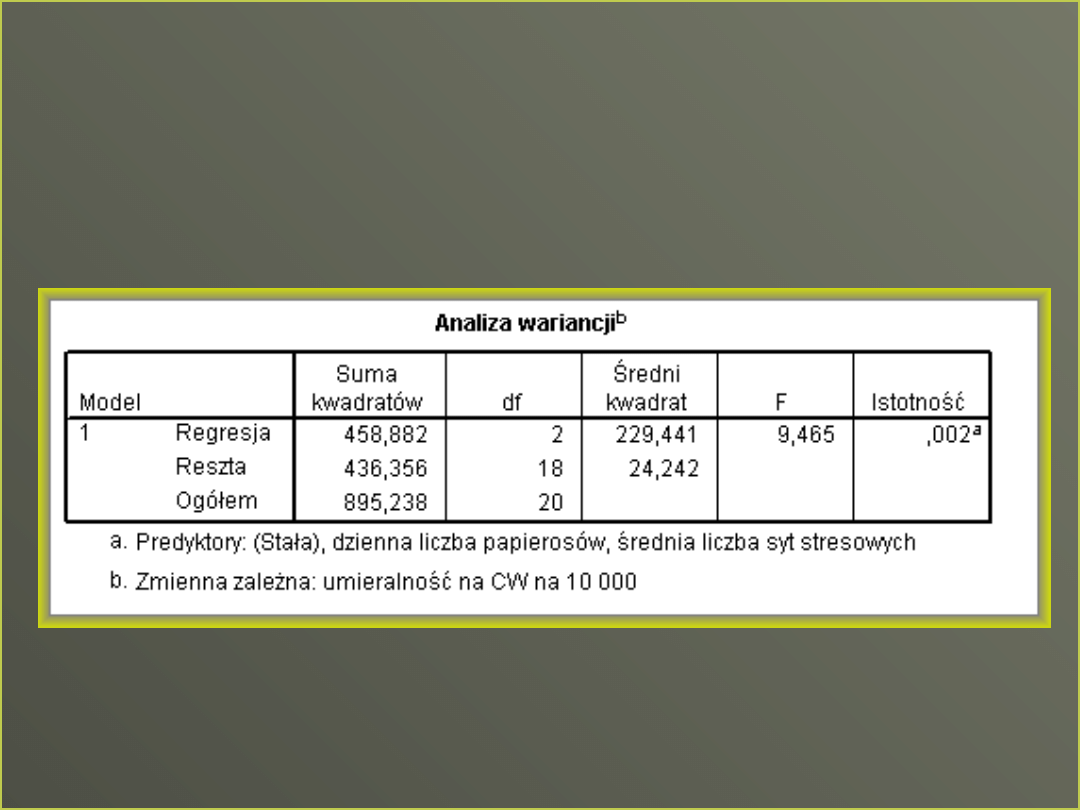
51% wariancji w CW jest wyjaśnione przez zmienność
w liczbie wypalanych papierosów i sytuacjach
stresowych
R-skorygowane: 45,8%

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Czy model jest istotny?

Czy model jest istotny?

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

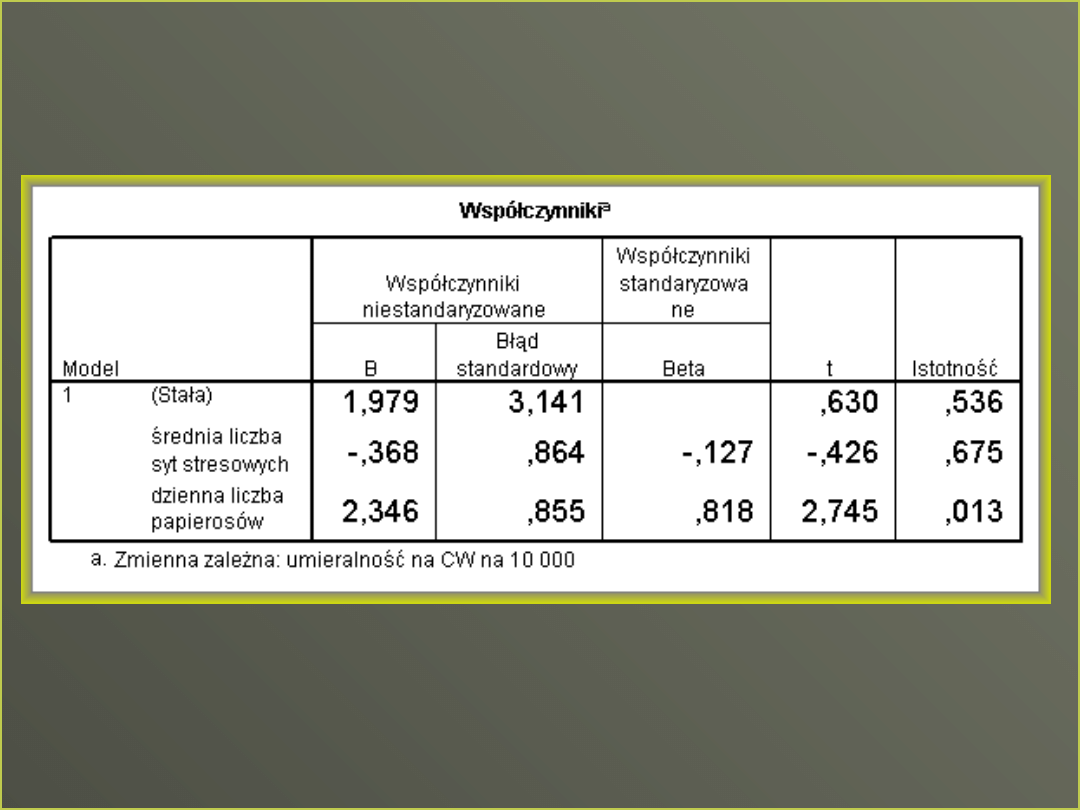
Współczynniki regresji

Współczynniki regresji



Stała i współczynniki dla każdego

Stała i współczynniki dla każdego

predyktora

predyktora



Przy szacowaniu współczynnika dla

Przy szacowaniu współczynnika dla

danej zmiennej wartości pozostałych

danej zmiennej wartości pozostałych

są utrzymywane na stałym poziomie

są utrzymywane na stałym poziomie

•

Najczęściej przyjmowana jest średnia

Najczęściej przyjmowana jest średnia



Równanie regresji wielokrotnej jest

Równanie regresji wielokrotnej jest

rozszerzeniem regresji prostej.

rozszerzeniem regresji prostej.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Interpretacja stałej nie ma zwykle sensu.

Interpretacja stałej nie ma zwykle sensu.

Przewidywanie zmiennej zależnej, gdy

Przewidywanie zmiennej zależnej, gdy

wszystkie predyktory równe 0

wszystkie predyktory równe 0

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Równanie regresji

Równanie regresji



Oddzielne współczynniki dla każdej

Oddzielne współczynniki dla każdej

zmiennej

zmiennej



Punkt przecięcia

Punkt przecięcia



Współczynnik dla papierosów jesdt

Współczynnik dla papierosów jesdt

dodatni, ale współczynnik dla stresu

dodatni, ale współczynnik dla stresu

jest negatywny

jest negatywny

•

Dlaczego?

Dlaczego?

979

,

1

368

.

346

,

2

ˆ

0

2

2

1

1













str

pap

b

X

b

X

b

Y

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Przewidywanie

Przewidywanie



Załóżmy, że

Załóżmy, że

liczba

liczba

papierosów

papierosów

=

=

1

1

0,

0,

syt.

syt.

stresowych

stresowych

= 5,

= 5,

10000

6

,

23

979

,

1

84

,

1

46

,

23

ˆ

na

Y









979

,

1

368

.

346

,

2

ˆ

0

2

2

1

1













str

pap

b

X

b

X

b

Y

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

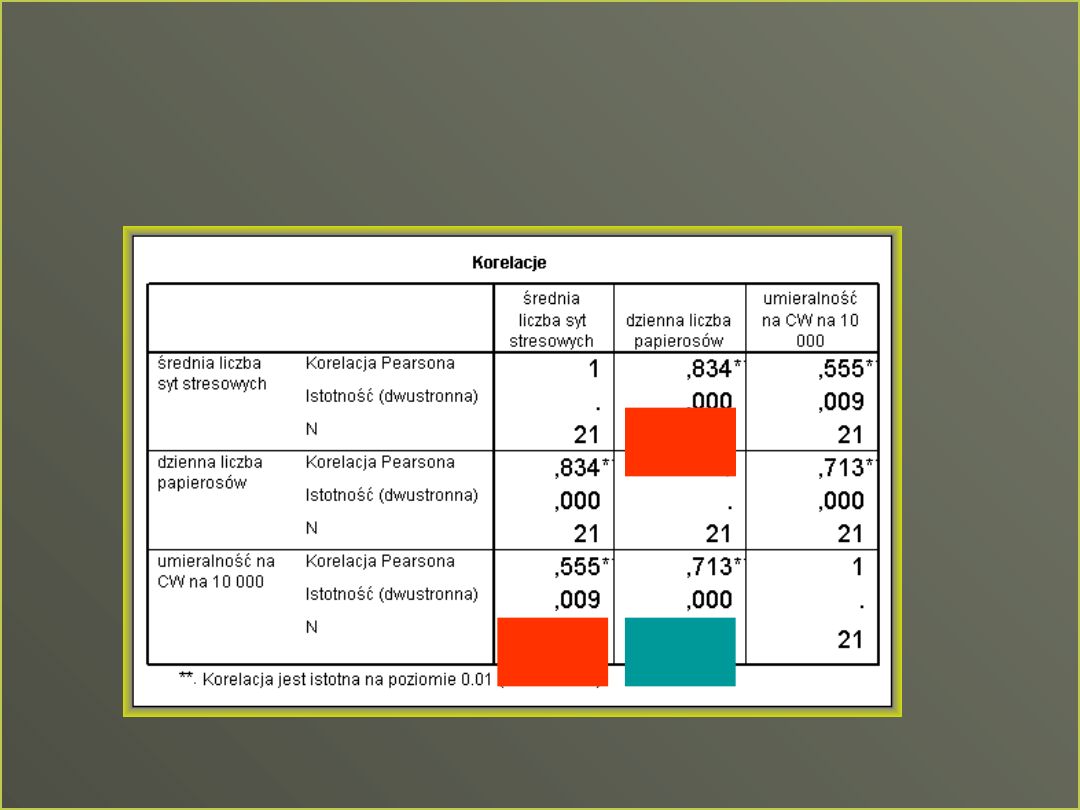
Problem skorelowanych

Problem skorelowanych

predyktorów

predyktorów



Korelacja cząstkowa –

Korelacja cząstkowa –

•

korelacja między dwiema zmiennymi Y i

korelacja między dwiema zmiennymi Y i

X1, po odrzuceniu z obu zmiennych,

X1, po odrzuceniu z obu zmiennych,

jakiejkolwiek wariancji, którą można

jakiejkolwiek wariancji, którą można

przypisać trzeciej zmiennej (X2).

przypisać trzeciej zmiennej (X2).

•

Patrzymy na związek dwóch zmiennych,

Patrzymy na związek dwóch zmiennych,

przy kontroli trzeciej

przy kontroli trzeciej

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Silniejszy wygrywa?

Silniejszy wygrywa?

R

2

=30,

8

R

2

=50,

8

R

2

=70

%

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

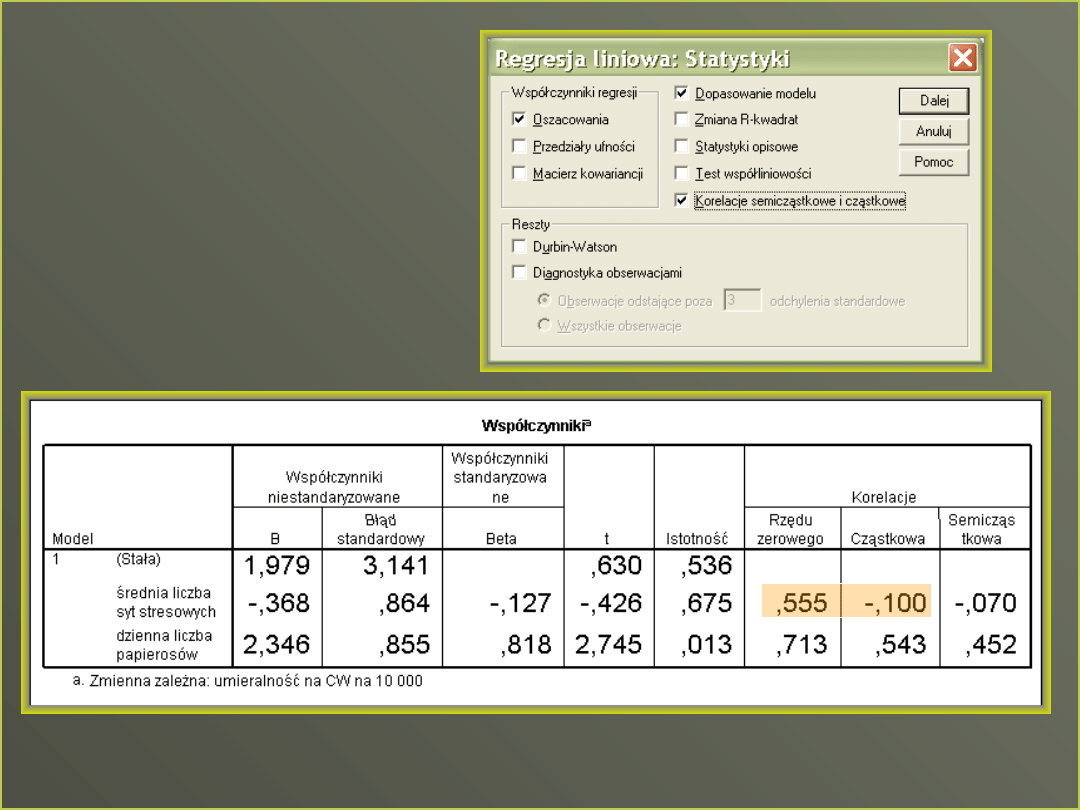
Idea korelacji cząstkowej

Idea korelacji cząstkowej

p

a

p

ie

ro

s

y

50,8%

Umieralność na CW

Syt. stresowe

30,8%

Unikalna
wariancja
w zmiennej
zależnej
wyjaśniona przez
papierosy

Unikalna
wariancja
w zmiennej
zależnej
wyjaśniona przez
syt. stresowe

Wariancja
w zmiennej
zależnej
wyjaśniona przez
oba predyktory

Przy korelacji
cząstkowej
kontrolujemy efekt
trzeciej zmiennej na
obie pozostałe

Umieralność na CW

Umieralność na CW

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Korelacje

Korelacje

cząstkowe

cząstkowe

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Nasi sąsiedzi

Nasi sąsiedzi



Jak widać, to, czy dana zmienna będzie dobrym

Jak widać, to, czy dana zmienna będzie dobrym

predyktorem zależy od sąsiedztwa z innymi zmiennymi w

predyktorem zależy od sąsiedztwa z innymi zmiennymi w

modelu i tego, czy są one ze sobą skorelowane

modelu i tego, czy są one ze sobą skorelowane

•

(gdyby nie były, wtedy nie zmieniałyby się współczynniki

(gdyby nie były, wtedy nie zmieniałyby się współczynniki

regresji w zależności od tego, która zmienna jest w modelu. (ta

regresji w zależności od tego, która zmienna jest w modelu. (ta

informacja jest ważna przy stosowaniu różnych metod

informacja jest ważna przy stosowaniu różnych metod

wprowadzania danych).

wprowadzania danych).



Patrząc na cząstkowe korelacje dostajemy czysty obraz

Patrząc na cząstkowe korelacje dostajemy czysty obraz

związku, przy kontroli innych zmiennych i widać, które

związku, przy kontroli innych zmiennych i widać, które

zmienne są lepszymi, a które gorszymi predyktorami.

zmienne są lepszymi, a które gorszymi predyktorami.

•

Sugerowane jest zrobienie regresji jeszcze raz, tym razem z

Sugerowane jest zrobienie regresji jeszcze raz, tym razem z

uwzględnieniem w równaniu tylko istotnych predyktorów

uwzględnieniem w równaniu tylko istotnych predyktorów

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Pytanka

Pytanka



Jaka jest różnica między regresją

Jaka jest różnica między regresją

wielokrotną a regresją prostą

wielokrotną a regresją prostą

?

?



Czy

Czy

R

R

2

2

może zmaleć jak wprowadzimy

może zmaleć jak wprowadzimy

kolejne predyktory do modelu

kolejne predyktory do modelu

?

?

•

A co będzie z wartością współczynnika R

A co będzie z wartością współczynnika R



Co to oznacza, że kontrolujemy wpływ

Co to oznacza, że kontrolujemy wpływ

trzeciej zmiennej

trzeciej zmiennej

?

?



W jaki sposób obliczamy wynik

W jaki sposób obliczamy wynik

przewidywany w regresji wielokrotnej

przewidywany w regresji wielokrotnej

?

?

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

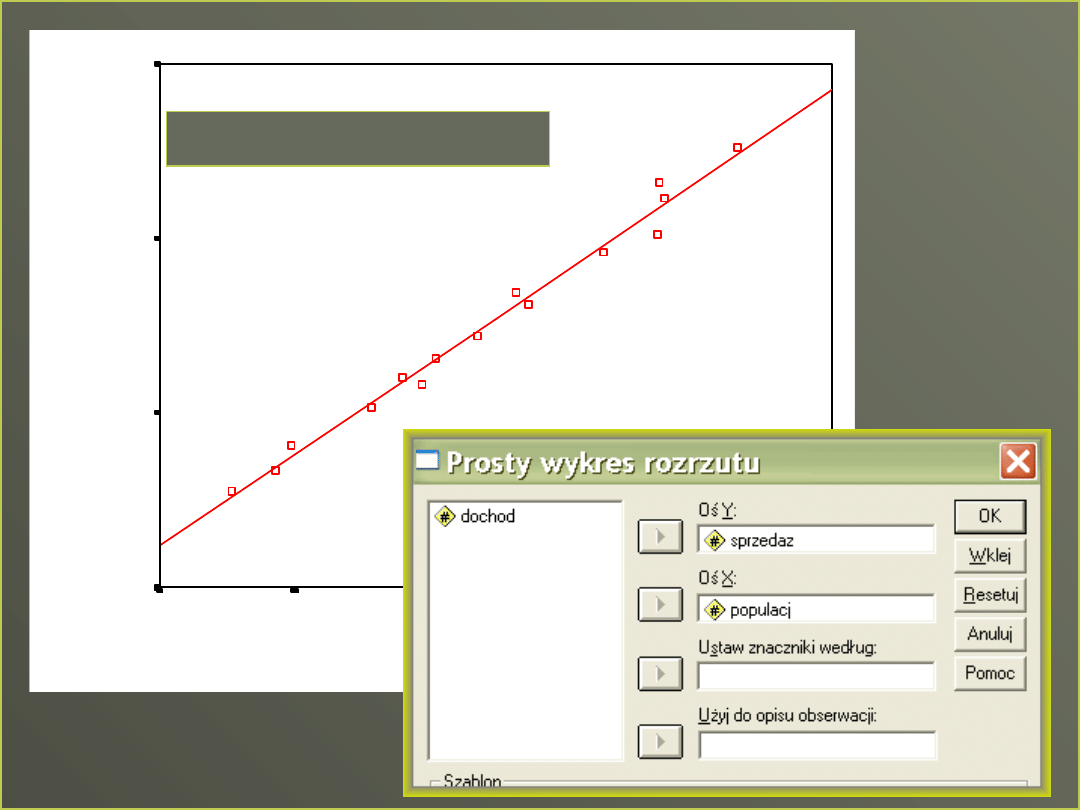
Sprzedaż balsamu do opalania

Sprzedaż balsamu do opalania

w majowy weekend

w majowy weekend



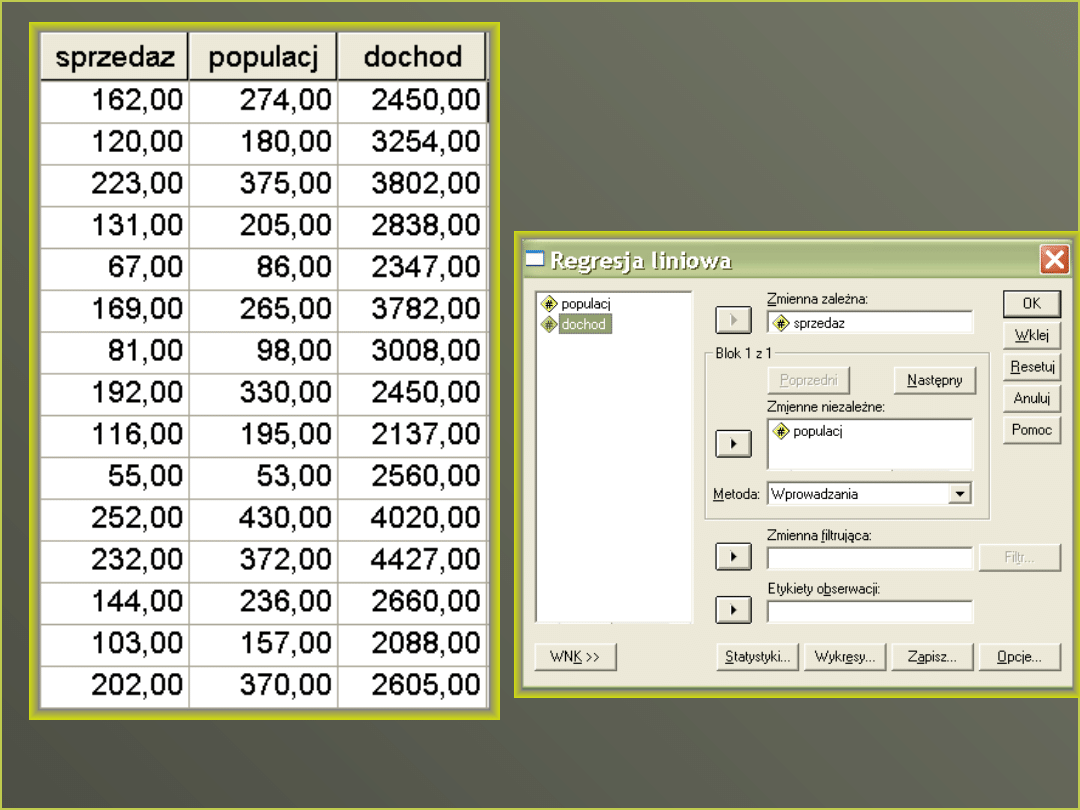
Interesuje nas przewidywana sprzedaż

Interesuje nas przewidywana sprzedaż

balsamu do opalania w majowy weekend w 15

balsamu do opalania w majowy weekend w 15

regionach Polski na podstawie dwóch

regionach Polski na podstawie dwóch

predyktorów:

predyktorów:

•

Liczby mieszkańców

Liczby mieszkańców

•

Średniego dochodu na głowę w danym regionie

Średniego dochodu na głowę w danym regionie



Możemy przeprowadzić dwie niezależne

Możemy przeprowadzić dwie niezależne

regresje liniowe dla każdego z predyktorów, a

regresje liniowe dla każdego z predyktorów, a

następnie sprawdzić pełny model z dwoma

następnie sprawdzić pełny model z dwoma

predyktorami

predyktorami

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Model - Podsumowanie

,993

a

,987

,986

7,3271

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), POPULACJ

a.

Analiza wariancji

b

52069,001

1 52069,001

969,860

,000

a

697,933

13

53,687

52766,933

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), POPULACJ

a.

Zmienna zależna: SPRZEDAZ

b.

Istotność modelu

98% wspólnej wariancji

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynniki

a

23,748

4,472

5,311

,000

,522

,017

,993

31,143

,000

(Stała)
POPULACJ

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: SPRZEDAZ

a.

Patrzymy na współczynnik b=0,522, istotny

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

POPULACJ

500

400

300

200

100

0

S

P

R

ZE

D

A

Z

300

200

100

0

Y’=23,748 +0,522X

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

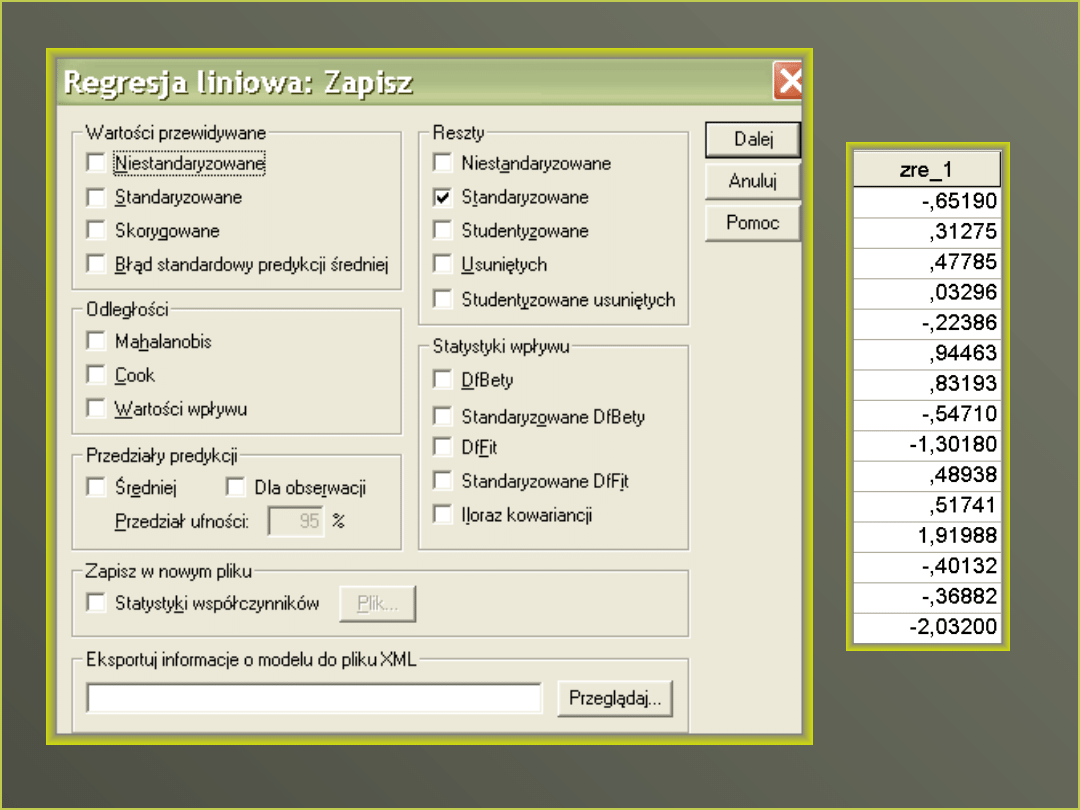
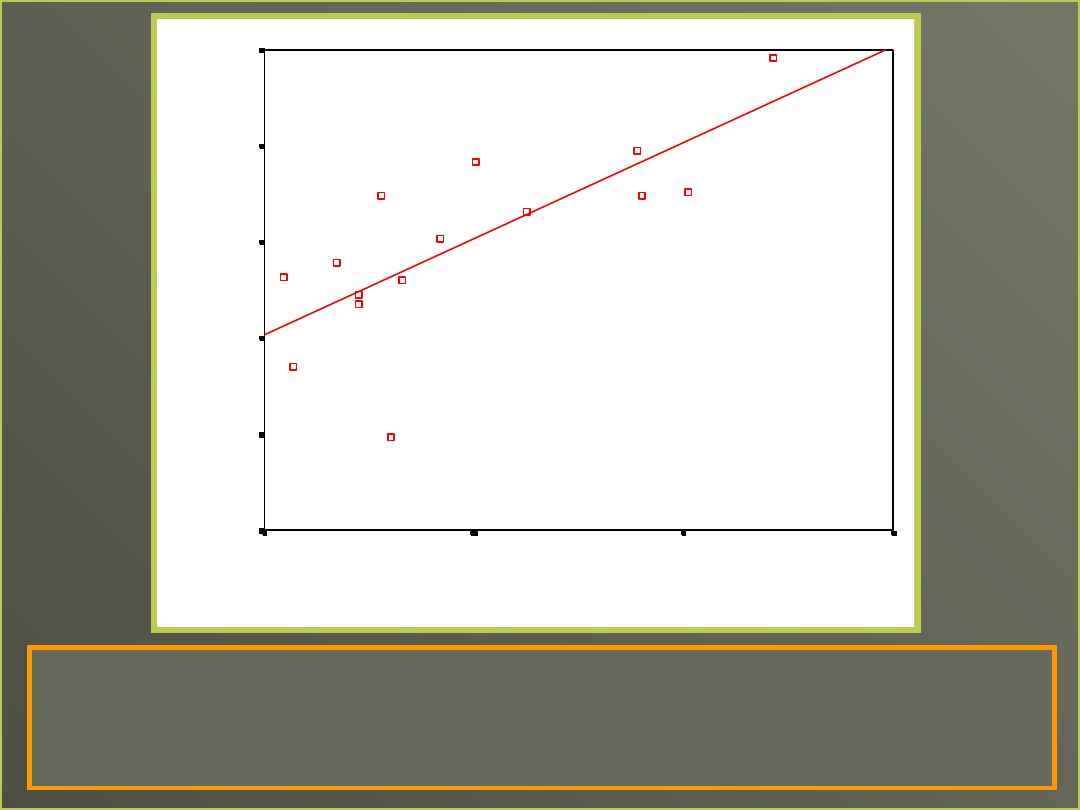
Wykres rozrzutu reszt i zmiennej niezależnej wskazuje na brak
związku i tak być powinno, gdy mamy dobry predyktor

•Stosuje się go do sprawdzenia, czy jest jakiś

•nieliniowy związek między zależną i predyktorem

•Reszty i predyktor nie powinny być skorelowane, ponieważ linia
regresji wyjaśnia większość wariancji zmiennej zależnej, to co
pozostaje to losowy szum w danych

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

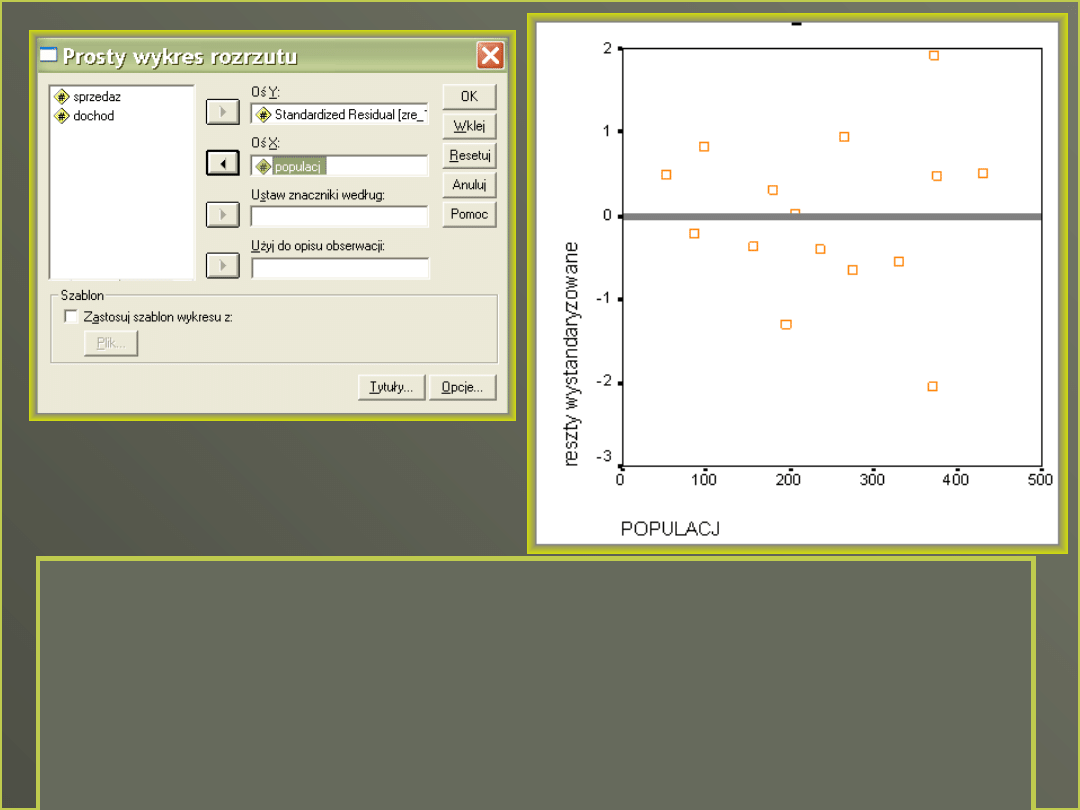
Sprawdźmy czy coś jeszcze może

Sprawdźmy czy coś jeszcze może

wyjaśnić druga zmienna

wyjaśnić druga zmienna

niezależna

niezależna

Można to zobaczyć robiąc

Można to zobaczyć robiąc

wykres rozrzutu reszt z

wykres rozrzutu reszt z

pierwszej regresji z drugim

pierwszej regresji z drugim

predyktorem

predyktorem

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

DOCHOD

5000

4000

3000

2000

S

ta

nd

ar

di

ze

d

R

es

id

ua

l

2

1

0

-1

-2

-3

Jeśli druga zmienna niezależna byłaby nieistotnym
predyktorem wykres ten powinien wyglądać losowo
Widać liniowy związek

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

DOCHOD

5000

4000

3000

2000

S

P

R

ZE

D

A

Z

300

200

100

0

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Model - Podsumowanie

b

,652

a

,425

,381

48,3161

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Analiza wariancji

b

22419,103

1 22419,103

9,604

,008

a

30347,831

13 2334,449

52766,933

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Współczynniki

a

-12,288

53,813

-,228

,823

5,477E-02

,018

,652

3,099

,008

(Stała)
DOCHOD

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: SPRZEDAZ

a.

Widać po R2, że
dopasowanie
tego modelu jest
mniejsze od
poprzedniego
modelu, widać to
również po
błędzie
standardowym

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Wprowadźmy obie zmienne do
modelu

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Model - Podsumowanie

b

,999

a

,998

,998

2,9903

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), POPULACJ, DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Analiza wariancji

b

52659,632

2 26329,816 2944,578

,000

a

107,302

12

8,942

52766,933

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), POPULACJ, DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Przy dodaniu
kolejnej
zmiennej do
modelu R2
zawsze wzrasta

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Model - Podsumowanie

b

,999

a

,998

,998

2,9903

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), POPULACJ, DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Model - Podsumowanie

,993

a

,987

,986

7,3271

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), POPULACJ

a.

Jeżeli R2 skorygowane z modelu z dwiema zmiennymi
jest mniejsze niż w modelu z 1 zmienną

wtedy nie ma sensu włączać drugiej zmiennej do

modelu

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza wariancji

b

52659,632

2 26329,816 2944,578

,000

a

107,302

12

8,942

52766,933

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), POPULACJ, DOCHOD

a.

Zmienna zależna: SPRZEDAZ

b.

Analiza wariancji

b

52069,001

1 52069,001

969,860

,000

a

697,933

13

53,687

52766,933

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), POPULACJ

a.

Zmienna zależna: SPRZEDAZ

b.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynniki

a

1,029

3,338

,308

,763

1,081E-02

,001

,129

8,127

,000

,484

,008

,920

58,154

,000

(Stała)
DOCHOD
POPULACJ

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: SPRZEDAZ

a.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Metody wprowadzenia

Metody wprowadzenia

zmiennych - krokowa

zmiennych - krokowa

Model - Podsumowanie

c

,993

a

,987

,986

7,3271

,987

969,860

1

13

,000

,999

b

,998

,998

2,9903

,011

66,053

1

12

,000

Model
1
2

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Zmiana

R-kwadrat

Zmiana F

df1

df2

Istotność

zmiany F

Statystyki zmiany

Predyktory: (Stała), POPULACJ

a.

Predyktory: (Stała), POPULACJ, DOCHOD

b.

Zmienna zależna: SPRZEDAZ

c.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Analiza wariancji

c

52069,001

1 52069,001

969,860

,000

a

697,933

13

53,687

52766,933

14

52659,632

2 26329,816 2944,578

,000

b

107,302

12

8,942

52766,933

14

Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem

Model
1

2

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), POPULACJ

a.

Predyktory: (Stała), POPULACJ, DOCHOD

b.

Zmienna zależna: SPRZEDAZ

c.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Współczynniki

a

23,748

4,472

5,311

,000

,522

,017

,993

31,143

,000

1,029

3,338

,308

,763

,484

,008

,920

58,154

,000

1,081E-02

,001

,129

8,127

,000

(Stała)
POPULACJ
(Stała)
POPULACJ
DOCHOD

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczy

nniki

standaryz

owane

t

Istotność

Zmienna zależna: SPRZEDAZ

a.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz



Zwróćmy uwagę również na to, że

Zwróćmy uwagę również na to, że

zmieniły się współczynniki b i bety

zmieniły się współczynniki b i bety

(zależne od tego, co wprowadzimy do

(zależne od tego, co wprowadzimy do

modelu)

modelu)



stąd jeśli interesuje nas predykcja

stąd jeśli interesuje nas predykcja

lepiej pozostać na poziomie prostej

lepiej pozostać na poziomie prostej

analizy regresji z 1 predyktorem, góra

analizy regresji z 1 predyktorem, góra

dwoma predyktorami – życie staje się

dwoma predyktorami – życie staje się

prostsze.

prostsze.

Materiały do wykładu

Materiały do wykładu

Izabela Krejtz

Izabela Krejtz

Regresja wielokrotna

Regresja wielokrotna



Rozszerzenie prostej regresji liniowej

Rozszerzenie prostej regresji liniowej



Sposób na stwierdzenie, w jaki sposób wiele

Sposób na stwierdzenie, w jaki sposób wiele

zmiennych wyjaśniających (predyktorów) jest

zmiennych wyjaśniających (predyktorów) jest

związanych ze zmienną wyjaśnianą (zależną)

związanych ze zmienną wyjaśnianą (zależną)

•

Zmienna zależna

Zmienna zależna

y,

y,

ale wiele predyktorów:

ale wiele predyktorów:

x1, x2, x3....

x1, x2, x3....



Daje informację o tym, jaki jest wpływ wszystkich

Daje informację o tym, jaki jest wpływ wszystkich

zmiennych wyjaśniających i każdej z osobna na

zmiennych wyjaśniających i każdej z osobna na

zmienną zależną

zmienną zależną



y= b1*x1 + b2*x2 + b3*x3.... + stała

y= b1*x1 + b2*x2 + b3*x3.... + stała

•

stała, jeśli wszystkie predyktory = 0

stała, jeśli wszystkie predyktory = 0



Przeprowadza się tak jak regresję liniową prostą,

Przeprowadza się tak jak regresję liniową prostą,

dodaje się tylko więcej zmiennych wyjaśniających

dodaje się tylko więcej zmiennych wyjaśniających