Pojęcie korelacji
szukanie związku
między dwiema
zmiennymi

Wykład 3

Co to oznacza że dwie zmienne
korelują ze sobą



Oznacza to, że ich wyniki zmieniają się
wspólnie



Jeśli zmieniają się wyniki na jednej
zmiennej, wyniki na drugiej zmieniają się w
przewidywalny sposób



Innymi słowy zmienne te nie są niezależne
od siebie



rączki

Wykres rozrzutu



Zazwyczaj używa się tego rodzaju wykresu do
pokazania współzależności pomiędzy dwoma
zmiennymi



Dwa wymiary pokazujące rozkład wyników dla
dwóch zmiennych



Każdy wymiar pokazuje wartości liczbowe
danej zmiennej



uwaga: najlepiej przedstawiać na tym typie
wykresu dane na mierzone, co najmniej, na
skali przedziałowej

Cel przeprowadzenia analizy
korelacji



Sprawdzenie czy istnieje związek
między dwiema zmiennymi



Określenie kierunku związku



Czy jest pozytywny, negatywny, czy równy zeru



Określenie siły związku między dwiema
zmiennymi



od 0 do 1 – bez względu na znak

Kierunek związku



Pozytywny



Wysokim wynikom na jednej zmiennej

towarzyszą wysokie wyniki na drugiej zmiennej;

a niskim wynikom na jednej – niskie na drugiej



Negatywny



Wysokim wynikom na jednej zmiennej

towarzyszą niskie na innej



sufit



Korelacja = zero



Oznacza, że nie ma liniowego związku między

zmiennymi

Kierunek związku



Związek między poziomem bezrobocia
a występkami



Szybkość mówienia prowadzącego
zajęcia a poziom zrozumienia materiału



Wiek siostry i brata

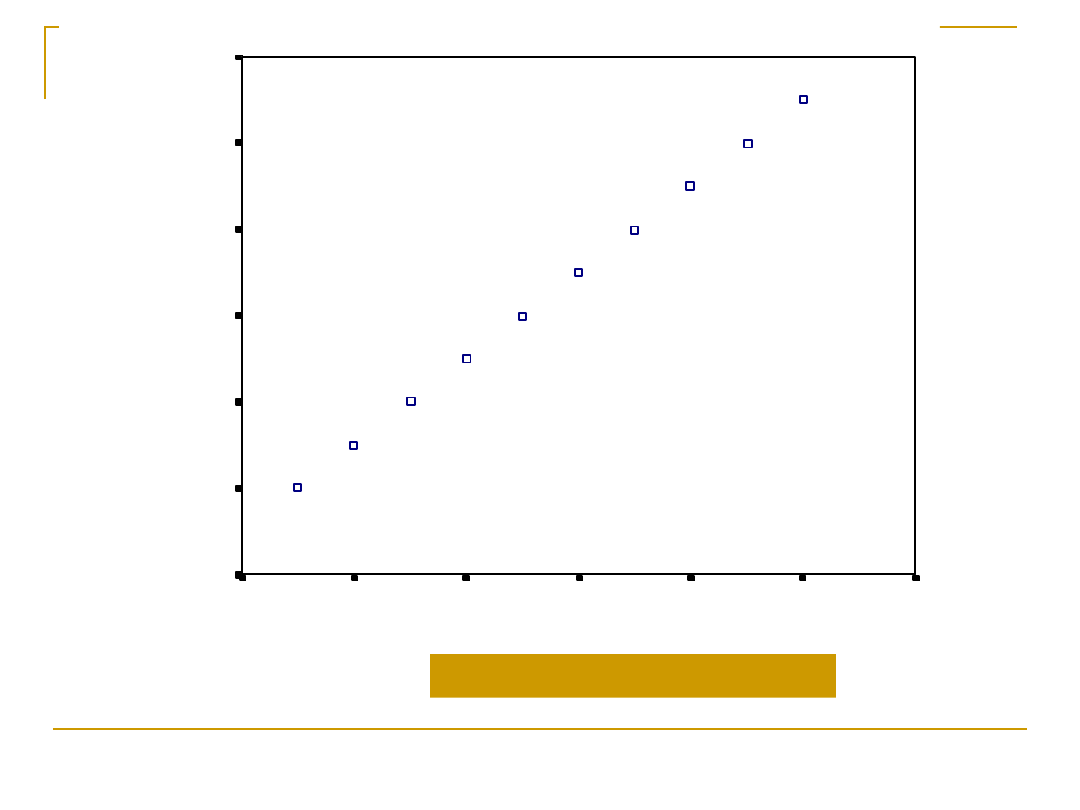
BRAT

14

12

10

8

6

4

2

S

IO

S

T

R

A

12

10

8

6

4

2

0

Idealna pozytywna korelacja

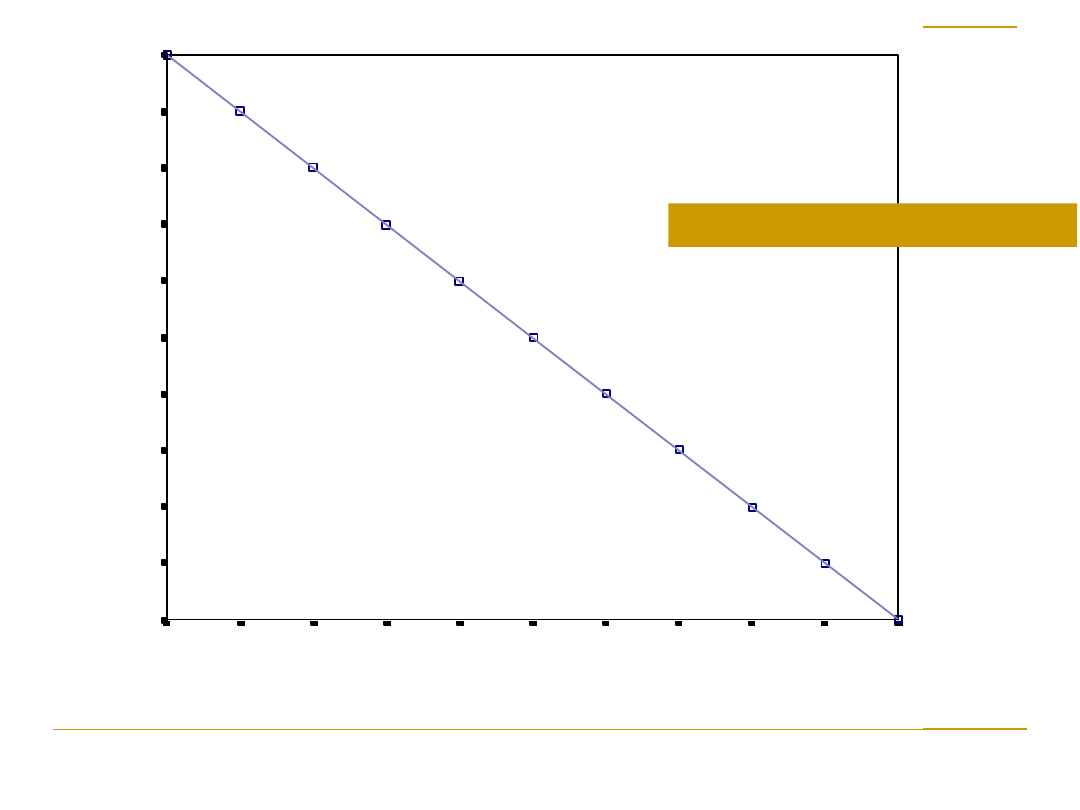
ZLOTOWKI

10

9

8

7

6

5

4

3

2

1

0

B

A

T

O

N

IK

I

10

9

8

7

6

5

4

3

2

1

0

Idealna negatywna korelacja

Siła korelacji – współczynnik
korelacji



Współczynnik korelacji może
przyjmować warości z przedziału:



(0; 1) , plus – pozytywna, 1 idealna



(-1; 0), minus – ujemny związek, 1 idealny



+1 =idealny związek



-1 = idelany związek



To, że współczynnik korelacji jest ujemny
nie oznacza, że jest mniej istotny, czy silny,
niż pozytywny

-1

idealna

+1

-0,9

+0,9

-0,8

silna

+0,8

-0,7

+0,7

-0,6

+0,6

-0,5

umiarkowana

+0,5

-0,4

+0,4

-0,3

słaba

+0,3

-0,2

+0,2

-0,1

+0,1

0

Współczynnik korelacji pokazuje jak bardzo punkty są skupione

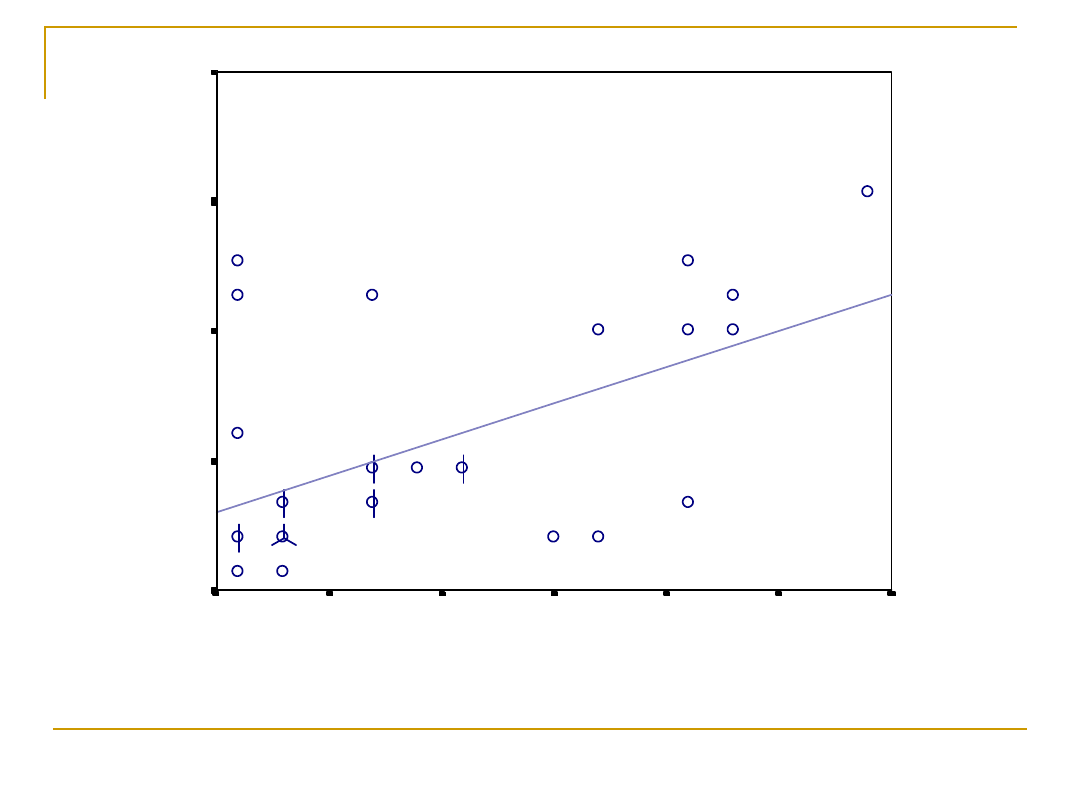
WIEK

70

60

50

40

30

20

10

W

IE

D

ZA

40

30

20

10

0

Korelacja umiarkowana r=0,54

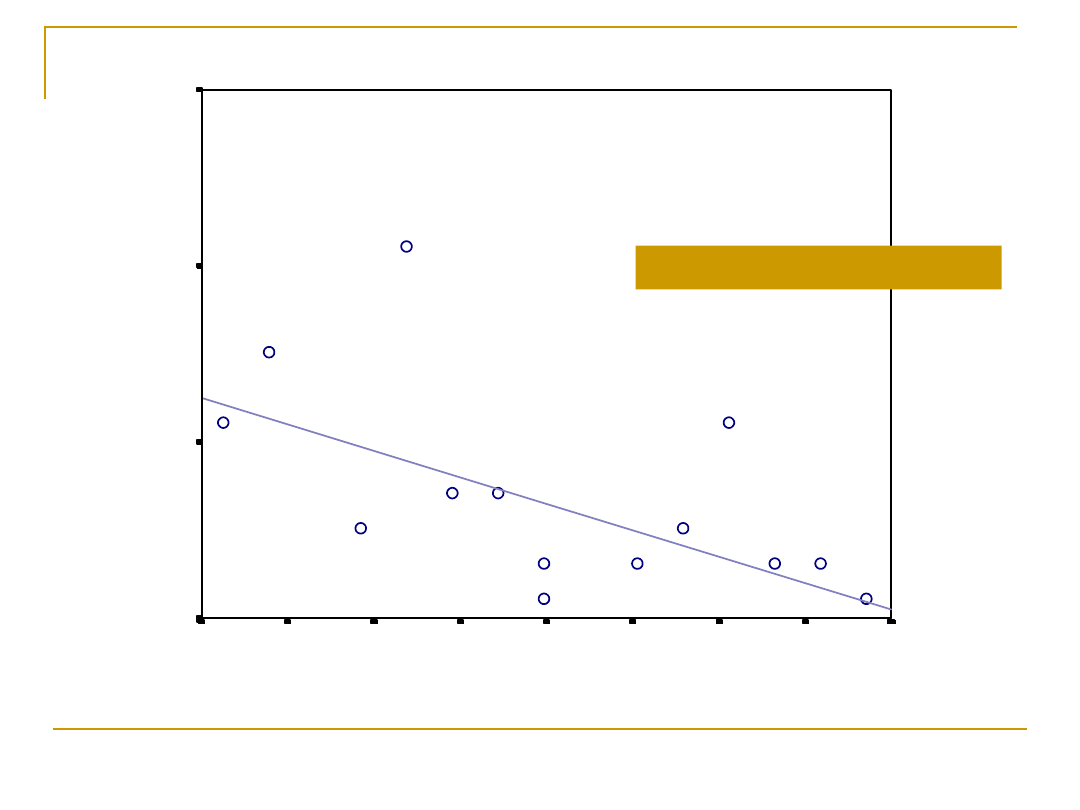
ciekawość poznawcza

18

16

14

12

10

8

6

4

2

un

ik

an

ie

w

ys

iłk

u

po

zn

aw

cz

eg

o

30

20

10

0

Korelacja ujemna r=-0,58

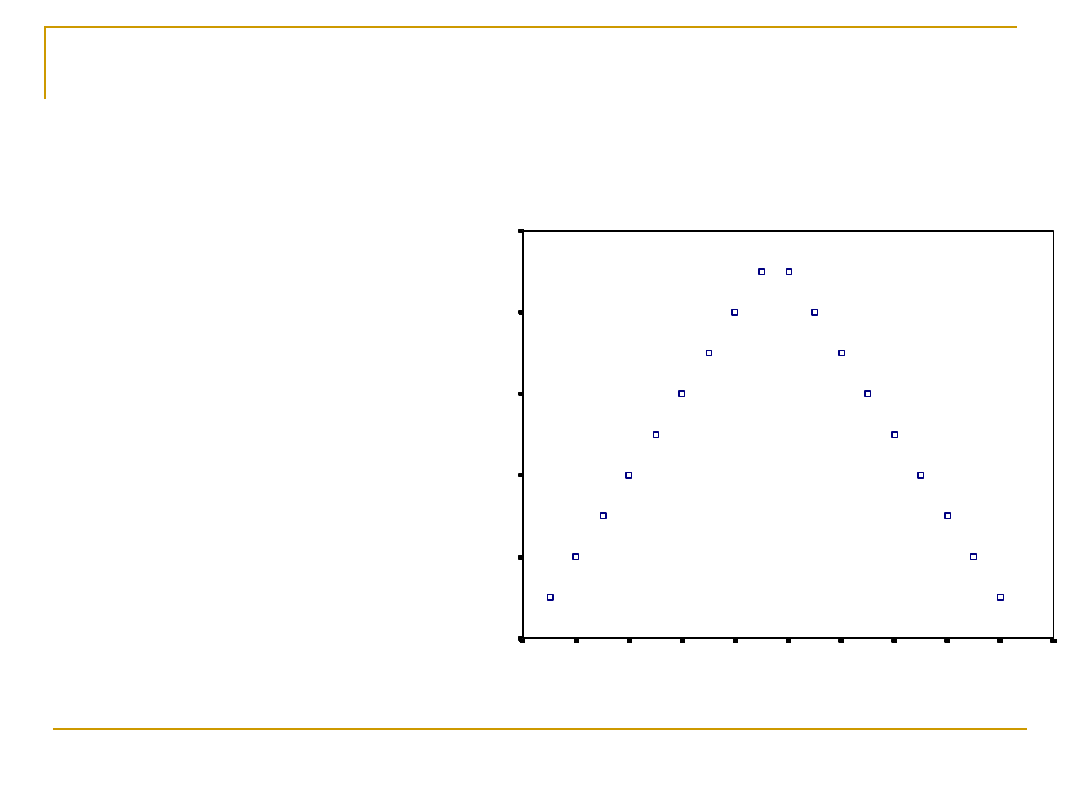
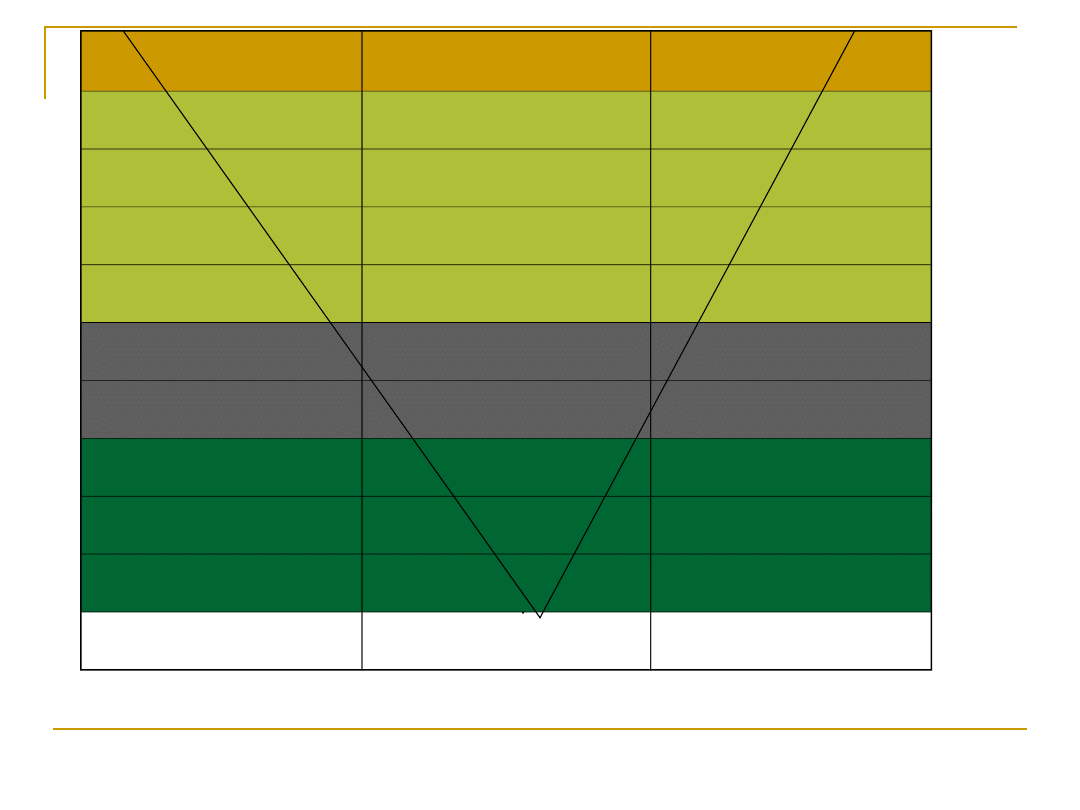
Jeśli współczynnik korelacji
=0



To jeszcze wcale
nie oznacza, że
dwie zmienne
nie są ze sobą
związane



Oznacza to, że
na pewno nie ma
między nimi
liniowego
związku

poziom pobudzenia

20

18

16

14

12

10

8

6

4

2

0

w

yk

on

an

ie

z

ad

an

ia

10

8

6

4

2

0

Współczynnik
r-Pearsona

Wyznaczniki atrakcyjności
interpersonalnej

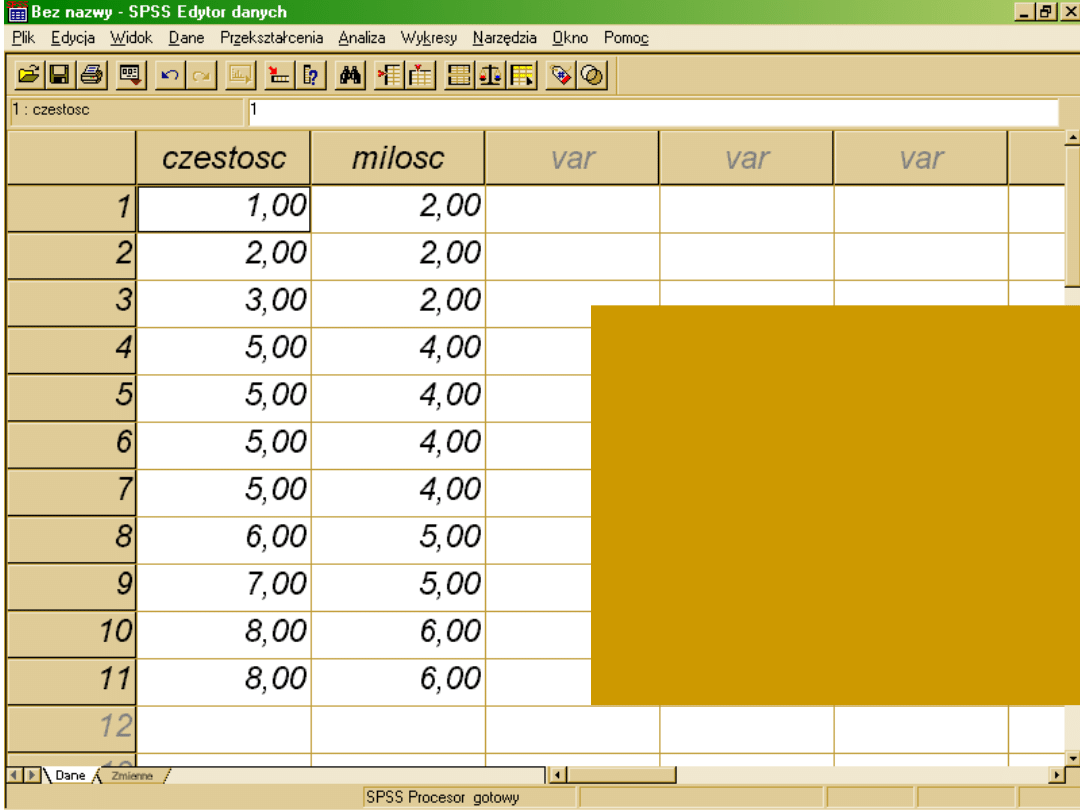
Częstość spoglądania w oczy – ile
razy spojrzeli sobie w oczy w
ciągu godziny

Poczucie bliskości – na skali od 1
do 6

Dane wprowadzane jak dla
schematu korelacyjnego – każda
ze zmiennych w oddzielnej
kolumnie

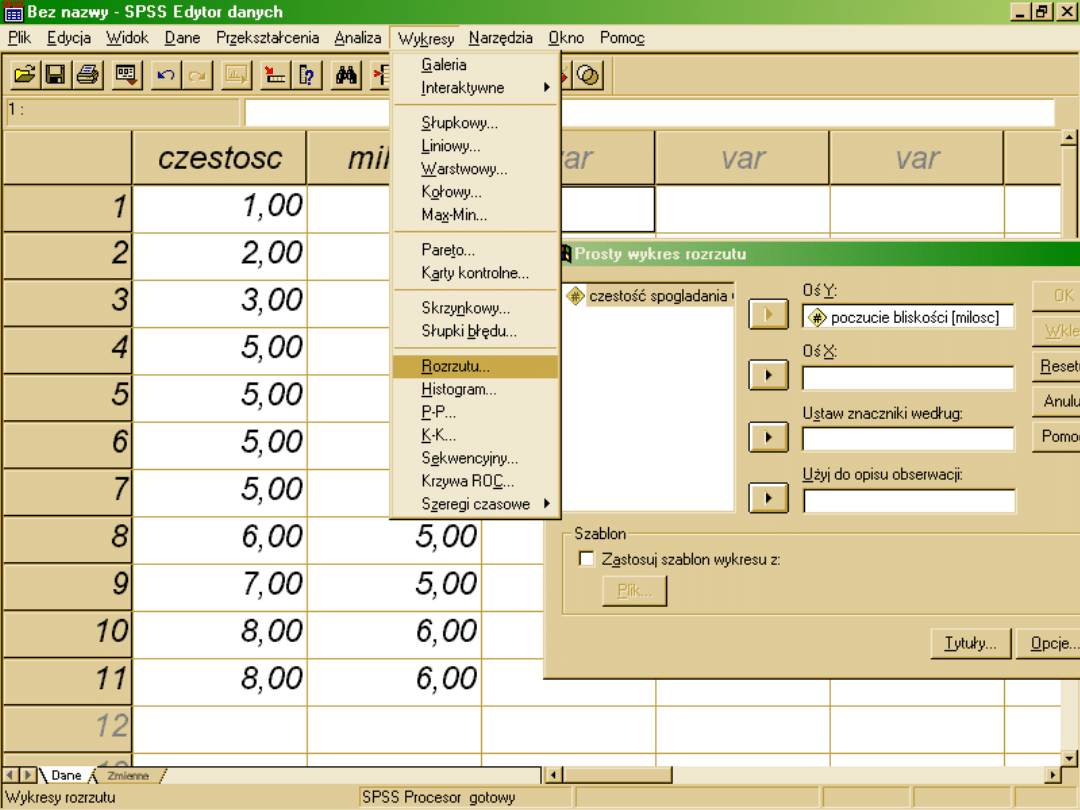
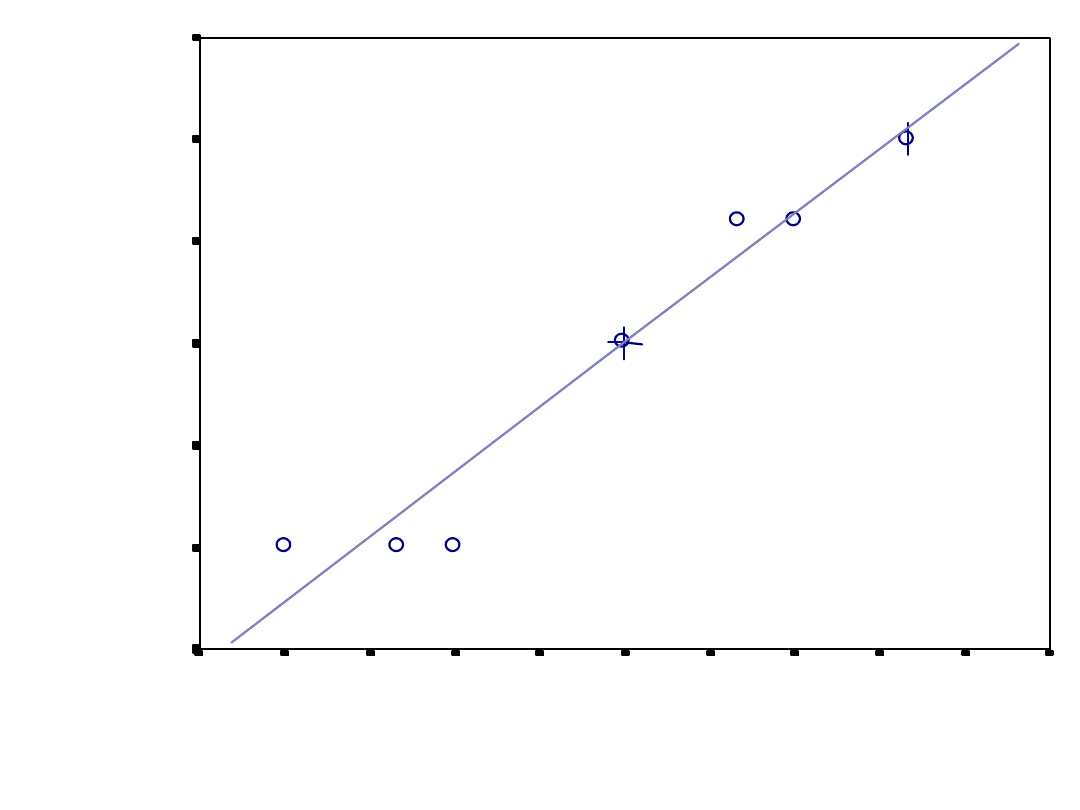
czestość spogladania w oczy

10

9

8

7

6

5

4

3

2

1

0

po

cz

uc

ie

b

lis

ko

śc

i

7

6

5

4

3

2

1

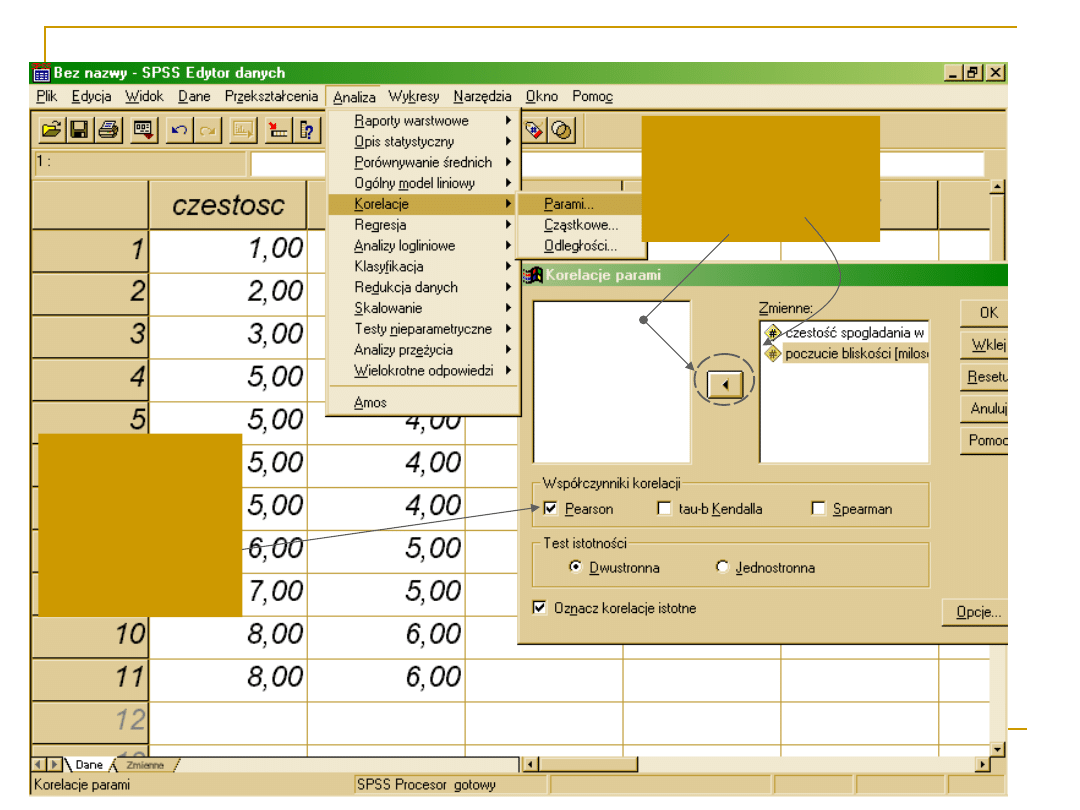
korelacja parami

Wybieramy

dwie zmienne

z listy

zmiennych

Zaznaczamy
korelację
Pearsona,
aby otrzymać
wskaźnik R-
Pearsona

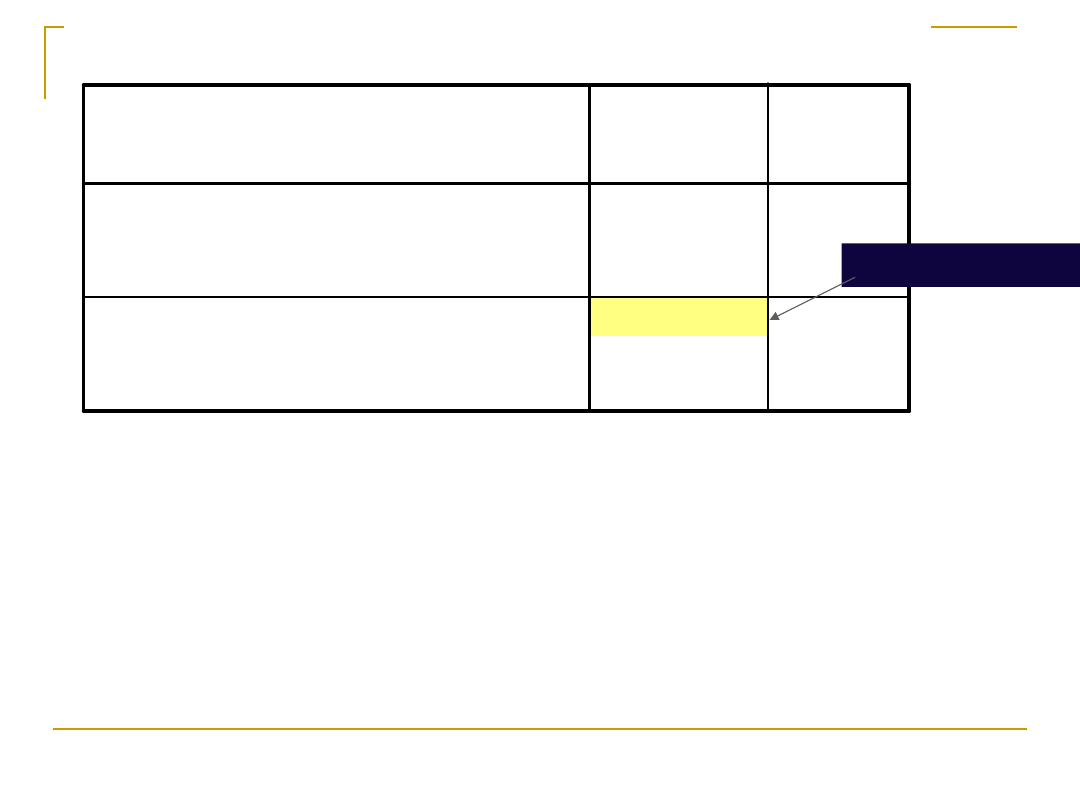
Korelacje

,976

11

Korelacja Pearsona

N
Korelacja Pearsona

N

czestość
spogladania w oczy

poczucie bliskości

czestość

spogladania

w oczy

poczucie

bliskości



Współczynnik korelacji Pearsona może przyjmować

wartości z przedziału -1 do 1.



Wartość ujemna wskazuje na negatywny związek między

zmiennymi (X maleje a Y wzrasta)



Wartość dodatnia pokazuje na związek pozytywny

pomiedzy zmiennymi (X rośnie i Y rośnie, X maleje i Y

maleje)

0,975665453382

Jak wyliczyć współczynnik r-
Pearsona



Ponieważ porównujemy wyniki dwóch zmiennych
mierzonych na różnych skalach, współczynnik
korelacji musi brać pod uwagę różne zakresy skali



Należy wystandaryzować wyniki obu zmiennych

Statystyki opisowe

11

1,00

8,00 5,0000

2,3000

11

2,00

6,00 4,0000

1,5000

11

czestość spogladania
w oczy
poczucie bliskości

N Ważnych (wyłączanie
obserwacjami)

N

Minimum Maksimum

Średnia

Odchylenie

standardowe

standaryzacja



Zmieniamy rozkład naszej zmiennej :



Średnia =0



Odchylenie standardowe =1



Wartości z leżące poniżej średniej są ujemne



Wartości większe od średniej mają z dodatnie

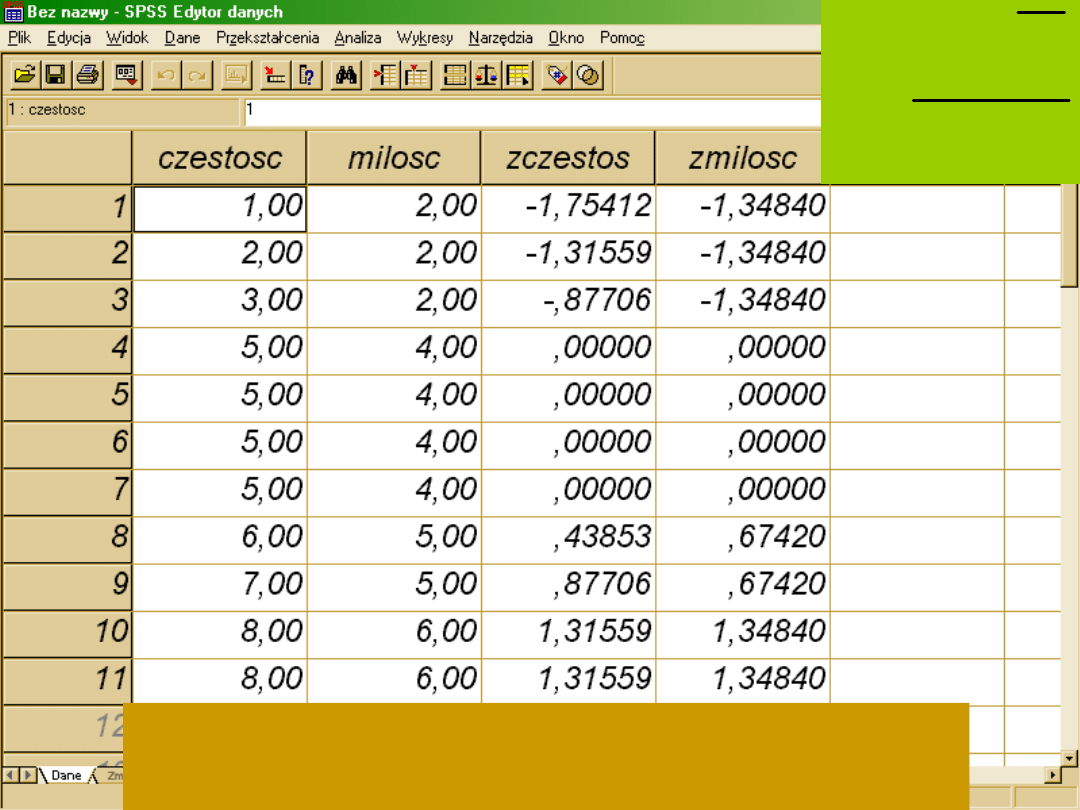
SD

X

X

z





Jeśli silna zależność to np. wyraźnie niskim wartościom z,
na jednej zmiennej to na drugiej zmiennej też.
Interesuje nas relatywne położenie wyników na obu skalach

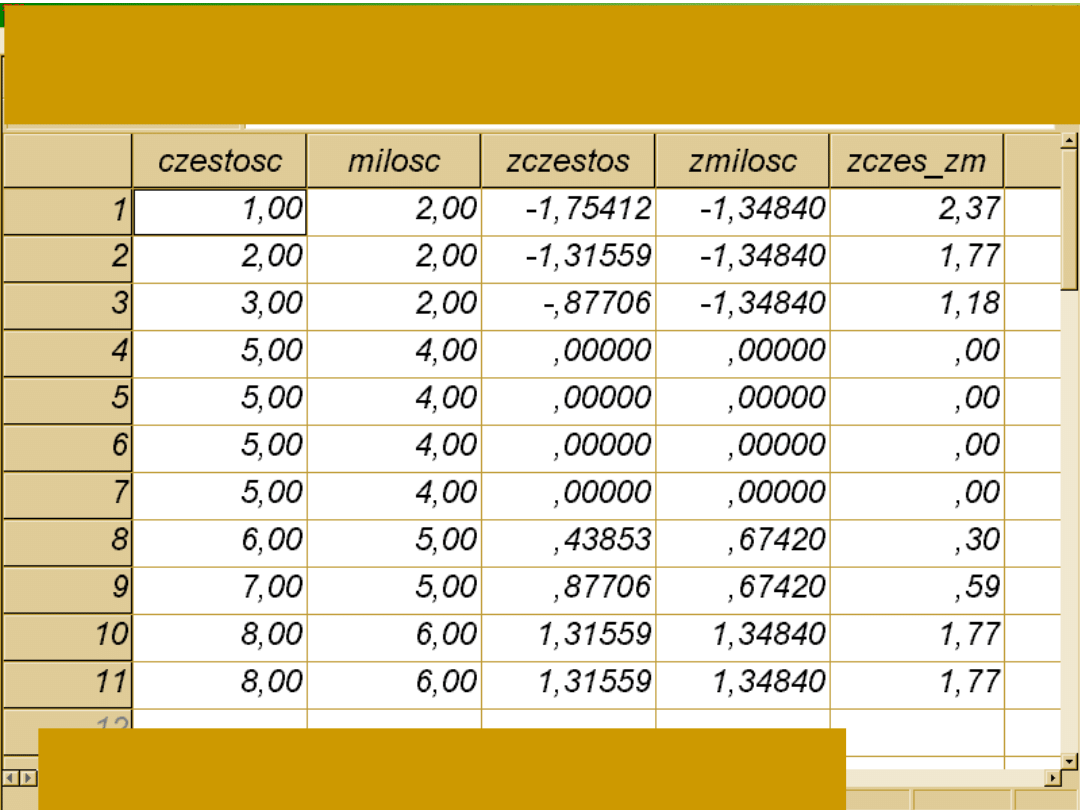
Następnie mnożymy wartości wystandaryzowane obu zmiennych
przez siebie
– uzyskujemny moment iloczynowy

sumujemy iloczyny i dzielimy przez liczbę
obserwacji - 1

wzór

1













N

z

z

r

x

y

SD

X

X

z

Kolejne kroki obliczania
współczynnika r-Pearsona



Wszystkie wyniki na obu skalach
zamieniamy na z (na podstawie
odpowiednich średnich i odchyleń
standardowych)



Obliczamy moment iloczynowy (mnożymy
odpowiednie wartości z przez siebie)



Dodajemy iloczyny do siebie



Dzielimy przez liczbę obserwacji minus 1

Wspólna zmienność wyjaśniona
przez współczynnik korelacji



Podnosząc współczynnik korelacji do
kwadratu, możemy dostać oszacowania
wspólnej wariancji (zmienności) obu
zmiennych

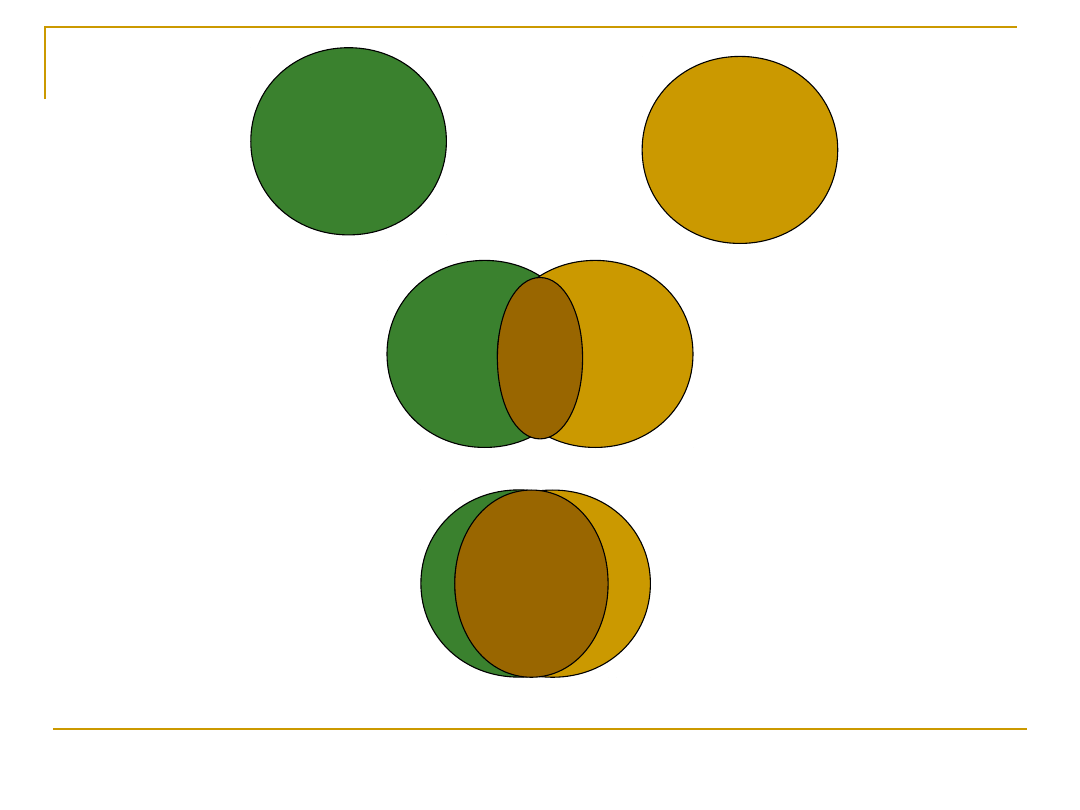
r=0

r=0.5 >> r

2

=0,25 >> 25%

r=-0.8 >> r

2

=0,64 >> 64%

64% zmienności jednej
zmiennej
może być wyjaśnione
przez zmienność
wartości drugiej
zmiennej