Analiza wariancji w schemacie z
powtarzanymi pomiarami

-

Schematy jednoczynnikowe

-

Schematy dwuczynnikowe

-

Schematy mieszane

Powtarzany pomiar w schemacie
jednoczynnikowym



Krótkie przypomnienie o czym rzecz i jakie

ma założenia



Pomiar zmiennej zależnej na skali ilościowej



Rozkład normalny zmiennej zależnej w każdym

pomiarze



Korelacje pomiędzy każdą parą pomiarów

(warunków eksperymentalnych) podobne;

innymi słowy:

wariancje różnic między dowolnymi

dwoma pomiarami podobne

(założenie o

sferyczności)

Jeszcze o F

F =

średni kwadrat pomiarów/ średni kwadrat błędu

MS pomiar x MS osób

Uwzględnia różnice
indywidualne

Pomiar 1

Pomiar 2

Pomiar 3

Osoba 1

1

2

4

Osoba 2

4

3

2

MS pomiar

MS miedzy
osobami

Gdy założenia spełnione – przykład o
alkoholu



W artykułach prasowych znajdujemy coraz

więcej doniesień o pozytywnych skutkach

picia alkoholu



Rozważane są np. krótkotrwałe i długotrwałe

skutki spożywania alkoholu



Pytanie: czy rodzaj spożywanego alkoholu

odgrywa jakąś rolę



Sprawdzano wpływ czystej wody, piwa oraz

wina na poziom koordynacji



Wskaźnik koordynacji: liczba poprawnie

wykonanych „jaskółek” (w ośmiu próbach)

Wino, piwo i jaskółki



Każdy badany najpierw wypijał wodę i robił
serię jaskółek, następnego dnia to samo z
piwem oraz winem



Kolejność picia wody, wina czy piwa losowa
(ważne ze względu na możliwy efekt
wytrenowania osób badanych w robieniu
jaskółki)



Pytanie: czy rodzaj wypitego płynu wpływał
na zdolność do robienia jaskółek?

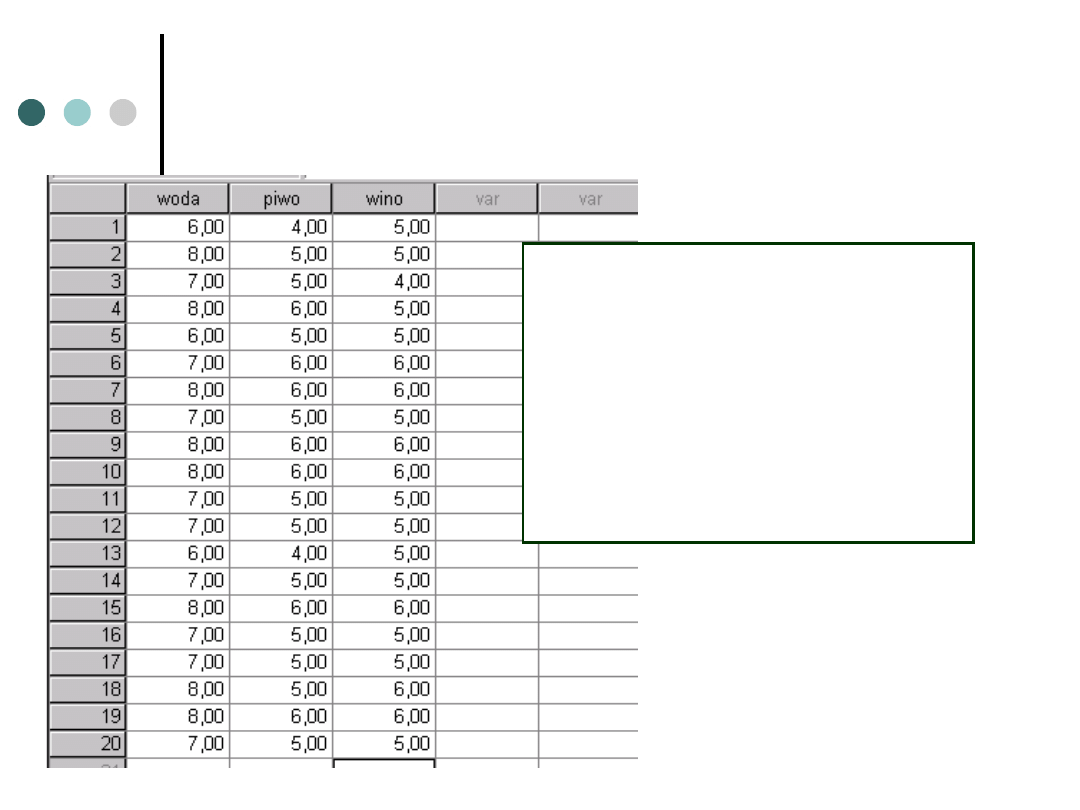
Jak wyglądają dane?

Każda osoba wykonywała
jaskółki po wypiciu zarówno
wody jak i piwa czy wina.
Nie potrzebujemy, w
przeciwieństwie do
schematów między
osobami, zmiennej
kategoryzującej.

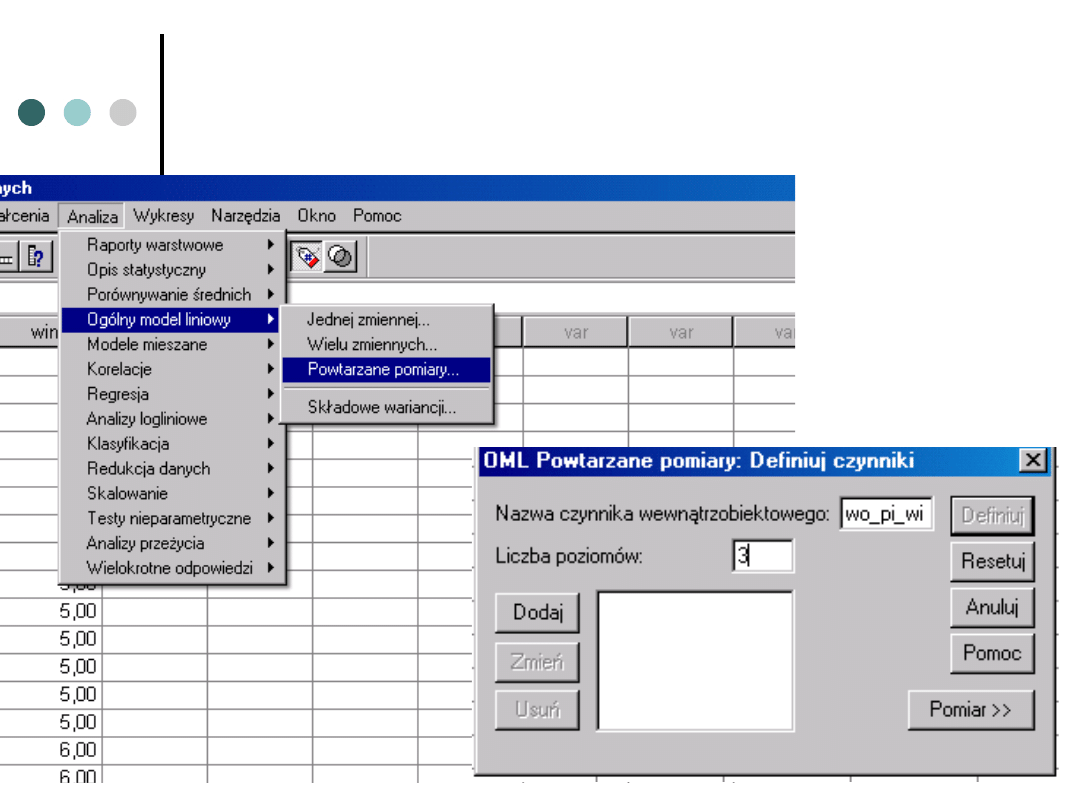
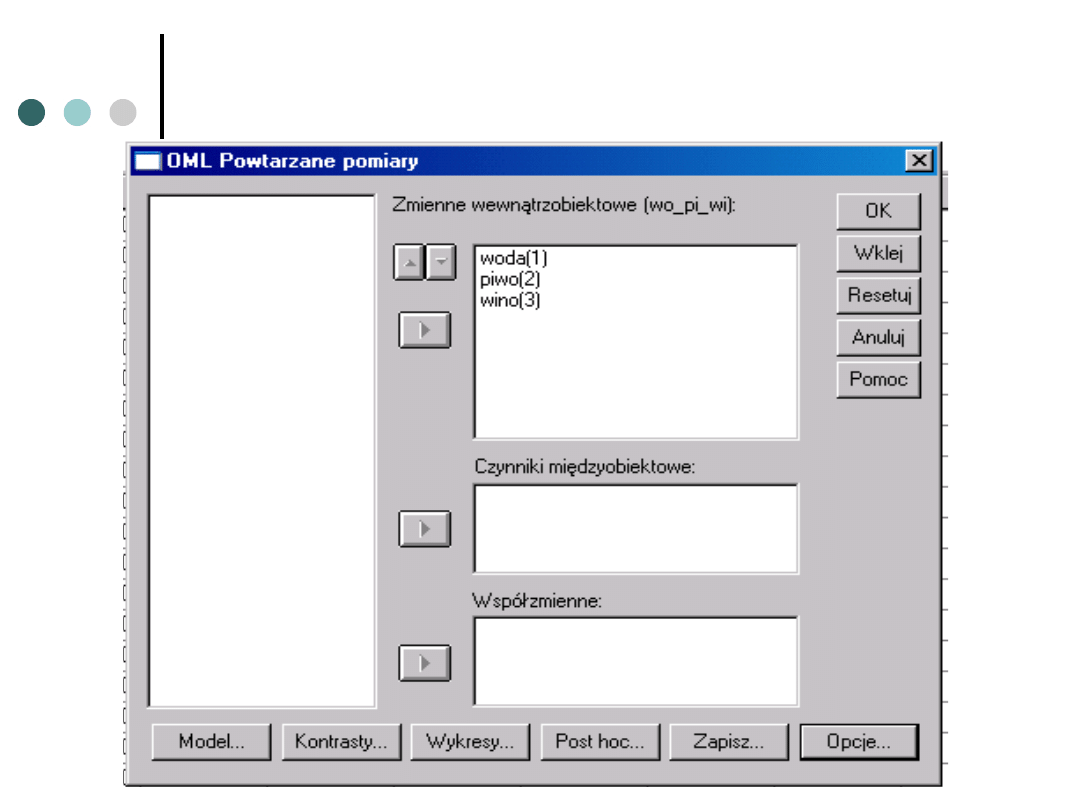
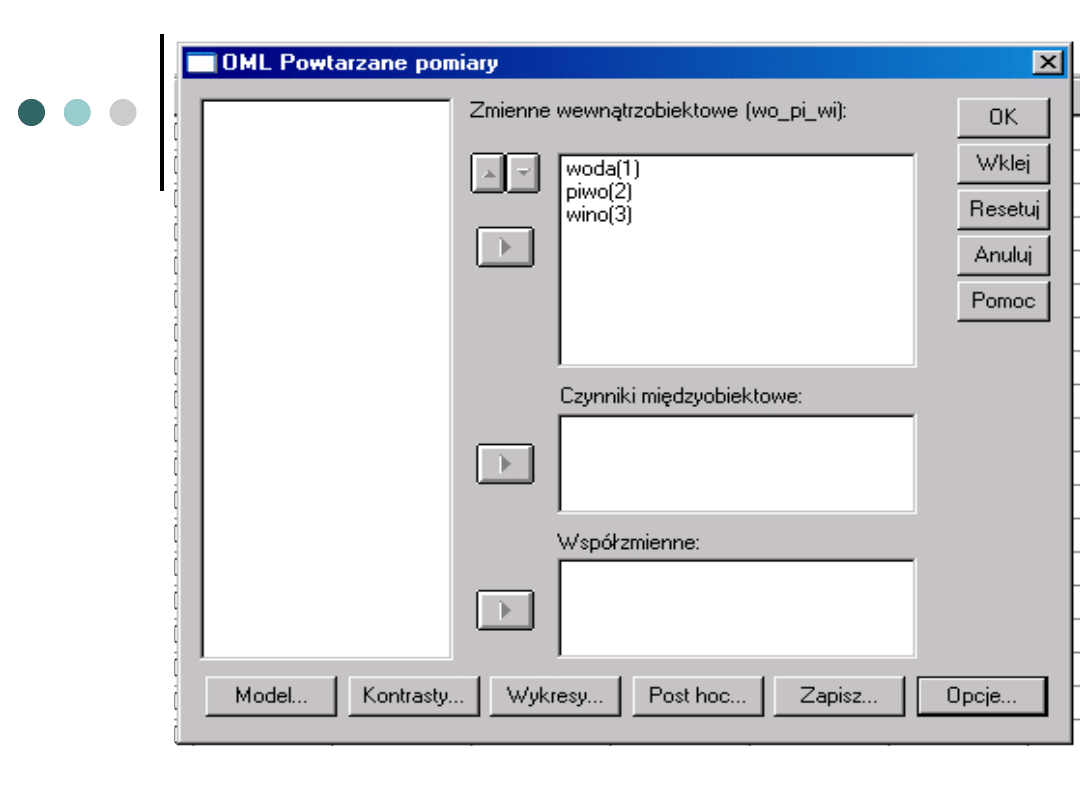
Powtarzane pomiary w SPSS

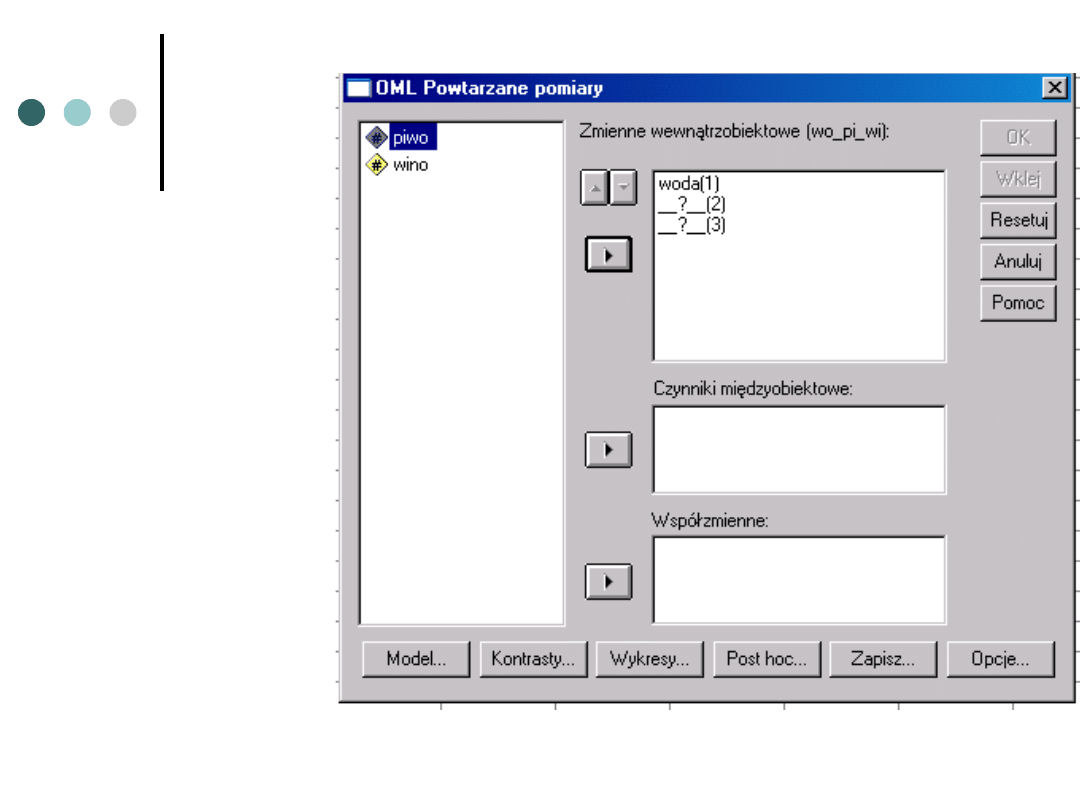
Definiujemy
zmienne,
które składają
się na nasz
czynnik, oraz
ich kolejność

Sprawdzamy założenia



Zmienna zależna – liczba wykonanych
poprawnie jaskółek



Rozkład normalny (K-S w każdym pomiarze:
woda - 0,156; piwo – 0,072; wino – 0,147)



Sferyczność – to założenie sprawdzane
specjalnym testem Mauchly’ego



H0:

wariancja

woda-piwo

=wariancja

woda-wino

=wariancja

piwo-wino

Testowanie założenia o sferyczności

W naszym przykładzie założenie to jest
spełnione (nie odrzucamy H0 testu
Mauchly’ego)

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,864

2,626

2

,269

,880

,963

,500

Efekt wewnątrzobiektowy
WO_PI_WI

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: WO_PI_WI

b.

Odczytujemy test F

Df

błędu

= 38, Df

błędu

=(N-1)*(k-1), wiemy, że trzy warunki

(df

pomiar

),

więc osób jest 20 (19*2=38; 19+1=20)

Zapisujemy: F(2,38) = 147,35; p<0,001; Ile osób zostało
przebadanych?

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

60,233

2

30,117

147,352

,000

60,233

1,761

34,205

147,352

,000

60,233

1,927

31,258

147,352

,000

60,233

1,000

60,233

147,352

,000

7,767

38

,204

7,767

33,458

,232

7,767

36,613

,212

7,767

19,000

,409

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
WO_PI_WI

Błąd(WO_PI_WI)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Statystyki opisowe



Które średnie różnią się w sposób istotny statystycznie?

Statystyki opisowe

7,2500

,7164

20

5,1500

,6708

20

5,1000

,7182

20

koordynacja po
szklance wody
koordynacja po piwie
koordynacja po winie

Średnia

Odchylenie

standardowe

N

?

?

Jak porównać średnie?

?

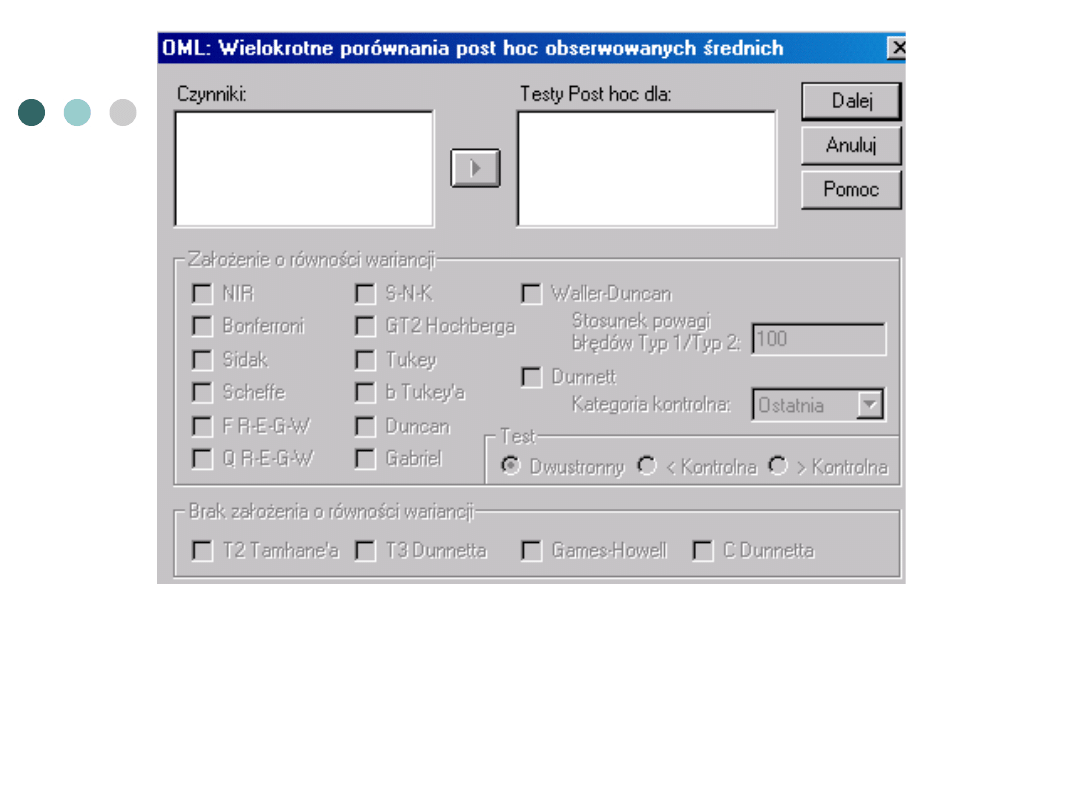
Nie ma możliwości wykonania testów post hoc dla
czynników w powtarzanym pomiarze w opcji post
hoc

?

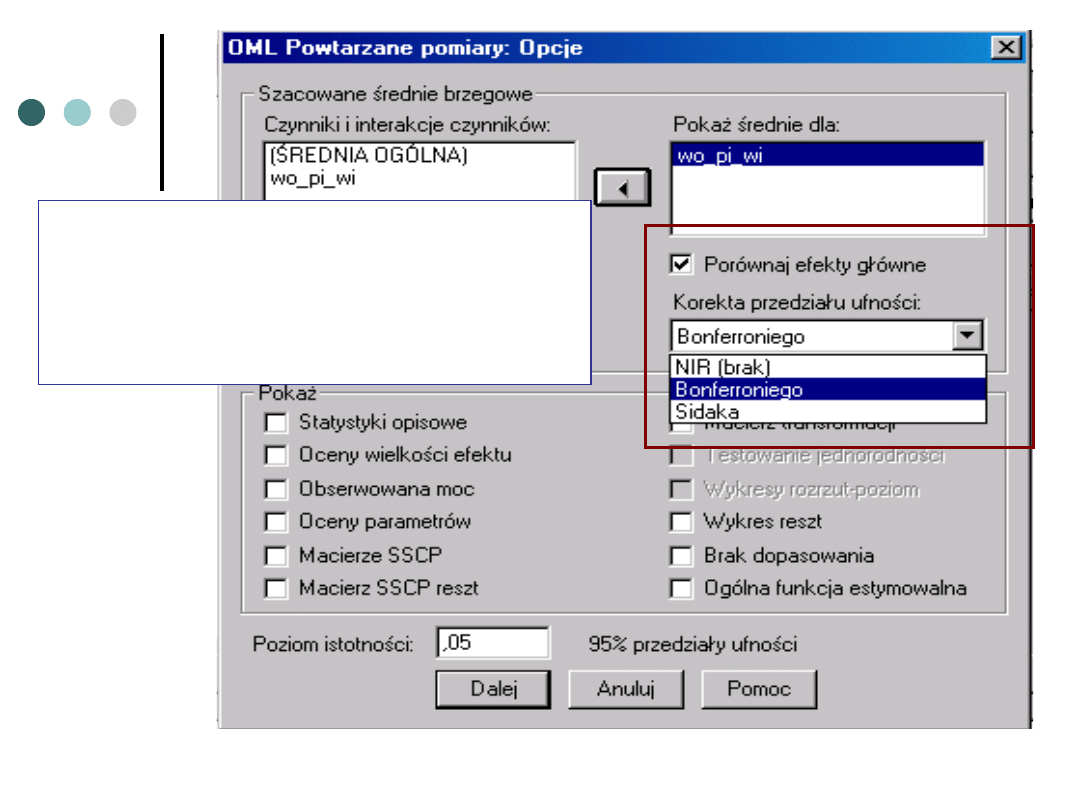
Zaznaczając tę opcję mamy
możliwość wykonania
porównań wielokrotnych, ale
tylko dla efektów głównych

Porównania parami

Miara: MIARA_1

2,100*

,124

,000

1,777

2,423

2,150*

,167

,000

1,714

2,586

-2,100*

,124

,000

-2,423

-1,777

5,000E-02

,135

,977

-,304

,404

-2,150*

,167

,000

-2,586

-1,714

-5,000E-02

,135

,977

-,404

,304

(J) WO_PI_WI
2
3
1
3
1
2

(I) WO_PI_WI
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Sidaka.

a.

Oszacowania

Miara: MIARA_1

7,250

,160

6,915

7,585

5,150

,150

4,836

5,464

5,100

,161

4,764

5,436

WO_PI_WI
1
2
3

Średnia

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności

Interpretacja? Po wypiciu szklanki wody osoby badane
wykonywały istotnie więcej (7,25) poprawnych jaskółek niż
po wypiciu piwa (5,15) czy wina (5,10). Rodzaj alkoholu nie
odgrywał roli.

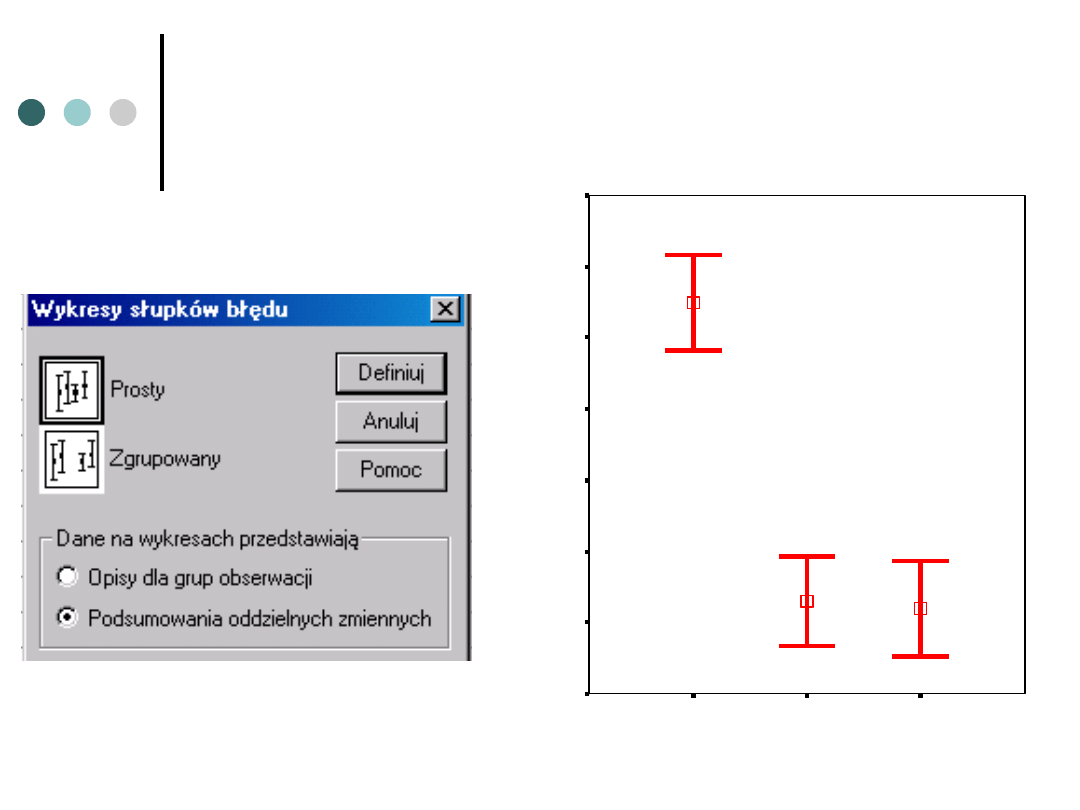
Można również inaczej



Robiąc słupki błędów

wino

piwo

woda

lic

zb

a

w

yk

on

an

yc

h

ja

sk

ół

ek

8,0

7,5

7,0

6,5

6,0

5,5

5,0

4,5

Gdy założenia nie spełnione –przykład
na temat skuteczności psychoterapii



Rozważano czy psychoterapia działa w ogóle
jak również w jakiś czas po jej zakończeniu



Badano poziom dobrostanu psychicznego:



Przed terapią



Bezpośrednio po jej zakończeniu



Kilka tygodni po zakończeniu



Czy taki plan badania optymalny?

Hipoteza badawcza 1 – badacz Ostrożny



Badacz Ostrożny

nie jest w stanie sformułować

hipotezy kierunkowej więc będzie testował

hipotezę niekierunkową - poszukującą różnic

między pomiarami – zrobi zatem

testy post hoc



Hipoteza zerowa zakłada, że nie będzie różnic

między średnimi dobrostanu w poszczególnych

pomiarach



Statystka F będzie obliczać proporcję różnic między

pomiarami w stosunku do składnika interakcyjnego

pomiaru i osób.

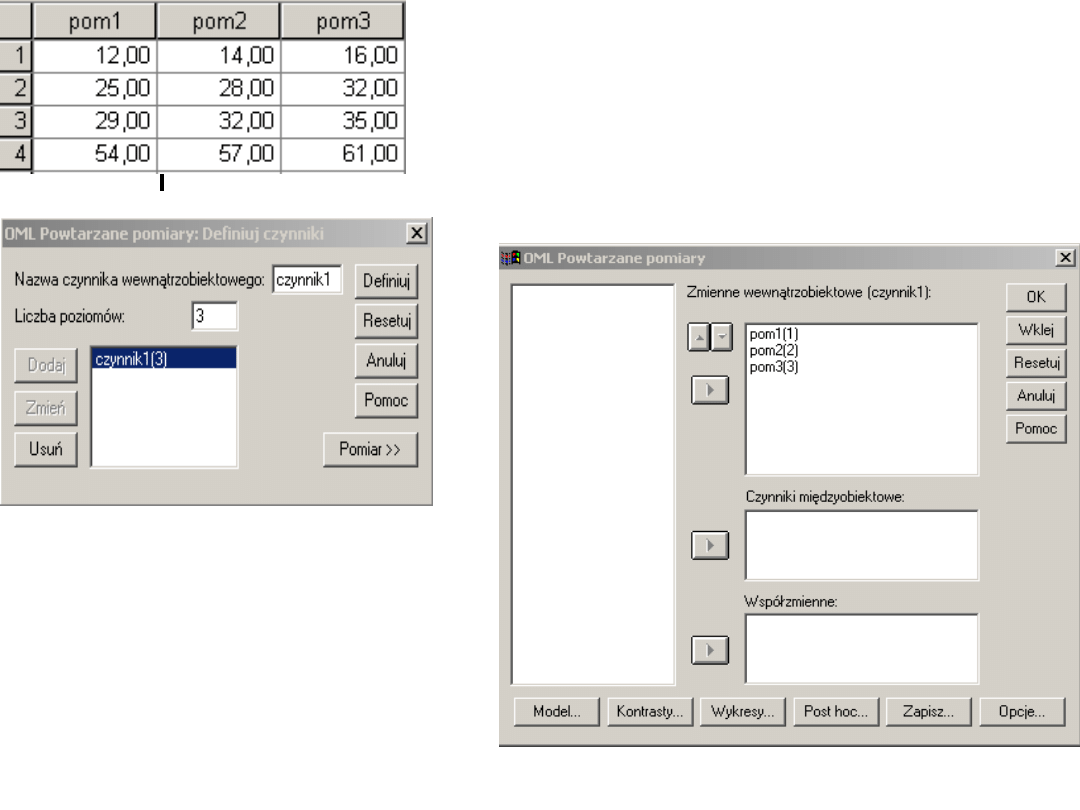
Przebadano cztery osoby…

Definiujemy ile jest

poziomów
powtarzanego
czynnika oraz
wybieramy zmienne

Założenie o sferyczności

Test sferyczności Mauchly'ego

Miara: MIARA_1

,066

5,422

2

,005

,517

,544

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

Założenie o sferyczności niespełnione – jakie kroki
podjąć?

SPSS oferuje trzy rodzaje poprawek w sytuacji
niespełnienia tego założenia

Opierają się one o miarę Epsilon – jej wartości oscylują
między

1/(k-1)

a

1

Homogeniczne
wariancje różnic
pomiarów

Brak homogeniczności
wariancji różnic
pomiarów

Poprawki na F – którą wybrać?



Najbardziej konserwatywna – dolna granica
epsilon = 1/(k-1), np. dla czynnika na trzech
poziomach wynosi 0,5



Greenhouse-Geisera wtedy, gdy duże
liczebności – dobra, gdy epsilon poniżej 0,75
(gdy wyżej zbyt konserwatywna)



Huynha-Feldt’a wtedy, gdy małe liczebności,
gdy epsilon powyżej 0,75

Test sferyczności Mauchly'ego

Miara: MIARA_1

,066

5,422

2

,005

,517

,544

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

Który F?

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

72,167

2

36,083

68,368

,000

72,167

1,034

69,768

68,368

,003

72,167

1,087

66,362

68,368

,003

72,167

1,000

72,167

68,368

,004

3,167

6

,528

3,167

3,103

1,020

3,167

3,262

,971

3,167

3,000

1,056

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Na czym polega poprawianie? Korekta stopni
swobody.

Odczytujemy, że są różnice między trzema pomiarami:

F(1; 3,1)=68,368; p<0,01

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

72,167

2

36,083

68,368

,000

72,167

1,034

69,768

68,368

,003

72,167

1,087

66,362

68,368

,003

72,167

1,000

72,167

68,368

,004

3,167

6

,528

3,167

3,103

1,020

3,167

3,262

,971

3,167

3,000

1,056

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Testy wielu zmiennych

b

,981

51,000

a

2,000

2,000

,019

,019

51,000

a

2,000

2,000

,019

51,000

51,000

a

2,000

2,000

,019

51,000

51,000

a

2,000

2,000

,019

Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a

Efekt
CZYNNIK1

Wartość

F

df hipotezy

df błędu

Istotność

Statystyka dokładna

a.

Plan: Intercept
Plan wewnątrzobiektowy: CZYNNIK1

b.

Alternatywa dla sferyczności

Znacznie rzadziej stosuje się poprawkę wartości statystyki F.
Statystyka F jest obliczana na podstawie statystyk z lewej
strony tabeli. Najczęściej stosowane to Lambda Wilksa (dla
więcej niż dwóch pomiarów) oraz Ślad Hotellinga (dla dwóch
pomiarów).

Zapis w tym przypadku będzie wyglądał następująco:

F(2,2) = 51; p<0,05; Lambda=0,019

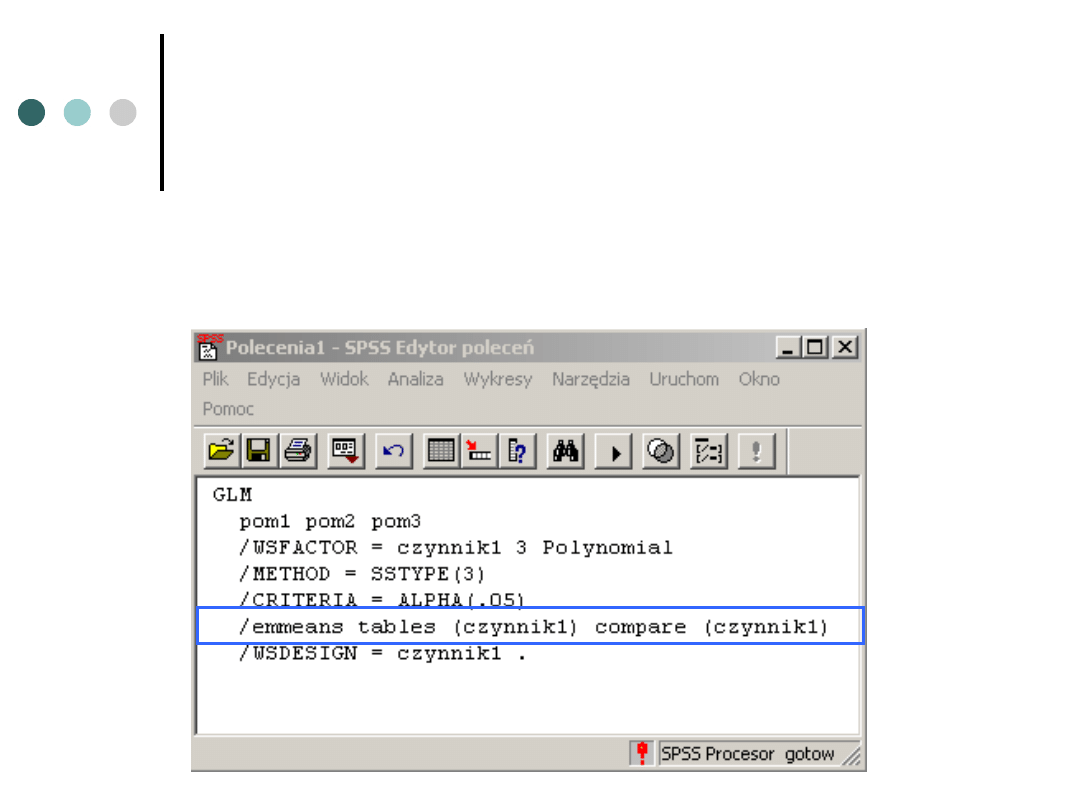
Testy post hoc



Hipoteza badacza Ostrożnego jest hipotezą niekierunkową i
dlatego wykonujemy testy post hoc. Korzystamy z syntaxa.

Skuteczność terapii

pomiar

skutki odroczone

skutki bezpośrednie

przed terapią

O

sz

ac

o

w

a

n

e

ś

re

d

n

ie

b

rz

e

g

o

w

e

37

36

35

34

33

32

31

30

29

Na podstawie porównań parami
możemy stwierdzić, że wszystkie
średnie różnią się między sobą.
Wykres pokazuje, że średni
dobrostan psychologiczny przed
terapią jest najniższy a w grupie
kilka miesięcy po terapii najwyższy.
Oznacza to, że psychoterapia odnosi
skutek i jest on długofalowy

Porównania parami

Miara: MIARA_1

-2,750*

,250

,002

-3,546

-1,954

-6,000*

,707

,003

-8,250

-3,750

2,750*

,250

,002

1,954

3,546

-3,250*

,479

,007

-4,773

-1,727

6,000*

,707

,003

3,750

8,250

3,250*

,479

,007

1,727

4,773

(J) CZYNNIK1
2
3
1
3
1
2

(I) CZYNNIK1
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

Pomiar

Przed

terapią

Skutki

bezpośredni

e

Skutki

odroczone

Poziom

dobrostanu

30a

32b

36c

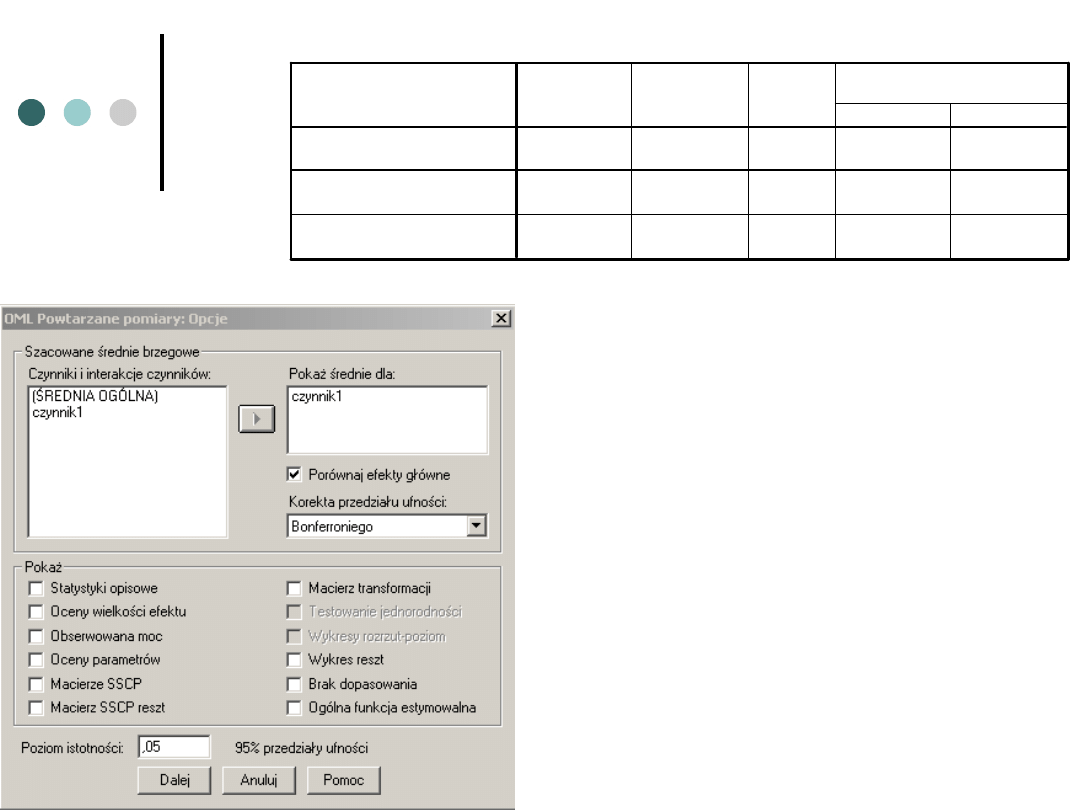
Porównania parami

b

Miara: MIARA_1

-2,750*

,250

,005

-3,964

-1,536

-6,000*

,707

,010

-9,434

-2,566

2,750*

,250

,005

1,536

3,964

-3,250*

,479

,020

-5,575

-,925

6,000*

,707

,010

2,566

9,434

3,250*

,479

,020

,925

5,575

(J) CZYNNIK1
2
3
1
3
1
2

(I) CZYNNIK1
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Bonferroniego.

a.

PLEC = mezczyzna

b.

Post hoc - Opcje

Uzyskujemy ten sam układ

średnich - wszystkie
średnie różnią się między
sobą - choć poziomy
istotności są już nieco
inne.

Hipoteza badawcza 2– badacz Odważny



Badacz Odważny

stwierdza na podstawie literatury,

że po psychoterapii błędna równowaga całego
systemu psychologicznego zostaje zaburzona co
umożliwia ustanowienie nowej, zdrowszej
równowagi.



Innymi słowy po terapii poziom dobrostanu będzie
systematycznie rósł. Badacz postawił zatem hipotezę
kierunkową i będzie poszukiwał prostoliniowego
układu średnich w poszczególnych pomiarach.



Badacz Odważny zastosuje

kontrasty

Jak układają się średnie?

Kontrast liniowy okazał się istotny

F(1,3)=72; p<0,01

i po obejrzeniu średnich na

wykresie uznajemy, że
dobrostan psychologiczny
systematycznie wzrasta po
psychoterapii.

Testy kontrastów wewnątrzobiektowych

Miara: MIARA_1

72,000

1

72,000

72,000

,003

,167

1

,167

3,000

,182

3,000

3

1,000

,167

3

,056

CZYNNIK1
Liniowy
Kwadratowy
Liniowy
Kwadratowy

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Skuteczność terapii

pomiar

skutki odroczone

skutki bezpośrednie

przed terapią

O

sz

ac

o

w

an

e

ś

re

d

n

ie

b

rz

e

g

o

w

e

37

36

35

34

33

32

31

30

29

Plany z dwoma czynnikami w
powtarzanym pomiarze



Złożony eksperyment, np. każda osoba badana
ocenia atrakcyjność różnych zdjęć (na skali 1-7)



Kobiecych oraz męskich



Wyrażających emocje: pozytywne, negatywne,
neutralne



Dwa czynniki wewnątrz osób: płeć osoby na fotografii
oraz rodzaj wyrażanej emocji



Sześć warunków eksperymentalnych

Kobieca
neutralna

Kobieca
negatywna

Kobieca
pozytywna

Męska neutralna Męska

negatywna

Męska
pozytywna

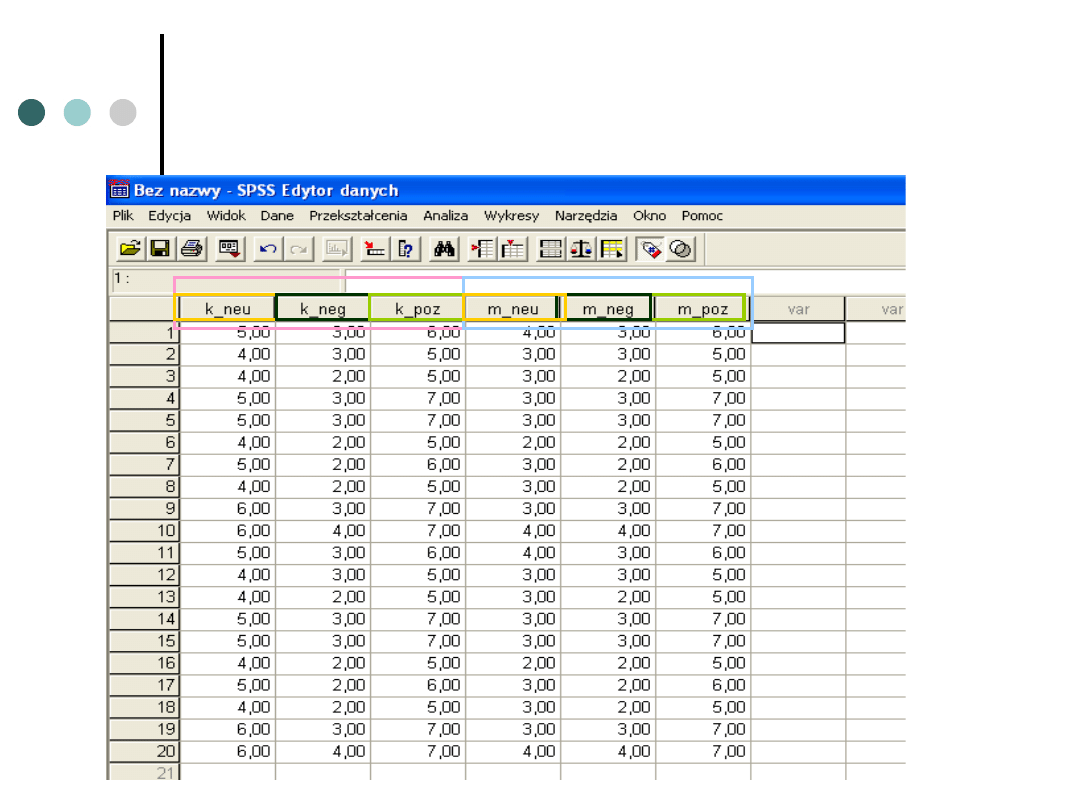
Jak wyglądają dane?

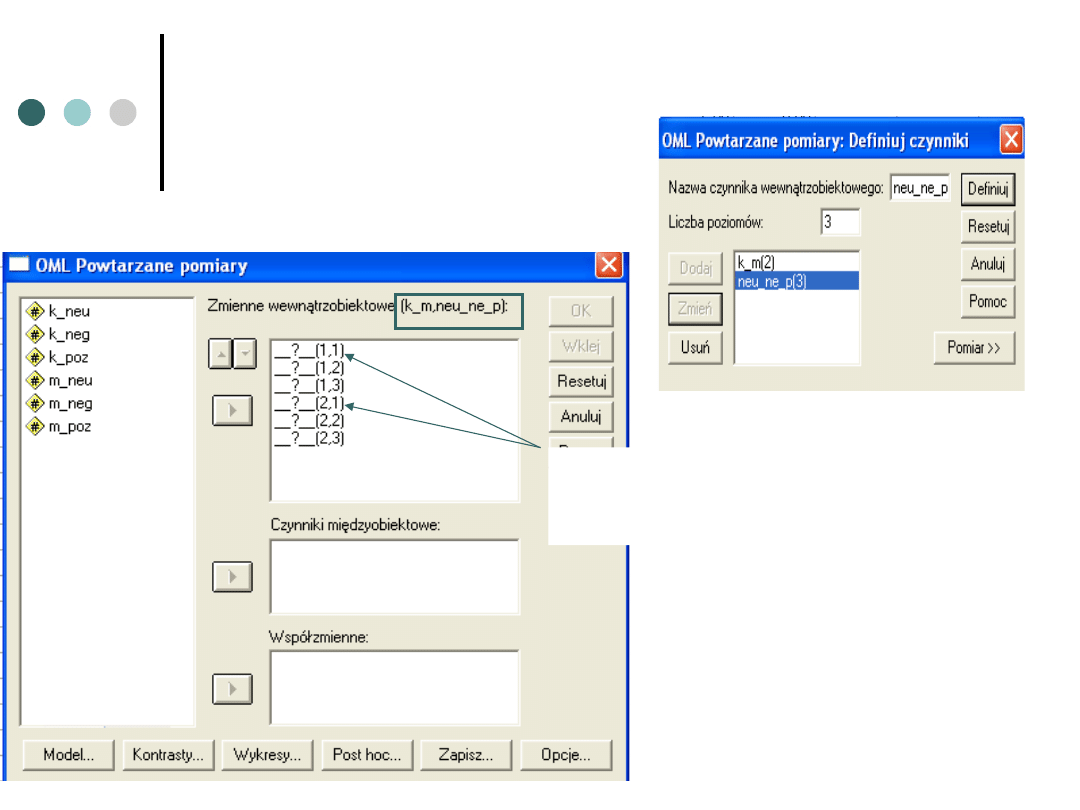
Jak wprowadzać takie dane do analizy

Bardzo ważna
kolejność zmiennych

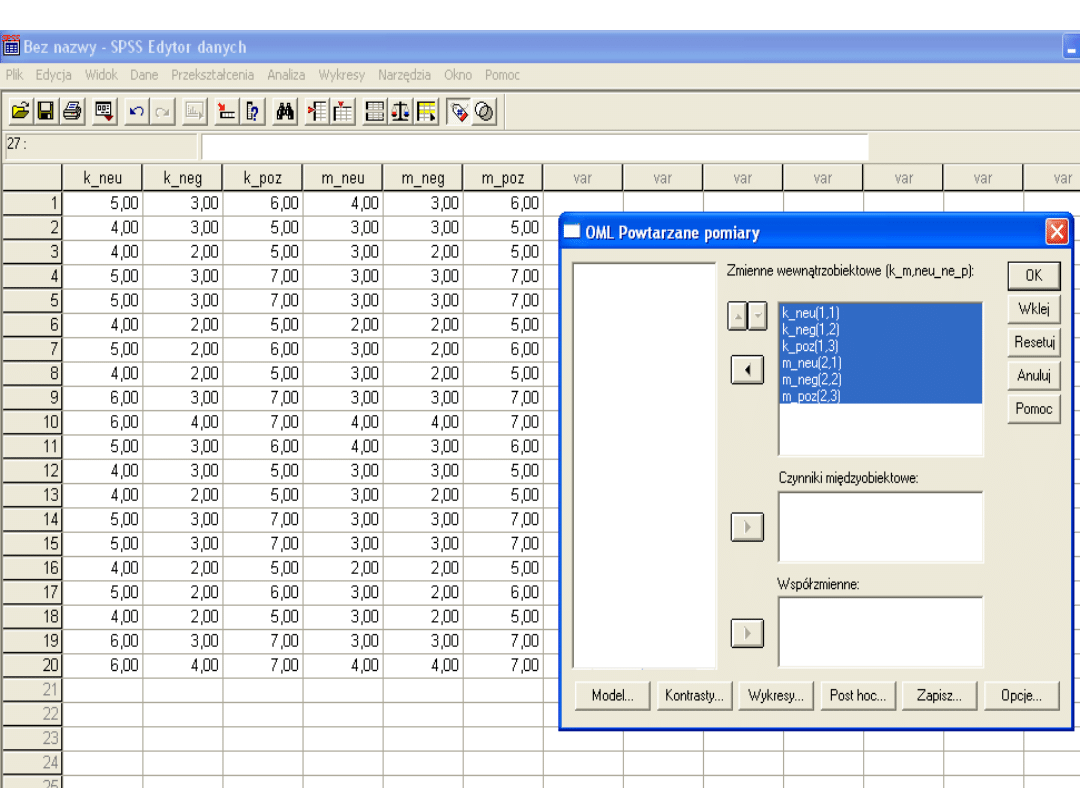
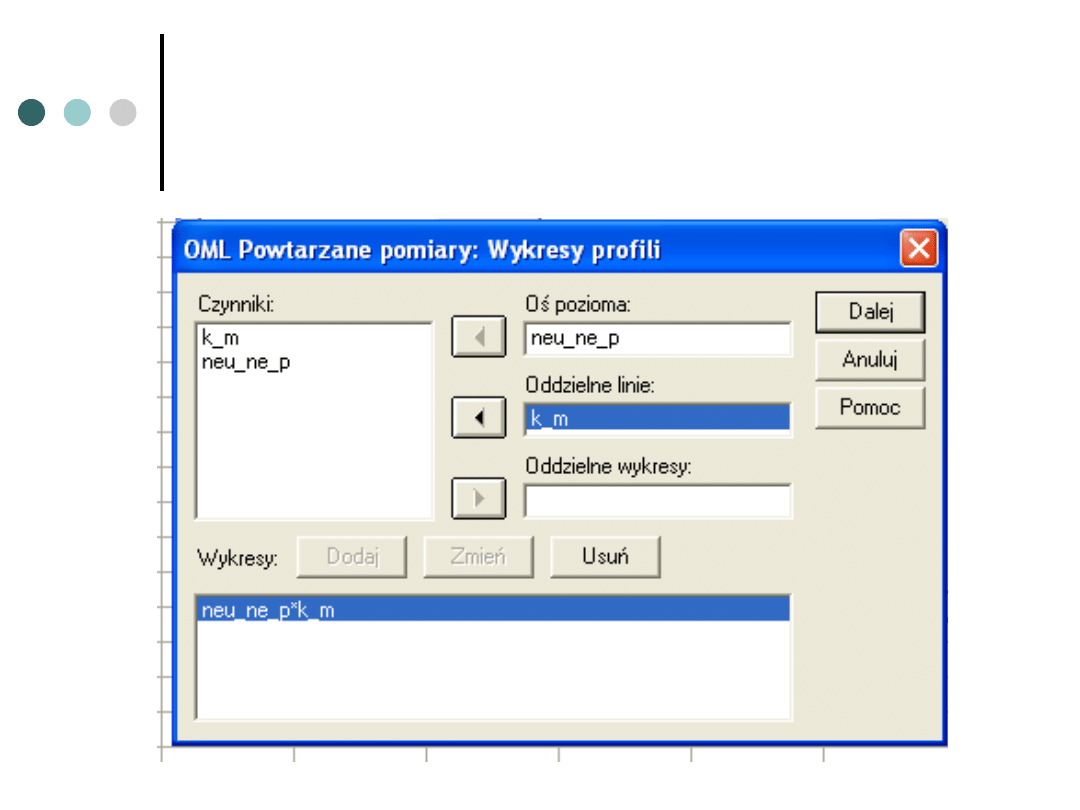
Warto zrobić wykres

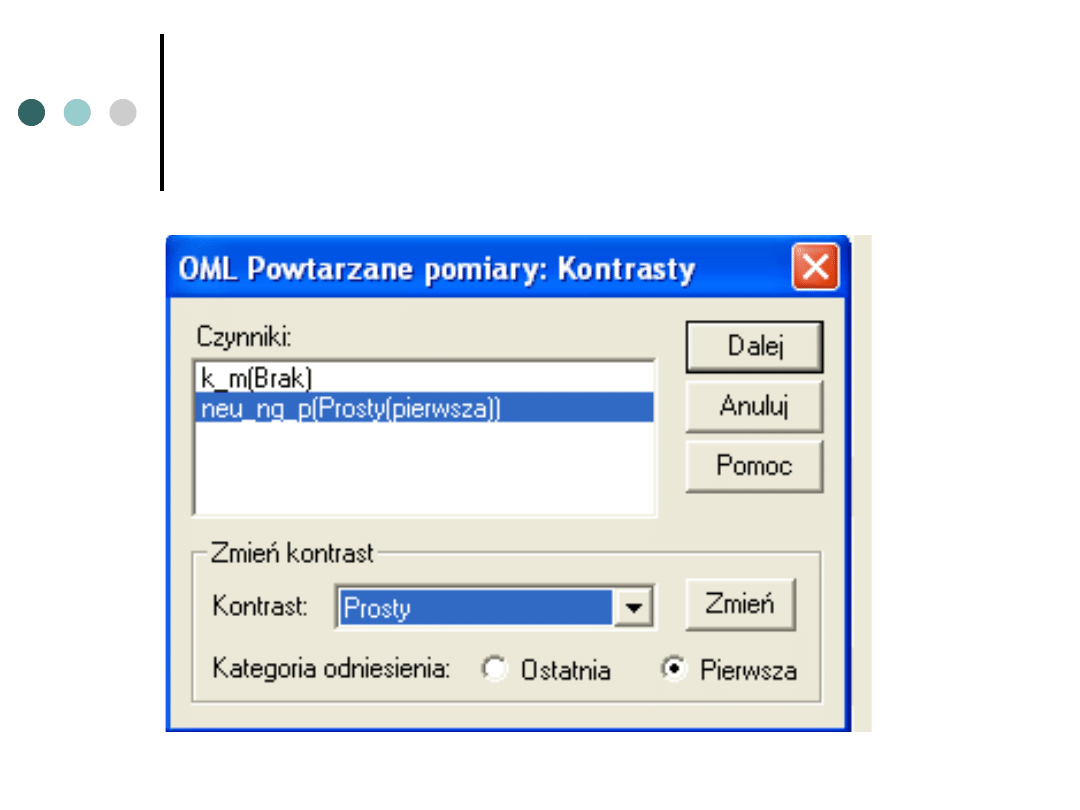
Kontrast dla czynnika na trzech
poziomach

Przydatne rzeczy na początek

Czynniki wewnątrzobiektowe

Miara: MIARA_1

K_NEU
K_NEG
K_POZ
M_NEU
M_NEG
M_POZ

NEU_NE_P
1
2
3
1
2
3

K_M
1

2

Zmienna

zależna

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

1,000

,000

0

,

1,000

1,000

1,000

,825

3,461

2

,177

,851

,926

,500

,652

7,702

2

,021

,742

,790

,500

Efekt wewnątrzobiektowy
K_M
NEU_NE_P
K_M * NEU_NE_P

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept
Plan wewnątrzobiektowy: K_M+NEU_NE_P+K_M*NEU_NE_P

b.

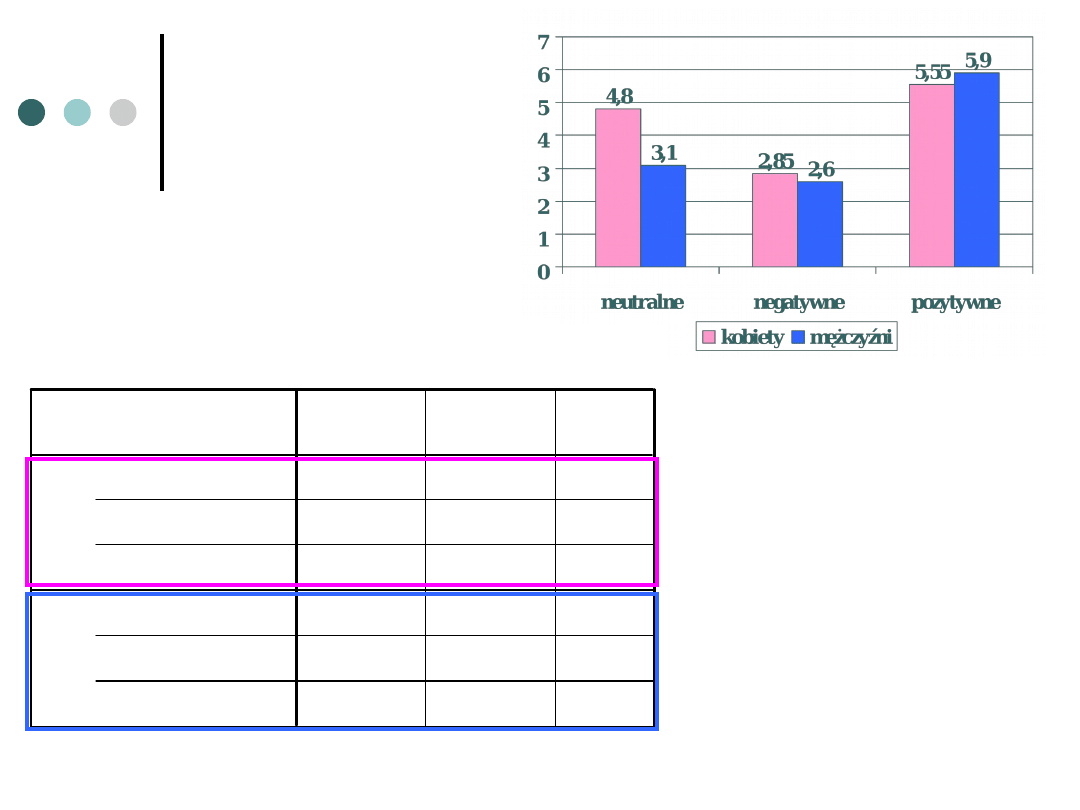
Statystyki opisowe

4,8000

,7678

20

2,8500

,7452

20

5,5500

,8870

20

3,1000

,5525

20

2,6000

,5026

20

5,9000

,9119

20

K_NEU
K_NEG
K_POZ
M_NEU
M_NEG
M_POZ

Średnia

Odchylenie

standardowe

N

Odczytujemy odpowiednie dla każdego efektu F

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

8,533

1

8,533

46,769

,000

8,533

1,000

8,533

46,769

,000

8,533

1,000

8,533

46,769

,000

8,533

1,000

8,533

46,769

,000

3,467

19

,182

3,467

19,000

,182

3,467

19,000

,182

3,467

19,000

,182

182,017

2

91,008

314,869

,000

182,017

1,702

106,927

314,869

,000

182,017

1,853

98,251

314,869

,000

182,017

1,000

182,017

314,869

,000

10,983

38

,289

10,983

32,343

,340

10,983

35,199

,312

10,983

19,000

,578

22,217

2

11,108

39,145

,000

22,217

1,484

14,975

39,145

,000

22,217

1,580

14,064

39,145

,000

22,217

1,000

22,217

39,145

,000

10,783

38

,284

10,783

28,187

,383

10,783

30,014

,359

10,783

19,000

,568

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
K_M

Błąd(K_M)

NEU_NE_P

Błąd(NEU_NE_P)

K_M * NEU_NE_P

Błąd(K_M*NEU_NE_P)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Jakie efekty uzyskaliśmy?

Efekt główny czynnika płeć osoby na zdjęciu:

F(1, 19)=46; p<0,001

Efekt główny rodzaju emocji:

F(2, 38)=315; p<0,001

Efekt interakcyjny płci i rodzaju emocji:

F(1; 28,2)=39; p<0,001

Dalszej interpretacji poddajemy właściwie tylko
efekt interakcyjny, bo oba efekty główne wynikają
z występowania efektu interakcyjnego

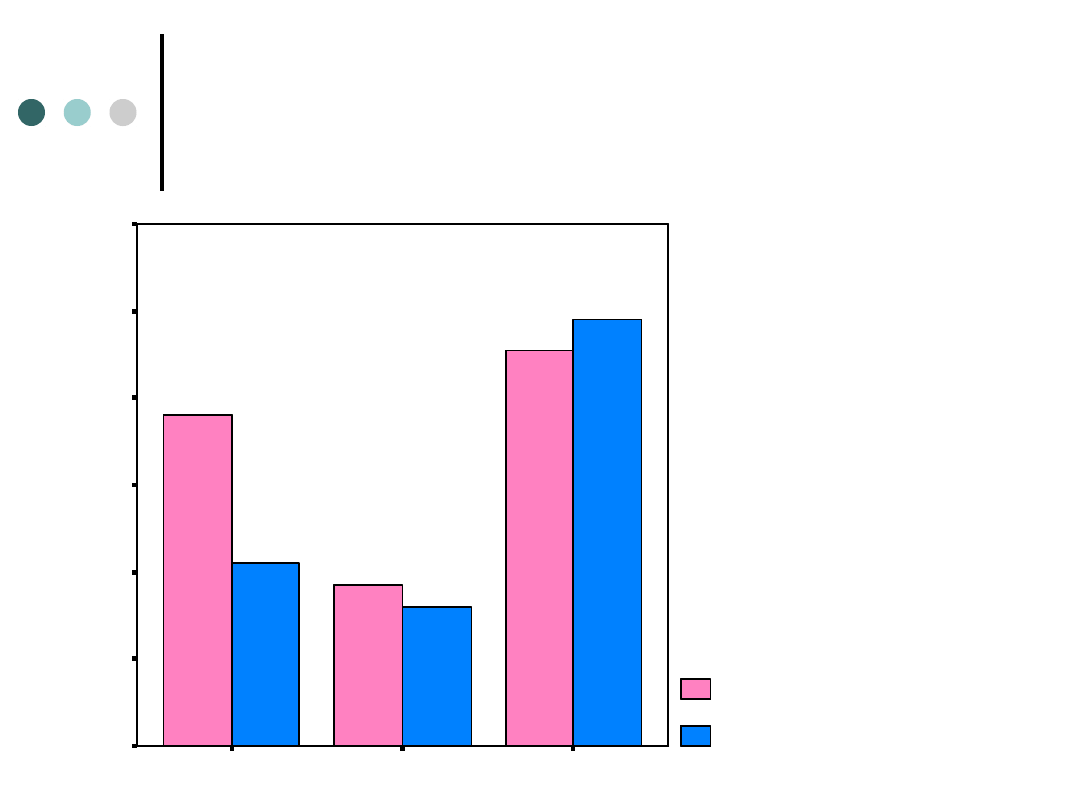
Na wykresie przedstawia się to tak

pozytywne

negatywne

neutralne

A

tr

ak

cy

jn

oś

ć

zd

ję

ci

a

7

6

5

4

3

2

1

K_M

kobiece

męskie

Które różnice
istotne
statystycznie?

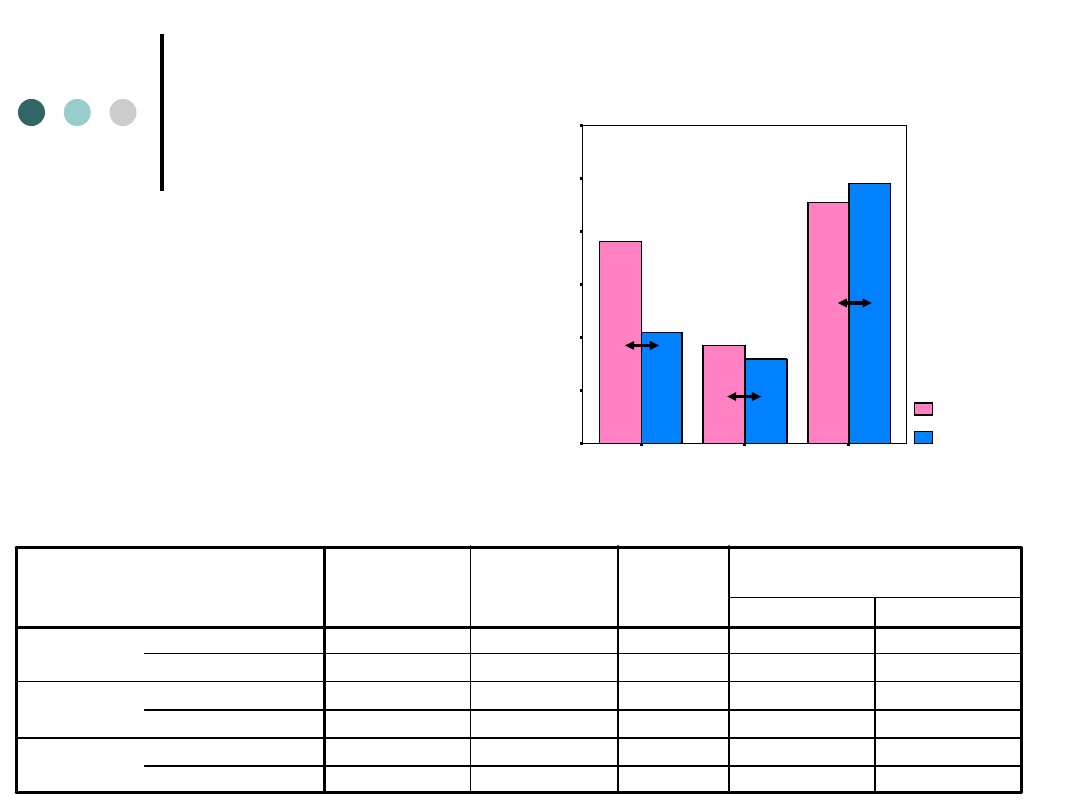
Jak interpretować interakcję?



Efekty proste płci osoby
w ramach każdego
poziomu czynnika
rodzaj emocji

pozytywne

negatywne

neutralne

A

tr

ak

cy

jn

oś

ć

zd

ję

ci

a

7

6

5

4

3

2

1

K_M

kobiece

męskie

*

Porównania parami

Miara: MIARA_1

1,700*

,147

,000

1,393

2,007

-1,700*

,147

,000

-2,007

-1,393

,250

,123

,056

-7,464E-03

,507

-,250

,123

,056

-,507

7,464E-03

-,350

,196

,090

-,760

5,956E-02

,350

,196

,090

-5,956E-02

,760

(J) K_M
2
1
2
1
2
1

(I) K_M
1
2
1
2
1
2

NEU_NG_P
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

Efekty proste rodzaju emocji

w ramach każdego

poziomu czynnika rodzaj

płci

Porównania parami

Miara: MIARA_1

1,950*

,135

,000

-,750*

,204

,002

-1,950*

,135

,000

-2,700*

,193

,000

,750*

,204

,002

2,700*

,193

,000

,500*

,115

,000

-2,800*

,186

,000

-,500*

,115

,000

-3,300*

,164

,000

2,800*

,186

,000

3,300*

,164

,000

(J) N_P_N
negat
pozyt
neutr
pozyt
neutr
negat
negat
pozyt
neutr
pozyt
neutr
negat

(I) N_P_N
neutr

negat

pozyt

neutr

negat

pozyt

K_M
K

M

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

*.
a.

Badanie w schemacie mieszanym
– jak reagujemy na stres?



Badacza interesowało, czy są różnice w reakcji

na stres przed, w trakcie i po rozmowie

rekrutacyjnej w grupie kobiet i mężczyzn.



Wiadomo z literatury, że kobiety mają

częstszą tendencję do „przeżuwania”

negatywnych emocji. Ta skłonność może być

też przyczyną utrzymywania się wysokiego

poziomu stresu nawet po zakończeniu

stresującej sytuacji.

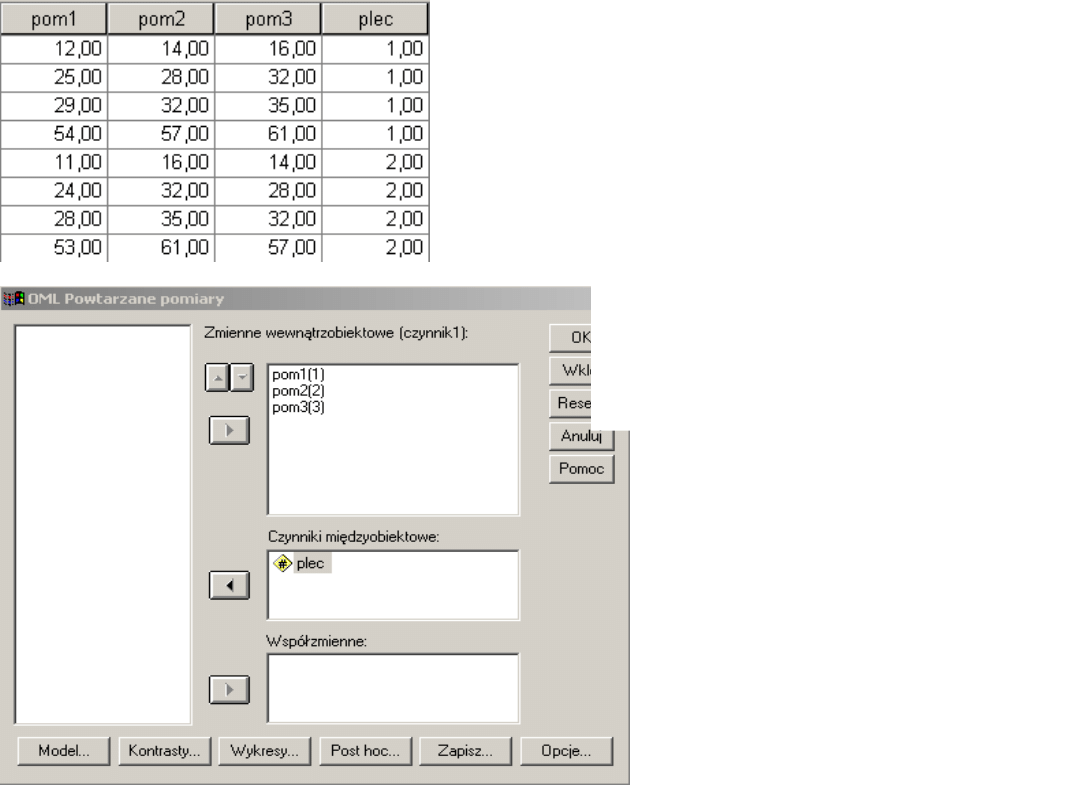
Schemat mieszany 2

(płeć) x 3 (dynamika

stresu)

Płeć jest czynnikiem

międzyobiektowym

Pomiar stresu przed, w

trakcie i po rozmowie

- zmienną

wewnątrzobiektową

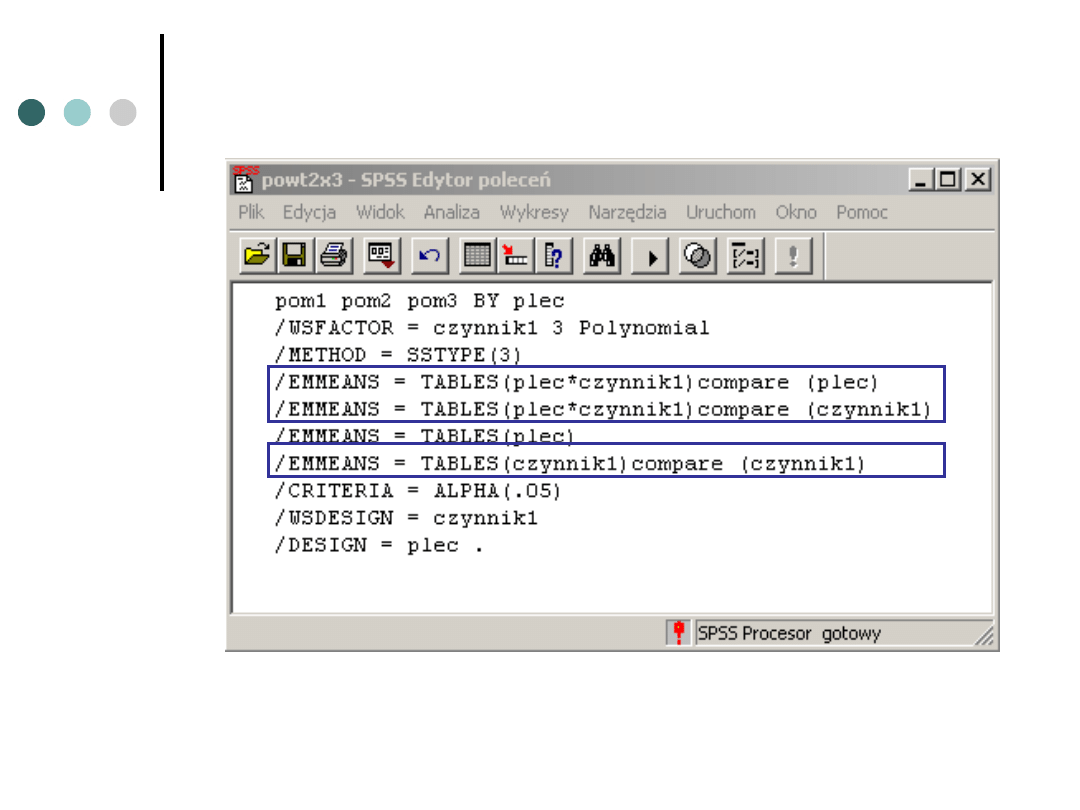
Możliwe efekty

Efekt główny płci

Efekt główny pomiaru

Efekt interakcyjny pomiaru x płci
Zakładany przez badacza

Sprawdzamy założenie o sferyczności
Założenie o sferyczności jest spełnione W(2)=0,983; p>0,05
Nie musimy korzystać z poprawek na niespełnione założenie

o sferyczności

Test sferyczności Mauchly'ego

b

Miara: MIARA_1

,983

,087

2

,957

,983

1,000

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

a

Testuje hipotezę zerową o proporcjonalności macierzy kowariancji błędów ortonormalizowanych przekształconych zmiennych
zależnych do macierzy jednostkowej.

Może być użyte do korygowania stopni swobody dla uśrednionych testów istotności. Skorygowane testy są przedstawione w
tabeli Testy efektów wewnątrzobiektowych.

a.

Plan: Intercept+PLEC
Plan wewnątrzobiektowy: CZYNNIK1

b.

Efekt główny płci

Nie uzyskaliśmy efektu głównego płci F(1,6)=0,001;

p>0,05 (n.i.)



To znaczy, że kobiety nie różnią się od mężczyzn

globalnym natężeniem stresu (łącznie dla wszystkich

pomiarów)

Testy efektów międzyobiektowych

Miara: MIARA_1
Zmienna przekształcona: Średnia

25741,500

1 25741,500

26,378

,002

,667

1

,667

,001

,980

5855,167

6

975,861

Źródło zmienności
Intercept
PLEC
Błąd

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Efekt główny pomiaru

Uzyskaliśmy efekt główny pomiaru F(2, 12)=120,1; p<0,001
Oznacza to, że poziom stresu osób badanych zmienia się w czasie

Ale jak się zmienia?

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

126,750

2

63,375

120,079

,000

126,750

1,966

64,472

120,079

,000

126,750

2,000

63,375

120,079

,000

126,750

1,000

126,750

120,079

,000

43,583

2

21,792

41,289

,000

43,583

1,966

22,169

41,289

,000

43,583

2,000

21,792

41,289

,000

43,583

1,000

43,583

41,289

,001

6,333

12

,528

6,333

11,796

,537

6,333

12,000

,528

6,333

6,000

1,056

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
CZYNNIK1

CZYNNIK1 * PLEC

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

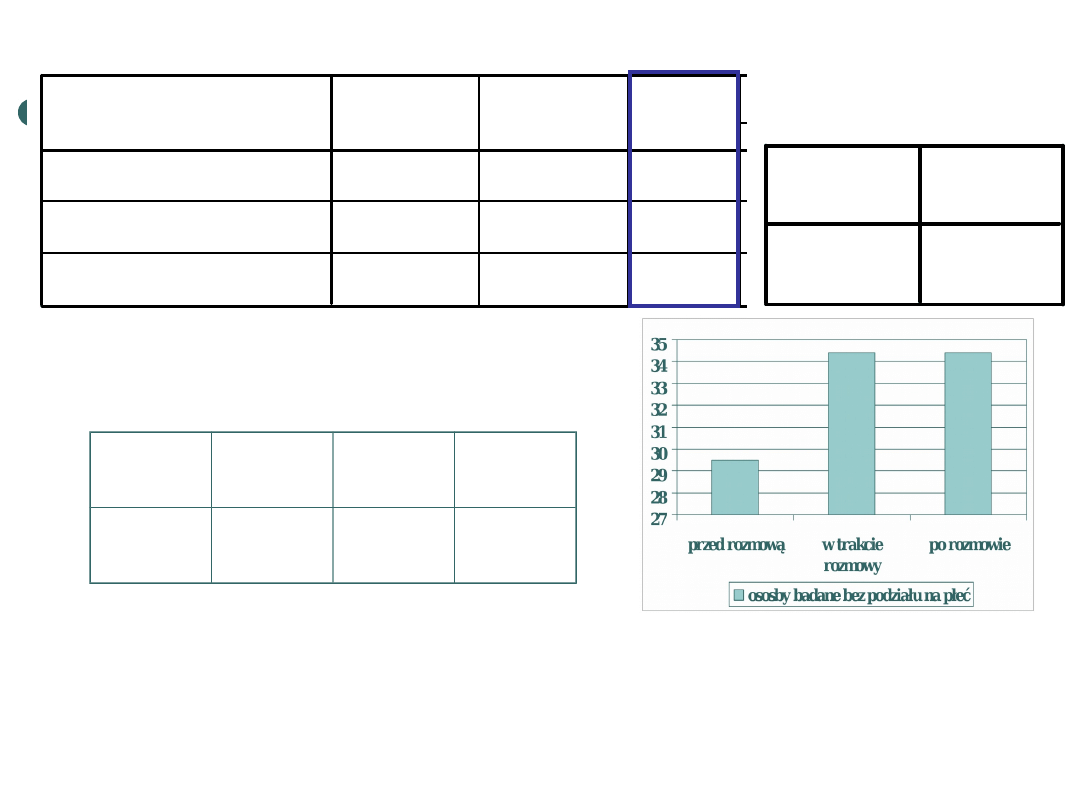
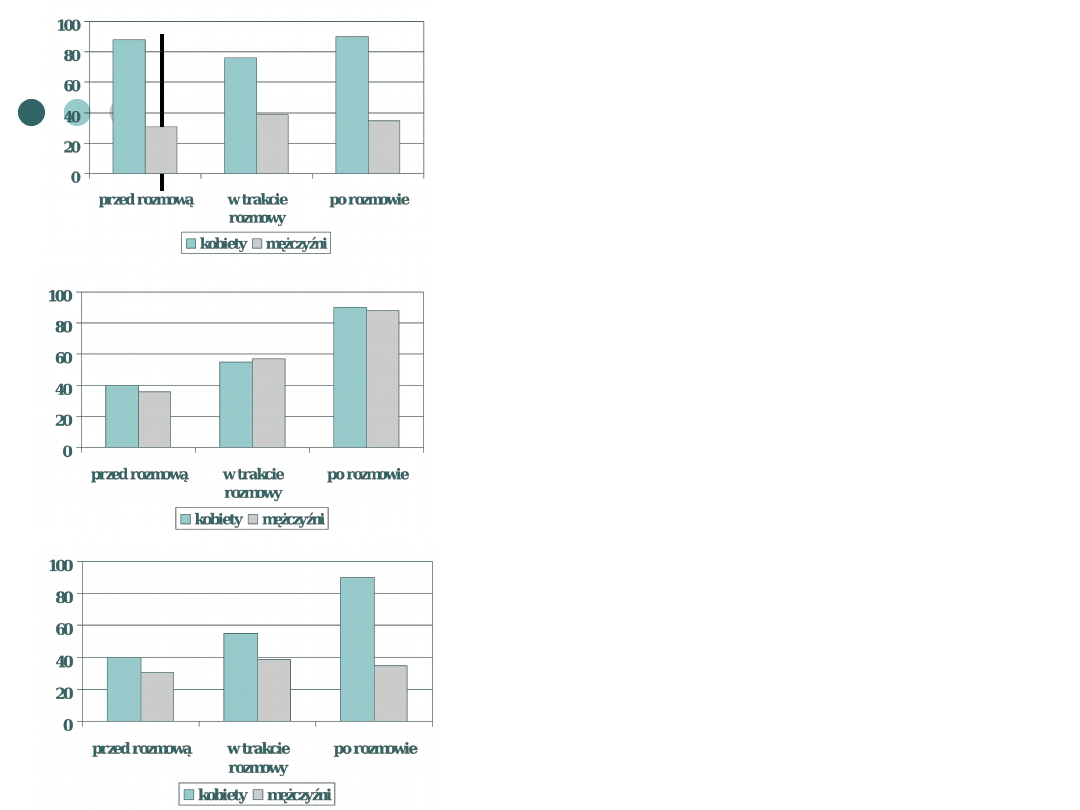
Poziom stresu przed rozmową jest niższy niż w trakcie i po. Nie ma

natomiast różnic między poziomem stresu w trakcie i po rozmowie

.

Porównania parami

Miara: MIARA_1

-4,875*

,375

,000

-5,793

-3,957

-4,875*

,375

,000

-5,793

-3,957

4,875*

,375

,000

3,957

5,793

,000

,339

1,000

-,828

,828

4,875*

,375

,000

3,957

5,793

,000

,339

1,000

-,828

,828

(J) CZYNNIK1
w trakcie
po
przed
po
przed
w trakcie

(I) CZYNNIK1
przed

w trakcie

po

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

Dolna granica Górna granica

95% przedział ufności dla

różnicy

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik braku poprawki).

a.

Oszacowania

Miara: MIARA_1

29,500
34,375
34,375

CZYNNIK1
przed
w trakcie
po

Średnia

Pomiar

Przed

W

trakcie

po

Poziom

stresu

29,5a 34,4b 34,4b

Efekt interakcyjny

Testy wielu zmiennych mówią nam, że

są różnice między pomiarami
wśród mężczyzn F(2,5)=54,8;
p<0,001, jak i wśród kobiet
F(2,5)72,9; p<0,001.

Nie wiemy tylko, które spośród trzech

średnich się różnią....

Testy wielu zmiennych

,956

54,815

a

2,000

5,000

,000

,044

54,815

a

2,000

5,000

,000

21,926

54,815

a

2,000

5,000

,000

21,926

54,815

a

2,000

5,000

,000

,967

72,955

a

2,000

5,000

,000

,033

72,955

a

2,000

5,000

,000

29,182

72,955

a

2,000

5,000

,000

29,182

72,955

a

2,000

5,000

,000

Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a
Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a

PLEC
mezczyzna

kobieta

Wartość

F

df hipotezy df błędu

Istotność

Każde F testuje proste wielowymiarowe efekty CZYNNIK1 w ramach każdej kombinacji poziomów
innych przedstawionych efektów. Testy te oparte są na liniowo niezależnych porównaniach parami
pomiędzy oszacowanymi średnimi brzegowymi.

Statystyka dokładna

a.

Porównania parami

Miara: MIARA_1

-2,750*

,530

,002

-6,000*

,530

,000

2,750*

,530

,002

-3,250*

,479

,000

6,000*

,530

,000

3,250*

,479

,000

-7,000*

,530

,000

-3,750*

,530

,000

7,000*

,530

,000

3,250*

,479

,000

3,750*

,530

,000

-3,250*

,479

,000

(J) CZYNNIK1
w trakcie
po
przed
po
przed
w trakcie
w trakcie
po
przed
po
przed
w trakcie

(I) CZYNNIK1
przed

w trakcie

po

przed

w trakcie

po

PLEC
mezczyzna

kobieta

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

a

W oparciu o estymowane średnie brzegowe.

Różnica średnich jest istotna na poziomie ,05

*.

Poprawka dla porównań wielokrotnych - Najmniejsza istotna różnica (równoważnik
braku poprawki).

a.

Pomiar

Przed

W trakcie

Po

Kobiety

29,a

36b

33c

Mężczyźni

30a

33b

36c

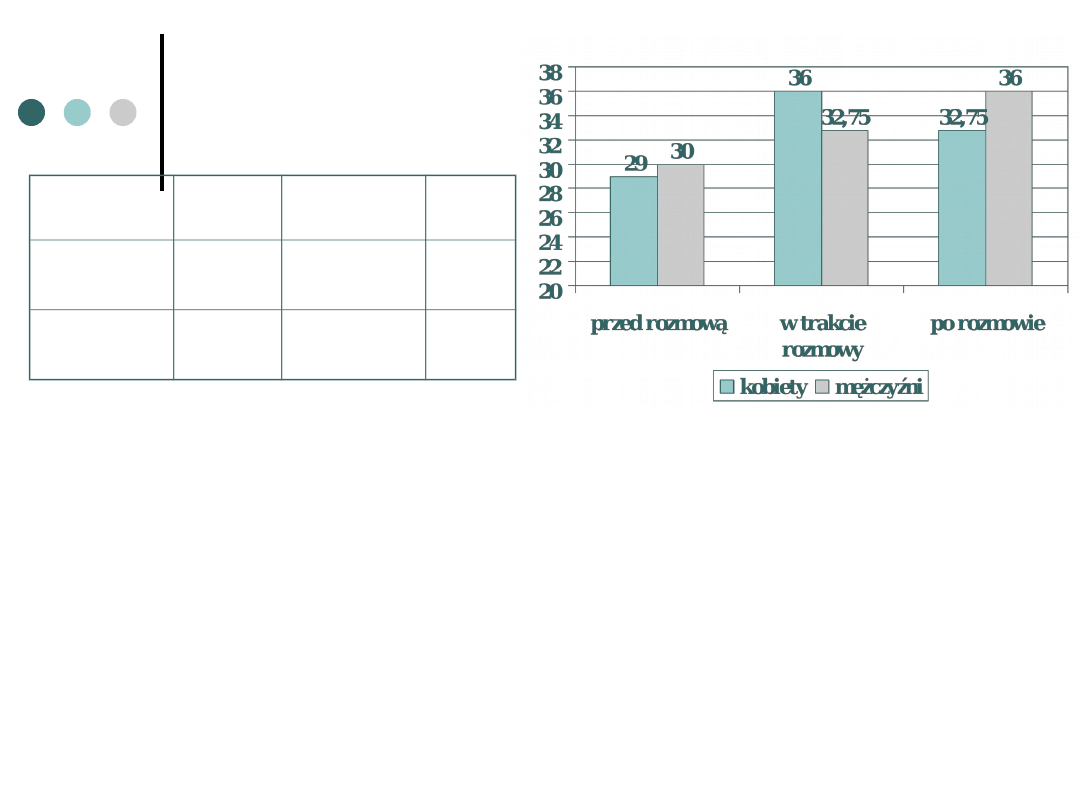
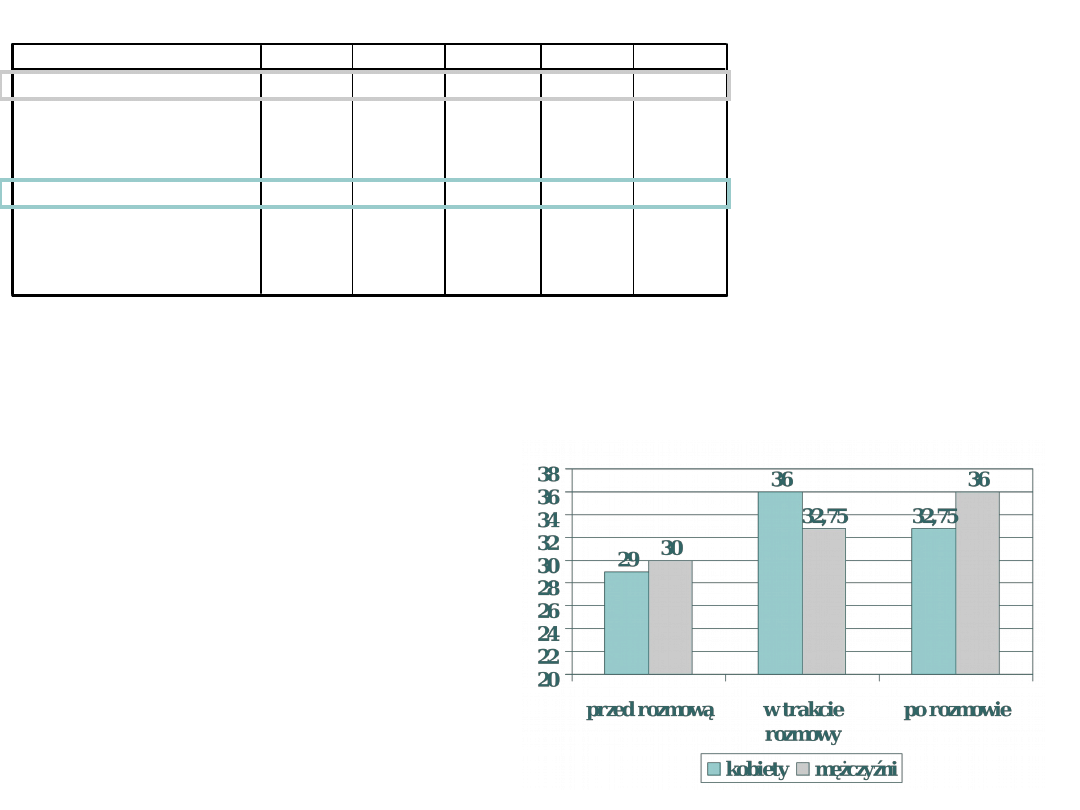
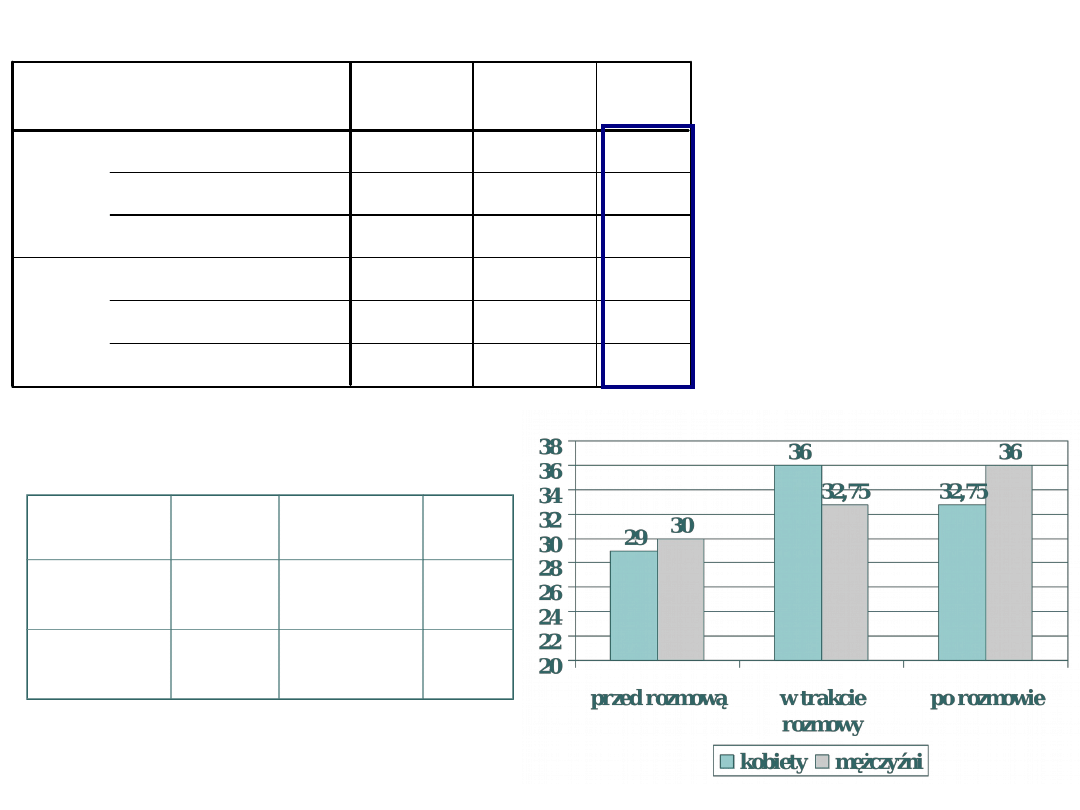
Pomiar

Przed

W trakcie

Po

Kobiety

29,a

36b

33c

Mężczyźni

30a

33b

36c

W grupie kobiet następuje wzrost poziomu stresu w
trakcie rozmowy, po rozmowie stres opada ale nie wraca
do początkowego poziomu tylko jest nadal nieco
podwyższony.

W grupie mężczyzn wzorzec wyników jest inny niż u
kobiet. Poziom stresu rośnie systematycznie – po
rozmowie nie opada tylko rośnie w stosunku do poziomu
stresu przed rozmową i w trakcie jej trwania.