Wyklad 6

Rozkład normalny

i prawdopodobieństwo cd.

…i wnioskowanie

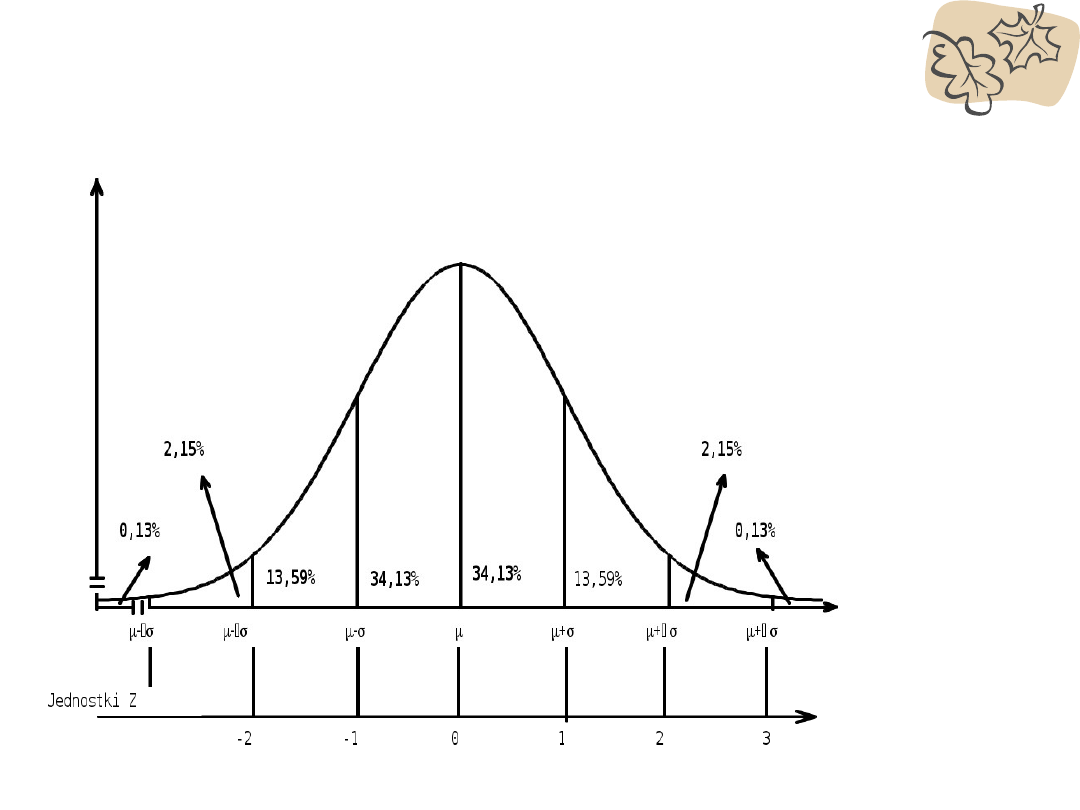
• Standardowy kształt krzywej umożliwia ustalenie
procenta przypadków poniżej lub powyżej dowolnego jej
punktu oraz procentów w zakresie pomiędzy dowolnymi
wartościami Z

• Możemy policzyć dokładny procent

przypadków między dowolnymi dwoma
punktami tej krzywej, wyrażonymi w postaci
wartości z.

Np. Dokładnie 68.59% przypadków znajduje

się między z = .62 i z = -1.68, a dokładnie
2.81% między .79 i .89.

• Procenty wyliczane na podstawie wzoru na

krzywą rozkładu normalnego – stąd tabele, w
których znajduje się procent przypadków
między daną wartością z a średnią (z = 0)

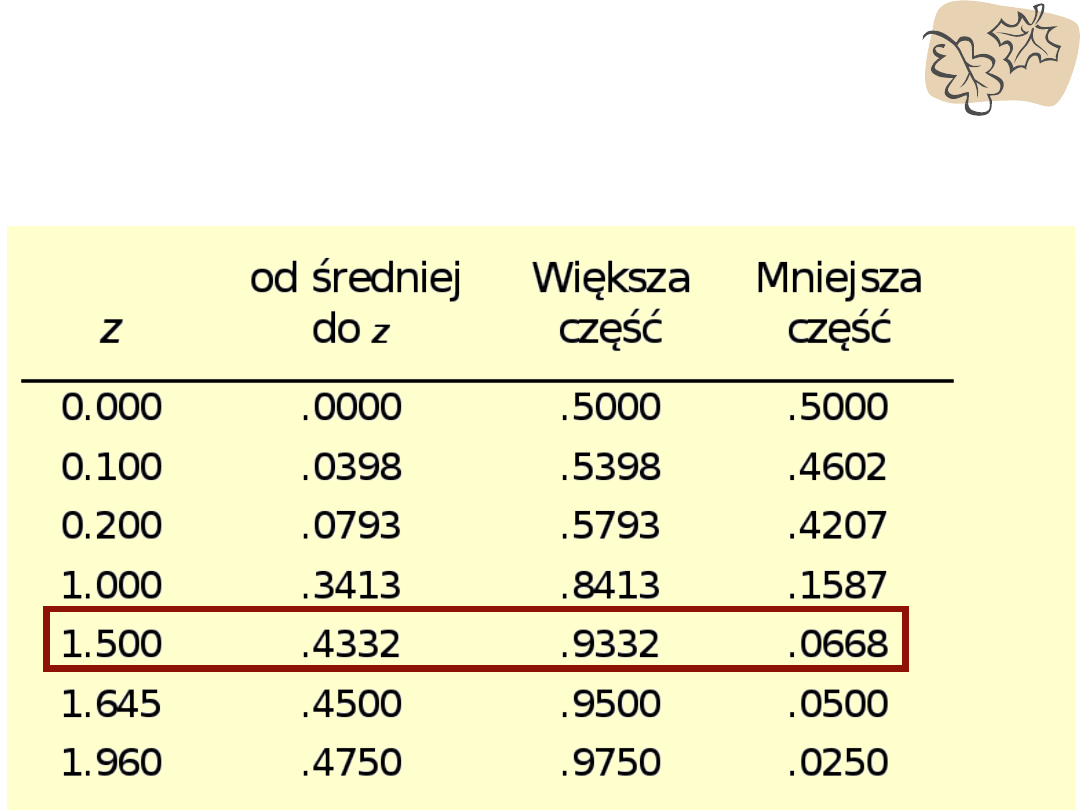
Tabele wartości z

• Korzystamy z tabel, aby znaleźć obszar pod krzywą

normalną, w tabeli są tylko pozytywne wartości z (ale skoro

rozkład jest symetryczny, to samo odnosi się do wartości

ujemnych z)

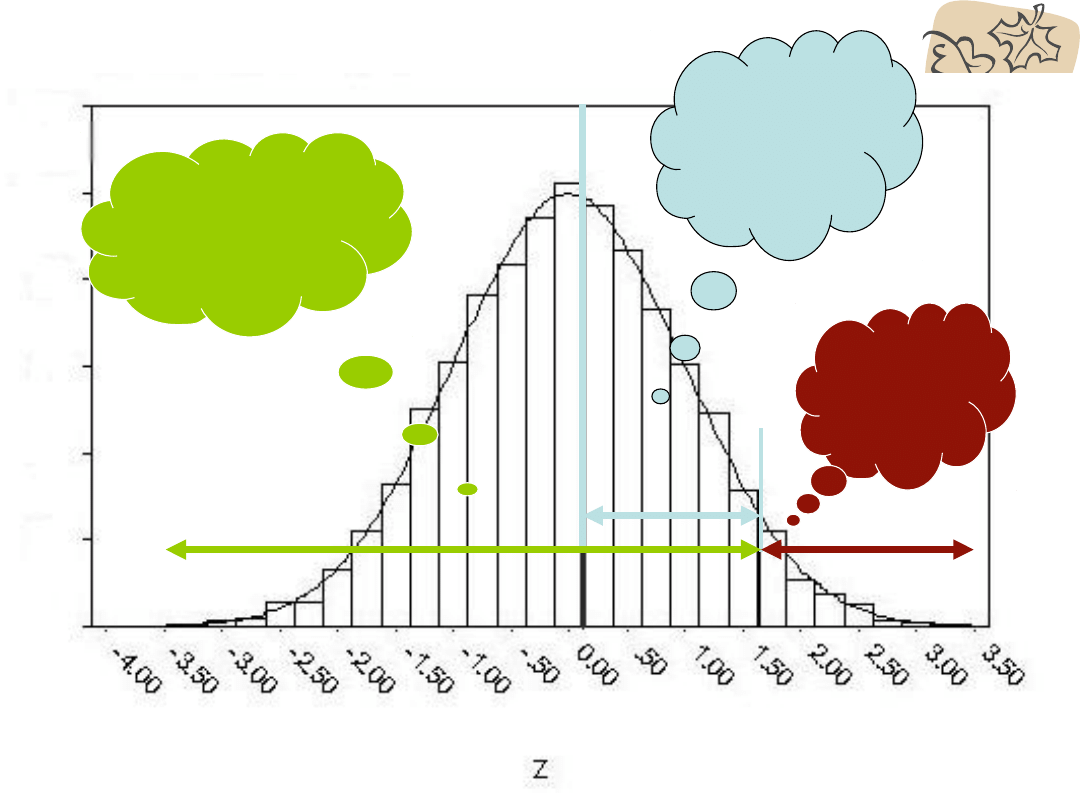
0,0668

Mniejsza

część

0,4332

od średniej

do wartości

z

Większa część

pod krzywą

normalną

0,9332

Korzystając z Tabeli wartości z

• Możemy obliczyć procent przypadków

znajdujących się powyżej danego wyniku

• W tym celu:
znajdź w tabeli wartość w kolumnie

„

procent od średniej do z

”

odpowiadającą uzyskanej wartości z;

- jeśli z jest dodatnie, odejmij ten wynik od

50,

- jeśli jest ujemne, dodaj ten wynik do 50.

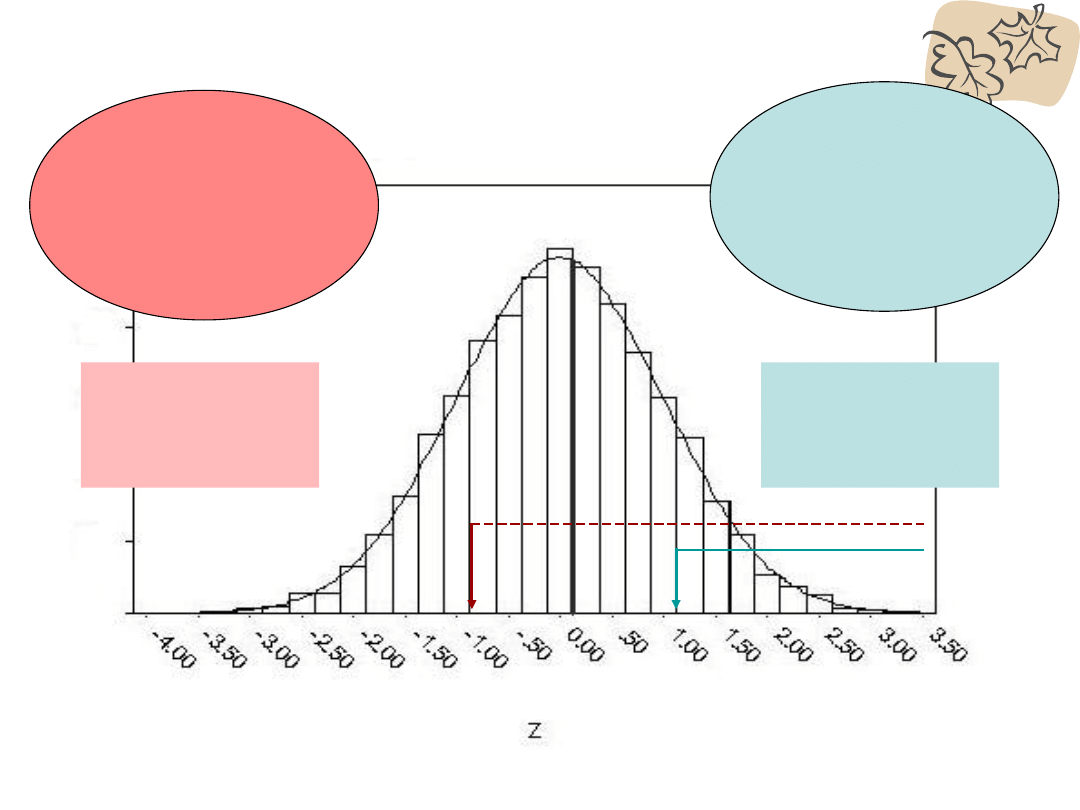
Gdy z dodatnie

odejmujemy odczytaną

wartość od 50

Gdy z ujemne

dodajemy do odczytanej

wartości 50

Wyniki powyżej danej
wartości z

Z = -1,0

% = 34 + 50 =
84

Z = 1,0

% = 50 - 34 =
16

• Możemy obliczyć procent przypadków

znajdujących się poniżej danego wyniku

• W tym celu:
znajdź w tabeli wartość w kolumnie

„

procent od średniej do z

” odpowiadającą

uzyskanej wartości z;

- jeśli z jest dodatnie, dodaj ten wynik od

50,

- jeśli jest ujemne, odejmij ten wynik do 50

Korzystając z Tabeli wartości z

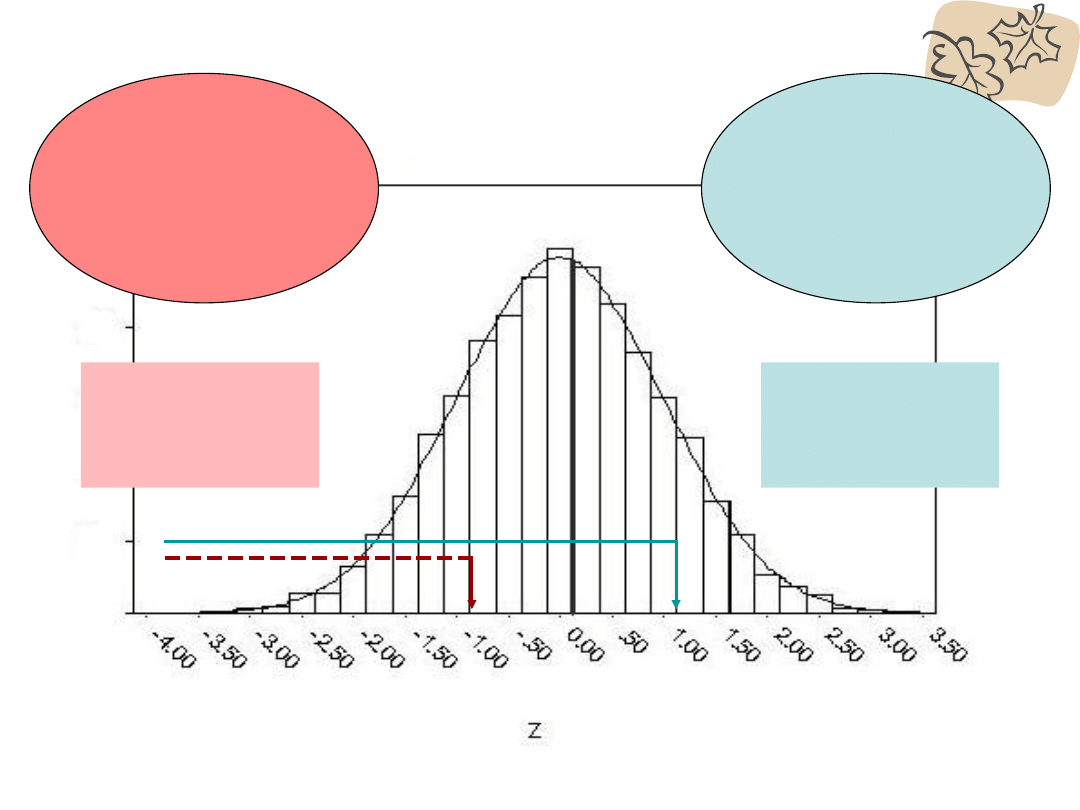
Gdy z ujemne

odejmujemy odczytaną

wartość od 50

Gdy z dodatnie

dodajemy do odczytanej

wartości 50

Wyniki poniżej danej wartości
z

Z = -1,0

% = 50 - 34 =
16

Z = 1,0

% = 50 + 34 =
84

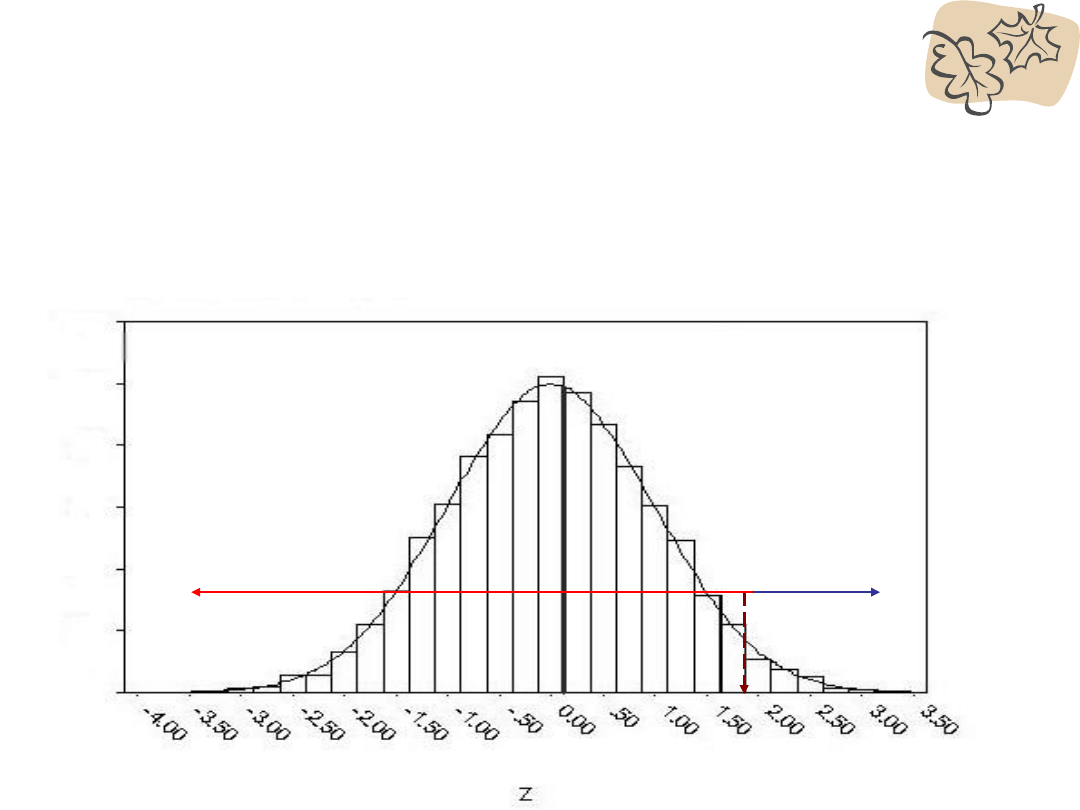
PRZYKŁAD

• IQ = 125, z = 1.56,

• na podstawie tabeli: z = 1,56 to % = 44.06

• z jest dodatnie:

• powyżej IQ = 125 znajduje się (50 - 44.06) =

5.94

% wyników

• poniżej IQ = 125 znajduje się (50 + 44.06) =

94.06

%

wyników.

5,94% powyżej

94,06% poniżej

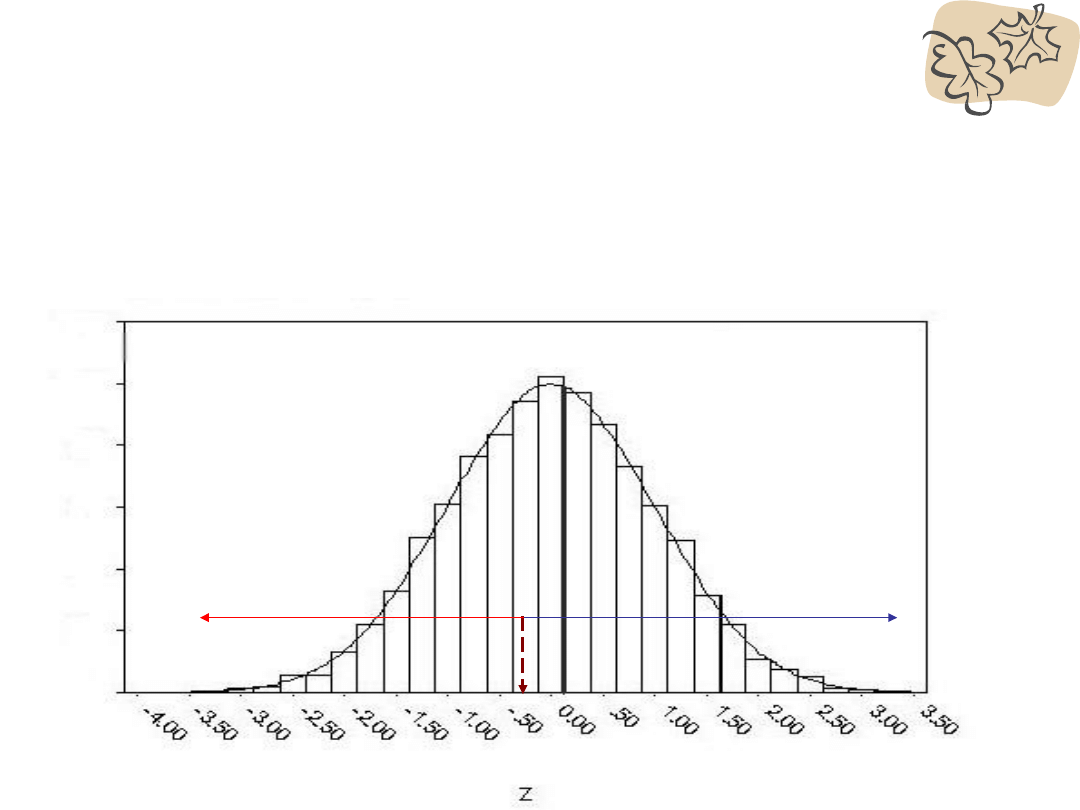
PRZYKŁAD
• IQ = 95, z = -.31
• na podstawie tabeli: % = 12.17
• z jest ujemne
• powyżej IQ = 95 znajduje się (50 + 12.17) =

62.17

% wyników

• poniżej IQ = 9 znajduje się (50 - 12.17) =

37.83

% wyników.

62,17% powyżej

37,83%
poniżej

Korzystając z Tabeli wartości z

• Możemy obliczyć dokładnie

– Jaki procent obserwacji będzie mieścił się w

przedziale między dowolnymi dwoma punktami na

krzywej normalnej wyrażonymi w wartościach z

– Np. procent między z= -1,5 a z= -1.0
Obszar między średnią a z=-1,5 = 0.4332
Obszar między średnią a z=-1.0 =

0.3413

Odejmujemy obszary 0.0919

– Widzimy, że około 9% obserwacji będzie mieściło

się w przedziale między z = -1.0 and z = -1.5

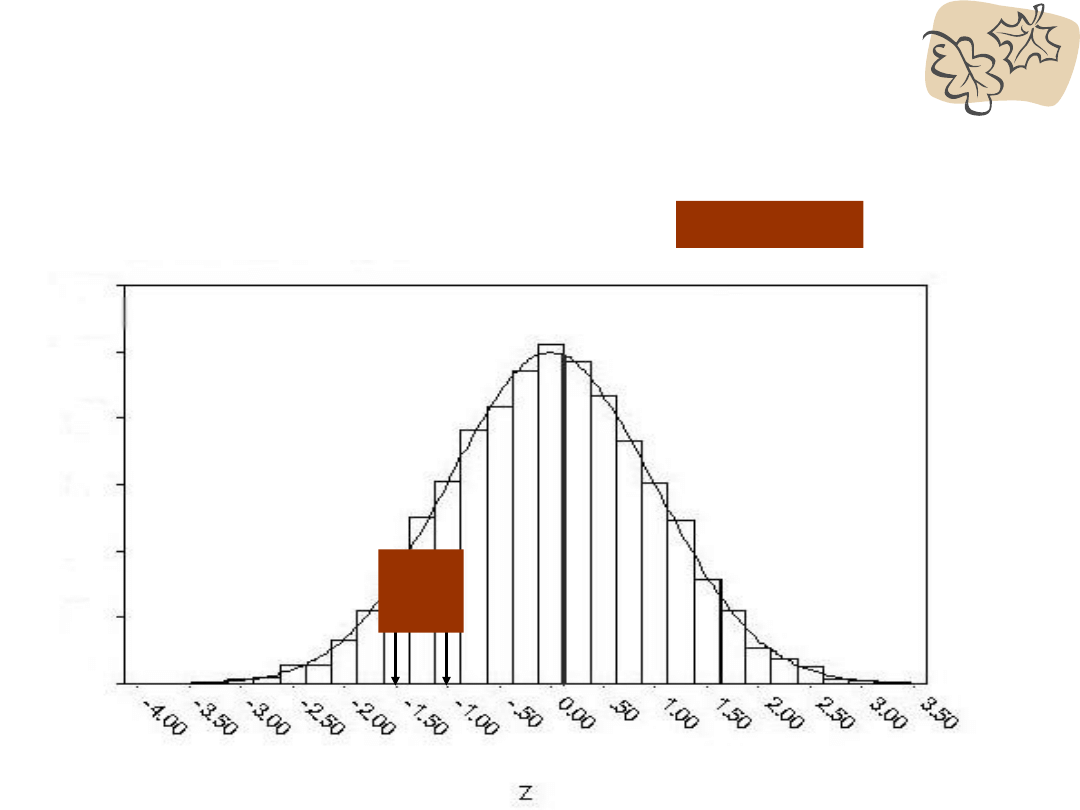
Jaki procent wyników znajduje się

między z=-1,5 a z=-1?

0,43

0,34

0,0
9

niewiele 

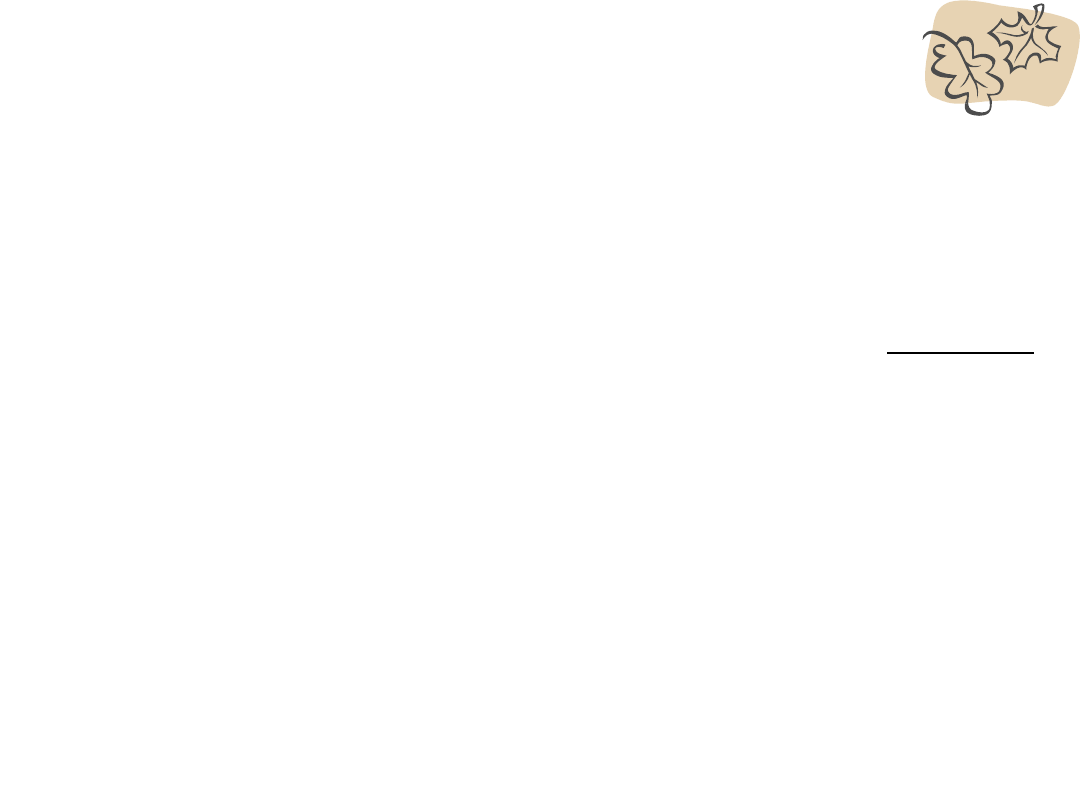
Korzystając z Tabeli wartości z

– Procent między z= -1,5 a z= 1.0
Obszar między średnią a z=-1,5 = 0.4332
Obszar między średnią a z=1.0 = 0.3413

Dodajemy obszary

0.7745

– Około 77% obserwacji będzie mieściło się w

przedziale między z = 1.0 and z = -1.5

Jaki procent wyników znajduje się

między z=-1,5 a z=1?

0,43

0,34

0,7
7

Jak powrócić do wyników surowych?

115

10

5

,

1

100

90

10

0

,

1

100



























x

x

SD

z

M

x

M

SD

x

z

Załóżmy, że dane pochodzą z rozkładu, gdzie

Średnia = 100

Odchylenie standardowe = 10

77% wyników
(między z = -1 a z =
1,5) pochodzących z
tego rozkładu mieści
się w granicach od 90
do 115

Od procentów do wyników surowych - regułki

• Procent wyników powyżej poszukiwanego, to:

- jeśli procent jest mniejszy od 50 najpierw

odejmij go od 50, potem znajdź w tabeli w

kolumnie drugiej procent najbliższy

otrzymanemu i odczytaj towarzyszącą mu

wartość z,

- jeśli jest większy od 50, odejmij go od 100,

potem znajdź w tabeli w kolumnie drugiej

procent najbliższy otrzymanemu i odczytaj

towarzyszącą mu wartość z, po czym postaw

przed nią znak minus: ta wartość z jest ujemna;

• Teraz, gdy masz już poszukiwaną wartość z

przekształć ją na wynik surowy.

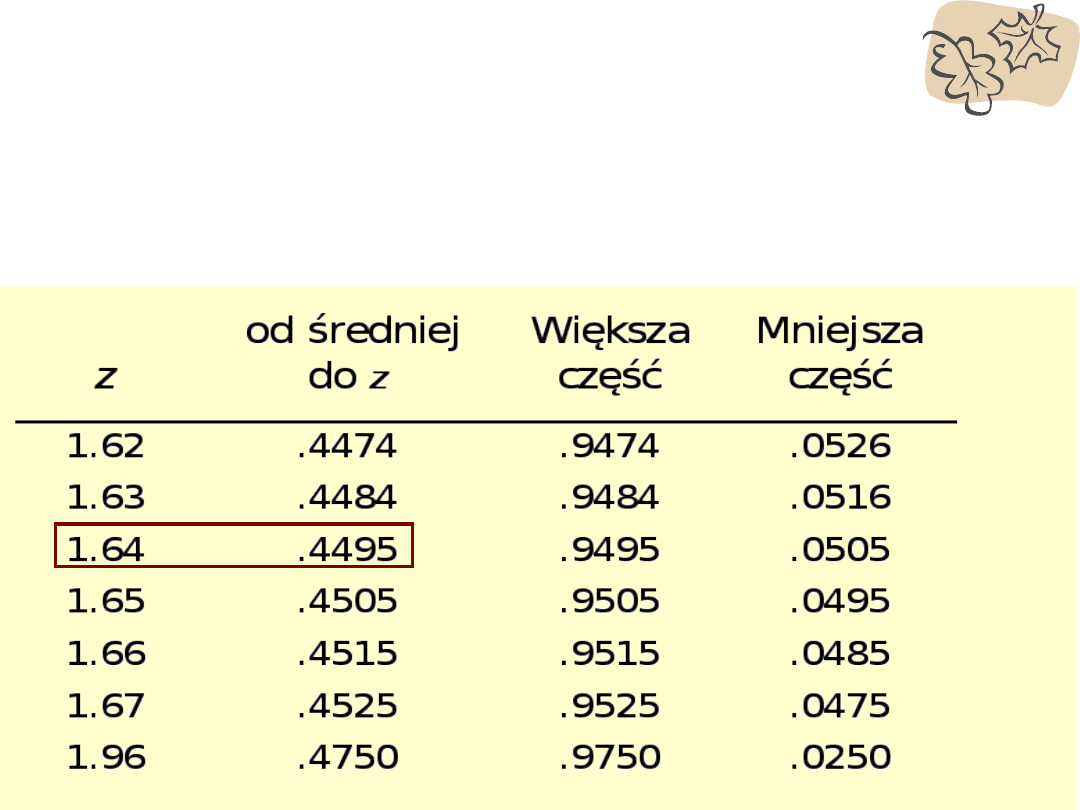
PRZYKŁAD

• IQ = ? M = 100, SD = 16

• % = górne 5%

• Zatem:

• % między średnią a wynikiem = 45%

• na podstawie tabeli najbliższy % = 44.95, z = 1.64

• X = M+ (z)(SD); X = 126.24

• Aby znaleźć się w górnych 5% potrzeba wyniku przynajmniej

126.24

• Procent wyników poniżej poszukiwanego, to:
- jeśli procent jest mniejszy od 50 najpierw odejmij

go od 50, potem znajdź w tabeli w kolumnie drugiej

procent najbliższy otrzymanemu i odczytaj

towarzyszącą mu wartość z, po czym postaw przed

nią znak minus: ta wartość z jest ujemna

- jeśli jest większy od 50, odejmij go od 100, potem

znajdź w tabeli w kolumnie drugiej procent

najbliższy otrzymanemu i odczytaj towarzyszącą

mu wartość z.

• Gdy masz już poszukiwaną wartość z przekształć ją

na wynik surowy.

PRZYKŁAD

• IQ = ?

• % = dolne 2.5%

• Zatem:

• % między średnią a wynikiem = 47.5%

• na podstawie tabeli najbliższy % = 47.5, z =

1.96

• ponieważ wynik jest poniżej średniej, z = -1.96

• X = M + (z)(SD); M = 100, SD = 16: X = 68.64

• Aby znaleźć się w dolnych 2.5% potrzeba

wyniku co najwyżej 68.64

PRAWDOPODOBIEŃSTWO

• Cel badań psychologicznych:
oznaczyć trafność teorii lub efektywność

procedury

• Do spełnienia jedynie w jakimś -

mniejszym lub większym - stopniu, nigdy

nie mamy całkowitej pewności

• Dlatego zjawiskiem centralnym dla nauki

oraz niezbędnym elementem procedur

wnioskowania statystycznego jest

prawdopodobieństwo

• Przejście od wyników badania do wniosków

dotyczących teorii czy procedur, których te

badania dotyczą

• Prawdopodobieństwo: „oczekiwana relatywna

częstość danego wyniku”

• Wynik to rezultat eksperymentu (lub dowolne

zdarzenie, np. że moneta upadnie orłem do góry lub

że jutro będzie padać).

• Relatywna częstość to częstość z jaką wynik się zdarza

w proporcji do tego, jak często mógłby się zdarzyć (np.

moneta orłem do góry może upaść osiem razy w

dwunastu rzutach, proporcja wynosi 8/12 czyli 2/3).

• Oczekiwana relatywna częstość wskazuje jakiej

proporcji spodziewalibyśmy się przy wielu zdarzeniach

(np. przy wielu rzutach monetą oczekujemy 50% czyli

1/2 orłów)

Obliczanie

prawdopodobieństwa

• Proporcja sukcesów oczekiwanych w danej sytuacji - czyli

liczba możliwych pozytywnych wyników (sukces)

podzielona przez liczbę wszystkich możliwych wyników.

• Np., przy obliczaniu prawdopodobieństwa wyrzucenia orła

podczas rzutów monetą, mamy do czynienia z jednym

sukcesem (orłem) na dwa możliwe wyniki (orzeł lub

reszka), co daje prawdopodobieństwo 1/2. Przy rzucie

pojedynczą kostką do gry prawdopodobieństwo uzyskania

dwóch oczek wynosi 1/6, ponieważ mamy jeden sukces

na sześć możliwych wyników.

Jednak prawdopodobieństwo wyrzucenia ‘3 lub mniej’

wynosi już 3/6 czyli 1/2. Jeśli w sali jest 200 osób z czego

50 ma czerwone czapki, to prawdopodobieństwo

wybrania losowo osoby w czerwonej czapce wynosi

50/200 czyli 1/4.

Zakres

prawdopodobieństwa

• Prawdopodobieństwo to proporcja i w związku z tym

nie może być mniejsze od 0 ani większe od 1 (od 0

do 100%).

Prawdopodobieństwo równe 0 to brak szansy na

zdarzenie, a równe 1 to całkowita pewność

zdarzenia.

• Prawdopodobieństwo wyrażone symbolicznie
Zazwyczaj do oznaczenia prawdopodobieństwa

używa się litery p. Wartość prawdopodobieństwa

podaje się w postaci ułamka dziesiętnego (p = 0.5),

choć czasami w postaci ułamka zwykłego (1/2) lub

procentu (50%). Często też korzysta się z możliwości

wyrażenia tego, że prawdopodobieństwo jest

mniejsze lub większe od jakiejś wartości (p < .01).

Prawdopodobieństwo a

rozkład normalny

• Prawdopodobieństwo – proporcja

przypadków – rozkłady częstości

• Rozkład normalny – rozkładem częstości
• Znany procent przypadków między

dwiema dowolnymi wartościami z

• Oznacza to, że znane jest

prawdopodobieństwo wybrania w sposób
losowy przypadku, który znajduje się
między tymi samymi wartościami z. Np.
między z od 0 do 1 znajduje się 34%
przypadków, więc prawdopodobieństwo
wylosowania jednego z nich wynosi p =
0,34

Próba a populacja

Populacja – pewna grupa, zbiór elementów; ograniczona,

nieograniczona

populacja kobiet w wieku rozrodczym, populacja

myszoskoczków

Próba – zbiór ograniczony

Metody próbkowania
• Próba losowa – losowanie indywidualne vs. zbiorowe
Losujemy uczniów z całej puli vs. losujemy szkoły
• Próba kwotowa (dobrana by zachować strukturę społeczną –

socjologia)

Jeśli wiemy, że w generalnej zbiorowości jest 8% osób z

wykształceniem wyższym to tyle procent osób z wyższym
wykształceniem musi się znaleźć w naszej próbie

• Próba celowa nieprobabilistyczna (grupy kliniczne – np. osoby

depresyjne)

Ochotnicy – czy to dobry wybór?

Brzeziński (2002) podsumowuje, że ochotnicy mają:
• Wyższy poziom wykształcenia
• Wyższy status
• Wyższy poziom inteligencji
• Wyższy poziom aprobaty społecznej
• Raczej kobiety
• Wyższy poziom potrzeby stymulacji

• Nie znamy parametrów populacji
• Zakładamy normalny rozkład

zmiennej w populacji

• Próba - wnioski na temat parametrów

zmiennej w populacji, w której ma
ona rozkład normalny (z pewnym
prawdopodobieństwem)..

Próba i populacja:

garnek kaszy – łyżka kaszy

Średnia, wariancja i odchylenie standardowe
populacji to parametry populacji. Są to zatem
niewiadome, które staramy się estymować na
podstawie informacji na temat próby. Nie
próbujemy całej kaszy, a jedynie łyżeczki. „Jest
gotowa” to estymacja na całą populację.

Parametry

populacji

Statystyki próby

Podstawa:

Wyniki całej

populacji

Tylko wyniki próby

Zazwyczaj

nieznane

Obliczane na

podstawie danych

Symbole:

Średnia



X lub M

Odchylenie

std



s lub SD

Wariancja



2

s

2

lub SD

2

Populacja i próba

Testowanie hipotez

• Rozkład normalny jest rozkładem

teoretycznym. Może służyć zatem
jako swego rodzaju wzorzec do
porównywania i wyciągania
wniosków.

Uczymy ufoludka kolorów

W badaniach psychologicznych okazało się, że

to co jest przez ludzi uznawane za kolor

czerwony nie jest wartością dyskretną.

Nie da się wytłumaczyć jak wygląda kolor

czerwony, więc trzeba stworzyć wzorzec

czerwonego.

Następnie każdy prezentowany kolor

porównujemy ze wzorcem – możemy określić

jak bardzo on odbiega od czerwonego.

Przykład: Czerwony to:

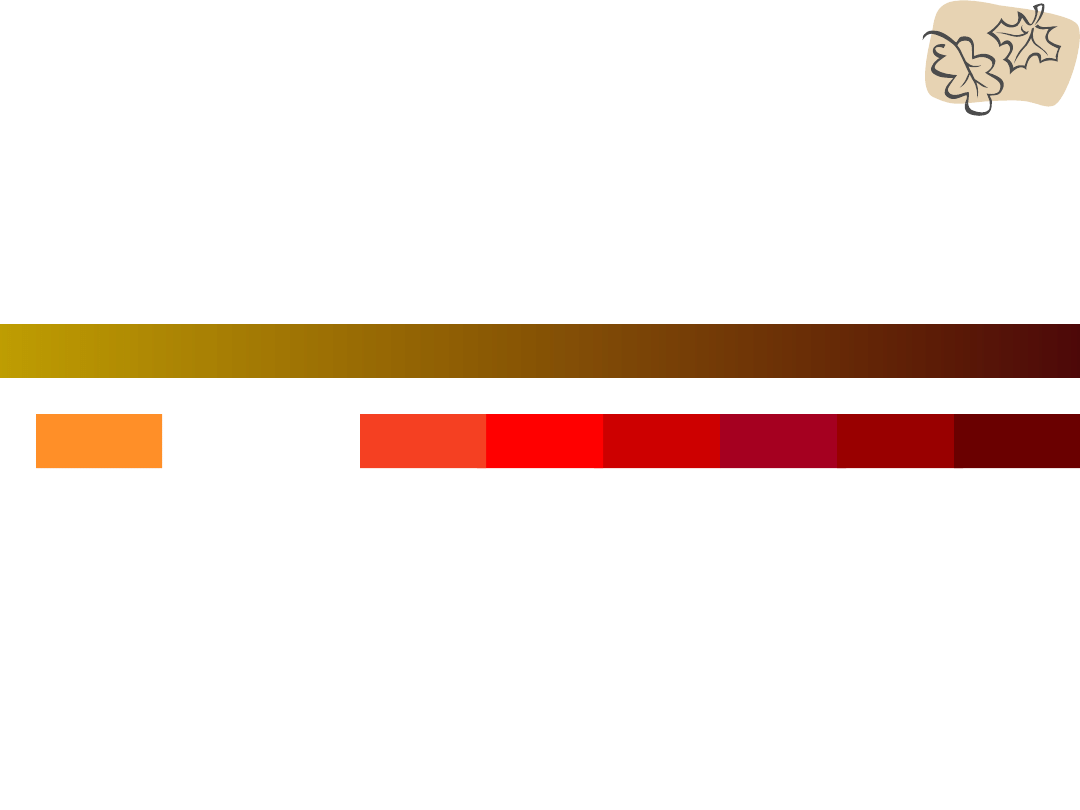
Jeśli ustawiamy te kolory według wzorca to
znajdą odzwierciedlenie nasze intuicyjne oceny
co do typowości danego paska jako koloru
czerwonego.

Na tym także opiera się wnioskowanie
statystyczne

Przykład 1 Czy Jaś jest wybitnym

łakomczuszkiem czy też typowym

zjadaczem czekolady?

• Wiemy, że teoretyczny rozkład

zmiennej „lubienie czekolady” jest
rozkładem normalnym.

• Wiemy też, że Jaś może zjeść

dziennie 3 czekolady, natomiast
przeciętnie osoby badane dziennie
jedzą 1 czekoladę (sd=0,25)

• Jakie jest prawdopodobieństwo, że Jaś

jest typowym zjadaczem czekolady?

Przykład 2 Czy klasa do której

chodzi Jaś to wyjątkowe rozrabiaki?

Rozkład teoretyczny zachowań agresywnych jest

rozkładem normalnym.

Wiemy, że klasa do której chodzi Jaś przeciętnie

wymyśla 20 psikusów tygodniowo (średnia 5
psikusów tygodniowo sd=5)

Jakie jest prawdopodobieństwo, że klasa Jasia

jest typową klasą szkolną?

Przykład 3 Te dzieci są jakieś dziwne

Psycholog pracujący w szkole zorganizował

specjalne zajęcia kreatywności. Jedna z klas
zachowywała się jakoś dziwnie – dzieci nie
angażowały się w zadania, które psycholog
wymyślił. Psycholog stwierdził, że możliwe są
dwie sytuacje: albo zadania są zbyt proste dla
dzieci, albo zbyt trudne

Zmierzył zatem poziom rozumienia tekstu

(Zmienna ta ma rozkład normalny

Klasa miała średnią 60 punktów a zatem zadania

były zbyt łatwe dla dzieci (średnią 30 sd=4).

Dzieci są dziwne ale „dziwne” znaczy tutaj

wyjątkowo zdolne

Wnioskowanie statystyczne

kolejne kroki

1.

Hipoteza badawcza

–

Klasa Jasia to wyjątkowe rozrabiaki
Te dzieci są jakieś dziwne

2.

Wybór grup do porównań

Poziom agresji w typowej grupie
Poziom rozumienia w typowej grupie

3.

Hipoteza zerowa (przeciwieństwo

hipotezy badawczej):

Klasa Jasia to typowe dzieci (Klasa Jasia nie

różni się od normalnej grupy)

Te dzieci charakteryzuje przeciętny poziom

rozumienia tekstu (Dzieci nie różnią się

poziomem rozumienia od typowej grupy)

Wnioskowanie statystyczne

kolejne kroki

4.

Charakterystyki rozkładu który

będzie wzorcem

5.

Od którego momentu wynik jest

nietypowy

• Poziom istotności

p<0,05
p<0,01
p<0,001

• Wartość krytyczna

Ile wynosi w jednostkach

standardowych wartość graniczna

Poniżej której jest 95% osób
Poniżej której jest 99% osób
Poniżej której jest 99,9% osób

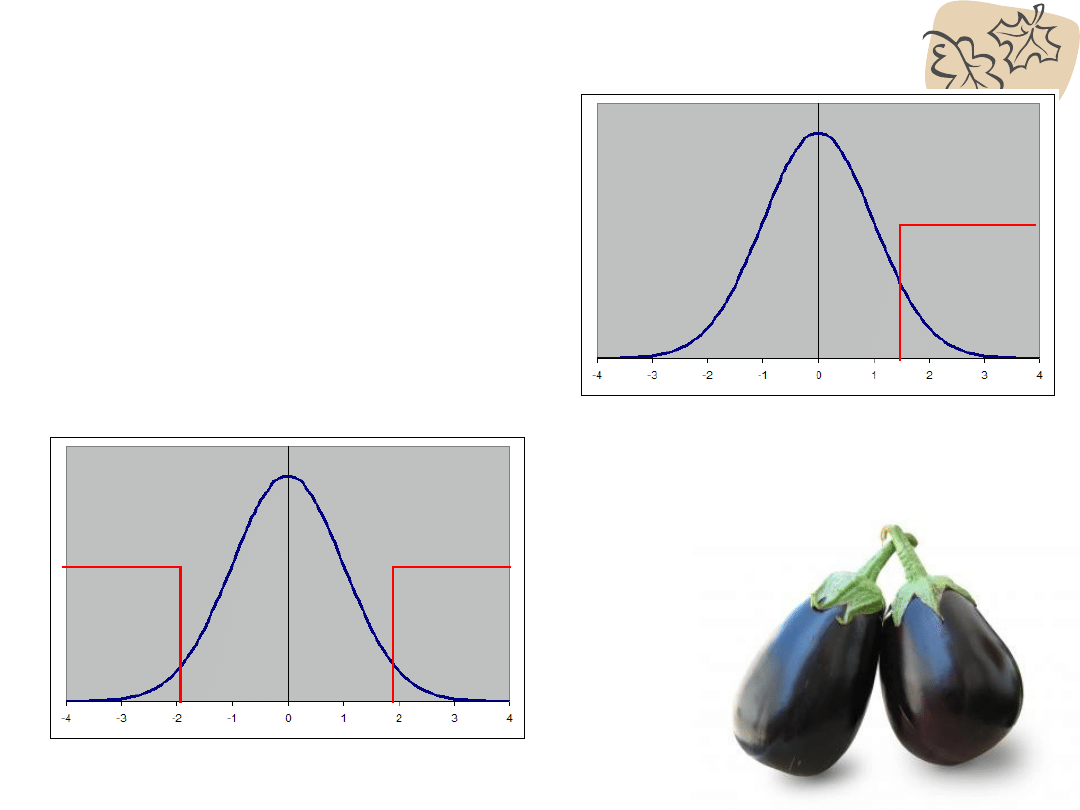
Hipotezy dwustronne i jednostronne

Klasa Jasia to wyjątkowe rozrabiaki
Zakładamy p<0,05 – ale interesuje nas tylko prawy

kraniec rozkładu – wysokie wyniki w skali agresji

Te dzieci są jakieś dziwne
Zakładamy p<0,05 – ale interesują
nas oba krańce rozkładu – zarówno
wysokie jak i niskie wyniki

Poziom
agresji

Poziom rozumienia
tekstu

5%

1,64 Z

2,5%

-1,96

Z

2,5%

1,96 Z

Hipotezy jednostronne i dwustronne

Czy dzieci uznane przez rodziców za uzdolnione

rzeczywiście takie są?

Czy osoby depresyjne mają
trudności z zapamiętywaniem?

Czy osoby poszukujące doznań
lubią sporty ekstremalne?

Czy osoby o wysokim ilorazie
inteligencji są lubiane przez
rówieśników?

Czy osoby o wysokiej potrzebie aprobaty
społecznej różnią się poziomem altruizmu od
osób o niskiej potrzebie aprobaty?

Czy kobiety i mężczyźni różnią się
umiejętnościami prowadzenia samochodu?

Testy statystyczne

Każdy test statystyczny składa się z następujących

specyficznych elementów:

• Hipotezy zerowej i alternatywnej
• Rozkładu, który stanowi podstawę podejmowania

decyzji

• Statystyki, której rozkład jest podstawą

wnioskowania (musimy wiedzieć jak ta statystyka
jest liczona, żeby zrozumieć o co chodzi – do tej
pory była to statystyka Z)

• Stały element – poziom istotności
W psychologii przyjmuje się trzy poziomy graniczne

p<0,05; p<0,01; p<0,001