Wnioskowanie

statystyczne

Facet działający pod pseudonimem Student

Krótkie powtórzenie kolejnych kroków

wnioskowania statystycznego – czyli

marudzenie o pieniądzach

Co dzisiaj?

Dwa rodzaje błędów: Zbyt słabe, albo zbyt

mocne okulary

WNIOSKOWANIE STATYSTYCZNE to szczególny
rodzaj postępowania badawczego, które
dostarcza uzasadnienia dla dokonania kroku
indukcyjnego od znanych właściwości próby
(fragmentu rzeczywistości) do nieznanych (i
badanych) właściwości populacji

Jak wnioskować o

ogromnej populacji

na

podstawie

niewielkiej próby

?

Robimy to zawsze z pewnym prawdopodobieństwem
popełnienia błędu

- wyróżnienie zbioru obiektów tworzących

próbę (losowy dobór)

- wyszczególnienie liczby i rodzaju

zmiennych, za pomocą których
charakteryzujemy populację (zmienne
zależne, zmienne niezależne, zmienne
towarzyszące)

- określenie rodzaju skal pomiarowych,

zastosowanych do wyrażenia wyników

- sprecyzowanie założeń co do charakteru

rozkładu zmiennych (najczęściej chodzi o
rozkład normalny)

Błąd próby

• Jeśli wylosujemy próbę z populacji:

– Średnia w tej próbie może być

większa/mniejsza od średniej w populacji

– Właśnie to, w jakim stopniu statystyka próby

(np. średnia) różni się od odpowiedniego

parametru w populacji (np. średniej w

populacji) określa się błędem próby.

– Im większa badana próba tym mniejszy błąd i

większe prawdopodobieństwo, że średnia z

próby jest bliska średniej w populacji

Wnioskowanie statystyczne

kolejne kroki

1. Hipoteza badawcza

–

Klasa Jasia to wyjątkowe rozrabiaki
Te dzieci są jakieś dziwne
(Robimy badanie)

2. Hipoteza zerowa

(przeciwieństwo hipotezy

alternatywnej):

Klasa Jasia nie różni się od populacji
Dzieci nie różnią się poziomem rozumienia

od typowej grupy

3. Wybór wzorca do porównań

(rozkładu teoretycznego)

Poziom agresji w populacji
Poziom rozumienia w populacji

Wnioskowanie statystyczne

kolejne kroki

Od którego momentu wynik jest

nietypowy

• Poziom istotności (alfa)

p<0,05
p<0,01
p<0,001

• Wartość krytyczna

Ile wynosi w jednostkach

standardowych wartość

graniczna

Poniżej której jest 95% osób
Poniżej której jest 99% osób
Poniżej której jest 99,9% osób

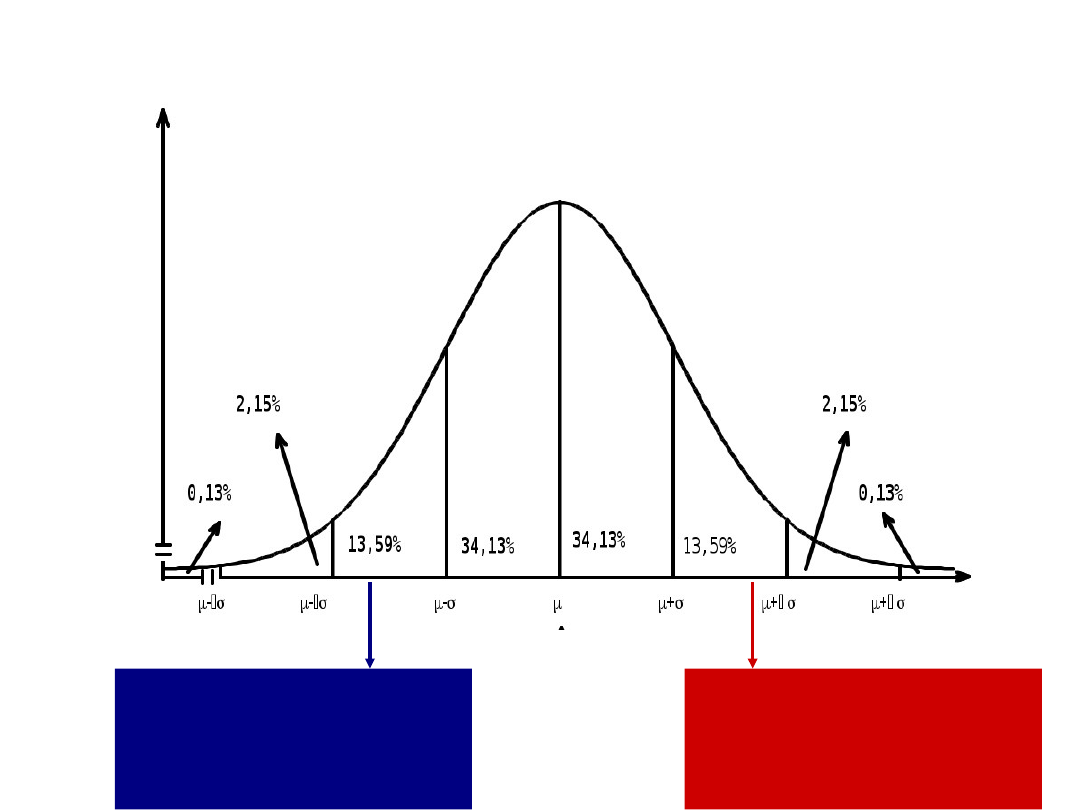
Z = 1,64; powyżej
tej wartości 5
%wyników

Z = -1,64; poniżej
tej wartości 5
%wyników

WAŻNA
DECYZJA
ŻYCIOWA

Jakiego wybrać
kawalera?

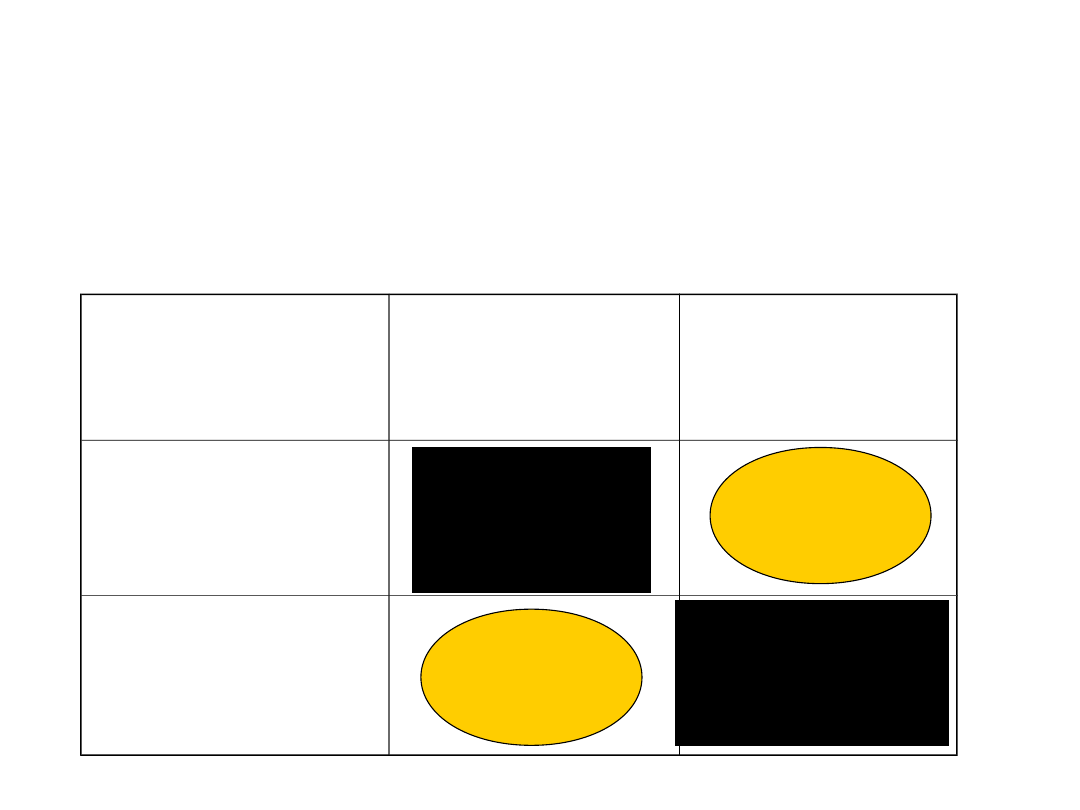
• Dwie możliwości

On jest

dobry

On jest zły

ODRZUCAMY

AKCEPTUJEMY



Utracona miłość



Męczarnia w domu





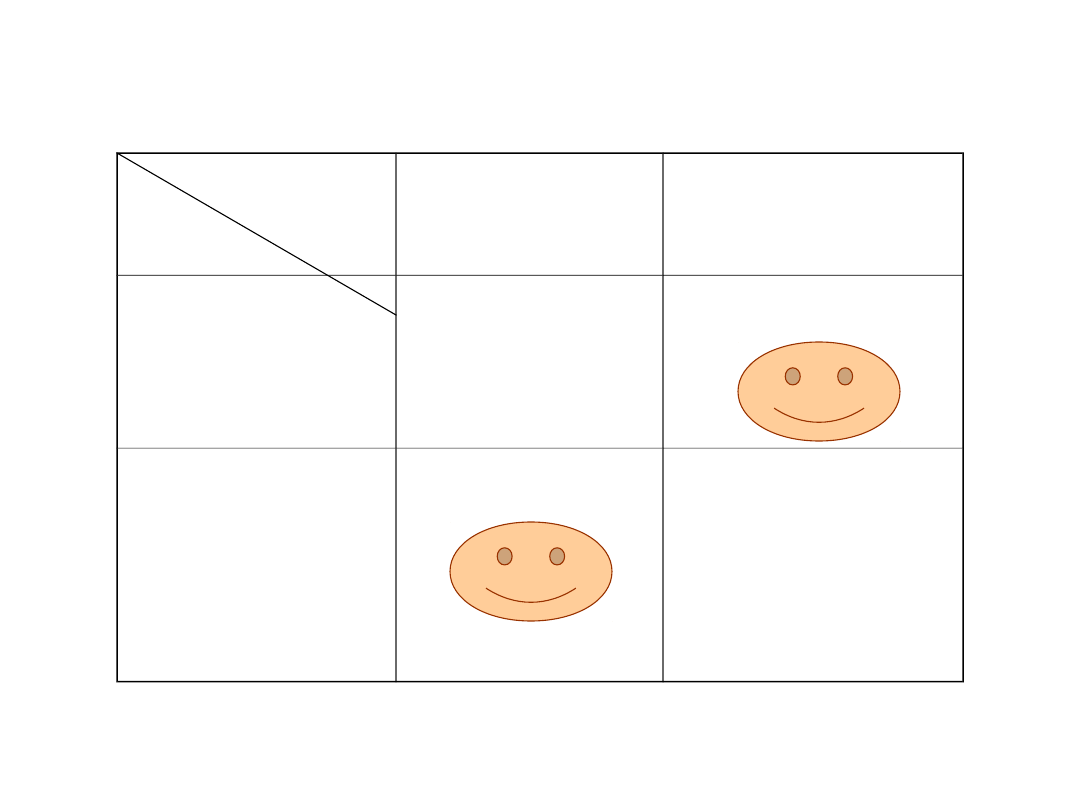
H0

prawdziwa

H0
fałszywa

ODRZUCAMY

błąd I

błąd I

rodzaju

rodzaju

NIE

ODRZUCAMY

błąd II

błąd II

rodzaju

rodzaju

Co możemy zrobić z hipotezą zerową?

Ryzyko (prawdopodobieństwo) popełnienia błędu I
rodzaju nazywane jest poziomem istotności –

w

badaniach staramy się zminimalizować ten błąd

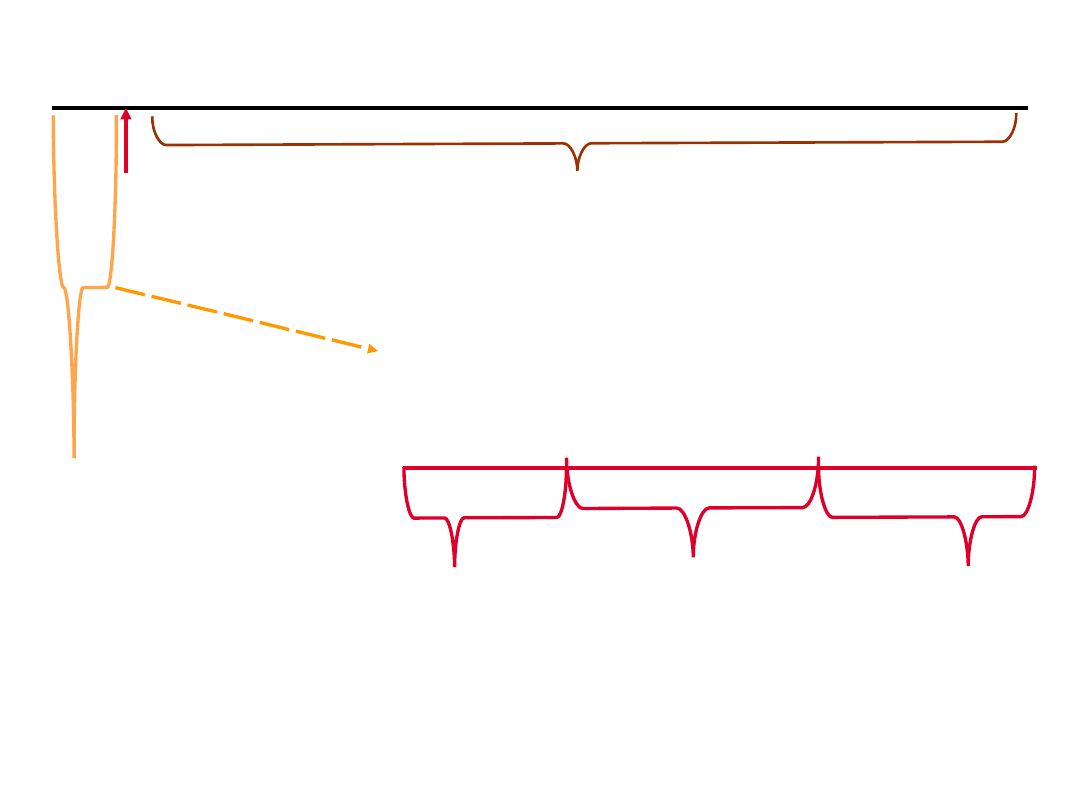
prawdopodobieństwo popełnienia błędu I
rodzaju (α)

0

1

0,0
5

nie mamy podstaw do
odrzucenia H0

odrzucamy
H0

Jak zapisujemy poziom istotności?

0

0,0
5

0,0
1

0,00
1

p <
0,001

p <
0,01

p <
0,05

Testy statystyczne

Każdy test statystyczny składa się z

następujących specyficznych elementów:

• Hipotezy zerowej i alternatywnej

• Statystyki testu (musimy wiedzieć jak ta

statystyka jest liczona, żeby zrozumieć o co
chodzi – do tej pory była to statystyka Z)

• Rozkładu tej statystyki, który stanowi

podstawę podejmowania decyzji

• Stały element – poziom istotności

W psychologii przyjmuje się trzy poziomy

graniczne p<0,05; p<0,01; p<0,001

H

0

:

H

A

:

Hipotezy teoretyczne kierunkowe i

niekierunkowe

Czy dzieci uznane przez rodziców za uzdolnione

rzeczywiście takie są?

Czy osoby depresyjne mają
trudności z zapamiętywaniem?

Czy osoby poszukujące doznań
lubią sporty ekstremalne?

Czy osoby o wysokim ilorazie
inteligencji są lubiane przez
rówieśników?

Czy osoby o wysokiej potrzebie aprobaty
społecznej różnią się poziomem altruizmu od
osób o niskiej potrzebie aprobaty?

Czy kobiety i mężczyźni różnią się
umiejętnościami prowadzenia samochodu?

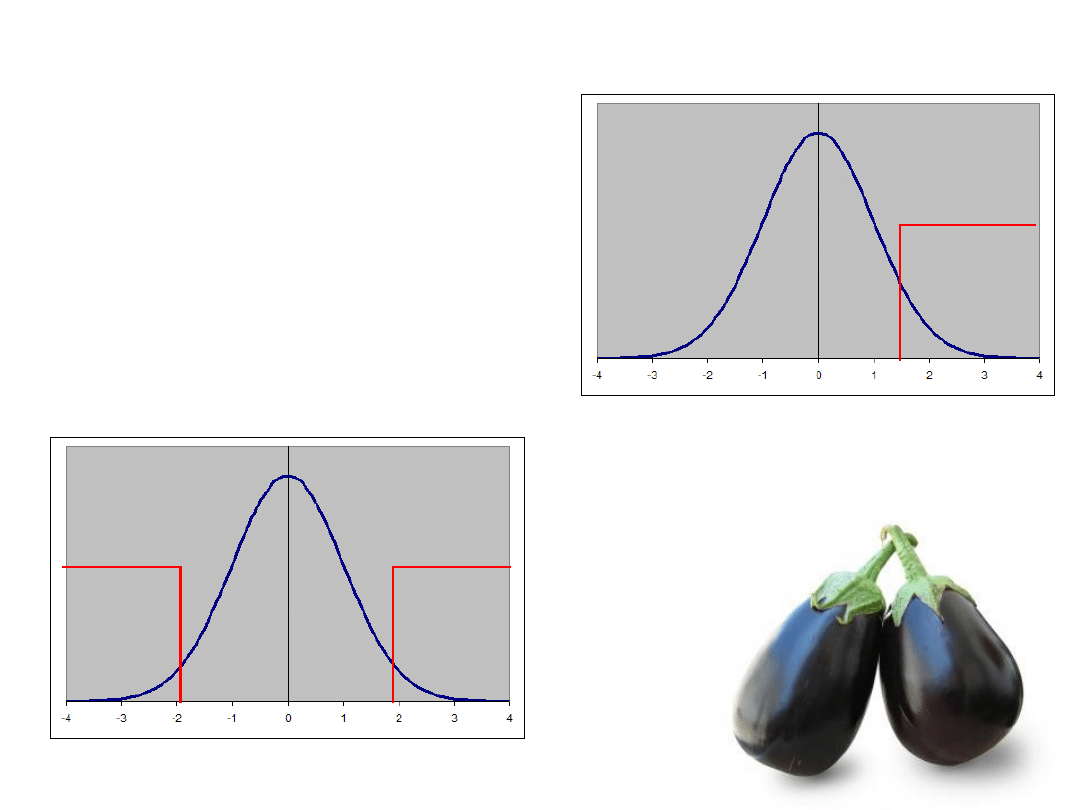
Hipotezy teoretyczne kierunkowe i

niekierunkowe

Klasa Jasia to wyjątkowe rozrabiaki
Zakładamy p<0,05 – ale interesuje nas tylko prawy

kraniec rozkładu – wysokie wyniki w skali agresji

Te dzieci są jakieś dziwne
Zakładamy p<0,05 – ale interesują
nas oba krańce rozkładu – zarówno
wysokie jak i niskie wyniki

Poziom
agresji

Poziom rozumienia
tekstu

5%

1,64 Z

2,5%

-1,96

Z

2,5%

1,96 Z

Hipotezy - podsumowanie

Hipotezy teoretyczne
sformułowane w języku teorii psychologicznej
• kierunkowe i niekierunkowe

Trening kreatywności menadżerów firmy „Krówka – ciągutka” poprawił ich

kreatywność

Policjanci, którzy przeczytali dowcipy o głupich policjantach zgłupieją.
Efekt memento mori – myśli o śmierci powodują zmianę ważności pewnych

elementów doświadczenia i zmianę zachowania

Hipoteza zerowa i alternatywna
sformułowane w języku technicznym – statystycznym

H

0

: Nie będzie różnic między średnią kreatywnością menadżerów przed i po

treningu kreatywności. (H

A

: Będą różnice)

H

0:

Policjanci, którzy czytali kawały będą w stanie wykonywać tyle samo

trudnych łamigłówek jak policjanci, którzy nie czytali kawałów (H

A

: Będą

różnice)

H

0:

Osoby, które poproszono o myślenie o własnej śmierci nie różnią się

średnią skłonnością do pomagania od osób, które nie zostały poddane tej

manipulacji (H

A

: Będą różnice)

Poziom teoretyczny – dotyczy zmiennej
teoretycznej (ekstrawersja)

hipoteza teoretyczna

Poziom operacyjny – operacjonalizujemy
zmienną teoretyczną (język wskaźników –
wyniki w kwestionariuszu ekstrawersji)

hipoteza operacyjna

Problemy? – jak znaleźć tę jedną, „prawdziwą”
operacjonalizację

Czy Polacy zarabiają średnią

krajową?

Jeden z badaczy zajmujących się psychologią

ekonomiczną postanowił sprawdzić, czy przeciętnie
Polacy zarabiają tyle ile wynosi średnia krajowa.
Badacz zauważył, że jego znajomi ciągle narzekają
na swoje dochody. Zaczął się zastanawiać, czy jest
aż tak źle, czy też narzekanie na pieniądze jest
zwyczajową wymianą uprzejmości.

Przebadał reprezentatywną 1000 osobową grupę

Polaków. Ustalił też, że średnie dochody w Polsce
wynoszą 2200 brutto a ich odchylenie standardowe
200 złotych (dane GUS – dane o populacji).

Nasi respondenci przeciętnie zarabiają 2700 złotych
Pytanie badawcze: Czy respondenci różnią się

poziomem dochodów od przeciętnego Polaka?

Hipoteza zerowa

:

Średni

dochód respondentów

nie

różni

się od średniej krajowej.

Hipoteza alternatywna

:

Średni

dochód respondentów

różni się

od średniej krajowej

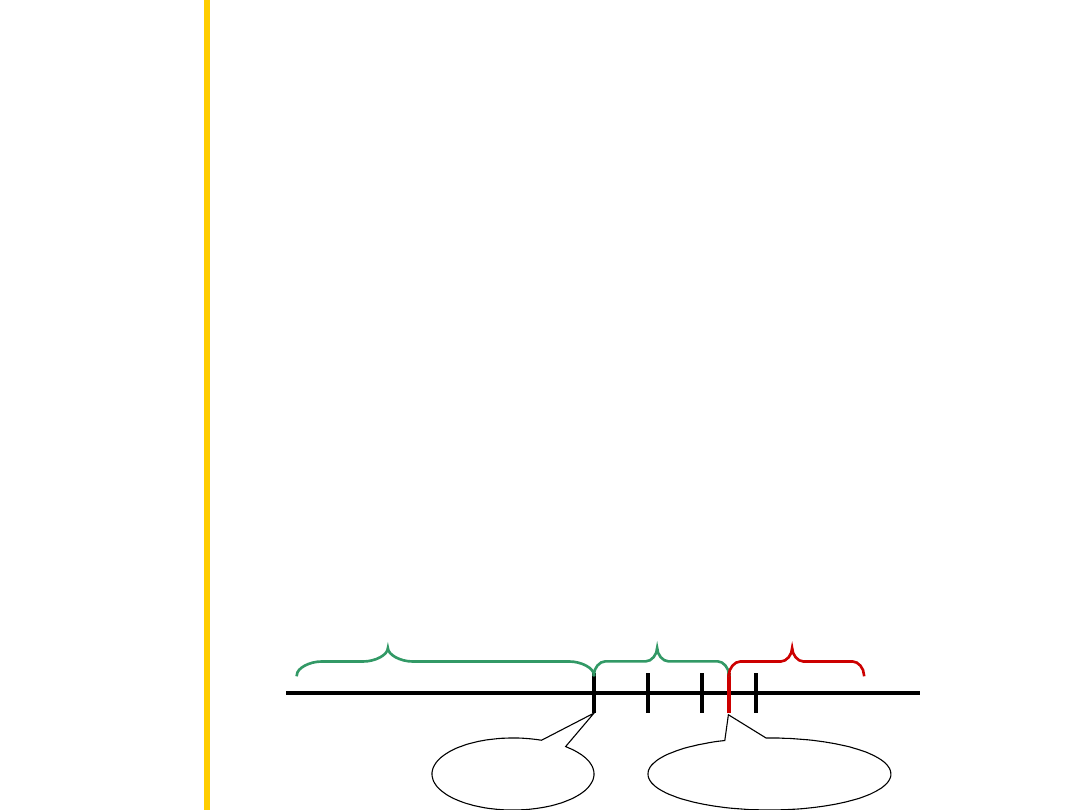
Czy Polacy zarabiają średnią krajową -

obliczenia

Standaryzujemy wynik uzyskany w naszym

badaniu traktując średni dochód krajowy
(wskaźnik GUS) jako punkt odniesienia

.

Z=(2700-2200)/200
Z=2,5

Posługując się rozkładem normalnym sprawdzamy

jakie jest prawdopodobieństwo uzyskania wyniku

powyżej Z=2,5

Zakładamy poziom istotności p<0,05

Dla Z=2,50 procent od średniej wynosi 49,38.

Dodajemy 50% poniżej średniej i mamy 99,38%.

Zatem powyżej tej wartości pozostaje mniej niż

5% zgodnie z zakładanym poziomem istotności.

Odrzucamy zatem hipotezę zerową i przyjmujemy

alternatywną.

Średn
ia

Wynik
2,5Z

50
%

49
%

Mniej niż
5%

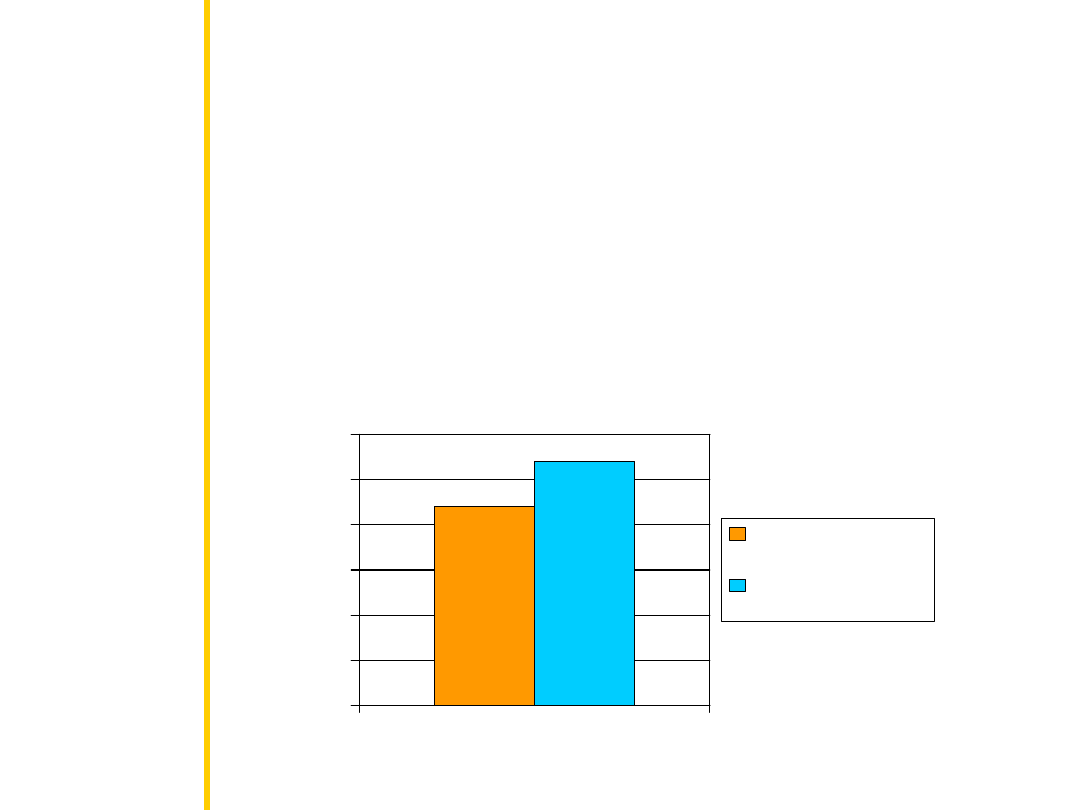
Czy Polacy zarabiają średnią krajową?

Jak to opisać

Na podstawie wykonanych obliczeń (Z=2,5; p<0,05)

możemy stwierdzić, że odrzucamy hipotezę zerową a
tym samym przyjmujemy alternatywną. A zatem
przebadana grupa nie zarabia średniej krajowej. Co
więcej na podstawie średnich (patrz wykres) możemy
stwierdzić, że nasi respondenci zarabiają przeciętnie
więcej niż wynosi średnia krajowa.

0

500

1000

1500

2000

2500

3000

dochody w złotych

średnia krajowa

dochody w

badanej grupie

Ale można też inaczej

Test T-Studenta dla jednej próby

Zamiast statystyki Z możemy się posłużyć statystyką T.

Tym bardziej, ż nie zawsze znamy parametry populacji.

Statystyka ta została zaproponowana przez Studenta,

który opracował także rozkład teoretyczny tej

statystyki. Rozkład statystyki T dla dużych grup ma

kształt zbliżony do rozkładu normalnego.

Student (w rzeczywistości Wiliam S. Gosset) stanął przed

poważnym pytaniem jak spowodować, żeby piwo

produkowane z różnych składników miało ten sam

smak, niezależnie od partii. Musiał opublikować swoją

pracę pod pseudonimem bo jego warzelnia bała się ze

sprzeda jej tajemnice i nie zezwoliła na publikację.

„Student” robił błędy obliczeniowe, najważniejsze notatki

robił na kopertach i nie lubił piwa

Podstawowe informacje o teście T dla

jednej próby

Zadaniem tego testu jest porównywanie średniej

grupowej z pewną stałą wartością.

Hipoteza zerowa: Nie ma różnic między średnią

grupową a pewną wartością (stałą), którą
znamy.

Hipoteza alternatywna: Są różnice między stała

a średnią grupową.

Decyzję podejmujemy licząc statystykę T i

odnosząc ją do rozkładu tej statystyki. Jak ją
policzyć?

Badania nad obżarstwem

Czy Amerykanie jedzą za dużo?
Badacz postanowił sprawdzić, czy Amerykanie są

otyli bo jedzą złe rzeczy, czy też jedzą zbyt
często. W tym celu przebadał 10 osób, mierząc
ile posiłków dana osoba zjadła w ciągu jednego
dnia.

Postawił hipotezę, że Amerykanie dlatego są

otyli, że jedzą zbyt wiele posiłków dziennie.

• Hipoteza zerowa: Średnia ilość posiłków

jedzonych przez Amerykanów nie różni się od
4.

• Hipoteza alternatywna: średnia ilość posiłków

różni się istotnie od 4.

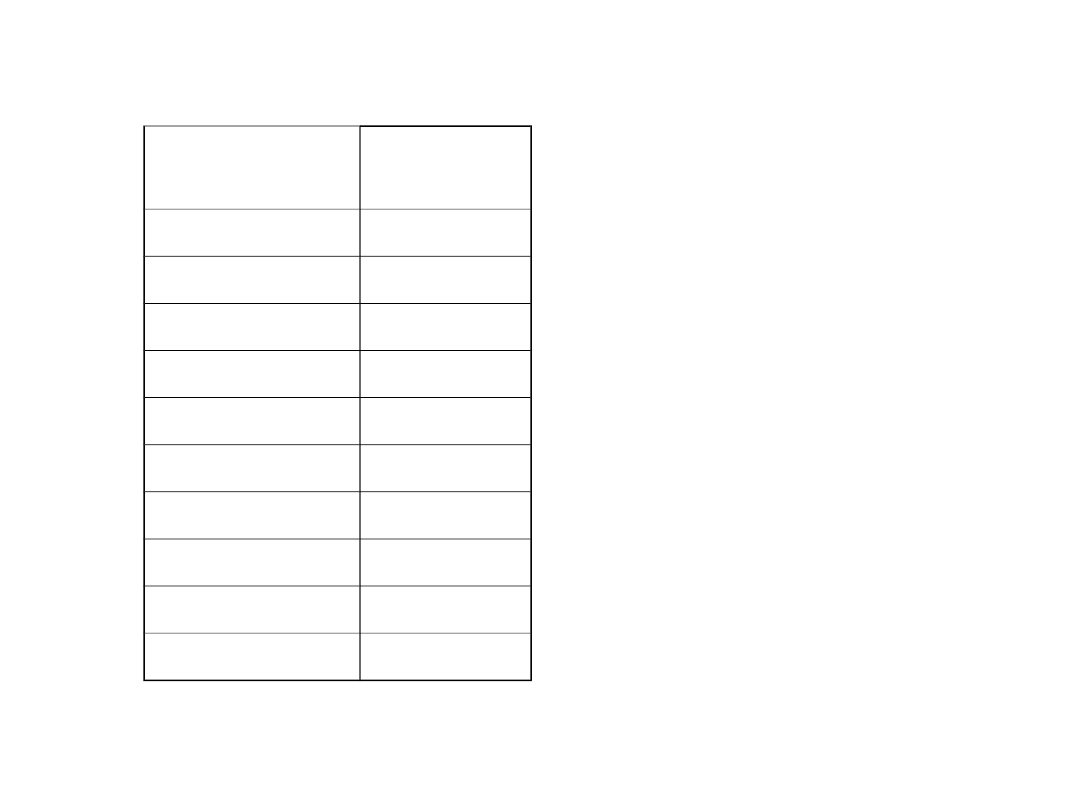
Wyniki badania

Na podstawie przebadanej

grupy można powiedzieć,
że Amerykanie jedzą
przeciętnie 2 posiłki

dziennie.

Liczba

posiłków

1 osoba

3

2 osoba

2

3 osoba

1

4 osoba

1

5 osoba

1

6 osoba

2

7 osoba

2

8 osoba

1

9 osoba

4

10 osoba

3

Liczenie statystyki T

Jedyne czego nam brakuje to odchylenie std. średniej

– to nie jest to samo co odchylenie std. wyników.

Średnia w
populacji

t =

Odchylenie std.
średniej

Średnia grupowa
-

S

t









Jak nie dostać wariacji nad wzorami

wariancji

Dwa wzory:

Opis statystyczny - próba

Suma kwadratów odchyleń wyników od

średniej

dzielona przez ich liczbę

(czyli

liczbę osób)

Wnioskowanie statystyczne - populacja

Dokonujemy oszacowania wariancji w

populacji na podstawie próby, więc

dzielimy licznik przez liczbę osób –1

Tak więc licząc odchylenie standardowe

średniej używamy właśnie tego
drugiego wzoru.

2

1

)

(









N

M

X

i



2

)

(

N

M

X

i









Odchylenie std. średniej

Wariancję wyników w próbie (1) dzielimy przez

liczbę osób (10) i pierwiastkujemy, żeby
uzyskać odchylenie standardowe średniej.

Odchylenie to wynosi 0,32

• Liczymy t=(2-3)/0,32=-3,125
Wiemy zatem, że wartość statystyki t w teście

dla jednej próby wynosi -3,125

Odczytywanie poziomu

istotności

Aby odczytać poziom istotności danej wartości testu T

musimy znać

liczbę stopni swobody

(df-degree of

freedom)– uzależnioną od liczby osób.

W teście T dla jednej próby stopnie swobody wynoszą

tyle ile liczba osób pomniejszona o 1 (czyli 9).

Stopnie swobody pojawiają się dlatego, że dla prób o

różnej wielkości rozkład jest troszkę inny.

Oprócz stopni swobody musimy wiedzieć, czy hipoteza

jest kierunkowa (wtedy

test jednostronny

), czy też

niekierunkowa – (wtedy

test dwustronny

)

Dla 9 stopni swobody (test jednostronny) wartość

krytyczna T, dla poziomu istotności p<0,05, wynosi

1,833 lub

–1,833.

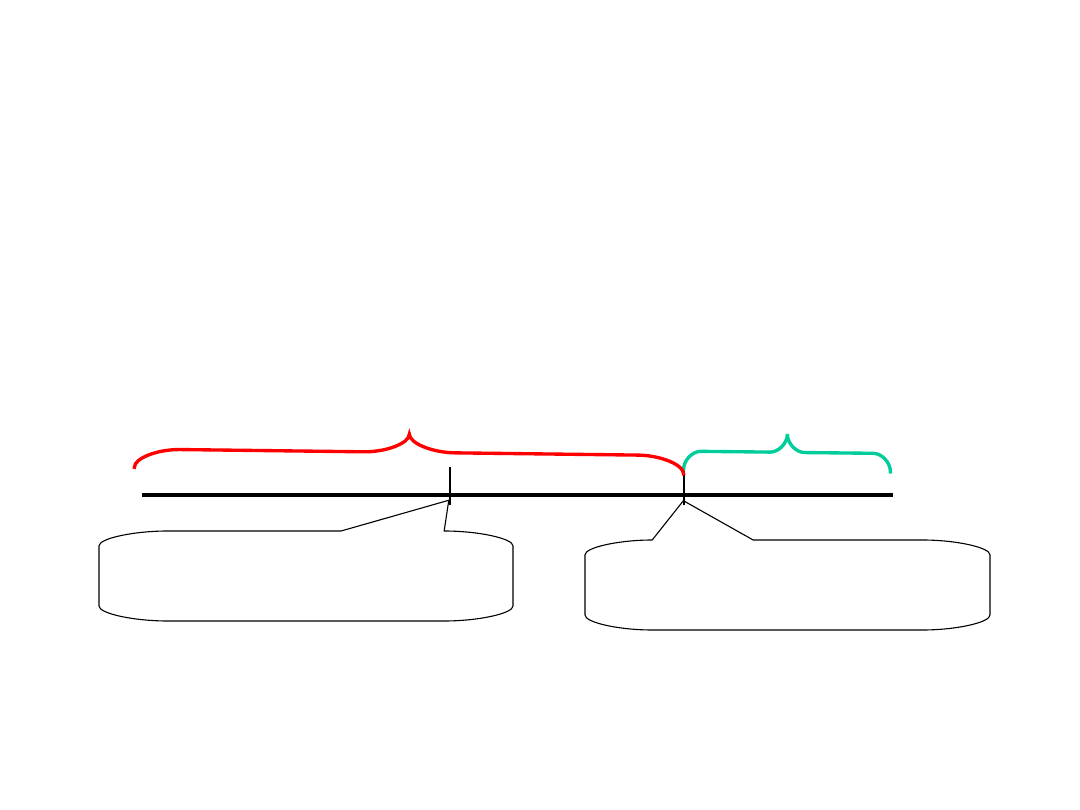
Porównujemy wartość graniczną i wartość

uzyskaną w obliczeniach – najlepiej na osi
liczbowej. Zaznaczamy zatem wartość
graniczną statystyki t oraz wartość t obliczoną
przez nas. Wartość t uzyskana w naszym
badaniu wpada w obszar odrzucenia.

Wartość krytyczna

statystyki T dla df=9

t= -1,833

Wartość statystyki t

uzyskana w naszym

badaniu t= -3,125

Obszar odrzucenia H0:
p<0,05

Wnioski

Tak więc na poziomie istotności p<0,05 odrzucamy

hipotezę zerową, że Amerykanie jedzą trzy posiłki

dziennie

t(9)=3,125; p<0,05

(Zapis APA).

Uwaga – przy wartości statystyki t nie piszemy znaku

„-”

Czy to oznacza, że nasza hipoteza się potwierdziła?
Niestety nie!
Myśleliśmy, że Amerykanie jedzą więcej niż trzy

posiłki, podczas, gdy średnia liczba posiłków

wynosi 2, czyli jest mniejsza niż średnia w

populacji.

Oznacza to, nasze poszukiwania wyjaśnienia otyłości

Amerykanów powinny iść nie w kierunku ilości

posiłków, ale ich wielkości.

Czy model rodziny 2+2

jeszcze funkcjonuje?

Statystyki dla jednej próby

4034

1,99

1,567

,025

LICZBA DZIECI

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

-,372

4033

,710

-,01

-,06

,04

LICZBA DZIECI

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 2

Wniosek: Na podstawie statystyk testu T-Studenta dla
jednej
próby nie ma podstaw do odrzucenia hipotezy zerowej
t(4033)=0,372; p>0,05. Zatem przeciętna polska rodzina
zawiera dwójkę dzieci