Statystyka

Wykład 13

Parametry populacji

Statystyki próby

Podstawa:

Wyniki całej populacji

Tylko wyniki próby

Zazwyczaj nieznane

Obliczane na podstawie

danych

Symbole:

Średnia



X lub M

Odchylenie std



s lub SD

Wariancja



2

s

2

lub SD

2

Populacja i próba

Relacje między odchyleniem standardowym i

wariancją

Odchylenie standardowe = pierwiastek z wariancji, czyli
Wariancja = OS (s) do kwadratu
• Jak policzyć?
2 4 6 8 10
• Średnia? 6
• -4 -2 0 2 4 (teraz suma = 0, więc podnosimy do

kwadratu)

• 16 4 0 4 16 (teraz sumujemy) – 40 i dzielimy przez N-1,

czyli

• 40/4 = 10 – mamy policzoną wariancję, żeby wyniki były

„bliższe” rzeczywistych, musimy je „odkwadracić”
(pierwiastkujemy, czyli obliczamy OS)

• Pierwiastek z 10, to 3,16 (w przybliżeniu )

Natężenie objawów choroby sierocej u dzieci z Domów Małego
Dziecka i Rodzinnych Domów Dziecka

Hipoteza1: Istnieją różnice w natężeniu objawów

choroby sierocej między dziećmi znajdującymi
się w Domu Małego Dziecka oraz tymi
wychowywanymi w Rodzinnym Domu Dziecka

(hipoteza niekierunkowa, dotycząca różnic)
Hipotez2: Natężenie objawów choroby sierocej u

dzieci wychowywanych w Rodzinnych Domach
Dziecka jest mniejsze niż u dzieci
znajdujących się pod opieką Domu Małego
Dziecka.

(hipoteza kierunkowa, dotycząca różnic)

Zmienne i sposoby ich pomiaru

1 zmienna

: rodzaj placówki opiekuńczej

Dom Małego Dziecka vs. Rodzinny Dom Dziecka
Zmienna jest

nominalna

i przyjmuje dwie

wartości

2 zmienna

: natężenie objawów choroby sierocej

Natężenie to było określane za pomocą

obserwacji – obserwator określał, czy natężenie
jest zerowe, małe, przeciętne, duże i bardzo
duże

Zmienna jest zatem

porządkowa

i przyjmuje 5

wartości

Podejmujemy decyzję jaki test należy zastosować

Opieramy się na informacjach na temat:
Rodzaju hipotez:
• różnice czy związek? różnice
Rodzaju i ilości zmiennych:
• dwie zmienne: jedna zmienna nominalna

dwuwartościowa, druga zmienna porządkowa

Test nieparametryczny: test U-Manna
Whitneya

Wyniki

Zamieniamy oceny obserwatora na wartości liczbowe zgodnie z

kluczem:

brak – 0, małe -1, przeciętne- 2, duże- 3, bardzo duże – 4.

Dzieci z Domu Małego
Dziecka

Dzieci z Rodzinnego Domu
Dziecka

Asia-małe, Zosia duże, Krzyś-
duże, Adam-przeciętne,
Robert- przeciętne, Patryk –

bardzo duże, Kasia- brak

Dagmara-brak, Artur – małe,
Tomek- brak, Stefan-
przeciętne, Milena-małe,

Danusia-brak, Małgosia - brak

Dzieci z Domu Małego Dziecka

Dzieci z Rodzinnego Domu
Dziecka

Asia - 1, Zosia - 3, Krzyś - 3,
Adam - 2, Robert - 2, Patryk – 4,
Kasia - 0

Dagmara - 0, Artur – 1,
Tomek - 0, Stefan - 2, Milena
- 1, Danusia - 0, Małgosia - 0

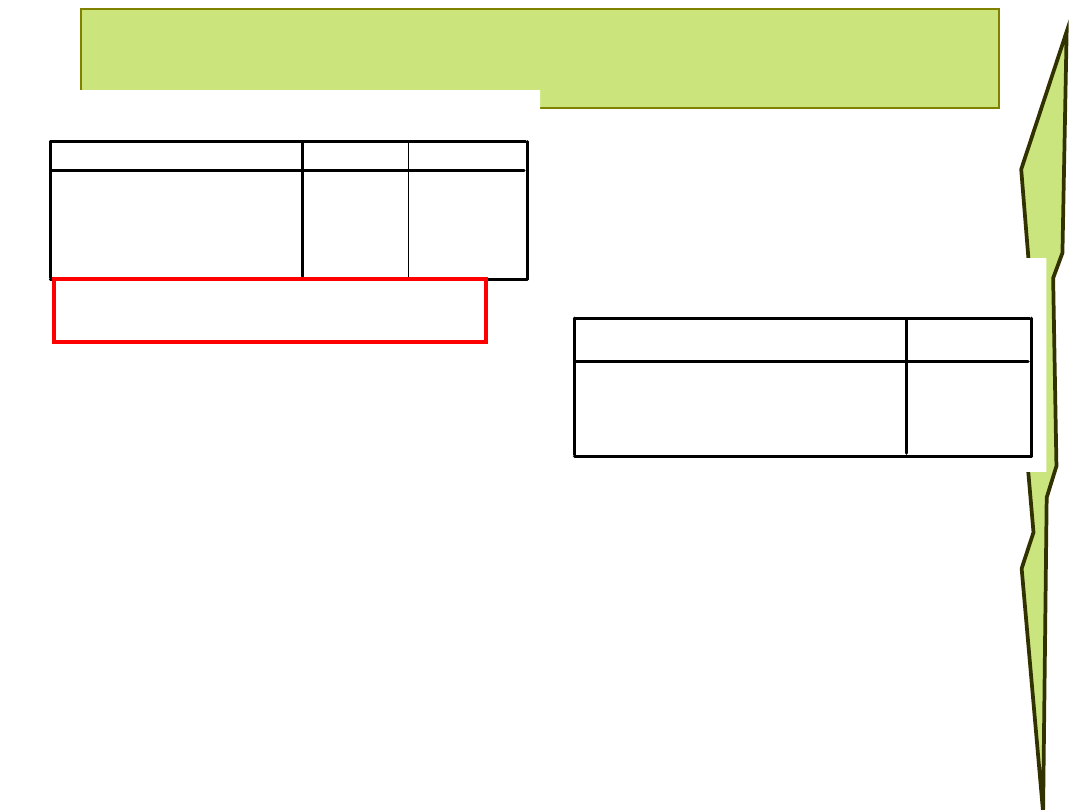
Liczymy statystyki opisowe zmiennych

Zmienna „rodzaj placówki” jest zmienną nominalną więc można policzyć tylko

modalną – w tym przypadku mamy dwie modalne – 1 (wartość podana na

wydruku) oraz 2. Widać to w tabeli częstości - grupy są równoliczne.

Zmienna „natężenie objawów choroby sierocej” może zostać opisana za

pomocą dwóch statystyk – modalnej równej 0 (co oznacza, że największa

liczba badanych dzieci nie przejawia objawów choroby sierocej) oraz

mediany równej 1 (co oznacza, że co najmniej połowa dzici ma objawy o

natężeniu niższym niż rzadkie).

Statystyki

14

14

0

0

1,0000

1,00

a

,00

Ważne
Braki danych

N

Mediana
Dominanta

DOM

CHOROBA

Istnieje wiele wartości modalnych. Podano
wartość najmniejszą.

a.

DOM

7
7

14

dom malego dziecka
rodzinny dom dziecka
Ogółem

Ważne

Częstość

Rangujemy wyniki

Ustawiamy wszystkie dzieci w kolejności od najmniejszego natężenia

objawów do najwyższego

Kasia – 0,

Dagmara - 0, Tomek – 0, Danusia – 0, Małgosia – 0,

Asia – 1,

Artur – 1, Milena – 1,

Adam – 2, Robert - 2,

Stefan – 2,

Zosia – 3, Krzyś –

3, Patryk – 4,

Zapisujemy same wartości liczbowe, żeby obliczyć rangi:

0

,

0, 0, 0, 0,

1,

1, 1,

2, 2,

2,

3, 3, 4

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,

(numerujemy)

3;

3; 3; 3; 3;

7;

7; 7;

10; 10;

10;

12,5; 12,5; 14 (rangujemy)

Dzieci z Domu Małego Dziecka

Dzieci z Rodzinnego Domu

Dziecka

Asia - 1, Zosia - 3, Krzyś - 3,
Adam - 2, Robert - 2, Patryk – 4,

Kasia - 0

Dagmara - 0, Artur – 1,
Tomek - 0, Stefan - 2, Milena

- 1, Danusia - 0, Małgosia - 0

Liczymy średnie rangi

3;

3; 3; 3; 3;

7;

7; 7;

10; 10;

10;

12,5; 12,5; 14 (rangujemy)

Rangi przypisujemy z powrotem do grup

Dzieci z Domu Małego Dziecka

Dzieci z Rodzinnego Domu
Dziecka

3; 7; 10; 10; 12,5; 12,5; 14
Uśredniamy = 9,86

3, 3, 3 3, 7, 7, 10
Uśredniamy = 5,14

Czy dobrze policzyliśmy?

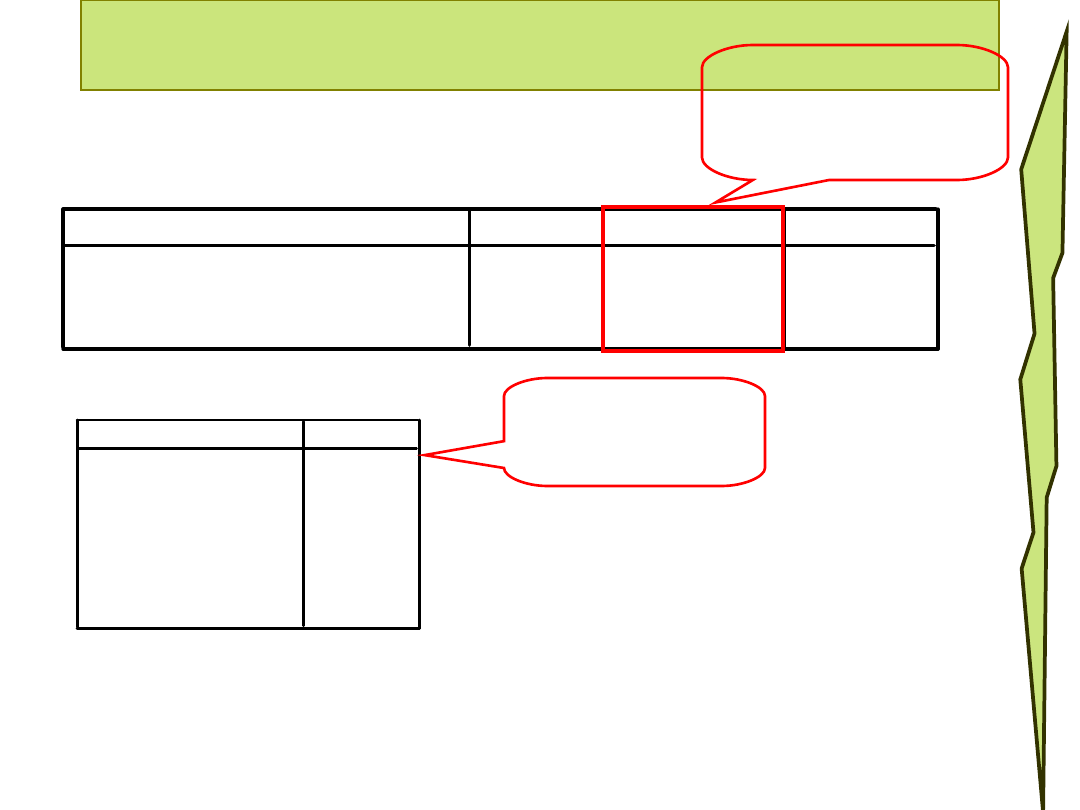
Wydruk

Rangi

7

9,86

69,00

7

5,14

36,00

14

DOM
dom malego dziecka
rodzinny dom dziecka
Ogółem

CHOROBA

N

Średnia ranga Suma rang

Statystyki testu

b

8,000

36,000

-2,179

,029

,038

a

U Manna-Whitneya
W Wilcoxona
Z
Istotność asymptotyczna
(dwustronna)
Istotność dokładna
[2*(jednostronna)]

CHOROBA

Nieskorygowane ze względu na wiązania.

a.

Zmienna grupująca: DOM

b.

Uff! Jest dobrze

– policzyliśmy

prawidłowo

!

Teraz

zapis:

U=8;

p<0,05

Formułujemy wniosek: Dzieci z
Domu małego Dziecka różnią się
natężeniem objawów choroby
sierocej od dzieci z Rodzinnego
Domu Dziecka. Średnie rangi
wskazują, że dzieci z Domu
Małego Dziecka mają wyższy
poziom objawów choroby
sierocej

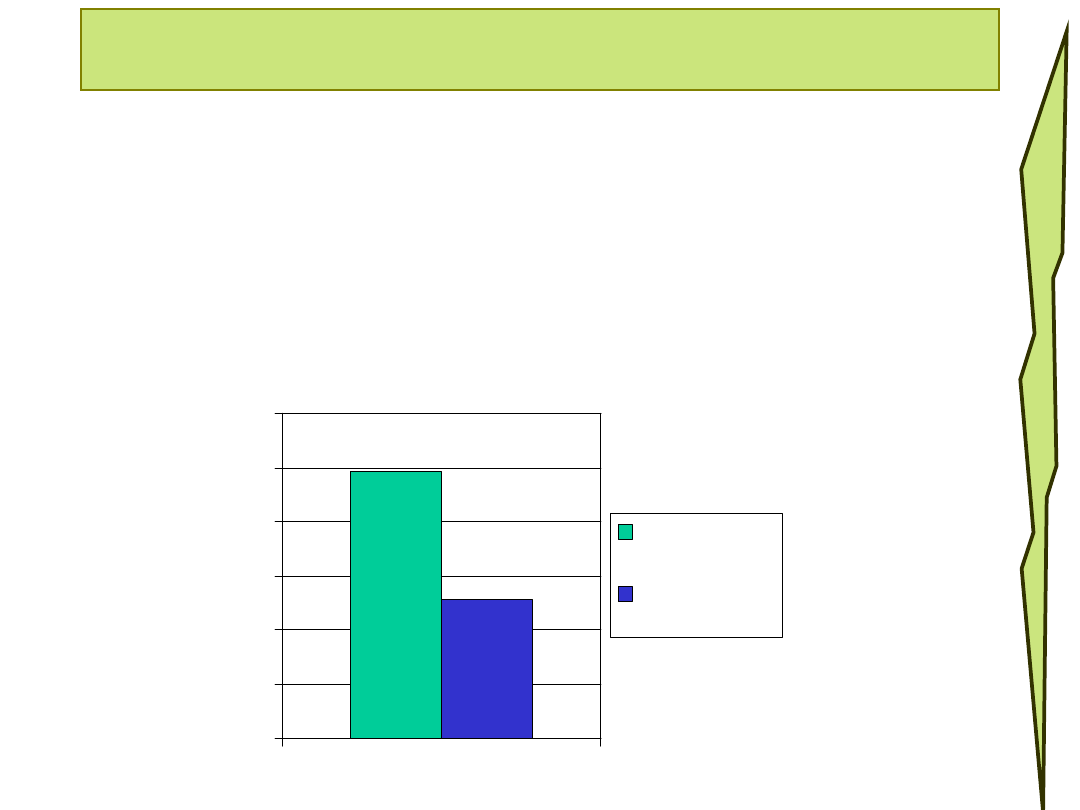
Wnioski – hipoteza 1

Hipoteza1: Istnieją różnice w natężeniu objawów choroby

sierocej między dziećmi znajdującymi się w Domu Małego
Dziecka oraz tymi wychowywanymi w Rodzinnym Domu
Dziecka

Formułujemy wniosek dotyczący hipotezy 1:
Dzieci z Domu małego Dziecka różnią się natężeniem

objawów choroby sierocej od dzieci z Rodzinnego
Domu Dziecka U=8; p<0,05. Średnie rangi wskazują,
że dzieci z Domu Małego Dziecka mają wyższy poziom
objawów choroby sierocej, co obrazuje wykres 1.

9,86

5,14

0

2

4

6

8

10

12

rodzaj placówki

na

tę

ze

ni

e

ob

ja

w

ów

c

ho

ro

by

s

ie

ro

ce

j

Dom Małego

Dziecka
Rodzinny Dom

Dziecka

Wnioski – hipoteza 1

Hipoteza2: Natężenie objawów choroby sierocej u dzieci

wychowywanych w Rodzinnych Domach Dziecka jest mniejsze
niż u dzieci znajdujących się pod opieką Domu Małego Dziecka.

Formułujemy wniosek dotyczący hipotezy 2:
Dzieci z Domu małego Dziecka różnią się natężeniem

objawów choroby sierocej od dzieci z Rodzinnego Domu
Dziecka U=8; p<0,05. Średnie rangi wskazują, że dzieci
z Domu Małego Dziecka mają wyższy poziom objawów
choroby sierocej.

Poziom istotności 0,038 dzielimy na pół – otrzymujemy

0,019. Ten poziom także zaokrąglamy do 0,05.

Tak więc wyniki są identyczne dla obu hipotez

Czy dziewczynki są chętniej umieszczane w Rodzinnych Domach

Dziecka niż w Domu Małego Dziecka (hipoteza trzecia)

Zmienne:
Rodzaj placówki – zmienna

nominalna, dwuwartościowa

Płeć – zmienna nominalna,

dwuwartościowa

Stosujemy test nieparametryczny –

chi

2

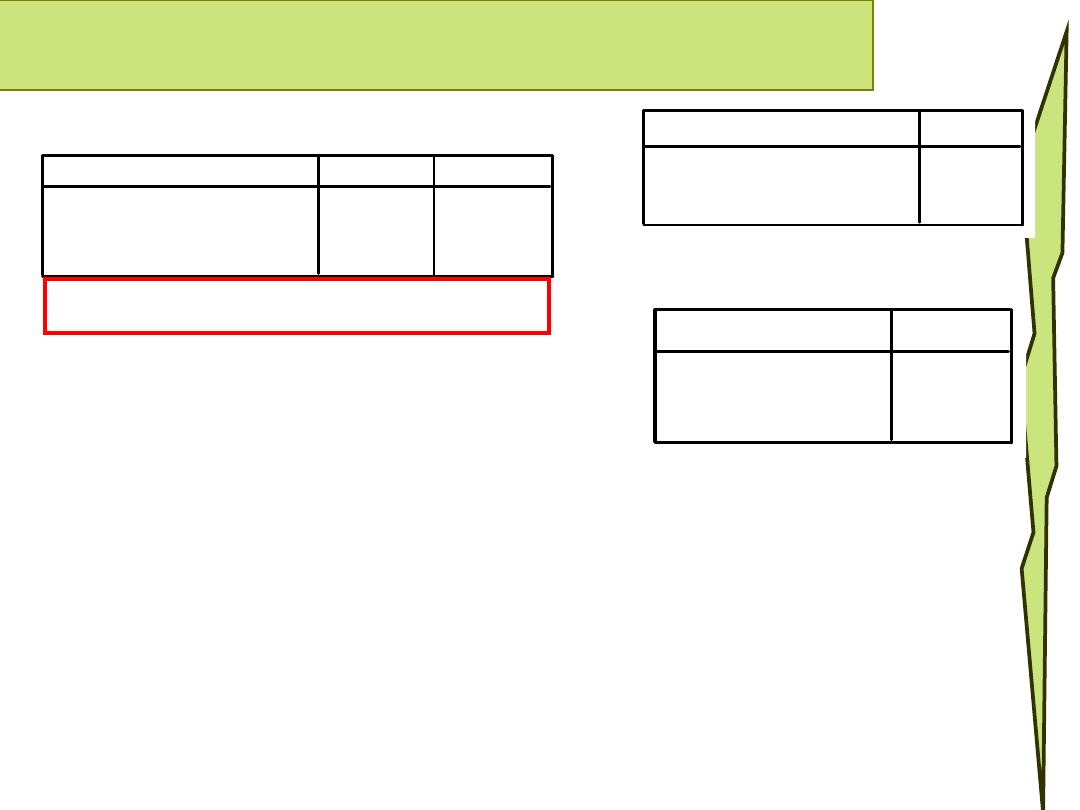
Obie zmienne są mierzone na skali nominalnej więc

możemy policzyć tylko modalne. Znowu pojawia się

komunikat, że „

Istnieje wiele wartości modalnych.

Podano wartość najmniejszą

”. Aby się przekonać ile

wynoszą wszystkie możliwe modalne liczymy

częstości. W tabelach częstości widać wyraźnie, że

grupy są równoliczne, a więc modalne w obu

przypadkach wynoszą 1 i 2.

Statystyki

14

14

0

0

1,00

a

1,00

a

Ważne
Braki danych

N

Dominanta

DOM

PLEC

Istnieje wiele wartości modalnych. Podano
wartość najmniejszą.

a.

DOM

7
7

14

dom malego dziecka
rodzinny dom dziecka
Ogółem

Ważne

Częstość

PLEC

7
7

14

dziewczynka
chłopiec
Ogółem

Ważne

Częstość

Statystyki opisowe zmiennych

Tabela liczebności – tabele krzyżowe

• Liczymy

liczebności brzegowe

• Liczymy

liczebności oczekiwane

(7 * 7) / 14 =

3,5

• Teraz liczymy dla każdej kratki
(obserwowane- oczekiwane)

2

/oczekiwane

((3 - 3,5)*(3 - 3,5)) / 3,5 = 0,071
((4 - 3,5)*(4 - 3,5)) / 3,5 = 0,071
• Chi

2

=0,071 + 0,071 + 0,071 + 0,071= 0,286

3/

3,5

4/

3,5

4/

3,5

3/

3,5

Dom Małego
Dziecka

Rodzinny
Dom
Dziecka

dziewczyn
ki

chłopcy

7

7

7

7

14

Wydruk

Tabela krzyżowa DOM * PLEC

3

4

7

3,5

3,5

7,0

4

3

7

3,5

3,5

7,0

7

7

14

7,0

7,0

14,0

Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana

dom malego dziecka

rodzinny dom dziecka

DOM

Ogółem

dziewczynka

chłopiec

PLEC

Ogółem

Testy Chi-kwadrat

,286

b

1

,593

14

Chi-kwadrat Pearsona
N

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

a.

100,0% komórek (4) ma liczebność oczekiwaną mniejszą
niż 5. Minimalna liczebność oczekiwana wynosi 3,50.

b.

Hurra!

Dobrze

policzyliśmy

!

Wniosek – nie ma
związku między płcią
dziecka a placówką w
jakiej się znalazło
Chi

2

(1,N=14)=0,286;

p>0,05.

Jak chodzą szczury?

Badano 50 szczurów, które wybierały

jedną z pięciu dróg. Oto jak wybrały:

• wejście A – 4
• wejście B – 5
• wejście C – 7
• wejście D – 9
• wejście E – 15

– Jakim testem sprawdzimy, która droga

jest najbardziej pożądana przez szczury?

Jak chodzą szczury?

Badano 50 szczurów, które wybierały

jedną z pięciu dróg. Oto jak wybrały:

• wejście A – 4
• wejście B – 5
• wejście C – 7
• wejście D – 9
• wejście E – 15

– Ile wynoszą liczebności oczekiwane dla

każdej celki?

Chi-kwadrat

W badaniu przedszkolnym nad atrakcyjnością zawodów

dwoje dzieci chciałoby być lekarzami, jedno

kominiarzem, zaś sześcioro aktorami. Jeśli testowana

byłaby hipoteza mówiąca o tym, że wszystkie zawody

są równie popularne, to liczba stopni swobody dla

testu chi kwadrat miałaby wartość:

• 1

• 2

• 3

• 9

Zwracamy uwagę na liczbę kategorii a nie liczbę osób

badanych

• Jeśli testowana byłaby hipoteza mówiąca o tym, że

wszystkie zawody są równie popularne, to liczebności

oczekiwane dla testu chi kwadrat wyniosą ….

Tabela 3 Testy Chi-kwadrat

22,739

a

3

,000

23,490

3

,000

,003

1

,958

145

Chi-kwadrat Pearsona
Iloraz wiarygodności
Test związku liniowego
N Ważnych obserwacji

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

,0% komórek (0) ma liczebność oczekiwaną mniejszą niż 5.
Minimalna liczebność oczekiwana wynosi 13,45.

a.

Tabela przedstawia wynik
testu chi2 dla dwóch
zmiennych nominalnych –
rodzaju zabawy i
preferowanego zwierzątka u
przedszkolaków. Wybierz
prawidłowy zapis wyniku
analizy, który należałoby
podać w raporcie z badania:
Chi2 (3) = 22,739; p>0,05
Chi2 (3) = 22,739; p<0,001
Chi2 (1) = 0,003; p>0,05
Chi2 (3) = 23,490; p<0,001

W opisie wyników badacz
zapomniał podać, ile kategorii
miała każda ze zmiennych. Na
ilu poziomach były kodowane
wspomniane zmienne:
2x4
3x4
4x4
3x3

Jak sobie poradzić na egzaminie?

Przy podejmowaniu decyzji czy odrzucić czy

też nie odrzucać hipotezy zerowej jesteśmy
narażeni na popełnienie dwóch błędów.
Błąd pierwszego rodzaju polega na:

– nie odrzucaniu hipotezy zerowej gdy jest

prawdziwa

– odrzuceniu hipotezy zerowej gdy jest prawdziwa
– odrzuceniu hipotezy zerowej gdy hipoteza

badawcza jest prawdziwa

– nie odrzuceniu hipotezy zerowej gdy hipoteza

badawcza jest prawdziwa

Zebraliśmy dane odnośnie poziomu

pesymizmu od osób będących na bezrobociu
oraz dane dotyczące ich percepcji
przyszłości, tego, na ile jest prawdopodobne,
że znajdą pracę. Interesował nas związek
między pesymizmem a wizją przyszłości.
Badanie przeprowadziliśmy w schemacie:

• różnicowym
• eksperymentalnym
• korelacyjnym
• mieszanym

W badaniu nad percepcją reklam wzięło

udział 40 studentek i 30 studentów.

Zarówno test Levena jak i test

Kołmogorowa-Smirnowa były nieistotne

statystycznie. Aby stwierdzić, czy istnieją

różnice między kobietami i mężczyznami

w odbiorze reklam, należy zastosować:

• test „t” dla prób niezależnych
• test „t” dla prób zależnych
• testy nieparametryczne, ze względu na

zaburzenia liczebności

• test korelacji r Pearsona

W ankiecie ulicznej pytano kobiety i

mężczyzn, czy będą głosować za, czy

przeciw wejściu Polski do Unii

Europejskiej (odpowiedzi: TAK, NIE,

NIE WIEM). W celu interpretacji

wyników należy zastosować test:

• test „t” dla prób niezależnych
• test chi kwadrat dla jednej zmiennej
• test chi kwadrat dla tabel krzyżowych
• test korelacji r Pearsona

Profesor Filutek zastanawiał się czy kolor

napoju wpływa na percepcję jego smaku.

Postanowił przeprowadzić eksperyment. Do

zwykłej oranżady dodał czerwonego

barwnika. Następnie grupę 15 osób poprosił

o degustację i ocenę (na skali typu Likerta)

smaku zwykłej i czerwonej oranżady. W celu

interpretacji wyników należy zastosować

test:

• test „t” dla prób niezależnych
• test „t” dla prób zależnych
• test Wilcoxona
• test korelacji r Pearsona

Ignacy

• Ignacy otrzymał w badaniu uprzedzeń

wobec mniejszości narodowych wynik 16

(rozkład wyników zgodny z rozkładem

normalnym, szacowana średnia w populacji

wynosi 14, a wariancja 4). Oznacza to, że:

• Ignacy uzyskał wynik niższy niż blisko 16%

populacji

• Ignacy jest bardziej uprzedzony niż około

84% ludzi w populacji

• blisko 2% ludzi w populacji jest mniej

uprzedzony niż Ignacy

• Ignacy jest bardziej uprzedzony niż ok.

34% ludzi w populacji

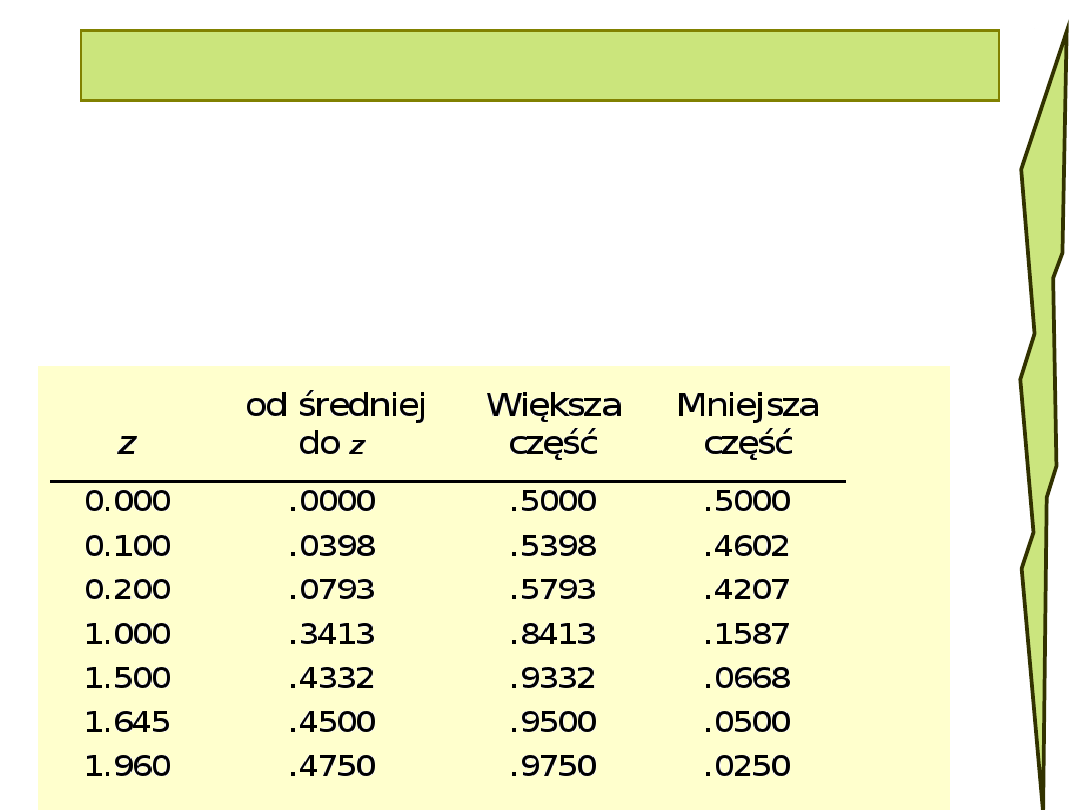
Ignacy

• Obliczamy Z dla wyniku Ignacego
• Z=(16-14)/2 = 1
• Wynik Ignacego 1OS powyżej

średniej

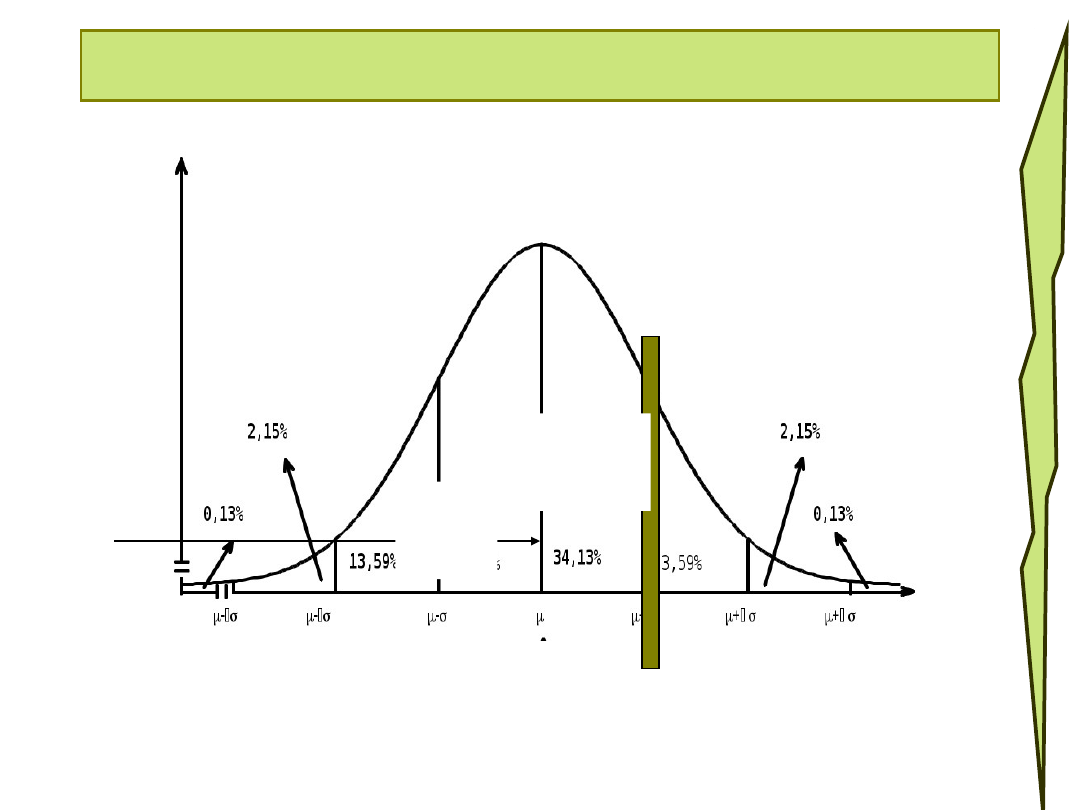
Ignacy

50
%

+34
%

Wynik Ignacego jest wyższy od 84%
populacji

Rangi raz jeszcze

• Pewna studentka pokusiła się o zrobienie

rankingu popularności różnych przedmiotów

w SWPS. Na pierwszym miejscu razem z

Psychologią Reklamy była Statystyka,

następnie Psychopatologia, na trzecim miejscu

Psychologia Rozwojowa razem z

Wprowadzeniem do społecznej, na ostatnim

Osobowość. Postanowiła przydzielić

odpowiednie rangi poszczególnym

przedmiotom. Jaką rangę będzie miała

Statystyka?

• 1

• wiązaną

• taką samą jak Psychopatologia

• 2

• Szeregujemy przedmioty:
1 1 Psychologia Reklamy, ranga: 1,5
2 1 Statystyka, ranga: 1,5
3 2 Psychopatologia, ranga: 3
4 3 Psychologia Rozwojowa, ranga: 4,5
5 3 Wprowadzeniem do społecznej,

ranga: 4,5

6 4 Osobowość, ranga: 6

Porównywaliśmy poziom wiary w magię przed i po

projekcji filmu „Harrry Potter – Komnata

Tajemnic”. Średni poziom wiary w czary przed

filmem wynosił M=2,6, po filmie M=4. W teście t

dla grup zależnych uzyskaliśmy następujący

wynik: t(24)=2,03; poziom istotności przy teście

dwustronnym p=0,12. Postawiliśmy hipotezę

kierunkową, mówiącą, że po filmie wiara w czary

wzrośnie. Czy stosując test jednostronny różnica

między porównywanymi pomiarami będzie

istotna na poziomie istotności p<0,05?

• Wynik istotny statystycznie, p<0,05?

• Wynik istotny statystycznie, p<0,06?

• Wynik nieistotny statystycznie, p<0,12?

• Wynik nieistotny statystycznie, p>0,05

• . Porównywano osoby słabo i silnie reaktywne

testem pamięci krótkotrwałej. Wyniki

uwidocznione są w Tabeli 4. O czym świadczą

wyniki testu Levena?

• Można przyjąć, że wariancje w grupach różnią

się istotnie

• Można przyjąć, że wariancje w grupach nie

różnią się istotnie

• Należy zastosować test nieparametryczny
• Należy zwiększyć liczbę osób badanych

Tabela 4 Test dla prób niezależnych

1,227

,283

8,434

18

,000

7,0000

,8300

5,2562

8,7438

8,434

15,987

,000

7,0000

,8300

5,2404

8,7596

Założono równość
wariancji
Nie założono
równości wariancji

PAMIEC

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

U czterech osób badanych zmierzono

poziom motywacji do osiągnięć i poziom

reaktywności (im wyższe wyniki na

skalach, tym wyższy poziom odpowiedniej

właściwości). Wyniki na skali motywacji

do osiągnięć wynosiły odpowiednio 8, 5,

5, 6. Wyniki na skali reaktywności

wynosiły odpowiednio 4, 7, 6, 5. Diagram

rozproszenia sugeruje istnienie:

• silnej korelacji ujemnej

• słabej korelacji dodatniej

• zależności krzywoliniowej w kształcie

odwróconego „U”

• silnej korelacji dodatniej

Przy założeniu poziomu istotności na poziomie p <0,01 (test

dwustronny):

• Stwierdzono istotną korelację tylko pomiędzy ceną i atrakcyjnością

opakowania

• Stwierdzono istotną korelację tylko pomiędzy ceną i jakością

• Stwierdzono istotną korelację zarówno pomiędzy ceną i jakością jak i

też pomiędzy ceną i atrakcyjnością opakowania

• Nie stwierdzono istotnych korelacji

Przy założeniu poziomu istotności na poziomie p <0,02 (test

jednostronny):

• Stwierdzono istotną korelację tylko pomiędzy ceną i atrakcyjnością

opakowania

• Stwierdzono istotną korelację tylko pomiędzy ceną i jakością

• Stwierdzono istotną korelację zarówno pomiędzy ceną i jakością jak i

też pomiędzy ceną i atrakcyjnością opakowania

• Nie stwierdzono istotnych korelacji

Korelacje

,680
,031

10

,810

,349

,004

,324

10

10

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

CENA

OPAK

JAKO

CENA

OPAK

JAKO

Współczynnik korelacji
• może być mniejszy niż 0, ale nie

mniejszy niż –1

• może być w wyjątkowych

przypadkach większy niż 1

• w przypadku bardzo słabych

zależności nie może być dodatni

• w przypadku bardzo silnych

zależności ma wartości bliskie zeru

Średnia w próbie jest :
• statystyką
• parametrem
• uzależniona od wielkości

wariancji

• dodatnio skorelowana z wielkością

populacji

Właściwości średniej

„Uśredniając ich obu można uznać, że są normalni”