Test na rozpoznawanie

Badanie nad agresją u dzieci – czy frustracja

wzmaga agresję?

• Badacz analizował wpływ frustracji na

poziom agresji u dzieci (frustracja
wywoływana nie otrzymaniem przez dziecko
obiecanej zabawki).

Wszystkim dzieciom została obiecana zabawka,
następnie część dzieci ją otrzymało, a część nie. Badacza
interesowała liczba agresywnych zachowań tego dnia
(zliczanych przez wychowawczynię w przedszkolu)

Zmienna niezależna?

Frustracja

versus

brak frustracji

Skala?

Nominalna

Zmienna zależna?

Agresja

liczba agresywnych zachowań

Skala?

Ilościowa

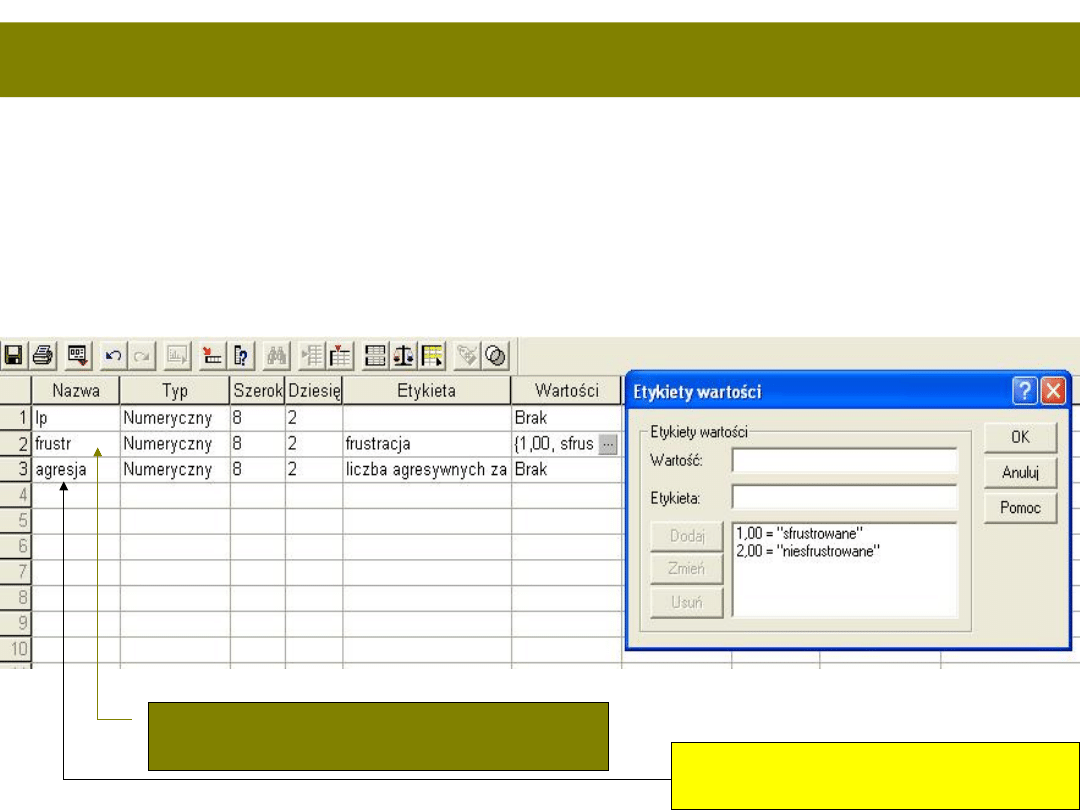
Co zrobi badacz po badaniu?

• Badaczowi udało się przebadać 45 dzieci, 26

nie było sfrustrowanych, 19 było sfrustrowane.

• Jak wpisać dane do SPSSa?

Zmienna niezależna – dzieli na grupy

powinniśmy ją zdefiniować

Zmienna zależna – ilościowa

Nie definiujemy wartości

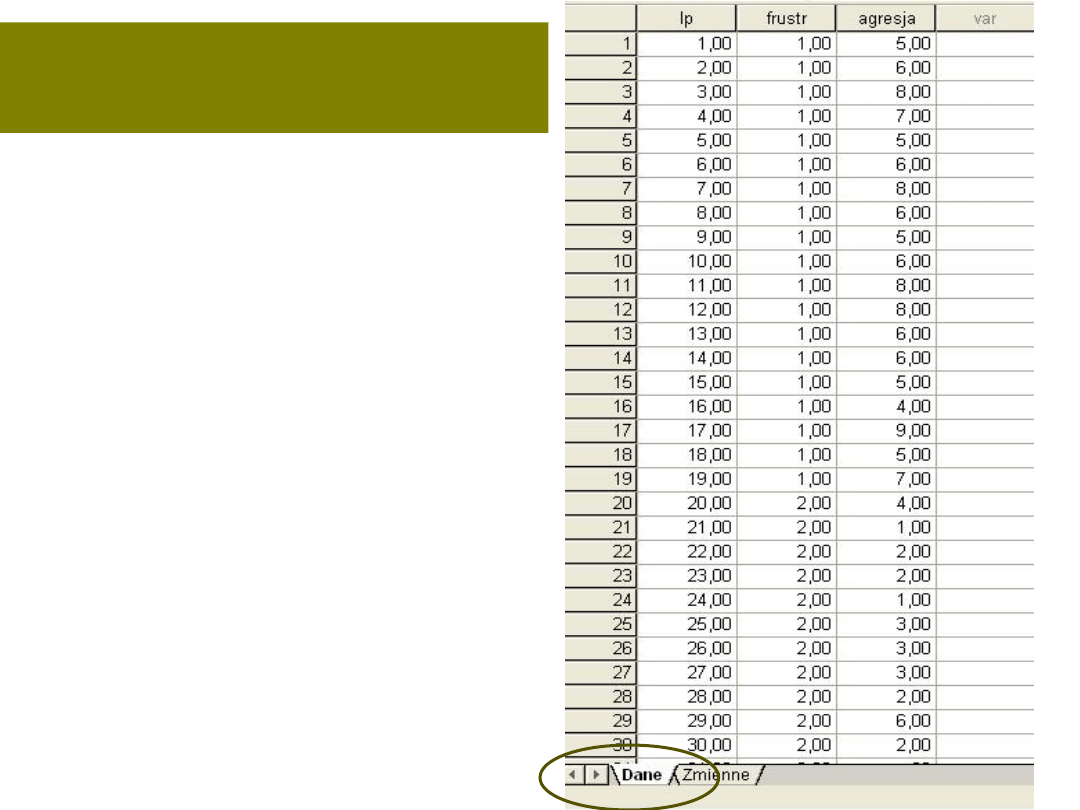
Co zrobi badacz po

badaniu?

• Wpisywanie?

– teraz już

proste

Zaczynają się poważne rzeczy – testowanie

hipotezy

• Jeżeli porównujemy dwie osobne

grupy, to użyjemy testu…

T-Studenta dla dwóch prób

niezależnych

Ale zanim przetestujemy, czy dzieciaki
sfrustrowane są bardziej agresywne niż
te nie sfrustrowane, musimy coś
sprawdzić

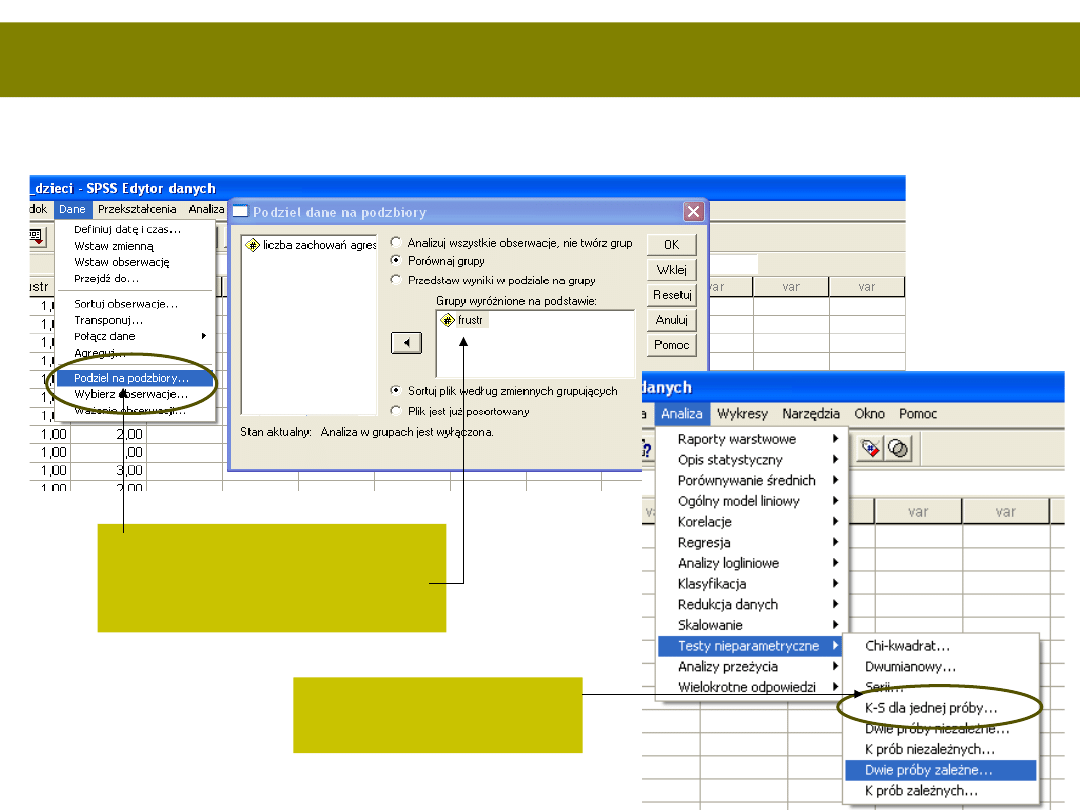
Oczywiście założenia

• O normalności rozkładu – test K-S w podziale na grupy

Zakładamy filtr na
podgrupy, Zmienna
dzieląca - frustracja

I wykonujemy test
K-S

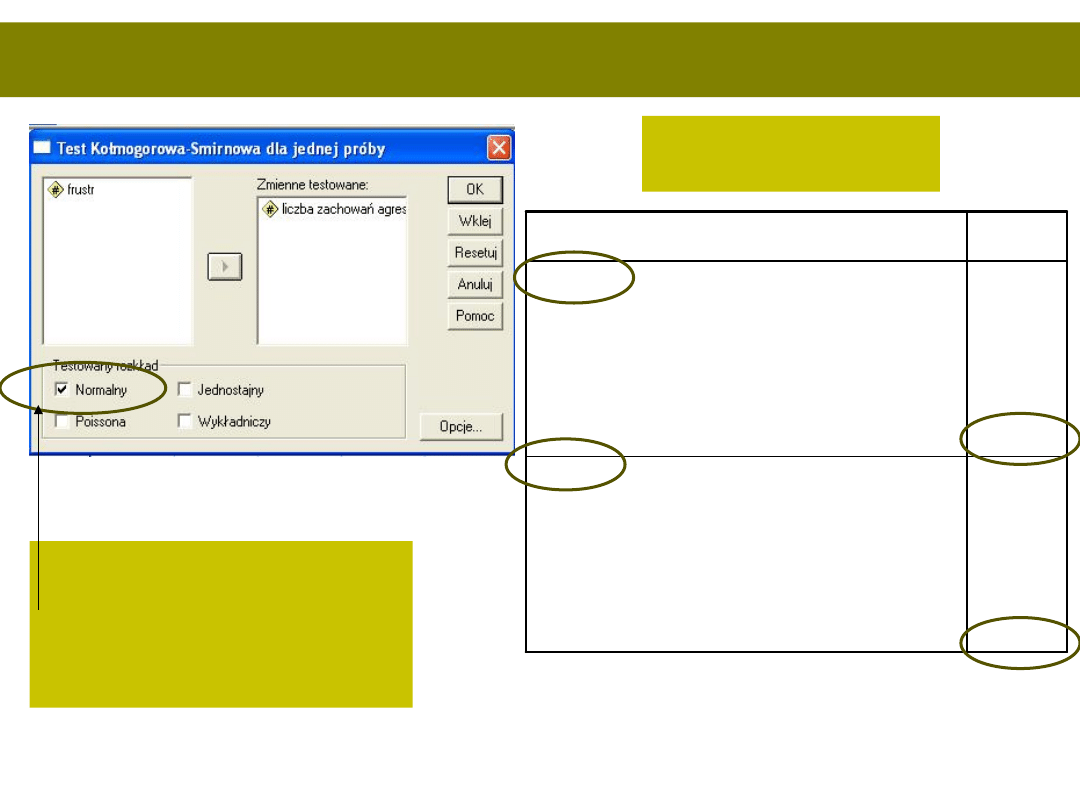
Normalność rozkładu…

Testujemy hipotezę
zerową:

Rozkład empiryczny =
rozkład normalny

Test Kołmogorowa-Smirnowa dla jednej próby

26

2,3077

1,1923

,204
,204

-,167

1,039

,230

19

6,3158

1,4550

,165
,165

-,140

,719

,680

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

FRUSTR
brak frustracji

frustracja

liczba

zachowań

agresywnych

Testowana jest zgodność z rozkładem normalnym.

a.

Obliczono na podstawie danych.

b.

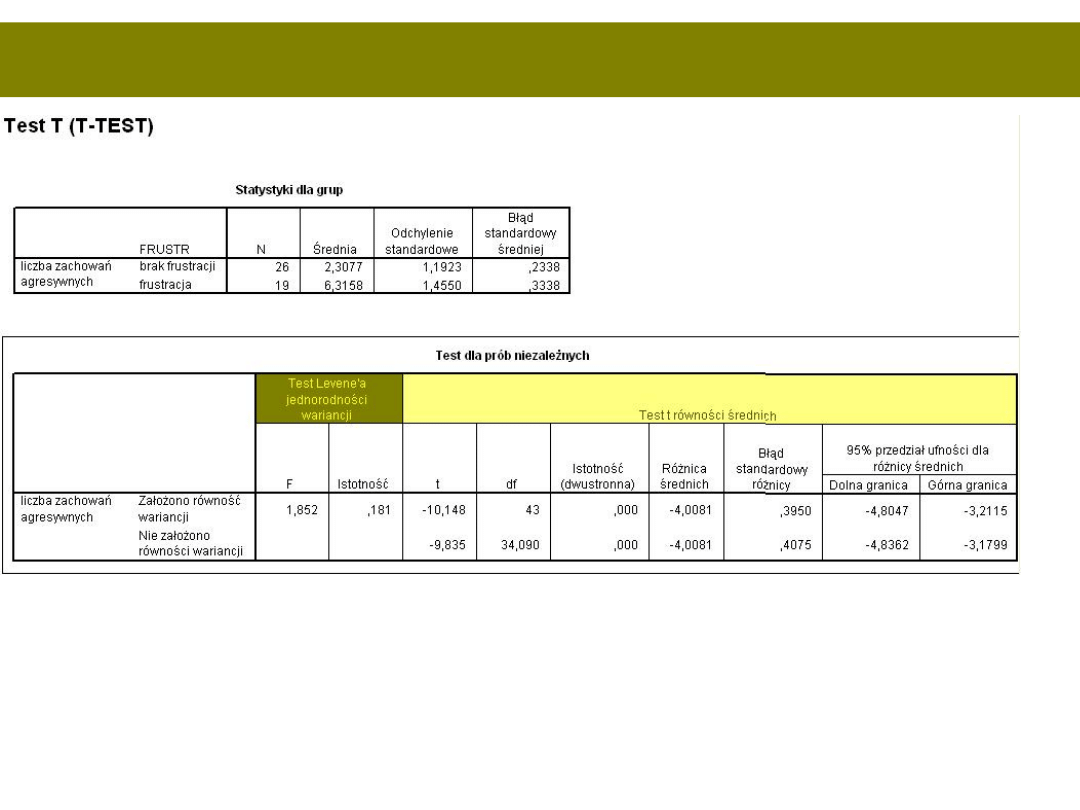
Wyniki testu w
raporcie:

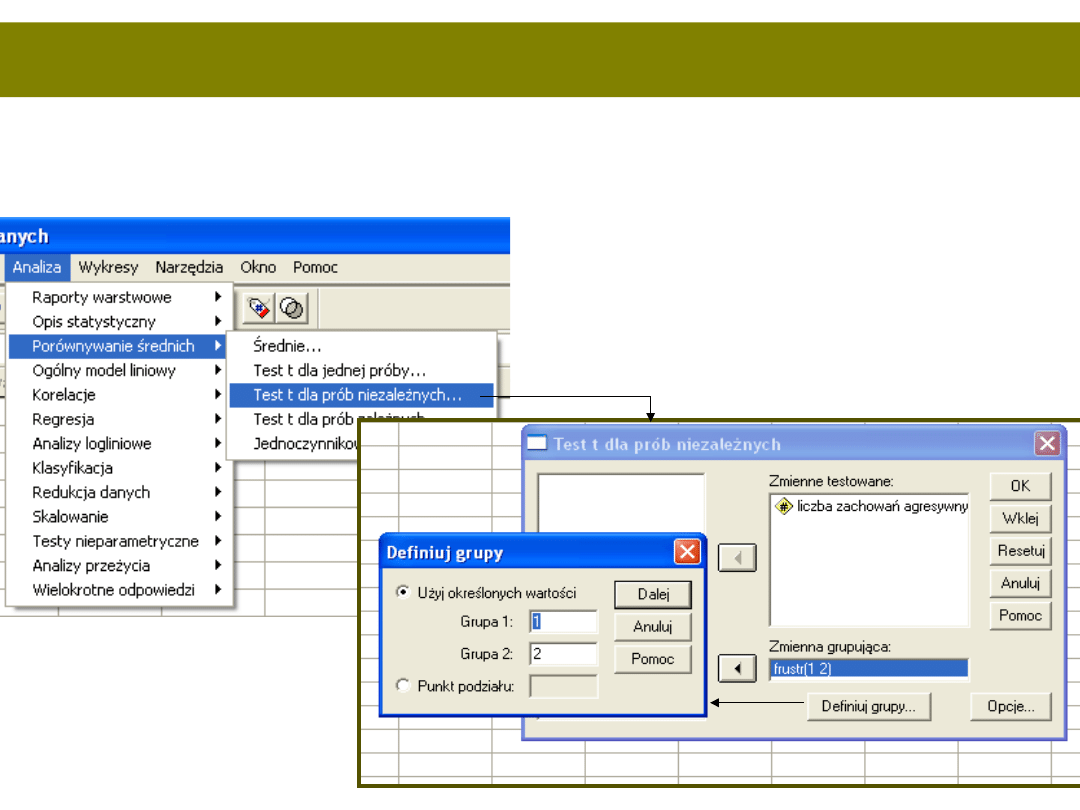
O równości wariancji

• To założenie jest automatycznie sprawdzany podczas

wykonywania testu

Stopnie
swobody

Liczymy, liczymy…

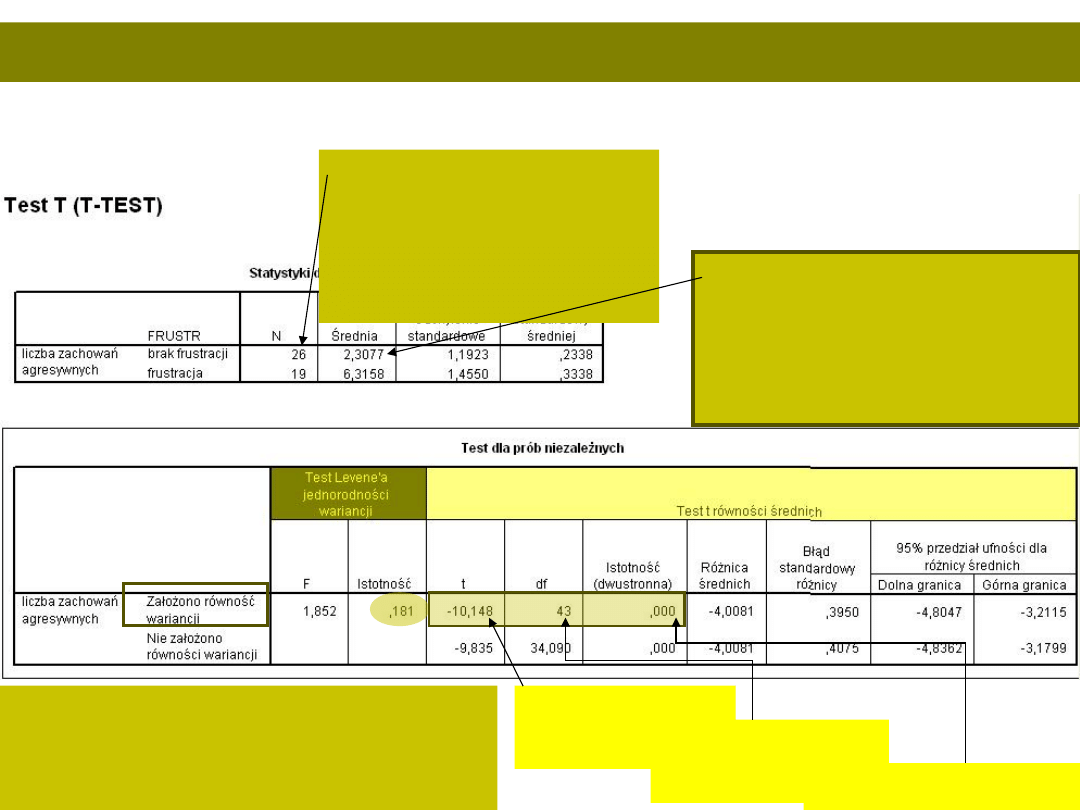
W raporcie pojawiają się
wyniki

Liczba osób w każdej
grupie, jeśli
nierówności nie
przekraczają 50%, to
jest OK

Średnie w każdej grupie,
widzimy, że grupa
frustrowana wykazuje
większą liczbę zachowań
agresywnych

Wariancje w grupach
homogeniczne – test Levene’a
nieistotny, wyniki testu T
odczytujemy a górnego
wiersza

Wartość
testu T

Poziom
istotności

Zapisujemy wynik

Jeśli już wszystko rozszyfrowaliśmy, zapisujemy:

T(43)=10,15; p<0,001 (M

frustrowana

=6,32;

M

kontrolna

=2,31)

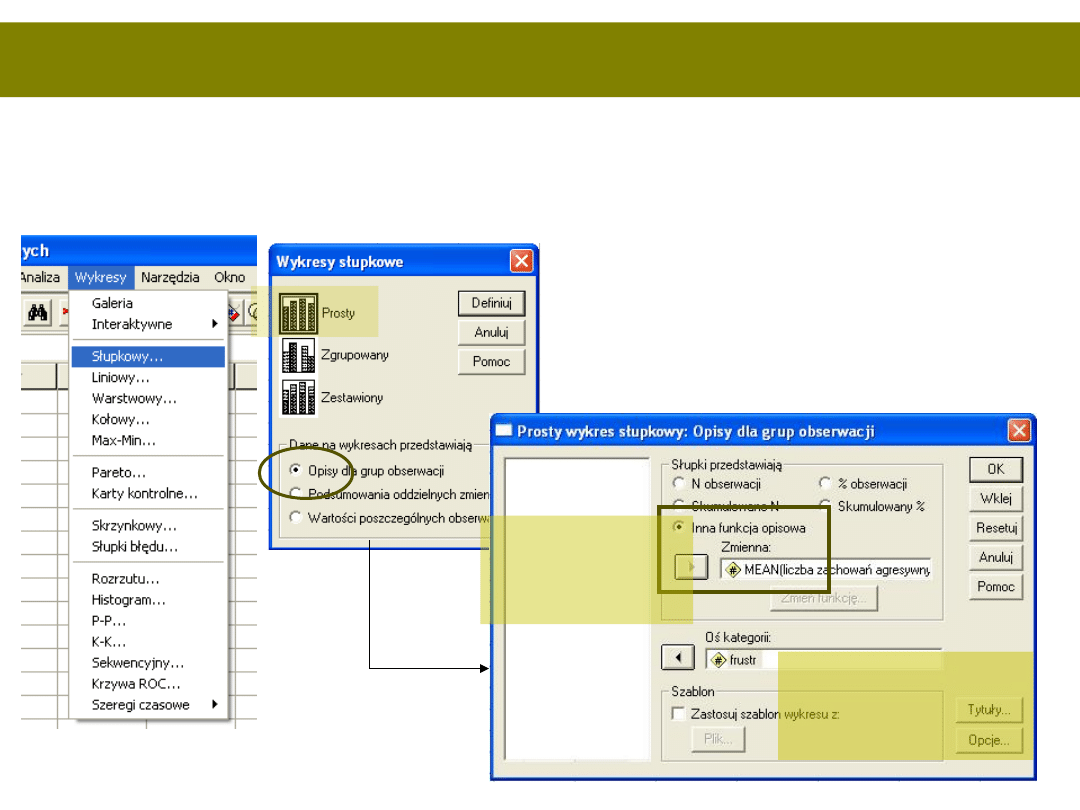
I jeszcze wizualizacja

• Dobrze jest pokazywać wyniki na wykresach,

czytający szybciej zrozumie o co chodzi

Zmienna
zależna -
ilościowa

Zmienna
niezależna -
grupująca

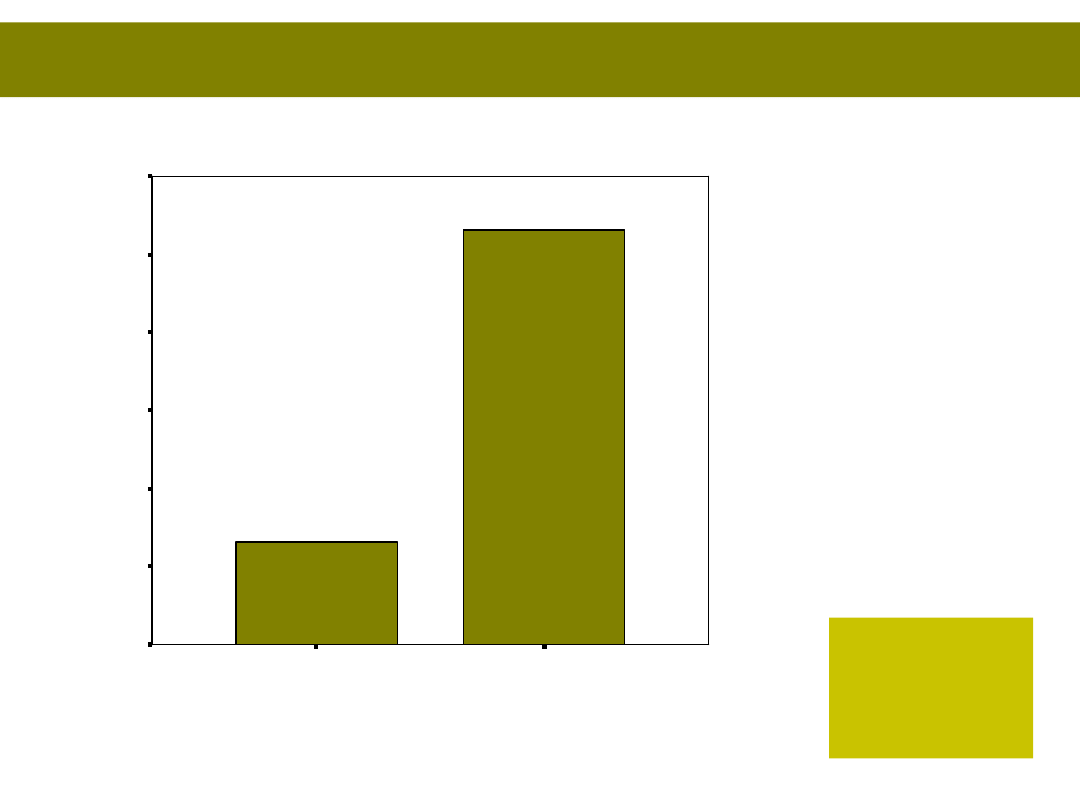
I mamy wykres

frustracja

brak frustracji

Ś

re

dn

ia

li

cz

ba

z

ac

ho

w

ań

a

gr

es

yw

ny

ch

7

6

5

4

3

2

1

Można
też zrobić
to inaczej

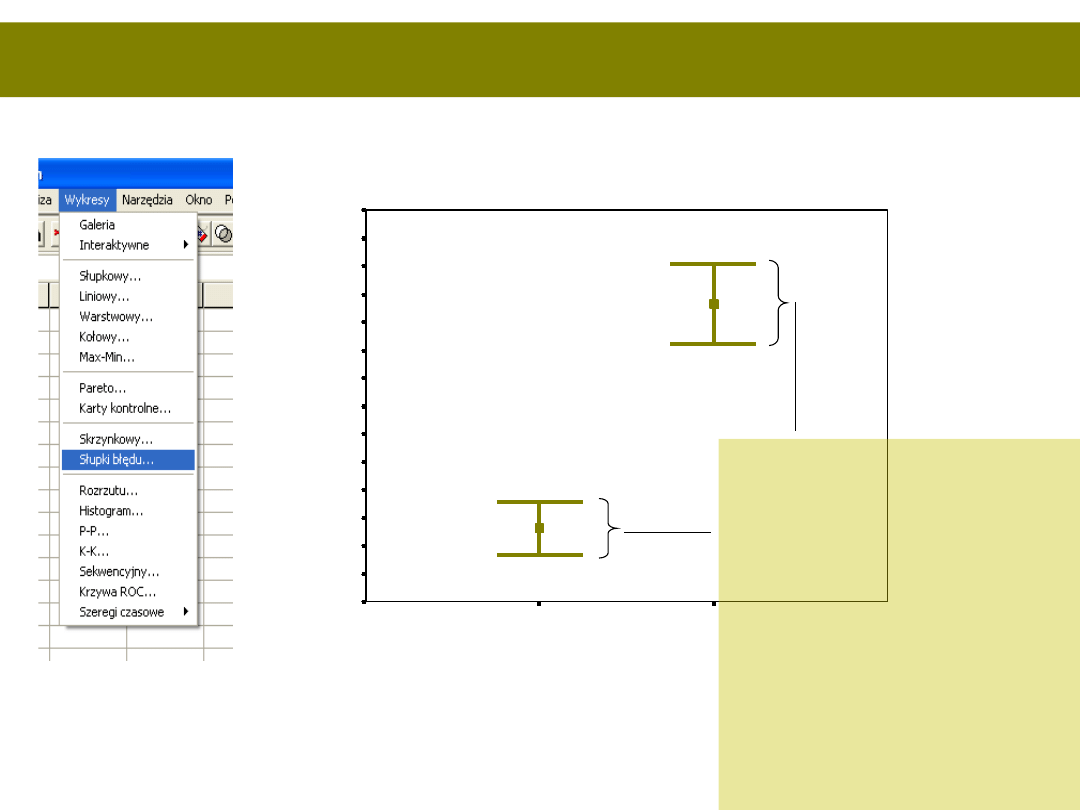
Wykres z przedziałami ufności…

19

26

N =

FRUSTR

frustracja

brak frustracji

95

%

P

U

li

cz

ba

z

ac

ho

w

ań

a

gr

es

yw

ny

ch

8,00

7,50

7,00

6,50

6,00

5,50

5,00

4,50

4,00

3,50

3,00

2,50

2,00

1,50
1,00

W tych przedziałach z
95%
prawdopodobieństwe
m znajduje się
średnia w każdej z
grup.

Jeśli określimy
prawdopodobieństwo
na np. 99% przedziały
będą większe, gdy na
np. 90% mniejsze

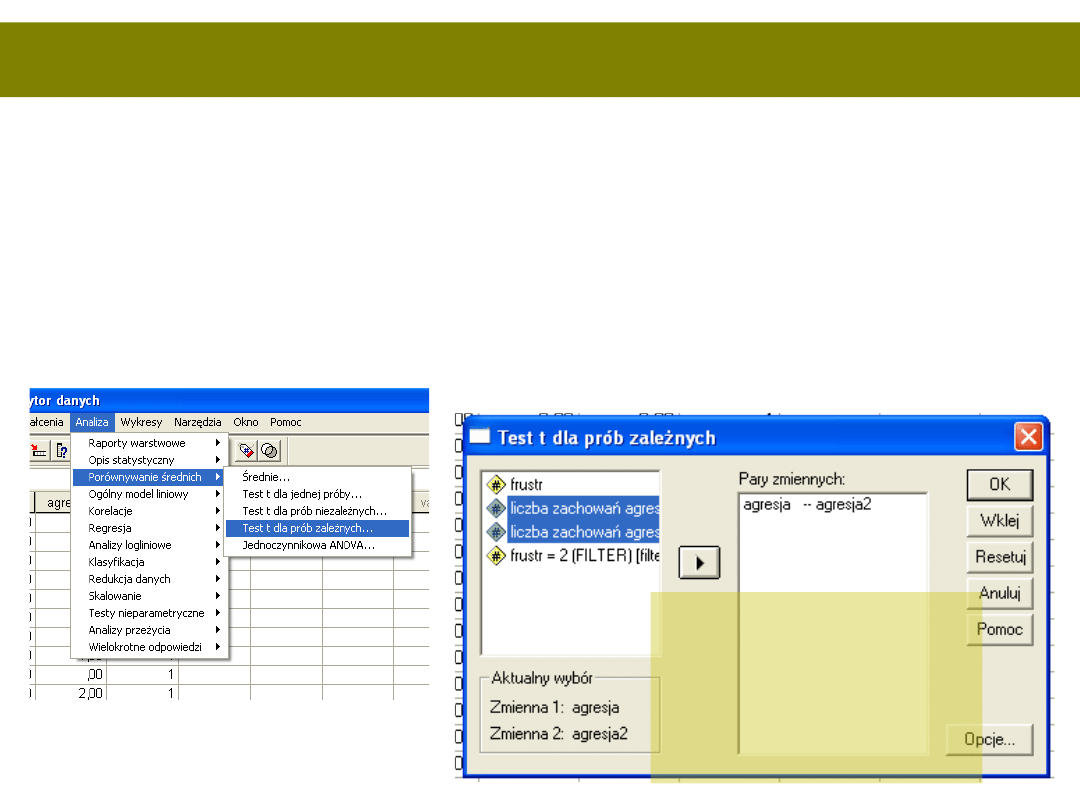
Teraz badamy dzieci sfrustrowane po

dwóch dniach

• Badacza interesowały czy po dwóch dniach u

dzieci sfrustrowanych spadnie poziom

agresji, dokonał powtórnej obserwacji

• Tym razem wyniki przetestujemy

Testem T-Studenta dla prób zależnych

Dwie zmienne
ilościowe –
dwukrotny pomiar
liczby zachowań
agresywnych

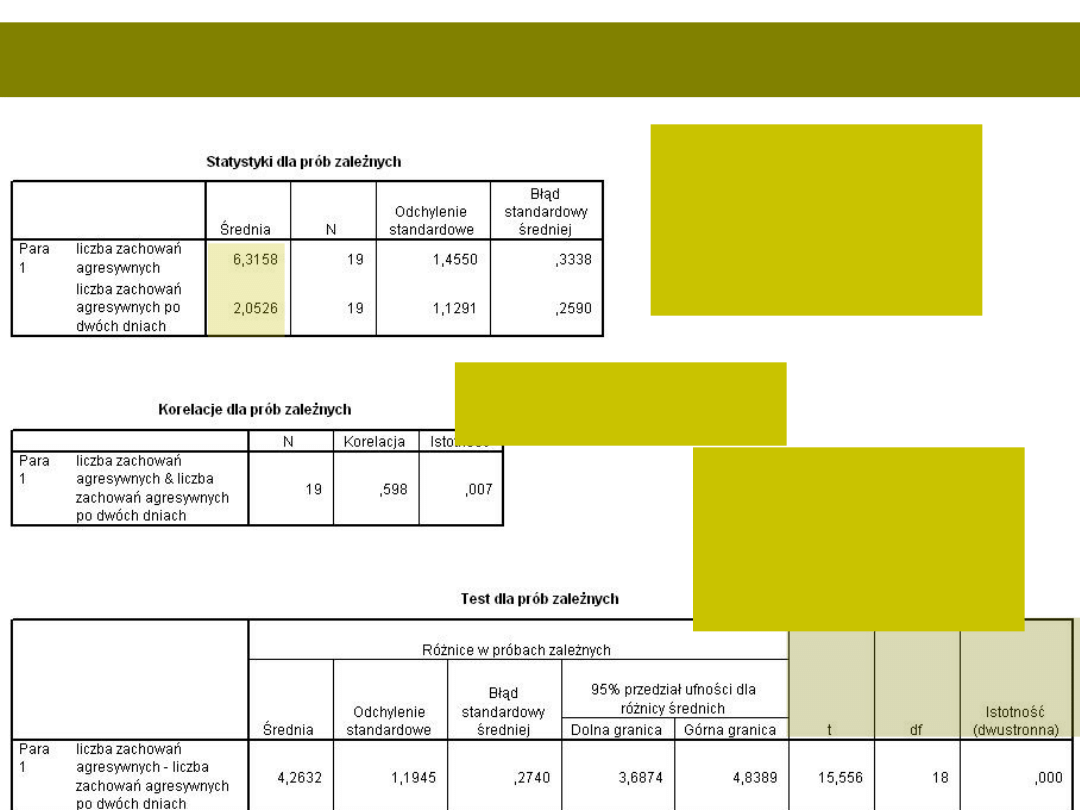
Cóż się okazało?

Po dwóch dniach
średnia liczby
zachowań
agresywnych jest
niższa

Korelacja r=0,6;
p<0,01

Wynik testu T:

T(18)=15,56;
p<0,001 (M

1

=6,32;

M

2

=2,05)

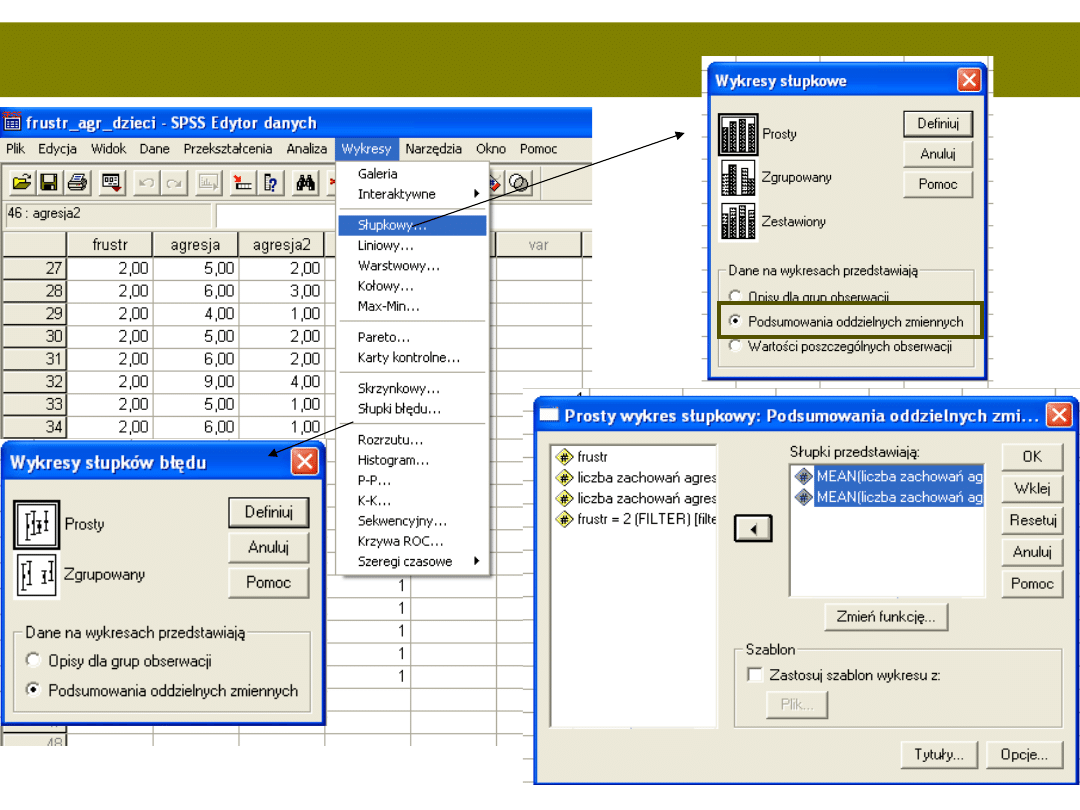
Jak to pokazać?

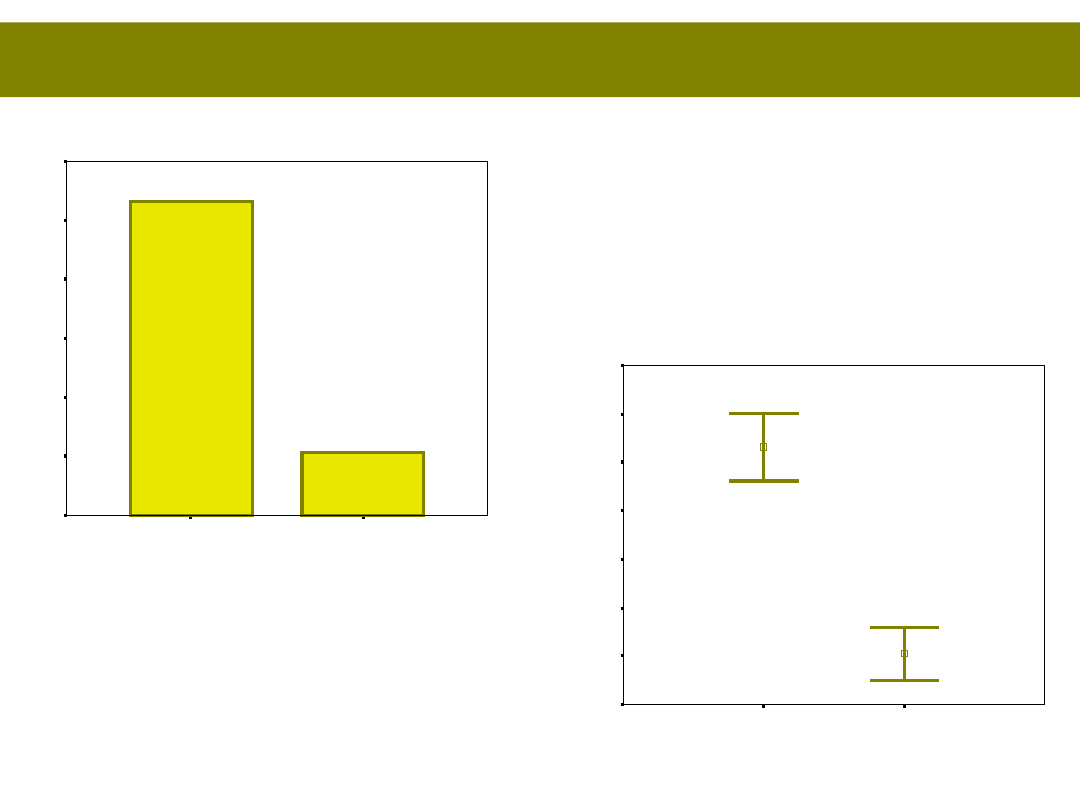
Wykresy

pomiar drugi

pomiar pierwszy

śr

ed

ni

a

lic

zb

a

za

ch

ow

ań

a

gr

es

yw

ny

ch

7

6

5

4

3

2

1

19

19

N =

pomiar drugi

pomiar pierwszy

śr

ed

ni

a

lic

zb

a

za

ch

ow

ań

a

gr

es

yw

ny

ch

8

7

6

5

4

3

2

1

Testy T-Studenta – testy

parametryczne

• Wymagają spełnienia szeregu założeń

przez nasze dane

– Zmienne na skali ilościowej
– Rozkład normalny zmiennych
– Równość wariancji

• Dzięki temu mają większą moc, czyli

Zdolność wykrywania małej, ale prawdziwej różnicy

w badanej próbie, przy jednoczesnej zdolności do
odrzucania mogących się pojawić
nierzeczywistych różnic

Zadanie do przemyślenia w domu....

Badacz postanowił sprawdzić, czy kobiety i

mężczyźni różnią się poziomem wykształcenia.

Zbadał 25 kobiet i 30 mężczyzn zadając im

pytanie „Na jakim poziomie skończyłeś edukację

szkolną?”. Badani mogli wybrać: szkoła

podstawowa, zawodowa, średnia, technikum,

szkoła wyższa”.

Jaki test statystyczny zastosowano do analizy

tego problemu?

a. Test T-Studenta dla jednej próby
b. Test T-Studenta dla dwóch prób niezależnych
c. Test T-Studenta dla dwóch prób zależnych
d. Test Kołmogorowa-Smirnowa
e. Test Levene’a

Jak dobrać właściwy test statystyczny do problemu?

Musimy się zastanowić:
Czy problem badawczy dotyczy różnic czy związku?
Ile mamy zmiennych?
Na jakich skalach mierzone są zmienne?
Badacz postanowił sprawdzić, czy kobiety i mężczyźni różnią

się poziomem wykształcenia. Zbadał 25 kobiet i 30
mężczyzn zadając im pytanie „Na jakim poziomie
skończyłeś edukację szkolną?”. Badani mogli wybrać:
szkoła podstawowa, zawodowa, liceum ogólnokształcące,
technikum, szkoła wyższa”.

Przedstawiony problem badawczy dotyczy różnic
między grupami

Mamy dwie zmienne: płeć i poziom
wykształcenia

Zmienna „płeć” jest mierzona na skali nominalnej,
zmienna „poziom wykształcenia” na

porządkowej

Ponieważ zmienna „poziom wykształcenia” jest
mierzona na

porządkowej

nie możemy użyć testu T-

Studenta, więc poznamy nowe testy –

testy

nieparametryczne

Nieparametryczne odpowiedniki testów T-Studenta

• Testy parametryczne

Statystyka testu opiera

się na parametrach,

czyli statystykach

opisowych które

można policzyć na

skali ilościowej:

średniej, wariancji lub

korelacji R-Pearsona

Przykłady:
Testy T-Studenta
Analiza wariancji
Test Levene’a
Analiza regresji

• Testy

nieparametryczne

Statystyka testu opiera

się na statystykach
opisowych które
można policzyć na
skali jakościowej:
liczebności, mediana

Przykłady:
U-Manna Whitneya
Z Kołmogorowa

Smirnowa

Test znaków
Test Wilcoxona

Dzisiaj zaczniemy od wojska

• Czy są różnice między tymi żołnierzami, którzy

mają osobisty bagnet i tymi, którzy nie mają

bagnetu w stopniu wojskowym?

Zmienna1: posiadanie bagnetu, brak bagnetu (skala

nominalna)

Zmienna2: stopień wojskowy (skala porządkowa)
Liczymy test U-Manna i Whitneya

Żołnierze, którzy posiadają
prywatny bagnet

Żołnierze, którzy nie posiadają
bagnetu

Podporucznik Stefan, podporucznik
Bogumił, kapral Wojtek, sierżant
Marek , sierżant Jan, sierżant
Kazimierz, podporucznik Bartłomiej,
kapral Mirek

Kapral Władek , kapral Ignacy ,
kapral Maciek , szeregowiec
Dziudzia, szeregowiec Lesio,
szeregowiec Franio, szeregowiec
Bambosz, sierżant Zbych

Ile było osób badanych?

 1 krok: Rangowanie

Najpierw ustawiamy wszystkie osoby w kolejności

od najniższej szarży do najwyższej, niezależnie od
tego do której grupy należą. Więc zaczynamy:

szeregowiec Dziudzia, szeregowiec Lesio,

szeregowiec Franio,

szeregowiec Bambosz,

kapral Wojtek, kapral Mirek

,

kapral Władek

,

kapral Ignacy, kapral Maciek,

sierżant Marek,

sierżant Jan, sierżant Kazimierz,

sierżant Zbych,

podporucznik Stefan, podporucznik Bogumił,
podporucznik Bartłomiej

Już „na oko” widać, że im niższa szarża tym bardziej

niebiesko – czyli żołnierze nie posiadają bagnetu.

Rangowanie – co dalej?

Teraz musimy ponumerować żołnierzy od 1 do 16 – to pierwszy krok

rangowania.

1 szeregowiec Dziudzia, 2 szeregowiec Lesio, 3 szeregowiec Franio,

4

szeregowiec Bambosz,

5 kapral Wojtek, 6 kapral Mirek

,

7

kapral

Władek

,

8

kapral Ignacy, 9 kapral Maciek,

10

sierżant Marek, 11

sierżant Jan, 12 sierżant Kazimierz,

13

sierżant Zbych,

14

podporucznik Stefan, 15 podporucznik Bogumił, 16 podporucznik
Bartłomiej

Nadajemy rangi – szeregowcy zajmują miejsca od 1 do 4, więc ich

ranga to 2,5 i tę rangę przypisujemy wszystkim szeregowcom.
Kaprale zajmują miejsca od 5 do 9, więc ich ranga to 7. Sierżanci
mają rangę 11,5. A jaką rangę nadamy podporucznikowi?

Teraz przepisujemy wszystkich żołnierzy, ale już z rangami:

2,5 szeregowiec Dziudzia, 2,5 szeregowiec Lesio, 2,5
szeregowiec Franio,

2,5 szeregowiec Bambosz,

7 kapral Wojtek,

7 kapral Mirek

,

7

kapral Władek

,

7

kapral Ignacy, 7 kapral

Maciek,

11,5

sierżant Marek, 11,5 sierżant Jan, 11,5 sierżant

Kazimierz,

11,5

sierżant Zbych,

15

podporucznik Stefan, 15

podporucznik Bogumił, 15 podporucznik Bartłomiej

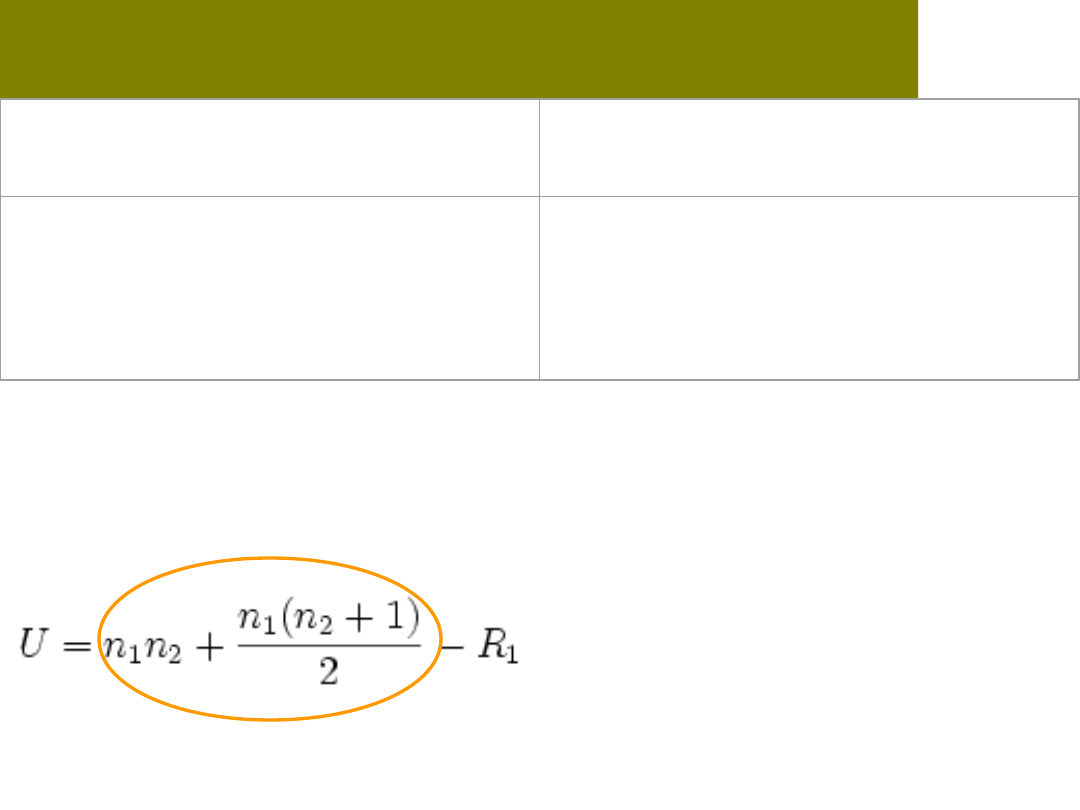
Teraz rozdzielamy żołnierzy z powrotem do grup

Teraz liczymy średnie z uzyskanych wcześniej rang. Średnia

ranga w grupie żołnierzy posiadających bagnet wynosi
11, 68 a średnia ranga dla osób nie posiadających
bagnetu wynosi 5,31

Żołnierze, którzy posiadają prywatny
bagnet

Żołnierze, którzy nie posiadają
bagnetu

Podporucznik Stefan, podporucznik
Bogumił, kapral Wojtek, sierżant Marek ,
sierżant Jan, sierżant Kazimierz,
podporucznik Bartłomiej, kapral Mirek

 
15; 15; 7; 11,5; 11,5; 11,5; 15; 7

Kapral Władek , kapral Ignacy , kapral
Maciek , szeregowiec Dziudzia,
szeregowiec Lesio, szeregowiec Franio,
szeregowiec Bambosz, sierżant Zbych

 
7; 7; 7; 2,5; 2,5; 2,5; 2,5; 11,5

n

1

- liczba osób w pierwszej

grupie

n

2

- liczba osób w drugiej

grupie

R

1

-suma rang w pierwszej

grupie

R-suma
wszystkich rang

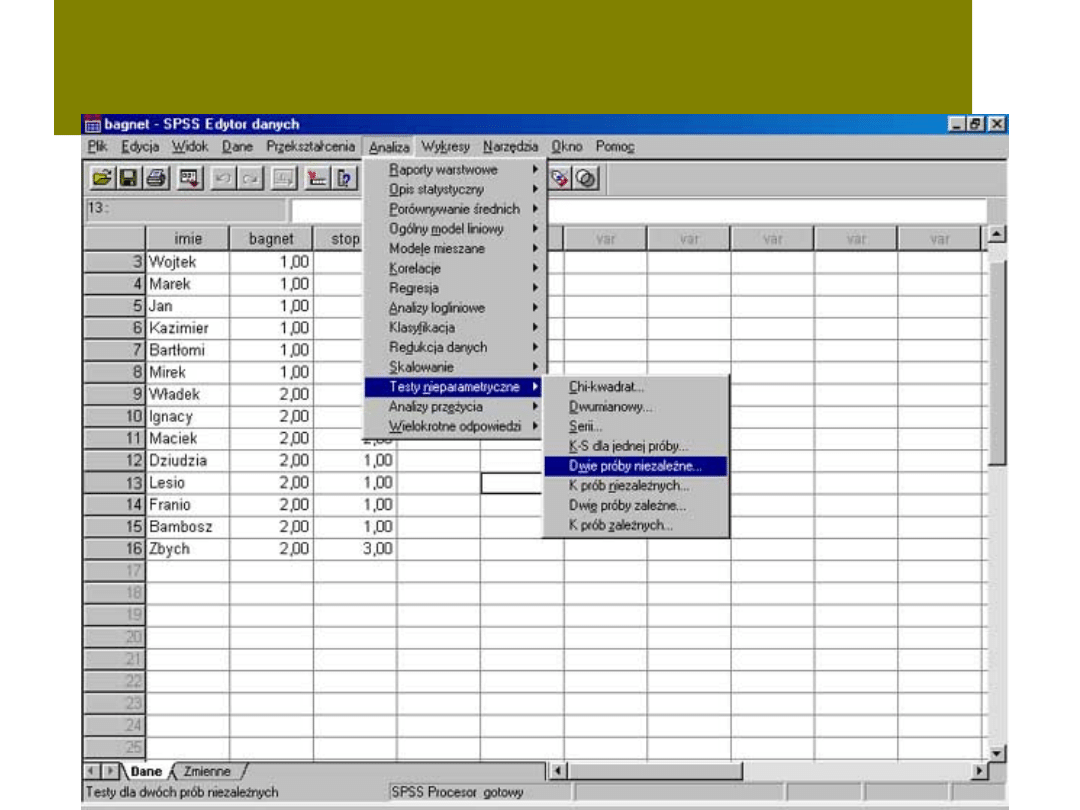
W Spss-ie znacznie łatwiej

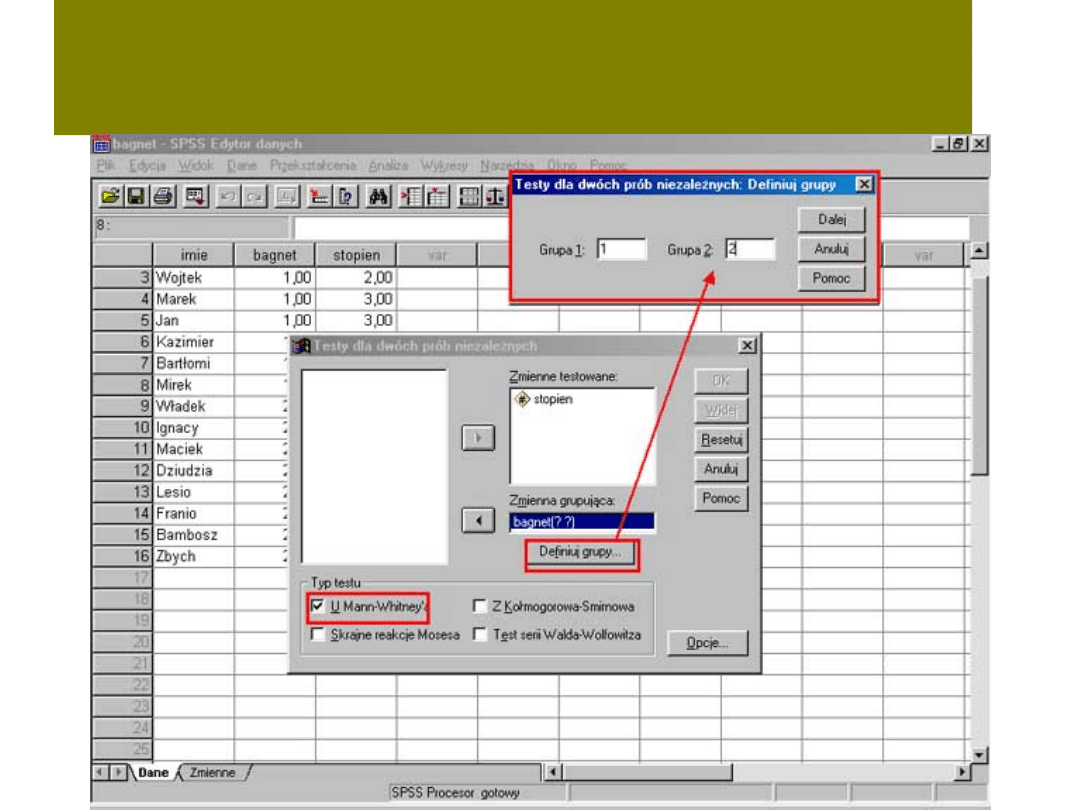
Okno przypomina to, które mamy w teście T-Studenta

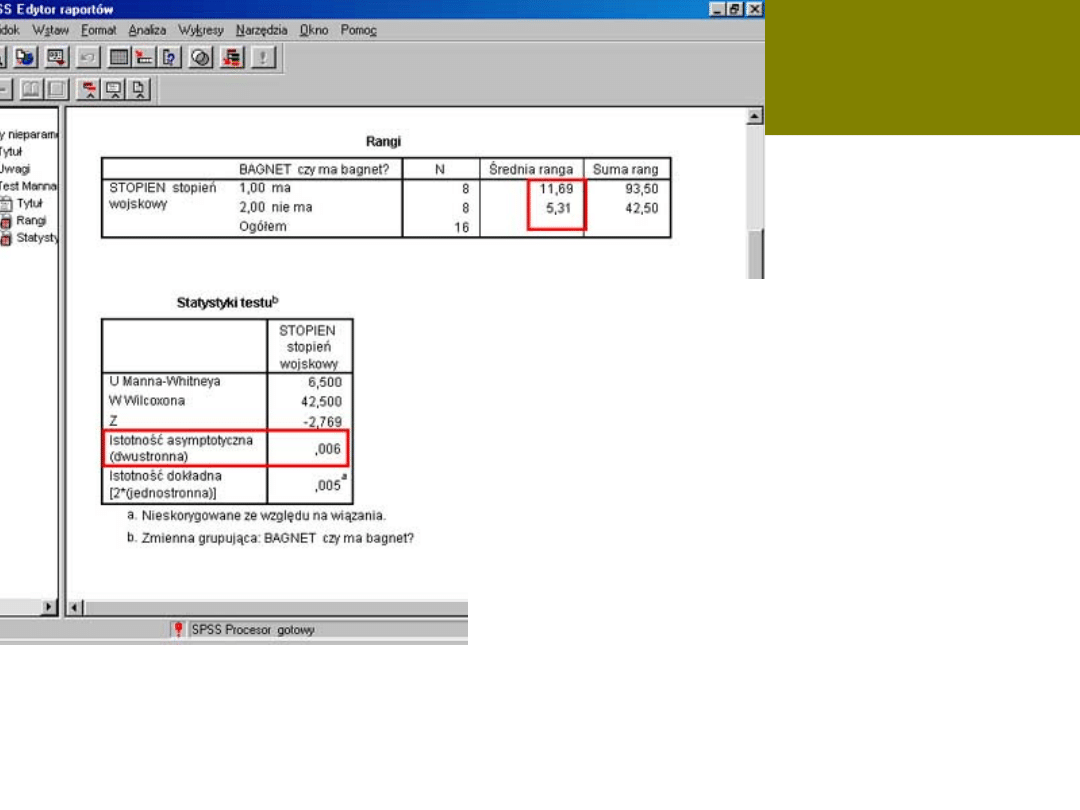
Wydruk

Zapis U=6,5; p<0,01

Wybierz właściwą interpretację
uzyskanego wyniku

•Żołnierze, którzy mają bagnet mają
też wyższy stopień wojskowy niż
żołnierze, którzy nie posiadają
bagnetu

•Nie ma różnic w randze żołnierzy,
którzy posiadają bagnet lub go nie
posiadają

•Żołnierze, którzy mają bagnet mają
też niższy stopień wojskowy niż
żołnierze, którzy nie posiadają
bagnetu

Test mediany

• Test mediany opiera się na podobnej

zasadzie jak test rang:

• Łączymy obie grupy razem i dla

wszystkich osób liczymy medianę

• Następnie dzielimy osoby z powrotem

do grup i sprawdzamy ile osób w danej
grupie ma wyniki powyżej a ile poniżej
mediany

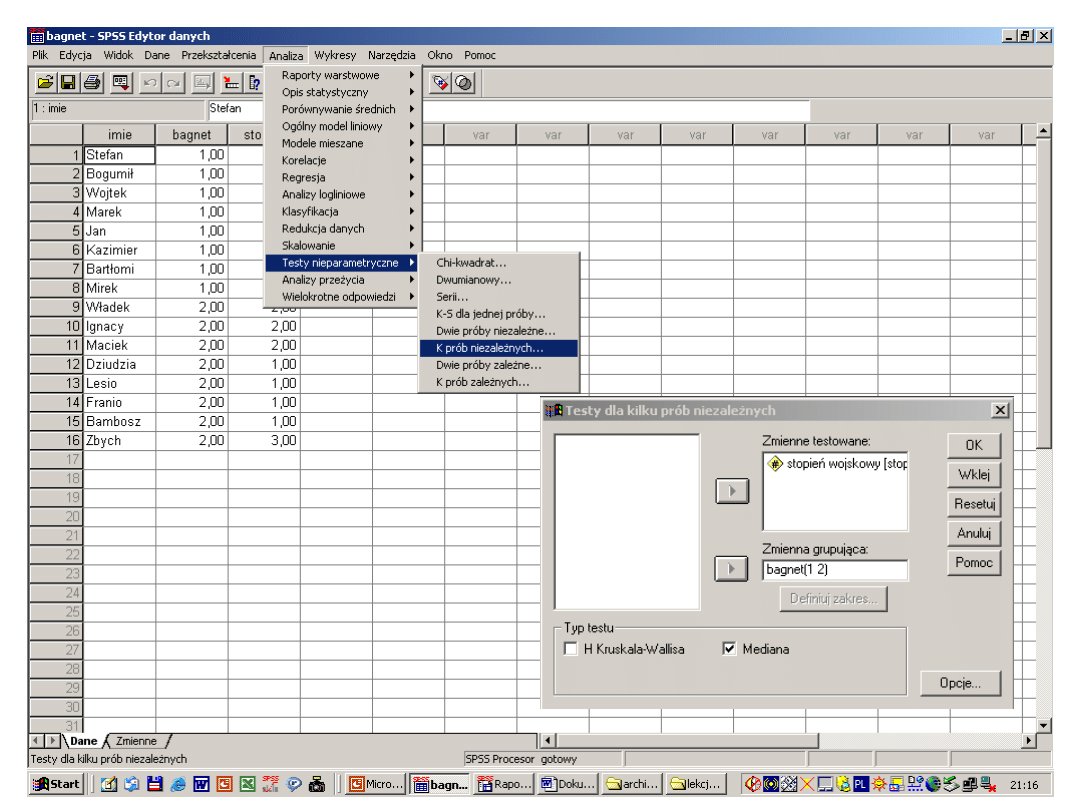
Test mediany- wydruk

Tabela częstości

6

1

2

7

> mediany
<= medianie

stopień wojskowy

ma

nie ma

czy ma bagnet?

Statystyki testu

a

16

2,0000

,041

N
Mediana
Istotność dokładna

stopień

wojskowy

Zmienna grupująca: czy ma bagnet?

a.

• Przebadano 10 cyrkowców wykonujących numer

„Żywy pocisk”. Lekarz oceniał ich stan zdrowia
przed i po skoku na skali zły, średni, dobry, bardzo
dobry.

• Ponieważ zmienne są porządkowe możemy

zastosować jedynie test nieparametryczny np. test
znaków lub test rang

Czy bycie cyrkowcem – żywą torpedą szkodzi

Test znaków

1 zły stan zdrowia
2 przeciętny stan

zdrowia

3 dobry stan zdrowia
4 bardzo dobry stan

zdrowia

Zliczamy ilość plusów

i minusów

9 plusów i 2 minusy

Obliczamy statystykę

testu znaków –
porównujemy
liczbę plusów i
minusów

|D|= Różnica między

liczbą plusów i
minusów

Z=(|D|-1)/ N

przed
wystrzeleni

em

po
wystrzele

niu

zna
k

2

3

+

1

2

+

3

4

+

2

4

+

3

4

+

4

3

-

3

2

-

2

3

+

1

4

+

1

3

+

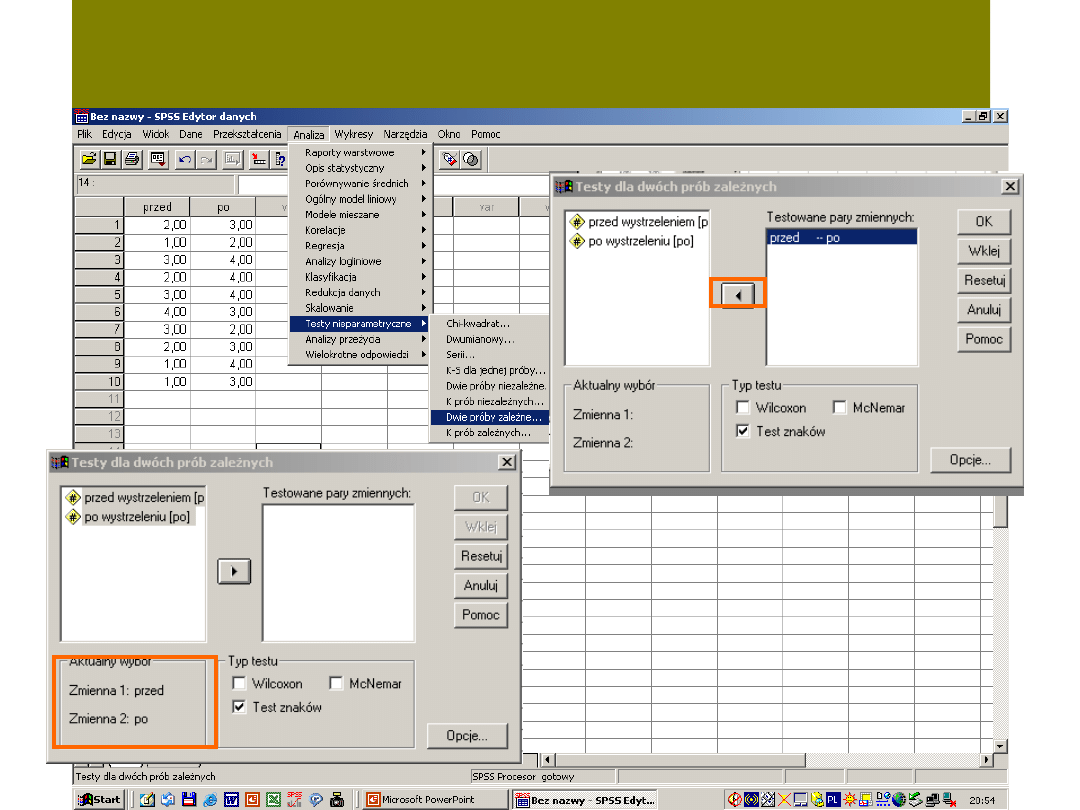
Test znaków – jak to zrobi w SPSS-ie

Test znaków - wydruk

Tabela częstości

2
8
0

10

Ujemne różnice

a

Dodatnie różnice

b

Wiązania

c

Ogółem

po wystrzeleniu -
przed wystrzeleniem

N

po wystrzeleniu < przed wystrzeleniem

a.

po wystrzeleniu > przed wystrzeleniem

b.

po wystrzeleniu = przed wystrzeleniem

c.

Statystyki testu

b

,109

a

Istotność dokładna
(dwustronna)

po

wystrzeleniu -

przed

wystrzeleniem

Użyto rozkładu dwumianowego.

a.

Test znaków

b.

Test Wilcoxona

-1, -1, 1, 1, 1, 1, 1, 2, 2, 3
(rangujemy według wartości bezwzględnych, ale zostawiamy minusy)
-4; -4; 4; 4; 4; 4; 4; 7,5; 7,5; 9

przed
wystrzeleni

em

po
wystrzele

niu

różnica rangi

2

3

1

4

1

2

1

4

3

4

1

4

2

4

2

7,5

3

4

1

4

4

3

-1

-4

3

2

-1

-4

2

3

1

4

1

4

3

9

1

3

2

7,5

Porównujem
y sumę rang
dodatnich i
sumę rang
ujemnych

Ile one
wynoszą

Test Wilcoxona

Rangi

2

a

4,00

8,00

8

b

5,88

47,00

0

c

10

Ujemne rangi
Dodatnie rangi
Wiązania
Ogółem

po wystrzeleniu -
przed wystrzeleniem

N

Średnia ranga Suma rang

po wystrzeleniu < przed wystrzeleniem

a.

po wystrzeleniu > przed wystrzeleniem

b.

po wystrzeleniu = przed wystrzeleniem

c.

Statystyki testu

b

-2,066

a

,039

Z
Istotność asymptotyczna
(dwustronna)

po

wystrzeleniu -

przed

wystrzeleniem

Na bazie ujemnych rang.

a.

Test znaków rangowanych Wilcoxona

b.

Jakiego testu użyć?

• Badacza interesowało, czy istnieją

różnice między osobami o niskim
statusie socjoekonomiczny i wysokim
statusie socjoekonomicznym pod
względem

– Wykształcenia (podstawowe, średnie ,

wyższe)

– Liczby dzieci
– Podatności na stres (niska, średnia,

wysoka)