Wykład 8

Testy T-Studenta

Standaryzacja1

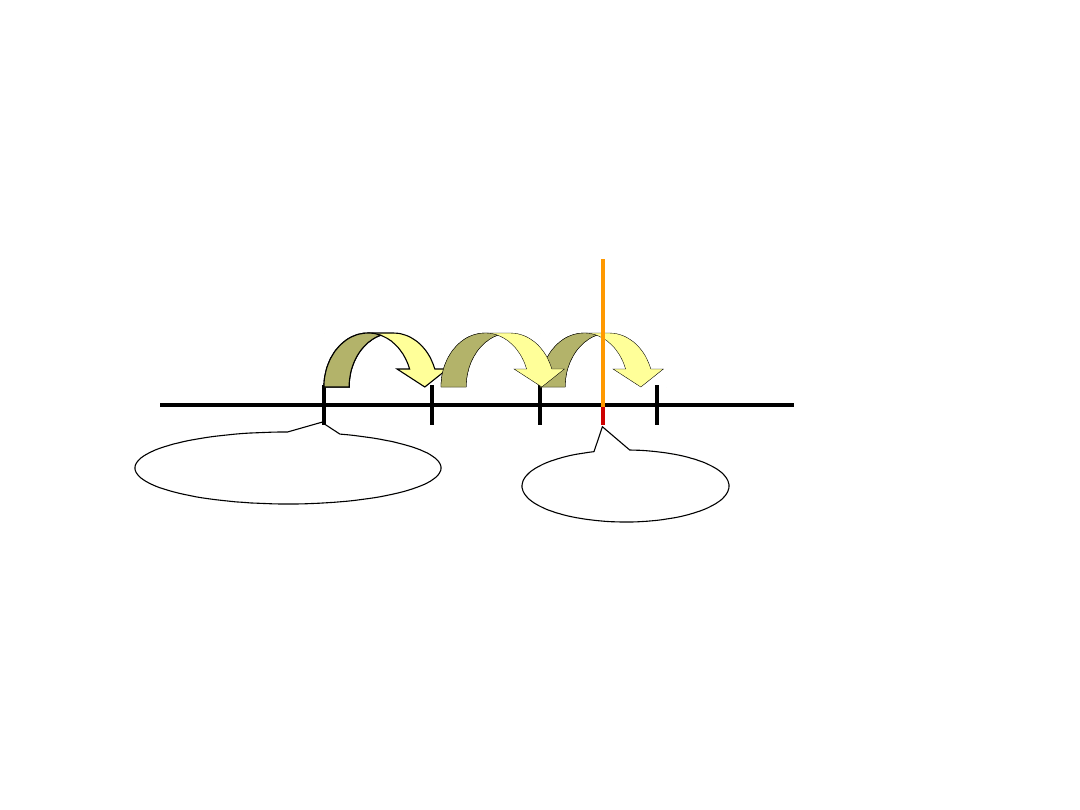
1. Zosia uzyskała wynik 15 punktów w skali

ekstrawersji (średnia wynosi 10 punktów,
odchylenie std. 2). Ile wynosi jej wynik w
jednostkach standardowych?

Średnia 10,
Z=0

Wynik
15

+1
Z

+0,5
Z

+1
Z

Standaryzacja2

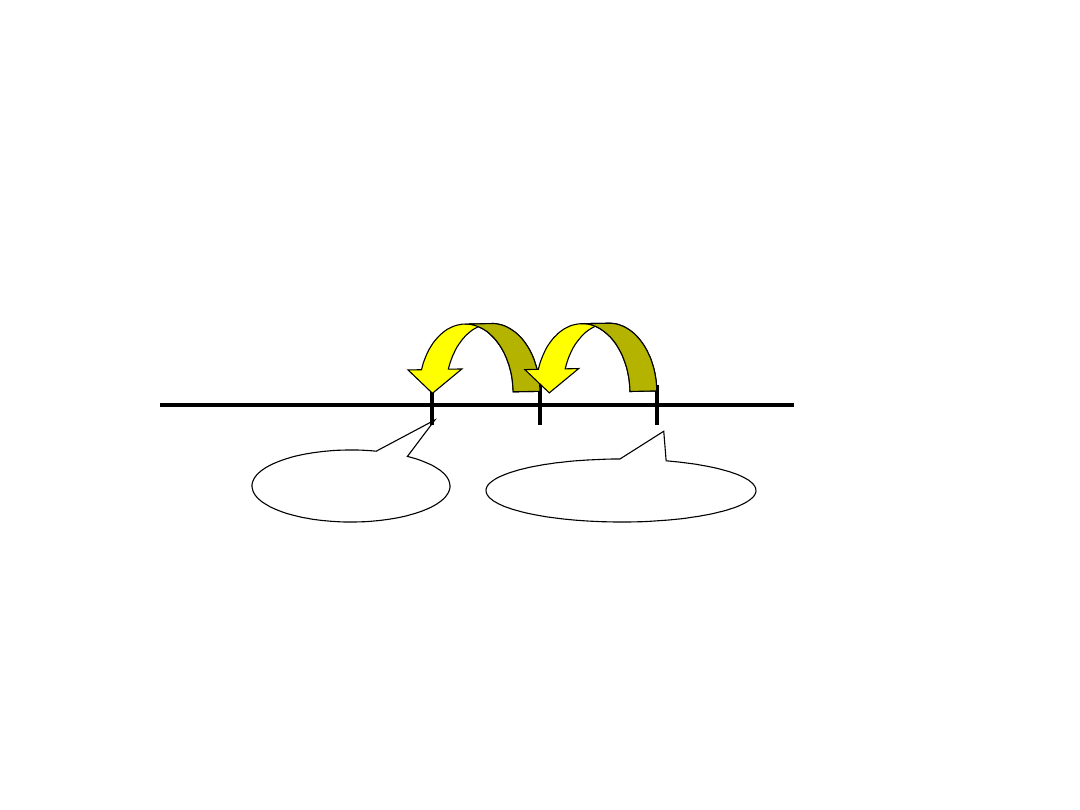
2. Adam uzyskał wynik 5 punktów w skali

neurotyczności (średnia wynosi 9 punktów,
odchylenie std. 2). Ile wynosi jego wynik w
jednostkach standardowych?

Średnia 9
Z=0

Wynik
5

-1Z

-1Z

Standaryzacja3

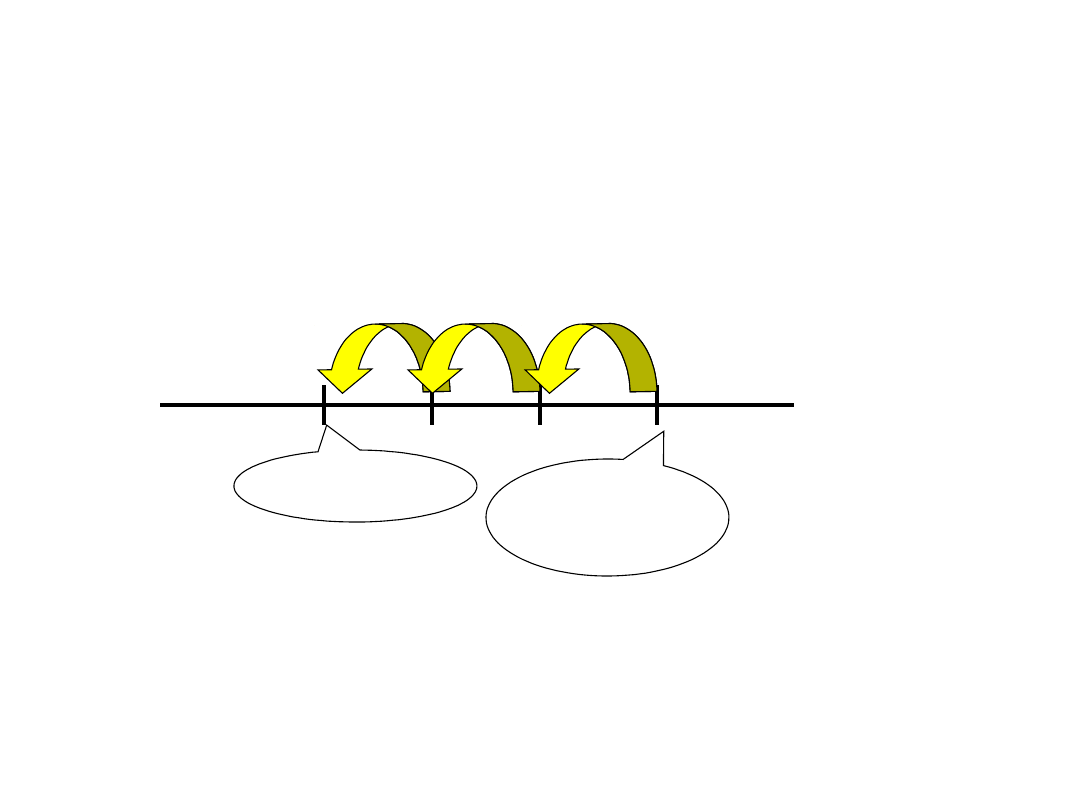
3. Adam uzyskał wynik –3Z w skali aprobaty

społecznej (średnia wynosi 24 punkty,
odchylenie std. 4). Ile punktów w tej skali
uzyskał Adam?

Z=0

Średnia
24

Wynik –
3Z

-
4pkt.

-
4pkt.

-
4pkt.

Standaryzacja4

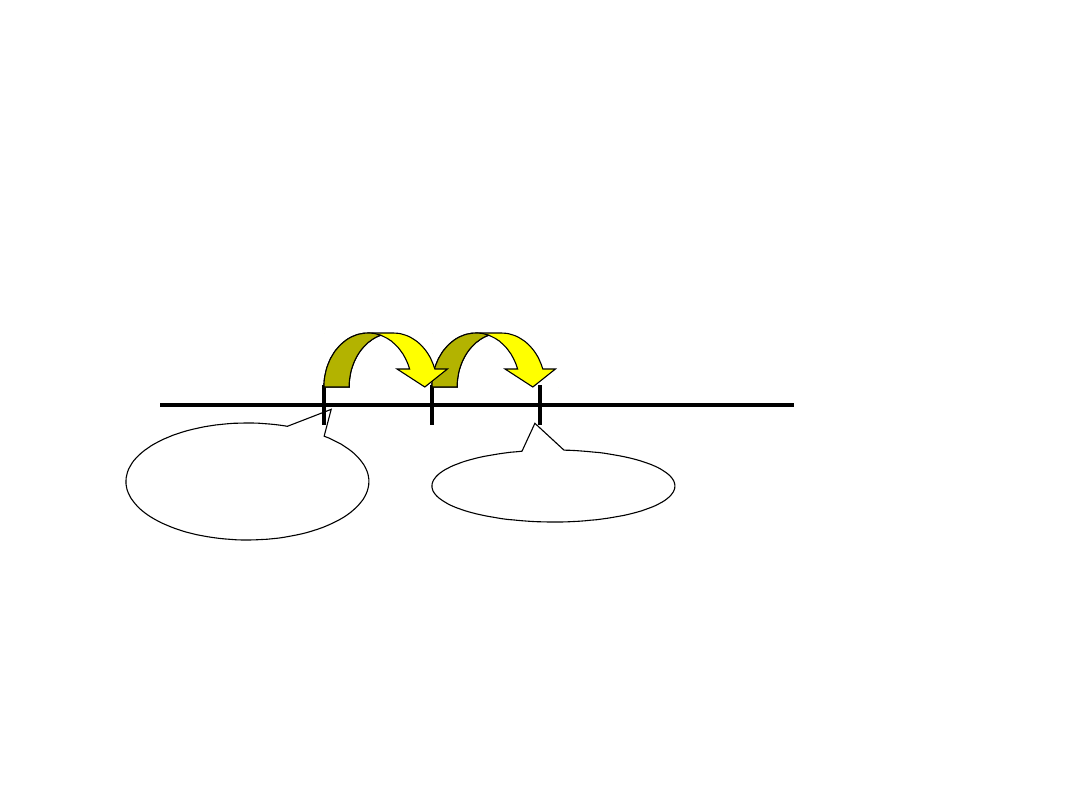
4. Kasia uzyskała wynik 2Z w skali depresji

(średnia wynosi 20 punktów, wariancja 4). Ile
punktów w tej skali uzyskała Kasia?

Z=0

Średnia
20

Wynik 2Z

+2pk
t.

+2pk
t.

Standaryzacja5

Zagadka

5. Dziadek Staś uzyskał wynik w skali artretyzmu

20 punktów. Rozkład zmiennej artretyzm jest
normalny, mediana wynosi 10 a odchylenie
std. 4 punkty. Przelicz wynik dziadka Stasia
na jednostki standardowe.

Rozwiązanie w przyszłym tygodniu....

Test T Studenta dla jednej próby

1.

Jak brzmi hipoteza zerowa testu T-Studenta dla jednej
próby?

a.

Są różnice między średnią grupową a pewną stałą

b.

Są różnice między średnią grupową a jej wariancją

c.

Nie ma różnic między średnią grupową a pewną stałą

d.

Nie ma różnic między średnią grupową a jej wariancją

2. Ile uzyskano stopni swobody w teście T-Studenta dla jednej

próby jeśli przebadano 35 osób

a.

36

b.

34

c.

35

d.

1

Test T Studenta dla jednej próby

Amisze – ciekawe osoby badane
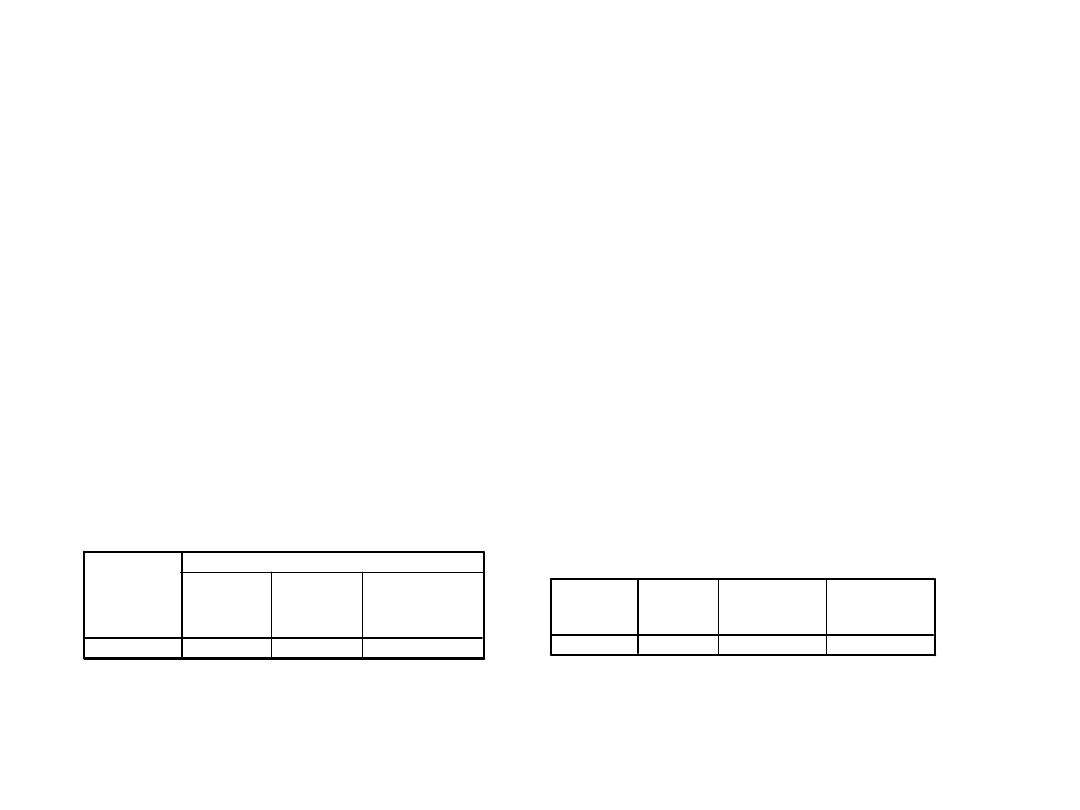
1.Popatrz na wydruk i powiedz, czy Amisze mają przeciętnie trójkę dzieci?
2. Ilu Amiszów zbadano?
3. Ile przeciętnie Amisze mają dzieci?
4. Jak zapisać poprawnie ten wynik?
•

a. T(11)=0,03; p<-3,767

•

b. T(0,03)=11; p<-3,767

•

c. T(11)=3,767; p=0,03

•

d. T(11)=3,767; p<0,05

Statystyki dla jednej próby

1,9167

,99620

,28758

lizba dzieci

Srednia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

-3,767

11

,003

lizba dzieci

t

df

Istotność

(dwustronna)

Wartość testowana = 3

Z pewnych badań
wynikało, że ludzie
nie powinni myć się
częściej niż raz
dziennie – wtedy
zachowają dobre
zdrowie.

Czy rzeczywiście
postępujemy zgodnie
z tymi szczytnymi
sugestiami?

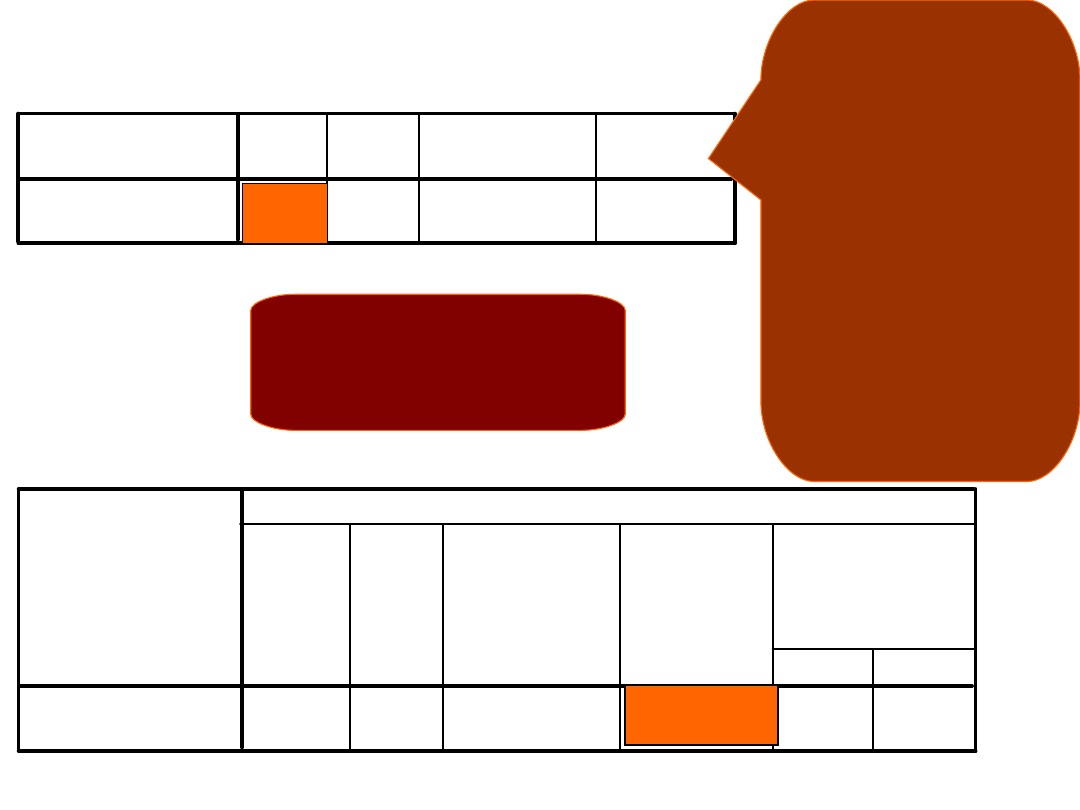
One-Sample Statistics

135

1,94

,826

,071

MYCIE jak często
się myjesz?

N

Mean Std. Deviation

Std. Error

Mean

One-Sample Test

13,226

134

,000

,94

,80

1,08

MYCIE jak często
się myjesz?

t

df

Sig. (2-tailed)

Mean

Difference

Lower

Upper

95%

Confidence

Interval of the

Difference

Test Value = 1

Błąd standardowy
średniej – określa
na ile może się ona
zmieniać w próbach
pobranych z tej
samej populacji. W
praktyce: jeśli iloraz
różnicy i błędu
większe od 2 lub
mniejsze od -2, to
porównywane
średnie pochodzą z
różnych rozkładów –
różnią się istotnie

Tutaj: 0,94/0,071=13,24

Chcemy wyciągać wnioski

o przyczynie…

Lub po prostu porównywać

dwie grupy…

A teraz o sytuacjach gdy….

PRZYCZYNY I SKUTKI

• Badania korelacyjne a badania

eksperymentalne

– Manipulujemy zmienną niezależną i

patrzymy jaki wpływ nasza manipulacja
wywiera na zmienną zależną

Jak wybrać odpowiedni plan

badawczy

• Wprowadzając do eksperymentu

zmienną niezależną (manipulację),

musimy zastanowić się czy będziemy

wykorzystywać ją jako zmienną

– między osobami (plany dla grup

niezależnych) – porównujemy różne grupy

osób

czy
– wewnątrz osób (plany dla grup zależnych) -

między warunkami badania, powtarzane

pomiary

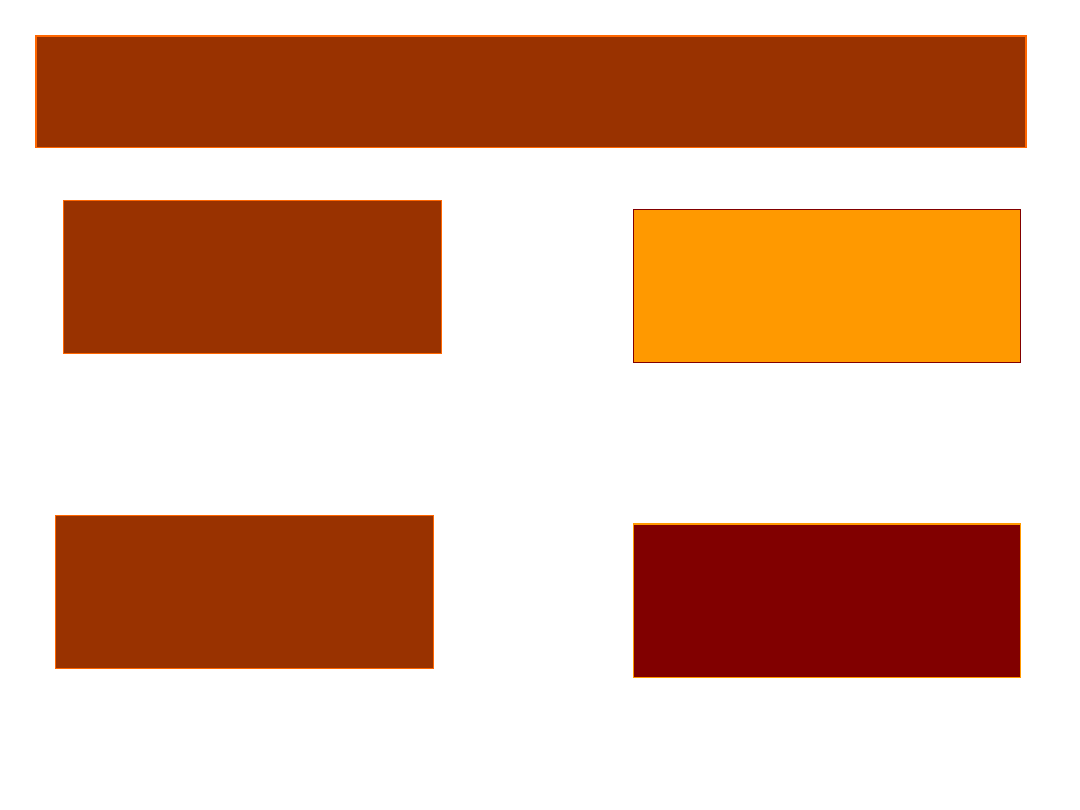
Schemat badania między osobami

(międzygrupowy)

Grupa eksperymentalna

vs

Grupa kontrolna

Grupa eksperymentalna II

Grupa eksperymentalna I

vs

Plan dla grup niezależnych

• Do jednej grupy wprowadzamy

manipulację eksperymentalną (np. głośną
muzykę), druga grupa jest kontrolna

– Eliminujemy zakłócenia związane z

wcześniejszym kontaktem z procedurą
badawczą

– Ale mamy do czynienia z różnicami

indywidualnymi między uczestnikami badania

• Wyjście z sytuacji – np. dobór parami i randomizacja

Schemat badania wewnątrz osób – jedna grupa

kilka razy badana

Pomiar 1

upływ czasu

manipulacja

Pomiar 2

Pomiar

1a –

zadanie werbalne

Pomiar

1b –

zadanie przestrzenne

Plan dla grup zależnych

• Dwukrotny pomiar (przed i po wprowadzeniu

manipulacji) na tej samej grupie osób

• Gdy kilka zadań na tej samej grupie i interesują

nas ich wzajemne relacje

• Główne zalety: mniejsza liczba uczestników

badania, mniej czasu do przeprowadzenia
badania,
– Przy trudno dostępnej próbie
– Odchodzi nam problem różnic indywidualnych

• Gdy powtarzany pomiar ryzyko wyuczenia

zadania

Chcemy ocenić skuteczność treningu

pamięci

• W planie dla grup

niezależnych

– jedna grupa trenuje

pamięć przez trzy
tygodnie
(eksperymentalna),
druga nie robi nic
niezwykłego
(kontrolna),

– na końcu wszystkim

robimy test pamięci

• W planie dla grup

zależnych

– mierzymy grupie

osób pamięć,
następnie grupa ta
trenuje pamięć
przez trzy tygodnie,

– po treningu robimy

powtórny test
pamięci

•

Test T-Studenta dla

Test T-Studenta dla

prób zależnych

prób zależnych

• Porównywanie

średnich dla 1 grupy

badanych (dwukrotny

pomiar tych samych

osób, te same osoby

w różnych warunkach

badania)

– Testowanie hipotezy

zerowej o braku

różnic między

średnimi w badaniu z

powtarzanym

pomiarem

•

Test T-Studenta dla

Test T-Studenta dla

prób niezależnych

prób niezależnych

• Porównywanie

średnich

pochodzących z

dwóch grup (różne

osoby w każdym z

warunków badania)

– Testowanie hipotezy

zerowej o braku

różnic między

średnimi w

porównywanych

populacjach

W
zależności
od planu,
w jakim
przeprowa-
dziliśmy
badanie, do
porównania
uzyskanych
średnich
powinniśmy
zastosować
odpowiedni

test T

Dokładniej o teście T-Studenta dla prób

niezależnych

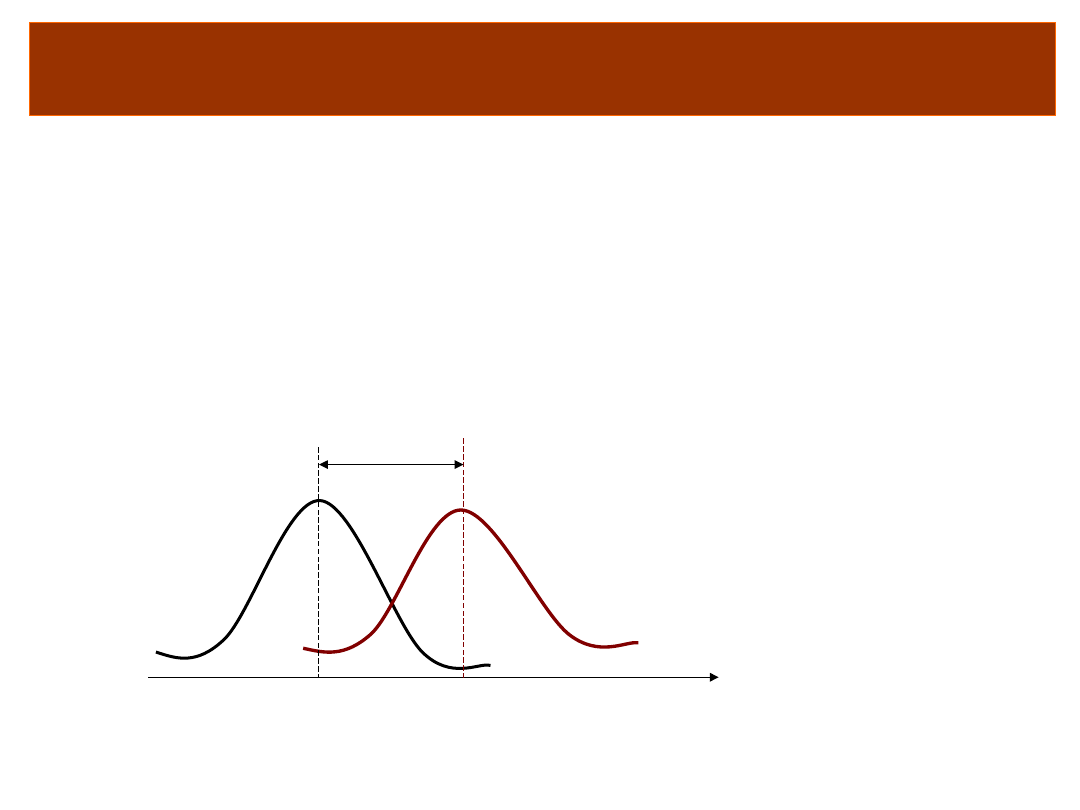
• Porównujemy dwie średnie

– jeśli się różnią możemy założyć, że

pochodzą z różnych populacji

M

1

M

2

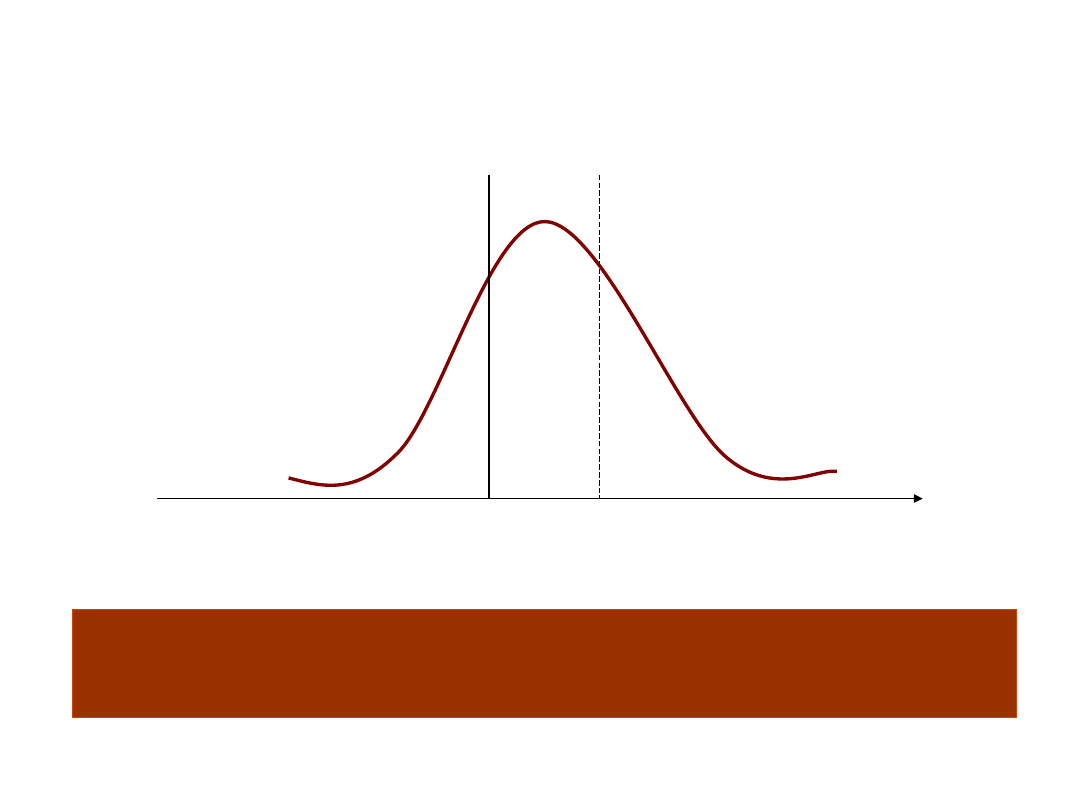
„Na oko” mogą się różnić nawet wtedy, gdy
pochodzą z tej samej populacji

M

1

M

2

Związane jest to z błędem pomiaru – nie mierzymy całej populacji,
tylko próbki – im większa próba, tym mniejszy błąd i lepsze
oszacowanie średniej

Żeby rozstrzygnąć, czy średnie się różnią czy nie, należy wykonać
pewne kroki…

• Formułujemy hipotezę badawczą

H

1

:

Dziewczynki w wieku przedszkolnym wykazują

wyższy poziom empatii niż chłopcy

• Stawiamy hipotezę zerową

H

0

:

Dziewczynki w wieku przedszkolnym wykazują

taki sam poziom empatii niż chłopcy

H1: M

ch

< M

dz

H0: M

ch

= M

dz

H0: M

ch

– M

dz

= 0

• Sprawdzamy założenia testu

– Pomiar zmiennej zależnej na skali co najmniej

przedziałowej

– Rozkład zmiennej zależnej w każdej grup nie

odbiega od normalnego (sprawdzamy np. K-S)

– Wariancje w porównywanych grupach są

homogeniczne (nie różnią się istotnie –

sprawdzamy testem Levene’a)

– Dobór osób do grup losowy
– Równoliczność grup

• Ustalamy poziom istotności (0,05) i

wartości krytyczne dla niego

• Wykonujemy obliczenia i podejmujemy

decyzję w sprawie hipotezy zerowej

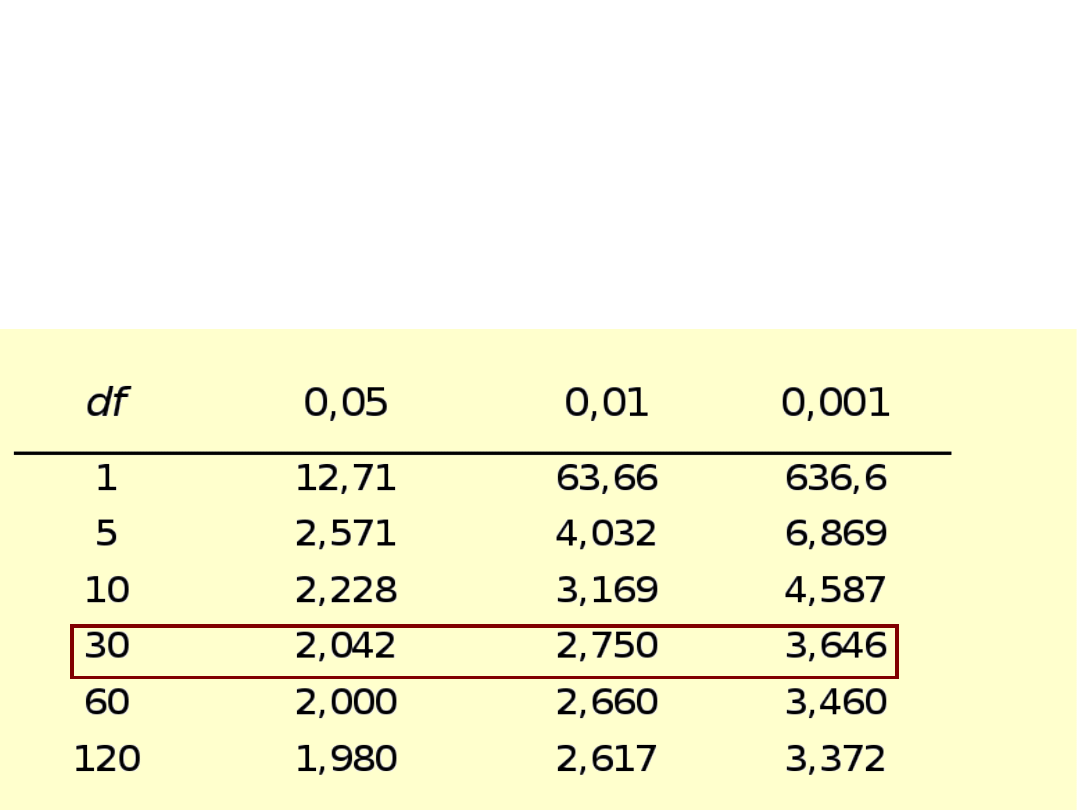
• Wartości krytyczne testu T są ściśle

powiązane ze stopniami swobody

• Stopnie swobody (df):

Sumaryczna liczba elementów danej próbki

lub próbek, która musi być znana, gdy

znana jest ogólna suma, aby można było

uzupełnić pozostałe elementy brakujące.

Jeśli mamy pięć elementów, których suma wynosi 16 i

wiemy, że cztery z nich wynoszą 1 5 4 i 3, to szybko

obliczamy, że pozostały element to…

Liczba stopni swobody w tym przypadku wynosi 4 (N-1)

Rozkład statystyki T zależy od jednego
parametru – stopni swobody; dla df > 30
jest nie do odróżnienia od
standaryzowanego rozkładu normalnego

Stopnie swobody a picie kawy

• Wyobraźmy sobie, że w naszej Szkole

w głównym holu zawsze stoją dwa
wielkie termosy: jeden z kawą i drugi
z herbatą

KAWA

HERBATA

Stopnie swobody a picie kawy

• Pewnego dnia z jednego termosu

znika napis

KAWA

Czy mielibyście problem z ustaleniem gdzie jest
herbata?

• Oczywiście nie, gdyż zbiorniki mają

tylko jeden stopień swobody – jeśli
znany jest jeden element – kawa – oraz
suma elementów – kawa i herbata –
wtedy nieznana zawartość drugiego
zbiornika nie może się zmienić, MUSI
tam być herbata

Stopnie swobody dla testu T-Studenta dla prób

niezależnych

• Na każdą grupę tracimy po jednym

stopniu swobody

• (n

1

-1)+ (n

2

-1)

• Jeśli przebadaliśmy po 20 osób w

każdej grupie to df=?

• W jednej 11 a w drugiej 13, df=?

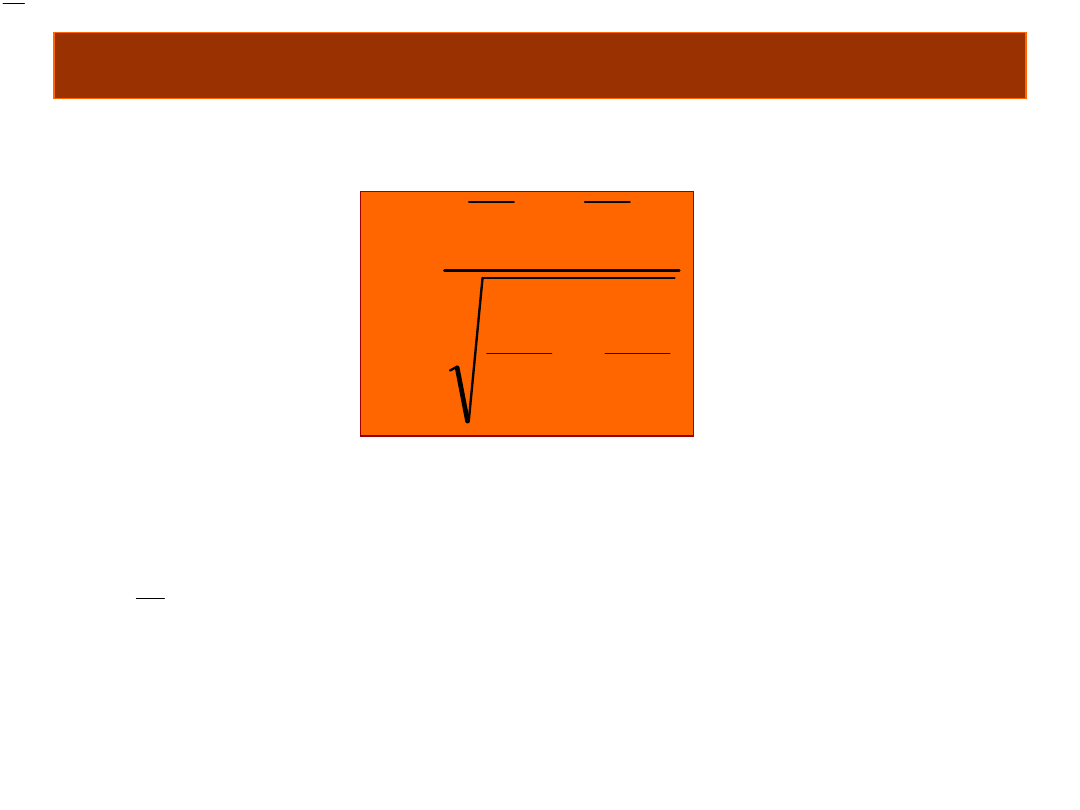
Jak policzyć ten test?

2

2

2

1

2

1

2

1

n

S

n

S

X

X

t







gdzie

– średnia w i-tej grupie, S

i

– odchylenie

standardowe w i-tej grupie, n

i

– ilość osób w i-

tej grupie

i

X

i

X

•

Na szczęście mamy SPSS, który wykona za nas brudną

robotę, czyli policzy wartość T i porówna z wartościami

krytycznymi

– Czy t = 2,1 jest istotne statystycznie, w momencie gdy przebadaliśmy

dwie grupy po 16 osób?

– Obliczamy df=N-2 (po jednym stopniu swobody dla każdej grupy), czyli
(16-1)+(16-1)=30
– Jest istotny na poziomie 0,05, ale nie na 0,01 i 0,001

Przykład z życia wzięty

• W pewnym badaniu sprawdzano, czy

osoby depresyjne różnią się od

niedepresyjnych pod względem

temperamentu, a dokładniej czynnika

aktywność (FCZ-KT)

• Postawiono hipotezę badawczą:

–

Osoby depresyjną osiągną niższe wyniki na

Osoby depresyjną osiągną niższe wyniki na

skali aktywności w porównaniu z

skali aktywności w porównaniu z

niedepresyjnymi

niedepresyjnymi

• Hipoteza kierunkowa, mamy prawo podzielić

„wydrukowany” poziom istotności przez 2, jeśli

wynik odwrotny od postulowanego, nie możemy

jej przyjąć

Na początku sprawdzamy

założenia

• Zmienna zależna została zmierzona na skali

ilościowej (punkty w kwestionariuszu FCZ-KT)

• Normalność rozkładu – testem K-S w podziale

na podgrupy

Sprawdzamy normalność rozkładu. H0 w teście K-S:
rozkład empiryczny = rozkład normalny

W obu grupach test K-S okazał się nieistotny – nie mamy
podstaw do odrzucenie H0 – tu się cieszymy  rozkład

nie odbiega od normalnego

One-Sample Kolmogorov-Smirnov Test

33

10,4545
4,29455

,126
,092

-,126

,725
,668

33

7,8788

4,78120

,119
,119

-,116

,683
,739

Std. Deviation

a,b

Absolute
Positive
Negative

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)

Std. Deviation

a,b

Absolute
Positive
Negative

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)

BDI
1,00 3-5

2,00 pow 9

AKTYWNOS

fcz-kt akt

Test distribution is Normal.

a.

Calculated from data.

b.

Pozostałe założenia odczytujemy z wydruku

testu T

•

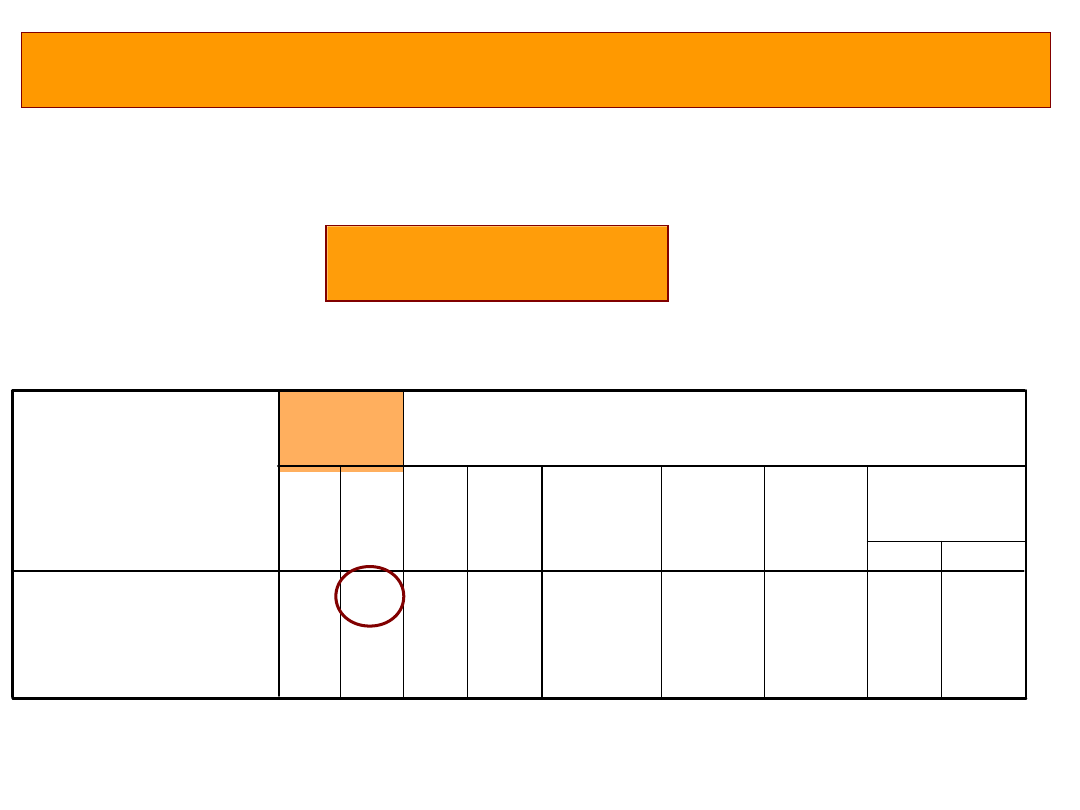
Założenie o równości wariancji – test Levener’a

2

2

2

1

0

:







H

Independent Samples Test

,236

,629 2,302

64

,025

2,5758

1,11875 ,34079 4,81072

2,302 63,276

,025

2,5758

1,11875 ,34030 4,81121

wariancje
homogeniczne
wariancje
niehomogeniczne

AKTYWNOS

F

Sig.

Levene's Test

for Equality of

Variances

t

df

Sig. (2-tailed)

Mean

Difference

Std. Error

Difference

Lower

Upper

95% Confidence

Interval of the

Difference

t-test for Equality of Means

Test Levene’a nieistotny, nie odrzucamy H0, wariancje
homogeniczne

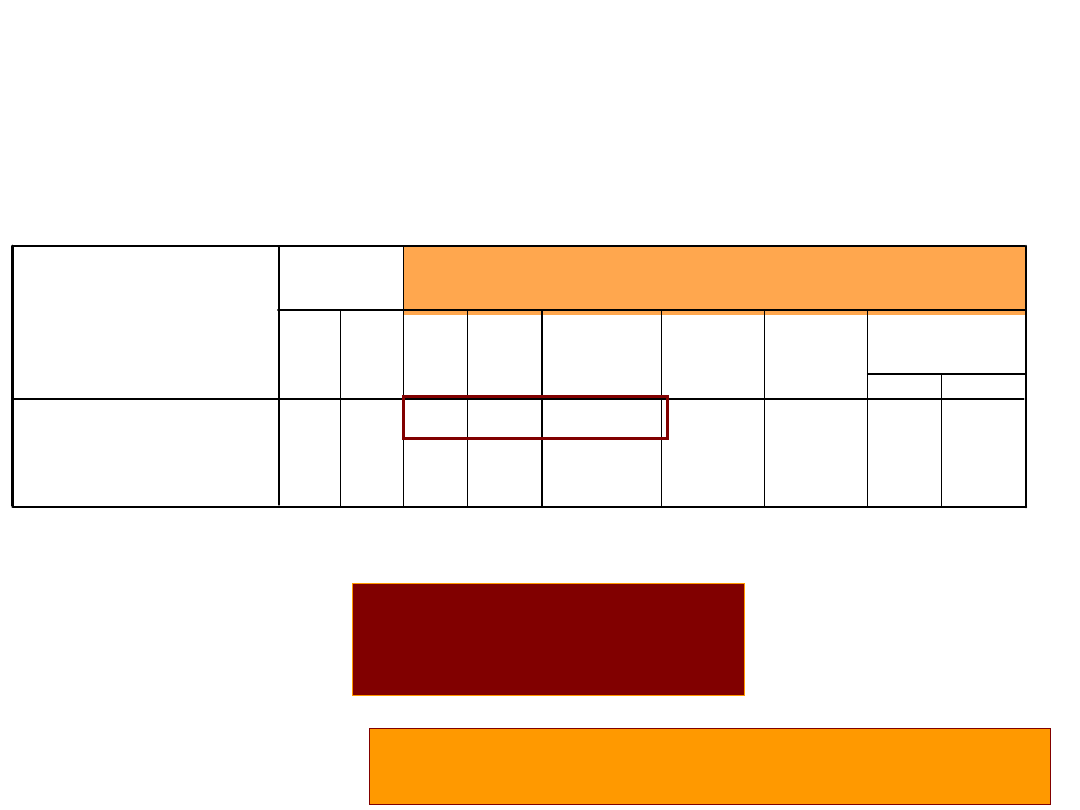
Odczytujemy wartość testu T

z górnego wiersza – wariancje homogeniczne

Independent Samples Test

,236

,629 2,302

64

,025

2,5758

1,11875 ,34079 4,81072

2,302 63,276

,025

2,5758

1,11875 ,34030 4,81121

wariancje
homogeniczne
wariancje
niehomogeniczne

AKTYWNOS

F

Sig.

Levene's Test

for Equality of

Variances

t

df

Sig. (2-tailed)

Mean

Difference

Std. Error

Difference

Lower

Upper

95% Confidence

Interval of the

Difference

t-test for Equality of Means

t(64) = 2,3;
p<0,05

Ile osób przebadano? df=64, df=N-2;
N=66

Wiemy, że się różnią, ale czy zgodnie z
hipotezą?

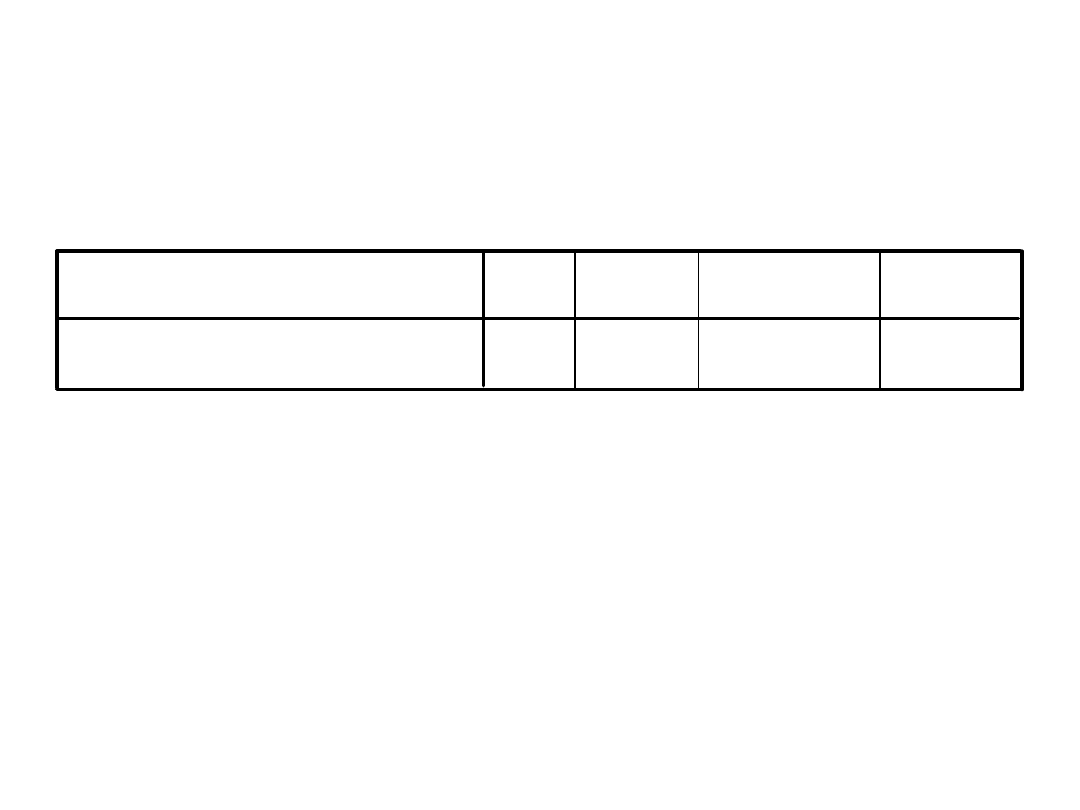
• Patrzymy do tabelki ze średnimi

Group Statistics

33 10,4545

4,29455

,74759

33

7,8788

4,78120

,83230

BDI
1,00 3-5
2,00 pow 9

AKTYWNOS fcz-kt akt

N

Mean

Std. Deviation

Std. Error

Mean

Średnie układają się zgodnie z
przewidywaniami, odrzucamy H0 i
przyjmujemy H1

Przy okazji widzimy, że grupy są równoliczne