Wykład 4

Statystyki opisowe cd. -

korelacje

Jesień za oknem… coraz więcej liści na drzewach?

Współczynniki korelacji

Relacja między dwiema zmiennymi
Wiadomo powszechnie, że im wyższy człowiek

tym ........ numer buta

Im wyższy człowiek tym ........... atrakcyjny

Statystyki opisowe

Dla pojedynczej zmiennej
• Średnia
• Odchylenie std.

Dla dwóch zmiennych
• Współczynniki korelacji

Właściwości średniej

Średnia służy charakterystyce określonej

grupy ale nie nadaje się do
charaketrystyki jednostki

• Paradoks kury i krowy
• Kura i krowa średnio mają trzy nogi,

choć to niewiele mówi o pojedynczym
egzemplarzu grupy, czyli krowie bądź
kurze.

• Odchylenie std.

• Jeżeli interesują nas powiązania pomiędzy dwiema

zmiennymi, tak naprawdę powinniśmy odpowiedzieć

na pytanie, czy:

zmiany w obrębie wartości jednej zmiennej (temperatura za

oknem) pociągają za sobą zmiany na drugiej zmiennej

(spadające liście)

• Oznacza to, że ich wyniki wspólnie się zmieniają

– Jeśli zmieniają się wyniki na jednej zmiennej,

wyniki na drugiej zmieniają się w
przewidywalny sposób

– Innymi słowy zmienne te nie są niezależne od

siebie

Dwie zmienne - przyczyna (zmienna niezależna)
i skutek (zmienna zależna).

Jednak jedynie w eksperymentach, możemy
naprawdę zaufać temu, która zmienna jest
niezależna, a która zależna.

Zanim przejdziemy do korelacji, kilka
słów luźnej dywagacji... o
przyczynowości

Rozważmy tę kwestię na przykładzie z
historii

DARWIN kontra
WALLACE

Pomyłka Wallace’a skutkowała niedocenianiem roli
doboru płciowego przez kilka dziesięcioleci

Współczynnik R-

Pearsona

Jak to policzyć?

Skala ilościowa

• Współczynnik korelacji R-Pearsona
Współczynnik wymyślony przez

Pearsona oznaczony został literą r.
Stosuje się go dla zmiennych
mierzonych na skali ilościowej.

Jak to liczono?

• W prehistorycznych czasach przedspssowych ten

współczynnik był liczony ręcznie (a właściwie

głownie)

• Jak?
• Według wzoru oczywiście:

r =



Z

X

Z

Y

/ N

gdzie:
r - współczynnik korelacji
Z

X

- wartość z dla każdego przypadku dla zmiennej x

Z

Y

- wartość z dla każdego przypadku dla zmiennej y

N - liczba przypadków

Kolejne kroki w liczeniu współczynnika korelacji

 

1. Przekształć wszystkie wyniki w wartości z.
Wymaga to obliczenia średniej i odchylenia
standardowego każdej zmiennej, a następnie
obliczenia wartości z dla każdego wyniku.

2. Pomnóż przez siebie wartość z wyniku na jednej
zmiennej i wartość z wyniku na drugiej zmiennej –
jest to tzw. moment iloczynowy.

3. Zsumuj momenty iloczynowe.

4. Podziel tę sumę przez liczbę przypadków. Pamiętaj,
aby użyć liczby przypadków, a nie liczby wyników.

 

Liczba nadzorowanych

pracowników (X)

Poziom stresu (Y)

Moment

iloczynowy

X

X - M

(X -

M)

2

Z

X

Y

Y - M (Y - M)

2

Z

Y

Z

X

Z

Y

6

-1

1

-0,42

7

1

1

0,38

-0,16

8

1

1

0,42

8

2

4

0,77

0,32

3

-4

16

-1,69

1

-5

25

-1092

3,24

10

3

9

1,27

8

2

4

0,77

0,98

8

1

1

0,42

6

0

0

0

0

 = 35

SS = 28

 = 30

SS = 34

 Z

X

Z

Y

= 4,38

M = 7

SD

2

= 5,60

M = 6

SD

2

= 6,80

r = 0,8

SD = 2,37

SD = 2,61

Wykorzystajmy te kroki do analizy przykładowych danych.

1. Przekształcić wszystkie wyniki na wartości z.

2. Policzyć moment iloczynowy dla każdego przypadku.

3. Suma: 4.38.

4. Podzielić przez liczbę przypadków.

r =  Z

X

Z

Y

/ N = 4.38 / 5 = .876

Interpretacja

• Interpretacja współczynnika r-Pearsona?
Współczynnik ten może przyjmować wartości

od (–1 do 1)

Siła (im bliżej 1 lub im bliżej – 1 tym silniejsza

zależność, zależność słaba gdy r znajduje się

blisko 0) i kierunek zależności (dodatni

kierunek – wysokie wartości jednej zmiennej

odpowiadają wysokim wartościom drugiej

zmiennej; ujemny kierunek wysokie wartości

jednej zmiennej odpowiadają niskim

wartościom drugiej zmiennej i na odwrót)

Macierz korelacji

• Współczynnik korelacji tej samej zmiennej z

nią samą wynosi 1 i jest umieszczony

po

przekątnej

• Szukamy tej części tabeli gdzie jest

skrzyżowana zmienna pracownicy oraz stres

(są dwie takie części)

Korelacje

1

,875

5

5

,875

1

5

5

Korelacja Pearsona
N
Korelacja Pearsona
N

PRACOW

STRES

PRACOW

STRES

Wykres rozrzutu

• Pokazuje współzależności pomiędzy

dwiema zmiennymi

• Dwa wymiary pokazujące rozkład

wyników dla dwóch zmiennych

• Każdy wymiar (oś) pokazuje wartości

liczbowe danej zmiennej

• Najlepiej dane mierzone co najmniej na

skali przedziałowej

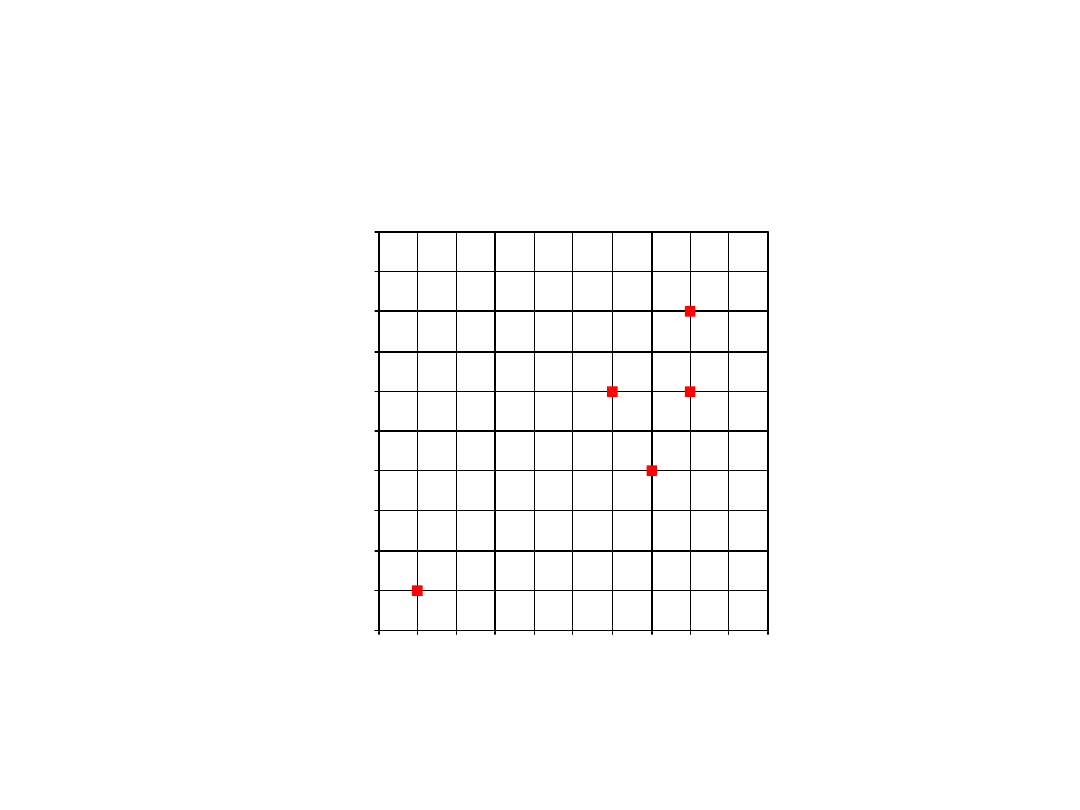
Wykres rozrzutu

STRES

10

9

8

7

6

5

4

3

2

1

0

P

R

AC

O

W

12

11

10

9

8

7

6

5

4

3

2

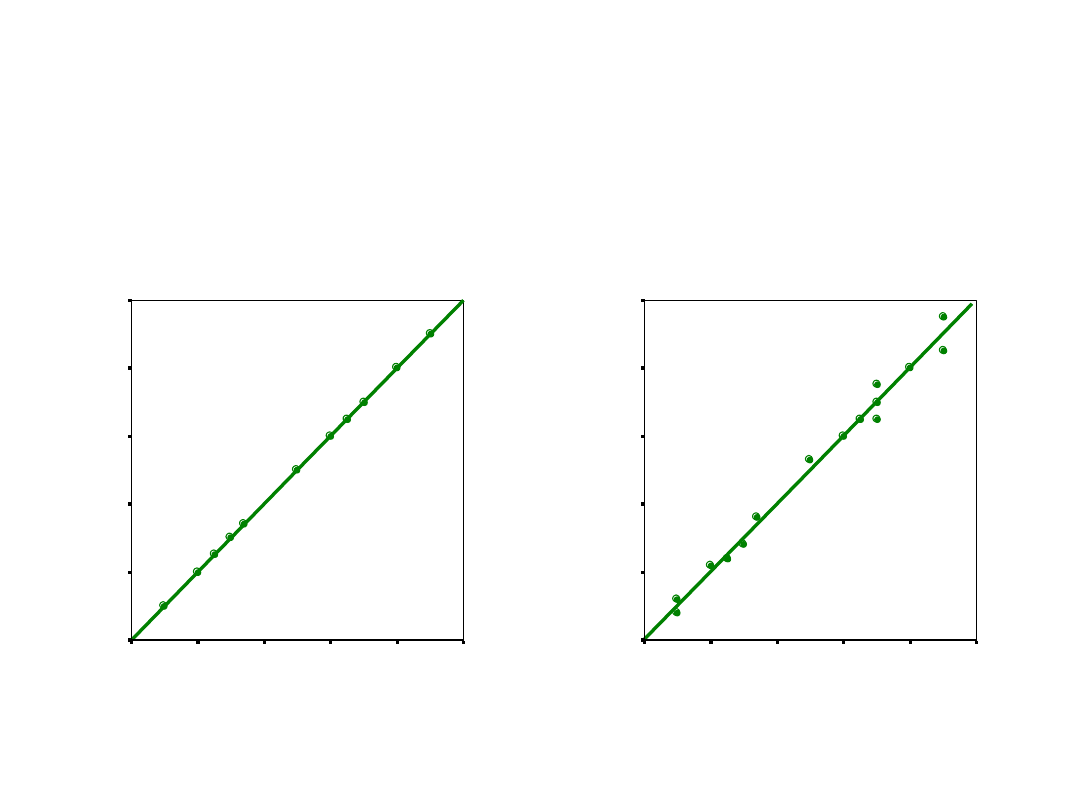
Wartości R na wykresach

wartości X

10

8

6

4

2

0

w

ar

to

śc

i Y

10

8

6

4

2

0

r=1,0

wartości X

10

8

6

4

2

0

w

ar

to

śc

i Y

10

8

6

4

2

0

r=0,99

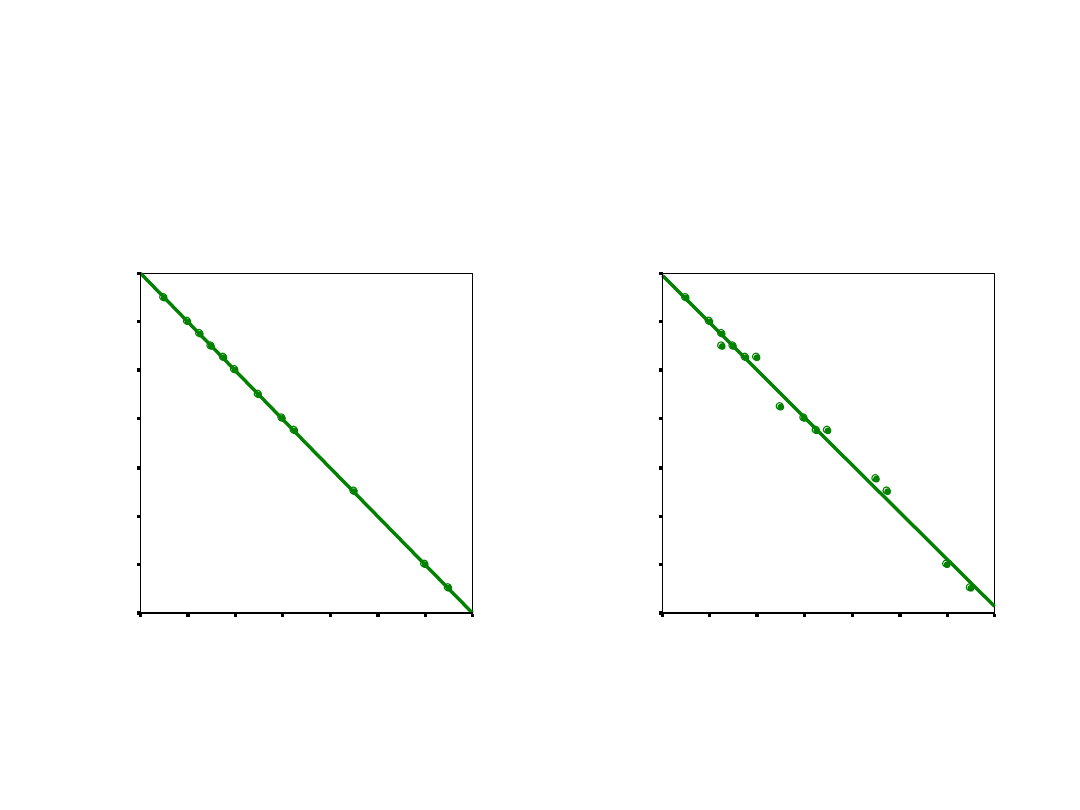
wartości X

4

2

0

-2

-4

-6

-8

-10

w

ar

to

śc

i Y

10

8

6

4

2

0

-2

-4

wartości X

4

2

0

-2

-4

-6

-8

-10

w

ar

to

śc

i Y

10

8

6

4

2

0

-2

-4

r = -1

r = -0,99

wartości X

18

16

14

12

10

8

6

4

2

0

-2

w

ar

to

śc

i Y

16

14

12

10

8

6

4

2

0

-2

wartości X

6,0

5,0

4,0

3,0

2,0

1,0

0,0

w

at

oś

ci

Y

6,0

5,0

4,0

3,0

2,0

1,0

0,0

r = 0,1

r = 0

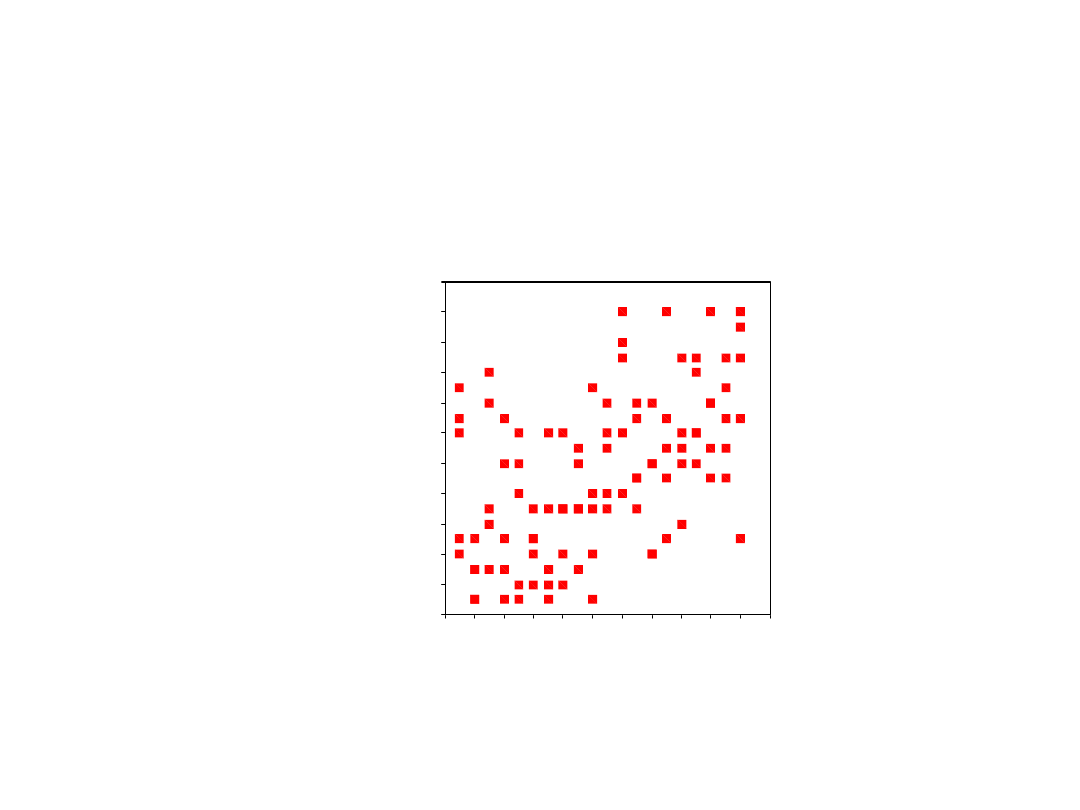
Zgadywanka

• Zgadnijcie, ile wynosi współczynnik korelacji

pokazanej na tym wykresie

Trudno ocenić na podstawie wykresu dlatego....

poziom asertywnosci

22

20

18

16

14

12

10

8

6

4

2

0

an

ty

p

at

ia

s

ro

d

o

w

is

ka

p

ra

cy

22

20

18

16

14

12

10

8

6

4

2

0

Zgadywanka -

rozwiązanie

Korelacje

1

,515**

100

100

,515**

1

100

100

Korelacja Pearsona
N
Korelacja Pearsona
N

poziom asertywnosci

antypatia srodowiska
pracy

poziom

asertywnosci

antypatia

srodowiska

pracy

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

Trudności ze

współczynnikiem

korelacji czyli korzyści

z oglądania obrazków

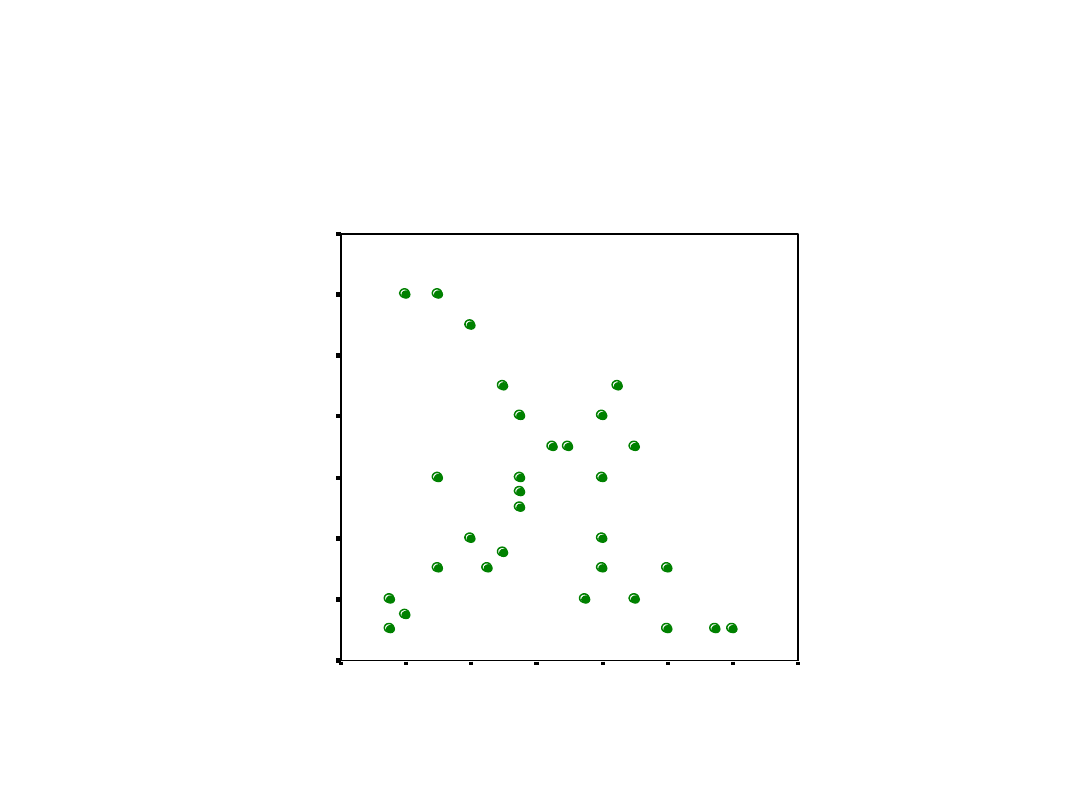
Testosteron i zdolności przestrzenne

r = -0,26 – słaby związek

A jak to wygląda na wykresie?

poziom testosteronu

14

12

10

8

6

4

2

0

zd

ol

no

śc

i p

rz

es

tr

ze

nn

e

14

12

10

8

6

4

2

0

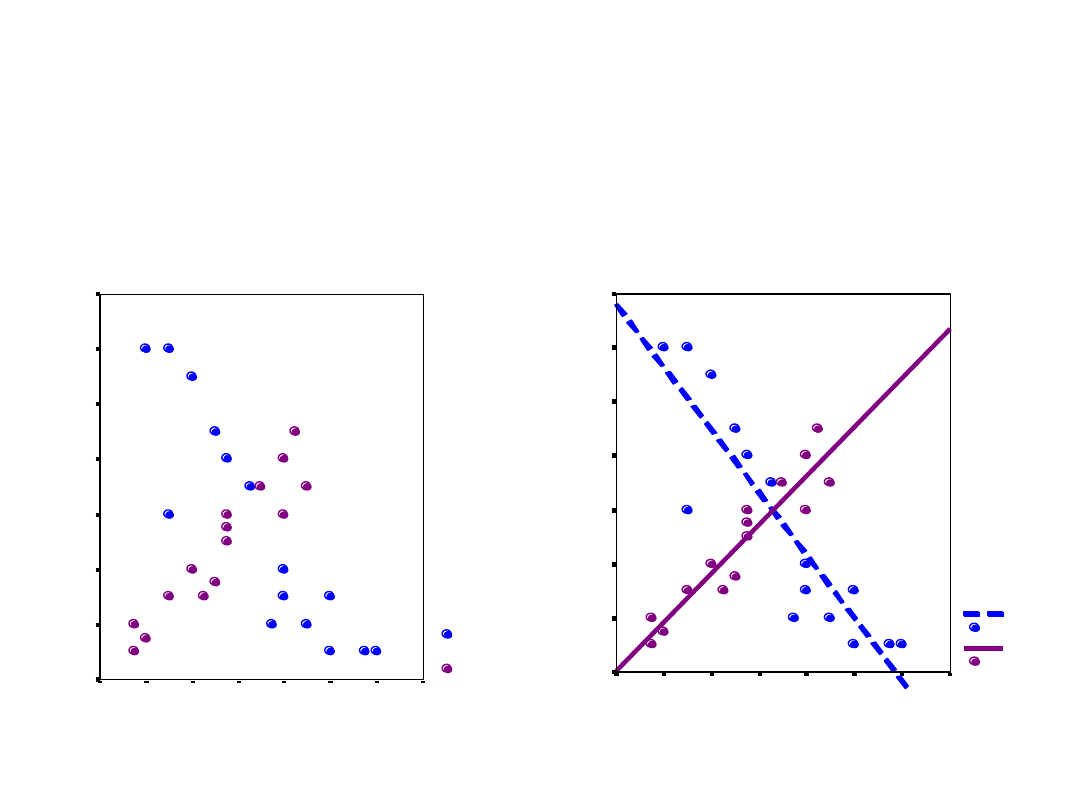
Co się stanie, gdy uwzględnimy
płeć?

poziom testosteronu

14

12

10

8

6

4

2

0

zd

ol

no

śc

i p

rz

es

tr

ze

nn

e

14

12

10

8

6

4

2

0

PŁEĆ

mężczyźni

kobiety

poziom testosteronu

14

12

10

8

6

4

2

0

zd

ol

no

śc

i p

rz

es

tr

ze

nn

e

14

12

10

8

6

4

2

0

PŁEĆ

mężczyźni

kobiety

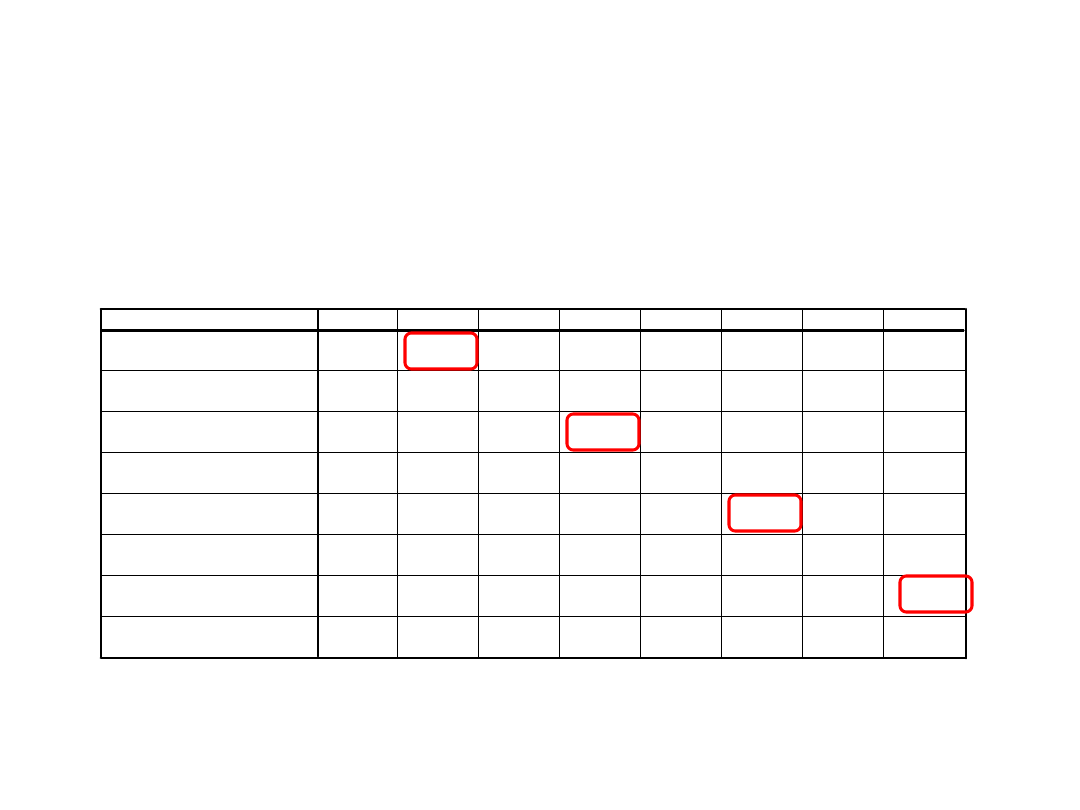
Macierz korelacji

dane anscombe.sav

Korelacje

1

,816**

,750**

,816**

,469

,816**

-,489

-,529

11

11

11

11

11

11

11

11

,816**

1

,816**

1,000**

,816**

1,000**

-,314

-,500

11

11

11

11

11

11

11

11

,750**

,816**

1

,816**

,588

,816**

-,478

-,718*

11

11

11

11

11

11

11

11

,816**

1,000**

,816**

1

,816**

1,000**

-,314

-,500

11

11

11

11

11

11

11

11

,469

,816**

,588

,816**

1

,816**

-,155

-,345

11

11

11

11

11

11

11

11

,816**

1,000**

,816**

1,000**

,816**

1

-,314

-,500

11

11

11

11

11

11

11

11

-,489

-,314

-,478

-,314

-,155

-,314

1

,817**

11

11

11

11

11

11

11

11

-,529

-,500

-,718*

-,500

-,345

-,500

,817**

1

11

11

11

11

11

11

11

11

Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N
Korelacja Pearsona
N

Y1

X1

Y2

X2

Y3

X3

Y4

X4

Y1

X1

Y2

X2

Y3

X3

Y4

X4

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

Korelacja jest istotna na poziomie 0.05 (dwustronnie).

*.

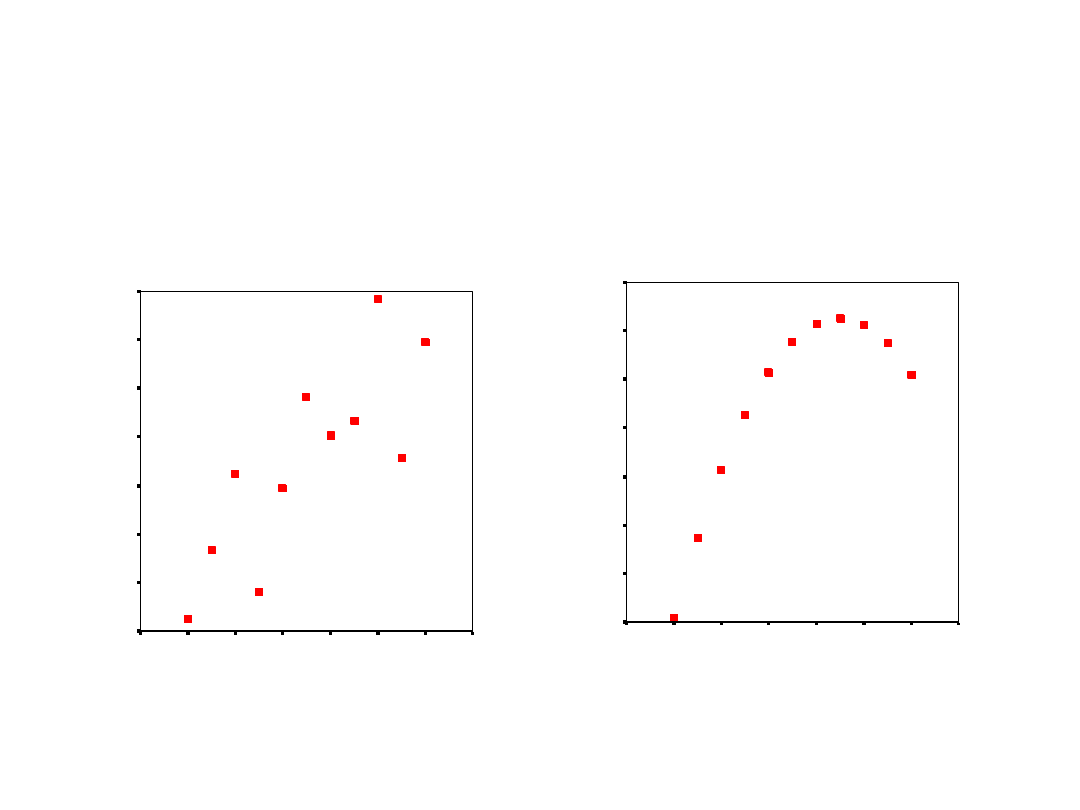
Wykresy rozrzutu

X1

16

14

12

10

8

6

4

2

Y

1

11

10

9

8

7

6

5

4

X2

16

14

12

10

8

6

4

2

Y

2

10

9

8

7

6

5

4

3

Mimo dobrego współczynnika r zależność
może być krzywoliniowa.

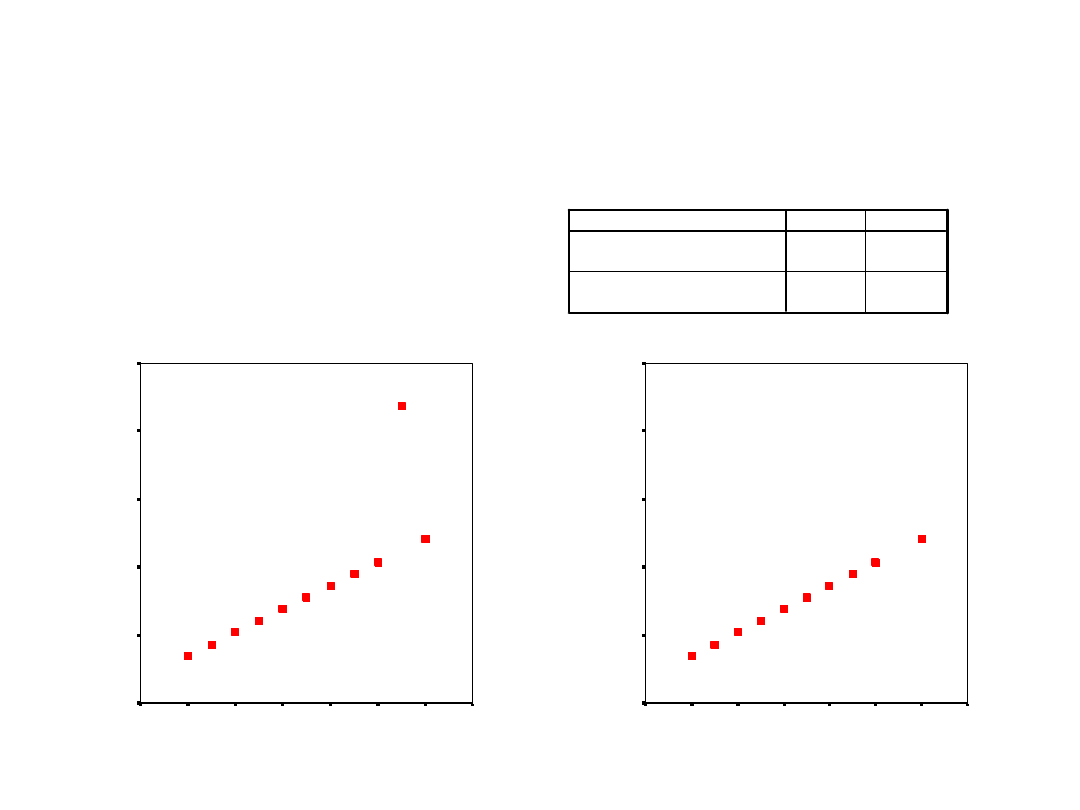
X3

16

14

12

10

8

6

4

2

Y

3

14

12

10

8

6

4

Korelacje

1

1,000**

10

10

1,000**

1

10

10

Korelacja Pearsona
N
Korelacja Pearsona
N

X3

Y3

X3

Y3

Korelacja jest istotna na poziomie 0.01
(dwustronnie).

**.

X3

16

14

12

10

8

6

4

2

Y

3

14,0

12,0

10,0

8,0

6,0

4,0

Wpływ dewianta – przypadek 1

Dewiant może osłabiać zależność, jeśli go
usuniemy (wykres po prawej) to zależność
jest idealna)

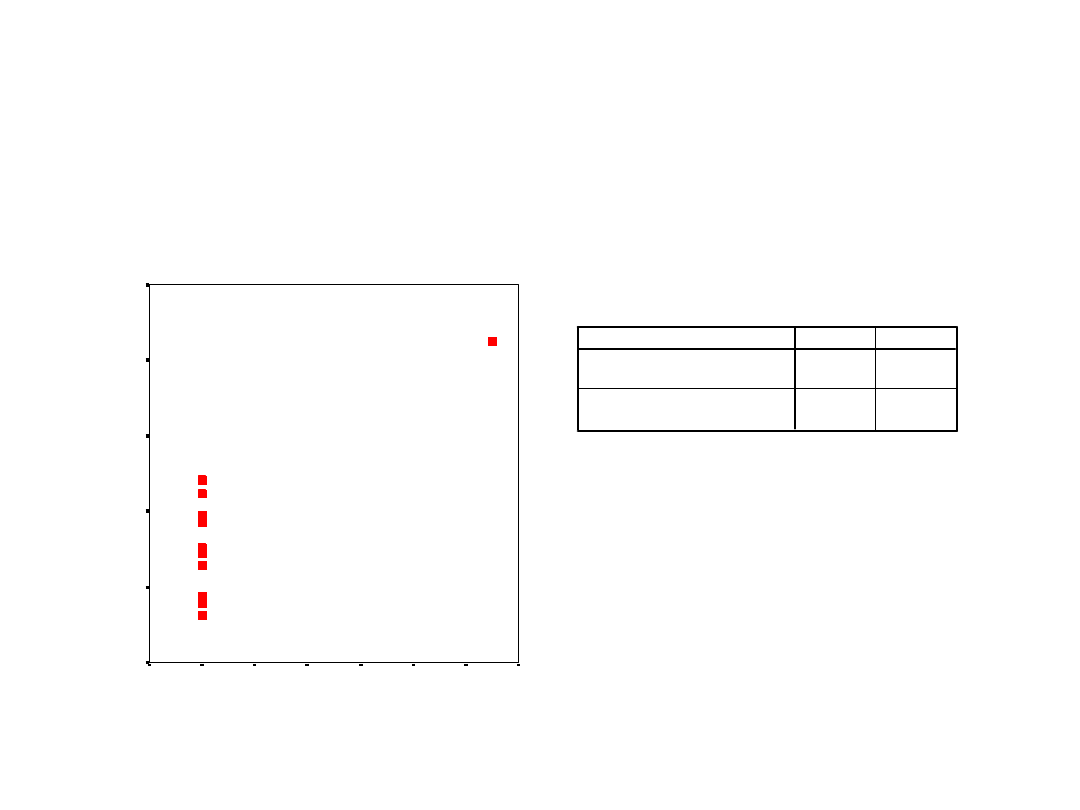
X4

20

18

16

14

12

10

8

6

Y

4

14

12

10

8

6

4

Korelacje

1

.

a

10

10

.

a

.

a

10

10

Korelacja Pearsona
N
Korelacja Pearsona
N

Y4

X4

Y4

X4

Obliczenia nie mogą być przeprowadzone, ponieważ
co najmniej jedna zmienna przyjmuje stałe wartości.

a.

Wpływ dewianta – przypadek 2

Dewiant może także wzmacniać współczynnik
korelacji. Zaciemnia to obraz sytuacji. Jeśli
usuniemy dewianta okaże się, że jedna ze
zmiennych nie ma odchylenia std, czyli ma tylko
stałe wartości

Dobór małżeński

Pytanie badawcze:

• Czy kobiety różnią się liczbą lat nauki od

mężczyzn?

• Czy istnieje związek między wykształceniem

męża i żony?

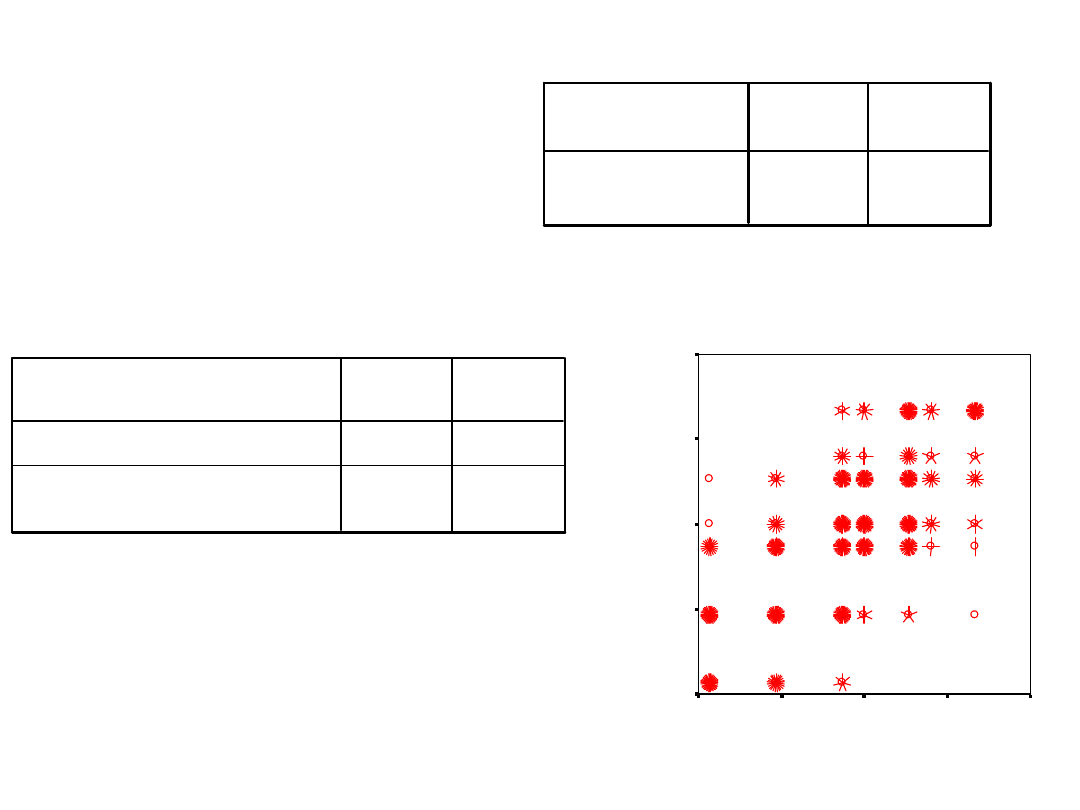
Korelacje

1

,444**

3838

3494

,444**

1

3494

3655

Korelacja Pearsona
N
Korelacja Pearsona
N

LAT NAUKI
SZKOLNEJ MATKI
LAT NAUKI
SZKOLNEJ OJCA

LAT NAUKI

SZKOLNEJ

MATKI

LAT NAUKI

SZKOLNEJ

OJCA

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

LAT NAUKI SZKOLNEJ MATKI

20

15

10

5

0

LA

T

N

A

U

K

I S

Z

K

O

LN

E

J

O

JC

A

20

15

10

5

0

Statystyki

3655

3838

394

211

11,94

10,29

Ważne
Braki danych

N

Średnia

LAT NAUKI

SZKOLNEJ

OJCA

LAT NAUKI

SZKOLNEJ

MATKI

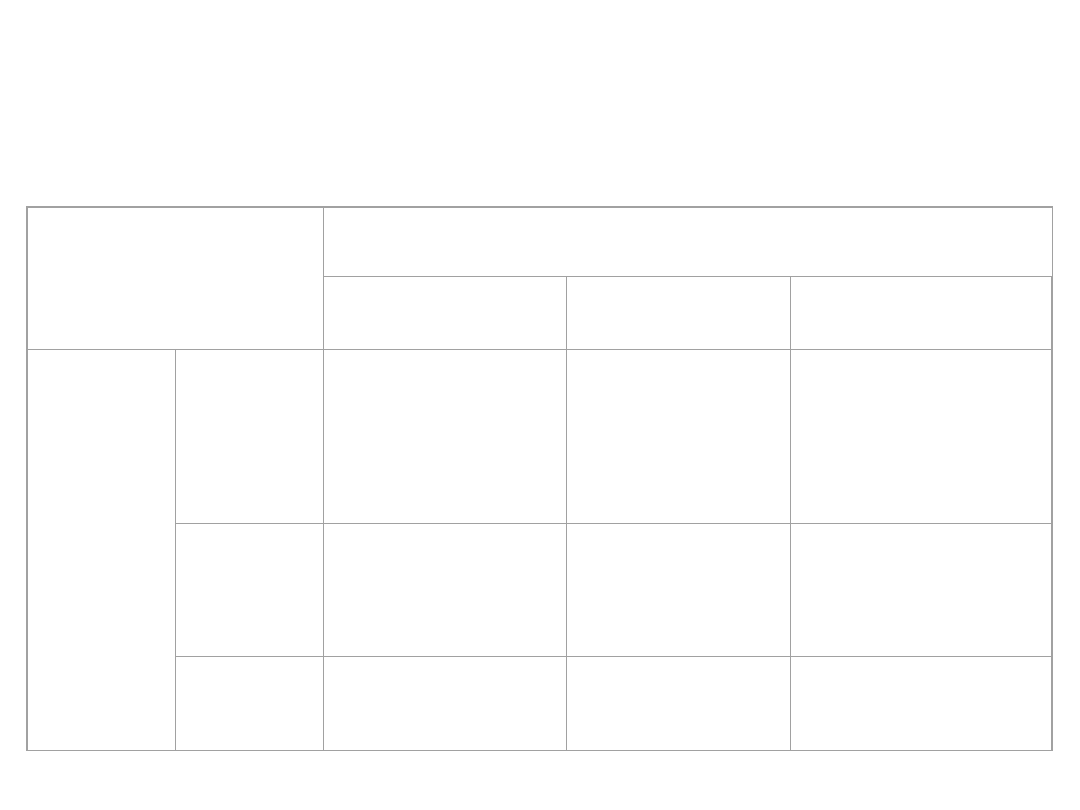
Współczynniki

korelacji - zestawienie

 

Zmienna niezależna

Skala nominalna

Skala
porządkowa

Skale ilościowe

Zmienn

a

zależna

Skala
nominal
na

Współczynnik
kontyngencji
Phi i V-
Cramera
Lambda
Współczynnik
niepewności

 

 

Skala
porządk
owa

Eta

Gamma
D-Sommersa
Tau-b
Kendalla
Tau-c Kendalla

 

Skale
ilościow
e

Eta

 

R-Pearsona
Rho-Spearmana

Współczynniki

korelacji dla

zmiennych

nominalnych

Zmienne nominalne – współczynniki przyjmują
wartości od 0 do 1 – możemy interpretować tylko
siłę zależności

Dla niektórych statystyk (np. Phi i V Cramera)
wartość 0,25 świadczy o silnej zależności

Zmienna nominalna i ilościowa – współczynnik
eta – zakres od 0 do 1

Zmienne porządkowe (Rho Spearmana)– wartości
od –1 do 1 – podobna interpretacja jak
współczynnika r-Pearsona.

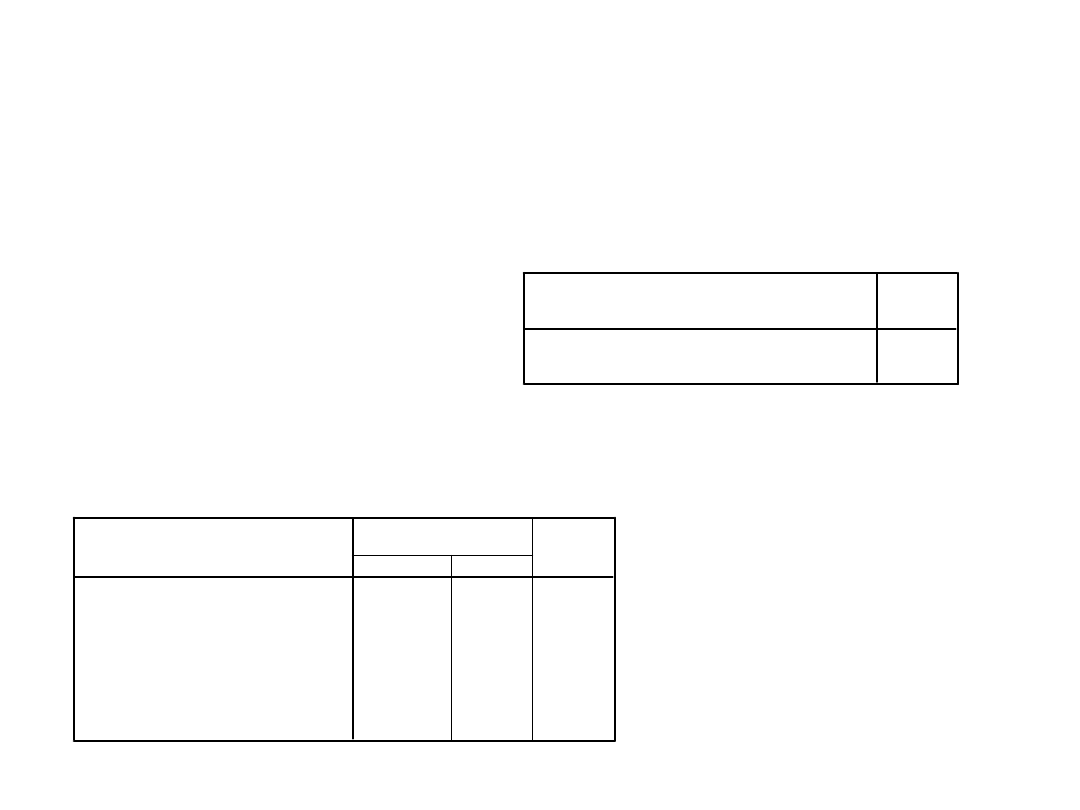
Czy długość nauki wiąże

się z płcią?

Miary kierunkowe

,210

Zmienna zależna: PLEC
RESPONDENTA: 1=M,
2=KOB

Eta

Nominalna przez
Przedziałowa

Wartość

Tabela krzyżowa LAT NAUKI SZKOLNEJ RESPONDENTA * PLEC RESPONDENTA:

1=M, 2=KOB

Liczebność

9

27

36

71

163

234

396

616

1012

665

475

1140

412

588

1000

72

219

291

165

169

334

1790

2257

4047

BRAK FORM WYKSZT
4 LATA/1
8 LAT/2
1O LAT/3,4
12 LAT/4,6
14 LAT/7,8
17 LAT/9

LAT NAUKI
SZKOLNEJ
RESPONDENTA

Ogółem

MEZCZYZNA

KOBIETA

PLEC RESPONDENTA:

1=M, 2=KOB

Ogółem

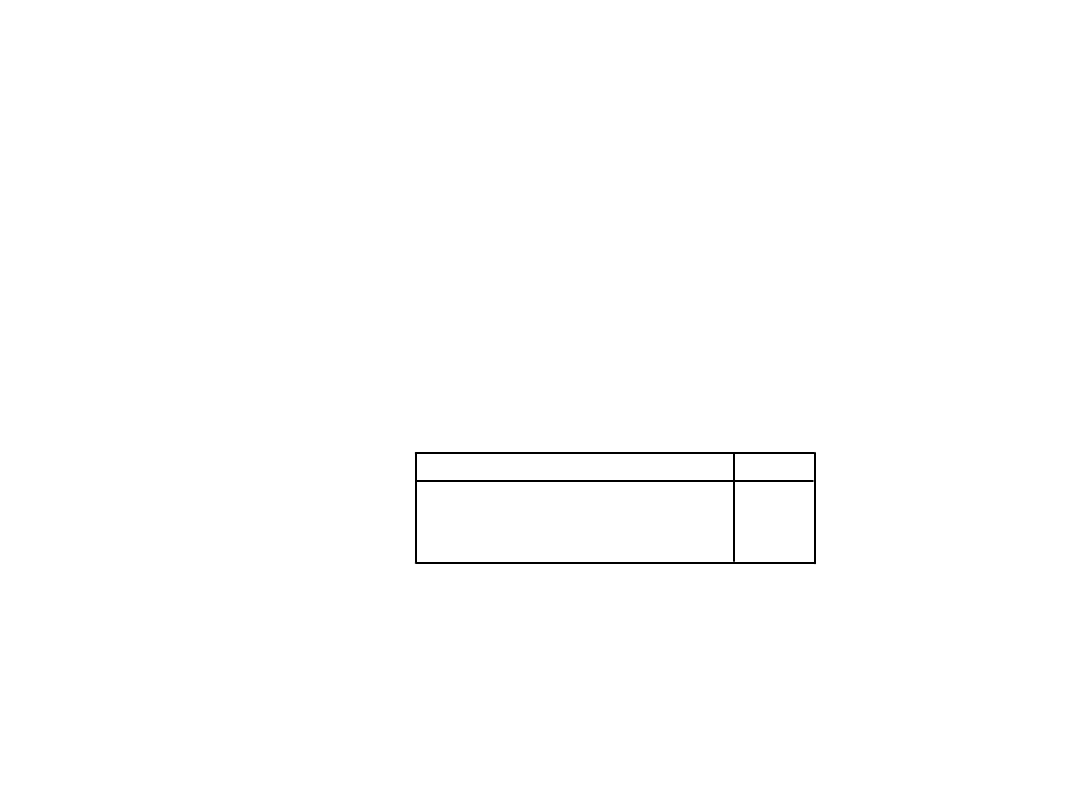
Czy któryś znak zodiaku

jest szczególnie marudny?

Liczymy współczynnik korelacji Phi i V Cramera

(dla zmiennych nominalnych) oraz tau-b

Kendalla (dla zmiennych porządkowych)

Niestety zależności nie ma....

Miary symetryczne

,114
,066

-,008

2388

Phi
V Kramera

Nominalna przez
Nominalna

tau-b Kendalla

Porządkowa przez
Porządkowa

N Ważnych obserwacji

Wartość

Nie zakładając hipotezy zerowej.

a.

Użyto asymptotycznego błądu standardowego, przy
założeniu hipotezy zerowej.

b.