Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

Rozkład normalny

Rozkład normalny jest teoretycznym modelem wielu zjawisk losowych. Zjawiska losowe to, najogólniej mówiąc,

takie zjawiska, co do których nie mamy pewności czy się pojawią czy nie, ani z jaką częstością. Nie jest więc
zjawiskiem losowym wschód słońca, ale zjawiskiem losowym jest, na przykład, wynik rzutu sześcienną kostką do gry,
czy to, jaki wzrost mają wylosowane do badania osoby. W statystyce mówimy o zmiennych losowych, które można
traktować jako matematyczne „odpowiedniki” zjawisk losowych. W badaniach, w których o własności populacji
wnioskuje się na podstawie losowej próbki tej populacji wszystkie interesujące badacza zmienne są traktowane jako
zmienne losowe. Stąd w analizach wykorzystujących wnioskowanie statystyczne duże znaczenie mają teoretyczne
rozkłady zmiennych losowych. Zajmiemy się tu tylko jednym z tych rozkładów, a mianowicie rozkładem normalnym.

Rozkład normalny o parametrach

µ

oraz

σ

oznaczany jest N(

µ

,

σ

).

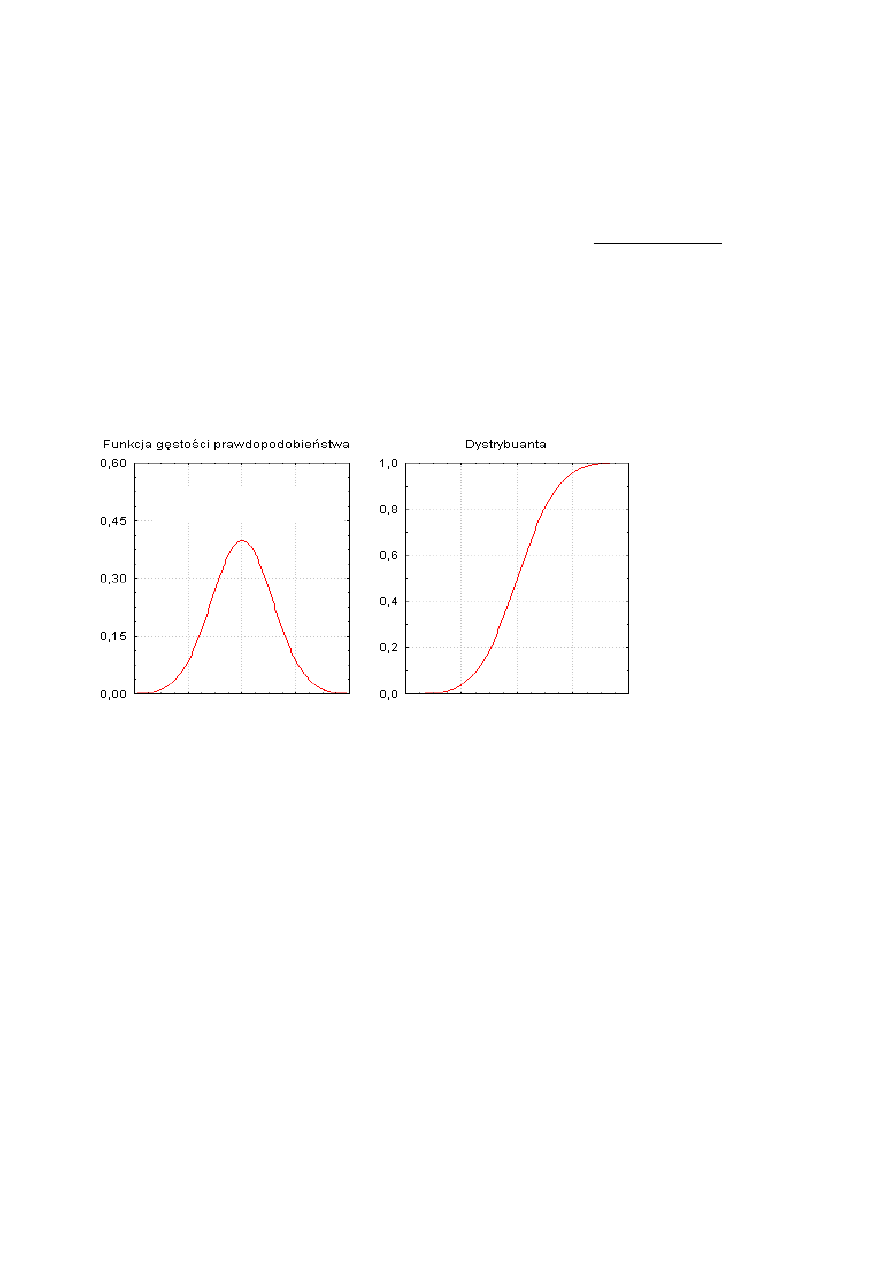
Na rysunku 1 przedstawiony jest wykres rozkładu normalnego, zwany krzywą Gaussa lub krzywą normalną oraz

jego dystrybuanta.

µ

Rys.1. Rozkład normalny N((

µ

,

σ

) oraz jego dystrybuanta.

Krzywa Gaussa ma kształt dzwonu o ramionach zbliżających się asymptotycznie do osi wartości zmiennej

(poziomej na rys.1)

Podstawowe własności krzywej Gaussa:

1.

krzywa osiąga maksimum w punkcie x =

µ

,

2.

jest symetryczna względem prostej przechodzącej przez punkt x =

µ

,

3. pole powierzchni pod krzywą jest skończone i równe 1.

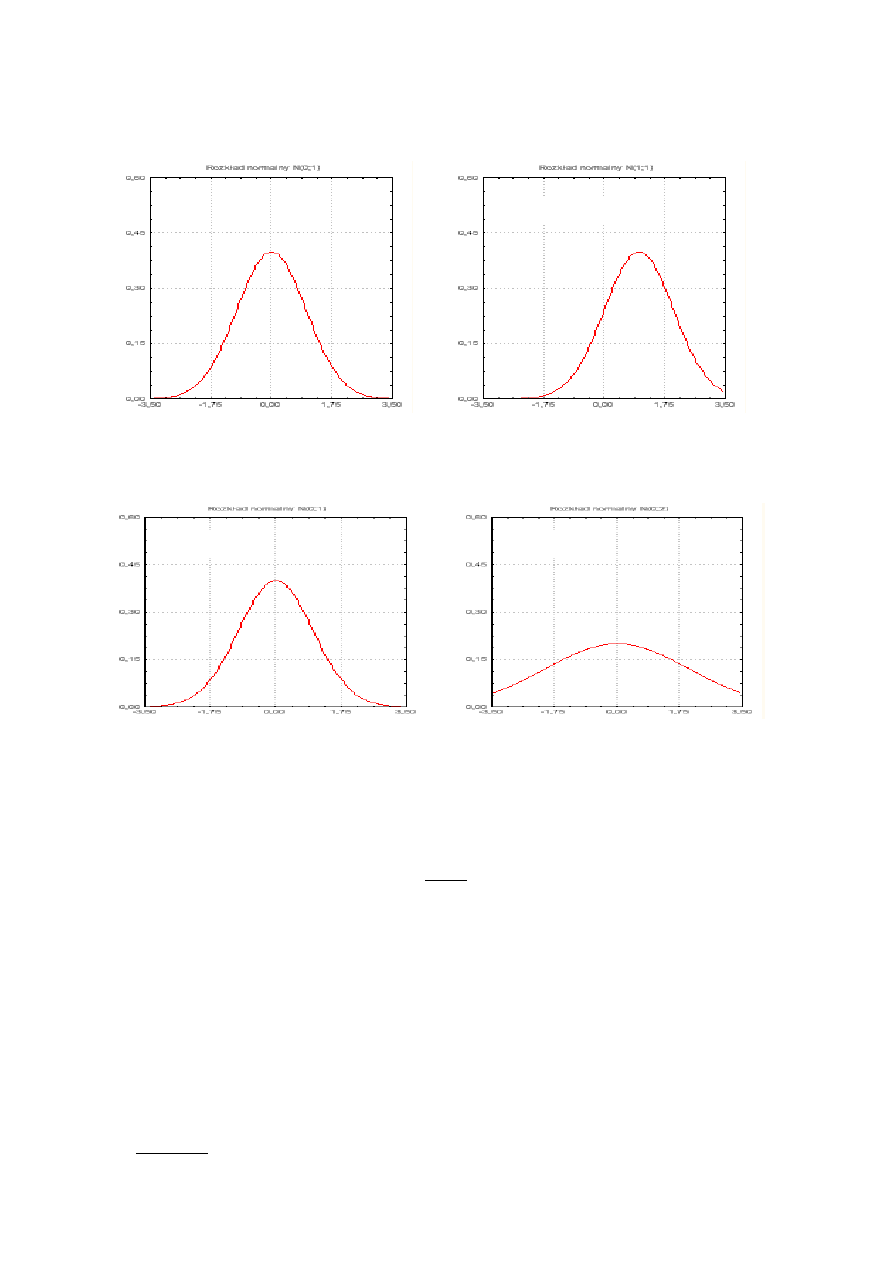
Rozkład normalny jest jednoznacznie określony przez swoje parametry. Dla różnych wartości parametrów

otrzymujemy różne krzywe. Na rysunku 2 przedstawione są rozkłady normalne o takim samym odchyleniu
standardowym, ale różnej średniej, a na rysunku 3 rozkłady normalne o takiej samej średniej, ale o różnym odchyleniu
standardowym.

Krzywa Gaussa N(

µ;σ)

Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

Rys.2. Krzywe normalne o różnej średniej i takim samym odchyleniu standardowym - N(0;1) oraz N(1; 1)

Rys.3. Krzywe normalne o takiej samej średniej i różnym odchyleniu standardowym -N(0; 1) oraz N(0; 2)

Rozkład normalny standaryzowany

Rozkładem normalnym standaryzowanym nazywany jest rozkład normalny o parametrach

µ

= 0 oraz

σ

= 1.

Wartości zmiennej losowej o rozkładzie normalnym N(

µ

,

σ

), można zawsze przekształcić na wartości standaryzowane,

czyli wartości zmiennej losowej o rozkładzie N(0; 1) według zależności:

σ

µ

−

=

x

z

, gdzie

z – wartość standaryzowana zmiennej losowej
x – wartość zmiennej losowej o rozkładzie N(

µ

,

σ

).

W zastosowaniach praktycznych często wygodnie jest operować wynikami standaryzowanymi. Na przykład wtedy,

gdy zachodzi potrzeba porównania danych wyrażonych w różnych jednostkach miary, albo danych z rozkładów o
różnych parametrach.

Przykład:
Przypuśćmy, że uczeń uzyskał w skoku w dal wynik 550 cm, przy czym rozkład wyników skoku w dal w jego grupie

wiekowej jest N(520cm, 20cm). Ten sam uczeń w biegu na 60 metrów uzyskał czas 7,9s, przy czym rozkład wyników
biegu na 60 metrów w jego grupie wiekowej jest N(7,1s; 0,6s). Należy ocenić, w której z tych dyscyplin uczeń ów
uzyskuje lepsze wyniki.

Aby tego dokonać wystarczy porównać jego wyniki standaryzowane. Obliczamy wynik standaryzowany skoku w

dal:

5

,

1

20

520

550

=

−

=

z

N(0;1)

N(0;2)

N(0;1)

N(1;1)

Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

oraz wynik standaryzowany biegu na 60 metrów:

3

,

1

6

,

0

1

,

7

9

,

7

=

−

=

z

Uczeń, o którym mowa, w obu tych dyscyplinach osiąga wyniki powyżej średniej (średni wynik standaryzowany

wynosi 0), ale lepszy jest w skoku w dal.

Interpretacja pola pod krzywą rozkładu

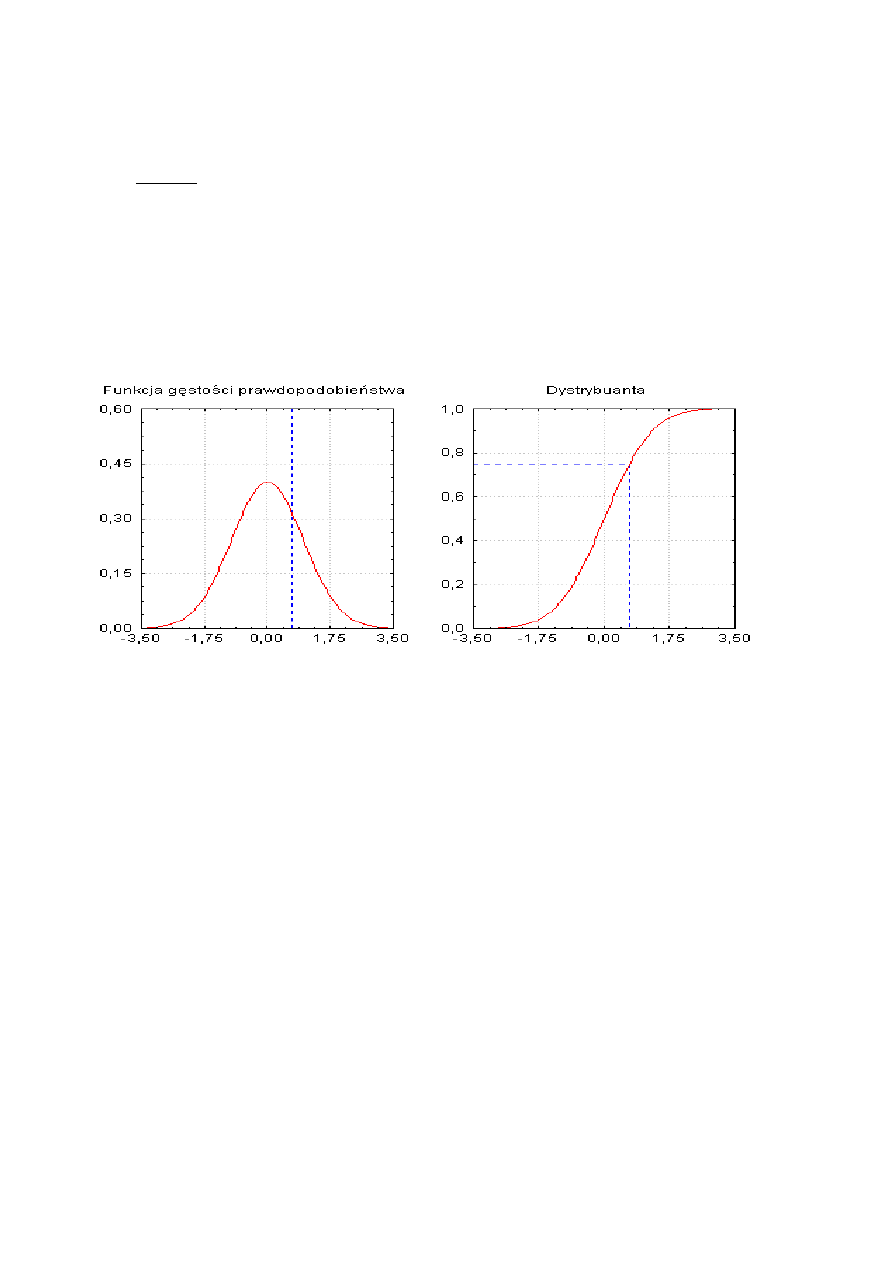
Pole powierzchni pod krzywą rozkładu określa prawdopodobieństwo realizacji określonego zdarzenia losowego.

I tak pole powierzchni na lewo od prostej wystawionej w punkcie x, równe jest prawdopodobieństwu zdarzenia, że
zmienna losowa X (której rozkład przedstawiony jest na rysunku 4) przyjmie wartość nie większą niż x. Pole to jest
zarazem równe wartości dystrybuanty w punkcie x.

x

x

Rys.4. Pole pod krzywą normalną a wartość dystrybuanty

W zastosowaniach praktycznych pole odpowiedniego obszaru pod krzywą rozkładu obliczamy, gdy chcemy uzyskać

odpowiedzi na pytania typu: jakie jest prawdopodobieństwo wylosowania z populacji (o znanym rozkładzie
analizowanej zmiennej) jednostki, która charakteryzuje się wartością tej zmiennej nie wyższą od danej, albo: jaką część
populacji stanowią jednostki, dla których zmienna nie przekracza określonej wartości.
Przykład: Rozkład wyników pewnego testu sprawności w populacji polskich szesnastolatków jest rozkładem normalnym
o średniej

µ

= 90 i odchyleniu standardowym

σ

= 10. Prawdopodobieństwo wylosowania szesnastolatka, którego wynik

w tym teście sprawności byłby nie wyższy niż 90 jest równe 0,5 (pole powierzchni pod krzywą rozkładu jest równe 1, a
prosta wystawiona w punkcie

µ

= 90, dzieli tę powierzchnię na dwie równe części z tej racji, że rozkład normalny jest

symetryczny). Inaczej: można się spodziewać, że spośród np. 100 losowo wybranych młodych ludzi z populacji
szesnastolatków, 50 uzyska w tym teście sprawności wynik nie wyższy niż 90. Jeszcze inaczej: można się spodziewać, że
50% populacji stanowi młodzież uzyskująca w tym teście wynik 90 lub niższy.

Skale standardowe

W badaniach właściwości człowieka stosowane są różne techniki i narzędzia badawcze. Powoduje to pewne

trudności przy analizie i porównywaniu otrzymanych danych. Wynik indywidualny uzyskany przy pomiarze danym
narzędziem (np. testem, kwestionariuszem) zależy bowiem nie tylko od własności osoby badanej lecz również od
własności zastosowanego narzędzia (np. liczby zadań lub pytań).

W celu ominięcia tych trudności dokonuje się pewnych przekształceń wyników surowych wykorzystujących

informację o rozkładzie tych wyników w większej grupie osób (zbiorowości statystycznej).

Jednym ze stosowanych przekształceń jest standaryzacja wyników surowych, poprzedzana często normalizacją

rozkładu empirycznego właściwości mierzonej danym narzędziem.

Standaryzacja indywidualnego wyniku surowego względem otrzymanego rozkładu empirycznego polega na

przekształceniu liniowym z = (x - M )/S, gdzie M jest średnią rozkładu wyników testu w zbiorowości, zaś S
odchyleniem standardowym tego rozkładu.

Rozkład wyników standaryzowanych jest rozkładem o średniej 0 i odchyleniu standardowym 1. Skośność i kurtoza

rozkładu wyników standaryzowanych są takie same jak rozkładu wyników surowych; przekształcenie liniowe bowiem

Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

(a takim przekształceniem jest standaryzacja według zależności z = (x - M )/S) nie zmienia „kształtu” rozkładu.
Zachowane zostaje też uporządkowanie wyników, tzn. jeżeli wynik surowy osoby A jest niższy niż osoby B, to również
wynik standaryzowany osoby A jest niższy niż wynik standaryzowany osoby B.

Przykład: Osoba A uzyskała w teście X liczącym 100 zadań wynik surowy 60 punktów, a w teście Y liczącym 25

zadań wynik 20 punktów. Oba testy mierzą różne właściwości i interesuje nas, w zakresie której z tych właściwości
osoba A uzyskała wyższy wynik względny, tzn. interesują nas jej wyniki, względem rozkładu empirycznego pomiarów
tych właściwości w grupie odniesienia, w której zastosowano test.

Przyjmijmy, że dla testu X średnia i odchylenie standardowe są równe M = 50 oraz S = 10, a dla testu Y

odpowiednio M = 12 oraz S = 4. Wówczas wynik standaryzowany uzyskany przez osobę A w teście X wynosi

z = (60 – 50)/10 = 1,00.
Wynik standaryzowany w teście Y zaś
z = (20-12)/4 = 2,00.
Możemy teraz stwierdzić, że osoba A wyższy względny wynik uzyskała w teście Y, co oznacza, że w zakresie

właściwości Y osoba ta sytuuje się wyżej na tle zbiorowości niż w zakresie właściwości X.

Względna pozycja osoby, jaką wyznacza wynik standaryzowany zależy całkowicie od postaci rozkładu badanej

właściwości w populacji. Jeżeli postać rozkładu nie jest znana, pozycja wyniku indywidualnego na tle populacji nie
może być dokładnie określona (nie możemy, na przykład, stwierdzić, jaki procent zbiorowości stanowią osoby o
wynikach niższych bądź wyższych). Z tego też powodu często przeprowadza się normalizację rozkładu otrzymanych
wyników.

Normalizacja rozkładu empirycznego polega na takim jego przekształceniu, aby rozkład przekształcony był

zbliżony jak najbardziej do rozkładu normalnego. Należy podkreślić, że normalizacja otrzymanego rozkładu
empirycznego danej właściwości ma sens jedynie wówczas, gdy zasadnym jest założenie o normalnym rozkładzie tej
właściwości w populacji.

Przekształcenie prowadzące do normalizacji zmienia skośność i kurtozę rozkładu empirycznego. Rozkład zmiennej

znormalizowanej ma własności takie same lub prawie takie same jak rozkład normalny, czyli jest symetryczny (lub
prawie symetryczny).

Po normalizacji rozkładu empirycznego wyniki surowe można przekształcić na wyniki wyrażone w jednostkach

jednej ze skal, które noszą wspólną nazwę skal znormalizowanych lub skal standardowych.

Podstawową skalą jest znormalizowana skala standardowa z, zwana skalą standardową z, lub krótko – skalą z

(jeżeli mówimy o skali standardowej zawsze odnosimy to pojęcie do skali zbudowanej na rozkładzie normalnym).

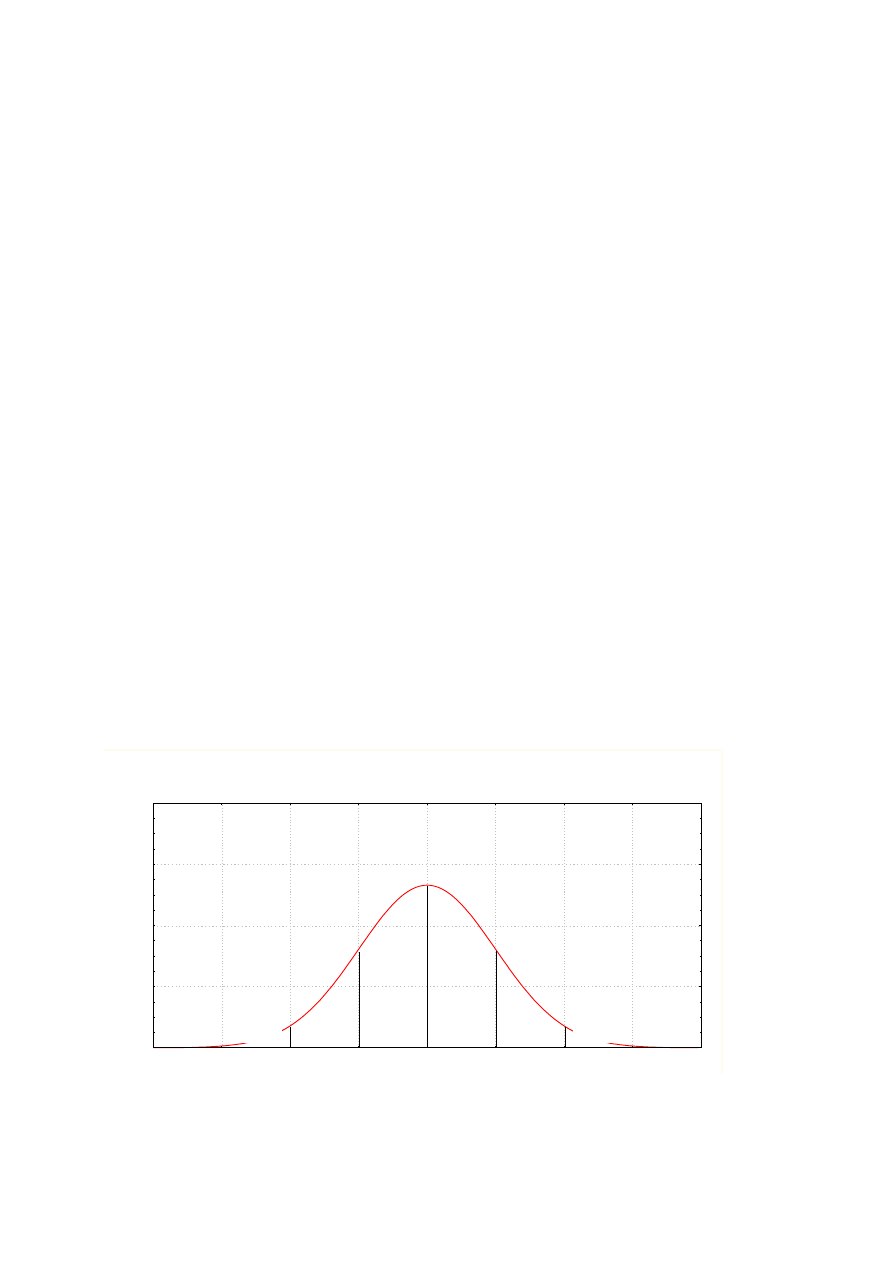
Rys.5. Rozkład normalny standaryzowany z zaznaczonymi wartościami pól pod krzywą rozkładu (podstawa skala z)

Na rysunku 5 przedstawiony jest rozkład normalny standaryzowany N(0,1) oraz wartości pól pod krzywą rozkładu

między wartościami różniącymi się o jedno odchylenie standardowe.

Wyrażenie wyniku surowego na skali standardowej umożliwia jego interpretację statystyczną wynikającą z

Funkcja gęstości prawdopodobieństwa

N(0,1)

0,00

0,15

0,30

0,45

0,60

-4

-3

-2

-1

0

1

2

3

4

0,341

0,341

0,136

0,136

0,021

0,021

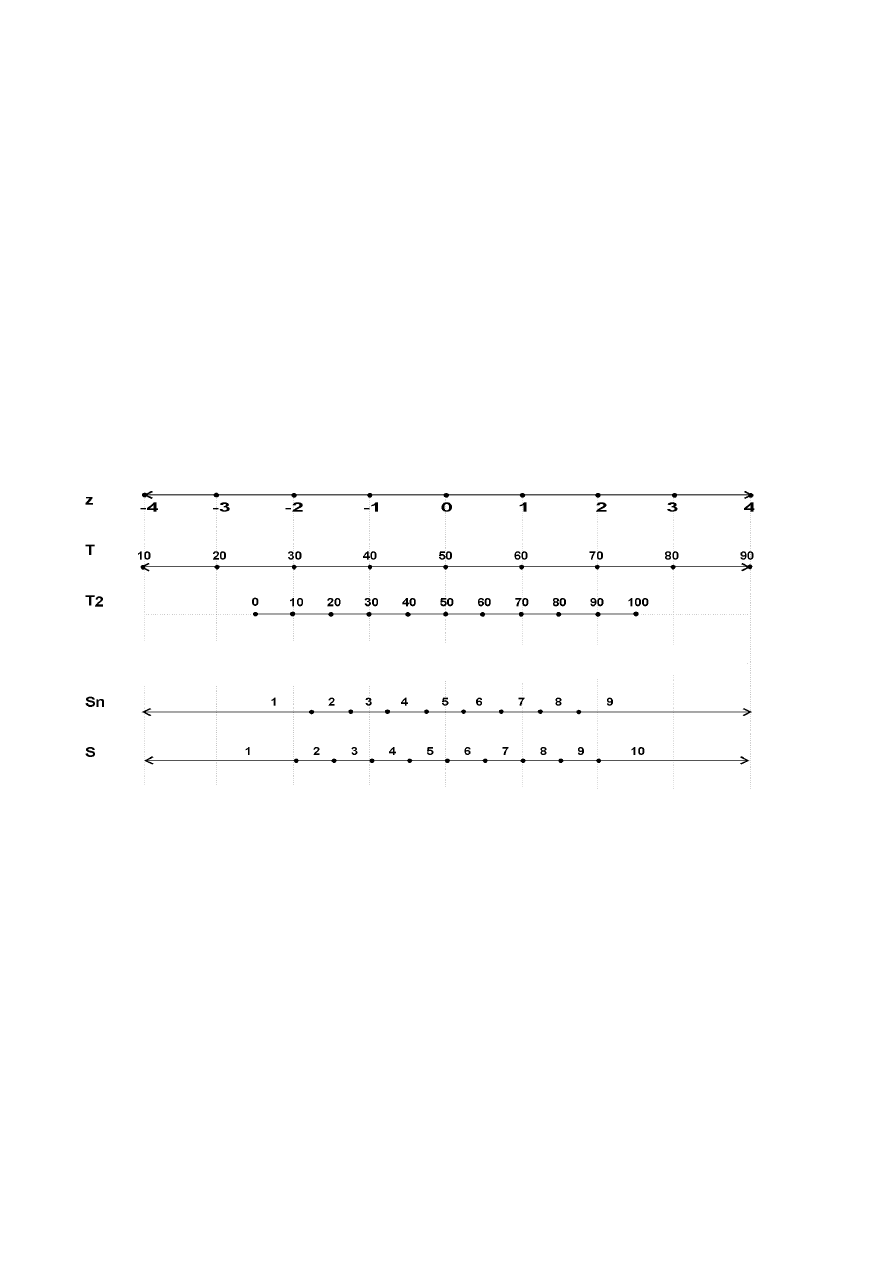
Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

własności rozkładu normalnego. Na przykład:

Pole pod krzywą między wartościami –1 a +1, czyli obszar odpowiadający wartościom różniącym się od średniej

nie więcej niż jedno odchylenie standardowe jest równe 0,68, co stanowi ok. 2/3 całego pola pod krzywą (nazywany
jest on obszarem wartości typowych). Można się zatem spodziewać, że ok.2/3 populacji stanowią osoby, których wynik
w teście (dla którego to testu przeprowadzono standaryzację) różni się od wyniku średniego nie więcej niż jedno
odchylenie standardowe. Albo inaczej: można się spodziewać, że na trzy losowo wybrane osoby 2 osiągną wynik nie
różniący się od średniej więcej niż o jedno odchylenie standardowe.

Oprócz podstawowej skali standardowej z stosowane są również skale standardowe punktowe, takie jak:

skala T, 100-punktowa, z jednostką równą 0,1 jednostki skali z (jest liniowym przekształceniem skali z według

zależności T = 50 + 10z ),

skala T

2

, 100-punktowa, z jednostką równą 0,2 jednostki skali z (jest liniowym przekształceniem skali z według

zależności T

2

= 50 + 20z),

oraz skale standardowe przedziałowe, takie jak:

skala staninowa Sn (standard nine), obejmująca 9 przedziałów równych 0,5 jednostki skali z,
skala stenowa S (standard ten), obejmująca 10 przedziałów równych 0,5 jednostki skali z.

Porównanie wymienionych skal z podstawową skalą standardową przedstawione jest na rysunku 6.

Rys.6. Podstawowa skala standardowa z a skale punktowe T i T

2

oraz skale przedziałowe Sn (staninowa) i S

(stenowa)

Źródło: Z.M.Zimny (red.); Pomiar dydaktyczny..., s.68

Statystyka w badaniach. Rozkład normalny

Urszula Augustyńska

Ćwiczenia i zadania

1. Symbol N(μ; σ) oznacza rozkład normalny o średniej μ i odchyleniu standardowym σ.
Naszkicuj wykres rozkładu normalnego N(4 ; 1), N(-2 ; 2), N(0 ;1).

2. Oblicz jakie wartości standaryzowane odpowiadają wartościom danych surowych pochodzących z rozkładu
normalnego N(15; 5):
a) x = 15

b) x = 15,5

c) x = 12

d) x = 10,5

3. Oblicz jakie wartości danych surowych dla rozkładu normalnego o średniej 30 i odchyleniu standardowym 3,
odpowiadają następującym wartościom danych standaryzowanych:
a) z = 1,4 b) z = 2,5 c) z = - 1,5 d) z = - 0,68

4. Jakie są wartości średniej i odchylenia standardowego dla rozkładu normalnego, w którym danym surowym
wynoszącym 45 punktów i 60 punktów odpowiadają dane standaryzowane
-1 oraz 2 ?

5. Rozkład normalny zmiennej losowej ma średnią 21 i odchylenie standardowe 3. Znajdź prawdopodobieństwo tego,
że zmienna losowa przyjmie:
a) wartość większą niż 21
b) wartość mniejszą niż 21
c) wartość większą niż 24
d) wartość mniejszą niż 24
e) wartość większą niż 18
f) wartość mniejszą niż 18
g) wartość większą niż 27
h) wartość mniejszą niż 12

6. Jeżeli wzrost 1000 studentów spełnia warunki rozkładu normalnego o średniej 174 cm i odchyleniu standardowym 6
cm, to ilu studentów tej grupy ma wzrost co najmniej 180 cm?

7. W populacji kobiet 20% ma wzrost powyżej 165 cm. Znajdź średnią rozkładu wzrostu jeżeli wiadomo, że odchylenie
standardowe wynosi 6 cm.