Rozkłady zmiennych losowych

Rozkład normalny

Rozkład normalny (rozkład Gaussa) jest rozkładem, któremu podlega wiele zjawisk świata fizycznego, np. waga oraz wzrost populacji ludzi.

Zmienna losowa X ma rozkład normalny z wartością oczekiwaną równą m i odchyleniem standardowym równym σ
, jeśli jej funkcja gęstości ma następującą postać:

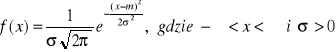
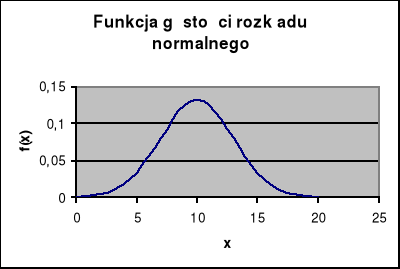
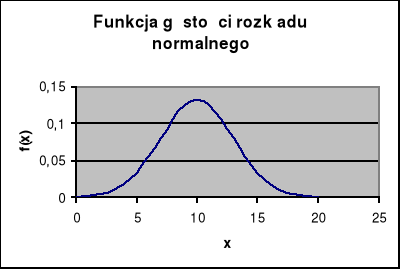
Wykres funkcji gęstości rozkładu normalnego określany jest jako krzywa normalna, która przyjmuje następującą postać:

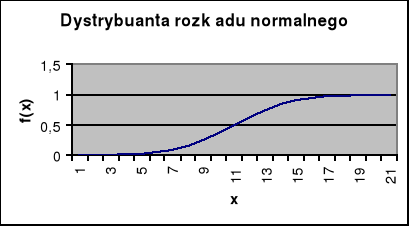
Dystrybuanta rozkładu normalnego ma postać:

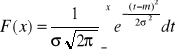
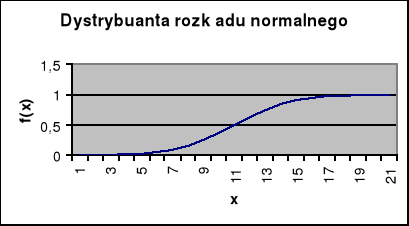
Wykres dystrybuanty zmiennej losowej
przyjmuje następującą postać:

Wartość oczekiwana i wariancja dla rozkładu normalnego wyrażane są następującymi wzorami:

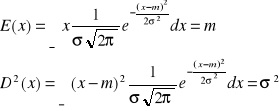
Parametr m oznacza średnią zmiennej losowej X o rozkładzie normalnym, natomiast parametr σ oznacza jej odchylenie standardowe.

Krzywa gęstości rozkładu normalnego ma następujące własności:

• jest symetryczna względem prostej x = m,

• osiąga maksimum równe
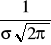
  dla x = m,

• jej ramiona mają punkty przegięcia dla x = m - σ oraz x = m + σ.

Wartość parametru m decyduje o położeniu krzywej normalnej względem osi x. Im średnia przyjmuje większe wartości, tym krzywa jest bardziej przesunięta w prawo. Wartość parametru σ determinuje natomiast „smukłość” krzywej. Im odchylenie standardowe jest większe, tym krzywa jest bardziej spłaszczona.

Możliwość sprowadzenia dowolnego rozkładu normalnego do postaci standardowego rozkładu normalnego, którego funkcja gęstości i dystrybuanta zostały stablicowane. Standardowym rozkładem normalnym nazywamy rozkład normalny ze średnią równą 0 oraz odchyleniem standardowym równym 1 i oznaczamy N(0,1).

Zmienną losową, która ma standardowy rozkład normalny oznacza się literą U, jej funkcję gęstości φ(u), natomiast dystrybuantę Φ(u).

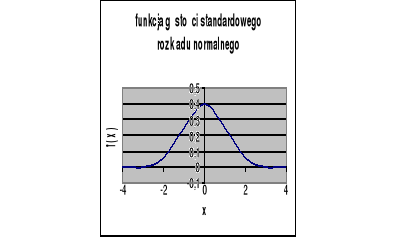
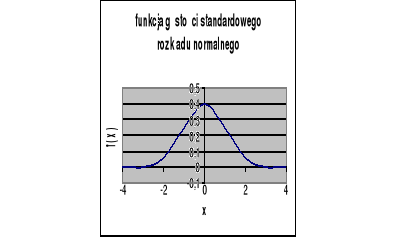
Wykres funkcji gęstości standardowego rozkładu normalnego przyjmuje następującą postać:

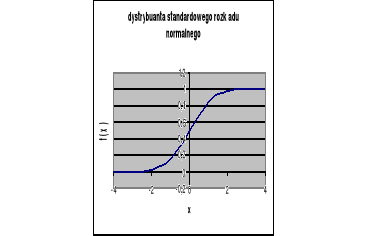
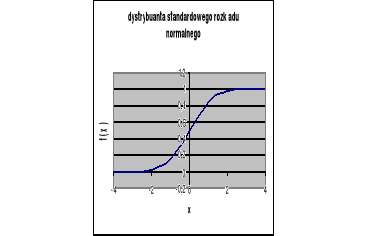
Wykres dystrybuanty standardowego rozkładu normalnego przyjmuje postać:

Dystrybuanta standardowego rozkładu normalnego charakteryzuje się następującymi własnościami:

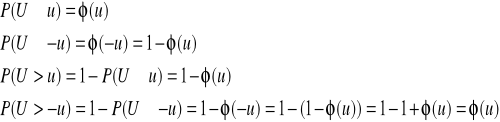
Ze względu na fakt, iż w tablicach najczęściej podawane są wartości tylko dla dodatnich u, przy wyznaczaniu wartości dla ujemnych u należy skorzystać z następujących własności funkcji φ(u) i Φ(u):

W celu obliczenia prawdopodobieństwa P(a < X ≤ b) należy skorzystać z operacji nazywanej standaryzacją. Jeśli zmienna losowa X ma rozkład
to zmienna standaryzowana
ma rozkład N(0,1). Na tej podstawie można wyznaczyć:

Wartości
i
odczytuje się z tablic dystrybuanty standardowego rozkładu normalnego.

Z rozkładem normalnym związana jest tzw. reguła trzech sigm, zgodnie z którą praktycznie wszystkie obserwacje dokonywane na zmiennej losowej o rozkładzie normalnym mieszczą się w przedziale (m-3σ, m+3σ). Reguła trzech sigm jest wykorzystywana w badaniach statystycznych do eliminacji obserwacji niewiarygodnych. Obserwacje niewiarygodne to obserwacje, których wartość różni się od średniej o więcej niż trzy odchylenia standardowe. Przyjmuje się, iż zmienne, które odbiegają tak znacznie od średniej mogą być skutkiem błędu pomiaru. Dla realizacji zmiennej losowej o dowolnym rozkładzie normalnym około 68,3% obserwacji mieści się w granicach jednego odchylenia standardowego wokół średniej, 95,5% obserwacji mieści się w granicach dwóch odchyleń standardowych i 99,7% w granicach trzech odchyleń standardowych.

---