Struktura

pasmowa ciał

stałych

 opis struktury elektronowej
 pasma energetyczne
 masa efektywna elektronu i
dziury

Wykład – 10 -

2

Prof. J. Zieliński

 

Terminy zaliczeń poprawkowych w semestrze letnim
2010/11
o 28 marzec

o 18 kwiecień

o 16 maj

o 13 czerwiec

Przypominam, że

Przypominam, że

 na wszystkie kolejne terminy poprawkowe
obowiązują karty zie-lone.

 Do zaliczenia można podejść po zaliczeniu ćwiczeń
rachunko-wych

 zaliczona w terminie zerowym teoria a nie wpisana

zaliczona w terminie zerowym teoria a nie wpisana

do indeksu została skreślona

do indeksu została skreślona

Zaliczenia zaczynają się o
godz. 15
sala 2 bud 5

W tym semestrze

Zaliczenie przedmiotu jest w formie egzaminu

> Aby móc przystąpić do egzaminu trzeba mieć
zaliczone ćwicze-nia i laboratoria. Pozytywne oceny
muszą być wpisane do karty o-cen i do indeksu.

Egzamin składa się z dwóch części:

- Pisemnej student pisze odpowiedź na 3 pytania z
zestawu 4-ech

- Ustnej odpowiedzi uzupełniające na pytania z
zestawu pisemne-go + inne pytania.

Właściwości elektronów w ciałach stałych

wynikają z ich oddziaływania między sobą i
oddziaływania z atomami (jonami) sieci. Jednakże
każde z tych oddziaływań jest skomplikowane.
Wystarczy sobie bowiem uświadomić, że w 1 cm

3

ciała stałego znajduje się około 10

23

elektronów i

jonów będących w ciągłym ruchu i oddziaływujących
na siebie.

W

celu

prześledzenia

wpływu

pola

elektrycznego na pozio-my energetyczne elektronów
w atomie, rozpatrzymy następujący wyidealizowany
przykład, który pozwala w sposób jakościowy zro-
zumieć zachodzące zjawiska. Rozmieścimy N atomów
sodu w wę-złach sieci przestrzennej odpowiadającej
kryształowi sodu, ale w tak dużych odległościach aby
można było pominąć ich wzajemne oddziaływanie. W
takim przypadku stany energetyczne elektronów będą
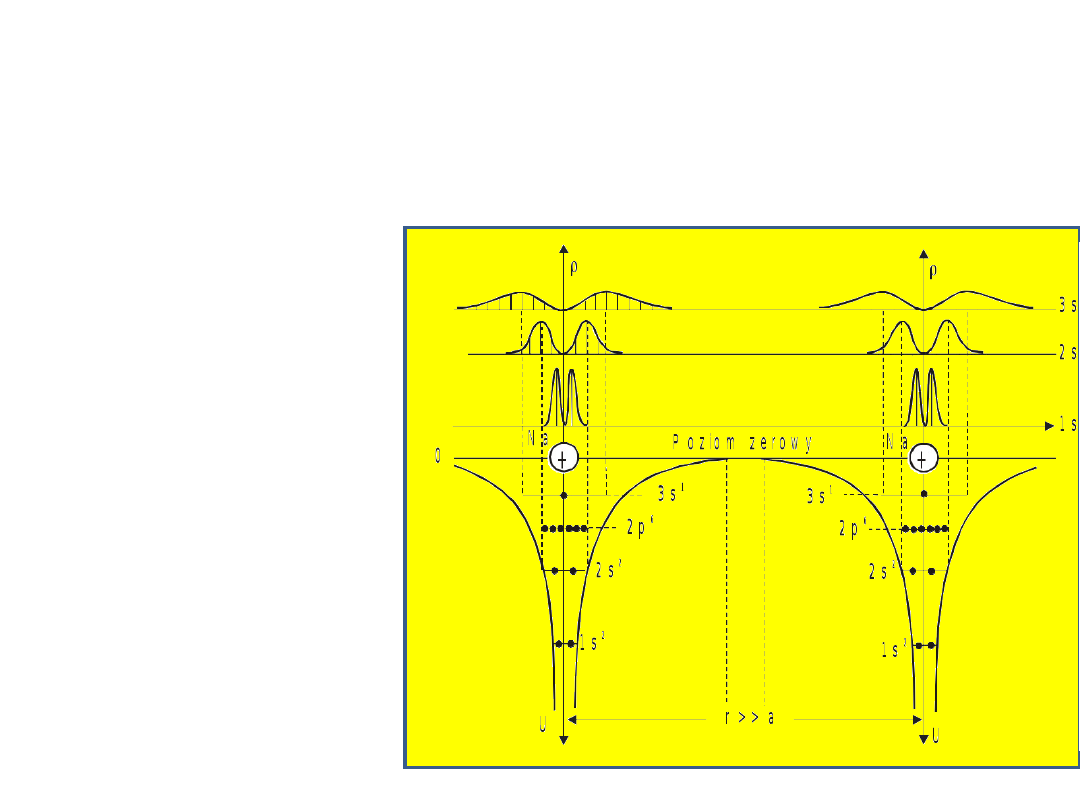
odpowiadały stanom atomu izolowanego. Na rys.
16.1a pokazano schemat poziomów energetycznych
dwóch izolowanych atomów sodu.

Izolowane (swobodne)

atomy sodu (Na)

• w atomie swobodnym

każdy poziom jest
2(2l+1)

krotnie

zdegenerowany

• dla N atomów liczba

pod-poziomów wynosi
2N(2l+1)

• bariera potencjału nie

ze-zwala elektronom
swo-bodnie poruszać
się mię-zy atomami

• elektrony

są

zlokalizowa-ne,
funkcje falowe nie za-
chodzą na siebie

W atomie tym jak wiadomo, poziomy

energetyczne 1s, 2s i 2p są zapełnione całkowicie, a
poziomy rozmieszczone powyżej 3s są wolne.

Zauważmy, że bariera potencjału nie pozwala
elektronom poruszać się swobodnie między
poszczególnymi atomami.

Poddajemy

teraz

sieć

jednorodnemu

ściskaniu

. W miarę zbliżania się atomów do siebie,

wzrasta ich oddziaływanie i w odległościach równych
parametrowi sieci (a = 0,43 nm) energia
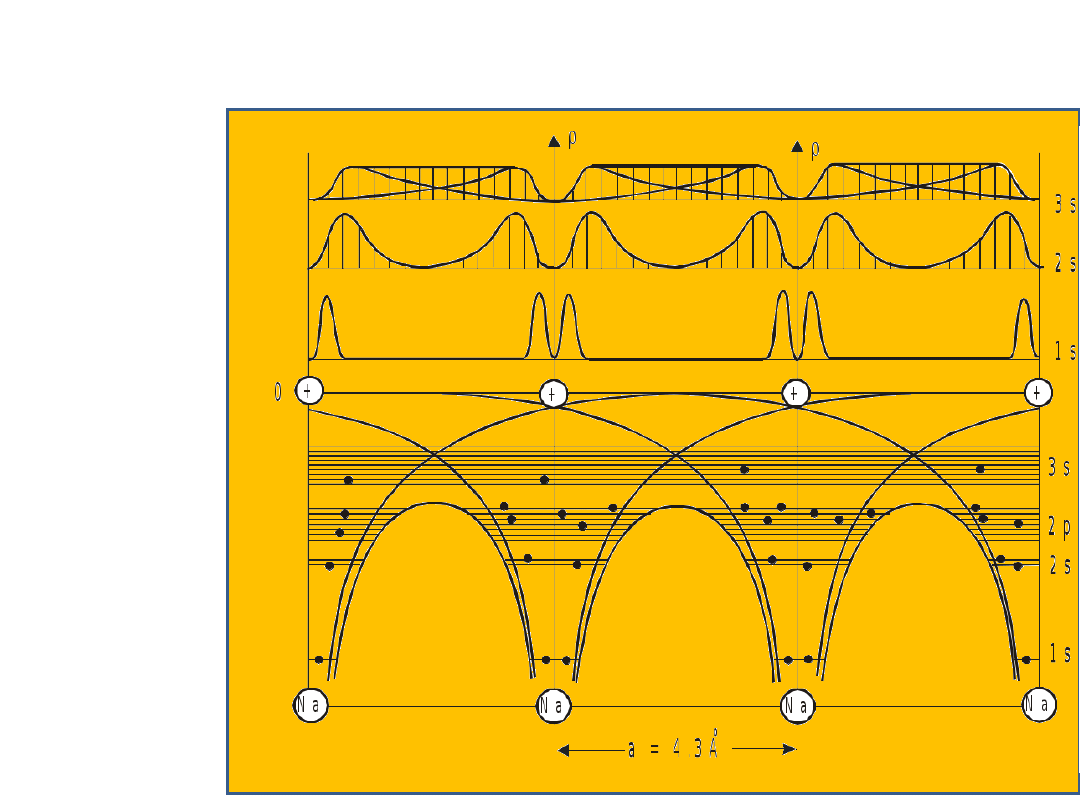
oddziaływania osiąga wartość minimalną. Na rys.
16.1b pokazano schemat poziomów energetycznych
elektronów

odpowiadający

zbliżeniu

atomów.

Widzimy,

że

krzywe

potencjalne

oddzielające

sąsiednie atomy częściowo zachodzą na siebie dając
wypadkową krzywą potencjalną, która przebiega
poniżej poziomu zerowego. Godnym uwagi jest fakt,
że wysokość ta jest nawet nieco mniejsza od
początkowego

położenia

poziomu

elektronów

walencyjnych 3s. Dlatego też elektrony walencyjne
uzyskują możliwość przechodzenia z jednego atomu
do

drugiego.

Elektrony

takie

nazywamy

swobodnymi

Zmiana stanu elektronów

przy zbliżaniu się atomów

•

obniżenie poziomu potencjału
poniżej stanu 3s

•

elektrony 3s stają się
swobodne

•

funkcje falowe tych
elektronów zachodzą na
siebie

•

funkcje falowe elektronów
wewnętrznych nie ulegają
zmianie

•

pojedyncze poziomy ulegają
rozszczepieniu tworząc pasmo

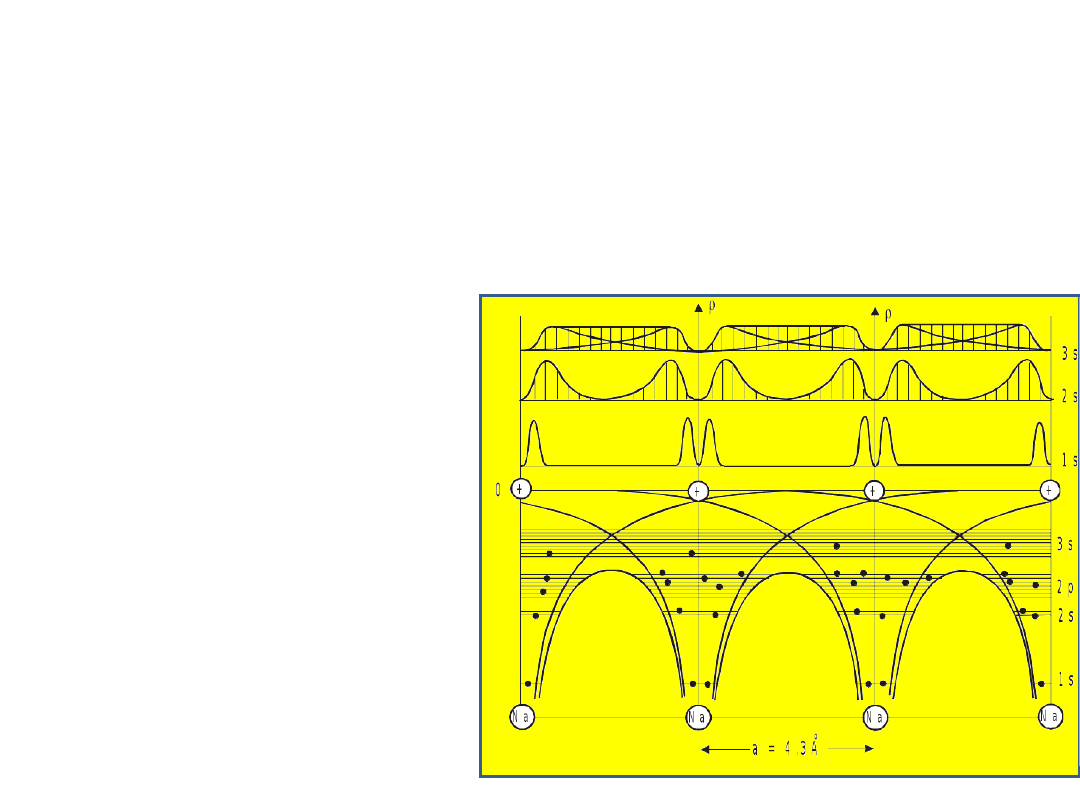
Przy odległościach równych stałej sieci 0,43 nm
otrzymujemy:

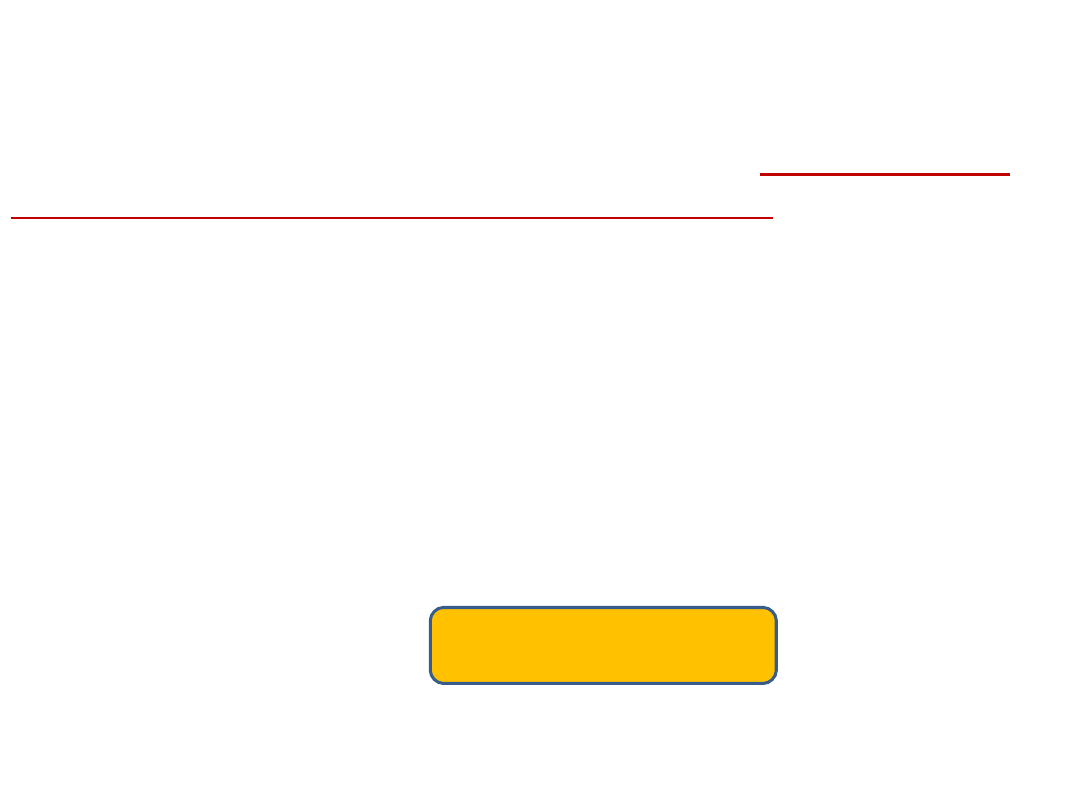
Zauważmy, że charakter funkcji falowych tych

elektronów jest taki, że zachodzą one na siebie w
takim stopniu, że tworzą chmurę o prawie
równomiernej gęstości, a to oznacza

stan pełnego

uwspólnienia elektronów walencyjnych

. Natomiast

chmury

elektro-nowe

wewnętrznych

powłok

elektronowych atomów nie pokrywają się i stany
elektronów wewnętrznych atomów kryształu pozostają
w zasadzie takie same jak w atomach izolowanych.
Należy ponadto zauważyć, że pojedyncze poziomy
atomowe uległy rozszczepieniu na zespoły poziomów
zwanych dozwolonymi pasmami energetycznymi.

Ponieważ prędkość ruchu elektronu jest rzędu 10

5

m/s, a

rozmiary ato-mu wynoszą 10

–10

m, to elektron

walencyjny znajduje się w danym wę-źle w czasie Δt =
10

–15

s co powoduje, że szerokość poziomu energe-

tycznego elektronu walencyjnego ΔE jest w przybliżeniu
równa .

eV

t

/

h

E

1









Jeżeli

poziomy

energetyczne

w

atomie

swobodnym były (2l+1) -krotnie zdegenerowane (bez
uwzględnienia spinu), to odpowiada-jące im pasma
energetyczne będą miały N(2l+1) podpoziomów (N –
ilość atomów); np. z poziomu p wytworzy się pasmo
składające się z 3N podpoziomów mogących zmieścić
6N elektronów. Jeżeli dalej uwzględnimy, że 1 g ciała
stałego zawiera N = 10

22

atomów i że każdy pojedynczy

poziom energetyczny rozpada się na N poziomów, to
przy szerokości pasma rzędu 1 eV odległości między
poziomami wynoszą około 10

–22

eV, co wskazuje, że nie

ma możliwości doświadczalnego ich rozróżnienia. O
takiej właśnie grupie poziomów mówimy jako o paśmie
dozwolonym uważając, że elektrony w tym paśmie
mają ciągły rozkład energii. Pasma te są rozdzielone
pasmami wzbronio-nymi.

Wyniki poglądowo przedstawione powyżej

uzyskuje

się

również

rozwiązując

kwantowo-

mechaniczne zagadnienia ruchu wielu elektronów w
polu ruchu jonów. Złożoność tego zagadnienia zmusza
nas do wprowadzenia szeregu uproszczeń. Dlatego
analizu-jąc zachowanie elektronów w sieci stosujemy
wiele

przybliżeń.

Dwoma

skrajnymi

przeciwstawnymi przybliżeniami są: przybliże-
nie

elektronów

prawie

swobodnych

i

przybliżenie elektronów silnie związanych

. W obu

tych przypadkach otrzymujemy zakresy energii
dozwolonych i zabronionych dla elektronów. Kształt
pasm energetycznych i ich zapełnienie przez elektrony
jest jednym z najpoważniejszych zagadnień w fizyce
ciała stałego.

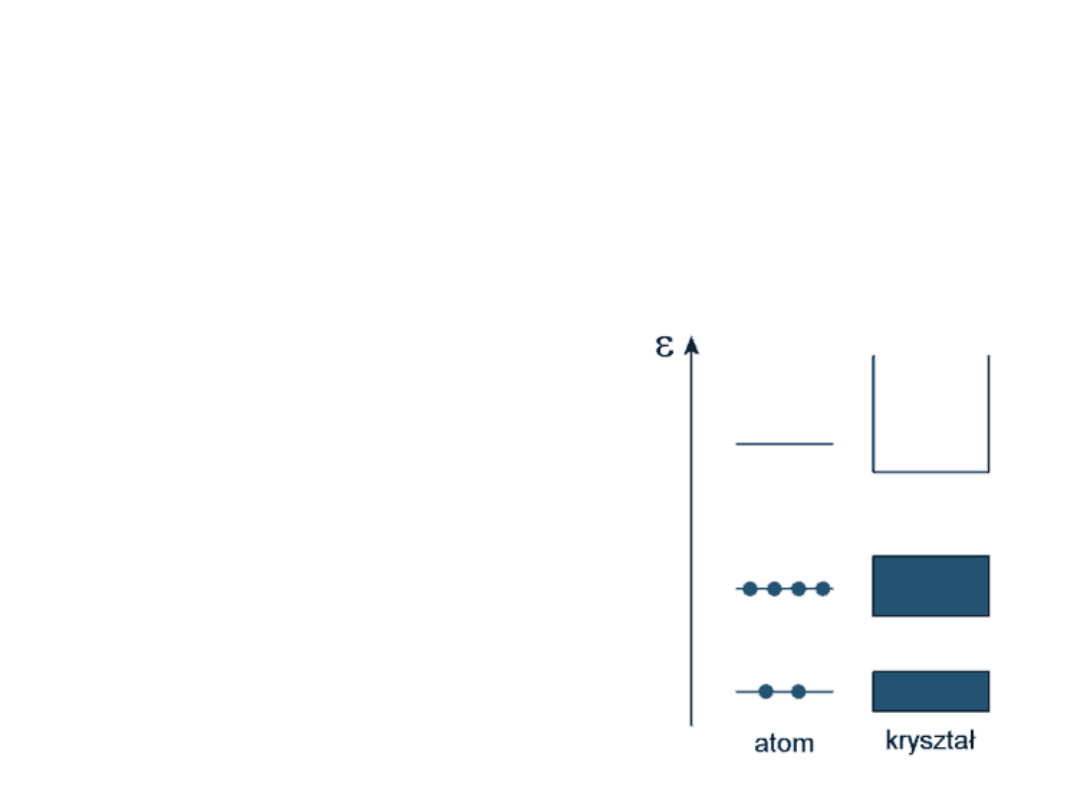
Co to jest teoria pasmowa

Teoria pasmowa jest kwantowo-
mechanicznym opisem zachowania
elektronów w krystalicznym ciele stałym

.

Nazwa

teoria

pasmowa

pochodzi od najważniejszej
cechy widma energety-cznego
w krysztale:

w

przeciwieństwie

do

dyskretnych

poziomów

dla

izolowanych atomów, widmo
energetyczne kryształu chara-
kteryzują

pasma

energii

dozwolonych

o

skończonej

szerokości

Równanie Schrodingera

Przyjęcie wspólnego potencjału U(r) umożliwia opis
stanów

ele-ktronowych

przy

pomocy

jedno-

elektronowych funkcji falo-wych.  Postać funkcji
falowych



i wartości własne energii E uzyskuje się

z rozwiązania równanie Schrödingera, które w przy-
padku jednowymiarowym ma znaną nam postać

Podstawą teorii pasmowej jest założenie, że
oddziaływania elektro-nów w ciele stałym można
opisać przy pomocy periodycznego po-tencjału U(r),
który nie zmienia się w wyniku przesunięcia o wektor
sieciowy R = n

1

a + n

2

b + n

3

c

U(r + R) = U(

r

)

 





0

2

2

2

2











x

U

E

m

dx

d



U(x + a) = U

(x)

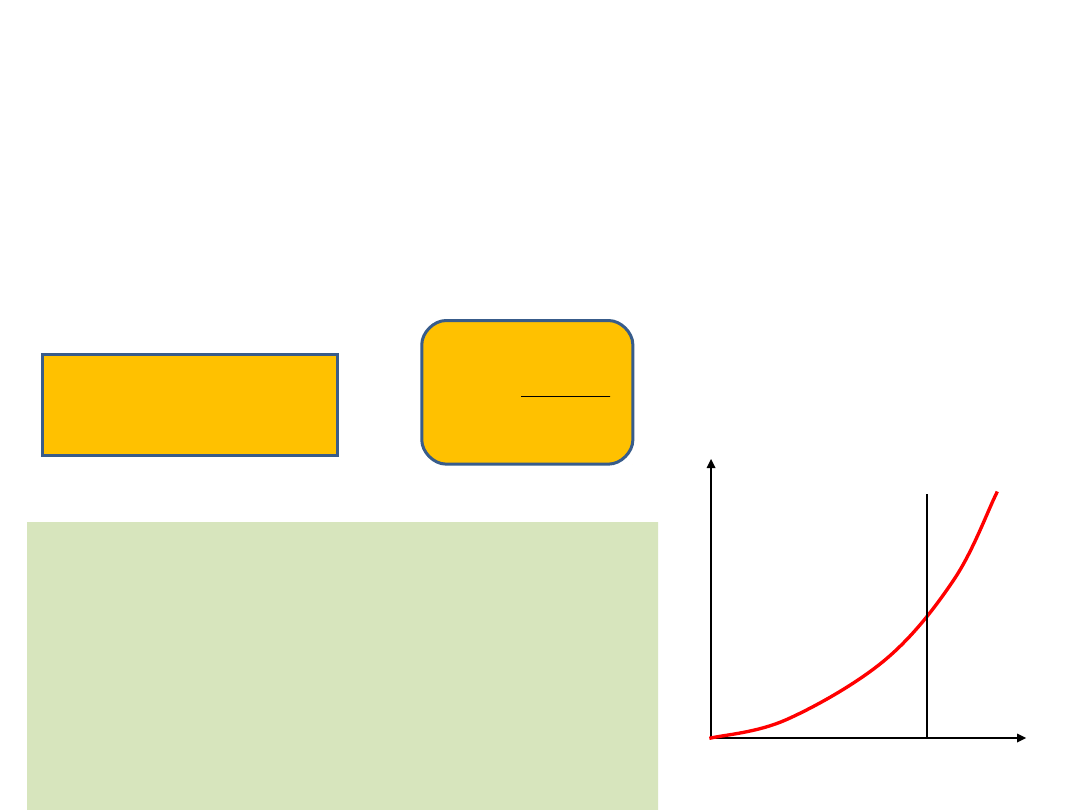
Model elektronów

swobodnych

m

k

E

2

2

2





E(k)

/a

k

Jedyne ograniczenie ruchu elektronów swobodnych jest
spowodowane

przez

powierzchnię

kryształu.

Z

równania Schrödingera wynika, że za-leżność energii od
wektora falowego jest quasi-ciągłą funkcją parabo-
liczną

Elektron praktycznie
może przyj-mować
dowolne wartości energii,
jedynie obsadzanie
stanów ener-getycznych
odbywa się zgodnie z
zakazem Pauliego

 

ikx

Ae

x 



Wady modelu elektronów

swobodnych

• przyjęcie stałego potencjału w

modelu elektronów swobodnych

nie

uwzglę-dnia

dyskretnej

struktury krystalicznej ciał stałych

• istotny wpływ na zachowanie

elektro-nów

odgrywa

ich

oddziaływanie z jonami sieci

• brak również uwzględnienia oddzia-

ływania elektronów pomiędzy sobą

• oba typy oddziaływań można

rozdzielić stosując różne rodzaje

przybliżeń:

jednoelektronowe,

elektronów prawie swobodnych lub

silnie związanych

E

x

0





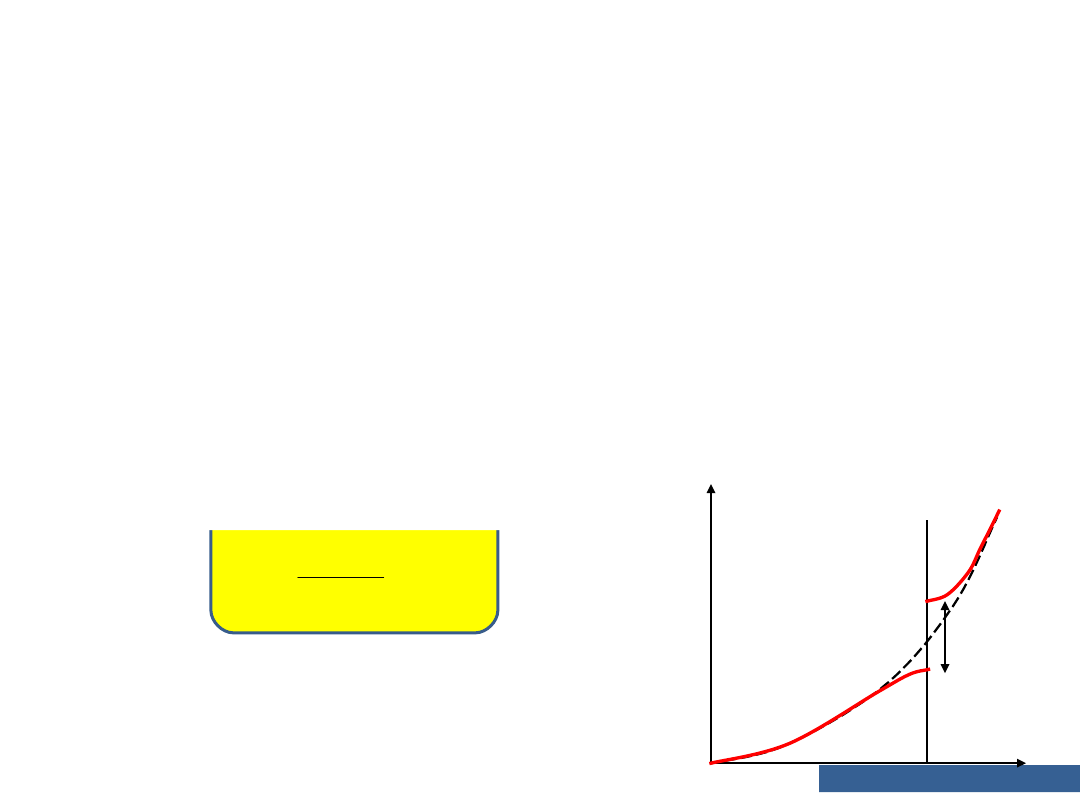
Przybliżenie elektronów

prawie swobodnych

Z rozwiązania równania Schrodingera wynika, że
energia elektro-nów o wektorach falowych leżących
na granicy tzw. strefy Bril-louina może przybierać
dwie wartości różniące się o 2V

g

– prowa-dzi to do

powstania nieciągłości energii

g

V

m

k

E





2

2

2



E(k)

/a

k

2V

g

Fale o tych wektorach falowych
ulegają całkowitemu odbiciu i nie
mogą rozcho-dzić się w krysztale -
powstaje fala stojąca.

Zakładamy, że potencjał U(r) działający na elektrony
poruszające się w krysztale jest tak mały, że można
potraktować go jako małe zaburzenie

W przybliżeniu elektronów słabo związanych
zakładamy, że energia oddziaływania elektronu z
siecią jest znacznie mniejsza od energii ki-netycznej.
Sytuacja taka ma miejsce w przypadku elektronów
najsła-biej związanych z atomami, czyli elektronów
przewodnictwa

w

meta-lach.

Pole

elektryczne

wytworzone przez jony jest kompensowane przez pole
wszystkich

pozostałych

elektronów

oprócz

rozpatrywane-go. Niewielkie, nieskompensowane pole
ma charakter okresowy o okresie równym stałej sieci. Z
okresowości tej wynika, że funkcja falo-wa opisująca
stan elektronu będzie funkcją Blocha.

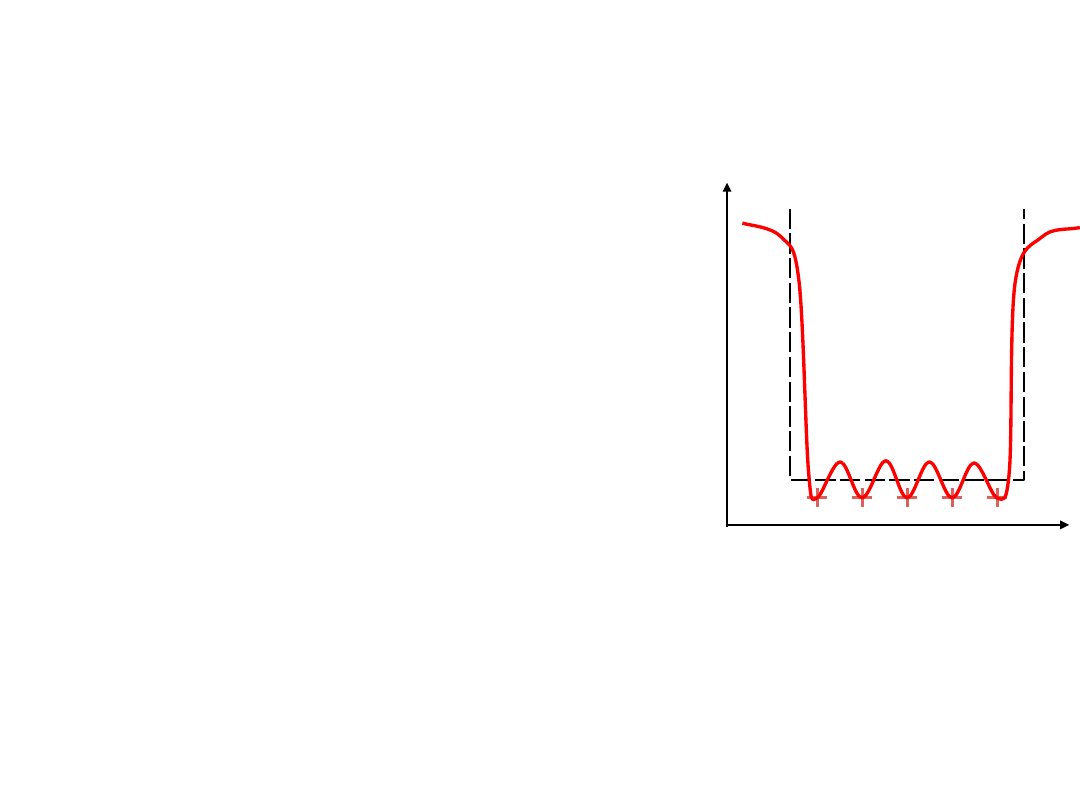
Aby

opisać

ruch

elektronu

w

polu

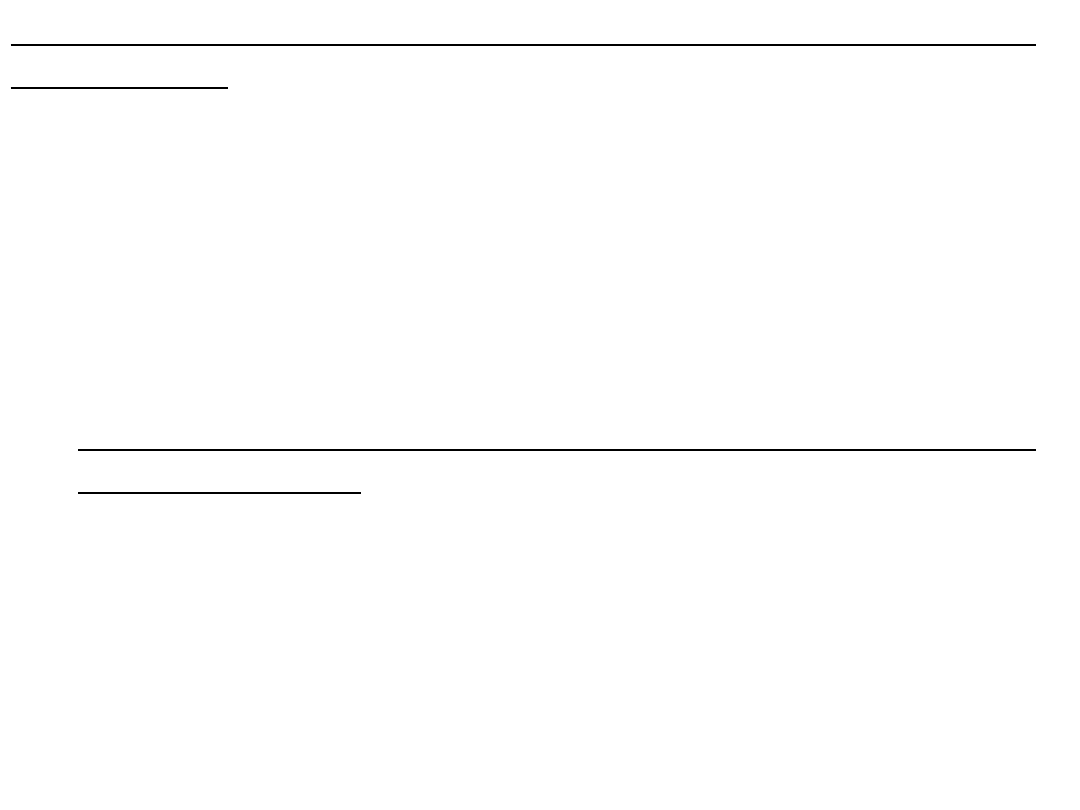
periodycznym, posłużymy się modelem Kröniga-
Penneya. W modelu tym potencjał rzeczywisty w
krysztale zastępujemy przez nieskończoną liczbę
prostokątnych barier potencjalnych o szerokości b i
wysokości U

o

. Studnia poten-cjału oddzielająca

bariery ma szerokość a i energię U

o

rys

Potencjał ten odtwarza wprawdzie w niewielkim
stopniu warunki występujące w krysztale, jednak
uzyskane

rozwiązanie

umożliwia

sformułowanie

pewnych ogólnych wniosków dotyczących zależności
dyspersyjnej dla elektronu w ośrodku periodycznym.
Potencjał jest więc okresowy o okresie d = a + b.
Zakładamy, że energia całkowita elektronu E < U

o

.

Równanie Schrödingera ma postać

0

2

2

2

2









E

m

dx

d







0

2

2

2

2











E

U

m

dx

d

o



dla 0 < x < a

dla –b < x < 0

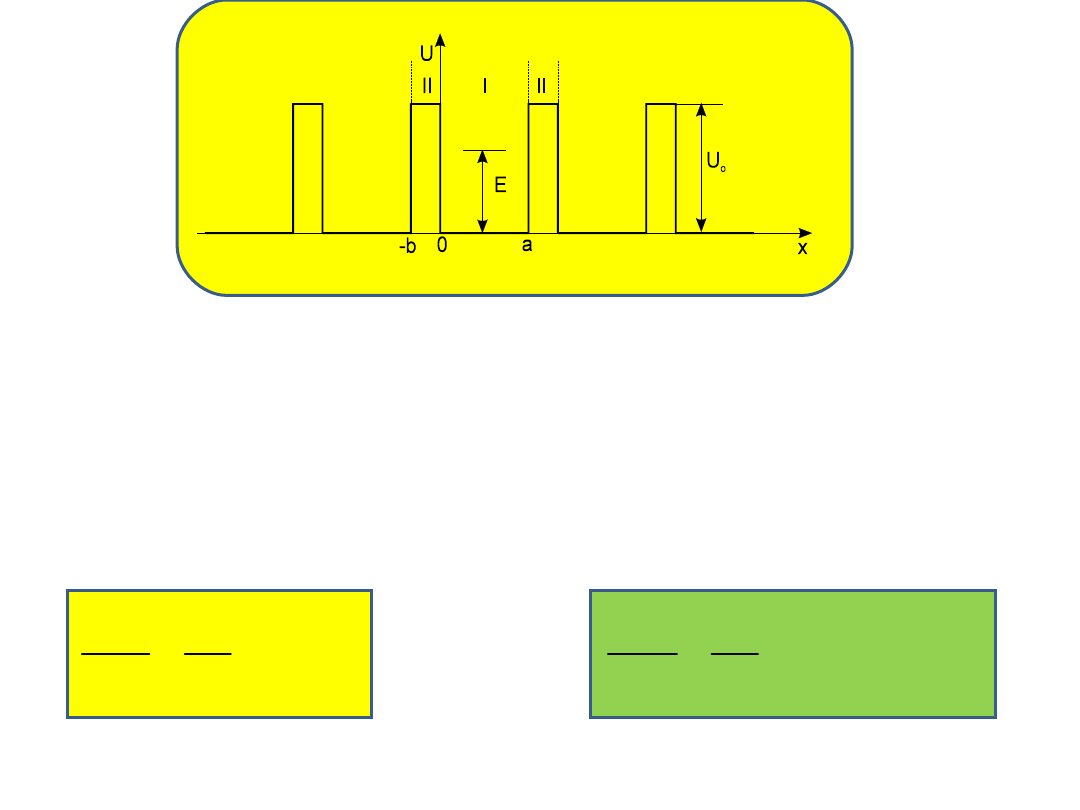
Rozwiązaniem powyższych równań są funkcje

x

i

x

i

e

B

e

A













1

1

1

x

x

e

B

e

A













2

2

2

dla 0 < x < a

dla –b < x < 0,

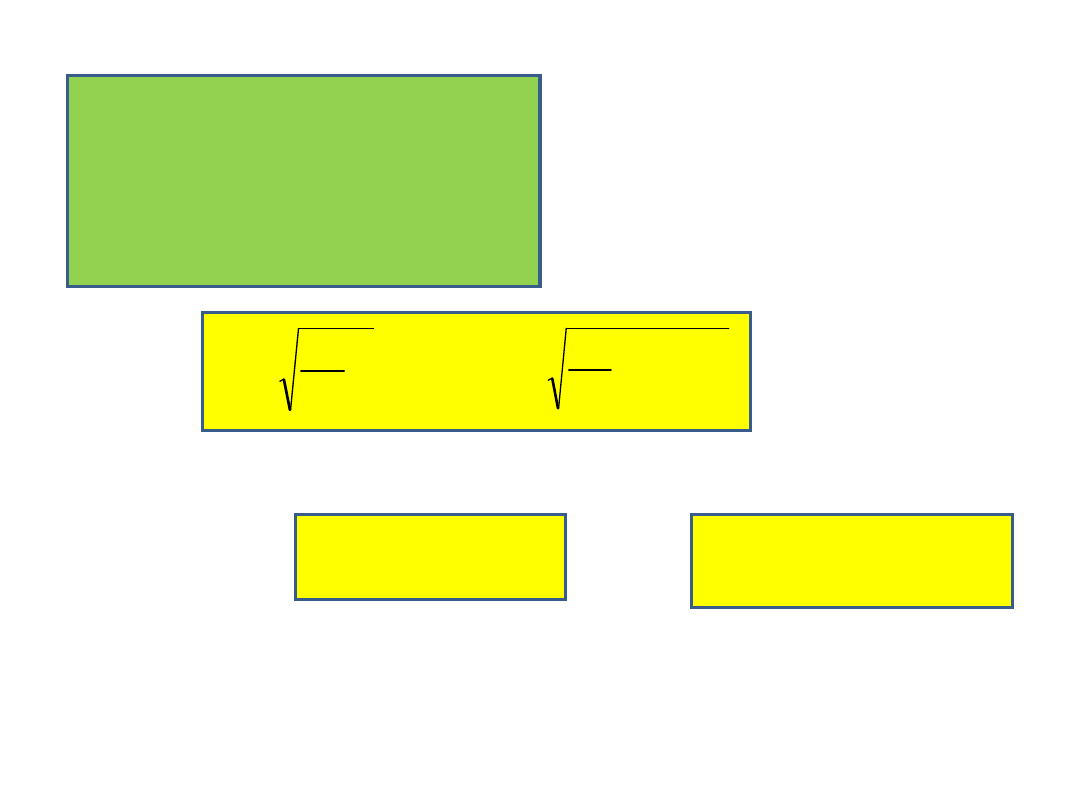
gdzie

E

m

2

2











E

U

m

o





2

2





Wiemy już, że jeśli potencjał jest periodyczny, to
funkcja Ψ(x) speł-nia warunek

   

ikx

e

x

u

x 



skąd

 

 

ikx

e

x

x

u







………

Po kolejnych podstawieniach otrzymujemy układ 4-
ech równań w których niewiadome stanowią A

1

, A

2

,

B

1

, B

2

:

2

2

1

1

B

A

B

A























2

2

1

1

B

ik

A

ik

B

k

i

A

k

i







































b

ik

b

ik

a

k

i

a

k

i

e

B

e

A

e

B

e

A



























2

2

1

1

































b

ik

b

ik

a

k

i

a

k

i

e

B

ik

e

A

ik

e

B

k

i

e

A

k

i













































2

2

1

1

Układ ten posiada niezerowe rozwiązanie tylko wtedy,
gdy wyznacznik macierzy współczynników przy A

1

, A

2

, B

1

,

B

2

równa się zeru





b

a

k

cos

a

cos

b

cosh

a

sin

b

sinh























2

2

2

Równanie to nakłada warunki na α i β, a co z tym się
wiąże i na dopu-szczalne wartości energii. Analiza tego
równania jest jednak dość uciążliwa. Dlatego
zastosujemy uproszczenie Kröniga i Penneya pole-
gające na założeniu, że U

o

dąży do nieskończoności,

natomiast b dąży do zera w taki sposób, że iloczyn U

o

b

pozostaje skończony.

Po uproszczeniu równanie ma postać

ka

cos

a

cos

a

a

sin

P











gdzie ; przyjęto też, że sinhβb = βb i cosh βb = 1.
Wielkość P można traktować jako miarę trudności
pokonywania bariery przez elektron.

- 3 

- 2 

2 

3 

 a

- 



- 1

+ 1

a

s in

a

a

s in

P









Równanie

wyraża

za-

leżność

energii

ele-ktronu
(poprzez a) od
liczby falowej k.
Na

rys.

przedstawiono
rozwiązanie
powyż-szego
równania meto-
dą graficzną

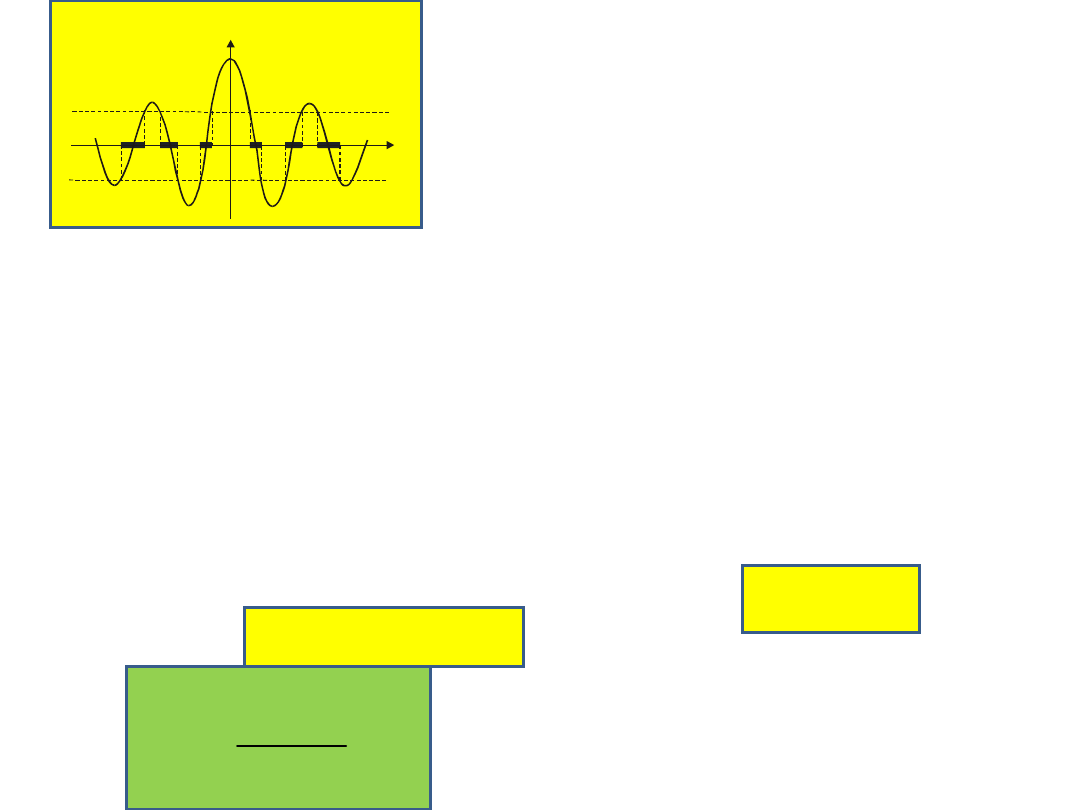
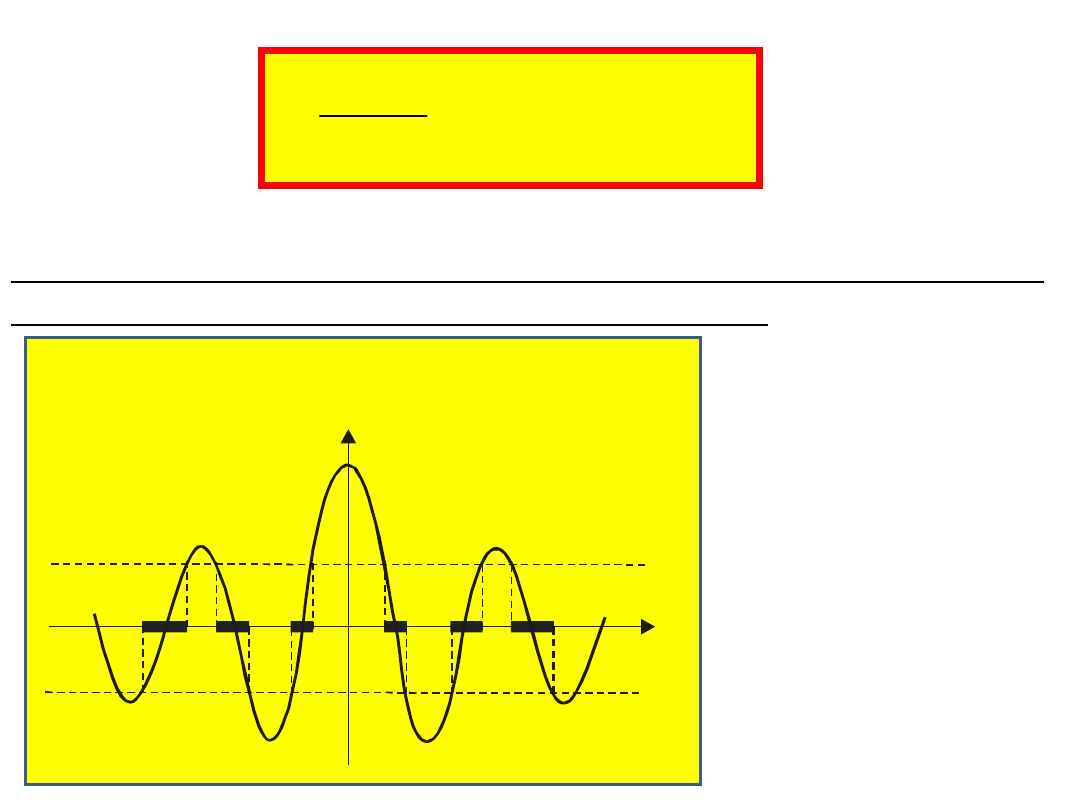
mieszczą się w przedziale [–1,1]. Wartości αa
spełniające ten warunek zaznaczono grubą linią.
Widać, że dopuszczalne wartości energii tworzą
pewne przedziały, tzw. pasma energetyczne.
Poszczególne pasma energetyczne oddzielone są przez
obszary o wzbronionych wartościach energii. W miarę
wzrostu αa (a więc wartości energii, gdyż a jest
ustalone) dozwolone pasma energetyczne stają się
coraz szersze. Szerokość pasm zależy także od
parametru P.

Ponieważ coska znajdujący się
po pra-wej stronie równania
jest zawarty w przedziale [–
1,1], a więc dopuszczalne
mogą być tylko te wartości αa,
dla któ-rych wartości lewej
strony równania

- 3 

- 2 

2 

3 

 a

- 



- 1

+ 1

a

s in

a

a

s i n

P









Ze wzrostem P pasma dozwolone zwężają się; w
szczególności gdy P>∞, równanie ma rozwiązanie tylko
wtedy gdy
czyli αa = nπ, a
Stąd

0



a

sin



3,....

2,

,

n







 1

2

2

2

2

2

n

ma

E







Otrzymujemy więc poziomy
dyskret-ne jak w
odosobnionej studni poten-
cjału.


a




a



2 

a



3 

a

3 

a

2 

a

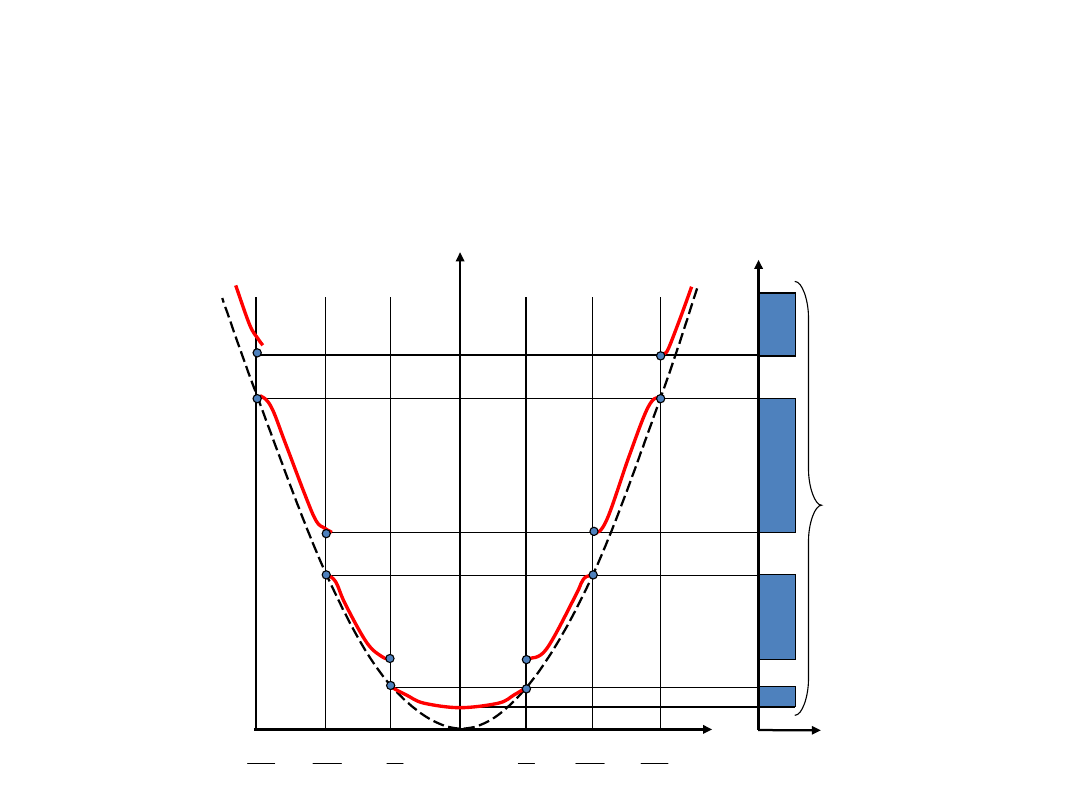
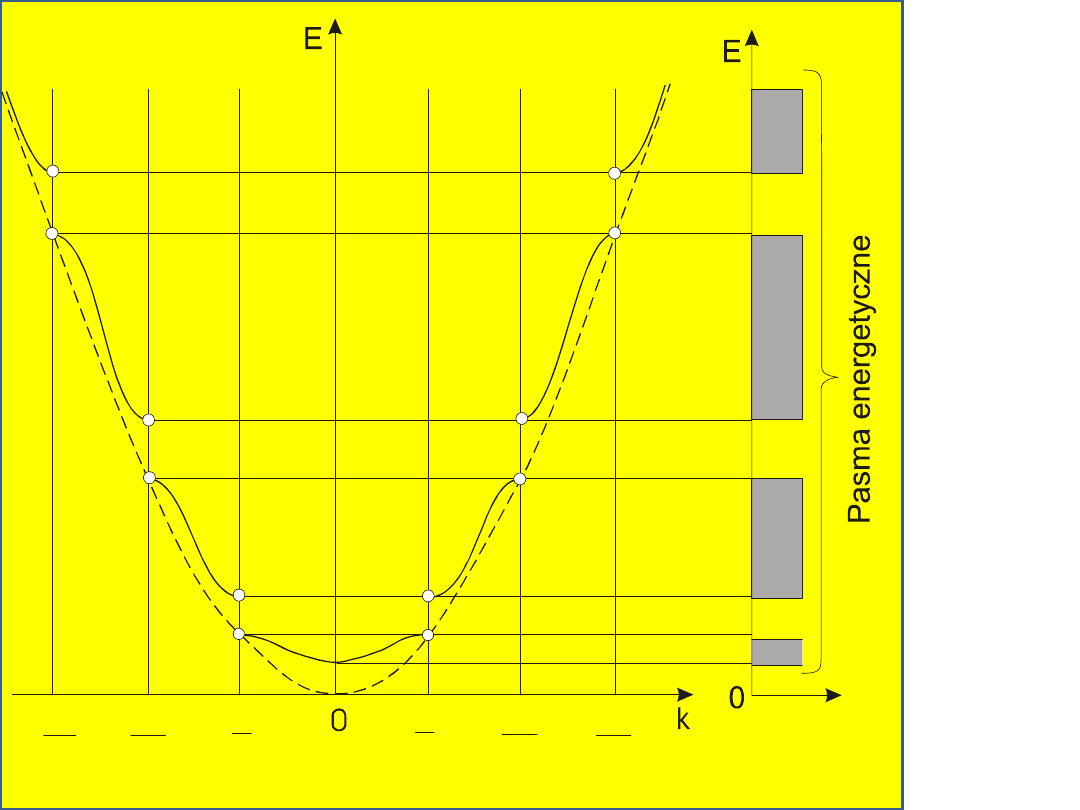
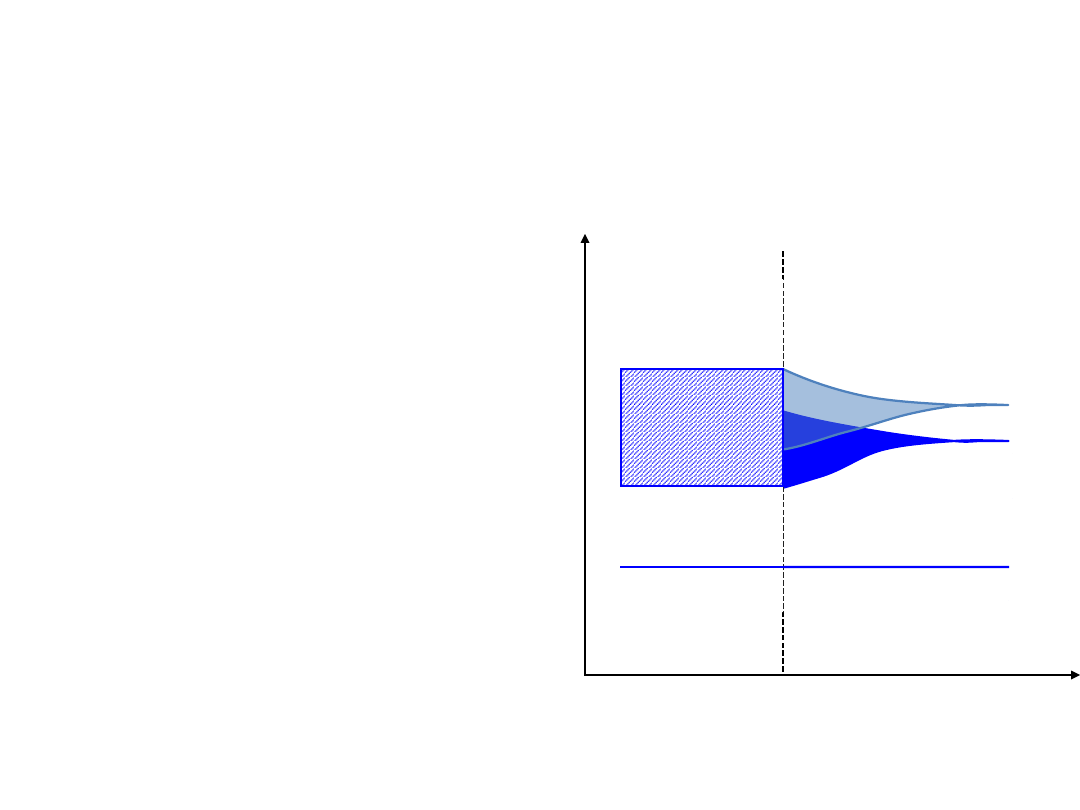
Zależność dyspersyjna

E(k)

E

E

k

0

0

a



a



2

a



3

a





a



2



a



3



p

a

sm

a

e

n

e

rg

e

ty

cz

n

e

Przybliżenie elektronów

silnie związanych

• jako punkt wyjścia przyjmujemy

funkcje falowe i zdegenerowane
poziomy energetyczne pojedyn-
czych atomów

• w wyniku zbliżania atomów

nastę-puje rozszczepienie
poziomów w pasma i
ewentualne przekrywanie
(zlewanie)

• szerokość pasma zależy od

prze-krywania odpowiednich
funkcji falowych

• głęboko leżące poziomy są

niezna-cznie poszerzone i
zachowują swój atomowy
charakter

odległość r

r

0

e

n

e

rg

ia

e

le

k

tr

o

n

u

E

1s

2s

2p

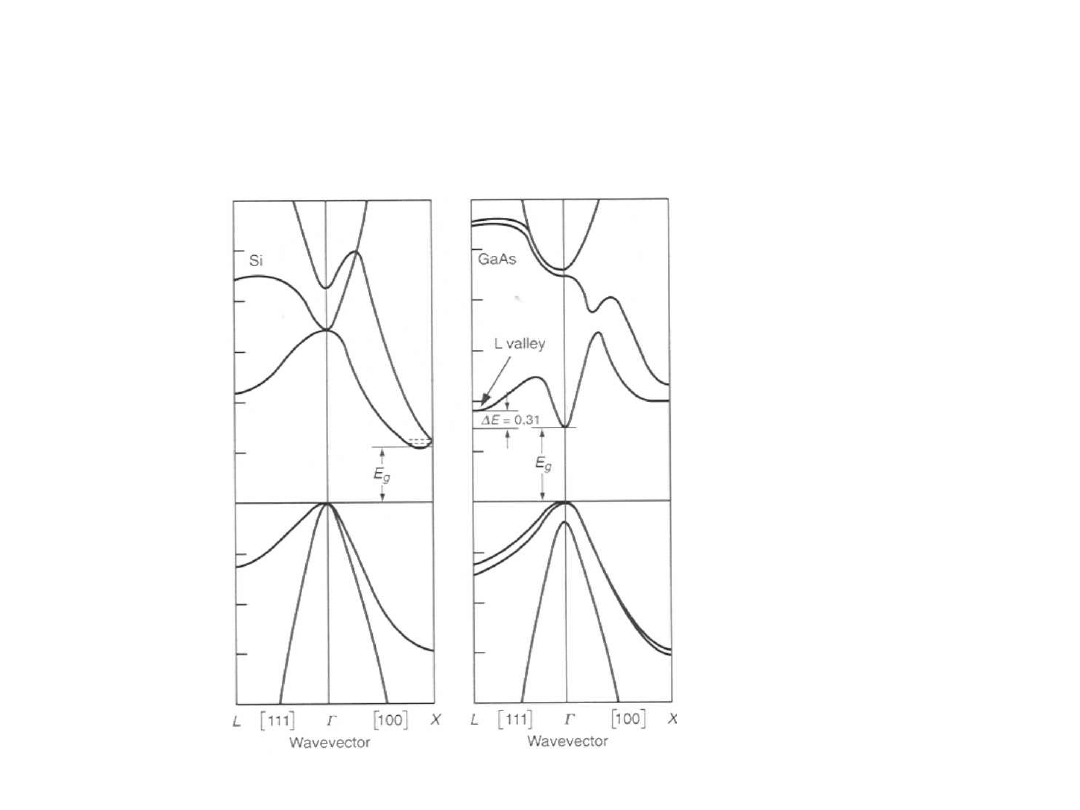
Kształt pasm Si i GaAs

Krzywe dyspersyjne

Zapełnianie pasm przez

elektrony

• izolatory i półprzewodniki - niższe pasma

całko-wicie zapełnione, wyższe poczynając

od pewne-go, całkowicie puste

• metale proste - nad całkowicie

zapełnionymi pasmami istnieje pasmo

zapełnione częściowo

• metale z pasmami nakładającymi się -

najwyższe całkowicie zapełnione pasmo,

zachodzi na poło-żone nad nim najniższe

pasmo puste, wtedy oba zapełniają się

częściowo

Pod względem charakteru zapełnienia pasm
przez elektrony możemy podzielić wszystkie
ciała na trzy grupy:

E

k

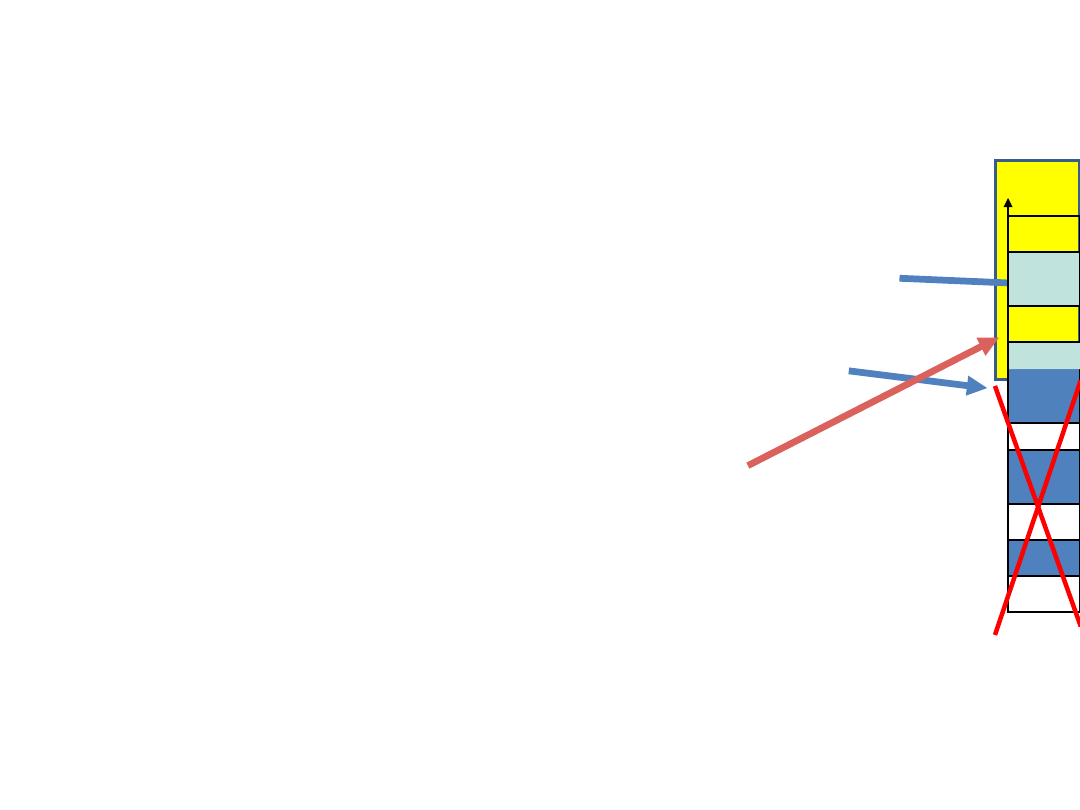
Podział ciał stałych

O własnościach fizycznych ciał stałych decydują:
• kształt i sposób obsadzenia elektronami dwóch

najważniej-szych pasm energetycznych

– pasma przewodnictwa - najniższego pasma nie

zapełnio-nego

– pasma podstawowego (walencyjnego) -

najwyższego pasma obsadzonego przez
elektrony

• odległość między tymi pasmami E

g

- zwana przerwą

energetyczną (pasmem zabronionym)

– izolatory E

g

> 3 eV - nie przewodzą prądu

– półprzewodniki E

g

< 3 eV, choć GaN ( 3,4eV)

diament (5,4eV)

– metale E

g

= 0 - pasma zachodzą na siebie

– ta sama substancja może mieć w pewnych warunkach

bądź właściwości półprzewodnikowe, bądź metaliczne

E

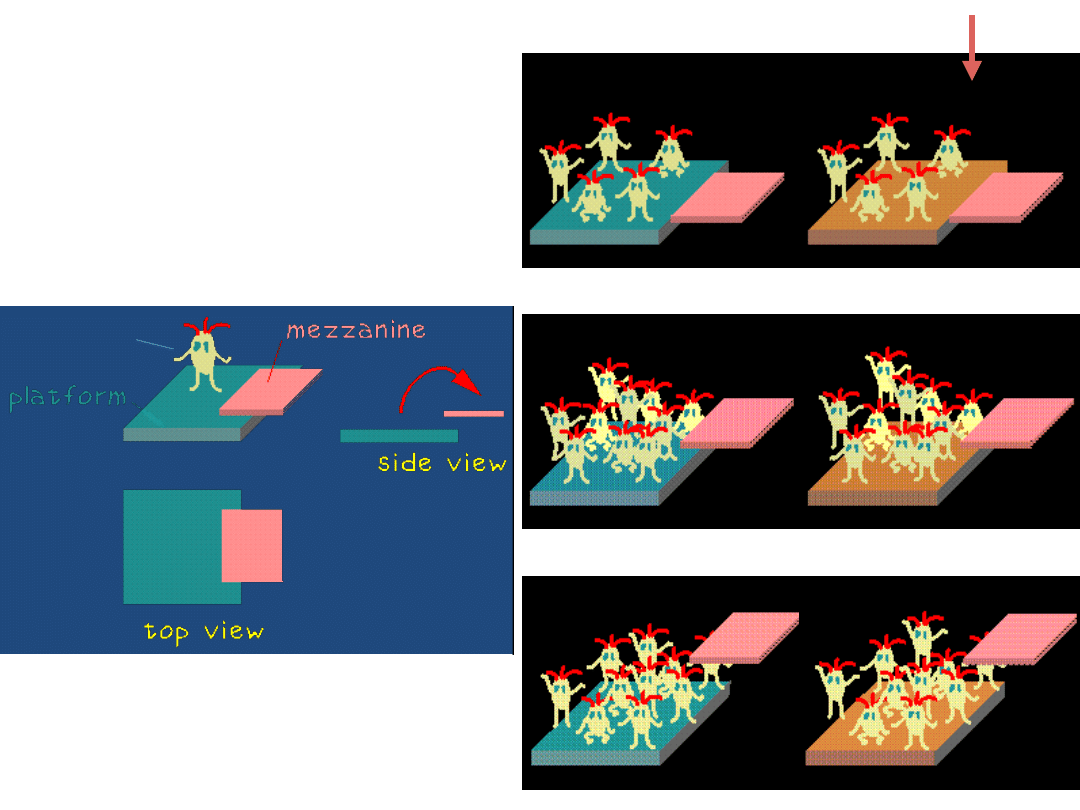
creature

przewodnik

półprzewodnik

izolator

Stworzenia próbują się
dostać
z platformy na antresolę.
W zależności od położenia
antresoli i temperatury
platformy wyróżniamy
trzy przypadki

grzanie