1

1

Elementy i operacje

symetrii

• http://math.boisestate.edu/~tconklin/

MATH124/Main/Notes/GroupTheory/Mo

lecular%20Symmetry.pdf

2

2

Symetria

• Symetria (

gr.

συμμετρια, od συμ, podobny

oraz μετρια, miara) – właściwość figury,

bryły lub ogólnie dowolnego obiektu

matematycznego (można mówić np. o

symetrii równań), polegająca na tym, iż

istnieje należące do pewnej zadanej klasy

przekształcenie nie będące identycznością,

które odwzorowuje dany obiekt na niego

samego. Brak takiej właściwości nazywany

jest asymetrią. W zależności od klasy

dopuszczalnych przekształceń wyróżnia się

rozmaite rodzaje symetrii. Tym samym

pojęciem określa się nie tylko obiekty, ale

też same przekształcenia.

3

3

Symetria

• Symetrycznym nazywamy każdy

przedmiot, który może mieć dwa

lub więcej ustawień w

przestrzeni, które nie dadzą się

pomiędzy sobą odróżnić.

4

4

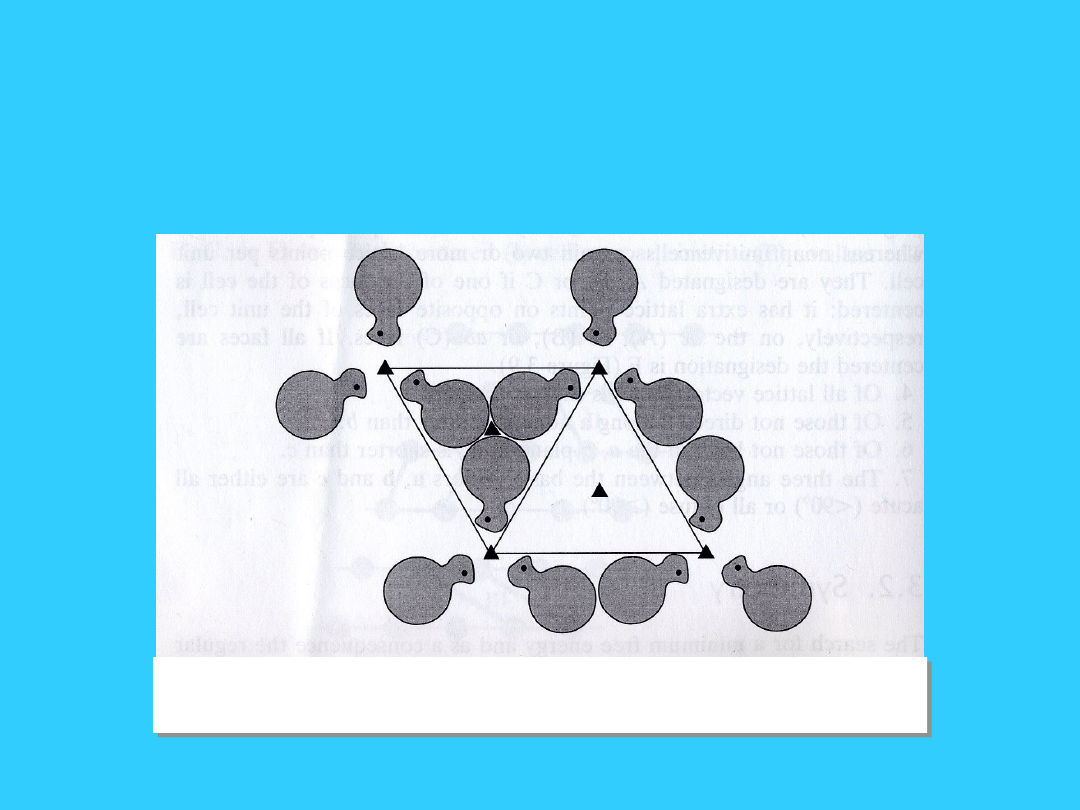
Elementy symetrii - oś

symetrii

Trzykrotna oś symetrii prostopadła do płaszczyzny
rysunku

Trzykrotna oś symetrii prostopadła do płaszczyzny
rysunku

symetria osiowa – przekształceniem
jest odbicie zwierciadlane figury
względem zadanej prostej zwanej
osią symetrii.

5

5

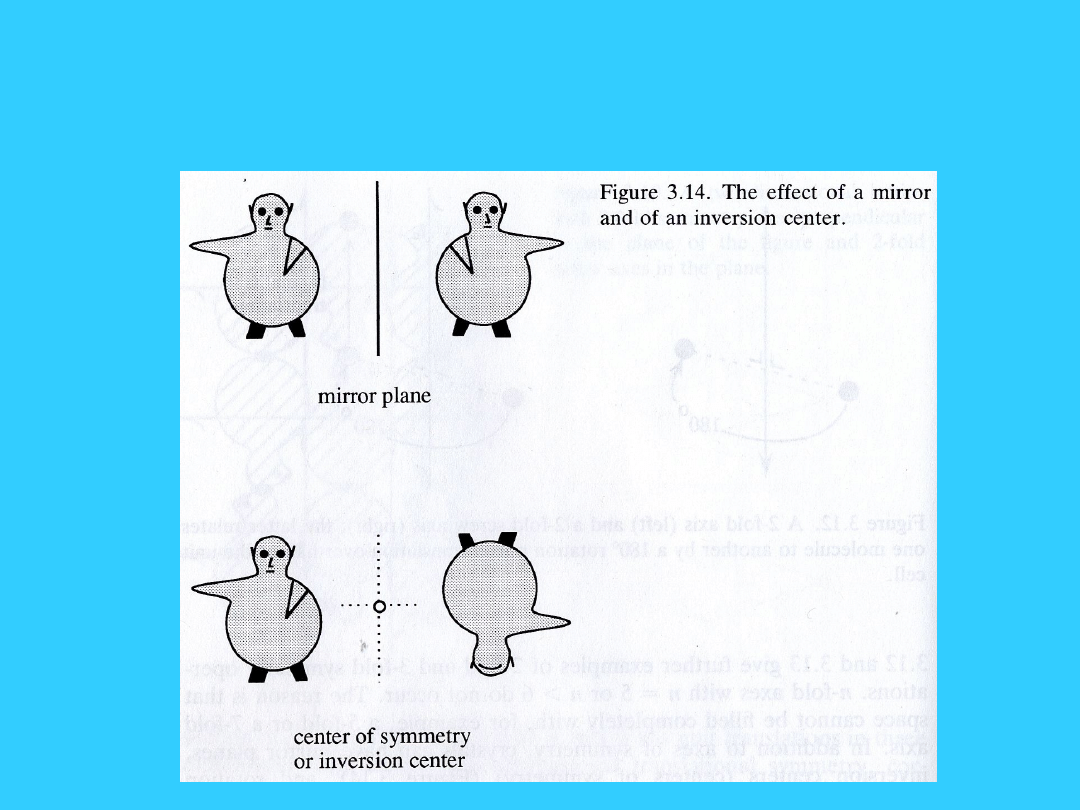
Elementy symetrii -

płaszczyzna symetrii i środek

symetrii

symetria płaszczyznowa –
przekształceniem jest odbicie
zwierciadlane figury względem
płaszczyzny zwanej płaszczyzną
symetrii

.

symetria środkowa

–

przekształceniem jest odbicie
zwierciadlane figury względem
ustalonego punktu zwanego środkiem
symetrii. Na płaszczyźnie symetria
środkowa jest złożeniem dwóch
symetrii osiowych o prostopadłych
osiach (lub obrót o kąt 180 stopni), w
przestrzeni jest złożeniem trzech
symetrii płaszczyznowych o
wzajemnie prostopadłych
płaszczyznach symetrii.

6

6

Elementy symetrii - translacja

• Przesunięcie

wszystkich

punktów o tą

samą

odległość i w

tym samym

kierunku.

7

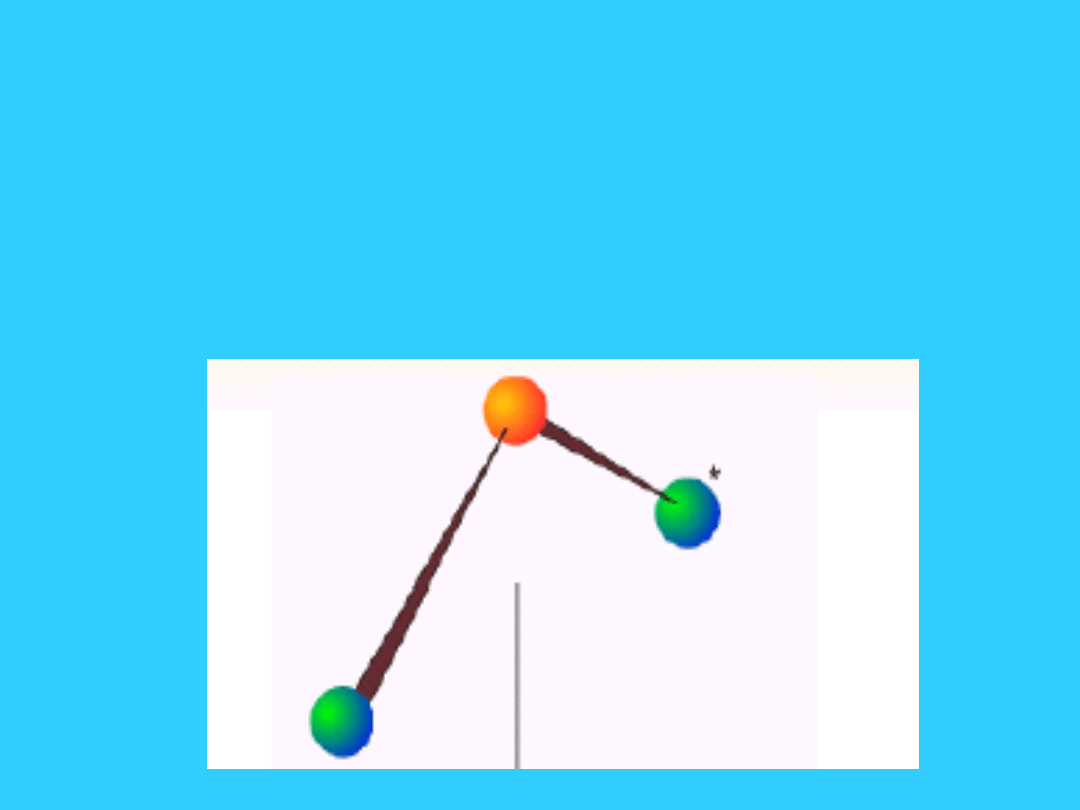
7

Elementy symetrii - element

tożsamościowy E

pozostawia cząsteczkę niezmienioną.

Wszystkie cząsteczki posiadają

przynajmniej ten element symetrii

8

8

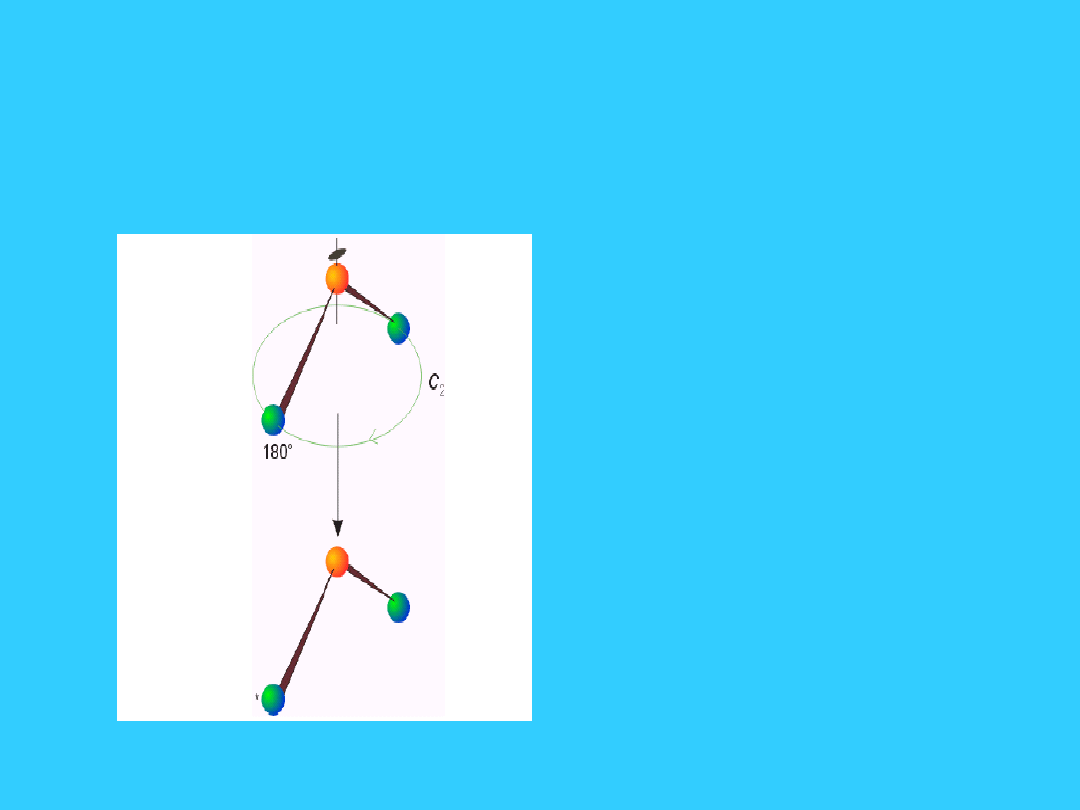
Elementy symetrii - oś

symetrii

(Oś o najwyższej krotności to

OŚ GŁÓWNA)

• n-krotna oś

symetrii

• obrót o kąt

360/n

• H

2

O

• *180, n = 2
• C

2

9

9

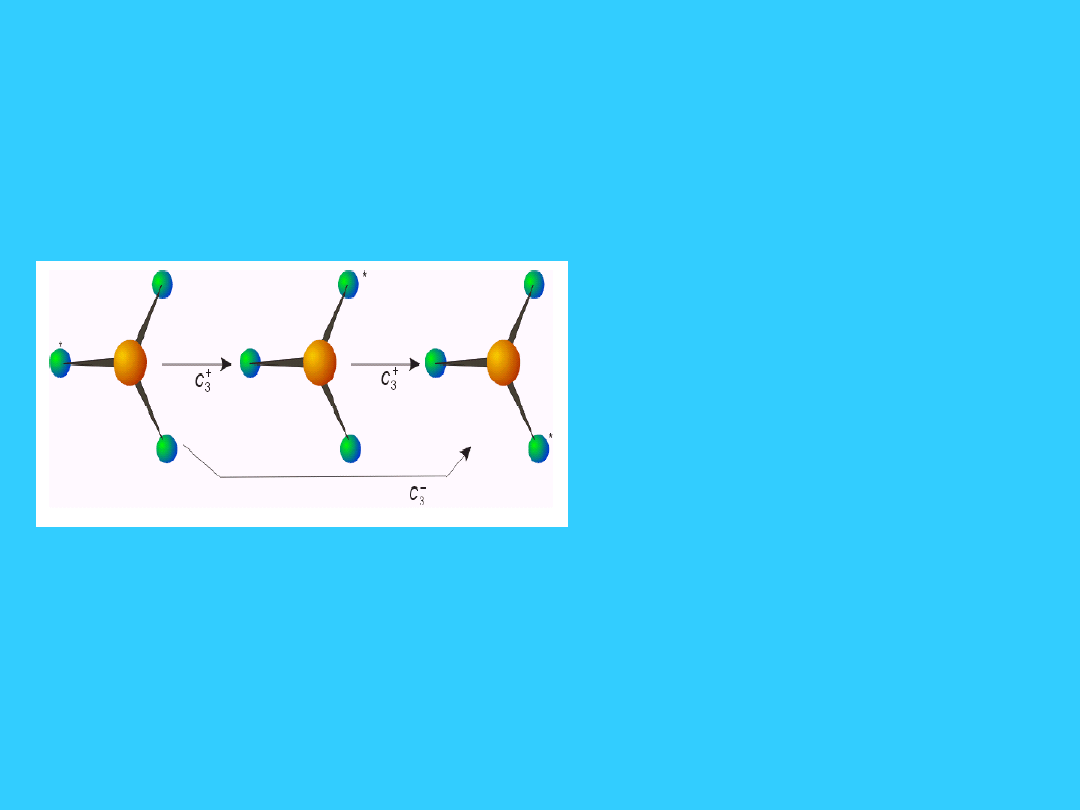
Elementy symetrii - oś

symetrii

• n-krotna oś

symetrii

• obrót o kąt

360/n

• NH

3

• *120, n = 3
• C

3

10

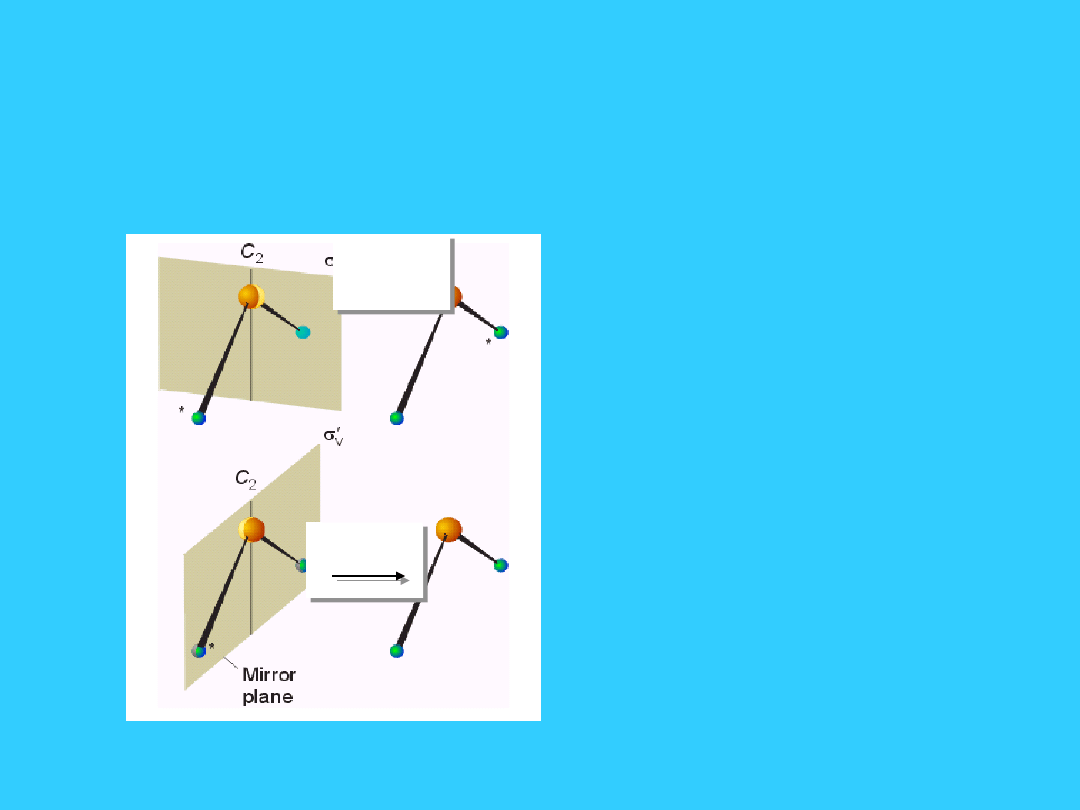
10

Elementy symetrii -

płaszczyzna symetrii



(

dzieli

cząsteczkę na 2 części

mające się do siebie jak

przedmiot do odbicia w

lustrze)

odbici
e

odbici
e

odbici
e

odbici
e

•



v

- płaszczyzna

symetrii, na której

leży główna oś

symetrii

(wertykalna)



h

- płaszczyzna

symetrii prostopadła

do osi głównej

(horyzontalna)

11

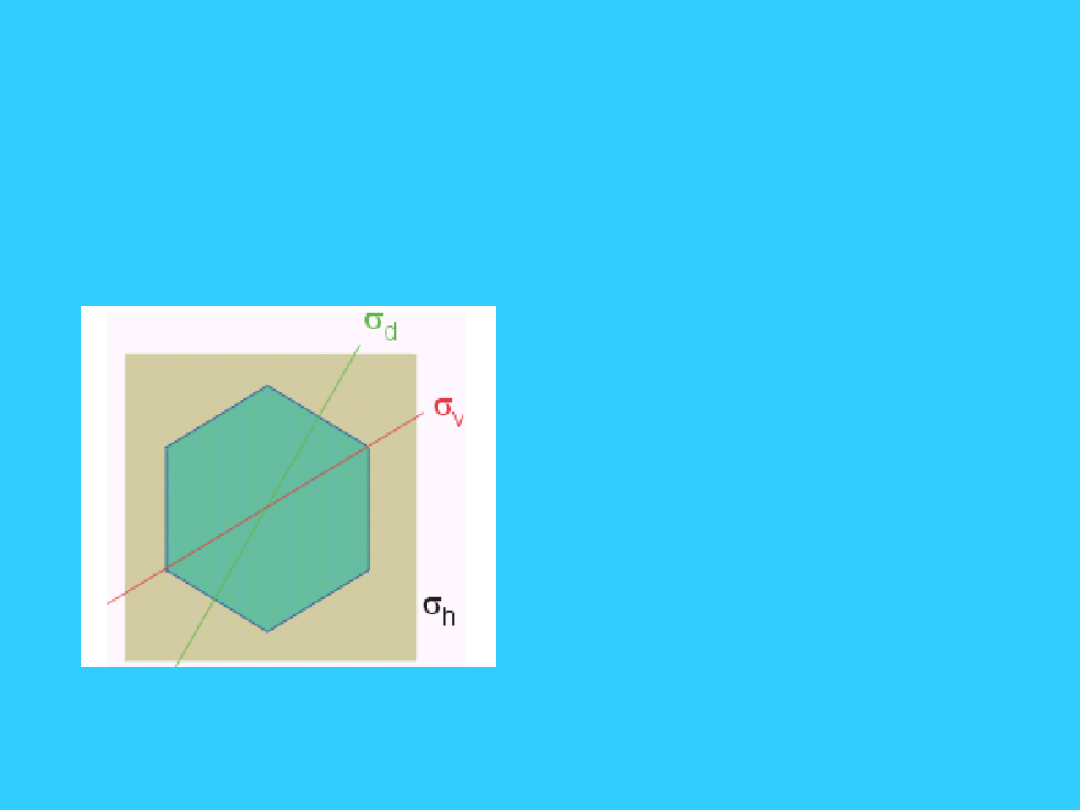
11

Elementy symetrii -

płaszczyzna symetrii





d

-

płaszczyzna

symetrii

skierowana

pomiędzy dwie

osie

dwukrotne

prostopadłe

do osi głównej

(diagonalna)

12

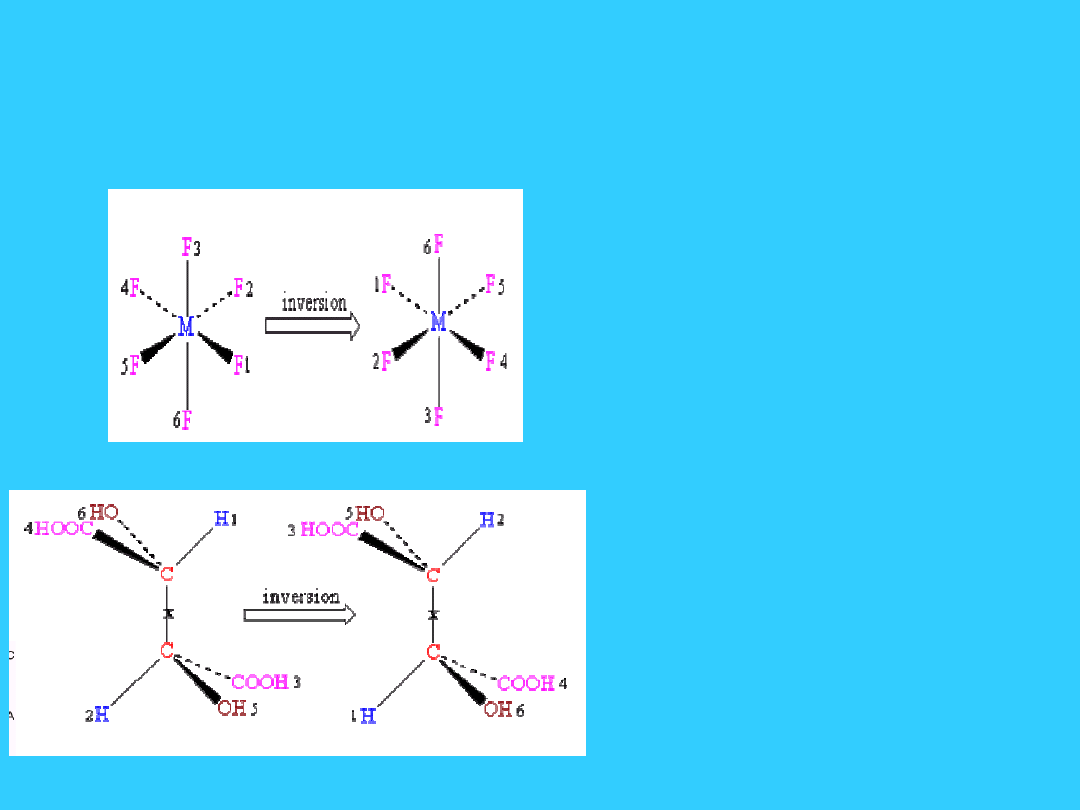
12

Elementy symetrii - inwersja

(i)

• Przekształca punkt o

współrzędnych (x, y,

z) w punkt o

współrzędnych (-x,

-y, -z)

• w oktaedrze

środkiem symetrii

jest środek oktaedru

• tetraedr nie ma

środka symetrii

13

13

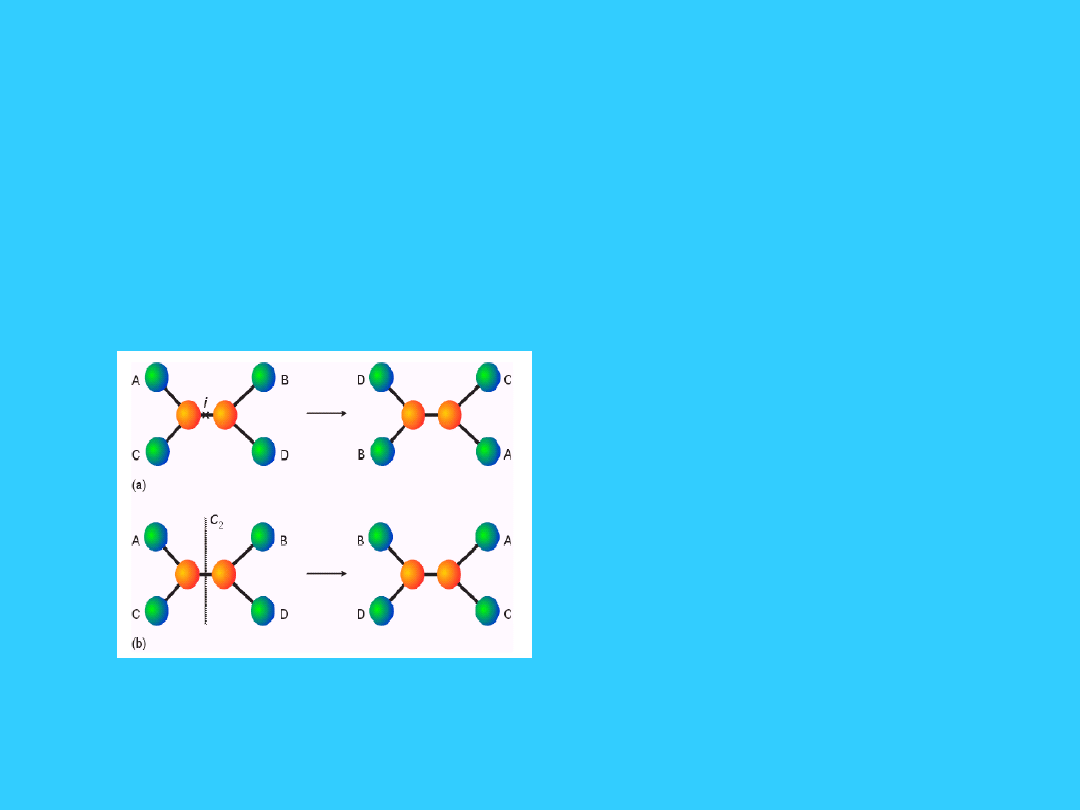
Elementy symetrii - oś i

środek symetrii

• Operacja

obrotu wokół

osi dwukrotnej

daje inny

rezultat niż

inwersja

14

14

Elementy symetrii - oś

przemienna n-krotna

• Obrót o kąt

360/n

• i następnie

odbicie w

płaszczyźnie

symetrii

prostopadłej

do osi obrotu

15

15

16

16

Zbiór wszystkich operacji symetrii,

jakie można wykonać na danej

cząsteczce

nazywamy punktową grupą symetrii.

17

17

18

18

Dutch graphic artist Maurits Cornelis

Escher (1898–1972)

The original Escher print

Circle Limit I.

19

19

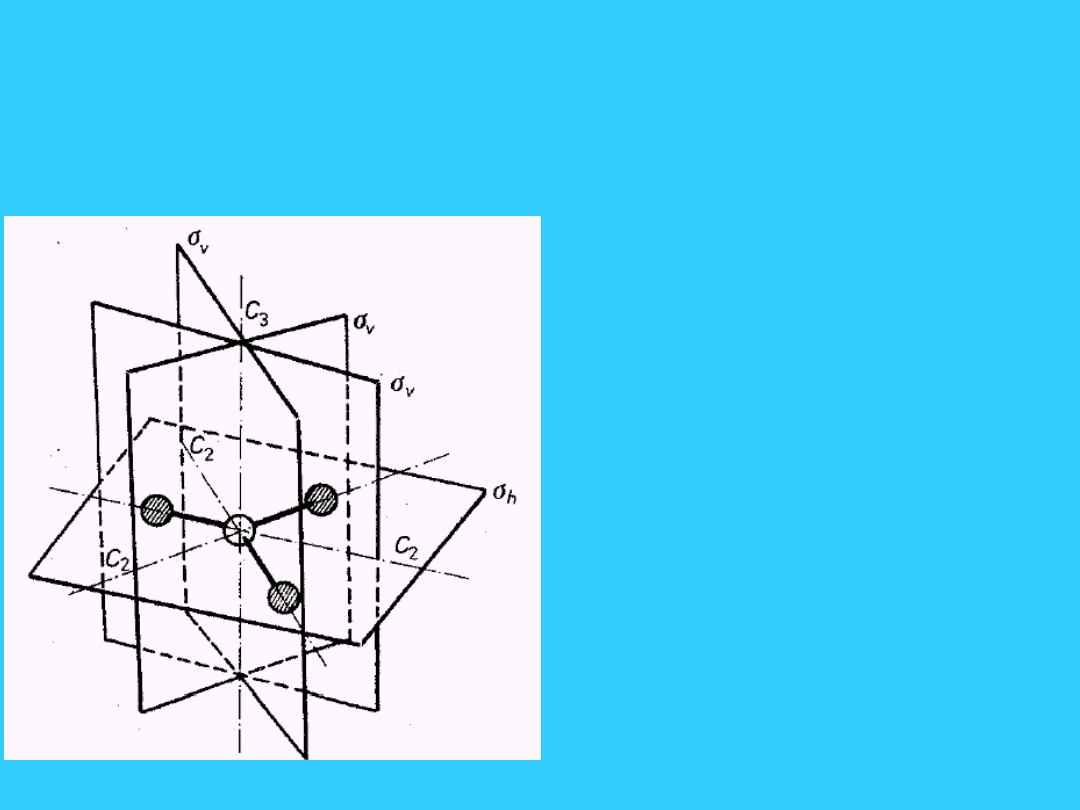
Cząsteczka BF

3

i jej elementy

symetrii

• Jest to cząsteczka

o hybrydyzacji atomu

centralnego typu sp

2

, a

więc o budowie płaskiej,

w której atomy fluoru

znajdują się w narożach

trójkąta równobocznego.

• Elementy

symetrii:

oś C

3

, 3 osie C

2

, 3 

v

i

1 

h

•D

3h

20

20

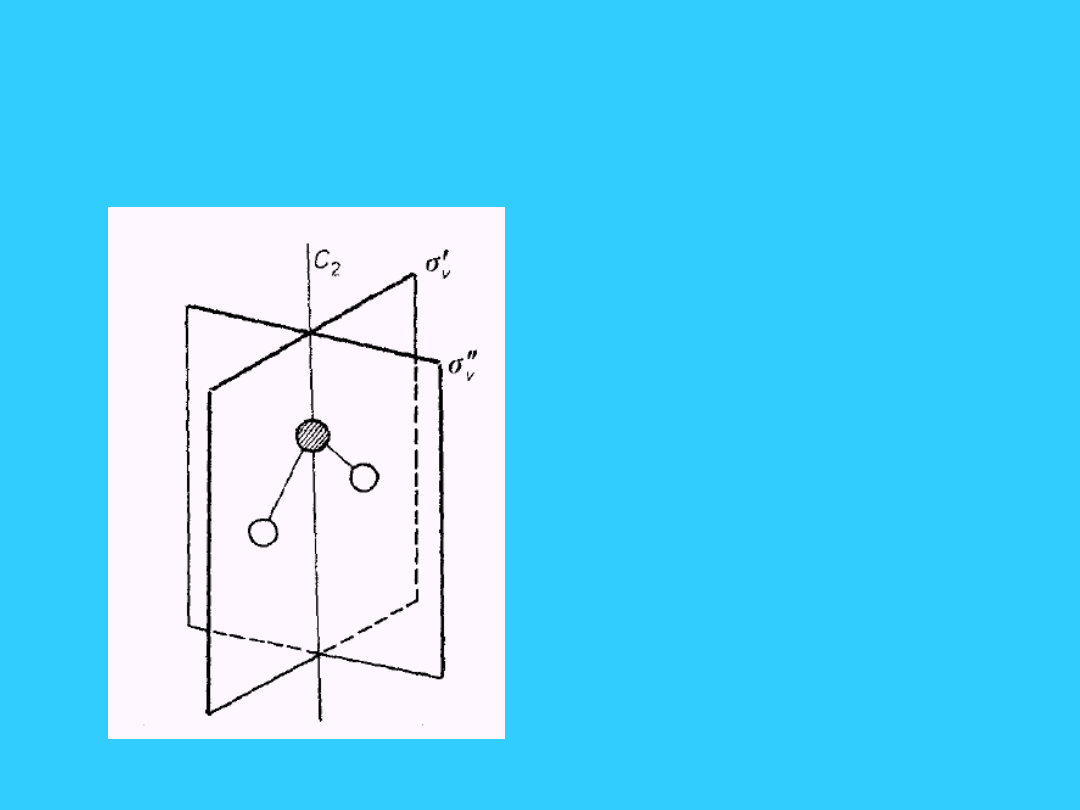
Cząsteczka H

2

O i jej elementy

symetrii (grupa punktowa C

2v

)

• Elementy

symetrii: oś

dwukrotna C

2

,

dwie płaszczyzny

symetrii typu 

v

tj. 

v

' i 

v

"

21

21

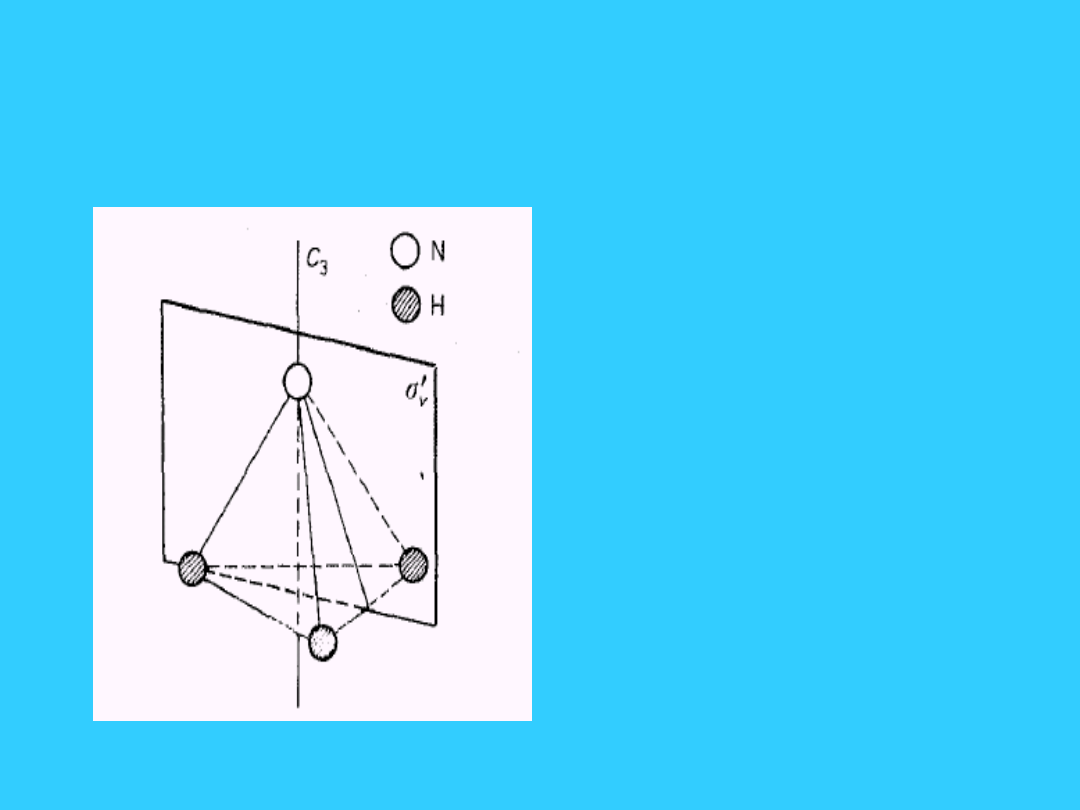
Cząsteczka NH

3

i jej elementy

symetrii (grupa punktowa C

3v

)

• Elementy symetrii:

oś C

3

,

• 3 płaszczyzny

symetrii 

v

tj. 

v

',



v

'' i 

v

''’ (na

rysunku pokazano

jedynie 

v

').

Pozostałe dwie

można otrzymać

przez obrót

płaszczyzny 

v

'

wokół osi C

3

o kąty

120  i 240 

22

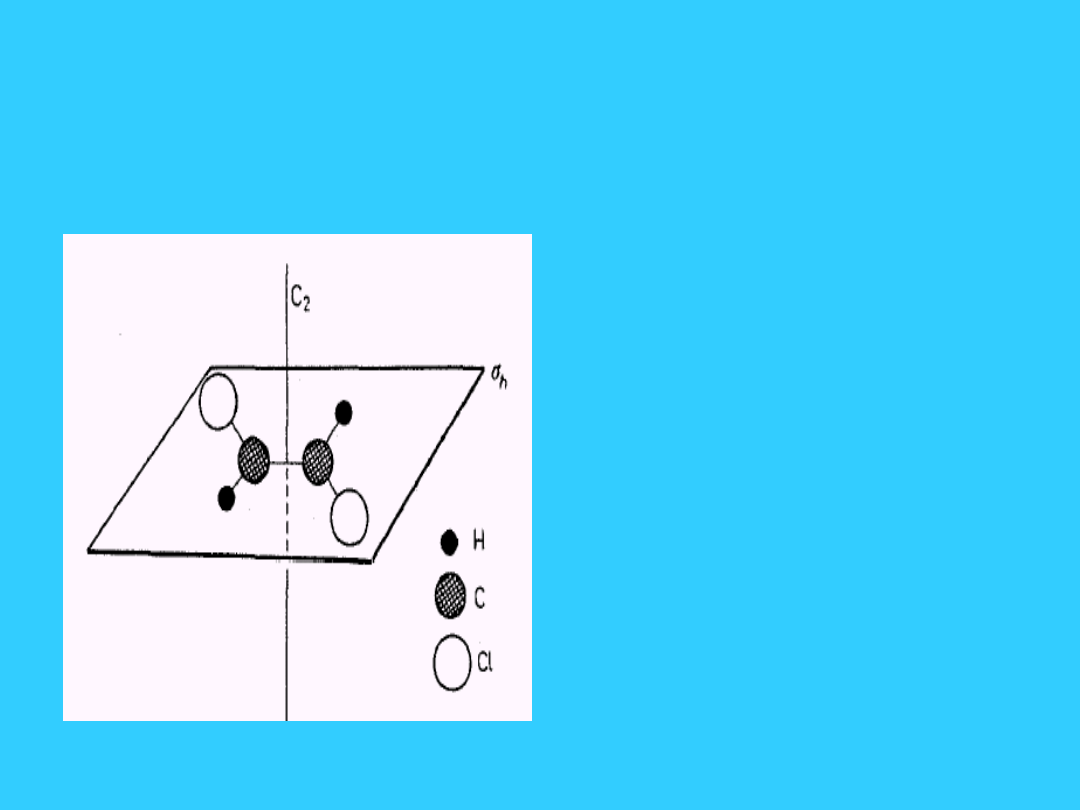
22

Cząsteczka trans-

dichloroetylenu i jej elementy

symetrii (grupa punktowa C

2h

)

• Elementy

symetrii: oś C

2

,

płaszczyzna

symetrii 

h

23

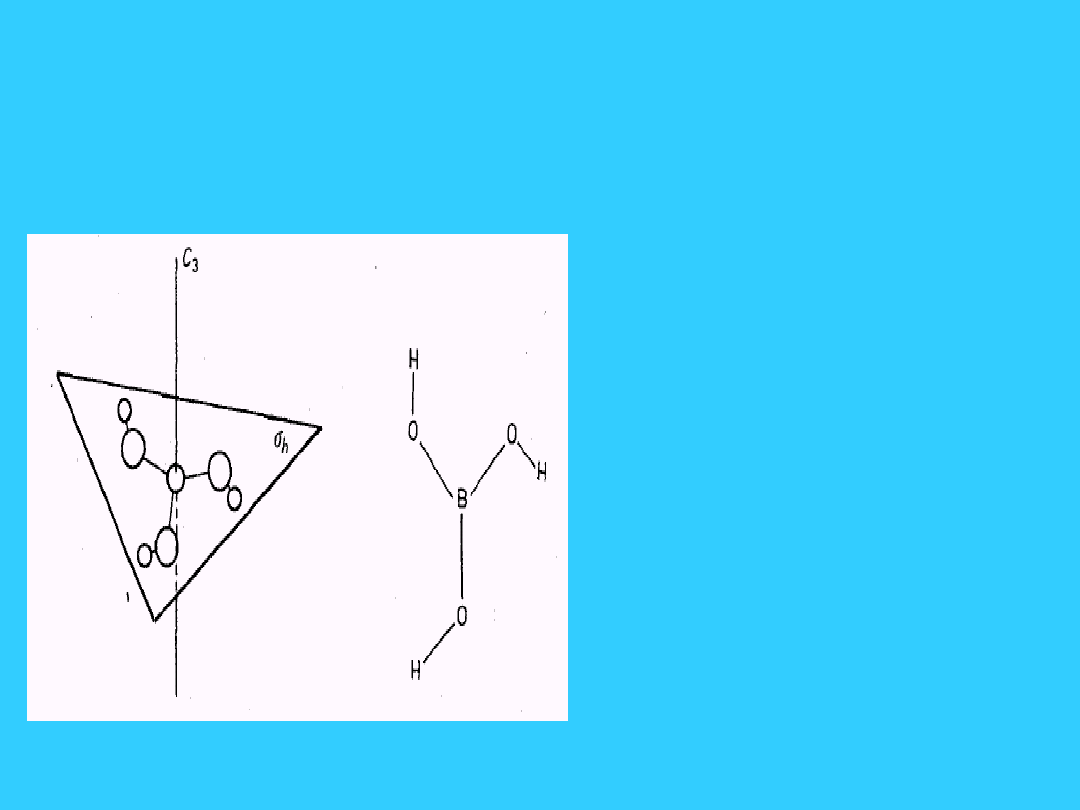
23

Cząsteczka B(OH)

3

i jej

elementy symetrii (grupa

punktowa C

3h

)

• Elementy

symetrii: oś

C

3

,

płaszczyzna

symetrii 

h

24

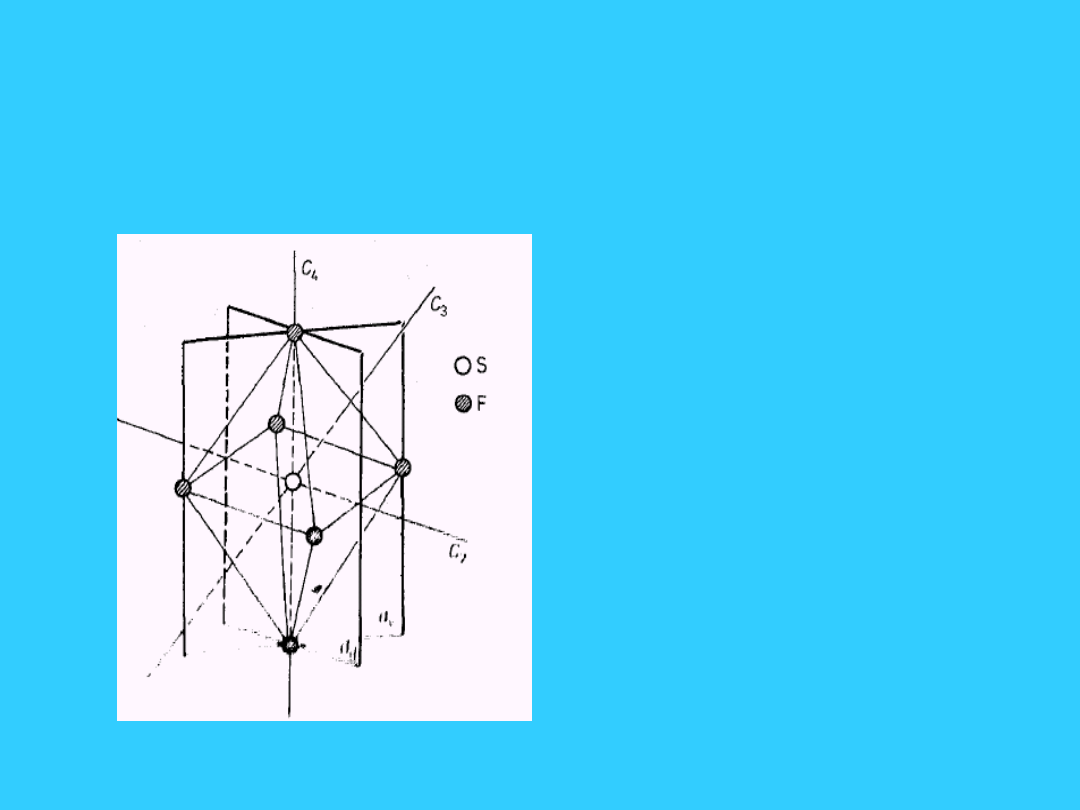
24

Cząsteczka SF

3

i jej elementy

symetrii (grupa punktowa O

h

)

• Elementy

symetrii: 3 osie

C

4

, 4 osie C

3

, 6

osi C

2

, środek

symetrii (i), 9

płaszczyzn

symetrii, 

d

płaszczyzna

symetrii (na

której leżą osie C

4

i C

2

), 3 osie S

4

, 4

osie S

6

.

25

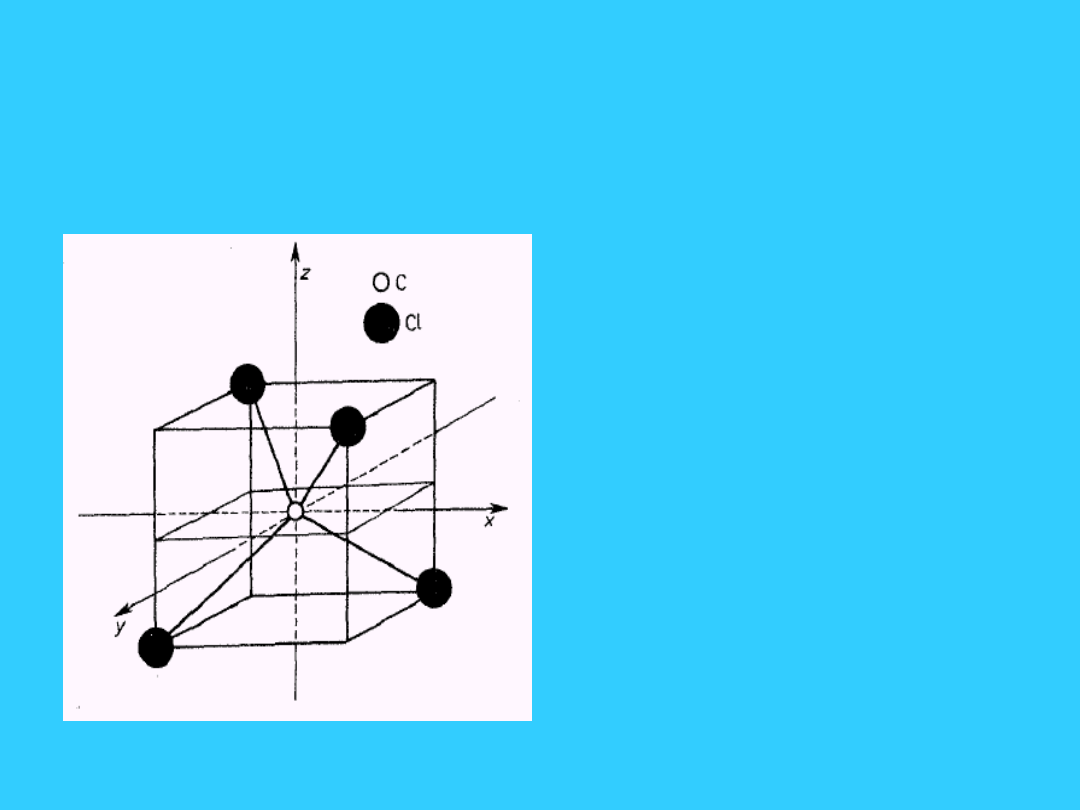
25

Cząsteczka CCl

4

i jej elementy

symetrii (grupa punktowa S

4

)

• Elementy

symetrii: oś S

4