SciLab. wpływ

temperatury i ciśnienia na

prężność parcjalną chloru

w wyniku rekacji Deacona.

2HCl + 0,5O

2

=H

2

O + Cl

2

ciśnienie parcjalne

Ciśnienie cząstkowe (ciśnienie parcjalne) - ciśnienie,

jakie wywierałby dany składnik mieszaniny gazów,

gdyby w tej samej temperaturze sam zajmował

objętość całej mieszaniny.

Ciśnienia cząstkowe można wyliczyć wykorzystując

równanie

gdzie:
pi - ciśnienie cząstkowe składnika "i"
ni - liczność (liczba moli) składnika "i"

p

i

=

n

i

/

(

s

+

sV

*

a

)

*

P

• Ciśnienie całego układu :

gdzie:
p - ciśnienie mieszaniny,
n - liczba moli,
k - łączna liczność składników

mieszaniny

Co obliczamy ?

• Szukane jest ciśnienie parcjalne

chloru w układzie reakcyjnym w
skład którego wchodzą cząsteczki
HCl O

2

Cl

2

H

2

O. Dane to liczba moli

poszczególnych składników. Ciśnienie
parcjalne liczymy dla różnych
temperatur reakcji. Zakładamy że
wszystkie te składniki występują w
postaci gazowej

 W pierwszej kolejności obliczamy stałą

równowagi termodynamicznej i tworzymy

wykres

dGHCl=[-95.92 -97.59 -99.09 -100.30 -102.38] ;
dGH2O=[-224.073 -214.18 -203.67 -192.760

-181.506];

dGreak=dGHCl*V(1,1)+dGH2O*V(1,4);
R=8.314*10^(-3);
lnKp=-dGreak./(R*T);
Kp=exp(lnKp)
f=1../T
xset('window',0)
plot(f,lnKp,'-o')
coefs=regress(f,lnKp)

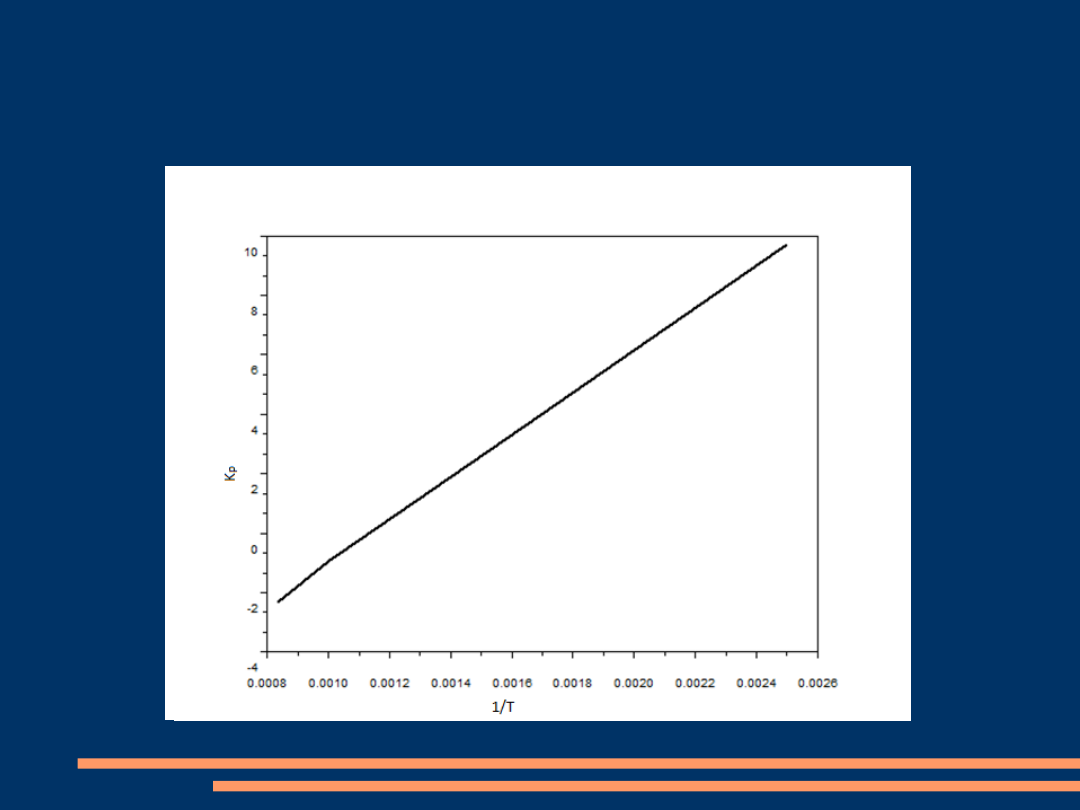
Wykres

 Dalej liczymy ciśnienie parcjalne w stanie równowagi, oraz używamy pętli „for”

w celu obliczenia stałych równowagi wyznaczonych dla konkretnych temperatur

w celu obliczenia p chloru w tej trmp. (skok temperatury co 100K)

s=sum(n0);
sV=sum(V);
P=1
function z=grze(a)
ni=n0+V*a
p=ni/(s+sV*a)*
z=Kp1-p(1,3)*p(1,4)*(p(1,1)^V(1,1))*(p(1,2)^V(1,2))
endfunction
a0=0.8
T1=400
for i=1:6
Ti(1,i)=T1+100*i
f1=1/Ti(1,i);
lnKp1=coefs(1,1)+coefs(2,1)*f1;
Kp1=exp(lnKp1)
[a,z,info(1,i)]=fsolve(a0,grze);
for j=1:4
nir(1,j)=n0(1,j)+V(1,j)*a;
if nir(1,j)<0 then write(%io(2),"zly punkt startu")
abort
end
end

 Tworzymy wykres zależności prężności parcjalnej chloru od temperatur

b info
xset('window',1)
plot(Ti,pCl2,'-o')
P1=[0.5 1 10 25 50]
Kp1=Kpr(1,1)
function z1=grze1(a)
ni=n0+V*a
p=P1(1,k)*ni/(sum(n0)+sum(V)*a)
z1=Kp1-(p(1,3)*p(1,4))*(p(1,1)^V(1,1))*(p(1,2)^V(1,2))
endfunction
a0=0.8
for k=1:5
[a,z1,info(1,k)]=fsolve(a0,grze1);
infp(1,k)=info(1,k);
for j=1:4
nir(1,j)=n0(1,j)+V(1,j)*a
if nir(1,j)<0 then write(%io(2),"zly punkt startu")
break
end
end

 Liczmy prężność parcjalną dla Cl

2

b(1,i)=a;
a0=a
pCl2(1,i)=n0(1,3)+V(1,3)*a;
pr=nir/sum(nir)*P;
Kpr(1,i)=pr(1,3)*pr(1,4)*pr(1,2)^V(1,2)*pr(1,1)^V(1,1)
end

 Wyniki:
Prężność parcjalna dla chloru w różnych temperaturach

wynosi :

8592818 Pa
8766365 Pa
9207877 Pa
9337179 Pa
9421098 Pa

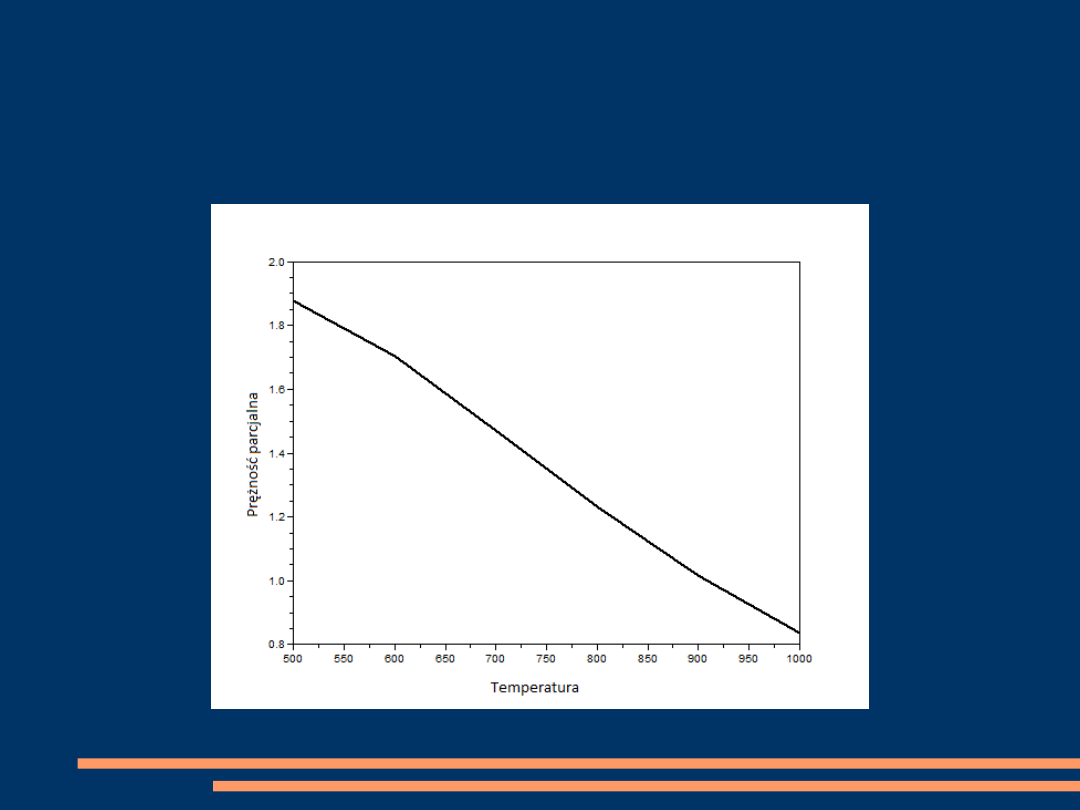
Wykres

Jakub

Mielcarek

Gr. 13T1

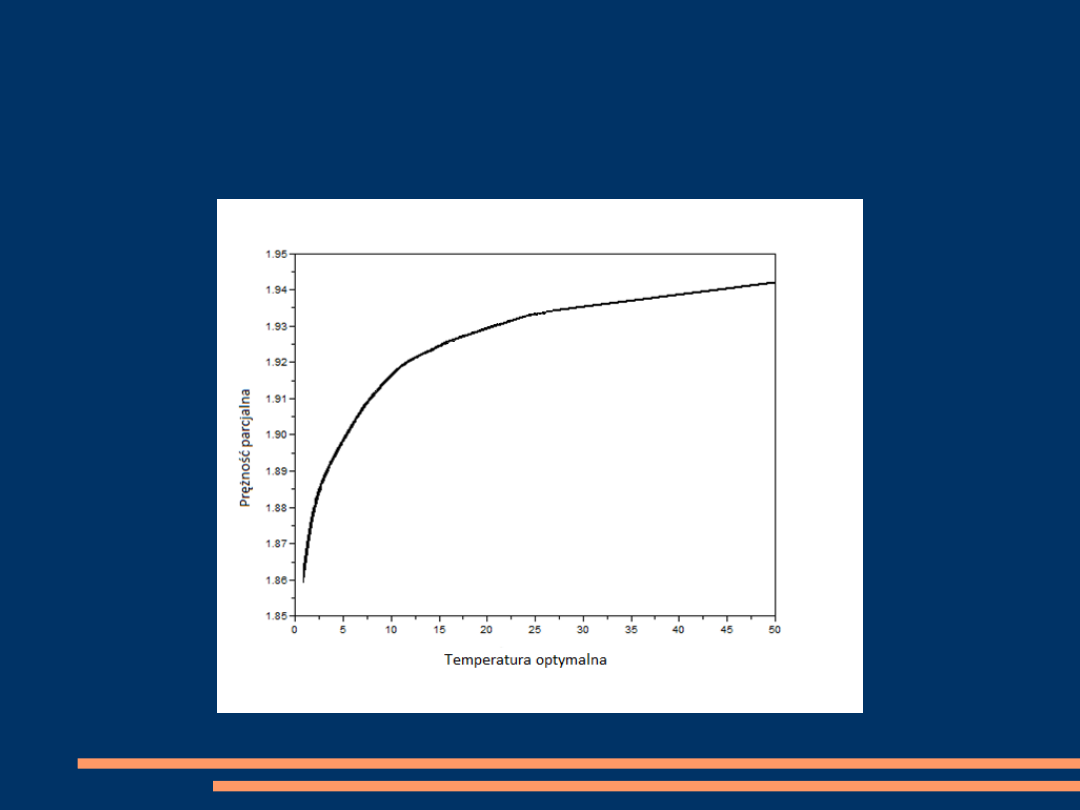
Wykres temperatury od

prężności parcjalnej Cl

2

.