A
S
D
S
U
A
U
B
U
C
U
D
T1 L T2
1
2
A B C D
Wszystkie parametry schematu zastępczego oraz moc i napięcie
sprowadzone są do jednego, wybranego poziomu napięcia.
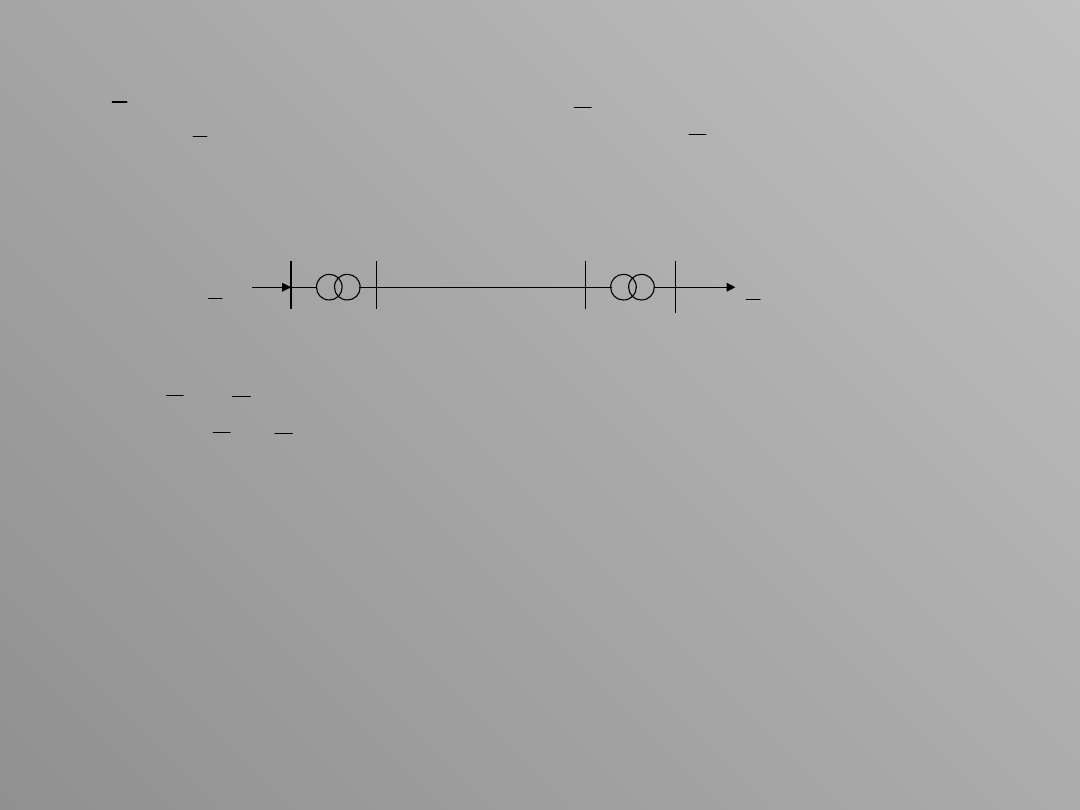
3. Dany jest układ przesyłowy pokazany na rysunku, z którego
odbierana jest moc . Napięcie na końcu układu wynosi .
Obliczyć moc dopływającą do układu oraz napięcie na
początku układu .
D
U
A
U
D
S
A
S
Dane: , , parametry podłużne i poprzeczne elementów
układu.
Obliczyć: , .
D
U
D
S
A
U
A
S
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
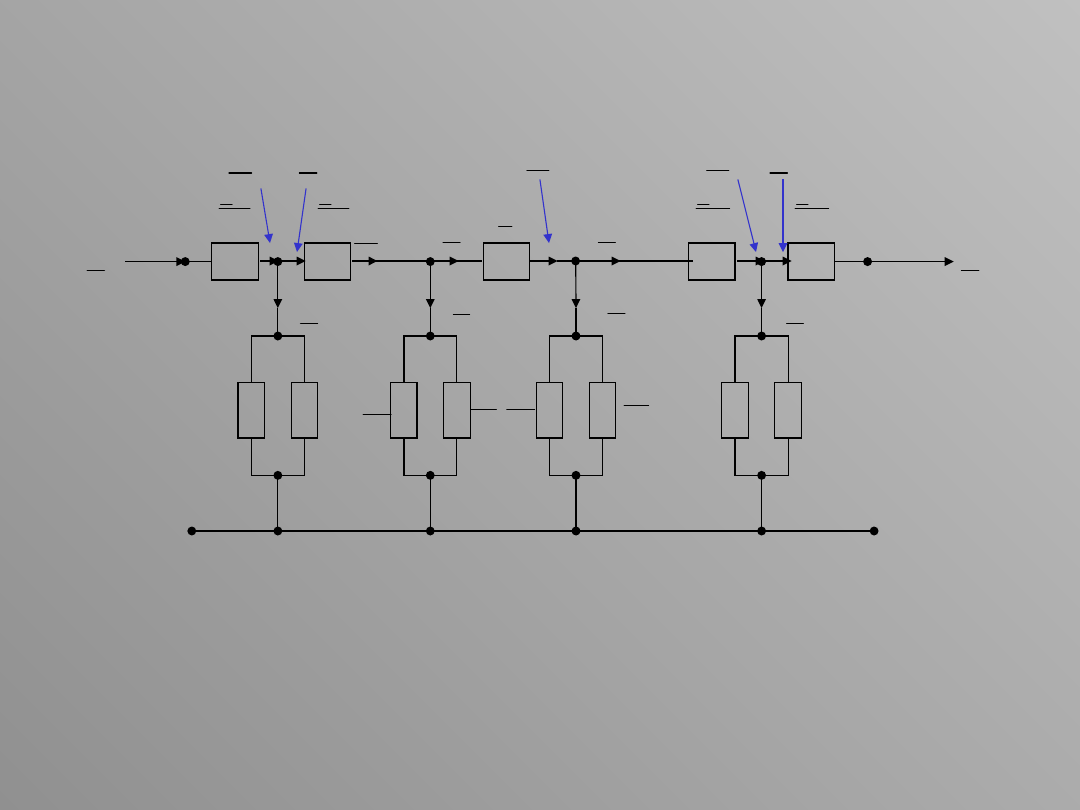
Jeśli znane jest napięcie na końcu układu , to napięcie na
początku układu jest równe
D
U
AD
D
A
U
U
U
- całkowita strata napięcia w układzie, przeliczona na wybrany
poziom napięcia
AD
U
1
1
2
2
A
B
BC
C
D
AD
U
U
U
U
U
U
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
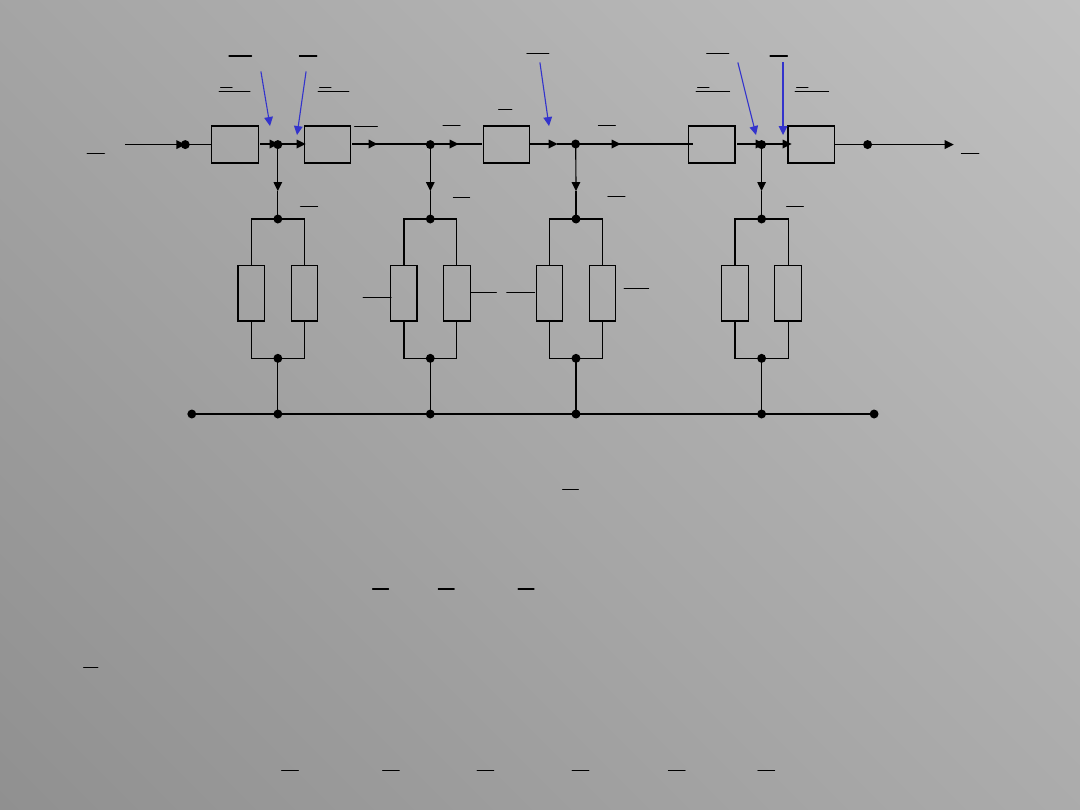
Strata napięcia w odcinku 2D jest równa
Napięcie w punkcie 2 jest równe
D
D
U
U
U
2
2
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
D
T
D
T
D
D
T
D
T
D
D
D
D
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
2
2
2
2
3
2
2
2
2
2
2
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
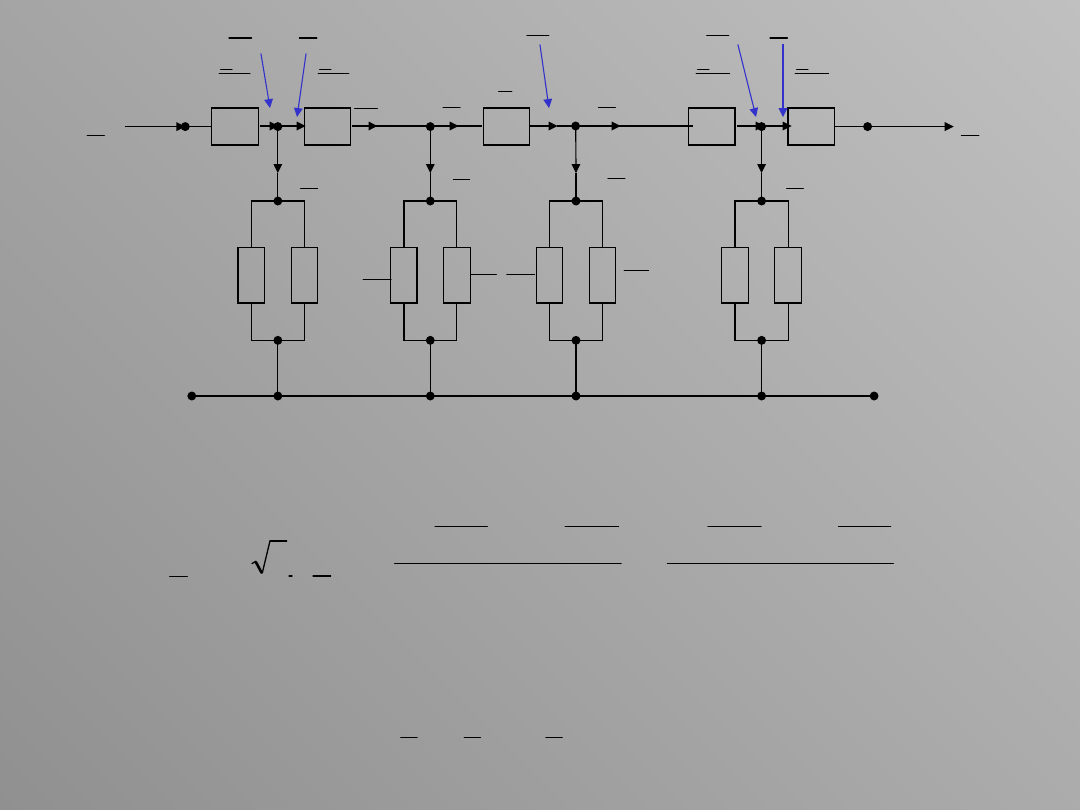
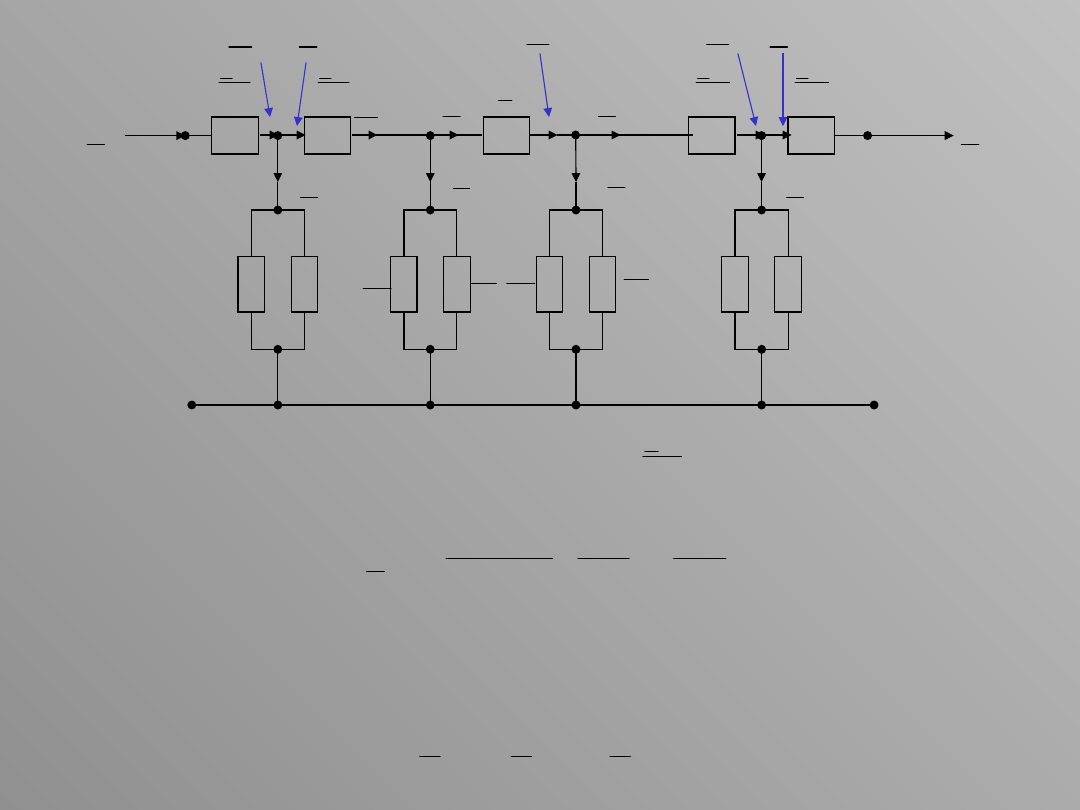
Przepływ mocy w odcinku 2D (przez impedancję ) powoduje
powstanie straty mocy (podłużna strata), która jest równa
2
2
T
Z
2
2
2
2
2
2
2
2
T
T
D
D
D
D
X
j
R
U
Q
P
S
Moc płynąca na początku odcinka 2D jest równa sumie mocy na
końcu tego odcinka i podłużnej straty mocy, powstającej w tym
odcinku
D
D
D
S
S
S
2
2
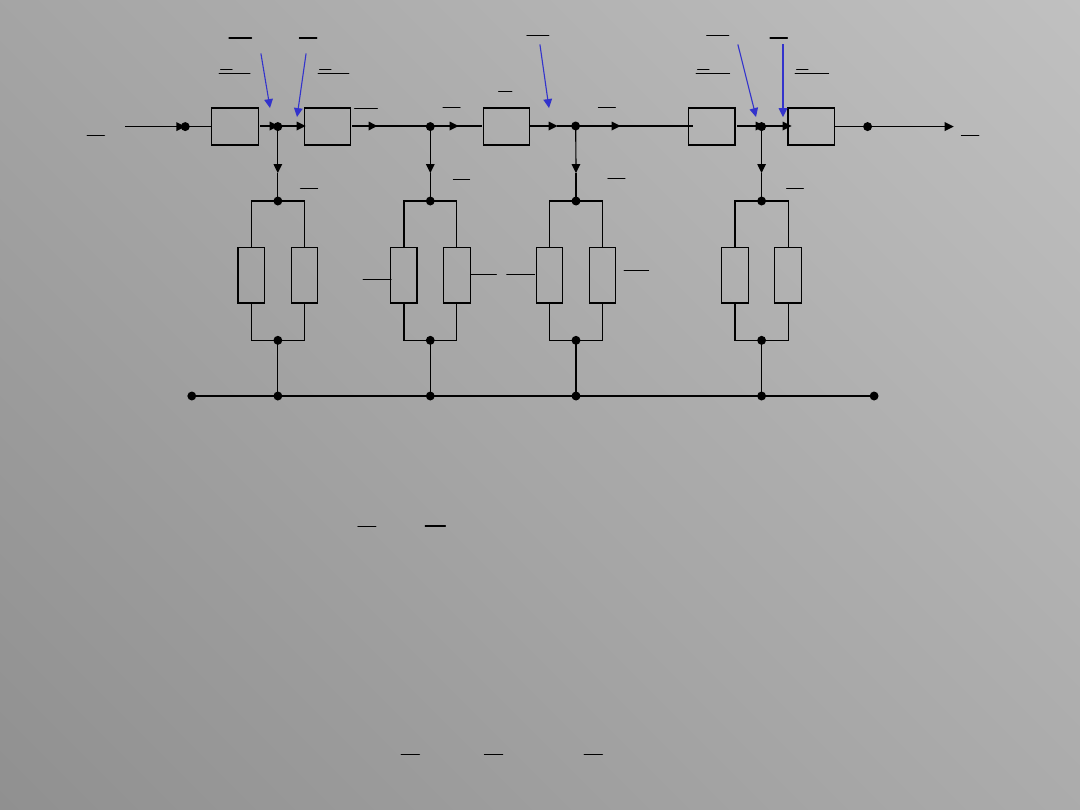
Moc płynąca przez przewodności poprzeczne transformatora
Moc płynąca w odcinku C2, dopływająca do punktu 2, zgodnie z
prawem Kirchhoffa, jest równa
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
2
2
2
2
2
2
2
2
U
jB
G
U
Y
S
T
T
*
T
2
2
2
S
S
S
D
'
C
Jest to moc o charakterze indukcyjnym.
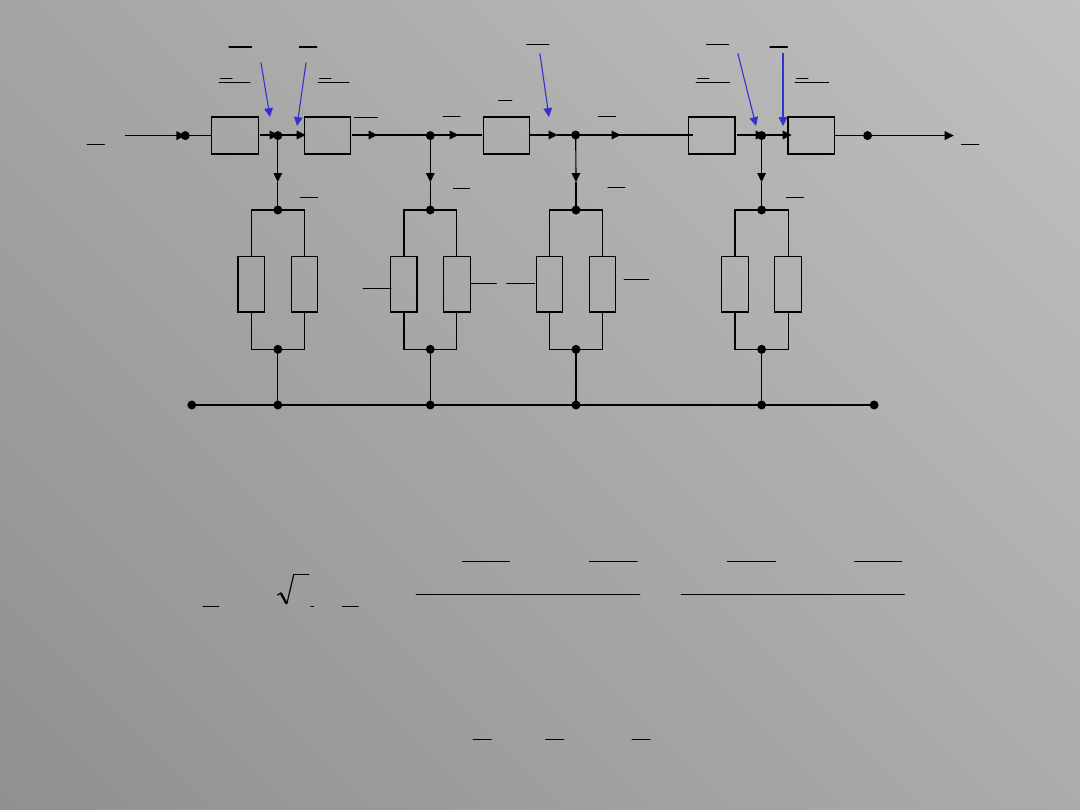
Przepływ tej mocy powoduje powstanie kolejnej straty napięcia na
połowie impedancji transformatora T2 – w odcinku C2
Napięcie w punkcie C jest równe
2
2
C
C
U
U
U
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
T
'
C
T
'
C
T
'
C
T
'
C
C
C
C
Przepływ mocy w odcinku C2 (przez impedancję ) powoduje
powstanie straty mocy (podłużna strata), która jest równa
2
2
T
Z
2
2
2
2
2
2
2
2
2
2
2
T
T
'
C
'
C
C
X
j
R
U
Q
P
S
Moc płynąca na początku odcinka C2 jest równa sumie mocy na
końcu tego odcinka i podłużnej straty mocy, powstającej w tym
odcinku
2
2
2
C
'
C
C
S
S
S
Teraz można obliczyć moc płynącą przez połowę przewodności
poprzecznej linii L (na końcu schematu zastępczego tej linii)
2
2
2
L
L
C
C
B
j
G
U
S
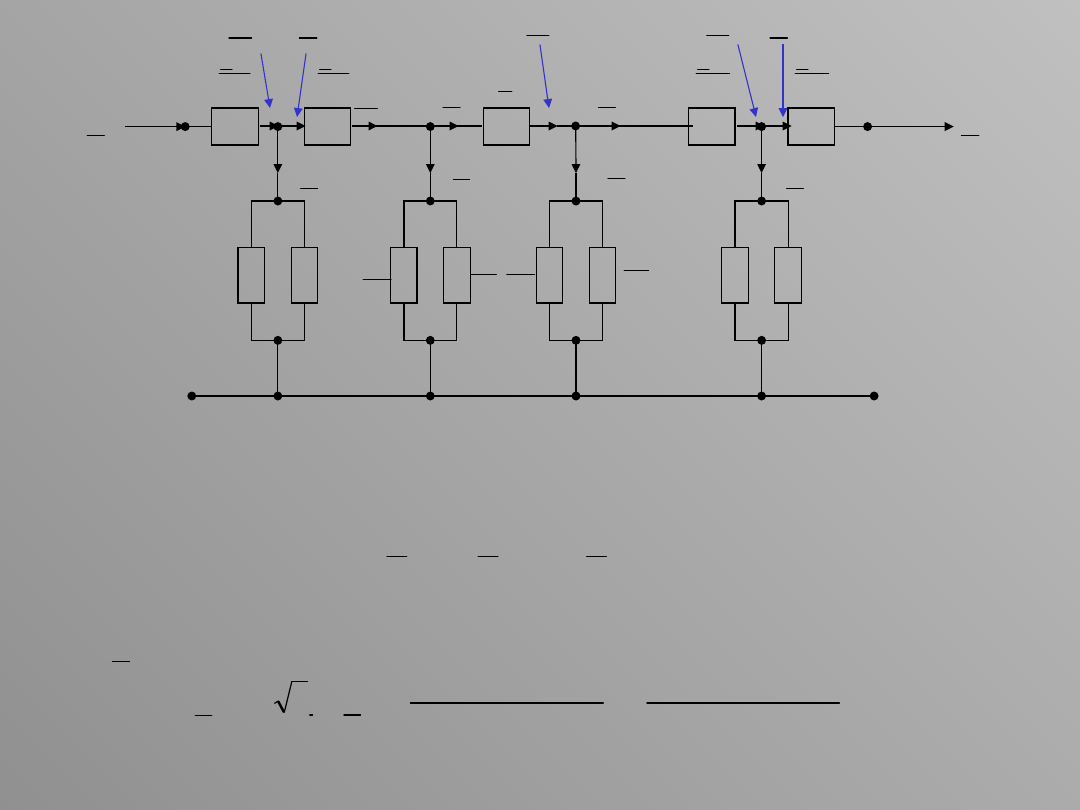
Jest to moc o charakterze pojemnościowym.
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
Moc płynąca w odcinku BC (dopływająca do punktu C) jest sumą
mocy wypływających z tego punktu
C
C
'
BC
S
S
S
2
Przepływ tej mocy powoduje powstanie straty napięcia na impedancji
linii Z
L
C
L
'
BC
L
'
BC
C
L
'
BC
L
'
BC
B
BC
BC
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
3
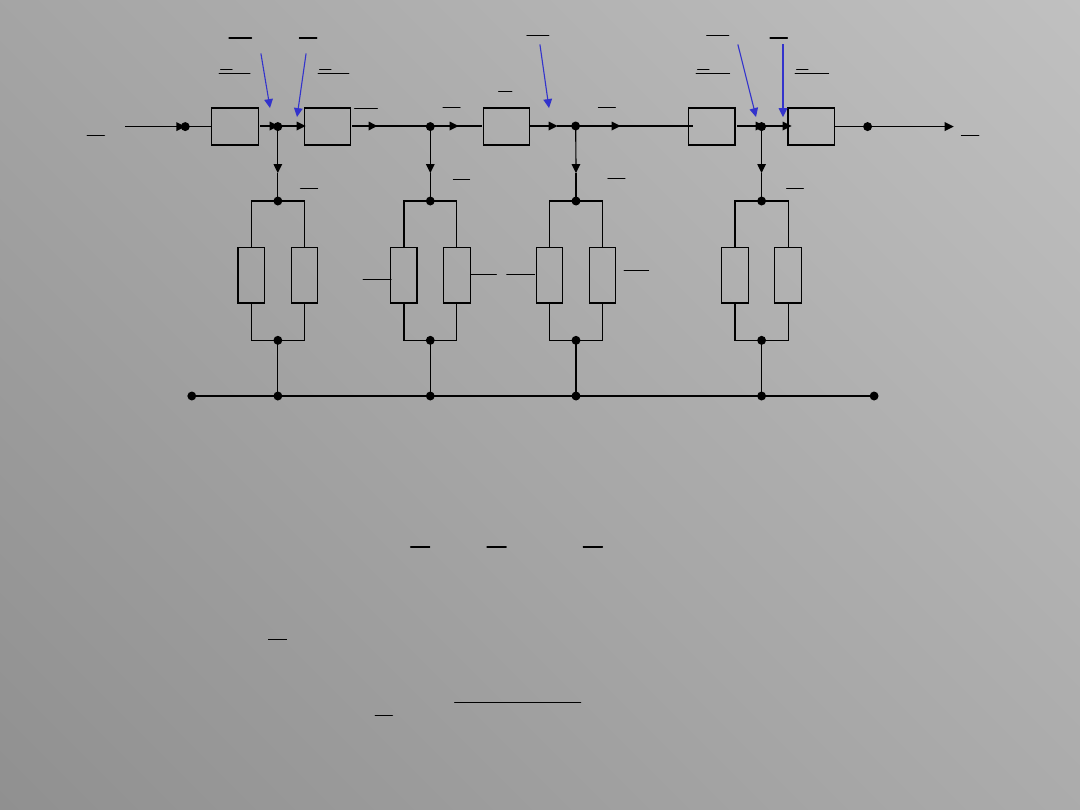
Napięcie w punkcie B jest więc równe
BC
C
B
U
U
U
Przepływ tej mocy powoduje również powstanie straty mocy na
impedancji linii Z
L
, która jest równa
L
L
C
'
BC
'
BC
BC
X
j
R
U
Q
P
S
2
2
2
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
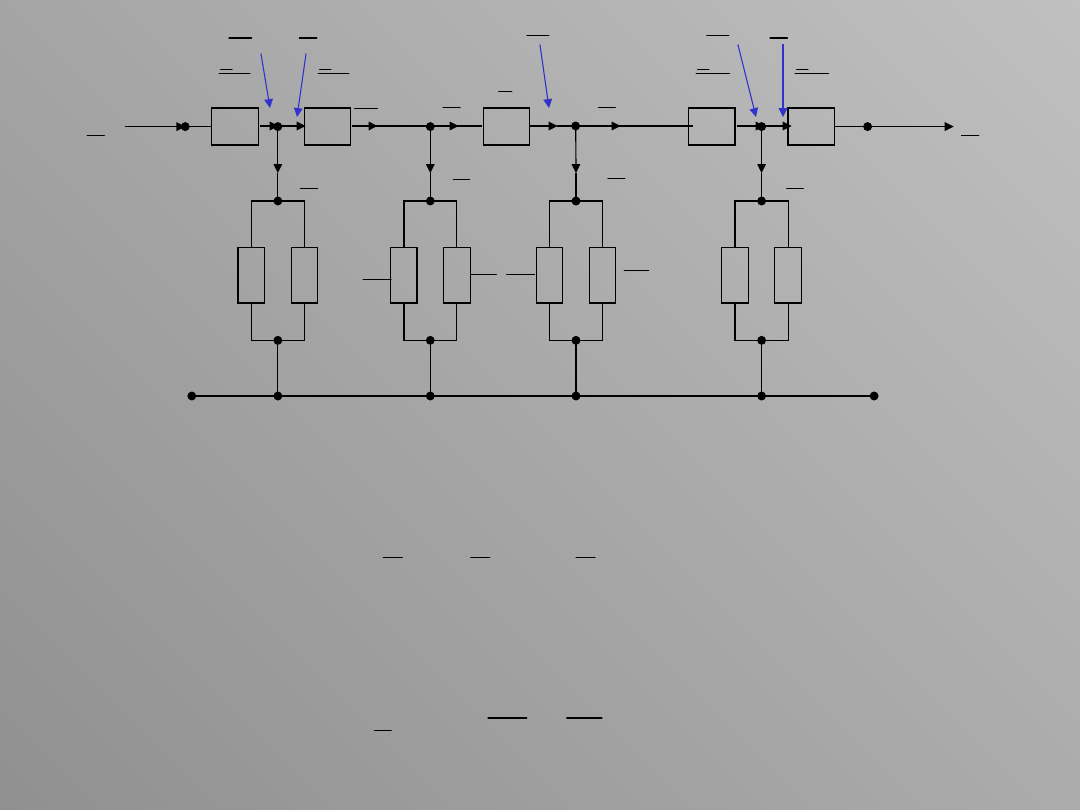
Moc płynąca na początku odcinka BC jest równa sumie mocy na końcu tego
odcinka i podłużnej straty mocy, powstającej w tym odcinku
BC
'
BC
BC
S
S
S
Moc płynąca przez połowę przewodności poprzecznej linii L (na początku
schematu zastępczego tej linii)
2
2
2
L
L
B
B
B
j
G
U
S
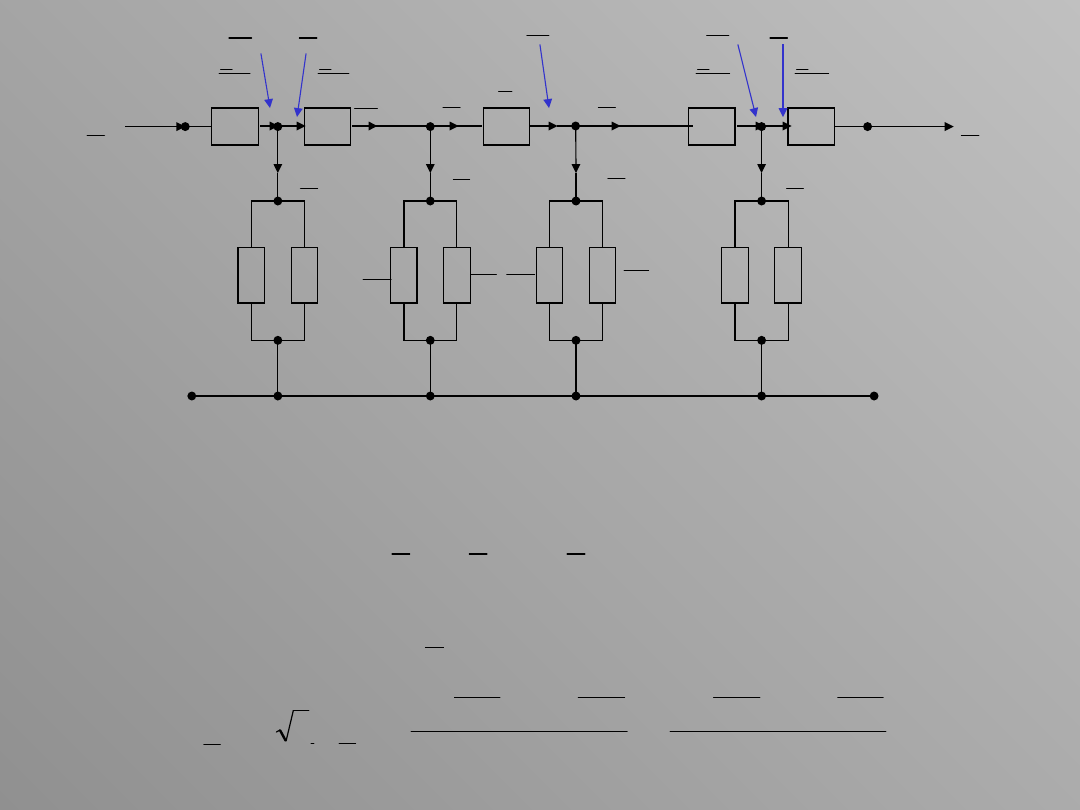
Moc płynąca w odcinku 1B (dopływająca do punktu B) jest sumą mocy
wypływających z tego punktu
Przepływ tej mocy powoduje powstanie straty napięcia na połowie
impedancji transformatora Z
T1
(w odcinku 1B)
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
B
BC
'
B
S
S
S
1
B
T
'
B
T
'
B
B
T
'
B
T
'
B
B
B
B
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
2
2
2
2
3
1
1
1
1
1
1
1
1
1
1
1
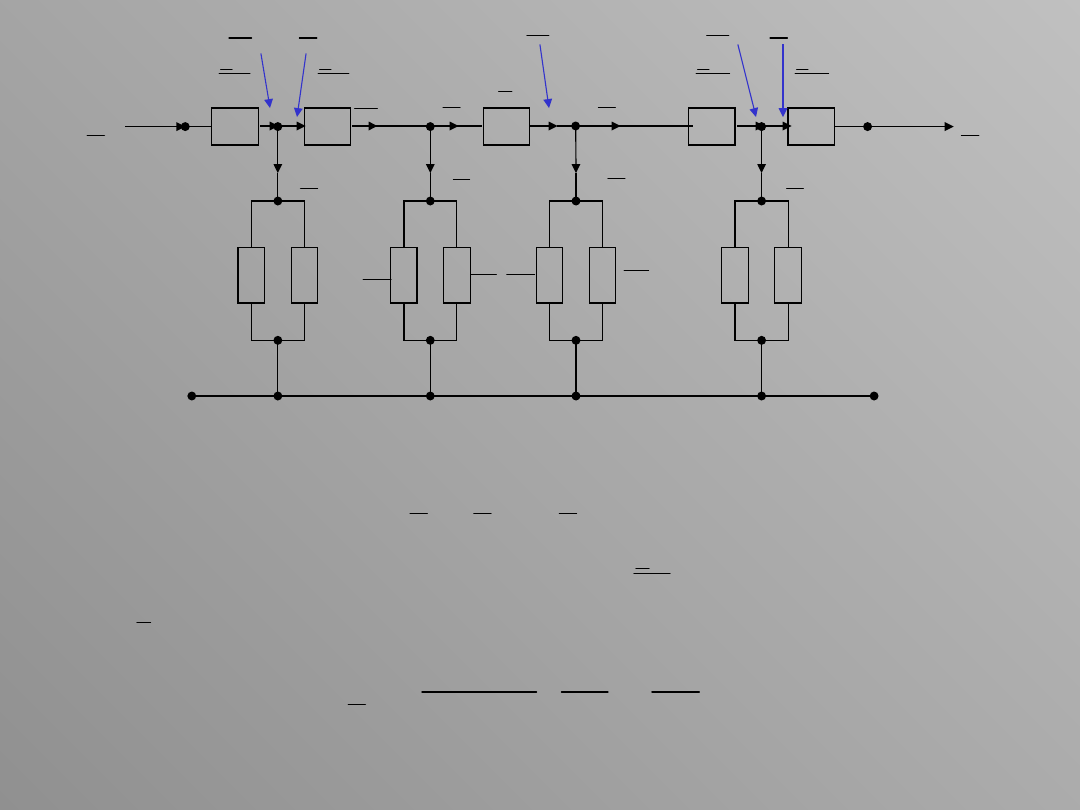
Napięcie w punkcie 1 jest równe
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
B
1
B
1
U
U
U
Przepływ mocy w odcinku 1B (przez impedancję ) powoduje
powstanie straty mocy (podłużna strata), która jest równa
2
1
T
Z
B
S
1
2
2
1
1
2
2
2
1
2
1
1
T
T
'
B
'
B
B
X
j
R
U
Q
P
S
Moc płynąca na początku odcinka 1B jest równa sumie mocy na końcu
tego odcinka i podłużnej straty mocy, powstającej w tym odcinku
B
'
B
B
S
S
S
1
1
1
Moc płynąca przez przewodność poprzeczną transformatora T1
2
1
1
1
2
1
1
1
U
jB
G
U
Y
S
T
T
*
T
Moc dopływająca do punktu 1
B
'
A
S
S
S
1
1
1
Przepływ tej mocy powoduje powstanie straty napięcia na połowie
impedancji transformatora Z
T1
(w odcinku A1)
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
3
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
T
'
A
T
'
A
T
'
A
T
'
A
A
A
A
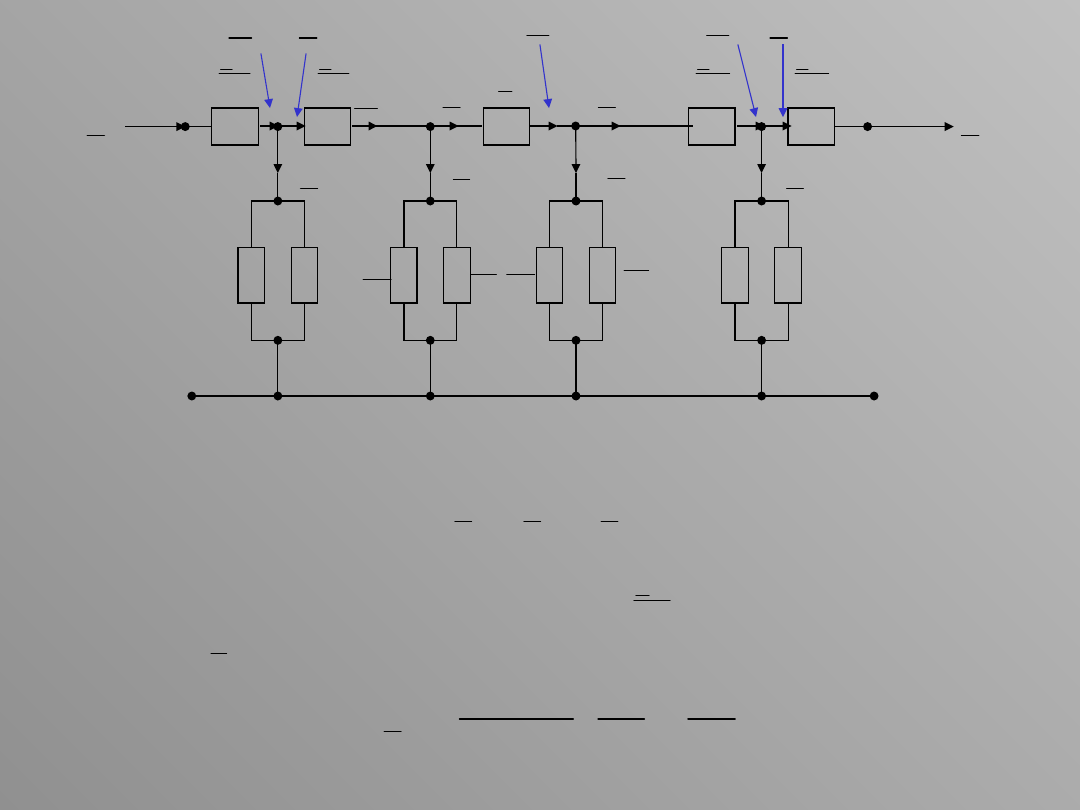
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
Napięcie na początku układu – w punkcie A – jest równe
1
1
A
A
U
U
U
Przepływ mocy w odcinku A1 (przez impedancję ) powoduje
powstanie straty mocy (podłużna strata), która jest równa
2
1
T
Z
1
A
S
2
2
1
1
2
1
2
1
2
1
1
T
T
'
B
'
B
A
X
j
R
U
Q
P
S
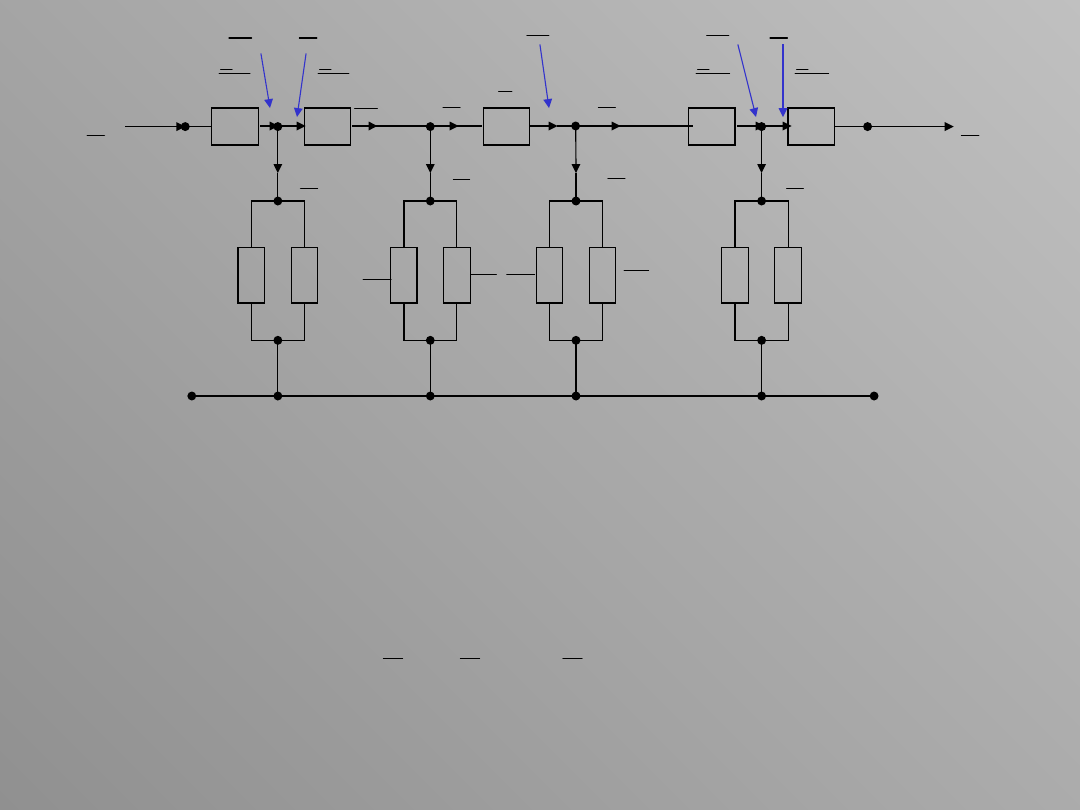
Moc płynąca na początku odcinka A1 jest równa sumie mocy na
końcu tego odcinka i podłużnej straty mocy, powstającej w tym
odcinku
1
1
A
'
A
A
S
S
S
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
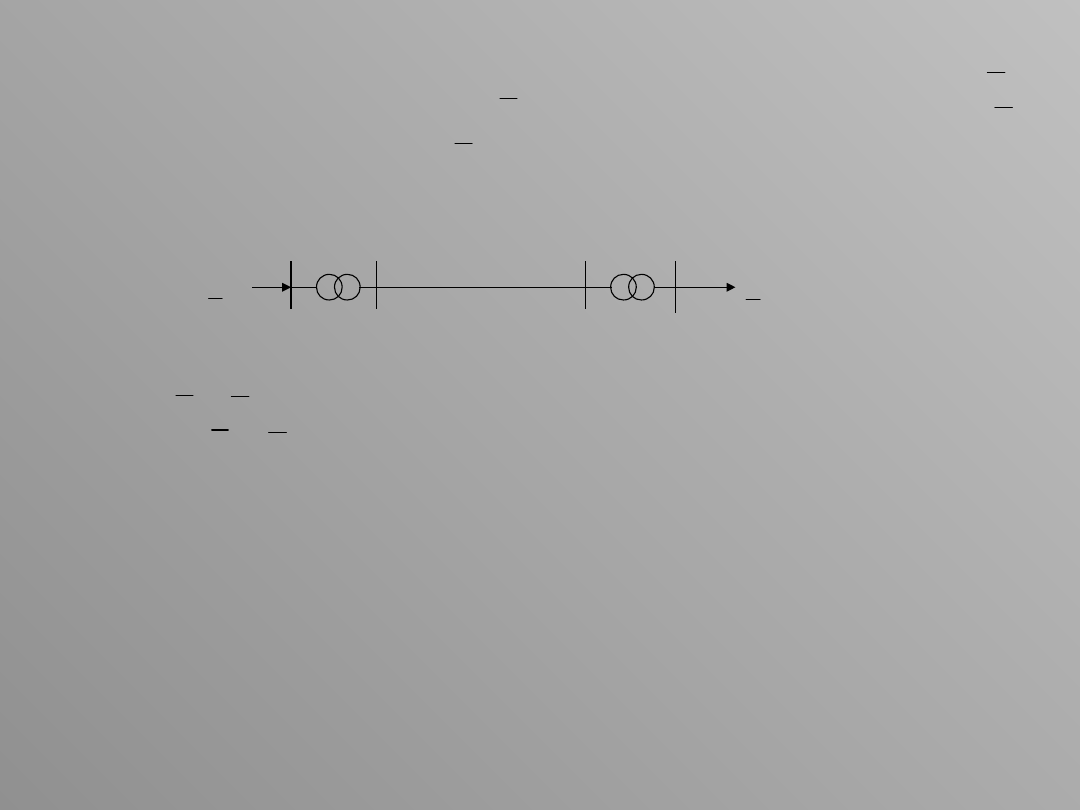
4. Dany jest układ przesyłowy pokazany na rysunku, do którego
dopływa moc . Napięcie na początku układu wynosi . Obliczyć
moc odbieraną z układu oraz napięcie na końcu układu .
A
S
D
U
D
S
A
U
A
S
D
S
U
A
U
B
U
C
U
D
T1 L T2
1
2
A B C D
Dane: , , parametry podłużne i poprzeczne elementów
układu.
Obliczyć: , .
D
U
D
S
A
S
A
U
Wszystkie parametry schematu zastępczego oraz moc i napięcie
sprowadzone są do jednego, wybranego poziomu napięcia.
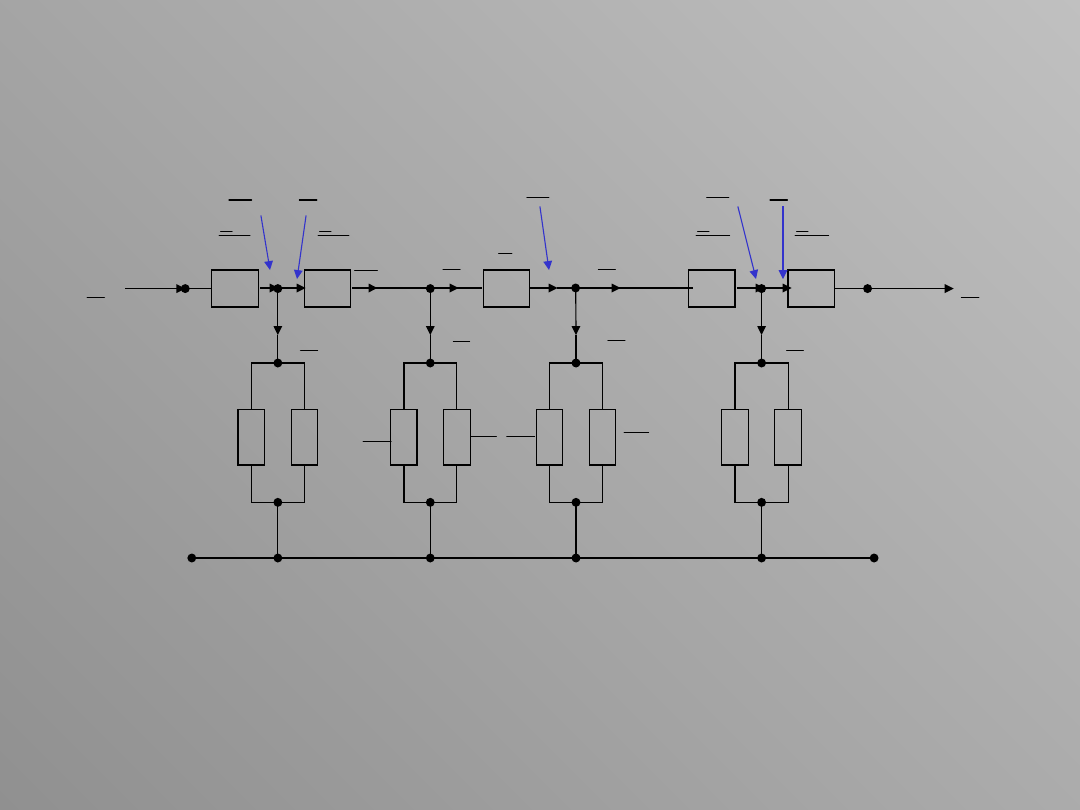
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
Jeśli znane jest napięcie na początku układu , to napięcie na
końcu układu jest równe
A
U
AD
A
D
U
U
U
- całkowita strata napięcia w układzie, przeliczona na wybrany
poziom napięcia
AD
U
1
1
2
2
A
B
BC
C
D
AD
U
U
U
U
U
U
Strata napięcia w odcinku A1 jest równa
Napięcie w punkcie 1 jest równe
A
A
U
U
U
1
1
A
T
A
T
A
A
T
A
T
A
A
A
A
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
2
2
2
2
3
1
1
1
1
1
1
1
1
1
1
1
Strata mocy w odcinku A1 jest równa
2
2
1
1
2
2
1
2
1
1
T
T
A
A
A
A
X
j
R
U
Q
P
S
Moc płynąca na końcu odcinka A1 jest równa różnicy mocy na
początku tego odcinka i podłużnej straty mocy, powstającej w tym
odcinku
1
1
A
A
'
A
S
S
S
Moc płynąca przez przewodności poprzeczne transformatora
Moc płynąca na początku odcinka 1B, zgodnie z prawem Kirchhoffa
2
1
1
1
2
1
1
1
U
jB
G
U
Y
S
T
T
*
T
B
'
A
B
S
S
S
1
1
1
Przepływ tej mocy powoduje powstanie kolejnej straty napięcia na
połowie impedancji transformatora T1 – w odcinku 1B
Napięcie w punkcie B jest równe
B
B
U
U
U
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
3
U
R
Q
X
P
j
U
X
Q
R
P
Z
I
U
T
B
T
B
T
B
T
B
B
B
B
Natomiast podłużna strata mocy na połowie impedancji
transformatora jest równa
2
2
1
1
2
1
2
1
2
1
1
T
T
B
B
B
X
j
R
U
Q
P
S
czyli moc płynąca na końcu tego odcinka jest równa
B
B
B
S
S
'
S
1
1
1
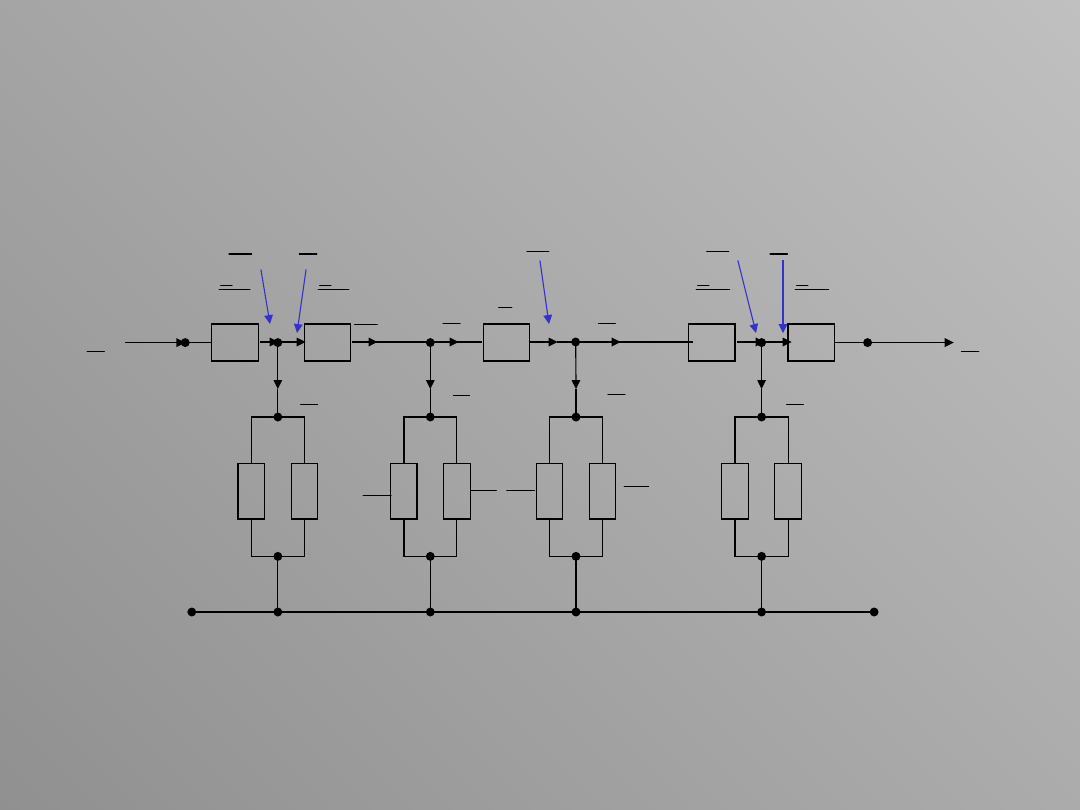
W ten sam sposób oblicza się straty napięcia i straty mocy w
kolejnych odcinkach układu
A 1 B C 2
D
2
1
T
Z
2
1
T
Z
L
Z
2
2
T
Z
2
2
T
Z
A
S
D
S
1
S
B
'
S
1
B
S
BC
S
C
S
2
C
S
2
S
1
T
G
2
1
L
T
G
B
2
2
L
L
G
B
2
L
B
2
T
G
2
T
B
B
S
1
1
A
'
S
BC
'
S
2
C
'
S
D
S
2
Document Outline