Introduction

Lecture Outline

• Introduction
• System Optimization
• Modeling
• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks
• Definitions
• Concluding Remarks

Lecture Outline

• Introduction

• System Optimization
• Modeling
• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks
• Definitions
• Concluding Remarks

Introduction

• In recent years we can observe very fast

development of computer networks

• Nowadays in most areas of human life computer

networks play a very significant role

• Thus, there is growing need to develop various

methods to improve network performance

• One of possible approaches is to provide effective

methods for optimization of computer networks

Globecom 2010, Miami, USA

Pinging www.nba.com

c:\>ping www.nba.com
Pinging a1570.gd.akamai.net [150.254.186.92] with 32 bytes of

data:

Reply from 150.254.186.92: bytes=32 time=5ms TTL=58
Reply from 150.254.186.92: bytes=32 time=5ms TTL=58
Reply from 150.254.186.92: bytes=32 time=6ms TTL=58
Reply from 150.254.186.92: bytes=32 time=5ms TTL=58

15000k

m  50

ms

Pinging www.nba.com

c:\>ping www.nba.com
Pinging a1570.gd.akamai.net [150.254.186.92] with 32 bytes of

data:

Reply from 150.254.186.92: bytes=32 time=5ms TTL=58
Reply from 150.254.186.92: bytes=32 time=5ms TTL=58
Reply from 150.254.186.92: bytes=32 time=6ms TTL=58
Reply from 150.254.186.92: bytes=32 time=5ms TTL=58

4

0

0

k

m

Akamai

• Akamai provides services to companies that

publish

content on the Internet

• The idea is to more

efficiently deliver content

to users

browsing the Web and downloading content

• Akamai

transparently mirrors

the source content (e.g.,

HTML, CSS, audio, video, software downloads) delivered
from customer servers

• Akamai has deployed the world’s largest globally-

distributed computing platform, with more than

95,000

servers

in 71 countries within nearly 1,900 networks

• Akamai delivers between

15-30% of all Web traffic

• Akamai delivers daily Web traffic reaching more than

5

Terabits per second

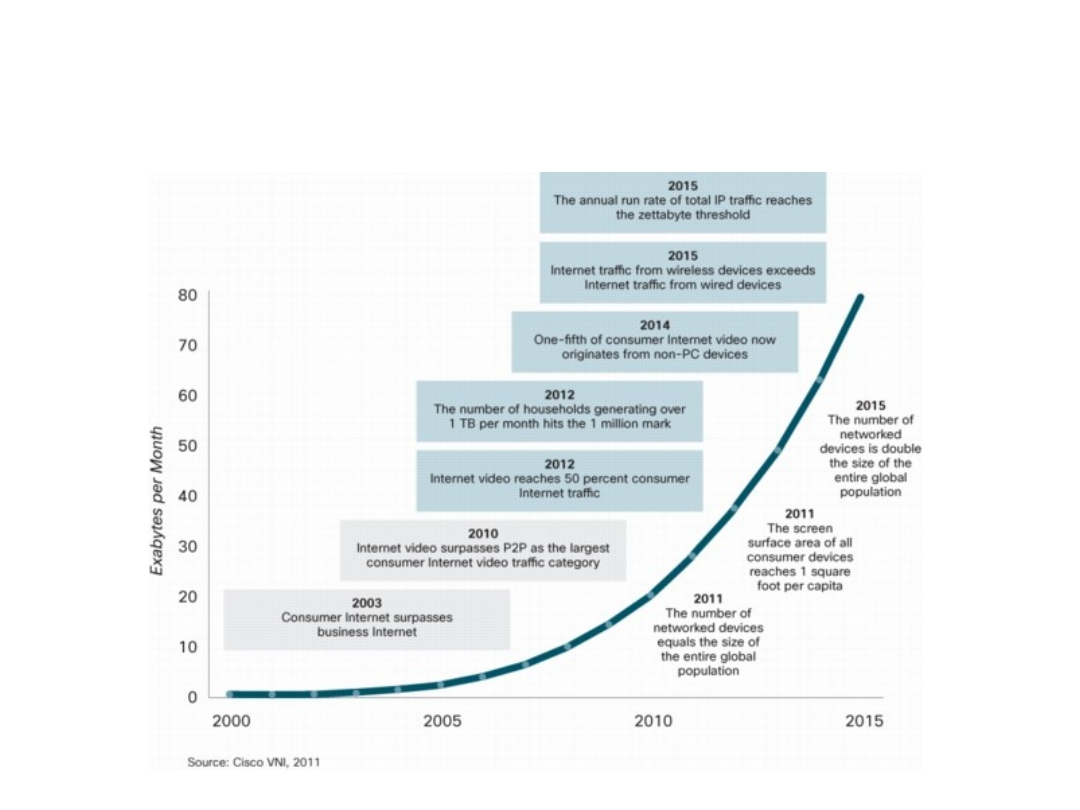
Traffic milestones

Global Consumer Internet Traffic, 2010-

2015, by Geography (EB per Month)

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2010-2015]

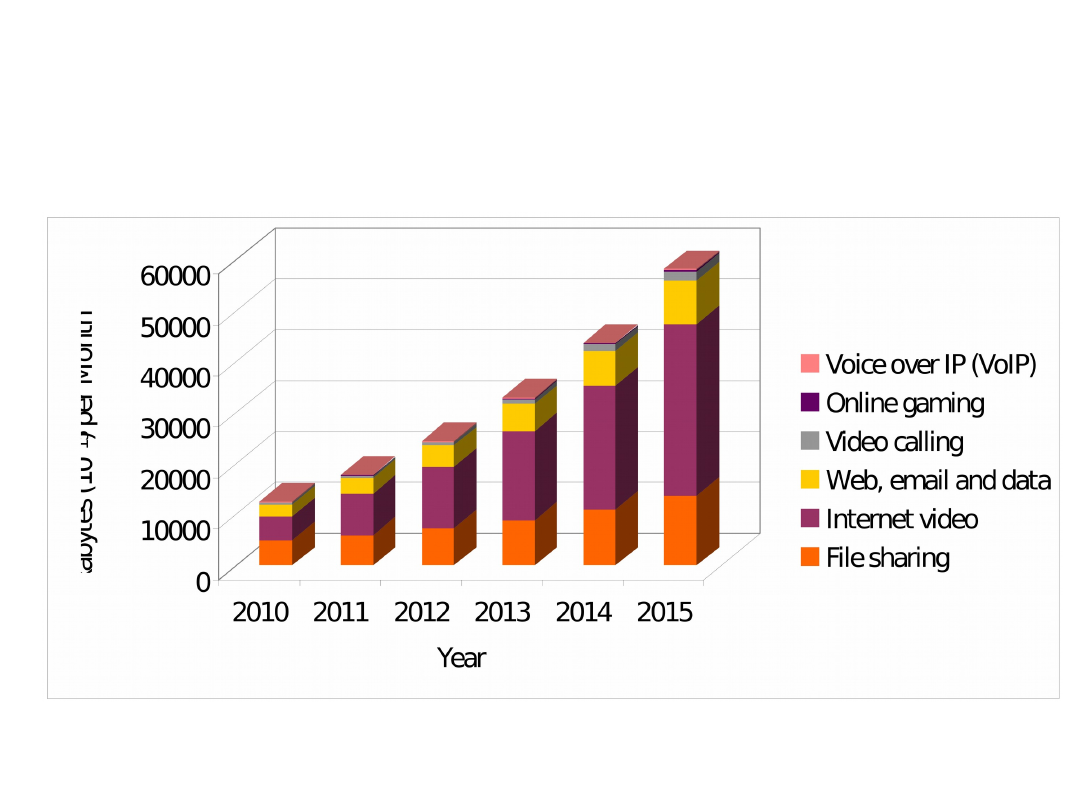
Global Consumer Internet Traffic, 2010-

2015, by Subsegment (EB per Month)

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2010-2015]

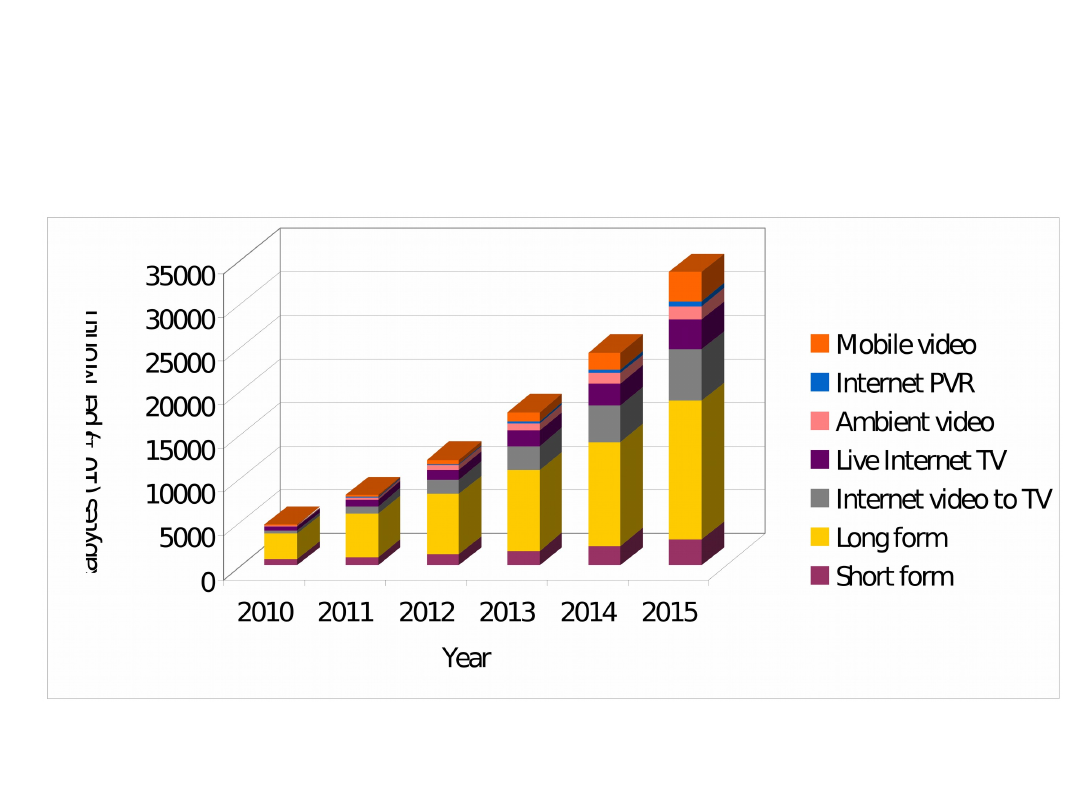
Global Consumer Internet Video, 2010-

2015, by Category (EB per Month)

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2010-2015]

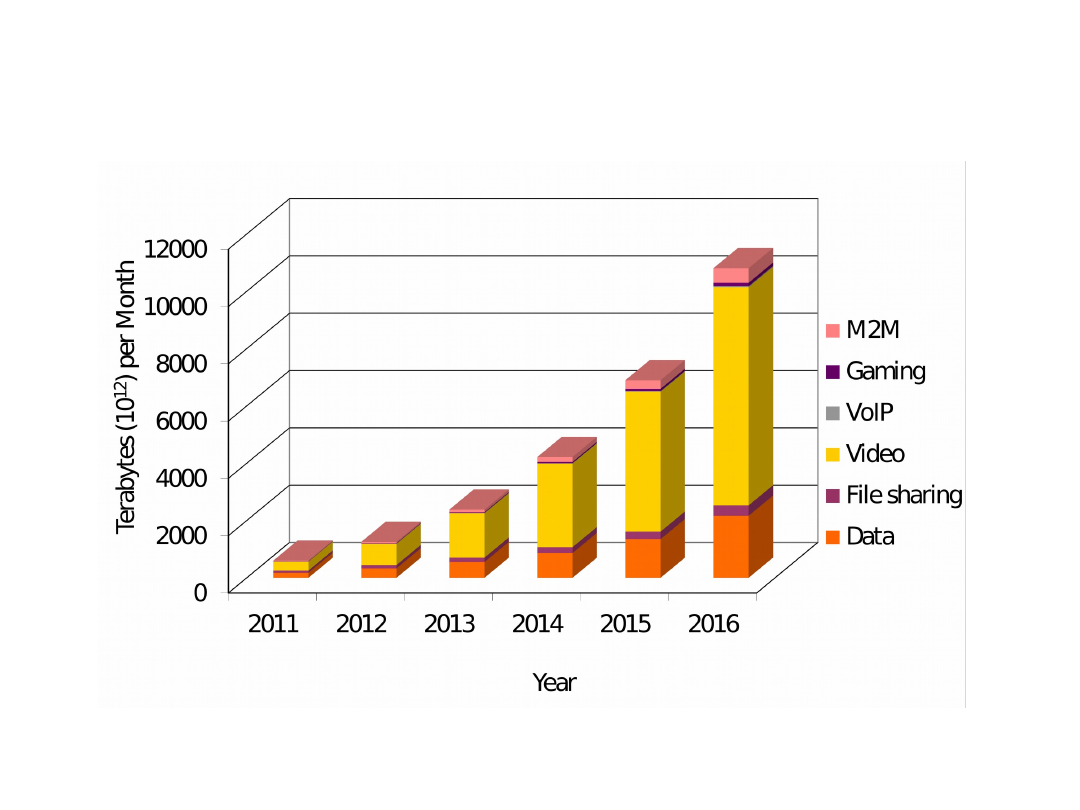
Global Mobile Data Traffic, 2011-2016,

by Application Category (TB per

Month)

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2011-2016]

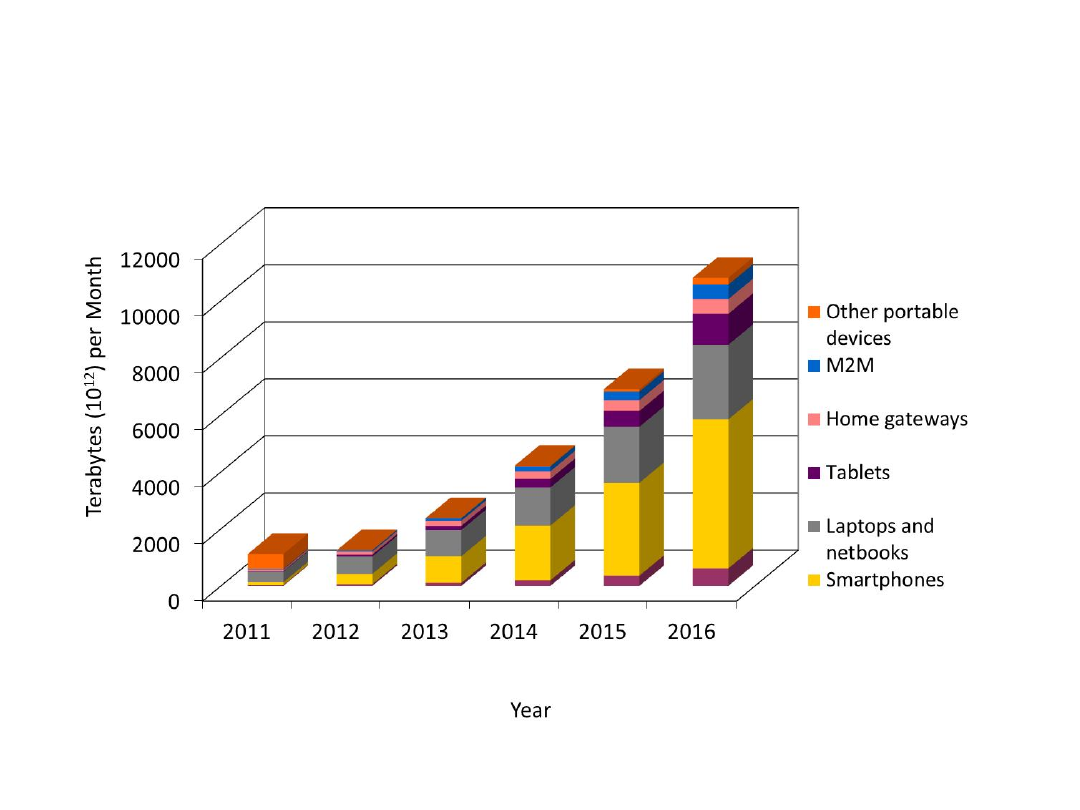
Global Mobile Data Traffic, 2011-2016,

by Device Type (TB per Month)

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2011-2016]

[Source: Cisco Visual Networking Index: Forecast and Methodology, 2011-2016]

Lecture Outline

• Introduction

• System Optimization

• Modeling
• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks
• Definitions
• Concluding Remarks

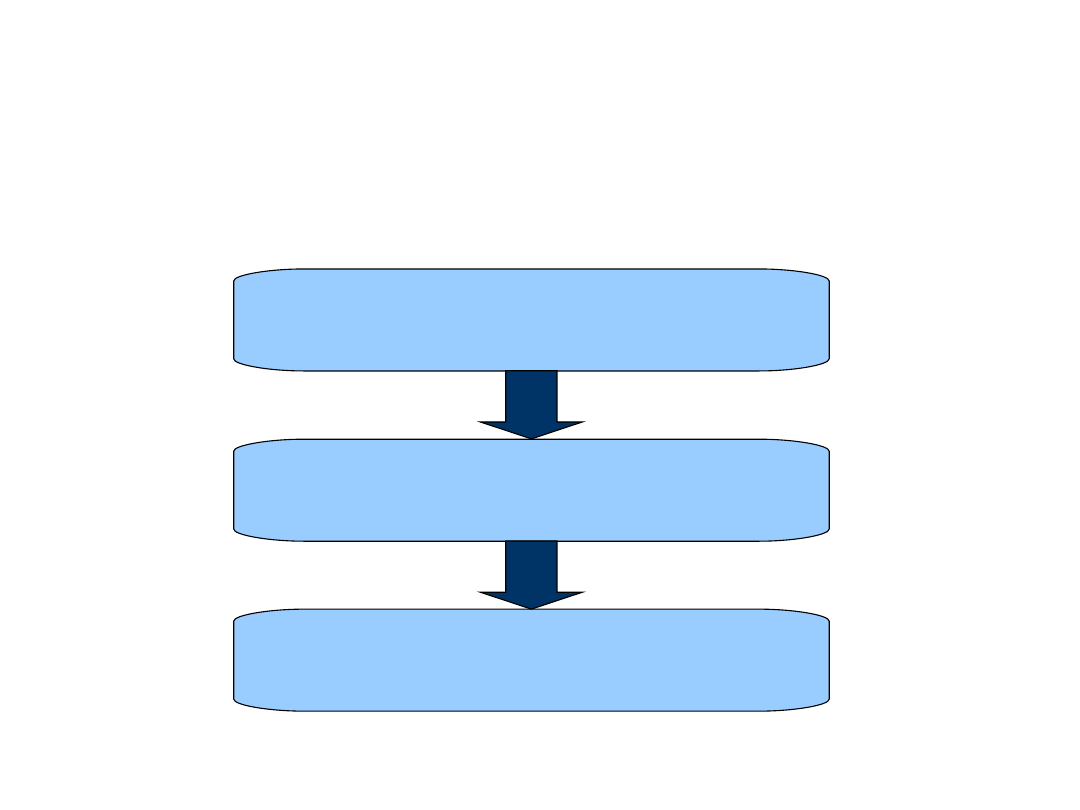
Modeling and Optimization

Problem Formulation

Modeling

Optimization

Optimization Goals

• Financial savings
• Operation improvement
• Work efficiency
• Improvement of reliability
• Improvement of security
• Reduction of resource consumption

Financial Savings Example

(1)

• SolveIT Software company was started by

Zbigniew Michalewicz

• One of systems offered by SolveIT Software

support to process of leasing cars selling in
General Motors

• Each year about 1 500 000 used cars return to

GM from leasing

• For each car a decision is to be made where to

send the car for selling, there are about 50 such
places in USA

Financial Savings Example

(2)

• The solution space (problem size) is

1500000

50

=6.4x10

308

• Savings about 100 USD per one car, yields 150

000 000 USD per year

• The proposed optimization system uses

computational inteligence and takse into
account many various constraints

• Additional advantage is the employment

reduction

Optimization Objectives

• Cost (e.g., capacity)
• Delay
• Throughput
• Reliability
• Security
• Resource consumption
• Etc.

Cost Objective Example (1)

• SolveIT Software System for GM
• The objective is to minimize to transport cost of

leasing cars for selling

• 8 cars can be transported on a one truck
• The cost of one truck is 800 USD
• Two possible objective functions:

– Linear function (approximation of real

situation, but easy for optimization)

– Piecewise linear function (difficult for

optimization)

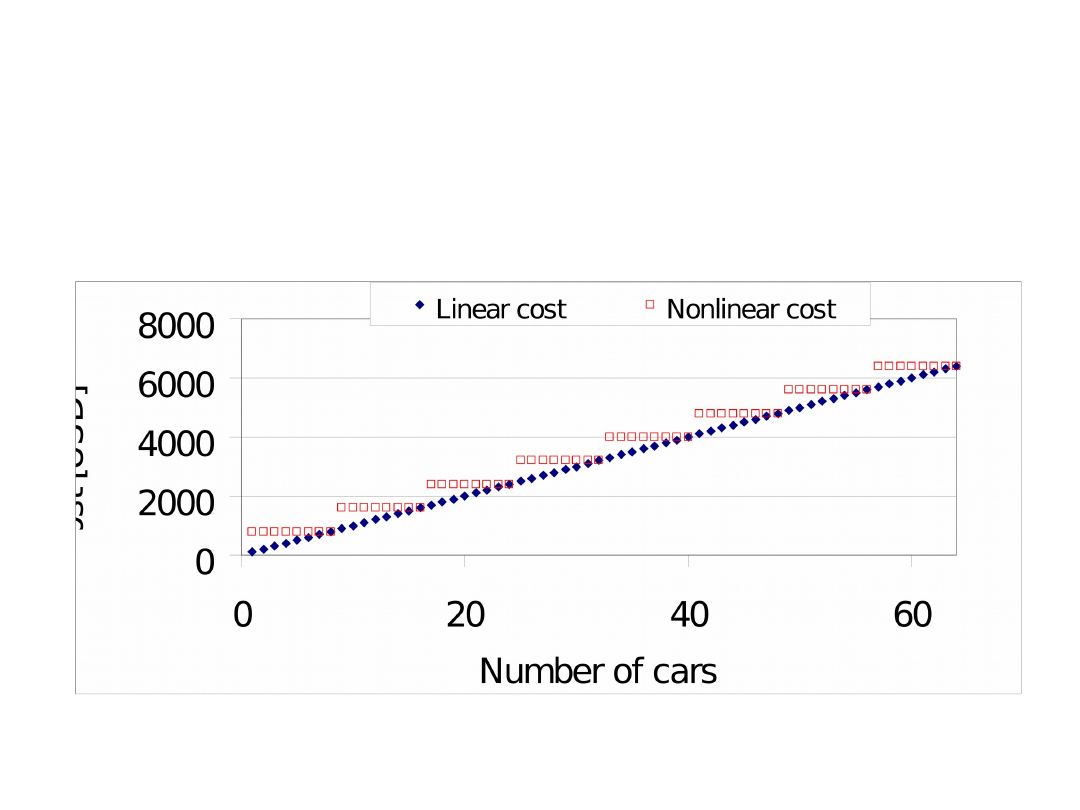
Cost Objective Example (2)

Reliability Objective

Example

• A reliable computer network topology is to be

designed, i.e., there must be at least two disjoint
paths for each node pair

• Paths can be:

– Link disjoint – the network is protected

against a single link failure

– Node disjoint – the network is protected

against a single node (e.g., router) failure

• 3 disjoint paths protect the network against a

double failure

Capacity Objective Example

• A computer network is to be designed to send the

given traffic and minimize the overall network cost

• The network cost is defined as the cost of capacity

installed on network links

• The capacity cost depends on the link length and

other factors

• The cost can be: linear, convex, piecewise linear,

nonlinear, etc.

Optimization Constraints

• Cost (e.g., capacity)
• Delay
• Throughput
• Reliability
• Security
• Resource consumption
• Etc.

Constraints Example (1)

• SolveIT Software System for GM takes into

account many constraints related to the process
of cars’ selling, e.g.,:

– White cars are not well sold in Florida
– Cabrio cars are not popular in Alaska
– There was an car crash caused by a AAA car in

Colorado, thus it will be difficult to sell AAA
cars for some time in Colorado

– Hybrid cars are very popular in California

Constraints Example (2)

• In the network design problem with capacity

objective there can be additional constraints:

– Network realibility, i.e., two disjoint paths for

each node pair for a given demand value

– Link capacity is upper and lower bounded

according to technological and physical
constraints (e.g., number of fibers, number of
ports in the router, etc.)

– Network delay cannot exceed a given threshold

Lecture Outline

• Introduction
• System Optimization

• Modeling

• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks
• Definitions
• Concluding Remarks

Modeling

• To enable optimization, first a mathematical

model of the considered problem must be
formulated

• The model includes variables, constants,

objective function and constraints

• The size of the model (i.e., number of variables

and constraints) should be as small as possible

• Since the most effective optimization methods

are developed for linear problems, often
nonlinear objective function and constraints are
approximated using linear functions

SolveIT Example (1)

indicies
c = 1,2,…,C

cars

p = 1,2,…,Pauction places
constants
t

cp

transport cost of car c to place p

color(c)

color of car c

brand(c)

brand (automaker) of car c

typeI(c)

type of car c

state(p)

state of auction place p

SolveIT Example (2)

variable
x

cp

= 1, if car c is sent to place p; 0, otherwise

objective
minimize 

c



p

x

cp

t

cp

constraints


p

x

cp

= 1, c = 1,2,…,C

x

cp

= 0, for color(c) = WHITE, state(p) = Florida

x

cp

= 0, for brand(c) = AAA, state(p) = Colorado

x

cp

= 0, for type(c) = cabrio, state(p) = Alaska

x

cp

= 1, for type(c) = hybrid, state(p) = California.

Network Design Example (1)

indices
d = 1,2,…,D

demands

p = 1,2,…,P

d

candidate paths for demand d

e = 1,2,…,Elinks
constants



edp

= 1, if link e belongs to path p realizing

demand d; 0, otherwise

h

d

volume of demand d



e

unit (marginal) cost of link e

Network Design Example (2)

variables
x

dp

flow allocated to path p of demand d

(continuous

non-negative)

y

e

capacity of link e (continuous non-negative)

objective
minimize F = 

e



e

y

e

constraints


p

x

dp

= h

d

, d = 1,2,…,D



d



p



edp

x

dp

 y

e

, e = 1,2,…,E.

Lecture Outline

• Introduction
• System Optimization
• Modeling

• Optimization Problems

• Algorithms and Optimization Methods
• Computer Networks
• Definitions
• Concluding Remarks

Kinds of Optimization Problems

(1)

• Without constraints
• With constraints
• Linear – objective function and all constraints are

linear

• Nonlinear – objective function or/and at least

one constraint is not linear

• Convex – objective function or/and at least one

constraint is convex

• Continuous – variables are continuous
• Integer – variables are integer

Kinds of Optimization Problems

(2)

• P problems (deterministic polynomial time) – the

solution can be found in polynomial time

• NP problems (nondeterministic polynomial time)

– the solution can be only verified (checked) in
polynomial time

• NP-hard (nondeterministic polynomial time hard)

problems is a class of problems that are, at least
as hard as the hardest problems in NP

• P versus NP problem is one of the most

imporatant unsolved problems

Examples of NP-hard

Problems

• Knapsack problem
• Hamiltonian path problem
• Travelling Salesman Problem (TSP)
• Vertex cover problem
• Graph coloring problem
• 3SAT problem

Problem Size

• The size of the problem is a function of the

number of variables and constraints

• The time needed to solve a problem depands on

the problem size as well as on the construct of
the objective function and constraints

Lecture Outline

• Introduction
• System Optimization
• Modeling
• Optimization Problems

• Algorithms and Optimization Methods

• Computer Networks
• Definitions
• Concluding Remarks

Algorithm

• In mathematics, computer science, and other

related subjects, an algorithm is an effective
method for solving a problem expressed as a
finite sequence of instructions

• The word "algorithm" comes from Muhammed

ibn Musa Alchwarizmi (ىسوم نبببب دمح م هللببا دبع وبأبو عبد الله محمد بن موسى

يمزراوخلببا), persian mathematician that lived in IX

century

• The algorithm can be implemented as computer

programs or some other device

Types of Algorithms (1)

• Polynomial time algorithms – the runninig time

of the algorithm can be limited by a polynomial,
which is a function of the problem size. Problems
that can be solved by polynomial time algorithm
are relatively simple

• Exponential time algorithms - the runninig time

of the algorithm is not polynomial. Problems that
do not have polynomial time algorithms can be
solved by methods like branch and bound

Types of Algorithms (2)

• Exact algorithms can find an optimal solution,

e.g., in the case of linear problems the Simplex
method is an exact algorithm, in the case of
integer problems, the branch and bound method
can provide the optimal solution

• Heuristics provide suboptimal results without

the guarantee of optimality, e.g., evolutionary
algorithm, tabu search, greedy search,
constructive algorithms

Types of Algorithms (3)

• Brute-force (exhaustive search)
• Divide and conquer
• Greedy method
• Linear programming
• Randomized (probabilistic)
• Artificial intelligence

Algorithm Complexity

• Bubble sorting of n element table

– O(n

2

)

• Binary search of sorted database including n

elements

– O(log

2

n)

• Brute force password hacking (n bits length)

– O(2

n

)

• Dijkstra algorithm (shortest path) for n vertex

graph

– O(n

2

)

• Brute force prime number n check

– O(n)

Polynomial versus

Exponential

• Polynomial

algorithm with
complexity 10

5

n

3

• Exponential

algorithm with
complexity 2

n

• 10

9

operations per

1 second

n

10

5

n

3

2

n

20

0.08 sec 0.001 sec

30

0.27 sec

1.07 sec

40

0.64 sec

17 min

50

1.25 sec

13 dni

60

2.16 sec

36 lat

Lecture Outline

• Introduction
• System Optimization
• Modeling
• Optimization Problems
• Algorithms and Optimization Methods

• Computer Networks

• Definitions
• Concluding Remarks

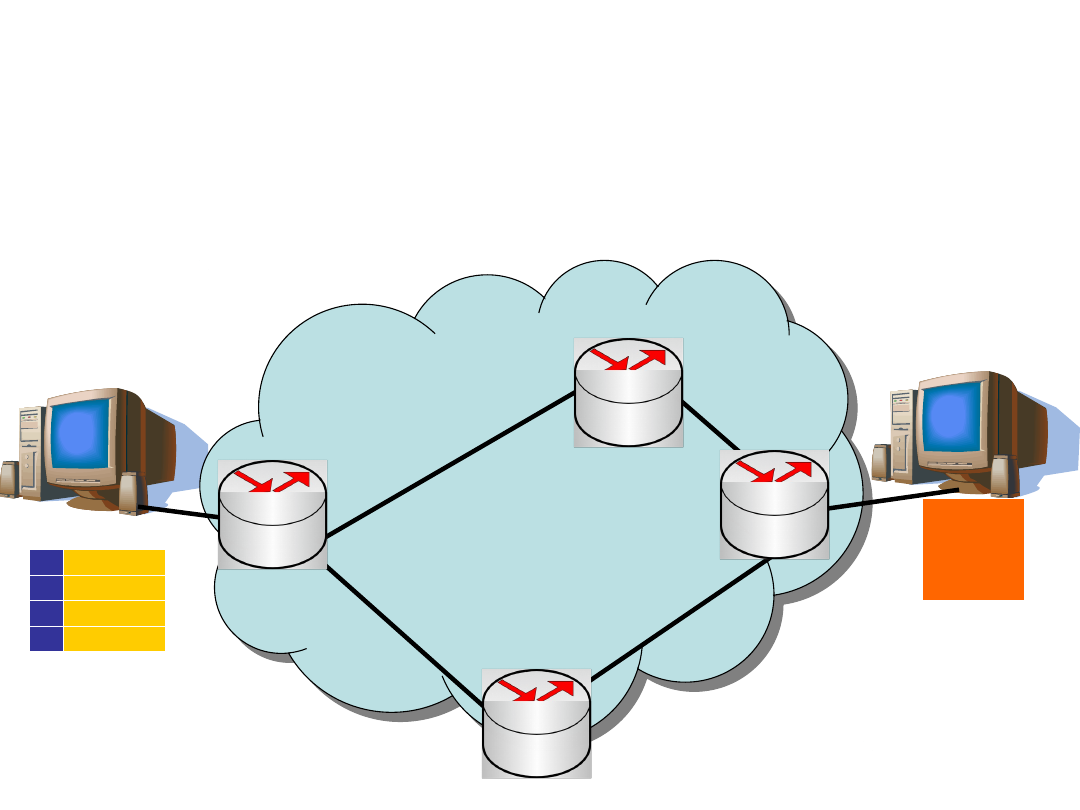
Store and Forward

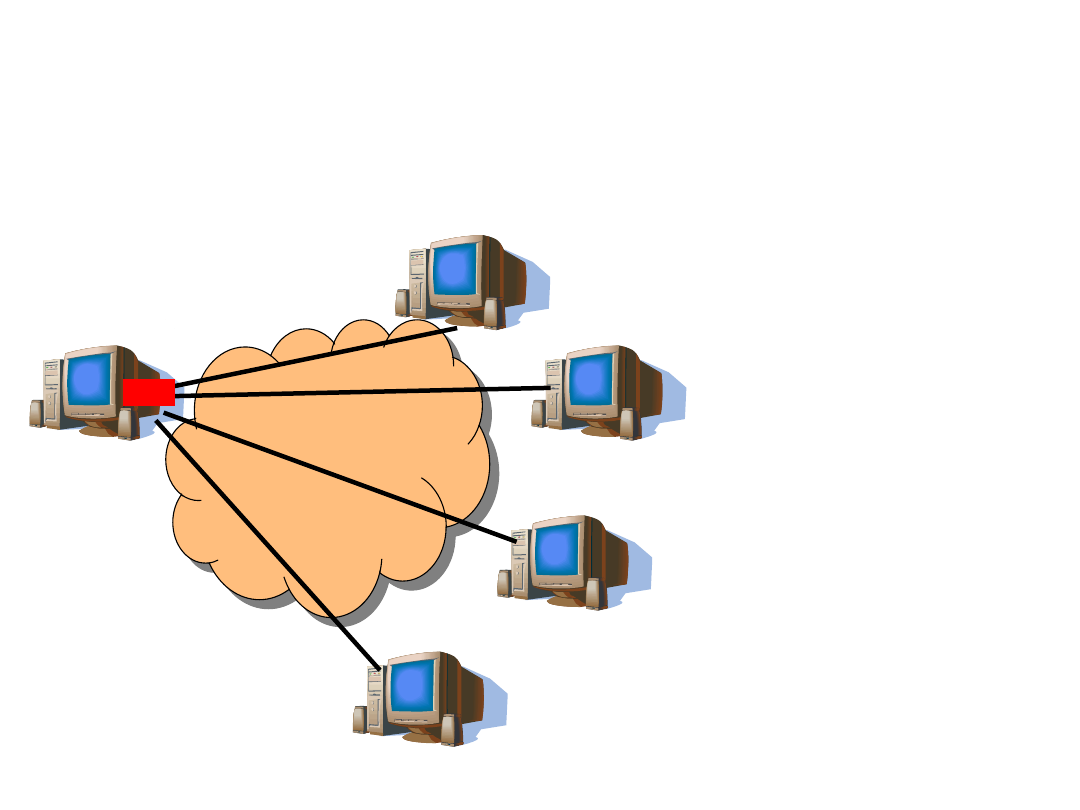
Unicast

• One-to-one – one

source and one
destination

• Examples: IP

protocol, VoIP, WWW

s

d

d

Broadcast

s

d

d

d

d

• One-to-all – one

source and all
destinations

• Examples: WiFi,

ARP, DHCP

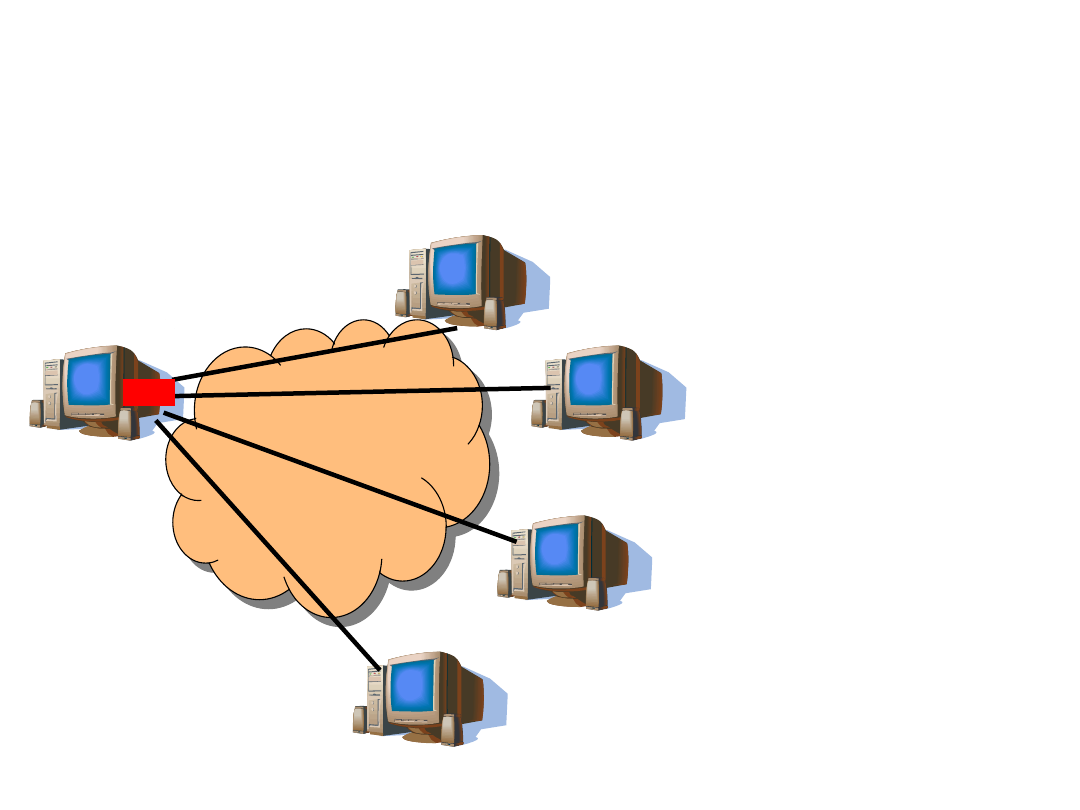
Multicast

s

d

d

• One-to-many –

one source and
selected
destinations

• Examples: IPTV,

Video on Demand,
internet radio

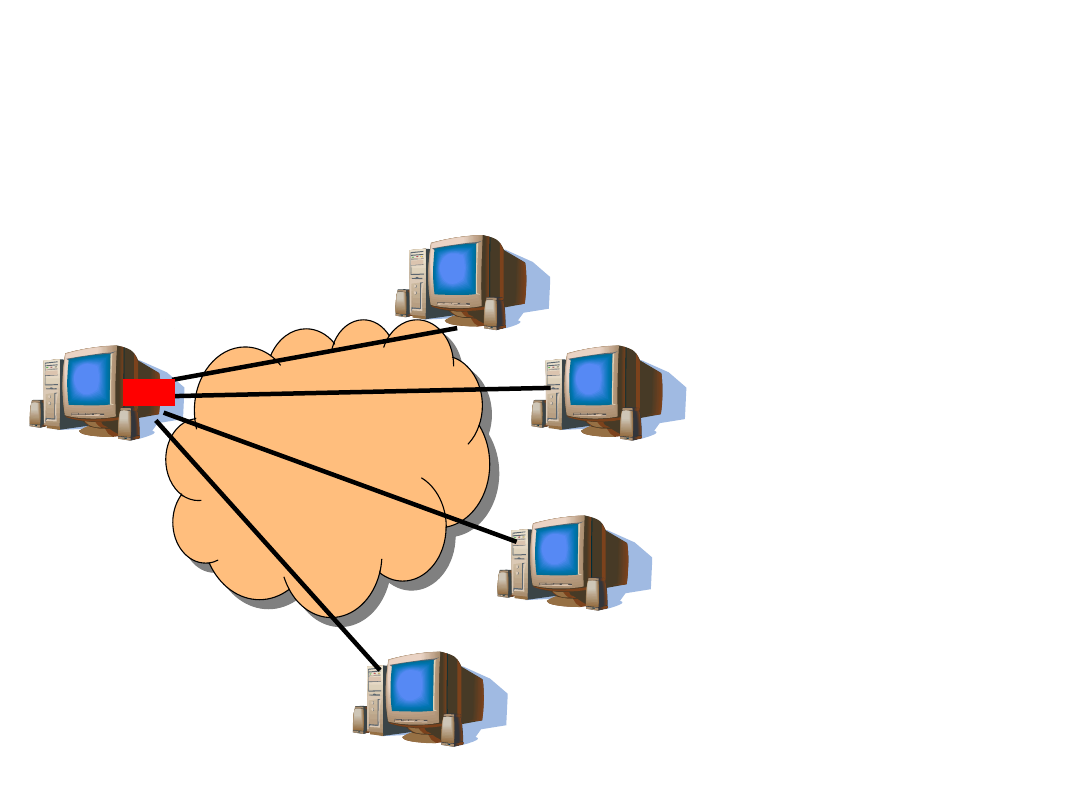
Anycast

s

d

d

• One-to-one-of-

many – one
source and one
selected
destination

• Examples: DNS,

CDN

Lecture Outline

• Introduction
• System Optimization
• Modeling
• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks

• Definitions

• Concluding Remarks

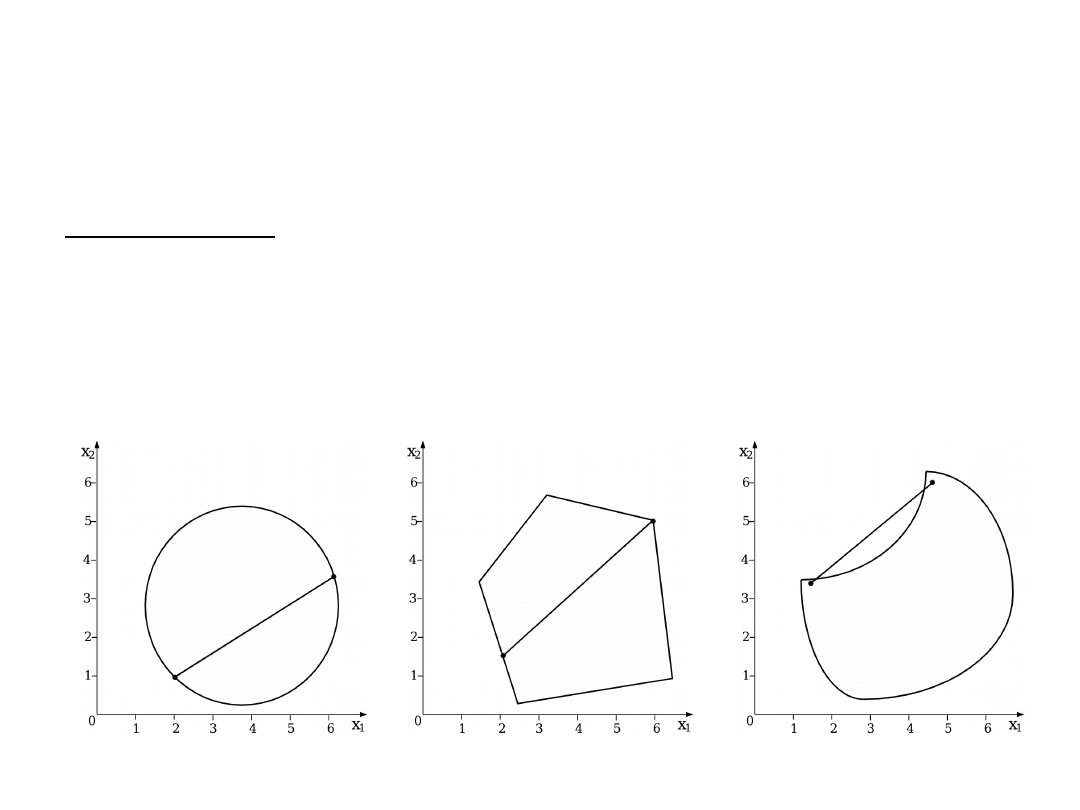
Definitions (1)

Definition. Set X  R

n

is convex, if for any two

points x

1

,x

2

 X

[x

1

,x

2

]={x : x =



x

1

+ (1 –



)x

2

, 0 





1}  X

Example of two dimension convex figures: circle,

eclipse, square

Defintions (2)

Definition. Function f : X  R

m

, X  R

n

, is linear, if

for every x

1

,x

2

 X and any real



1

i



2

that,



1

x

1

+



2

x

2

 X satisfied is

f(



1

x

1

+



2

x

2

) =



1

f(x

1

) +



2

f(x

2

)

Definition. Let X  R

n

be a convex set. Function f :

X  R

1

is convex, if for any x

1

,x

2

 X we have

f(



x

1

+ (1 –



)x

2

) 



f(x

1

) + (1 –



)f(x

2

), 



 [0;1]

If the inequality is sharp, the function is strictly

convex

Definition. Function f is concave, if –f is convex

and vice versa

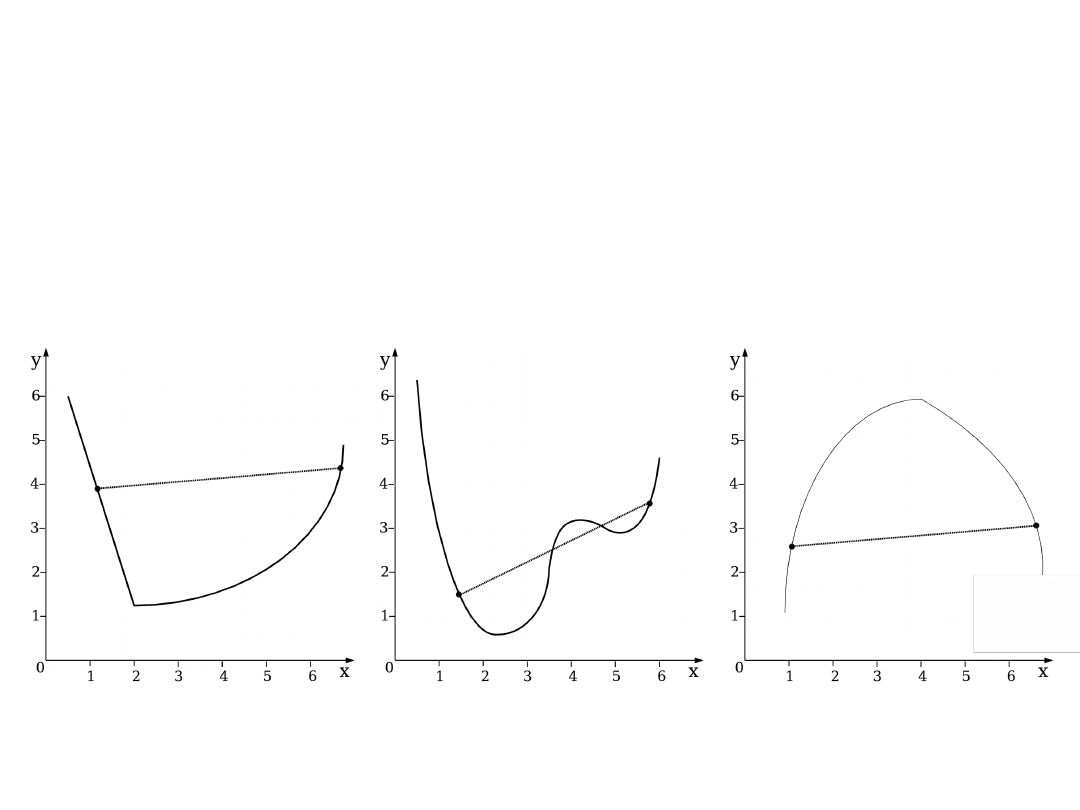
Examples

Convex

function

Nonconvex

function

Concave

function

Graphs (1)

• Graph G = <V, E> is a set of vertices (nodes)

v= 1,2,…,V and a set of edges (links) e= 1,2,
…,E that connect pairs of vertices

• A graph may be:

– undirected – there is no distinction between

the two vertices associated with each edge

– directed – every edge <v

1

, v

2

> is directed, v

1

is the source vertex and v

2

is the desitnation

vertex for this edge

• Network S = <G; h

1

,…, h

w

> is defined as a graph

G and a set of functions h

i

, that assign a real

number to each edge

Graphs (2)

• Let v

1

, v

2

,...,v

a

, (a > 1) be a sequence of various

nodes that
<v

i

,v

i+1

> is an oriented link for each i = 1,...,a-1

• Sequence of nodes and link v

1

, <v

1

,v

2

>, v

2

,..., v

a-1

, <v

a-

1

, v

a

>, v

a

is called a path

• The path cannot contain the same vertex more than

once

• A computer network is modeled by a graph in the

following way:

– vertices are network devices (routers, switches,

etc.)

– edges are network links (fibers, cables, radio links,

etc.)

Lecture Outline

• Introduction
• System Optimization
• Modeling
• Optimization Problems
• Algorithms and Optimization Methods
• Computer Networks
• Definitions

• Concluding Remarks

Concluding Remarks

• The design process of complex systems including

computer networks should include the phase of

mathematical modeling what enables the

application of optimization methods

• The model should be simple
• According the model, various kinds of

optimization methods are used

• The main goal of modeling and optimization is to

achieve expected benefits, mostly financial ones

• Many real problems encountered in computer

networks are NP- hard and optimal solution is

very difficult to be obtained

Further Reading

• A. Tanenbaum, Computer Networks, Ed. 4, Prentice Hall,

2003

• J. Kleinberg, E. Tardos, Algorithm Design, Addison Wesley,

2005

• M. Pióro, D. Medhi, Routing, Flow, and Capacity Design in

Communication and Computer Networks, Morgan Kaufman
Publishers 2004