1

PHYSICS

Newton

Einstein

Lectures for the 1

st

year

Electronics and Telecommunications

2

• Professor : Tadeusz Pisarkiewicz

Office in C1 building, Room 304,
office hours Thursday 1:00–2:00 PM,

[e-mail]

• Teaching Assistants:

Barbara Dziurdzia, e-mail:

[e-mail]

Konstanty Marszałek, e-mail:

[e-mail]

• Textbook: Fundamentals of Physics, parts 1 - 5,

D. Halliday, R. Resnick, J. Walker, Wiley & Sons, Inc.
Sudent web site

http://www.wiley/com/college/halliday

Resources

Resources

3

prof. Tom Murphy – UCSD:

• An attempt to rationalize the observed Universe in terms of

irreducible basic constituents, interacting via basic forces.

– Reductionism!

• An evolving set of (sometimes contradictory!) organizing

principles, theories, that are subjected to experimental
tests.

• This has been going on for a long time.... with considerable

success

What is

“Physics”

4

• Attempt to find unifying principles and properties e.g., gravitation:

Universal
Gravitation

“Unification” of forces

Kepler’s laws of
planetary motion

Falling apples

Reductionis

m

5

Many thousands

Many hundreds

Tens

3

An ongoing
attempt to deduce
the basic building
blocks

All the stuff you see around you

Chemical compounds

Elements (Atoms)

e,n,p

Superstrings?

Reductionism,

cont.

6

Fundamental interactions

•

gravitational interactions

example:

the force that holds the Moon in its orbit and makes an apple fall.

Newton’s law of gravitation

F - force of interaction between particles with masses m

1

and m

2

,

r – the distance between particles,
G = 6.67

x

10

-11

Nm

2

/kg

2

, the gravitational constant.

•

electromagnetic (EM) interactions

Basic interactions in everyday life (EM radiation, cohesion, friction,

chemical and biological processes, etc.) between electric charges and
magnetic moments

Coulomb’s law

Q

1

, Q

2

– point electric charges separated by distance r

ε

o

– permittivity constant, F – static el. force (attractive or repulsive)

2

2

1

r

m

m

G

F 

2

2

1

0

4

1

r

Q

Q

F





7

Fundamental interactions, cont.

•

strong interactions

Responsible for binding of nucleons to form nucleus (nuclei)
and for nuclear reactions.
Short-range interactions (~10

-15

m).

Simple laws of interaction do not exist.

•

weak interactions

Responsible for β decay and for disintegration of many elementary particles.
Short-range interactions (~10

-15

m), which do not give bound objects.

Comparison of interaction intensities

Interaction

Relative intensity

strong

1

EM

7.3

x

10

-3

weak

10

-5

gravit.

2

x

10

-39

8

Vector calculus

There are quantities that can be completely described by a number
and are known

as scalars

. Examples: temperature, mass.

Other physical parameters require additional information about
direction and are known as

vectors

. Examples: displacement,

velocity, force.

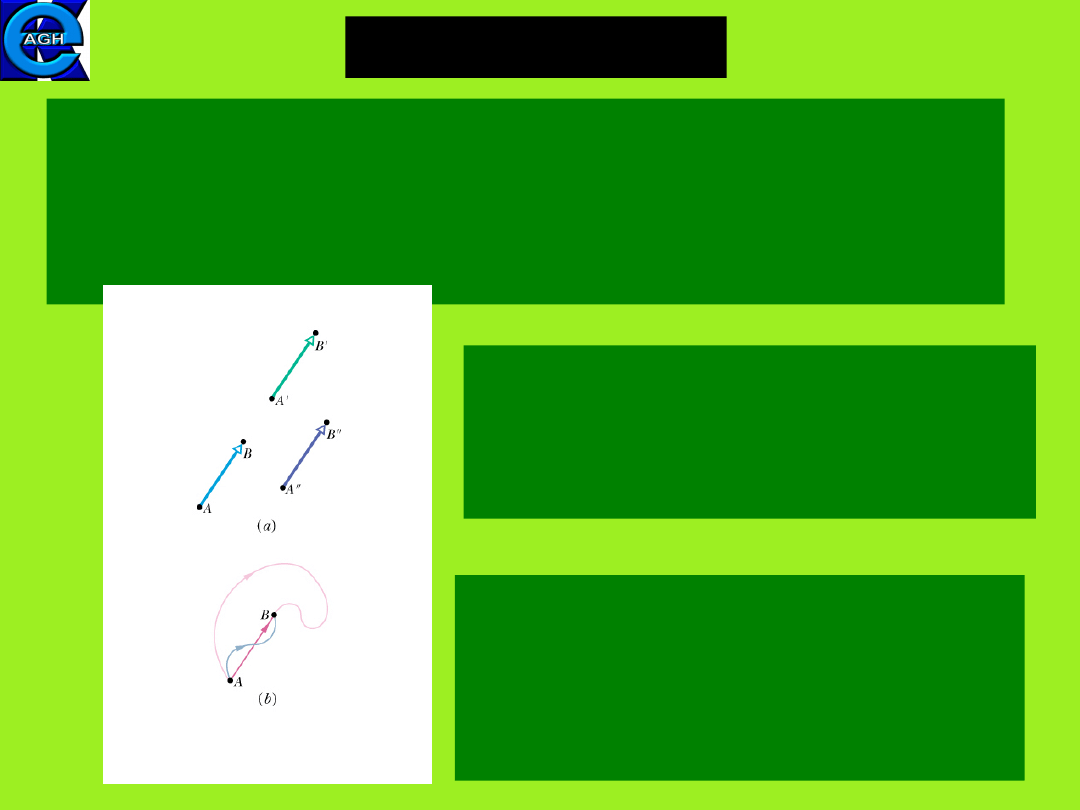
All vectors in Fig.(a) have the same
magnitude and direction. A vector can
be shifted without changing its value if
its length and direction are not
changed.

All three paths in (b) correspond to the
same
displacement vector.
Vectors are written in two ways: either
by using an arrow above or using
boldface print.

9

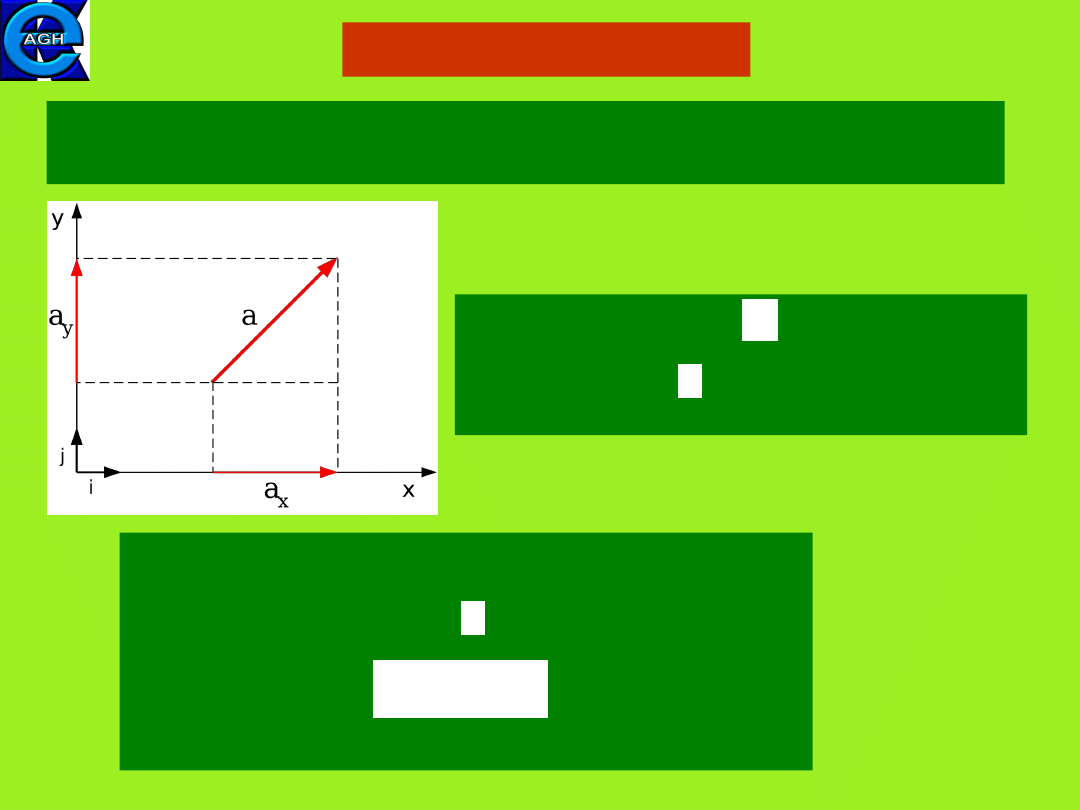
Vector components

Each vector can be resolved into components, e.g. by
projection on the axes of a rectangular coordinate system

The scalar component is obtained
by drawing perpendicularly straight
lines from the tail and tip of the
vector to the x axis.

By using unit vectors (vectors having magnitude
of exactly 1 and pointing in a particular direction)
one can express vector as

a

x

a

a

jˆ

a

iˆ

a

a

y

x







10

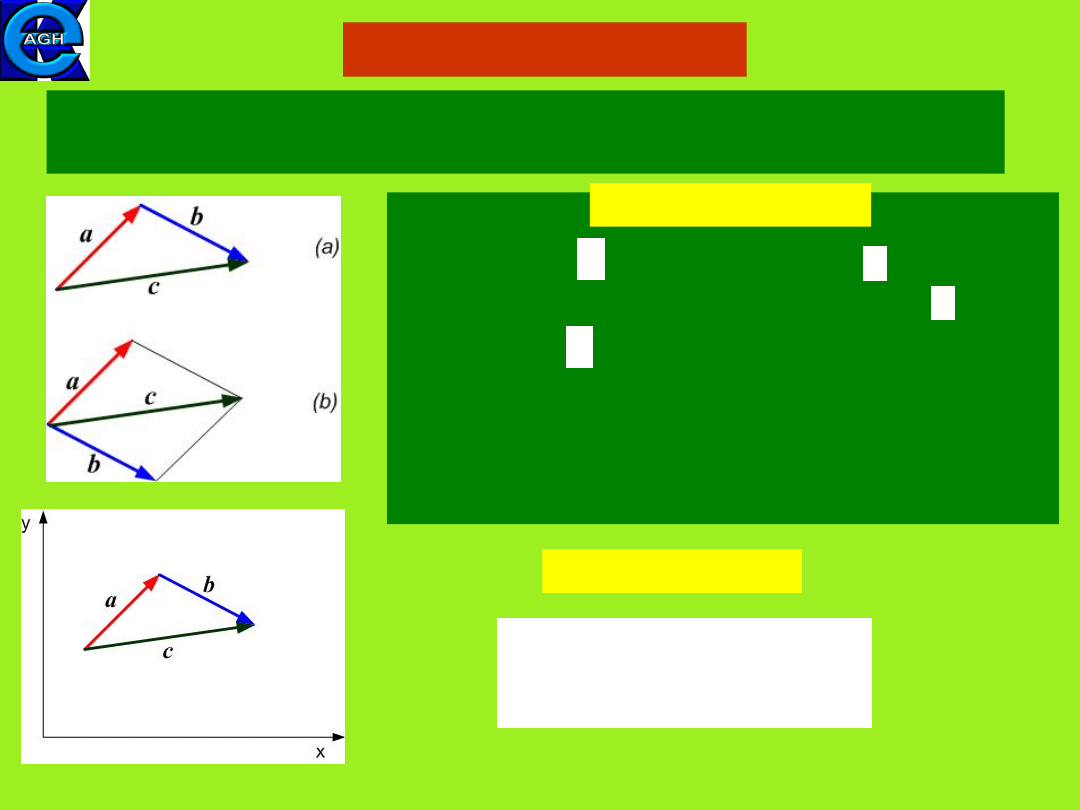
Addition of vectors

Vectors can be added geometrically or in a component form
(using algebraic rules).

(a) The tail of is placed at the tip of .

The resultant vector connects the tail of
and the tip of (

polygon method

).

(b) Vector sum is the diagonal connecting

common
vectors origin with the opposite corner of a
parallelogram (

parallelogram method

).

a

b



a

b



Geometric addition

Agebraic addition

jˆ

)

b

a

(

iˆ

)

b

a

(

c

jˆ

b

iˆ

b

jˆ

a

iˆ

a

b

a

c

y

y

x

x

y

x

y

x





























11

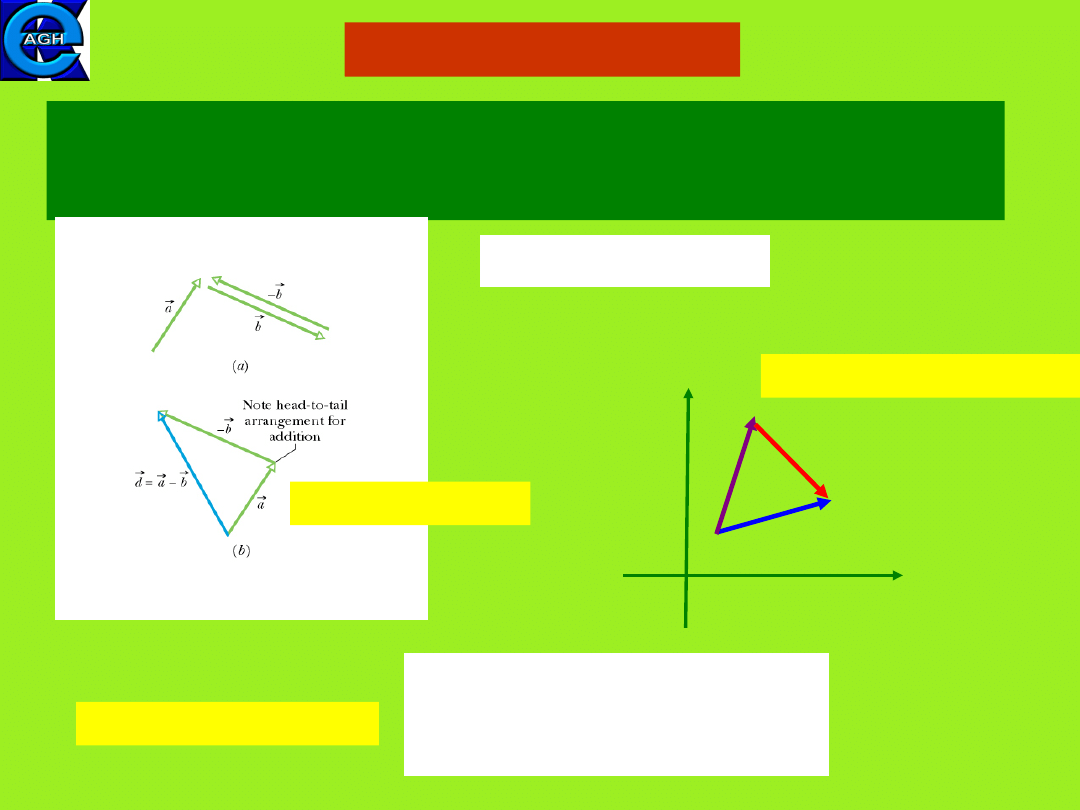
Vector subtraction

Vectors can be also subtracted geometrically or by
components.
The subtraction can be reduced to vector addition.

Agebraic subtraction

x

O

y

a

d



b



jˆ

)

b

a

(

iˆ

)

b

a

(

d

)

jˆ

b

iˆ

b

(

jˆ

a

iˆ

a

b

a

d

y

y

x

x

y

x

y

x





























)

b

(

a

b

a

d





















Parallelogram method

Polygon method

12

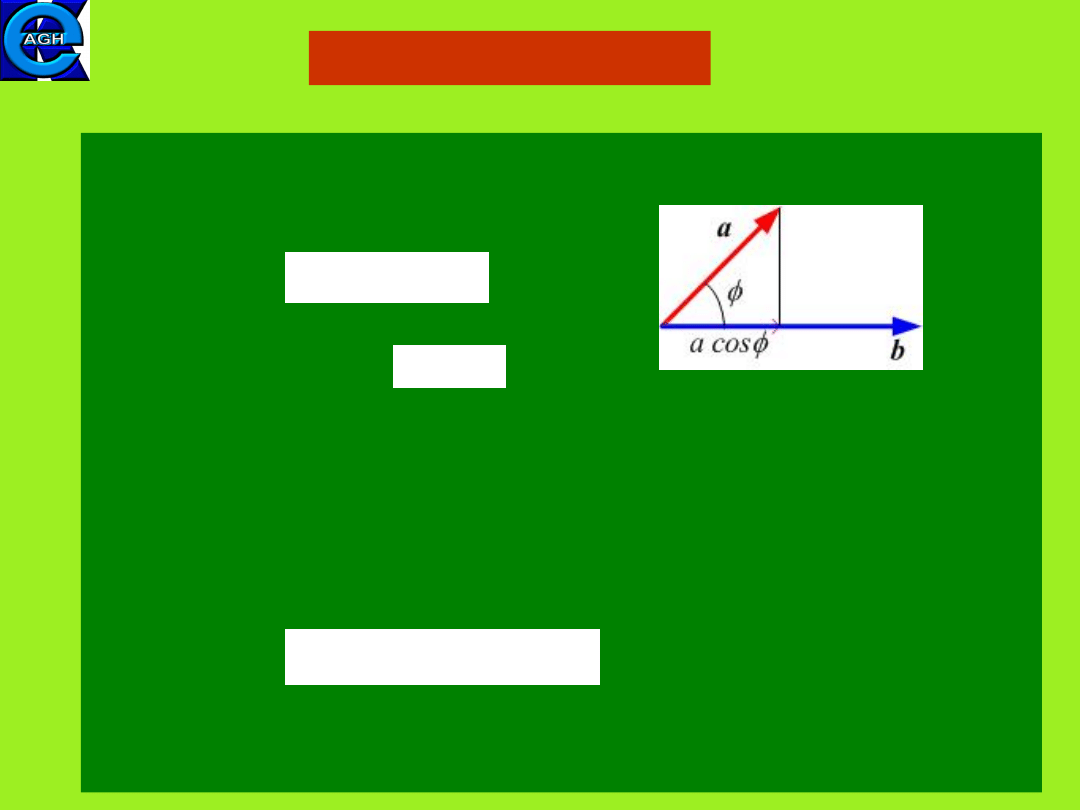
The scalar product

The scalar product (dot product) of two vectors gives scalar
and is defined as follows:

(orthogonality criterion: )

The dot product can be considered as the product of the
magnitude of one vector and the scalar component of the
second vector along the drection of the
first vector.

Using component notation one obtains for the dot product in
three dimentions:



cos

b

a

b

a









z

z

z

y

x

x

b

a

b

a

b

a

b

a













0



B

A





13

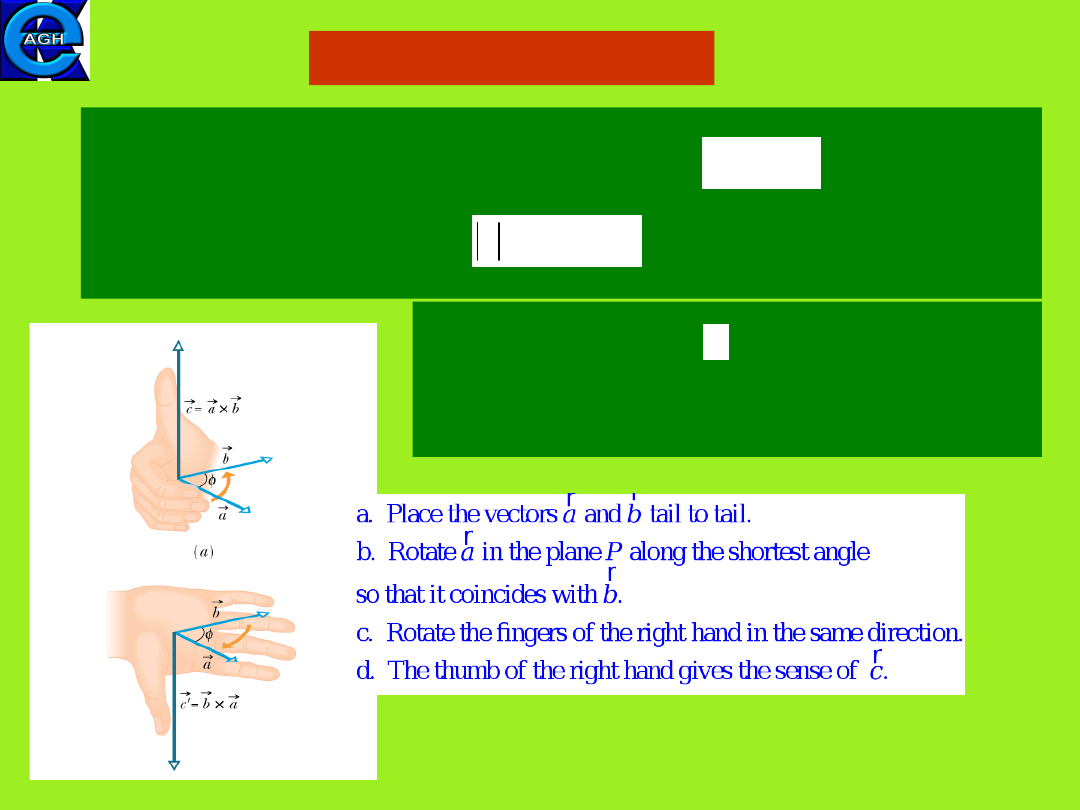
The vector product

The direction of vector is
perpendicular to the plane defined by
multiplied vectors and its sense is
given by the

right-hand rule

.

The vector product (cross product) of two vectors

is a vector, whose magnitude is .



sin

b

a

c 



b

a

c











c

14

The vector product, cont.

)

b

a

b

a

(

kˆ

)

b

a

b

a

(

jˆ

)

b

a

b

a

(

iˆ

b

b

b

a

a

a

kˆ

jˆ

iˆ

b

a

x

y

y

x

z

x

x

z

y

z

z

y

z

y

x

z

y

x





















In terms of vector components one calculates the
determinant:

The order of two vectors in the cross product is important:

)

(

a

b

b

a















