
APPLIED PHYSICS
for CIVIL ENGINEERS
Faculty of Civil Engineering
Silesian University of Technology (SUT)
Lecture (30 h) & classes (15 h) - 1
st
semester
dr hab. inż. Bogusława ADAMOWICZ, prof. nwz. Pol. Śl.
Institute of Physics, ul. Krzywoustego 2
building („new”) of Electrical Engineering Faculty
Office – room No. 422
Boguslawa.Adamowicz@polsl.pl

Course content
Heat
Fundamentals of thermodynamics
Heat transfer
Thermal properties of materials
Solar energy
Liquids
Fundamentals of liquid thermodynamics
Mass transport
Water vapour and humidity
Acoustics
Acoustic waves
Sound effects
Acoustics protection

Literature - textbooks
1.
P. A. Tipler, Physics for Scientists and Engineers, W.H. Freeman, 4th
Ed. (1998), 155 zl (ABE)
2.
M. Mansfield, C. O`Sullivan, Understanding Physics, Wiley & Sons,
Chichester (1998) (SUT Library)
3. Yunus A. Cengel, Heat Transfer. A Practical Approach 2nd
Ed.,McGraw-Hill, Boston 2003. 219 zł (ABE)
4. C.-E. Hagentoft, Introduction to Building Physics, Studentlitteratur AB
(2001). 229 zl (ABE).
5. Foundation of Engineering Acoustics, Academic Press, (SUT Library).
269 zl (ABE)

http://web.mit.edu/lienhard/www/ahtt.html
A Heat Transfer Textbook
,
3rd edition
John H. Lienhard IV, Professor, University of Houston
John H. Lienhard V, Professor, Massachusetts Institute
of Technology
Copyright (c) 2000-2005, John H. Lienhard IV and John
H. Lienhard V. All rights reserved.
On-line free access

Books - Physics for Civil Engineers course
Silesian University of Technology Library
General Physics
English through civil engineering / Mariusz Meller. - Koszalin : Wydaw. Politechniki Koszalińskiej,
1998
Glossary of building and civil engineering terms / British Standards Institution. - Oxford :
Blackwell Scientific Publ., 1993
The Penguin dictionary of building / James H. Maclean and John S. Scott. - 4th ed., [repr. with
minor rev.]. - London : Penguin Books, 1995
Modern physics for scientists and engineers / Stephen T. Thornton, Andrew Rex. - 2nd ed.. - Fort
Worth : Saunders College Publ., 2000
Advanced level physics / Michael Nelkon, Philip Parker. - 7th ed., repr.. - Oxford : Heinemann,
1998
Heat and mass transfer
Fundamentals of heat and mass transfer / Frank P. Incropera, David P. DeWitt. - 4th ed.. - New
York : John Wiley & Sons, 1996
Thermal energy conservation : building and services design / Weller J.W., Youle A.. - London :
Applied Science Publ., 1981
Building ventilation : theory and measurement / David Etheridge, Mats Sandberg. - Chichester :
John Wiley & Sons, 1996
Displacement ventilation / SKISTAD HAKON. - Taunton : Research Studies Press Ltd., 1994
Heat, air and moisture transfer in highly insulated building envelopes (Hamtie) / Hugo S.L.C.
Hens. - Birmingham : FaberMaunsell, 2002
Photovoltaic energy
Photovoltaic solar energy generation / A. Goetzberger, V.U. Hoffmann. - Berlin : Springer, 2005
Energy in architecture : the European passive solar handbook / / [Red.] Goulding John R., [red.]
Lewis J. Owen, [red.] Steemers Theo C.. - - Repr.. - London : B.T. Batsford Ltd, 1993
Acoustics
Encyclopedia of acoustics / Malcolm J. Crocker, ed.-in-chief. - New York : John Wiley & Sons
The master handbook of acoustics / F. Alton Everest. - 4th ed.. - New York : McGraw-Hill, 2001
Foundations of engineering acoustics / Frank Fahy. - San Diego : Academic Press, 2001
Active control of sound / P.A. Nelson and S.J. Elliott. - 3rd print.. - London : Academic Press, 1995

Literature in Polish
(1) Z. Kleszczewski, Fizyka klasyczna, skrypt Pol. Śl.
(2) S. Kończak, A. Klimasek, Wykłady z podstaw fizyki, wyd. Pol.
Ś
l. 2002
(3) A. Zastawny, Zarys fizyki, wyd. Pol. Śl. 1997
(4) Cz. Bobrowski, Fizyka – krótki kurs, WNT, W-wa, 1998
(wyd.VI)
(5) J. Orear, Fizyka, WNT, W-wa, 1998
(6) A. Januszajtis – Fizyka dla politechnik, PWN, W-wa, 1977
(7) R. Resnick, D. Halliday, Fizyka, PWN, W-wa
(8) R. Feynman, Wykłady z Fizyki, PWN, W-wa

Scope of Physics
Physical phenomena
Fundamental interactions and elemental
particles
Physical values
Unit systems
Mathematical and physical models

Physics – basis for technology
Thermodynamics →
→
→
→
engines (transport), buildings (architecture)
Electromagnetism →
→
→
→
telephone, radio, tv
Optics →
→
→
→
optical fibres →
→
→
→
telecommunication
Solid state physics →
→
→
→
micro- and nanoelectronics
Quantum physics →
→
→
→
lasers, quantum computers
Nuclear physics →
→
→
→
energetics
World of physical phenomena
10
20
10
10
10
0
10
-10
10
-20
Age of the Universe
Man
Neutrons
Miuon, hiperion
Resonanses
T
(
se
conds
)
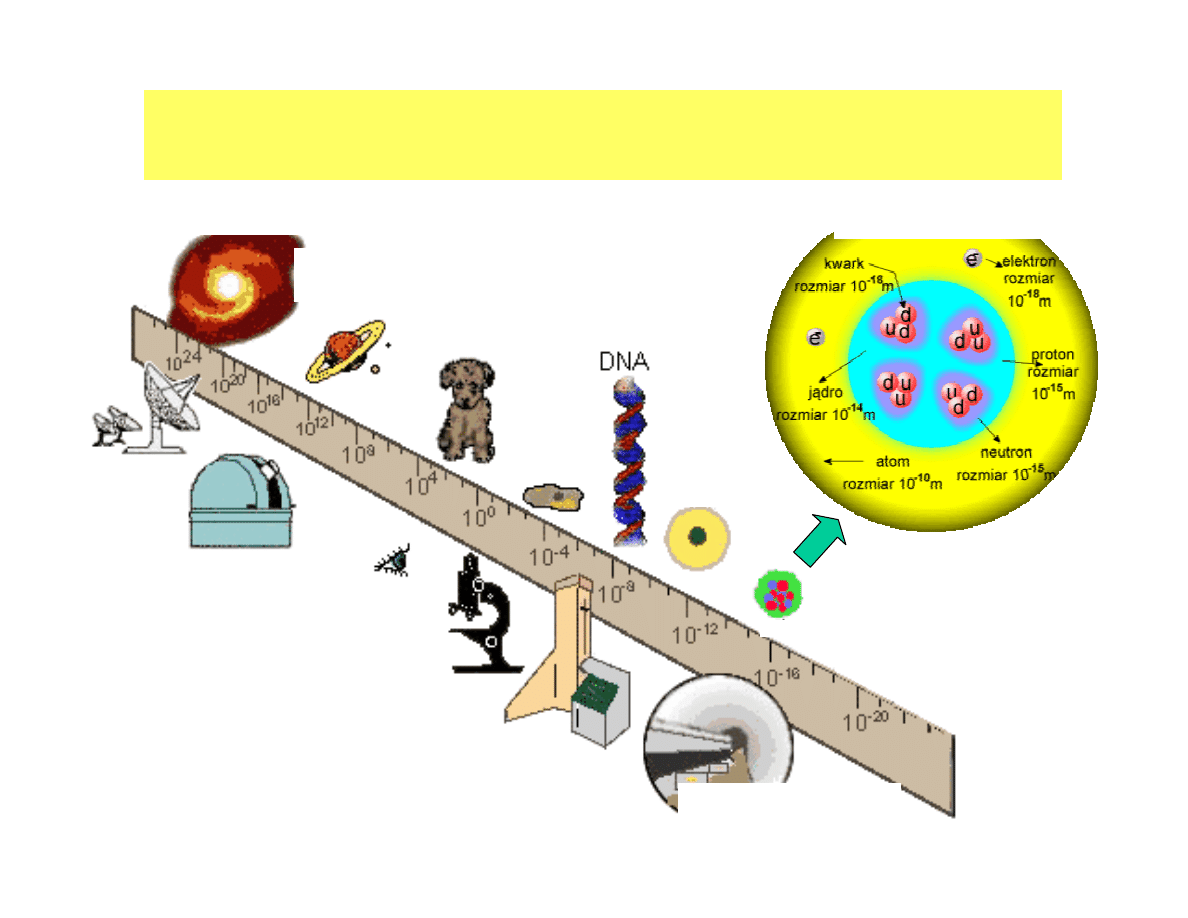
World of physical phenomena
Galaxy
Cell
Atom
Nucleus
mete
rs
Accelerator
Nucleus
Microscope
Atom structure

Physical laws are the same
in the whole UNIVERSE
Physical laws are the same
in the whole UNIVERSE
Physics
– fundamental natural science
→
→
→
→
Exploring fundamental and
universal properties of matter and
phenomena in the surrounding world
World of physical phenomena

Understanding
the Universe
Albert Einstein (1905)
The World Year of
Physics 2005

Structure of matter – elemental „blocks”
Elemental particles (2001)
Quarks - 3 colours
3 generations of quarks and
leptons
Quarks and leptons
have no structure probably
Q
U
A
R
K
S
L
E
P
T
O
N
S

Interaction
Intensity
Gravitational 10
-39
Electromagnetic
10
-3
Weak 10
-5
Strong 1
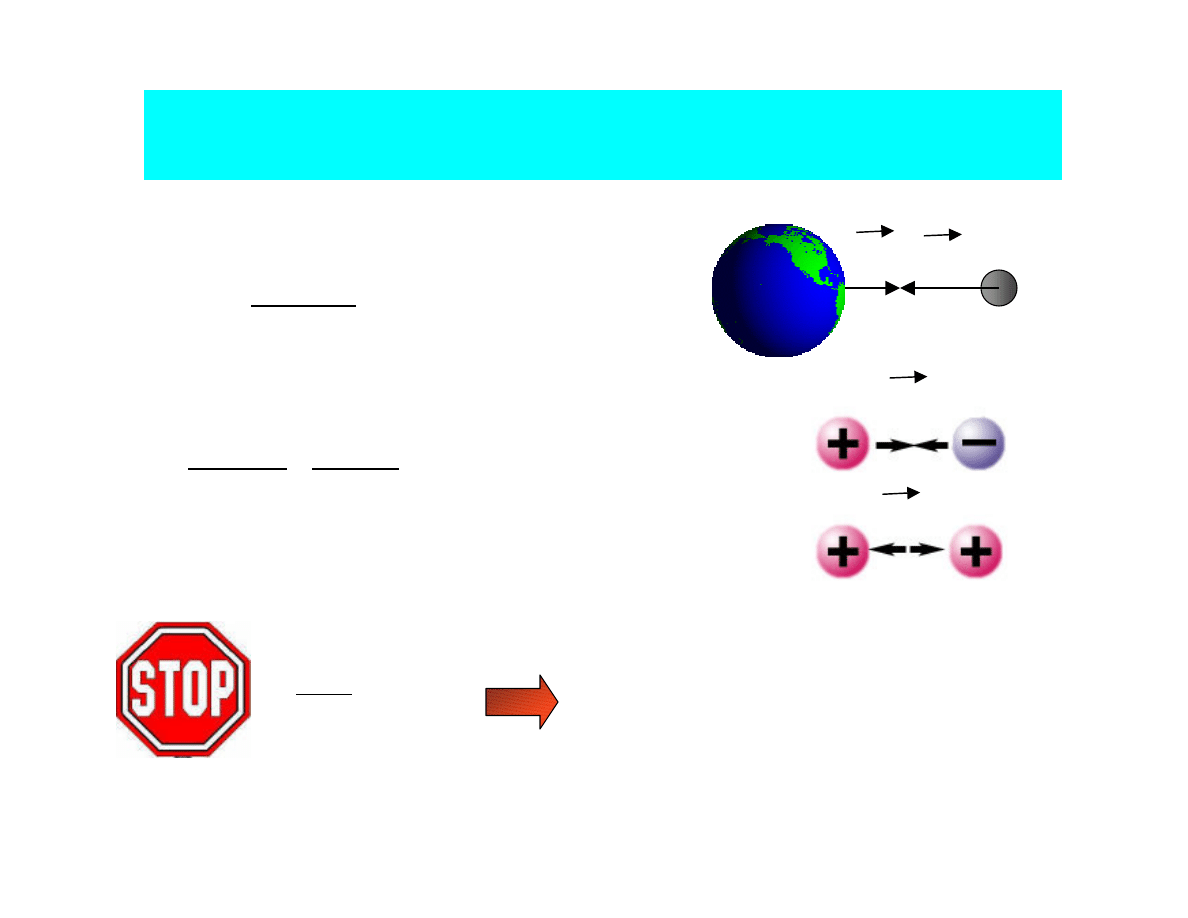
Fundamental interactions
gravitational
electromagnetic
weak
strong
World of physical phenomena
2
2
1
r
m
m
G
F
g
⋅
=
2
2
1
0
4
1
r
q
q
F
e
⋅
=
πε
gravitation -
Newton`s law
electrostatics -
Coulomb`s law
42
10
=
g
e
F
F
In microworld – little role of
gravitation
F
g
F
g
F
e
F
e

Methodology of Physics
METHOD:
-
observation
-
measurement
-
analysis of experimental data
→
→
→
→
hypothesis →
→
→
→
model →
→
→
→
physical law
Physical values
– properties of bodies or phenomena which can
be compared
quantitatively (numerically)
with the same
properties of different bodies or phenomena
• EXPERIMENT • MATHEMATICAL MODEL
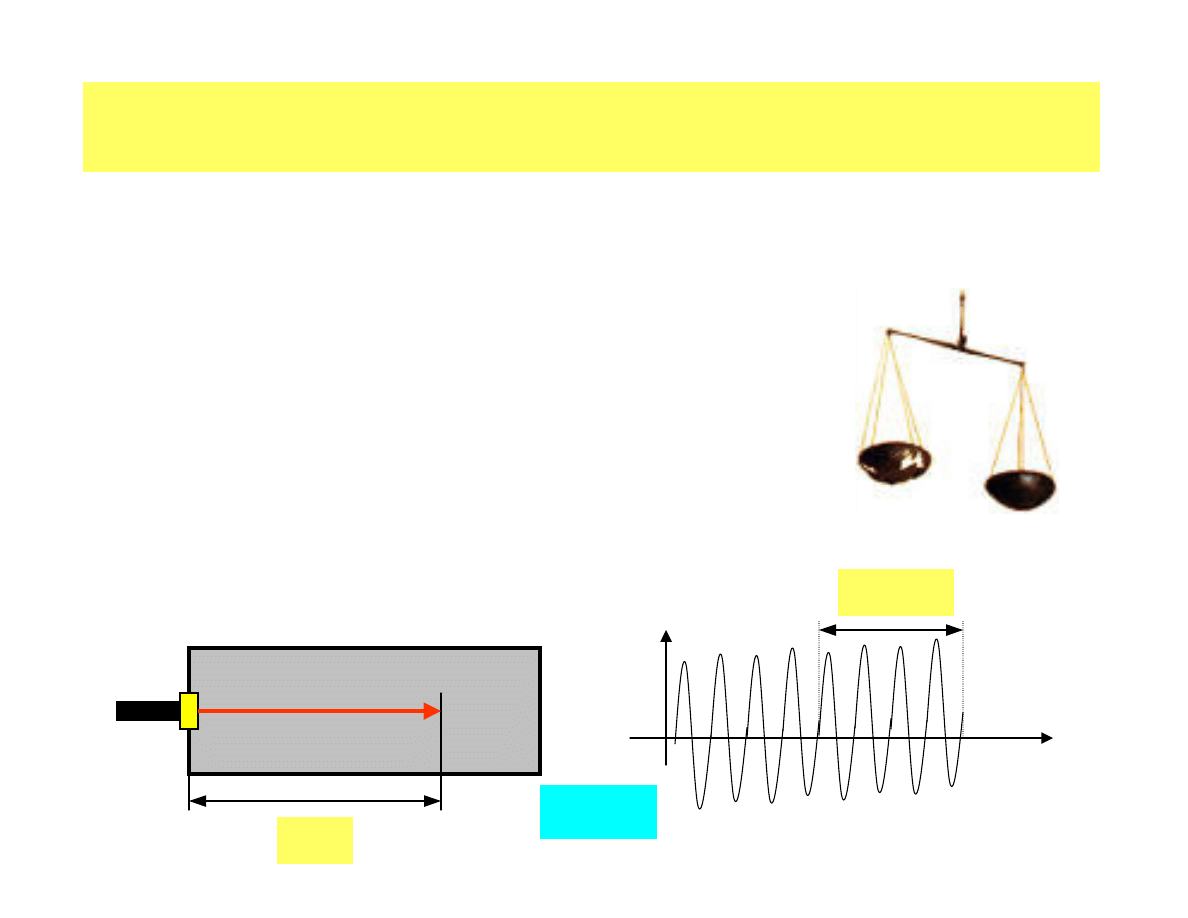
Measurement
of physical value – comparison with a
unit
value.
Physical measurements – always charged with an
uncertainty.
Fundamental units - system
SI
Length
1 meter (m)
Mass
1 kilogram (kg)
Time 1 second (s)
Current intensity 1 amper (A)
Temperature 1 kelvin (K)
Light intensity
1 candela (cd)
Amount of substance
1 mole (mole)
1 m
t
t = 1s
Cs
133
vacuum
t = 1/299792458 s
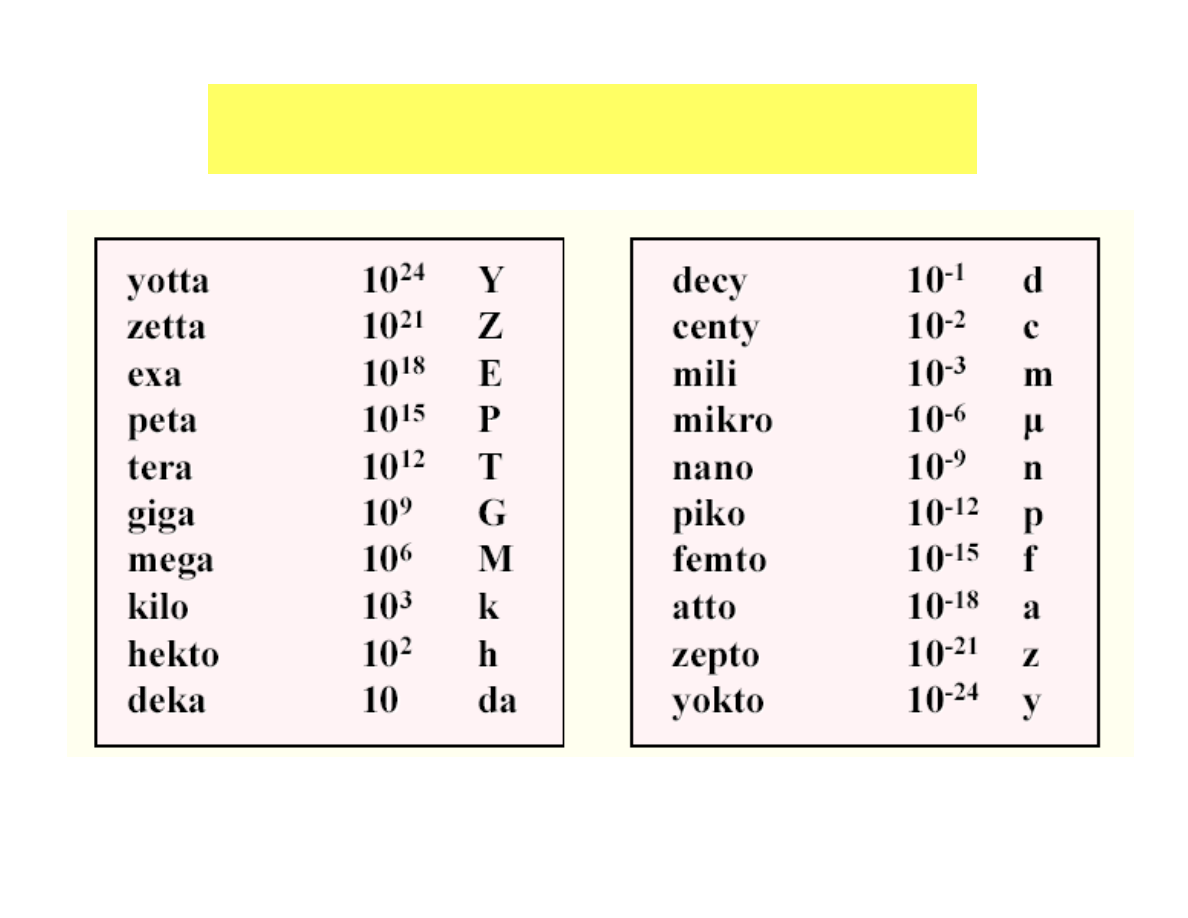
Related units

Important physical constants
ligth velocity in vacuum
Planck constant
electron mass
electron charge
Avogadro number
Boltzmann constant
gravitational constant

I have found the solution ! But what for...

Physics
classical
quantum
non-relativistic
relativistic
h
= 6.62·10
-34
J·s
XXI century
XX century
PHYSICS
c
= 3·10
8
m/s
light velocity
Planck constant
non-quantum
quantum

Kinematics
•
Fundamental quantities
•
Displacement and trajectory
•
Velocity and acceleration
•
Examples of motion
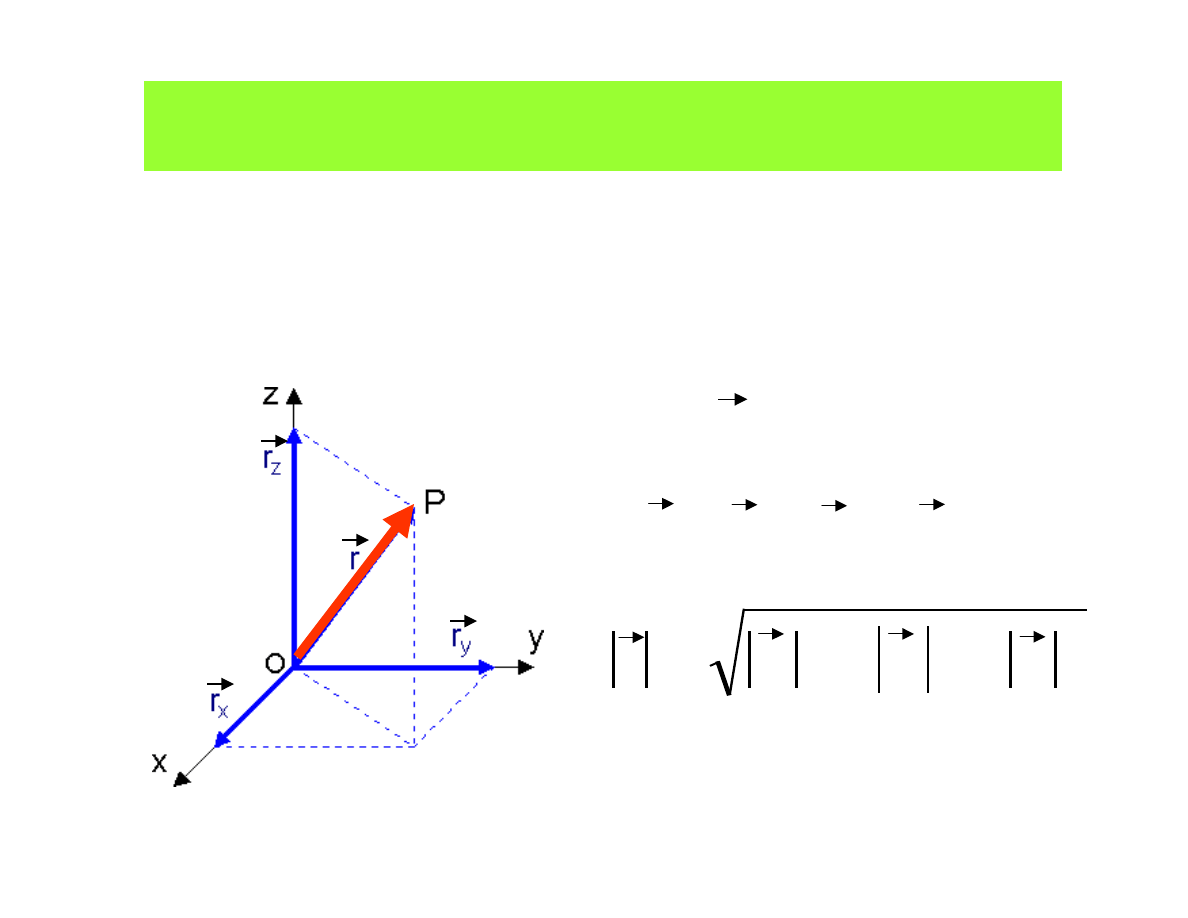
Fundamental quantities
Scalar
– mass, time, temperature
Vectors
– velocity, acceleration, force
Vector r and its components
z
y
x
r
r
r
r
+
+
=
2
2
2
z
y
x
r
r
r
r
+
+
=
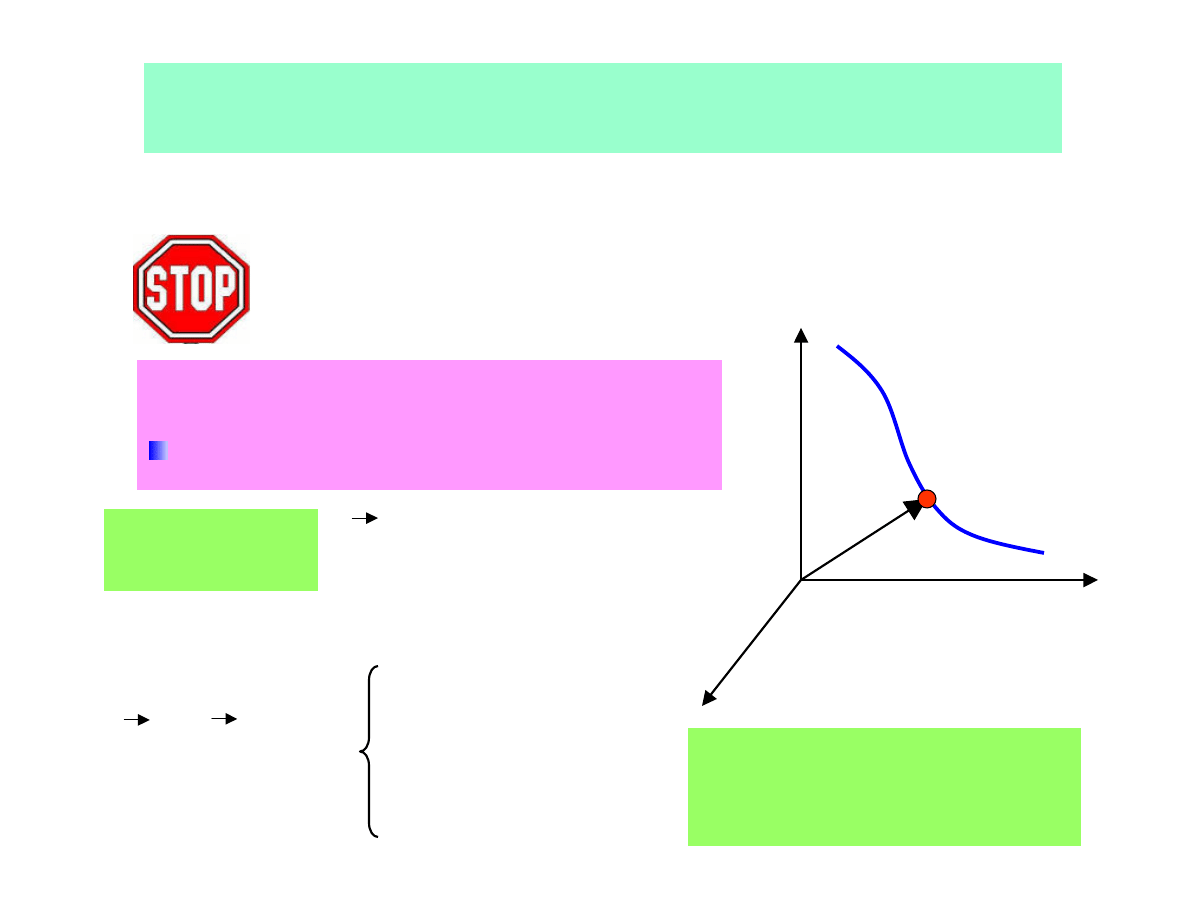
Displacement and trajectory
Motion
- change in relative position among bodies versus time
→
reference system
Material point :
mass with negligible sizes (volume)
Trajectory –
all points corresponding
to the position of the point P
y
x
z
0
trajectory
P(x,y,z)
r(t)
Motion is not absolute but relative !
In the rectangular (Cartesian)
coordinate system:
)
(
)
(
)
(
t
z
z
t
y
y
t
x
x
=
=
=
Position of
the point P
r
- vector of displacement
)
(t
r
r =
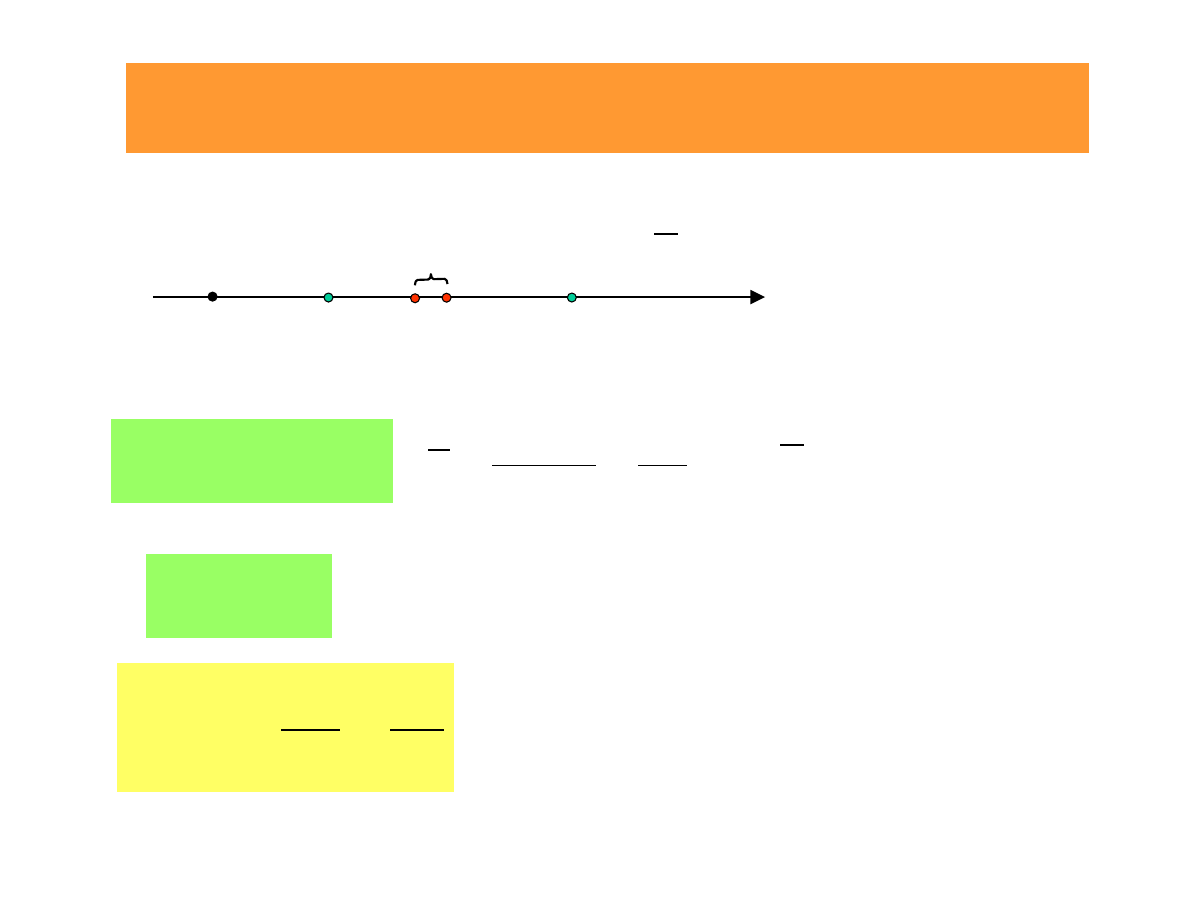
Average velocity
t
s
t
t
s
s
∆
∆
=
−
−
=
1
2
1
2
v
m/s
)
v
(
=
Rectilinear motion of a material point
Displacement – coordinate
s = s(t)
– function of time
∆
t
→
0
Velocity
dt
ds
t
s
t
=
∆
∆
=
→
∆
0
lim
v
Derivative of the displacement
with respect to time
0
s
1
s
2
A
1
A
2
t
1
t
2
B
1
B
2
B
1
B
2
= ∆s in ∆t
∆s
dt
s
t
t
∫
=
∆
2
1
v
Definite integral of time over time
Integration of a function
dx
x
dF
x
f
)
(
)
(
=
Indefinite integral of the function
f(x):
∫
+
=
C
x
F
dx
x
f
)
(
)
(
Definite integral of the
function f(x)
in the limits x
1
i x
2
:
)
(
)
(
)
(
1
2
2
1
x
F
x
F
dx
x
f
x
x
−
=
∫
Example:
C
x
n
a
dx
ax
n
n
+
+
=
+
∫
1
1
Rectilinear uniform motion
V = const
Initial condition: t = 0, s = 0 ⇒
s = vt
Rectilinear variable motion
V – dependent on time: in the moments t
1
(t
2
) – the velocity v
1
(v
2
)
Average acceleration
t
v
∆
∆
=
a
2
/
)
(
s
m
a =
Acceleration
dt
v
t
v
lim
0
d
a
t
=
∆
∆
=
→
∆
2
2
)
(
dt
s
d
dt
ds
dt
d
a
=
=
∫
=
∆
2
1
)
(
v
t
t
dt
t
a
⇒

Rectilinear motion with constant acceleration
a
a
a
a
= const
a
a
a
a
>
0 – accelerated motion
a
a
a
a
<
0 - retarded motion
at
adt
t
∫
=
=
∆
0
v
Velocity changes
Initial condition:
t = 0, v = v
0
Velocity
v
:
v – v
0
=
a
a
a
a
t
⇒
v = v
0
+
a
a
a
a
t
Displacement:
2
0
0
0
0
2
1
v
)
v
(
v(t)
at
t
dt
at
dt
s
t
t
+
=
+
=
=
∆
∫
∫
or:
2
0
0
2
1
v
at
t
s
s
s
+
=
−
=
∆
Initial condition: t = 0, s = s
0
⇒
2
0
0
2
1
v
at
t
s
s
+
+
=
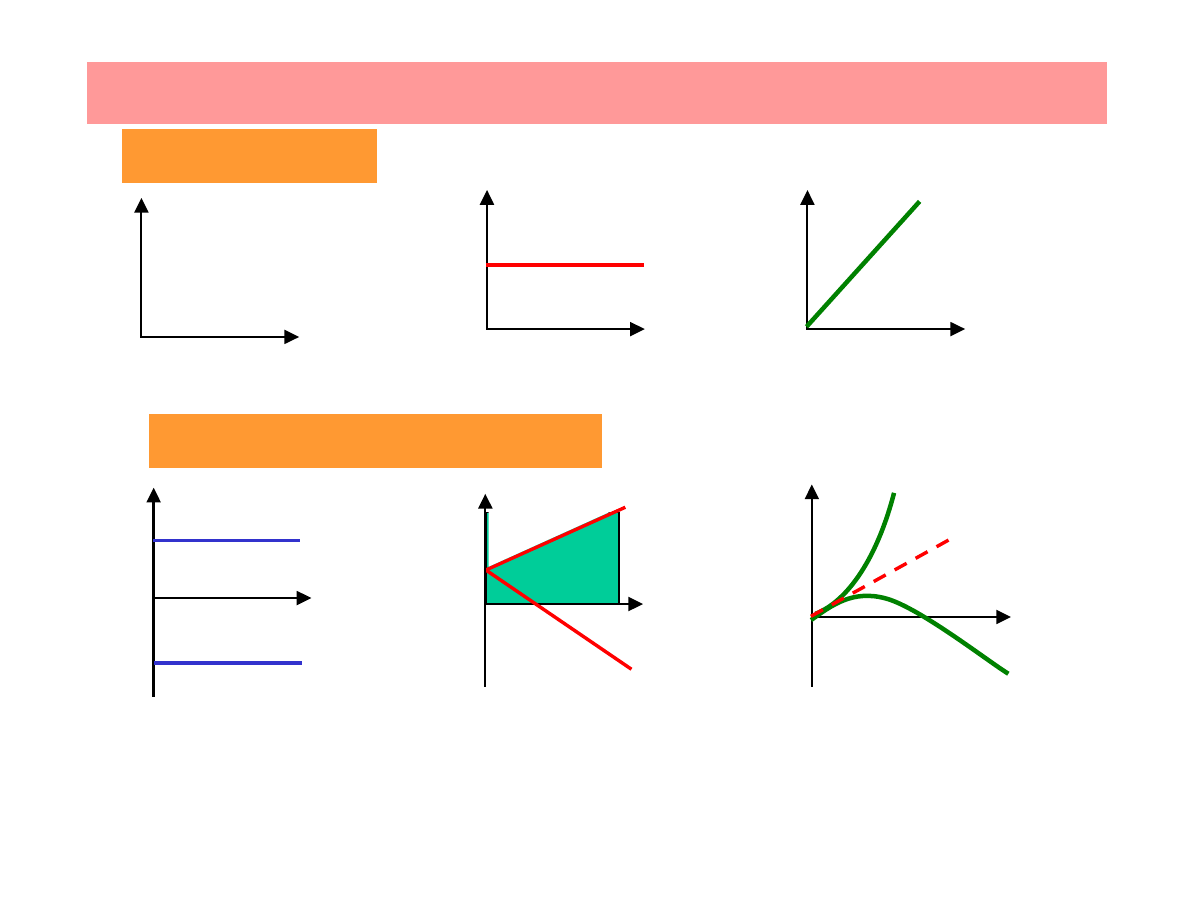
Graphical presentation of the rectilinear motion
a
a
a
a
=0
a
t
Uniform motion
v = const
v
t
s = vt
s
t
Uniformly accelerated motion
a
a
a
a
>0
a
t
a
a
a
a
<0
a
a
a
a
>0
s
t
a
a
a
a
<0
tangent slope – v(t)
v
t
a
a
a
a
<0
v
0
a
a
a
a
>0
path - area under
the curve v(t)
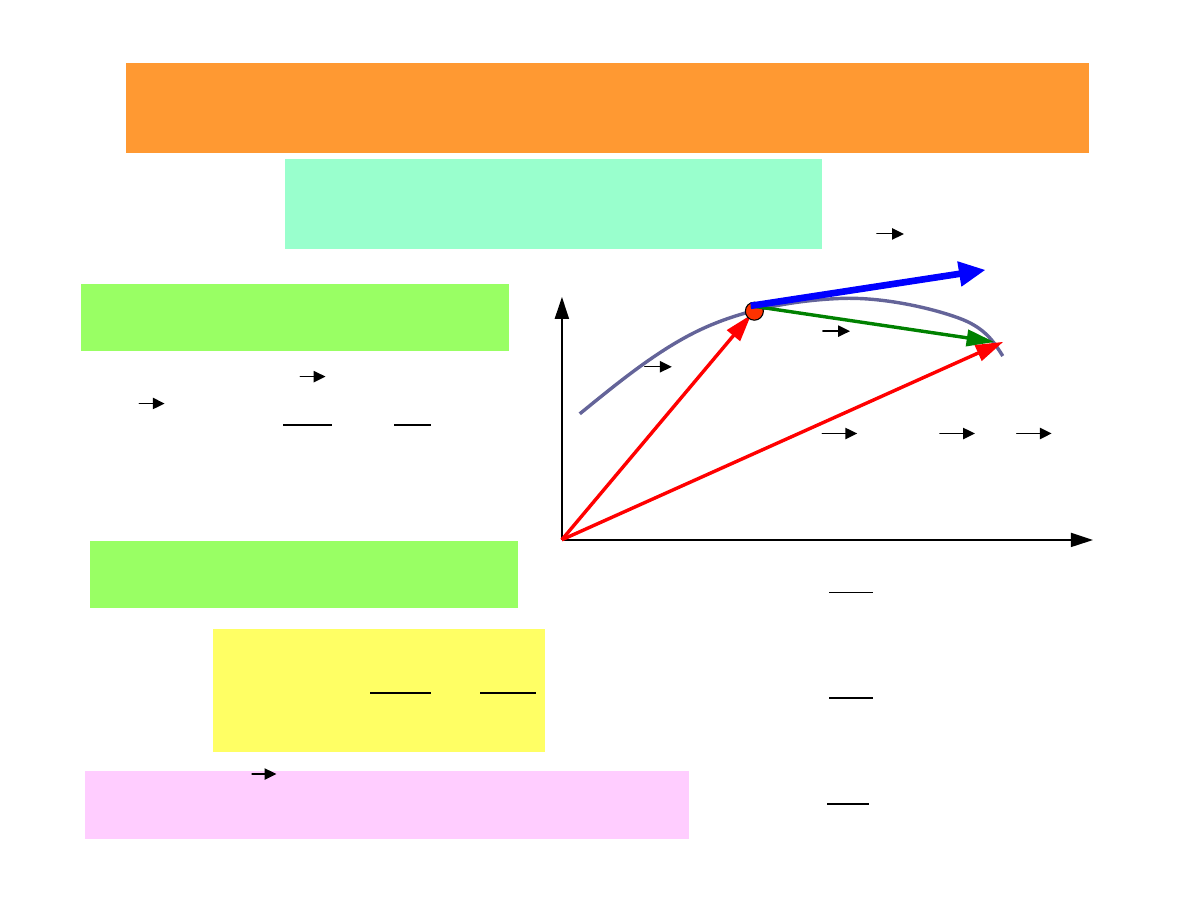
Velocity as a vector
x
y
r(t)
Curvilinear motion
dt
r
d
t
r
t
r
v
r
=
∆
∆
=
→
∆
0
lim
v
Velocity
Vektor
v
is always tangent to
the trajectory
dt
dz
dt
dy
dt
dx
=
=
=
z
y
x
v
v
v
Average velocity
∆
∆
=
s
m
t
r
average
v
∆
∆
∆
∆
r
V
r(t+∆
∆
∆
∆
t) =
r(t)
+
∆
∆
∆
∆
r
P

Acceleration as a vector
2
2
0
v
v
lim
dt
r
d
dt
d
t
a
t
r
r
r
r
=
=
∆
∆
=
→
∆
Acceleration
2
2
z
2
2
y
2
2
x
dt
v
dt
v
dt
v
dt
z
d
d
a
dt
y
d
d
a
dt
x
d
d
a
z
y
x
=
=
=
=
=
=
Average acceleration
∆
∆
=
2
v
s
m
t
a
average
1
v
2
v
2
v
v
∆
A
V
a
a
t
a
n
R
dt
d
a
t
v
=
R
a
n
2
v
=
n
t
a
a
a
+
=
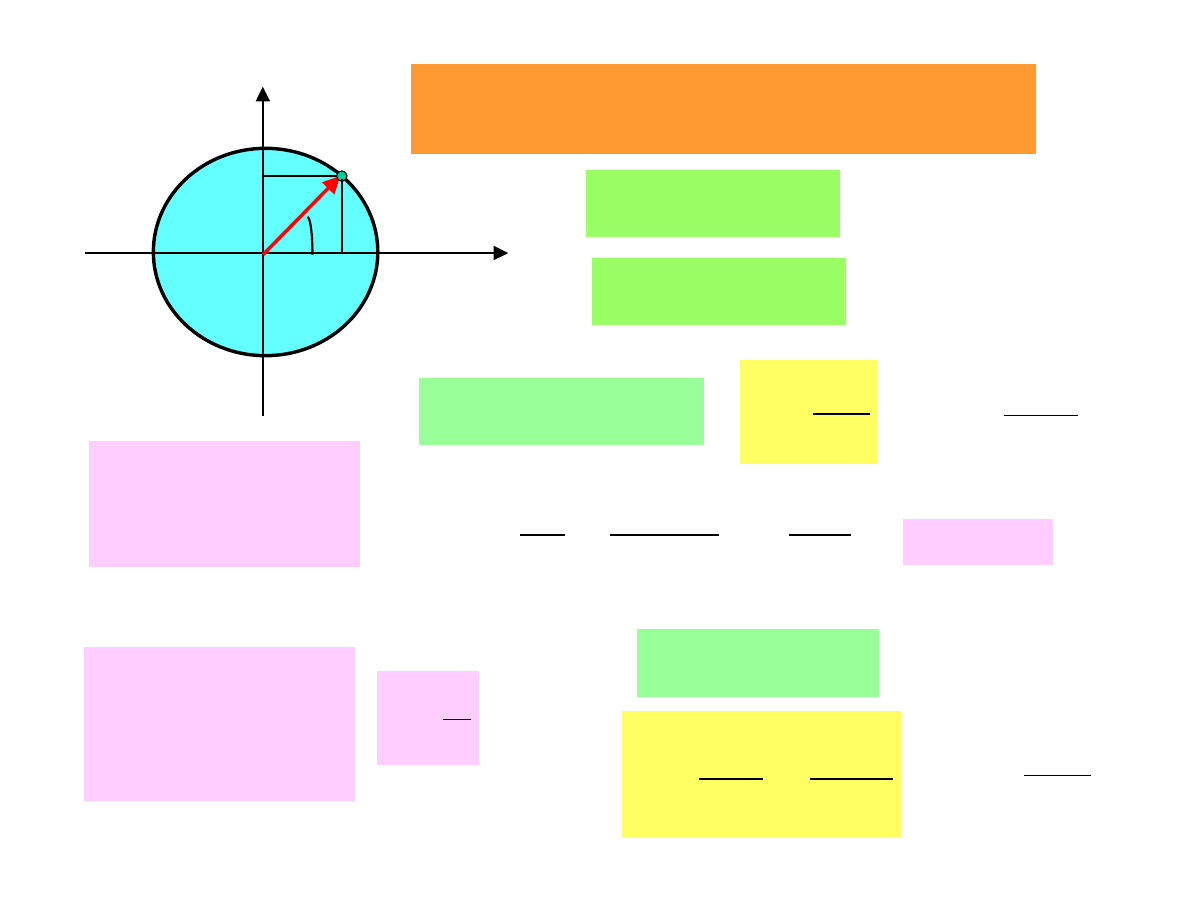
Motion in a circle
Angular path
α
α
α
α
(rad)
Linear path
s =
α
α
α
α
r
X
y
α
α
α
α
P
0
x
Y
r
dt
d
r
dt
r
d
α
α
=
=
=
)
(
dt
ds
v
ω
r
=
v
Angular velocity
dt
d
α
ω
=
s
rad
=
)
(
ω
Angular
acceleration
2
2
dt
d
dt
d
α
ω
ε
=
=
2
)
(
s
rad
=
ε
Period of motion
T
– time of a path
α
= 2π
When ω = const then
T = 2π
π
π
π
/ ω
ω
ω
ω
herc
s
f
−
=
−1
)
(
Hz
Frequency f
–
number of
revolution per
unit time
T
f
1
=
hertz (Hz)
Wyszukiwarka
Podobne podstrony:
ZMPST 01 Introduction
Lecture 01 Introduction
01 Introduction
Lab 01 Introductin to UNIX System
01 Introductionid 2824 Nieznany (2)
01 Introducere
01 introduction
ZMPST 01 Introduction
01 Introduction
01 introduction
Boellmann Suite gothique 01 introduction choral
01 Introduction
01 Introduction to Chassis Dynamics
01 01 Introduction
więcej podobnych podstron