
ZASTOSOWANIE LOGIKI
ROZMYTEJ
DO
STEROWANIA
ZROBOTYZOWANYCH
SYSTEMÓW
WYTWARZANIA

Spośród znanych metod sztucznej inteligencji, stosowanych w
planowaniu i doborze strategii działania, harmonogramowaniu oraz
sterowaniu
zrobotyzowanych
systemów
wytwarzania
można
wymienić:
Systemy eksperckie, zwane też ekspertowymi lub doradczymi.
Metody
oparte
o
mechanizm
wnioskowania
rozmytego
wykorzystujące teorię zbiorów rozmytych i logikę rozmytą (Fuzzy
Logic).
Sztuczne sieci neuronowe.
Metody wykorzystujące algorytmy genetyczne.
Systemy agentowe i wieloagentowe.
Do rozwiązania zadań harmonogramowania i sterowania produkcją w
zrobotyzowanych systemach wytwarzania zastosowano logikę rozmytą
(Fuzzy Logic).

Zastosowania Fuzzy Control w obszarze
sterowania i automatyzacji produkcji
Stosowanie zbiorów rozmytych budzi nadal wiele kontrowersji, które
są często wynikiem niezrozumienia tej teorii, jak i przeceniania jej możliwości.
Jako motto dla jej stosowania niech będzie cytat: “Rozmytość nie jest przecież
ani rezygnacją z precyzji pojęć, ani też jej pochwałą, lecz próbą względnie
ścisłego ujmowania wyrażeń nieostrych, z którymi mamy do czynienia nie
tylko w życiu codziennym, lecz także w naukach ścisłych jak i społecznych”.
Obszary zastosowania logiki rozmytej w szeroko rozumianym
sterowaniu maszynami i produkcją dzisiaj określić można następująco:
Przejmowanie funkcji klasycznych regulatorów typu PID przez regulatory
rozmyte w coraz większej grupie urządzeń automatyki przemysłowej
(szczególnie w przypadku układów o zmiennych parametrach). Powód
stosowania tutaj logiki rozmytej wynika z niemożliwości wykonania regulatora
PID działającego idealnie w układach o zmiennych parametrach. Stosując
logikę
rozmytą
unika
się
budowania
skomplikowanego
modelu
matematycznego, zastępując go zbiorami reguł i funkcji przynależności [5, 6,
13].
Sterowanie pracą, a także dobór strategii działania elastycznych
zautomatyzowanych systemów produkcyjnych [9, 10, 11].
Dobór parametrów i sterowanie procesami obróbczymi (np.: toczenie,
frezowanie, szlifowanie) [2, 3 , 4].
Sterowanie,
głównie
w
zastosowaniach
dotyczących
zagadnień
pozycjonowania w robotach.
Diagnozowanie maszyn, gdzie zbiory rozmyte znalazły zastosowanie do
szybszego łatwiejszego wyróżniania różnego rodzaju cech sygnałów i
określania ich wartości w celu zidentyfikowania i porównania do
reprezentanta klasy [7].
Modelowanie układów mechanicznych, szczególnie w zakresie badania
istotności uproszczeń i relacji pomiędzy odpowiednimi członami modelu
empirycznego, a układu fizycznego [15].

2. Podstawy sterowania
rozmytego
W klasycznej logice dwuwartościowej element należy lub nie
należy do zbioru. W logice rozmytej, wprowadzone jest pojęcie funkcji
przynależności (term), która w zbiorach rozmytych jest oszacowaniem
stopnia (najczęściej w przedziale 0, 1) wystąpienia określonego elementu
w poszczególnych zbiorach.
Harmonogramowanie
i
sterowanie
z
wykorzystaniem
wnioskowania rozmytego nie polega na budowie modelu układu
sterowanego (jak w sterowaniu tradycyjnym), ale opiera się na wiedzy
pozyskanej od doświadczonych ekspertów, którzy w stanie wyrazić swoja
wiedze w postaci werbalnej. Wiedza o tym jak należy sterować może być
wyrażona w postaci twierdzeń lingwistycznych.

Stopień przynależności (najczęściej w przedziale 0,1) zmiennej X
i
- w
zależności od jej wartości do zbioru, czyli jej stan - określa (oszacowuje)
funkcja przynależności (term). Można wyodrębnić standardowe klasy
funkcji przynależności, np. kwadratowe, typu e
f(x)
, hiperboliczne lub ich
kombinacje, a także trójkątne, prostokątne, itp. Kształt funkcji
przynależności zależy od charakterystyki sterowanego urządzenia. Zwykle
oszacowuje się stopień przynależności zmiennej X
i
do kilku zbiorów
(znaczników)
stanu
jej
wartości.
Obecnie najczęściej stosowane są funkcje trójkątne z trzema (rys. 9.9a) lub
pięcioma znacznikami (rys. 9.9b), w których przyjmuje się stopnie
wartościowania:
trzy:
(M-mały
Ś-średni,
D-duży),
pięć (BM-bardzo mały, M-mały, Ś-średni, D-duży i BD-bardzo duży).
Wartość
zmiennej
(unormowana)
Wartość
zmiennej
(unormowana)
1
D
Ś
M
BM
Stopień
przynależności
Stopień
przynależności
1
D
Ś
M
0
0
1
0
0
1
a)
b)
BD
Przytoczone przykłady są najczęściej stosowane w modelowaniu systemu
rozmytego. W rzeczywistości funkcją przynależności może być dowolna funkcja
mieszcząca się w zakresie: y = [0 ,1]. Dobór kształtu funkcji jest ważnym
elementem budowania sterownika wnioskowania rozmytego i ma duży wpływ na
proces rozmywania (fuzyfikacji) i wyostrzania (defuzyfikacji), a wybór ten zależy
od ilości posiadanej informacji o systemie oraz od jakości metod strojenia
modelu. Oprócz wymienionych funkcji stosuje się również: symetryczną funkcję
Gaussa, niesymetryczną funkcję Gaussa, funkcję sigmoidalną.
1
a b c d e f g h i
0
Reguła 2
Reguła 1
0 Y 1
0
X2
1
0 X1 1
0 Y
1
0 X2 1
0 X1 1
J eżeli X1=duży i X2=średni to Y=średni
J eżeli X1=średni i X2=mały to Y = mały
Defuzyfikacja
Fuzyfikacja
X2
X1
Y
1
1
1
1
1
1
MAX
M
I
N
M
I
N
Środek ciężkości
uzyskanej figury
Proces wnioskowania polega w pierwszym etapie na poszukiwaniu minimum
wartości dla każdej przyjętej reguły, tzn. wyborze najmniejszej wartości
spośród zbiorów wejściowych objętych analizowaną regułą. Blokiem
wynikowym jest zbiór rozmyty Y, mający miano określonej wielkości
fizycznej. W bloku “Defuzyfikacja” następuje końcowe wnioskowanie oparte
na każdej z zasad podstawowych w ten sposób, że końcową wartością jest
maksimum spośród podstawowych zbiorów rozmytych. Ustalenie maksimum
pozwala na uwzględnienie wszystkich zasad (reguł) podstawowych. Taki
proces wnioskowania nosi nazwę zasady min/max i jest podobny do sposobu
myślenia człowieka.
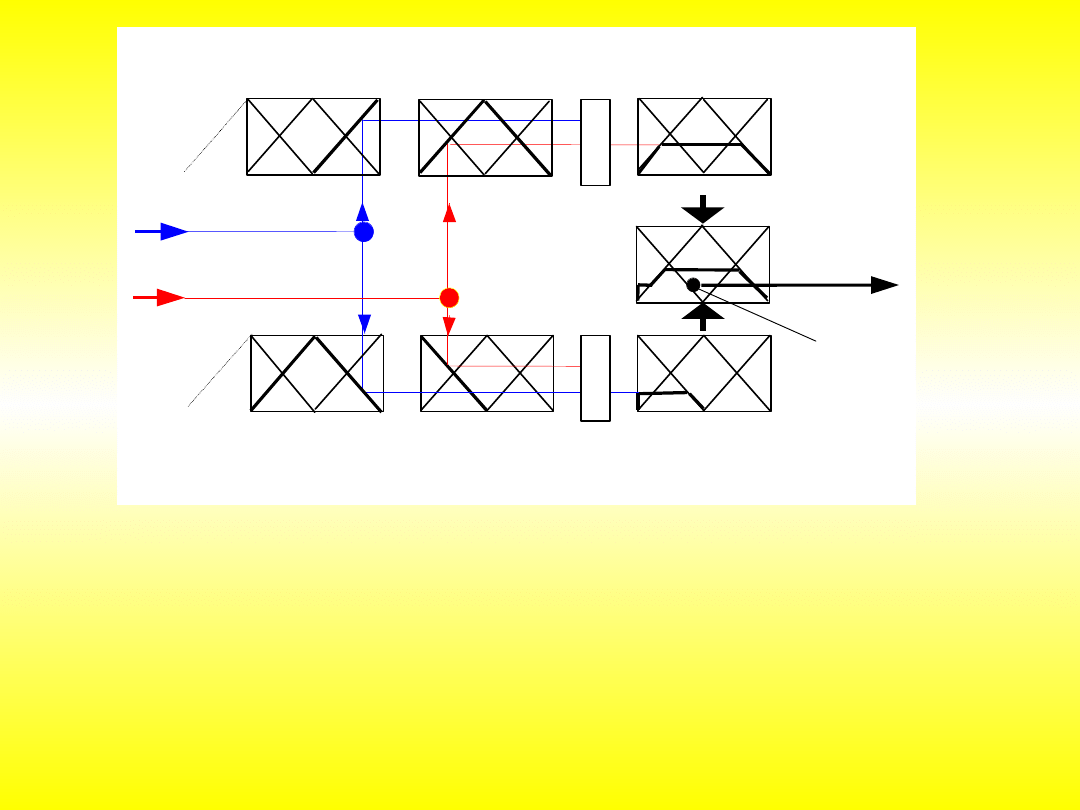
Rozmywanie często określa się mianem fuzzyfikacji. Proces ten polega na
transformacji wartości z dziedziny liczb rzeczywistych na wartości z
dziedziny zbiorów rozmytych. Przebieg tego procesu przedstawia rys. 4.8
[RPR97]. W bloku rozmywania obliczane są stopnie przynależności każdej
ostrej wartości wejściowej x1 i x2 dla poszczególnych wejściowych zbiorów
rozmytych Ai i Bj. W tym celu niezbędne jest podanie dokładnie
zdefiniowanych funkcji przynależności: µAi(x1), µBj(x2) dla zbiorów
rozmytych wszystkich wejść.
Blok rozmywania na wyjściu zwraca obliczone stopnie przynależności dla
wszystkich wejść. Liczba wyników jest zależna od precyzji rozmywania,
czyli liczby zastosowanych funkcji przynależności dla danej zmiennej
lingwistycznej
1
A
1
B
1
A
2
B
2
μ(x
1
)
μ(x
2
)
μ
A1
(x
1
)
μ
A2
(x
2
)
μ
B2
(x
2
)
μ
B1
(x
2
)
x
1
X
1
X
2
x
2

Przesłanki mogą posiadać jeszcze bardziej rozbudowana postać, a zastosowane
operatory nie muszą być tego samego rodzaju, tak jak jest to pokazane
poniżej:
JEŚLI (x1 =A1 ) I (x2 =B2) LUB (x1 =A2 ) I (x2 =A1) TO ( y
= C
1
) , (4.8)
gdzie : A
i
są zmiennymi lingwistycznymi pierwszej zmiennej
wejściowej,
B
i
są zmiennymi lingwistycznymi drugiej zmiennej wejściowej,
C
q
są zmiennymi lingwistycznymi danej wyjściowej.
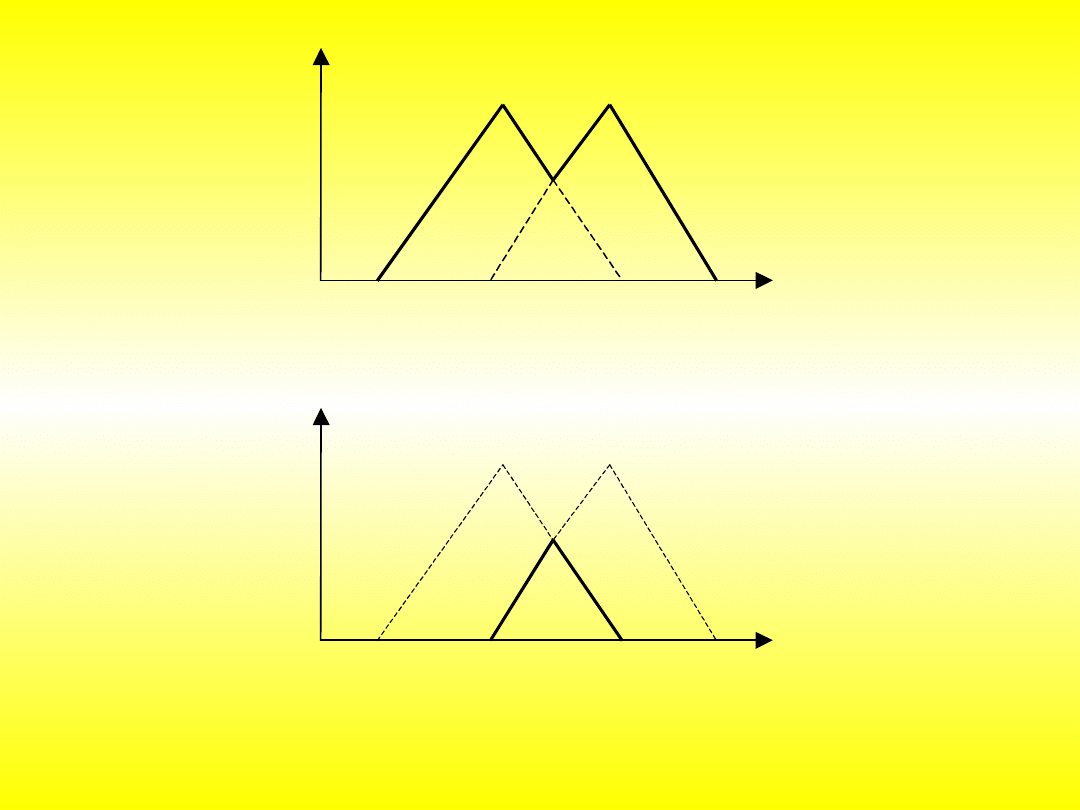
Zasadniczą rolę w budowie i działaniu reguł mają same operatory logiczne,
które stanowią pewien łącznik między przesłankami prostymi. Operator
LUB oznacza sumowanie zbiorów (rys. 4.10), a operator I oznacza iloczyn
zbiorów (rys.4.11). Przy zastosowaniu operatora typu I wartość stopnia
spełnienia przesłanki danej reguły jest równy wartości minimalnej ze
wszystkich stopni przynależności, reprezentujących wszystkie przesłanki
danej reguły. Analogicznie odbywa się to z regułami, w których są
zastosowane operatory typu LUB. Różnica polega na tym, że stopień
spełnienia danej przesłanki nie przyjmuje wartość minimalną, lecz
maksymalną z dostępnych stopni przynależności danej reguły [Piegat99].
1
A
(X)
B
(X)
X
1
A
(X)
B
(X)
X
Rys. 4.10. Wykres zbioru rozmytego powstałego w wyniku działania
operatora
LUB
Rys. 4.11. Wykres zbioru rozmytego powstałego w wyniku działania
operatora
I
SUMA
ILOCZYN

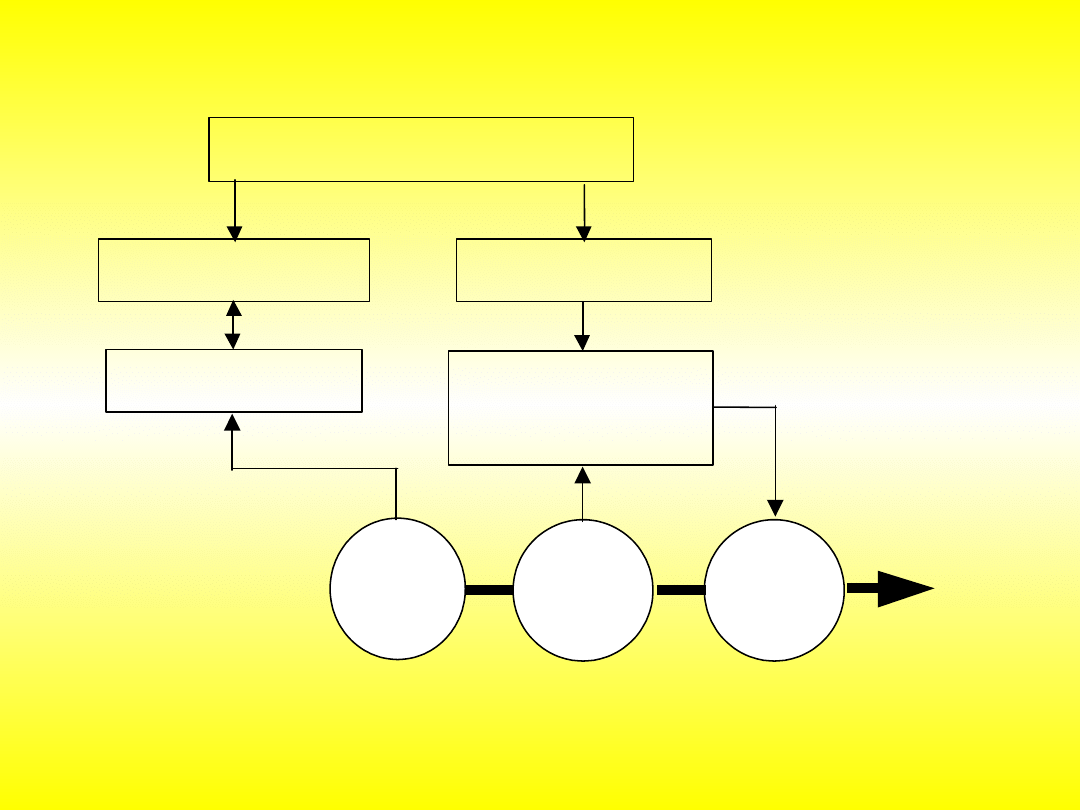
Przykład sterowania ruchem w osi robota
Mikrosterownik rozmyty
Przetwornik C/A
Procesor jednoukładowy
Analogowy regulator
prędkości
Licznik rewersyjny
Prądnica
tacho-
metryczna
Silnik
Przetwornik
obrotowo-
impulsowy
Rys. Schemat blokowy sterowania pojedynczej osi robota

Zbiór reguł wnioskowania może przedstawiać się jak poniżej:
1. Jeżeli A i D to +20
min (A,D) =
0,70
2. Jeżeli A i E to +110
min (A,E) = 0,20
3. Jeżeli A i F to 0
min (A,F) = 0
4. Jeżeli B i D to +1
min (B,D) =
0
5. Jeżeli B i E to 0
min (B,E) = 0
6. Jeżeli B i F to -1
min (B,F) = 0
7. Jeżeli C i D to 0
min (C,D) = 0
8. Jeżeli C i E to -10
min (C,E) = 0
9. Jeżeli C i F to -20
min (C,F) = 0
Procedura wnioskowania znajduje wygrywającą regułę używając metody min/max .
Dla każdej reguły, spośród ujętych w niej funkcji przynależności, zostaje
wyznaczona ta dla której stopień przynależności ma najmniejszą wartość.
Następnie z otrzymanych w ten sposób wartości zostaje znaleziona maksymalna.
Dla pokazanego przykładu regułą wygrywającą jest reguła 1, dla której minimalna
wartość stopnia przynależności jest równa 0,70 i jest największa dla wszystkich
reguł (patrz obliczenie z prawej strony reguł). Reguła 1 z której pochodzi
znaleziony w ten sposób stopień przynależności jest regułą wygrywającą i
odpowiadająca jej wartość przyrostu prędkości równa 20 zostaje podana na
wyjście regulatora prędkości
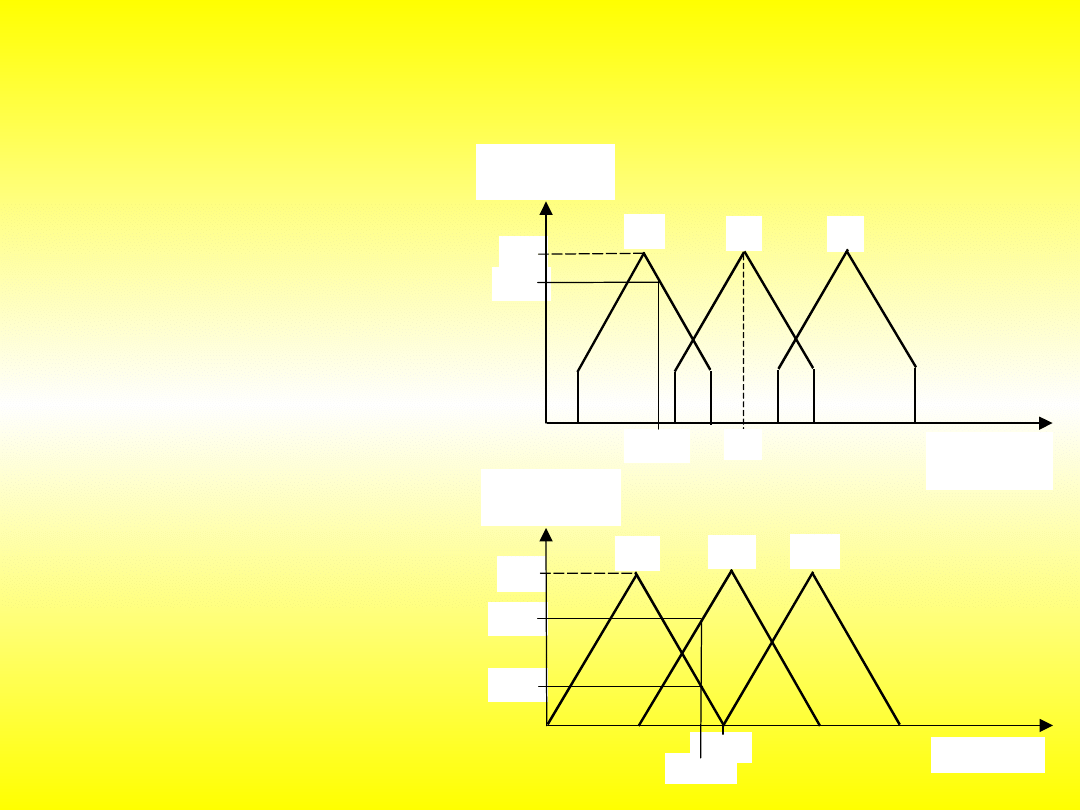
Na rys. pokazano przykładowy zbiór funkcji przynależności dla
wykorzystywanych sygnałów położenia i prędkości. Przyjmując wartość
uchybu położenia 0 dla zerowej odchyłki od położenia zadanego i 100 dla
zadanej wartości prędkości, pokazane na rys. funkcje przynależności
można interpretować następująco:
90
100
0,20
0,70
1,0
-0,6
0,8
1,0
0
A
B
C
Uchyb
położenia
Prędkość
D
E
F
Stopień
przynależności
Stopień
przynależności
•A: bieżące położenie znajduje się
na lewo od położenia zadanego
(uchyb położenia jest mniejszy od
zera),
•B: odchylenie od położenia
zadanego jest małe,
•C: bieżące położenie znajduje się
na prawo od położenia zadanego
(uchyb położenia jest większy od
zera),
•D: aktualna wartość prędkości
jest mniejsza od zadanej,
•E: aktualna prędkość jest w
pobliżu wartości zadanej,
•F: aktualna wartość prędkości
jest większa od zadanej.
Dla danych wejściowych:
uchyb położenia –0,60,
aktualna prędkość 90%
wartości zadanej, które wynoszą:
A(-0,6) = 0,80 B(-0,6) = 0 C(-0,6)
= 0
D(90) = 0,20 E(90) = 0,70 F(90)
= 0

i
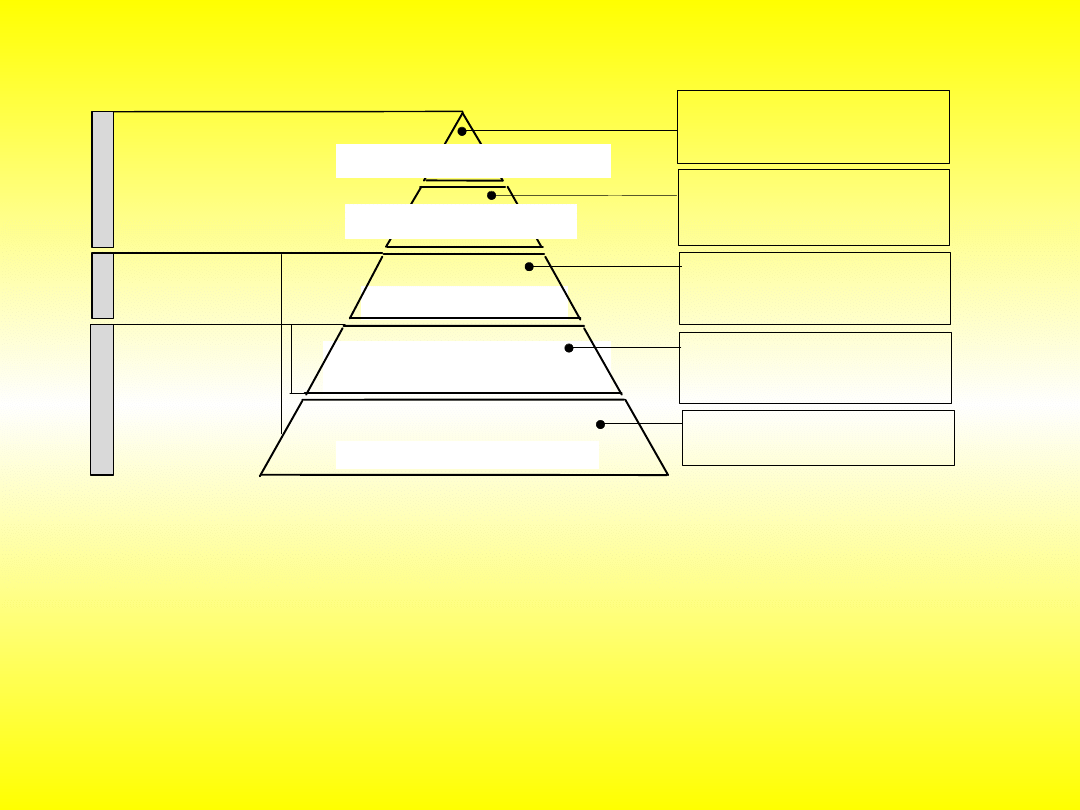
Harmonogramowanie
produkcji
Planowanie produkcji
Decyzje makroekonomiczne
Planowanie strategiczne
Sterowanie produkcją
Długookresowe
(lata)
Średnookresowe
(miesiące,
tygodnie, dni)
Bieżące
(godziny, minuty)
FSM
MM
Stopa procentowa.
Polityka podatkowa.
Zamówienia rządowe itd.
Harmonogramowanie produkcji.
Śledzenie produkcji i usuwanie
zakłóceń
Oprogramowanie sterowników
CNC, PLC
Partie produkcyjne
równocześnie wytwarzane.
Obciążenie maszyn
Asortyment produkcji.
Zasoby: obrabiarki, narzędzia,
przyrządy, transport, magazyn
.
Harmonogramowanie produkcji
jest zadaniem wyznaczenia rozdziału, w czasie i
przestrzeni, dostępnych zasobów produkcyjnych tak, aby zaspokoić zapotrzebowanie
na produkowane przedmioty przy najlepszym wykorzystaniu tych zasobów.
Harmonogram obejmuje następujące zadania:
1.
Ustalenie czasów poszczególnych operacji w sposób gwarantujący wymagane terminy.
2.
Wybór środków wytwarzania – dostosowanie maszyn oraz urządzeń wytwórczych w
sposób gwarantujący realizację zadań i uniknięcie kolejek.
3.
Rozdział materiałów – gwarantujący ciągłość pracy i termin realizacji zadań.
Sterowanie produkcją
to kierowanie pracą maszyn i urządzeń przez wpływanie na
parametry i przebieg ich pracy w celu zrealizowania harmonogramu, czyli
programowa i fizyczna realizacja wygenerowanego harmonogramu.
Zastosowanie logiki rozmytej do harmonogramowania
sterowania zrobotyzowanych systemów wytwarzania
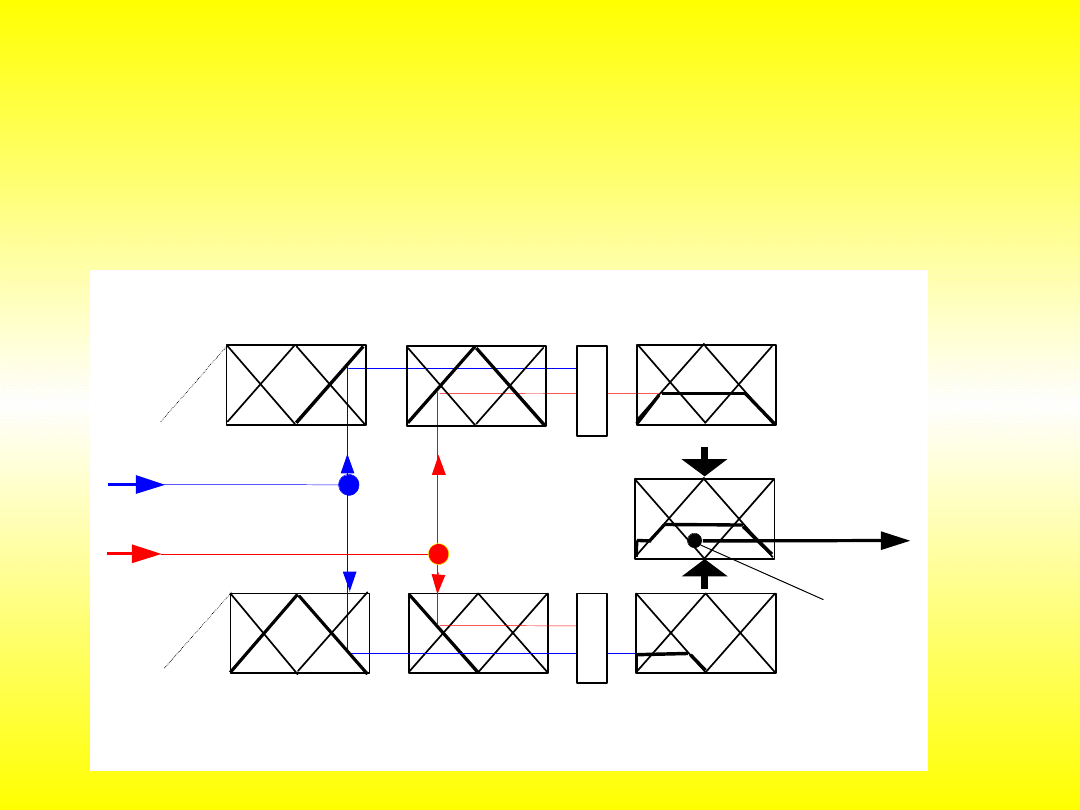
Reguła 2
Reguła 1
0 Y 1
0
X2
1
0 X1 1
0 Y
1
0 X2 1
0 X1 1
J eżeli X1=duży i X2=średni to Y=średni
J eżeli X1=średni i X2=mały to Y = mały
Defuzyfikacja
Fuzyfikacja
X2
X1
Y
1
1
1
1
1
1
MAX
M
I
N
M
I
N
Środek ciężkości
uzyskanej figury
Jeżeli czas przezbrojenia (X1) jest duży i czas obróbki (X2) jest średni to priorytet
(Y) jest średni
Jeżeli czas przezbrojenia (X1) jest średni i czas obróbki (X2) jest mały to
priorytet (Y) jest mały
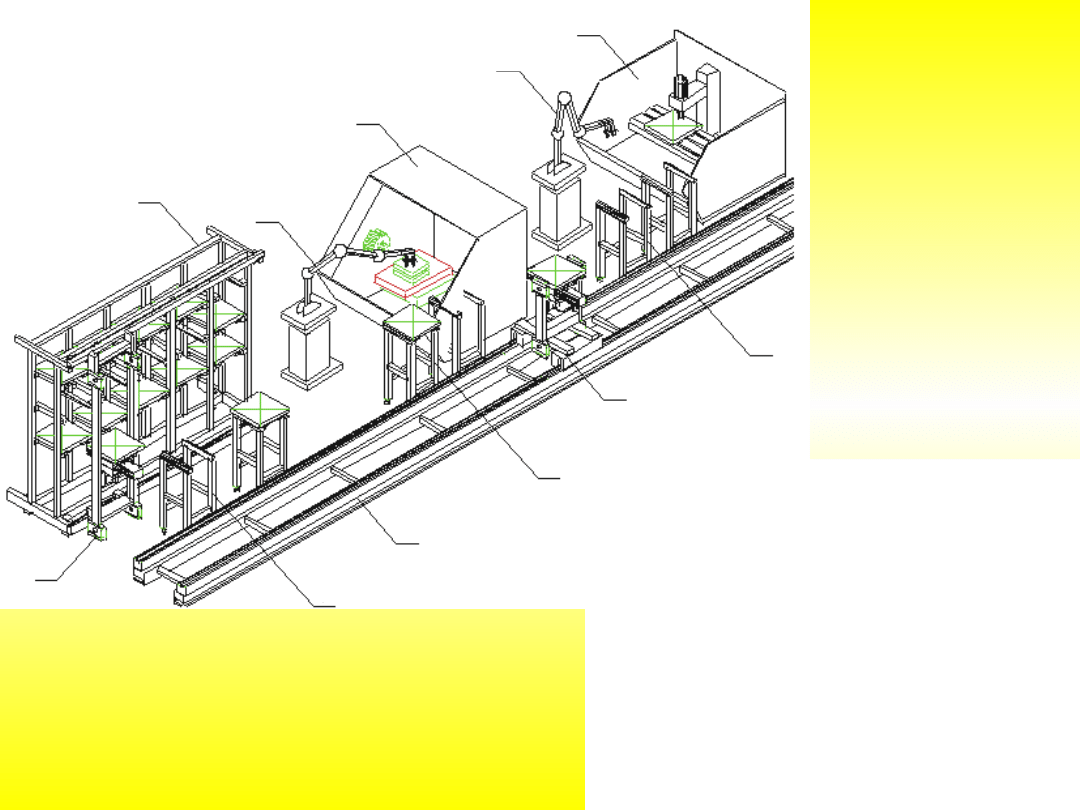
2
1
3
5
6
4
7
8
9
11
10
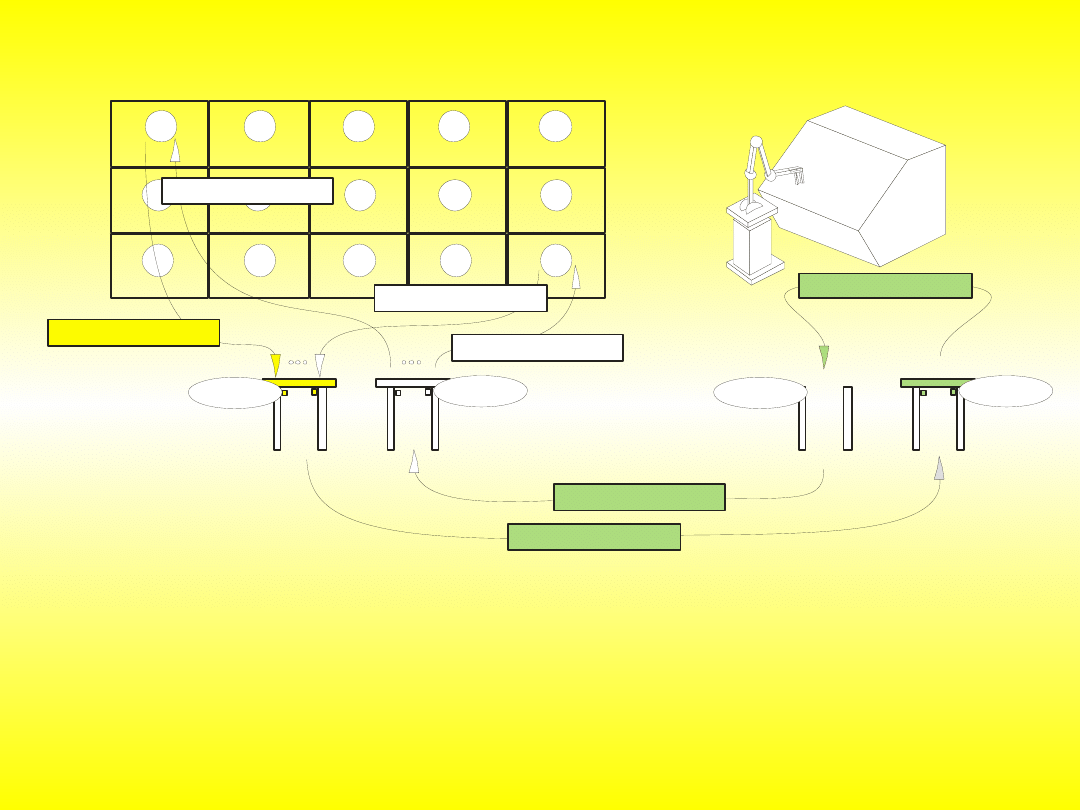
Konfiguracja badawczego
miniaturowego elastycznego systemu
wytwarzania:
1) magazyn regałowy,
2) układarka regałowa,
3) szynowy wózek transportowy,
4) tor jezdny,
5) tokarka M1,
6) frezarka M2,
7) robot tokarki,
8) robot frezarki,
9) stanowiska odkładcze układarki
regałowej,
10) stanowiska odkładcze tokarki,
11) stanowiska odkładcze frezarki


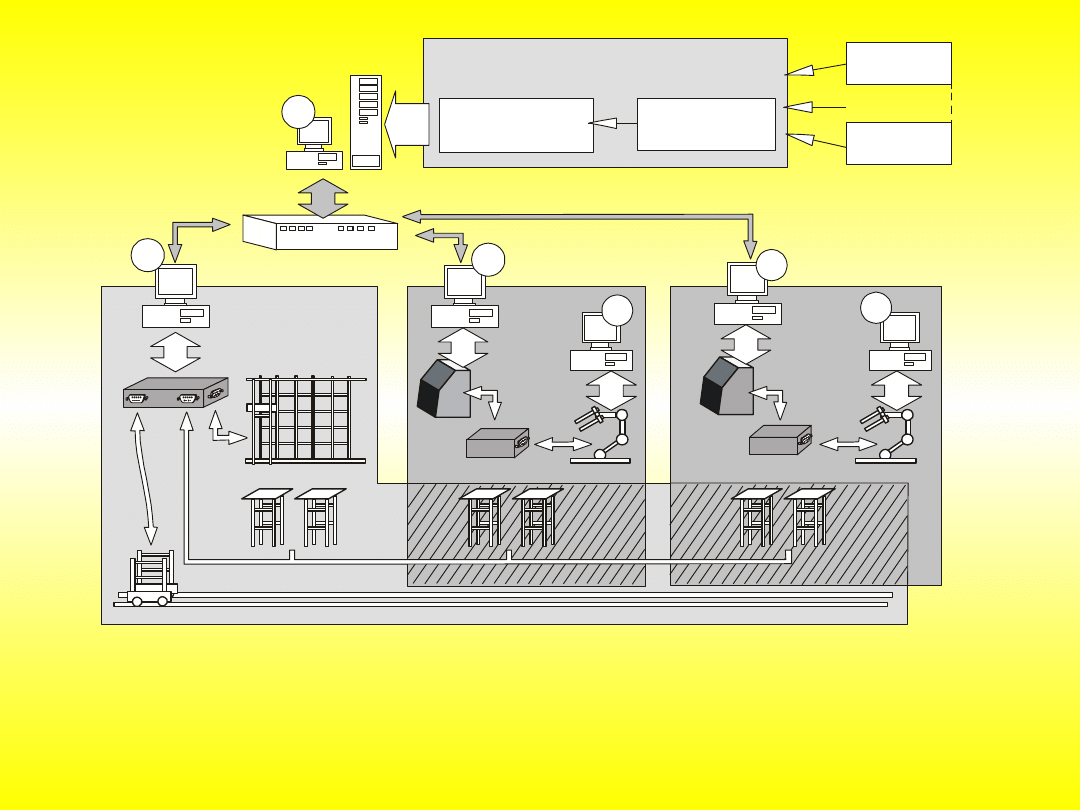
•
Architektura podsystemu sterowania
1
H U B
2
4
5
3
6
O R G A N I Z A C Y J N E P R Z Y G O T O W A N I E
P R O D U K C J I
Z L E C E N IE N
Z L E C E N IE 1
H A R M O N O G R A M
P R O C E D U R Y
S T E R U J Ą C E
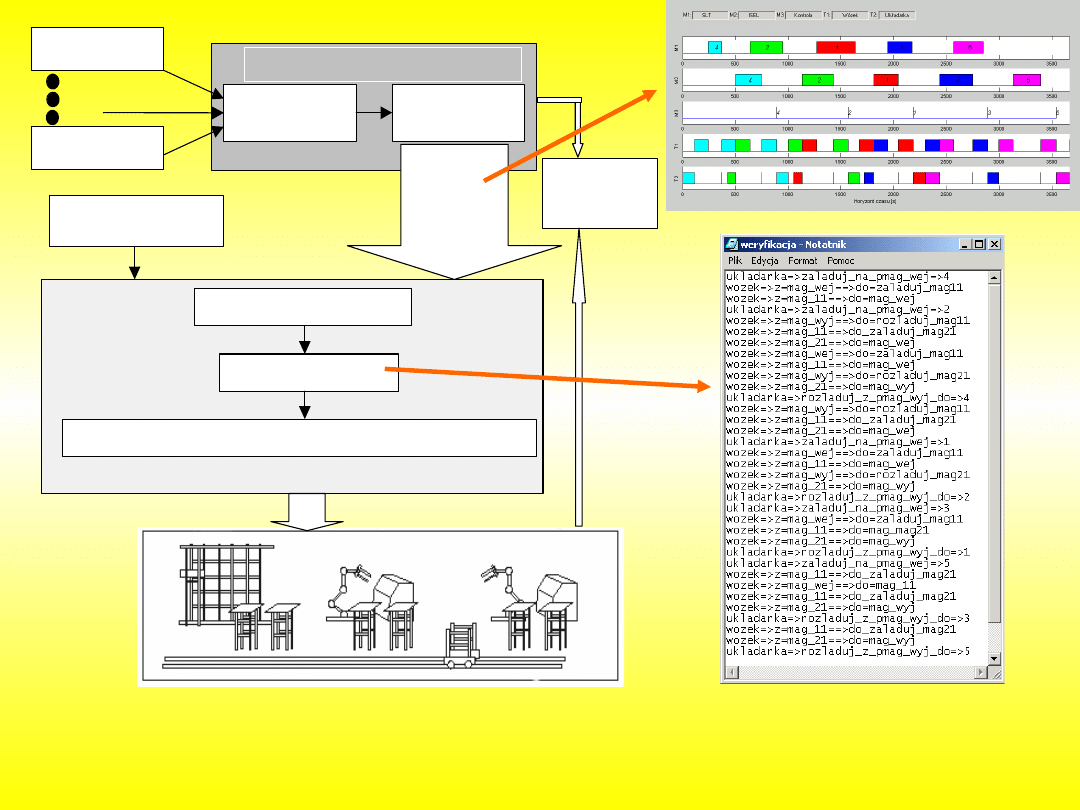
Planowanie i harmonogramowanie wytwarzania przy sterowaniu
scentralizowanym
wg harmonogramu generowanego off-line
wg harmonogramu generowanego off-line
Z l e c e n i e 1
Z l e c e n i e n
M o d e l
S y s t e m u
B a d a n i a
S y m u l a c y j n e
O p r o g r a m o w a n ie s y m u l a c y j n e
W e r y fi k a c j a
w y n i k ó w
s y m u l a c j i
D a n e w p r o w a d z o n e
p r z e z o p e r a t o r a
A l g o r y t m s t e r o w a n i a
I n t e r p r e t a c j a h a r m o n o g r a m u
P r o c e d u r y s t e r o w a n i a d l a p o s z c z e g ó l n y c h u r z ą d z e ń w y k o n a w c z y c h
O p r o g r a m o w a n ie s t e r u j ą c e s y s t e m e m w y t w a r z a n i a
H a r m o n o g r a m
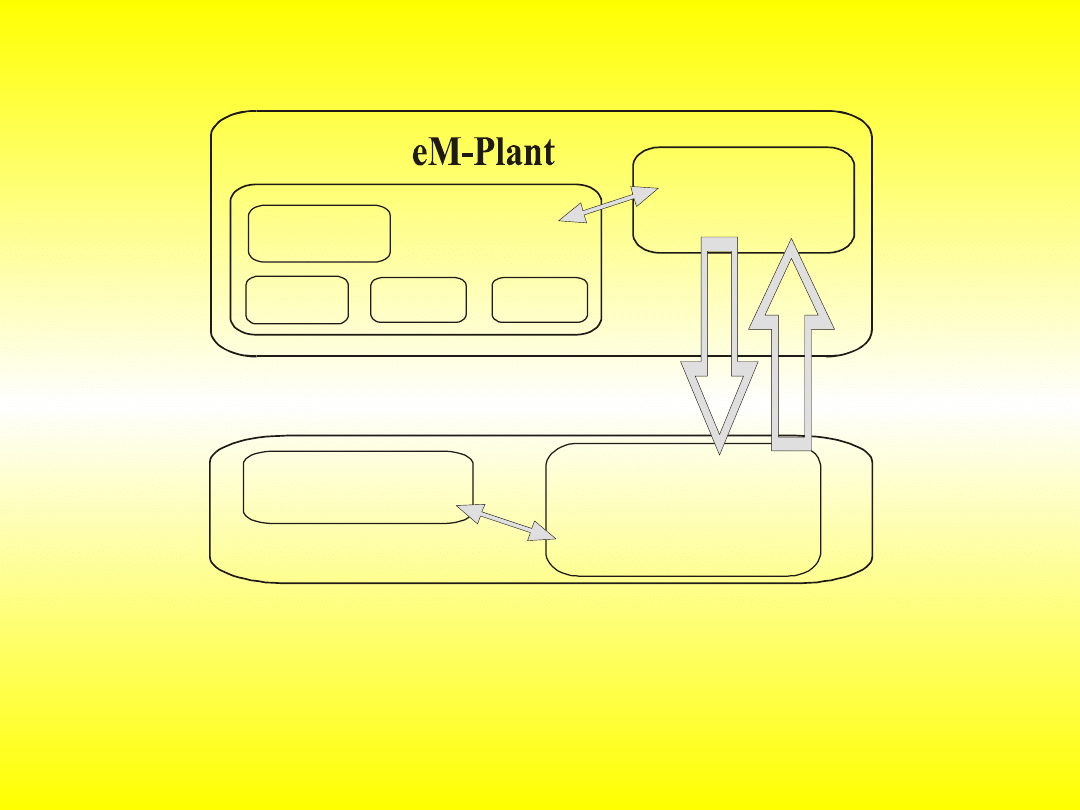
•Idea sterowania modelem systemu z wykorzystaniem logiki
rozmytej
•Schemat współdziałania trzech programów podczas
symulacji w programie eM-Plant wg reguł rozmytych
U k ł a d a r k a
“ b a z a _ r e g u ł .f t r ”
W ó z e k
M 2
M 1
M o d e l
s y s t e m u
O b i e k t -
" F il e I n t e r f a c e "
F L L o a d e r
F u z z y T e c h
"p
yt
an
ie
.tx
t”
"o
dp
ow
ie
dź
.tx
t”
+
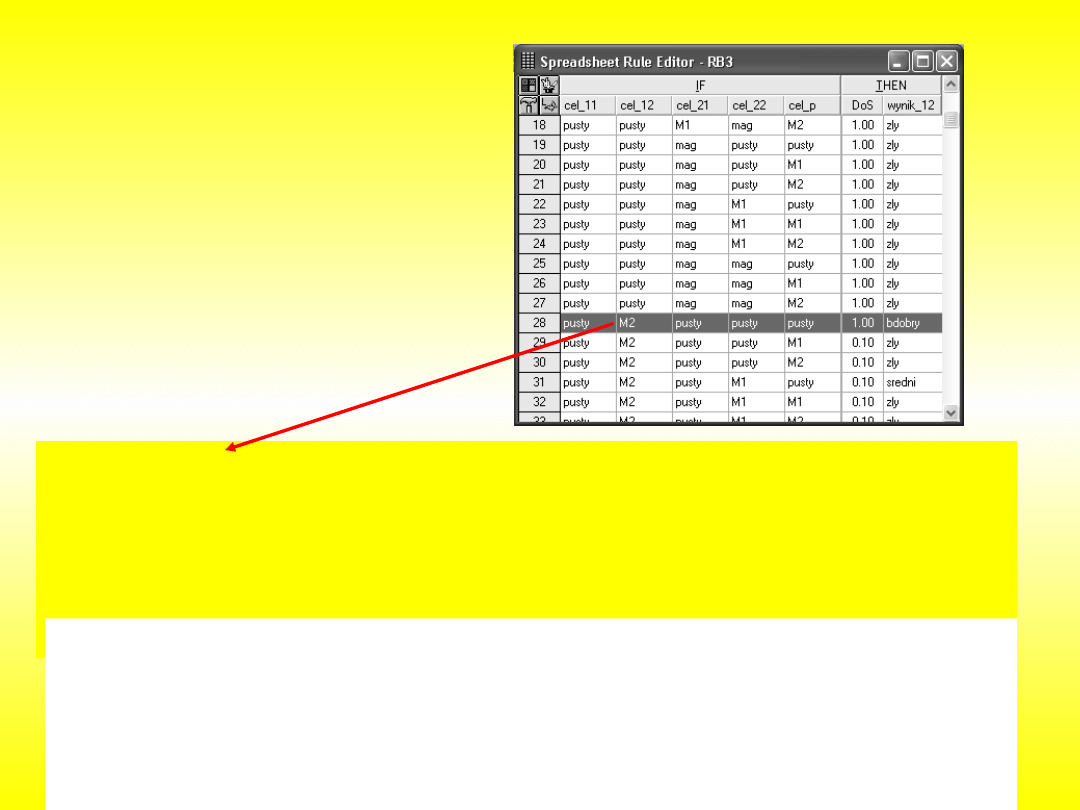
Jeżeli stanowisko odkładcze mag_11 jest wolne (cel_11=pusty) i paleta na
stanowisku odkładczym mag_12 jest gotowa do odebrania z marszrutą
technologiczną M2 (cel_12=M2) i stanowisko odkładcze mag_21 jest wolne
(cel_21=pusty) i stanowisko odkładcze mag_22 jest wolne (cel_22=pusty) i
stanowisko odkładcze mag_wyj jest wolne (cel_p=pusty)
to wybór
przemieszczenia palety z mag_12 do magazynu wyjściowego mag_wyj jest
bardzo dobry
Przykład reguł rozmytych dla oceny ruchu układarki regałowej do
stanowisk odkładczych przedstawiono poniżej.
if (mag_11<>0) and (mag_12=0) and (mag_21<>0) and (mag_22<>0) and
(s11<>0) and (s12=0) and (s21<>0) and(s22<>0) then begin
if M1 then startw6;
if M2 then startw5;
if M3 then startw16;
if M4 then startw15;
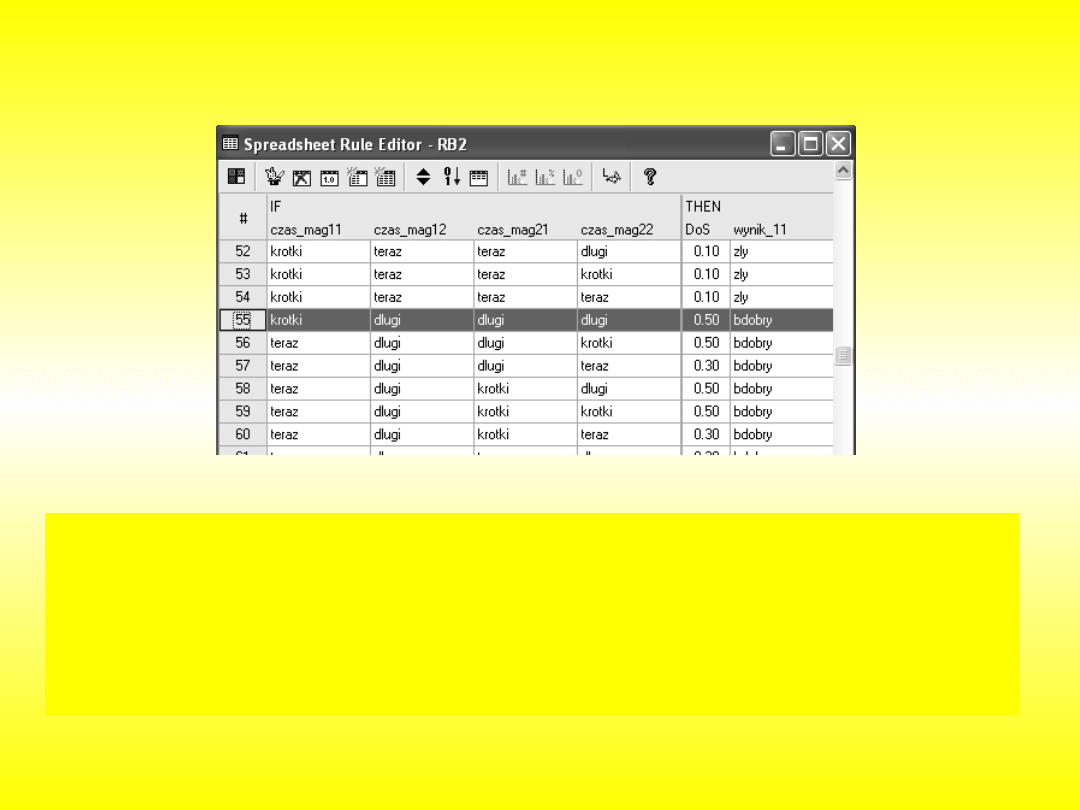
Jeżeli czas przewidziany do zakończenia obróbki przedmiotów na stanowisku
mag_11 jest krótki (czas_mag11=krótki)
i przedmiotów na stanowisku mag_12 jest długi (czas_mag12=długi)
i przedmiotów na stanowisku mag_21 jest długi (czas_mag21=długi)
i przedmiotów na stanowisku mag_22 jest długi (czas_mag22=długi)
to wybór przemieszczenia palety z mag_11 jest bardzo dobry (waga reguły
50%).
Przykład reguł rozmytych dla oceny ruchu wózka szynowego do
stanowisk odkładczych przedstawiono poniżej.
W trakcie pracy systemu na bieżąco pobierane są sygnały zwrotne
dotyczące stanu poszczególnych podsystemów (układarki, wózka, robotów,
obrabiarek). Sygnałami zwrotnymi są: zakończenie pracy obrabiarek,
zakończenie obróbki wszystkich części umieszczonych na palecie, obecność
palety w magazynie regałowym i na stanowiskach odkładczych, stan
obrabiarek i robotów.
PODSYSTEM
STEROWANIA
OBIEKT
STEROWANIA
ESW
WY NIK
ZAKŁÓCENIE
SYGNAŁY
STERUJĄCE
ESW
SYGNAŁY
WEJŚCIOWE
ZLECENIA
SYGNAŁY STANU OBIEKTU
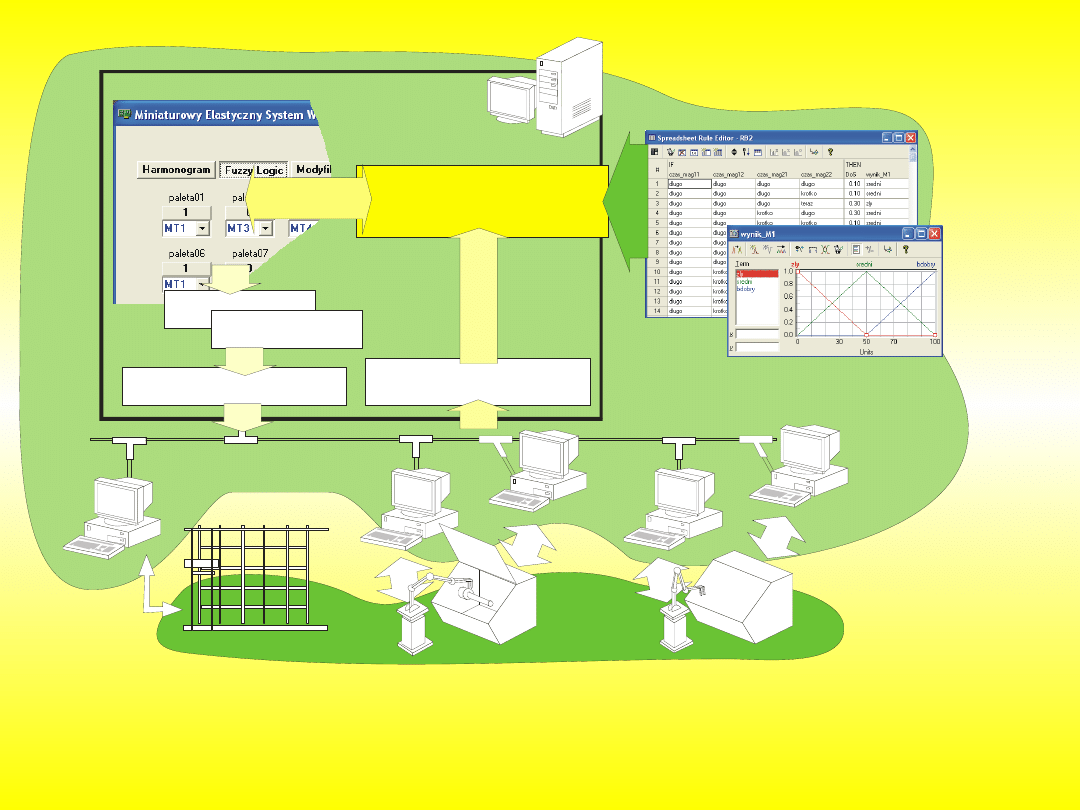
Taki sposób sterowania pracą systemu wytwarzania to
regulacja.
Podczas sterowani on-line, na podstawie sygnałów zwrotnych
program wnioskowania rozmytego podejmuje decyzje dotyczące kolejnych
operacji w systemie wytwarzania.
•
Schemat blokowy automatycznej regulacji ESW
GŁÓWNY PROGRAM STERUJĄCY
PROGRAM
WNIOSKOWANIA
ROZMY TEGO
BAZY REGUŁ
K
O
M
P
IL
A
C
JA
p y t a n i e?
o d p o w i e d ź
HARMONOGRAM
PROCEDURY STERUJĄCE
NOWY
HARMONOGRAM
SYGNA ŁY O STANIE
OBIEKT U
ESW
OBIEKT REGULACJI
REGULATOR
7
6
11
PODPR O G RA M 15
PODPROGRAM 1
PODPROG RAM 41
PODPROGRAM 64
POD PR O G RAM 16
PODPROGRAM 30
PODPROGRAM 55
1
m ag_ wej
m ag_ wy j
15
3
4
5
8
9
14
10
12
13
2
m ag _ 11
m ag _12
M1 - TO KARKA
Podprogramy sterujące

4. Badania
doświadczalne
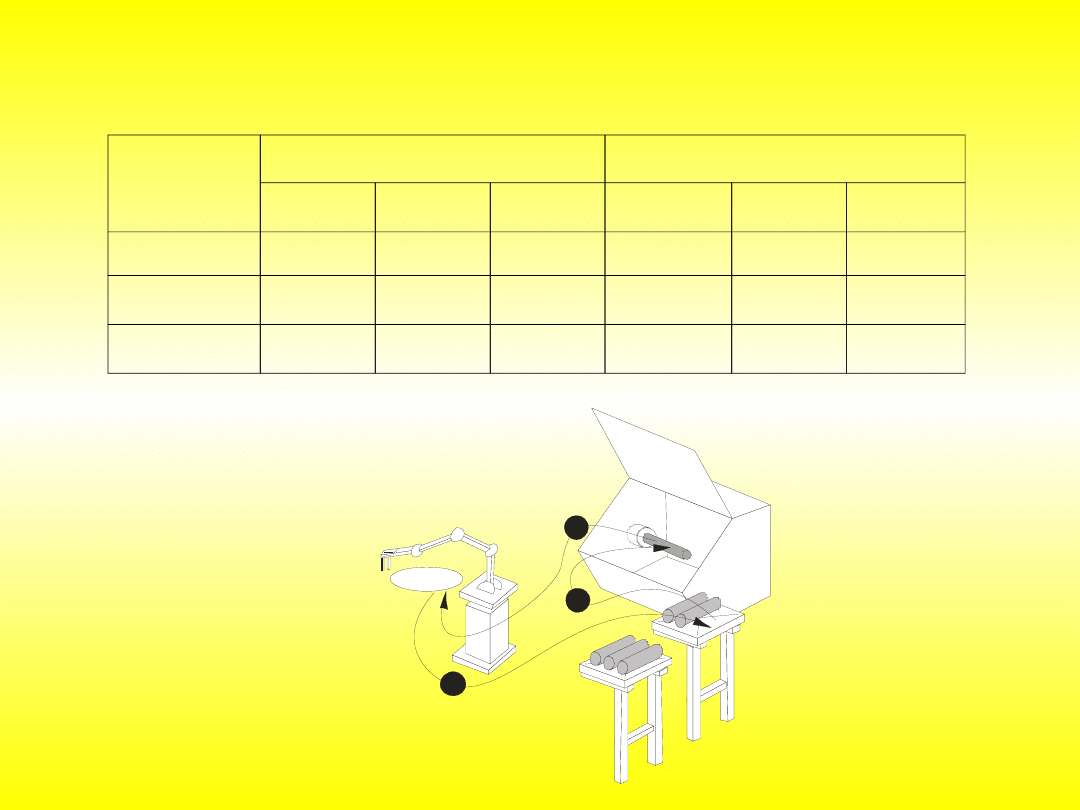
Pokazano przykłady weryfikacji dla dwóch przypadków.
I W pierwszym przypadku zweryfikowano harmonogram utworzony przy
użyciu modelu operacyjnego.
II W drugim przypadku weryfikowano modele symulacyjne opracowane w
programie eM-Plant wykorzystując logikę rozmytą.
Ad I Zakłada się wykonanie pięciu przedmiotów w partiach transportowych
po trzy sztuki według przepływowej formy organizacji na dwóch
stanowiskach technologicznych.
Tabela 1. Czasy zadań technologicznych na obrabiarkach M1 i M2 (Podane czasy
uwzględniają czasy maszynowe oraz czasy pomocnicze (manipulacji) związane z wymianą
partii przedmiotów na obrabiarkach)
Z1/3
1
2
3
4
5
M1
115
95
69
34
85
M2
65
85
92
68
75

Wygenerowano harmonogramy w oparciu o metody Johnson’a, Browna-
Lomnickiego, Branch&Bound. Do weryfikacji wybrano metodę rozszerzoną
B&B, dającą najkrótszy sumaryczny czas realizacji wszystkich zadań
produkcyjnych.
Tabela 2. Rezultaty weryfikacji dla modelu B&B
Etapy weryfikacji
Model
Czas realizacji wszystkich zadań
[godz:min:s]
Harmonogramowanie
01:01:04
Sterowanie
B&B
01:05:00
Względny błąd w stosunku do
obiektu rzeczywistego [%]:
- 6%

Ad. 2. W drugim przypadku zweryfikowano model symulacyjny opracowany
w programie eM-Plant wykorzystując reguły FIFO i logikę rozmytą.
Zestawienie eksperymentów i czasy zadań technologicznych zestawiono w
tablicach 3 i 4.
Wyniki realizacji zlecenia przy sterowaniu off-line i on-line
przedstawiają tabele 5, 6, 7 i 8.
Nr
eksperymentu
Metoda
harmono-
gramowania
Liczba
przedmiotów
Marszruta
technologiczna
Kolejność realizacji
zleceń
P2
Fuzzy Logic
15
MT1
Z1, Z2, Z3, Z4, Z5
P7
FIFO
15
MT1
Z1, Z2, Z3, Z4, Z5
P10
Fuzzy Logic
45
MT1, MT2, MT3,
MT4
Z6, Z14, Z14, Z14,
Z14, Z10, Z10, Z6,
Z6, Z6, Z6, Z6, Z6,
Z10, Z10
P11
FIFO
45
MT1, MT2, MT3,
MT4
Z6, Z14, Z14, Z14,
Z14, Z10, Z10, Z6,
Z6, Z6, Z6, Z6, Z6,
Z10, Z10
Tabela 3. Zestawienie eksperymentów

Tabela 4. Czasy maszynowe dla tokarki i frezarki w realizowanych zleceniach
Czasy maszynowe
tokarka M1
Czasy maszynowe
frezarka M2
Numer zlecenia
s
s
Z1
129
81
Z2
101
121
Z3
71
65
Z4
81
181
Z5
200
30
Z6
71
31
Z7
200
181
Z8
128
Z9
101
Z10
71
Z11
81
Z12
200
Z13
181
Z14
31
Czas załadunku [s]
Czas rozładunku [s]
t_min
t_śred
t_max
t_min
t_śred
t_max
Przedmiot 1
45,71
45,93
46,26
38,26
38,59
38,84
Przedmiot 2
46,38
46,65
46,91
39,20
39,48
39,71
Przedmiot 3
47,02
47,46
47,62
40,15
40,43
40,71
Tabela 5. Czasy manipulacyjne robota przegubowego
2
3
1
BAZA
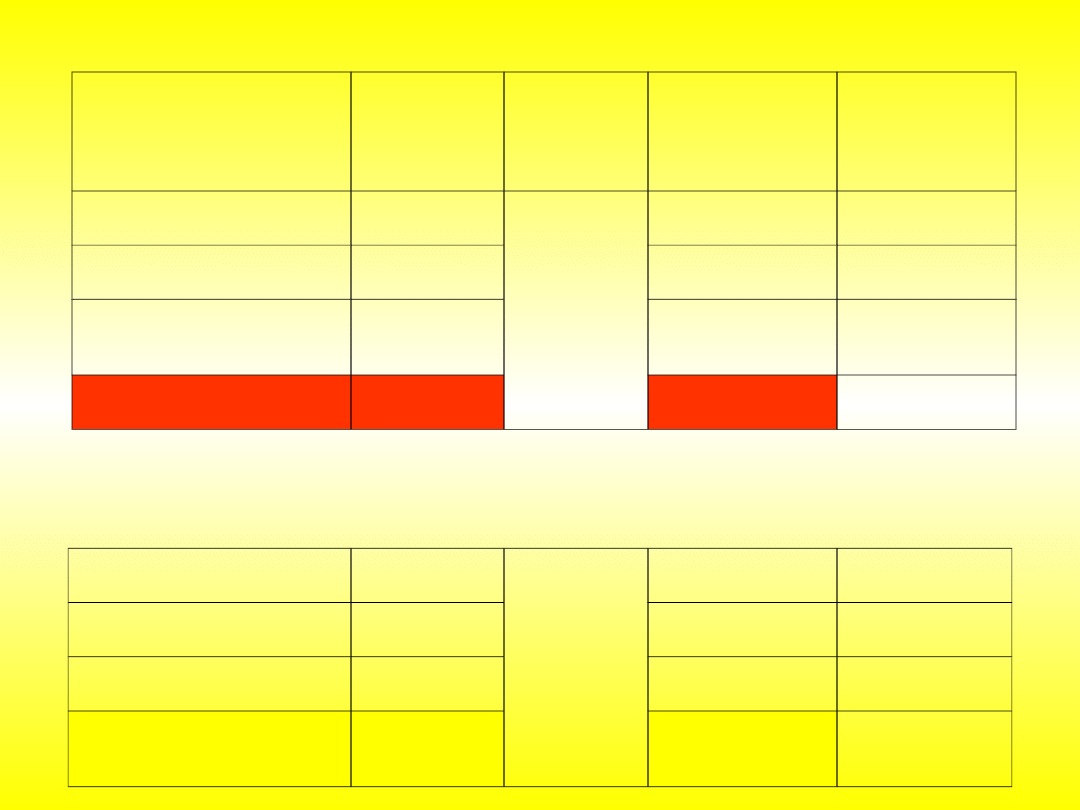
Tabela 6. Wyniki weryfikacji symulacji w programie eM-Plant dla modelu działającego
wg reguł FIFO (Eksperyment P2)
Eksperyment
Nr palety/
liczba
przedmiotó
w
Kolejność
pobierania
palet
Czas realizacji
zlecenia
[godz:min:s]
Względny błąd
w stosunku do
obiektu
rzeczywistego
[%]
Symulacja w eM-Plant
dla minimalnych czasów
5/3
{11; 12;
13; 14;
15}
1:03:15,46
-3,39
Symulacja w eM-Plant
dla średnich czasów
5/3
1:03:33,81
-2,92
Symulacja w eM-Plant
dla maksymalnych
czasów
5/3
1:03:54,29
-2,39
Sterowanie systemem
wg harmonogramu
5/3
1:05:28,33
-
Symulacja w eM-Plant dla
minimalnych czasów
5/3
{13; 14;
12; 11;
15}
1:08:47,56
-3,47
Symulacja w eM-Plant dla
średnich czasów
5/3
1:09:08,68
-2,98
Symulacja w eM-Plant dla
maksymalnych czasów
5/3
1:09:30,95
-2,46
Sterowanie systemem wg
harmonogramu
5/3
1:11:16,15
-
Tabela 7. Wyniki weryfikacji symulacji w programie eM-Plant dla modelu działającego wg
reguł rozmytych (Eksperyment P7)
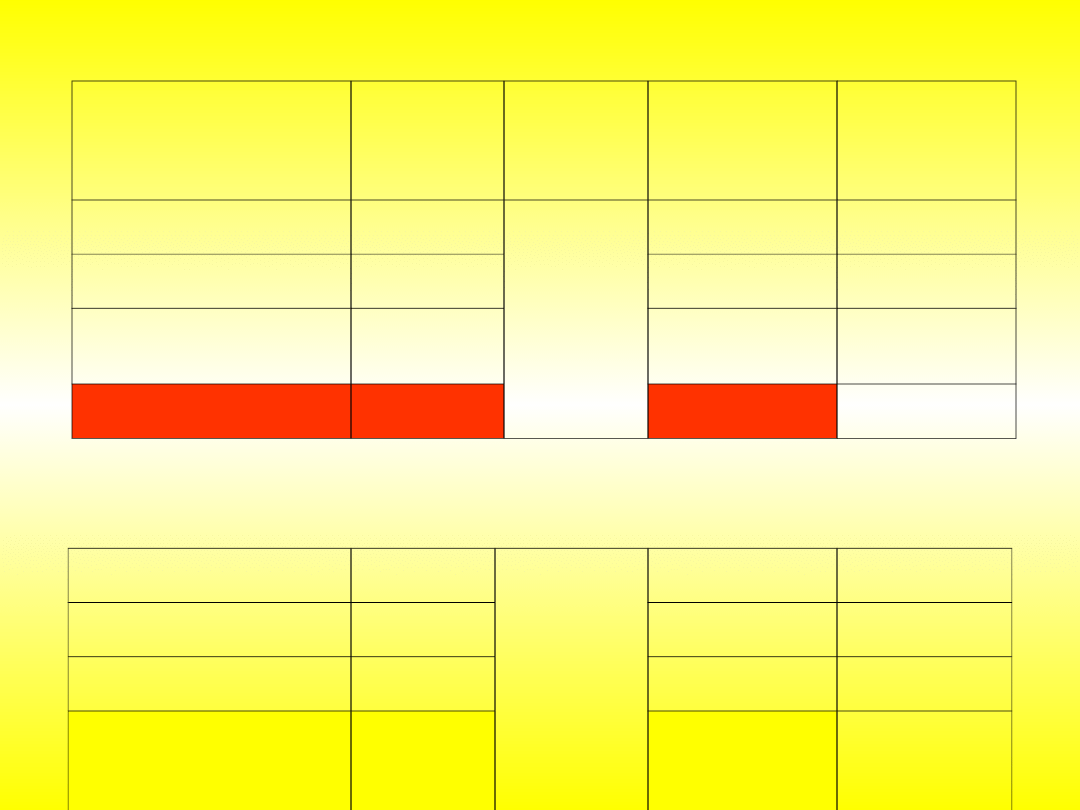
Table 9. Wyniki weryfikacji symulacji w programie eM-Plant dla modelu działającego wg
reguł FIFO (Eksperyment P11)
Eksperyment
Nr palety/
liczba
przedmiotó
w
Kolejność
pobierania
palet
Czas realizacji
zlecenia
[godz:min:s]
Względny błąd
w stosunku do
obiektu
rzeczywistego
[%]
Symulacja w eM-Plant
dla minimalnych czasów
15/3
{11; 8; 9;
12; 10, 13,
14, 15, 6,
1, 2, 7, 3,
4, 5}
1:30:28,42
-3,84
Symulacja w eM-Plant
dla średnich czasów
15/3
1:31:00,10
-3,28
Symulacja w eM-Plant
dla maksymalnych
czasów
15/3
1:31:29,47
-2,76
Sterowanie systemem
wg harmonogramu
15/3
1:34:05,42
-
Symulacja w eM-Plant dla
minimalnych czasów
15/3
{11; 12;
13; 14; 15,
6, 7, 8, 9,
10, 1, 2, 3,
4, 5
1:53:17,63
-3,77
Symulacja w eM-Plant dla
średnich czasów
15/3
1:53:58,19
-3,20
Symulacja w eM-Plant dla
maksymalnych czasów
15/3
1:54:38,21
-2,63
Sterowanie systemem wg
harmonogramu
15/3
1:57:44,04
-
Tabela 8. Wyniki weryfikacji symulacji w programie eM-Plant dla modelu działającego wg
reguł rozmytych (Eksperyment P10)
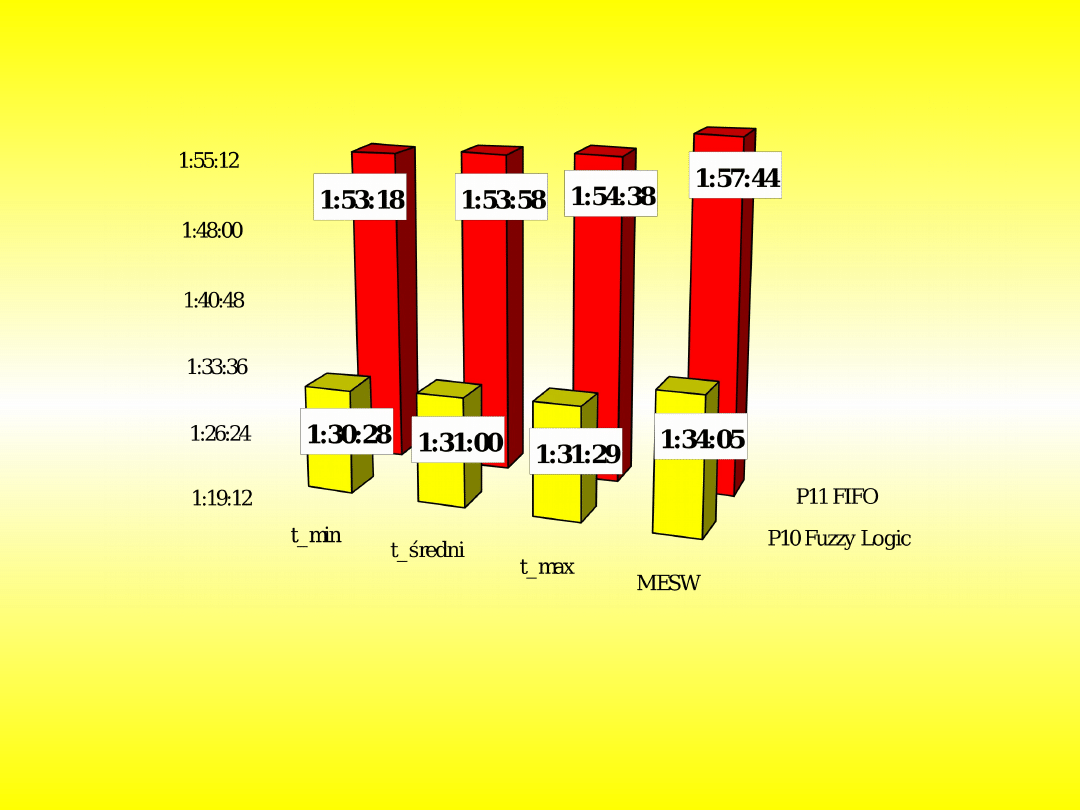
Wyniki weryfikacji symulacji w programie eM-Plant dla modelu
działającego wg reguł rozmytych i FIFO (Eksperyment P10 and P11)
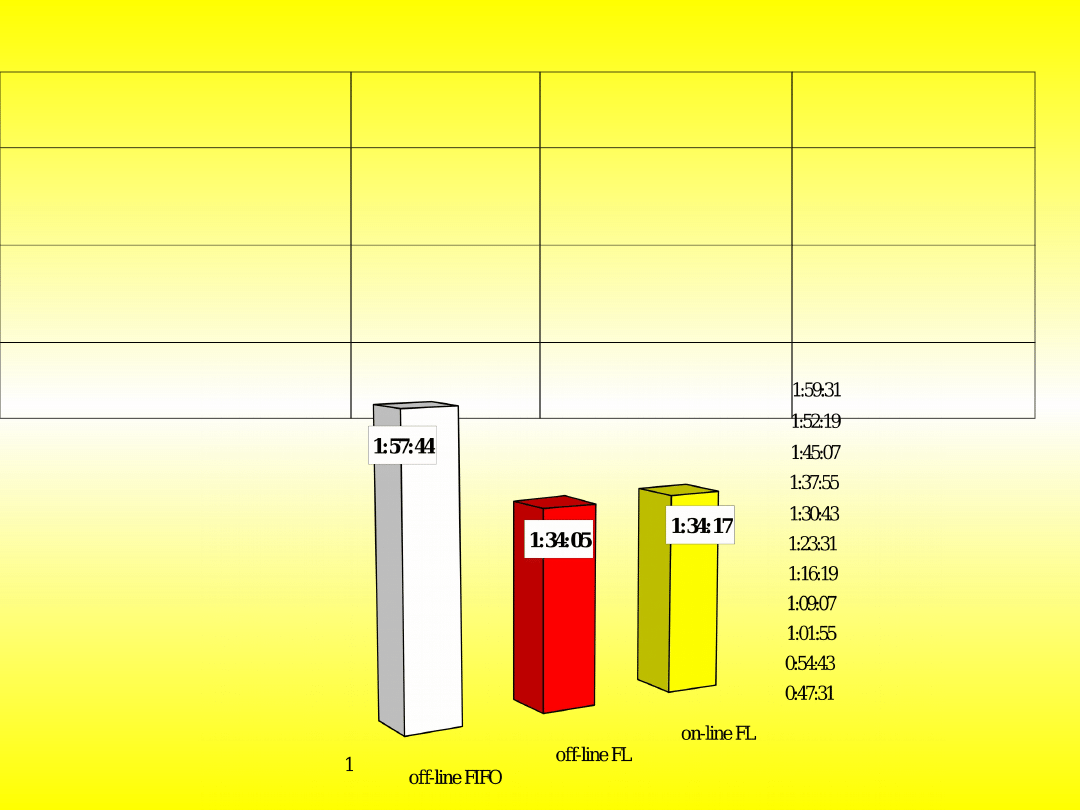
Eksperyment
Liczba
palet/przedmiot
ów
Kolejność pobierania
palet
Czas realizacji
wszystkich zadań
[godz:min:s]
Sterowanie systemem na
podstawie harmonogramu
wygenerowanego w eM-Plant
wg reguł FIFO (off-line)
15/3
{11; 12; 13; 14, 15,
6, 7, 8, 9, 10, 1, 2,
3, 4, 5 }
1:57:44,04
Sterowanie systemem na
podstawie harmonogramu
wygenerowanego w eM-Plant
wg reguł rozmytych (off-line)
15/3
{11; 8; 9; 12; 10;
13; 14; 15; 6; 1; 2;
7; 3; 4; 5}
1:34:05,42
Sterowanie systemem on-line
wg reguł rozmytych
15/3
{11; 8; 9; 12; 10;
13; 14; 15; 6; 1; 2;
7; 3; 4; 5}
1:34:17,22
Tabela 9. Wyniki sterowania systemem na podstawie harmonogramów wygenerowanych w eM-Plant wg
reguł FIFO i reguł rozmytych (off-line - Eksperyment P10 and P11) oraz sterowania systemem on-line

Po weryfikacji, dla zmierzonych, rzeczywistych czasów jazdy
układarki, wózka i robotów oraz czasów maszynowych obróbki
zestawionych w tabeli 10 przeprowadzono badania symulacyjne dla
różnych wariantów zadań produkcyjnych. Celem badań była analiza pracy
systemu dla zestawów zleceń różniących się liczbą części na paletach (i =
1, 2, 3) oraz sprawdzenie wpływu zastosowanych strategii sterowania na
kryteria oceny pracy systemu.
Marszruta
techn.
Liczba
palet
Czas
maszynowy
tokarka M1
Czas
maszynowy
frezarka M2
Czas
przezbrojenia
tokarki M1
Czas
przezbrojenia
frezarki M2
MT1
4
03:20
03:52
02:16
01:56
MT2
4
03:01
03:56
02:04
02:16
MT3
4
05:30
---
01:46
---
MT4
3
---
04:51
---
02:36
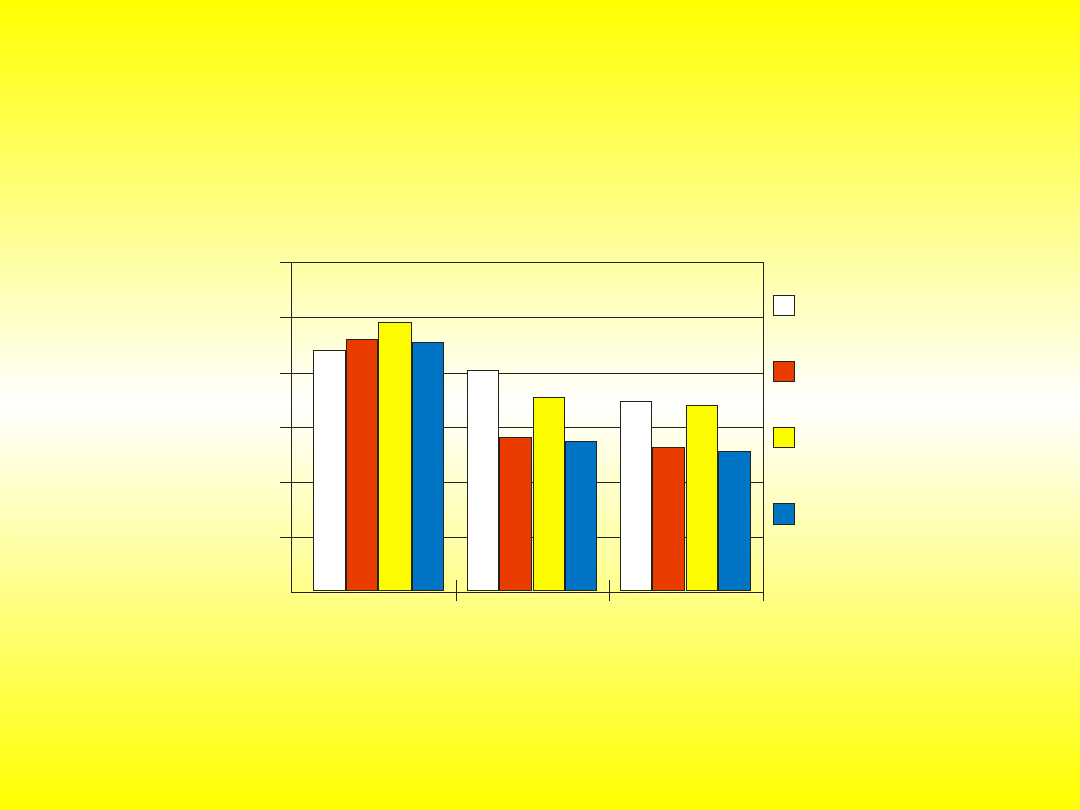
Średnie czasy obróbki jednego przedmiotu dla czterech modeli i różnej
liczby przedmiotów na paletach
Uwzględniono 4 modele różniące się algorytmami sterowania dla
układarki regałowej i wózka transportowego:
Model I – wózek FIFO, układarka FIFO (First-Input-First-Output),
Model II – wózek FIFO, układarka FL (Fuzzy Logic),
Model III – wózek FL, układarka FIFO,
Model IV – wózek FL, układarka FL.
150
200
250
300
350
400
ŚREDNI CZAS
OBRÓBKI
JEDNEGO
PRZEDMIOTU
[s]
LICZBA PRZEDMIOTÓW NA PALECIE
1 PRZEDMIOT
2 PRZEDMIOTY
3 PRZEDMIOTY
WÓZEK - FIFO
UKŁADARKA - FIFO
WÓZEK - FIFO
UKŁADARKA - FL
WÓZEK - FL
UKŁADARKA - FIFO
WÓZEK - FL
UKŁADARKA - FL
100
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
Wyszukiwarka
Podobne podstrony:
Fuzzy Logic I SCILAB
Fuzzy logic
Fuzzy Logic III id 182424 Nieznany
Fuzzy Logic II id 182423 Nieznany
A New Low Cost Cc Pwm Inverter Based On Fuzzy Logic
3 fuzzy logic I
fuzzy logic
Fuzzy Logic I SCILAB
A New Low Cost Cc Pwm Inverter Based On Fuzzy Logic
pole placement Fuzzy Logic
13 GEP fuzzy
Dolby Surround eller Dolby Surround Pro Logic
Fuzzy Navel Jell
projekt leafnode, logic
RATIONALITY AND SITUATIONAL LOGIC IN POPPER
więcej podobnych podstron