
Pole Placement Approaches for Linear and Fuzzy
Systems
S. Preitl
*
, R.-E. Precup
*
, P.A. Clep
*
, I.-B. Ursache
*
, J. Fodor
**
and I. Škrjanc
***
*
Dept. of Automation and Applied Informatics, “Politehnica” University of Timisoara, Timisoara, Romania
**
Institute of Intelligent Engineering Systems, Budapest Tech Polytechnical Institution, Budapest, Hungary
***
Laboratory of Modelling, Simulation and Control, University of Ljubljana, Ljubljana, Slovenia
stefan.preitl@aut.upt.ro, radu.precup@aut.upt.ro, alexandru.clep@aut.upt.ro, bogdan.ursache@aut.upt.ro,
fodor@bmf.hu, igor.skrjanc@fe.uni-lj.si
Abstract—The paper investigates several pole placement
methods in the linear case and suggests a new pole
placement method by means of fuzzy linear equations. The
linear methods concern the constant real part poles, the
poles places on a circle, Butterworth configurations without
and with the correction of the imaginary part, the pole-zero
cancellation, and the poles placed on an ellipse. Low order
systems are considered. The pole placement methods are
compared by the digital simulation of control systems’
behaviors with respect to the modification of the reference
input. The conclusions are useful for continuous control
systems, and they can be extended easily to digital control
systems including quasi-continuous ones.
I.
I
NTRODUCTION
The well accepted necessity behind the pole placement
design of state feedback control system (SFCS) is justified
due to [1]:
-
The performance specifications including the stability
request, the sensitivity analysis and the performance
indices defined in systems’ dynamic behaviors
(overshoot, settling time, etc.) can be defined
adequately.
-
The implementation of the state feedback controllers
(SFCs) can be accomplished easily by pole placement
ensuring an elegant way to insert supplementary
nonlinear functionalities such as limitations and Anti-
Windup-Reset (AWR) measures.
-
The pole placement for single input-single output
(SISO) systems allows the univocal determination of
the state feedback gain matrix. The problem is not
solved in case of multi input-multi output (MIMO)
systems where the degrees of freedom need additional
constrains [1-4].
The SFCS performance indices are influenced directly
by the SFC design. Many methods are available with this
regard because the placement of poles and zeros ensures
the desired control system behavior and performance.
Therefore the classical subject of pole placement is still
actual and present in the literature [5-8].
The paper presents the basic rules of pole placement
(with the placement of zeros in certain cases). The
approaches deal with constant real part poles, poles placed
on a circle, Butterworth configurations without and with
the correction of the imaginary part, and pole-zero
cancellation. Also, another advantageous method
mentioned in [9] and characterized by the poles placed on
an ellipse is suggested and analyzed here.
The SFC gain matrix is obtained usually in case of
SISO linear control systems in terms of Ackermann’s
formula given the state mathematical model of the
controlled plant and the desired / imposed positions of
poles. Ackermann’s formula can be viewed as a linear
equation or a system of linear equations given the desired
characteristic polynomial of the closed-loop system (the
SFCS). However in real-world applications the designer
might encompass a difficult task in imposing crisp
positions of the poles accounting for the set of constraints
regarding the SFCS behavior. So the first idea of this
paper is to accept the poles characterized by fuzzy
numbers and positions imposed in the framework of the
new ellipse-based pole placement method from the linear
case. Nevertheless, the plant model can be subject to
uncertainties and the second idea of this paper is to
consider the plants characterized by linear models with
fuzzy parameters. Therefore the SFC gain matrix will be
obtained as the solution to a system of fuzzy linear
equations. The method is simple and straightforward
compared to similar methods reported in [5-8], [10].
The paper is organized as follows. The next Section
presents methods for pole placement for linear SFCSs and
addresses the pole-zero cancellation issue. Section III is
dedicated to the ellipse-based pole placement method.
Aspects concerning the new pole placement method based
on fuzzy linear equations are highlighted in Section IV.
Case studies for third, fourth and fifth order SFCSs are
presented in Section V together with a comparative
analysis of several pole placement methods. Section VI
outlines the concluding remarks.
II. P
OLE
P
LACEMENT
M
ETHODS FOR
L
INEAR
S
YSTEMS
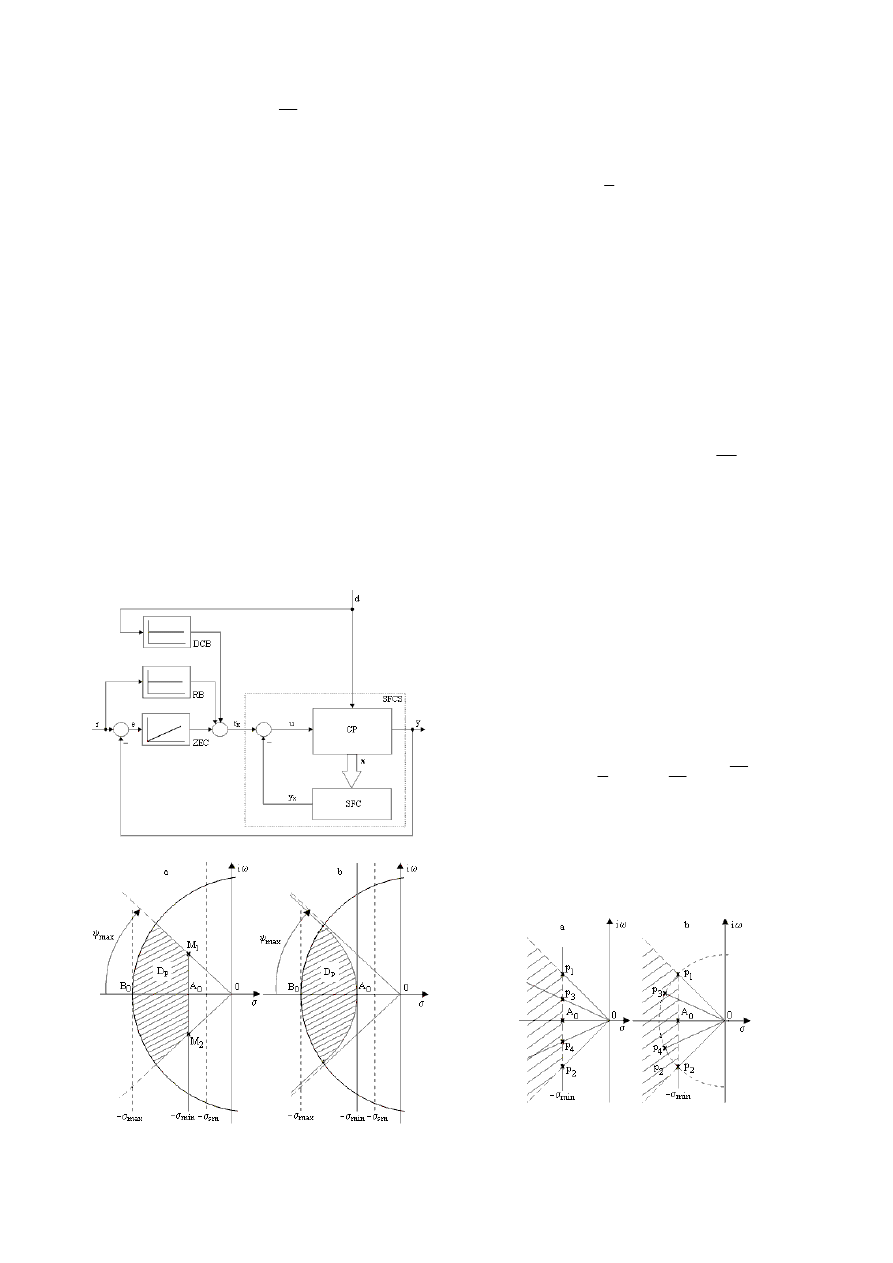
The classical SFCS structure extended with zero error
controller (ZEC), reference block (RB) and disturbance
compensation block (DCB) is presented in Fig. 1 (with CP
– controlled plant). The general principles concerning pole
placement designs applied to SFCSs are well known:
-
Due to the stability conditions, the poles must be
placed in the left-hand half-plane
0
}
Re{
<
s
keeping
a stability margin delimited by
sm
σ
−
.
-
The pole placement must ensure as small as possible
settling times in system’s transients. This leads to the
necessity for the absolute value of the real part of all
1-4244-2407-8/08/$20.00 ©2008 IEEE
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.
poles (
n
k
i
p
k
k
k
,
1
,
=
ω
+
σ
=
with
n
– system’s
order),
|
|
|
}
Re{
|
k
k
p
σ
=
, to be as big as possible, and
|
|
|
|
}
Im{
k
k
k
p
σ
≤
ω
=
. The last requirement can be
expressed under the form of the condition
|
|
|
|
max
σ
<
σ
k
.
-
The choice of an extremely big value of
|
|
max
σ
implies difficulties to be avoided: big values of the
SFC gains, increased sensitivity with respect to
disturbance inputs, additional power at the actuator
level, etc.
Because of these motives, the literature does not offer
ideal or univocal recommendations on the pole placement.
In addition, the recommendations become less and less
accurate when the system order increases.
The above mentioned principles are expressed in terms
of the recommended domain of feasible poles D
p
illustrated in Fig. 2 in two versions, a and B. The version a
presented in Fig. 2 a is used frequently. The limitations
imposed through the values of
min
σ ,
max
σ and
max
ψ
depend on the maximum imposed settling time, the
overshoot
1
σ and the damping factor specific to the
transients, ρ and the constraints related to the
implementation of the SFC. One usual relationship is
)
3
(
2
/
min
max
>
σ
σ
, (1)
Fig. 1. Extended structure of state feedback control system
Fig. 2. Two versions of the domain of feasible poles
and the minimum value
min
σ is correlated often with the
following sum:
¦
=
ν
ν
≤
σ
n
p
n
1
min
|
}
Re{
|
1
. (2)
The value of
M
ψ is usually about 45
o
. The maximum
value,
max
σ , is fixed arbitrarily but in correlation with the
constraints related to the implementation of the SFC.
The first placement rule, which is common to many
methods, involves the hard constraint on the position of
two dominant poles p
1
and p
2
corresponding to the points
M
1
and M
2
in Fig. 2 a. The rule involves also the soft
constraint on the positions of the other poles p
3
, p
4
, etc. in
the domain D
p
. The classical methods of pole placement
concern the placement of the remaining (n–2) poles, they
are presented as follows and referred to as I to IV.
I. All poles fulfill the placement condition
n
p
p
,
3
,
}
Re{
}
Re{
min
2
,
1
=
ν
σ
−
=
=
ν
. (3)
The poles are placed on a parallel line to the imaginary
axis according to Fig. 3 a.
II. The poles are placed on a circle of radius
0
ω
centered in the origin. The circle contains the poles p
1
and
p
2
poles. The angle between two consecutives poles is
constant (Fig. 3 b).
Both methods are easy to use, but II ensures smaller
settling time. The performance of the SFCSs designed by
the methods I and II are satisfactory, but the settling time
takes generally big values.
III. The Butterworth configuration corresponds to the
poles of Butterworth filters. This method is recommended
when the CP and the SFCS do not have dominant zeros.
The placement condition is
n
n
n
i
p
,
1
]},
2
)
1
2
(
2
[
exp{
0
=
ν
π
−
+
π
ω
=
ν
. (4)
The method places the poles on a on a circle of radius
0
ω centered in the origin according to Fig. 4. For n>2 the
placed poles drop outside the recommended domain so the
system becomes more and more oscillating. Three
possibilities of pole placements can be used. They
correspond to three Butterworth circles:
Fig. 3. Poles with constant real part (a) and placed on a circle (b)
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.
Fig. 4. Butterworth configurations
-
the internal Butterworth circle of radius
min
σ with the
poles
n
p
i
,
1
,
=
ν
ν
, resulting in the slowest SFCS,
-
the medium Butterworth circle of radius
min
0
2
σ
=
ω
with the poles
n
p
m
,
1
,
=
ν
ν
,
-
the external Butterworth circle of radius
'
0
ω with the
poles
n
p
e
,
1
,
=
ν
ν
, resulting in the fastest SFCS.
Only the settling times differ for the three previously
presented versions. The larger the system order is the
larger the overshoot will be.
IV. The minimization of the ITAE performance
criterion [11]
³
∞
=
0
d
|
)
(
|
t
t
e
t
I
, (5)
sets indirectly the pole placement. The calculation of the
integral becomes complicated for n >10.
V. If the controlled plant contains zeros, they will be
preserved in the SFCS structure that will exhibit more and
more oscillating transients as the zeros become more
dominant. That is the reason why it is advised to place the
poles such that they cancel the zeros as follows:
-
zeros placed in the left-hand half-plane are canceled
by poles taking the same values (Fig. 5 a),
-
zeros placed in the right-hand half-plane are canceled
by poles placed symmetrically on the imaginary axis
(Fig. 5 b).
If the cancellation process is imperfect, its favorable effect
will be lost. This is important when the zeros are close to
the imaginary axis.
Fig. 5. Pole-zero cancellation
III.
E
LLIPSE
-
BASED
P
OLE
P
LACEMENT
M
ETHOD
The idea behind this new method is to impose rigidly
that the two dominant poles p
1
and p
2
to be placed in the
points M
1
and M
2
(Fig. 2 a) with
min
2
,
1
}
Re{
σ
−
=
p
and
the other poles
n
p
,
3
,
=
ν
ν
, are placed on an ellipse
centered in the origin and passing through the points M
1
,
M
2
and B
0
(Fig. 2). The coordinates of the imposed poles
are illustrated in Fig. 6 (the domain D
p
is inside the dashed
region) and calculated according to the following steps:
-
Step 1. The values of
min
σ and
max
σ are set
accounting for the desired control system
performance indices and the constraints related to the
implementation of the SFC. Next the values of
0
ω
and
'
0
ω are determined.
-
Step 2. The poles
n
p
e
,
1
,
=
ν
ν
, are placed making use
of the external Butterworth configuration
n
n
n
i
p
e
,
1
]},
2
)
1
2
(
2
[
exp{
'
0
=
ν
π
−
+
π
ω
=
ν
. (6)
The first two poles must fulfill the condition
min
2
,
1
}
Re{
σ
−
=
p
. (7)
-
Step 3. Two situations arise depending on the position
of the point
)
0
,
(
'
0
'
0
i
B
ω
−
with respect to the point
)
0
,
(
max
0
i
B
σ
−
indicating the fastest Butterworth
filter. Firstly, if
'
0
B is placed on the right-hand side of
0
B , then no correction is needed. Secondly, if
'
0
B is
placed on the left-hand side of
0
B , then it will be
necessary to analyze whether the designed solution
fulfills the performance indices and constraints. If
not, then the position of
'
0
B will be position is
bounded to
0
B and a compromise to the value of
min
σ will needed possibly by approach to the origin.
Hence the control system becomes slower and the
abscissa of those poles will set the abscissa of the new
poles placed on the ellipse.
Fig. 6. Ellipse-based pole placement
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.

-
Step 4. The poles
n
p
i
,
1
,
=
ν
ν
, are placed on the
internal Butterworth circle
n
n
n
i
p
i
,
1
]},
2
)
1
2
(
2
[
exp{
'
min
=
ν
π
−
+
π
σ
=
ν
, (7)
where the radius
'
min
σ is calculated in (8):
2
/
2
)
2
2
sin(
0
'
min
ω
=
π
+
π
σ
n
, (8)
for
1
=
ν
and
o
45
max
=
ψ
. These ordinate of these
poles will fix the ordinate of the new poles placed on
the ellipse.
-
Step 5. The dominant poles
p
1
and
p
2
are imposed to
be placed in the points
M
1
and
M
2
belonging to the
medium Butterworth circle of radius
min
0
2
σ
=
ω
for
o
45
max
=
ψ
but moved away from the poles
n
p
m
,
1
,
=
ν
ν
.
-
Step 6. Making use of (8), the
n
poles will be placed
on an ellipse centered in the origin and passing
through the points
M
1
,
M
2
and
'
0
B
:
.
,
,
1
),
2
2
sin(
)
2
2
cos(
'
0
'
min
'
min
'
0
ω
<
σ
=
ν
π
+
π
σ
+
π
+
π
ω
=
ν
n
n
i
n
p
(9)
The equation of that ellipse is
1
)
/
(
)
/
(
2
'
min
2
'
0
=
σ
ω
+
ω
σ
. (10)
It may degenerate to a circle under certain conditions.
IV.
P
OLE
P
LACEMENT
M
ETHOD
B
ASED ON
F
UZZY
L
INEAR
E
QUATIONS
Ackermann’s formula can be employed easily in case of
SISO linear systems resulting in the SFC gain matrix
k
T
:
)
(
]
1
...
0
0
[
1
A
S
k
P
T
−
−
=
, (11)
where
S
is the controllability matrix, with its well
accepted expression.
]
...
[
1
b
A
b
A
b
S
−
−
=
n
. The
matrix polynomial term
)
(
A
P
is obtained from the
desired characteristic polynomial of the closed-loop
system (the SFCS) calculated from the imposed poles
n
p
,
1
,
=
ν
ν
:
∏
=
ν
ν
−
=
n
p
s
s
P
1
)
(
)
(
. (12)
In uncertain environments, the crisp equation obtained
from the transformation of (11):
]
1
...
0
0
[
)
(
1
−
=
−
S
A
k
P
T
, (13)
can be viewed as a fuzzy equation. Unlike crisp equations,
which imply the identity of the left and right-hand
expressions, fuzzy equations do not necessarily carry this
implication. Several definitions of fuzzy equations are
given in [12] accepting the fuzzy sets A, B on R, a real
crisp variable x, and considering * an operator satisfying
Zadeh’s extension principle. Two such definitions are:
-
A type-Į equation is defined as A*x=B; the equation
means that the fuzzy set A*x is the same as the fuzzy
set B.
-
A type-Ȗ equation is defined as A*x§B; this definition
is one of the weak equalities and it is interpreted as
B
x
A
∈
=
*
if
≥∈
)
.
*
(
B
x
A
S
, where S is some scalar
measure of the similarity between two fuzzy sets and
∈
is a suitable threshold value.
In case of fuzzy numbers, a fuzzy linear equation is in
form of
B
x
A
~
~
~
=
, where A
~
, B
~
and x~ are fuzzy numbers.
It is well know that there exist no inverse numbers under
fuzzy numbers arithmetic addition and multiplication
respectively.
If F is a mathematical function involving fuzzy
parameters, then a number X can not be found generally
such that F(X)=B. Even if a solution does exist it becomes
difficult to find. A procedure to determine the degree to
which a proposed solution satisfies a given equation to
settle for a solution which only makes the given equation
only approximately true has been suggested in [13].
Large applicability in control systems can be found for
matrix equations
b
x
A
~
~
~
=
where
1
]
~
[
~
×
=
n
j
x
x
,
n
n
ij
a
×
=
]
~
[
~
A
is a matrix with fuzzy numbers as entries and
1
]
~
[
~
×
=
n
i
b
b
is a vector of fuzzy numbers. Differently expressed, the
fuzzy linear equation is
n
i
b
x
a
i
n
j
j
ij
,
1
,
~
~
~
1
=
=
¦
=
. (14)
Systems of linear interval equations are obtained taking
the Į-levels of (14). But these interval equations are hard
to solve, consequently the exact solution does not always
exists, and a first solution has been proposed in [14]. The
idea of this paper is to consider the equations (13) in the
framework of (14) accounting for the fuzzy modeling of
the controlled plant and the fuzzy pole placement.
V. C
ASE
S
TUDIES
The following six versions of pole placement methods
have been considered for third, fourth and fourth order
linear SFCSs: poles placed on the medium Butterworth
circle (B-m), poles placed on the external Butterworth
circle (B-e), poles resulted from the minimization of the
ITAE performance criterion (abbreviated by ITAE), poles
placed on a parallel line to the imaginary axis in terms of
the method I (M-I), poles placed on a circle of radius
0
ω
centered in the origin in terms of the method II (M-II), and
poles placed in terms of the ellipse-based pole placement
method presented in Section III (abbreviated EBPP). For
all six versions it is accepted that
'
0
B is placed on the
right-hand side of
0
B and
22
.
3
/
1
'
0
max
≤
ω
σ
≤
. The pole
configurations are calculated and presented in Table I
corresponding to all six pole placement versions.
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.
TABLE I.
P
OLE
C
ONFIGURATIONS
Method Case
study
n=3
n=4
n=5
B-m
–0.5
±0.866i,
–1
–0.3827
±0.924i,
–0.924
±0.3827i
–0.309
±0.5877i,
–0.809
±0.951i,
–1
B-e
–0.707
±1.2247i,
–1.4142
–0.707
±1.707i,
–1.707
±0.707i
–0.707
±2.176i,
–1.851
±1.345i,
–2.288
ITAE
–0.521
±1.068i,
–0.707
–0.424
±1.263i,
–0.626
±0.414i
–0.3764
±1.292i,
–0.575
±0.534i,
–0.8955
M-I
–0.707
±0.707i,
–0.707
–0.707
±0.707i,
–0.707
±0.3824i
–0.707
±0.707i,
–0.707
±0.293i,
–0.707
M-II
–0.707
±0.707i,
–1
–0.707
±0.707i,
–0.966
±0.2588i
–0.707
±0.707i,
–0.924
±0.3824i,
–1
EBPP
–0.707
±0.707i,
–1.4142
–0.707
±0.707i,
–0.707
±0.292i
–0.707
±0.707i,
–1.851
±0.437i,
–2.288
The controlled plant is characterized by the following
transfer functions [9]:
.
s
1
.
0
,
s
166
.
0
,
s
25
.
0
,
s
5
.
0
,
s
1
),
/
1
)(
/
1
)(
/
1
)(
/
1
)(
/
1
(
)
(
s,
1
.
0
,
s
25
.
0
,
s
5
.
0
,
s
1
),
/
1
)(
/
1
)(
/
1
)(
/
1
(
)
(
,
s
1
.
0
,
s
5
.
0
,
s
1
),
/
1
)(
/
1
)(
/
1
(
)
(
5
4
3
2
1
5
4
3
2
1
4
3
2
1
4
3
2
1
3
2
1
3
2
1
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
T
T
T
T
T
s
T
s
T
s
T
s
T
s
T
s
P
T
T
T
T
s
T
s
T
s
T
s
T
s
P
T
T
T
s
T
s
T
s
T
s
P
(15)
The SFCS structure is presented in Fig. 7, where d
1
and d
2
are disturbance inputs. The application of Ackermann’s
formula (11) for the three case studies gives the SFC
matrices presented in Table II.
The behaviors of the designed SFCSs can be analyzed
considering the effects in the system response with respect
to the modification of the reference input, the disturbance
input. The behavior in the frequency domain can be
analyzed, too [9]. The parametric modifications of the
controlled plant can be analyzed in both the frequency and
the time domain in terms of the sensitivity analysis and
eventually the robustness one.
Only the system behavior with respect to the unit step
modification of the reference input is presented here. With
this regard the several linguistic terms corresponding to
the performance indices defined in the time variation of
the controlled output are defined:
-
definitions for the overshoot
1
σ : VG (very good) for
%
7
%
0
1
<
σ
≤
, G (good) for
%
11
%
7
1
<
σ
≤
, A
(acceptable) for
%
15
%
11
1
<
σ
≤
, AQ (acceptable
but questionable) for
%
15
1
≥
σ
,
-
definitions for the first settling time
1
t : VG for
s
05
.
0
s
0
1
<
≤ t
, G for
s
07
.
0
s
05
.
0
1
<
≤ t
, A for
s
1
.
0
s
07
.
0
1
<
≤ t
, AQ for
s
1
.
0
1
≥
t
,
-
definitions for the settling time
s
t : VG for
s
08
.
0
s
0
<
≤
s
t
, G for
s
12
.
0
s
08
.
0
<
≤
s
t
, A for
s
15
.
0
s
12
.
0
<
≤
s
t
, AQ for
s
15
.
0
≥
s
t
,
-
definitions for the IAE performance criterion
³
∞
=
0
d
|
)
(
|
t
t
e
J
: VG for
5
.
0
0
<
≤ J
, G for
1
5
.
0
<
≤ J
, A for
5
.
1
1
<
≤ J
, AQ for
5
.
1
≥
J
.
Therefore the behavior of the fifth order system case study
in (15) with respect to the reference input is highlighted in
Table III.
TABLE II.
S
TATE
F
EEDBACK
C
ONTROLLER
M
ATRICES
Method Case
study
n=3
n=4
n=5
B-m
[.05 .1 .2]
[.13 .0334
.0865 .263]
[.0021 .0067
.0218 .0072 .324]
B-e
[.14 .2 .203]
[.013 .206
.291 .403]
[.131 .105
.261 .457 .74]
ITAE
[.05 .107
.175]
[.012 .0327
.0833 .21]
[.0021 .0071
.0229 .0833 .28]
M-I
[.035 .1 .212]
[.007 .027
.008 .203]
[.0009 .0045
.02 .0931 .354]
M-II
[.05 .107
.241]
[.0125 .042
.118 .335]
[.0021 .009
.033 .1312 .426]
EBPP [.707
.15
.283]
[.037 .096
.221 .4828]
[.0172 .0496
.131 .3593 .74]
Fig. 7. State feedback control system used in case studies
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.
TABLE III.
P
ERFORMANCE
I
NDICES OF
F
IFTH
O
RDER
S
YSTEM
C
ASE
S
TUDY
(15)
IN
U
NIT
S
TEP
M
ODIFICATION OF
R
EFERENCE
I
NPUT
Method Performance
index
ı
1
t
1
t
s
J
B-m G VG A
VG
B-e G VG VG
AQ
ITAE G G VG
VG
M-I AQ AQ G VG
M-II AQ AQ A G
EBPP VG G
(VG) VG A
VI.
C
ONCLUSION
The ellipse-based pole placement method suggested
here for linear control systems exhibits the following
advantages with respect to other ellipse-based methods
reported in the literature:
-
The method does not require sophisticated either
reasoning and / or calculus.
-
The method ensures the univocal placement of poles
inside the recommended domain.
-
The dominant poles are placed in the very favorable
points M
1
and M
2
of the recommended domain that
ensures good SFCS performance indices
characterized by very good overshoot
(
%
5
%
4
1
≤
σ
≤
) and small settling time.
-
The real part of the remaining (n–2) poles is
increasing and their imaginary part is decreasing. This
results in fast and well damped SFCS transients.
-
The method is subject to easy implementation in
terms of algorithms and computer-aided design due to
its systematic six steps formulation.
However the single shortcoming, which is generally met
in all the other pole placement methods, is the rational
setting of
min
σ and
'
0
ω .
The pole placement method based on fuzzy linear
equations method proves to be easily understandable for
the designer and practitioner. Hence this original method
can be implemented in the framework of low-cost
automation solutions when the numerical problems
associated with it can be solved.
Both methods proposed here, the ellipse-based one and
the fuzzy linear equations-based one, can be extended to
the designs of state feedback observers by pole placement.
Extension to quasi-continuous digital control, digital
control, implementations, additional tests and applications
[15-20] represent directions of future research.
The linguistic characterization defined in the previous
Section allows the fuzzy characterization of system’s
behavior. This aspect leads to the idea of a new adaptive
fuzzy control system to be tackled in the future research.
A
CKNOWLEDGMENT
This work was supported by the cooperation between
Budapest Tech Polytechnical Institution and “Politehnica”
University of Timisoara (PUT), and University of
Ljubljana and PUT, in the framework of the Hungarian-
Romanian and Slovenian-Romanian Inter-governmental S
& T Cooperation Programs. The support from the
CNCSIS and CNMP of Romania is acknowledged. The
contribution of Mrs. Dipl. Ing. Angela Porumb in the early
phase of this project is appreciated.
R
EFERENCES
[1] B. C. Kuo and F. Golnaraghi, Automatic Control Systems, 8
th
Edition. New York: John Wiley & Sons, 2002.
[2] J. Ackermann, “Entwurf durch Polvorgabe,” Regelungstechnik,
vol. 25, pp. 173–179, April 1977.
[3] H. -R. Buehler, “Minimierung der Norm des Rückführvektors bei
der Polvorgabe,” Automatisierungstechnik, vol. 34, pp. 152–155,
April 1986.
[4] U. Konigorski, “Entwurf robuster, strukturbeschränkter
Zustandsregelungen durch Polgebietsvorgabe mittels
Straffunktionen,” Automatisierungstechnik, vol. 35, pp. 457–463,
Sept. 1987.
[5] W. Assawinchaichote and S. K. Nguang, “Fuzzy H
∞
output
feedback control design for singularly perturbed systems with pole
placement constraints: an LMI approach,” IEEE Trans. Fuzzy
Syst., vol. 14, pp. 361–371, June 2006.
[6] Y. G. Sun, L. Wang, G. Xie, and M. Yu, “Improved overshoot
estimation in pole placements and its application in observer-based
stabilization for switched systems,” IEEE Trans. Autom. Control,
vol. 51, pp. 1962–1966, Dec. 2006.
[7] Y. Kaiyang and R. Orsi, “Static output feedback pole placement
via a trust region approach,” IEEE Trans. Autom. Control, vol. 52,
pp. 2146–2150, Nov. 2007.
[8] U. Helmke, J. Rosenthal, and X. Wang, “Pole placement results
for complex symmetric and Hamiltonian transfer functions,” in
Proc. 46
th
IEEE Conference on Decision and Control, New
Orleans, LA, 2007, pp. 3450–3453.
[9] S. Preitl and A. Porumb, “About poles placement for sate feedback
control systems design,” in Proc. First International Conference
on Technical Informatics CONTI’94, Timisoara, Romania, 1994,
vol. 3, pp. 119–128.
[10] F. Liu, “Fuzzy pole placement design with H
∞
disturbance
attenuation for uncertain nonlinear systems,” in Proc. 2003 IEEE
Conference on Control Applications, Istanbul, Turkey, 2003, vol.
1, pp. 392–396.
[11] R. C. Dorf and R. H. Bishop, Modern Control Systems, 9
th
Edition.
Upple Saddle River, NJ: Prentice-Hall, 2007.
[12] D. Dubois and H. Prade, Fuzzy Sets and Systems: Theory and
Applications. New York: Academic Press, 1980.
[13] D. P. Filev and R. Yager, “Operations on fuzzy numbers via fuzzy
reasoning,” Fuzzy Sets and Systems, vol. 91, pp 137–142, Oct.
1997.
[14] J. Buckley and Y. Qu, “Solving systems of linear fuzzy
equations,” Fuzzy sets and Systems, vol. 43, pp 33–43, Sept. 1991.
[15] K. Tanaka, T. Ikeda, and H. O. Wang, “Fuzzy regulators and
fuzzy observers: relaxed stability conditions and LMI-based
designs,” IEEE Trans. Fuzzy Syst., vol. 6, pp. 250–265, May 1998.
[16] L. Horváth and I. J. Rudas, Modeling and Problem Solving
Methods for Engineers. Burlington, MA: Academic Press,
Elsevier, 2004.
[17] A. Sala, T. M. Guerra, and R. Babuška, “Perspectives of fuzzy
systems and control,” Fuzzy Sets and Systems, vol. 156, pp. 432–
444, Dec. 2005.
[18] I. Skrjanc, S. Blazic, and O. Agamennoni, “Interval fuzzy model
identification using l
∞
-norm,” IEEE Trans. Fuzzy Syst., vol. 13,
pp. 561–568, Dec. 2005.
[19] T. Orlowska-Kowalska and K. Szabat, “Control of the drive
system with stiff and elastic couplings using adaptive neuro-fuzzy
approach,” IEEE Trans. Ind. Electron., vol. 54, pp. 228–240, Feb.
2007.
[20] R. -E. Precup, S. Preitl, and P. Korondi, “Fuzzy controllers with
maximum sensitivity for servosystems,” IEEE Trans. Ind.
Electron., vol. 54, pp. 1298–1310, June 2007.
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:51 from IEEE Xplore. Restrictions apply.
Wyszukiwarka
Podobne podstrony:
Fuzzy Logic I SCILAB
Fuzzy logic
Fuzzy Logic III id 182424 Nieznany
Fuzzy Logic II id 182423 Nieznany
Fuzzy logic
pole placement robot design id Nieznany
A New Low Cost Cc Pwm Inverter Based On Fuzzy Logic
3 fuzzy logic I
fuzzy logic
Fuzzy Logic I SCILAB
robust pole placement
A New Low Cost Cc Pwm Inverter Based On Fuzzy Logic
regional pole placement
A pole placement approach to multivariable control of manipulators
więcej podobnych podstron