
1
Abstract—This paper addresses a systematic controller
design for the TCSC device in power systems based on a Linear
Matrix
Inequality
(LMI)
pole
placement
technique.
Requirements of performance can be expressed in terms of
LMI’s. In our formulation we combine a
∞
H
controller design
with some regional pole placement constraints using LMI’s.
The application of this controller, which is presented as an
example in this paper, is effective in improving the damping
ratio of a two-area four-machine test system. Furthermore,
good damping ratio can be achieved and maintained over a
larger range of operation with this LMI pole placement
controller than with a conventionally designed
∞
H
controller.
Another benefit of this approach is that it results in a fixed
parameter controller.
I.
I
NTRODUCTION
OWER system operating conditions vary with system
configuration and load level in a complex manner.
Obtaining a robust controller to damp system oscillations is a
primary objective in the controller design in power systems.
The most commonly used controller is the power system
stabilizer (PSS), which is installed at the generator so that it
can damp both local oscillations and inter-area oscillations.
With the successful application of FACTS devices in larger
systems, a lot of interest has arisen in designing
supplementary damping controllers (SDC) for FACTS
devices in recent years. Several papers [1, 2] have shown the
significant impact of SDC in damping inter-area system
oscillations. There are several approaches which mainly use
a linear time invariant (LTI) controller to guarantee the
robust stability and robust performance after describing the
changes of operating condition as uncertainties [3].
Normally the problem is formulated as a weighted mixed
sensitivity design. References [4,5] dealt with the
∞
H
controller design in order to guarantee the robust stability
and performance. The standard Riccati solution to this
The Authors are with Department of Electrical and Computer
Engineering, Iowa State University, Ames, IA, 50011 USA (corresponding
author Qian Liu e-mail: qliu@ iastate.edu).
problem will usually cause some pole-zero cancellation
problems and requires careful weighting function selection.
It is clearly known that the design objective of a conventional
∞
H
controller is to minimize the infinity norm from some
output signals to some input signals. But the obtained
∞
H
controller with the minimal infinity norm does not guarantee
the closed loop system with a largest damping ratio at some
critical modes because the
∞
H
norm index is not directly
related to the damping issue. Though we can carefully select
some weighting functions to get the better controller, the
conventional
∞
H
controller design still has its intrinsic limit
in achieving this specific goal.
Recently the Linear Matrix Inequality (LMI) approach
has been successfully applied in the control area [6]. The
stability problem can be formulated as LMI’s. In addition,
other specific objectives from the time domain performance
can be easily expressed in terms of some LMI’s. Previously
these would have been translated into some weighting
function selection. In this paper, a supplementary controller
for a TCSC device in power systems is designed with this
LMI pole placement technique.
The LMI based pole placement SDC is applied to a
two-area four-machine system. The simulation results show
that the designed controller can enhance the damping ratio
for the inter-area oscillations in a much wider operating
range than the conventionally designed
∞
H
controller,
which doesn’t take the pole placement into account.
Section II of this paper introduces the LMI pole
placement controller design technique. The test system is
described in Section III. Details of the robust pole placement
output-feedback controller are addressed in Section IV.
Simulation results of its application in the test system are
shown in Section V as well as comparisons with a
conventionally designed
∞
H
SDC. Conclusions are drawn
in Section VI.
LMI Pole Placement Based Robust Supplementary
Damping Controller (SDC) for A Thyristor
Controlled Series Capacitor (TCSC) Device
Qian Liu, Vijay Vittal, Fellow, IEEE, Nicola Elia
P
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.

2
II.
REGIONAL
POLE
PLACEMENT
VIA
LMI
OPTIMIZATION
The objective of the controller design is to place the
closed loop poles in some regions while still satisfying some
infinity norm constraints at the same time. It is clearly known
that the transient response of a linear system is related to the
location of its poles [7]. For example, the step response of a
second–order system with poles
d
n
j
ω
ζω
λ
±
−
=
is fully
characterized in terms of the undamped natural frequency
λ
ω =
n
, the damping ratio
ζ
, and the damped natural
frequency
d
ω
. Confining the closed-loop poles to some
region can ensure a minimum damping ratio
θ
ζ
cos
=
,
which is the objective of this damping problem in the power
systems.
A.
LMI regions
Definition 1: A LMI region is the any subset D of the
complex plane that can be defined as
{
}
0
:
<
+
+
∈
=
T
M
z
zM
L
C
z
D
(1)
where
L
and
M
are real matrices such that
L
L
T
=
.
The matrix-valued function
T
M
z
zM
L
z
f
+
+
=
)
(
D
is
called the characteristic function of D. Some typical LMI
regions are shown in Fig. 1:
(1) Half-plane
α
−
<
)
Re(
z
:
0
2
)
(
<
+
+
=
α
z
z
z
f
D
(2) Disk centered at (-q,0) with radius r:
0
)
(
<
−
+
+
−
=
r
z
q
z
q
r
z
f
D
;
(3) Conic sector with apex at the origin and inner angle
θ
2 (
)
,
0
,
0
(
θ
S
):
0
)
(
sin
)
(
cos
)
(
cos
)
(
sin
)
(
<
+
−
−
+
=
z
z
z
z
z
z
z
z
z
f
θ
θ
θ
θ
D
LMI region is a subset of the complex plane that is
representable by an LMI in
z
and
z
.
B.
Quadratic
D
-stable
Definition 2: The system
Ax
x
=
&
is called D -stable if
all its poles lie in D.
Theorem 1: The matrix A is D-stable if and only if there
exists a symmetric matrix X such that
0
)
,
(
<
X
A
M
D
,
0
>
X
where
T
T
AX
M
AX
M
X
L
X
A
M
)
(
)
(
:
)
,
(
⊗
+
⊗
+
⊗
=
D
(2)
In the case of confining the poles in a conic sector of
)
,
0
,
0
(
θ
S
,
,
0
=
L
−
=
θ
θ
θ
θ
sin
cos
cos
sin
M
(3)
Based on Theorem 1, the system matrix has poles in
)
,
0
,
0
(
θ
S
if and only if
0
)
(
sin
)
(
cos
)
(
cos
)
(
sin
<
+
−
−
+
T
T
T
T
A
X
AX
AX
A
X
A
X
AX
A
X
AX
D
D
D
D
D
D
D
D
θ
θ
θ
θ
(4)
Note that when this D is the entire left–half plane, this
notion reduces to asymptotic stability, which is characterized
in LMI terms by the Lyapunov theorem [8].
C.
The
∞
H
constraint
The classical
∞
H
robust controller design in the mixed
sensitivity problem [9] is represented as
γ
≤
KS
W
T
W
S
W
3
2
1
,
(5)
where
γ
is the upper bound on the
∞
H
norm.
The
∞
H
constraint is equivalent to the existence of a
solution
0
>
∞
X
to the LMI
0
2
<
−
−
+
∞
∞
∞
∞
I
D
X
C
D
I
B
C
X
B
A
X
X
A
cl
cl
T
cl
T
cl
T
cl
cl
T
cl
cl
γ
(6)
where
cl
cl
cl
cl
D
C
B
A
,
,
,
are
D
C
B
A
,
,
,
matrices of the closed
loop system.
By combining the pole placement constraint in (4) with the
∞
H
constraint in (6), we restrict our goal to the following
suboptimal formulation of
∞
H
synthesis with pole
placement constraints.
The controller design objective is to find
0
>
X
and a
controller
)
(s
K
that satisfy (3) and (4) with
D
X
X
X
=
=
∞
.
The difficulty is that there are non-linearities in both (3) and
(4). These can be solved by make appropriate changes of
controller variables. The details can be found in [10, 11].
θ
r
α
Fig. 1. LMI region
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
3
III.
T
EST
S
YSTEM
A.
Test System
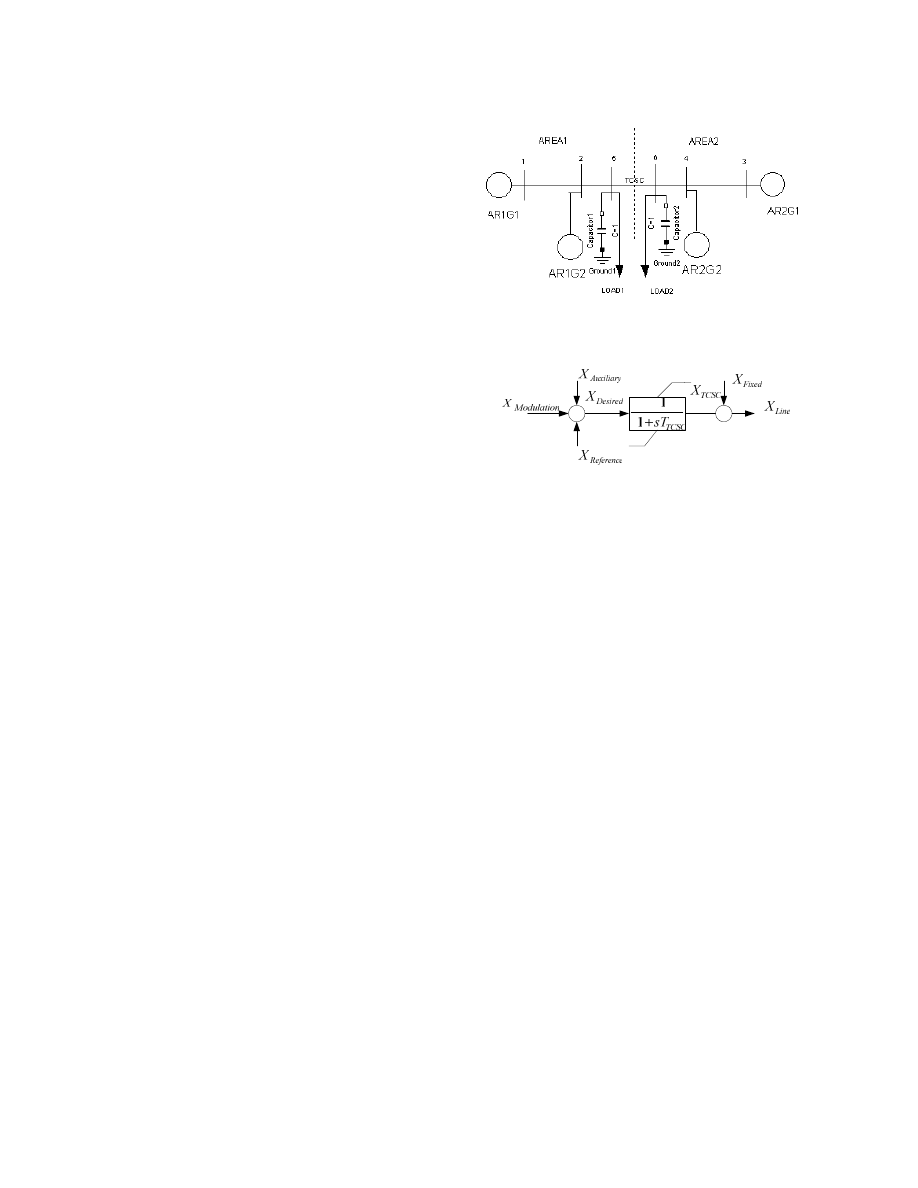
A two-area four-machine system [12] is used in this paper
for the simplicity of demonstration. This system has been
specially designed by Ontario Hydro for fundamental studies
of inter-area oscillations in power systems. The system has
the complexity to verify the efficiency of the proposed
procedure and is characterized by the presence of both
inter-area and local modes.
The test system consists of two identical areas, each
including two generators with the same power output and a
load. All generators are represented by the two-axis model
[13] equipped with (IEEE AC4A) ETMSP Type-30 [13]
Excitation system. Thus each generator with its exciter is
modeled by seven first-order nonlinear differential
equations. The loads are modeled as constant impedances.
A TCSC has been placed in series with the transmission line
to extend the power transfer capability. The diagram of this
system is shown in Fig. 2.
B.
TCSC model
Fig. 3 shows a block diagram for the TCSC model for
typical transient and oscillatory stability studies [14]. An
open loop auxiliary signal (
Auxiliary
X
) could be the output
of a power scheduling controller, which is used to extend the
power transfer limit and improve transient stability. A small
modulation input (
Modulation
X
) is produced by a
supplementary damping controller, which will be discussed
later in this paper. The desired compensation level is set by a
reference input (
Reference
X
).
The TCSC thyristor firing and other delays are usually
represented by a single lag of about 15ms. It will not be
modeled here for simplicity because it does not significantly
impact the electromechanical modes. In this paper, we
restrict ourselves to the design of the damping controller for
the inter-area mode.
C.
State Space Description of The System
The power system is represented by a differential
algebraic model that captures the differential dynamics of the
various components and the algebraic relationship that
governs the network.
)
,
(
0
)
,
(
.
Y
X
G
Y
X
F
X
=
=
(7)
The above equations can be linearized at a specific
operating point in the following manner:
u
B
w
B
Ax
x
2
1
+
+
=
&
u
D
w
D
x
C
z
12
11
1
+
+
=
(8)
u
D
w
D
x
C
y
22
2
2
+
+
=
We want to find an output-feedback controller in the state
space form as follows:
y
B
x
A
x
k
k
k
k
+
=
&
y
D
x
C
u
k
k
k
+
=
(9)
Usually a robust controller is designed based on a nominal
operating point (OP) with the plant uncertainty represented
as appropriate weighting functions [15]. The obtained
controller can improve the damping ratio at some operating
points. The damping performance, however, doesn’t relate
well to its achieved
∞
H
norm. Without carefully selecting
weighting functions, the obtained controller can even worsen
the closed loop system damping. Therefore, it takes a lot of
efforts to select the appropriate weighting functions because
there is no clear and explicit connection between the
weighting functions and the damping ratio of the closed loop
system. With the introduction of the pole placement
constraints, the system damping issue can be directly
addressed and enhanced in a very wide operating range.
IV.
S
UPPLEMENTARY
D
AMPING
C
ONTROLLER FOR A
TCSC
DEVICE
We want to obtain a damping controller for the TCSC to
provide sufficient damping for the inter-area oscillatory
modes in the test system at all six operating points, which are
characterized by a 100-600MW range of power transfer from
area 1 to area 2 with a compensation level range of 0-50%. A
0% TCSC compensation level is used at P
tie
=100MW and
200MW while a 50% TCSC compensation level is used at
P
tie
=300MW to 600MW. The operating point at
P
tie
=400MW is chosen as a nominal case in the controller
synthesis. The absolute value of the tie-line current is used
as the output feedback control signal due to its largest
Fig. 2. The two-area four-machine test system
Fig. 3. The block diagram for the TCSC model for typical stability studies
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
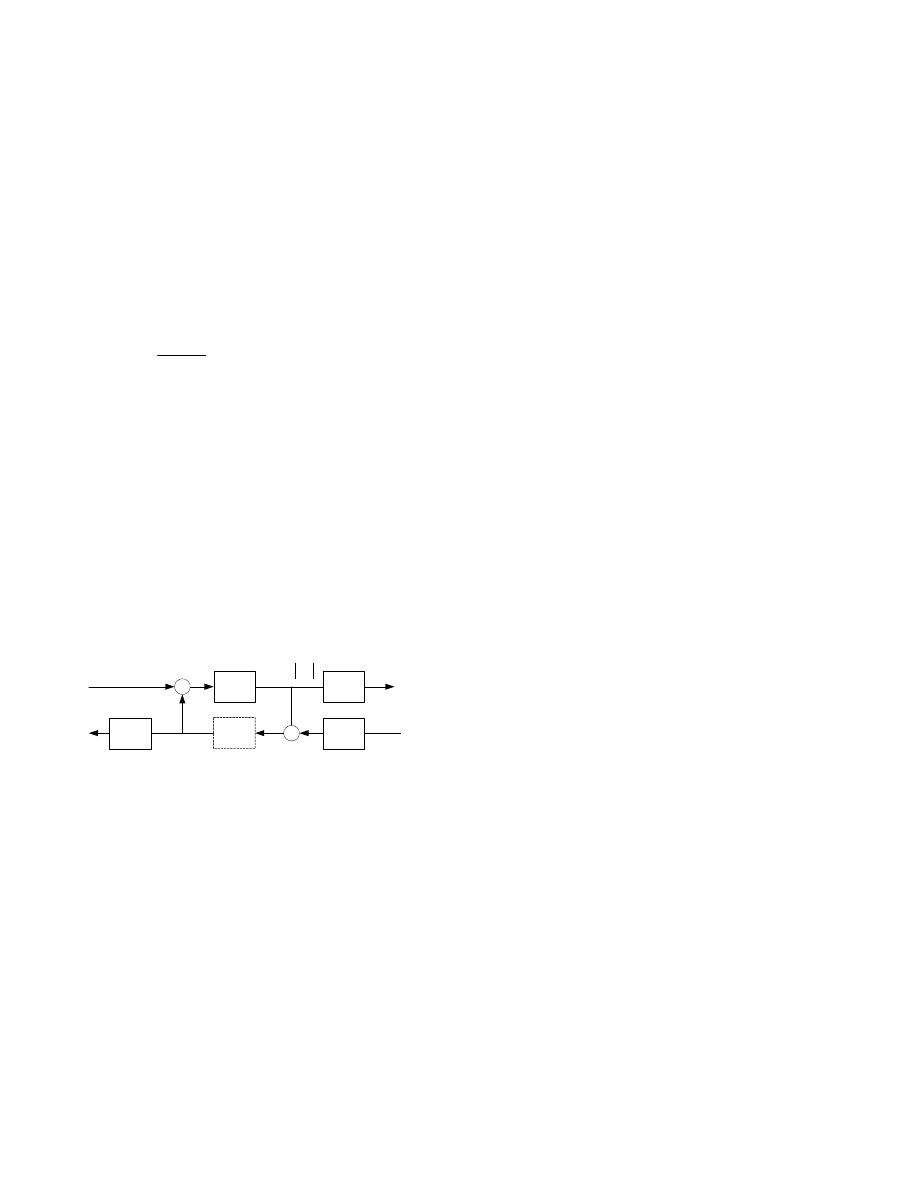
4
observability of the poorly damped modes. The setup of this
controller design problem is shown in Fig. 4, where P
represents the system model of the 2-area power system and
the primary part of the TCSC device. The K in this figure is
the controller we want to design. The output of this controller
is fed into the summing point of the TCSC device as the
Modulation
X
signal in Fig. 2. The major objective of the
controller design is to improve the damping instead of the
reference tracking or disturbance rejection. In the SDC
setup, because the regional pole placement constraint will be
imposed in terms of LMI’s, the weighting function is not a
critical issue so that we simply set them as
12
.
1
1
+
=
s
W
perf
,
1
=
u
W
,
1
.
0
=
noise
W
.
The original system obtained under the nominal OP is of
27
th
order. Then it is reduced to 4
th
order by using a Hankel
norm [16] reduction. To get a better damping,
o
63
=
θ
is
used to define the conic sector to ensure a minimum damping
ratio of 45% at the nominal OP while maintaining the
damping ratio good enough at all of the other five OPs.
LMI toolbox in MATLAB is used to form the three LMIs
(10) (11) (12), which are derived from (4), (6) with the
changes of some controller parameters in order to make the
problem convex and linear [14].
0
R
I
I
S
>
(10)
perf
W
noise
W
u
W
P
K
tie
I
d
noise
ref
TCSC
dV
_
Fig. 4. Supplementary damping controller (SDC) design setup
0
T
T
R
I
L
M
M
I
S
⊗
+
⊗ Φ +
⊗ Φ
<
(11)
11
21
21
22
0
T
Ψ
Ψ
<
Ψ
Ψ
(12)
The LMI of (10) sets the constraint of
0
>
X
; the second
LMI imposes the pole region constraint; and the last one
imposes
the
∞
H
constraint.
The
details
of
22
21
11
,
,
,
Ψ
Ψ
Ψ
Φ
can be found in [16]. Therefore, a 5
th
order controller is obtained, which is of the same order as the
augmented open loop system.
The parameters of the obtained controller are shown in
the Appendix. A washout filter of
)
10
1
/(
10
s
s
+
is applied in
series with the controller to maintain the original steady state
gain of the open loop system.
V.
P
ERFORMANCE RESULTS
Apply this supplementary damping controller (SDC) to the
test system. A conventional
∞
H
controller that is designed
based on the same nominal OP without pole placement
constraints is tested in the two-area system at the same time.
Small signal analysis is performed using EPRI’s MASS
[9] software package. Table 1 shows the damping ratio of the
system with the pole placement based
∞
H
SDC, without
SDC and with the conventional
∞
H
SDC.
The frequency jump of the poorly damped modes from
P
tie
=200MW to P
tie
=300MW is due to the compensation
level change of the TCSC device.
From Table 1, it is obvious that the closed loop system
with the LMI based pole placement SDC has the largest
damping ratio at all six OPs. The damping ratio at the
nominal case of P
tie
=400MW is 19.71%, which is smaller
than the expected value in the design phase. It is reasonable
because the system at the design phase is different from the
real system due to the linearization and model reduction.
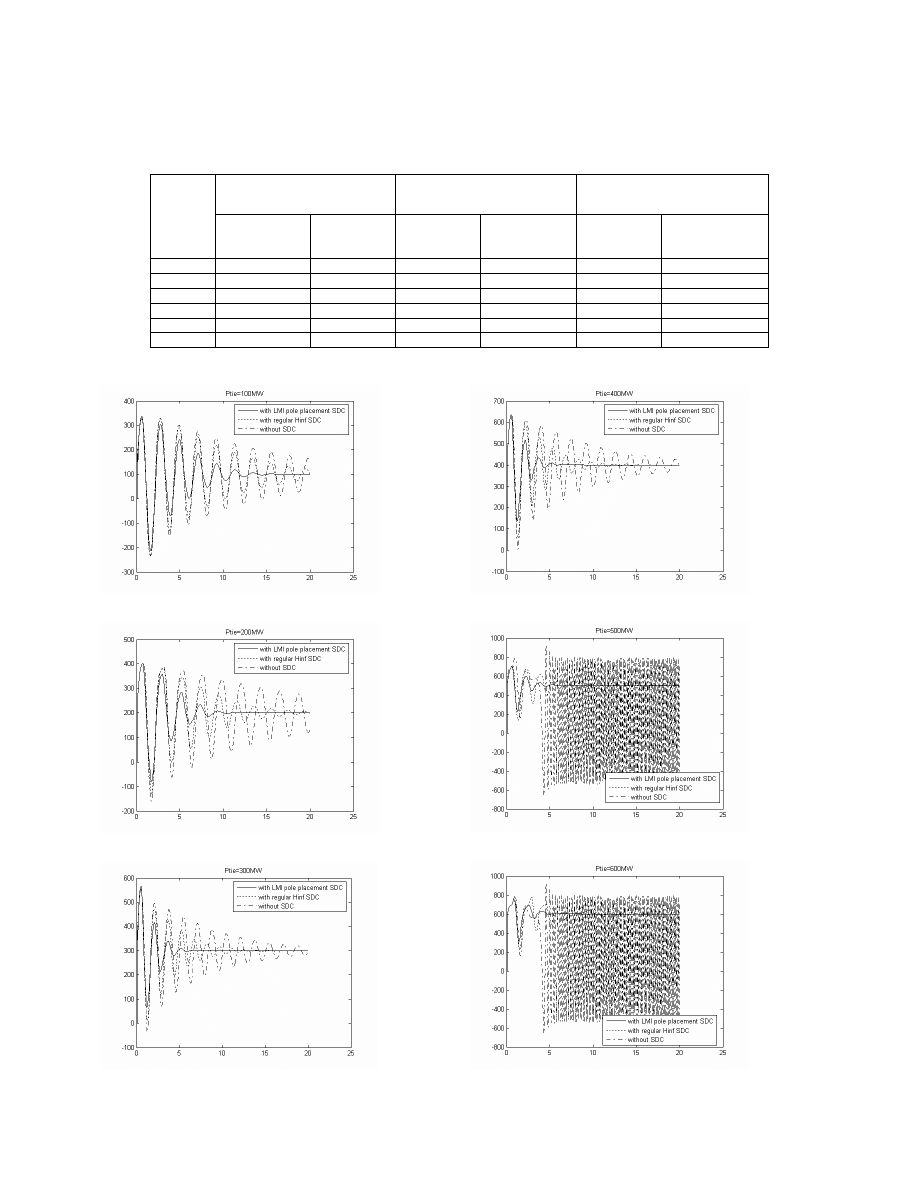
Nonlinear time domain simulation is performed using
ETMSP [9] software. A three-phase short circuit fault is
applied at bus 5 for 100 ms; the tie-line real power flow is
monitored. The simulation results are shown in Fig. 5~10.
Comparisons are made between the system with the LMI
based pole placement SDC, with conventional
∞
H
SDC and
without SDC.
From figures 6-10 it is very clear that the inter-area modes
are well damped from P
tie
=100MW to P
tie
=600MW. The
system takes a longer time to be settled down to its
equilibrium point at P
tie
=100MW than at P
tie
=600MW even
though the result from the small signal analysis shows the
damping ratio at P
tie
=100MW is greater than the damping
ratio at P
tie
=600MW. This inconsistency between the small
signal results and the transient results is due to the
non-linearity being taken into account in the transient
simulation. Another important point to mention is that the
transient response looks better with the increase in the level
of P
tie
. That is to say, the controller is more effective when
the power transfer level between areas is much higher. The
TCSC device is a series-connected device that is installed
between the tie-line, which makes it totally different from
other FACTS devices in the way that it affects the
controllability
in
this
problem.
Furthermore,
the
controllability increases with the increase of the power
transfer level between the two areas. Consequently, the
benefit of this controller is its increasing effect in an
increasing stressed power network. In other words, with the
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
5
TABLE
I
D
AMPING RATIO COMPARISON BETWEEN CLOSED LOOP SYSTEM WITH POLE PLACEMENT BASED
SDC
AND CONVENTIONAL
∞
H
SDC
Pole placement based
∞
H
SDC
∞
H
SDC
Without SDC
Ptie
(MW)
Frequency
(Hz)
Damping
ratio
(%)
Frequency
(Hz)
Damping ratio
(%)
Frequency
(Hz)
Damping ratio
(%)
100
0.4821
18.08
0.5225
8.04
0.4750
2.81
200
0.4774
34.64
0.5443
10.45
0.4549
2.68
300
0.8413
23.35
0.7318
9.69
0.6011
3.80
400
0.8518
19.71
0.7393
9.73
0.5829
3.61
500
0.8427
17.68
0.7346
9.53
0.5575
3.31
600
0.8167
16.29
0.7151
9.04
0.5193
2.74
Fig. 5. Three phase fault at Ptie=100MW
Fig. 6. Three phase fault at Ptie=200MW
Fig. 7. Three phase fault at Ptie=300MW
Fig. 8. Three phase fault at Ptie=400MW
Fig. 9. Three phase fault at Ptie=500MW
Fig. 10. Three phase fault at Ptie=600MW
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.

6
increase of the inter-area power transfer stress, the
supplementary damping controller of TCSC will be more
and more efficient.
VI. CONCLUSIONS
Instead of using an adaptive controller for TCSC, a
parameter-fixed controller is used to achieve better
damping ratio at all of the six operating points. This
controller is designed by imposing the regional pole
placement constraints. From its application in a two-area
four-machine system, it is obvious that the benefit of this
controller in enhancing the system damping is much greater
than the conventional
∞
H
controller. This LMI based pole
placement SDC is easier to design compared with the
conventional
∞
H
controller design in the way that the
performance requirement is explicitly formed in terms of
LMIs instead of being included in a complex weighting
function selection. The approach is practical and provides a
fixed structure controller. The designed controller is robust
and it can improve the system damping over a very wide
operating range. It is also shown that the controller
becomes more and more effective with the increase of
power transfer level between the two areas.
In future work this approach will be tested on a larger
test system to verify its efficacy.
A
PPENDIX
Zeros and poles of the controller:
−
−
−
−
+
−
−
=
−
−
+
−
−
−
+
−
=
9734
.
0
8880
.
7
7159
.
5
3030
.
3
7159
.
5
3030
.
3
2906
.
66
,
2054
.
1
4285
.
0
2054
.
1
4285
.
0
4665
.
4
3021
.
3
4665
.
4
3021
.
3
i
i
p
i
i
i
i
z
Controller matrices:
[
]
0
877
.
3
418
.
5
298
.
3
727
.
0
314
.
9
3812
.
7
0251
.
17
0121
.
0
19
.
14
0026
.
0
524
.
38
649
.
37
625
.
241
945
.
63
438
.
1322
570
.
83
040
.
83
975
.
547
087
.
143
348
.
3033
135
.
0
001
.
0
368
.
5
080
.
0
468
.
10
507
.
65
423
.
71
565
.
458
863
.
118
121
.
2535
062
.
0
108
.
0
568
.
2
069
.
0
043
.
2
=
−
−
−
−
=
−
=
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
k
k
k
k
D
C
B
A
R
EFERENCES
[1]
Bikash C. Pal and Alun H. Coonick. “A Linear Matrix Inequality
Approach to Robust Damping Control Design in Power Systems
with Superconducting Magnetic Energy Storage Device”, IEEE
Trans. on Power Systems, Vol.15, No.1, February 2000.
[2]
Jaw-Kuen Shiau and Glauco N. Taranto, “Power Swing Damping
Controller Design Using an Iterative Linear Matrix Inequality
Algorithm”, IEEE Trans. on Control Systems Technology, vol. 7,
No. 3, May 1999.
[3]
M.Klien, L.X. Le, G.J. Rogers, and S. Farrokhpay, “
∞
H
Damping
Controller Design in Large Power Systems”, IEEE Trans. on Power
Systems, vol. 10, no. 1, Feburary 1995, pp158-166.
[4]
G. N. Taranto, J. K. Shiau, “Robust Decentralized Control Design
for Damping Power System Oscillations”, Proceeding of the 33rd
Conference on Decision and Control, Lake Buena Vista, FL,
December 1994.
[5]
Qihua Zhao, Jin Jiang, “Robust SVC Controller Design for
Improving Power System Damping”, IEEE Trans. on Power
Systems, Vol.10, No.4, November 1995.
[6]
P. Gahinet, and P. Apkarian, “A linear Matrix Inequality Approach
to
∞
H
Control”, Int. J. Robust and Nonlinear Contr., 4 (1994), pp.
421-448.
[7]
J. Ackermann, Robust Control: Systems with Uncertain Physical
Parameters, London Springer_Verlag, 1993.
[8]
P. Gahinet, A. Nemirovski, A. J. Laub, and M. Chilali, The LMI
Control Toolbox, Natick, MA: The MathWorks, 1995.
[9]
S. Skogestad and I. Postlethwaite, “Multivariable Feedback Control
Analysis and Design”, John Wiley and Sons, 1996.
[10]
M. Chilaili and P. Gahinet, “
∞
H
Design with Pole Placement
Constraints: an LMI approach,” IEEE Trans. On Automatic Control,
vol. 41, o. 3, pp. 358-367, Mar. 1996.
[11]
C. Scherer, P. Gahinet, and M. Chilali, “Multiobjective
Output-feedback Control via LMI Optimization,” IEEE Trans. On
Automatic Control, vol. 42, no. 7, pp896-911, July 1997.
[12]
M. Klein, G. J. Rogers, and P. Kundur, “ A Fundamental Study of
Inter-area Oscillations in Power Systems,” IEEE Trans. on Power
systems, vol. PWRS-6, no. 3, pp. 914-921, Aug. 1991.
[13]
P. Kundur, G. J. Rogers, and D.Y. Wong, “Extended Transient
Midterm Stability Program Package: Version 2.0, user’s manuals”,
EPRI EL-6648, December 1989.
[14]
John J. Paserba (M) and Nicholas W. Miller (SM), “A Thyristor
Controlled Series Compensation Model for Power System Stability
Analysis”, IEEE Trans. on Power Delivery, Vol. 10, No. 3, July
1995.
[15]
Qihua Zhao and Jin Jiang, “A TCSC Damping Controller Design
Using Robust Control Theory”, Electrical & Energy System, Vol.
20, No. 1, pp.25-33, 1998.
[16]
D.J. Limebeer and M. Green, Linear Robust Control: Prentice-Hall,
1995.
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
Wyszukiwarka
Podobne podstrony:
pole placement robot design id Nieznany
robust pole placement
pole placement Fuzzy Logic
A pole placement approach to multivariable control of manipulators
Alpejski region turystyczny 2
Struktura regionalna
Polityki WE 3 Regionalna
zasady i problemy koordynacji polityki regionalnej 6
Porównanie dwóch regionalnych strategii innowacji
Geografia Regionalna
Regiony turystyczne Europy 2008
gospodarka regionalna 3 teorija
Mój region w średniowieczu
Regiony turystyczne Europy
Bliskowschodni kompleks bezpieczeństwa Przyczyny destabilizacji w regionie
Edukacja na Kaszubach; przykłady edukacji regionalnej i regionalizacji nauczania
Znieczulenie regionalne ból
Zasady polityki regionalnej UE
więcej podobnych podstron