SYMBOL NEWTONA

PERMUTACJE

SILNIA

Dla n>1 symbol n! (czyt: n silnia) oznacza 
iloczyn kolejnych liczb naturalnych od 1 do n.

n!=1·2·3·4·……·n

Przyjmujemy, że:      

0!=1

                          1!=1

 

2!=2
3!=1·2·3=6
4!=1·2·3·4=24
5!=1·2·3·4·5=120
6!=1·2·3·4·5·6=720
7!=1·2·3·4·5·6·7=5040
8!=1·2·3·4·5·6·7·8=40320
9!=1·2·3·4·5·6·7·8·9=362880
10!=1·2·3·4·5·6·7·8·9·10=3628800

  4!=1·2·3·4=24

  4!=3! ·4=24

  5!=1·2·3·4·5=120

  5!=3!·4·5=120

  5!=4!·5=120

  6!=5!·6=720

  6!=4!·5·6=720

  6!=3!·4·5·6=720

  8!=4!·5·6·7·8=40320

  8!=5!·6·7·8=40320

  8!=6!·7·8=40320

  8!=7!·8=40320

PRZYKŁADY:

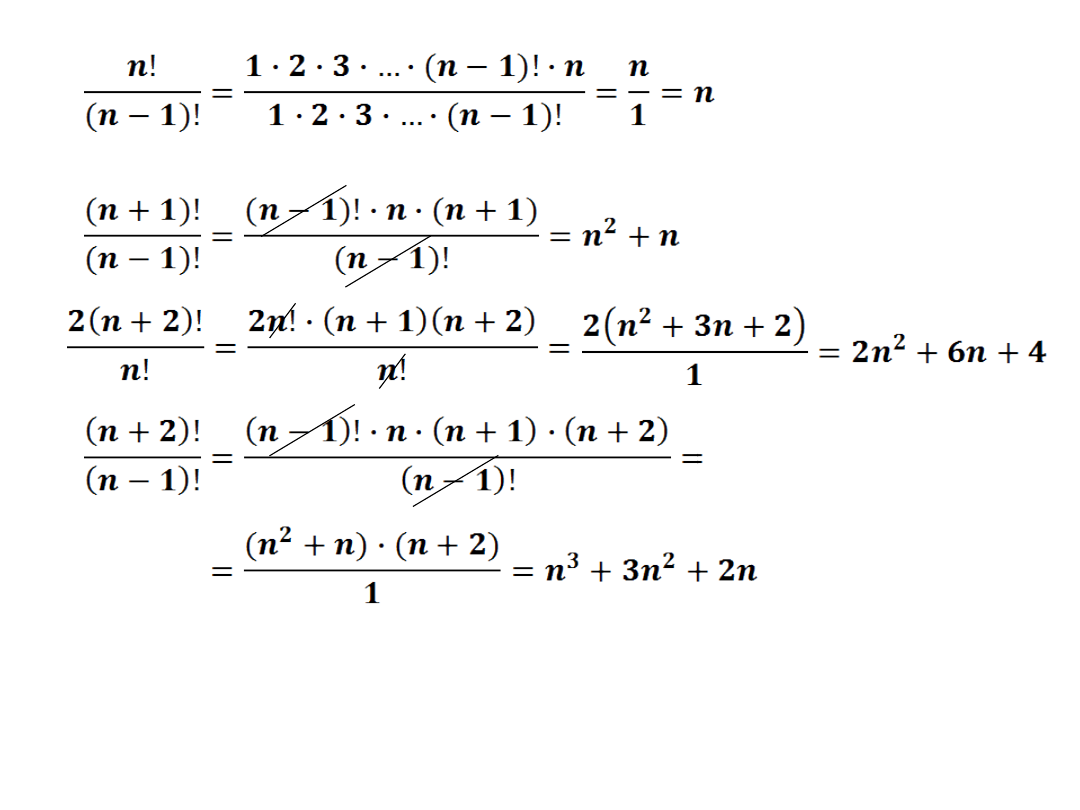
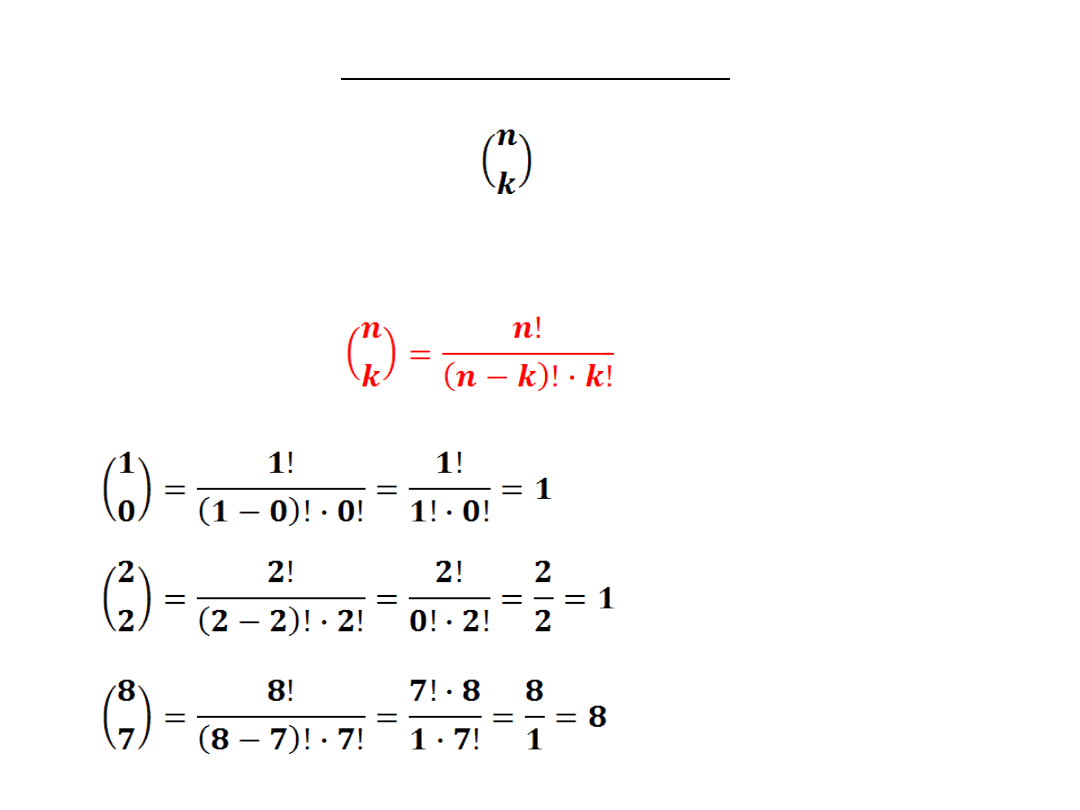
SYMBOL NEWTONA

Jeżeli k≤n to wyrażenie      (czytamy: n nad k) 

nazywamy symbolem Newtona.

PRZYKŁADY:

PERMUTACJE

Permutacją n-elementową zbioru n-

elementowego nazywamy każdy n-wyrazowy 

ciąg utworzony ze wszystkich elementów tego 

zbioru.

Permutacje n-elementowe oznaczamy: P

n

P

n

=n!

Ćw.1. Na ile sposobów można ustawić 6 osób w kolejce?

                   P

6

=6!=1·2·3·4·5·6=720

   Odp.: Sześć osób można ustawić na 720 sposoby.

Ćw.2. Na ile sposobów można ustawić liczby: 1,2,3,4, aby 

        stworzyć liczby czterocyfrowe?

                   P

4

=4!=1·2·3·4=24

   Odp.: Można utworzyć 24 liczby czterocyfrowe.

Ćw.3. W gonitwie bierze udział 11 koni. Ile jest wyników 

        zakończenia gonitwy? (zakładamy, że każdy koń 

dobiegnie 

        do mety i żadne dwa nie przebiegną razem).

                   P

11

=11!=1·2·3·4·5·6·7·8·9·10·11= 39916800

Odp.: Jest 39916800 wyników zakończenia gonitwy.

Ćw.4. Na ile sposobów może usiąść 5 osób na ławce tak, 
aby 
        KASIA i BASIA będące w tej grupie siedziały obok 
siebie:
a)w dowolnej kolejności
b)w kolejności BASIA-KASIA

Ad.a)
Pięć osób może usiąść na ławce w kolejności:

                 

K B _ _ _                        

                     _ K B _ _
                     _ _ K B _
                     _ _ _ K B

  

4·2! ·3!=4·2·6=48

Ad.b)
Pięć osób może usiąść na ławce w kolejności:

                 B K _ _ _                        
                 _ B K _ _
                 _ _ B K _
                 _ _ _ B K

4·3!=4·6=24

Odp.: Pięć osób może usiąść na 48 w pierwszym i 24 
sposoby 
       w drugim przypadku.

Kasia i Basia mogą się między sobą 
zmieniać na 2! sposoby; pozostałe 3 osoby 
zmienią się na 3! sposoby. Schemat obok 
przedstawia 4 możliwe ustawienia 5 osób.

Basia i Kasia nie mogą się zmieniać między 
sobą, pozostałe 3 osoby zmienią się na 3! 
sposoby. Schemat obok przedstawia 4 
możliwe ustawienia 5 osób.

Ćw.5. Cyfry 5,6,7,8 ustawiamy w ciąg. Oblicz ilość 
możliwych  ustawień cyfr w liczbie jeżeli:

a)liczby stoją na dowolnym miejscu

     P

4

=4!=1·2·3·4=24

b) na pierwszym miejscu stoi cyfra 8

     P

3

=3!=1∙2∙3=6

c) na pierwszym miejscu stoi cyfra 6, a na ostatnim cyfra 
5

     P

2

=2!=2

d) na początku są liczby parzyste

     2!∙2!=4

Ćw.6. Ile można utworzyć liczb pięciocyfrowych z cyfr 
2,3,4,5,6 

w których otrzymana liczba jest:

a)dowolna pięciocyfrowa

      P

5

=5!=1∙2∙3∙4∙5=120 

 
b)parzysta (na miejscu ostatnim musi stać cyfra 2 lub 4 
lub 6)

  3∙4!=3∙24=72

c)nieparzysta (na miejscu ostatnim musi stać cyfra 3 lub 
5)

  2∙4!=2∙24=48

d)podzielna przez 5 (na miejscu ostatnim musi stać cyfra 
5)

  P

4

=4!=1∙2∙3∙4=24