Metoda symboliczna
czyli
trochę rzemiosła
Założenia
1. Układ jest BIBO stabilny,
2. Wszystkie pobudzenia w obwodzie, czyli wszystkie niezależne
źródła (napięciowe i prądowe) są generatorami przebiegów
sinusoidalnych o takiej samej pulsacji
ω
0
.
Wówczas składowe ustalone wszystkich przebiegów w obwodzie
(tzn. wszystkich napięć i prądów) są przebiegami sinusoidalnymi
( )
(
)
{
}
( )
(
)
{
}
0
0
j
j
0
j
j
z
z
z
z
0
z
2 sin
2 Im
e
,
e
2 sin
2 Im
e
,
e
i
j
t
i
i
i
i
i
i
t
j
j
j
j
j
j
e t
E
t
E
E
E
i
t
I
t
I
I
I
ω
θ
ω
η
ω
θ
ω
η
=
+
=
=
=
+
=
=
Oznaczymy pobudzenia
(tzn. wszystkich napięć i prądów) są przebiegami sinusoidalnymi
o pulsacji
ω
0
.

Wówczas składowe ustalone wszystkich prądów i napięć
gałęziowych będą mieć postać
( )
(
)
{
}
( )
(
)
{
}
0
0
j
j
0
j
j
0
2 sin
2 Im
e
,
e
2 sin
2 Im
e
,
e
u k
i k
t
k
k
k
k
u k
k
t
k
k
k
k
i k
k
u
t
U
t
U
U
U
i t
I
t
I
I
I
ω
ψ
ω
ψ
ω
ψ
ω
ψ
=
+
=
=
=
+
=
=
gdzie k jest numerem gałęzi.
Będziemy również oznaczać
Będziemy również oznaczać
( )
( )
{
}
( )
( )
{
}
0
0
j
j
2 Im
e
2 Im
e
itd.
t
k
k
k
k
t
k
k
k
k
u
t
U
u
t
U
i t
I
i t
I
ω
ω
⇔
=
⇔
=
⇌
⇌
co oznacza, że sinusoidalnej funkcji czasu o pulsacji
ω
0
przyporządkowujemy w sposób wzajemnie jednoznaczny jej
wartość skuteczną zespoloną.
Przypomnienie
{
}
0
j
Im
e
0
0
t
W
W
ω
≡ ⇔
=
I prawo Kirchhoffa
( )
0
k k
k
a i t
∈
≡
∑
K
K — zbiór gałęzi incydentnych z wybranym
węzłem (lub ogólniej — tworzących
przekrój), a
k
=
±
1
{
}
0
0
j
j
2 Im
e
2 Im
e
0
t
t
k
k
k
k
k
k
a
I
a I
ω
ω
∈
∈
=
≡
∑
∑
K
K
0
k
k
k
a I
∈
=
∑
K
I prawo Kirchhoffa w postaci symbolicznej
W każdym węźle obwodu algebraiczna suma
wartości skutecznych zespolonych prądów
jest równa 0.
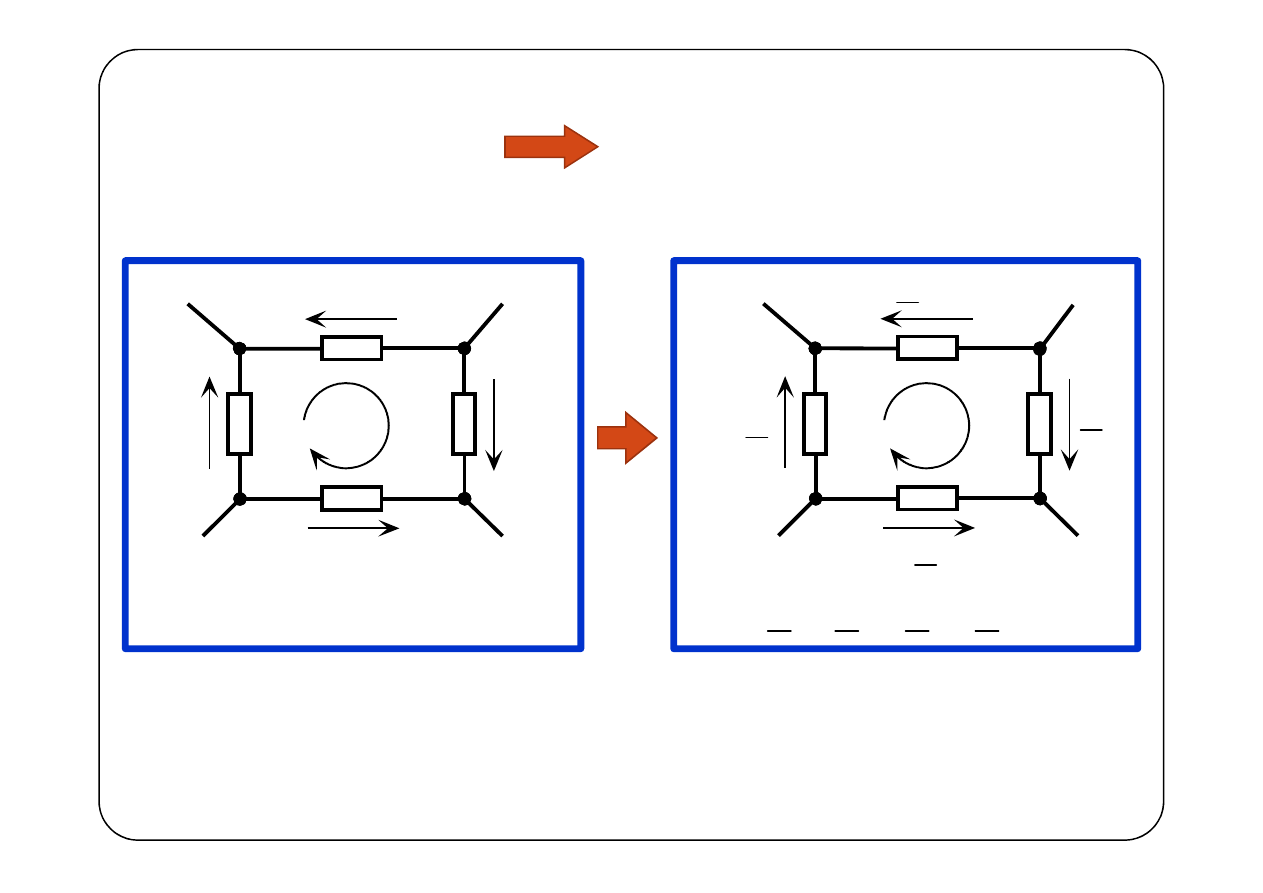
Schemat obwodu Symboliczny schemat zastępczy
( )
1
i t
( )
2
i t
1
I
2
I
( )
3
i t
3
I
( ) ( ) ( )
1
2
3
0
i t
i t
i t
−
+
−
=
1
2
3
0
I
I
I
− + − =
II prawo Kirchhoffa
( )
0
i
i
i
b u t
∈
≡
∑
L
L — zbiór gałęzi tworzących oczko,
b
i
=
±
1
{
}
0
0
j
j
2 Im
e
2 Im
e
0
t
t
i
i
i
i
i
i
b
U
b U
ω
ω
∈
∈
=
≡
∑
∑
L
L
0
i
i
i
b U
∈
=
∑
L
II prawo Kirchhoffa w postaci symbolicznej
W każdym oczku w obwodzie algebraiczna
suma wartości skutecznych zespolonych
napięć jest równa 0.
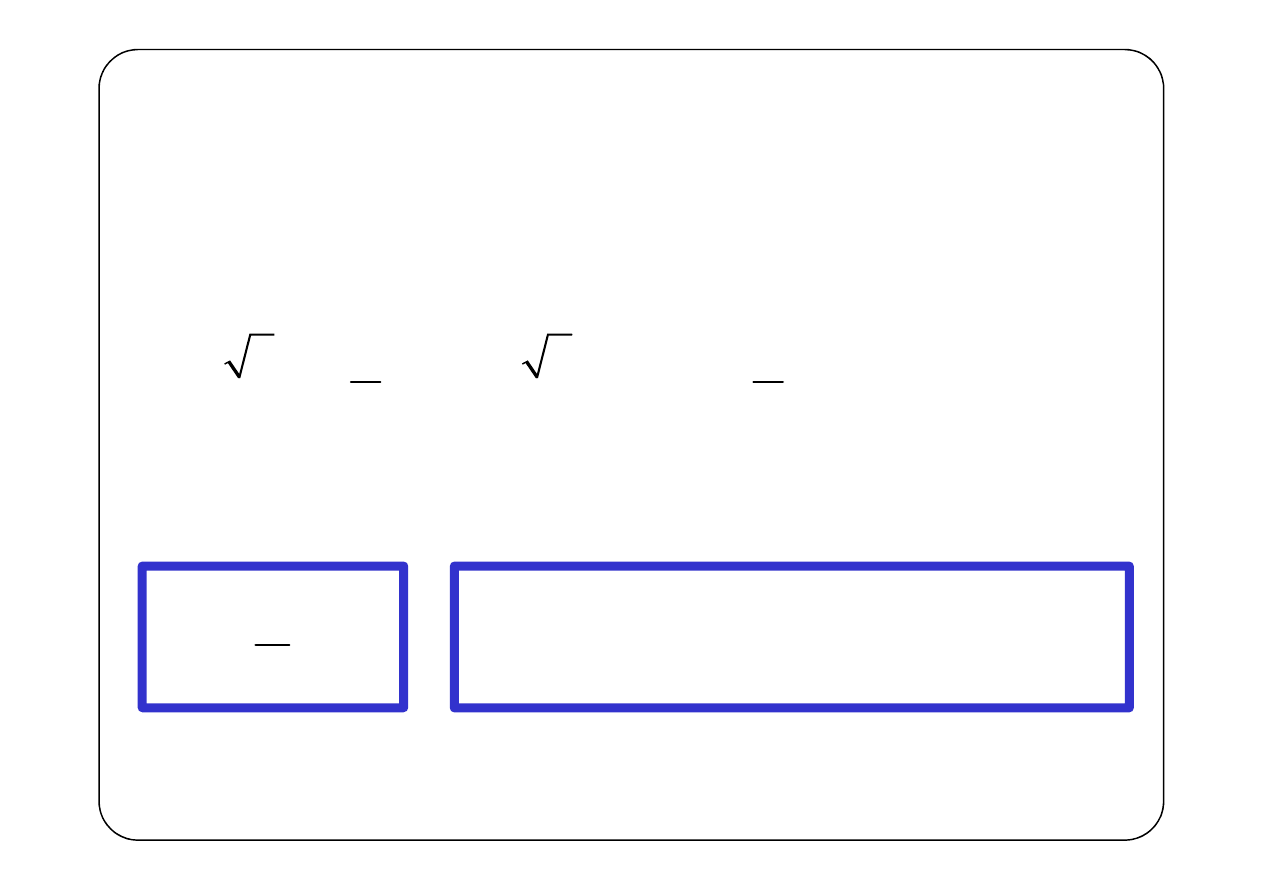
Schemat obwodu Symboliczny schemat zastępczy
( )
1
u t
( )
2
u
t
( )
3
u t
1
U
2
U
3
U
( )
4
u
t
4
U
( )
( )
( )
( )
1
2
3
4
0
u t
u t
u t
u
t
−
+
−
+
=
1
2
3
4
0
U
U
U
U
−
+
−
+
=
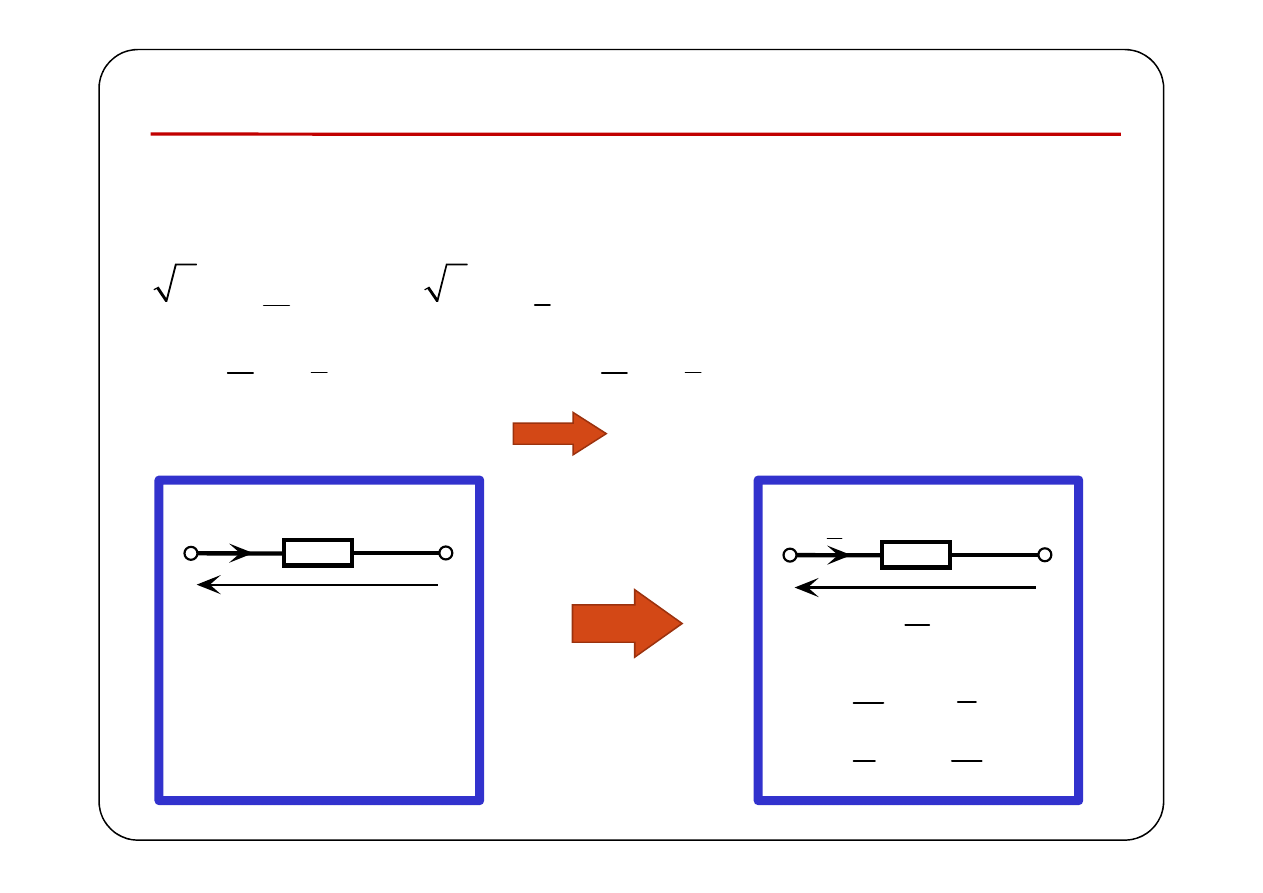
Prawo Ohma
Rezystor
( )
( )
{
}
{ }
(
)
{
}
0
0
0
j
j
j
2 Im
e
2 Im
e
Im
e
0
0
t
t
t
u t
Ri t
U
R
I
U
RI
U
RI
ω
ω
ω
=
≡
−
≡
⇔
−
=
Schemat obwodu
Symboliczny schemat zastępczy
Schemat obwodu
Symboliczny schemat zastępczy
( )
u t
( )
i t
R
( )
( )
( )
( )
u t
Ri t
i t
Gu t
=
=
R
I
U
U
RI
I
GU
=
=
Schemat obwodu
Symboliczny schemat zastępczy
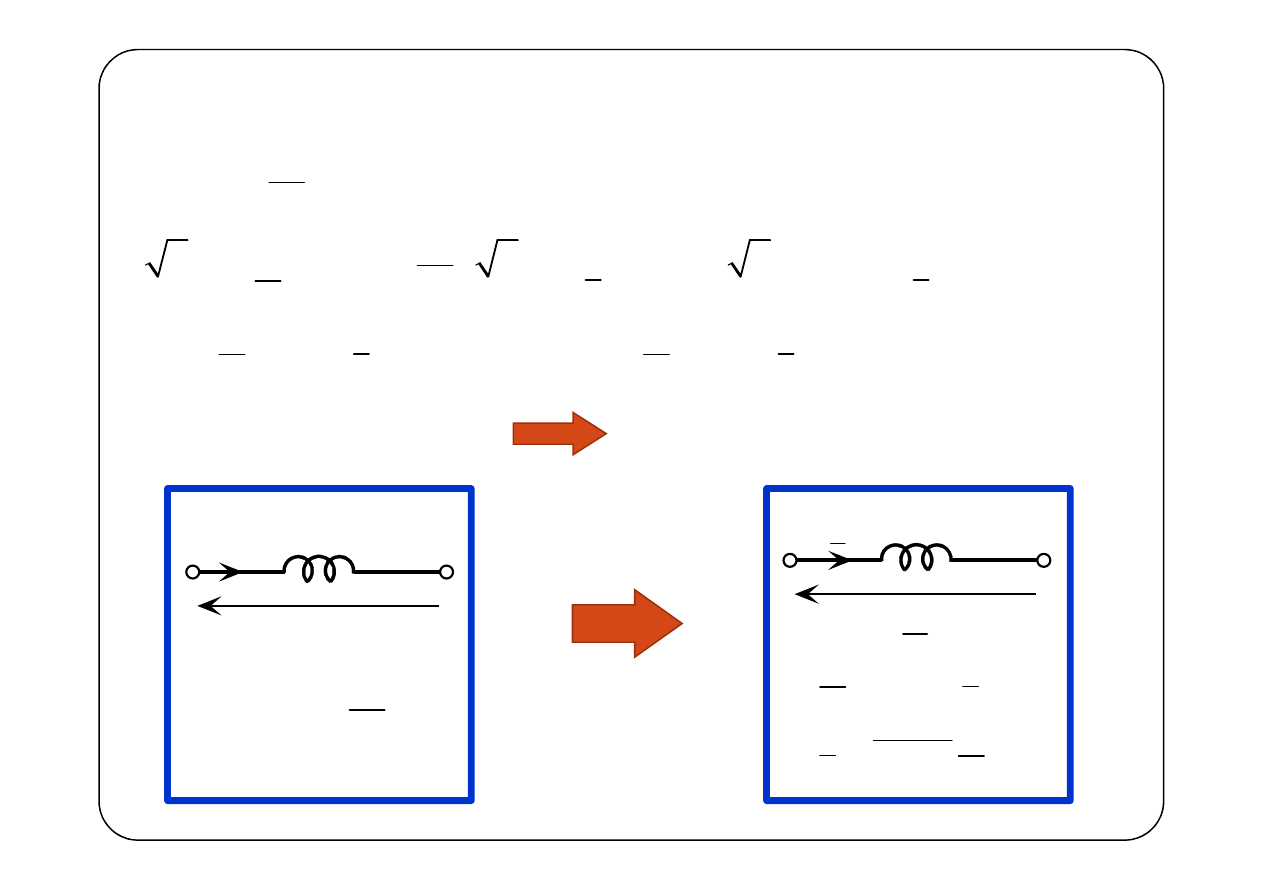
Induktor
( )
{
}
{ }
{
}
(
)
{
}
0
0
0
0
j
j
j
0
j
0
0
d
d
d
2 Im
e
2 Im
e
2 Im j
e
d
Im
j
e
0
j
0
t
t
t
t
i
u t
L
t
U
L
I
LI
t
U
LI
U
LI
ω
ω
ω
ω
ω
ω
ω
=
=
=
−
≡
⇔
−
=
Schemat obwodu
Symboliczny schemat zastępczy
L
U
I
0
0
j
1
j
U
L I
I
U
L
ω
ω
=
=
( )
i t
( )
u t
L
( )
d
d
i
u t
L
t
=
Schemat obwodu
Symboliczny schemat zastępczy
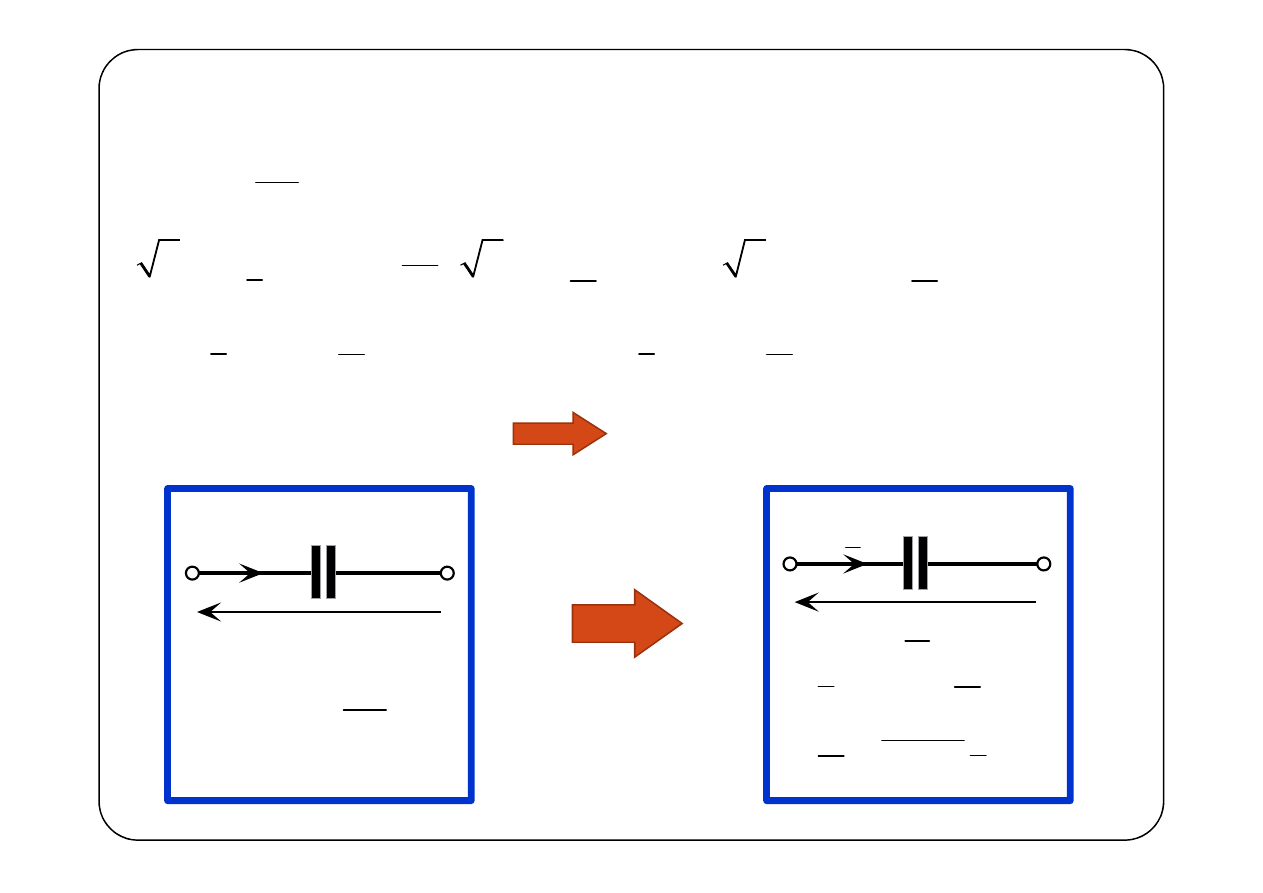
Kondensator
( )
{ }
{
}
{
}
(
)
{
}
0
0
0
0
j
j
j
0
j
0
0
d
d
d
2 Im
e
2 Im
e
2 Im j
e
d
Im
j
e
0
j
0
t
t
t
t
u
i t
C
t
I
C
U
CU
t
I
CU
I
CU
ω
ω
ω
ω
ω
ω
ω
=
=
=
−
≡
⇔
−
=
Schemat obwodu
Symboliczny schemat zastępczy
C
U
I
0
0
j
1
j
I
C U
U
I
C
ω
ω
=
=
( )
i t
( )
u t
C
( )
d
d
u
i t
C
t
=
Prawa Kirchhoffa i prawo Ohma w postaci symbolicznej nie różnią
się od odpowiednich praw w postaci operatorowej (przy zerowych
warunkach początkowych) jeżeli transformaty napięć i prądów
zastąpimy odpowiednimi wartościami skutecznymi zespolonymi oraz
dokonamy formalnego podstawienia s = j
ω
0
.
Równania symboliczne, opisujące obwód, można uzyskać z równań
operatorowych poprzez podstawienia:
( )
U
s
U
→
i pominięcie źródeł pochodzących od warunków początkowych.
( )
( )
( )
( )
z
z
0
j
k
k
k
k
U
s
U
I
s
I
E s
E
I
s
I
s
ω
→
→
→
→
→
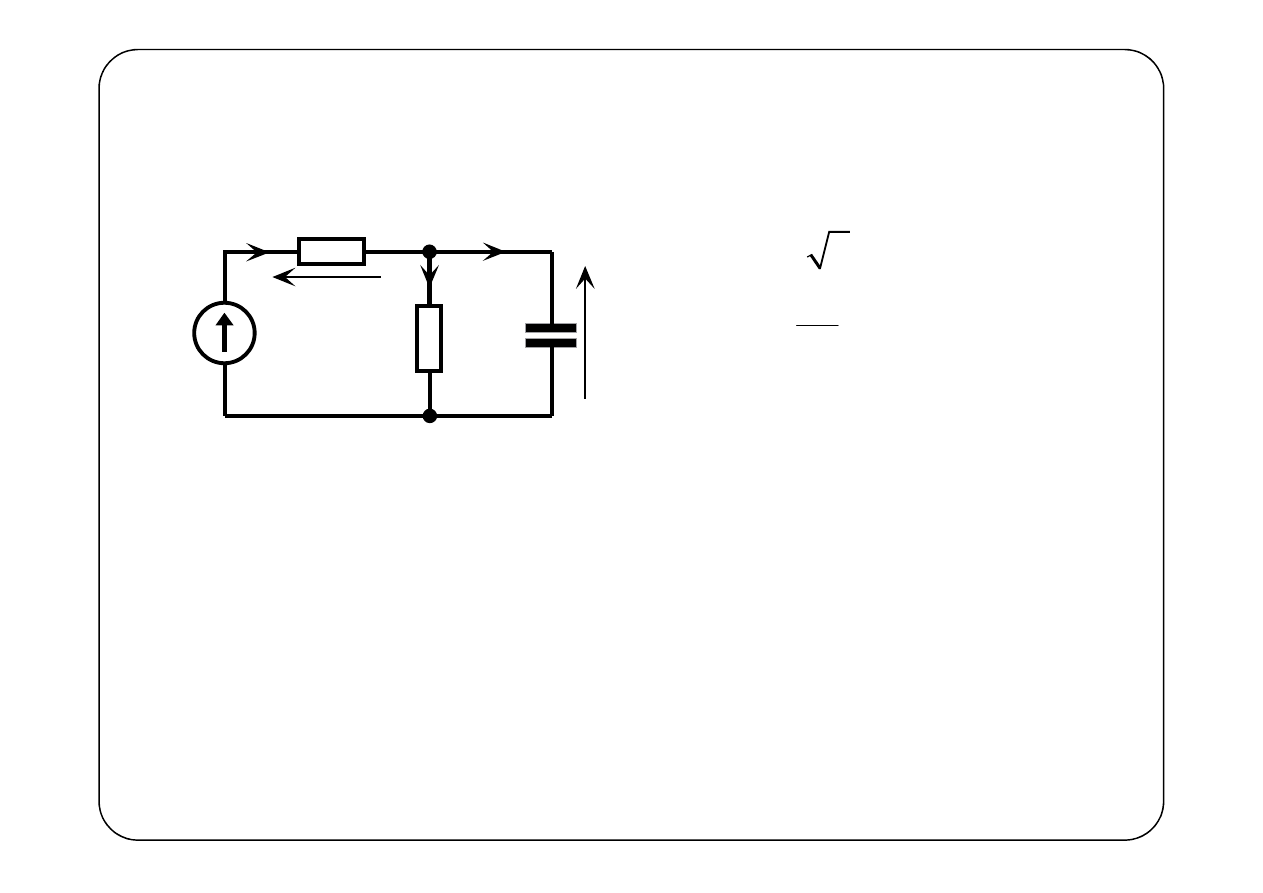
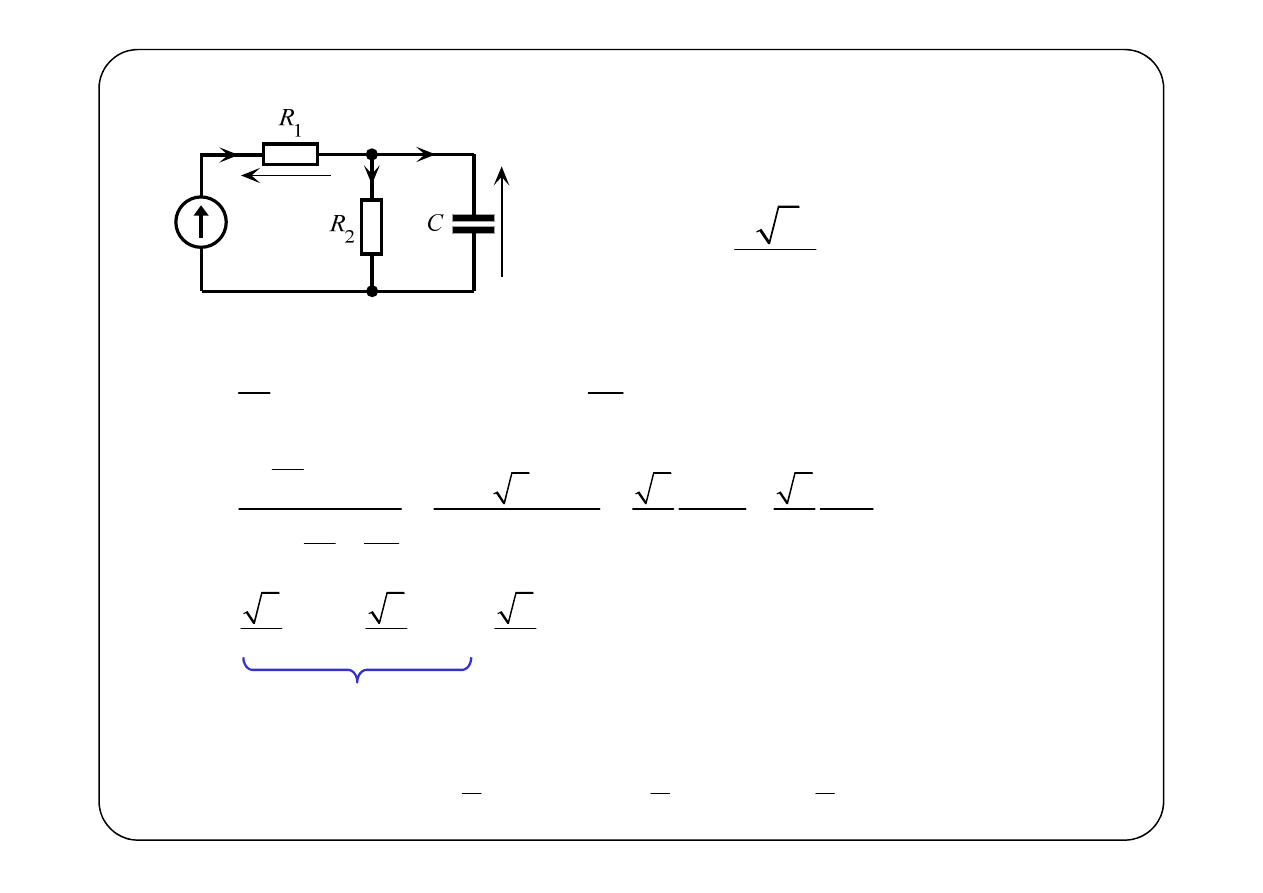
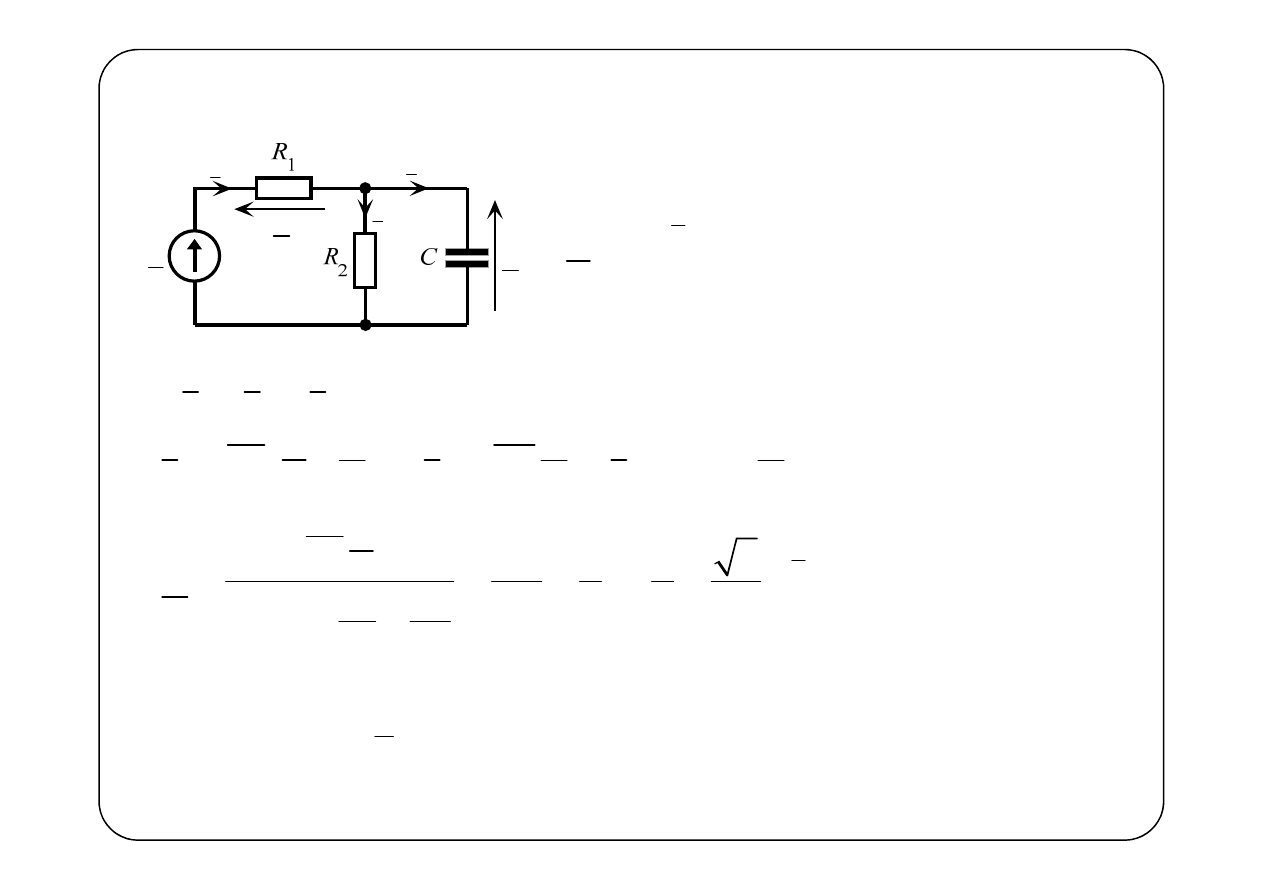
Przykład
R
1
R
2
C
( )
e t
( )
1
u t
( )
1
i t
( )
2
i
t
( )
3
i t
( )
u t
( )
( )
(
)
0
1
2
rad
s
2 2 cos
V,
1
,
2 Ω,
2 Ω,
1F.
e t
t
t
R
R
C
ω
=
⋅
=
=
=
=
1
Wyznaczyć składową ustaloną napięcia u(t)
Metoda operatorowa
( )
E s
( )
1
U
s
( )
1
I
s
( )
2
I
s
( )
3
I
s
( )
U s
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
1
2
3
1
2
0,
1
1
,
,
,
1
I
s
I
s
I
s
I
s
E s
U s
I
s
U s
I
s
sCU s
R
R
−
+
+
=
=
−
=
=
( )
2
2 2
1
s
E s
s
=
+
( )
( )
(
)
(
)
( )
( )
1
2
2
1
2
1
2
2
1
2
1
,
1
1
2
2
1
1
1
1
2
2
2
sin
cos
e
2
2
2
t
E s
R
s
s
U s
s
s
s
s
sC
R
R
u t
t
t
t
−
+
=
=
=
−
+
+
+
+
+
+
=
+
−
1
składowa ustalona
W stanie ustalonym:
( )
( )
π
π
π
4
4
4
sin
cos
cos
sin
sin
u t
t
t
t
=
⋅
+
⋅
=
+
Metoda symboliczna
E
1
U
1
I
2
I
3
I
U
π
j
2
2e
j2
E
=
=
[
]
1
2
3
1
2
3
0
0,
1
1
,
,
j
,
I
I
I
I
E U
I
U
I
CU
R
R
ω
− + + =
=
−
=
=
[
]
1
2
3
0
1
2
π
j
1
4
0
1
2
,
,
j
,
1
j
1
1
2
j
e
1
1
1+j
2
2
2
j
I
E U
I
U
I
CU
R
R
E
R
U
C
R
R
ω
ω
=
−
=
=
=
=
= +
=
+
+
( )
( )
π
4
sin
V.
u t
t
=
+
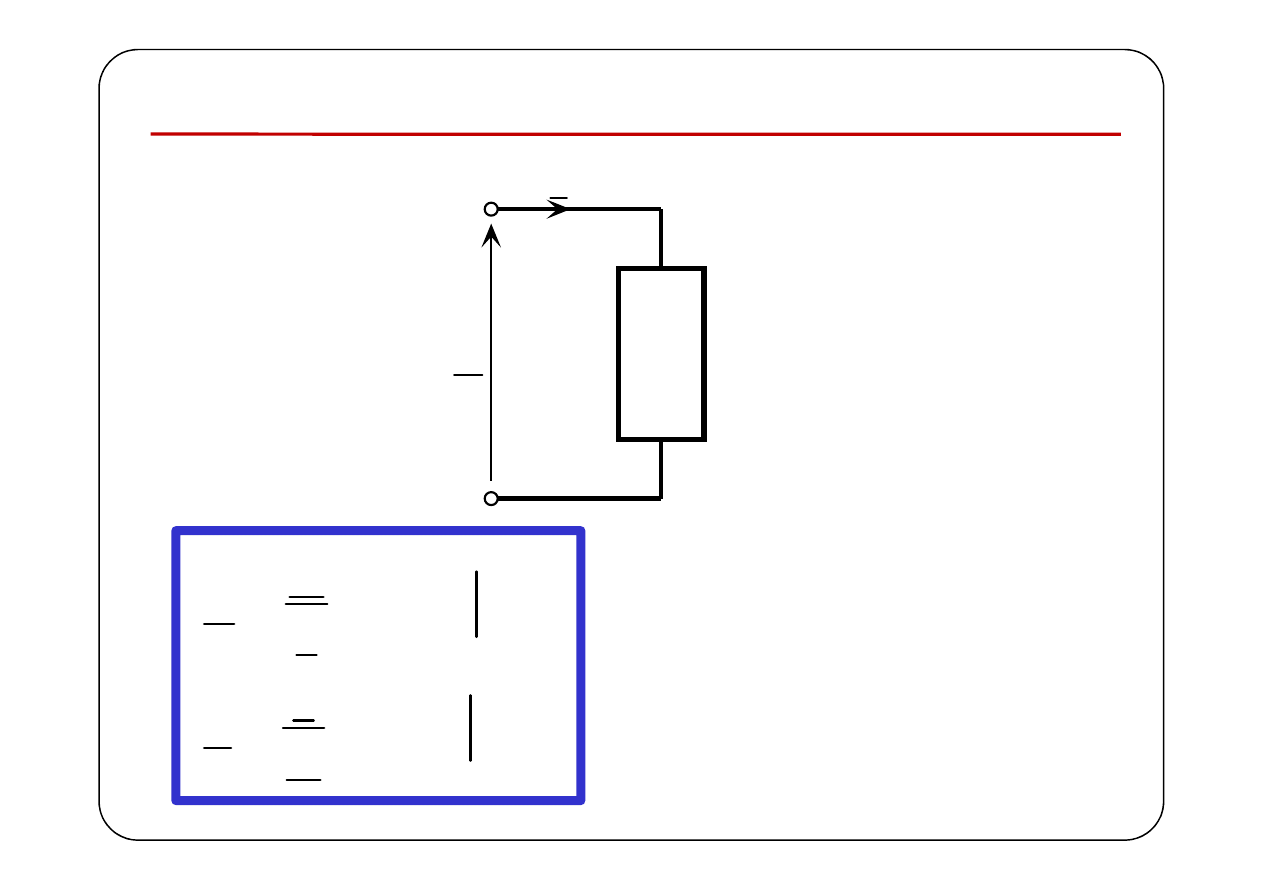
Impedancja i admitancja zespolona
U
I
( )
( )
0
0
j
j
s
s
U
Z
Z s
I
I
Y
Y s
U
ω
ω
=
=
=
=
≜
≜
impedancja zespolona
admitancja zespolona
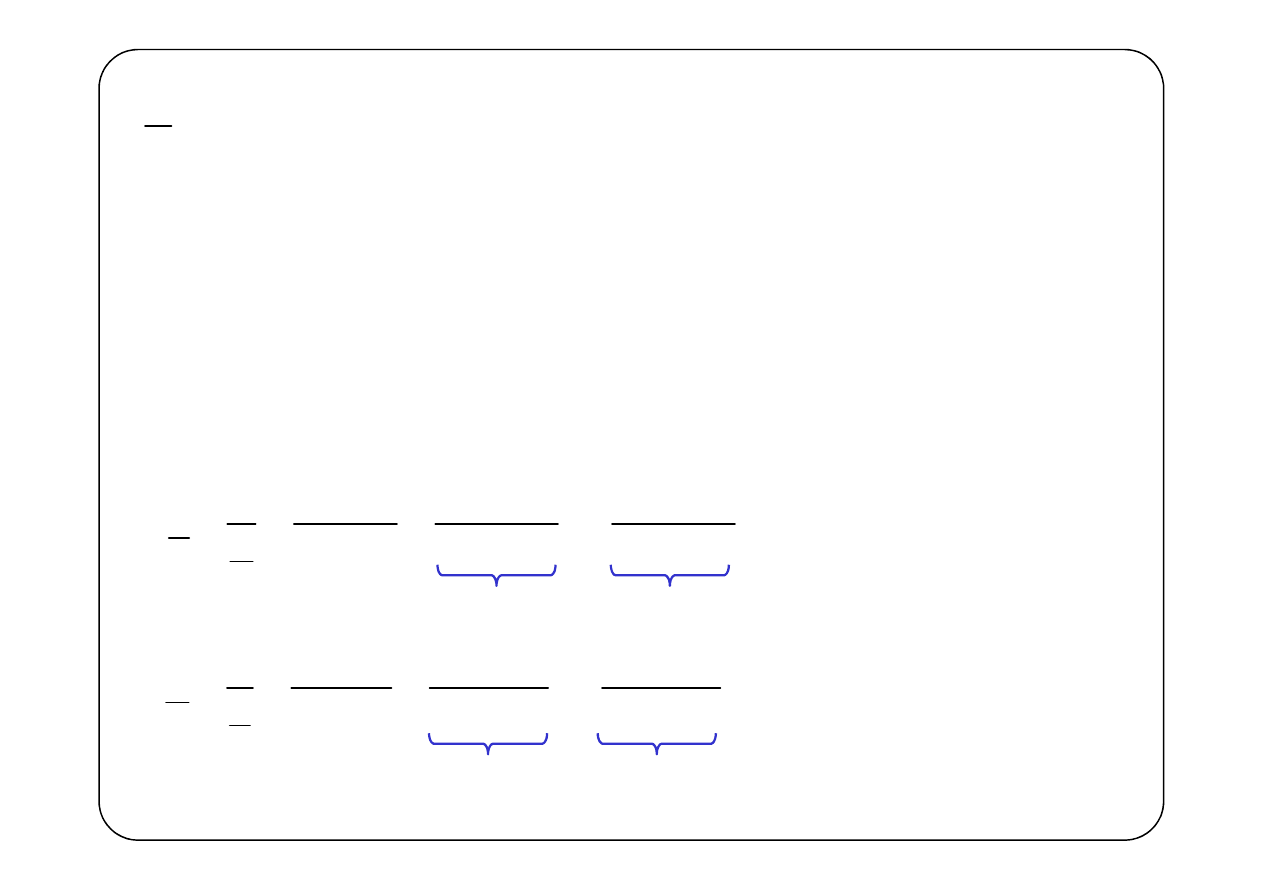
j
Z
R
X
= +
R — część rezystancyjna impedancji zespolonej (rezystancja)
X — część reaktancyjna impedancji zespolonej (reaktancja)
j
Y
G
B
= +
G — część konduktancyjna admitancji zespolonej (konduktancja)
X — część susceptancyjna admitancji zespolonej (susceptancja)
2
2
2
2
1
1
j
j
j
R
X
Y
G
B
Z
R
X
R
X
R
X
−
= =
=
+
= +
+
+
+
G
B
2
2
2
2
1
1
j
j
j
G
B
Z
R
X
Y
G
B
G
B
G
B
−
= =
=
+
= +
+
+
+
R
X
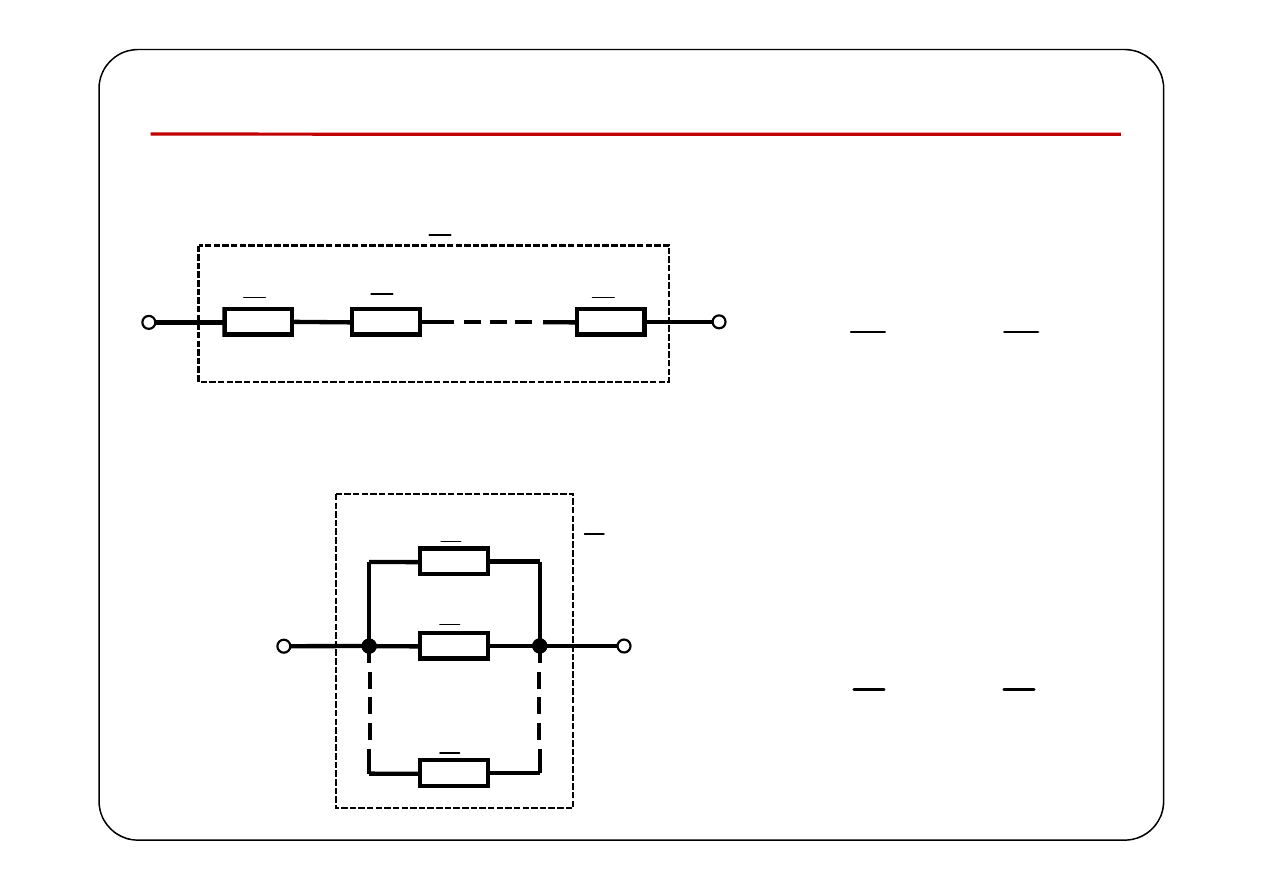
Łączenie dwójników
Połączenie szeregowe
1
Z
n
Z
2
Z
Z
1
n
k
k
Z
Z
=
=
∑
Połączenie równoległe
1
Y
2
Y
n
Y
Y
1
n
k
k
Y
Y
=
=
∑
Połączenie równoległe
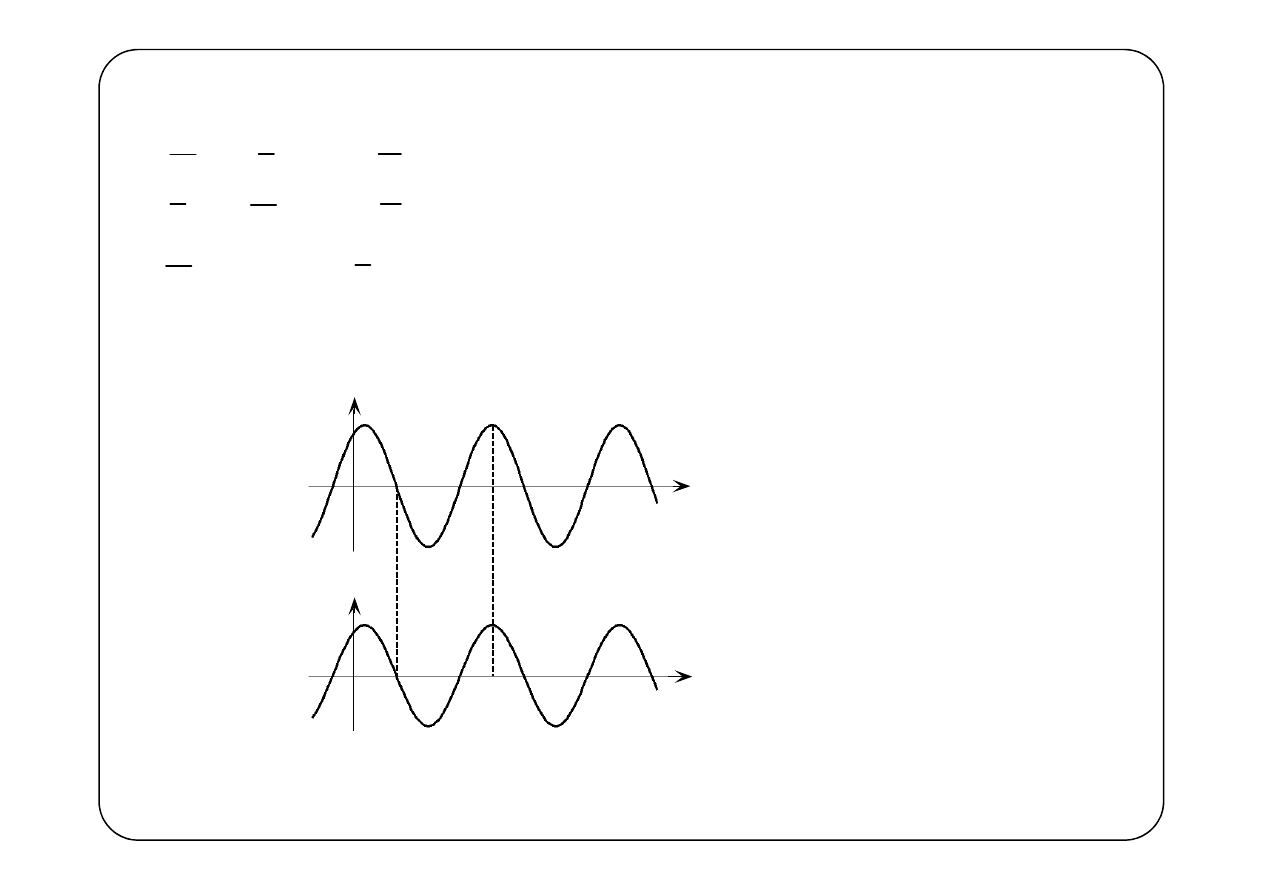
Rezystor
U
RI
Z
R
I
GU
Y
G
=
→
=
=
→
=
u
i
u
i
j
j
j
j
u
i
e
,
e
e
e
U
U
I
I
U
RI
ψ
ψ
ψ
ψ
ψ
ψ
=
=
=
⇒
=
( )
u t
( )
i t
t
t
Faza napięcia jest taka
sama jak faza prądu
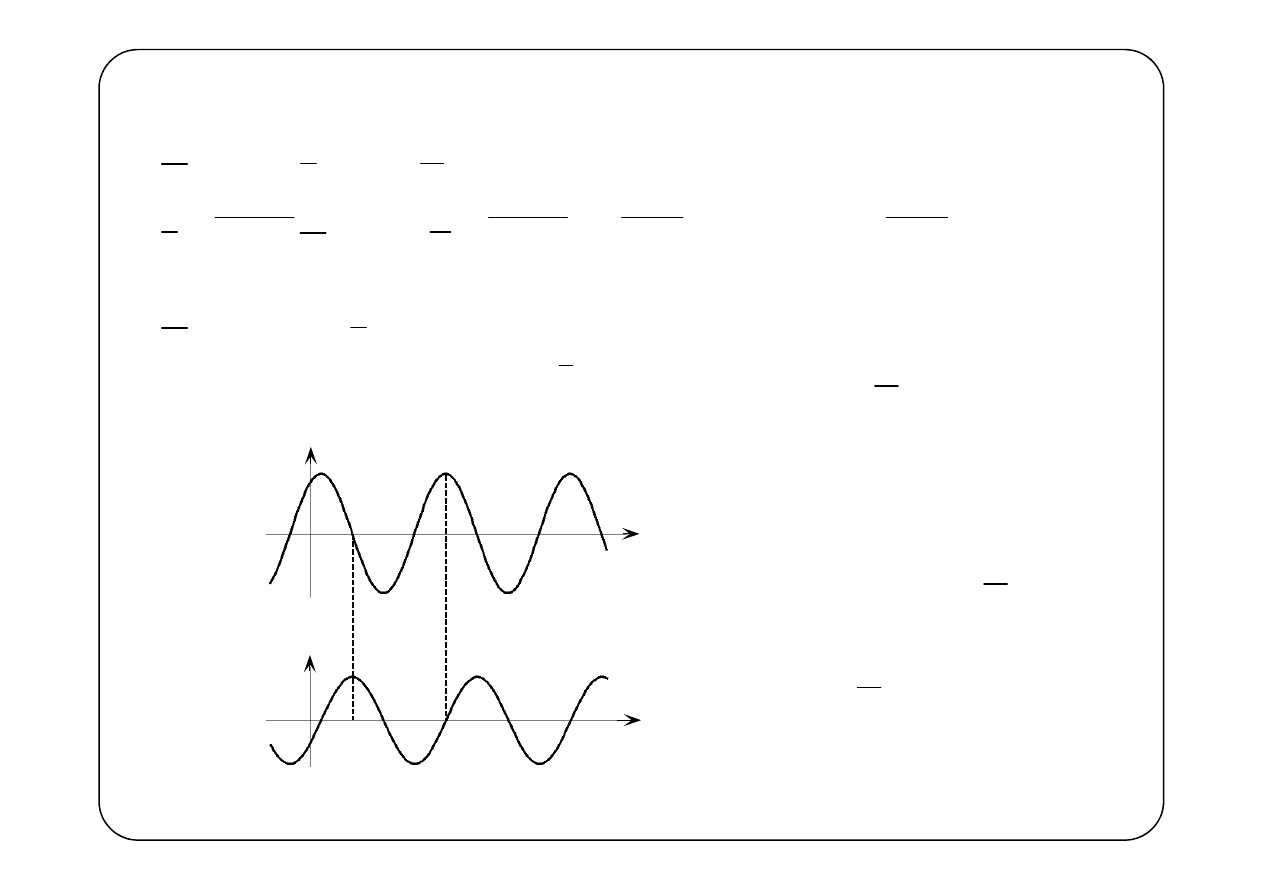
Induktor
0
0
0
0
0
0
0
j
j
j ,
0
1
1
1
1
j
j ,
0
j
j
U
LI
Z
L
X
X
L
I
U
Y
B
B
L
L
L
L
ω
ω
ω
ω
ω
ω
ω
=
→
=
=
=
>
−
=
→
=
=
=
= −
<
u
i
u
i
i
j
j
π
j
j
j
j
2
0
0
u
i
e
,
e
π
e
j
e
e e
2
U
U
I
I
U
LI
LI
ψ
ψ
ψ
ψ
ψ
ω
ω
ψ
ψ
=
=
=
=
⇒
=
+
( )
u t
( )
u t
( )
i t
t
t
Fazy napięcia i prądu
różnią się o kąt
(Napięcie „wyprzedza”
prąd o )
2
π
2
π
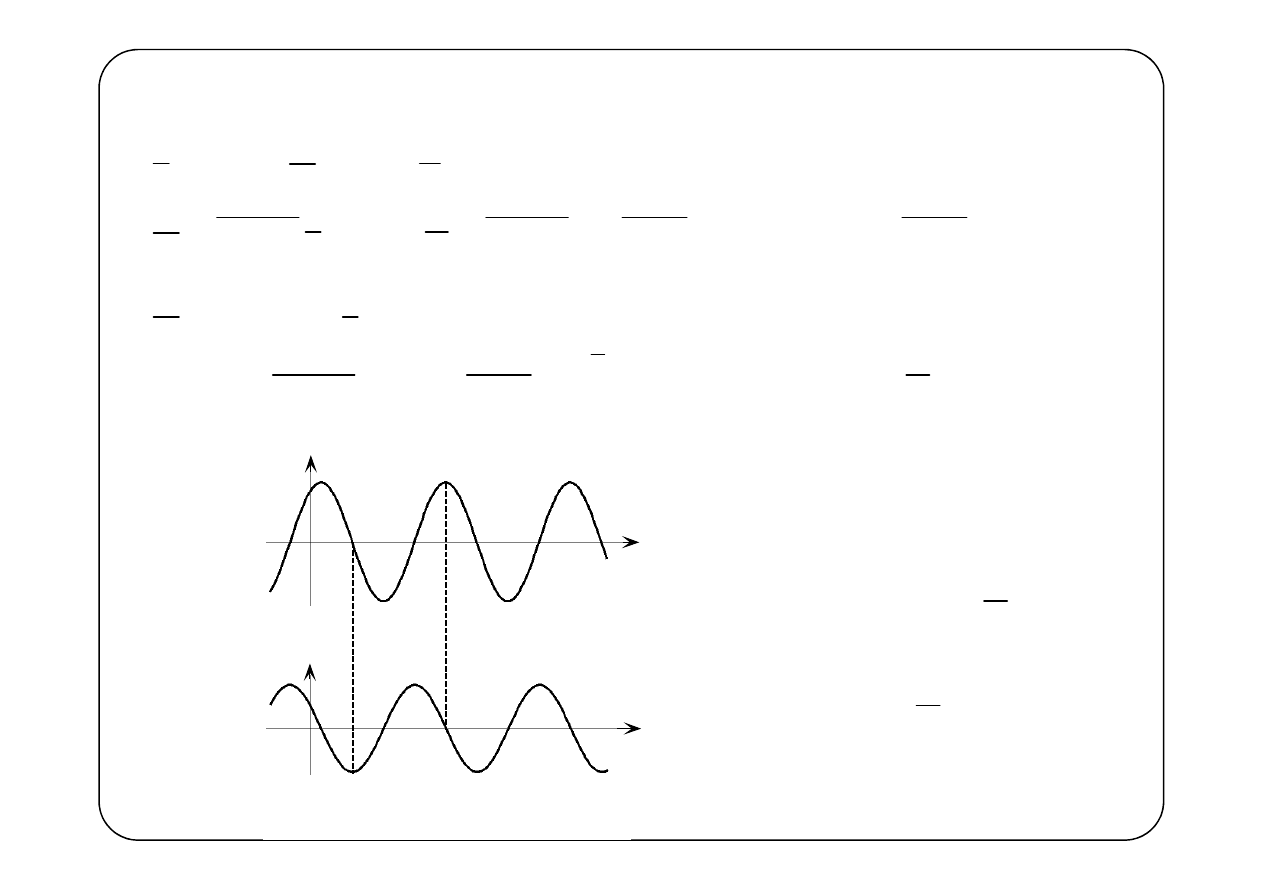
Kondensator
0
0
0
0
0
0
0
j
j
j ,
0
1
1
1
1
j
j ,
0
j
j
I
C U
Y
C
B
B
C
U
I
Z
X
X
C
C
C
C
ω
ω
ω
ω
ω
ω
ω
=
→
=
=
=
>
−
=
→
=
=
=
= −
<
u
i
u
i
i
j
j
π
j
j
j
j
2
u
i
0
0
e
,
e
1
1
π
e
e
e
e
j
2
U
U
I
I
U
I
I
C
C
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ω
ω
−
=
=
=
=
⇒
=
−
( )
u t
( )
u t
( )
i t
t
t
Fazy napięcia i prądu
różnią się o kąt
(Prąd „wyprzedza”
napięcie o )
2
π
2
π
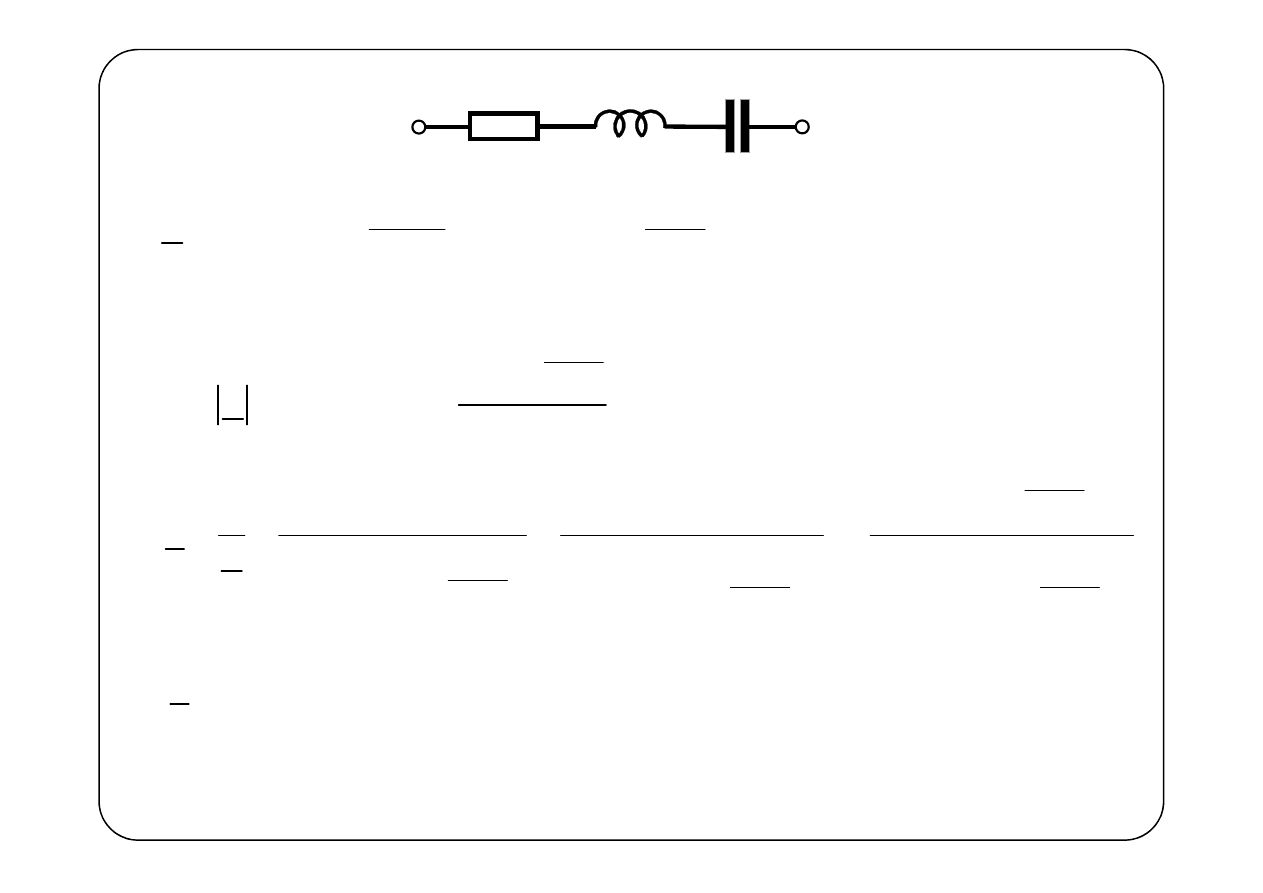
R
L
C
j
0
0
0
0
0
0
1
1
j
j
e
j
1
,
arc tg
Z
R
L
R
L
Z
C
C
L
C
Z
Z
R
ϕ
ω
ω
ω
ω
ω
ω
ϕ
= +
+
= +
−
=
−
=
=
gdzie
0
0
2
2
2
2
0
0
0
0
0
0
1
1
1
j
1
1
1
j
L
C
R
Y
Z
R
L
R
L
R
L
C
C
C
ω
ω
ω
ω
ω
ω
ω
ω
−
−
= =
=
+
+
−
+
−
+
−
j
e
Y
Y
ϕ
−
=
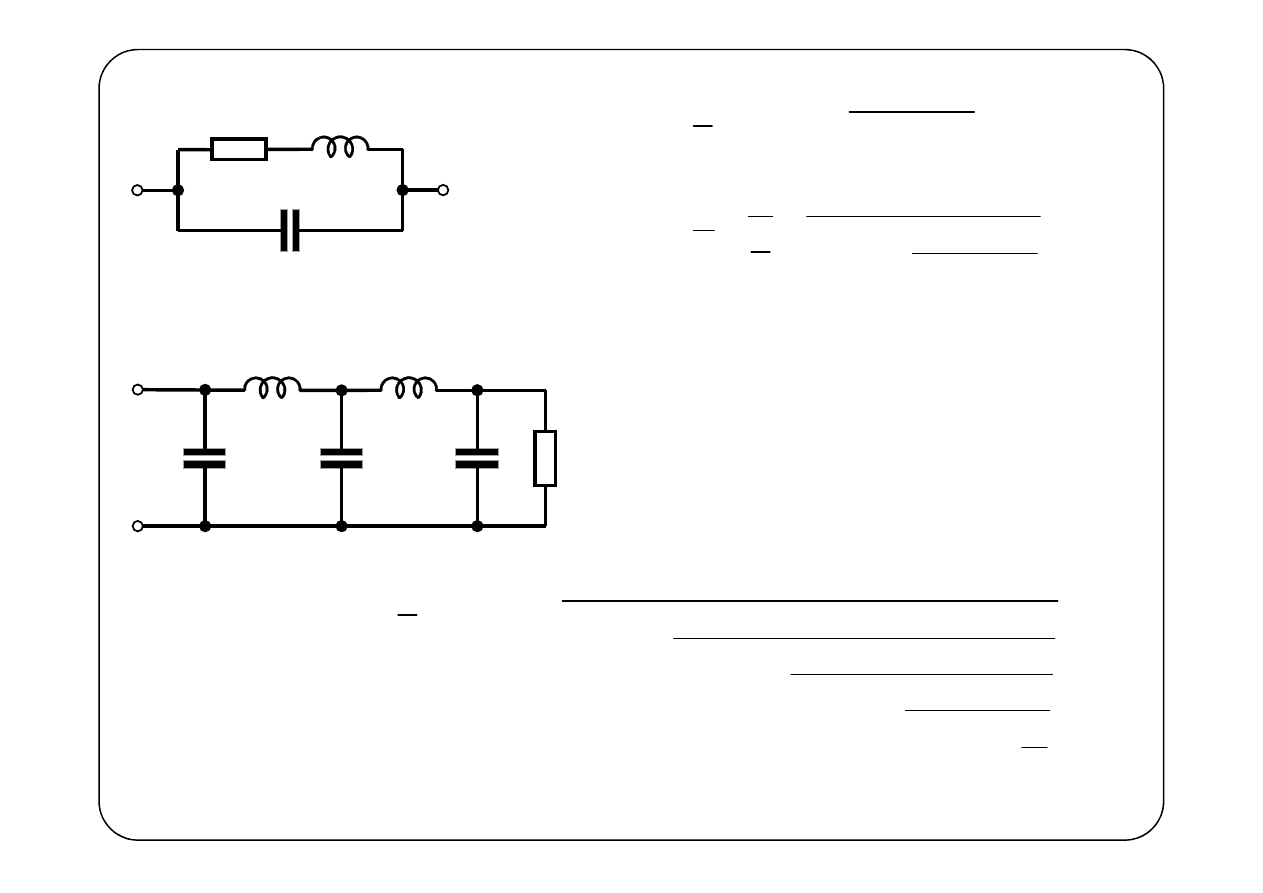
R
L
C
0
0
0
0
1
j
j
1
1
1
j
j
Y
C
R
L
Z
Y
C
R
L
ω
ω
ω
ω
=
+ +
= =
+ +
C
C
C
1
L
2
L
R
1
C
2
C
3
C
R
0
1
0
1
0
2
0
2
0
3
1
j
1
j
1
j
1
j
1
j
Y
C
L
C
L
C
R
ω
ω
ω
ω
ω
=
+
+
+
+
+
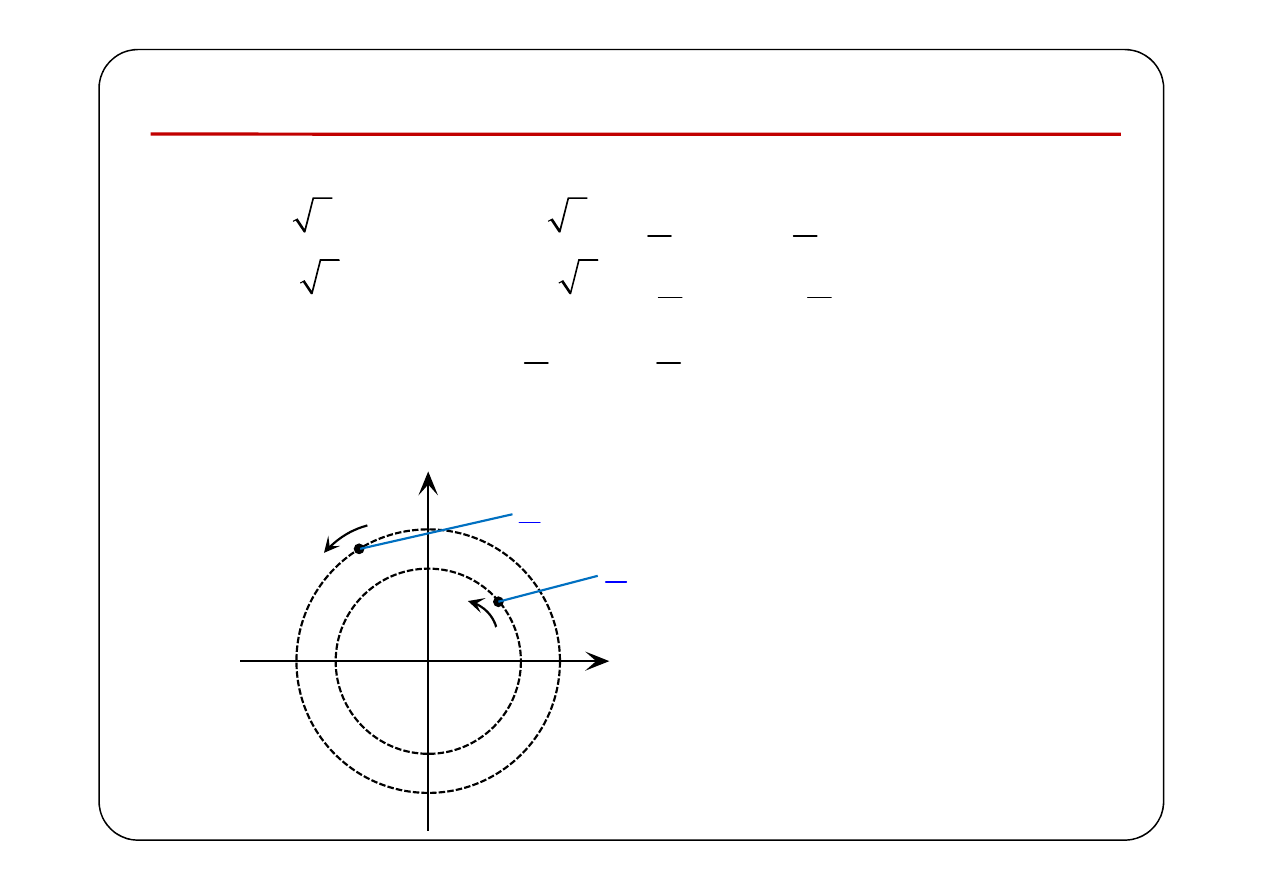
Wykres wskazowy
Rozważmy dwa napięcia sinusoidalne
( )
(
)
{
}
( )
(
)
{
}
0
1
0
2
j
j
1
1
1
1
0
1
1
j
j
2
2
2
2
0
2
2
2 sin
2 Im
e
,
e
2 sin
2 Im
e
,
e
t
t
u t
U
t
U
U
U
u
t
U
t
U
U
U
ω
ψ
ω
ψ
ω
ψ
ω
ψ
=
+
=
=
=
+
=
=
Każda z zespolonych funkcji
reprezentuje na płaszczyźnie
zespolonej punkt poruszający się po okręgu o promieniu odpowiednio
równym U
1
i U
2
z taką sama prędkością kątową
ω
0
.
0
0
j
j
1
2
e
i
e
t
t
U
U
ω
ω
0
ω
0
ω
Im
Re
0
j
1
e
t
U
ω
0
j
2
e
t
U
ω
Odległość między
punktami jest stała!
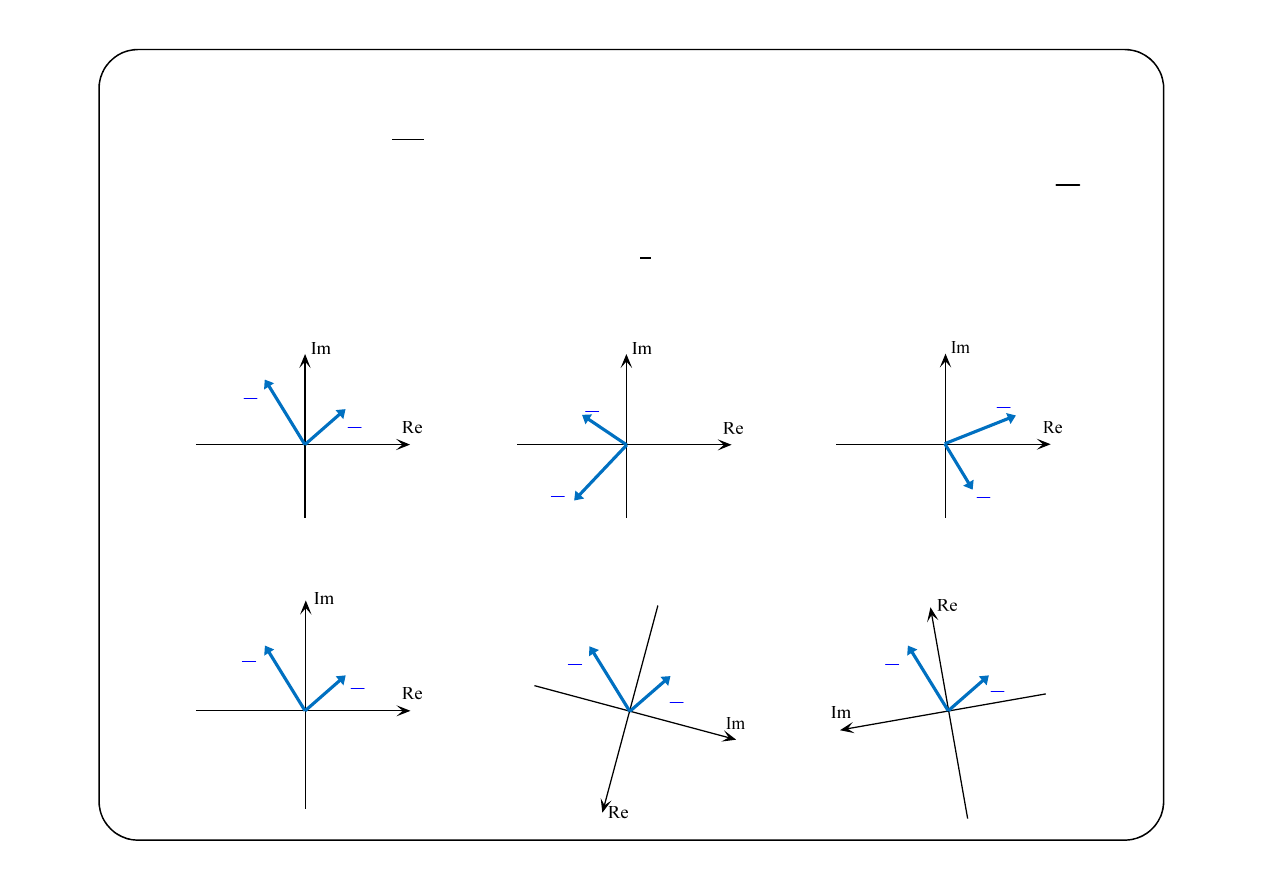
Definicja
Wskazem napięcia U będziemy nazywać strzałkę o długości U, łączącą
początek układu współrzędnych z punktem reprezentującym funkcję
na płaszczyźnie zespolonej w dowolnej, ale ustalonej, chwili czasu t.
Identycznie definiujemy wskaz prądu I.
0
j
e
t
U
ω
1
U
1
U
2
U
2
U
t = t
1
t = t
2
t = t
3
1
U
2
U
1
U
1
U
1
U
2
U
2
U
2
U
Lub równoważnie
Definicja
Wykresem wskazowym nazywamy zbiór wskazów napięć i prądów
w obwodzie elektrycznym w ustalonej chwili czasu t, np. t = 0.
(Oczywiście obowiązuje cały czas założenie, że wszystkie napięcia i prądy
w obwodzie są przebiegami sinusoidalnymi o takiej samej pulsacji).
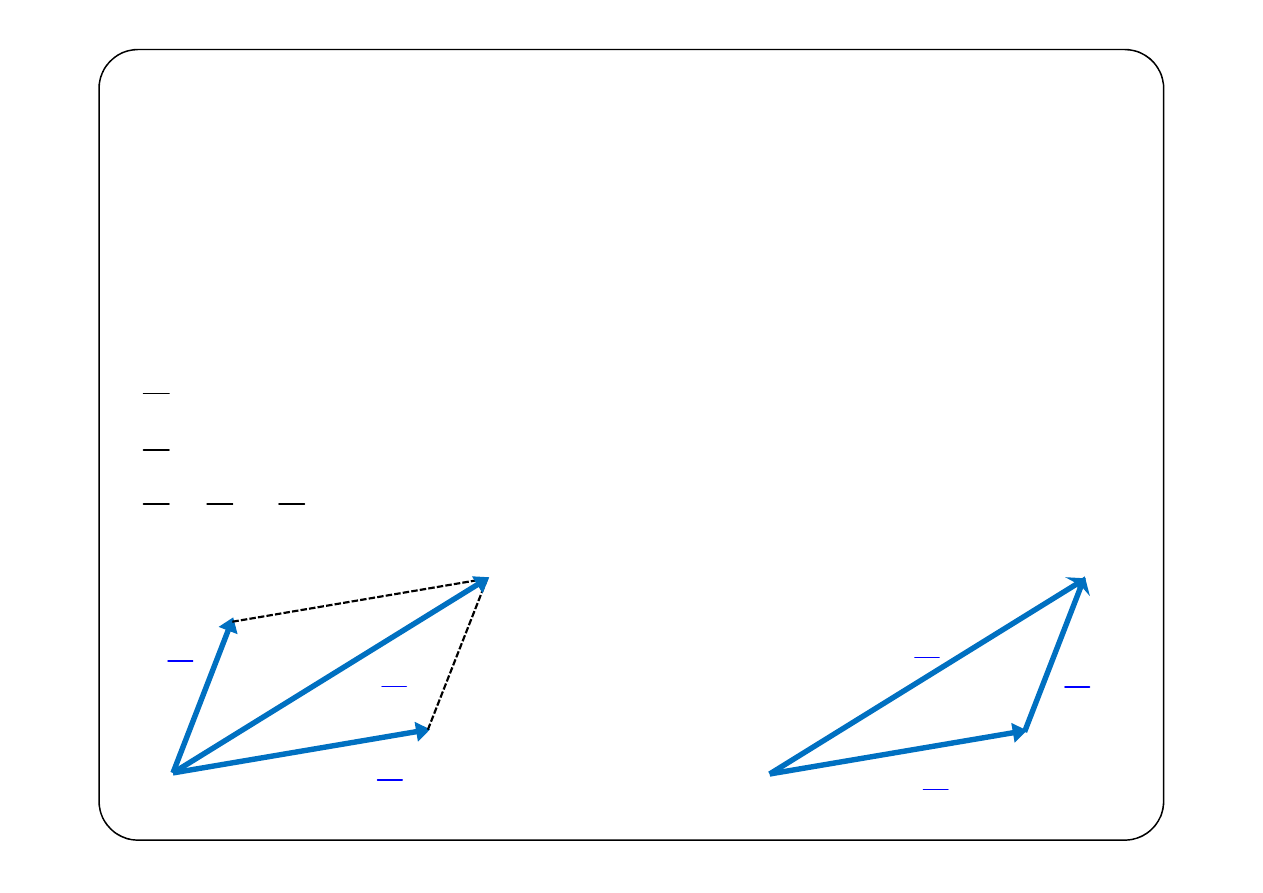
Dodawanie wskazów
1
2
j
1
1
1
1
1
1
j
2
1
2
2
2
2
e
cos
j
sin
e
cos
j
sin
U
U
U
U
U
U
U
U
ψ
ψ
ψ
ψ
ψ
ψ
=
=
+
=
=
+
(
) (
)
2
1
2
2
2
2
1
2
1
1
2
2
1
1
2
2
e
cos
j
sin
cos
cos
j
sin
sin
U
U
U
U
U
U
U
U
U
U
U
ψ
ψ
ψ
ψ
ψ
ψ
=
=
+
=
+
=
+
+
+
1
U
2
U
U
1
U
2
U
U
albo tak
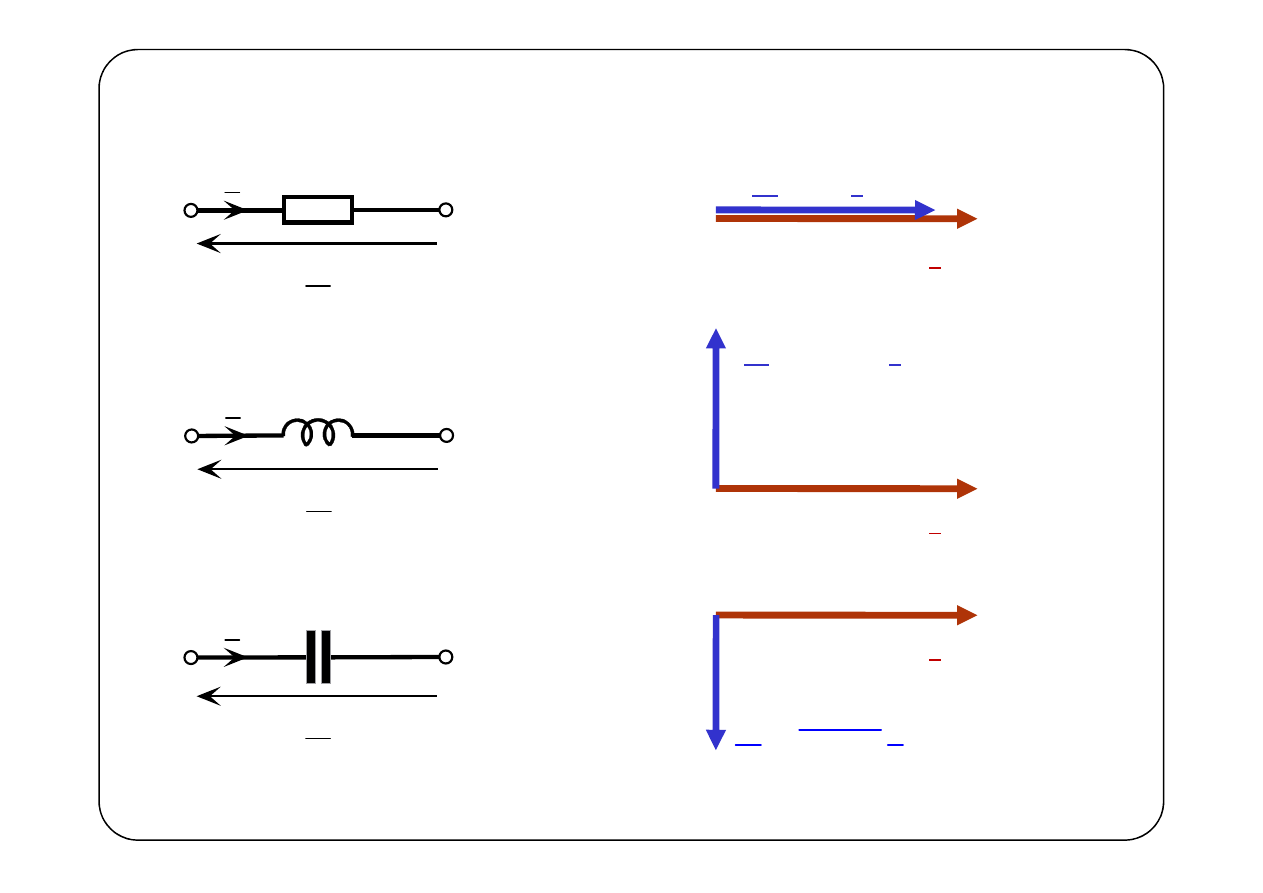
Przykłady
I
U
R
I
U = R I
I
L
U = j
ω
0
L I
U
I
I
U
C
I
0
1
j
U
I
C
ω
=
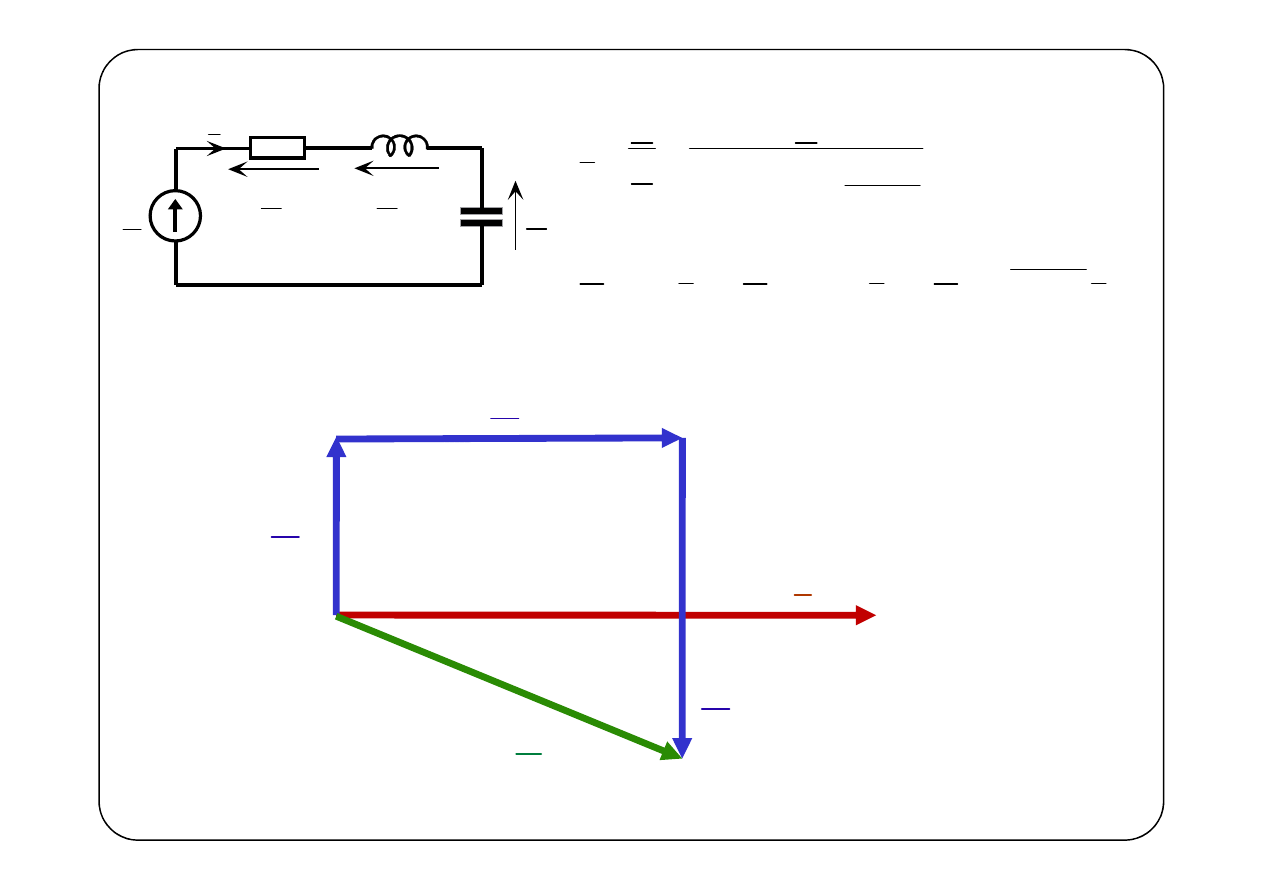
E
R
L
C
I
R
U
L
U
C
U
0
0
0
0
,
1
j
j
1
,
j
,
j
R
L
C
E
E
I
Z
R
L
C
U
RI
U
I
U
I
C
ω
ω
ω
ω
= =
+
+
=
=
=
R
U
I
L
U
C
U
E
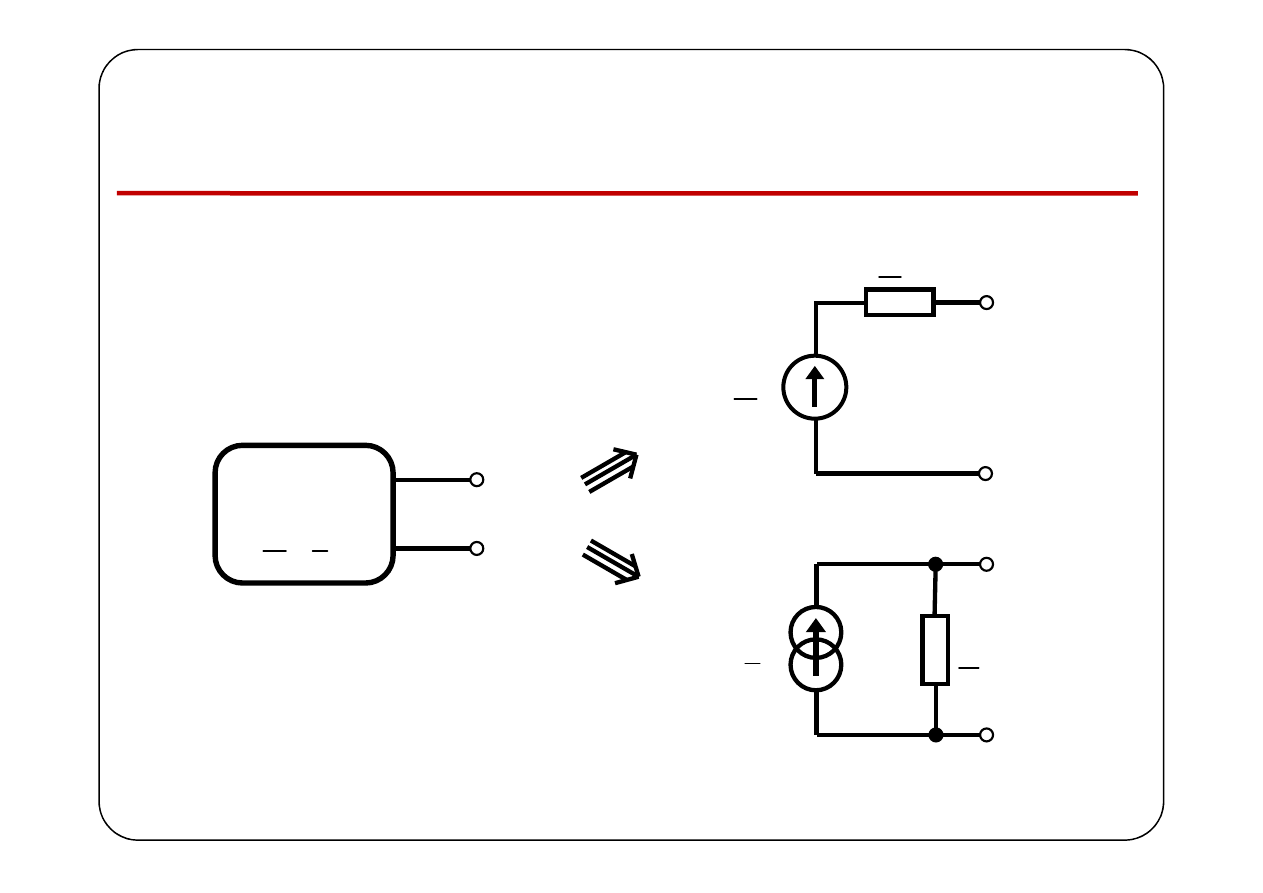
Twierdzenie Thévenina i Nortona
w postaci symbolicznej
A
T
E
T
Z
Twierdzenie
Thévenina
A
B
A
B
B
z
SLS
,
E I
N
Y
N
I
Twierdzenie
Nortona
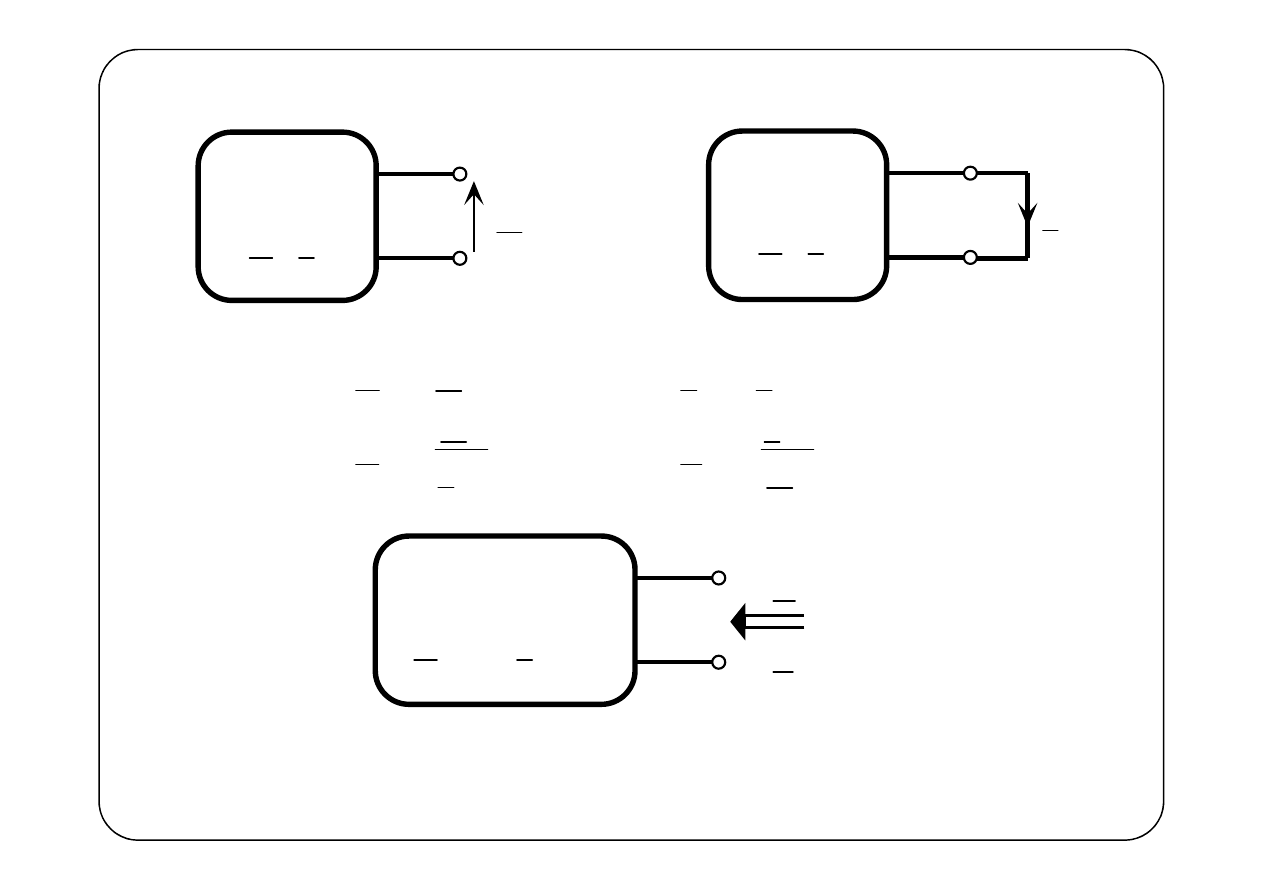
z
SLS
,
E I
z
SLS
,
E I
0
U
zw
I
T
N
zw
0
0
zw
E
U
I
I
U
I
Z
Y
=
=
=
=
0
zw
T
N
zw
0
Z
Y
I
U
=
=
z
SLS
0,
0
E
I
=
=
T
N
Z
Y
Nie wyłączamy źródeł sterowanych!!!
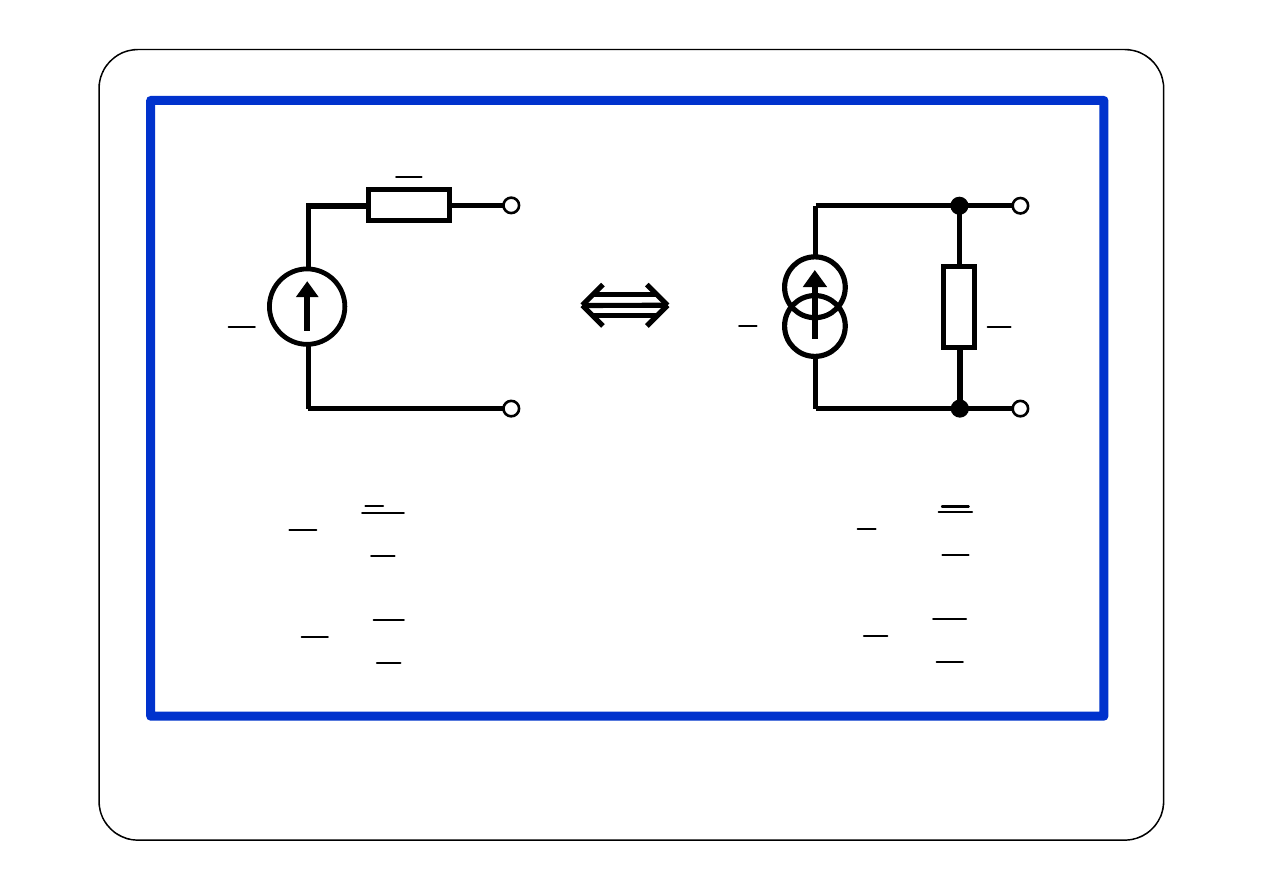
E
Z
z
I
Y
z
1
I
E
Y
Z
Y
=
=
⇐
z
1
E
I
Z
Y
Z
=
=
⇒
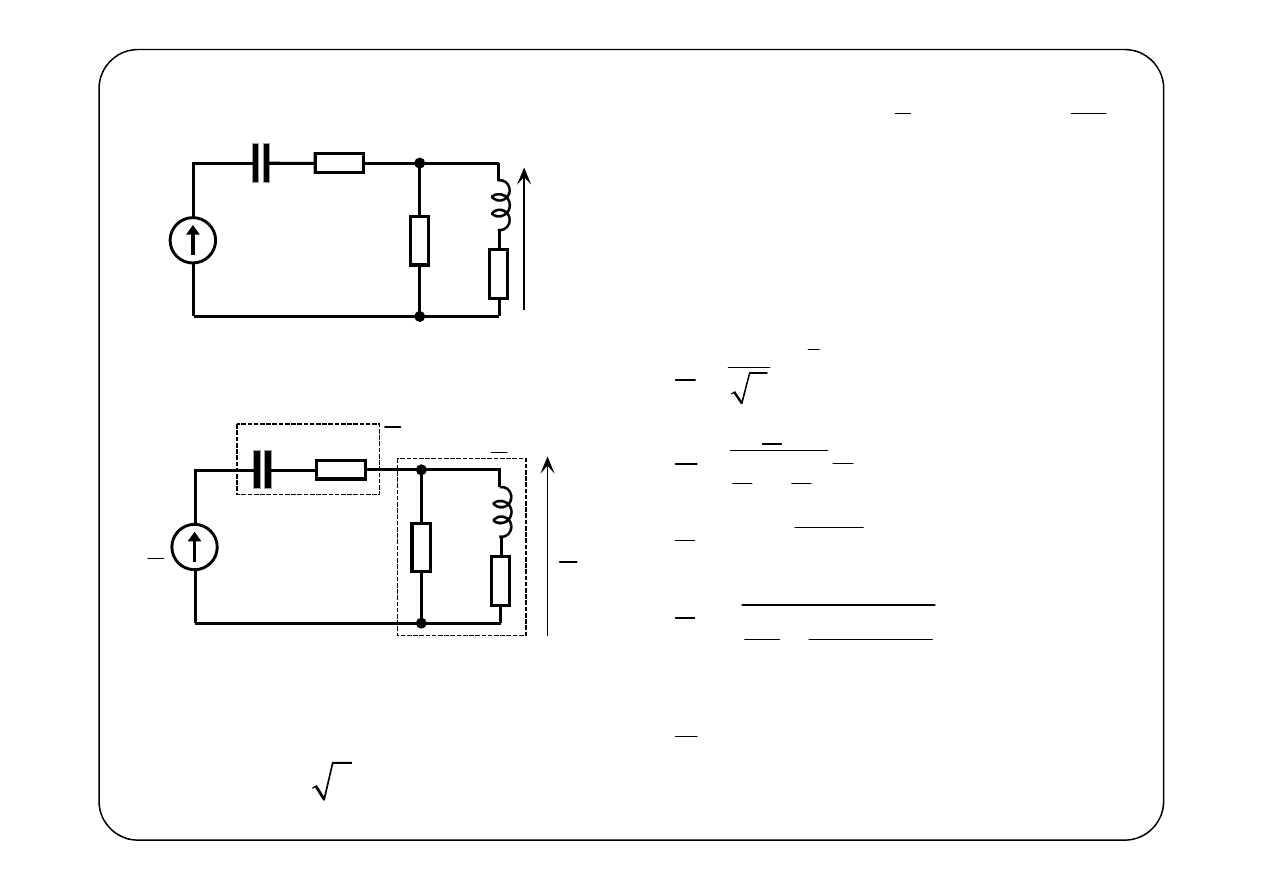
Przykład 1.
( )
e t
C
`1
R
2
R
L
3
R
( )
u t
( )
(
)
( )
0
0
1
2
3
π
rad
4
s
20 sin
V,
2
,
1Ω,
1Ω,
1Ω,
1H,
1F.
?
e t
t
R
R
R
L
C
u t
ω
ω
=
−
=
=
=
=
=
=
=
π
j
4
2
20
e
10
j10
2
E
Z
U
E
−
=
=
−
=
C
`1
R
1
Z
2
Z
Symboliczny schemat zastępczy
2
1
2
1
1
0
2
2
3
0
j0,3217
1
1
j0,5
j
1
0, 75
j0,25
1
1
j
6
j2
6, 325e
U
E
Z
Z
Z
R
C
Z
R
R
L
U
ω
ω
−
=
+
=
+
= −
=
=
+
+
+
= − =
( )
(
)
0
6,325 2 sin
0,3217 V.
u t
t
ω
=
−
E
C
`1
R
2
R
L
3
R
U
2
Z
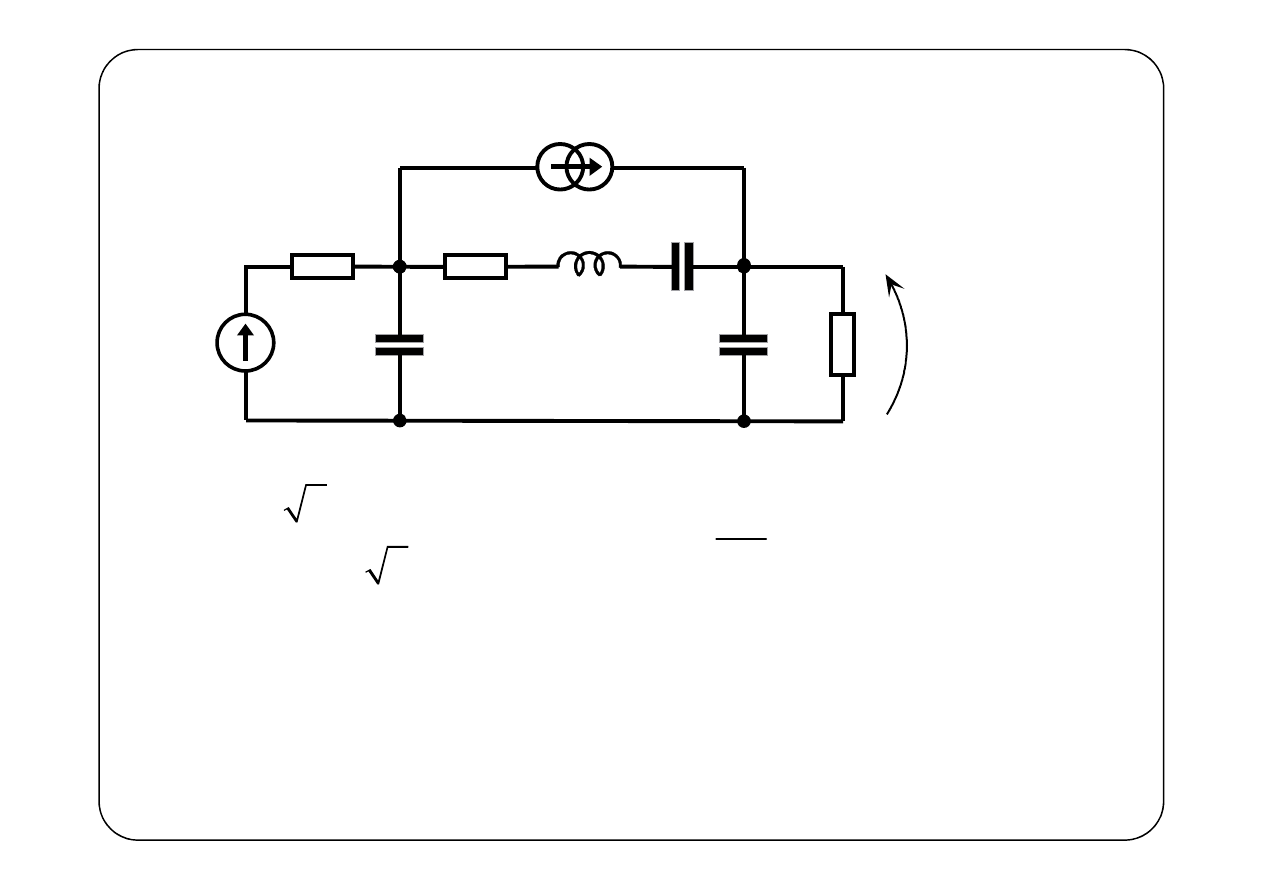
Przykład 2.
( )
e t
1
R
2
R
3
R
L
1
C
2
C
3
C
( )
z
i t
( )
u t
( )
( )
( )
0
6
0
3
z
0
1
2
3
1
2
3
4 2 sin
V,
rad
10
,
s
5 10
2 cos
A,
500 Ω,
1 kΩ,
2 kΩ,
2 mH,
1nF,
500 pF,
500 pF.
?
e t
t
i t
t
R
R
R
L
C
C
C
u t
ω
ω
ω
−
=
=
= ⋅
=
=
=
=
=
=
=
=
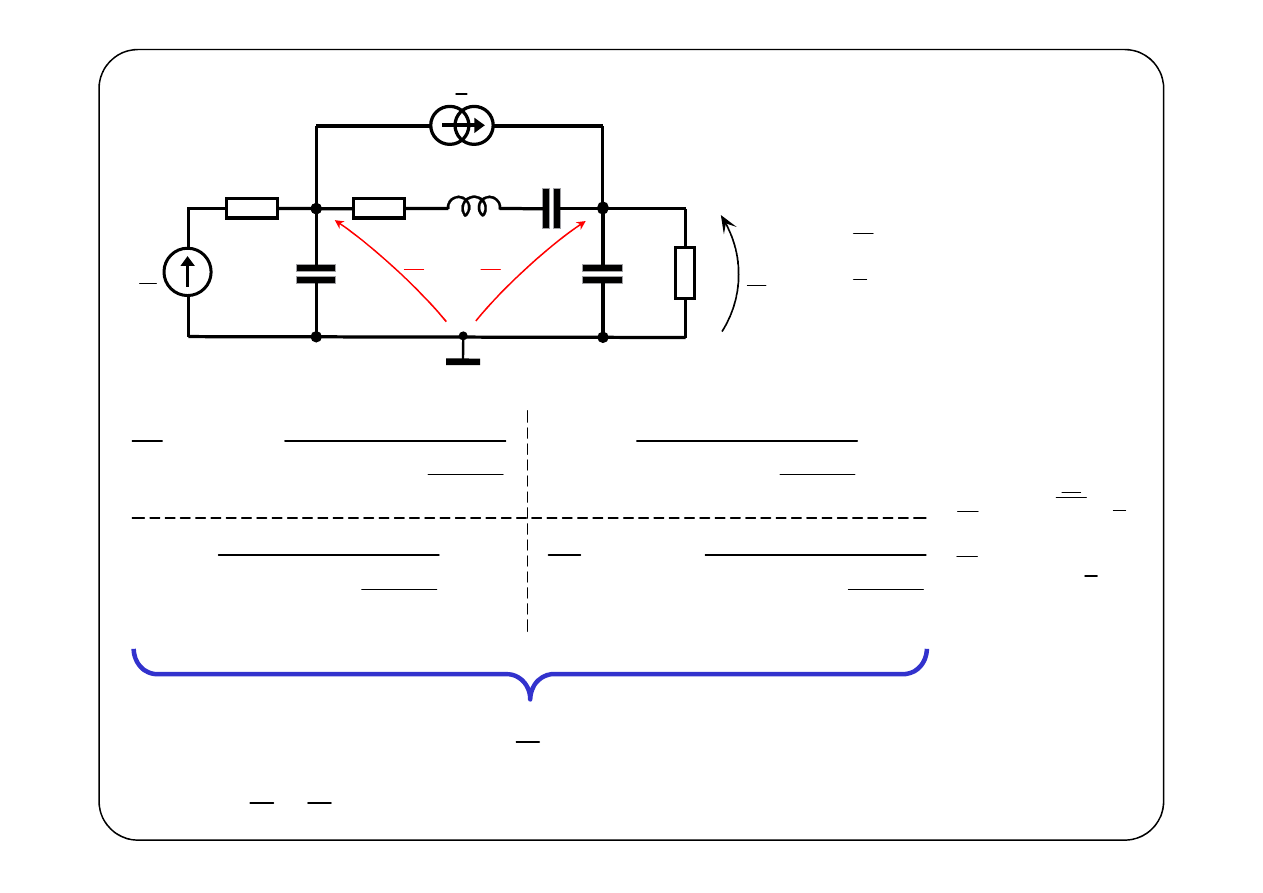
E
1
R
2
R
3
R
L
1
C
2
C
3
C
z
I
U
1
2
n1
U
n2
U
3
z
4
j 5 10
E
I
−
=
=
⋅
0
1
1
1
1
j
1
1
C
R
ω
+
+
−
0
1
1
2
0
2
0
0
2
0
2
z
n1
1
n2
0
3
z
3
2
0
2
0
0
2
0
2
j
1
1
j
j
j
j
1
1
1
j
1
1
j
j
j
j
C
R
R
L
R
L
E
C
C
I
U
R
U
C
I
R
R
L
R
L
C
C
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
−
+
+
+
+
−
=
−
+
+
+
+
+
+
n2
U
U
=
n
Y
3
3
3
3
3
n1
3
3
3
3
n2
3 10
j10
10
8 10
j 5 10
10
1,5 10
j 0,5 10
j 5 10
U
U
−
−
−
−
−
−
−
−
−
⋅
+
−
⋅
−
⋅
=
−
⋅
+
⋅
⋅
Po uproszczeniu przez 10
–3
n1
n2
3
j
1
8
j 5
1
1,5
j 0,5
j 5
U
U
+
−
−
=
−
+
2
n2
U
U
∆
=
=
∆
n2
n
2
n
n
j0,494
3
j
8
j5
det
3
j10
1
j5
det
3
j3
3
j10
2,167
j1,167
2, 46e
3
j3
U
U
U
=
=
∆
+
−
∆ =
= +
−
∆ =
= +
+
=
=
+
=
+
Y
( )
(
)
0
2, 46 2 sin
0, 494 V.
u t
t
ω
=
+
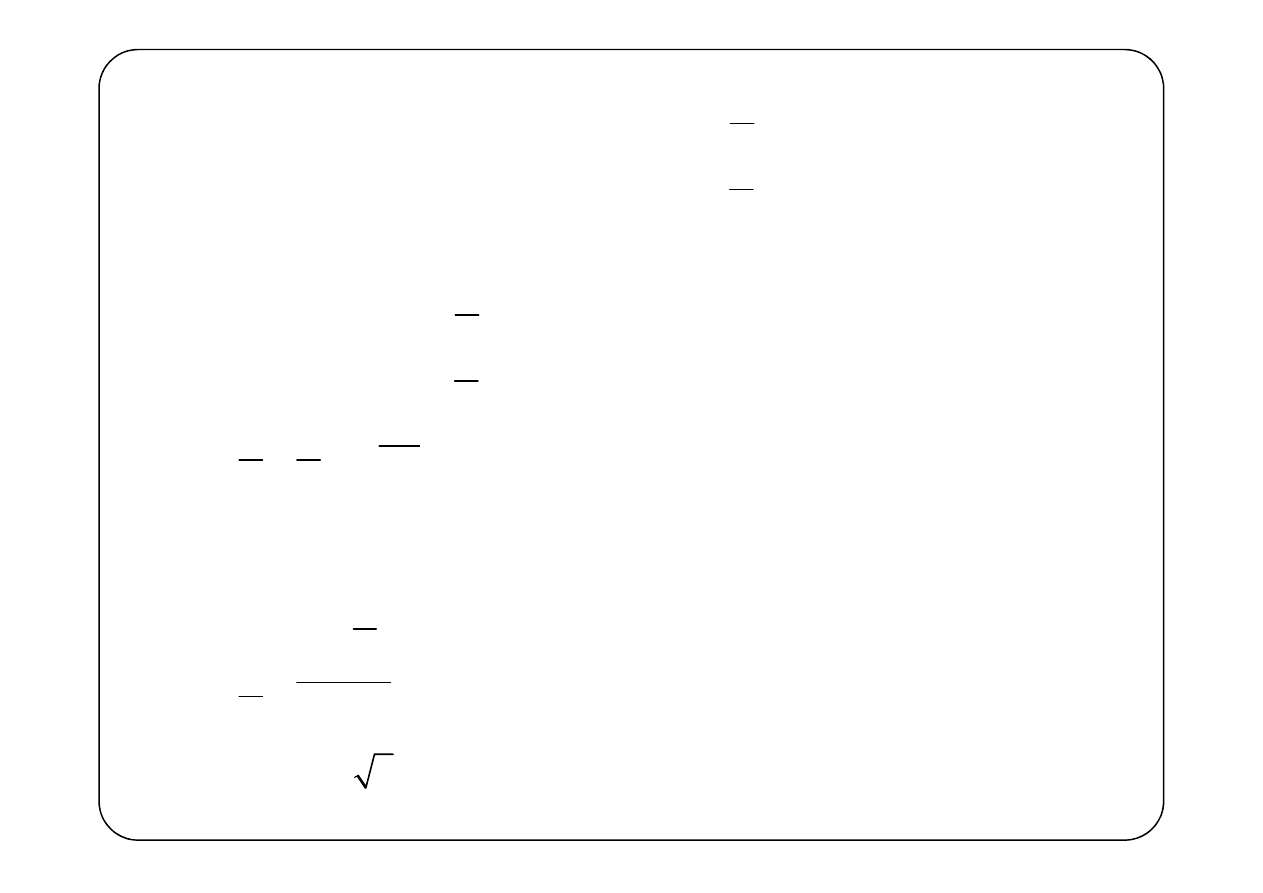
Przykład 3.
1
R
2
R
3
R
1
C
2
C
L
( )
e t
( )
i t
( )
( )
(
)
( )
0
1
2
3
1
2
π
rad
4
s
1
1
2
2
1
2
2sin
V,
1
,
1Ω,
Ω,
Ω,
1F,
2 F,
H.
?
e t
t
R
R
R
C
C
L
i t
ω
=
−
=
=
=
=
=
=
=
=
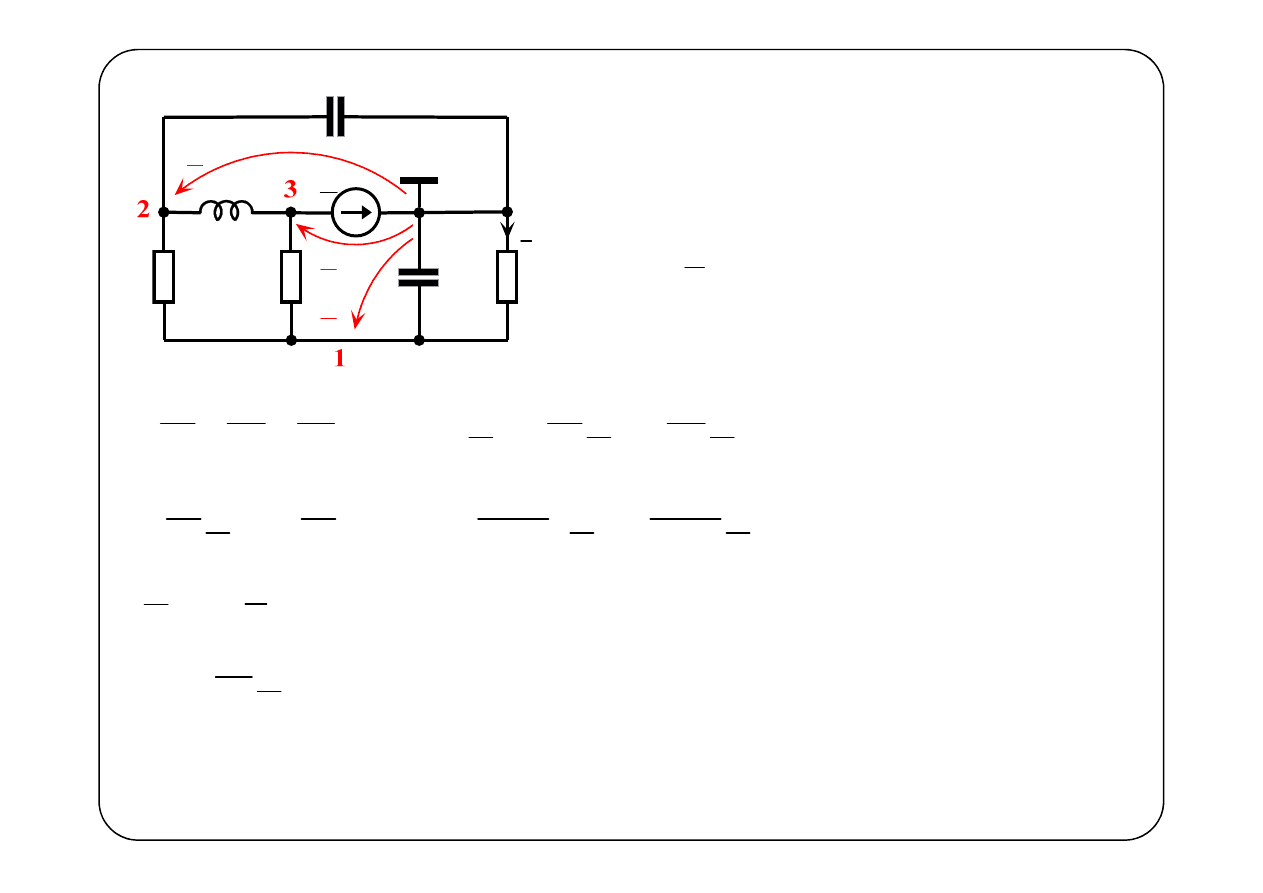
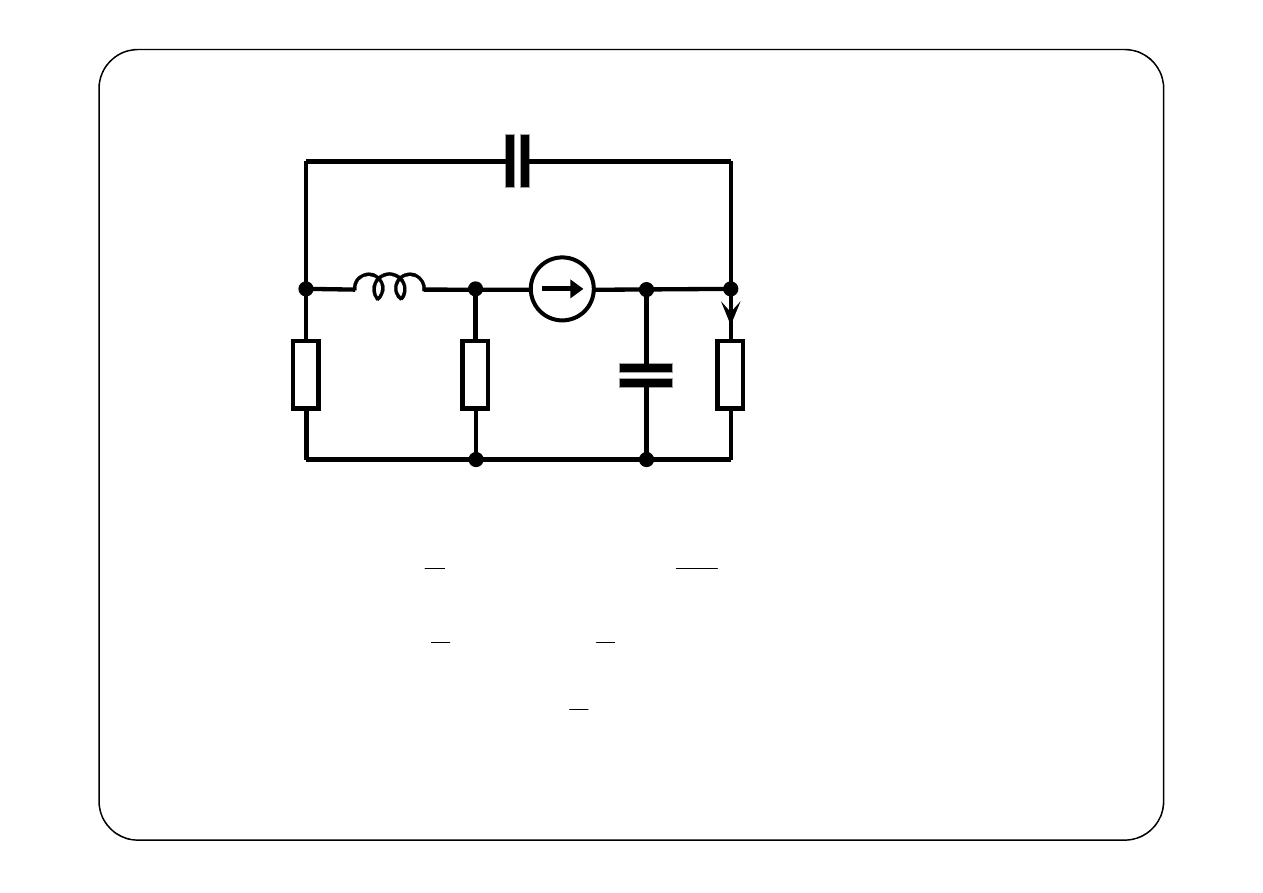
1
R
2
R
3
R
1
C
2
C
L
E
I
n1
U
n2
U
n3
U
1
j
E
= −
n1
n2
n3
0
2
1
2
3
1
2
1
1
1
1
1
j
0
C
U
U
U
R
R
R
R
R
ω
+
+
+
−
−
=
1
2
3
1
2
n1
n2
n3
0
1
1
1
0
0
n3
1
1
1
1
j
0
j
j
R
R
R
R
R
U
C
U
U
R
R
L
L
U
E
ω
ω
ω
−
+
+
+
−
=
= −
n1
3
1
I
U
R
= −
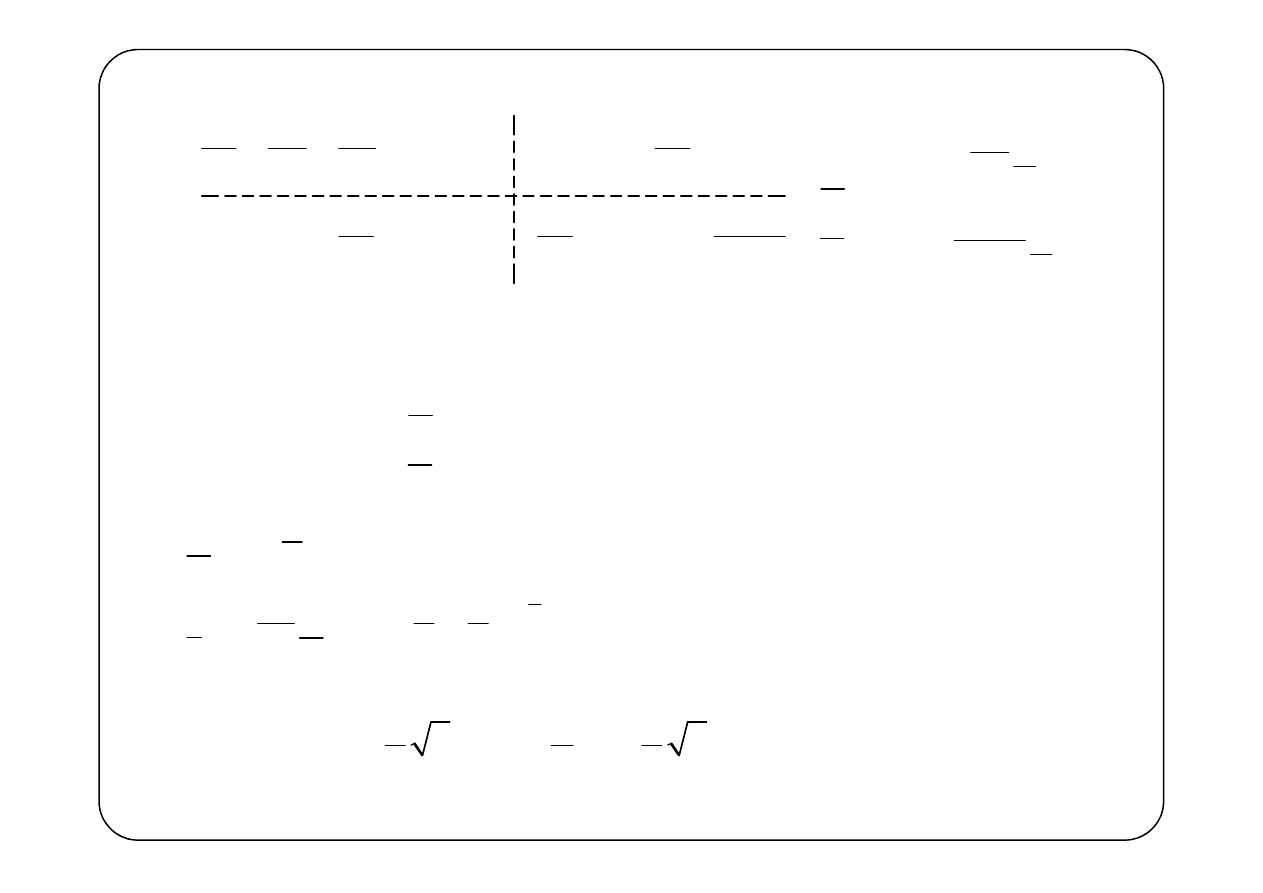
0
2
1
2
3
1
2
n1
n2
0
1
1
1
0
0
1
1
1
1
1
j
1
1
1
1
j
j
j
C
E
R
R
R
R
R
U
U
C
E
R
R
L
L
ω
ω
ω
ω
+
+
+
−
−
=
−
+
+
−
Po podstawieniu danych
n1
5
j2
1
1
j
1
1
j
2
j2
U
U
+
−
− +
=
−
−
+
n2
1
1
j
2
j2
U
−
−
+
n1
π
j
2
n1
3
2
j
3
1
4
4
j
e
3
3
U
I
U
R
−
=
= −
= −
=
( )
( )
4
π
4
2 sin
2 cos A.
3
2
3
i t
t
t
=
−
= −
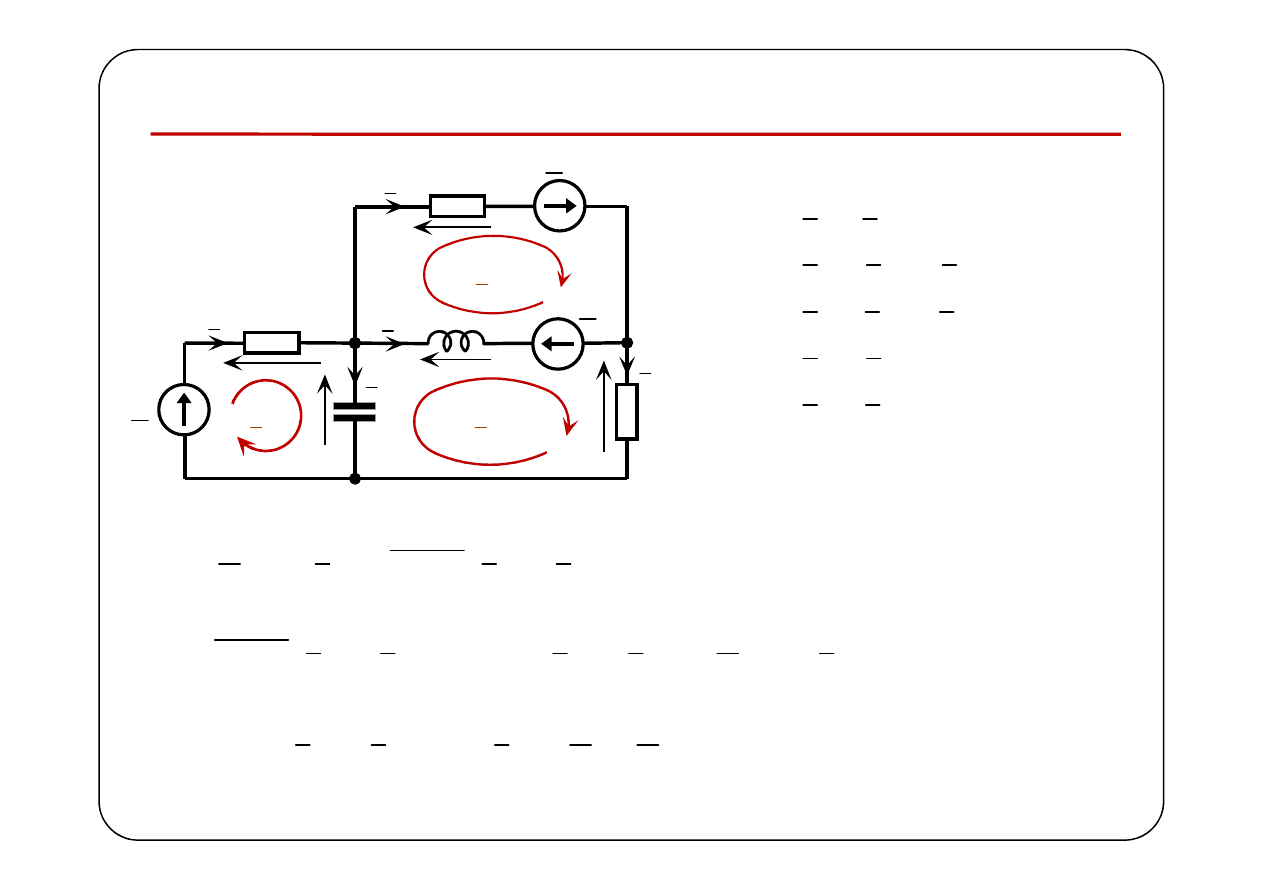
Metoda prądów oczkowych
1
E
2
E
3
E
1
R
2
R
3
R
C
L
m1
I
m2
I
m3
I
1
I
2
I
3
I
4
I
5
I
1
m1
2
m2
m3
3
m1
m2
4
m3
5
m2
I
I
I
I
I
I
I
I
I
I
I
I
=
=
−
=
−
=
=
(
)
1
m1
m1
m2
1
0
1
0
j
E
R I
I
I
C
ω
− +
+
−
=
1.
(
)
(
)
m1
m2
m2
m3
2
m2
0
3
0
1
j
0
j
I
I
L I
I
E
R I
C
ω
ω
−
−
+
−
+
+
=
2.
(
)
m2
m3
m3
3
2
0
2
j
0
L I
I
R I
E
E
ω
−
−
+
−
−
=
3.
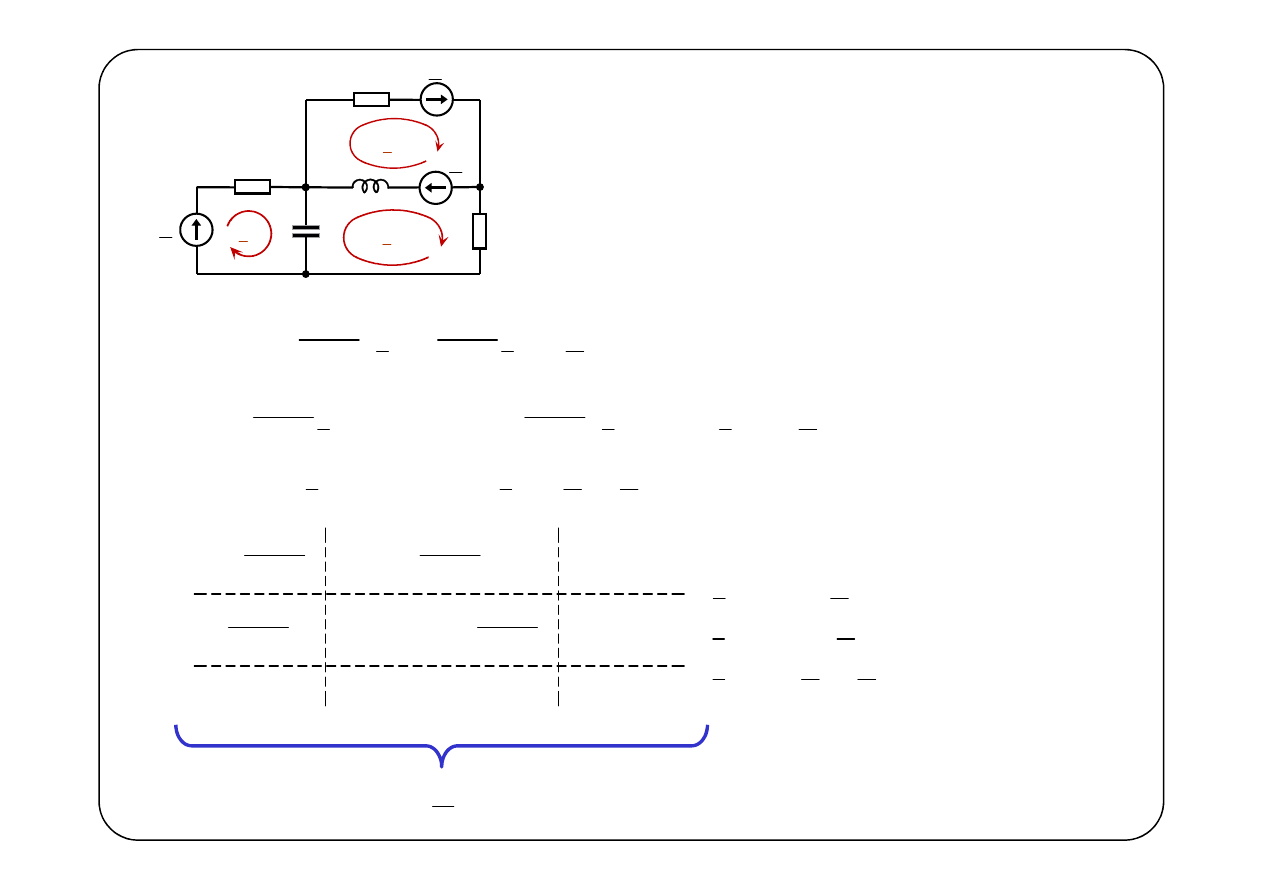
1
E
2
E
3
E
1
R
2
R
3
R
C
L
m1
I
m2
I
m3
I
m1
m2
1
1
0
0
m1
m2
m3
2
3
0
0
0
0
1
1
j
j
1
1
j
j
j
j
R
I
I
E
C
C
I
R
L
I
LI
E
C
C
ω
ω
ω
ω
ω
ω
+
−
=
−
+
+
+
−
= −
1.
2.
(
)
0
0
m2
m3
2
3
0
2
0
j
j
j
j
C
C
LI
R
L I
E
E
ω
ω
ω
ω
−
+
+
=
+
3.
1
0
0
m1
1
m2
2
3
0
0
0
0
m3
2
3
0
2
0
1
1
0
j
j
1
1
j
j
j
j
0
j
j
R
C
C
I
E
R
L
L
I
E
C
C
I
E
E
L
R
L
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
+
−
=
−
+
−
+
m
Z
— macierz zespolonych impedancji oczkowych
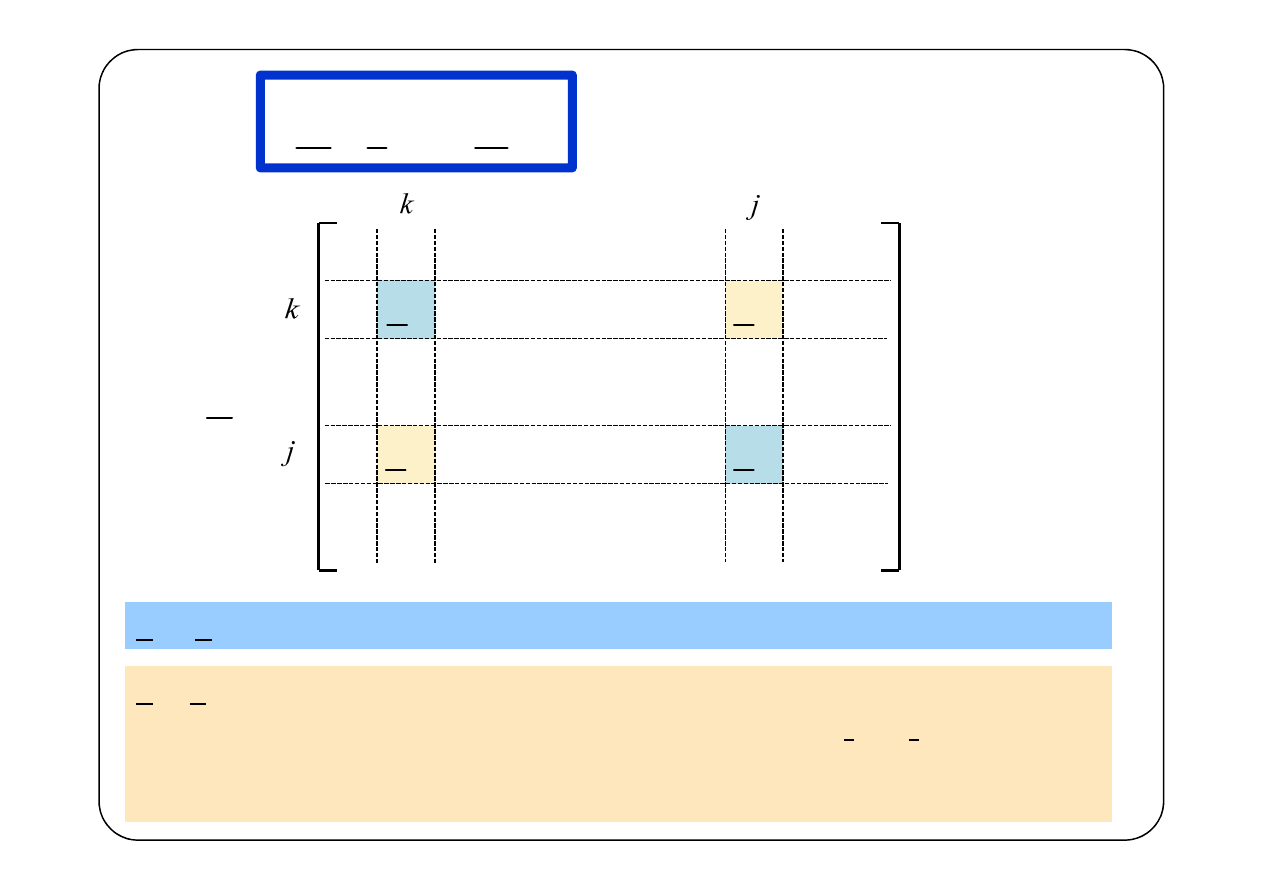
m
m
m
=
Z I
E
m
=
Z
Z
kk
Z
kj
Z
Z
jk
Z
jj
Z
Z
kk
, (Z
jj
) — suma impedancji zespolonych gałęzi tworzących oczko k, (j)
Z
jk
, Z
kj
— impedancje zespolone gałęzi należących jednocześnie do
oczek k i j, wzięte ze znakiem „+” gdy prądy I
mk
i I
mj
płyną we
wspólnej gałęzi w tym samym kierunku, lub ze znakiem „–” gdy
płyną w kierunkach przeciwnych
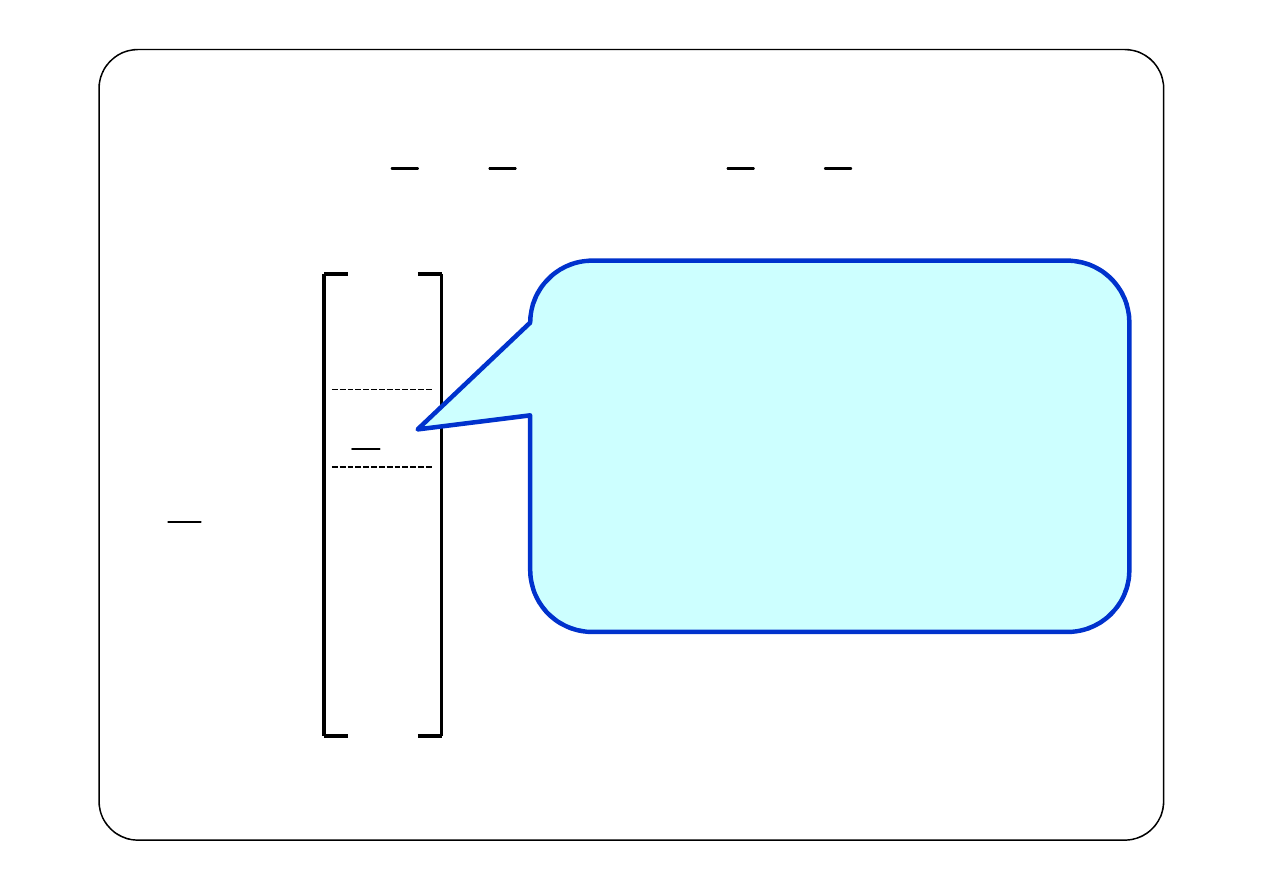
Układ RLC, e
t
m
m
,
czyli
kj
jk
Z
Z
=
=
Z
Z
k
mk
E
Algebraiczna suma wartości
skutecznych zespolonych SEM
źródeł napięciowych, znajdujących
się w oczku k, przy czym SEM
m
=
E
mk
E
skierowaną zgodnie z orientacją
oczka bierzemy ze znakiem plus,
a skierowaną przeciwnie — ze
znakiem minus
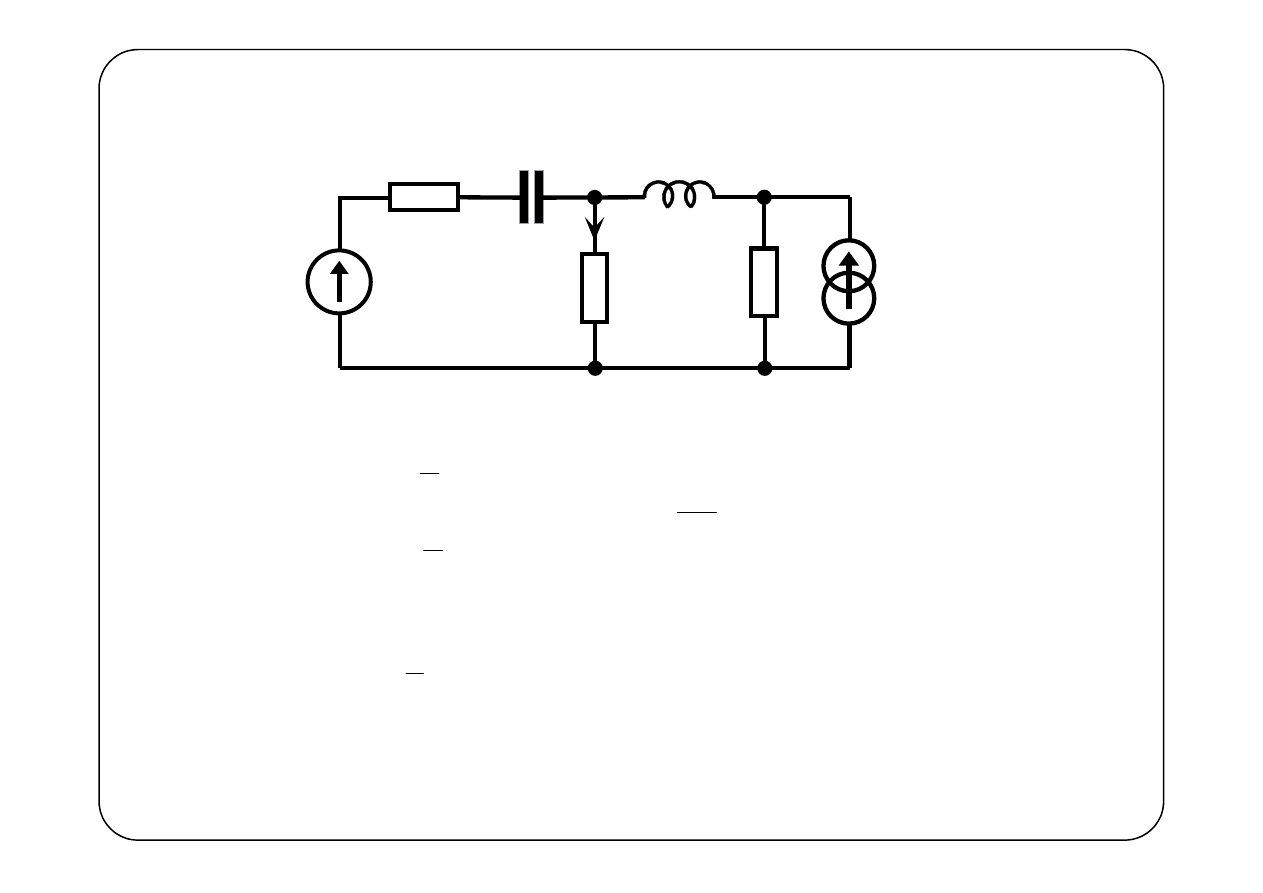
Przykład 1.
( )
e t
( )
z
i t
1
R
2
R
3
R
C
L
( )
i t
( )
( )
π
=
+
( )
( )
( )
( )
(
)
( )
0
z
1
2
3
π
4
rad
s
π
4
1
2
2sin
V,
1
2 sin
A,
1Ω,
1Ω,
2 Ω,
2 H,
F.
?
e t
t
i t
t
R
R
R
L
C
i t
ω
=
+
=
=
−
=
=
=
=
=
=
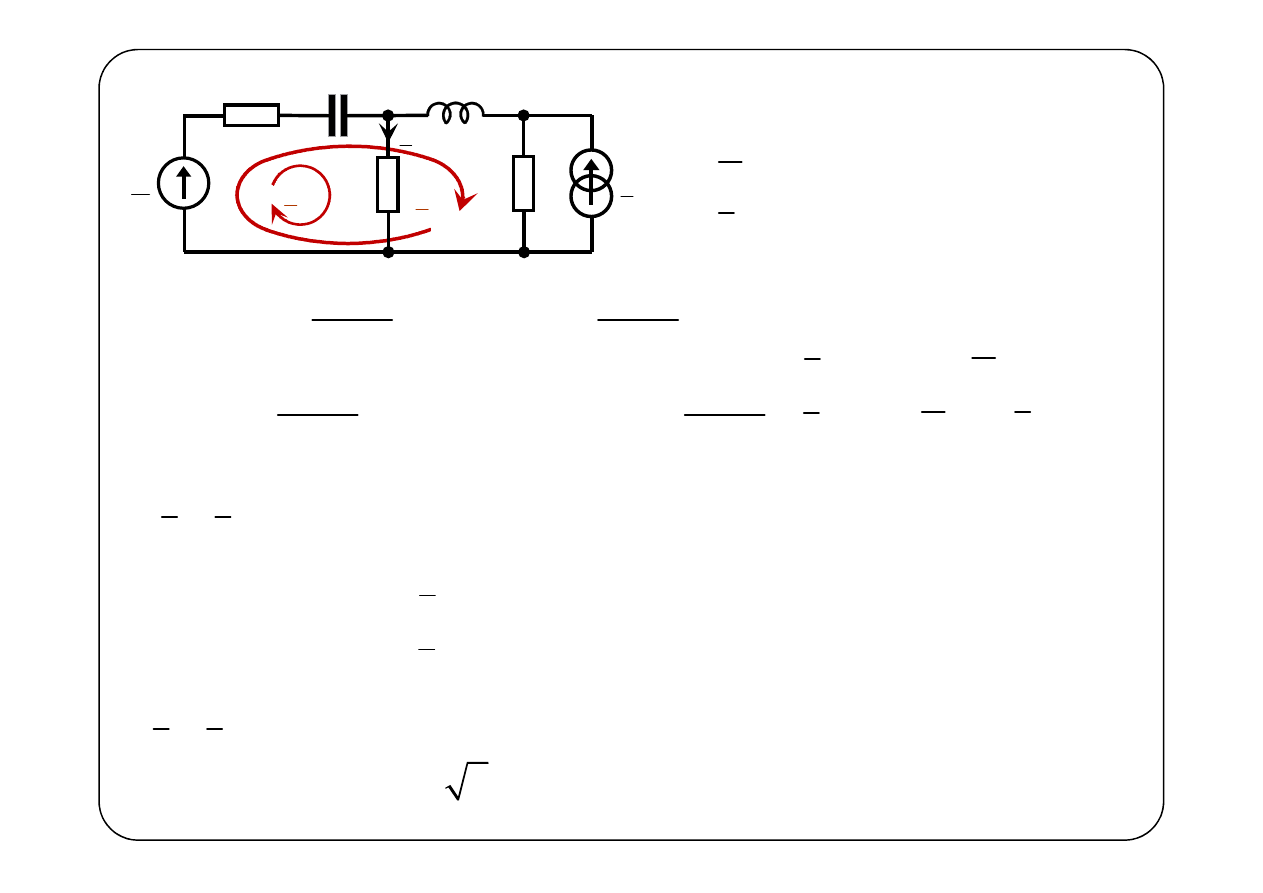
E
z
I
1
R
2
R
3
R
C
L
I
m1
I
m2
I
z
1
j
1 j
E
I
= +
= −
1
2
1
0
0
m1
z
m2
3
1
1
3
0
0
0
1
1
j
j
1
1
j
j
j
R
R
R
C
C
E
I
E
R I
I
R
R
R
L
C
C
ω
ω
ω
ω
ω
+
+
+
=
−
+
+
+
+
0
0
j
j
C
C
ω
ω
m1
I
I
=
m1
m2
j2,138
m1
2
j2
1 j2
1
j
1 j2
3
1
j3
0,1647
j0, 2588
0, 3068e
I
I
I
I
−
−
−
+
=
−
− +
=
= −
−
=
( )
(
)
0, 3068 2 sin
2,138 A.
i t
t
=
−
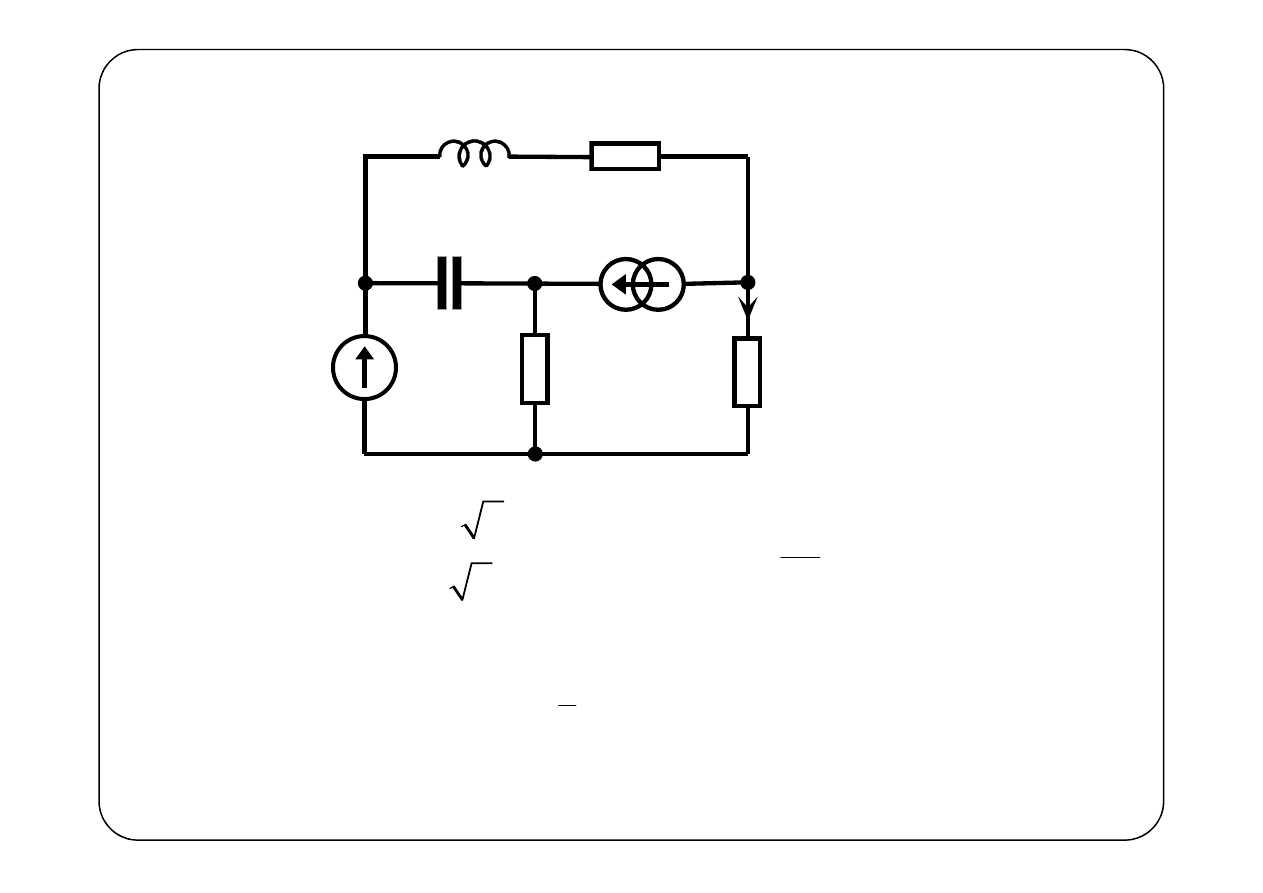
Przykład 2.
( )
e t
( )
z
i t
1
R
2
R
3
R
L
C
( )
i t
( )
( )
(
)
( )
0
z
1
2
3
rad
s
1
2
2 2 sin V,
1
2 cos A,
2 Ω,
1Ω,
3Ω,
2 H,
F.
?
e t
t
i t
t
R
R
R
L
C
i t
ω
=
=
=
=
=
=
=
=
=
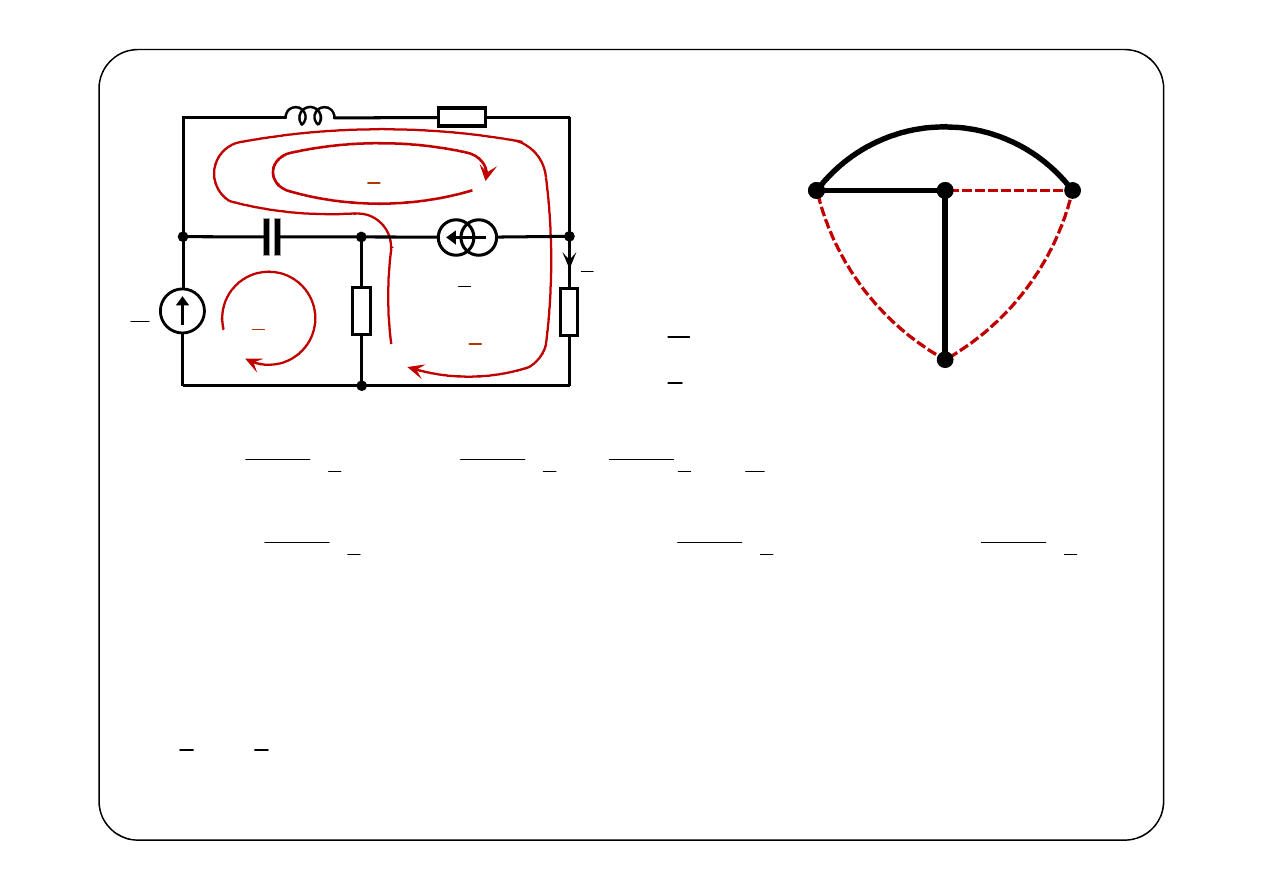
E
z
I
1
R
2
R
3
R
L
C
I
m1
I
m2
I
m3
I
z
2
j
E
I
=
=
1
1
1
R
I
R
I
I
E
+
−
+
−
=
1.
m1
m2
m3
1
1
0
0
0
m1
m2
m3
1
1
2
3
0
3
0
0
0
0
1
1
1
j
j
j
1
1
1
j
j
0
j
j
j
R
I
R
I
I
E
C
C
C
R
I
R
R
R
L
I
R
L
I
C
C
C
ω
ω
ω
ω
ω
ω
ω
ω
+
−
+
−
=
−
+
+
+
+
+
+
+
+
+
=
1.
2.
Dla oczka 3. nie potrafimy napisać równania na podstawie II prawa Kirchhoffa
(nie znamy napięcia na źródle prądowym). Zastępujemy je równaniem
m3
z
I
I
=
3.
Po podstawieniu równania
3.
do
1.
i
2.
i uporządkowaniu
z
1
1
0
0
0
m1
m2
1
1
2
3
0
z
3
0
0
0
0
1
1
1
j
j
j
1
1
1
j
j
j
j
j
E
I
R
R
C
C
C
I
I
R
R
R
R
L
R
L
I
C
C
C
ω
ω
ω
ω
ω
ω
ω
ω
+
+
− −
=
− −
+
+
+
+
−
+
+
m2
I
I
=
m1
m2
j1,107
m2
2
j2
2
j2
4
2
j2
6
j3
0,5
j 1,118e
I
I
I
I
−
−
− +
=
− +
−
=
=
− =
( )
(
)
1,118 2 sin
1,107 A.
i t
t
=
−
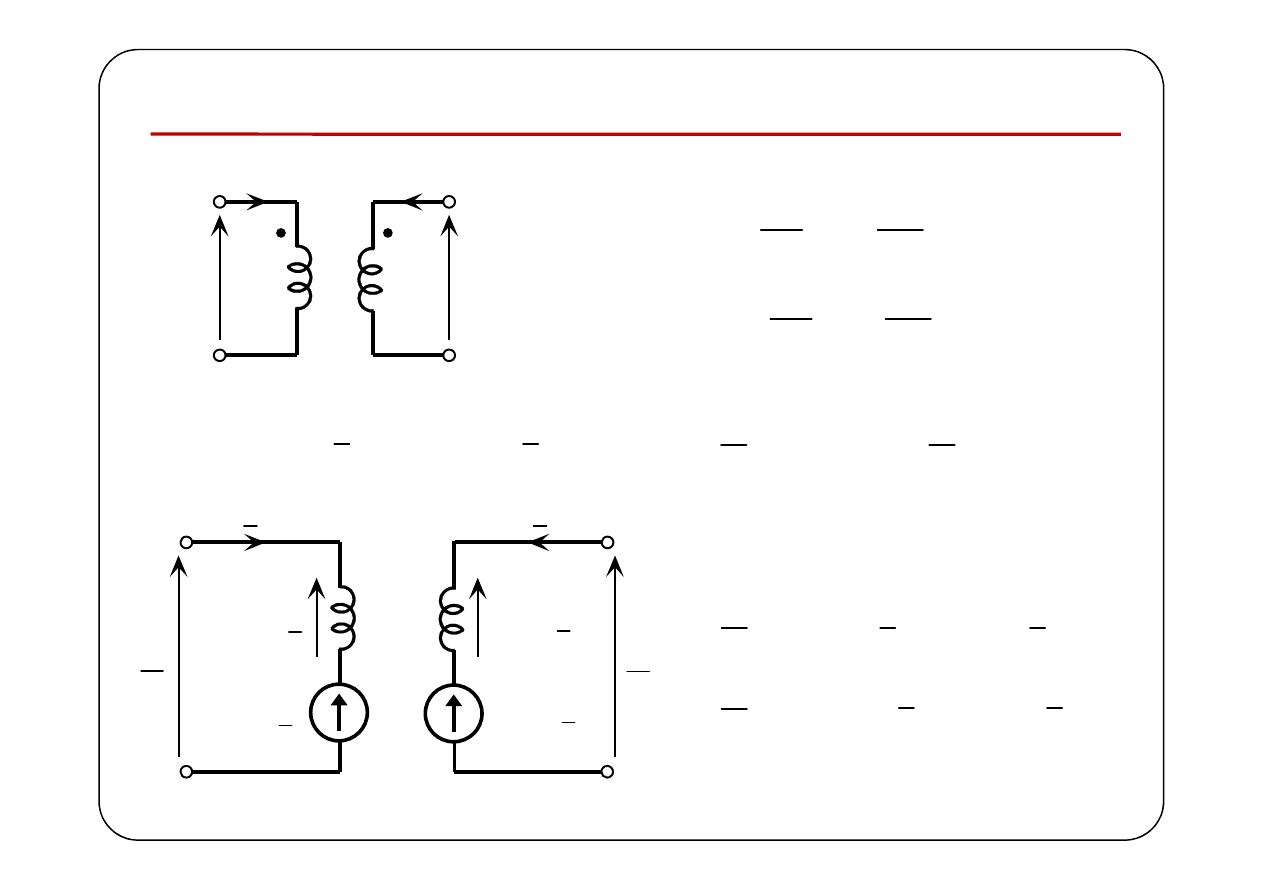
Induktory sprzężone magnetycznie
( )
1
u t
( )
2
u
t
( )
1
i t
( )
2
i t
1
L
2
L
M
( )
( )
1
2
1
1
1
2
2
2
d
d
d
d
d
d
d
d
i
i
u t
L
M
t
t
i
i
u
t
M
L
t
t
=
+
=
+
( )
( )
( )
( )
1
2
1
2
1
2
1
2
i t
I
i t
I
u t
U
u
t
U
⇌
⇌
⇌
⇌
( )
( )
( )
( )
1
2
1
2
1
2
1
2
i t
I
i t
I
u t
U
u
t
U
⇌
⇌
⇌
⇌
1
2
1
0
1
0
1
2
2
0
1
0
2
j
j
j
j
U
L I
M I
U
M I
L I
ω
ω
ω
ω
=
+
=
+
1
U
2
U
1
I
2
I
1
L
2
L
2
0
j
M I
ω
1
0
j
M I
ω
1
0
1
j
L I
ω
2
0
2
j
L I
ω
M — indukcyjność wzajemna, [M] = H
Warunek fizycznej realizowalności:
lub
k — współczynnik sprzężenia
2
1
2
0
L L
M
−
≥
1
2
1
M
k
L L
=
≤
Zaciski jednoimienne (zaznaczone na schemacie np. kropkami) — początki
Zaciski jednoimienne (zaznaczone na schemacie np. kropkami) — początki
(lub końce) uzwojeń. Jeżeli prądy i
1
(t) i i
2
(t) jednocześnie wpływają do
zacisków
jednoimiennych
(lub
wypływają
z
nich),
to
strumienie
magnetyczne wytworzone przez te prądy sumują się.
Reguła strzałkowania źródeł sterowanych pochodzących od sprzężenia:
jeżeli prądy
i
1
(t)
i
i
2
(t)
jednocześnie wpływają do zacisków
jednoimiennych (lub wypływają z nich), to źródła sterowane strzałkujemy
przeciwnie do prądu w gałęzi, w której się znajdują.
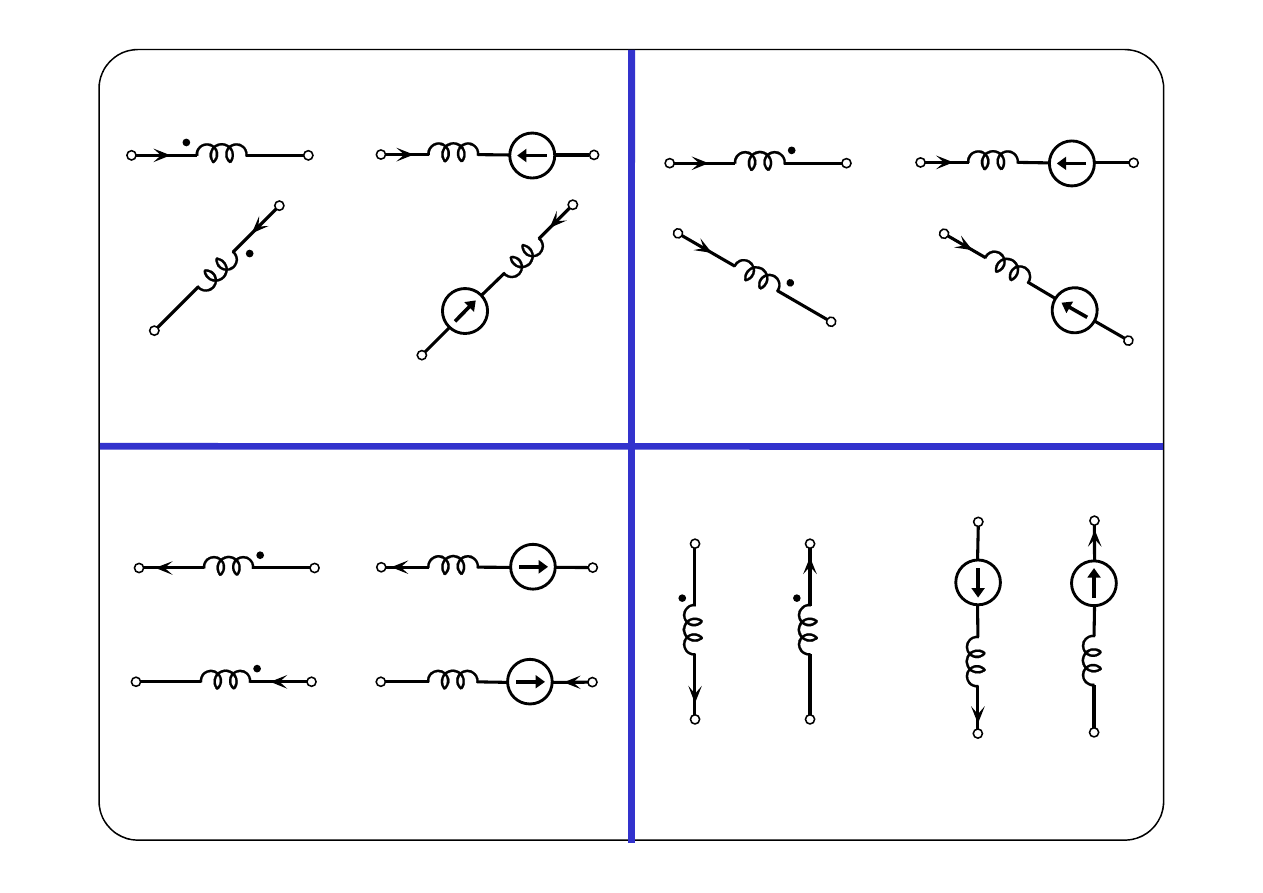
⇌
⇌
⇌
⇌
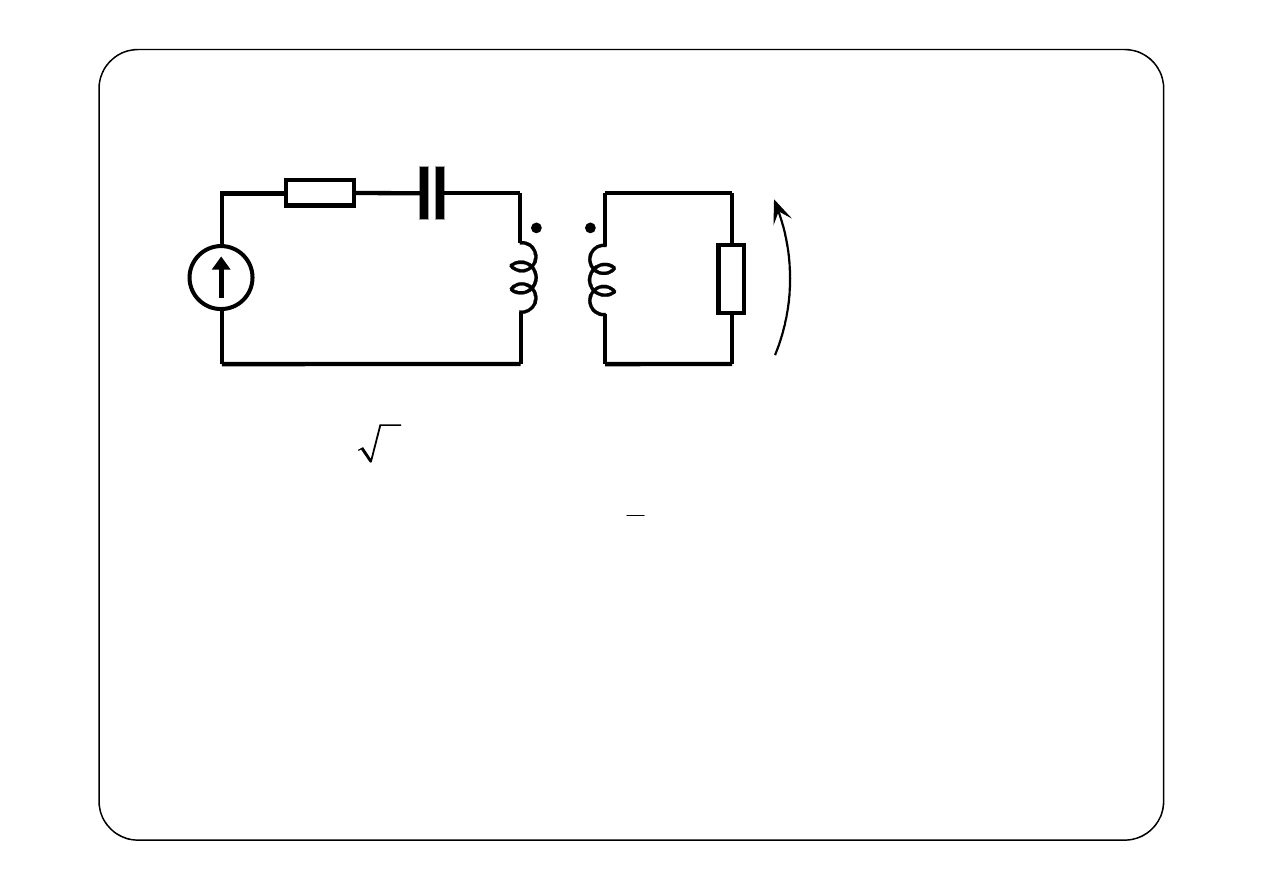
Przykład 1.
( )
e t
1
R
2
R
C
1
L
2
L
M
( )
u t
( )
5 2 sin V,
e t
t
=
( )
( )
1
2
1
2
1
4
5 2 sin V,
2 Ω,
1Ω,
F,
4 H,
2 H,
1H,
?
e t
t
R
R
C
L
L
M
u t
=
=
=
=
=
=
=
=
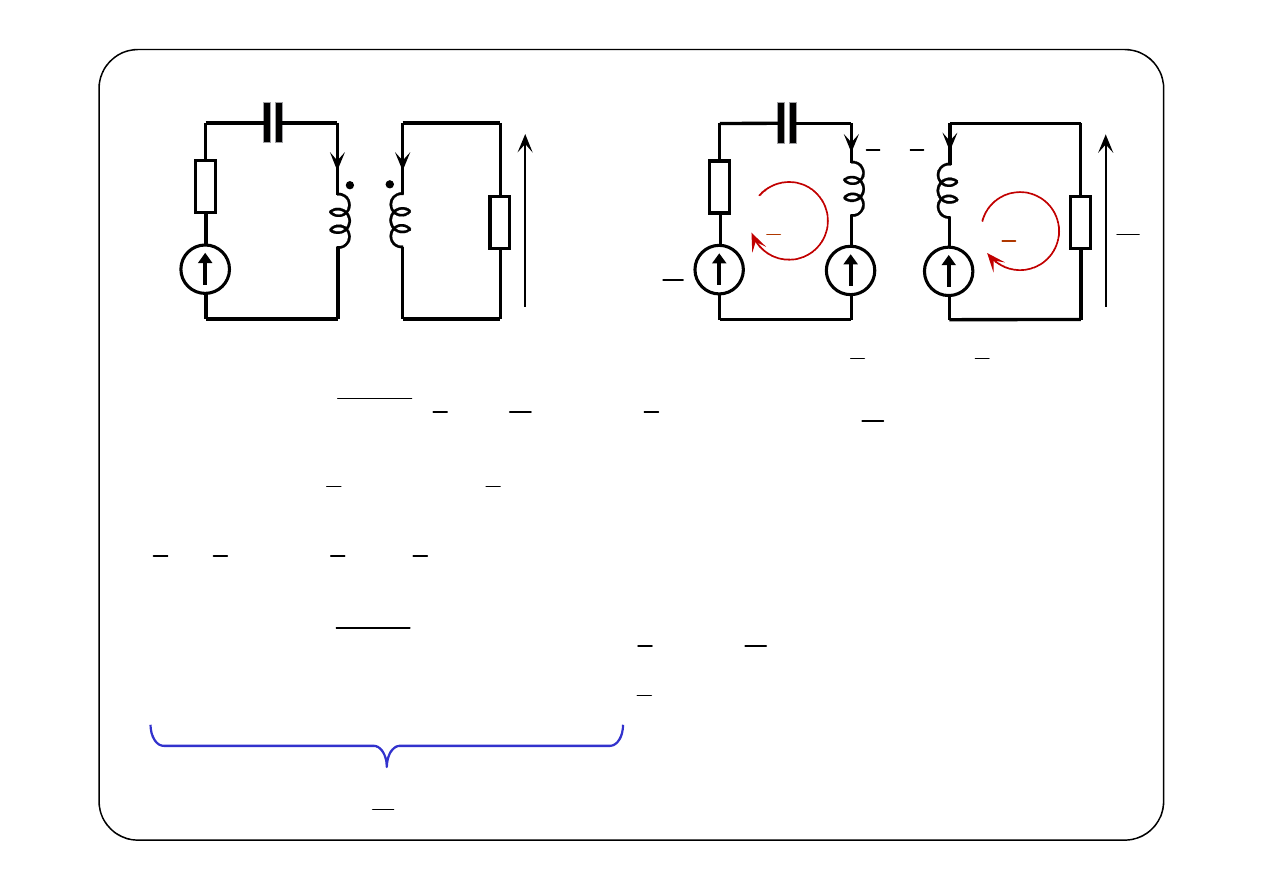
( )
e t
1
R
2
R
C
1
L
2
L
M
( )
u t
( )
1
i t
( )
2
i t
(
)
m1
2
1
0
1
0
0
1
j
j
j
R
L
I
E
M I
C
ω
ω
ω
+
+
= −
E
1
R
2
R
C
1
L
2
L
U
1
I
2
I
2
0
j
M I
ω
1
0
j
M I
ω
m1
I
m2
I
5
E
=
(
)
m2
1
2
0
2
0
j
j
R
L
I
M I
ω
ω
+
=
1
m1
2
m2
,
I
I
I
I
=
= −
1
0
1
0
m1
0
m2
0
2
0
2
1
j
j
j
0
j
j
R
L
M
I
E
C
I
M
R
L
ω
ω
ω
ω
ω
+
+
−
=
−
+
m
Z

( )
(
)
m1
m2
m2
j 0,6435
m2
2
2
j
5
j
1 2 j
0
0,8
j0, 6
0,8
j0, 6
e
2 sin
0, 6435 V.
I
I
I
U
R I
u t
t
−
=
−
+
=
+
=
=
+
=
=
+
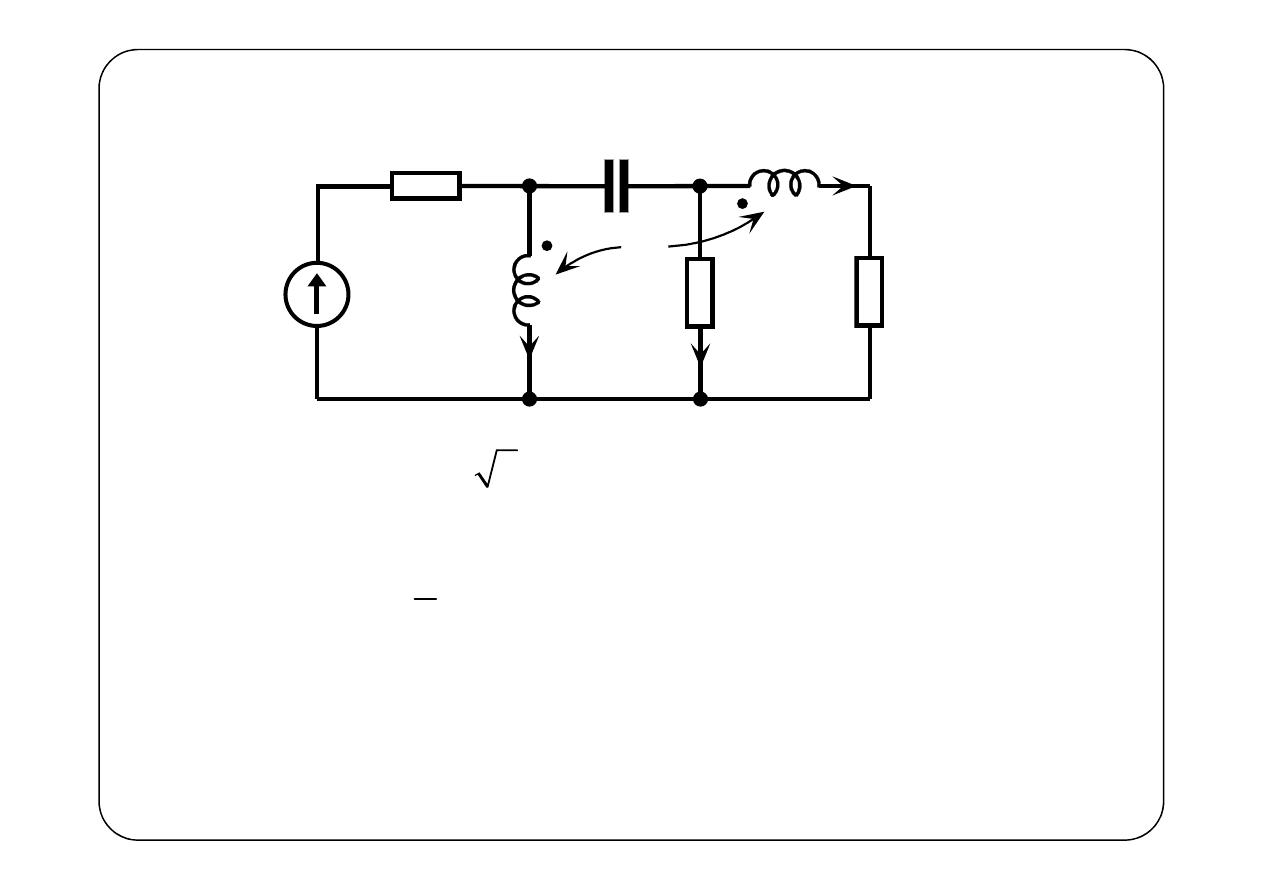
Przykład 2.
M
( )
e t
1
R
1
L
C
2
R
3
R
2
L
( )
1
i t
( )
2
i t
( )
i t
( )
( )
1
2
3
1
2
15 2 sin V,
1Ω,
1Ω,
1Ω,
2 F,
1
H,
4 H,
1H.
2
?
e t
t
R
R
R
C
L
L
M
i t
=
=
=
=
=
=
=
=
=
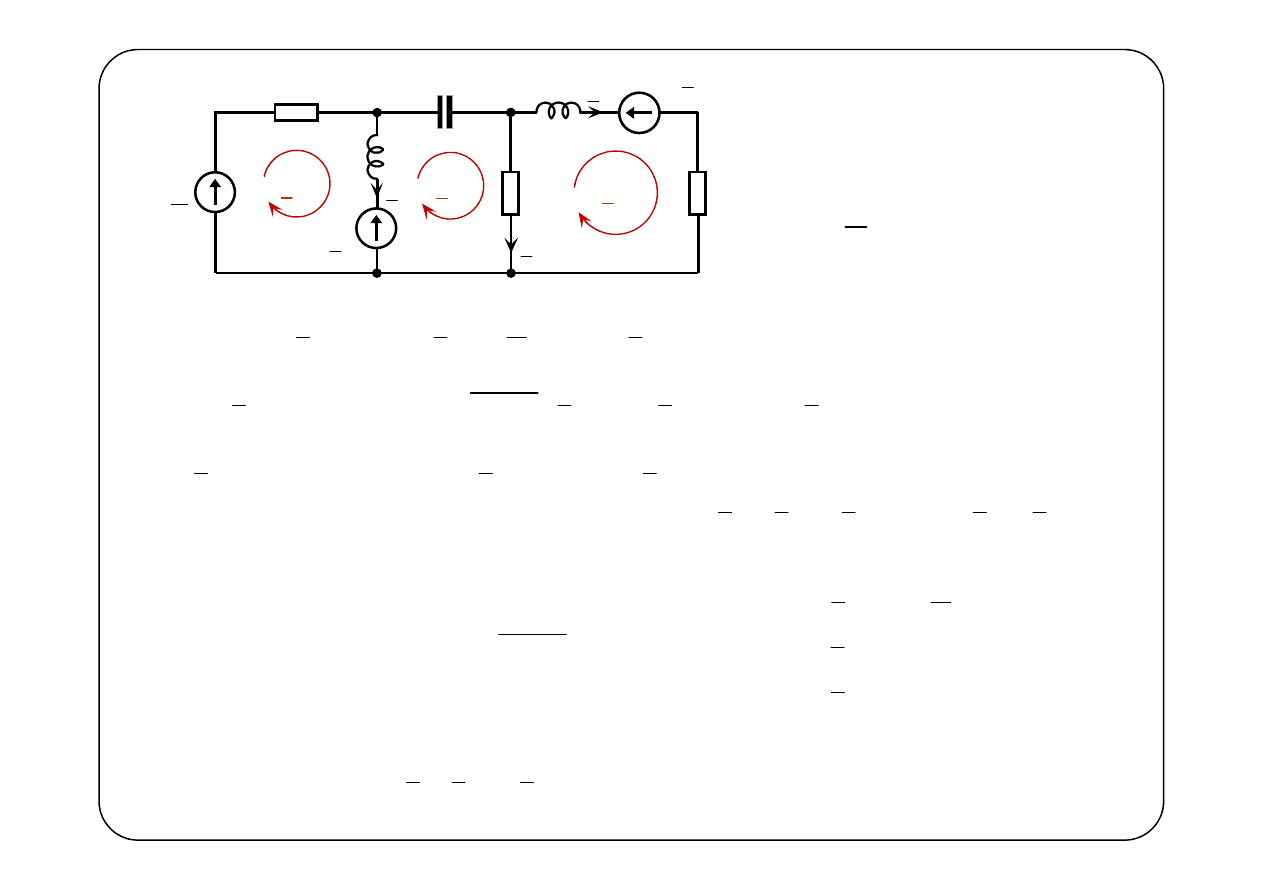
1
R
E
C
1
L
2
L
2
R
3
R
1
I
2
I
1
0
j
M I
ω
2
0
j
M I
ω
m1
I
m2
I
m3
I
I
15
E
=
(
)
(
)
m1
m2
2
1
0
1
0
1
0
m1
m2
m3
2
0
1
2
0
1
2
0
0
j
j
j
1
j
j
j
j
j
j
R
L I
L I
E
M I
L I
R
L
I
R I
M I
C
R I
R
R
L
I
M I
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
= −
−
+
+
+
−
=
−
+
+
+
= −
(
)
m2
m3
1
2
2
3
0
2
0
j
j
R I
R
R
L
I
M I
ω
ω
−
+
+
+
= −
1
m1
m2
2
m3
I
I
I
I
I
=
−
=
1
0
1
0
1
0
m1
m2
0
1
2
0
1
2
0
0
m3
0
2
0
2
3
0
2
j
j
j
1
j
j
j
0
j
0
j
j
j
R
L
L
M
I
E
L
R
L
R
M
I
C
I
M
R
M
R
R
L
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
+
− −
=
− −
+
+
m2
m3
I
I
I
=
−

m1
m2
m3
1
j0,5
j0,5
j
15
j0,5
1
1
j
0
j
1
j
2
j4
0
I
I
I
+
−
−
− −
=
− −
+
m2
m3
2
j4
3
j
I
I
= − +
= − +
j1,249
1
j3
3,162e
I
I
I
=
−
= +
=
j1,249
m2
m3
1
j3
3,162e
I
I
I
=
−
= +
=
( )
(
)
3,162 2 sin
1, 249 A.
i t
t
=
+
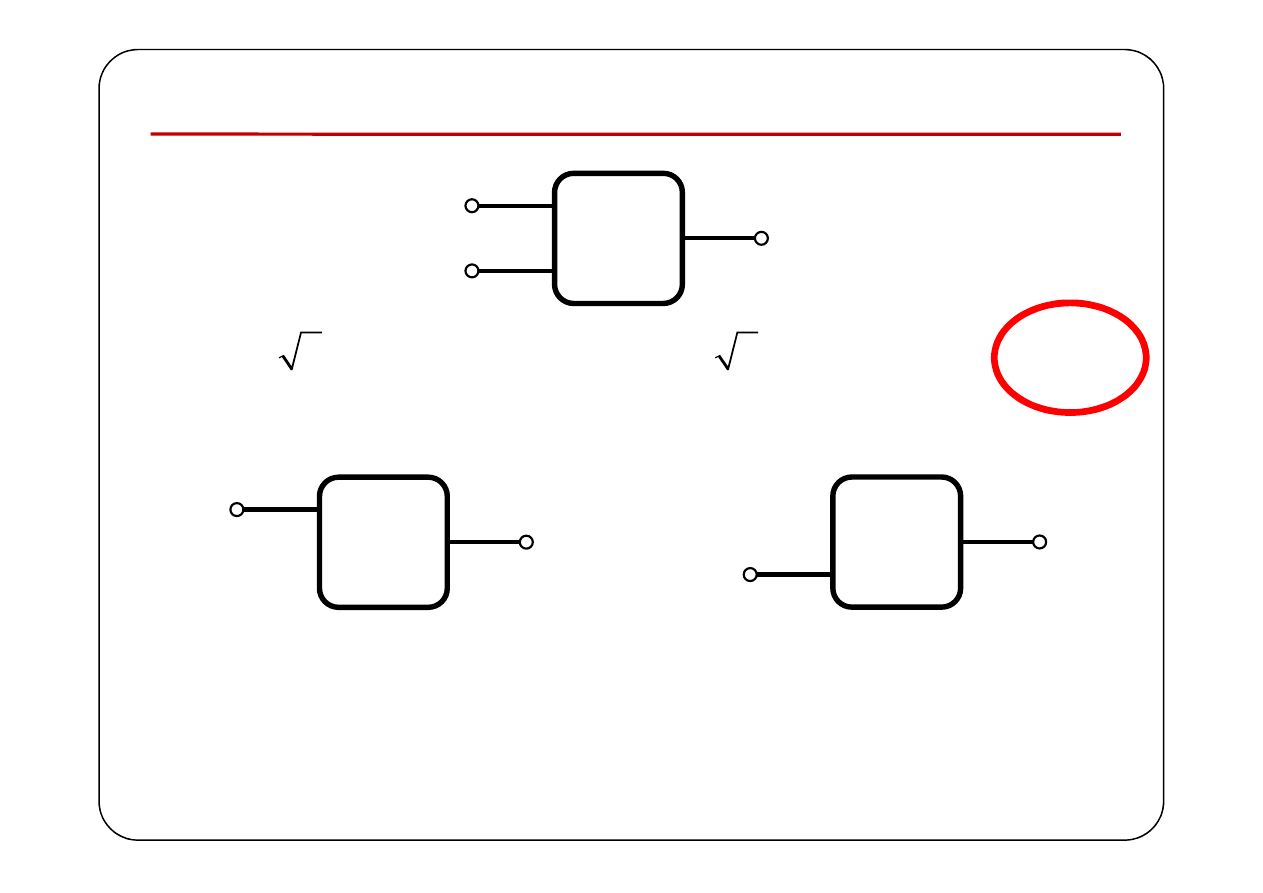
Pobudzenia sinusoidalne o różnych pulsacjach
SLS
( )
1
p t
( )
2
p t
( )
r t
( )
(
)
( )
(
)
1
1
01
1
2
2
02
2
01
02
2 sin
,
2 sin
,
p t
P
t
p t
P
t
ω
θ
ω
θ
ω
ω
=
+
=
+
≠
Nie wolno zastosować metody symbolicznej!
SLS
( )
1
p t
( )
1
r t
SLS
( )
2
p t
( )
2
r t
( )
2
0
p
t
=
( )
1
0
p t
=
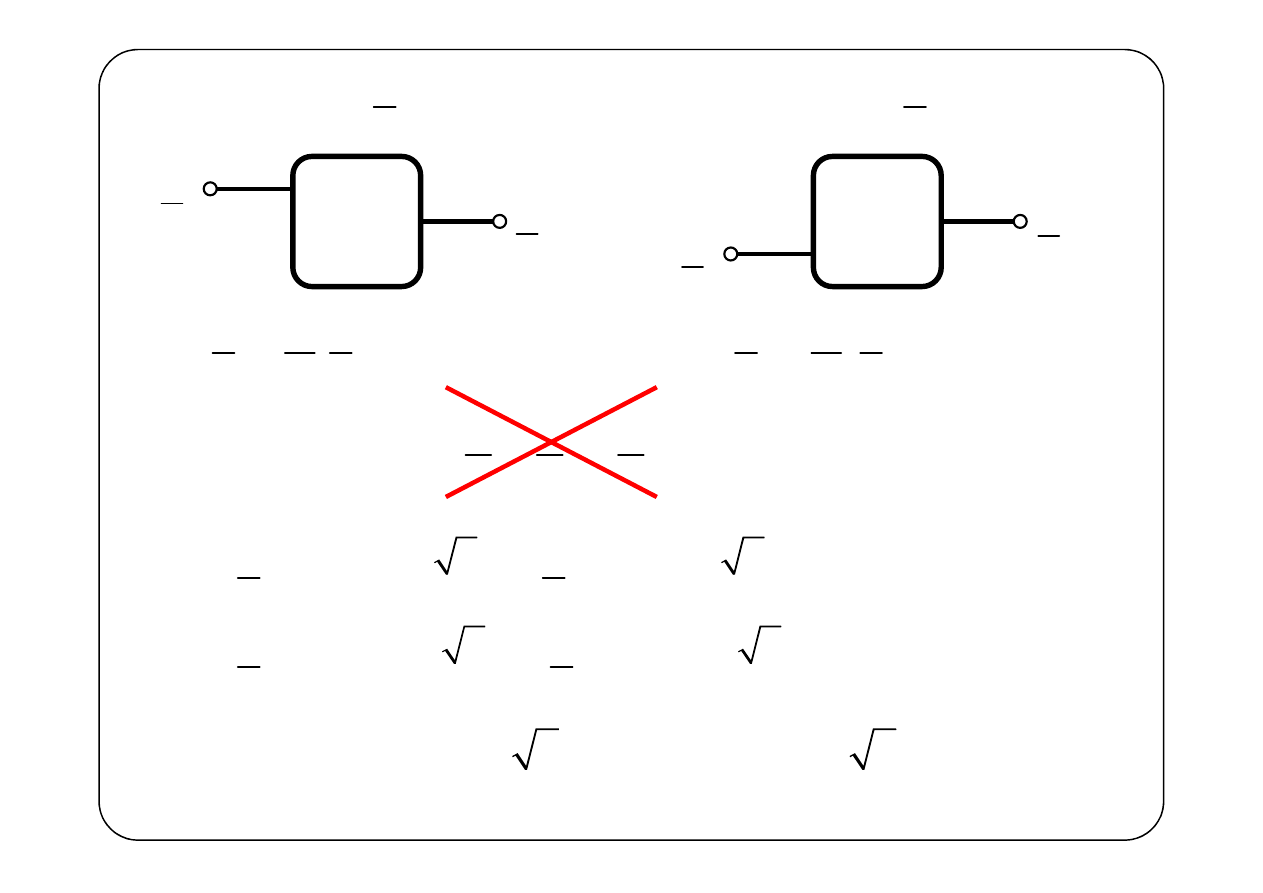
Każdy z powyższych układów można analizować metodą symboliczną
Zgodnie z twierdzeniem o superpozycji:
( ) ( ) ( )
1
2
r t
r t
r t
=
+
SLS
1
P
1
R
( )
1
1
01
;
p t
P
ω
⇌
1
j
1
1
1
1
e
R
H P
R
η
=
=
( )
2
2
02
;
p t
P
ω
⇌
SLS
2
P
2
R
2
j
2
2
2
2
e
R
H P
R
η
=
=
1
2
R
R
R
=
+
Źle!!!
1
2
R
R
R
=
+
Źle!!!
( )
{
}
(
)
( )
{
}
(
)
01
02
j
1
1
1
1
01
1
j
2
2
2
2
02
2
2 Im
e
2 sin
2 Im
e
2 sin
R
r t
R
R
t
R
r t
R
R
t
ω
ω
ω
η
ω
η
=
=
+
=
=
+
⇌
⇌
( ) ( ) ( )
(
)
(
)
1
2
1
01
1
2
02
2
2 sin
2 sin
r t
r t
r t
R
t
R
t
ω
η
ω
η
=
+
=
+
+
+
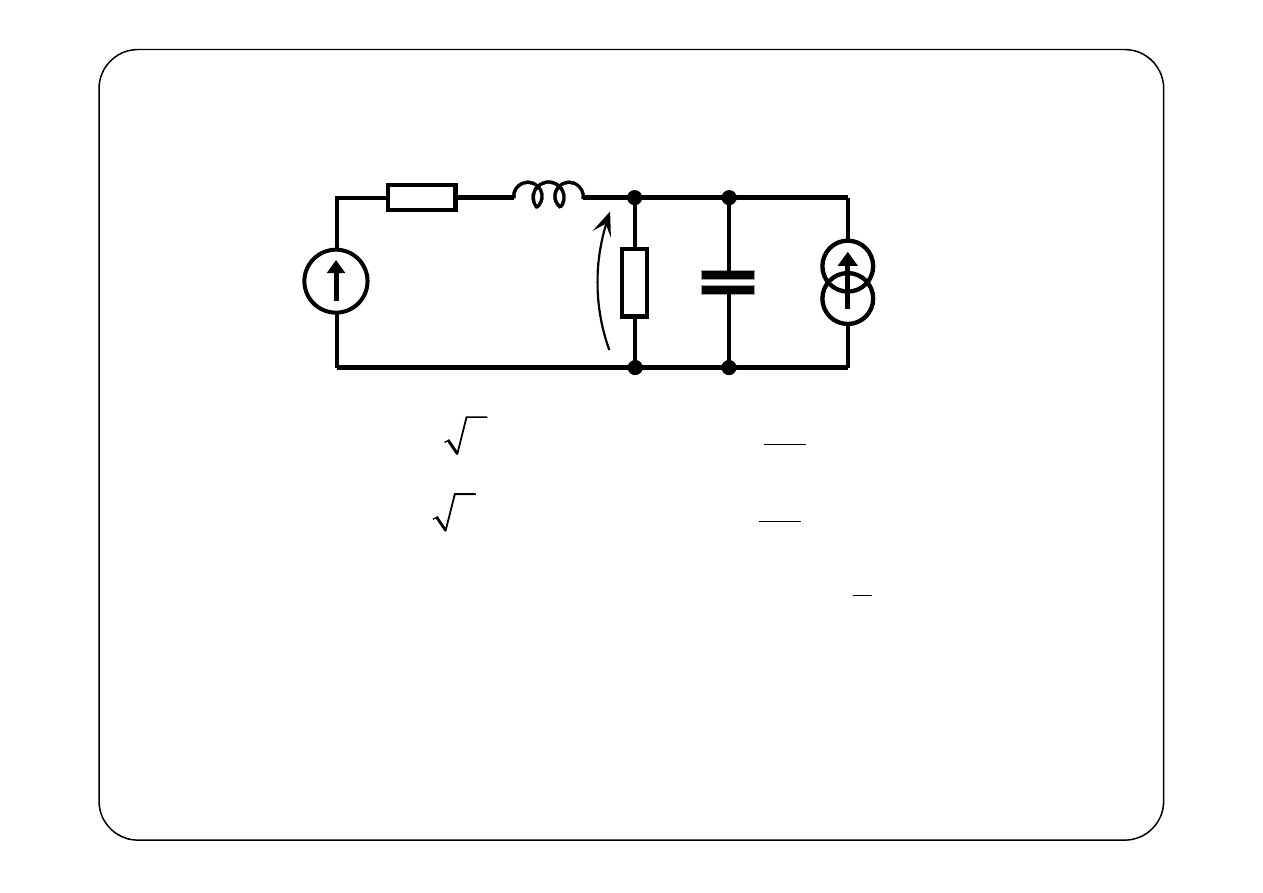
Przykład 1.
( )
e t
( )
z
i t
1
R
2
R
L
C
( )
u t
( )
(
)
01
rad
s
2 2 sin 2 V,
2
e t
t
ω
=
=
( )
(
)
( )
(
)
( )
01
z
02
1
2
s
rad
s
1
2
2 2 sin 2 V,
2
2 cos A,
1
1Ω,
2Ω,
1H,
F.
?
e t
t
i t
t
R
R
L
C
u t
ω
ω
=
=
=
=
=
=
=
=
=
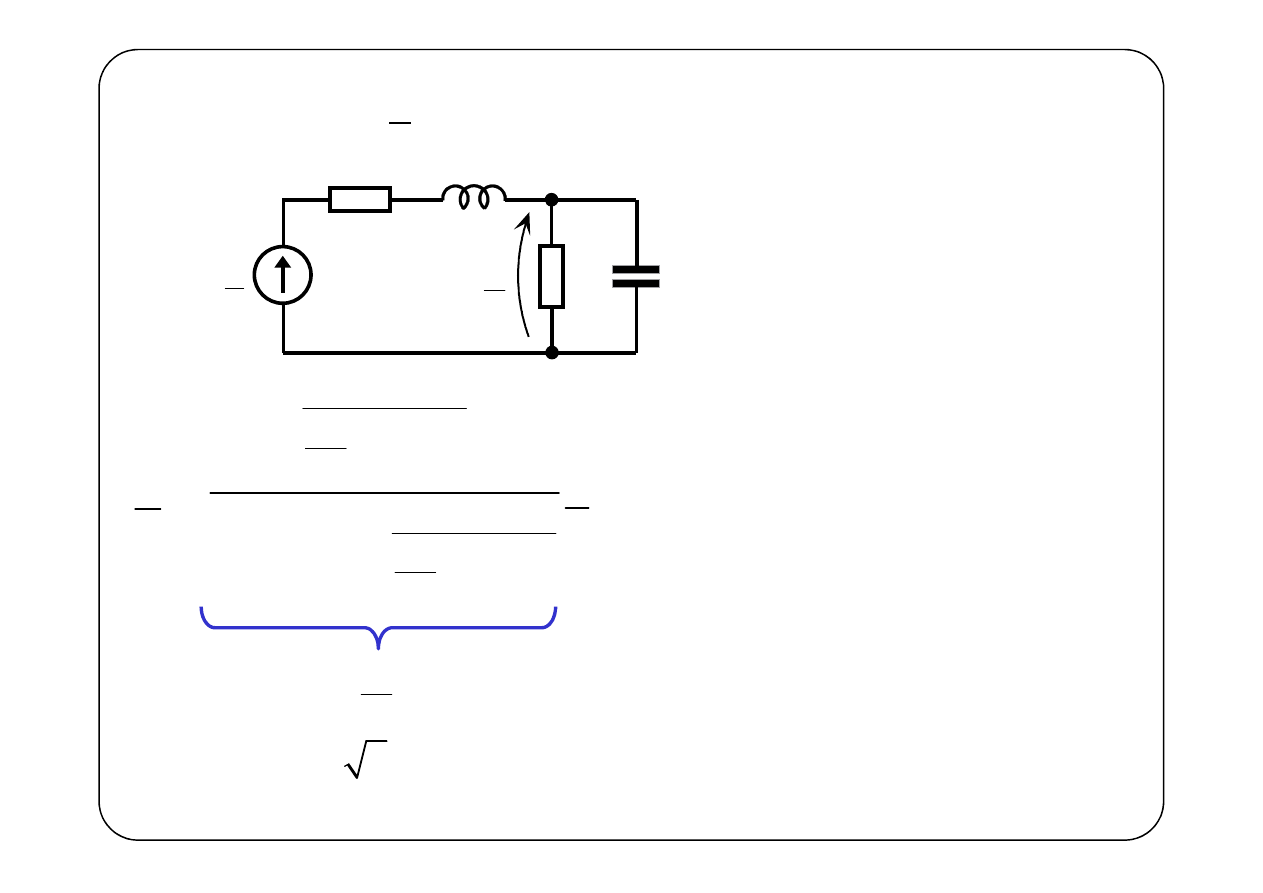
A.
i
z
(t) = 0, E = 2;
ω
01
= 2
E
1
R
2
R
L
C
U
′
1
1
j
C
ω
+
01
j1,816
2
1
01
01
2
1
j
0, 2353
j0, 9412
0, 9702e
1
j
1
j
C
R
U
E
R
L
C
R
ω
ω
ω
−
+
′ =
= −
−
=
+
+
+
( )
(
)
0, 9702 2 sin 2
1,816
u t
t
′
=
−
1
H
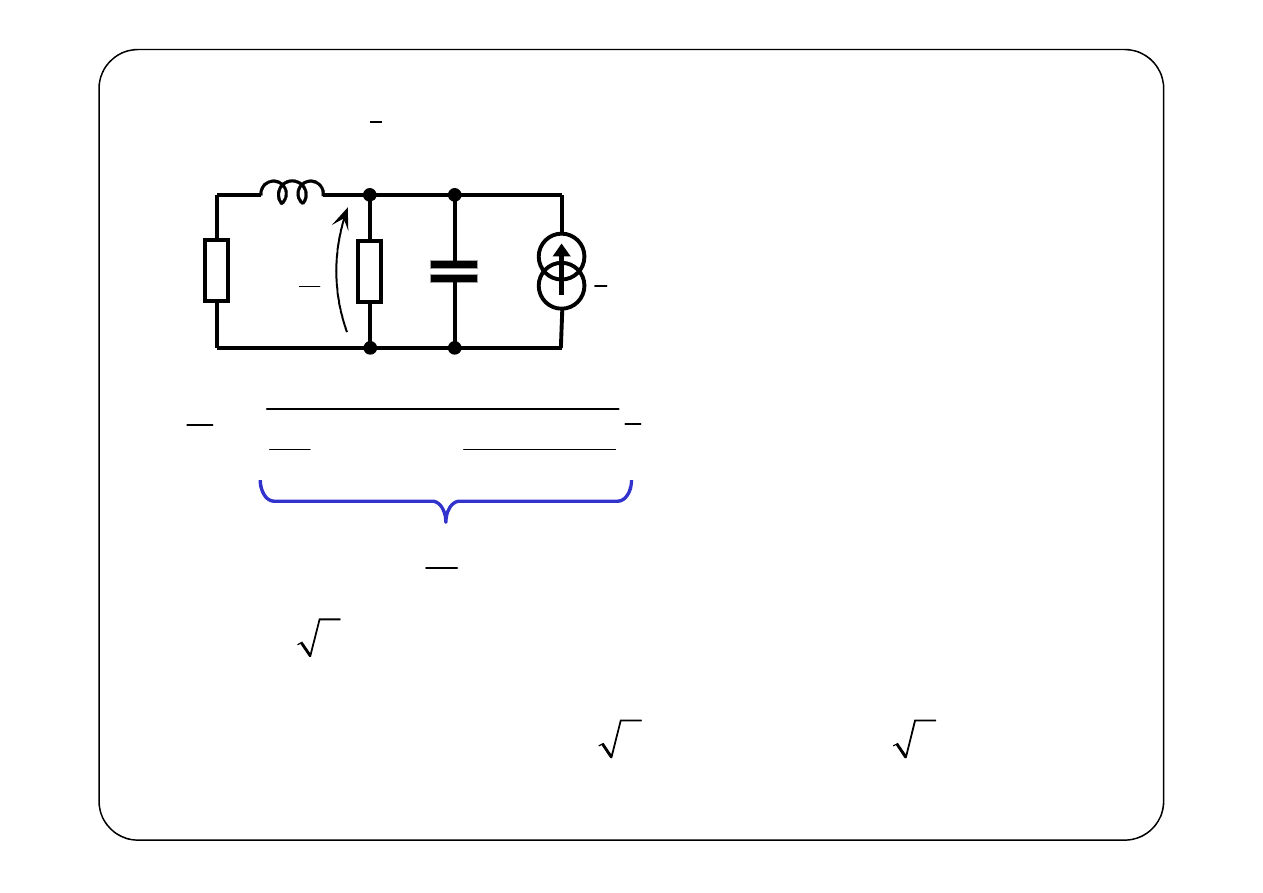
B.
e(t) = 0, I
z
= j;
ω
02
= 1
z
I
1
R
2
R
L
C
U
′′
z
1
j
1
1
j
U
I
C
ω
ω
′′ =
=
+
+
+
02
2
1
02
1
1
j
j
C
R
R
L
ω
ω
+
+
+
( )
2 cos
u t
t
′′
=
( )
( )
( )
(
)
0, 9702 2 sin 2
1,816
2 cos V.
u t
u t
u t
t
t
′
′′
=
+
=
−
+
2
H
Moc w obwodzie przy pobudzeniu sinusoidalnym
Dwójnik
SLS
( )
u t
( )
i t
Moc chwilowa dostarczona do dwójnika:
( ) ( ) ( )
p t
u t i t
=
Zakładamy, że prąd i napięcie mają postać:
( )
(
)
( )
(
)
0
i
0
u
2 sin
2 sin
i t
I
t
u t
U
t
ω
ψ
ω
ψ
=
+
=
+
Zakładamy, że prąd i napięcie mają postać:
( )
(
) (
)
0
u
0
i
2
sin
sin
p t
UI
t
t
ω
ψ
ω
ψ
=
+
+
=
(
)
(
)
2sin sin
cos
cos
x
y
x
y
x
y
=
− −
+
(
)
(
)
u
i
0
u
i
cos
cos 2
UI
UI
t
ψ ψ
ω
ψ ψ
=
−
−
+
+
U
I
Z
u
i
j
j
j
e
e
j
e
U
U
I
I
Z
R
X
Z
ψ
ψ
ϕ
=
=
= +
=
(
)
u
i
j
j
j
j
u
i
e
e
e
e
,
,
i
U
Z I
Z
I
ZI
U
U
ZI
ϕ ψ
ψ
ψ
ϕ
ψ
ϕ ψ
+
=
=
=
=
=
= +
u
i
( )
(
)
0
i
cos
cos 2
2
p t
UI
UI
t
ϕ
ω
ψ ϕ
=
−
+
+
( )
p t
t
Wartość średnia
P
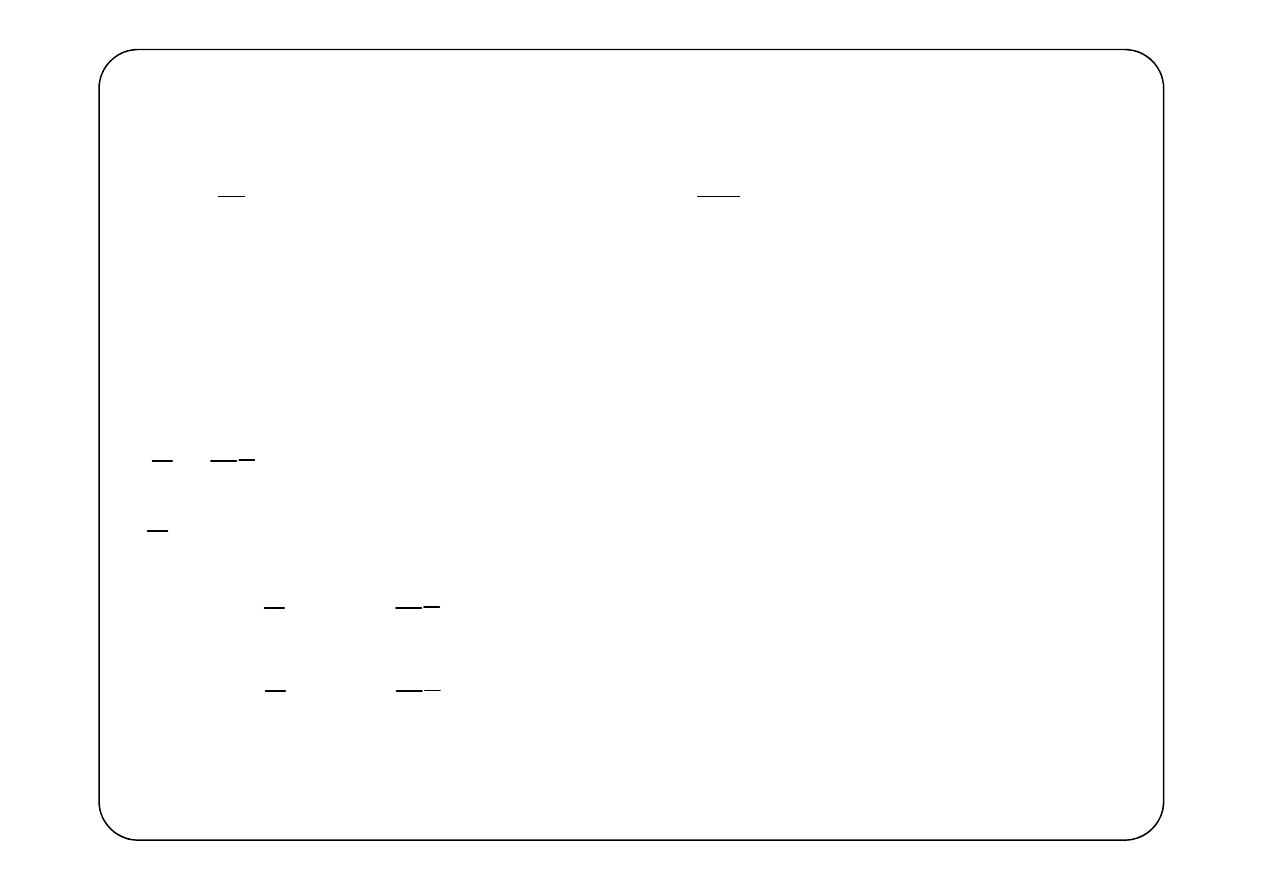
Wartość średnia mocy chwilowej
( )
0
0
0
1
2π
d
cos
,
t
T
t
P
p t
t
UI
T
T
ϕ
ω
+
=
=
=
∫
P — moc czynna, [P] = W
cos
ϕ
— współczynnik mocy
u
i
j
j
j
e
e
e
cos
j
sin
j
S
U I
U
I
UI
UI
UI
P
Q
ψ
ψ
ϕ
ϕ
ϕ
−
∗
=
=
=
+
= +
≜
u
i
e
e
e
cos
j
sin
j
S
U I
U
I
UI
UI
UI
P
Q
ϕ
ϕ
=
=
=
+
= +
≜
S
— moc pozorna zespolona
{ }
{ }
{ }
{ }
Re
Re
cos
Im
Im
sin
P
S
U I
UI
Q
S
U I
UI
ϕ
ϕ
∗
∗
=
=
=
=
=
=
Q — moc bierna, [Q] = VAr
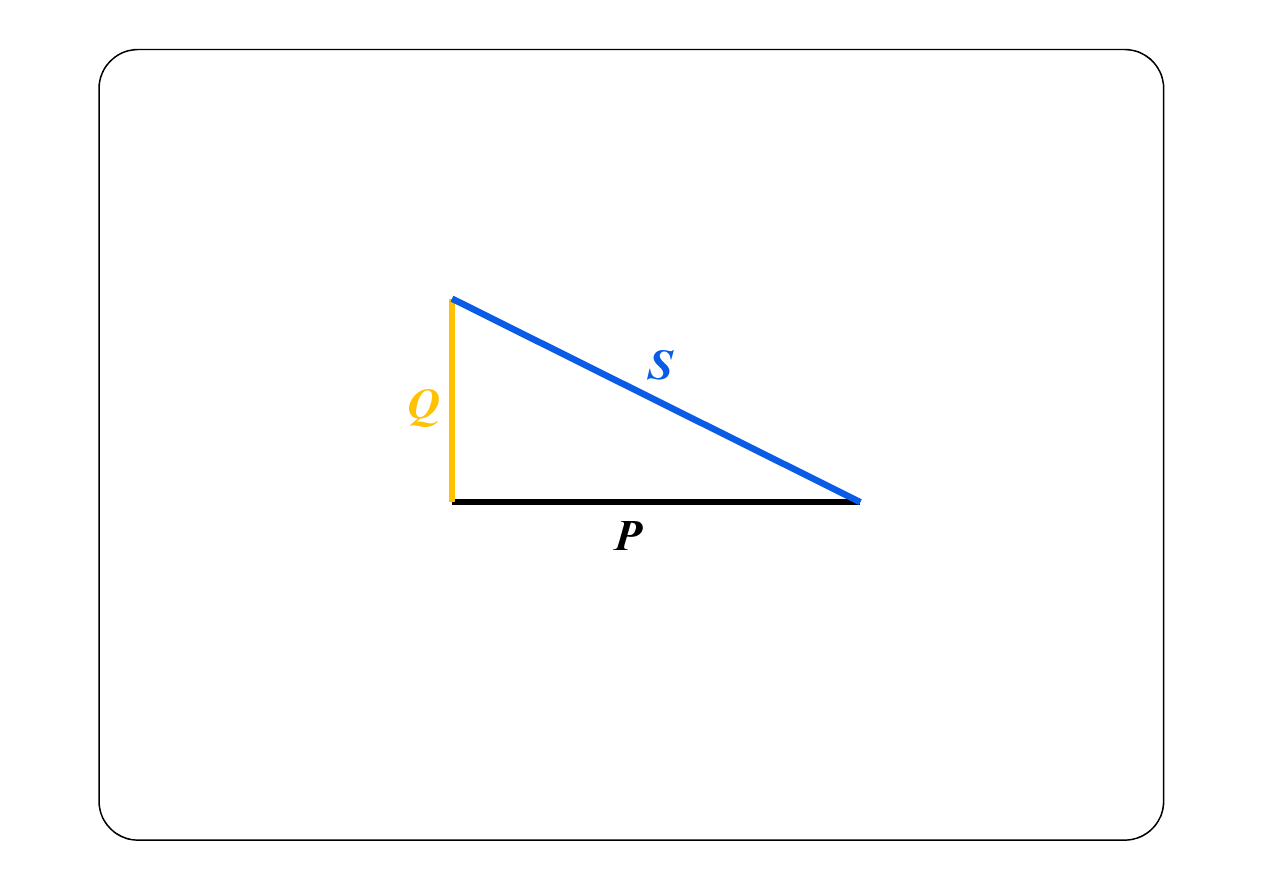
2
2
2
S
P
Q
=
+
S — moc pozorna, [S] = VA
„Trójkąt mocy”
cos
sin
S
I
U
I
U
I
Q
P
U
ϕ
ϕ
=
=
=
moc pozorna
moc czynna
moc bierna
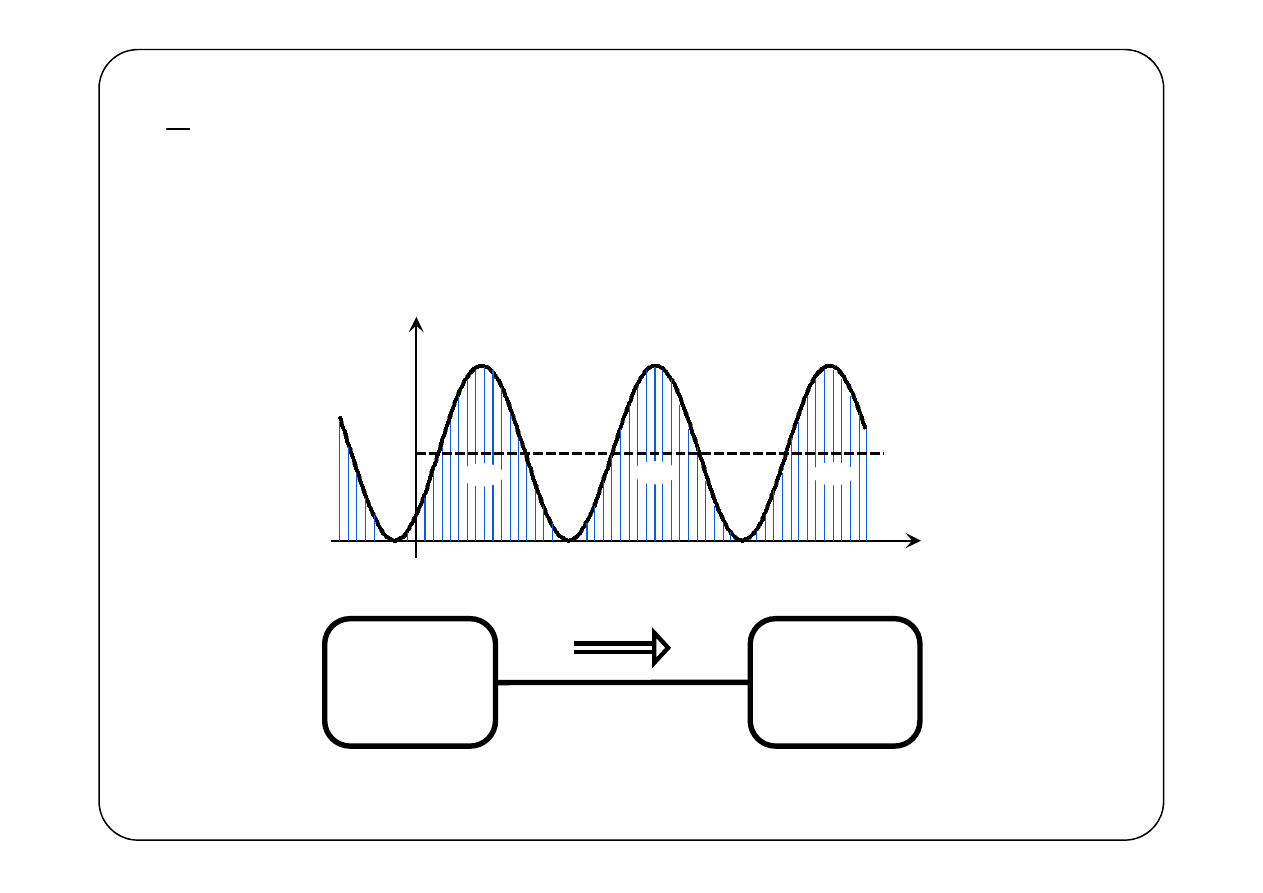
0
0,
cos
1
Z
R
ϕ
ϕ
= >
⇒
=
=
( )
(
)
0
i
cos 2
2
p t
UI
UI
t
P
UI
ω
ψ
=
−
+
=
( )
p t
P
+
+
+
t
P
Generator
Odbiornik
P
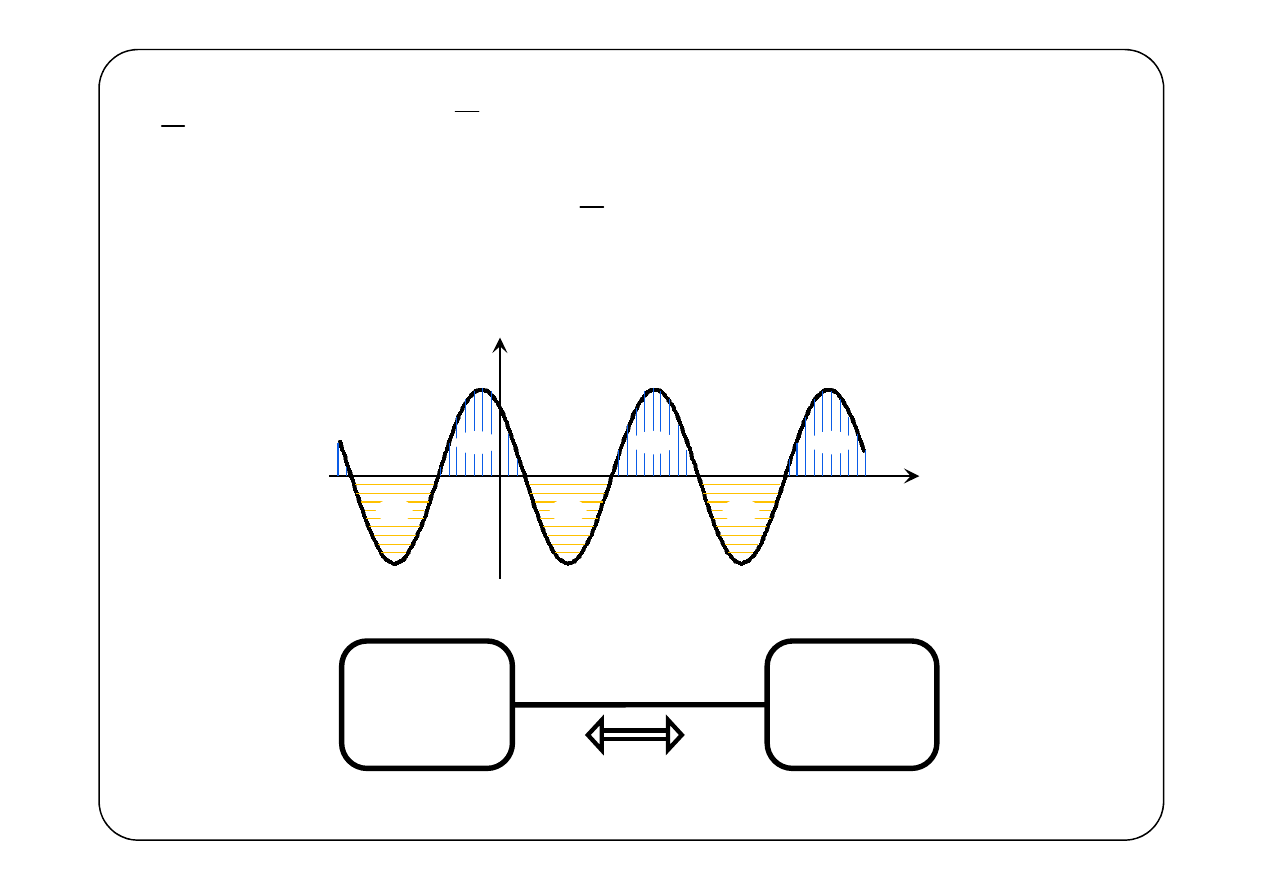
π
j
,
cos
0
2
Z
X
ϕ
ϕ
=
⇒
= ±
=
( )
(
)
0
i
0
i
π
cos 2
2
sin 2
2
2
0
p t
UI
t
UI
t
P
ω
ψ
ω
ψ
= −
+
±
= ±
+
=
+
+
+
( )
p t
t
+
+
+
t
−−−−
−−−−
−−−−
Generator
Odbiornik
0
P
=
Q
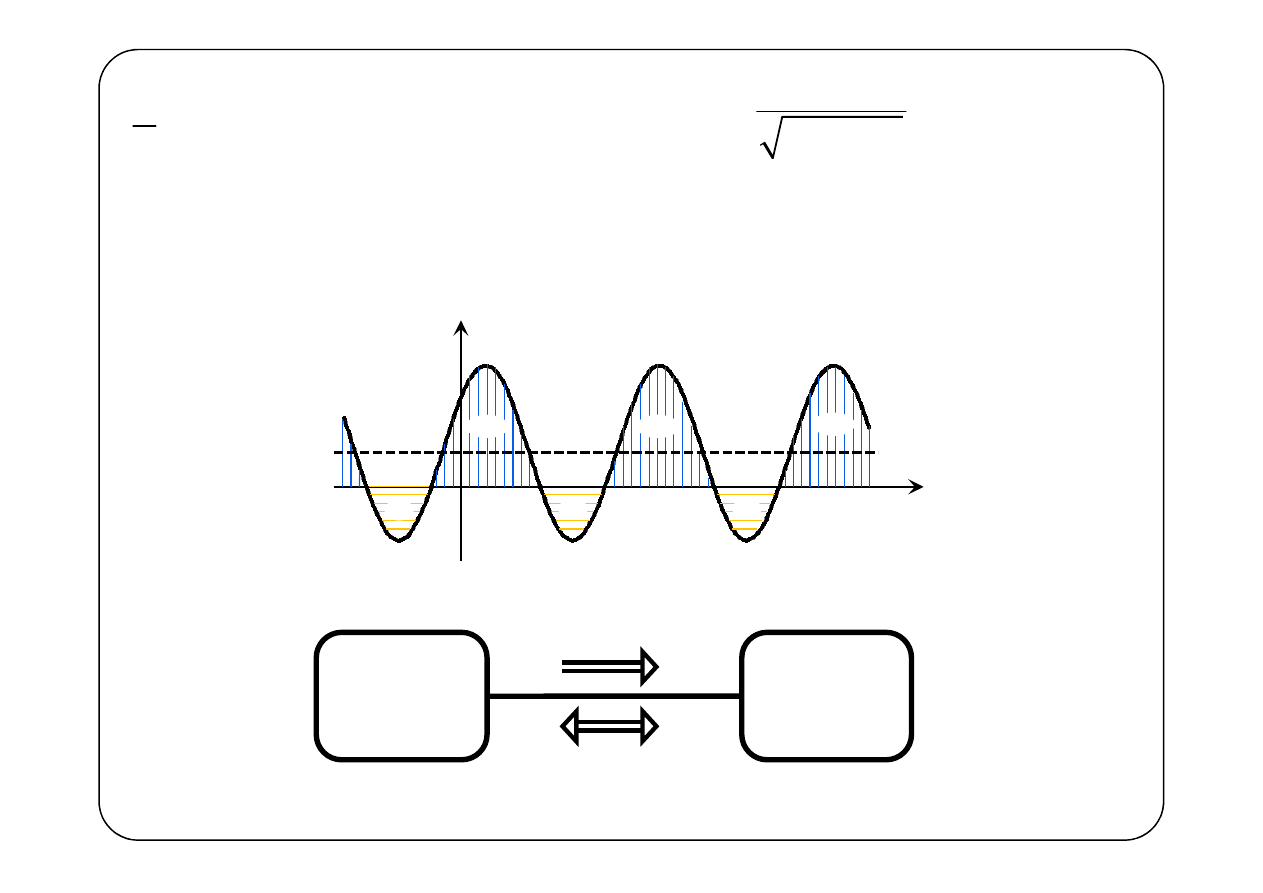
2
2
j
,
0,
0
cos
,
0
cos
1
R
Z
R
X
R
X
R
X
ϕ
ϕ
= +
>
≠
⇒
=
<
<
+
( )
(
)
0
i
cos
cos 2
2
cos
p t
UI
UI
t
P
UI
ϕ
ω
ψ ϕ
ϕ
=
−
+
+
=
+
+
+
( )
p t
P
t
−−−−
−−−−
−−−−
Generator
Odbiornik
P
Q
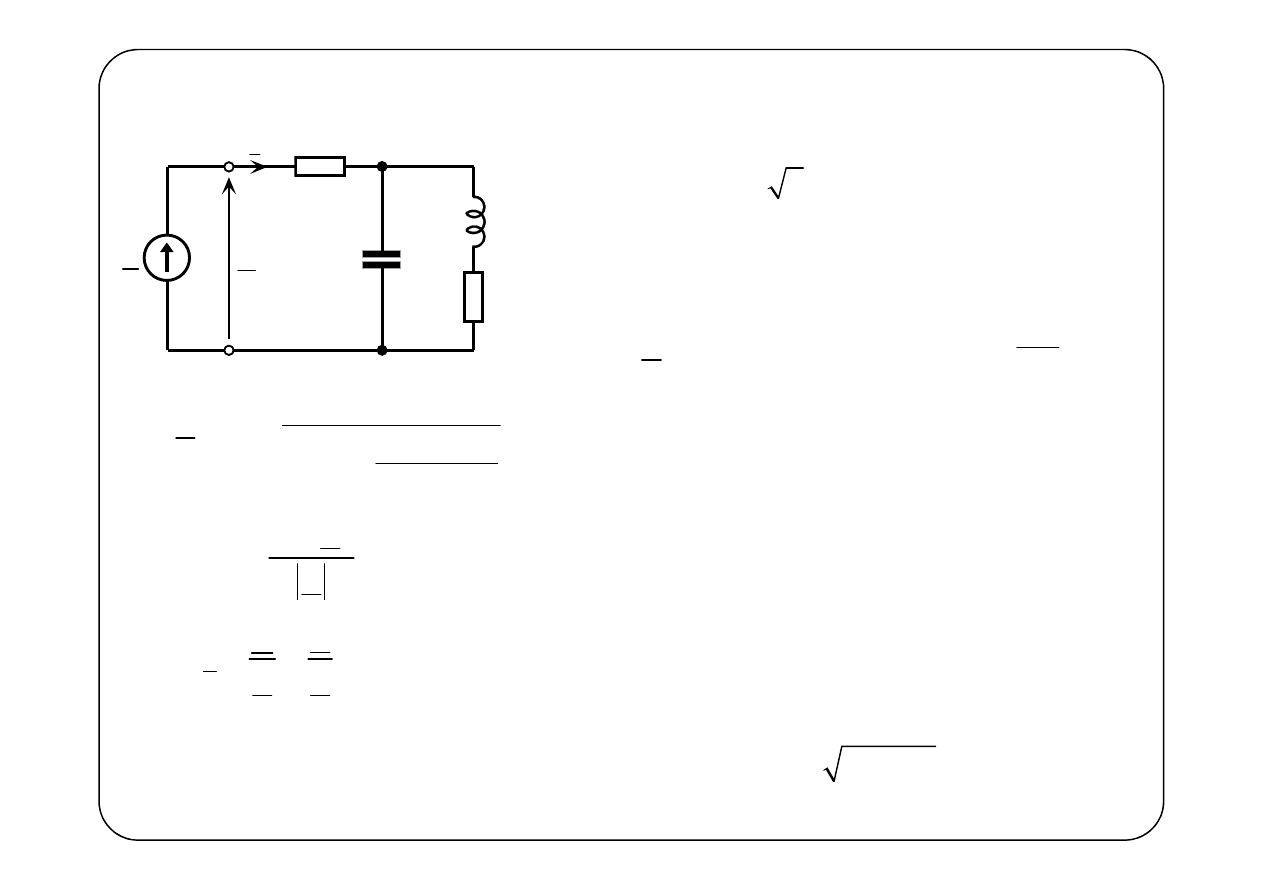
Przykład
E
1
R
2
R
L
C
I
U
( )
0
0
1
2
0
0
230 2 sin
V,
50 Hz,
1kΩ,
100 Ω,
5 H,
20 nF.
rad
230 V,
2π
100π
e t
t
f
R
R
L
C
E
f
s
ω
ω
=
=
=
=
=
=
=
=
=
(
)
1
1
1102
j1587 Ω
1
j
Z
R
C
ω
=
+
=
+
+
{ }
0
2
0
1
j
j
Re
cos
0, 5074
C
R
L
Z
Z
ω
ω
ϕ
+
+
=
=
j
j0,964
0, 0679
j0,978
0,119e
e
i
U
E
I
I
Z
Z
ψ
−
=
=
=
−
=
=
2
2
27, 4 VA,
cos
15, 6 W,
22, 5 VAr
S
EI
P
EI
Q
S
P
ϕ
=
=
=
=
=
−
=
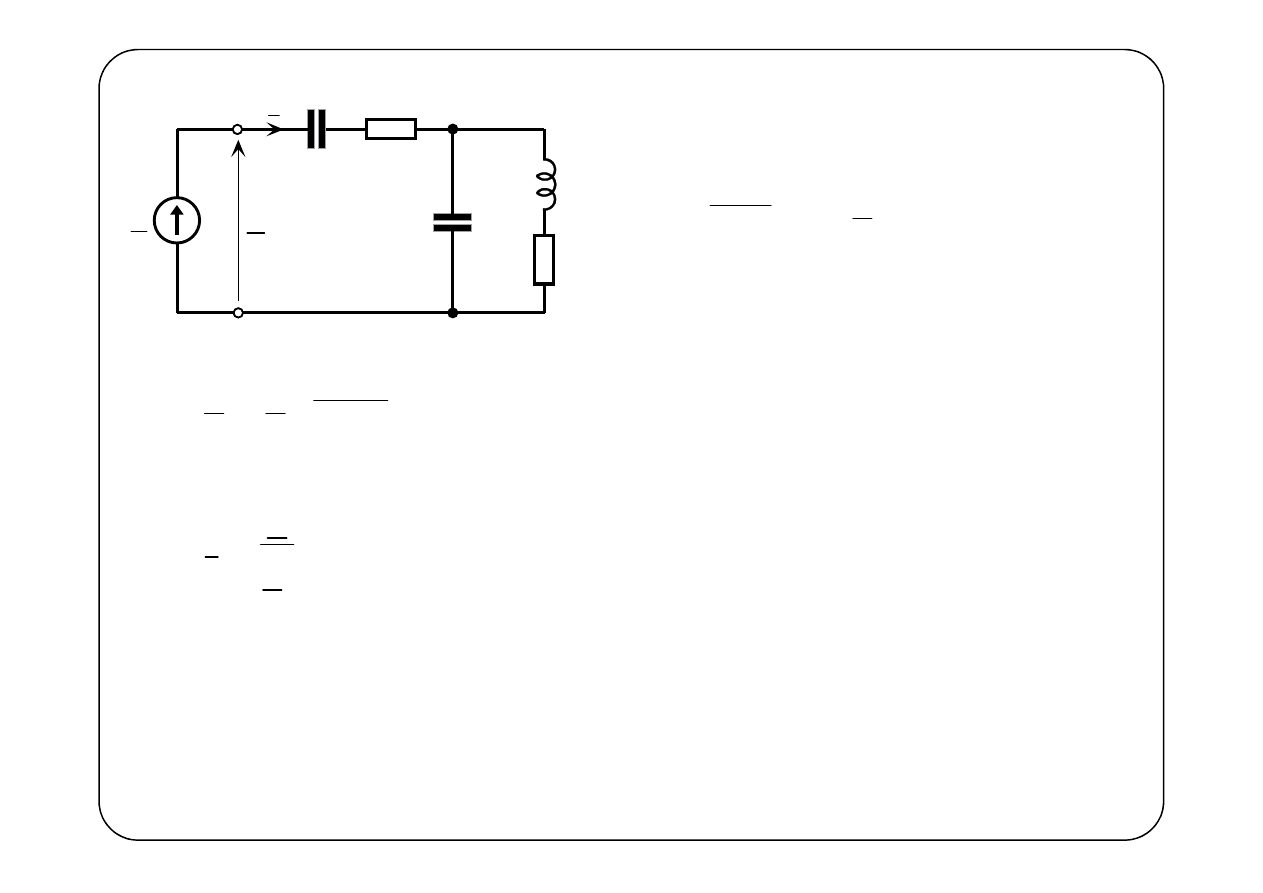
E
1
R
2
R
L
C
I
′
U
C
′
{ }
0
6
1
Im
1587
2 10 F
Z
C
C
ω
−
=
=
′
′ ≈ ⋅
0
1
1102 Ω
j
Z
Z
C
ω
′ = +
=
′
cos
1
ϕ
=
0, 209 A
E
I
Z
′ =
=
′
48 VA,
cos
48 W,
0
S
EI
P
EI
Q
ϕ
′
′
′
′
′
=
=
=
=
=
,
I
I
P
P
′
′
>
>
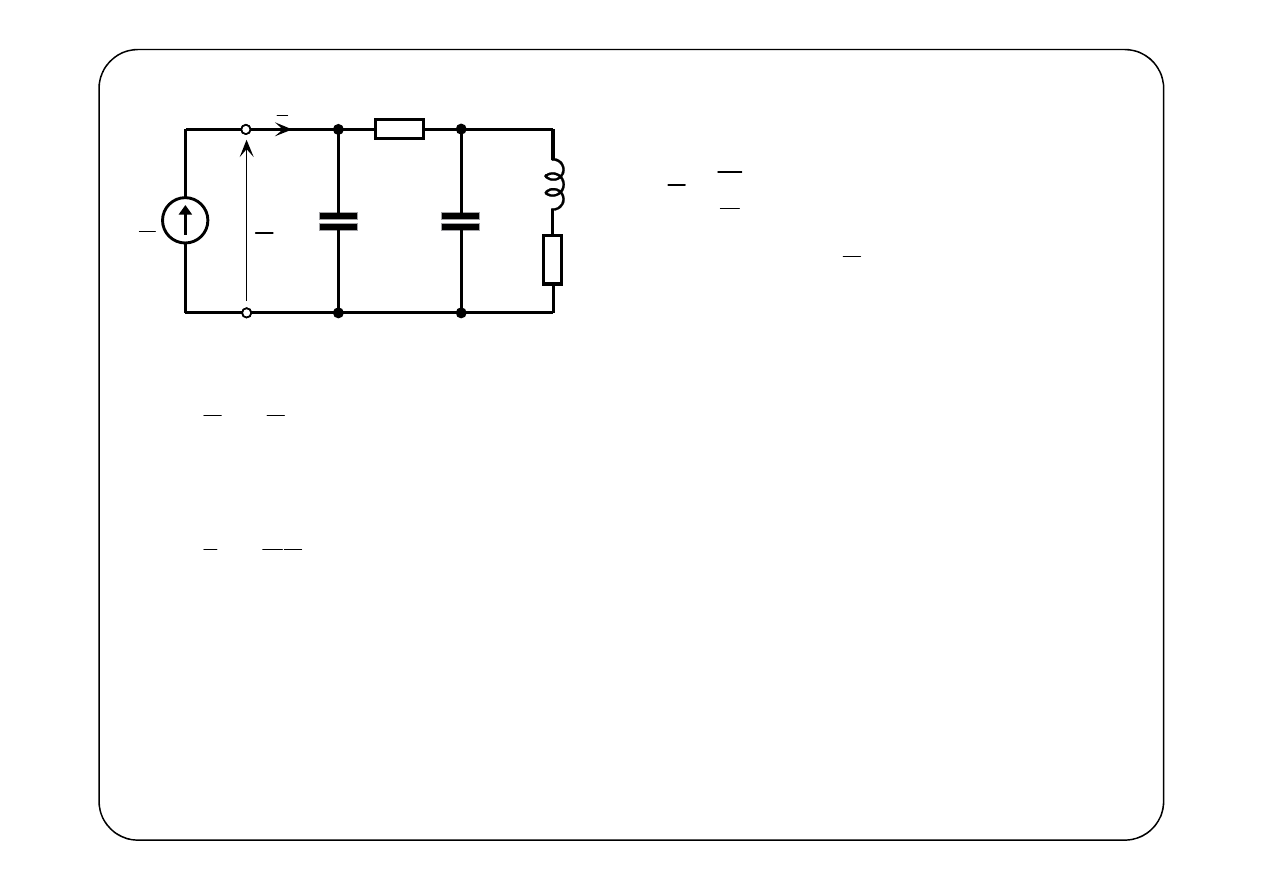
E
1
R
2
R
L
C
I
′′
U
C
′′
(
)
{ }
3
3
0
6
1
0, 295
j0, 425 10 S
j
Im
0, 425 10
1, 35 10 F
Y
Z
C
Y
C
ω
−
−
−
=
=
−
⋅
′′ = −
=
⋅
′′ =
⋅
3
0
j
0, 295 10 S
cos
1
Y
Y
C
ω
ϕ
−
′′
′′
= +
=
⋅
=
cos
1
ϕ
=
0, 0679 A
I
EY
′′
′′
=
=
15, 6 VA,
cos
15, 6 W,
0
S
EI
P
EI
Q
ϕ
′′
′′
′′
=
=
=
=
=
,
I
I
P
P
′′
′′
<
=
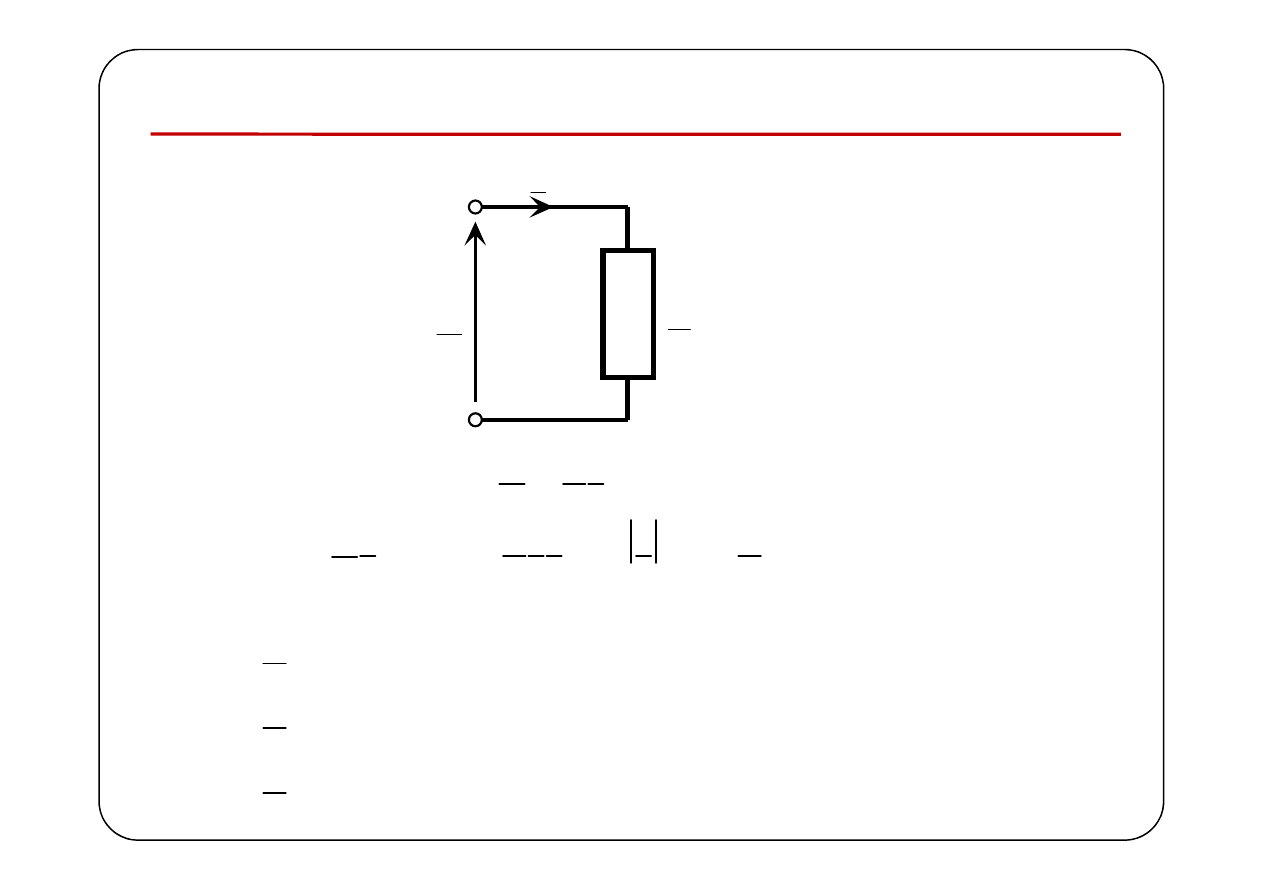
Pasywność dwójnika
U
I
Z
U
Z I
=
{ } { }
{ }
2
Re
Re
Re
P
U I
Z I I
I
Z
∗
∗
=
=
=
{ }
{ }
{ }
Re
0
0
Re
0
0
Re
0
0
Z
P
Z
P
Z
P
>
⇔
>
=
⇔
=
<
⇔
<
dwójnik pobiera energię
dwójnik dostarcza energię
Definicja 1.
Dwójnik nazywamy ściśle pasywnym, jeżeli jest on odbiornikiem
energii przy pobudzeniu sinusoidalnym o dowolnej pulsacji
ω
0
.
Dwójnik będzie ściśle pasywny gdy
przy dowolnej
pulsacji
ω
0
.
Ponieważ , więc warunek ścisłej pasywności
można zapisać jako
{ }
Re
0
Z
>
( )
0
j
s
Z
Z s
ω
=
=
gdzie
( )
( )
j
j
s
Z
Z s
ω
ω
=
=
( )
{
}
Re
j
0,
Z
ω
ω
>
− ∞ < < ∞
Definicja 2.
Dwójnik o impedancji Z(s) nazywa się dwójnikiem pasywnym gdy
( )
{
}
Re
j
0,
Z
ω
ω
≥
− ∞ < < ∞
Warunek pasywności (ścisłej pasywności) oznacza, że całkowita
energia dostarczona do dwójnika w dowolnej chwili czasu jest
nieujemna (dodatnia), czyli dla dowolnego t
( )
( )
( )
( )
d
0
d
0
t
t
w t
p
w t
p
τ τ
τ τ
−∞
−∞
=
>
=
≥
∫
∫
dwójnik ściśle pasywny
dwójnik pasywny
Definicja 3.
Dwójnik o impedancji Z(s) nazywa się dwójnikiem bezstratnym gdy
( )
{
}
Re
j
0,
Z
ω
ω
≡
− ∞ < < ∞
Całkowita energia dostarczona do dwójnika bezstratnego jest
równa 0, czyli
( )
( )
d
0
W
w
p
τ τ
∞
−∞
=
∞ =
=
∫
Dwójniki bezstratne są dwójnikami pasywnymi (ale nie są
dwójnikami ściśle pasywnymi)

Definicja 4.
Dwójnik, który nie jest pasywny nazywa się dwójnikiem aktywnym.
Dwójniki zbudowane z elementów RLCM są dwójnikami
( )
{
}
0
Re
j
0
Z
ω
<
Dwójnik o impedancji Z(s) jest więc aktywny,
gdy istnieje takie
ω
0
, że
Dwójniki zbudowane z elementów RLCM są dwójnikami
pasywnymi (ale niekoniecznie ściśle pasywnymi).
Dwójniki zbudowane z elementów LCM są dwójnikami
bezstratnymi.
Dwójniki SLS, zawierające źródła sterowane, mogą być
pasywne, ściśle pasywne, bezstratne lub aktywne.
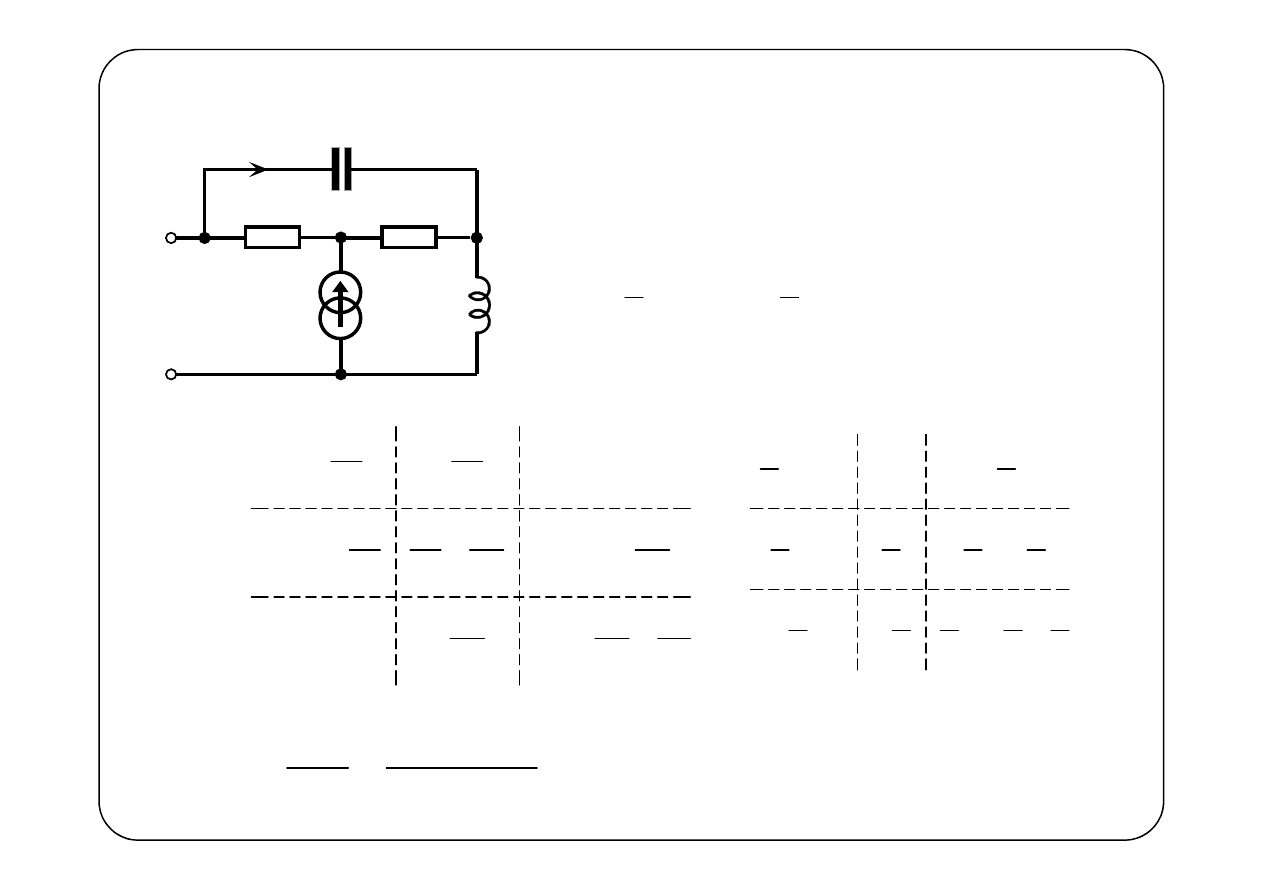
1
R
2
R
C
L
( )
i t
( )
i t
α
1
2
1
1
2
2
1Ω,
2 Ω,
H,
F,
1.
R
R
L
C
α
=
=
=
=
=
Przykład
1
1
1
1
sC
sC
+
−
−
1
2
3
( )
2
n11
n
2
6
2
s
s
Z s
s
∆
+ +
=
=
∆
+
( )
1
1
n
1
1
2
2
2
2
1
1
1
1
1
1
2
2
1
1
1
1
1
3
1
1
1
2
2
2
2
1
1
1
1
2
1
1
1
2
2
2
2
sC
sC
s
s
R
R
Y
s
sC
sC
s
s
R
R
R
R
s
s
sC
sC
s
R
R
sL
α
α
+
−
−
+
−
−
= −
−
+
−
= −
−
−
−
−
+ +
−
−
+
+
j
s
ω
=
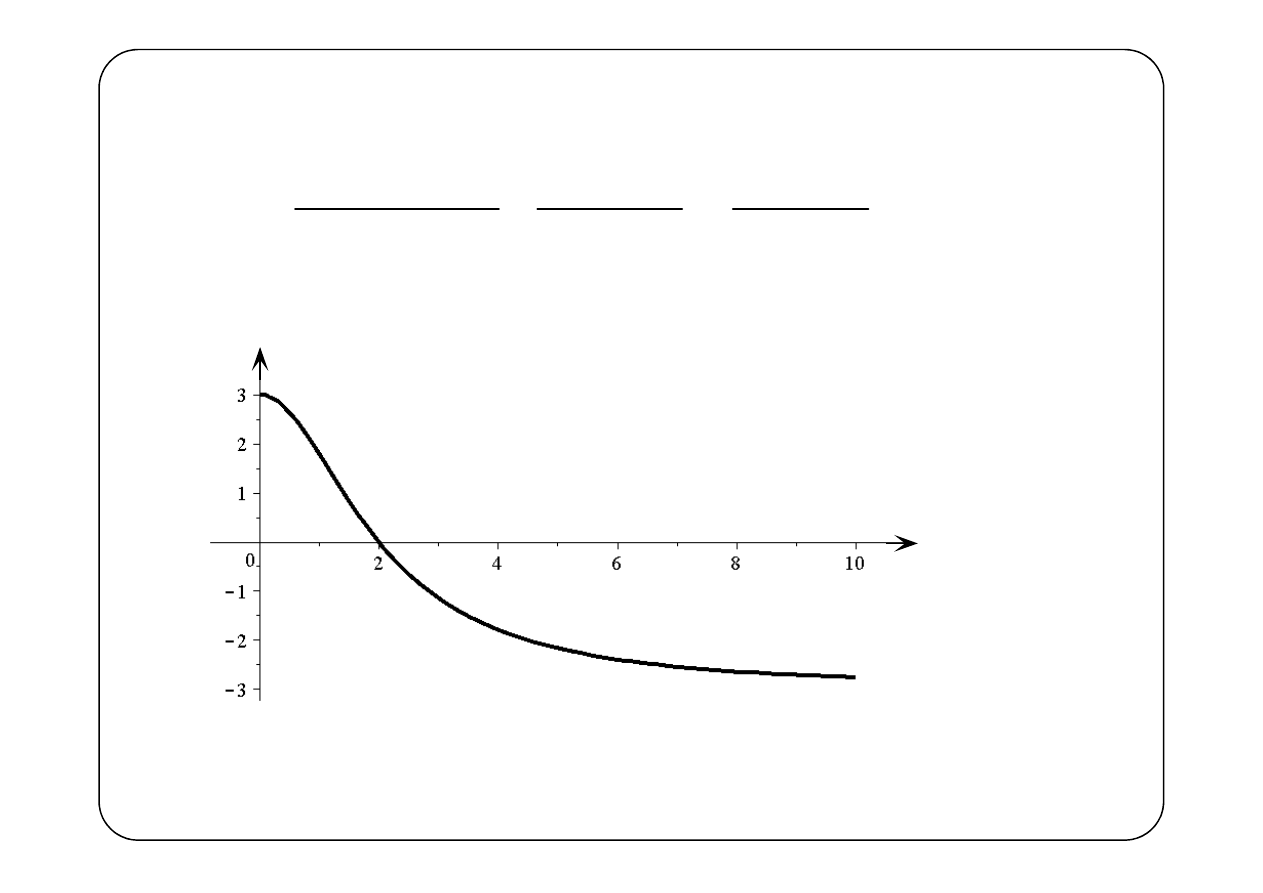
( )
2
2
3
2
2
2
j
6
3
12
2
4
j
j
j
2
4
4
Z
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
+
+
−
+
−
=
=
+
+
+
+
( )
{
}
Re
j
Z
ω
ω
Dwójnik jest aktywny
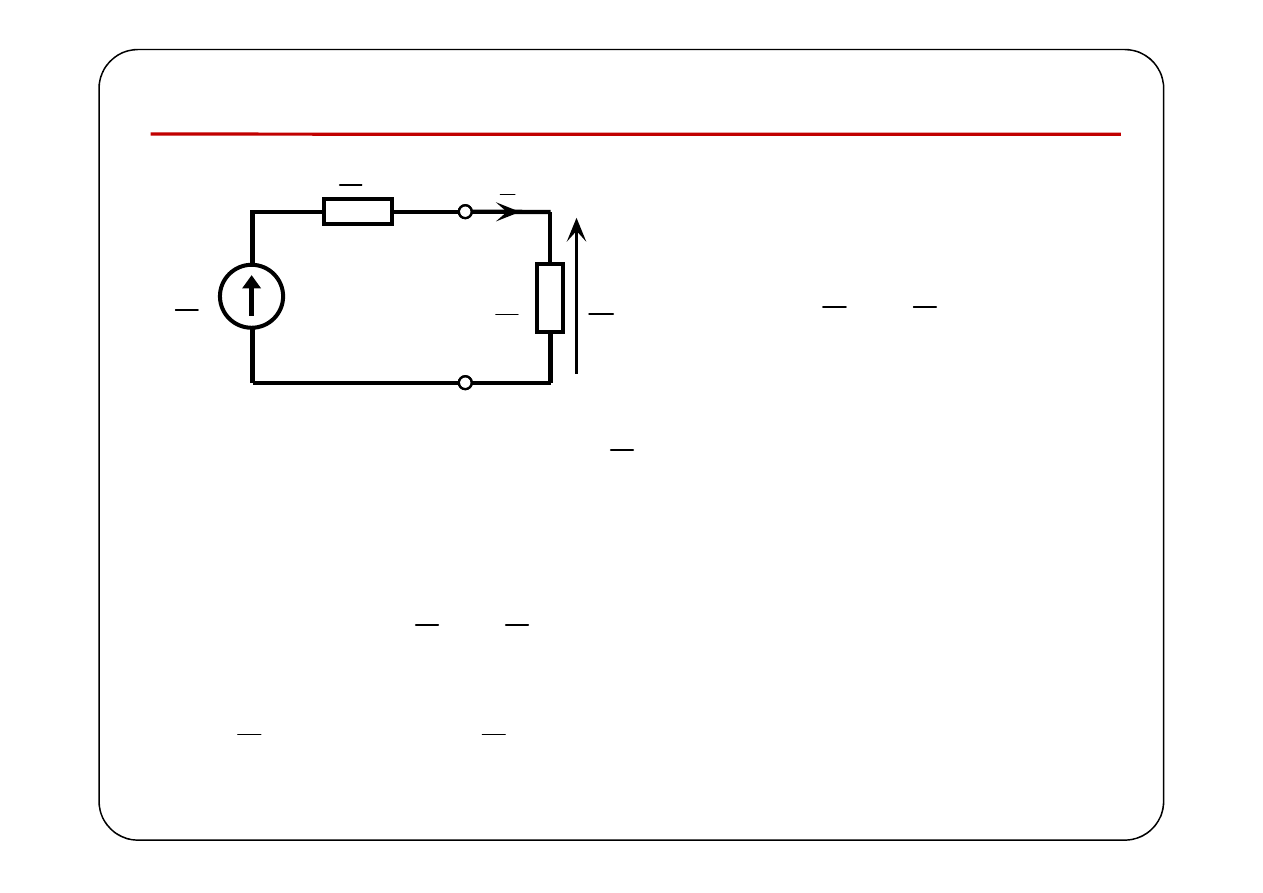
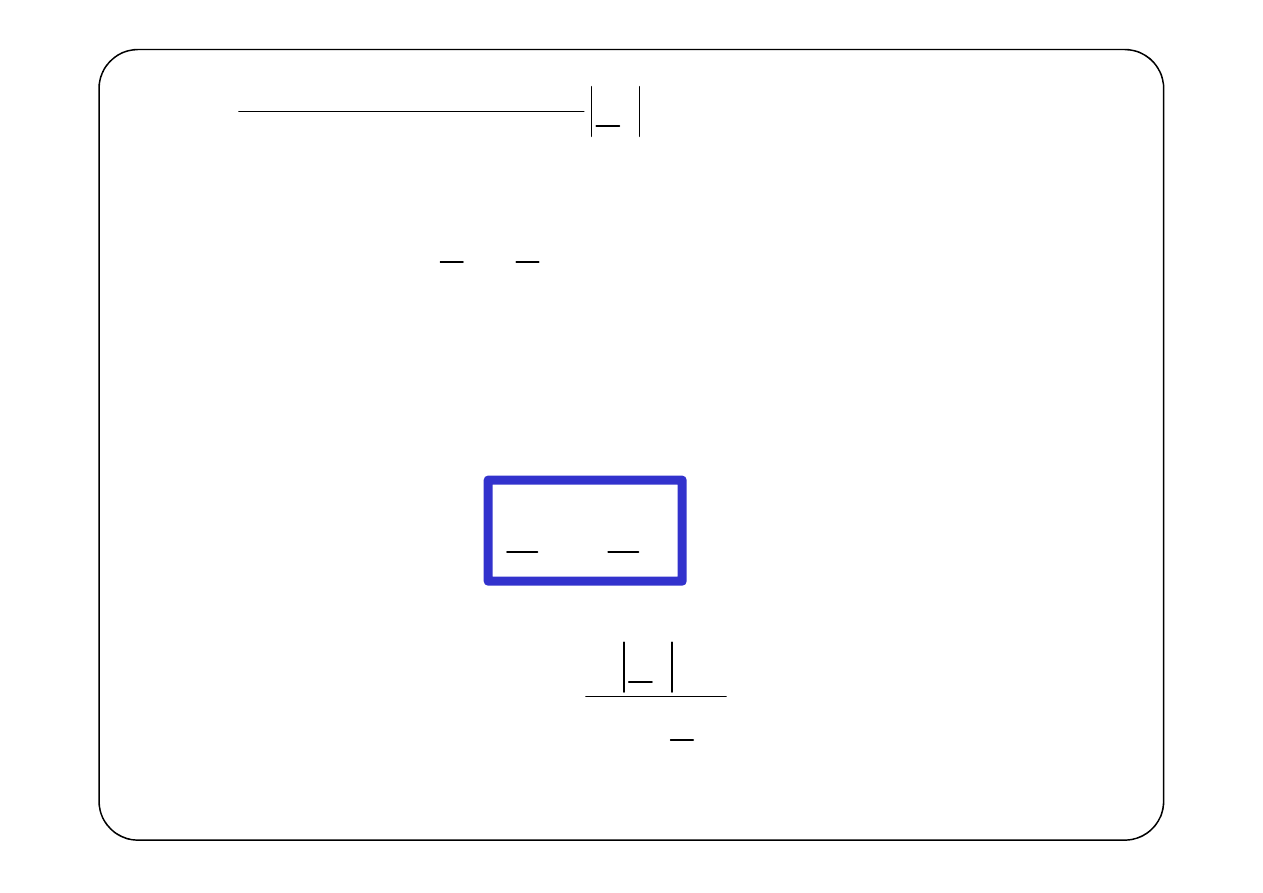
Dopasowanie obciążenia do generatora
Zadane
g
g
i
E
Z
Należy znaleźć impedancję
dwójnika reprezentującego
0
Z
g
E
g
Z
0
Z
I
U
Należy znaleźć impedancję
dwójnika reprezentującego
obciążenie, taką, aby do obciążenia przekazana została
maksymalna moc czynna.
0
Z
Zakładamy, że są impedancjami dwójników ściśle
pasywnych, czyli
g
0
i
Z
Z
{ }
{ }
g
0
Re
0
i
Re
0
Z
Z
>
>
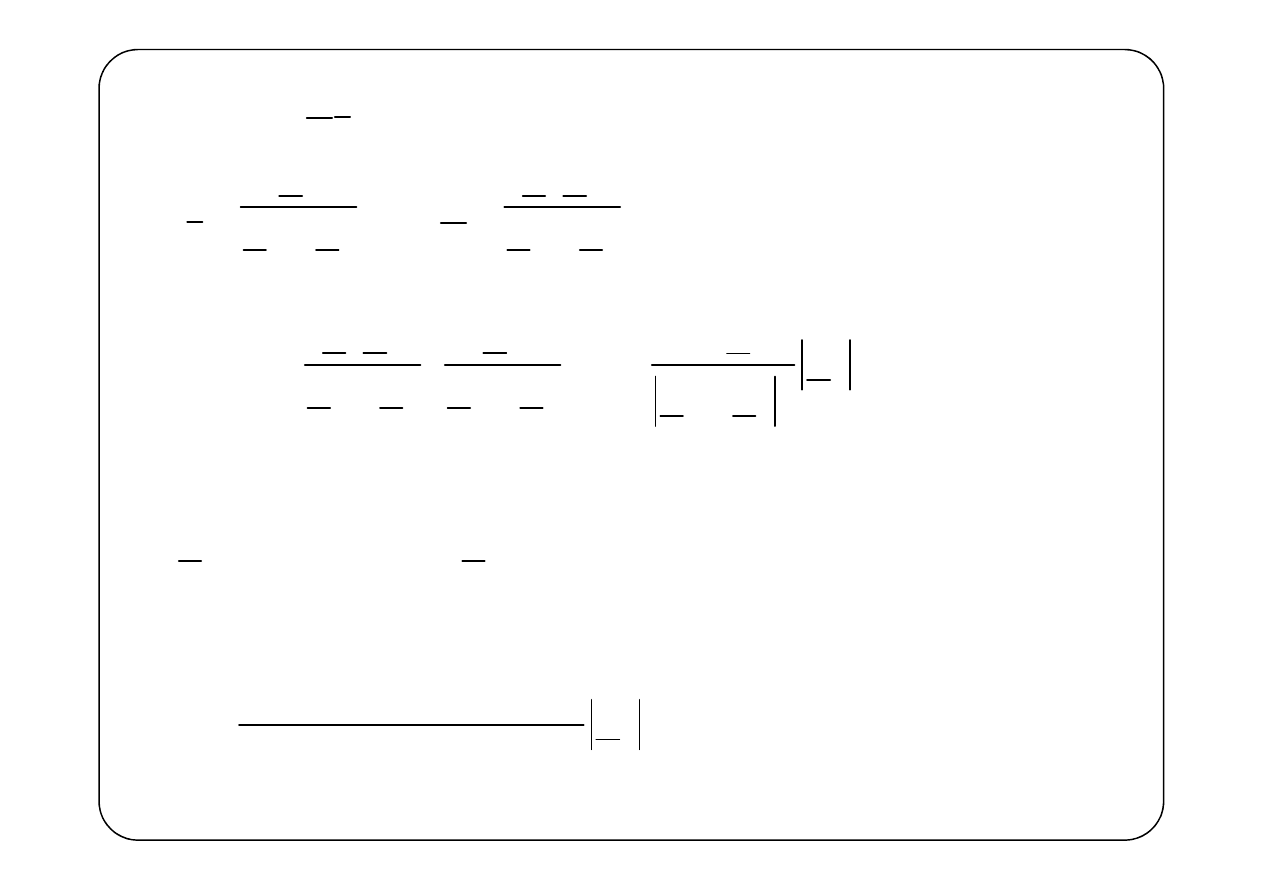
{ }
2
0
g
g
0
g
2
g
0
g
0
g
0
Re
Re
Z E
E
Z
P
E
Z
Z
Z
Z
Z
Z
∗
=
=
+
+
+
g
0
g
g
0
g
0
,
E
Z E
I
U
Z
Z
Z
Z
=
=
+
+
{ }
Re
P
U I
∗
=
Oznaczmy:
g
0
g
g
0
0
j
,
j
Z
R
X
Z
R
X
=
+
=
+
Wówczas
(
) (
)
2
0
g
2
2
g
0
g
0
R
P
E
R
R
X
X
=
+
+
+
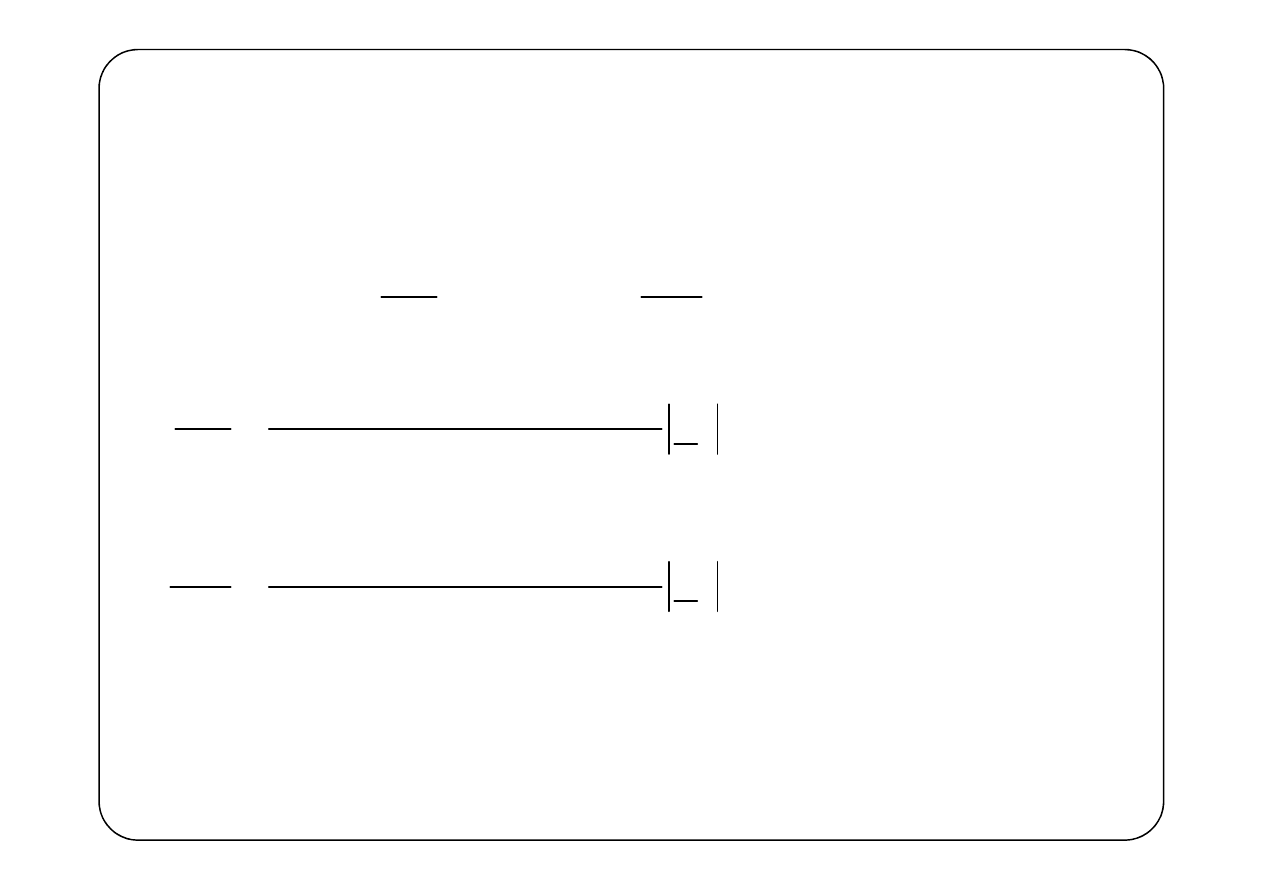
Należy znaleźć maksimum funkcji w obszarze
(
)
0
0
,
P R X
0
0
0
,
R
X
<
< ∞
− ∞ <
< ∞
Warunkami koniecznymi istnienia lokalnego ekstremum są:
0
0
0
i
0
P
P
R
X
∂
∂
=
=
∂
∂
(
)
(
) (
)
2
2
2
2
g
0
g
0
g
2
2
2
0
R
R
X
X
P
E
R
−
+
+
∂ =
=
∂
(
) (
)
(
)
(
) (
)
g
2
2
2
0
g
0
g
0
2
g
0
0
g
2
2
2
0
g
0
g
0
2
0
R
R
R
X
X
X
X
R
P
E
X
R
R
X
X
∂
+
+
+
−
+
∂ =
=
∂
+
+
+
Jedynym rozwiązaniem w rozważanym obszarze jest
0
g
0
g
i
R
R
X
X
=
= −
(
) (
)
2
0
g
2
2
g
0
g
0
R
P
E
R
R
X
X
=
+
+
+
0
g
0
g
0
g
R
R
Z
Z
X
X
∗
=
⇒
=
= −
Z przesłanek fizycznych wynika, że w wyznaczonym punkcie funkcja
ma lokalne maksimum, które jest jednocześnie największą
wartością funkcji w rozważanym obszarze.
Warunkiem dopasowania jest więc
(
)
0
0
,
P R X
Warunkiem dopasowania jest więc
0
g
Z
Z
∗
=
W warunkach dopasowania
{ }
2
g
max
g
4 Re
E
P
P
Z
=
=
Moc P
max
nazywa się mocą dysponowaną generatora
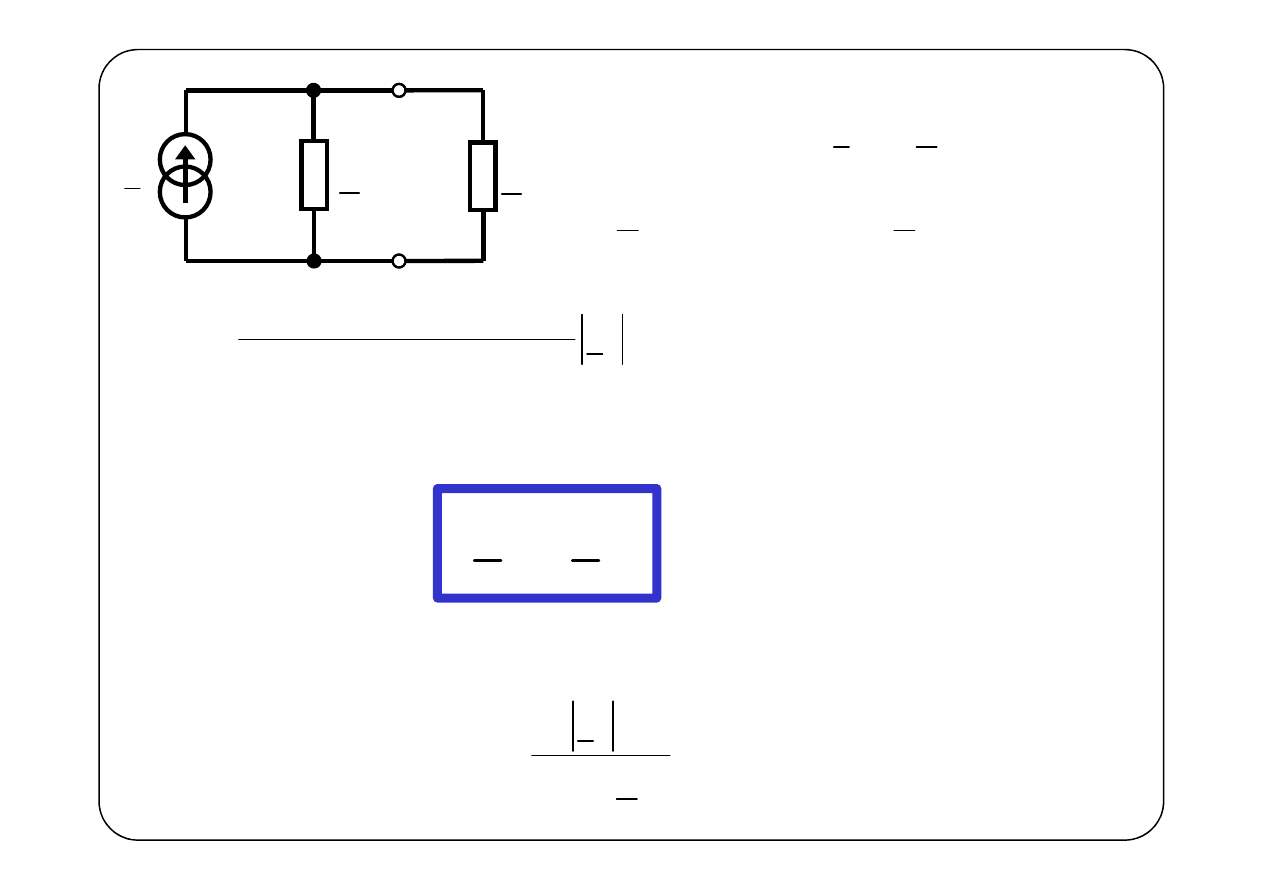
g
I
g
Y
0
Y
Zadane
g
g
i
I
Y
g
0
g
g
0
0
j
,
j
Y
G
B
Y
G
B
=
+
=
+
(
) (
)
2
0
g
2
2
g
0
g
0
G
P
I
G
G
B
B
=
+
+
+
Warunek dopasowania
Warunek dopasowania
0
g
Y
Y
∗
=
Moc dysponowana generatora
{ }
2
g
max
g
4 Re
I
P
Y
=
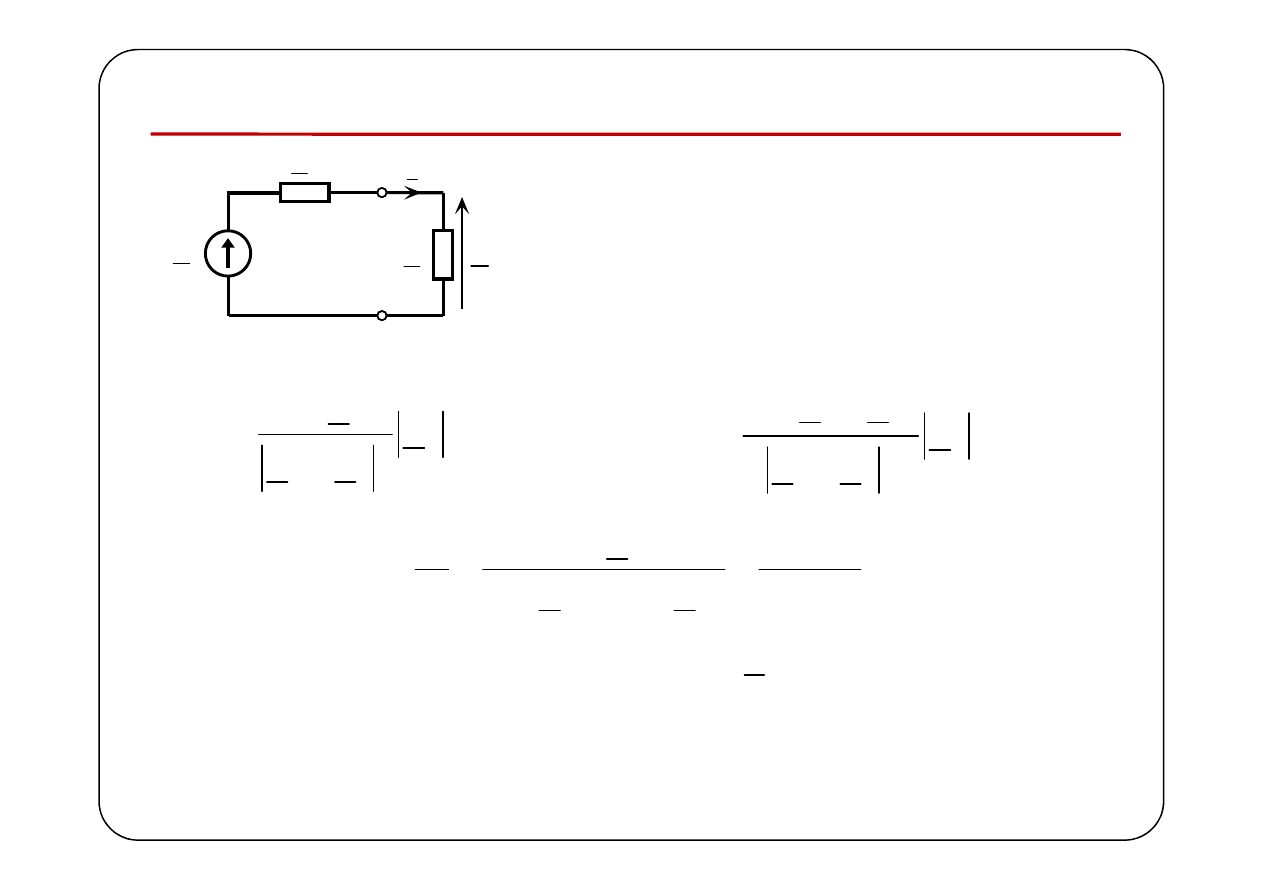
Sprawność przekazywania mocy
g
E
g
Z
0
Z
I
U
{ }
2
0
g
2
Re Z
P
E
=
+
{
}
2
g
0
g
g
2
Re Z
Z
P
E
+
=
+
Moc wydzielona w obciążeniu
Moc wytworzona w generatorze
g
2
g
0
P
E
Z
Z
=
+
g
g
2
g
0
P
E
Z
Z
=
+
{ }
{ }
{ }
0
0
g
g
0
g
0
Re
Re
Re
Z
R
P
P
R
R
Z
Z
η
=
=
=
+
+
W warunkach dopasowania (R
0
= R
g
):
1
2
η
=
Dopasowania na maksimum mocy czynnej nie stosuje się w energetyce!!!
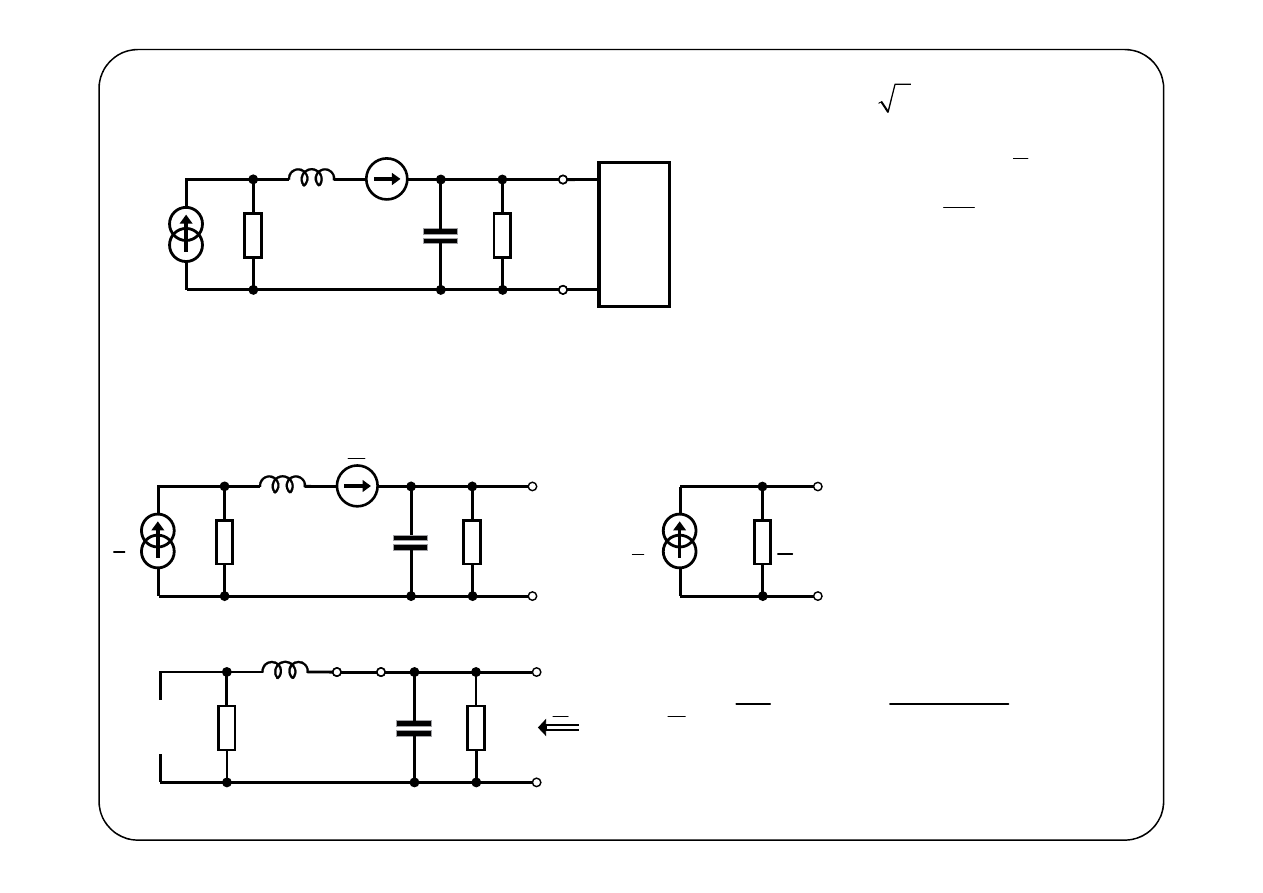
Przykład 1.
N
( )
e t
( )
z
i t
1
R
L
C
2
R
( )
( )
(
)
0
z
0
6
0
1
2
π
4
rad
5 2 cos
V,
0, 2sin
A,
10
,
50Ω,
100Ω,
50µH,
50 nF.
s
e t
t
i t
t
R
R
L
C
ω
ω
ω
=
=
−
=
=
=
=
=
Należy zaprojektować taki dwójnik N, aby wydzieliła
się w nim maksymalna moc czynna
E
E
z
I
1
R
L
C
2
R
≡
N
I
N
Y
1
R
L
C
2
R
N
Y
(
)
N
0
2
1
0
1
1
j
j
0, 02
j0, 04 S
Y
C
R
R
L
ω
ω
=
+
+
=
+
=
+
E
z
I
1
R
L
C
2
R
zw
I
π
j
z
1
4
zw
1
0
N
zw
0, 05
j0, 05
0, 05 2e
j
R I
E
I
R
L
I
I
ω
−
+
=
=
−
=
+
=
N
I
N
Y
0
Y
{ }
{ }
0
N
0
0
0
6
0
0
N
N
0
1
1
0, 02
j0, 04
j
1
1
50
Ω
,
25 10 H.
Re
Im
Y
Y
R
L
R
L
Y
Y
ω
ω
−
∗
=
=
−
=
−
=
=
= −
=
⋅
0
R
0
L
{ }
2
N
max
N
0, 0625 W
4 Re
I
P
Y
=
=
0
0
0
0
0
6
0
0
1
10
j20
j
10 Ω,
20 10 H
Z
R
L
Y
R
L
ω
−
′
′
=
=
+
=
+
′
′
=
=
⋅
0
R
′
0
L
′
Wyszukiwarka
Podobne podstrony:
metoda symboliczna
metoda symboliczna
METODA SYMBOLI DŹWIĘKOWYCH, Studia
Metoda symboli dźwiękowych, Diagnoza i terapia pedagogiczna
Metoda symboliczna (2)
metoda symboli dzwiękowych, Pedagogika
Metoda Symboli Dźwiękowych wg B
metoda symboliczna
Metoda symboli dźwiękowych, Studia
metoda symboliczna 3
W14 Metoda symboliczna i pojęcie impedancji ppt
WYKŁAD 4 METODA SYMBOLICZNA i pojęcie impedancji
METODA SYMBOLI DŹWIĘKOWYCH PREZENTACJA
Metoda komunikacji symbolicznej Blissa
Metoda magnetyczna MT 14
więcej podobnych podstron