
33. Algorytmy zapewnienia
jakości i niezawodności
mikrosystemów
.
Ireneusz Bylica

Niezawodność
Niezawodność - jest to właściwość obiektu
mówiąca o tym, czy pracuje on poprawnie
(spełnia
wszystkie powierzone mu funkcje i czynności)
przez wymagany czas i w określonych
warunkach
eksploatacji (w danym zespole czynników
wymuszających).

Niezawodność
( )
{
}
Pr
R t
t t
=
�
Niezawodność obiektu jest określona
przez prawdopodobieństwo
wystąpienia zdarzenia opisanego
definicją
Gdzie:
• R(t) – niezawodność
• t – czas pracy bez uszkodzenia
• – założony (wymagany) czas pracy bez
uszkodzenia

Niezawodność
Jednym ze sposobów charakteryzowania
zdolności do spełnienia wymagań jest
podanie prawdopodobieństwa, że obiekt,
który spełnia wymagania przy danym t, np.
w danej chwili t, w następnym przedziale
Δt przestanie je spełniać.

Niezawodność
Rozważa się, jaka część obiektów, które nie uległy
uszkodzeniu w przedziale (0, t), prawdopodobnie
stanie się niezdatna (niesprawna) w przedziale (t,
t+dt).
Tę niezdatną część obiektów oznacza się przez
λ(t)dt.
Zaś λ(t) nazywa się funkcją ryzyka, funkcją
intensywności ubywania lub funkcją intensywności
uszkodzeń.
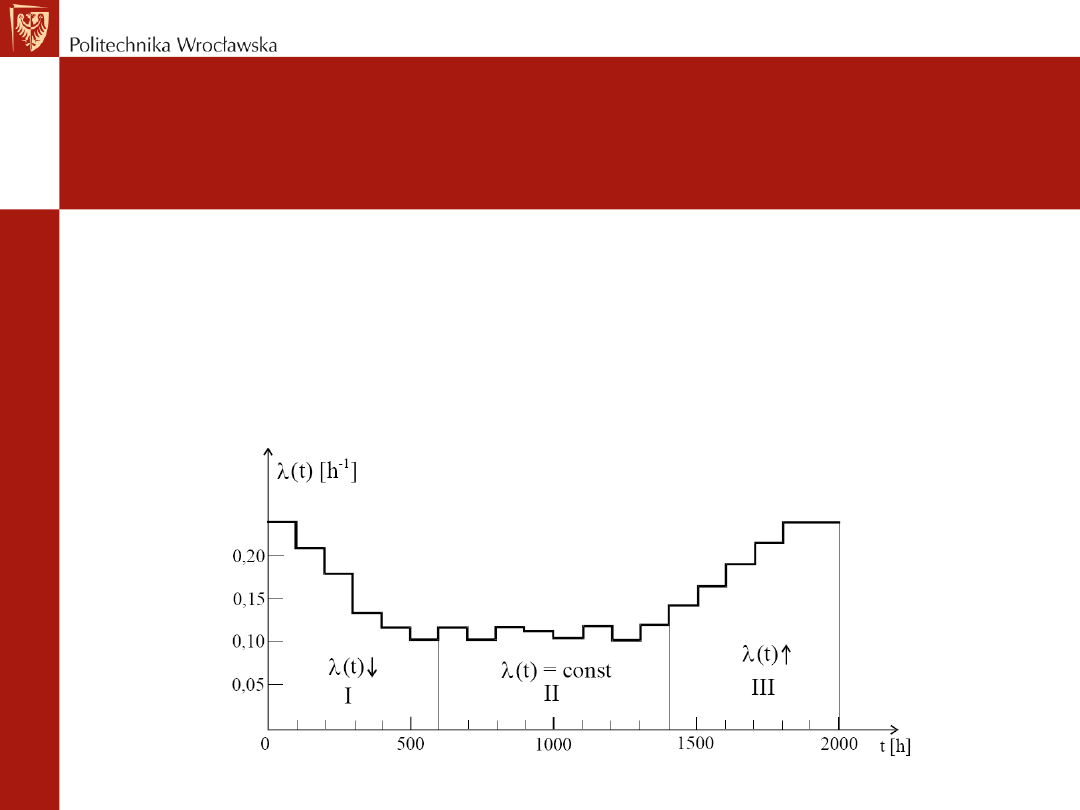
• Gdy λ(t) zwiększa się, intensywność uszkodzeń zwiększa się,
niezawodnościowe właściwości obiektów pogarszają się.
• Gdy λ(t) maleje, niezawodnościowe właściwości obiektów
polepszają się. W każdym następnym przedziale Δt ubywa
mniejszy procent obiektów niezdatnych ze zbioru zdatnych.
Niezawodność

Naprawialność -
prawdopodobieństwo
przywrócenia prawności obiektowi w
określonym czasie (0, τ) jest miarą
naprawialności. W przypadku ogólnym
naprawialność zależy od właściwości samego
obiektu i od warunków w jakich przywraca mu
się sprawność.
Niezawodność

Niezawodność
Kres życia obiektu przychodzi, gdy nie przywraca
się jego sprawności. Obiektowi nie przywraca się
sprawności ze względów ekonomicznych, a także
nieracjonalnych (np. ze względów na możliwości,
modę, gust, estetykę, obyczaje i inne).
Obiekty, którym nie przywraca się utraconej
sprawności, nazywa się obiektami
nienaprawialnymi (np. mikrosystemy, układy
scalone). Kres życia takiego obiektu nadchodzi z
chwilą zjawienia się pierwszej niesprawności.

Niezawodność obiektu nienaprawialnego, zdefiniowana
jako prawdopodobieństwo przeżycia, określają funkcje
R(t), λ(t) lub f(t) lub parametry tych funkcji, przy czym:
• R(t) – funkcja niezawodności
• λ(t) – funkcja intensywności uszkodzeń
• f(t) – funkcja gęstości prawdopodobieństwa, która opisuje
rozkład trwałości obiektów
Niezawodność obiektu może być scharakteryzowana również
przez zbiór danych z obserwacji zbioru obiektów lub
otrzymanych z prób niezawodności obiektów.
Niezawodność

W teorii i inżynierii niezawodności przyjmuje się, że
funkcją, która najlepiej charakteryzuje zmiany
niezawodności dowolnego obiektu technicznego
jest funkcja intensywności uszkodzeń λ(t). Z jej
przebiegu można wyciągnąć wiele wniosków
natury teoretycznej i praktycznej, a także
wyznaczyć:
• funkcję niezawodności
Niezawodność

• funkcję zawodności (dystrybuantę)
• funkcję gęstości prawdopodobieństwa
Niezawodność

Niezawodność

Znajomość przebiegu funkcji λ(t) umożliwia
producentowi i użytkownikowi, podejmowanie
ważnych decyzji praktycznych w zakresie:
• ustalania niezbędnych okresów starzenia wstępnego
produkowanych obiektów
• ustalenia wielkości i asortymentu części zamiennych
• planowania optymalnej pracy serwisu technicznego, służb
remontowych
• ustalenia optymalnych okresów wymian profilaktycznych
elementów i zespołów
• ustalania optymalnych okresów eksploatacji obiektów
• innych działań techniczno-ekonomicznych (okres gwarancji)
Niezawodność

W wielu przypadkach eksperymentalne przebiegi
funkcji λ(t) można aproksymować funkcjami
analitycznymi (teoretycznymi rozkładami
prawdopodobieństwa jak np. rozkładem
wykładniczym, beta, Weibulla lub kompozycją tych
rozkładów).
Rzeczywiste przebiegi funkcji λ(t) konkretnego
obiektu, zależnie od przyjętej strategii
eksploatacji, mogą być bardzo różne i mogą być
celowo kształtowane.
Niezawodność

Jednym z najprostszych modeli probabilistycznych
czasu zdatności obiektu nieodnawialnego jest
zmienna losowa T, której intensywność uszkodzeń
jest stała, tzn. niezależna od czasu
Rozkład wykładniczy
Niezawodność
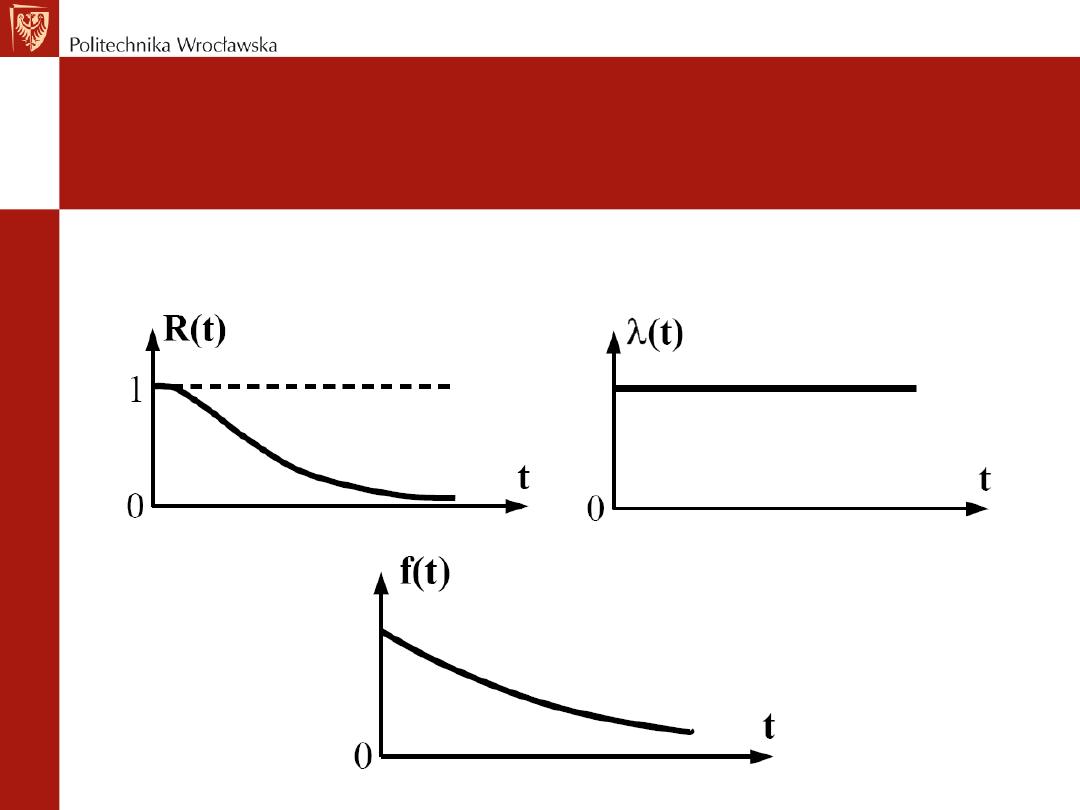
Charakterystyki funkcyjne rozkładu wykładniczego
Niezawodność

Rozkład Weibulla jest bardziej ogólny niż
wykładniczy. Jest on stosowany, gdy intensywność
uszkodzeń jest zmienną o przebiegu
monotonicznym. Rozkładem tym opisuje się
między innymi trwałość zmęczeniową materiałów i
konstrukcji mechanicznych. Intensywność
uszkodzeń określa wzór
Niezawodność

Rozkład Weibulla
Gdy
•
– otrzymuje się rozkład
wykładniczy
•
– otrzymuje się rozkład Reyleigha
Niezawodność
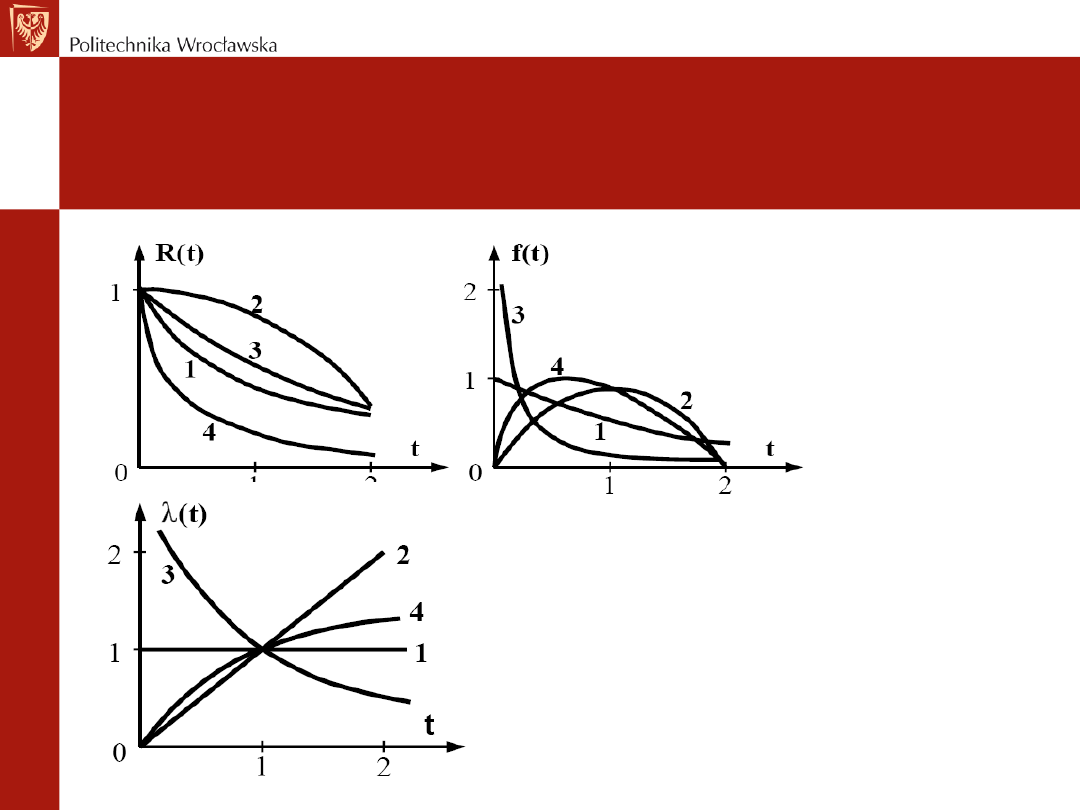
Charakterystyki funkcyjne rozkładu:
• – wykładniczego (
• – Rayleigha (
• 3 – o malejącej intensywności
uszkodzeń (
• 4 - o rosnącej intensywności
uszkodzeń (
3
3
Niezawodność

Rozkład normalny
Niezawodność
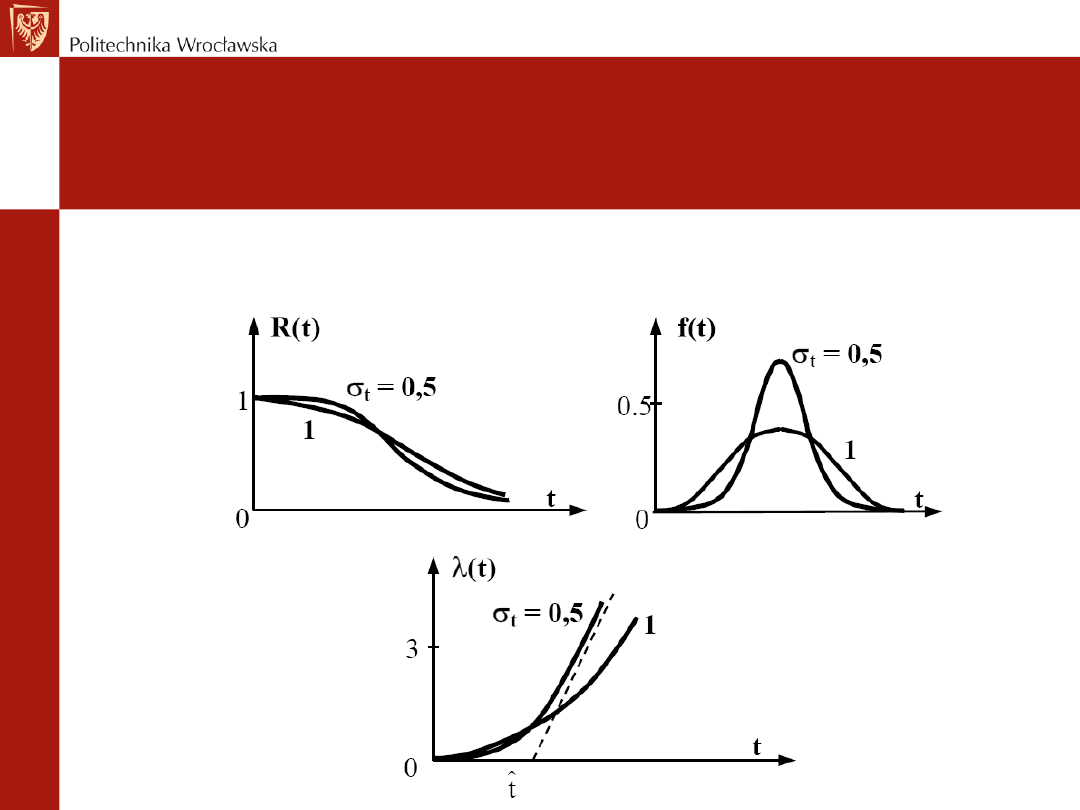
Charakterystyki funkcyjne rozkładu normalnego
Niezawodność

Niezawodność w IC
PowerPC 970
miliony
tranzystorów
Procesor
Ilość
tranzystorów
Rok produkcji
Intel 44
3
97
Intel 88
97
Intel 88
4
974
Intel 888
9
979
Intel 886
34
98
Intel 8386
7
98
Intel 8486
989
Pentium
3
993
AMD K
4 3
996
Pentium II
7
997
AMD K6
8 8
997
Pentium III
9
999
AMD K6-II
3
999
Niezawodność w IC

Procesor
Ilość
tranzystorów
Rok produkcji
AMD K7
999
Pentium 4
4
Itanium
Barton
4 3
3
AMD K8
9
3
Itanium
3
Itanium z 9MB cache
9
4
Cell
4
6
Core Duo
9
6
Core Quad
8
6
Dual-Core Itanium
7
6
Niezawodność w IC

Niezawodność w
mikrosystemach

Niezawodność w
mikrosystemach
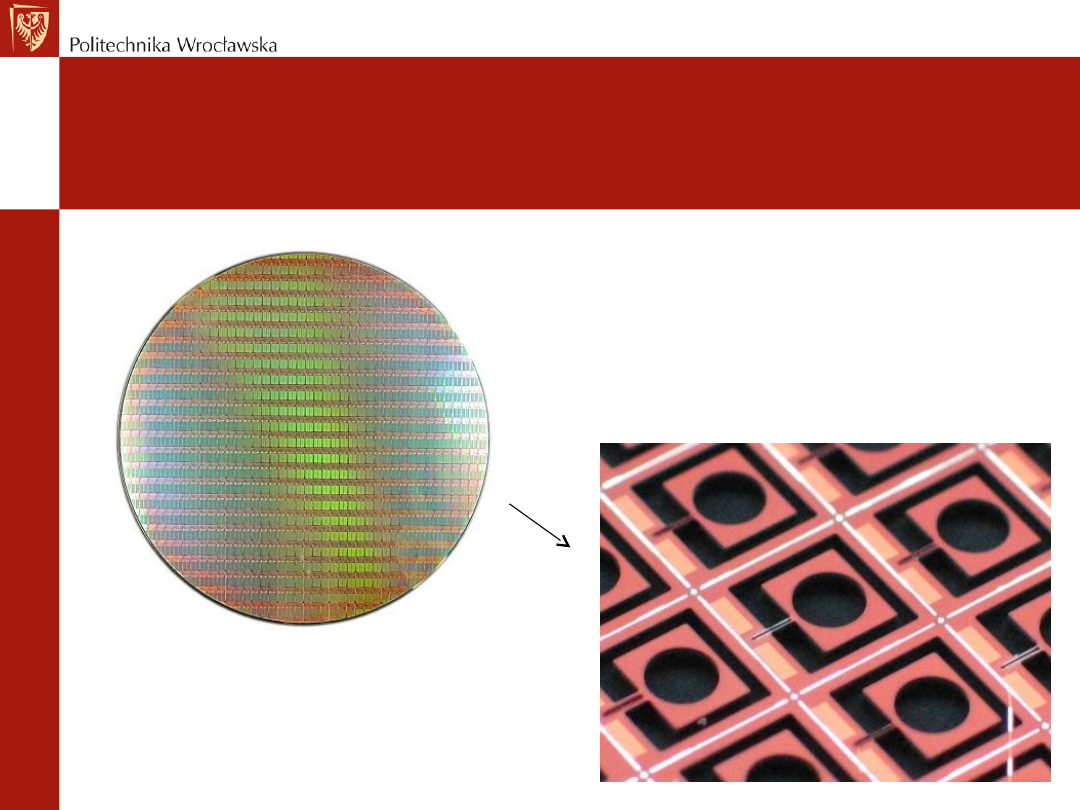
Z jednego podłoża krzemowego
można uzyskać nawet kilkaset
mikrostruktur
Niezawodność w
mikrosystemach

Technologie stosowane w produkcji mikrosystemów
korzystają z wielu technik znanych z produkcji
układów scalonych. Z tego powodu algorytmy
stosowane do zapewnienia ich niezawodności są
podobne. Algorytmy te obejmują:
• pomiary międzyoperacyjne
• wytwarzanie struktur próbnych i testowych
• pomiary ostrzowe
• pomiary końcowe
Niezawodność w
mikrosystemach

Pomiary międzyoperacyjne
Niezawodność w
mikrosystemach
Pomiędzy
ważniejszymi
etapami
technologicznymi przeprowadza się pomiary
dostarczające
informacji
o
wynikach
bieżących
procesów
technologicznych.
Pozwala to np. ocenić głębokość wnikania
domieszki po procesie implantacji i na tej
podstawie poprawiać parametry danego
procesu (a co za tym idzie – gotowych
struktur) w przyszłości.

Niezawodność w
mikrosystemach
W skład każdej struktury próbnej wchodzą
elementy składowe umożliwiające ocenę
poszczególnych procesów technologicznych
oraz zależności między tymi procesami.
Umożliwiają one określenie m.in.. napięcia
przebicia
złącza
p-n,
upływności,
rezystywności powierzchniowej, itp.
Struktury próbne

Niezawodność w
mikrosystemach
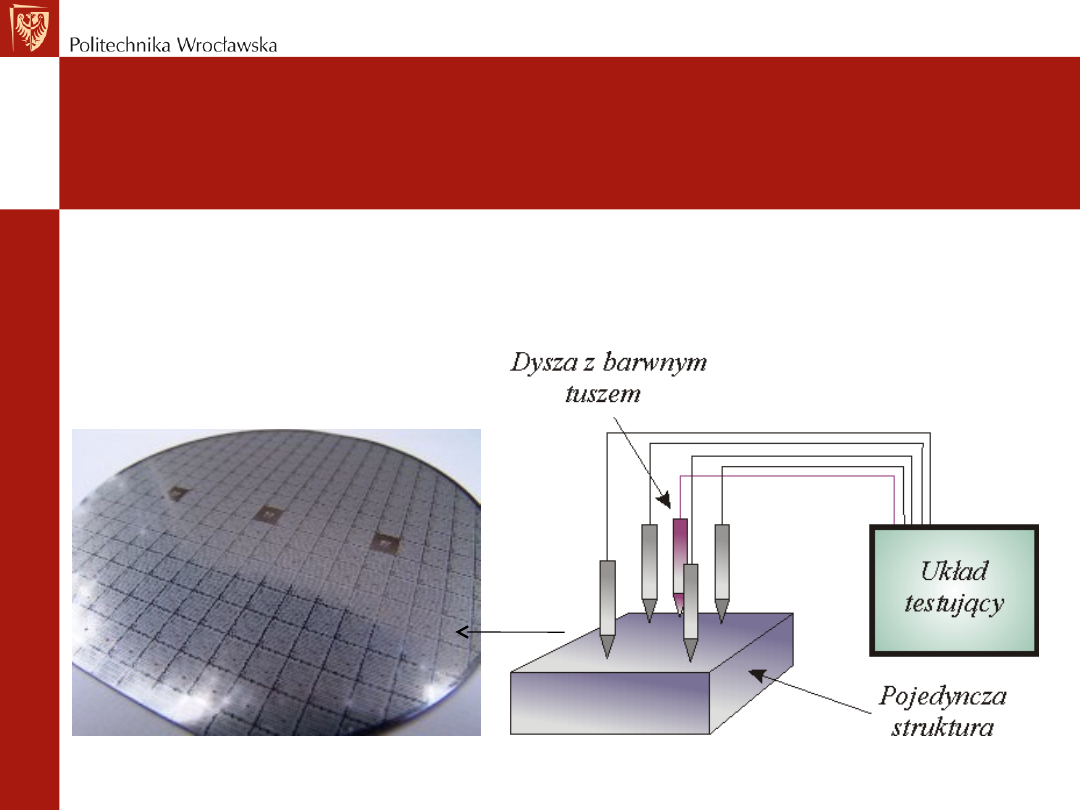
Pomiary ostrzowe
Przeprowadza się je przed podziałem płytki na
poszczególne struktury. Elementy wadliwe
oznaczane są kroplą barwnego tuszu. Po
operacji podziału są usuwane w trakcie
selekcji
optycznej.
Usuwane
są
także
struktury o wadliwej geometrii (np. pęknięte
przy podziale).
Niezawodność w
mikrosystemach
Pomiary ostrzowe

Niezawodność w
mikrosystemach
Pomiary końcowe
Po montażu i hermetyzacji w ramach pomiarów końcowych
przeprowadza się testy mechaniczno-klimatyczne. Stosuje się
następujące wymuszenia:
• wysoka temperatura
• niska temperatura
• duża wilgotność względna
• niskie ciśnienie
• cykle temperaturowe
• mgła solna
• wibracje
• udary
• stałe przyspieszenie

Niezawodność w
mikrosystemach
Pomiary końcowe
Rodzaje prób zależą od przeznaczenia elementów i
wymaganego poziomu jakości:
• elementy standardowe
• elementy profesjonalne
• elementy o podwyższonej niezawodności
• elementy do zastosowań specjalnych

Niezawodność w
mikrosystemach
Pomiary końcowe
Pomiary w grupie A obejmują sprawdzenie:
• wymiarów
• oznakowań
• podstawowych parametrów elektrycznych

Niezawodność w
mikrosystemach
Pomiary końcowe
Pomiary w grupie B dodatkowo obejmują:
•
testy
mechaniczno-klimatyczne
(wytrzymałość
mechaniczna wyprowadzeń, szczelność, lutowność, udary
wielokrotne, spadki temperatury, itp.)
• sprawdzenie odporności na narażenia elektryczne
(polaryzacja wsteczna, obciążenie większą mocą itp.)

Niezawodność w
mikrosystemach
Pomiary końcowe
Pomiary w grupie C to dodatkowe testy selekcyjne:
• cykle temperaturowe
• krótkotrwałe udary i wibracje
•kontrola szczelności
•praca w warunkach granicznych
•wygrzewanie

Niezawodność w
mikrosystemach
Pomiary końcowe
Pomiary w grupie D pozwalają określić niezawodność
przy pracy w warunkach specjalnych. Ich rodzaj
zależy od narażeń środowiskowych jakim będzie
poddany mikrosystem. Testy te mogą badać np.
odporność na pleśń, mgłę solną, itp.

Niezawodność w
mikrosystemach
Pomiary końcowe
W pomiarach końcowych stosuje się także:
• mikroskopię w podczerwieni (lokalizacja
naprężeń)
• radiometrię w podczerwieni (otrzymana mapa
rozkładu temperatury na powierzchni płytki pozwala
ocenić jakość połączeń, kontaktów, zlokalizować rysy
i pęknięcia)
• mikroskopię elektronową
• metody rentgenograficzne

Dla losowej próbki obiektów przeprowadza się badania
statystyczne. Na ich podstawie wnioskować można o słuszności
określonych hipotez statystycznych (np. prawdopodobieństwa
wystąpienia zdarzenia losowego) oraz estymacji nieznanych
wartości chwilowych rozkładu funkcji niezawodności.
Wyróżnia się dwie grupy badań statystycznych:
•
metody
nieparametryczne
–
o
charakterystyce
probabilistycznej
zdarzenia
losowego
wnioskuje
się
bezpośrednio
•
metody parametryczne – charakterystyki probabilistyczne
wyznacza się pośrednio przez wyznaczenie z doświadczalnych
charakterystyk probabilistycznych określonych parametrów
Niezawodność w
mikrosystemach
Pomiary statystyczne

Jakość
„
pewien stopień doskonałości”
Platon
Cyceron tworząc łaciński termin filozoficzny dla
określenia greckiego pojęcia, wprowadził słowo
qualitas , które przeszło do niektórych języków
romańskich i germańskich, np. quality w języku
angielskim.

Jakość
•Zgodność z celem.
•Zgodność ze specyfikacją czyli zero braków.
•Stopień doskonałości wyrobu lub usługi.
•Zespół cech i charakterystyk wyrobu lub usługi,
które noszą w sobie zdolność zaspokojenia
określonej potrzeby.
•Właściwość jednostki odnosząca się do jej
zdolności zaspokojenia wymagań jakościowych.

Jakość
•Strata jaką produkt wyekspediowany na rynek powoduje
w
społeczeństwie,
różna
od
jakiejkolwiek
straty
spowodowanej przez funkcję wewnętrzną wyroby (wg.
Genichi Tahuchiego)
•Wielkość odwrotnie proporcjonalna do zmienności pewnej
charakterystyki liczbowej / mierzalnej przedmiotu (wg.
Douglasa C. Montgomerego)
Współcześnie definicje kładą większy nacisk na
społeczne aspekty jakości, a konkretnie odnoszą się
do jakości produktu i jego wartości użytkowej.

Cechy jakości produktu
•
Funkcjonalność:
Funkcjonalność:
– użyteczność – stopień realizacji oczekiwanych
funkcji
– praktyczność – komfort użytkowania, łatwość
obsługi
– niezawodność - zdolność do pracy
bezusterkowej
– trwałość – okres zachowania cech użytkowych
– bezpieczeństwo użytkowania

Cechy jakości produktu
•
Satysfakcjonowanie:
Satysfakcjonowanie:
– ekskluzywność – prestiż nabywcy związany z
posiadaniem produktu lub jego marką
– estetyczność – pozytywne odczucia osobiste
– prezentacja – forma zaoferowania (warunki
sprzedaży: otoczenie, obsługa, sposób dostawy,
opakowanie, certyfikaty, referencje)
•
Koszt nabycia
Koszt nabycia
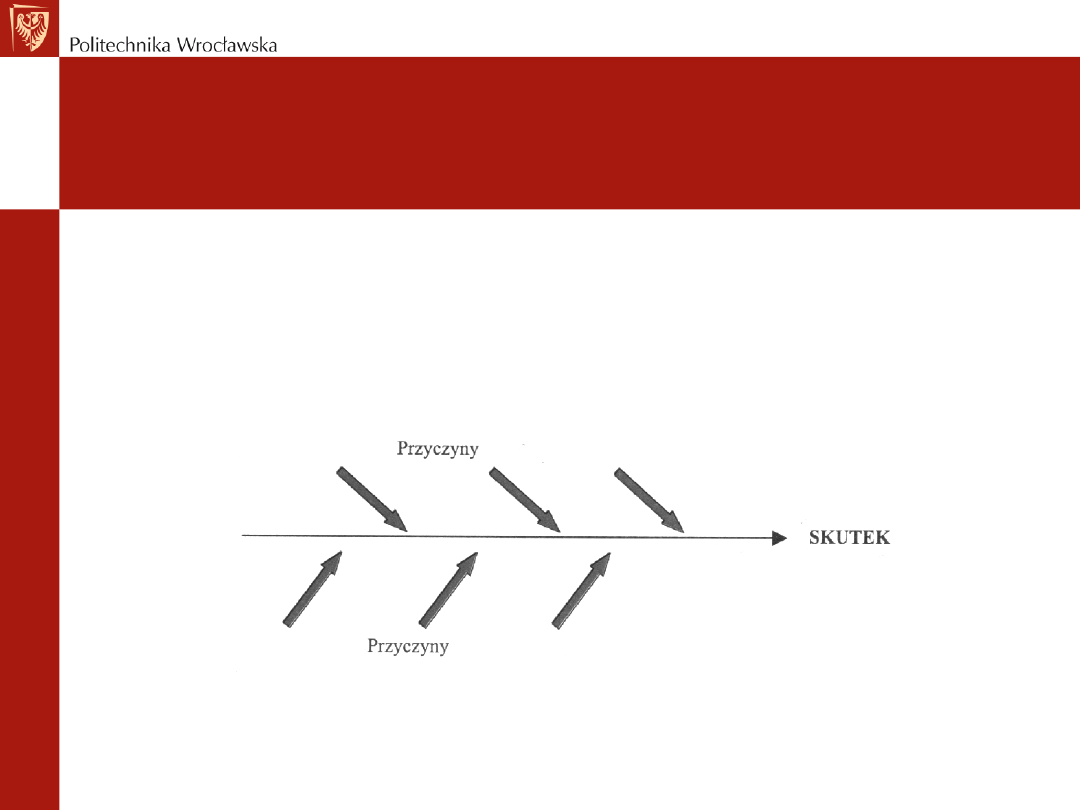
Metody i techniki sterowania
jakością
• Diagram przyczynowo skutkowy Ishikawy –
graficzna reprezentacja analizy wzajemnych
powiązań przyczyn wywołujących problem.
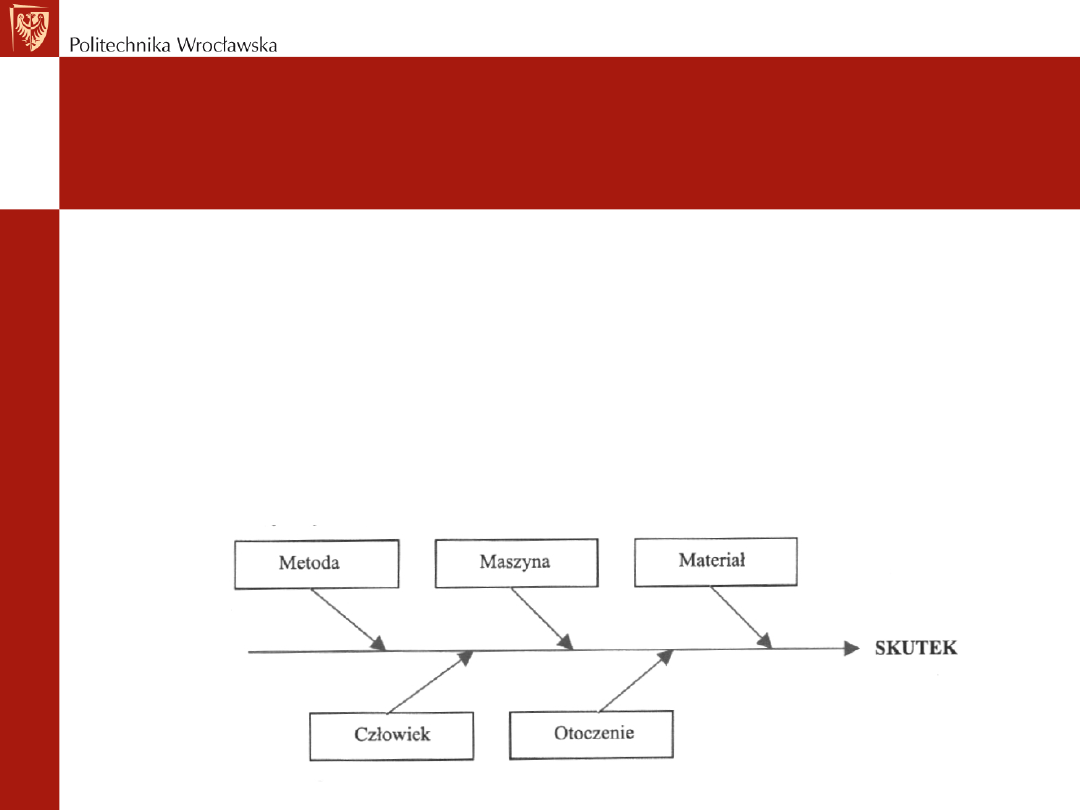
Metody i techniki sterowania
jakością
Przyczyny 5M:
Przyczyny 5M:
•
człowiek (Man)
• materiał (Material)
• sprzęt/maszyna (Machine)
• stosowana metoda (Method)
• kierownictwo (Management)

Metoda ABCD Suzuki
Metoda ABCD Suzuki – jest stosowana w
sytuacji,
gdy nie wiadomo, które z przyczyn mają
większy, a
które mniejszy, a nawet minimalny wpływ na
rozpatrywaną kwestię.
Metody i techniki sterowania
jakością

Etapy metody:
Etapy metody:
• uporządkowanie przyczyn
• sporządzenie
oraz
wypełnienie
tabeli
indywidualnych wyborów rangi
• sporządzenie oraz wypełnienie tabeli zbiorczej
• uszeregowanie przyczyn według rangi
Metody i techniki sterowania
jakością

Diagram Pareto – jest narzędziem umożliwiającym
hierarchizację czynników wpływających na badane
zjawisko
Tryb postępowania:
Tryb postępowania:
• Określenie liczy przyczyn
• Wybranie kategorii wpływającej na analizowane zjawisko
• Określenie przedziały czasowego analizy
• Zgromadzenie danych
• Tworzenie tabel, skalowanie osi
• Tworzenie wykresów słupkowych w porządku malejącym
• Obliczenie i naniesienie na wykres wartości skumulowanych
• Dokonanie analizy wykresu
Metody i techniki sterowania
jakością
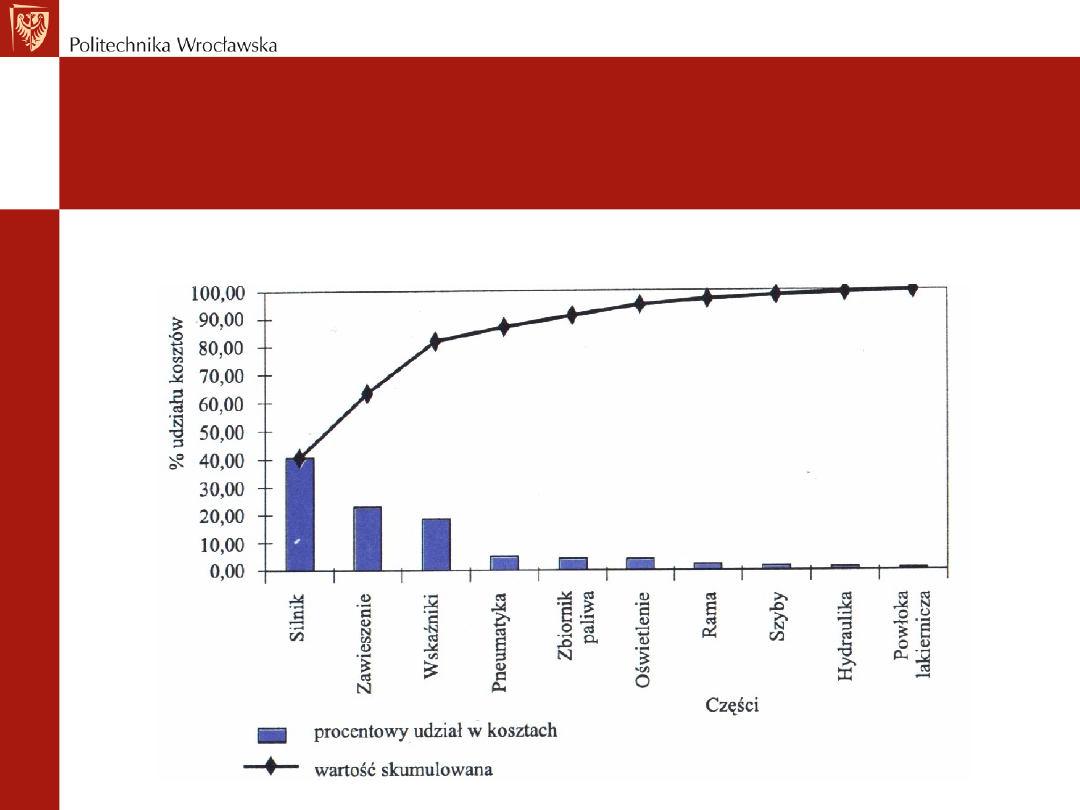
Metody i techniki sterowania
jakością
Diagram Pareto
Diagram Pareto

Metody i techniki sterowania
jakością
FMEA – analiza skutków i przyczyn potencjalnych
błędów.
Pozwala na
Pozwala na
:
:
• Rozpoznanie i ocenę potencjalnych błędów,
mogących wystąpić w wyrobie lub procesie oraz
skutków ich wystąpienia
• Identyfikacje działań, które mogłyby wyeliminować
lub przynajmniej ograniczyć szansę wystąpienia
potencjalnych błędów
• Dokumentacje procesu

Etapy:
Etapy:
• Identyfikacja wszystkich elementów wyrobu lub
funkcji rozpatrywanego procesu w kolejności
technologicznej
• Sporządzenie listy możliwych błędów
• Przygotowanie listy prawdopodobnych skutków tych
błędów
• Opracowanie listy przyczyn możliwych błędów i
prawdopodobieństwa ich wykrycia
• Przyporządkowanie możliwym błędom wartości
ryzyka
Metody i techniki sterowania
jakością

Metody statystyczne:
Metody statystyczne:
• SPC (Statistical Process Control)
• Karta kontrolna
• Arkusze analityczne
• Histogramy
• Analiza wariancji (ANOVA)
Metody i techniki sterowania
Metody i techniki sterowania
jakością
jakością
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
Wyszukiwarka
Podobne podstrony:
33 Algorytmy zapewnienia jakości i niezawodności mikrosystem
33 Algorytmy zapewnienia jakości i niezawodności mikrosystem
Sytemy zapewnienia jakości`, Systemy Zapewnienia Jakości, Systemy Zapewnienia Bezpieczeństwa Zdrowot
Metody zapewniania jakości opieki zdrowotnej
4 Zapewnienie jakości i DPL
22(45) Zapewnienie jakości oprogramowaniaid 29565 ppt
Projekt plan zapewnienia jakości (2)
rozwój norm dotyczących systemów zapewnienia jakosci, Marketing
Systemy Zapewnienia Jakosci Wyklady
więcej podobnych podstron