Optyka
geometryczna

Podstawowe pojęcia optyki
geometrycznej

Bezwzględny współczynnik
załamania

v

c

n 

c

– prędkość światła w próżni

v < c

– prędkość światła w danym

ośrodku

>
1

Aksjomaty

Światło w ośrodku jednorodnym

propaguje się po liniach prostych

nazywanych promieniami świetlnymi

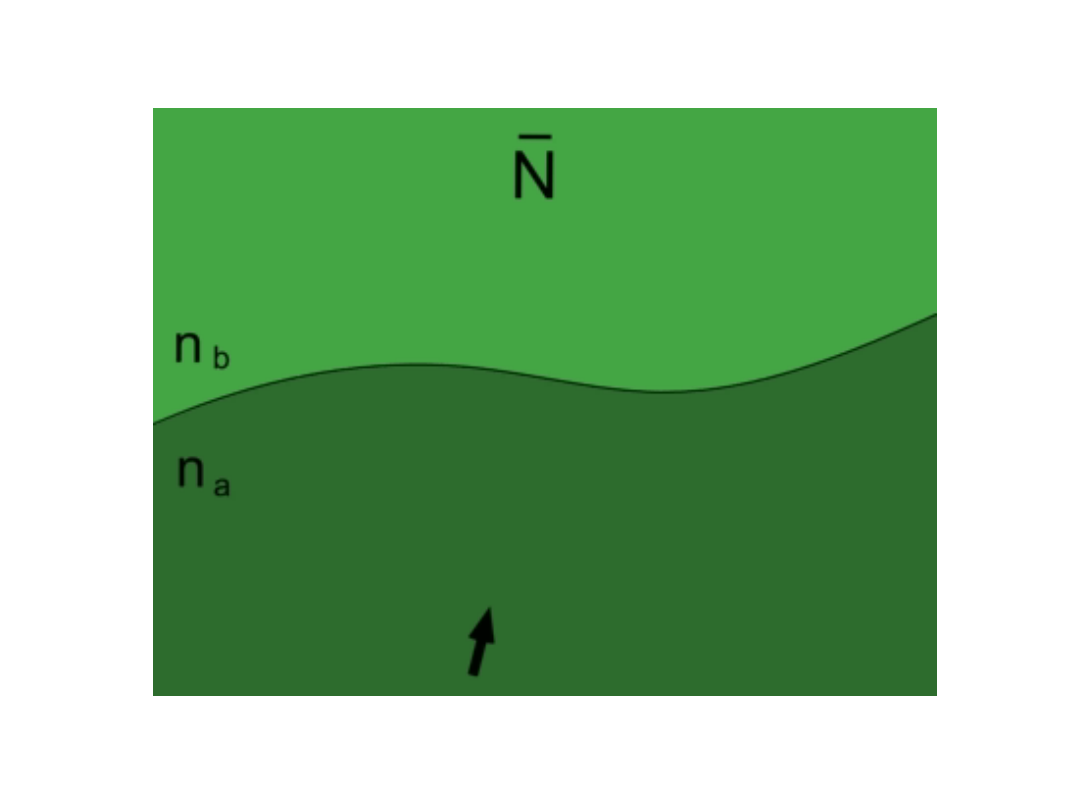
Aksjomaty

cd

n

b

< n

a

n

a

N

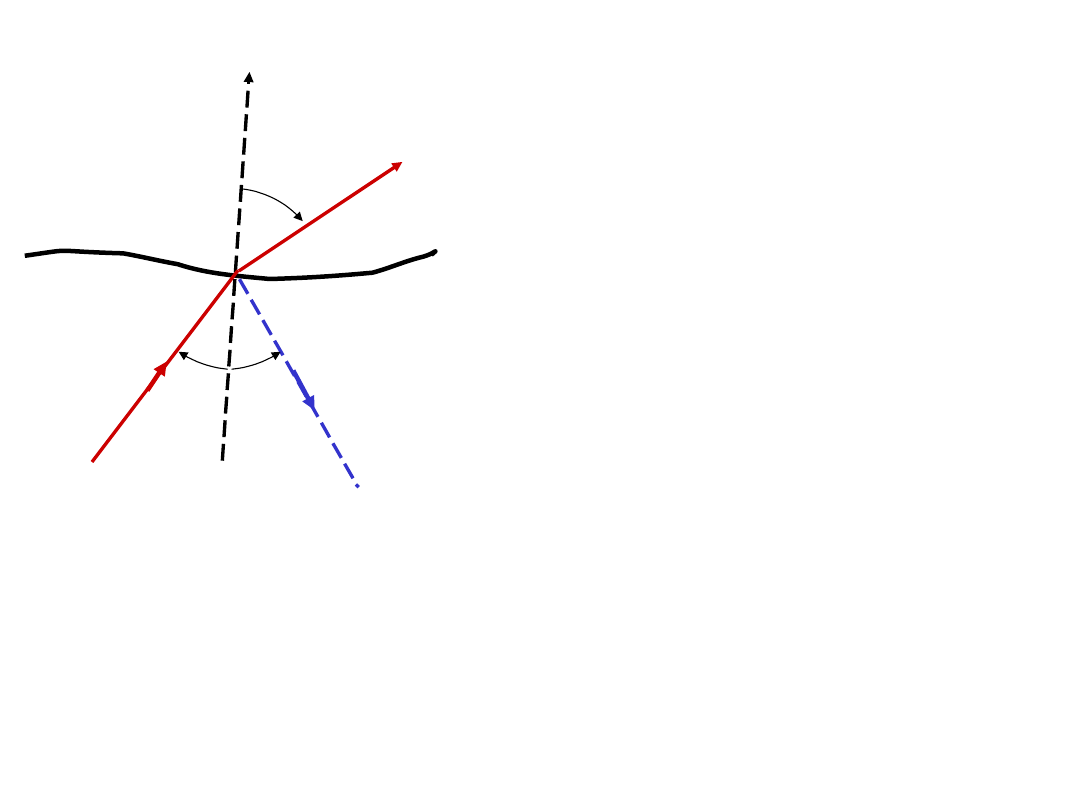
Prawo
załamania

b

b

a

a

sin

n

sin

n







Promień padający, normalna

N

i promień załamany leżą

w tej samej płaszczyźnie



a

Promień

padający



b

Promień

załamany

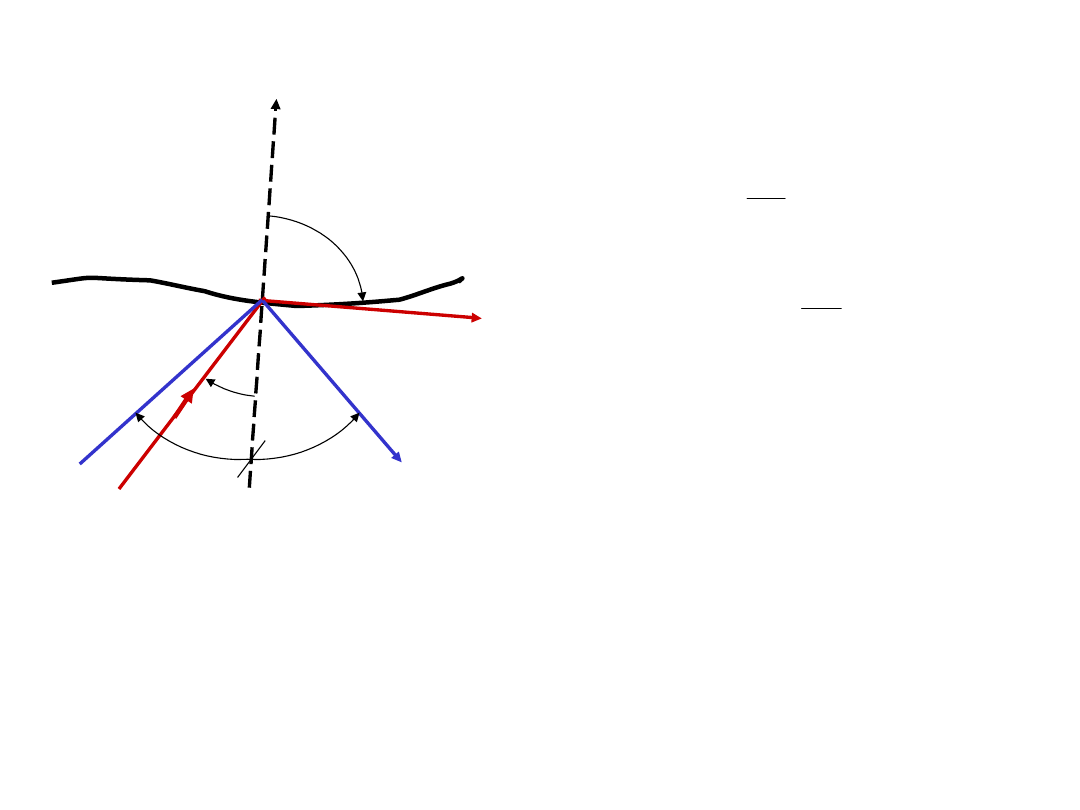
Prawo
odbicia

a

a

'







Promień padający, normalna

N

i promień

odbity leżą w tej samej płaszczyźnie

’

a

Promień

odbity

Całkowite wewnętrzne
odbicie

n

b

< n

a

n

a

N



ag

Promieni

e

padające



bg

=

/2

Promień

załamany

graniczny

’

a



a

Ponieważ

n

a

>

n

b

1

sin

n

n

sin

ag

b

a

bg









i

1

n

n

sin

a

b

ag







Dla promienia



a

>



ag

1

sin

b





Promień ulega

całkowitemu wewnętrznemu

odbiciu

według prawa
odbicia

a

a

'







Zastosowanie w
światłowodach

Względny współczynnik
załamania

Bezwzględny współczynnik załamania
powietrza

760

p

273

/

t

1

a

1

n









0

[nm]

334 546 656

1530

a

[10

6

]

303 293 291

288

t

– temperatura w

0

C

p

–

ciśnienie w

mm Hg

n 

1.0003

Zmiana z temperaturą dla p
= 760

t

10

n

6











1

2

1

2

2

1

n

n

v

c

v

c

v

v

n







1

– ośrodek odniesienia

najczęściej

powietrze

n

2

n

1

–

bezwzględne

współczynniki
załamania

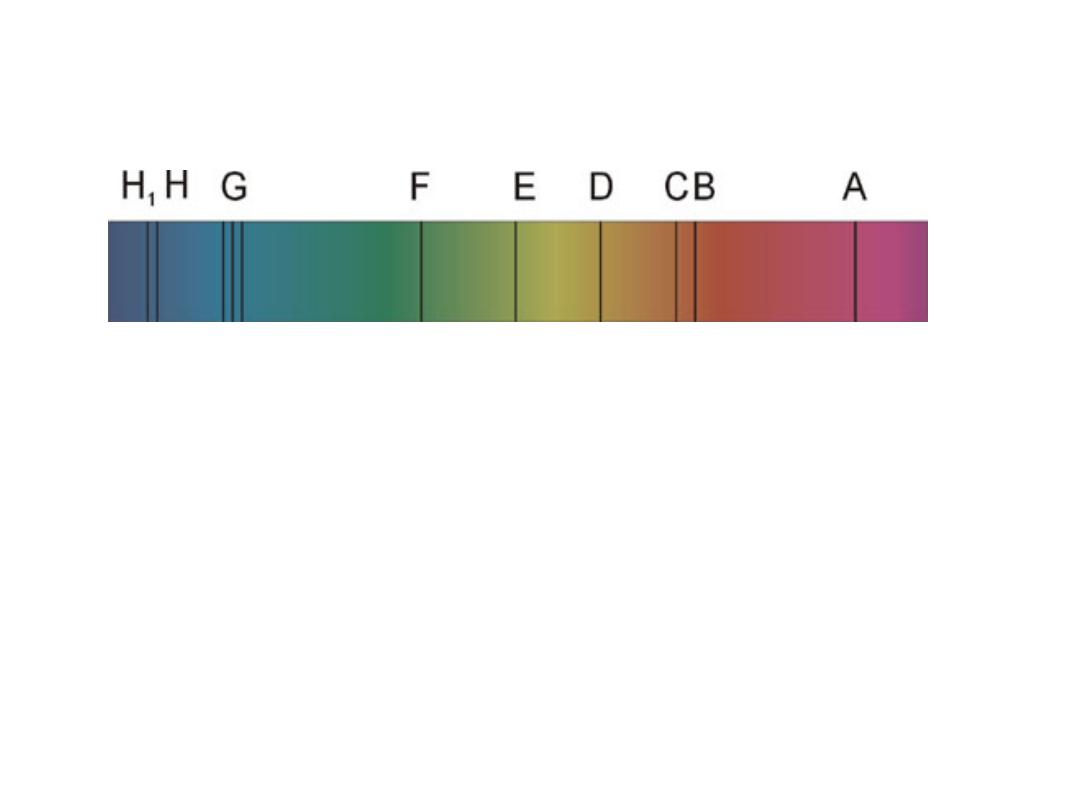
Właściwości dyspersyjne i absorpcyjne
materiałów

Widmo
słońca

linie (Josefa)
Fraunhofera

i365

g435 F486 e546 d587 C656

t1014 nm

Hg Hg H Hg He H

Hg

220 365 435.6 656.3 [nm] 1.014
5 [m]

Kwarc topiony

1.528 1.475 1.467 1.456 1.450

x

Sz. kronowe

x 1.539 1.526 1.514 1.507

x

Sz. flintowe

x 1.815 1.774 1.721 1.715

x

Krzem

x x x x x

3.422

German

x x x x x

4.017

KBr

1.853 1.606 1.583 1.555 1.544

1.534

UV n

i

n

g

n

C

n

t

IR

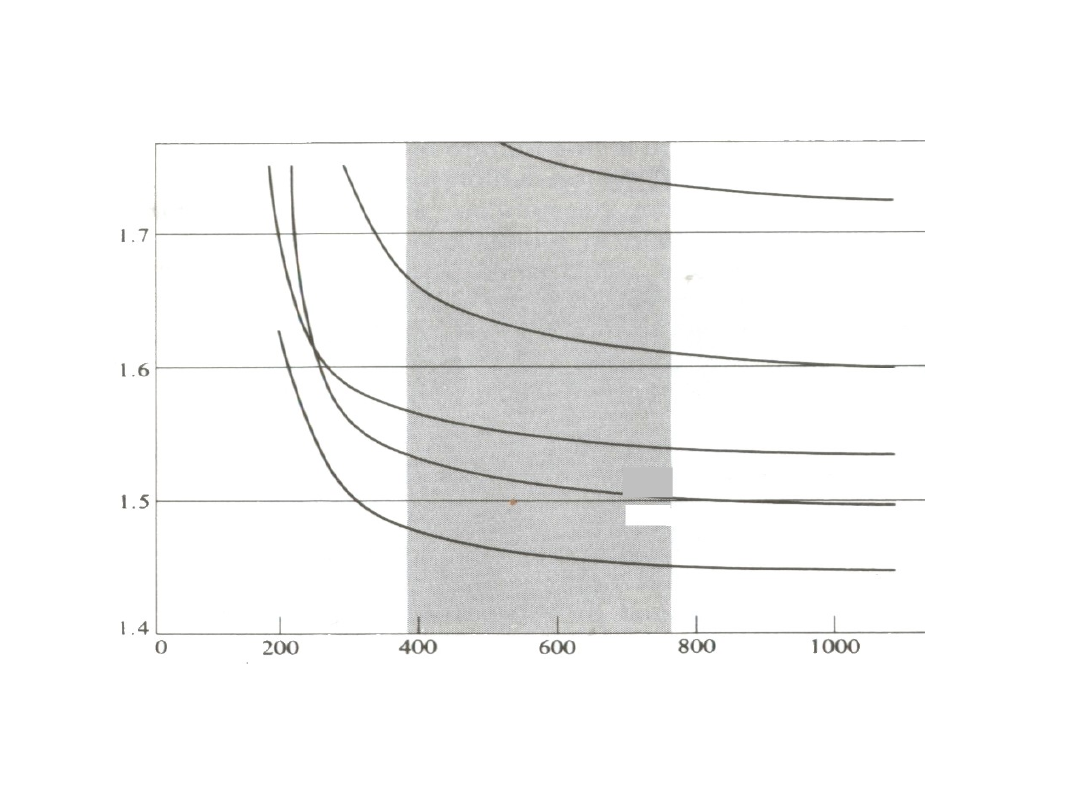
Wsp

ółc

zy

nn

ik

za

ła

ma

nia

Długość fali



nm

Szkło
kwarcowe

Kron

Kwarc

Lekki
flint

Ci

ęż

ki

flint

Krzywe dyspersyjne
materiałów

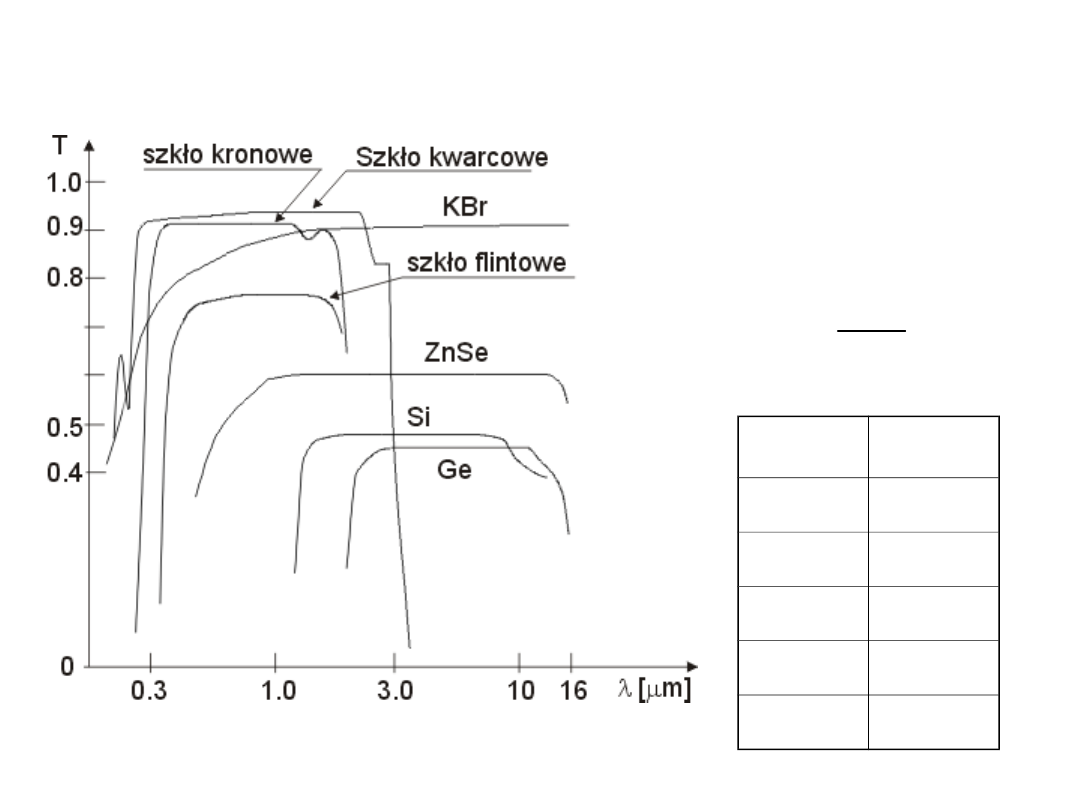
Właściwości transmisyjne
płytki

Współczynniki

odbicia

powierzchni

materiał -

powietrze

2

1

n

1

n





















n

[%]

1.5

4.0

1.6

5.3

1.8

8.1

2.0

11.1

4.0

36.0

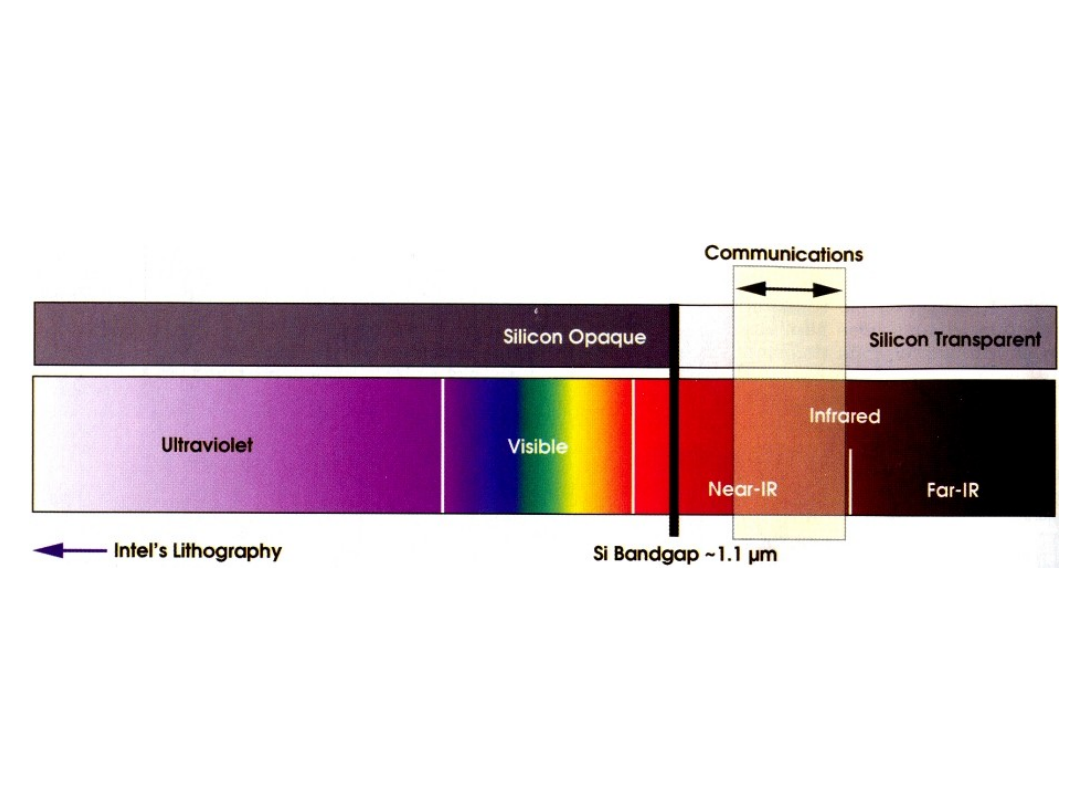
Pasma absorpcyjne krzemu zaznaczone na
czarno

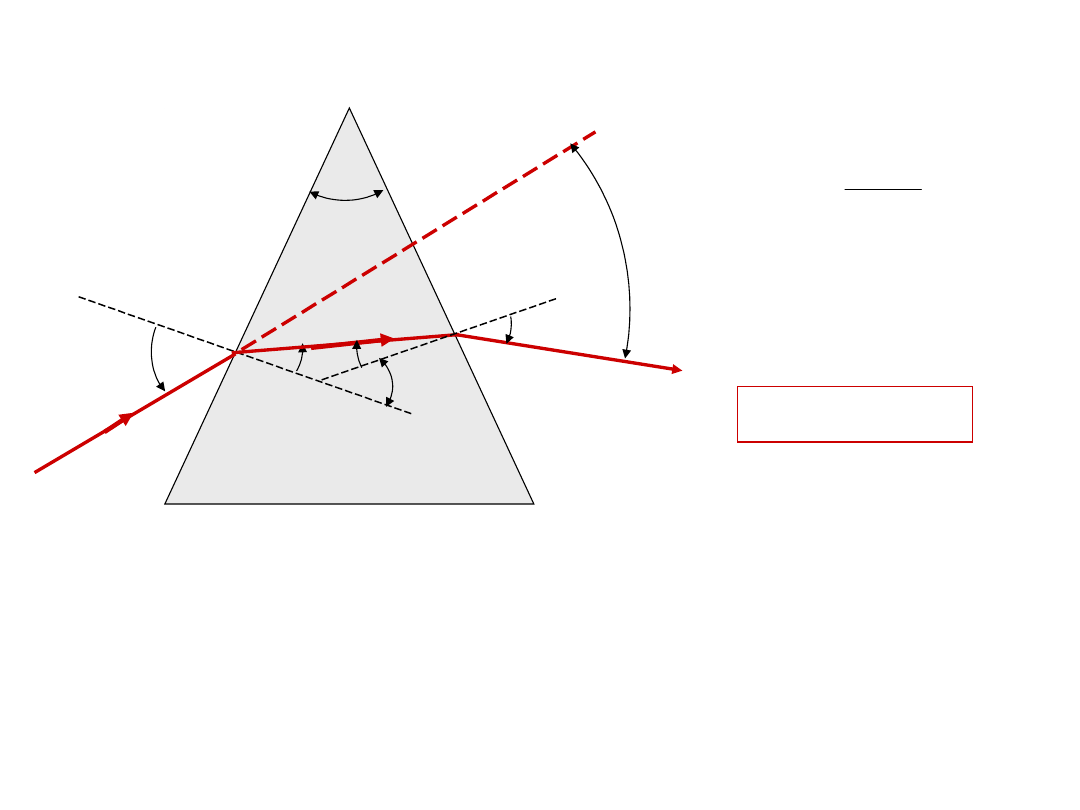
Pryzmat

Reguła znaków



n =
1

n =
1

n

’

2



-

1

-’

1

n

sin

'

sin

1

1









2



1

2

'











2

2

sin

n

'

sin





















1

2

'

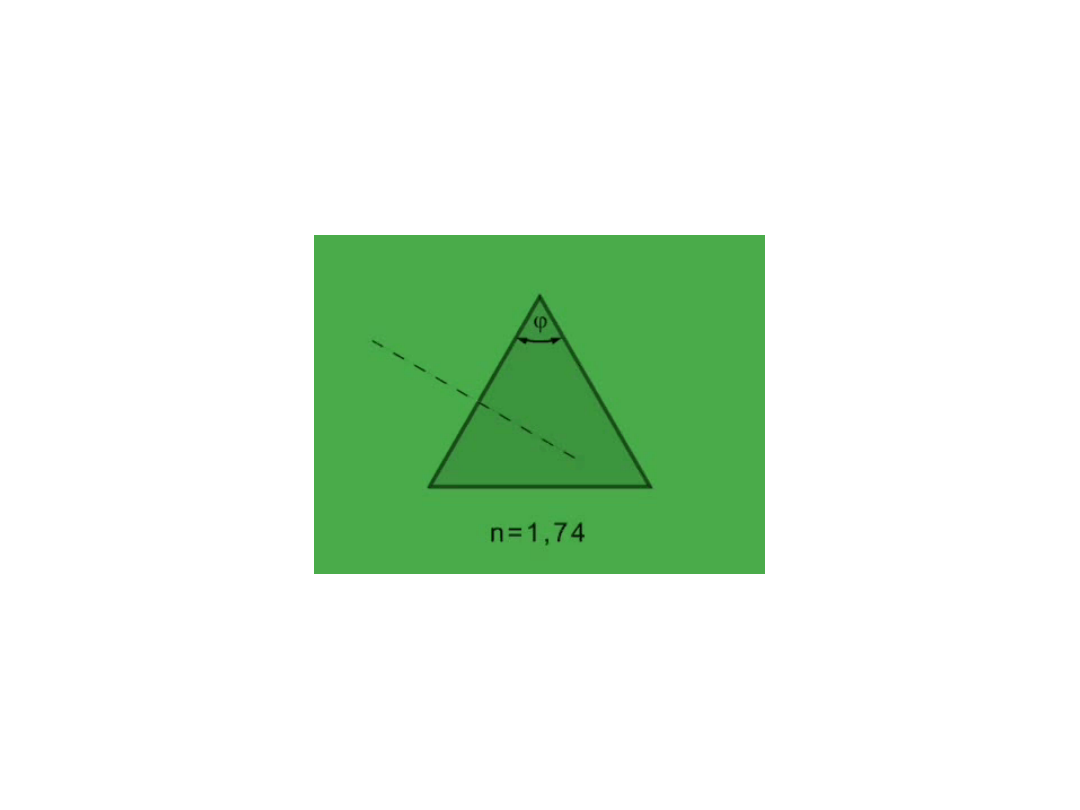
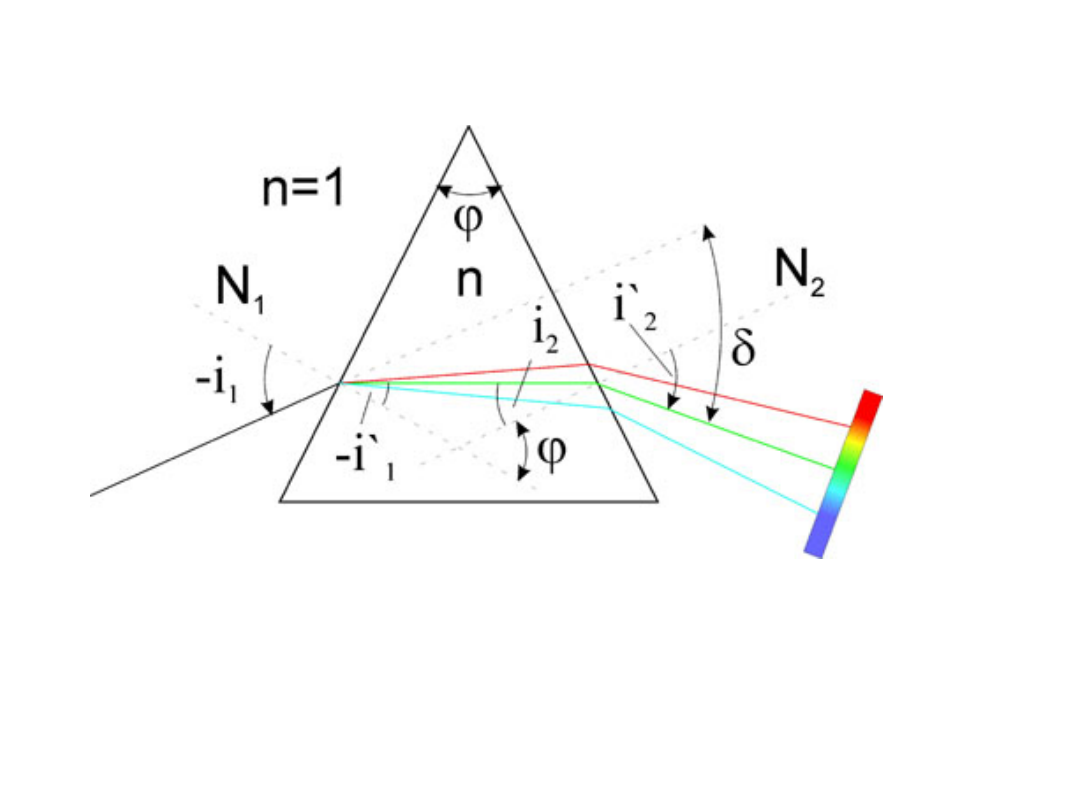
Pryzmat

 

 



















1

2

'

Św

iatł

o

bia

łe

Tęcza.swf

Układ
optyczny

obszar o pewnym rozkładzie współczynnika
załamania

Cel
budowy

Zbiór powierzchni o skokowej zmianie

współczynnika

załamania

Ograniczony obszar o ciągłej jego zmianie

układ

gradientowy

Przykłady:

Przekształcenie przestrzeni przedmiotowej w

obrazową w celu zarejestrowania informacji o

przedmiocie przez odbiornik

Optyka

Fotonika
dodatkowo

Kształtowanie wiązki np. laserowej

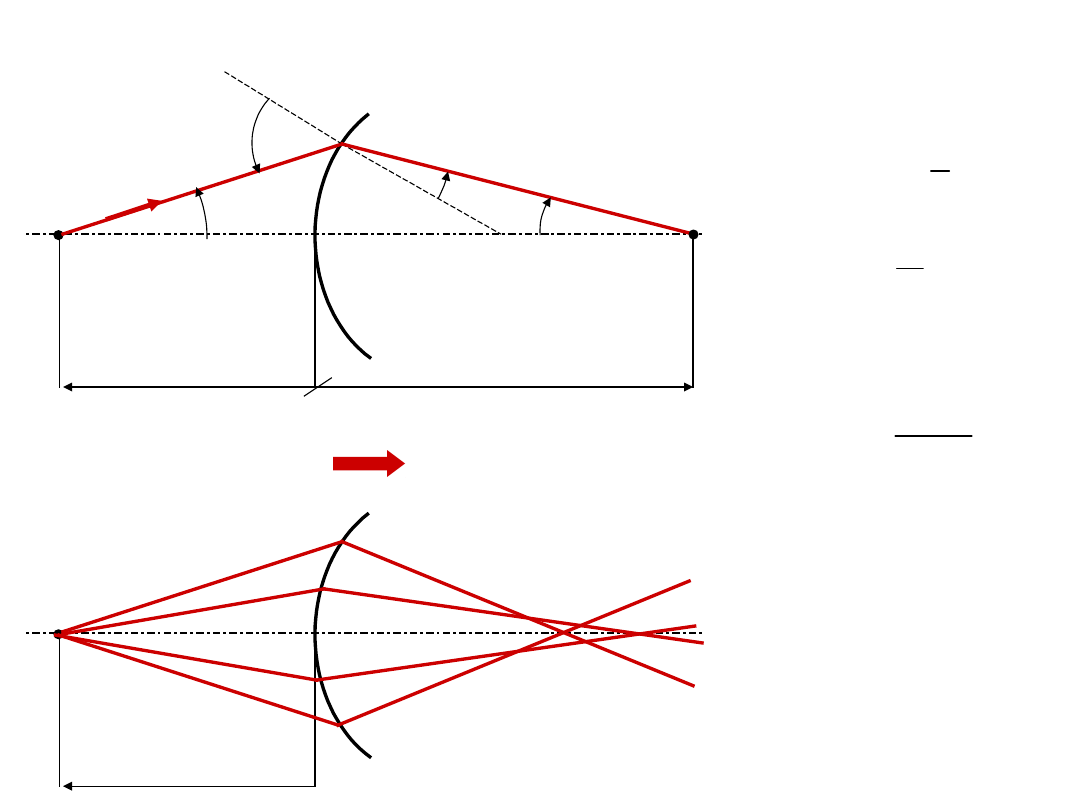
Powierzchnia sferyczna

układ

elementarny

n

n’

O

r

P

-S

-u

-

u

sin

r

S

1

sin











 





P’

u’

-’

S’







sin

'

n

n

'

sin











'

u

'

u



















'

u

sin

'

sin

1

r

'

S

Dane wejściowe

P

(S,u)

Dane wyjściowe

P’

(S’,u’

)

P

-S

 

u

'

S

'

S 

Aberracja

sferyczna

pow_sfer.swf

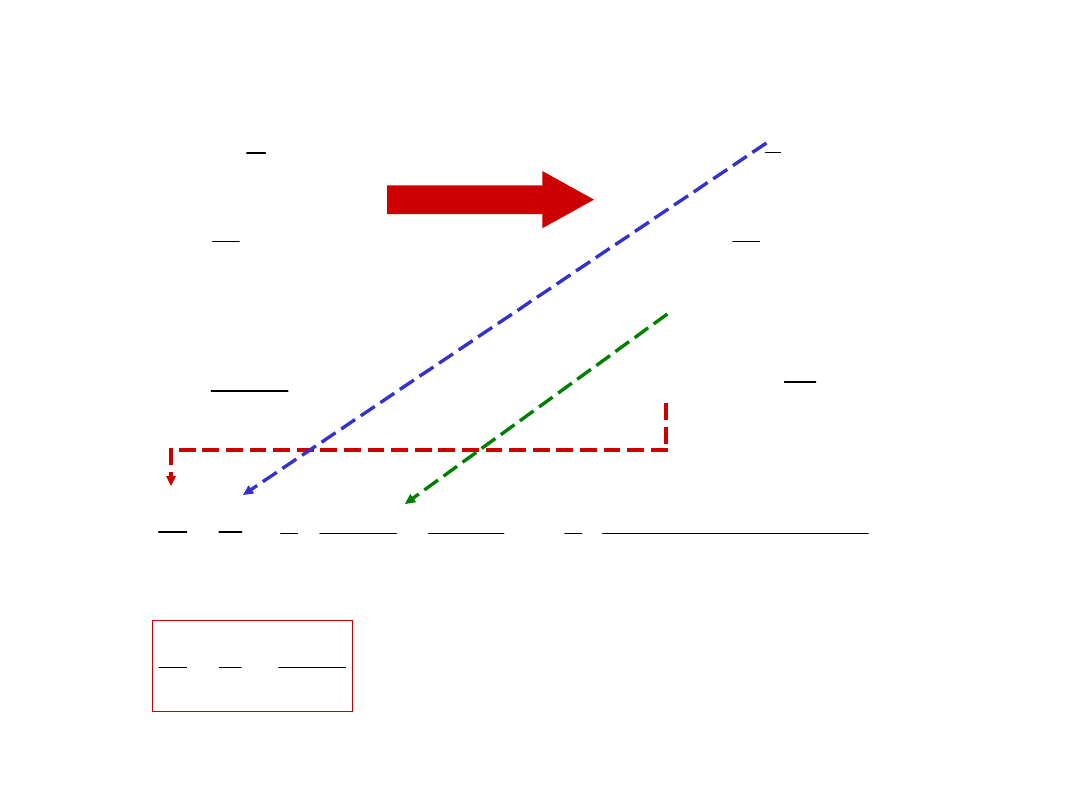
Układ elementarny – przestrzeń przyosiowa

sinx  x





s

n

'

s

'

n

r

n

'

n

s

n

'

s

'

n







u

sin

r

S

1

sin











 











sin

'

n

n

'

sin











'

u

'

u



















'

u

sin

'

sin

1

r

'

S

u

r

s

1











 











'

n

n

'











'

u

'

u



















'

u

'

1

r

'

s

S’  s’ S  s



 

























u

u

n

u

'

n

r

1

























u

nu

'

'

u

'

u

'

n

r

1

W przestrzeni
przyosiowej

s’

jest niezależne od

małego

u

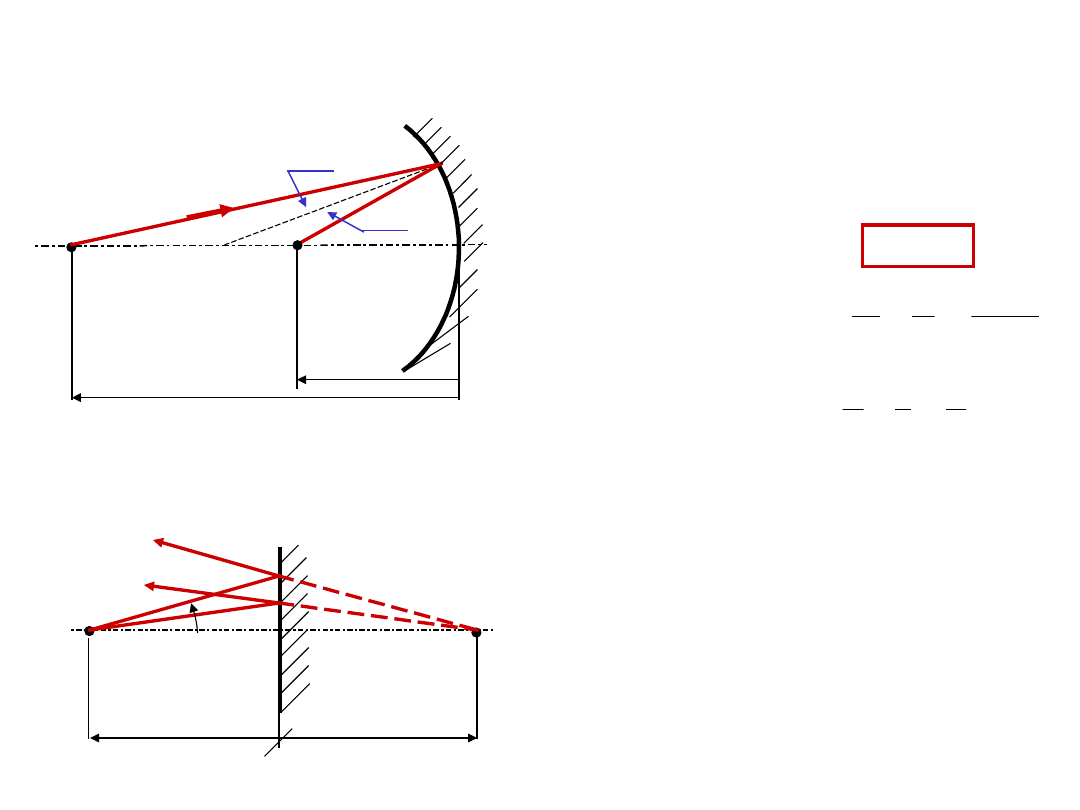
Zwierciadło w przestrzeni przyosiowej

P

-s

P’

-
s’



-’

Zgodnie z regułą znaków

’ =

-

co formalnie dla prawa
załamania





 n

'

'

n

oznacza

n

'

n 



r

n

'

n

s

n

'

s

'

n







Po podstawieniu
do

r

2

s

1

'

s

1





dla zwierciadła

Zwierciadło płaskie

r





mamy

s

'

s 



P

P’

-s = - S

s’ = S’

-u

Obraz

P’

bezaberracyjny

S’ = -S

niezależnie od kąta

u

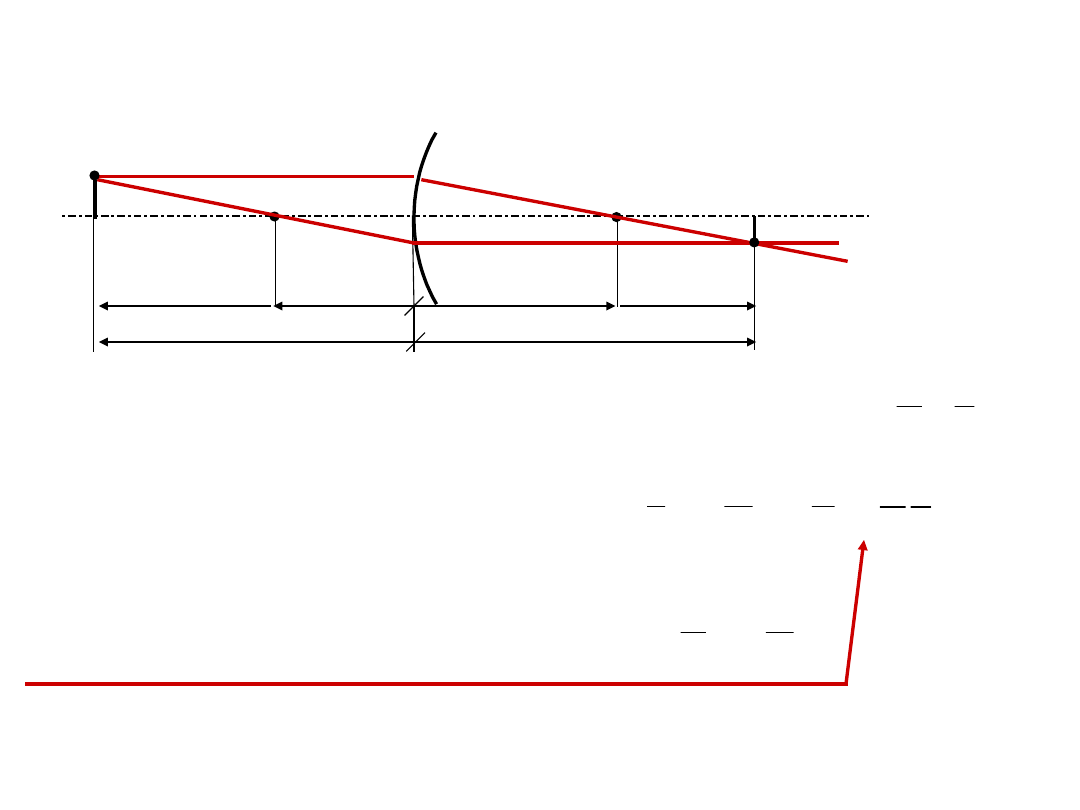
Odwzorowanie przez układ elementarny

w przestrzeni

przyosiowej

Powiększenie
poprzeczne

x

f

'

f

'

x

l

'l













Wzór Newtona

'

f

'

xx 

Ale

f

s

x

'

f

'

s

'

x











1

s

f

'

s

'

f





s

'

s

'

n

n



n

n’ >
n

F

F’

-f

f’

Przedmiot

P

Obraz

P’

-l’

l

-x

-s

x’

s’

po
uwzględnieniu

'

f

'

s

'

x

f

s

x









n

'

n

f

'

f





oraz

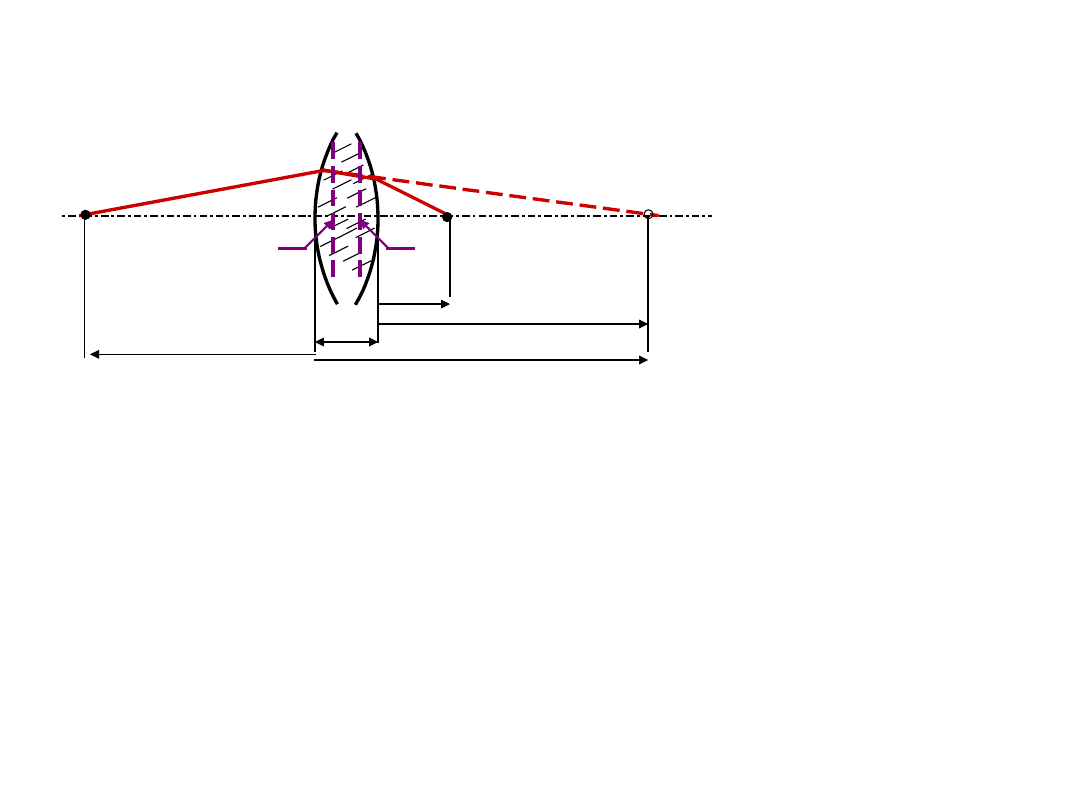
Soczewka w przestrzeni
przyosiowej

2

1





 

Powiększenie



dla

soczewki

W celu znalezienia obrazu dawanego przez

soczewkę

wystarczy znać

położenie jej

płaszczyzn głównych

H, H’

i ognisk

F, F’

n = 1

n

n = 1

d

P’

1

 P

2

s’

2

P’

2

-s

1

P

1

s

2

s’

1

Płaszczyzny główne



H

=

1

H

H’

Dotyczy to również obiektywu, lub innego układu

optycznego

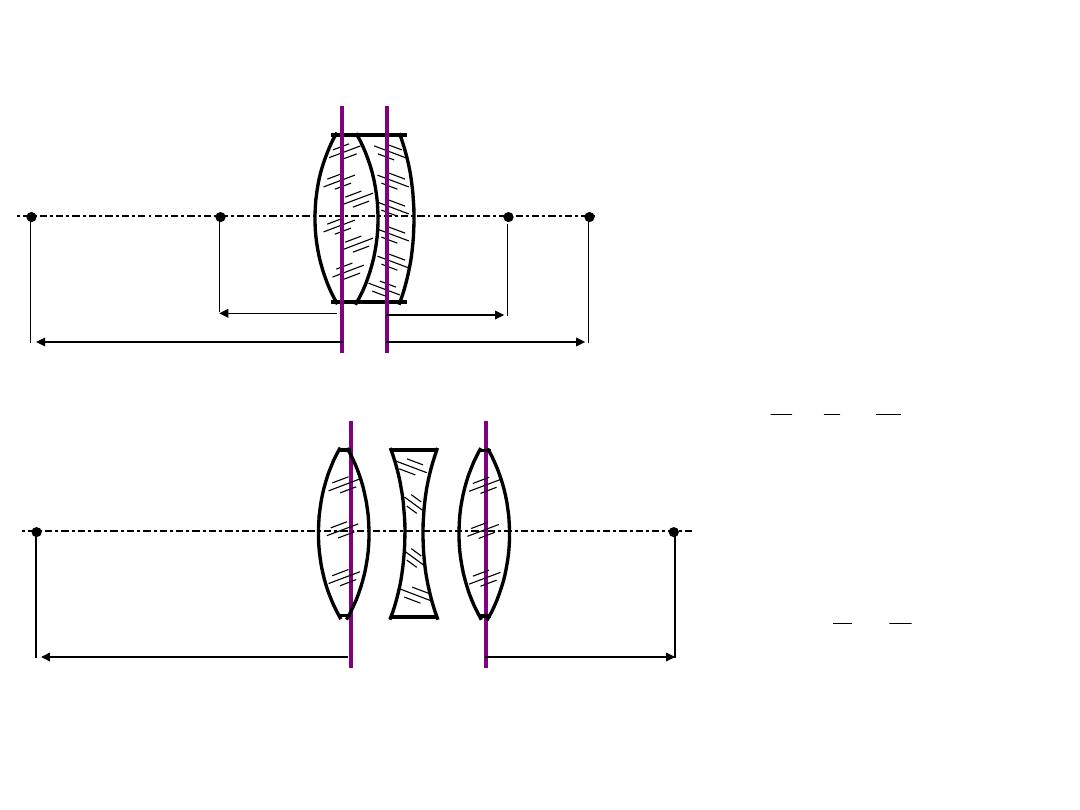
Obiektywy w powietrzu

f’ = -f

Znane ogniskowa

f’

i położenie

F

i

F’

albo

znane ogniskowa

f’

i

położenie

H

i

H’

f’

f’

s’

-s

F

F’

H

H’

P

P’

s’

-s

H

H’

P

P’

'

f

1

s

1

'

s

1





Położenie obrazu

P’

s

'

s

l

'l







Powiększenie

poprzeczne

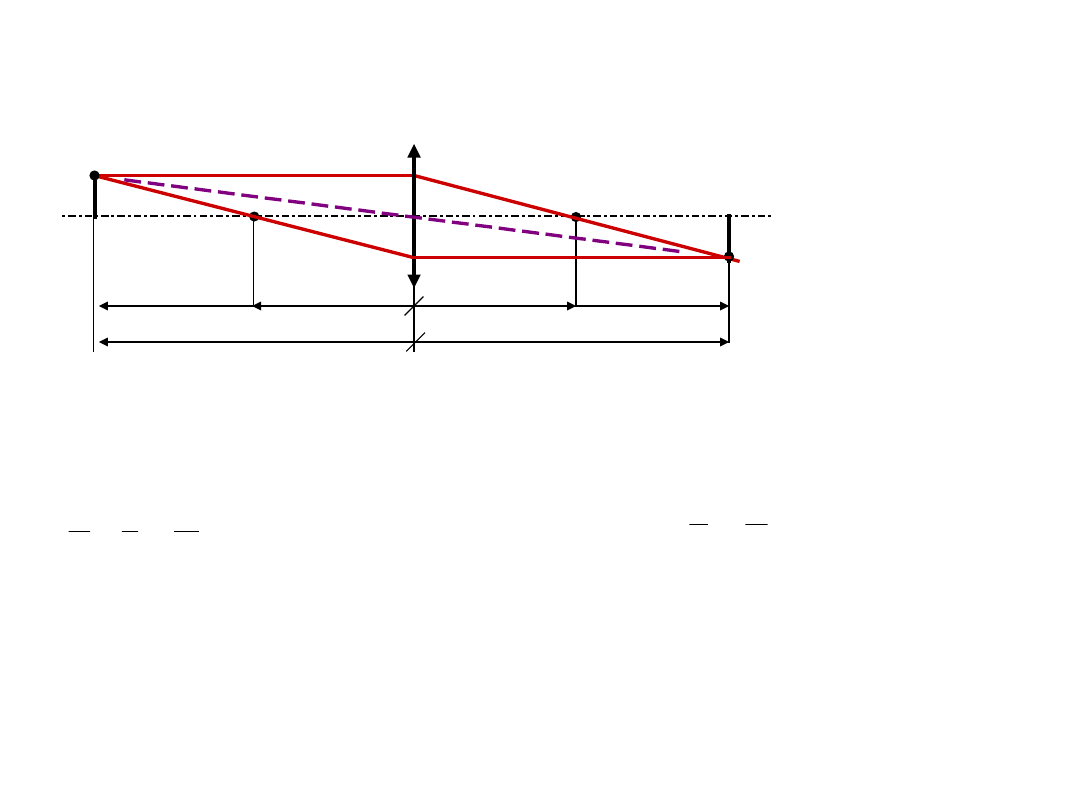
n =
1

n =
1

F

F’

f’

f’

P

P’

-l’

l

-x

-s

x’

s’

H H’

Obiektyw jako układ
cienki

s

'

s

l

'l







Powiększenie

poprzeczne

'

f

1

s

1

'

s

1





Położenie obrazu

P’

2

'

f

'

xx 



lub

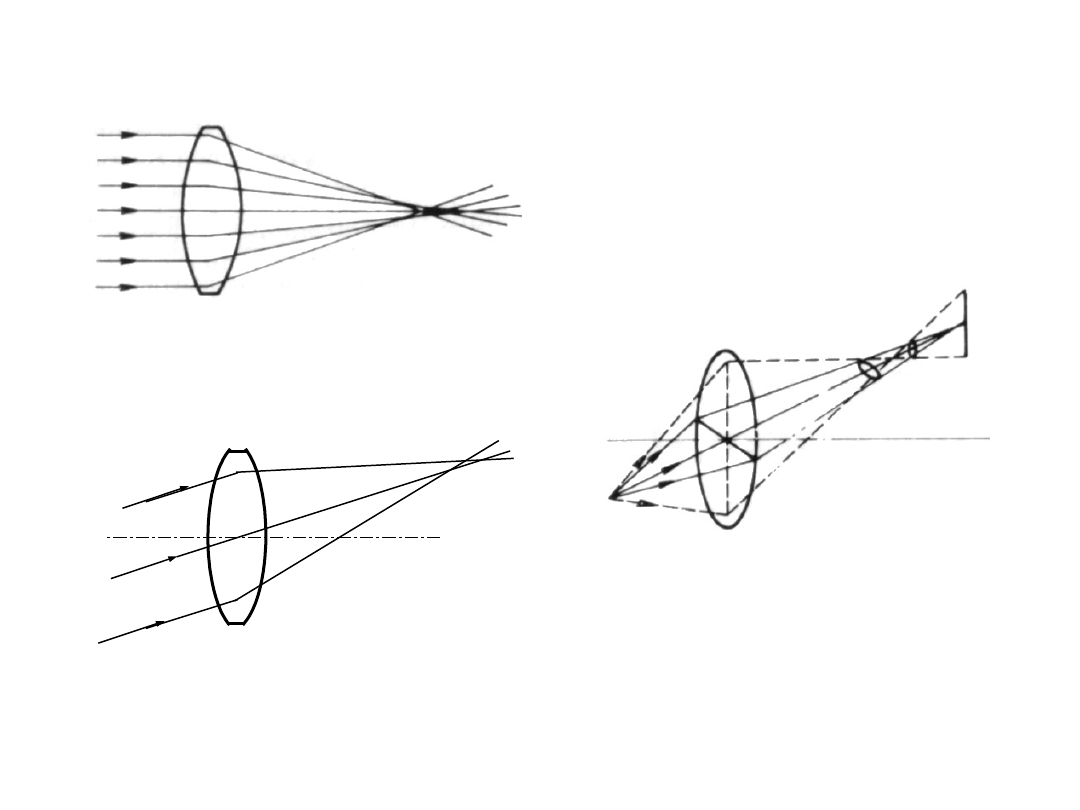
Aberracje obiektywu

- aberracje

monochromatyczne

Aberracja
sferyczna

Astygmatyzm

Koma

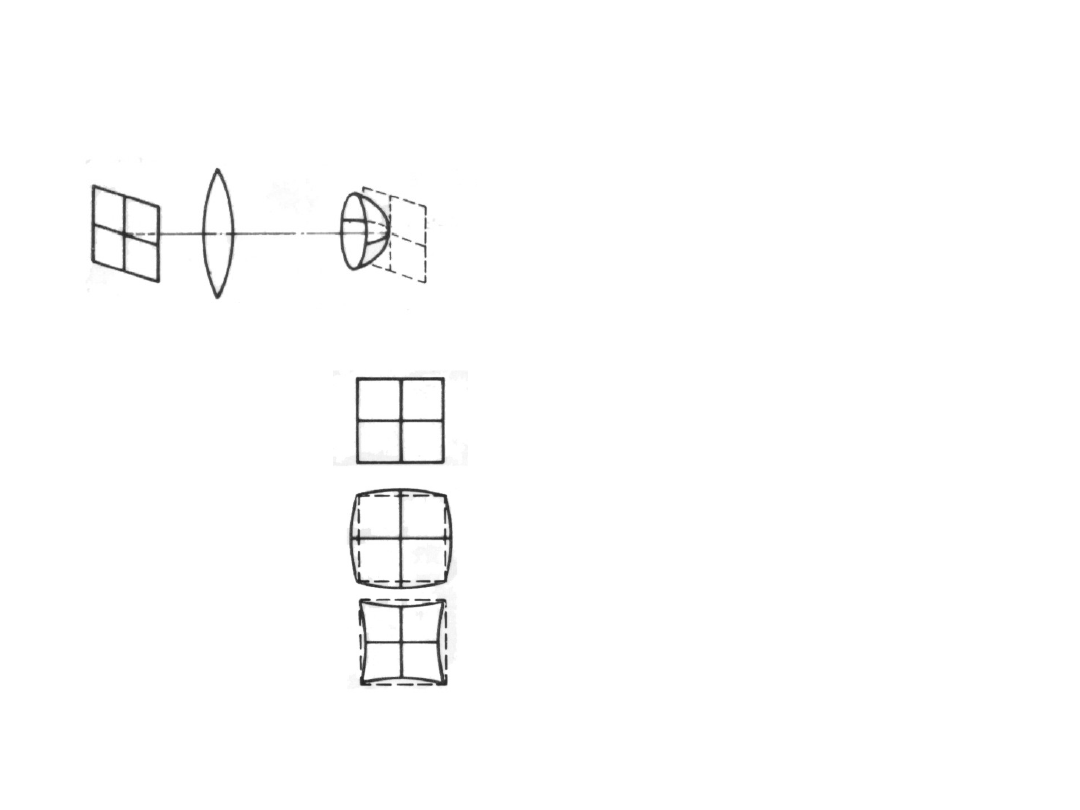
Aberracje obiektywu

- aberracje

monochromatyczne cd

Krzywizna pola

Przedmiot

Obraz

Dystorsja

Obraz
bezdystorsyjny

beczkowata

jaśkowata

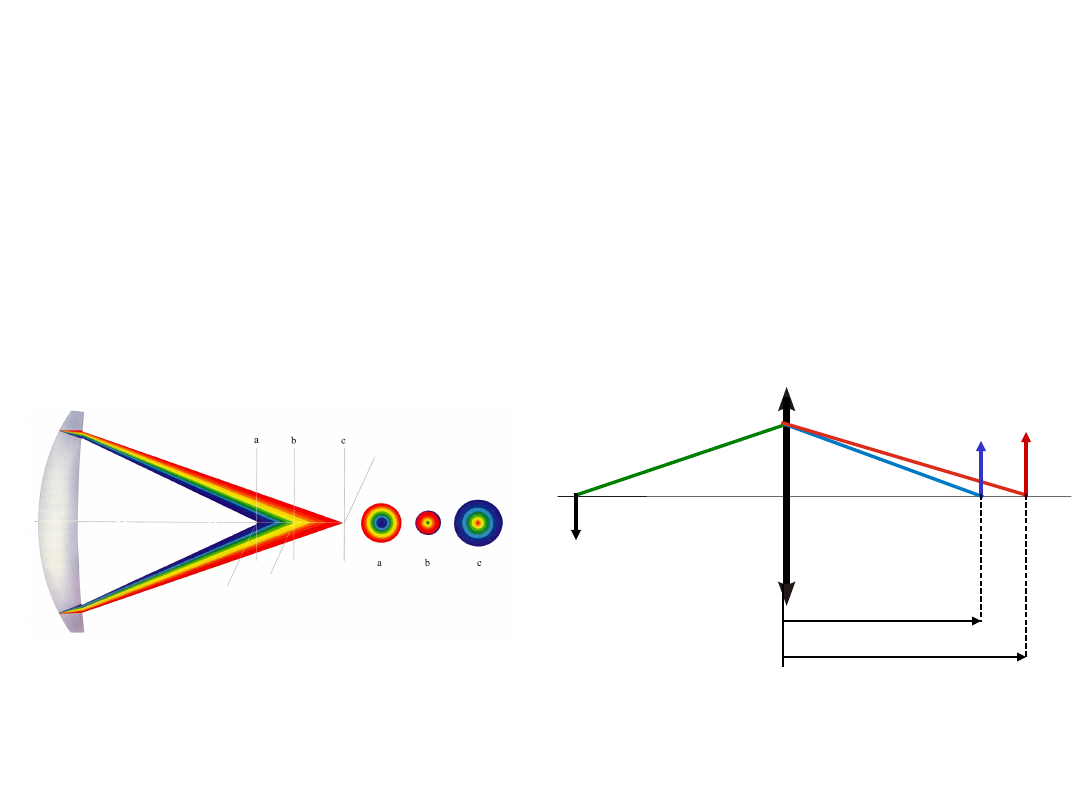
Aberracje obiektywu

- aberracje

chromatyczne

Ogniskowa

f’

położenia płaszczyzn głównych

H H’

położenia ognisk

F F’

są funkcjami





położenie obrazu i jego powiększenie są również
funkcją



chromatyzm położenia

chromatyzm
powiększenia

P

P’

F

P’

C

s’

F

s’

C