1 /14

Problem decyzyjny

• Firma AGA produkuje dwa szampony A i B. Litr A sprzedaje po 9zł a litr B sprzedaje
po 5zł. Celem firmy jest osiągnięcie jak największej wartości produkcji.

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

(funkcja celu)

Gdzie

x1 – produkcja szamponu A w litrach,

x2 – produkcja szamponu B w litrach

• Szampony produkowane są z trzech składników: Z1, Z2 i Z3. Wyprodukowanie 1 litra

szamponu A wymaga zużycia 20 dag składnika Z1, 40 dag składnika Z2 i 30 dag

składnika Z3. Natomiast w przypadku szamponu B zużycie składników Z1, Z2 i Z3

wynosi odpowiednio 30, 10 i 20 dag. Na najbliższy miesiąc zasoby tych składników
wynoszą

odpowiednio 60, 30 i 40 kg.

0,2x

1

+ 0,3x

2

<= 60

0,4x

1

+ 0,1x

2

<= 30

warunki ograniczające (zbiór decyzji

dopuszczalnych)

0,3x

1

+ 0,2x

2

<= 40

(x

1

, x

2

) – decyzja (zmienne

decyzyjne)

2 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

•Czy decyzja (x

1

, x

2

) = (60, 90) jest decyzją

dopuszczalną?

NIE, bo

0,2*60 + 0,3*90 = 39 < 60 (warunek spełniony)

0,4*60 + 0,1*90 = 33 > 30

(warunek niespełniony)

0,3*60 + 0,2*90 = 36 < 40 (warunek spełniony)

0,2x

1

+ 0,3x

2

<= 60

0,4x

1

+ 0,1x

2

<= 30

0,3x

1

+ 0,2x

2

<= 40

Przykład 1

•Czy przy tak sformułowanym problemie, jak
powyżej, decyzja

(x

1

, x

2

) = (50, 20) jest

decyzją dopuszczalną?

TAK, bo

0,2*50 + 0,3*20 = 16 < 60 (warunek
spełniony)

0,4*50 + 0,1*20 = 22 < 30 (warunek
spełniony)

0,3*50 + 0,2*20 = 19 < 40 (warunek
spełniony)

3 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

Decyzja optymalna - najlepsza decyzja dopuszczalna

20
0

x

1

x

2

30
0

75

30
0

1

2

13
3

3

f(x

1

,x

2

)

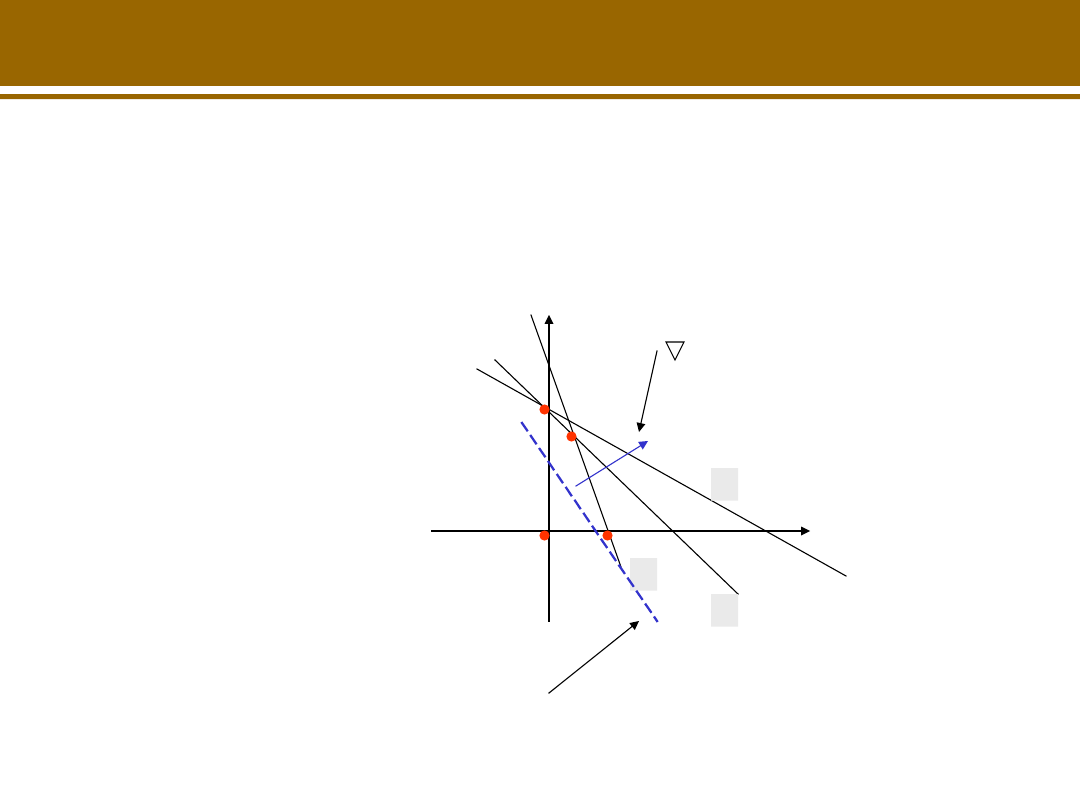
Warstwica funkcji f(x

1

, x

2

) dla wybranej wartości z

np. dla z=450 f (x

1

, x

2

): 9x

1

+ 5x

2

= 450 (prosta przecinająca oś 0x

1

w pkt.

50, 0x

2

w pkt. 90

Kierunek najszybszego
wzrostu wartości funkcji,
czyli wektor pochodnych
cząstkowych

f = [9 5]

lub (nachylenie

prostej:

–

9/5)

4 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

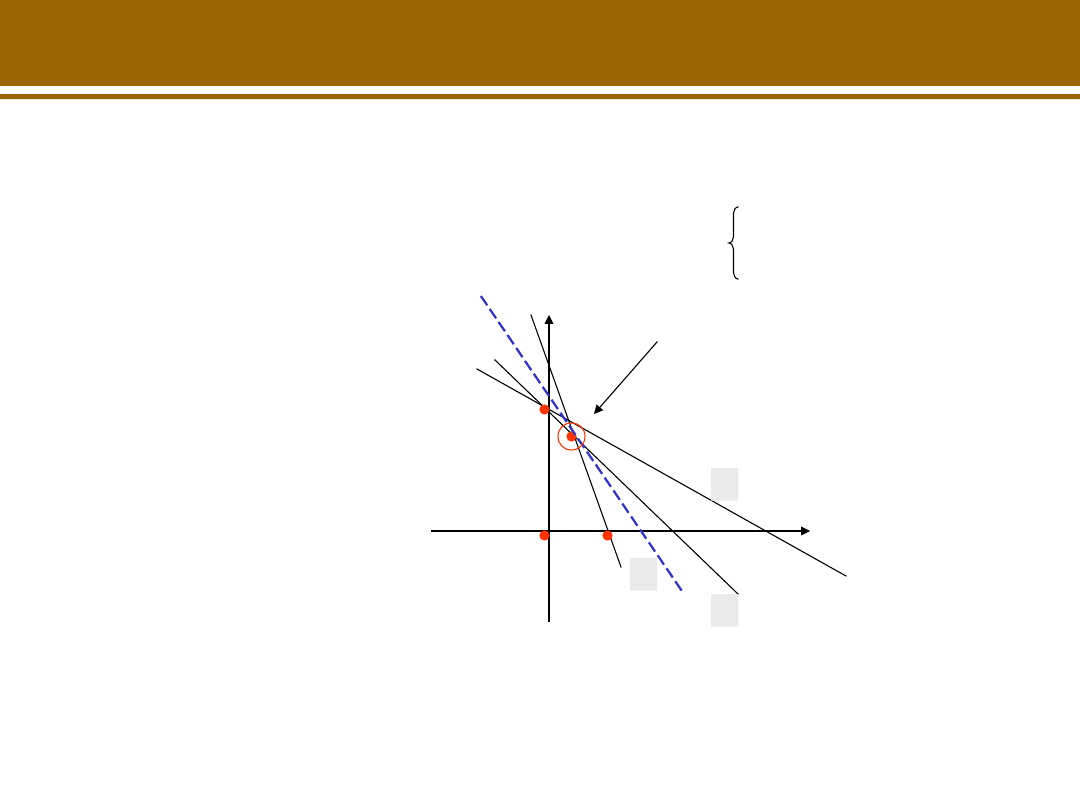
Decyzja optymalna - najlepsza decyzja dopuszczalna

Decyzja optymalna
(40,140)

20
0

x

1

x

2

30
0

75

30
0

1

2

13
3

3

0,4x

1

+ 0,1x

2

=

30

0,3x

1

+ 0,2x

2

=

40

5 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

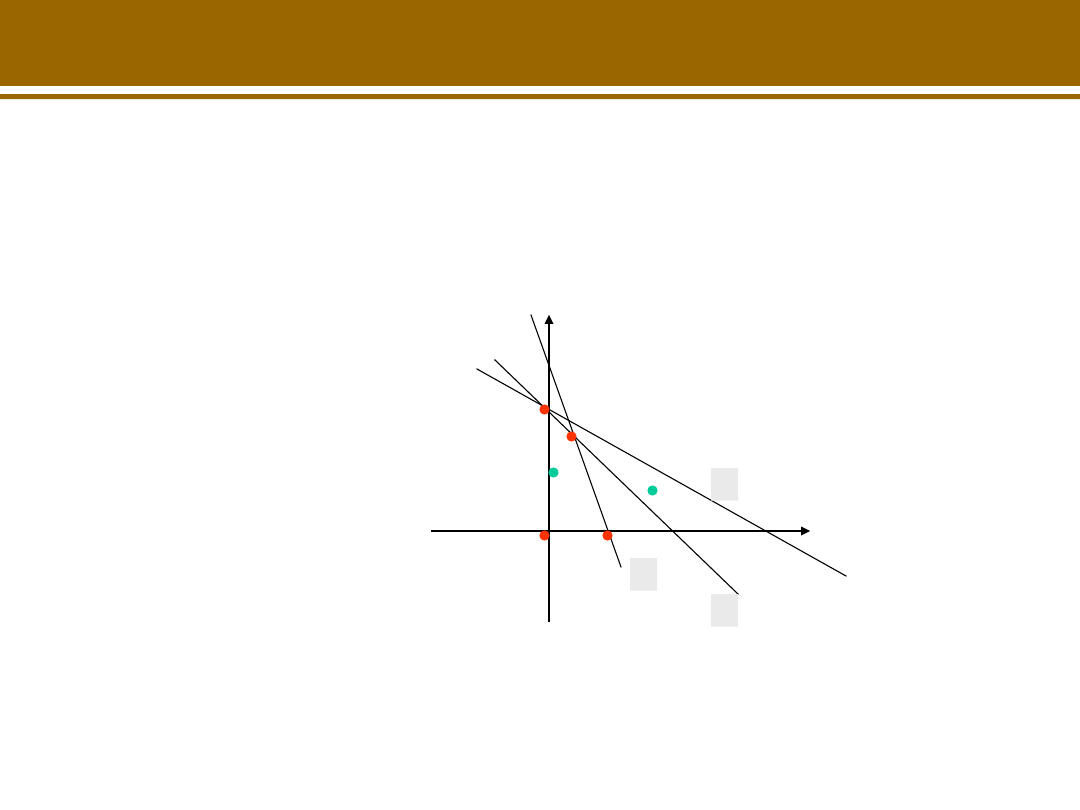
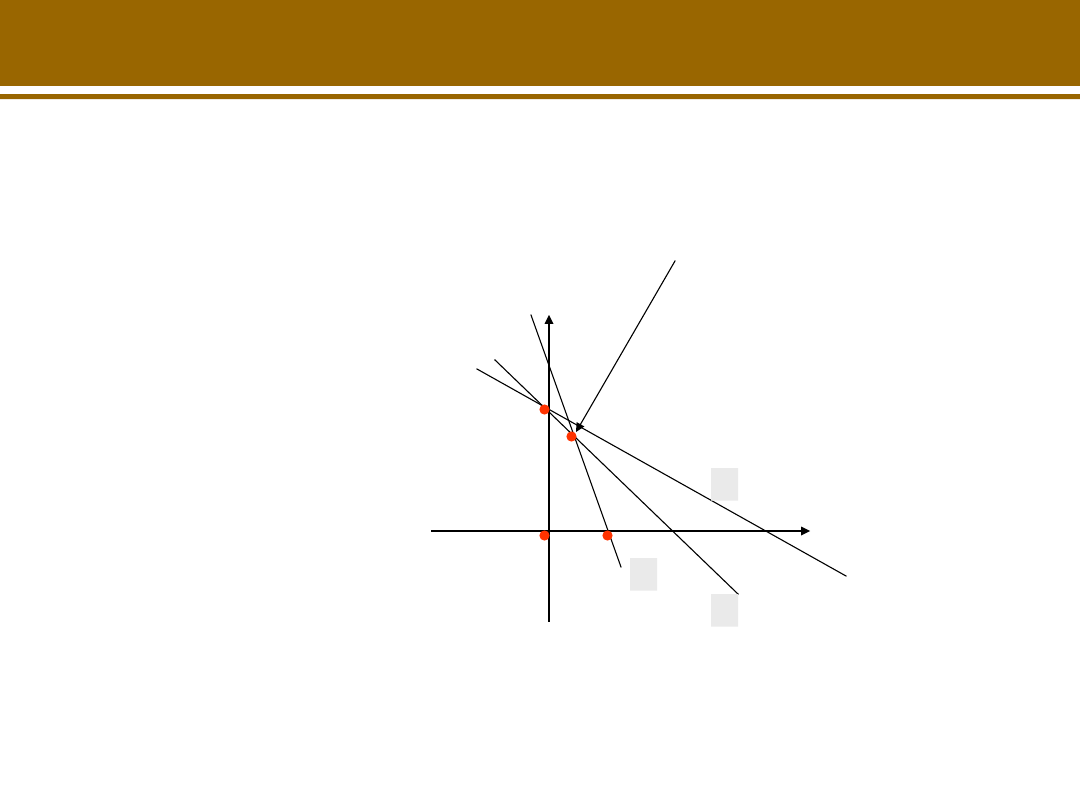
Przykład 2

• Czy punkt A jest decyzją dopuszczalną?

NIE

• Które warunki są spełnione w punkcie A?

Tylko 1

• Czy punkt B jest decyzją dopuszczalną?

TAK

• Czy w punkcie B korzystamy

ze wszystkich składników

do produkcji szamponu?

TAK, bo produkujemy szampon B (x2)

do którego potrzebne są wszystkie

Trzy składniki

20
0

x

1

x

2

30
0

75

30
0

1

2

13
3

3

A

B

6 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

20
0

x

1

x

2

30
0

75

30
0

1

2

13
3

3

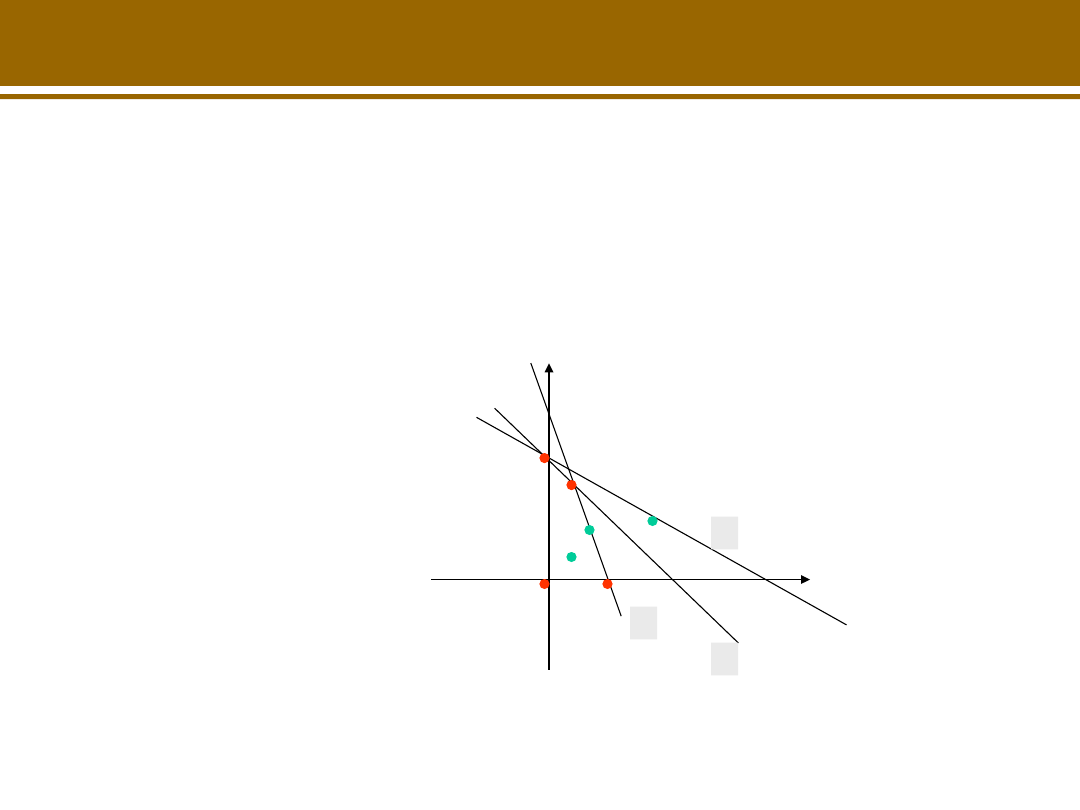
Warunki 2 i 3 są napięte, warunek 1 jest luźny

Brakuje składników 2 i 3 do wyprodukowania
większej ilości szamponów, natomiast zapasy
składnika 1 są nie w pełni wykorzystane

7 /14

Problem decyzyjny

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

x

2

• Które warunki są napięte, a które luźne w punkcie A?

1 jest napięty a

2 i 3 brakuje (żaden nie jest luźny)

• Które warunki są napięte, a które luźne w punkcie B?

Wszystkie trzy

luźne

• Które warunki są napięte, a które luźne w punkcie C?

2 napięty, a 1 i

3 luźne

Przykład 3

20
0

x

1

30
0

75

30
0

1

2

13
3

3

A

B

C

8 /14

Problem decyzyjny

• Jaka decyzja jest optymalna jeśli cena szamponu B
wynosi 2,25zł?

Przykład 4

f(x

1

, x

2

) = 9x

1

+

2,25

x

2

->

max

1. 0,2x

1

+ 0,3x

2

<=

60

2. 0,4x

1

+ 0,1x

2

<=

30

3. 0,3x

1

+ 0,2x

2

<=

40

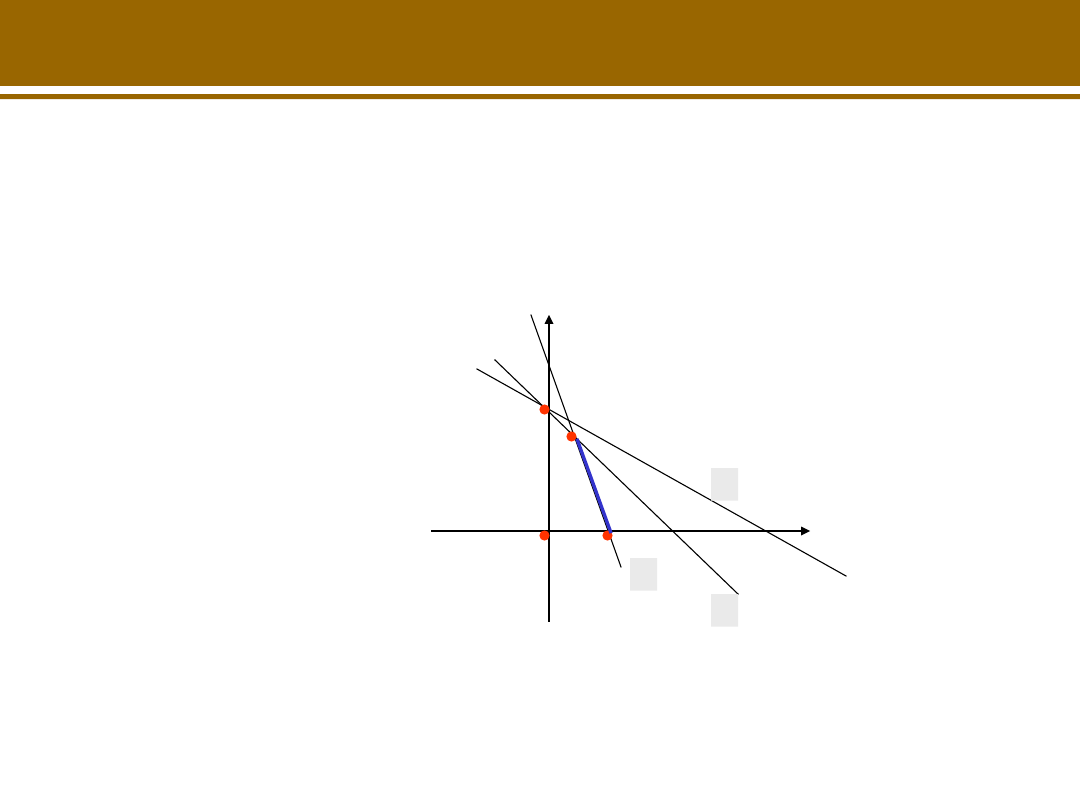
Nachylenie prostej –9/2,25 =
-4

Zatem warstwica jest równoległa
do prostej wyznaczającej drugi
warunek

Rozwiązaniem jest zbiór alternatywnych decyzji
optymalnych

– odcinek o końcach (75,0) i (40,140). Rozwiązań

optymalnych jest

nieskończenie wiele

.

x

2

20
0

x

1

30
0

75

30
0

1

2

13
3

3

9 /14

Problem decyzyjny

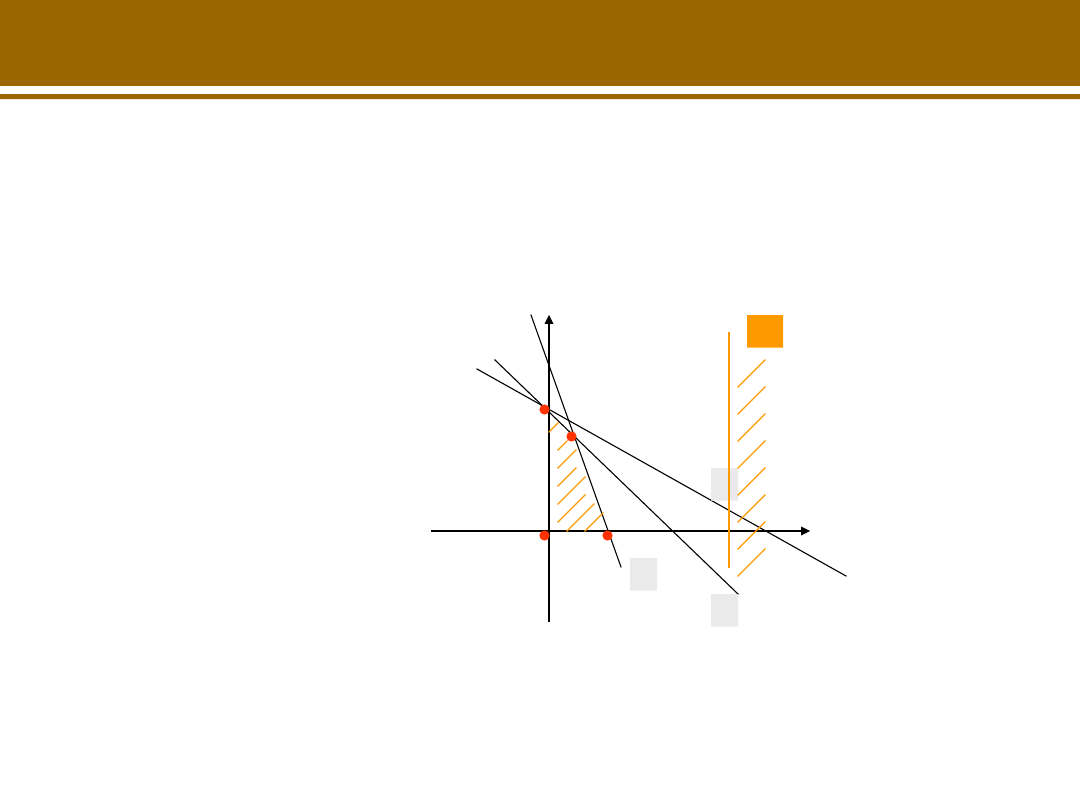
• Jaka decyzja jest optymalna jeśli nałożymy dodatkowy
warunek: firma musi wyprodukować co najmniej 200 litrów
szamponu A?

Przykład 5

f(x

1

, x

2

) = 9x

1

+ 5x

2

-> max

1. 0,2x

1

+ 0,3x

2

<= 60

2. 0,4x

1

+ 0,1x

2

<= 30

3. 0,3x

1

+ 0,2x

2

<= 40

4. x

1

>= 200

x

2

20
0

x

1

30
0

75

30
0

1

2

13
3

3

4

Nie istnieje decyzja optymalna, ponieważ jest to zadanie
sprzeczne (zbiór decyzji dopuszczalnych jest pusty).

10 /14

Problem decyzyjny

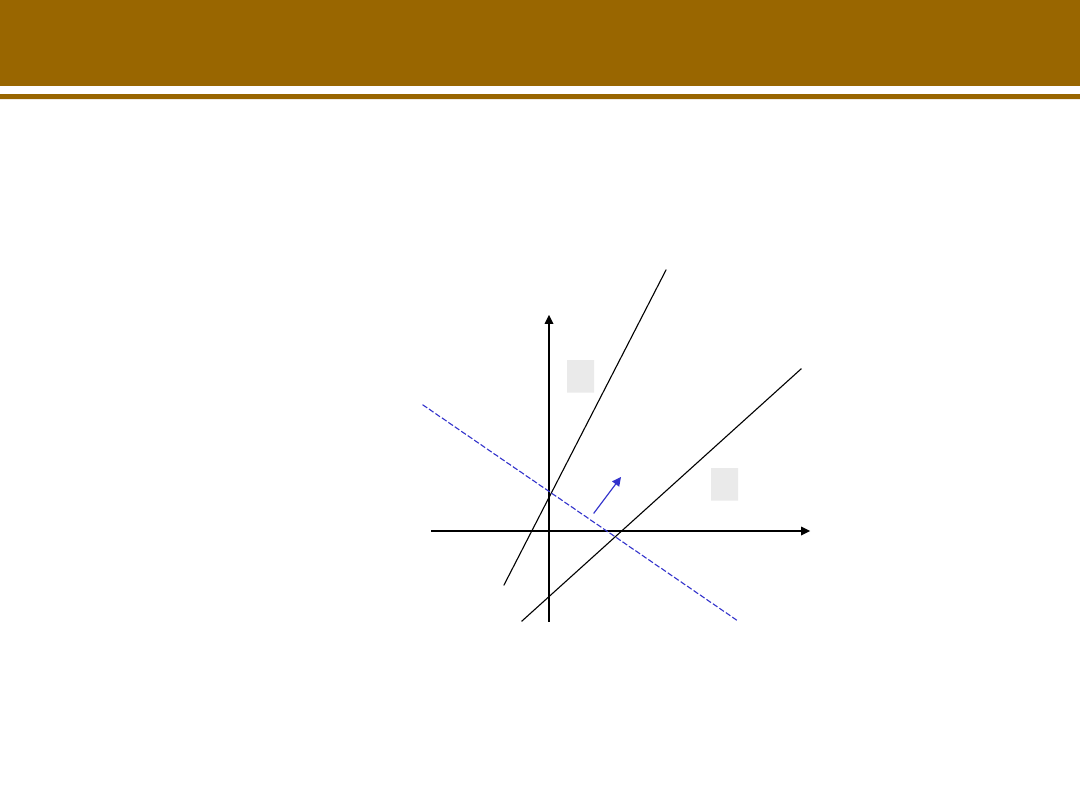
Funkcja celu nieograniczona:

2x

1

+ 3x

2

-> max

x

1

– x

2

<=3

-2x

1

+ x

2

<=1

x

2

x

1

1

2

11 /14

Zadanie programowania liniowego

f(x

1

, x

2

, x

3

... x

n

) = c

1

x

1

+ c

2

x

2

+ ... + c

n

x

n

-> max/min

Przy warunkach
a

11

x

1

+ a

12

x

2

+ ... + a

1n

x

n

<= b

1

a

21

x

1

+ a

22

x

2

+ ... + a

2n

x

n

<= b

2

...

a

m1

x

1

+ a

m2

x

2

+ ... + a

mn

x

n

<= b

m

Współczynniki funkcji celu

Zadanie PL z n zmiennymi decyzyjnymi:

Wyraz wolny warunku