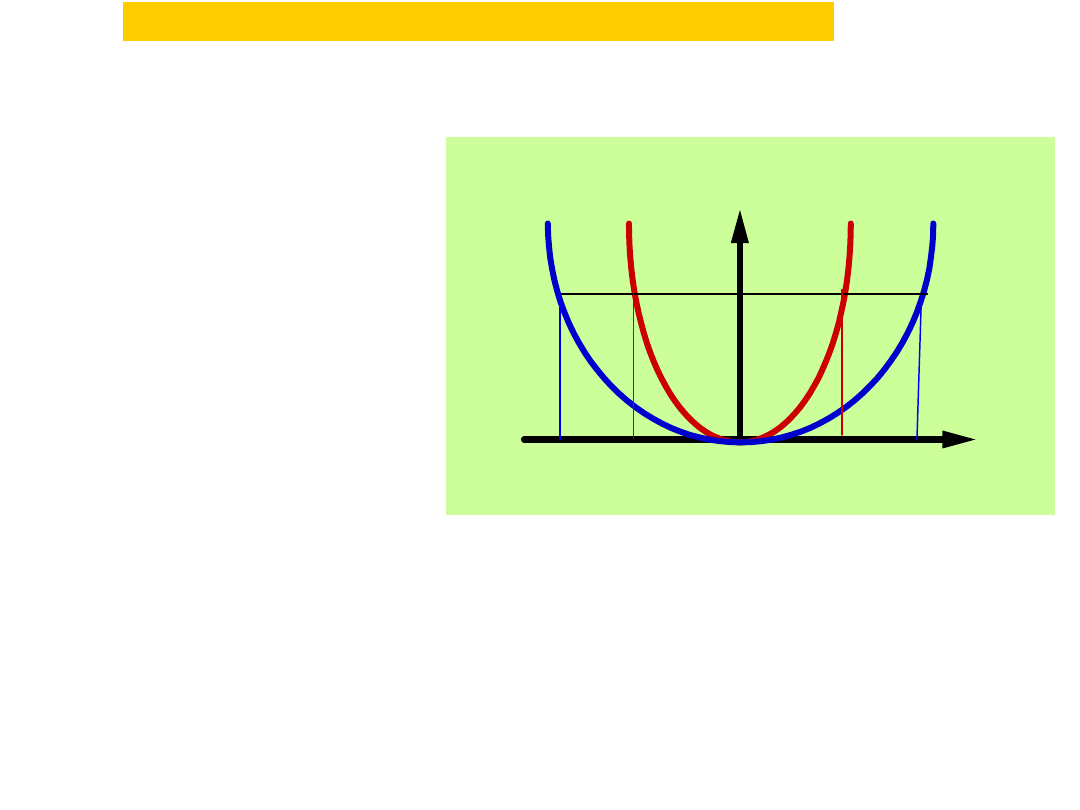
V(x) = 1/2k2x2

V

x

-A2

A2

k1>k2

E

V(x) = 1/2k1x2

-A1

A1

k

1

 k

2

Appendix 

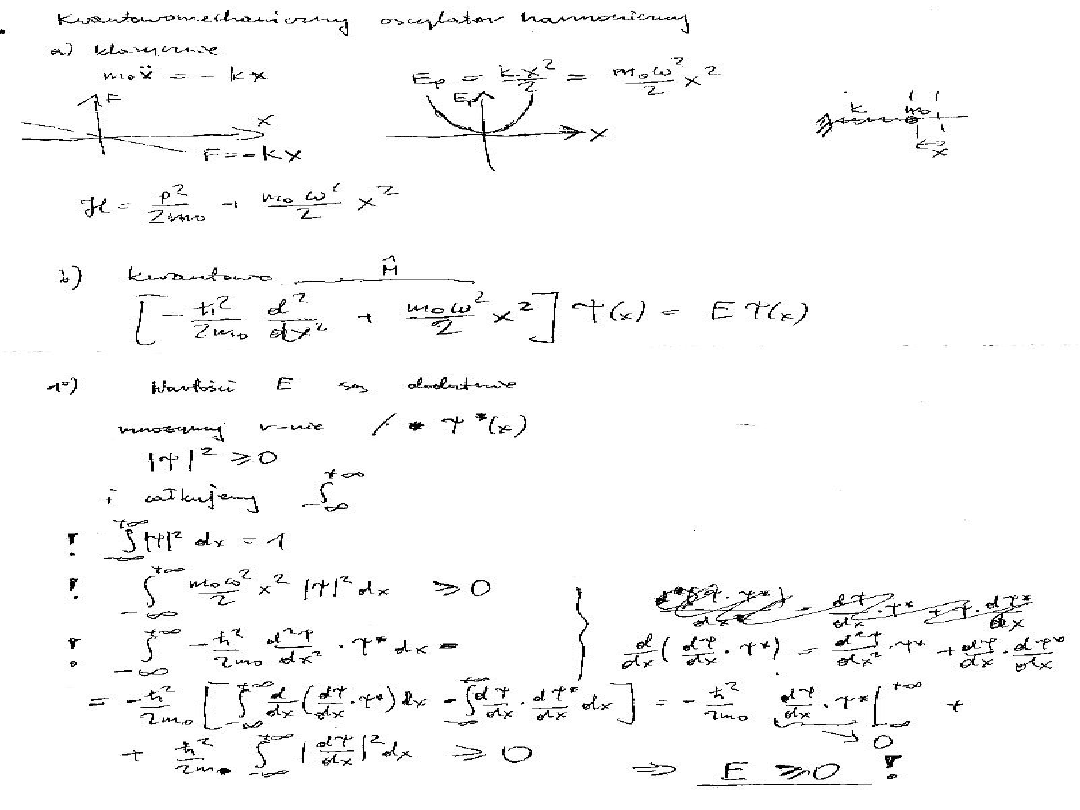
:  Classical harmonic oscillator

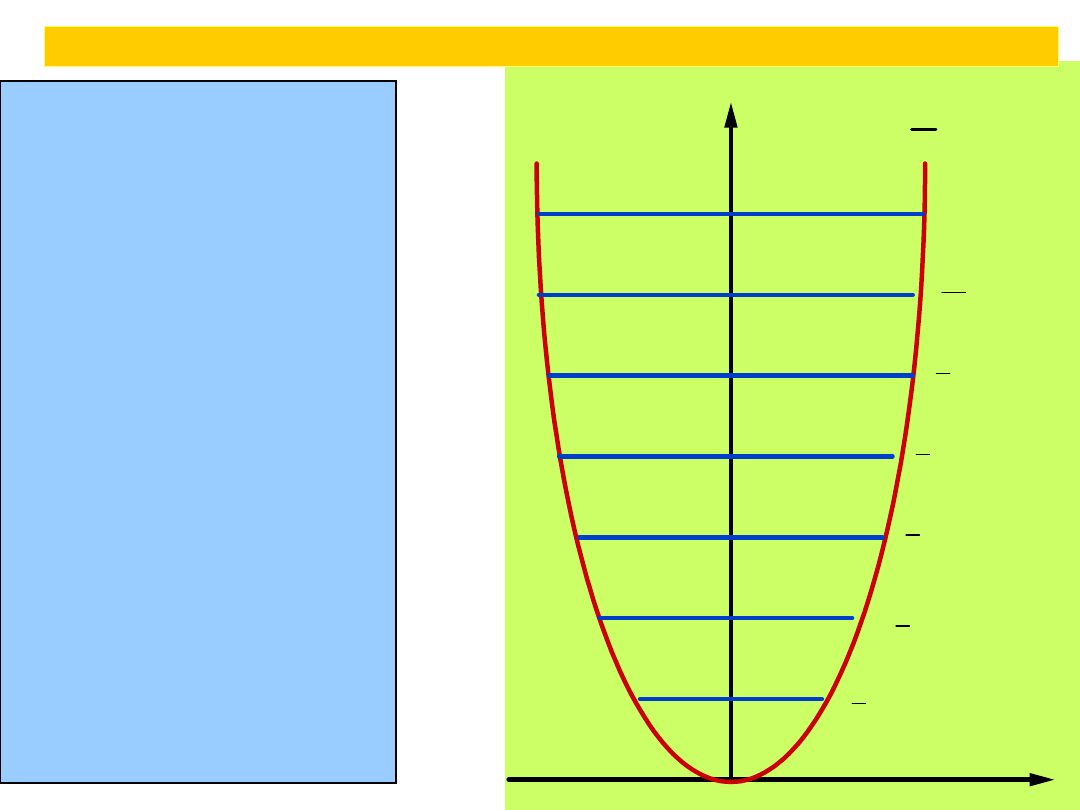
The parabolic potential energy V = 

1

/

2

kx

2

 a harmonic oscillator, where x is

the displacement from equilibrium. The

narrowness of the curve depends on

the force constant k: the larger the

value of k, the narrower the well.

E

  

1

2

h

  

3
2

h

  

5
2

h

  

7
2

h

x

  

9
2

h

  

11

2

h

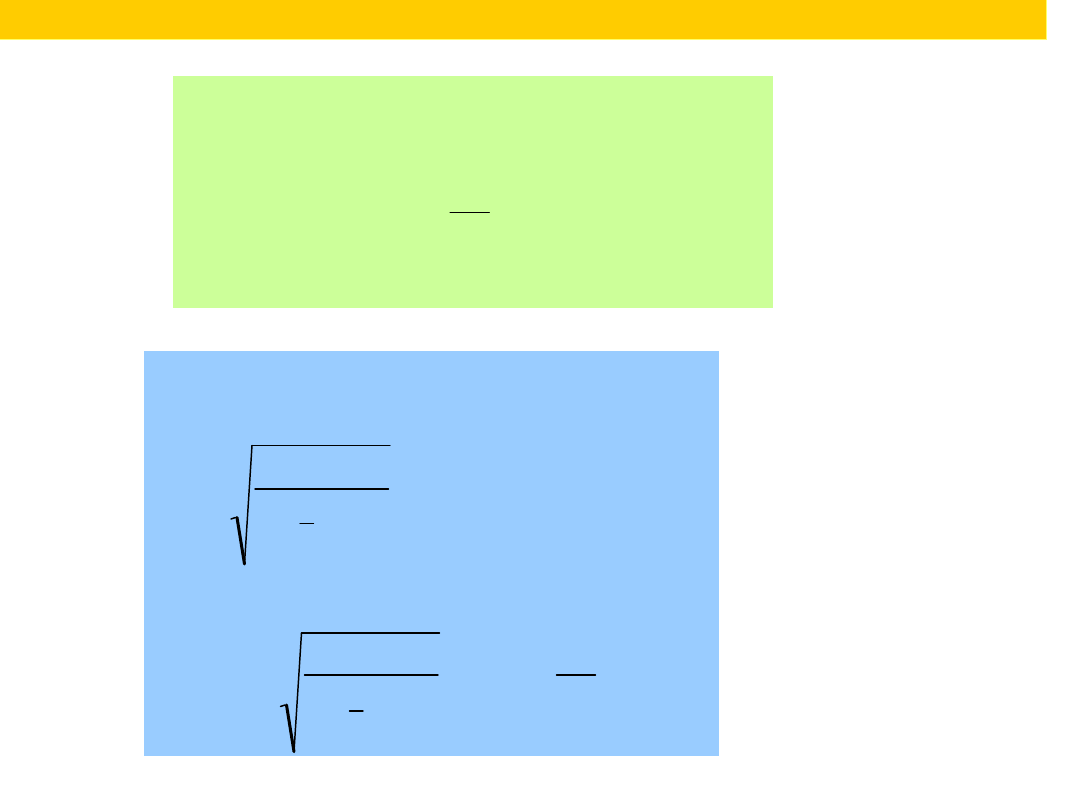
The energy

levels of a

harmo

nic

oscillator

are evenly

spaced with

separation

·, with  =

(k/m)

1/2

.

Even in its

lowest state,

an oscillator

has an

energy

greater

than zero.

Harmonic oscillator...Quantum mechanically .Energy levels

v 0

v 1

v 2

v 3

v 4

v 5

v 6

  

E h



(

1

2

 v)

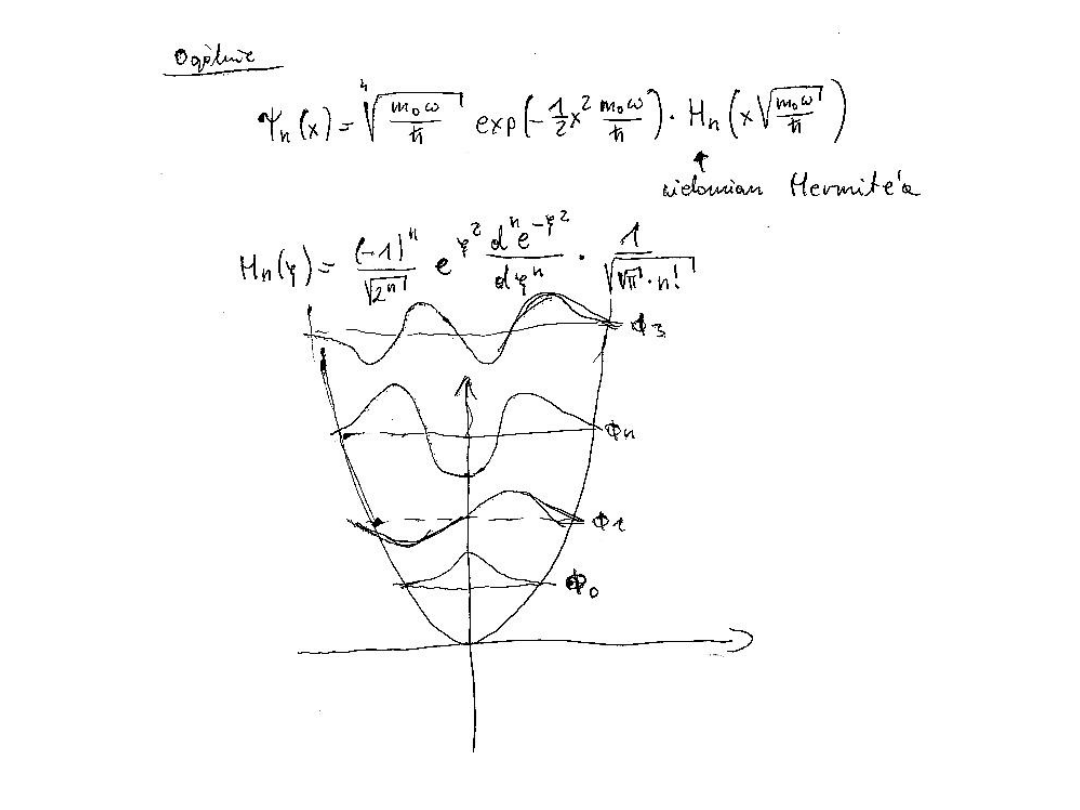
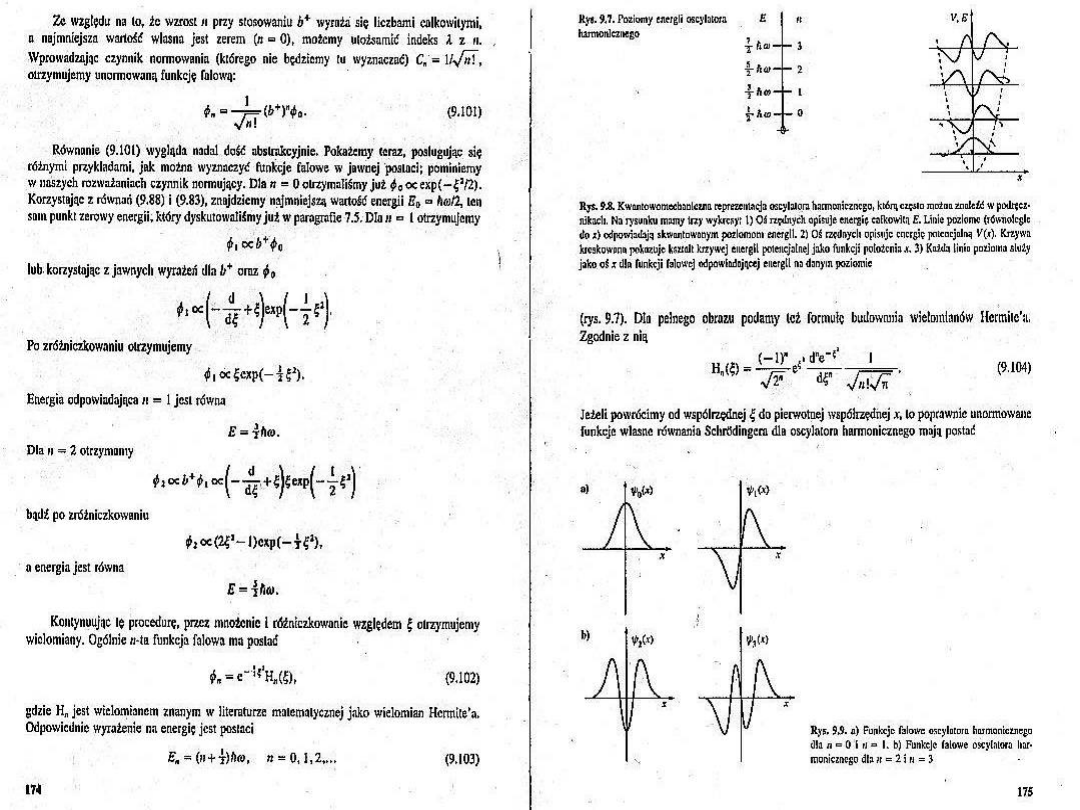
We have  the general solution



v

(x)N

v

exp

y

2

2

















 H

v

(y) ;   y=x/

Harmonic oscillator...Quantum mechanically.... Wavefunction

It is readilly shown that 

N

v



1



1

2

2

v

v!

so



v

(x) 

1



1

2

2

v

v!

exp 

y

2

2









 H

v

(y)

Harmonic oscillator...Quantum mechanically.... Wavefunction

_________________________

v             H

v

_________________________

0              1

1              2y

2              4y

2

-2

3               8y

3

-  12y

4              16y

4

- 48y

2

+12

5              32y

5

  -160y

3

+120y

6             64y

6

- 48y

4

+72y

2

-120

_____________________________      

Hermit

 polynominals

Note

 that H

v

 for v odd (1,

3,5,7,..)

is odd 

:  H

v

(y)  = - H

v

( y)

Note

 that H

v

 for v even (0,

2,4,6,8...)

is even 

:  H

v

(y)  = H

v

( y)

Harmonic oscillator...Quantum mechanically.... Wavefunction



v

(x) N

v

exp 

y

2

2

















 H

v

(y)

Particle can

be found 

outside

clasical region

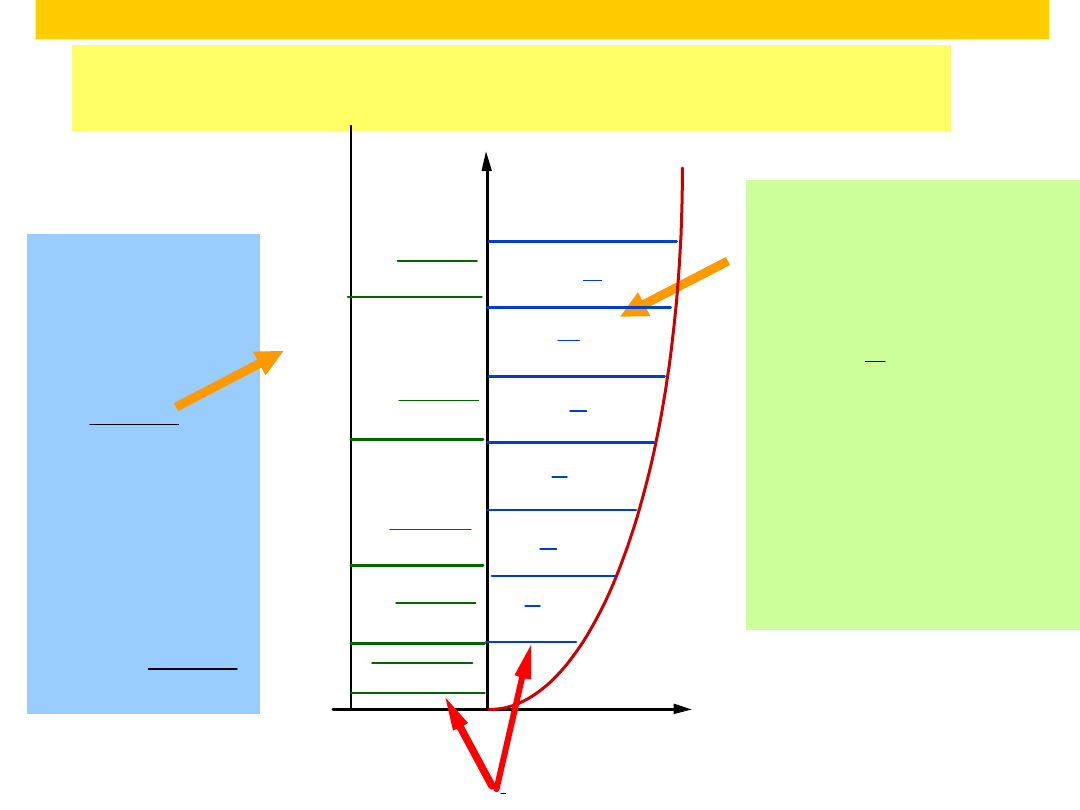
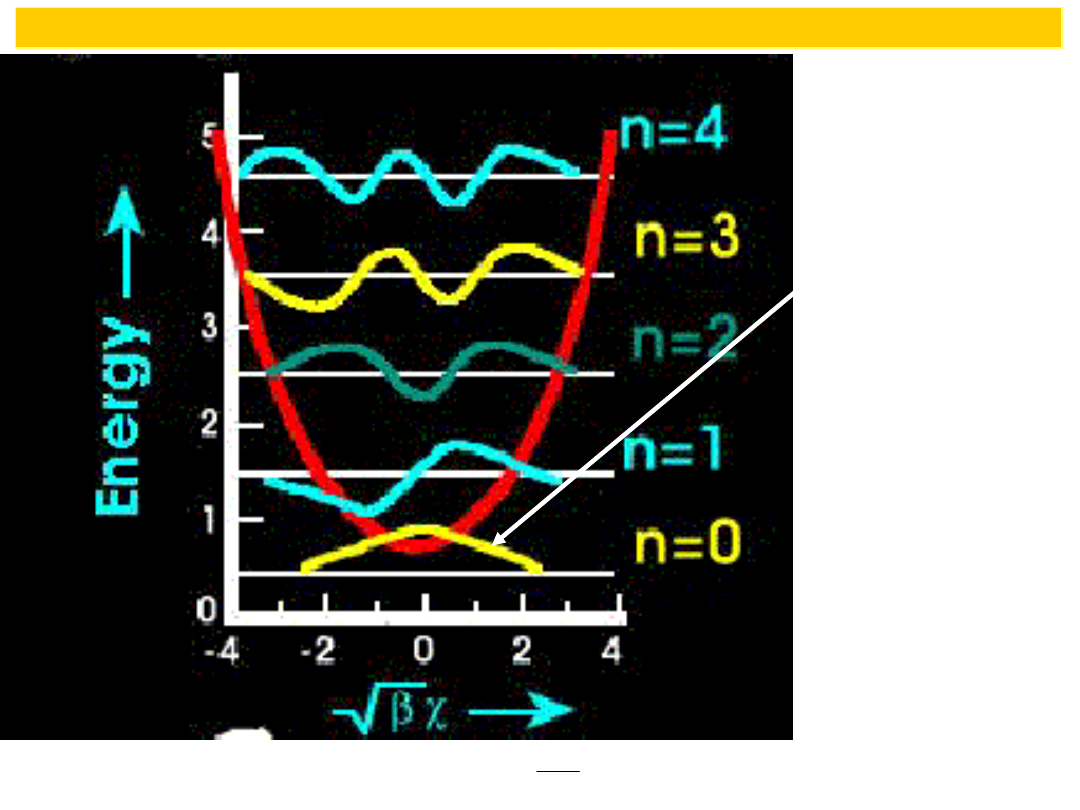
Comparison

 of energy levels in harmonic oscillator

and particle in a box

  

Energy levels for 
harmonic oscillator

E =h(

1

2

 v)

v 0,1,2,3

Spacing

E h

  

Energy levels
in particle in
box

E =

n

2

h

2

8mL

2

n 1,2,3

E 

(2n 1)

h

2

8mL

2

E

  

1

2 h



  

3
2

h

  

5

2 h

  

7

2 h

  

9

2 h

  

11

2  h

v=0

v=1

v=2

v=3

v=4

v=5

Harmonic oscillator

Particle-in-box

n=1

n=2

n=3

n=4

n=5

  

h

2

8mL

2

  

4 h

2

8mL

2

  

9 h

2

8mL

2

  

16 h

2

8mL

2

  

25 h

2

8mL

2

Zero-point Energy

Harmonic oscillator...Quantum mechanically .Energy levels

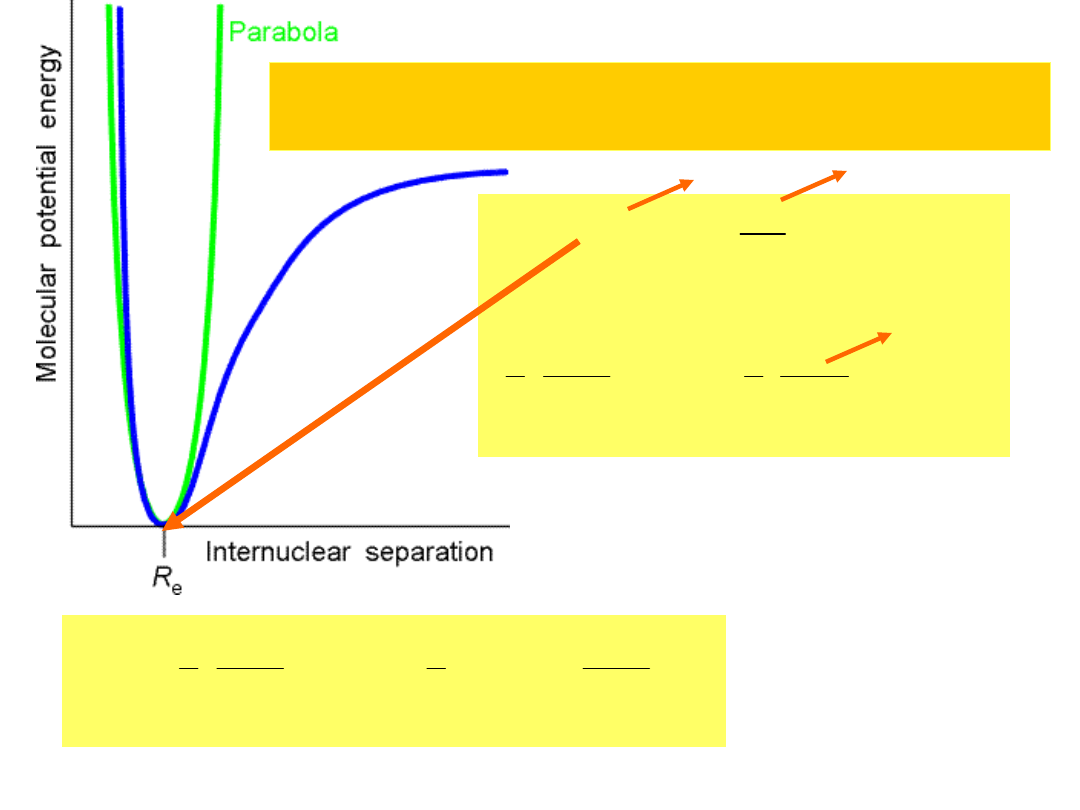
Harmonic oscillator...Quantum mechanically..

Vibration Spectroscopy

V(R)V(R

e

) (

dV
dR

) R

e



1
2

(

d

2

V

dR

2

)R

e

2



1
8

(

d

3

V

dR

3

)R

e

3

 ...

Taylor expansion

0

small

0

V(R)

1
2

(

d

2

V

dR

2

)R

e

2



1
2

kR

e

2

;(

d

2

V

dR

2

)k

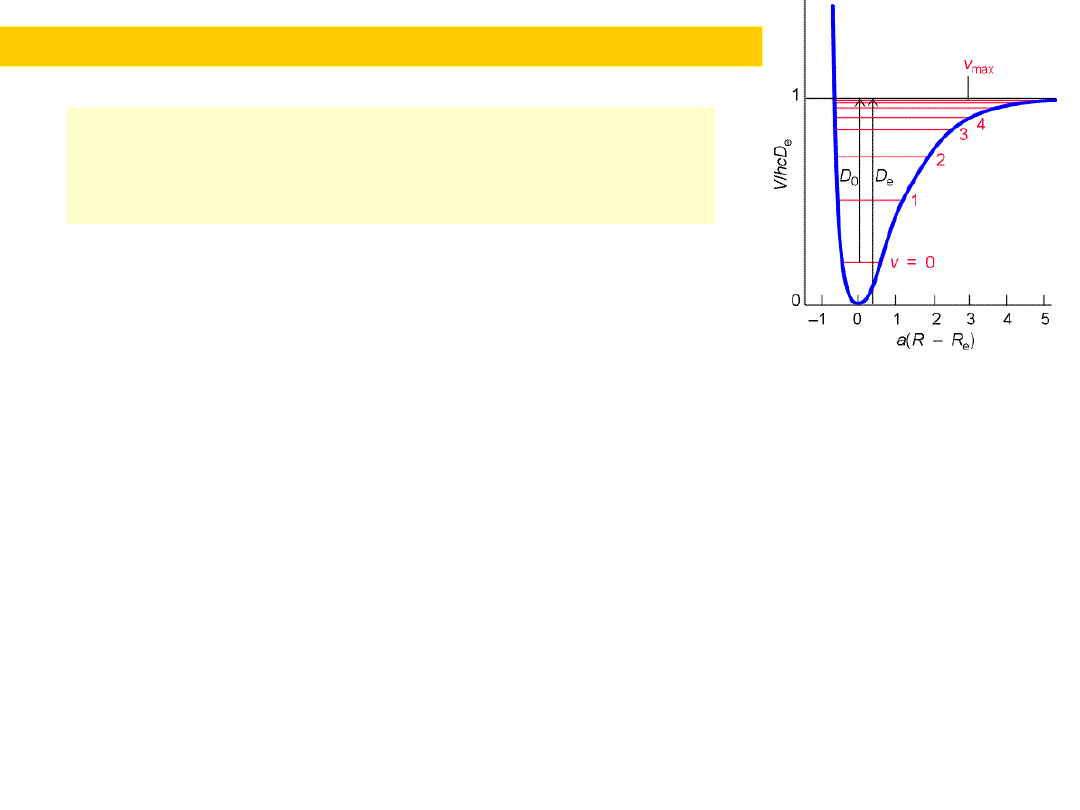
Harmonic oscillator...Quantum mechanically

We note relation between bond energy D ;

 bond order and force constant k   

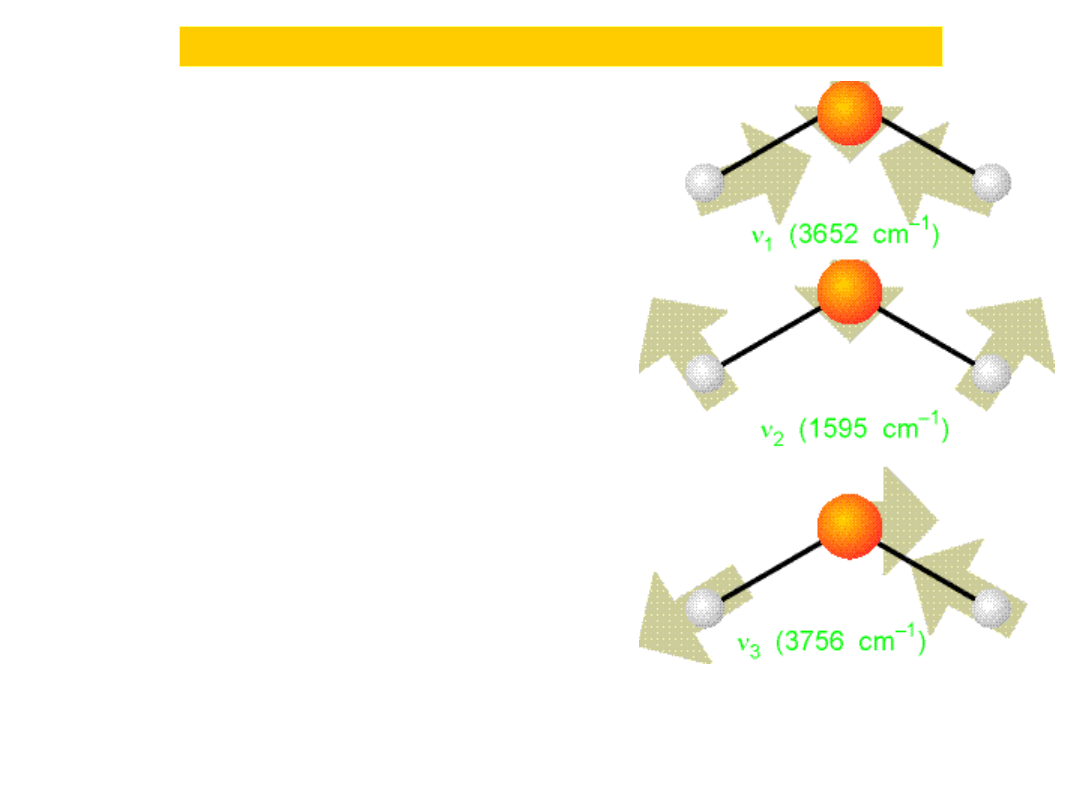
Harmonic oscillator...Quantum mechanically

The three
normal

modes of

H

2

O. The

mode v

2

 is

predominant

ly bend

ing,

and o

ccurs

at lower
wavenumber

than the
other two.