
I
T
P
W
ZPT
1
Struktury układów logicznych
FPGA
Field Programmable Gate Array
W dzisiejszych technologiach układy logiczne
to nie tylko bramki!
Coraz większego znaczenia
nabierają technologie, w których
podstawowym elementem
konstrukcyjnym są komórki logiczne
(Logic Cell)
Logic Cell
… a dla tych struktur klasyczne
metody syntezy - w szczególności
minimalizacja - są nieskuteczne

2
Dekompozycja funkcjonalna jest metodą znaną od dawna,
ale jej intensywny rozwój dokonuje się od niedawna.
Sytuacja jest podobna do rozwoju nowoczesnych metod
minimalizacji, który to rozwój zapoczątkowany został
pojawieniem się układów scalonych z milionami bramek
logicznych.
Jedyną różnicą jest fakt, że technologie struktur
komórkowych pojawiły się znacznie później i metody ich
syntezy nie są jeszcze wbudowane do systemów
komercyjnych.

I
T
P
W
ZPT
3
Dekompozycja funkcjonalna
Skuteczność dekompozycji jest tak ogromna, że mimo jej
braku w narzędziach komercyjnych należy się z tymi
metodami zapoznać i stosować w praktyce projektowania
układów cyfrowych za pośrednictwem narzędzi
uniwersyteckich.
Dekompozycję funkcji boolowskich omówimy w dwóch
ujęciach:
a) metoda klasyczna (znana od dawna...)
b) metoda nowoczesna (dostosowana do złożoności
dzisiejszych technologii)
I
T
P
W
ZPT
4
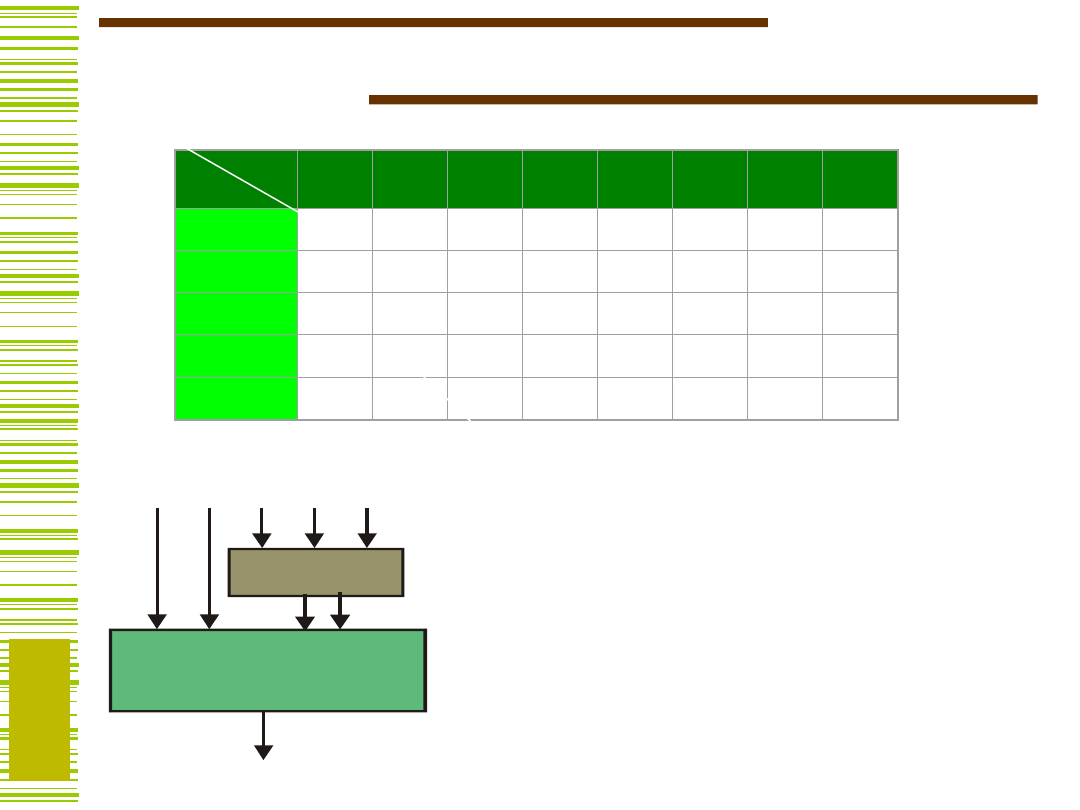
Metoda klasyczna
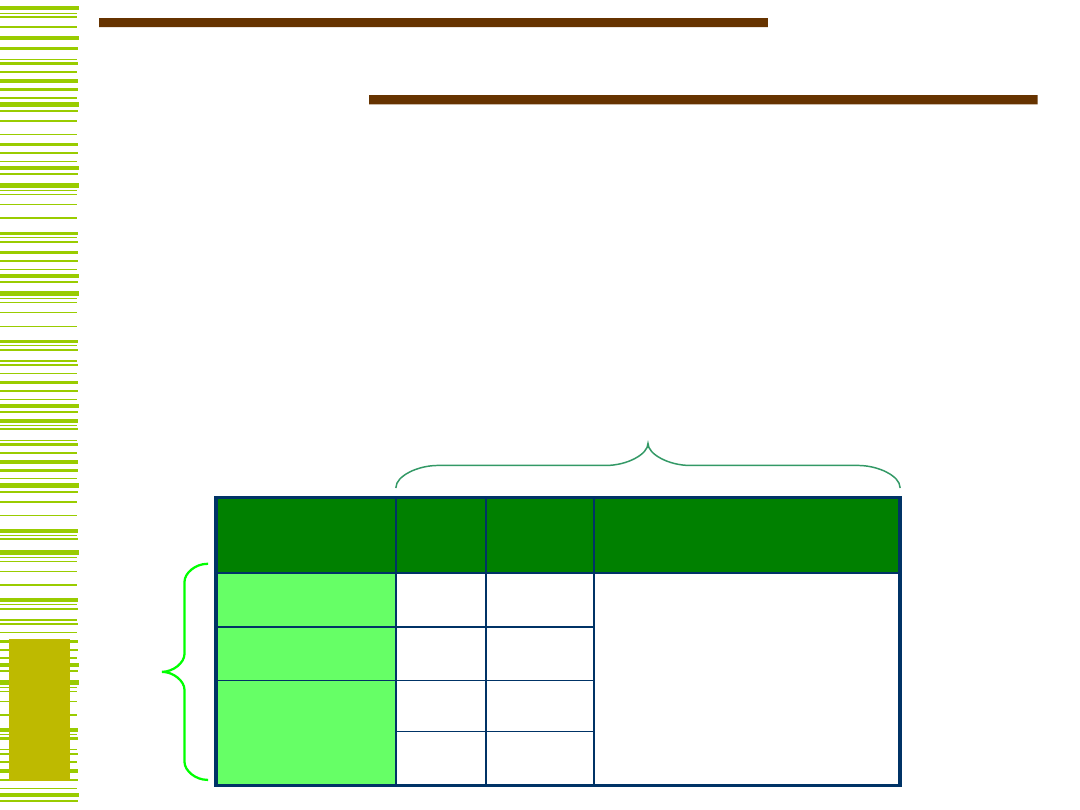
Tablicą dekompozycji funkcji f nazywamy macierz
dwuwymiarową o kolumnach etykietowanych wartościami
zmiennych funkcji f ze zbioru B oraz o wierszach
etykietowanych wartościami zmiennych funkcji f ze
zbioru A
A
B
0
1
01
1
0
00
001
000
x
1
x
2
x
3
x
4
x
5
Elementami
macierzy M są
wartości, jakie
przyjmuje funkcja f
na wektorach
złożonych z
odpowiednich
etykiet
i-tego wiersza i j-
tej kolumny.
... to metoda tablicowa, graficzna, której podstawowe
operacje wykonywane są na tzw. tablicy dekompozycji
I
T
P
W
ZPT
5
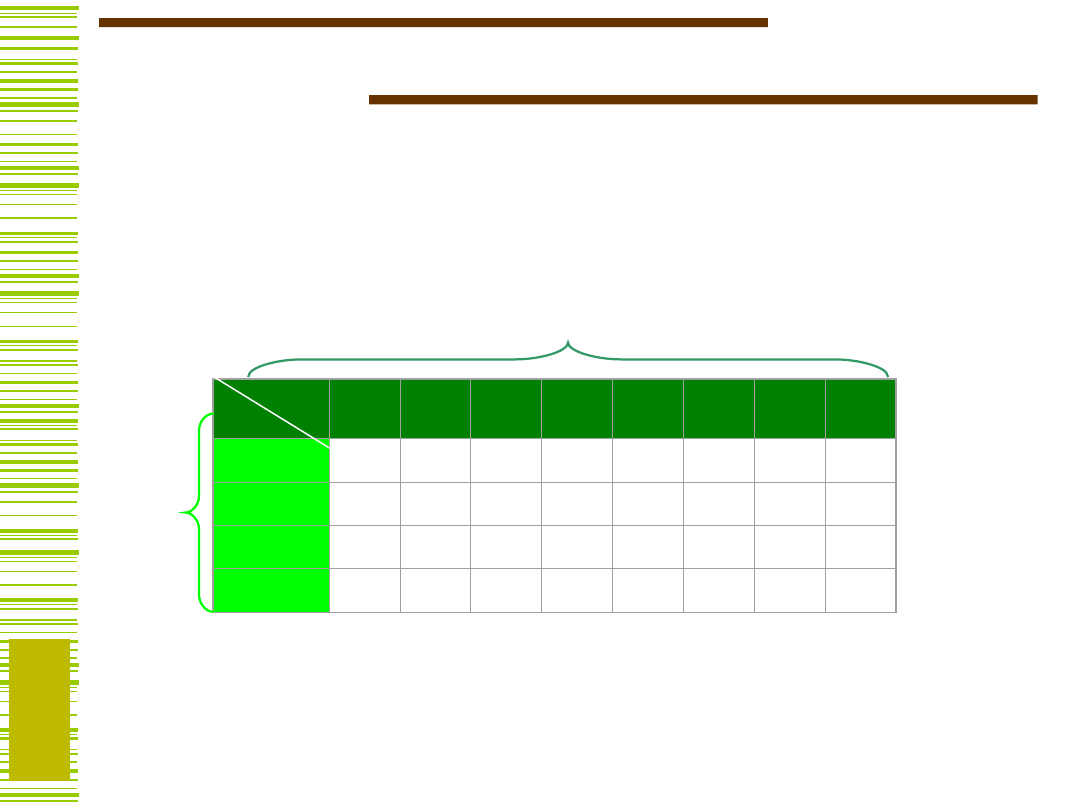
Krotność kolumn
Liczbę istotnie różnych kolumn tej macierzy ze względu na
ich zawartość nazywamy ich krotnością i oznaczamy
symbolem (A|B).
x
1
x
2
x
3
x
4
x
5
00
0
00
1
01
0
10
0
11
0
10
1
01
1
11
1
00
1
1
1
1
0
0
0
0
01
0
1
1
1
0
0
0
0
10
0
0
0
0
0
0
0
0
11
0
0
0
0
1
1
1
0
A
B
Krotność
kolumn =
4
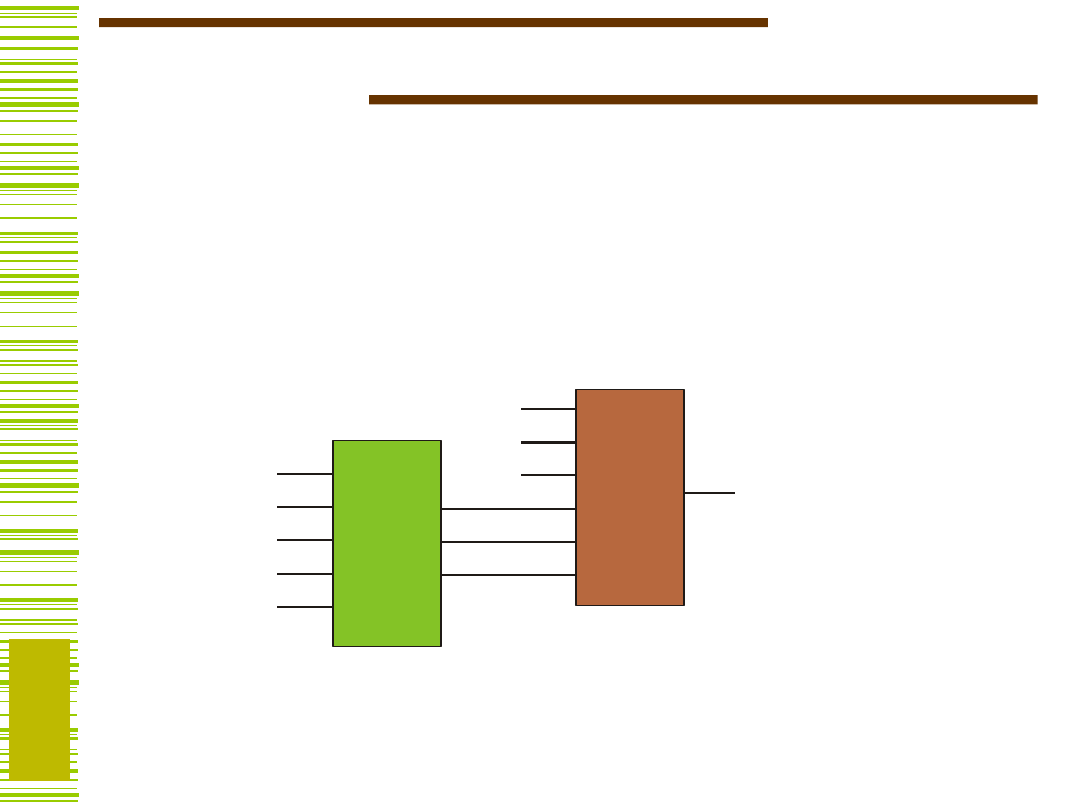
I
T
P
W
ZPT
6
Klasyczne twierdzenie o
dekompozycji
Niech będzie dana funkcja boolowska f oraz
podział zbioru zmiennych wejściowych funkcji f
na dwa rozłączne zbiory A i B, to wówczas:
f(A,B) = h(g
1
(B),.., g
j
(B),A) (A|B)
2
j
.
B
A
g
h
f
B (bound set), A (free set)
I
T
P
W
ZPT
7
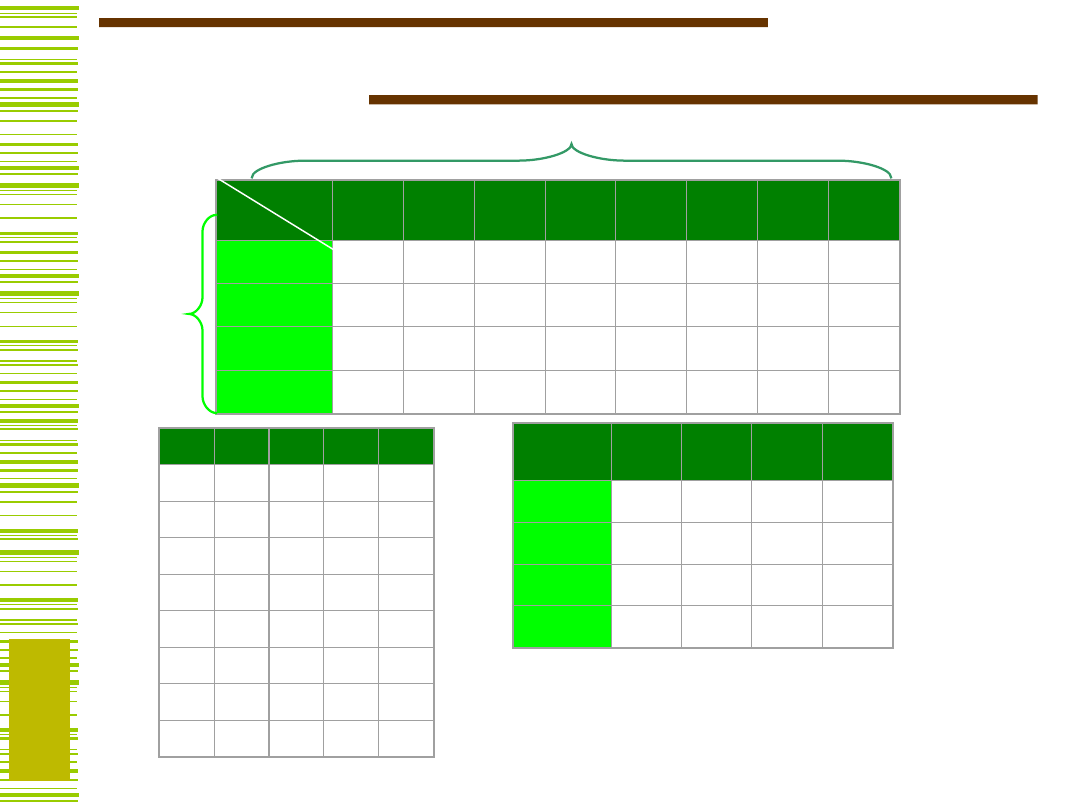
Przykład
x
1
x
2
x
3
x
4
x
5
00
0
00
1
01
0
10
0
11
0
10
1
01
1
11
1
00
1
1
1
1
0
0
0
0
01
0
1
1
1
0
0
0
0
10
0
0
0
0
0
0
0
0
11
0
0
0
0
1
1
1
0
A
B
x
1
x
2
x
3
g
1
g
2
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
1
0
1
1
0
0
1
1
1
0
1
1
1
1
1
g
1
g
2
x
4
x
5
00
01
10
11
0 0
1
1
0
0
0 1
0
1
0
0
1 0
0
0
0
0
1 1
0
0
1
0
Istnieje dekompozycja !
f = h(x
4
, x
5
, g
1
(x
1
, x
2
, x
3
), g
2
(x
1
, x
2
, x
3
))
I
T
P
W
ZPT
8
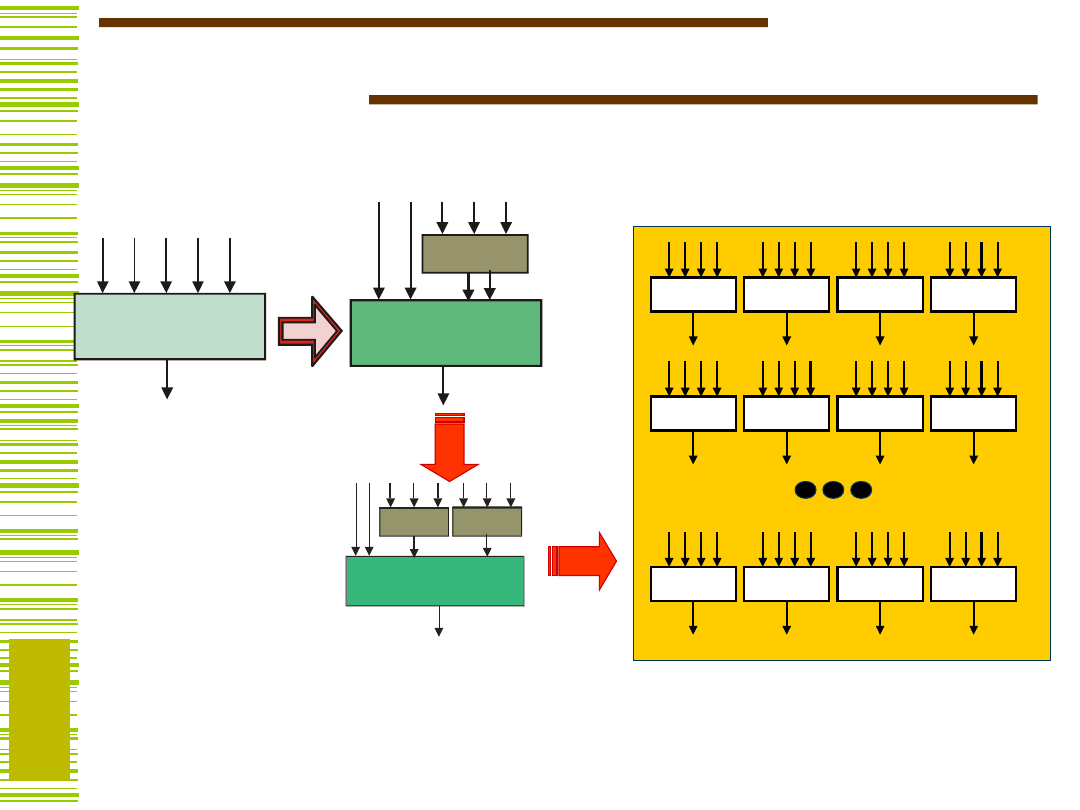
Praktyczne znaczenie
dekompozycji..
x
1
x
2
x
3
x
4
x
5
f
x
1
x
2
x
3
x
4
x
5
g
h
g
1
g
2
h
..dla struktur FPGA
I
T
P
W
ZPT
9
Przykład trochę trudniejszy
cde
a b
000
001
010
011
100
101
110
111
00
1
–
0
1
–
0
1
0
01
–
–
–
–
1
1
–
–
10
–
0
1
0
0
–
0
1
11
0
1
–
–
–
–
–
–
K0
K1
K2
K3
K4
K5
K6
K7
Istnieje dekompozycja !
f = h(a,b,g
1
(c,d,e), g
2
(c,d,e))
c d
e
a b
g
h
I
T
P
W
ZPT
10
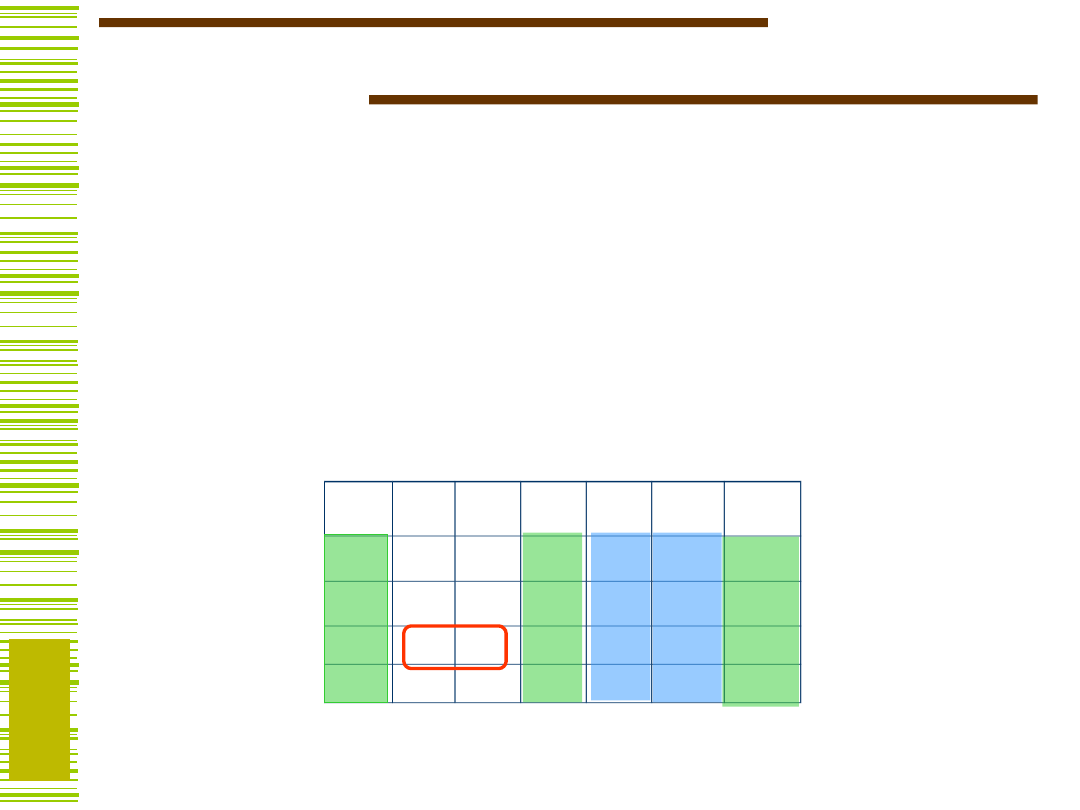
Relacja zgodności kolumn
Jak obliczać dekompozycję
I
T
P
W
ZPT
11
K1
K2
K3
K4
K5
K6
K7
1
-
0
1
-
0
1
-
-
-
-
1
1
-
-
0
1
0
0
-
0
0
1
-
-
-
-
0
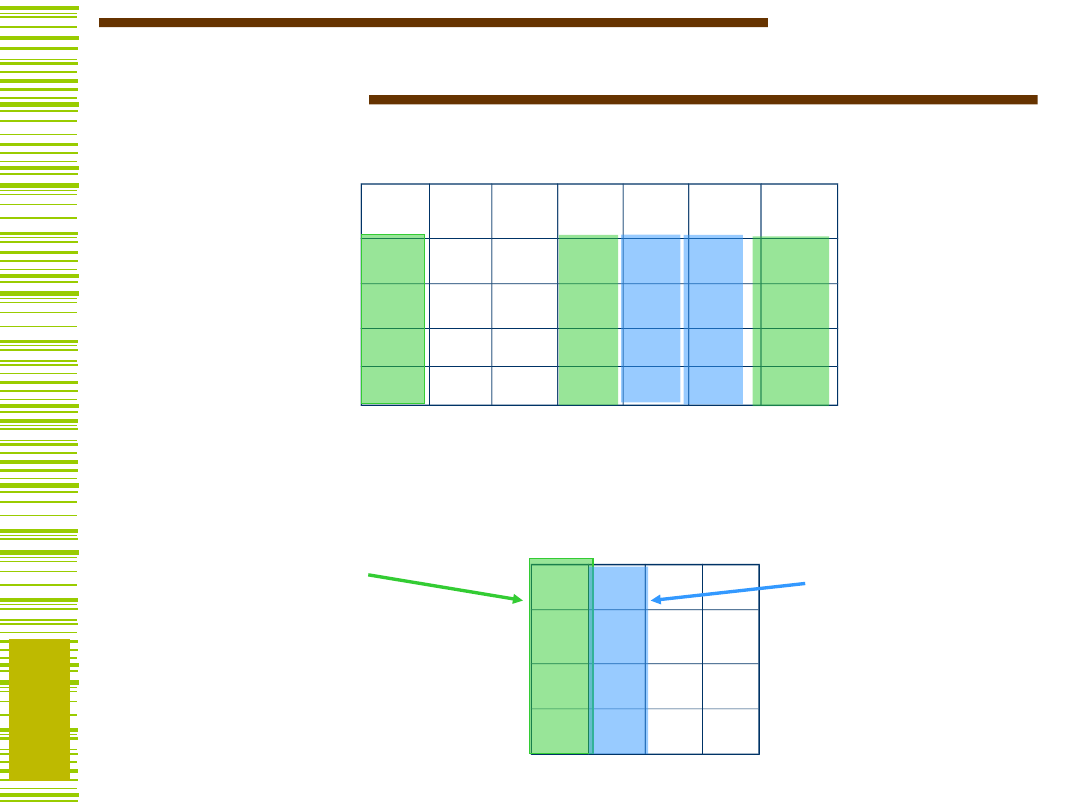
Relacja zgodności kolumn
Kolumny {k
r
, k
s
} są zgodne, jeśli nie istnieje wiersz i,
dla którego elementy K
ir
, K
is
są określone i różne,
tzn. odpowiednio: 0, 1 albo 1, 0.
I
T
P
W
ZPT
12
{K1,K4,K7}
Relacja zgodności kolumn
K1
K2
K3
K4
K5
K6
K7
1
-
0
1
-
0
1
-
-
-
-
1
1
-
-
0
1
0
0
-
0
0
1
-
-
-
-
0
{K5,K6}
1
-
0
0
0
1
0
-
Kolumny zgodne można „sklejać”

I
T
P
W
ZPT
13
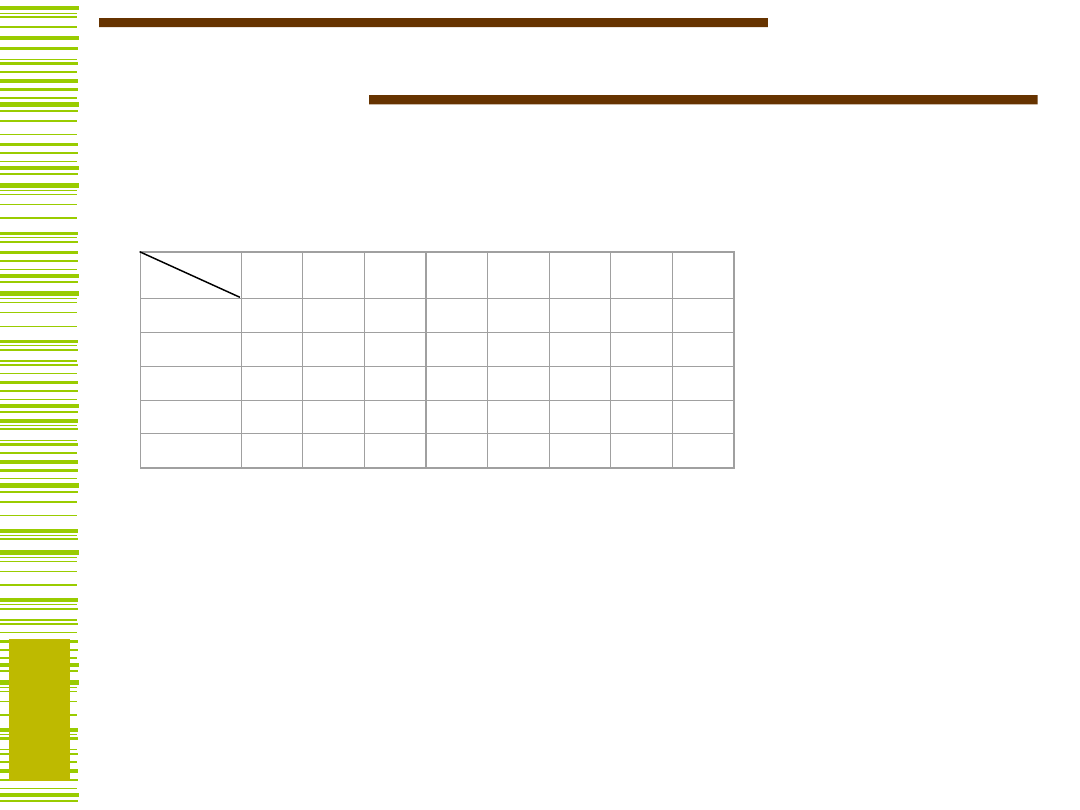
Obliczanie dekompozycji...
Wyznaczyć relację zgodności kolumn, czyli
wypisać wszystkie pary sprzeczne.
Wyznaczyć relację zgodności kolumn, czyli
wypisać wszystkie pary sprzeczne.
Wyznaczyć rodzinę maksymalnych zbiorów
kolumn zgodnych (maksymalnych klas zgodnych
– MKZ).
Wyznaczyć rodzinę maksymalnych zbiorów
kolumn zgodnych (maksymalnych klas zgodnych
– MKZ).
Z rodziny tej wyselekcjonować minimalną
podrodzinę
(w sensie liczności) rozłącznych zbiorów
zgodnych pokrywającą zbiór K wszystkich kolumn
tablicy dekompozycji.
Z rodziny tej wyselekcjonować minimalną
podrodzinę
(w sensie liczności) rozłącznych zbiorów
zgodnych pokrywającą zbiór K wszystkich kolumn
tablicy dekompozycji.
I
T
P
W
ZPT
14
Przykład - obliczanie klas
zgodności
cde
a b
00
0
00
1
01
0
01
1
10
0
10
1
11
0
11
1
00
1
–
0
1
–
0
1
0
01
–
–
–
–
1
1
–
–
10
–
0
1
0
0
–
0
1
11
0
1
–
–
–
–
–
–
K0
K1
K2
K3
K4
K5
K6
K7
K0, K1 sprzeczna
K0, K2 sprzeczna
K0, K3
zgodna
Pary
sprzeczne:
K0, K4
zgodna
0,1
0,2
0,5
0,7
1,2
1,7
2,3
2,4
2,6
3,5
3,7
4,7
5,6
6,7
I
T
P
W
ZPT
15
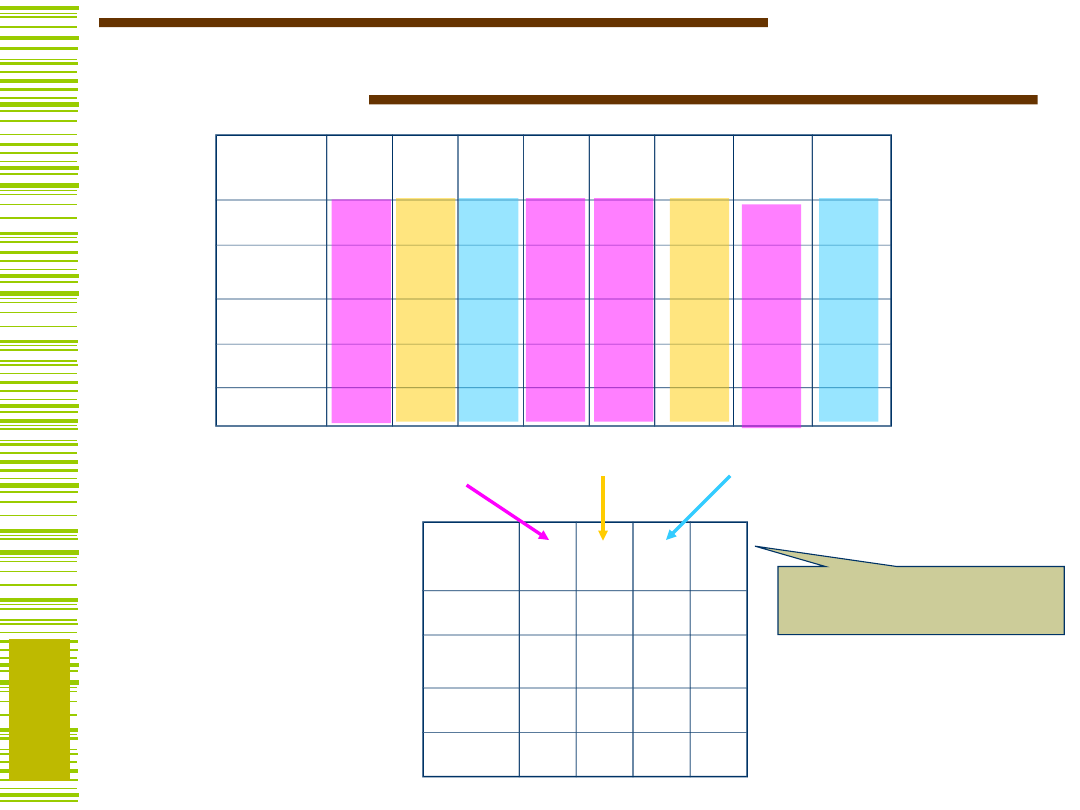
Przykład – obliczanie klas
zgodności
Stosując algorytm MKZ (był omawiany na PUL)
obliczamy rodzinę Maksymalnych Klas Zgodnych
kolumn:
0,3,4,6
1,3,4,6
1,4,5
2,5,7
0,3,4,
6
Wybieram
y:
1,5
0,3,4,6
2,7
Rodzina rozłącznych
zbiorów kolumn
zgodnych:
1,4,
5
2,5,
7
Kolumny powtarzające się
usuwamy
Komentarz: formalnie obliczamy
pokrycie..
Kolumny ze zbiorów
zgodnych można
sklejać!
I
T
P
W
ZPT
16
Sklejanie kolumn – funkcja h
cde
ab
00
0
00
1
01
0
01
1
10
0
101
110
111
00
1
-
0
1
-
0
1
0
01
-
-
-
-
1
1
-
-
10
-
0
1
0
0
-
0
1
11
0
1
-
-
-
-
-
-
K0
K1
K2
K3
K4
K5
K6
K7
g
1
g
2
ab
00 01 11 10
00
1
0
0
-
01
1
1
-
-
10
0
0
1
-
11
0
1
-
-
{K0,K3,K4,K6}
{K1,K5}
{K2,K7}
Kodowanie?
Może być dowolne
I
T
P
W
ZPT
17
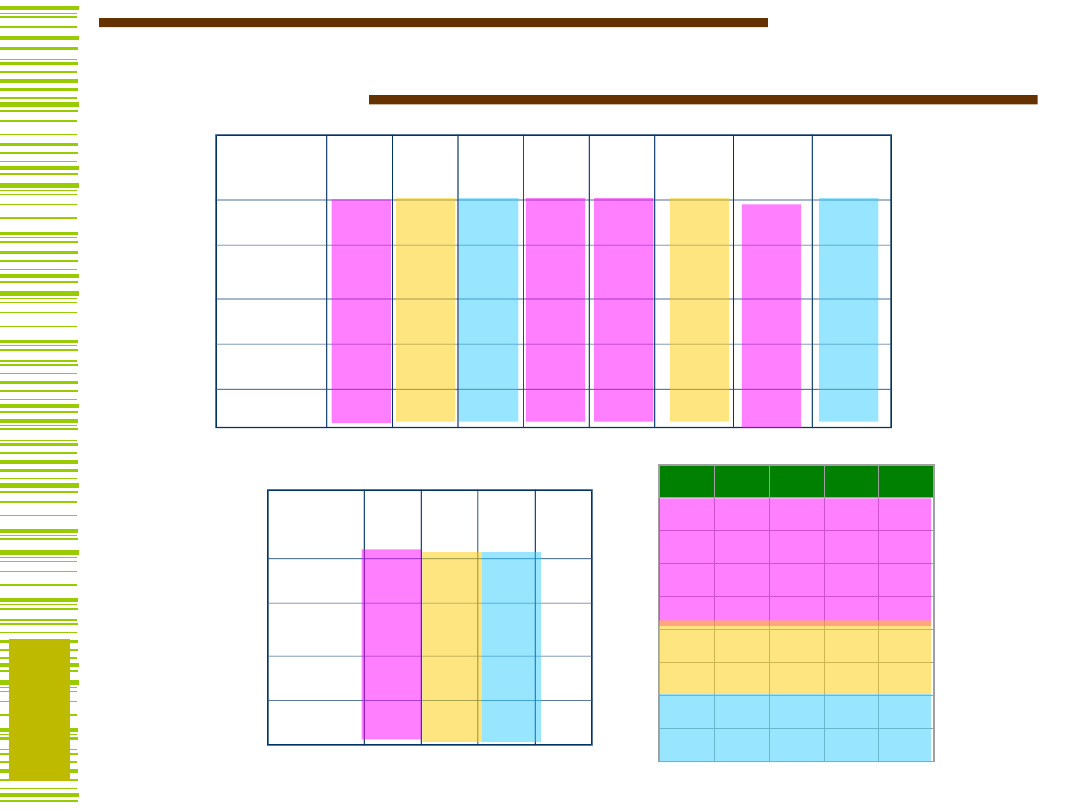
Kodowanie kolumn – funkcja g
cde
ab
00
0
00
1
01
0
01
1
10
0
101
110
111
00
1
-
0
1
-
0
1
0
01
-
-
-
-
1
1
-
-
10
-
0
1
0
0
-
0
1
11
0
1
-
-
-
-
-
-
K0
K1
K2
K3
K4
K5
K6
K7
g
1
g
2
ab
00 01 11 10
00
1
0
0
-
01
1
1
-
-
10
0
0
1
-
11
0
1
-
-
c
d
e
g
1
g
2
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
0
0
0
1
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
I
T
P
W
ZPT
18
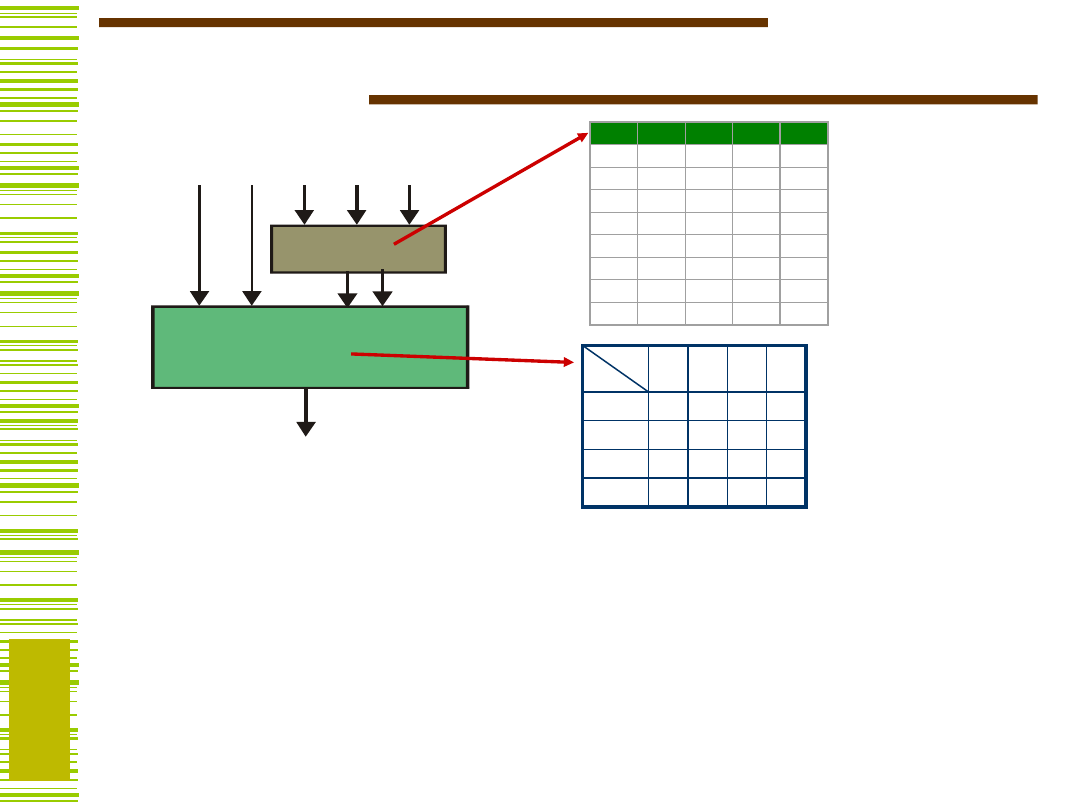
Co uzyskaliśmy
c d
e
a b
g
h
Opis funkcji g i h tablicami prawdy
wystarczy dla realizacji w strukturach FPGA
Ale funkcje g i h można obliczyć jawnie…
czyli po procesie dekompozycji można je minimalizować
c
d
e
g
1
g
2
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
0
0
0
1
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
-
-
-
-
1
0
-
1
-
0
1
1
1
0
1
0
0
1
0
0
1
1
0
0
10
11
01
00
g
1
g
2
ab
I
T
P
W
ZPT
19
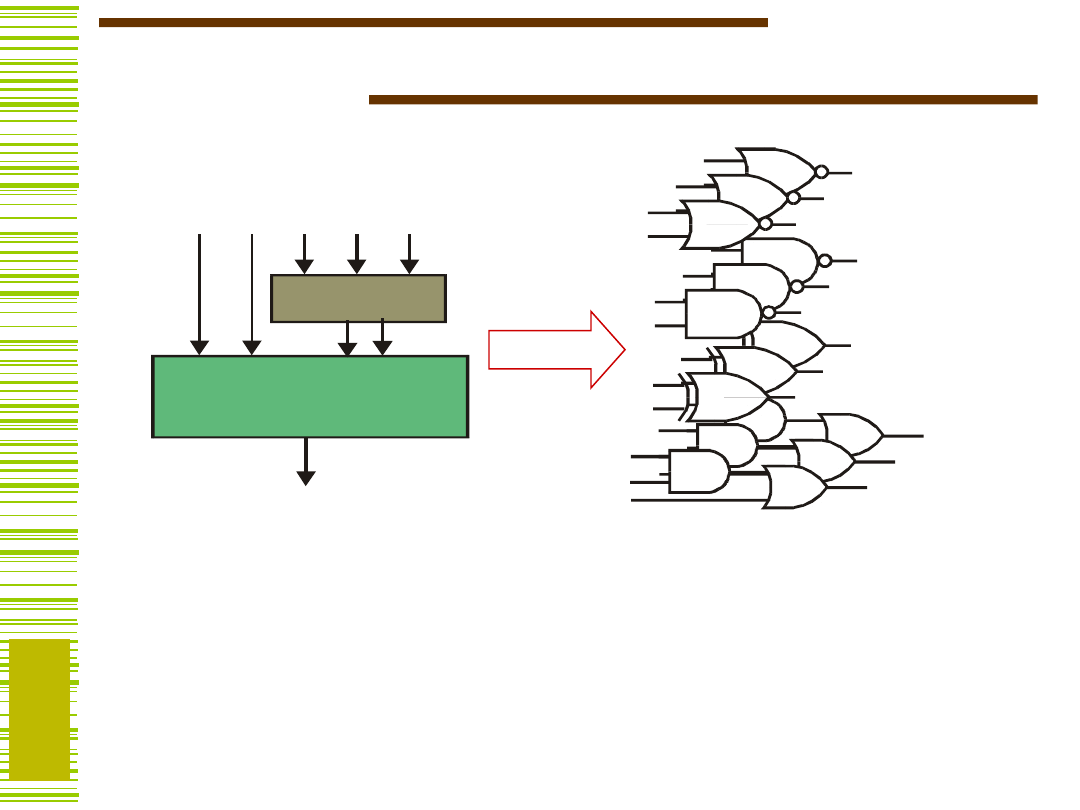
uzyskując w rezultacie …
c d
e
a b
g
h
…strukturę na bramkach
..ale to nas nie interesuje!!!
I
T
P
W
ZPT
20
Przykład (bardziej skomplikowany) -
TL27
x
3
x
5
x
6
x
7
x
8
x
9
x
1
0
f
1
1
1
1
0
1
0 0
1
0
1
0
1
0
0 0
0
0
1
1
1
1
0 0
1
1
0
1
0
1
1 0
0
0
1
0
0
1
1 0
0
0
1
0
1
1
0 0
1
1
0
0
1
1
0 0
0
1
1
0
0
0
0 0
0
0
0
0
0
1
0 0
1
1
1
1
0
1
1 1
0
0
1
0
1
0
0 1
0
1
1
0
0
1
1 1
0
1
0
0
0
0
0 1
0
0
1
1
1
1
1 1
1
0
0
0
1
1
0 1
1
0
1
0
0
0
1 1
1
1
0
1
0
0
1 1
1
1
1
1
1
1
1 1
1
0
0
0
0
0
0 1
0
1
0
0
1
1
1 1
1
0
0
1
1
1
1 1
1
1
0
0
0
1
0 1
1
1
1
1
1
0
1 1
0
1
1
1
0
0
0 1
.type fr
.i 10
.o 1
.p 25
001011101
0 0
101001010
0 0
010001111
0 0
101110101
1 0
110001001
1 0
010001011
0 0
111010011
0 0
010011000
0 0
010100001
0 0
011111101
1 1
000001010
0 1
110111001
1 1
010010000
0 1
010001111
1 1
001000011
0 1
111101000
1 1
111110100
1 1
111111111
1 1
001000000
0 1
110110011
1 1
001000111
1 1
111110001
0 1
101011110
1 1
011000011
0 1
010011100
0 1
.e
x
7
x
8
x
9
x
3
x
5
x
6
x
1
0
f
1 0 1 1 1 1 0
0
0 1 0 1 0 1 0
0
1 1 1 0 0 1 0
0
1 0 1 1 1 0 1
0
0 0 1 0 0 1 1
0
0 1 1 0 0 1 0
0
0 1 1 1 1 0 0
0
0 0 0 0 1 1 0
0
0 0 1 0 0 0 0
0
1 0 1 1 1 1 1
1
0 1 0 0 0 1 0
1
0 0 1 0 1 1 1
1
0 0 0 0 1 0 0
1
1 1 1 0 0 1 1
1
0 1 1 1 0 0 0
1
0 0 0 1 0 1 1
1
1 0 0 1 1 0 1
1
1 1 1 1 1 1 1
1
0 0 0 1 0 0 0
1
0 1 1 0 1 0 1
1
1 1 1 1 0 0 1
1
0 0 1 1 1 0 0
1
1 1 0 1 1 1 1
1
1 0 0 0 1 1 0
1
A
B
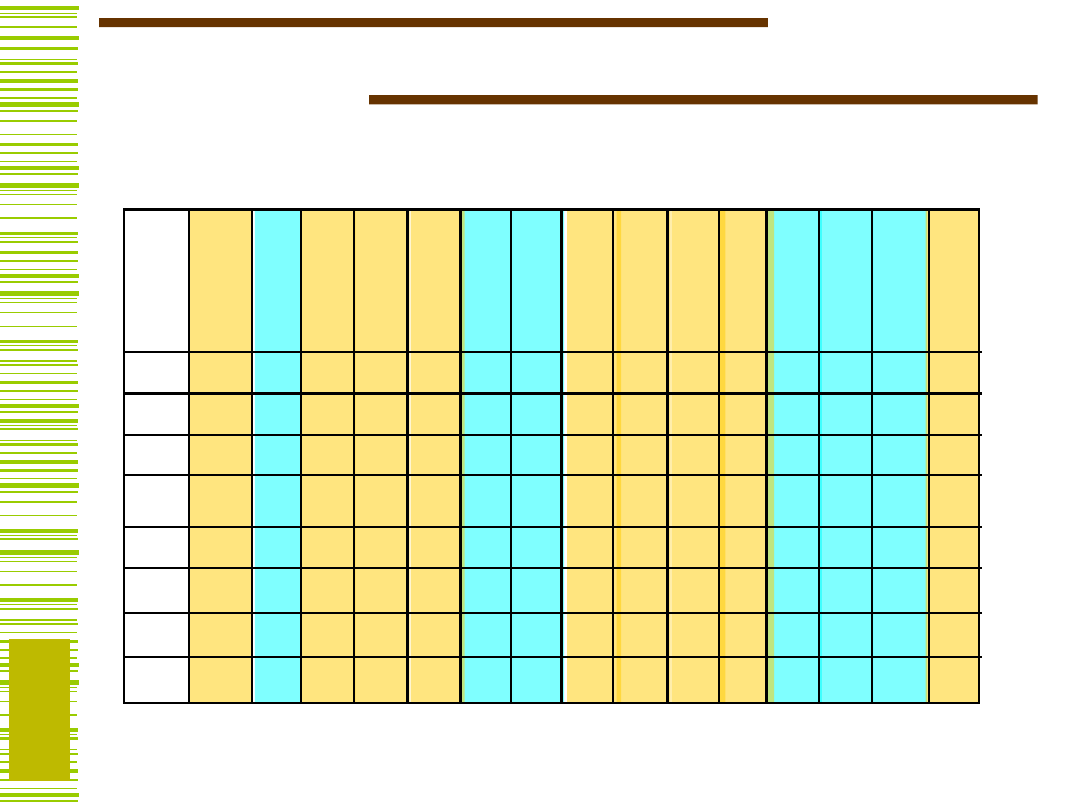
I
T
P
W
ZPT
21
Tablica dekompozycji dla funkcji
TL27
0
0
0
0
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
00
0
–
–
–
1
–
0
–
1
–
–
1
–
–
–
–
00
1
0
–
0
–
–
–
1
–
–
–
–
1
–
–
–
01
0
–
1
–
–
–
–
–
–
–
0
–
–
–
–
–
01
1
–
0
–
–
1
–
–
1
–
–
–
0
–
–
–
10
0
–
–
–
–
–
1
–
–
–
–
–
–
1
–
–
10
1
–
–
–
–
–
–
–
–
–
–
–
–
0
0
1
11
0
–
–
–
–
–
–
–
–
–
–
–
–
–
–
1
11
1
–
–
1
–
–
–
–
–
1
–
–
–
–
–
1
x
3
x
5
x
6
x
10
x
7
x
8
x
9
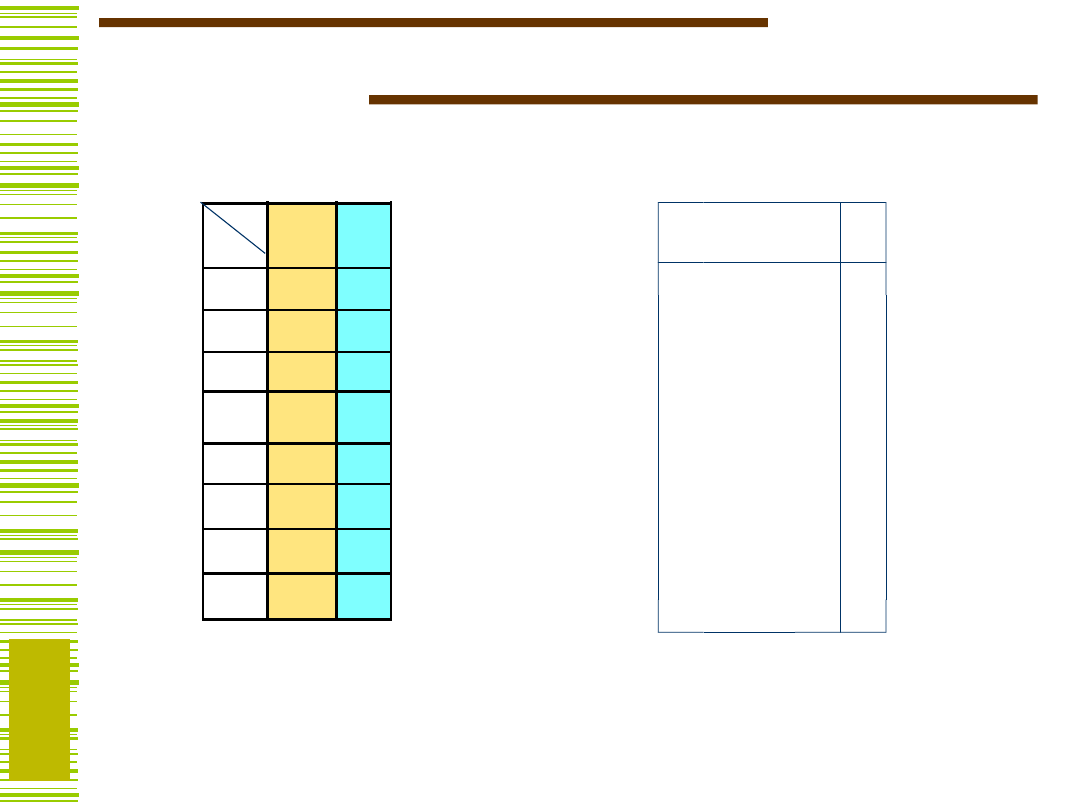
I
T
P
W
ZPT
22
Tablica dekompozycji dla funkcji
TL27
00
0
1
1
0
0
00
1
0
1
01
0
0
1
01
1
1
0
10
0
–
1
10
1
1
0
11
0
1
–
11
1
1
–
x
7
x
8
x
9
g
x
3
x
5
x
6
x
1
0
G
0
0
0
0
0
0
0
1
0
1
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
1
0
1
1
1
1
1
0
0
0
0
1
1
1
1
0
H
G
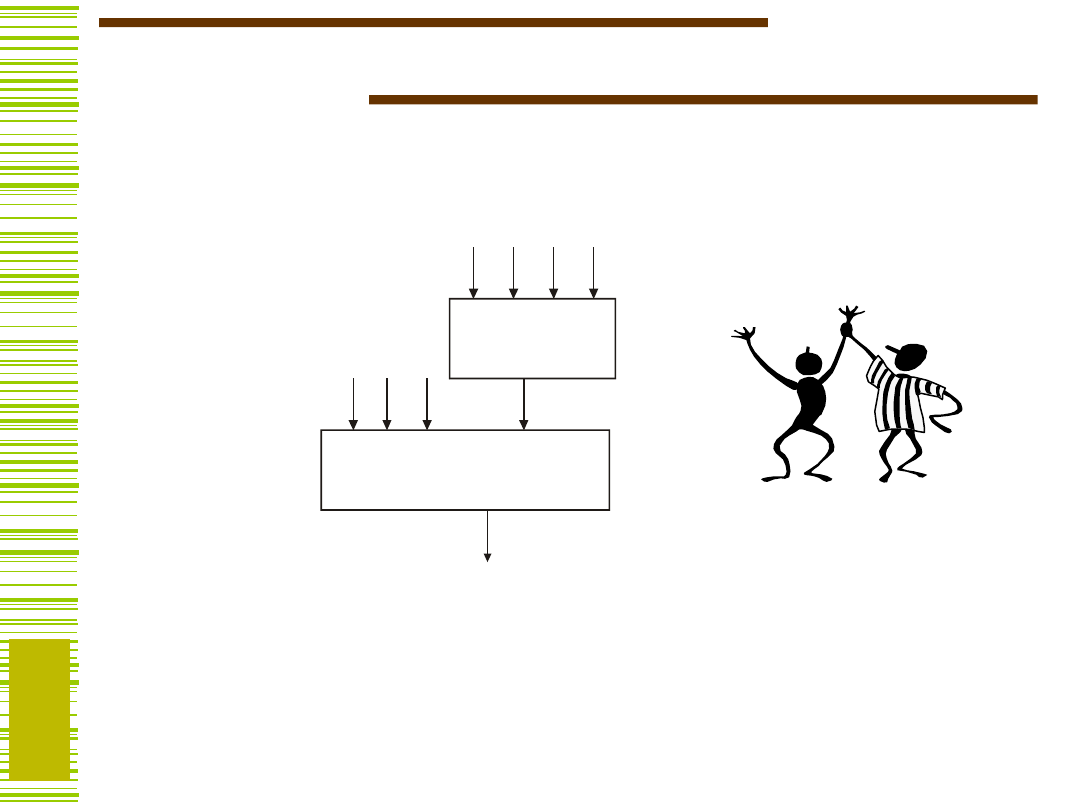
I
T
P
W
ZPT
23
Praktyczny wynik dekompozycji funkcji
TL27
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
1 0
Tylko 2
komórki
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
I
T
P
W
ZPT
24
Zagadka
QUARTUS
25 kom. (FLEX)
lub 27 kom.
(Stratix)!!!
Na ilu komórkach zrealizuje tę
funkcję amerykański system
QUARTUS?
Niesamowita
skuteczność procedur
dekompozycji!!!
I
T
P
W
ZPT
25
Jak usprawnić obliczanie MKZ?
W metodzie dekompozycji
jednym z najważniejszych
algorytmów jest algorytm
obliczania maksymalnych klas
zgodności
W celu sprawniejszego obliczania MKZ
wprowadzimy metodę wg par
zgodnych:
a) metodę bezpośrednią
b) metodę iteracyjną
a) metodę bezpośrednią
b) metodę iteracyjną
I
T
P
W
ZPT
26
Metoda bezpośrednia
a, b
b, c
a, c
{a, b, c}
a, b, c
a, b, d
b, c, d
a, c, d
{a, b, c, d}
i.t.d.
Pary zgodne:

I
T
P
W
ZPT
27
Przykład – obliczanie klas
zgodności
1,4,5
1,4,6
2,5,7
3,4,6
0,3,4,6
Maksymalne klasy
zgodności:
0,3
0,4
0,6
1,3
1,4
1,5
1,6
2,5
2,7
3,4
3,6
4,5
4,6
5,7
0,3,
4
0,4,
6
0,3,
6
1,3,
4
1,3,
6
1,3,4,6
1,4,5
2,5,7

I
T
P
W
ZPT
28
Algorytm MKZ wg par zgodnych
E – relacja zgodności (e
i
,e
j
) E
E – relacja zgodności (e
i
,e
j
) E
R
j
= { e
i
| i < j oraz (e
i
,e
j
) E}
R
j
= { e
i
| i < j oraz (e
i
,e
j
) E}
RKZ
k
RKZ
k+1
KZ RKZ
k
RKZ
k
RKZ
k+1
KZ RKZ
k
a) R
k+1
= , RKZ
k+1
jest powiększana o klasę KZ = {k+1}
a) R
k+1
= , RKZ
k+1
jest powiększana o klasę KZ = {k+1}
b) KZ R
k+1
= , KZ bez zmian
b) KZ R
k+1
= , KZ bez zmian
c) KZ R
k+1
, KZ’ = KZ R
k+1
{k+1}
c) KZ R
k+1
, KZ’ = KZ R
k+1
{k+1}

I
T
P
W
ZPT
29
Przykład
R
0
=
R
0
=
R
1
=
R
1
=
R
2
=
R
2
=
R
3
=
R
3
=
R
4
=
R
4
=
R
5
=
R
5
=
0,1
0,1
0,1,3
0,1,3
1,2,4
1,2,4
R
j
= { e
i
| i < j oraz (e
i
,e
j
) E}
R
j
= { e
i
| i < j oraz (e
i
,e
j
) E}
E
:
E
:
0,3
0,4
0,6
1,3
1,4
1,5
1,6
2,5
2,7
3,4
3,6
4,5
4,6
5,7
R
6
=
R
6
=
0,1,3,4
0,1,3,4
R
7
=
R
7
=
2,5
2,5

I
T
P
W
ZPT
30
Przykład
R
0
=
R
0
=
R
1
=
R
1
=
R
2
=
R
2
=
R
3
=
R
3
=
R
4
=
R
4
=
R
5
=
R
5
=
{0,1}
{0,1}
{0,1,3}
{0,1,3}
{1,2,4}
{1,2,4}
R
6
=
R
6
=
{0,1,3,4}
{0,1,3,4}
R
7
=
R
7
=
{2,5}
{2,5}
{0}
{0}{1}
{0}{1} {2}
{0,3}{1,3}{2}
{0,3,4}{1,3,4}{2}
{4,5}{1,4,5}{2,5}{0,3,4}{1,3,4}
{1,4,6}
{2,5,7}
{0,3,4,6}{1,3,4,6}
{2,5}
{1,4,5}
{0,3,4,6}{1,3,4,6}{5,7}{1,4,5}
Rodzina MKZ

I
T
P
W
ZPT
31
Przykład…
0,3
0,4
0,6
1,3
1,4
1,5
1,6
2,5
2,7
3,4
3,6
4,5
4,6
5,7
Pary zgodne:
Pary sprzeczne:
0,1
0,2
0,5
0,7
1,2
1,7
2,3
2,4
2,6
3,5
3,7
4,7
5,6
6,7
I
T
P
W
ZPT
32
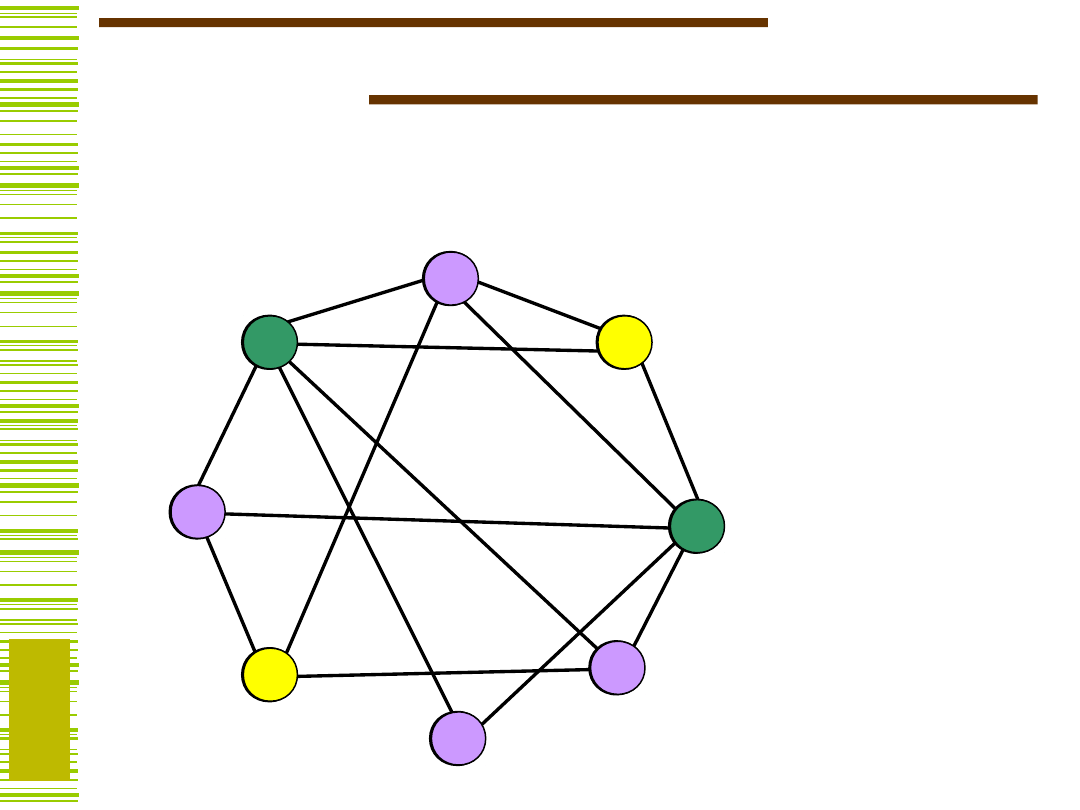
Graf niezgodności
(0,1), (0,2), (0,5), (0,7), (1,2), (1,7), (2,3),
(2,4), (2,6), (3,5), (3,7), (4,7), (5,6), (6,7)
0
1
2
3
4
5
6
7
i jego kolorowanie
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
Wyszukiwarka
Podobne podstrony:
ELC dek klas
ELC dek r p
2 zarzadz klas behawid 21012 ppt
Teza o ¶mierci klas
8(45) Diagramy klas cz2
Ocena opisowa dla uczniĂłw klas I III
Cem por klas
ANALIZA WYNIKÓW EGZAMINU GIMNAZJALNEGO DLA UCZNIÓW KLAS III
Krzyżówki do lektur dla klas 1 3
miao wykl 6 projektowanie klas Nieznany
Język Angielski Poziom II Sprawdziany Kompetencji dla klas IV VI
Spotkanie 3 Dziecko Maryi nie krzywdzi innych, Spotkania Dzieci Maryi, Dzieci klas I-III
Konkurs dla klas pierwszych liceum ogólnokształcącego
Przejawy niedost. społ. wśród uczniów klas gimnazjalnych, studia, II ROK, Resocjalizacja
PLAN WYNIKOWY DLA KLAS 1 wdr, Studia, Wychowanie do życia w rodzinie
Dyktanda dla klas II -III, Ortografia
więcej podobnych podstron