1

Wydział Mechaniczny

Technologiczny
Politechniki Śląskiej w

Gliwicach
Dr inż.. Iwona Wosik

2

Szeregowanie

Szeregowanie

polega na uporządkowaniu

polega na uporządkowaniu

operacji w czasie i przestrzeni zgodnie z

operacji w czasie i przestrzeni zgodnie z

warunkiem procesu produkcyjnego tak, aby

warunkiem procesu produkcyjnego tak, aby

określone kryterium efektywności osiągało

określone kryterium efektywności osiągało

wartość ekstremalną.

wartość ekstremalną.

Podstawowe cele szeregowania:

Podstawowe cele szeregowania:

•         Skrócenie cyklu produkcyjnego,

•         Skrócenie cyklu produkcyjnego,

•         Usprawnienie organizacji pracy.

•         Usprawnienie organizacji pracy.

Szeregowanie

Szeregowanie

3

Zmierza ono do ustalenia optymalnego

Zmierza ono do ustalenia optymalnego

harmonogramu kolejności wykonania operacji

harmonogramu kolejności wykonania operacji

na m stanowiskach, dla n przedmiotów,

na m stanowiskach, dla n przedmiotów,

zdeterminowanego przede wszystkim przez :

zdeterminowanego przede wszystkim przez :

       

       

kolejność wykonywanych operacji

kolejność wykonywanych operacji

Szeregowanie

Szeregowanie

4

Ustalenie najlepszego harmonogramu

Ustalenie najlepszego harmonogramu

kolejności wykonywania operacji często

kolejności wykonywania operacji często

sprawia problem przedsiębiorstwom, które

sprawia problem przedsiębiorstwom, które

dążą do

dążą do

skrócenia czasu produkcji

skrócenia czasu produkcji

.

.

Z myślą o rozwiązaniu tych problemów

Z myślą o rozwiązaniu tych problemów

opracowano kilka metod. Metody

opracowano kilka metod. Metody

szeregowania są podstawowym narzędziem

szeregowania są podstawowym narzędziem

planowania operatywnego.

planowania operatywnego.

Problem

5

1.zbiór N zadań produkcyjnych oczekuje na

realizację począwszy od momentu t = 0. Każde
zadanie wymaga M

operacji

operacji, każda operacja jest

realizowana na innym stanowisku spośród M
dostępnych,

2.kolejność realizacji operacji jest identyczna
dla wszystkich zadań,

3. operacje nie mogą być przerywane,

4.czasy przygotowawczo-zakończeniowe dla
urządzeń nie są zależne od kolejności zadań,

5.każda operacja ma określony czas trwania
równy sumie czasu przygotowawczo-
zakończeniowego i czasu wykonania serii
wyrobów.

Istota problemu szeregowania
zadań

6

Istnieje wiele metod rozwiązujących

problem szeregowania, m.in. metody

przybliżone do których zaliczamy:

• Metodę Palmera
• Metodą Gupty

7

Metoda Palmera

Metoda Palmera

Palmer opracował algorytm porządkujący

zadania wg spadku czasów obróbki,
opierając się na spostrzeżeniu, że zadania
umieszczone na początku sekwencji
optymalnej powinny mieć czasy obróbki
zwiększające się w miarę przechodzenia
zadania przez kolejne stanowiska, zadania
umieszczone na końcu – czasy zmniejszające
się.

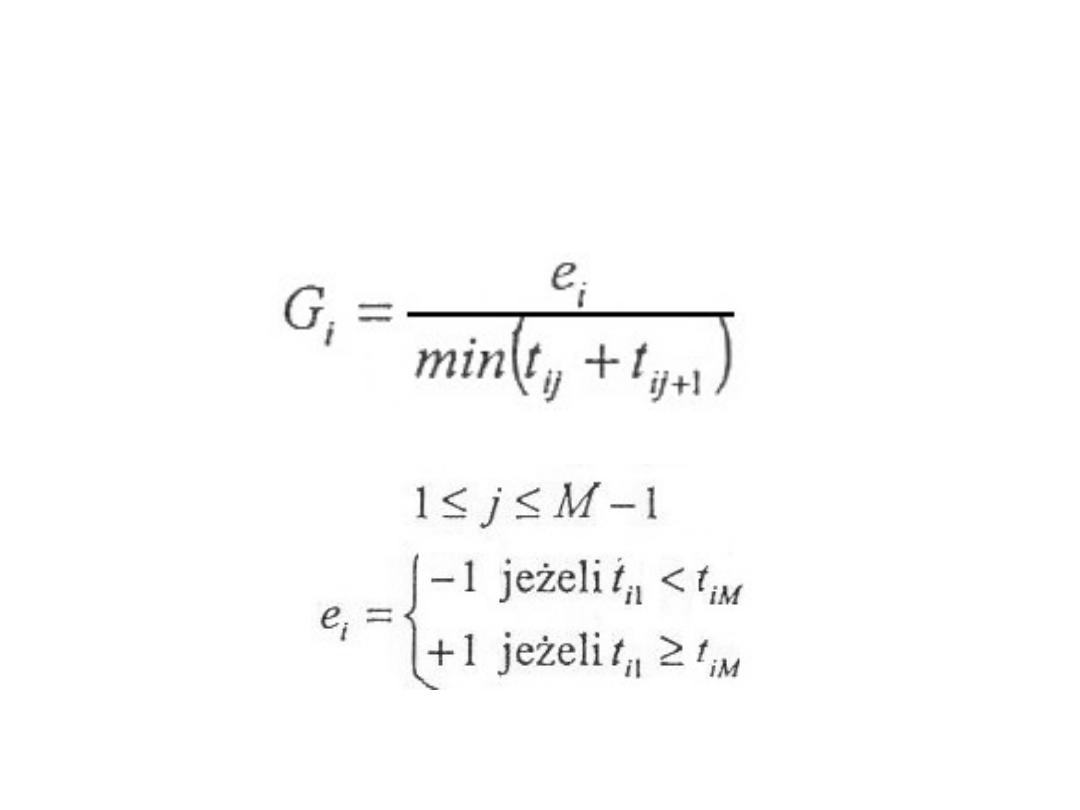
8

Metoda Gupty

Metoda Gupty

Metoda Gupty polega na wyznaczeniu dla każdego

Metoda Gupty polega na wyznaczeniu dla każdego

wskaźnika G

wskaźnika G

i

i

wg wzoru:

wg wzoru:

Gdzie za współczynnik e

Gdzie za współczynnik e

i

i

przyjmuje się:

przyjmuje się:

9

Metoda Palmera

Metoda Palmera

Dla każdego zadania oblicza się wskaźnik SI

i

ze

wzoru:

SIi = (M-1)xtiM+(M-3)xtiM-1+(M-5)xtiM-2+…- (M-

3)xti2-(M-1)xti1

gdzie:
M- liczba stanowisk pracy,
t

iM

– czas jednostkowy operacji i-tego zadania

na stanowisku M,

t

iM-j+1

– czas jednostkowy operacji i-tego

zadania na stanowisku M-j+1.

10

Długość cyklu produkcyjnego obliczana jest

Długość cyklu produkcyjnego obliczana jest

według wzoru:

według wzoru:

C

max

= max(C

iM

)

Przy czym:

C

11

=t

11

oraz C

ij

= t

ij

+ max(C

i,j-1

, C

i-1,j

)

Wyznaczenie długości cyklu
produkcyjnego

11

P

P

rzykład

rzykład

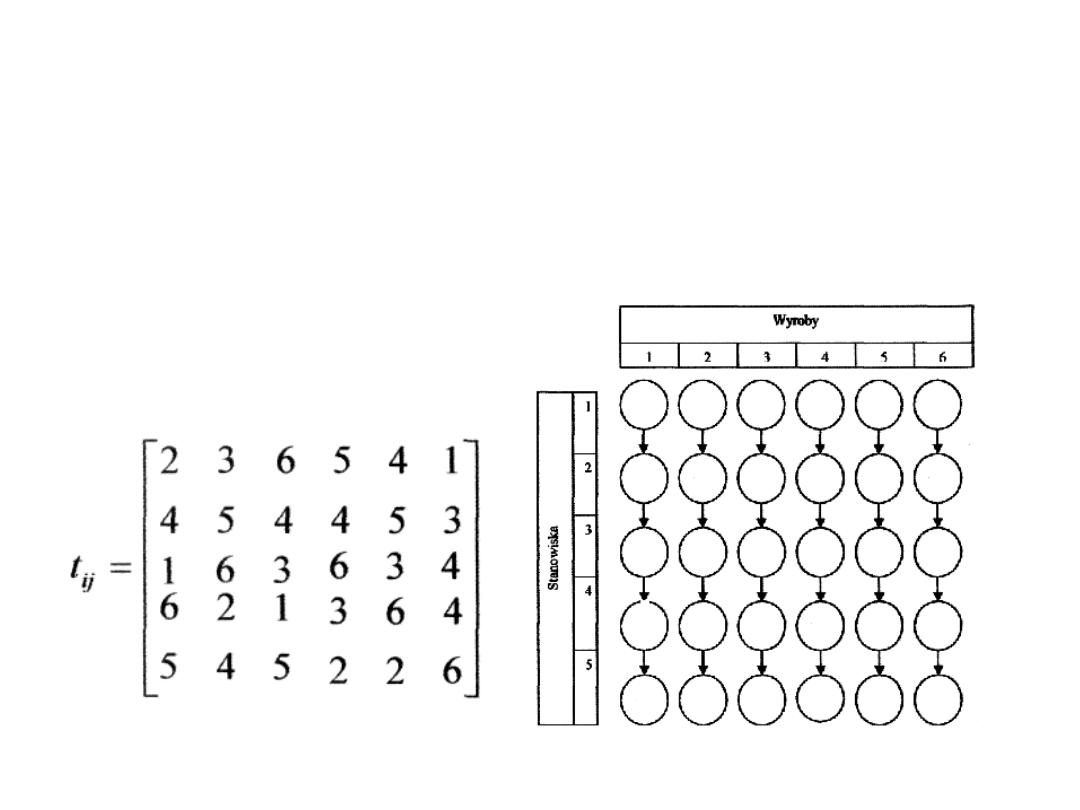
Należy ustalić optymalny harmonogram obróbki sześciu przedmiotów na

Należy ustalić optymalny harmonogram obróbki sześciu przedmiotów na

pięciu maszynach. Czasy obróbki j detalu na i maszynie zawiera macierz [t

pięciu maszynach. Czasy obróbki j detalu na i maszynie zawiera macierz [t

ij

ij

],

],

Kolejność wykonania operacji jest ustalona na poniższym rysunku.

Kolejność wykonania operacji jest ustalona na poniższym rysunku.

12

Rozwiązanie przykładu metodą

Palmera

Wyznaczamy wartości współczynnika

SI

i

dla wszystkich wyrobów

SI

i

= (M-1)xt

iM

+(M-3)xt

iM-1

+(M-5)xt

iM-2

- (M-3)xt

i2

-(M-

1)xt

i1

= 4x t

15

+ 2x t

14

+ 0x t

13

- 2x t

12

- 4x t

11

13

Wartości współczynnika SI

i

dla i= 1,2,3,4,5,6

wynoszą:

S1 = 20+12-8-8= 16
S2 = 16+4-10-12= -2
S3 = 20+2-8-24= -10
S4 = 8+6-8-20= -14
S5 = 8+12-10-16= -6
S6 = 24+8-6-4= 22

Porządkujemy wartości SI w ciąg malejący:

Porządkujemy wartości SI w ciąg malejący:

S6>S1>S2>S5>S3>S4

S6>S1>S2>S5>S3>S4

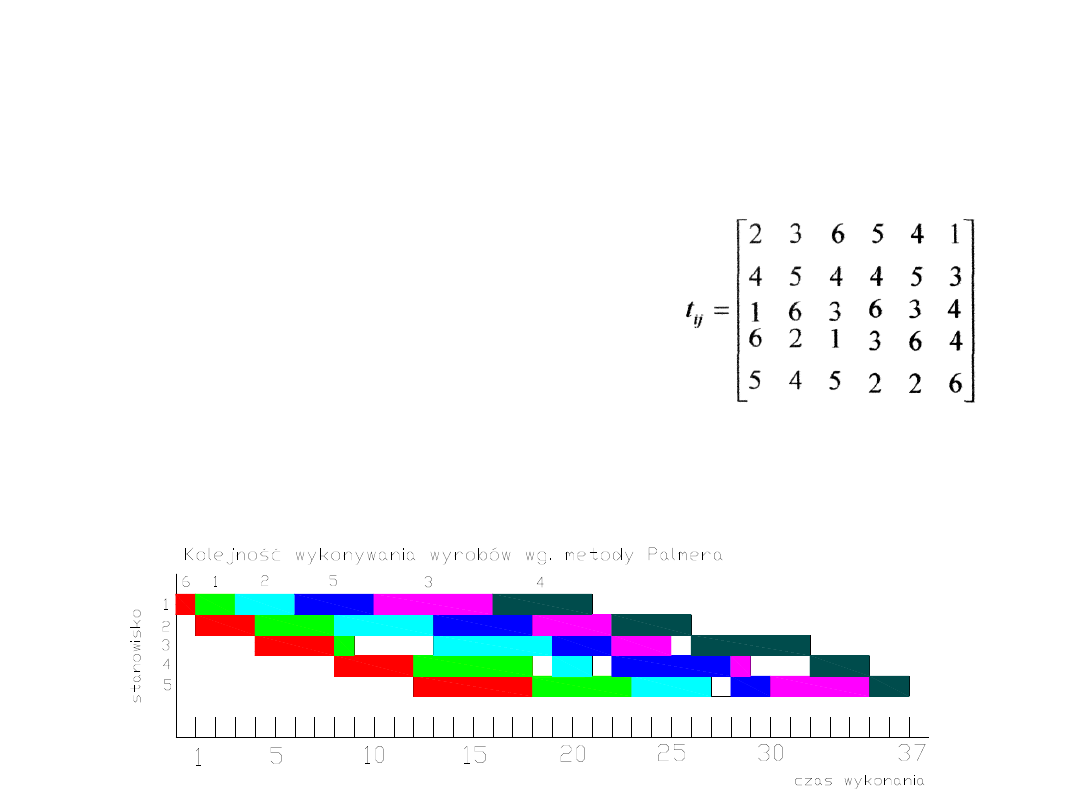
Uzyskaliśmy następującą optymalną

Uzyskaliśmy następującą optymalną

kolejność obróbki wyrobów :

kolejność obróbki wyrobów :

6 l 2 5 3 4.

6 l 2 5 3 4.

14

Długość cyklu produkcyjnego – metoda

Długość cyklu produkcyjnego – metoda

Palmera

Palmera

6.
C

11

=t

11

=1

C

12

=t

12

+C

11

=3+1=4

C

13

=t

13

+C

12

=4+4=8

C

14

=t

14

+C

13

=4+8=12

C

15

=t

15

+C

14

=6+12=18

1.
C

21

=t

21

+C

11

=2+1=3

C

22

=t

22

+max(C

21

C

12

)=4+4

=8
C

23

=t

23

+max(C

22

C

13

)=1+8

=9
C

24

=t

24

+max(C

23

C

14

)=6+1

2=18
C

25

=t

25

+max(C

24

C

15

)=5+1

8=23
2.
C

31

=t

31

+C

21

=3+3=6

C

32

=t

32

+max(C

31

C

22

)=5+8

=13
C

33

=t

33

+max(C

32

C

23

)=6+1

3=19
C

34

=t

34

+max(C

33

C

24

)=2+1

9=21
C

35

=t

35

+max(C

34

C

25

)=4+2

3=27

5.
C

41

=t

41

+C

31

=4+6=10

C

42

=t

42

+max(C

41

C

32

)=5+13

=18
C

43

=t

43

+max(C

42

C

33

)=3+19

=22
C

44

=t

44

+max(C

43

C

34

)=6+22

=28
C

45

=t

45

+max(C

44

C

35

)=2+28

=30
3.
C

51

=t

51

+C

41

=6+10=16

C

52

=t

52

+max(C

51

C

42

)=4+18

=22
C

53

=t

53

+max(C

52

C

43

)=3+22

=25
C

54

=t

54

+max(C

53

C

44

)=1+28

=29
C

55

=t

55

+max(C

54

C

45

)=5+30

=35
4.
C

61

=t

61

+C

51

=5+16=21

C

62

=t

62

+max(C

61

C

52

)=4+22

=26
C

63

=t

63

+max(C

62

C

53

)=6+26

=32
C

64

=t

64

+max(C

63

C

54

)=3+32

=34
C

65

=t

65

+max(C

64

C

55

)=2+35

=37

15

Kolejność wyrobów (metoda Palmera) 6, 1, 2, 5, 3, 4.

Wyrób 6

1

4

8

12

18

Wyrób 1

3

8

9

18

23

Wyrób 2

6

13

19

21

27

Wyrób 5

10

18

22

28

30

Wyrób 3

16

22

25

29

35

Wyrób 4

21

26

32

34

37

16

Rozwiązanie przykładu metodą

Gupty

•

Obliczamy wskaźnik G

Obliczamy wskaźnik G

i

i

odnoszący się do poszczególnych

odnoszący się do poszczególnych

detali:

detali:

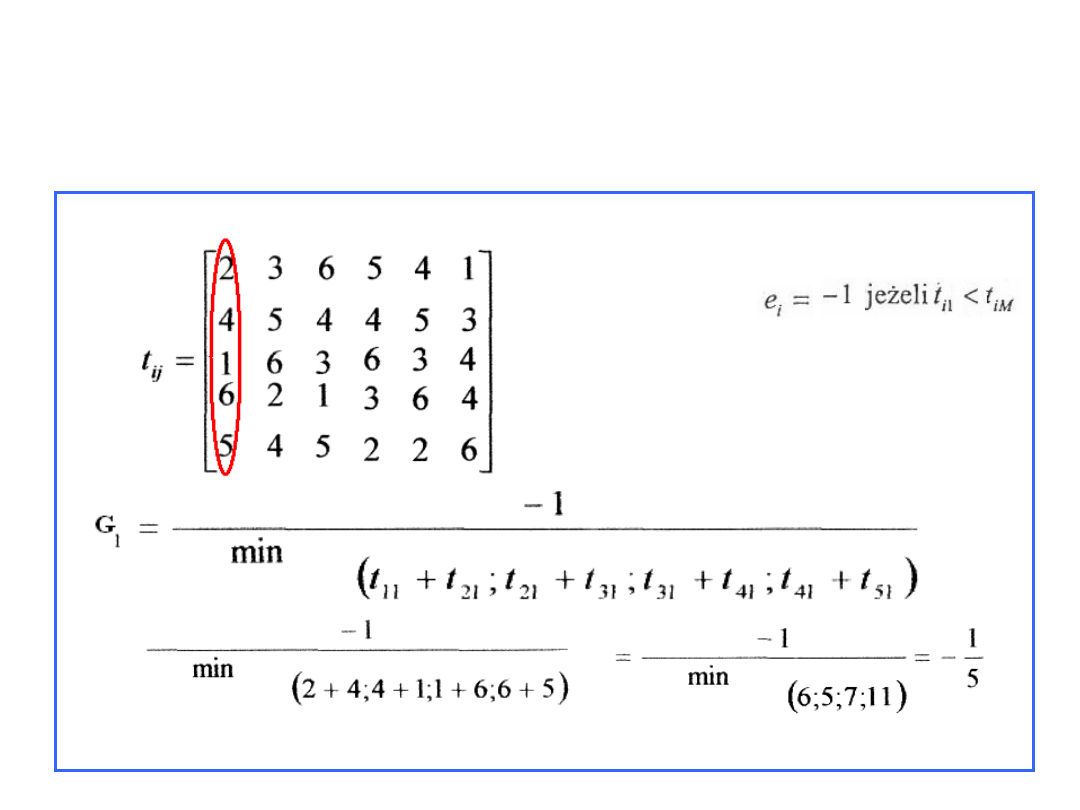
Wyrób 1

G1= -1/5=-0,2

Warunek:

17

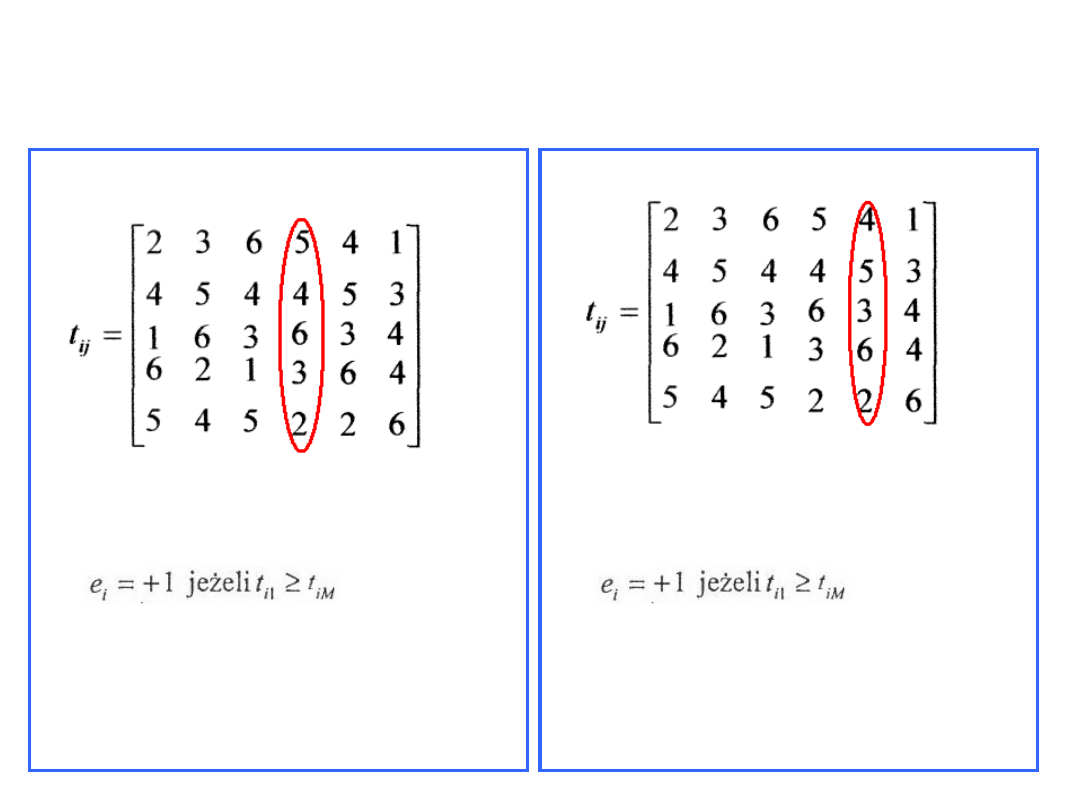
Wyrób nr.2

Wyrób nr.3

min tz

lj

+ tz

lj

+1 (8;11;8;6)=6

Warunek:

min tz

lj

+ tz

lj

+1 (10;7;4;6)=4

Warunek:

G2=-1/6=-0,16

G3=1/4=0,25

18

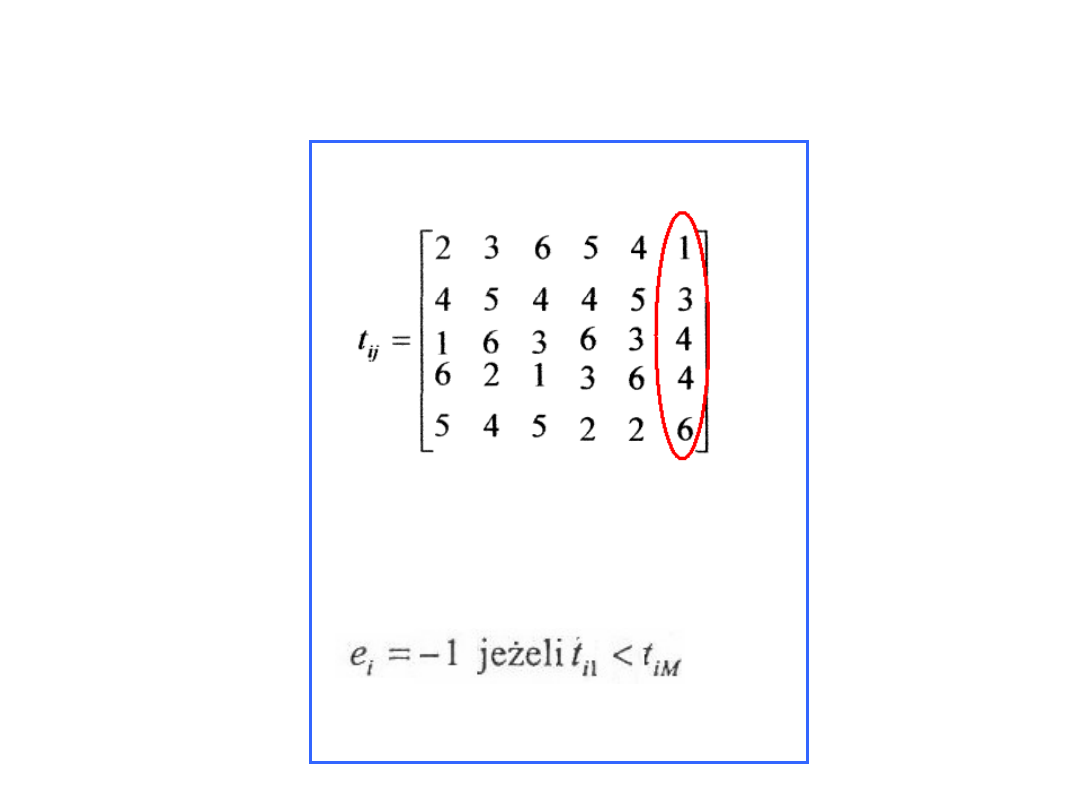
Wyrób nr.5

Wyrób nr.4

min tz

lj

+ tz

lj

+1 (9;10;9;5)=5

Warunek:

min tz

lj

+ tz

lj

+1 (9;8;9;8)=8

Warunek:

G4=1/5=0,2

G5=1/8=0,125

19

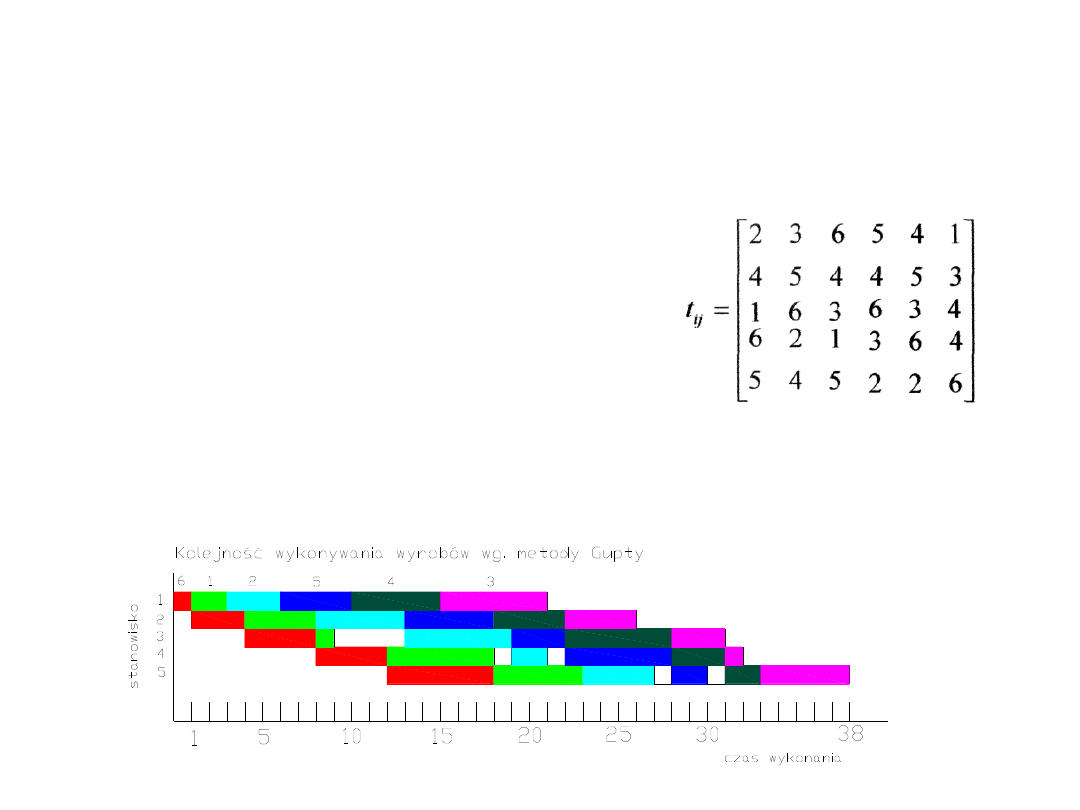
Wyrób
nr.6

min tz

lj

+ tz

lj

+1 (4;7;8;10)=4

Warunek:

G6=-1/4=-025

20

Ustawiamy wskaźniki Gi

Ustawiamy wskaźniki Gi

w ciąg rosnący:

w ciąg rosnący:

G6<G1<G2<G5<G4<G3

G6<G1<G2<G5<G4<G3

Na podstawie powyższego ciągu otrzymaliśmy następującą

Na podstawie powyższego ciągu otrzymaliśmy następującą

kolejność zapuszczania wyrobów do obróbki:

kolejność zapuszczania wyrobów do obróbki:

612543

612543

G1

G2

G3

G4

G5

G6

-0,2

-0,16

0,25

0,2

0,125 -0,25

21

Długość cyklu produkcyjnego – metoda Gupty

6.
C

11

=t

11

=1

C

12

=t

12

+C

11

=3+1=4

C

13

=t

13

+C

12

=4+4=8

C

14

=t

14

+C

13

=4+8=12

C

15

=t

15

+C

14

=6+12=18

1.
C

21

=t

21

+C

11

=2+1=3

C

22

=t

22

+max(C

21

C

12

)=4+

4=8
C

23

=t

23

+max(C

22

C

13

)=1+

8=9
C

24

=t

24

+max(C

23

C

14

)=6+

12=18
C

25

=t

25

+max(C

24

C

15

)=5+

18=23
2.
C

31

=t

31

+C

21

=3+3=6

C

32

=t

32

+max(C

31

C

22

)=5+

8=13
C

33

=t

33

+max(C

32

C

23

)=6+

13=19
C

34

=t

34

+max(C

33

C

24

)=2+

19=21
C

35

=t

35

+max(C

34

C

25

)=4+

23=27

5.
C

41

=t

41

+C

31

=4+6=10

C

42

=t

42

+max(C

41

C

32

)=5+13=

18
C

43

=t

43

+max(C

42

C

33

)=3+19=

22
C

44

=t

44

+max(C

43

C

34

)=6+22=

28
C

45

=t

45

+max(C

44

C

35

)=2+28=

30
4.
C

51

=t

51

+C

41

=5+10=15

C

52

=t

52

+max(C

51

C

42

)=4+18=

22
C

53

=t

53

+max(C

52

C

43

)=6+22=

28
C

54

=t

54

+max(C

53

C

44

)=3+28=

31
C

55

=t

55

+max(C

54

C

45

)=2+31=

33
3.
C

61

=t

61

+C

51

=6+15=21

C

62

=t

62

+max(C

61

C

52

)=4+22=

26
C

63

=t

63

+max(C

62

C

53

)=3+28=

31
C

64

=t

64

+max(C

63

C

54

)=1+31=

32
C

65

=t

65

+max(C

64

C

55

)=5+33=

38

22

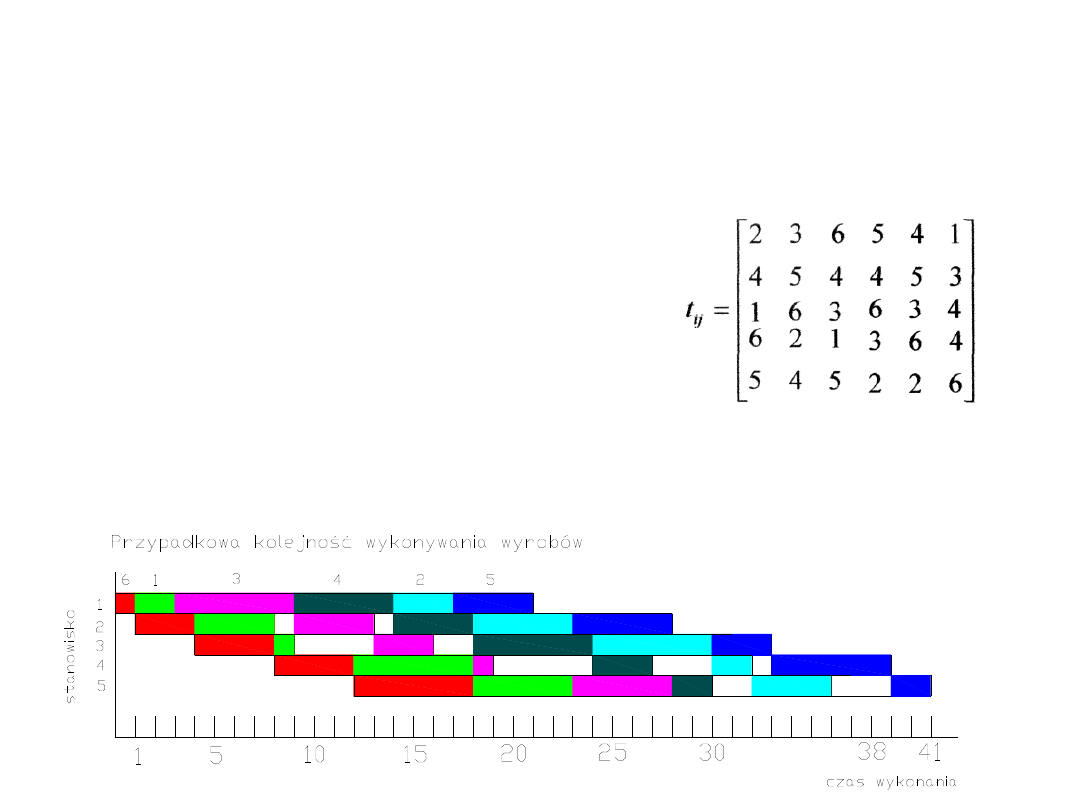
Kolejność wyrobów (metoda Gupty):6, 1, 2, 5,

Kolejność wyrobów (metoda Gupty):6, 1, 2, 5,

4, 3.

4, 3.

Wyrób 6

1

4

8

12

18

Wyrób 1

3

8

9

18

23

Wyrób 2

6

13

19

21

27

Wyrób 5

10

18

22

28

30

Wyrób 4

15

22

28

31

33

Wyrób 3

21

26

31

32

38

23

Długość cyklu produkcyjnego – dowolna
kolejność

6.
C

11

=t

11

=1

C

12

=t

12

+C

11

=3+1=4

C

13

=t

13

+C

12

=4+4=8

C

14

=t

14

+C

13

=4+8=12

C

15

=t

15

+C

14

=6+12=18

1.
C

21

=t

21

+C

11

=2+1=3

C

22

=t

22

+max(C

21

C

12

)=4+

4=8
C

23

=t

23

+max(C

22

C

13

)=1+

8=9
C

24

=t

24

+max(C

23

C

14

)=6+

12=18
C

25

=t

25

+max(C

24

C

15

)=5+

18=23
3.
C

31

=t

31

+C

21

=6+3=9

C

32

=t

32

+max(C

31

C

22

)=4+

9=13
C

33

=t

33

+max(C

32

C

23

)=3+

13=16
C

34

=t

34

+max(C

33

C

24

)=1+

18=19
C

35

=t

35

+max(C

34

C

25

)=5+

23=28

4.
C

41

=t

41

+C

31

=5+9=14

C

42

=t

42

+max(C

41

C

32

)=4+

14=18
C

43

=t

43

+max(C

42

C

33

)=6+

18=24
C

44

=t

44

+max(C

43

C

34

)=3+

24=27
C

45

=t

45

+max(C

44

C

35

)=2+

28=30
2.
C

51

=t

51

+C

41

=3+14=17

C

52

=t

52

+max(C

51

C

42

)=5+

18=23
C

53

=t

53

+max(C

52

C

43

)=6+

24=30
C

54

=t

54

+max(C

53

C

44

)=2+

30=32
C

55

=t

55

+max(C

54

C

45

)=4+

32=36
5.
C

61

=t

61

+C

51

=4+17=21

C

62

=t

62

+max(C

61

C

52

)=5+

23=28
C

63

=t

63

+max(C

62

C

53

)=3+

30=33
C

64

=t

64

+max(C

63

C

54

)=6+

33=39
C

65

=t

65

+max(C

64

C

55

)=2+

39=41

24

Kolejność wyrobów przypadkowa 6, 1, 3, 4, 2, 5.

Wyrób 6

1

4

8

12

18

Wyrób 1

3

8

9

18

23

Wyrób 3

9

13

16

19

28

Wyrób 4

14

18

24

27

30

Wyrób 2

17

23

30

32

36

Wyrób 5

21

28

33

39

41

25