Łańcuchy Markowa

1. Wstęp
2. Prawdopodobieństwo, niezależność

prawdopodobieństwo warunkowe

3. Definicja łańcucha Markowa
4. Klasyfikacja stanów
5. Ewolucja prawdopodobieństw
6. Stacjonarność
7. Odwracalność

Wstęp

Andrey Andreevich
Markov
Андрей Андреевич
Марков
(1856-1922)

Wstęp

• fizyce,
• chemii, biochemii,
• biologii, biologii molekularnej,
• genetyce,
• informatyce, teorii algorytmów, teorii

optymalizacji

Łańcuchy Markowa powstały jako modele w
rachunku prawdopodobieństwa uogólniające
pojęcie niezależności.
Obecnie są stosowane praktycznie we wszystkich
gałęziach nauki, w szczególności w:

Wstęp

W konstrukcji Łańcucha Markowa istotne

znaczenie mają pojęcia:

- stanu (stanów)
- przejść (przeskoków) pomiędzy stanami
- własności Markowa

Będziemy się koncentrować na łańcuchach

Markowa o skończonej liczbie stanów:

1

2

3

N

….

Prawdopodobieństwo

n

n

A

P

A



)

(

n

n

A

P

A

n

lim

)

(







Prawdopodobieństwo zdarzenia A, P(A), jest
miarą częstości występowania A przy
wielokrotnym powtarzaniu eksperymentu:

Geometryczna definicja
prawdopodobieństwa:



A

Prawdopodobieństwo







A

A

C

P( ) = 1

A

C

= \ A

P(A

C

) = 1 – P(A)

Prawdopodobieństwo

Jeśli A i B się wykluczają (A  B = )

to:

P(A  B) = P(A) + P(B)

Ogólnie:
P(A  B) = P(A) + P(B) – P(A

 B )

A

B

A  B

Niezależność

Zdarzenia A i B są niezależne

wtedy i tylko wtedy gdy:

P( A  B) = P(A) P(B)

Zamiast A  B często będziemy pisać A,B

P( A  B) =P(A,B)

Prawdopodobieństwo

warunkowe

)

(

)

,

(

)

(

)

(

)

|

(

B

P

B

A

P

B

P

B

A

P

B

A

P







A

B

A  B

Reguła łańcuchowa

C)

B

P(A|B,C)P(

C

P

C

B

P

C

B

P

C

B

A

P

C

P

C

B

A

P

C

B

A

P

|

)

(

)

,

(

)

,

(

)

,

,

(

)

(

)

,

,

(

)

|

,

(









Przykład

Drukarka laserowa drukując stronę testową

może

(a) zgnieść papier,
(b)doznać uszkodzenia mechanizmu

drukującego.

Prawdopodobieństwo zgniecenia papieru wynosi

0.001, prawdopodobieństwo uszkodzenia

mechanizmu przy zgnieceniu papieru wynosi

0.01.

Jakie jest prawdopodobieństwo, że drukując

stronę testową drukarka zgniecie papier i

dozna uszkodzenia mechanizmu drukującego?

Rozwiązanie przykładu

A – drukarka doznaje uszkodzenia

mechanizmu

B – drukarka gniecie papier
C – drukarka drukuje stronę testową
P(A|B,C)=0.01
P(B|C)=0.001

P(A,B|C) = P(A|B,C) P(B|C) =

0.00001

Reguła łańcuchowa

)

|

(

,

|

,

)

|

,

,

(

D

C

D)P

C

D)P(B

P(A|B,C

D

C

B

A

P



… i tak dalej

Wzór na

prawdopodobieństwo

całkowite

B

1

, B

2

, …, B

K

- zdarzenia wzajemnie

wykluczające się:
B

i

 B

j

= ,

oraz:
B

1

 B

2

 …  B

K

= 







K

i

i

i

B

P

B

A

P

A

P

1

)

(

)

|

(

)

(



K

i

i

B

A

A

1







Wzór na prawdopodobieństwo całkowite:

Przykład

Supermarket kupuje jabłka od dwóch

dostawców, 30% od pierwszego i 70%
od drugiego. Wśród jabłek od
pierwszego dostawcy jest 1% zepsutych
a od drugiego 2% zepsutych.

Wybieramy losowo jabłko w

supermarkecie. Jakie jest
prawdopodobieństwo, że będzie
zepsute?

Rozwiązanie przykładu

A – zepsute jabłko
B

1

– jabłko od pierwszego dostawcy

B

2

– jabłko od drugiego dostawcy

P(B

1

) = 0.3

P(B

2

) = 0.7

P(A|B

1

) = 0.01

P(A|B

2

) = 0.02

P(A) = P(A|B

1

) P(B

1

) + P(A|B

2

) P(B

2

) =

= 0.01*0.3 + 0.02*0.7 =

0.017

Łańcuch Markowa

Łańcuch Markowa X

k

jest

procesem losowych przeskoków

pomiędzy dyskretnymi stanami

Indeks k oznacza chwile czasowe
pomiędzy przeskokami

Stany

1

2

3

N

….

Prawdopodobieństwa przejść

z X

k

= i do X

k+1

= j

p

ij

= P( X

k+1

= j | X

k

= i )

Macierz prawdopodobieństw

przejść



























NN

N

N

N

N

p

p

p

p

p

p

p

p

p

P

...

...

...

...

...

...

...

2

1

2

22

21

1

12

11

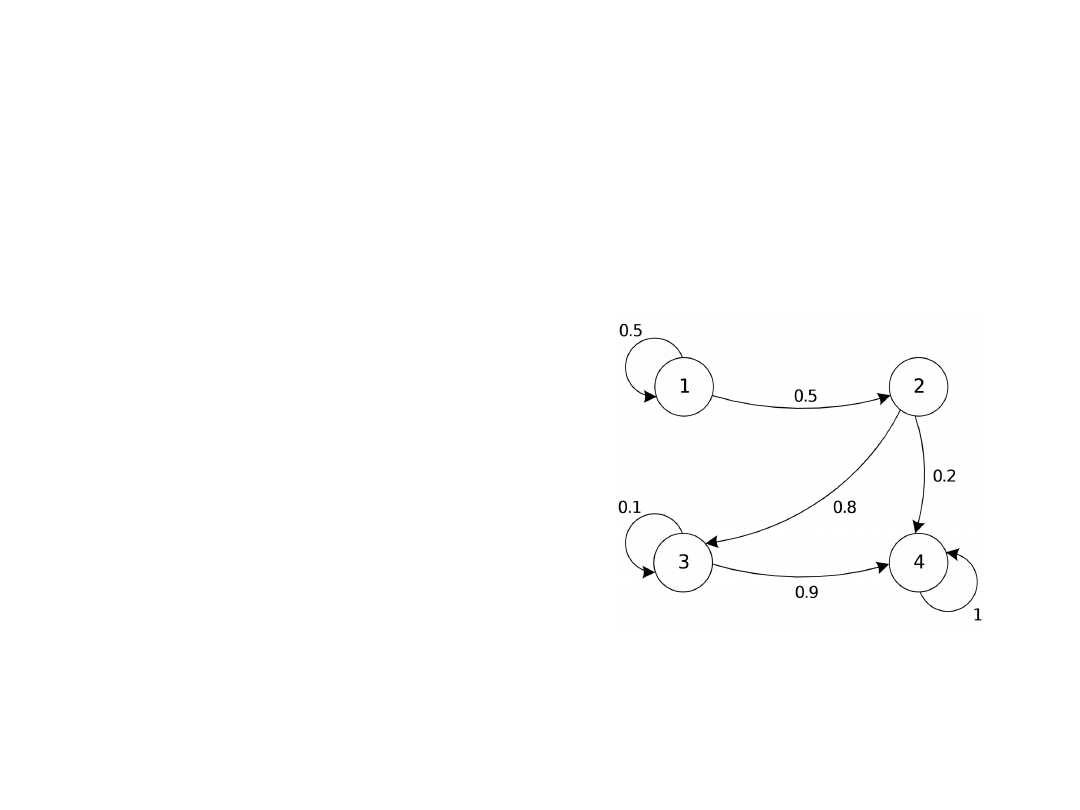
Macierz prawdopodobieństw

przejść i graf przejść



























1

0

0

0

9

.

0

1

.

0

0

0

2

.

0

8

.

0

0

0

0

0

5

.

0

5

.

0

P

Własność Markowa

P( X

k+1

= j | X

k

= i ) = P( X

k+1

= j | X

k

= i , X

k-1

= i

1

,…,

X

k-r

= i

k-r

)

Własność Markowa oraz

reguła łańcuchowa prowadzą

do wniosku

P[i

0

, i

1

,...,i

K

] =

i0

p

i0,i1

p

i1,i2

p

K-1,K

gdzie


i0

= P[ X₀ = i₀ ]

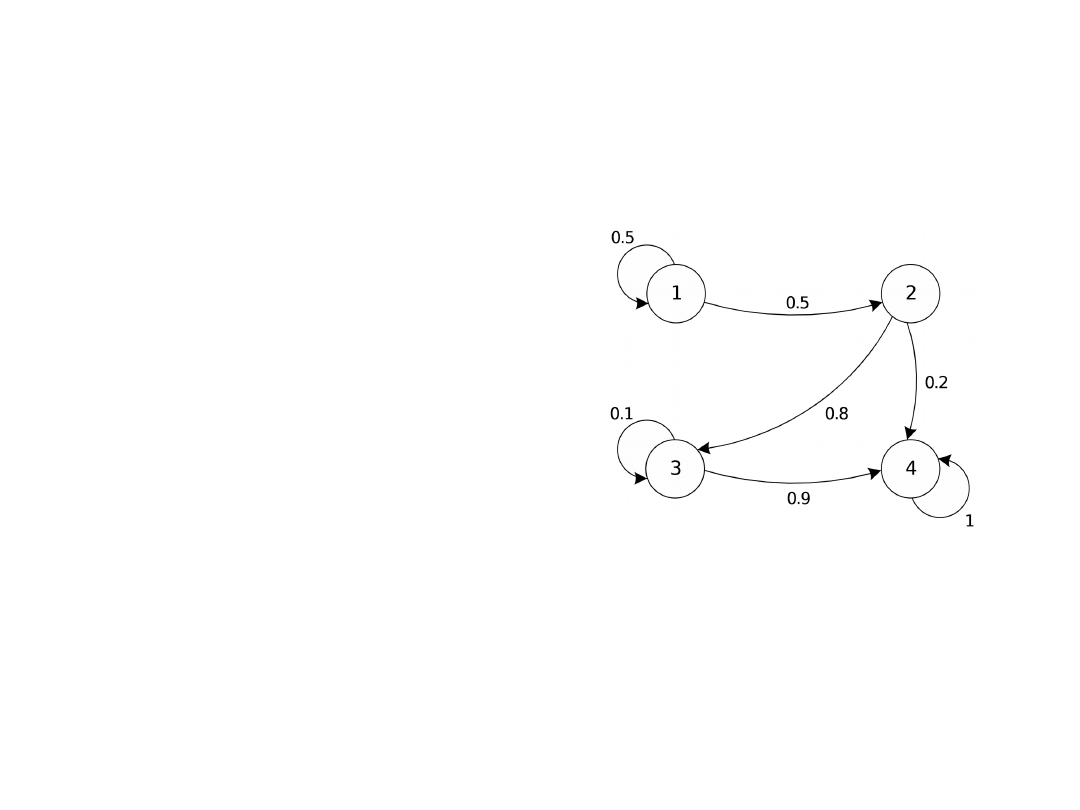
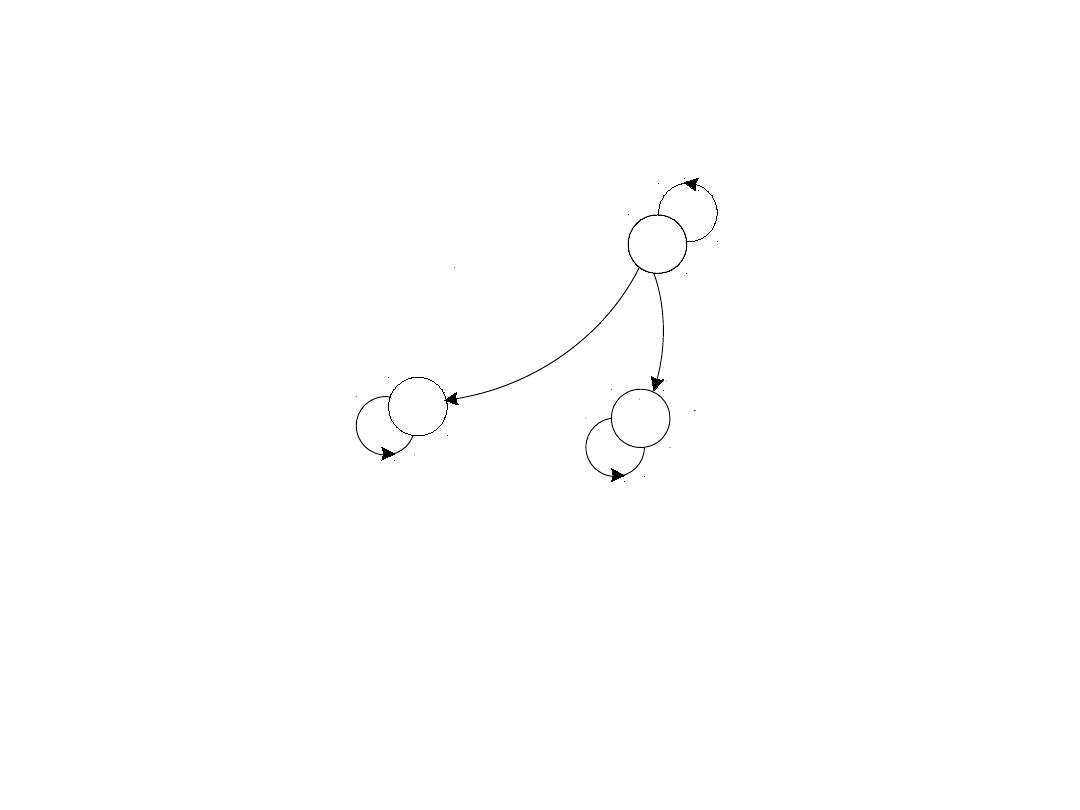
Przykład

Dla łańcucha Markowa:

gdzie X

1

= 1, mamy

P[1, 1, 2, 3, 4, 4] = 0.5*0.5*0.8*0.9*1=0.18

Rozkład

prawdopodobieństwa stanów

]

2

.

0

,

7

.

0

,

1

.

0

[

)]

1

(

),

1

(

),

1

(

[

)

1

(

3

2

1













]

0

,

0

,

1

[

)]

0

(

),

0

(

),

0

(

[

)

0

(

3

2

1













)

0

(



Jeśli w chwili k=0 X

0

=1 to

nazywa się rozkładem prawdopodobieństw stanów w chwili 0

Z kolei:

nazywa się rozkładem prawdopodobieństw stanów w chwili k

)

(k



1

3

2

.

0.2

0.7

0.1

1

1

Ewolucja rozkładów

prawdopodobieństw stanów

)]

1

(

...

)

1

(

)

1

(

[

)

1

(

2

1

N











)]

(

...

)

(

)

(

[

)

(

2

1

k

k

k

k

N











.
.
.

.
.
.

)]

0

(

...

)

0

(

)

0

(

[

)

0

(

2

1

N











Ewolucja rozkładów

prawdopodobieństw stanów

)]

1

(

...

)

1

(

)

1

(

[

)

1

(

2

1

N











)]

0

(

...

)

0

(

)

0

(

[

)

0

(

2

1

N











Zadanie: znamy

policzyć

Ewolucja rozkładów

prawdopodobieństw stanów

Nk

N

k

k

k

p

p

p

k

X

P

)

0

(

...

)

0

(

)

0

(

]

)

1

(

[

)

1

(

2

2

1

1























Zastosowanie wzoru na prawdopodobieństwo całkowite

Ewolucja rozkładów

prawdopodobieństw stanów

(1) =

(0) P

)]

0

(

...

)

0

(

)

0

(

[

2

1

N

































NN

N

N

N

N

p

p

p

p

p

p

p

p

p

...

...

...

...

...

...

...

2

1

2

22

21

1

12

11

)]

1

(

...

)

1

(

)

1

(

[

2

1

N







(1) = (0) P
(2) = (0) P*P

…..

(k) = (0) P

k

Ewolucja rozkładów

prawdopodobieństw stanów

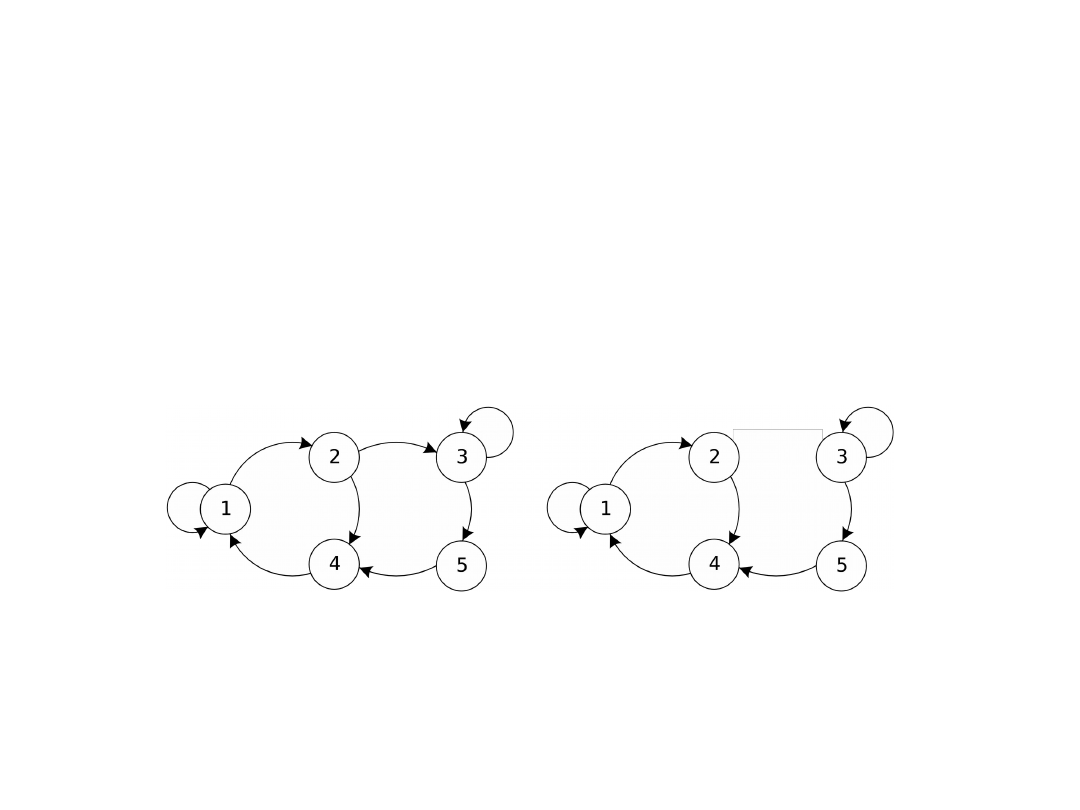
Nieprzywiedlność

Łańcuch Markowa jest nieprzywiedlny

jeśli z dowolnego stanu można
przejść do każdego innego

nieprzywiedlny

przywiedlny

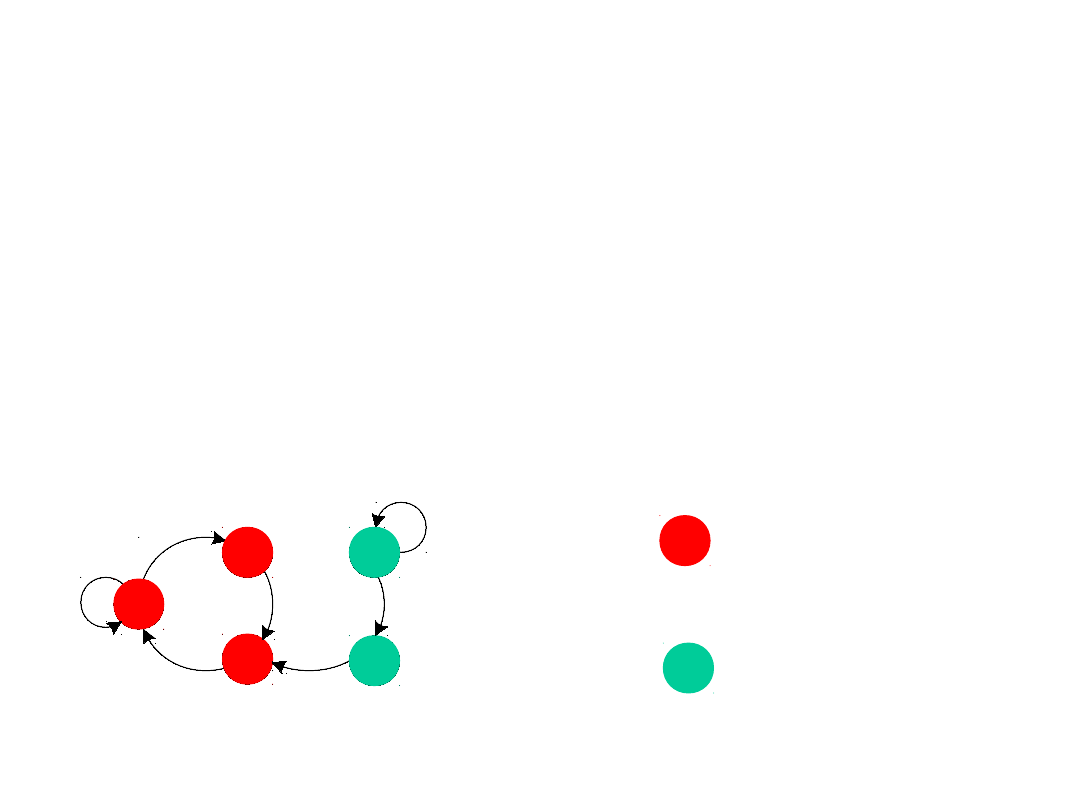
Stany powracające i

przejściowe

Stan łańcucha Markowa nazywa się

powracającym, jeśli startując z tego stanu

wrócimy do niego z

prawdopodobieństwem 1. Stan, który nie

jest powracający nazywa się

przejściowym.

1

4

5

2

3

- powracające

- przejściowe

Stany okresowe

Łańcuch aperiodyczny

Łańcuch Markowa, którego żaden

stan nie jest okresowy nazywa się
aperiodycznym

Ergodyczność

Stan jest ergodczny jeśli jest

aperiodyczny i powracający. Łańcuch
jest ergodyczny jeśli wszystkie jego
stany są ergodyczne.

Jeśli łańcuch ma skończoną liczbę stanów

i jest nieprzywiedlny i aperiodyczny to
jest ergodyczny

Rozkład niezmienniczy



S

= 

S

P

Rozkład stacjonarny

)

(

)

(

lim

k

k













Jak policzyć rozkład

stacjonarny?



S

= 

S

P

Z układu równań:

Łańcuch jest stacjonarny

jeśli

)

(

)

0

(









Jeśli łańcuch Markowa jest

ergodyczny

to granica (k) gdy k  , istnieje, nie

zależy od początkowego rozkładu (0)

oraz

S

k

k











)

(

lim

Łańcuch Markowa z

odwróconym czasem

X

k

, X

k1

, X

k-2

….

)

(

)

1

(

]

[

]

|

[

]

[

]

|

[

1

1

1

k

p

k

i

X

P

j

X

i

X

P

j

X

P

i

X

j

X

P

p

i

ji

j

k

k

k

k

k

k

reversed

ij

































Odwracalne łańcuch

Markowa

Łańcuch Markowa nazywa się odwracalnym

jeśli

ij

reversed

ij

p

p



Łańcuch odwracalny jest łańcuchem stacjonarnym

Odwracalność – warunek

lokalnego bilansu

)

(

)

1

(

k

p

k

p

i

ji

j

reversed

ij









Si

ji

Sj

reversed

ij

p

p







Stacjonarność

pociąga za
sobą:

ji

Sj

ij

Si

p

p







Warunek lokalnego

bilansu: