POŁĄCZENIA CIERNE

 Wprowadzenie
 Sposoby montażu
 Obciążalność połączeń ciernych
 Rozkłady naprężeń w elementach

łączonych

 Zależność miedzy wciskiem skutecznym

a naciskiem na powierzchni styku

 Obciążalność elementów złącza

połączenia ciernego

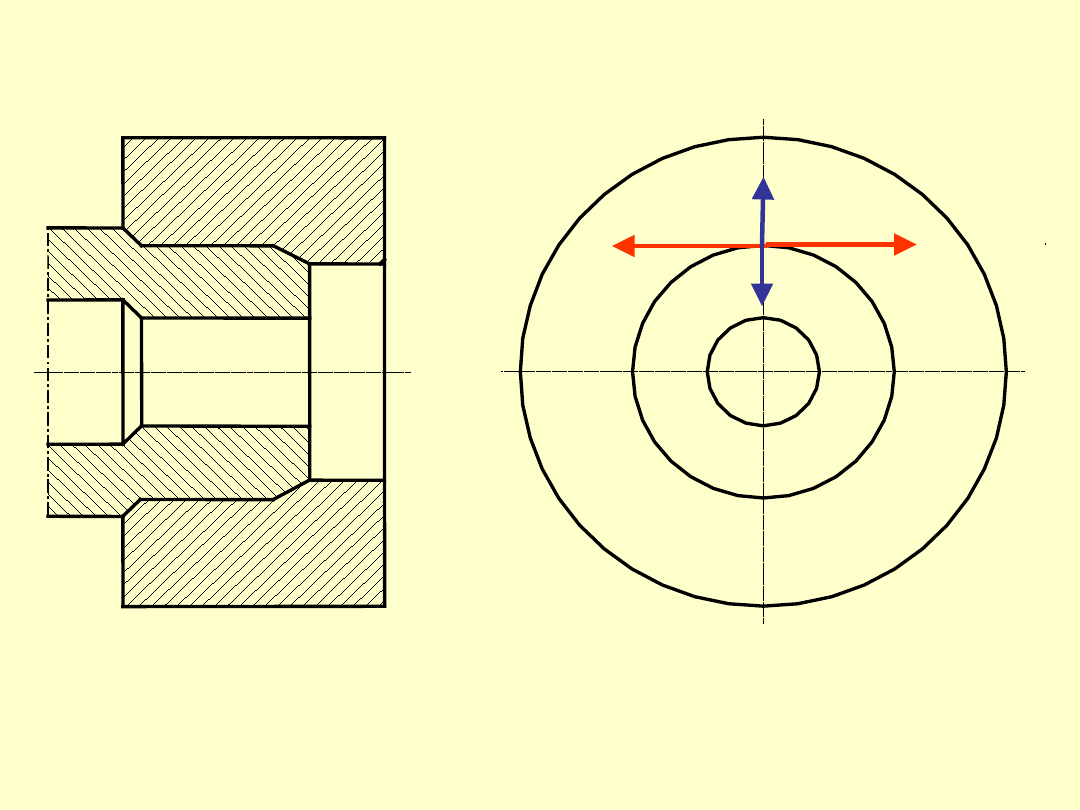
Połączenie cierne – połączenie
spoczynkowe o sprężyście
odkształconych, gładkich powierzchniach
styku czopa i oprawy.

W budowie maszyn i okrętownictwie
takie połączenia są szeroko stosowane
np. do osadzania kół zębatych na wałach
lub kołnierzy na wałach w sztywnych
sprzęgłach kołnierzowych linii wałów
okrętowych.

Suma odkształceń czopa i oprawy
stanowi tzw. wcisk skuteczny, który
wywołuje docisk w polu styku.

Docisk ten pozwala przenieść obciążenie
(siłę lub moment skręcający) za pomocą
sił tarcia pojawiającego się na
powierzchni styku.



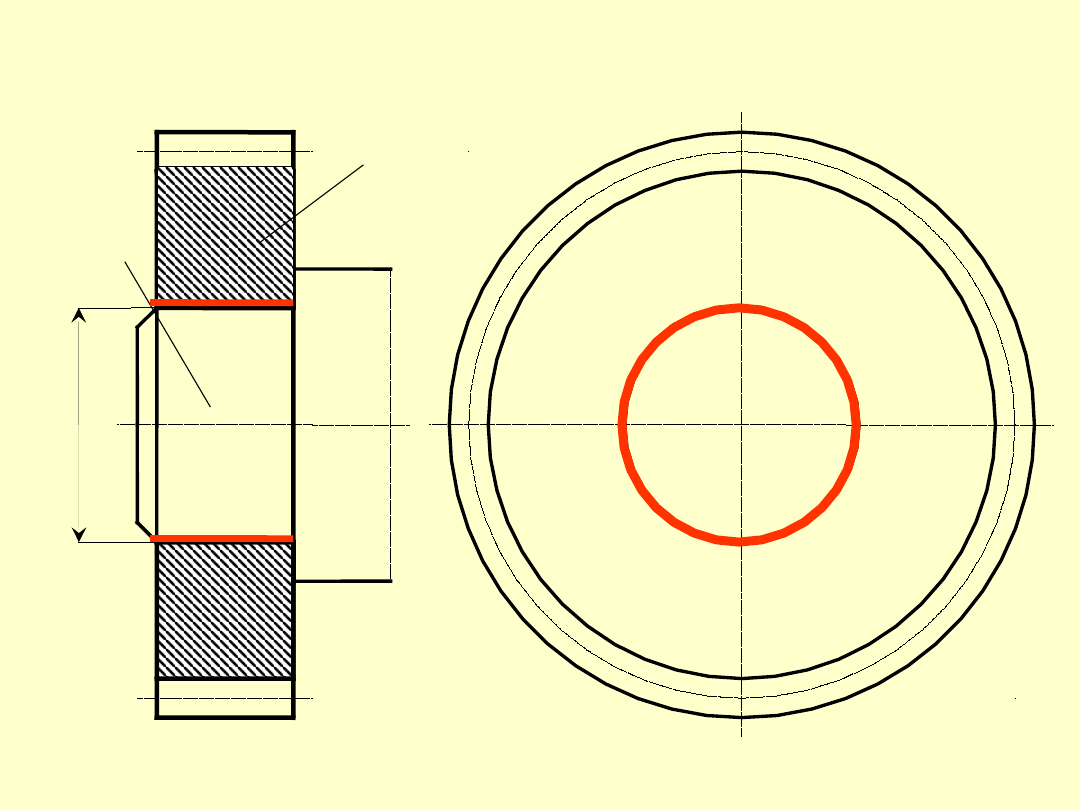
8

0

H

7

/s

6

czop

oprawa

Zalety:

prostota konstrukcji,

zwartość złącza,

łatwość wykonania,

dokładne osiowanie elementów

łączonych,

duża obciążalność złącza – statyczna i

dynamiczna.

Wady:

duże naprężenia montażowe

(niebezpieczne dla materiałów
kruchych),

utrudniony montaż,

możliwość zmiany wcisku podczas

pracy (temperatura lub siła
odśrodkowa).

Sposoby montażu

W zależności od sposobu montażu
rozróżnia się połączenia:

wtłaczane (prasa hydrauliczna),
skurczowe (nagrzewanie oprawy

do max. 300400C).

rozprężane (oziębianie czopa),
kombinowane.

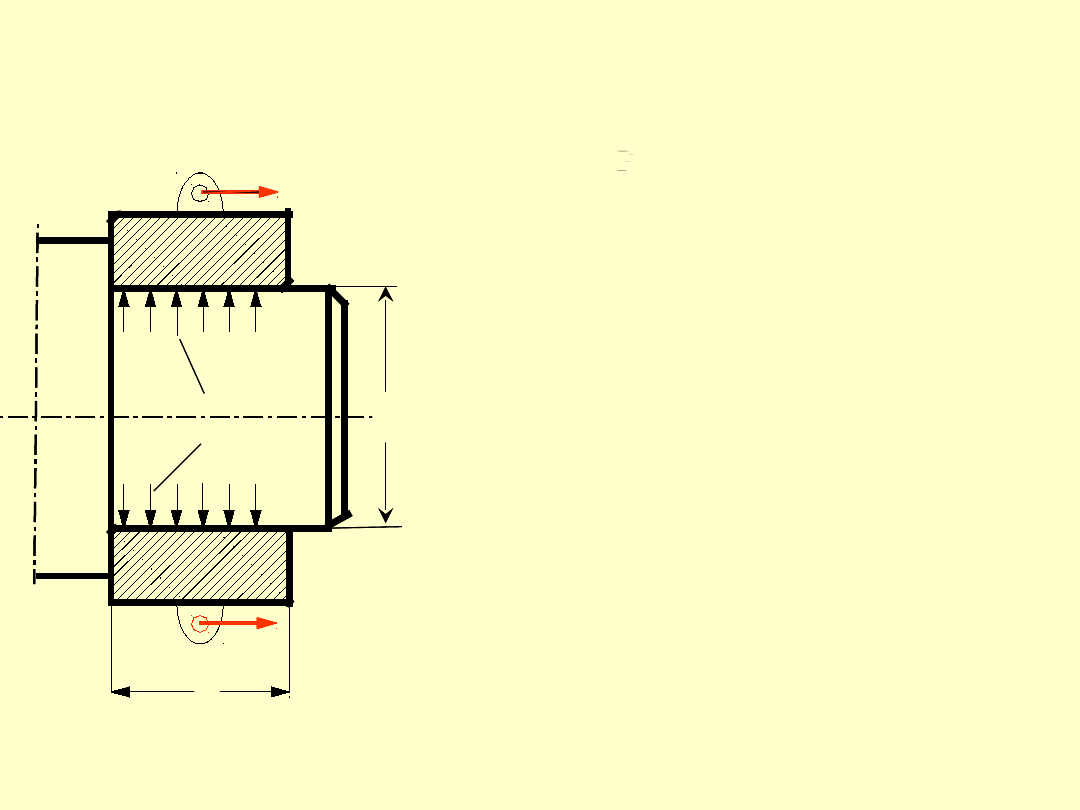
Obciążalność połączeń ciernych

I. Obciążenie siła styczną

P

T

do powierzchni styku.

Obciążenie to przenoszone
będzie za pomocą sił
tarcia.
W związku z tym:

P

T



T

Wiemy jednak, że:

N

T







(1)

P

T

l

p

d

P

T

/2

l

p

d

P

T

/2

W naszym przypadku siła nacisku

N

będzie

wypadkową z nacisków

p

na powierzchni

styku:

F

p

N

F

N

p









(2)

gdzie:

F

– pole powierzchni styku równe:

l

d

F









(3)

Wykorzystując zależności (1), (2) i (3)
uzyskujemy:

(4)

Po przekształceniu otrzymujemy zależność na
wymagany nacisk

p

wym

na powierzchni styku

zapewniający obciążalność złącza siła

P

T

:

(5)

l

d

p

F

p

N

T

P

T































l

d

P

p

T

wym













Siła potrzebna do rozłączenia złącza jest
zwykle o 30% do 50% większa od siły

P

T

.

II. Obciążenie momentem skręcającym

M

l

d

M

Obciążenie to
przenoszone będzie za
pomocą sił tarcia.

W związku z tym:

M



M

T

=

T



d/2

Wykorzystując uprzednio wyznaczone
zależności (1), (2) i (3) otrzymamy:

2

2

2

2

d

l

d

p

d

F

p

d

N

d

T

M































(6)

Po przekształceniu otrzymujemy zależność na
wymagany nacisk

p

wym

na powierzchni styku

zapewniający obciążalność złącza momentem

M

:

l

d

M

p

wym









2

2





(7)

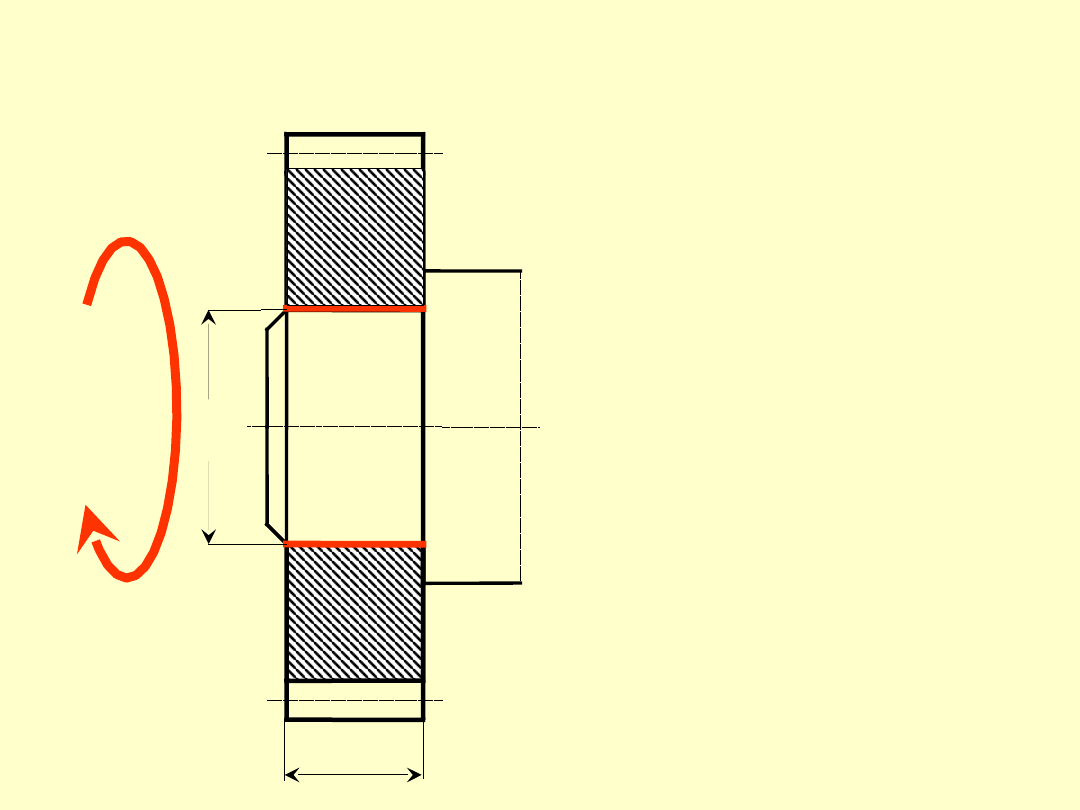
Rozkłady naprężeń w elementach
łączonych

d

z1

d

w

2



1

/2



2

/2

W połączeniach ciernych wcisk skuteczny

w

w =



1

+



2

,

zależy od wcisku pomiarowego

w

pom

w

pom

= d

z1

-d

w2

,

stanowiącego różnicę średnic czopa

d

z1

i

oprawy

d

w2

przed zamontowaniem złącza.

Rozkłady naprężeń w elementach
łączonych



T



T



R



R



T

–

naprężenia obwodowe



R

–

naprężenia

promieniowe

W wyniku odkształcenia elementów łączonych w
czopie i oprawie pojawią się naprężenia:





T

– naprężenia obwodowe,





R

– naprężenia promieniowe.

W czopie i oprawie na ich powierzchni styku
naprężenia promieniowe są równe naciskom
powierzchniowym:



R

= p

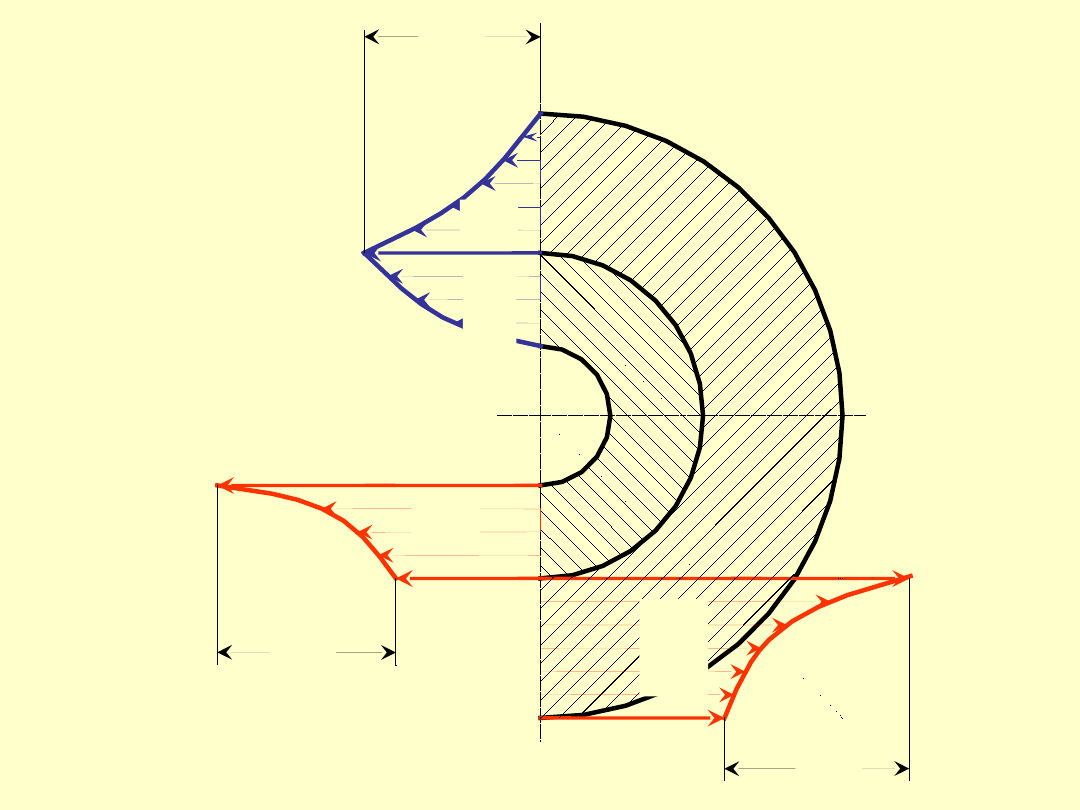
p

p

p



R2



R1



T1



T2

(+

)

(-)

(-)

(-

)



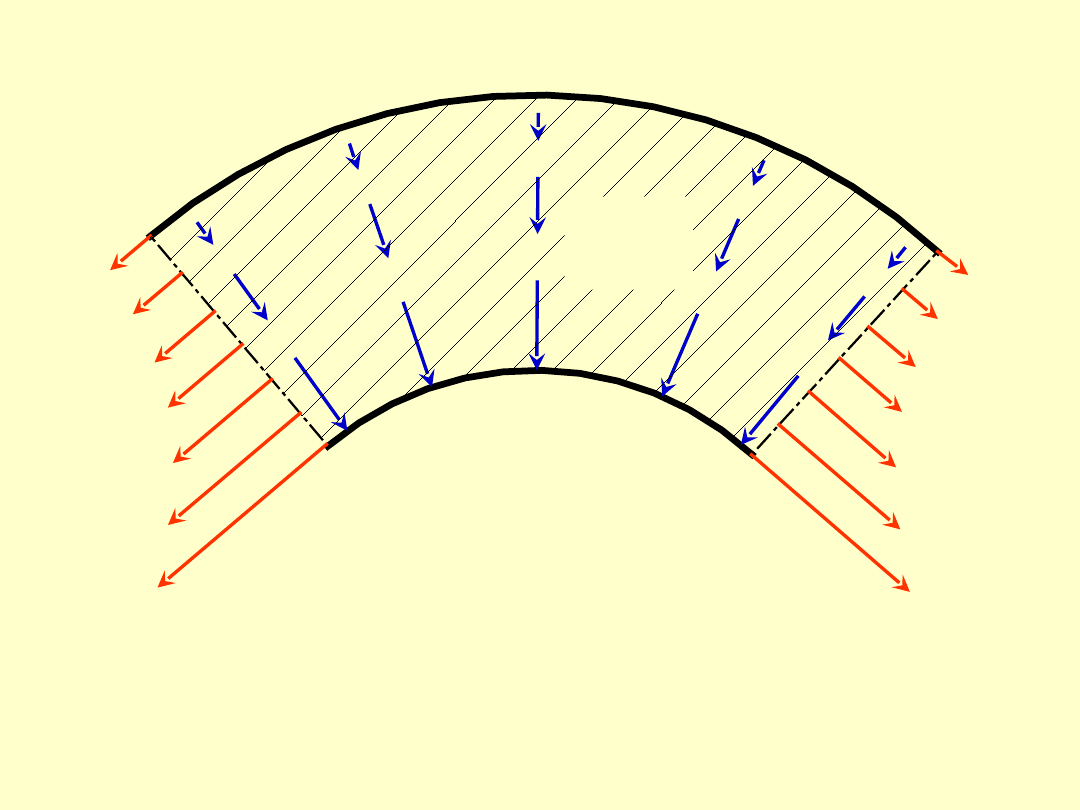
T2



T2



R1

Wycinek oprawy

Zależność miedzy wciskiem

skutecznym a naciskiem na

powierzchni styku

W celu wyznaczenia zależności miedzy
wciskiem skutecznym

w

a naciskiem na

powierzchni styku

p

wykorzystuje się:

 twierdzenie Lame’go (zagadnienie

związane z wytrzymałością
materiałów,

 pojęcie współczynnika wydrążenia.

Twierdzenie Lame’go mówi o tym, że
suma naprężeń obwodowego



T

i

promieniowego



R

w każdym punkcie

przekroju danego pierścienia ma wartość
stałą.



T

1

+



R1

= const



T

2

+



R2

= const

Wiemy jednak, że na powierzchni styku
naprężenia promieniowe



R

zarówno w

czopie jak i oprawie są równe naciskom
powierzchniowym

p

.



R1

=



R2

=

p

Dla uproszczenia oznaczmy naprężenia
obwodowe



T

na powierzchni styku

odpowiednio jako:



T1

=



1



T2

=



2

d

d

d

d

x

z

w

1

1

1

1





2

2

2

2

d

d

d

d

x

z

w





d

w

1

d

z

1

d

w

2

d

z

2

d

1

d

2

d

x

1

– współczynnik wydrążenia czopa,

x

2

– współczynnik wydrążenia oprawy.

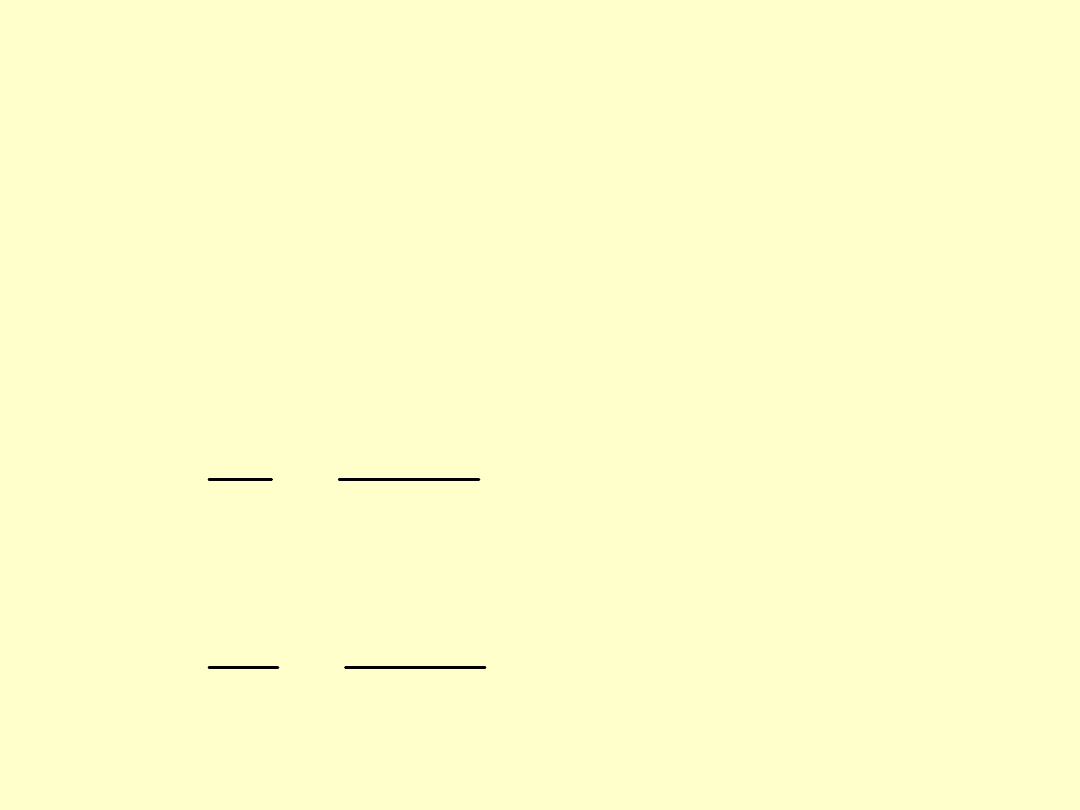
Wykorzystując twierdzenie Lame’go
można wykazać, że na powierzchni styku
czopa i oprawy stosunek naprężeń
obwodowych



T

=



do naprężeń

promieniowych



R

=

p

można wyrazić za

pomocą współczynnika wydrążenia

x

.

oprawy

dla

x

x

p

czopa

dla

x

x

p

1

1

1

1

2

2

2

2

2

2

1

2

1

1

















(1)

(2)

Dla jednoosiowego stanu naprężenia,
odkształcenie względne



części można wyrazić

za pomocą prawa Hooke’a:

E







gdzie:



- naprężenia występujące w odkształcanej

części,

E

– moduł sprężystości wzdłużnej materiału

odkształcanej części (moduł Younga).

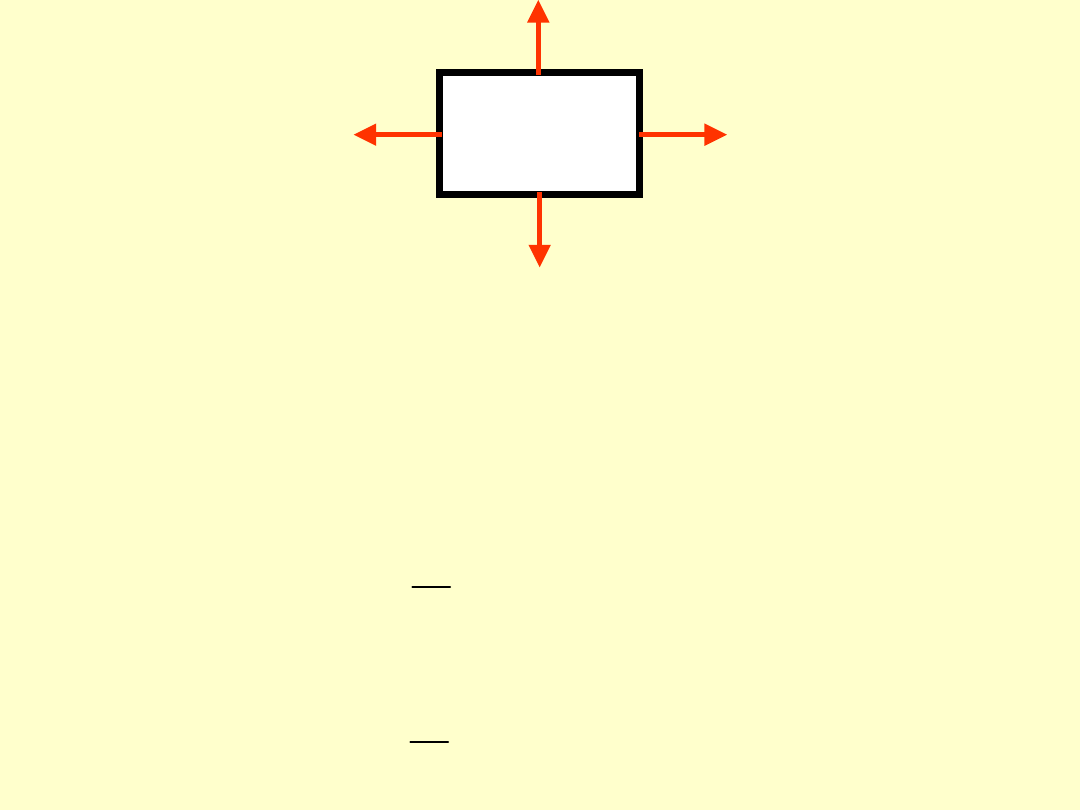
Prawo Hooke’a dla dwuosiowego stanu
naprężenia materiału izotropowego wyraża się
następującymi zależnościami między
składowymi stanu naprężenia



x

,



y

:

P

y

P

x

P

x

P

y





y

x

x

v

E











1





x

y

y

v

E











1

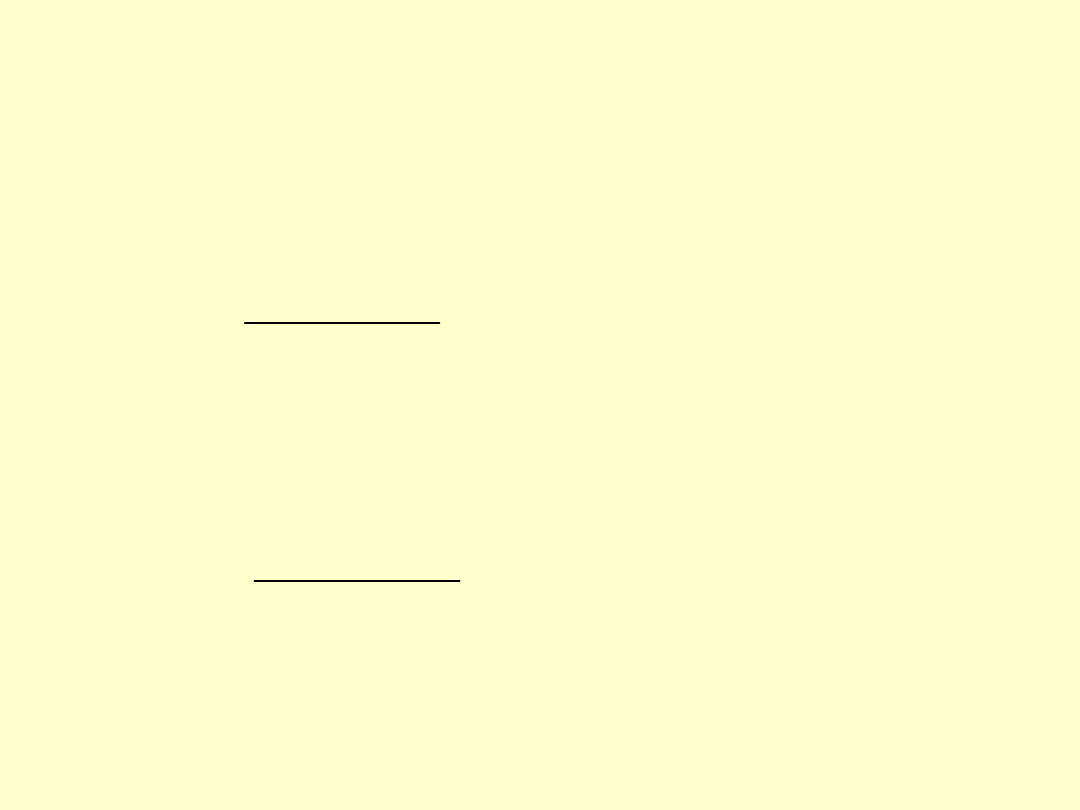
Wyznaczmy odkształcenia względne elementów
łączonych:

 dla czopa:





1

1

1

1

E

p











 dla oprawy:





2

2

2

2

E

p











(3)

(4)

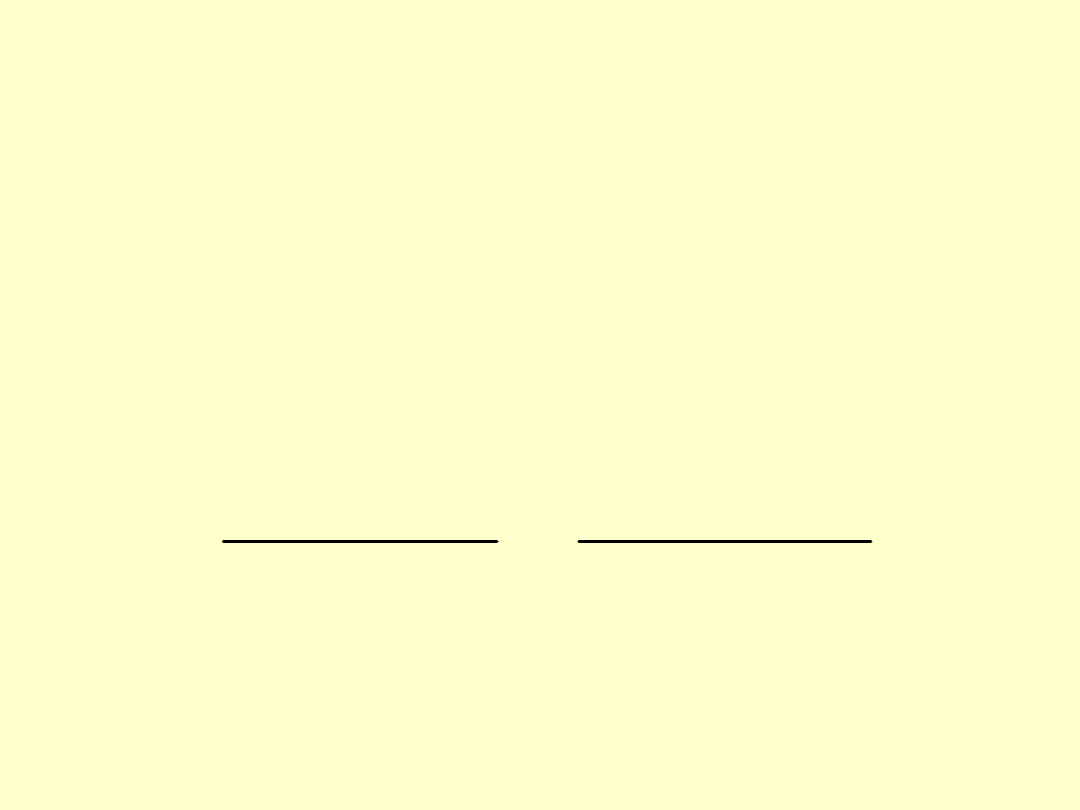
Całkowity wcisk względny



będzie sumą

odkształceń względnych czopa



1

i oprawy



2

:

2

1











Podstawiając zależności na odkształcenia
względne czopa (3) i oprawy (4) uzyskuje się:

2

2

2

1

1

1

E

p

E

p



















(5)

(6)

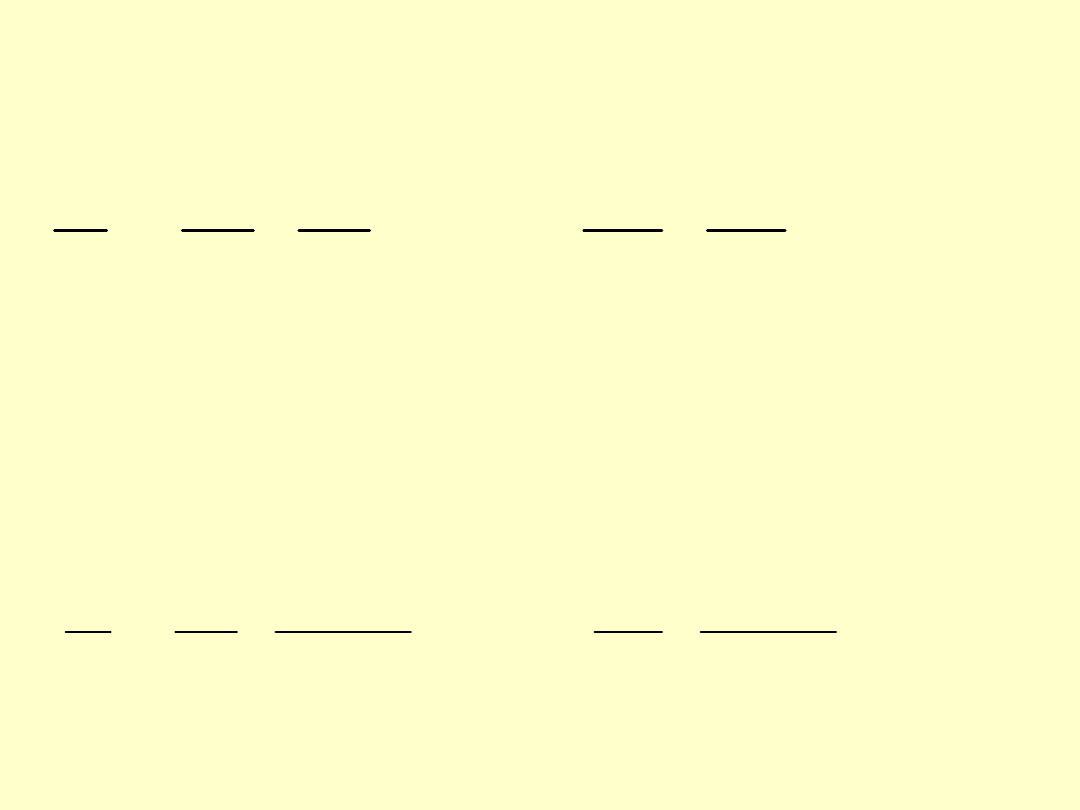
Podzielmy obie strony równania (5) przez

p

:

Jeżeli jednak postawimy zależności (1) i (2) to
otrzymamy:

































2

2

2

1

1

1

1

1

v

p

E

v

p

E

p







(7)

(8)









































2

2

2

2

2

2

1

2

1

2

1

1

1

1

1

1

1

1

v

x

x

E

v

x

x

E

p



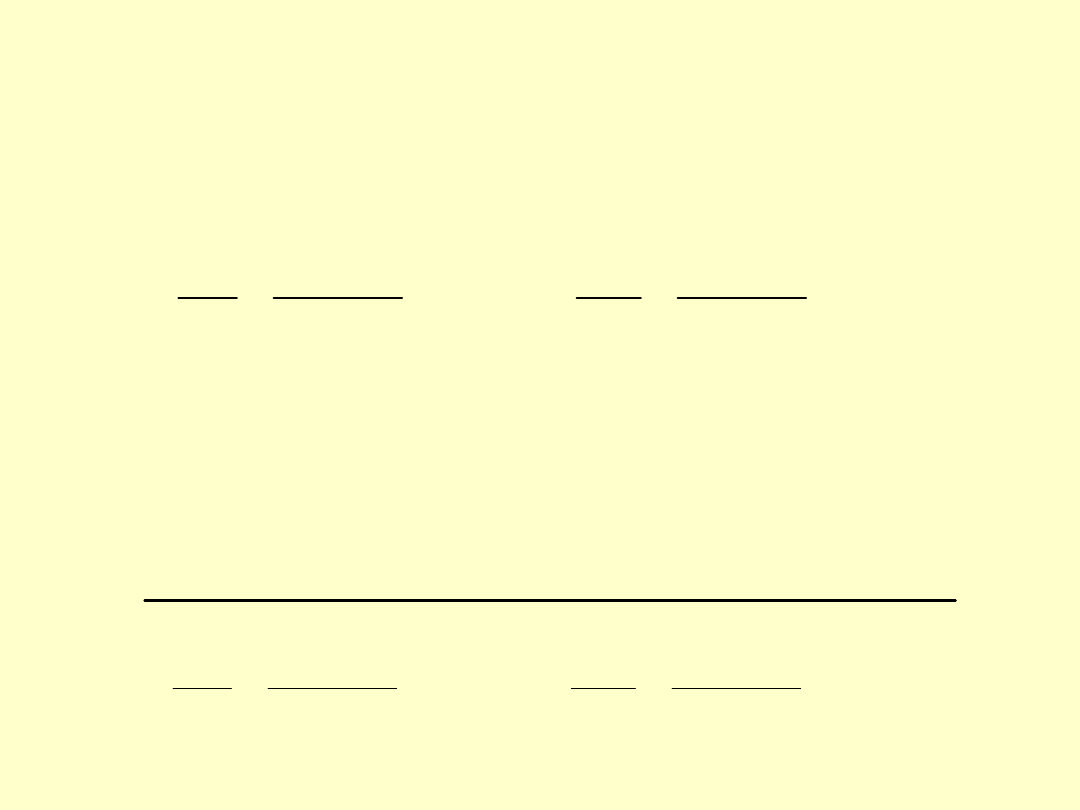
Zależność między wciskiem



a naciskiem na

powierzchni styku

p

wyraża się następującą

zależnością:

lub zależność między naciskiem na powierzchni
styku

p

a wciskiem



:

(9)

(10)





















































2

2

2

2

2

2

1

2

1

2

1

1

1

1

1

1

1

1

v

x

x

E

v

x

x

E

p























































2

2

2

2

2

2

1

2

1

2

1

1

1

1

1

1

1

1

v

x

x

E

v

x

x

E

p



Zależności (8) i (9) pozwalają obliczyć dwa

podstawowe zadania związane z połączeniem
ciernym:

Zadanie I.

 Dana jest pasowanie, np.

120 H7/s6

,

 Z tego pasowanie obliczamy wcisk

bezwzględny

w

,

 Dla tego wcisku obliczamy wcisk względny



=

w

/d (d – średnica nominalna pasowanego

połączenia),

 Wykorzystując zależność (9) obliczamy

nacisk

p

,

 Dla tego nacisku obliczamy dopuszczalną

obciążalność złącza (siła

P

lub moment

skręcający

M

).

Zadanie II.

 Dane jest obciążenie złącza (siła

P

lub

moment skręcający

M

),

 Dla tego obciążenia obliczamy nacisk

p

,

 Wykorzystując zależność (8) obliczamy

wcisk względny



,

 Dla tego wcisku względnego obliczamy

wcisk

bezwzględny

w

,

 Wcisk bezwzględny

w

pozwala nam dobrać

odpowiednie pasowanie zapewniające
poprawną pracę połączenia ciernego.

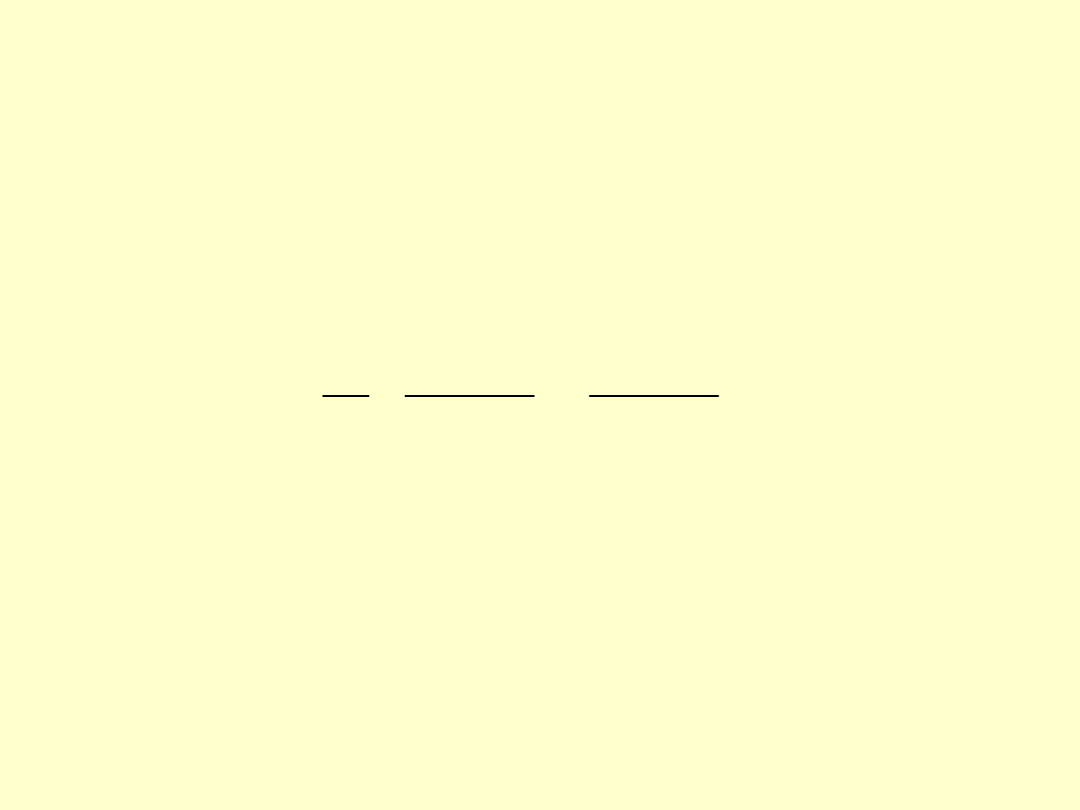
Jeżeli czop i oprawa zostaną wykonane z tego
samego materiału (

E

=

E

1

=

E

2

oraz



=



1

=



2

)

to zależność (8) przyjmie postać:

(11)

























2

2

2

2

2

1

2

1

1

1

1

1

x

x

x

x

E

p



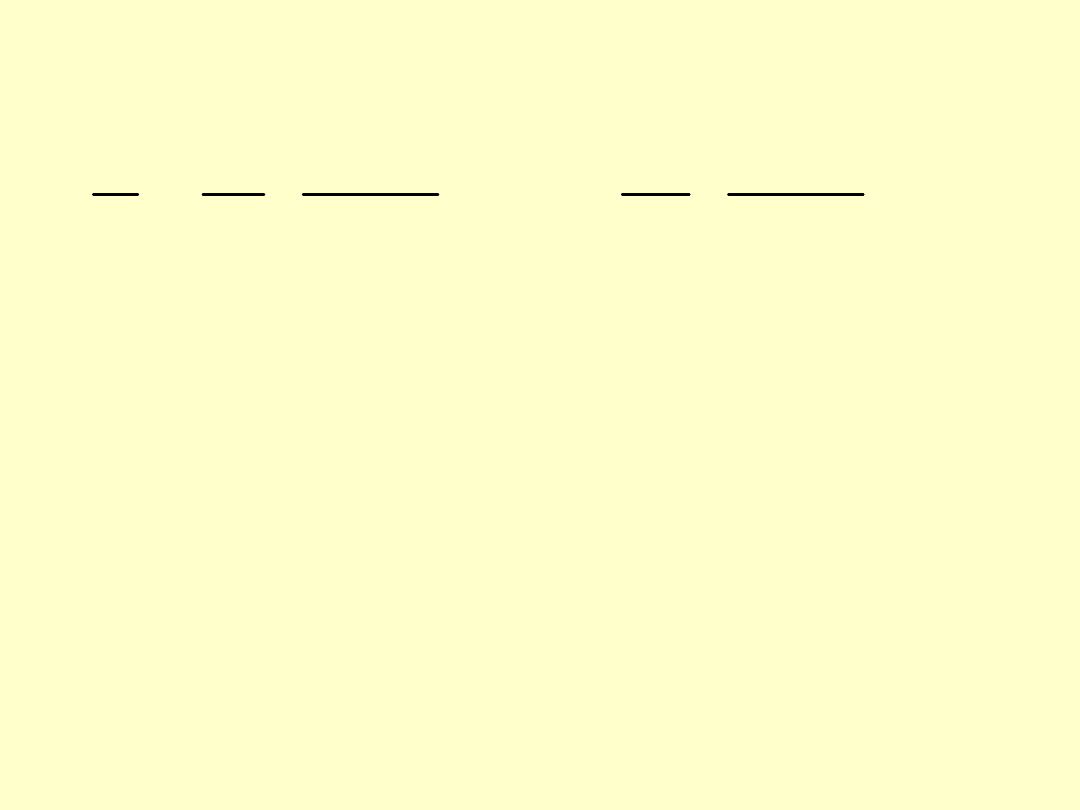
Analiza równania wyrażającego stosunek
miedzy odkształceniem względnym



a

naciskiem

p

pokazuje, że skuteczność

połączenia ciernego zależy od cech
geometrycznych (współczynniki wydrążenia

x

1

i

x

2

) oraz cech materiałowych (

E

1

i

E

2

oraz



1

i



2

).









































2

2

2

2

2

2

1

2

1

2

1

1

1

1

1

1

1

1

v

x

x

E

v

x

x

E

p



Obciążalność elementów złącza

połączenia ciernego

Warunek wytrzymałościowy dla elementów
złącza wykonanych z materiałów ciągliwych
praktycznie nie istnieje. Wynika to z faktu, że
odkształcenia wywołane największym wciskiem
nie mogą wywołać pęknięcia elementu. A
zatem należy sprawdzić warunek stosowalności
wzoru:

p

o



p

e

gdzie:

p

e

–

nacisk odpowiadający początkowi

występowania odkształceń plastycznych w
najbardziej obciążonym obszarze elementu
słabszego,

p

o

– obliczeniowy

nacisk w polu styku.

Wartość

p

e

wyznacza się zgodnie z hipotezą

największej energii odkształcenia
postaciowego:

 dla czopa drążonego:





2

1

1

1

1

58

0

x

,

R

p

e

e





 dla oprawy:





2

2

2

2

1

58

0

x

,

R

p

e

e





gdzie:

2

2

e

e

R

p

- współczynnik obciążalności elementu
wykonanego z materiału ciągliwego.

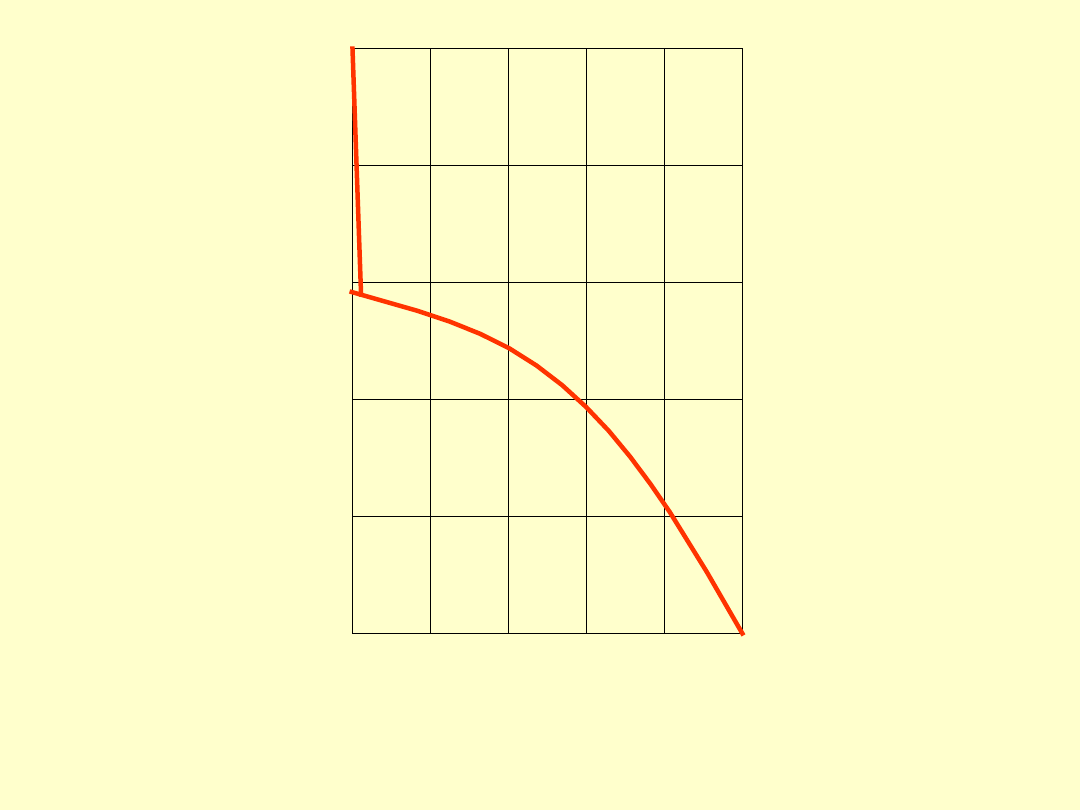
0

0,
2

0,
4

0,
6

0,
8

1,
0

współczynniki wydrążenia czopa

x

1

lub oprawy

x

2

dla materiału

ciągliwego

w

sp

ó

łc

zy

n

n

ik

i

o

b

ci

ą

ża

ln

o

śc

i

cz

o

p

a

p

e

1

/

R

e

1

l

u

b

o

p

ra

w

y

p

e

2

/

R

e

2

0,
2

0,
4

0,
8

0,
6

1,
0

Analiza wykresu pokazuje, że w przypadku
czopa drążonego jego obciążalność jest dużo
mniejsza w porównaniu z czopem pełnym.

Nawet niewielki otwór w czopie powoduje
spadek obciążalności czopa aż o 48%.