Dobór materiałów

konstrukcyjnych

Prezentacja: „Właściwości

mechaniczne materiałów”

Autorzy:

Rafał Antczak

Krzysztof Grzeszak

Zagadnienia prezentacji

• Moduł sprężystości
• Granica plastyczności
• Odkształcenie
• Zmęczenie materiału
• Wytrzymałość na rozciąganie

Moduł sprężystości

• Jest to iloraz wartości naprężenia do

odkształcenia sprężystego,

spowodowanego przez to naprężenie.

• Rozróżniamy:
• moduł Younga - współczynnik sprężystości

wzdłużnej

• moduł Kirchoffa - współczynnik

sprężystości poprzecznej

• moduł sprężystości objętościowej -

współczynnik sprężystości

Moduł Younga

• Wielkość uzależniająca

odkształcenie liniowe ε materiału

od naprężenia σ jakie w nim

występuje w zakresie odkształceń

sprężystych.

• Jednostką modułu Younga jest

paskal. Jest to wielkość określająca

sprężystość materiału.

• Moduł Younga jest hipotetycznym

naprężeniem, które wystąpiłoby

przy dwukrotnym wydłużeniu

próbki materiału, przy założeniu,

że jej przekrój nie ulegnie zmianie

(założenie to spełnione jest dla

hipotetycznego materiału o

współczynniku Poissona υ=0).







E

Moduł Kirchoffa

• Jest to współczynnik

uzależniający odkształcenie
postaciowe materiału od
naprężenia, jakie w nim
występuje. Jednostką modułu
Kirchhoffa jest paskal. Jest to
wielkość określająca
sprężystość materiału.

• We wzorze: τ - naprężenia

ścinające, γ - odkształcenie
postaciowe

• Moduł Kirchhoffa dla

materiałów izotropowych
bezpośrednio zależy od
modułu Younga i
współczynnika Poissona.







G

Współczynnik sprężystości

• Jest to odwrotność

współczynnika ściśliwości

• We wzorze: K -

współczynnik sprężystości
[Pa], k - współczynnik
ściśliwości [1/Pa]

k

K

1



Wartości modułu Younga dla

przykładowych materiałów

[GN/m^2]

• Cyna: 39-54
• Cynk: 34-130
• Glin (aluminium): 62-

73

• Miedź: 79-130
• Srebro: 69-79
• Szkło: 49-79

• Wolfram: 354
• Polimery: 0,01-7
• Tytan: 100
• Ceramika: 300-600
• Diament: 1000
• Stal: 215 (w zależności

od gatunku)

Granica plastyczności

• Granica plastyczności to

naprężenie, po którego
osiągnięciu następuje
pierwszy spadek siły
rozciągającej próbkę.

• Górna granica sprężystości

określona jest wzorem, w
którym: Re - naprężenie w
granicy plastyczności,
F - siła obciążająca próbkę
w granicy plastyczności,
S - pole przekroju próbki
pod działaniem siły F.

S

F



Re

Przykładowe wartości granicy

plastyczności dla kilku

materiałów

[MN/m^2]

• Granica plastyczności jest trudna

do ustalenia, gdyż nie istnieje

dokładnie określona wartość, lecz

jedynie przedział wartości,

ponieważ dla wielu materiałów

brak wyraźnego przejścia ze stanu

sprężystego w stan plastyczny.

• Polimery: 1-100

• Stale, stopy niklu: 200-2000

• Stopy miedzi: 60-950

Odkształcenie

• Jest to miara deformacji ciała poddanego

siłom zewnętrznym.

• Aby mówić o odkształceniu, należy wyróżnić

dwa stany ciała: początkowy i końcowy. Na
podstawie różnic w położeniach punktów w
tych dwóch stanach można wyznaczać
liczbowe wartości odkształcenia.

• Zależność pomiędzy stanem odkształcenia, a

naprężenia określa m.in. Prawo Hooke'a.

Odkształcenie dzielimy na:

• Sprężyste - takie odkształcenie, które ustępuje po usunięciu

siły, która je spowodowała. Odkształcenia sprężyste

występują w każdej konstrukcji budowlanej, maszynie,

urządzeniu. Najczęściej spotykanymi odkształceniami są:

rozciąganie, ściskanie, skręcanie. Reakcją na rozciąganie jest

przyciąganie się cząsteczek, zaś na ściskanie odpychanie się.

Odkształcenia sprężyste nie występuje w ciałach idealnie

plastycznych (ich przybliżeniem jest np. glina).

• Plastyczne – odkształcenie, które nie ustępuje po usunięciu

naprężenia, które je wywołało.

• Liniowe - to zmiana kształtu wzdłuż jednego z wymiarów

detalu. Odkształcenia liniowe mogą nastąpić pod wpływem

siły zewnętrznej (siła skupiona), wewnętrznej (siła

sprężystości), zmiany temperatury itp. Odkształcenia liniowe

podłużne dzieli się na ściskanie i rozciąganie.

• Postaciowe - to zmiana kształtu (odkształcenie) ośrodka

ciągłego przy zachowaniu długości odcinków równoległych do

osi układu współrzędnych. Przykładem odkształcenia

postaciowego może być ścinanie lub skręcanie.

• Objętościowe

Odkształcenie liniowe

• Przy rozpatrywaniu

uproszczonego przypadku

rozciągania, bądź ściskania, czyli

odkształcenia liniowego pręta

tylko wzdłuż jego długości, biorąc

pod uwagę dwa dowolnie

wybrane punkty wewnątrz

nieobciążonego ciała, można

określić odległość pomiędzy nimi.

W chwili obciążenia tego ciała

siłami zewnętrznymi następuje

jego deformacja, a w wyniku tego

zmienia się odległość pomiędzy

rozpatrywanymi punktami.

Odkształcenie liniowe ε w

dowolnym punkcie ciała jest

granicą ilorazu różnicy odległości

do odległości wyjściowej, gdy

odległość wyjściowa zmierza do

zera.

L

L

L







lim

0



Odkształcenie postaciowe

• Podobnie rozważa się zmiany miar

kątowych w bezpośrednim otoczeniu
punktu. Odkształcenie kątowe γ jest
granicą ilorazu różnicy kąta
pomiędzy dwoma dowolnie
wybranymi odcinkami w ciele
nieobciążonym i obciążonym, gdy
długości tych odcinków zmierzają do
zera.

Odkształcenie objętościowe

• Chociaż odkształcenia liniowe ε i

kątowe γ w pełni definiują stan
odkształcenia, możliwe jest
wyznaczenie innych
charakterystycznych wartości
odkształceń. Jednym z nich jest
odkształcenie objętościowe, które
jest miarą zmiany objętości ciała.

Zmęczenie materiału

• Jest to zjawisko pękania materiału pod wpływem

cyklicznie zmieniających się naprężeń.

• Obciążenia zmęczeniowe – są obciążeniami zmiennymi

w czasie, typowymi obciążeniami dla różnorodnych

części i podzespołów maszyn. Odpowiadające im

naprężenia nazywane są naprężeniami zmiennymi lub

naprężeniami zmęczeniowymi. Przebieg obciążeń

zmiennych w czasie jest określany jako widmo

obciążenia. Może przebiegać nieregularnie,

przypadkowo lub w sposób ustalony, gdy segmenty

obciążenia powtarzają się, co jest charakterystyczne

dla obciążenia okresowo zmiennego, które nazywane

jest obciążeniem cyklicznym. W ciągu jednego okresu

zachodzi pełen cykl zmian obciążenia, a analogicznie

do tego pełen cykl zmian naprężenia.

Zmęczenie materiału

• Szczególnym przypadkiem obciążenia okresowo zmiennego jest

obciążenie sinusoidalnie zmienne. Obciążenie te zostało przyjęte za

podstawę wyznaczania właściwości zmęczeniowych materiałów i

elementów konstrukcji. Cykl naprężeń sinusoidalnie zmiennych jest

opisany przez parametry: naprężenie maksymalne cyklu σmax,

naprężenie minimalne cyklu σmin, okres zmian T lub jego odwrotność:

częstotliwość zmian f.

• Wytrzymałość zmęczeniowa lub granica zmęczenia, lub wytrzymałość

trwała na zmęczenie to najwyższy poziom cyklicznego naprężenia

który nie powoduje zniszczenia próbek poddanych badaniu do

umownej, granicznej liczby cykli. Innymi słowy wytrzymałość

zmęczeniowa to graniczna amplituda naprężeń, poniżej której

materiał nie ulega zniszczeniu (przy danej liczbie cykli - liczba cykli to

wynik pojedynczego badania zmęczeniowego)

• Ocenia się, że spośród zniszczonych podczas eksploatacji ruchomych

części maszyn, 90 % stanowią zniszczenia zmęczeniowe.

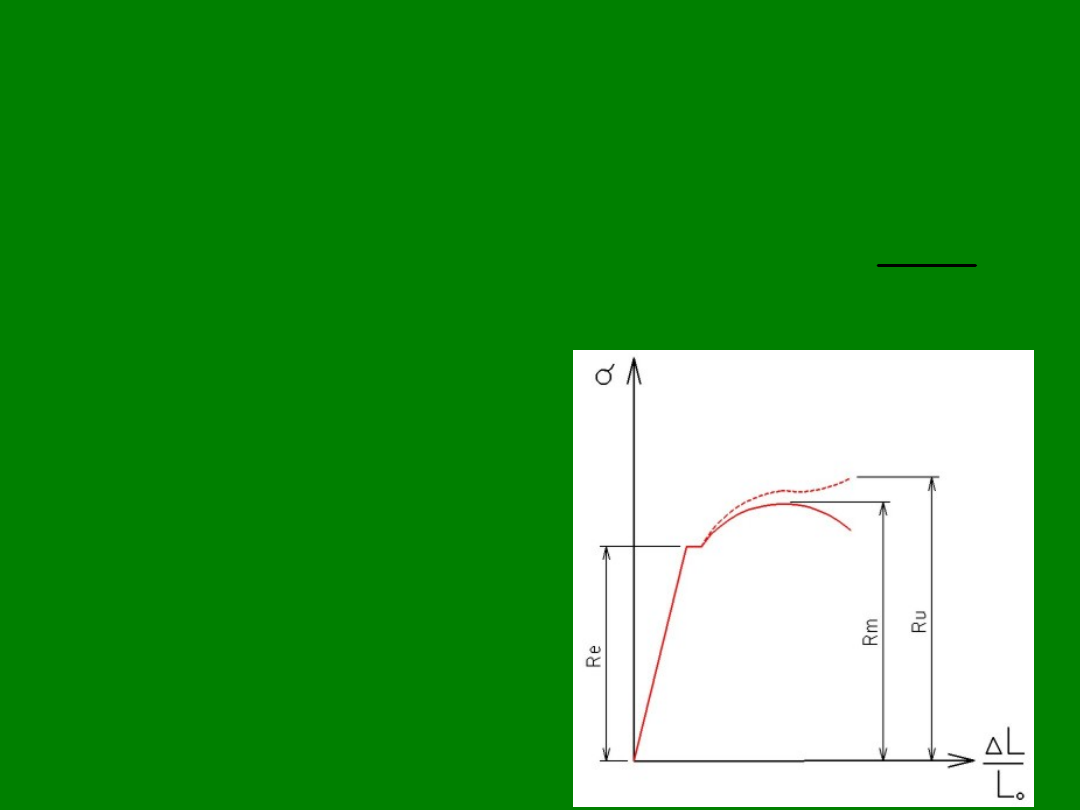
Wytrzymałość na

rozciąganie

• Oznaczana w polskich

normach jako Rm.

• Jest to naprężenie

odpowiadające

największej sile

niszczącej Fm

uzyskanej w czasie

prowadzenia próby

rozciągania,

odniesionej do

pierwotnego przekroju

poprzecznego tej

próbki S.

S

F

R

m

m



Wytrzymałość na

rozciąganie

• Wytrzymałość na rozciąganie

ustala się podczas statycznej

próby rozciągania.

• Jest to podstawowa metoda

badań wytrzymałościowych

dla metalowych materiałów

konstrukcyjnych.

• W statycznej próbie

rozciągania rozciąga się

odpowiednio wykonany pręt o

przekroju okrągłym

wykorzystując urządzenie

zwane zrywarką. W czasie

próby rejestruje się zależność

przyrostu długości próbki od

wielkości siły rozciągającej

oraz rejestruje się granicę

sprężystości, przewężenie

próbki i siłę zrywającą próbkę.

Wartości Rm dla wybranych

materiałów

[MN/m^2]

• Diament: 50000
• Ceramiki: 4000-10000
• Stale, stopy niklu: 400-2000
• Stopy miedzi: 250-1000
• Polimery: 1-120

Dziękujemy za uwagę