Podstawy mechaniki

górotworu

Stan naprężenia w górotworze

nienaruszony i naruszonym

eksploatacją górniczą

Wykład III

Dr inż. Wojciech
PREIDL

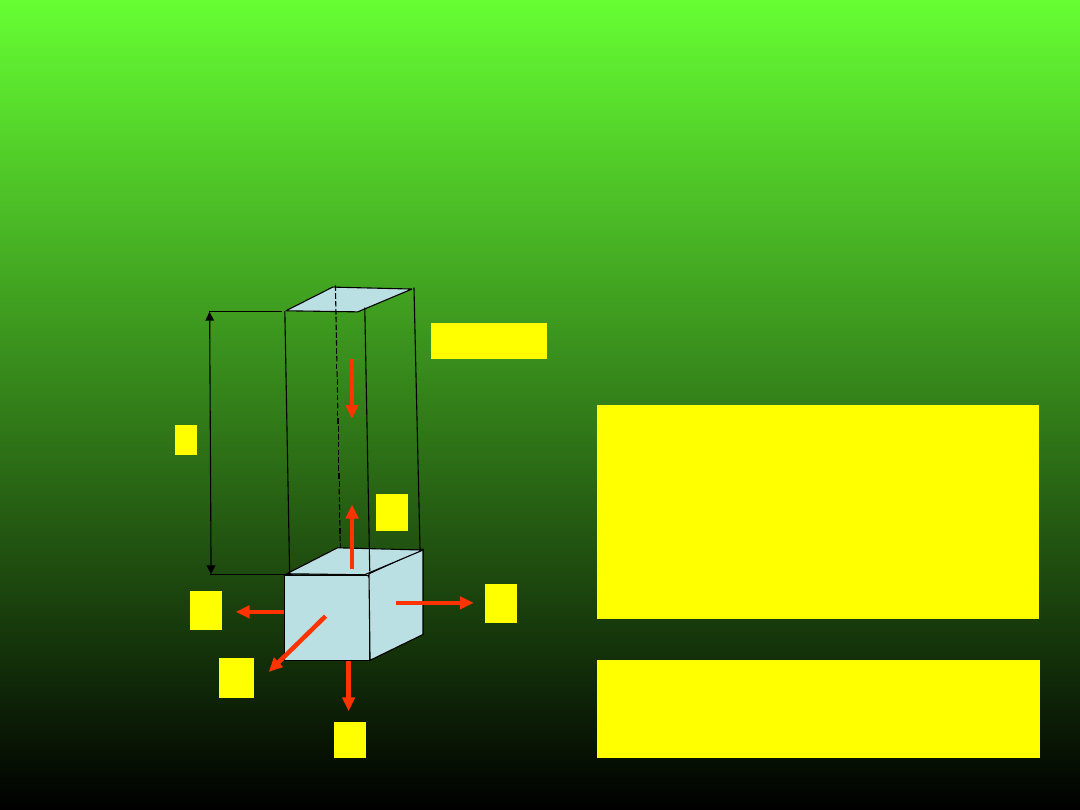
Stan naprężęnia w górotworze nie jest jednoosiowy pionowy.
Cząstki pod wpływem ciężaru dążą do zwiększenia swych
wymiarów poprzecznych. Efektem tego procesu jest ciśnienie
boczne.

I. Górotwór nienaruszony eksploatacją
górniczą

h

z











z



x



y



x



z



h

Ciężar słupa skalnego o

podstawie jednostkowej













y

z

x

x

x

z

y

y

y

x

z

z

E

E

E





























































0

.

2

,

.

1















z

y

x

z

x

x

h















h

h

x

y

z

x

y

z



















































1

1

Po podstawieniu:

m

p

p

p

z

z

y

x

x

y

1



















h

m

p

p

h

p

y

x

z























1

1

Dla małych głębokości naprężenia w
górotworze zbliżone są do stanu
jednoosiowego

z

x

p

p

%

20

10



Natomiast na dużych głębokościach stan
naprężenia zbliża się do stanu
hydrostatycznego

z

y

x

p

p

p





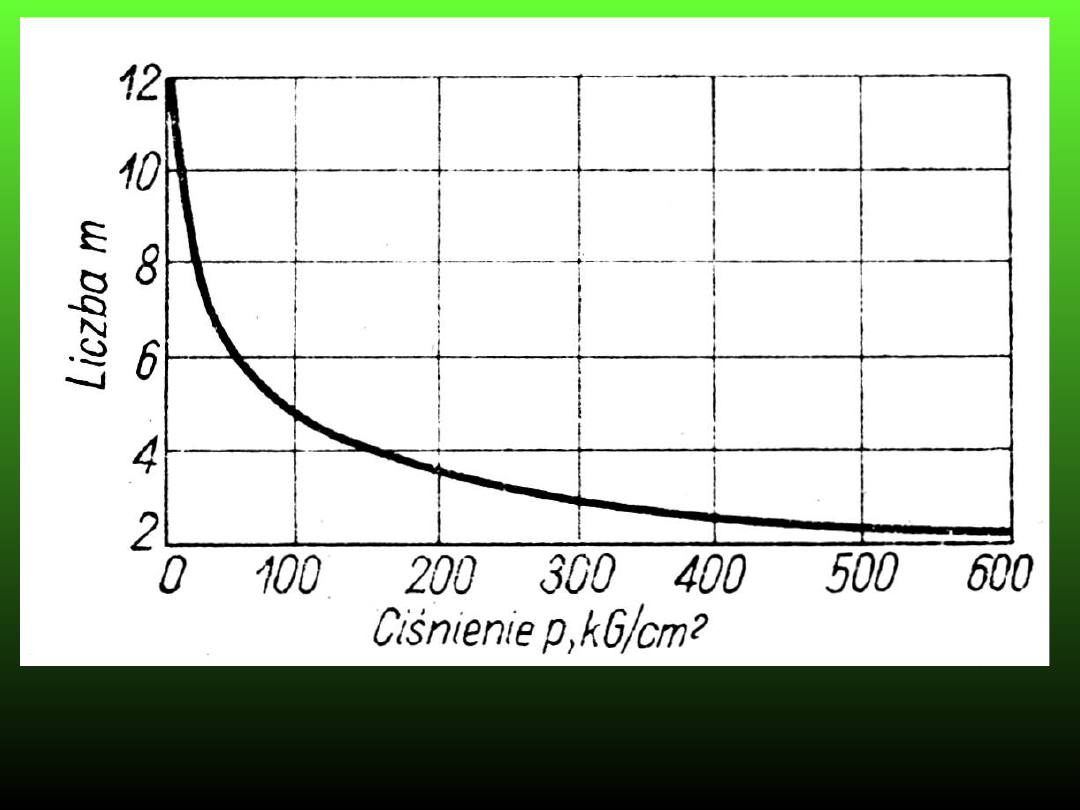
Liczba Poissona nie jest wartością stałą. Zmienia się wraz ze wzrostem
obciążenia, dążąc do wartości m=2, co odpowiada założeniu nieściśliwości
materiału.

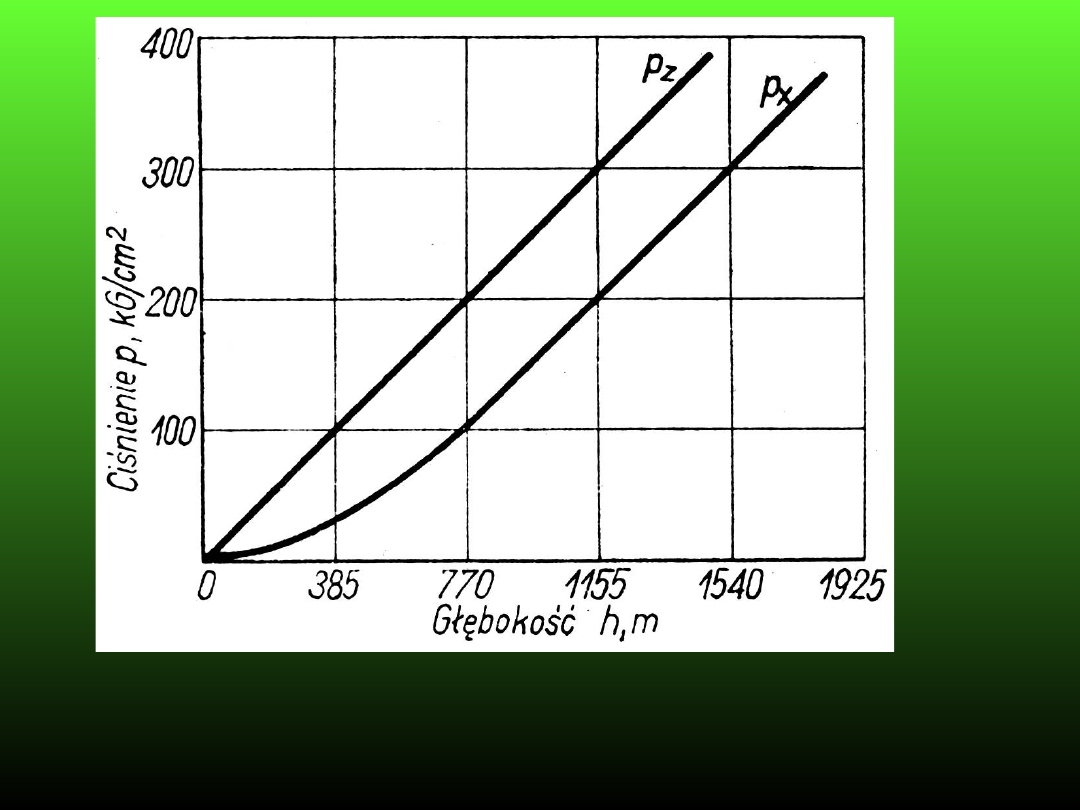
Skały na dużych głębokościach znajdują się w stanie ukrytej
plastyczności. Jak wynika z hipotezy niezmienników różnica pomiędzy
ciśnieniem pionowym p

z

a ciśnieniem poziomym p

x

=p

y

ma wartość

stałą.

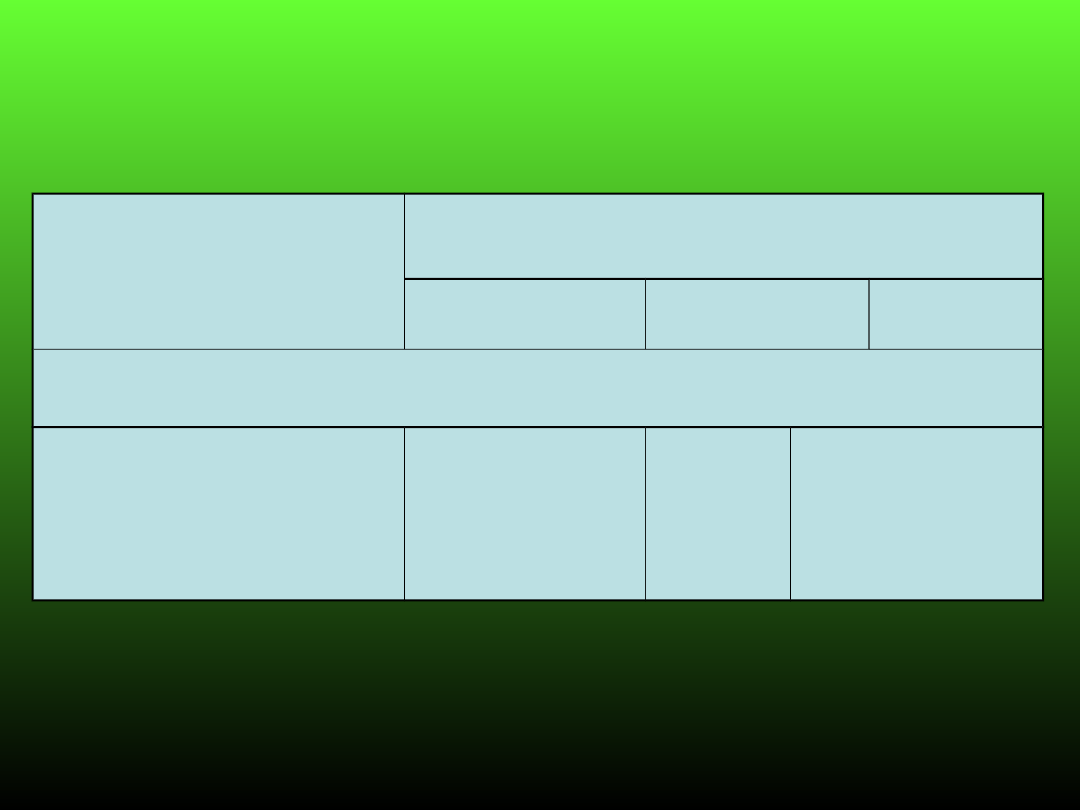
Rodzaj skały

Głębokość m

122

620

1200

wartość liczby m

Piaskowiec
Łupek

Węgiel

20

12

3

9

7

2,5

4

3,5

2

Wartości liczby Poissona dla skał formacji

węglowej

wg Assosation des Ingenieurs sortes de Liege

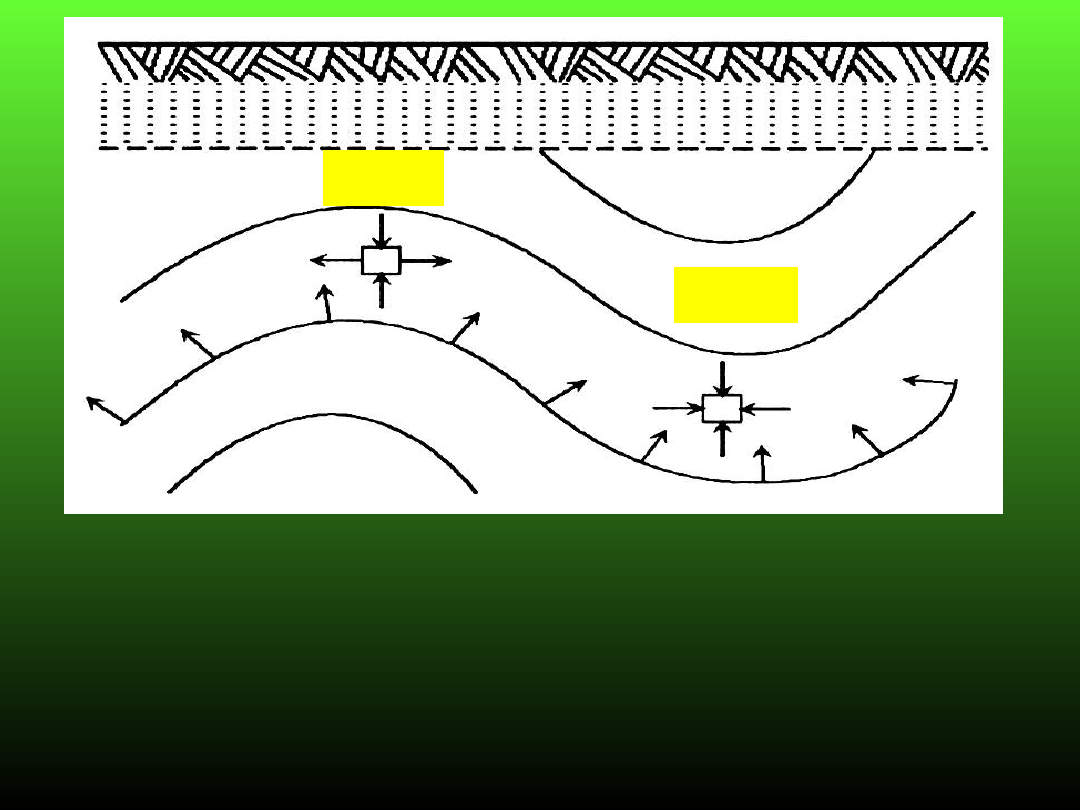
W siodłach tektonicznych siły boczne są rozciągające natomiast
w nieckach są ściskające. W nieckach siły tektoniczne sumują
się
z siłami poziomymi w efekcie wartość ciśnień poziomych może
przewyższyć wartość ciśnień pionowych

z

x

p

p 

z

x

p

p 

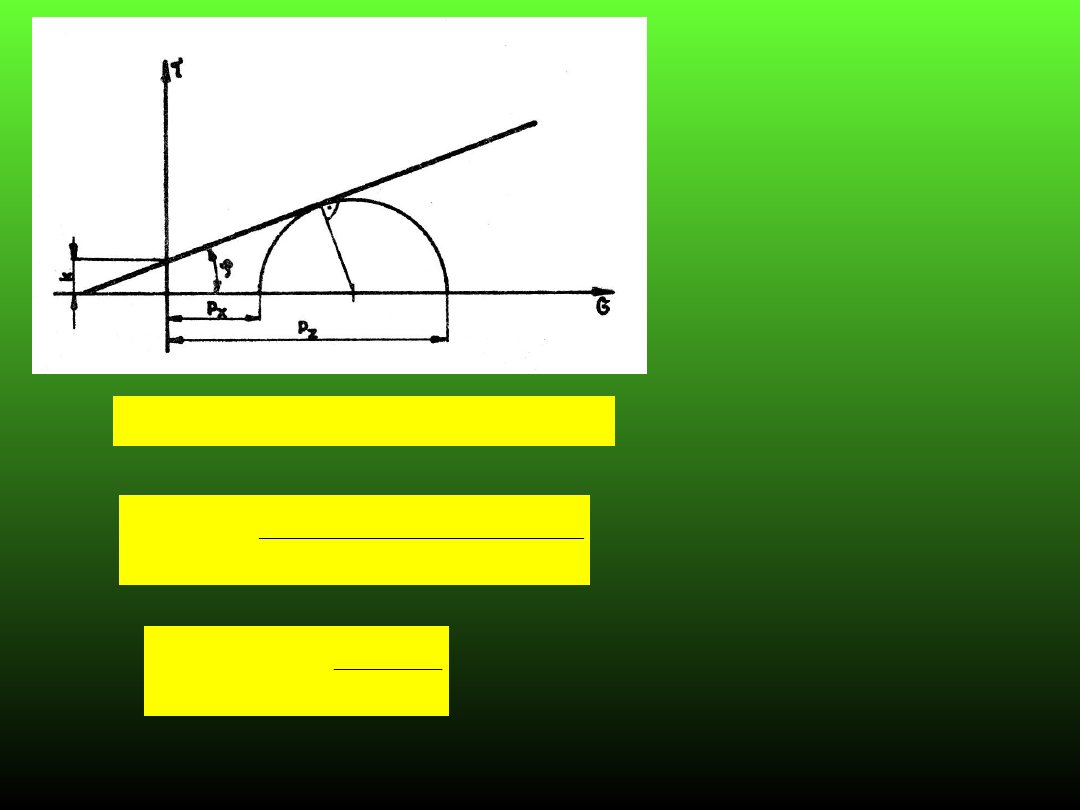
Warunek równowagi
granicznej dla górotworu
o budowie ziarnisto-
spoistej









cos

2

sin















k

p

p

p

p

x

z

x

z











sin

1

cos

2

sin

1















k

p

p

p

z

y

x

Ponieważ dla górotworu
o budowieziarnisto-sypkiej
k=0





sin

1

sin

1











z

y

x

p

p

p

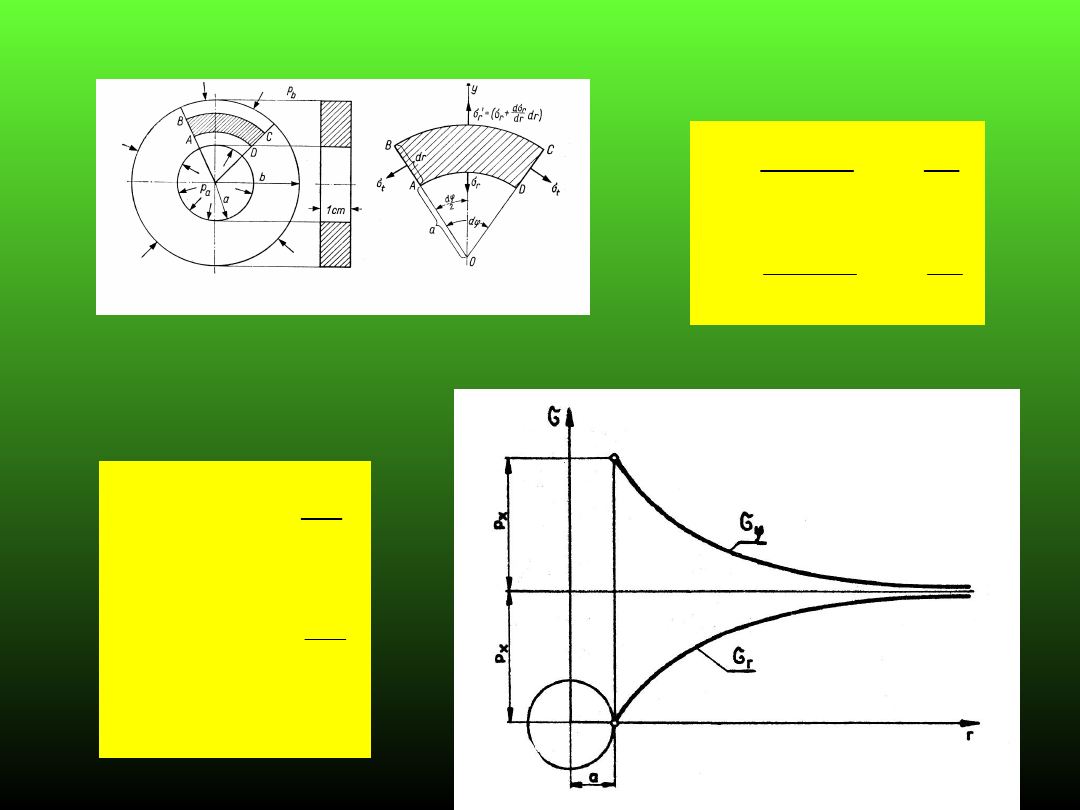
Stan naprężenia w sąsiedztwie wyrobisk
korytarzowych

Zagadnienie
Lame’go

Wyrobisko pionowe































































r

z

x

x

r

r

a

p

r

a

p

2

2

2

2

1

1













































2

2

2

2

2

2

2

2

2

2

1

1

r

a

a

b

b

p

r

a

a

b

b

p

b

b

r







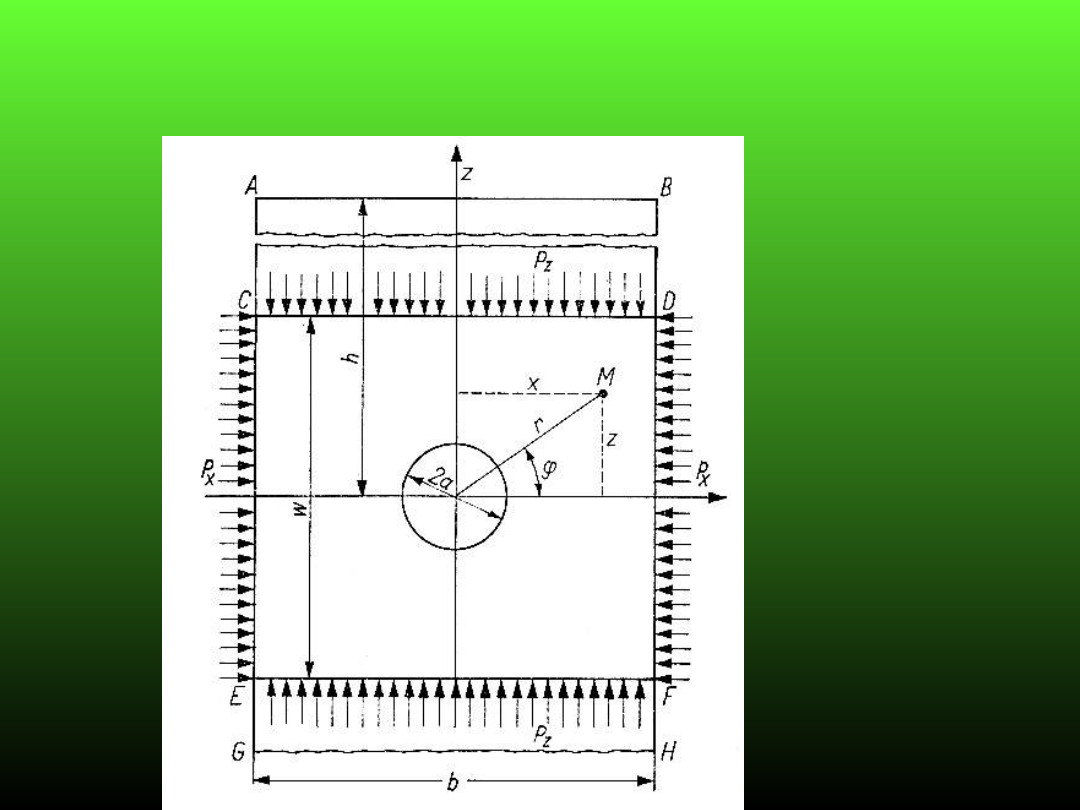
Stan naprężenia w sąsiedztwie wyrobisk

korytarzowych

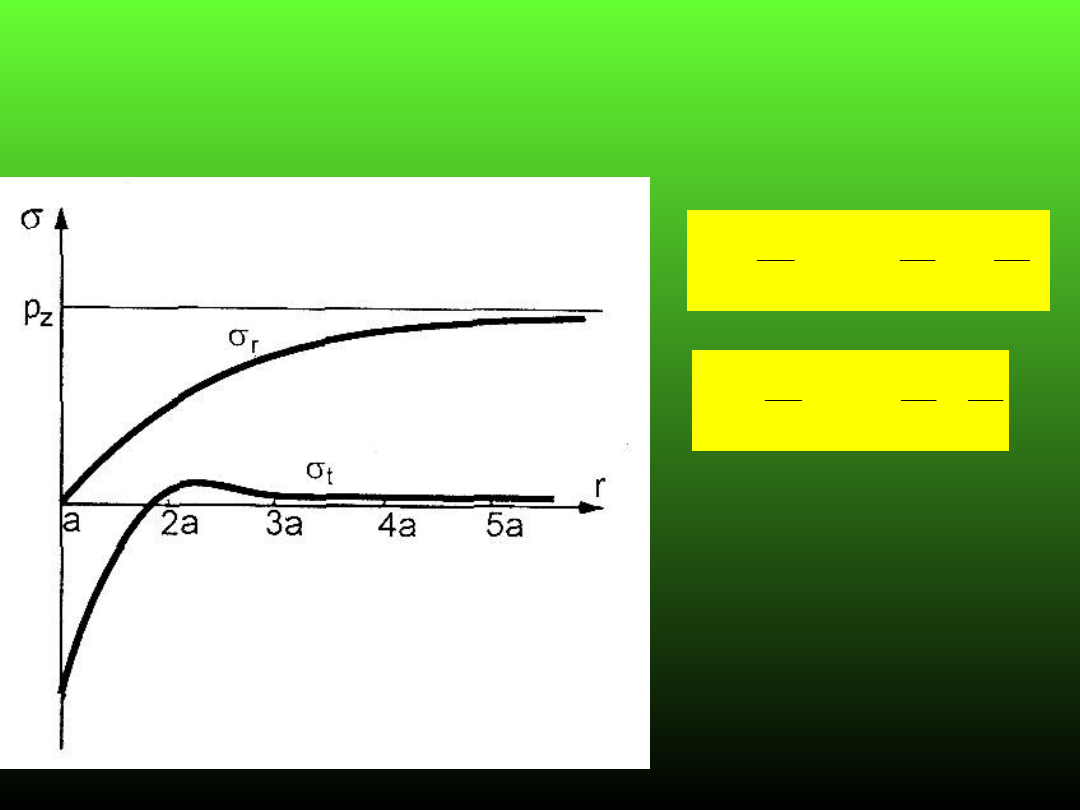
Wyrobisko poziome o przekroju kołowym

P

z

> p

x

=

p

y

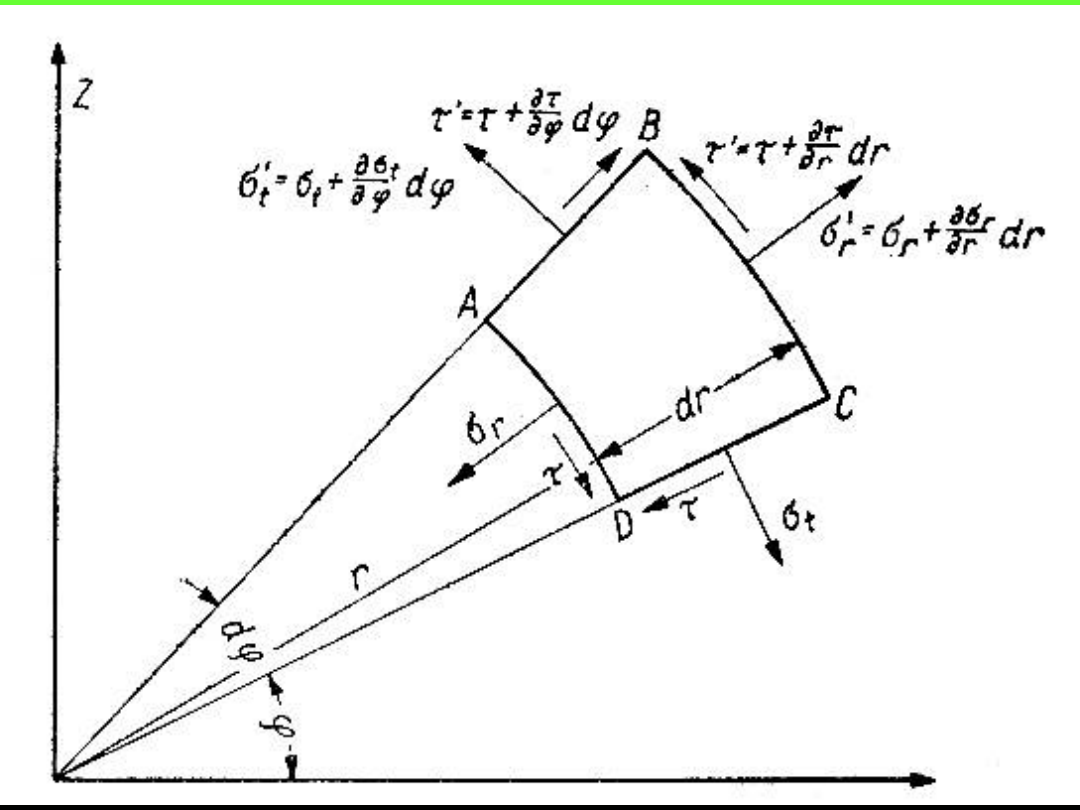
Równania stanu naprężenia dla przypadku
p

z

> p

x

























































































2

cos

3

4

1

1

2

2

cos

3

4

1

1

2

4

4

2

2

2

2

4

4

2

2

2

2

r

a

r

a

r

a

p

r

a

r

a

r

a

p

x

z

r



















































































2

cos

3

1

1

2

2

cos

3

1

1

2

4

4

2

2

4

4

2

2

r

a

r

a

p

r

a

r

a

p

x

z







2

sin

3

2

1

2

4

4

2

2





























r

a

r

a

p

p

x

z

r

a

r 

0



r



















2

cos

2

1

2

cos

2

1













x

z

p

p

0







r





r















2

cos

1

2

2

cos

1

2













x

z

r

p

p

















2

cos

1

2

2

cos

1

2













x

z

p

p







2

sin

2







x

z

r

p

p

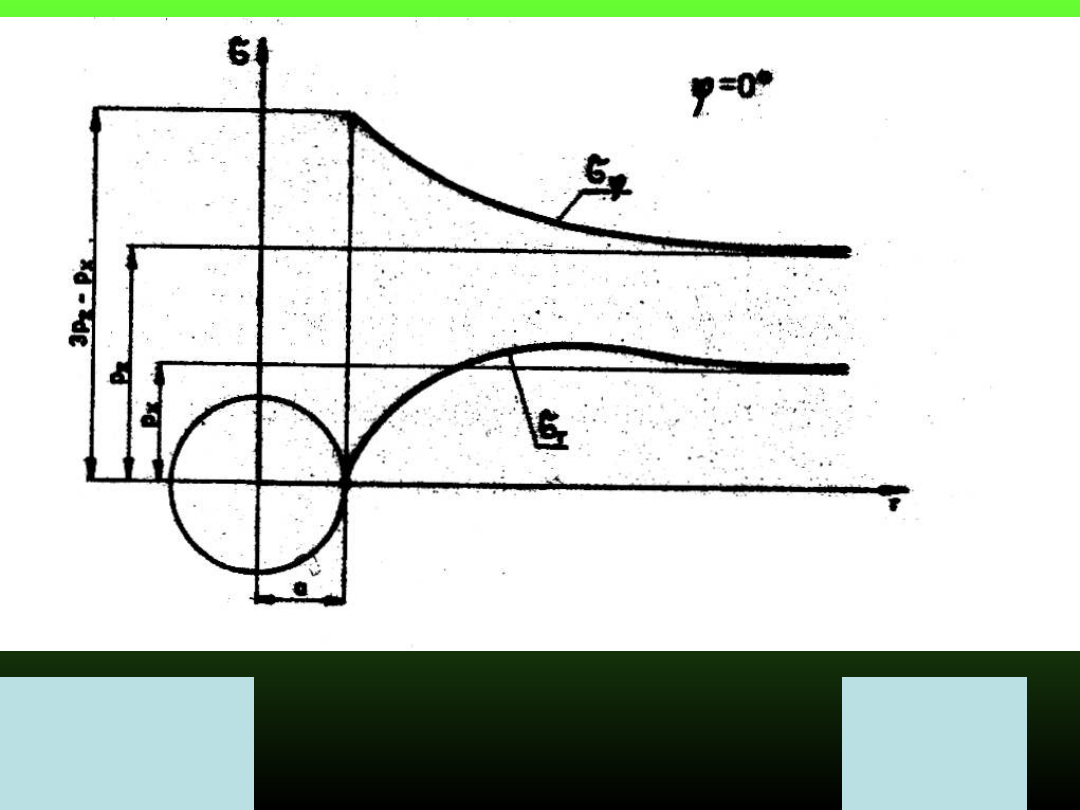
0

3







r

x

z

p

p







x

r

z

p

p











Naprężenia w ociosach
wyrobiska

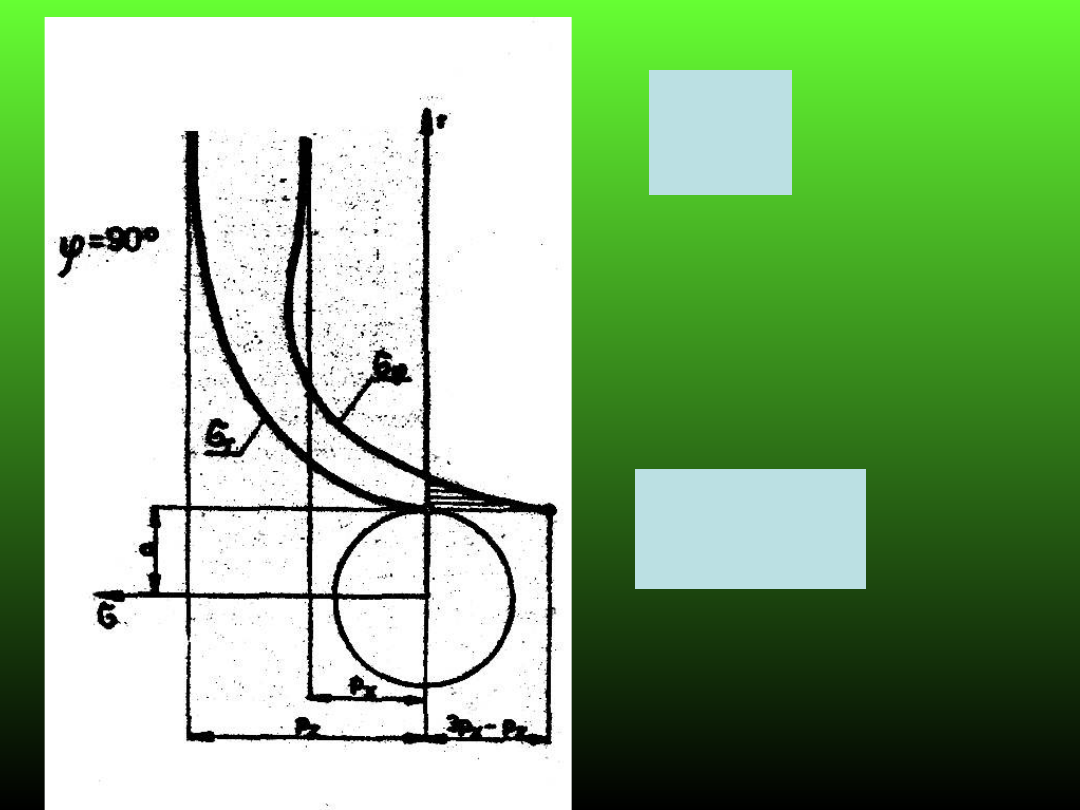
0

3







r

z

x

p

p







z

r

x

p

p











Naprężenia

w stropie

wyrobiska

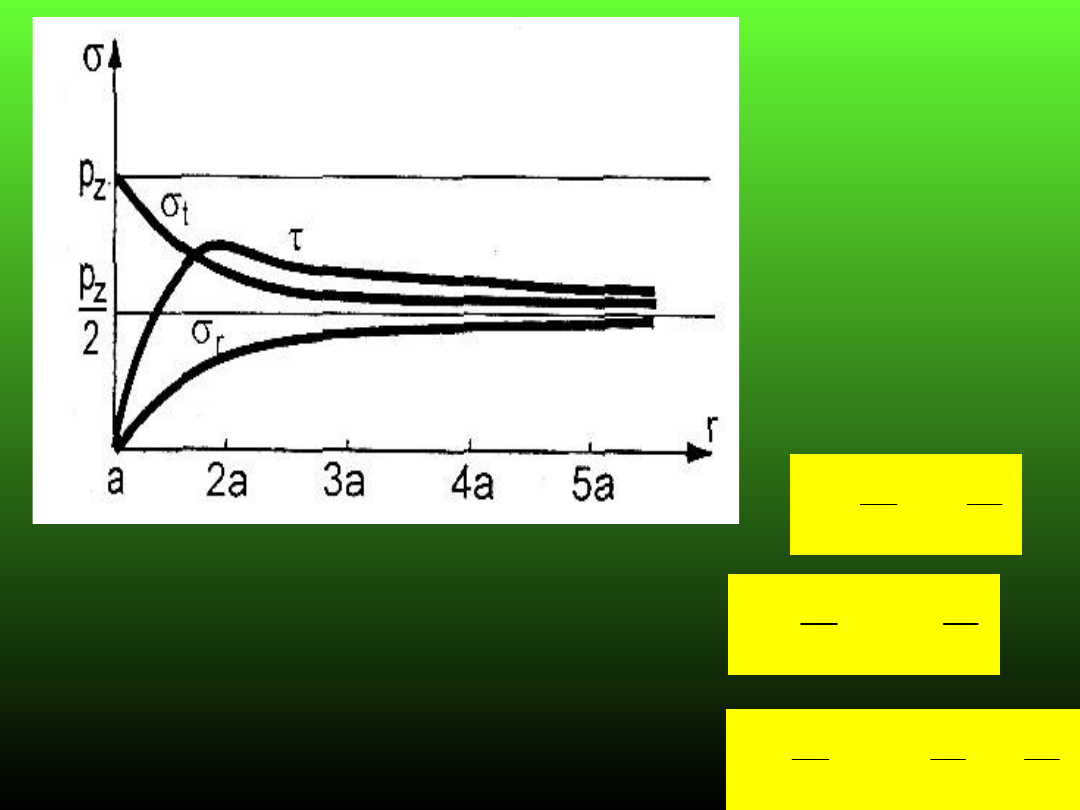
Równania stanu naprężenia dla przypadku
p

x

= 0















































2

cos

3

4

1

1

2

4

4

2

2

2

2

r

a

r

a

r

a

p

z

r













































2

cos

3

1

1

2

4

4

2

2

r

a

r

a

p

z







2

sin

3

2

1

2

4

4

2

2





























r

a

r

a

p

p

x

z

r

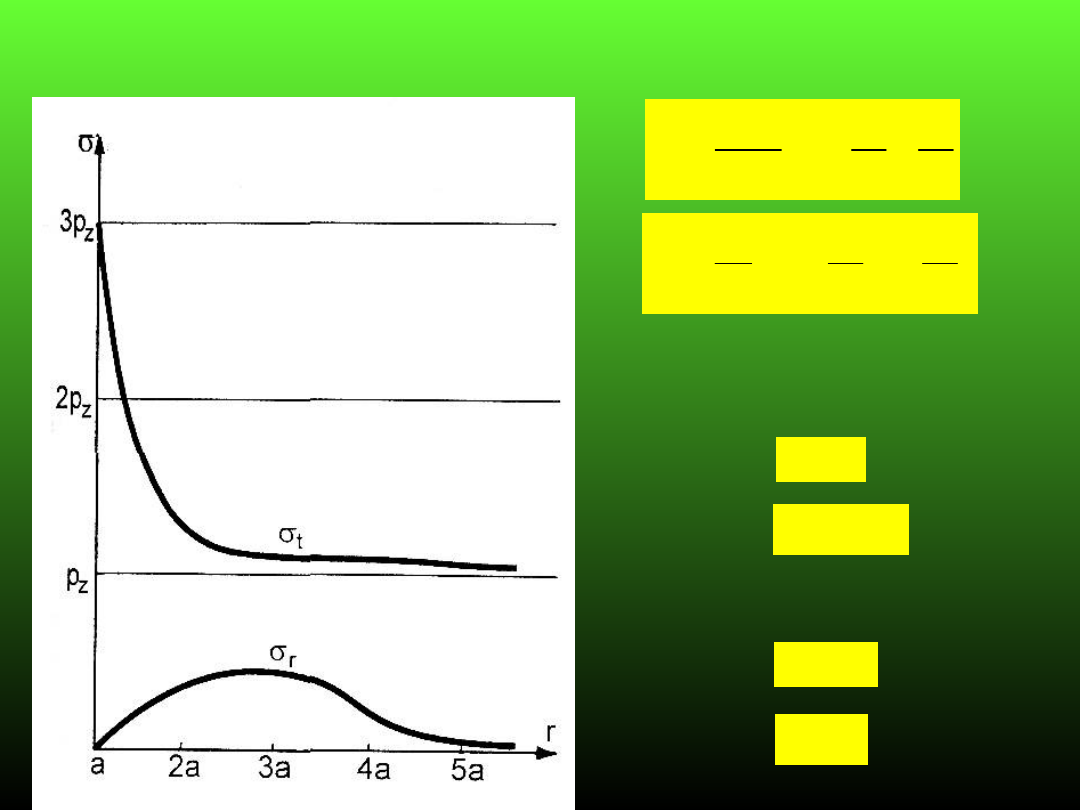
f = 0

0

i f = 180

0

strop i spąg wyrobiska

r = a

r = 

2

2

2

2

1

2

3

r

a

r

a

p

z

r















































4

4

2

2

3

2

2

r

a

r

a

p

z





0



r



z

p



3





z

r

p





0







f = 90

0

i f = 270

0

ociosy wyrobiska

























4

4

2

2

3

5

2

2

r

a

r

a

p

z

r



2

2

4

4

3

1

2

r

a

r

a

p

z



























f = 45

0

i f = 135

0

„naroża” wyrobiska



















2

2

1

2

r

a

p

z

r























2

2

3

2

2

r

a

p

z





























4

4

2

2

3

2

1

2

r

a

r

a

p

z





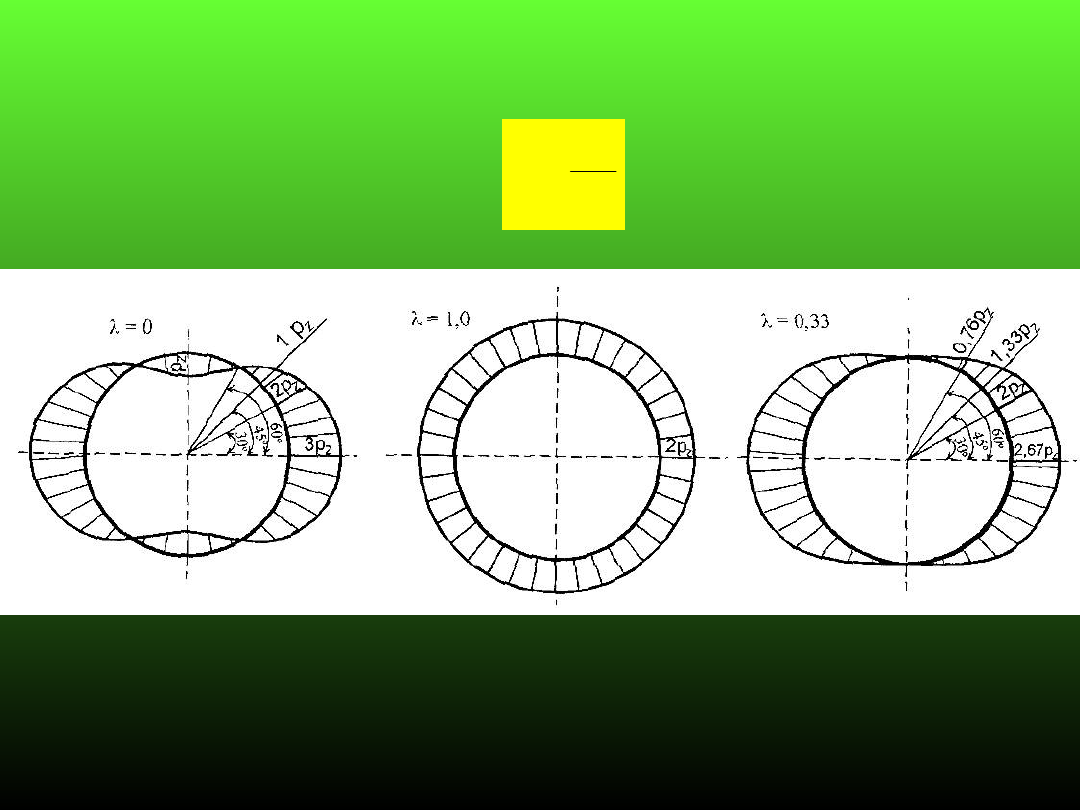
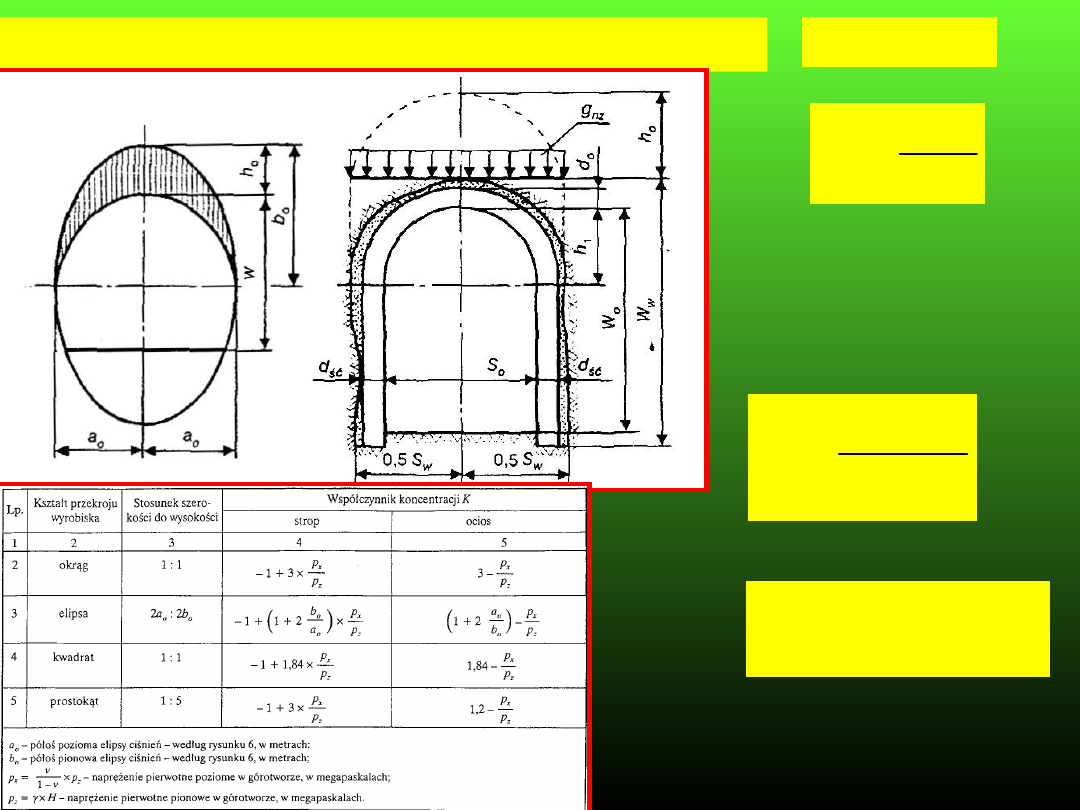
Rozkład naprężeń obwodowych na konturze wyrobiska w
zależności od:

z

x

p

p





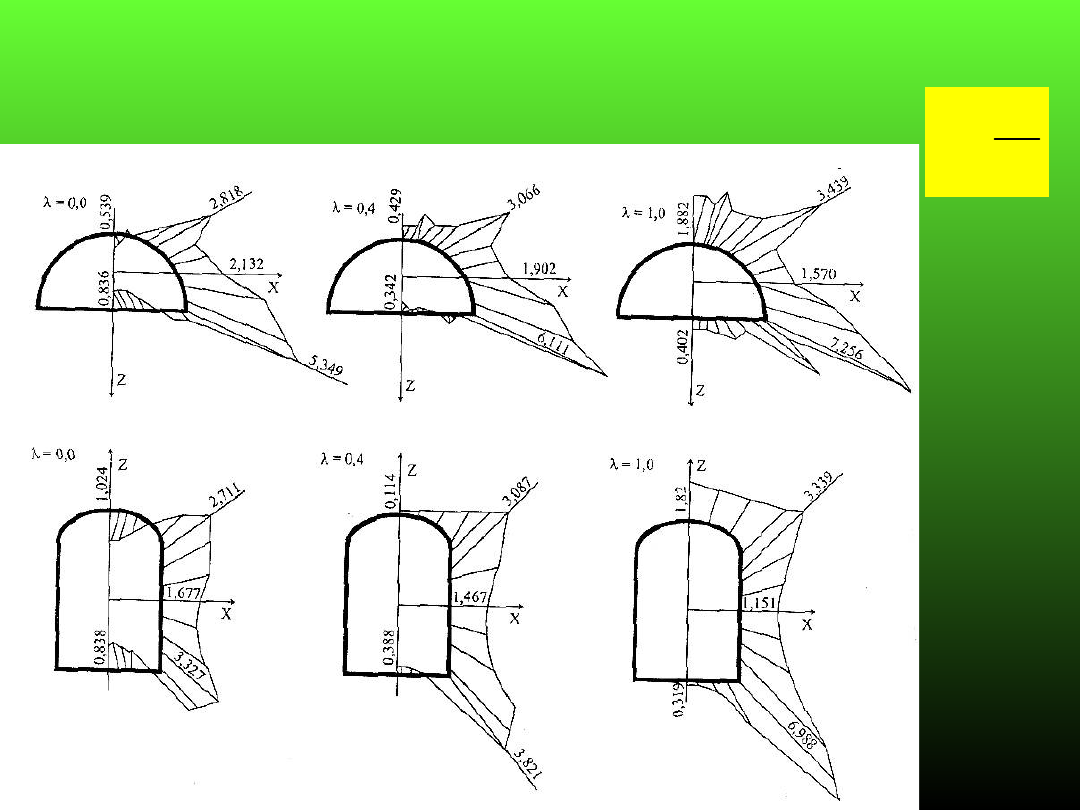
Rozkład naprężeń obwodowych na konturze wyrobiska w
zależności od:
- kształtu wyrobiska
- wartości stosunku l

z

x

p

p





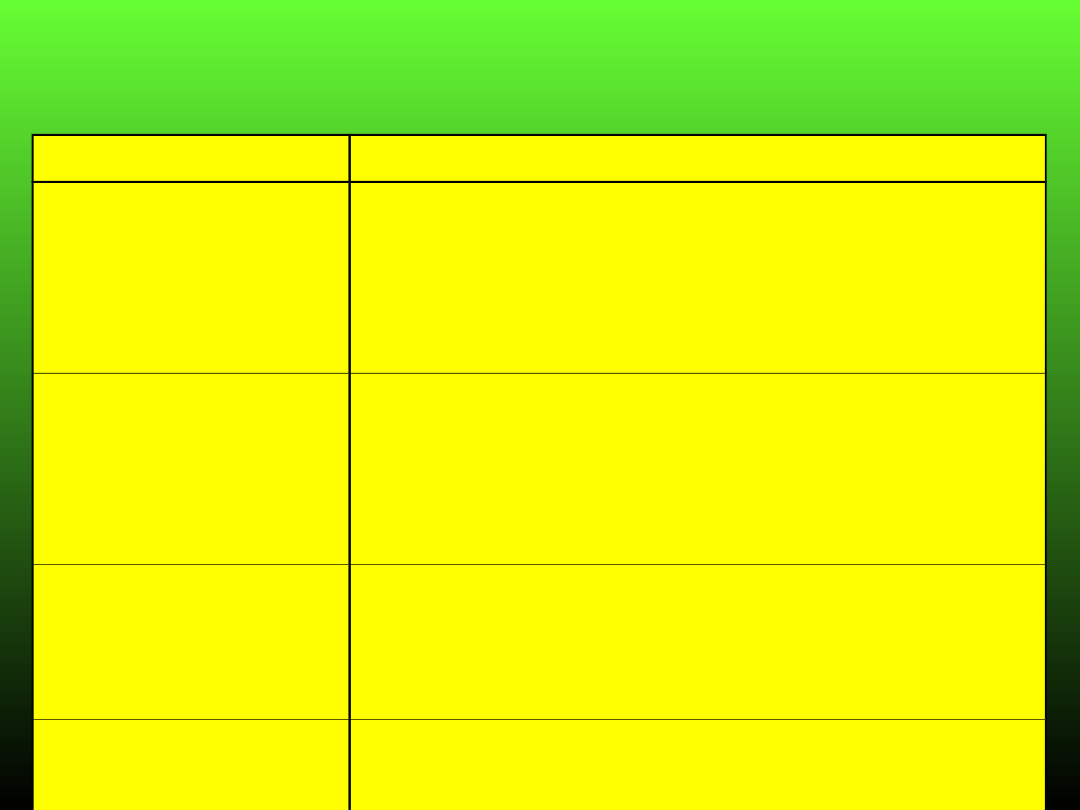
Kształt

Charakterystyka

Prostokątny

Stwarza możliwość pełnego wykorzystania

przekroju. Podstawowa wada to duża
koncentracja naprężeń w narożach oraz
trudności w utrzymaniu stateczności
ociosów

Sklepieniowy

Dobre możliwości wykorzystania przekroju
poprzecznego. Stosunkowo korzystny
rozkład naprężeń w stropie wyrobiska. Duża

koncentracja naprężeń w narożach przy
spągu wyrobiska

Łukowy

Korzystny rozkład naprężeń wokół

wyrobiska. Wykorzystanie przekroju gorsze
niż w przypadku kształtu prostokątnego i
sklepieniowego

Kołowy

Najkorzystniejszy rozkład naprężeń przy
działaniu na obudowę wszechstronnych

ciśnień górotworu. Wykorzystanie przekroju
najgorsze z omawianych

Charakterystyka geomechaniczna typowych

kształtów wyrobisk korytarzowych

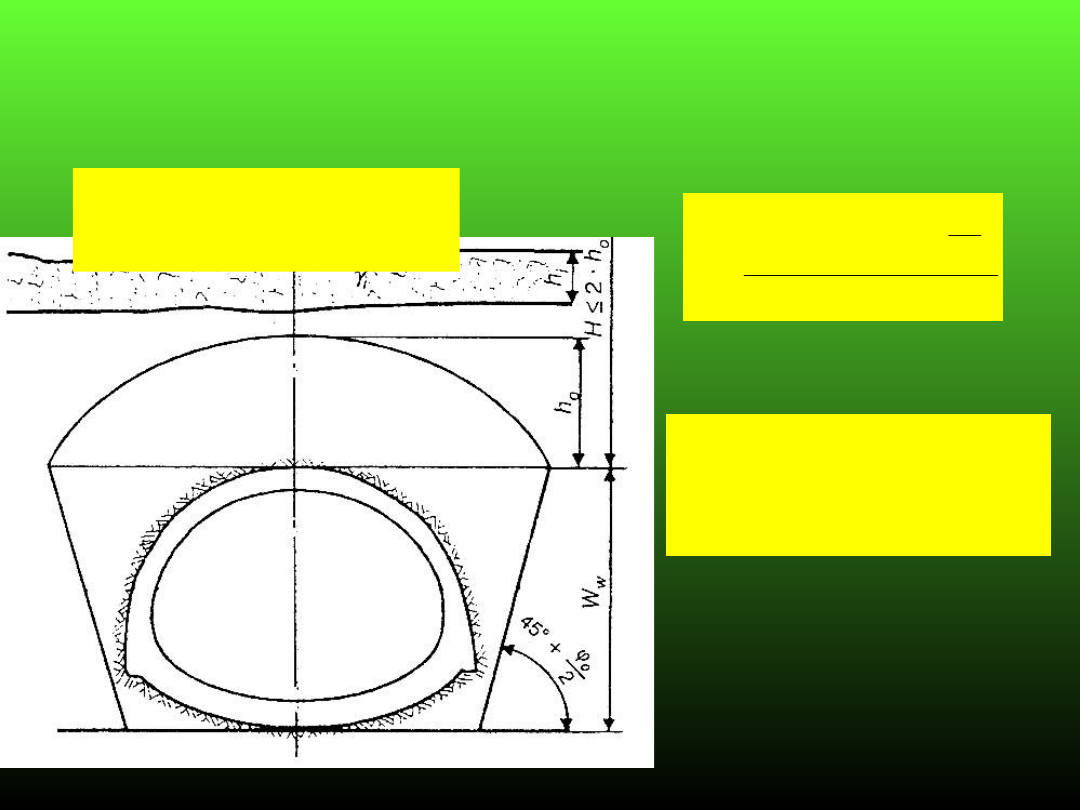
Modele obciążenia obudowy wyrobiska

korytarzowego

wg. PN-G-05020/1997

Model I
H<2h

0

 











J

i

i

i

r

i

Nz

h

q

1

0



s

w

tg

tg

s

h

























2

45

5

,

0

0

0

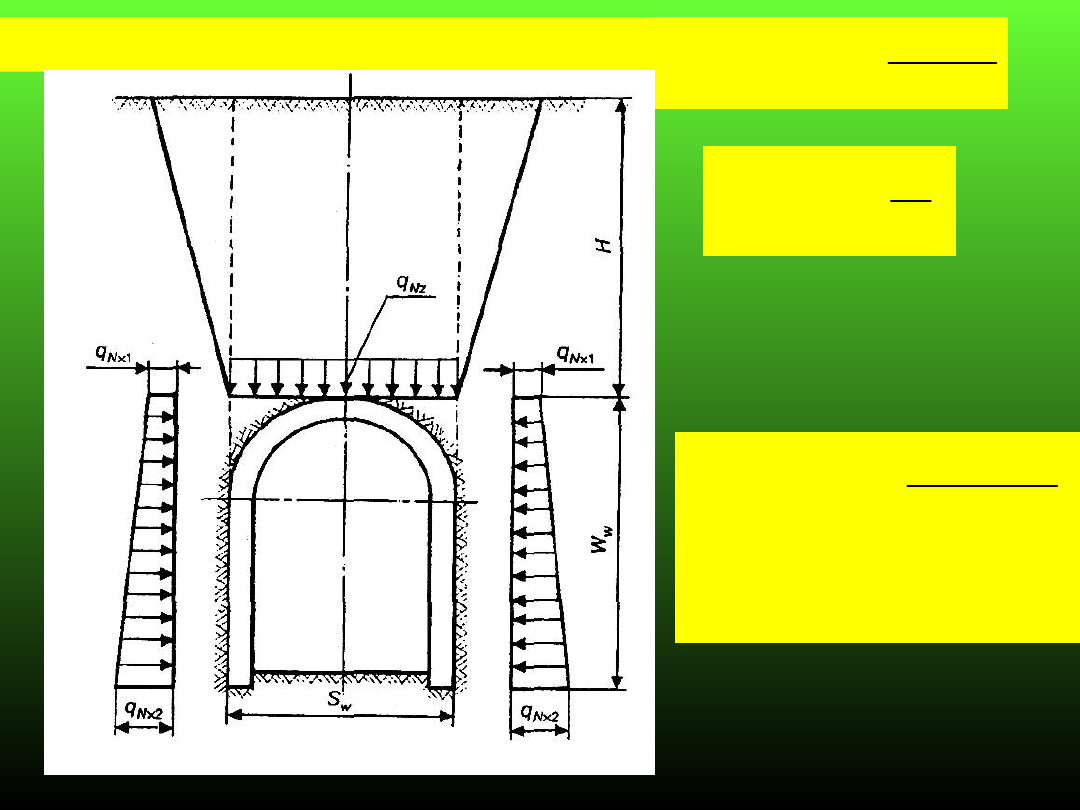
Model II wg. Bierbaumera

s

w

tg

s

H

h















2

0

2

















2

45

2

g

tg

























































w

Nz

Nx

Nz

Nx

w

g

Nz

w

q

q

q

q

s

tg

H

H

q

0

2

1

0

1

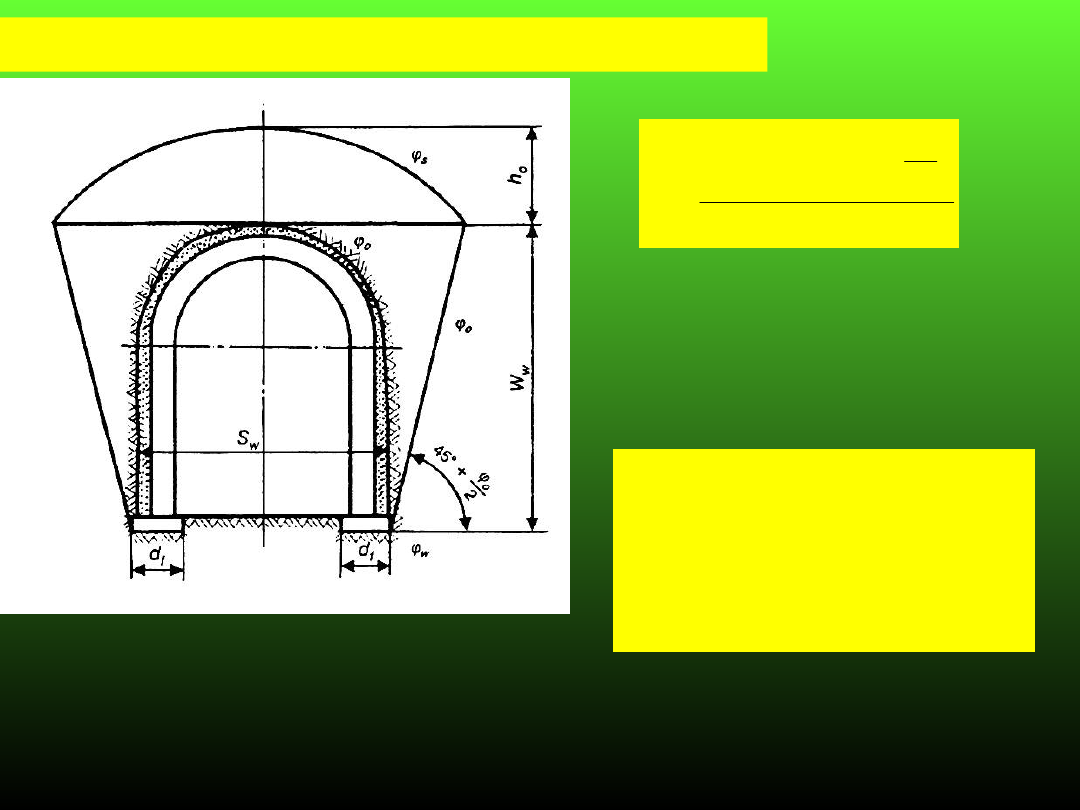
Model III wg. Cymbariewicza

s

w

tg

tg

s

h

























2

45

5

,

0

0

0





























w

Nz

Nx

Nz

Nx

Nz

w

q

q

q

q

h

q

0

2

1

0

0

Nad wyrobiskiem wytwarza się
sklepienie, a ociosy nie przejmują w
pełni ciężaru nadkładu. Ciśnienie
deformacyjne nie występuje

Model IV wg. Protodiakonowa

kr

H

H

h







0

2

0







K

R

H

cg

kr

K – współczynnik
koncentracji naprężeń
wg tabeli

s

w

tg

s

h







2

0

0

0

h

q

Nz







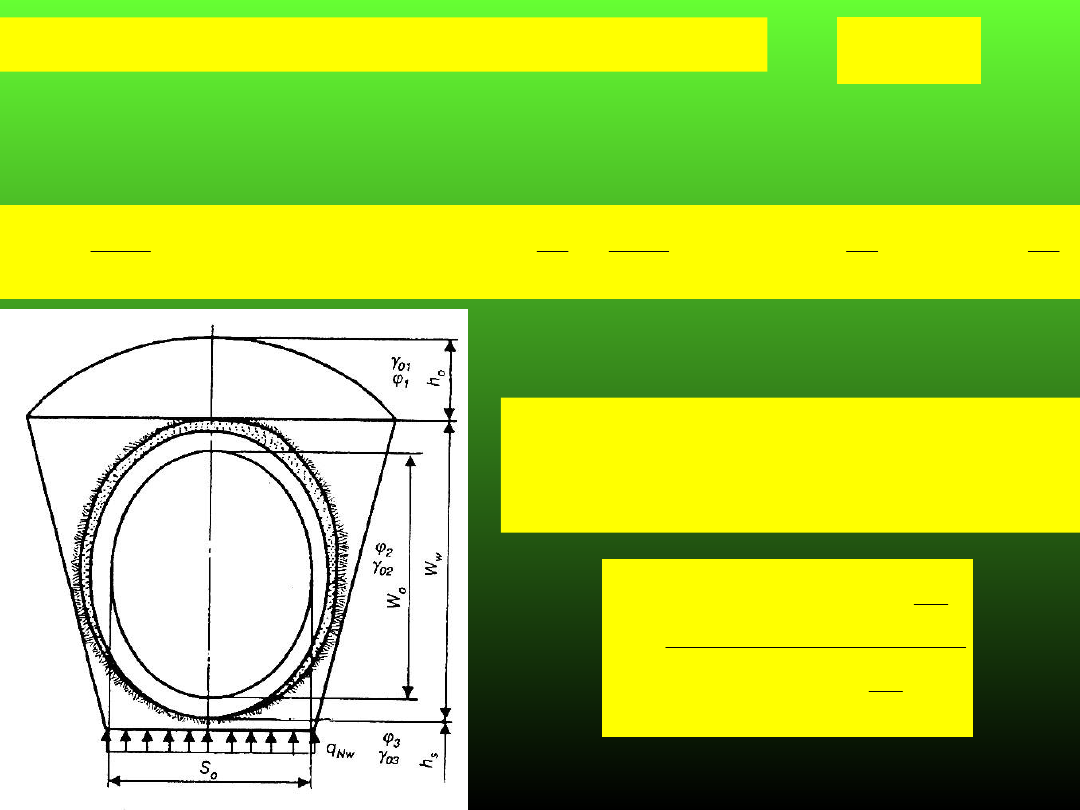
Model V (ciśnienie spągowe)

0



Nw

q

Należy przyjmowac jednocześnie z modelami od I

do IV

























































































2

45

2

45

2

2

45

2

2

3

0

3

0

2

2

3

3

0

2

0

2

02











tg

tg

h

s

tg

h

w

h

h

s

q

s

w

o

w

s

s

w

Nw

f

3

– pozorny kąt tarcia skał

spągowych
h

s

– głębokość wypiętrzania spągu









































2

45

1

2

45

3

4

3

4





tg

tg

h

w

h

o

w

s

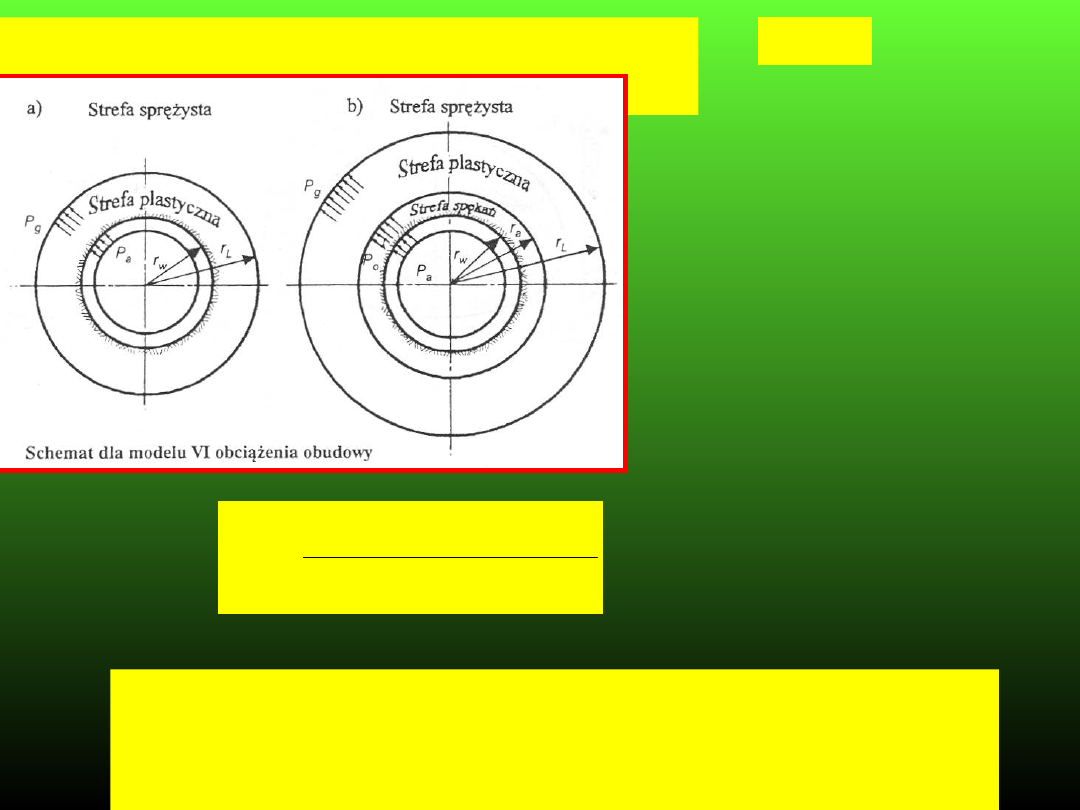
Model VI (ciśnienień
deformacyjnych)

kr

H

H 

Przypadki wystąpienia
strefy niesprężystej wokół
wyrobiska wyróżnia się w
zależności od wartości
przemieszczeń konturu
wyrobiska U

w



 



w

g

g

z

L

g

w

r

E

p

p

r

U













2

1



r

L

- zasięg strefy plastycznej

r

w

– promień wyrobiska w wyłomie

p

g

– naprężenie radialne na granicy strefy plastycznej i

sprężystej
p

z

– pierwotne ciśnienie pionowe

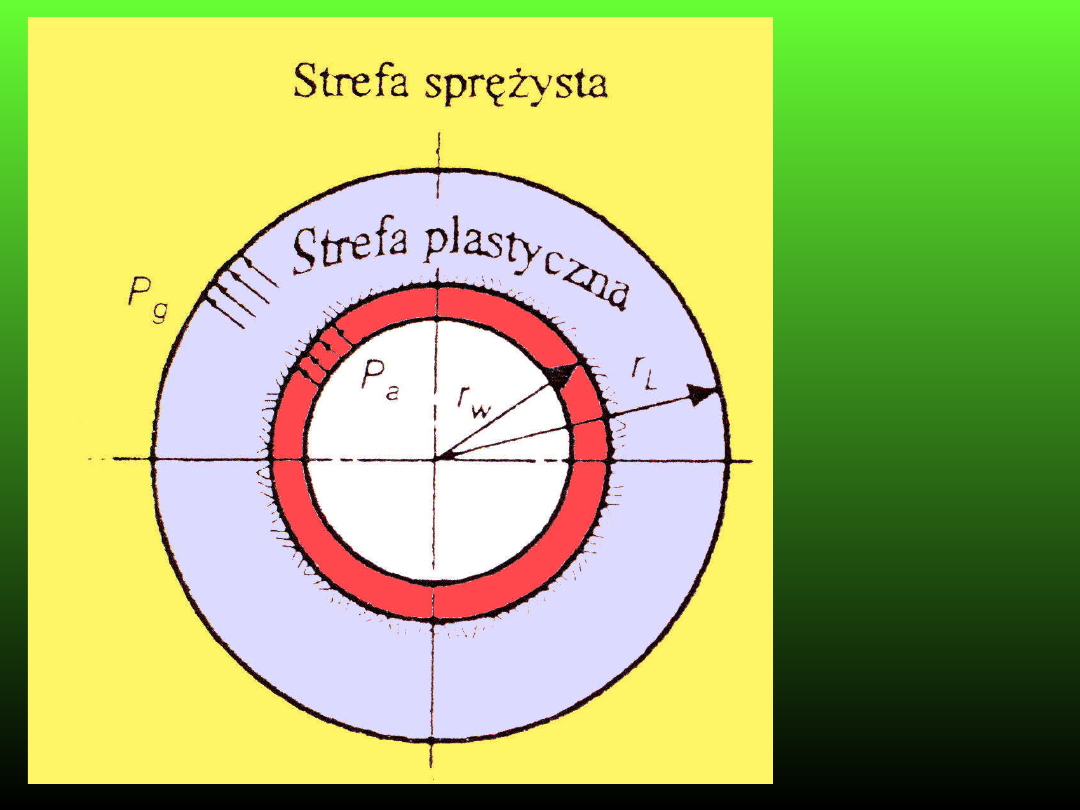
Ośrodek

II

strefowy

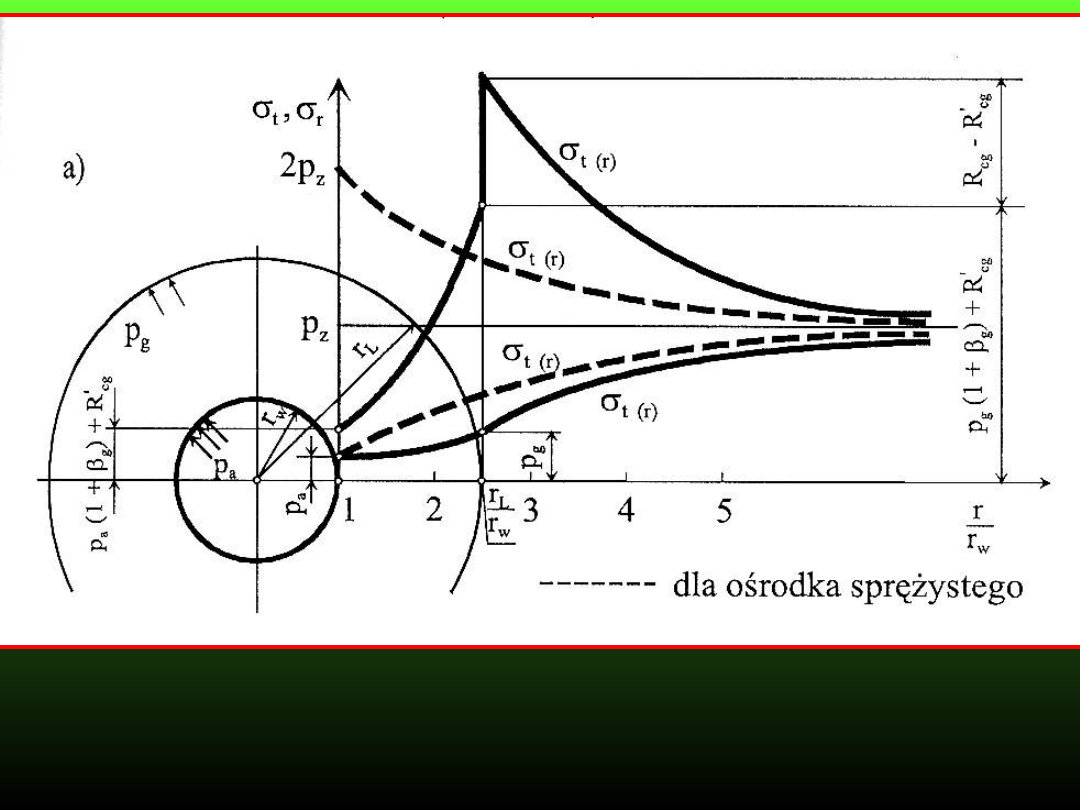
Rozkład naprężeń wokół wyrobiska kołowego w ośrodku

sprężysto-plastycznym

a) przypadek
gdy

ng

w

w

r

U







g

g

a

cg

g

g

w

L

p

R

p

r

r







1

'



























P

a

– podporność wstępna

obudowy

g

g

g







sin

1

sin

2











cg

cg

R

R







6

,

0

4

,

0

'





w

L

o

Nz

r

r

q































w

Nz

Nx

Nz

Nx

w

q

q

q

q

0

2

1

















2

45

2

g

tg





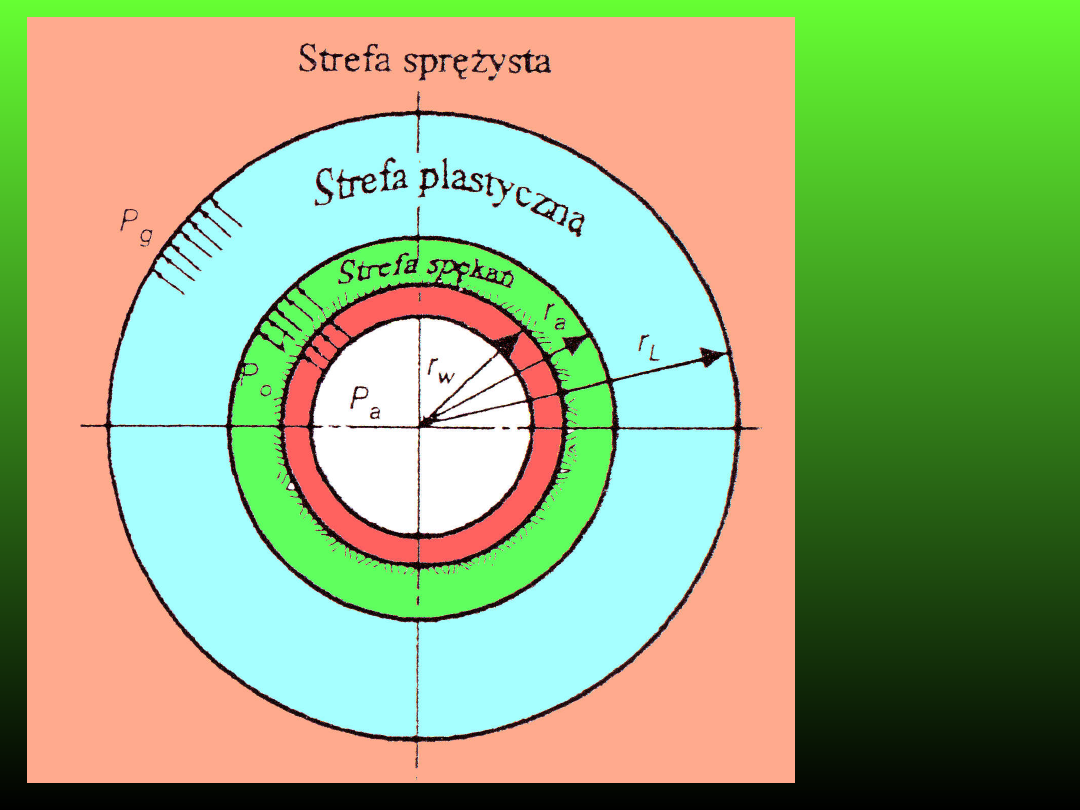
Ośrodek

III

strefowy

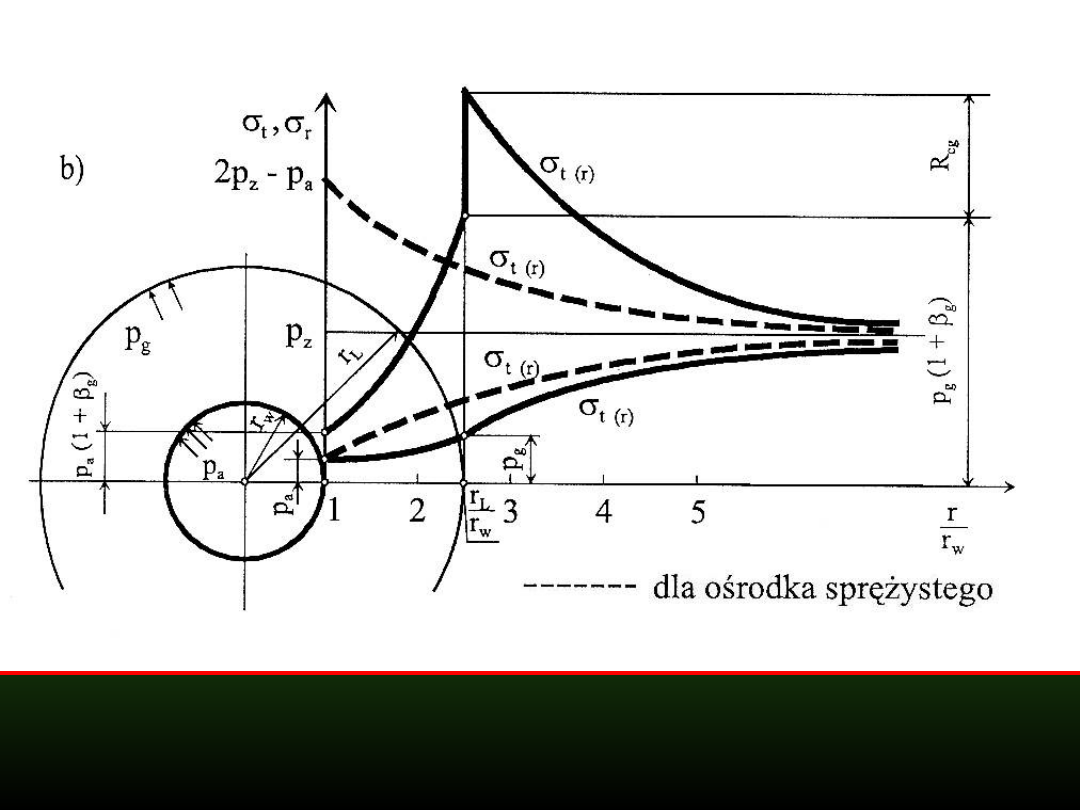
Rozkład naprężeń wokół wyrobiska kołowego w ośrodku

sprężysto-spękanym

b) przypadek
gdy

ng

w

w

r

U







g

g

a

cg

g

g

a

L

p

R

p

r

r







1

'































w

a

o

Nz

r

r

q































w

Nz

Nx

Nz

Nx

w

q

q

q

q

0

2

1

















2

45

2

g

tg





g

cg

z

g

R

p

p











2

2

g

o

g

w

a

p

p

r

r



1



















 



g

cg

g

ng

g

z

g

g

cg

g

g

o

R

E

p

p

R

p

p

g













'

'

1



































r

L

– zasięg strefy plasrtycznej

r

a

– zasięg strefy spękań

p

g

– naprężenie radialne na granicy strefy sprężystej i

plastycznej
p

o

– naprężenie radialne na granicy strefy spękanej i

plastycznej
p

a

– podporność początkowa obudowy