Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

• Każde ciało stałe, ciecz lub gaz, emituje

promieniowanie termiczne w postaci fal
elektromagnetycznych, a także absorbuje je z
otoczenia. Promieniowanie ma widmo ciągłe.

• DEF:

Ciało doskonale czarne absorbuje całe

promieniowanie termiczne, które nań pada.

• Przykładem CDC jest przedmiot pokryty sadzą

lub czernią bizmutową.

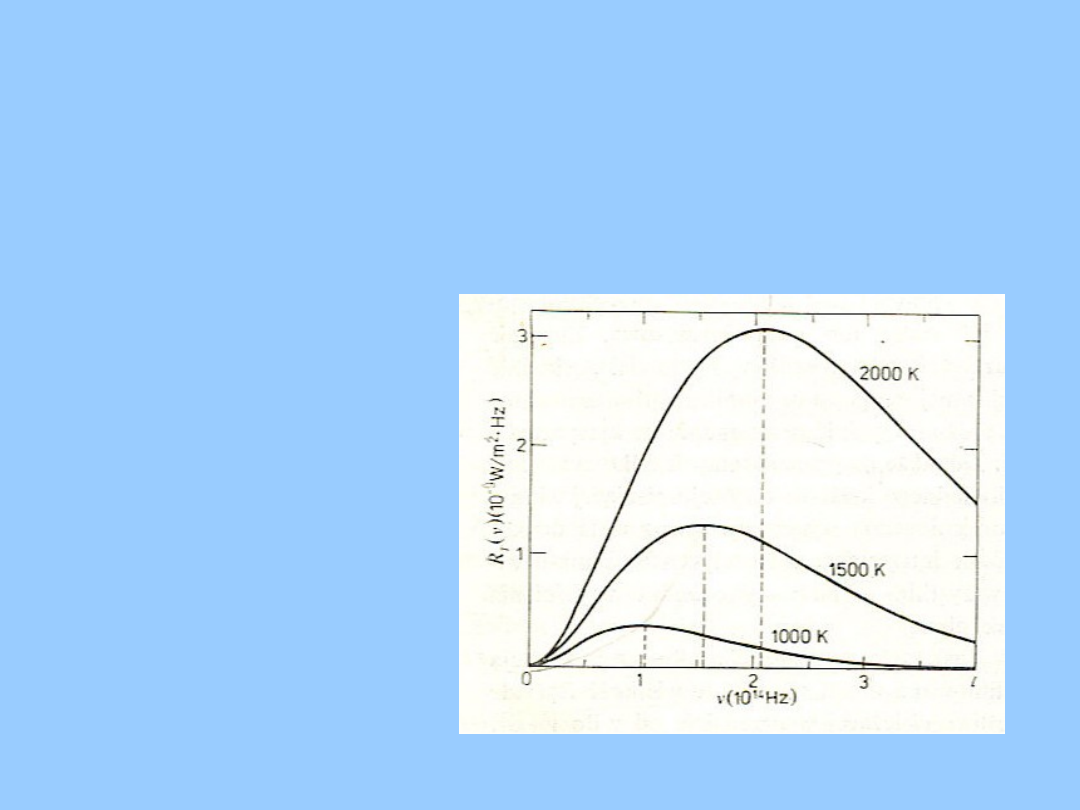
• Rozkład widmowy promieniowania CDC

charakteryzuje funkcja R

T

(v) zwana zdolnością

emisyjną ciała (def: wielkość R

T

(v)dv jest

równa energii promieniowania o
częstotliwości leżącej w przedziale od v do v +
dv, wysyłanego w ciągu jednostki czasu przez
jednostkę powierzchni ciała mającego
temperaturę bezwzględną T)

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

• Częstotliwość

odpowiadająca

maksimum zdolności

emisyjnej wzrasta

liniowo ze wzrostem

temperatury.

• Całkowita moc

wyemitowana przez

powierzchnię

jednostkową (pole

pod krzywą)

gwałtownie rośnie z

temperaturą.

Całkowita zdolność emisyjna R

T

jest całką ze

zdolności emisyjnej R

T

(v) po wszystkich

częstotliwościach v. Jest ona równa całkowitej
energii wyemitowanej w ciągu jednostki czasu z
jednostki powierzchni ciała doskonale czarnego o
temperaturze T.

Ilościowo ujmuje ten fakt empiryczne prawo

Stefana:

R

T

= σT

4

,

gdzie σ = 5,67 * 10

-8

W/(m

2

* K

4

) jest stałą Stefana-

Boltzmana.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

• Prawo przesunięć Wiena.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

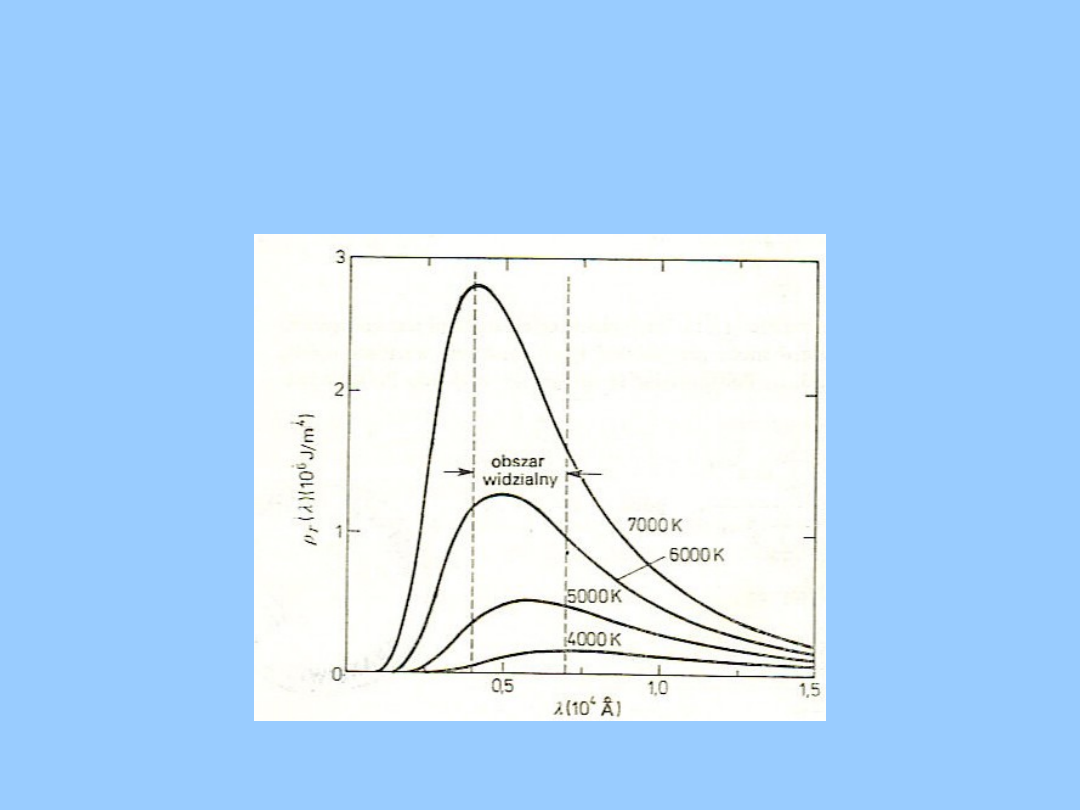
Analizując widmo promieniowania CDC

widzimy, że wraz ze wzrostem temperatury T

widmo promieniowania ulega przesunięciu w

stronę wyższych częstotliwości. Fakt ten

wyraża tzw. prawo przesunięć Wiena:
v

max

~ T czyli 

max

*T=const.

gdzie v

max

jest częstotliwością

a 

max

długością

fali dla której R

T

(v) ma w danej temperaturze

T wartość maksymalną (wraz ze wzrostem T

częstotliwość v

max

ulega przesunięciu w

kierunku wyższych częstotliwości).

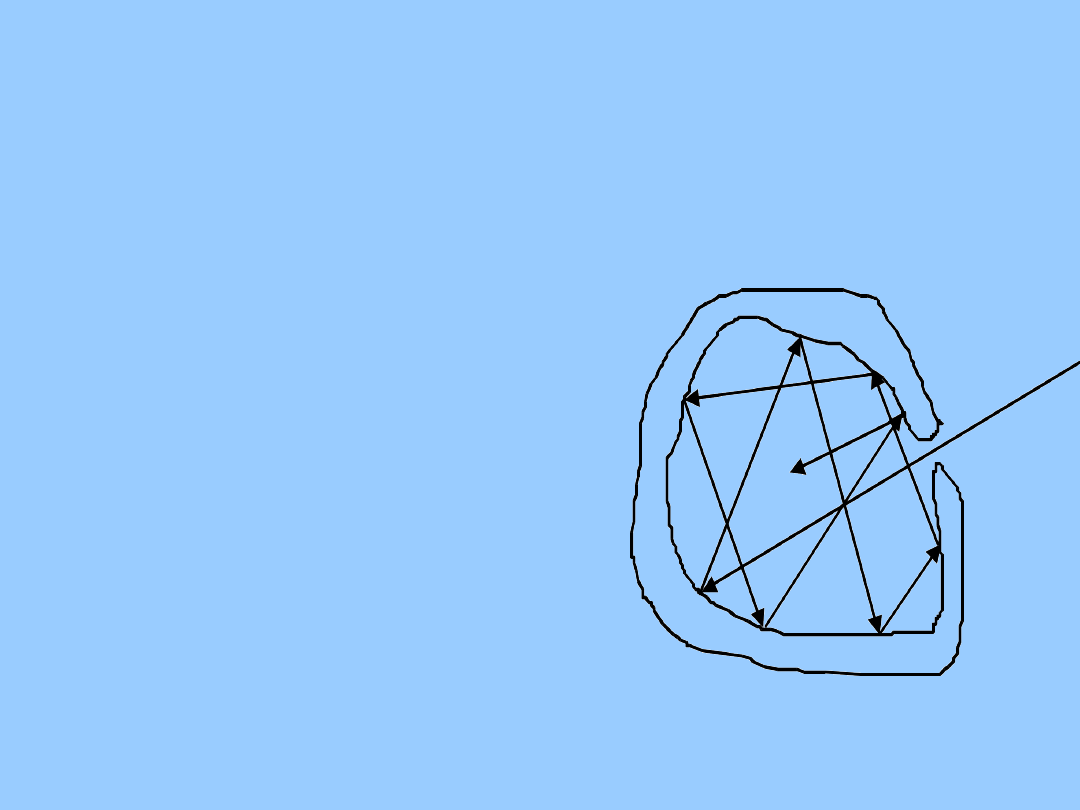
• Model ciała doskonale czarnego.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Nieprzezroczyste ciało

zawierające wnękę z bardzo

małym otworem wejściowym,

którego ścianki ogrzane są w

jednorodny sposób do

temperatury T.
Promieniowanie padające na

otwór z zewnątrz jest po

wielokrotnych odbiciach od

wewnętrznych ścian wnęki

całkowicie pochłaniane.

Wewnętrzne ściany wnęki także

emitują promieniowanie, część

jego wychodzi na zewnątrz. Otwór

pochłania i emituje

promieniowanie jak ciało

doskonale czarne

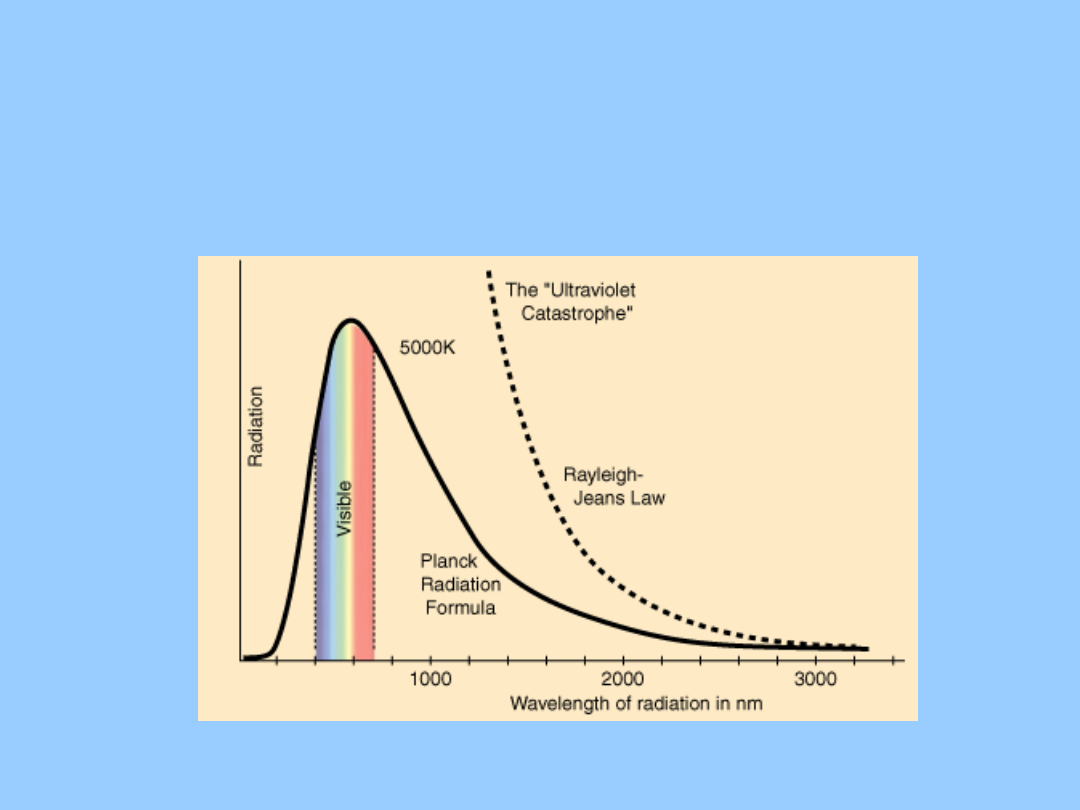
• Prawo Rayleigh’a – Jeans’a

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

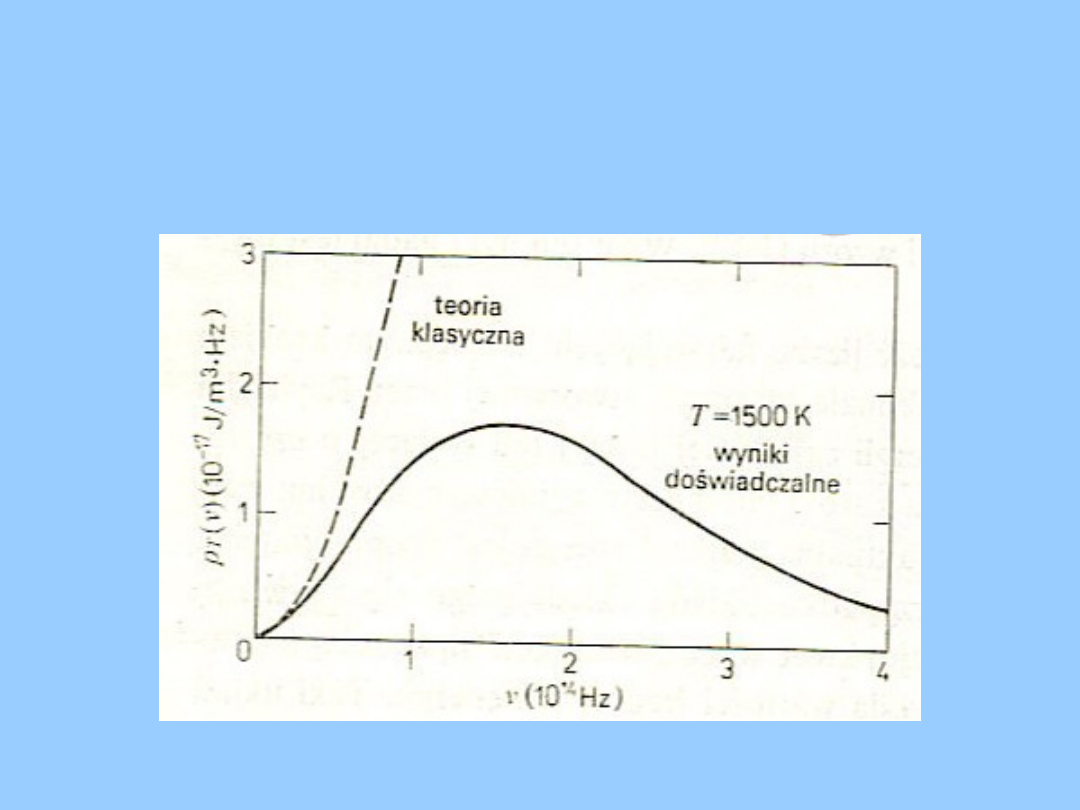
Pod koniec XIX w. Rayleigh i Jeans obliczają energie

promieniowania we wnęce. Stosują klasyczną teorię

pola elektromagnetycznego do pokazania, że

promieniowanie wewnątrz wnęki ma charakter fal

stojących (węzły na ścianach wnęki). Zgodnie z fizyką

klasyczną, energia każdej fali może przyjmować

dowolną wartość od zera do nieskończoności, przy

czym energia jest proporcjonalna do kwadratu

amplitudy. Następnie Rayleigh i Jeans obliczyli wartość

średniej energii w oparciu o prawo ekwipartycji energii i

w oparciu o nią znaleźli widmową zdolność emisyjną: 
R

T

(v) = ( 8πv

2

/ c

3

)* kT,

gdzie c jest prędkością światła w próżni, a k stałą

Boltzmanna, k = 1,38 * 10

–23

J/K.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Rayleigh’a –
Jeans’a
„katastrofa w
nadfiolecie”

• Teoria Wiena:

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

T

c

e

c







2

1

5

1





• Założenia Plancka – oscylator

kwantowy.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Planck szukał przyczyny rozbieżności doświadczenia z prawem

R-J. Postanawia naruszyć prawo ekwipartycji energii, na

którym opierał się jego dowód. Przyjmuje, że atomy ścian

zachowują się jak oscylatory harmoniczne, które emitują (i

absorbują) energię do wnęki, z których każdy ma

charakterystyczną częstotliwość drgań. Dalej przyjmuje, że:
I. Oscylator nie może mieć dowolnej energii, lecz tylko energie

dane wzorem:
E = nhv
gdzie v oznacza częstość oscylatora, h stałą (Plancka),

n pewną liczbę całkowitą (zwaną obecnie liczbą kwantową). Z

powyższego wzoru wynika, że energia jest skwantowana i

może przyjmować tylko ściśle określone wartości. Tu jest

zasadnicza różnica, bo teoria klasyczna zakłada dowolną,

ciągłą wartość energii od zera do nieskończoności.

II. Oscylatory nie wypromieniowywują (ani pobierają)

energii w sposób ciągły, lecz porcjami, czyli kwantami,

podczas przejścia z jednego stanu w drugi. Wtedy to:

ΔE = Δnhv = hv

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Na podstawie swoich hipotez Planck otrzymał
następującą funkcję rozkładu

R

T

(v) = ( 8πv

2

/ c

3

) * (hv / (e

hv/kT

- 1)) ,

Doświadczalna wartość stałej Plancka,

h = 6,62 * 10

-34

J*s.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Kwantyzacja energii może wydawać się dość absurdalnym

założeniem i niezgodnym z naszym doświadczeniem. Jak ta

hipoteza stosuje się do znanych nam oscylatorów, np. sprężyna

o masie m = 1 kg i stałej sprężystości k = 20 N/m wykonująca

drgania o amplitudzie 1 cm.

Częstotliwość drgań własnych:

Wartość energii całkowitej:
 
Jeżeli energia jest skwantowana to jej zmiany dokonują się

skokowo przy czym E = hv. Względna zmiana energii wynosi

więc:

E/E = 4.7·10

-31

Żaden przyrząd pomiarowy nie jest wstanie zauważyć tak

minimalnych zmian energii.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Hz

m

k

v

71

.

0

2

1







J

kA

E

3

2

10

1

2

1









Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Wyniki badań nad widmami zdolności emisji

promieniowania podczerwonego znalazły

sporo zastosowania:

• kamer działające na podczerwień

(szpiegowskie)

• różna aparatura techniczna (np. profilowanie

opon i ich bieżników tak by temperatury

powstałe na skutek tarcia im nie szkodziły)

• mierzenie temperatur - pirometry
• ogrzewanie - promienniki.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Promieniowanie emitowane przez gorące ciało można

wykorzystać do wyznaczenia jego temperatury. Mierzy się
ich zdolność emisyjną dla wybranego zakresu długości fal. Z
prawa Plancka wynika, że dla dwu ciał o temperaturach T

1

i

T

2

stosunek natężeń promieniowania o długości fali



wynosi:

 

Jeżeli T

1

przyjmiemy jako standardową temperaturę odniesienia

to możemy wyznaczyć T

2

wyznaczając doświadczalnie I

1

/I

2

.

Do tego służy

pirometr.

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

1

1

2

1

2

1







kT

hc

kT

hc

e

e

I

I





Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

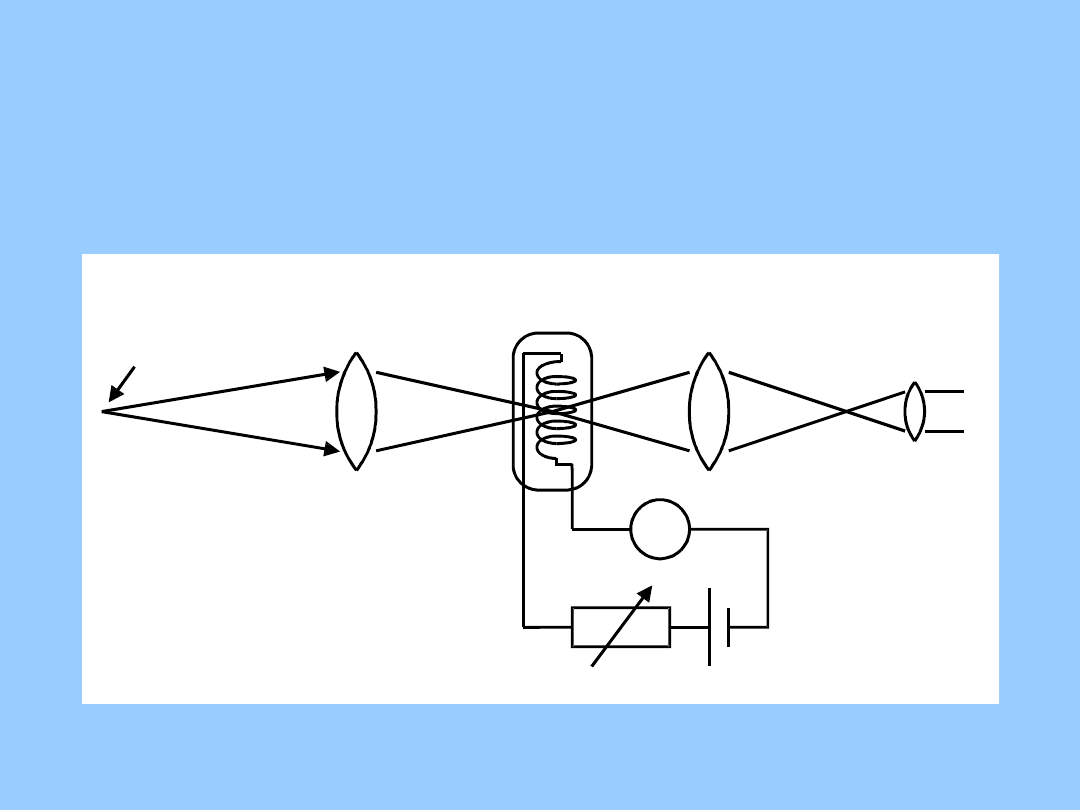
A

źródło

promieniowania

włókno pirometru

mikroskop

Pirometr – budowa

Fizyka współczesna

Promieniowanie Ciała Doskonale

Czarnego (CDC)

Współczesny
pirometr
cyfrowy

1895 -

Wilhelm Roentgen badał własności

promieni katodowych:

•

Rura katodowa czynna -> leżący w pobliżu

rury ekran pokryty platynocyjankiem baru

świecił.

•

Rura owinięta w czarnym papierem ->

ekran świecił.

•

Klisza fotograficzna w czarnym papierze

umieszczona obok rury katodowej ->

uległa naświetleniu.

Fizyka współczesna

Promieniowanie Roentgena

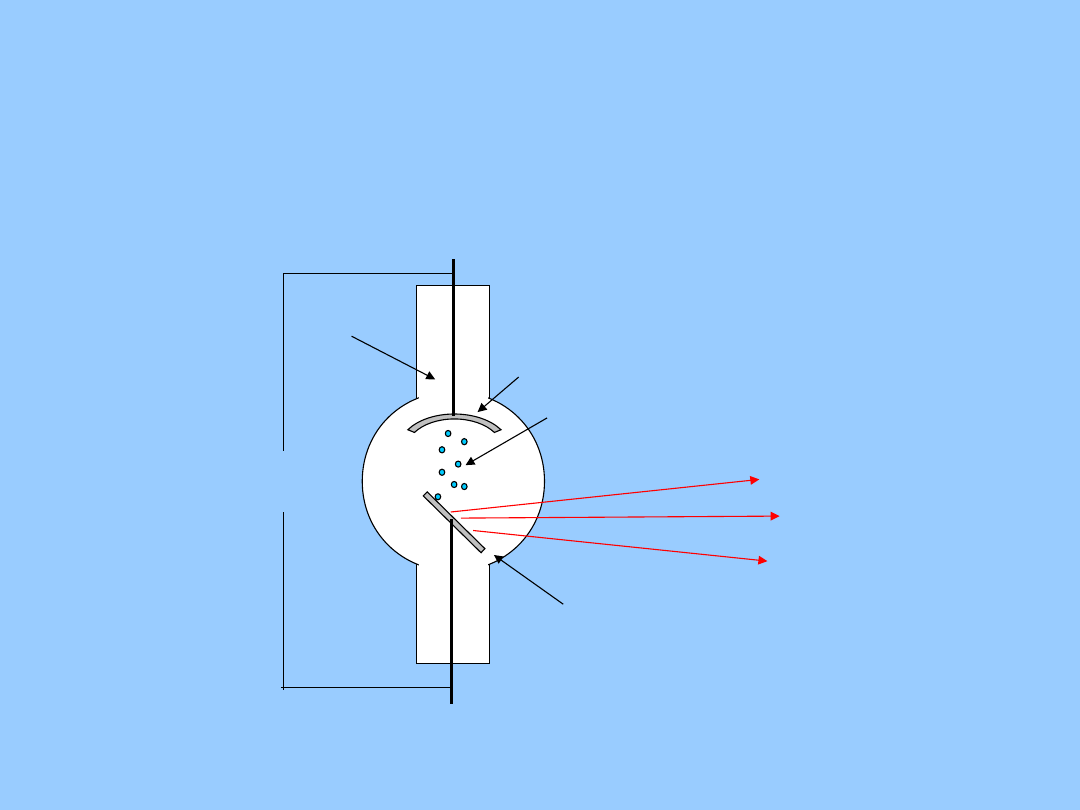
anoda:
Cu, Mo, W,
Ni

próżnia

katoda

wysokie U
ponad 1.5kV

przyśpieszane
elektrony

promienie X

Fizyka współczesna

Promieniowanie Roentgena

Promieniowanie X (Roentgena) jest to

strumień kwantów promieniowania
elektromagnetycznego, powstający w
wyniku hamowania strumienia
elektronów na anodzie (antykatodzie.
Promieniowanie to rozchodzi się w
postaci fali elektromagnetycznej, której
długość zawiera się w granicach od 10
do 0,001 nm.

Fizyka współczesna

Promieniowanie Roentgena

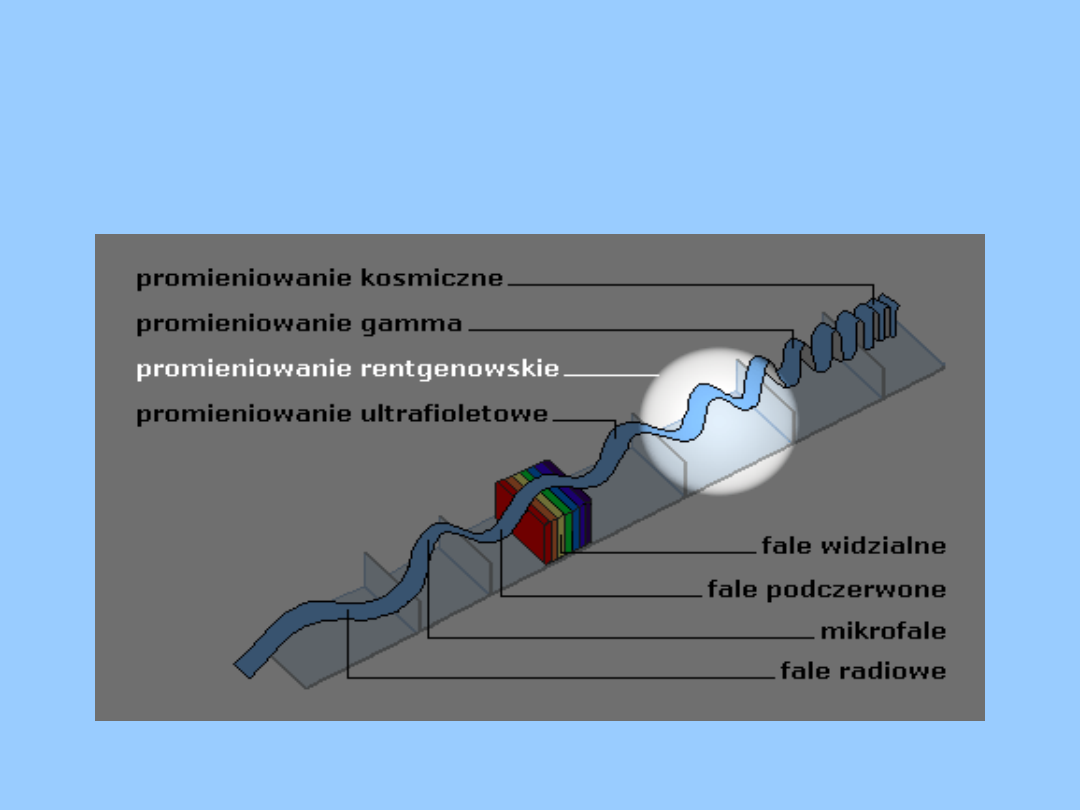
Fizyka współczesna

Promieniowanie Roentgena

Promieniowanie rentgenowskie

powstaje na dwóch drogach:

• jako

promieniowanie hamowania

w polu kulombowskim jąder atomów

materiału anody - elektron jest

wyhamowany i odbity przez atom,

emitując przy tym energię w postaci

promieniowania rentgenowskiego,

Fizyka współczesna

Promieniowanie Roentgena

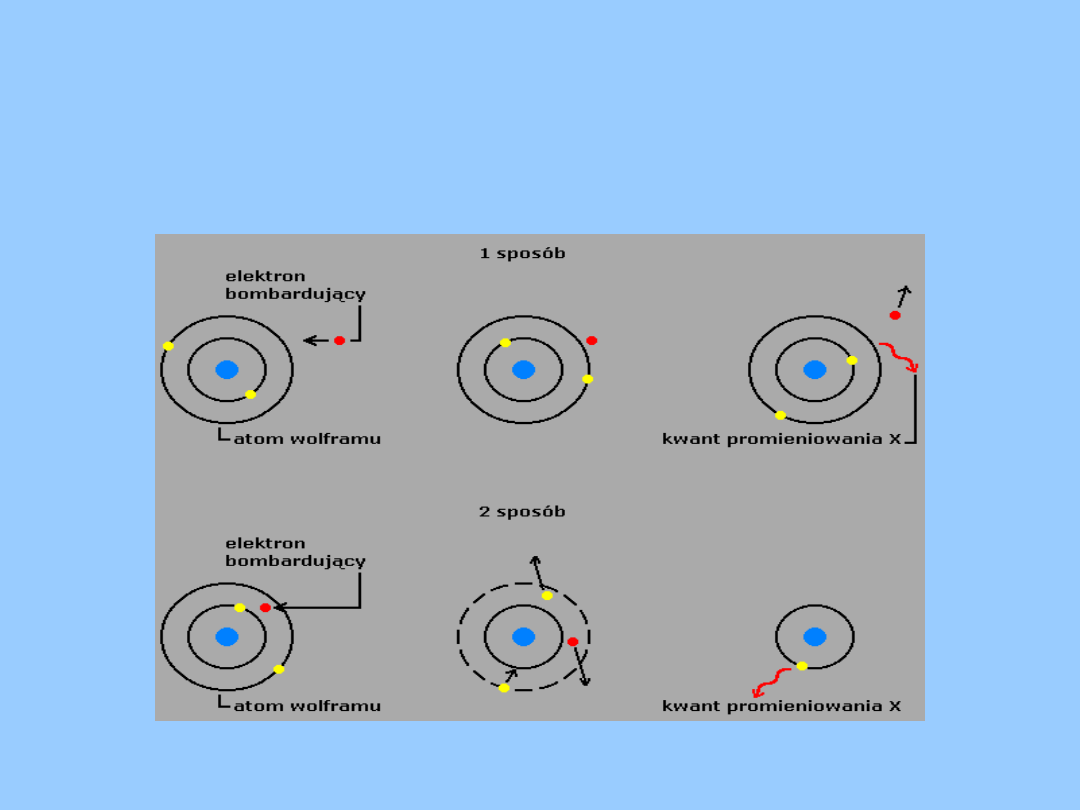
• jako

promieniowanie

charakterystyczne

(oddziaływanie z

elektronami wewnętrznych powłok

atomów materiału anody) - elektron

wybija z wewnętrznej orbity atomu

jeden z jego elektronów. Wówczas

promieniowanie rentgenowskie

powstaje wskutek przejścia elektronu z

orbity zewnętrznej na miejsce

wybitego wcześniej elektronu.

Fizyka współczesna

Promieniowanie Roentgena

Fizyka współczesna

Promieniowanie Roentgena

Fizyka współczesna

Promieniowanie Roentgena

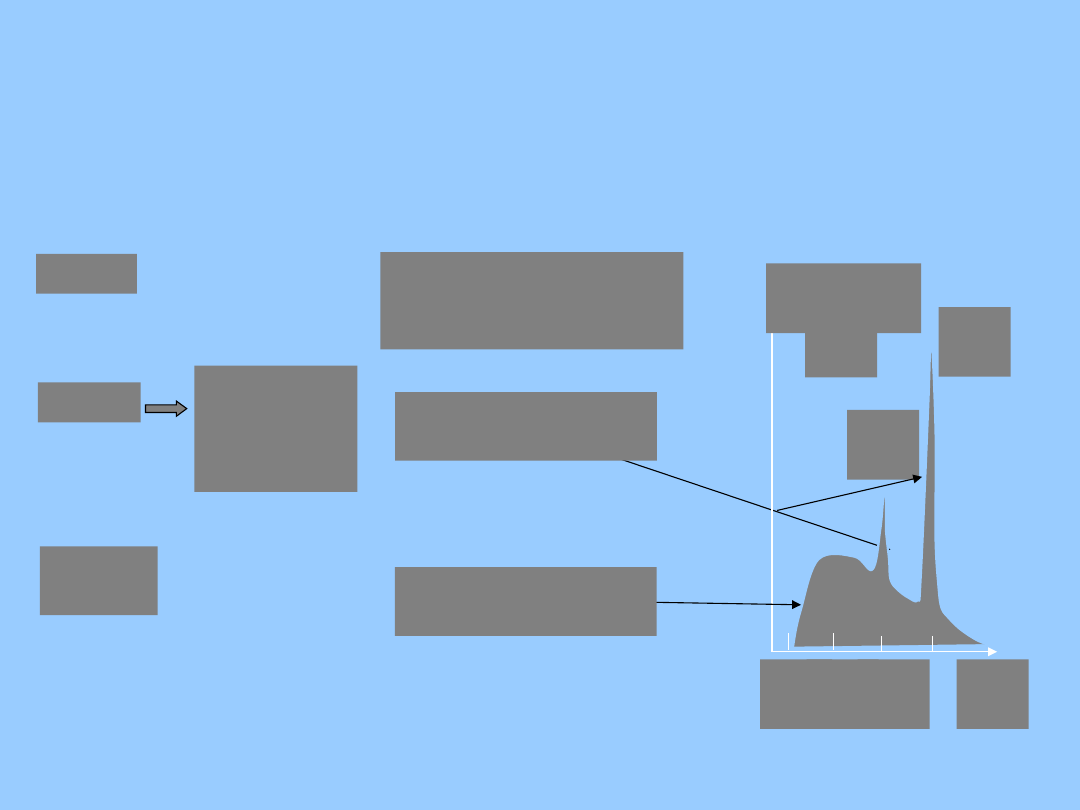
emisja

(Ĺ)

0.4 0.5

0.6

K



K



Mo

intensywnoś
ć

atom
kw.

widmo

fluorescenc
ja
rentgenow
ska

szybkie elektrony
hamowane są na
anodzie

promieniowanie
charakterystyczne

promieniowanie
hamowania

Fizyka współczesna

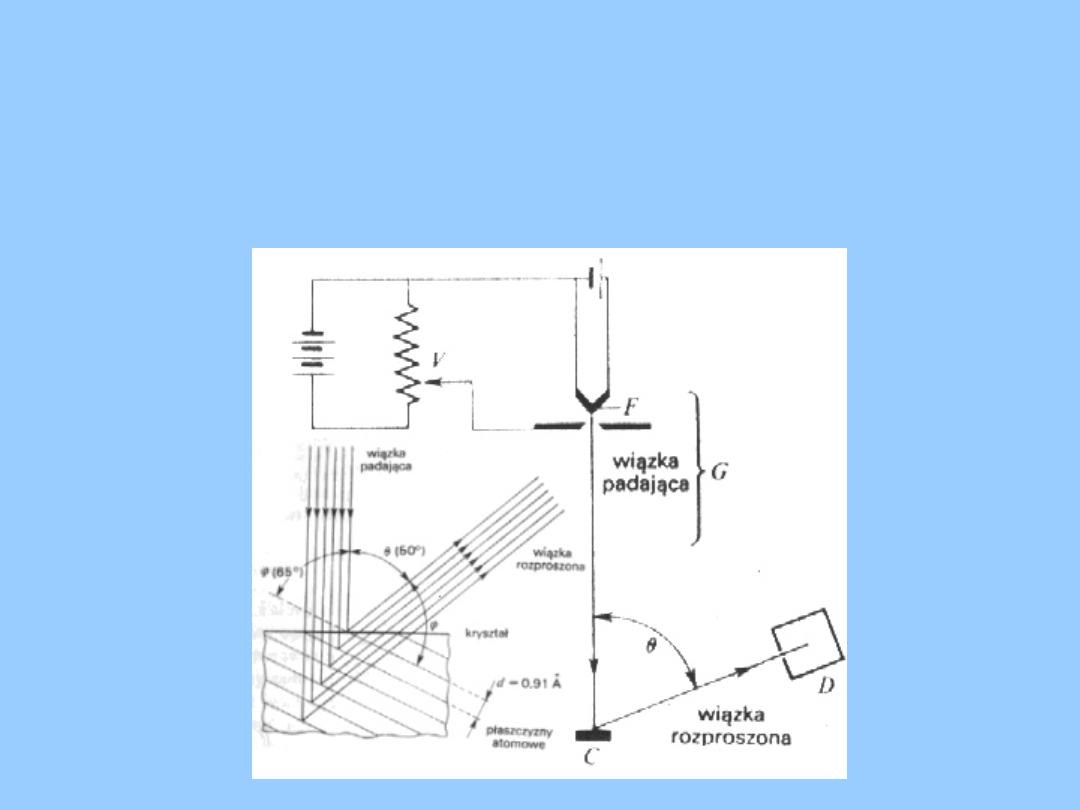
Promieniowanie Roentgena

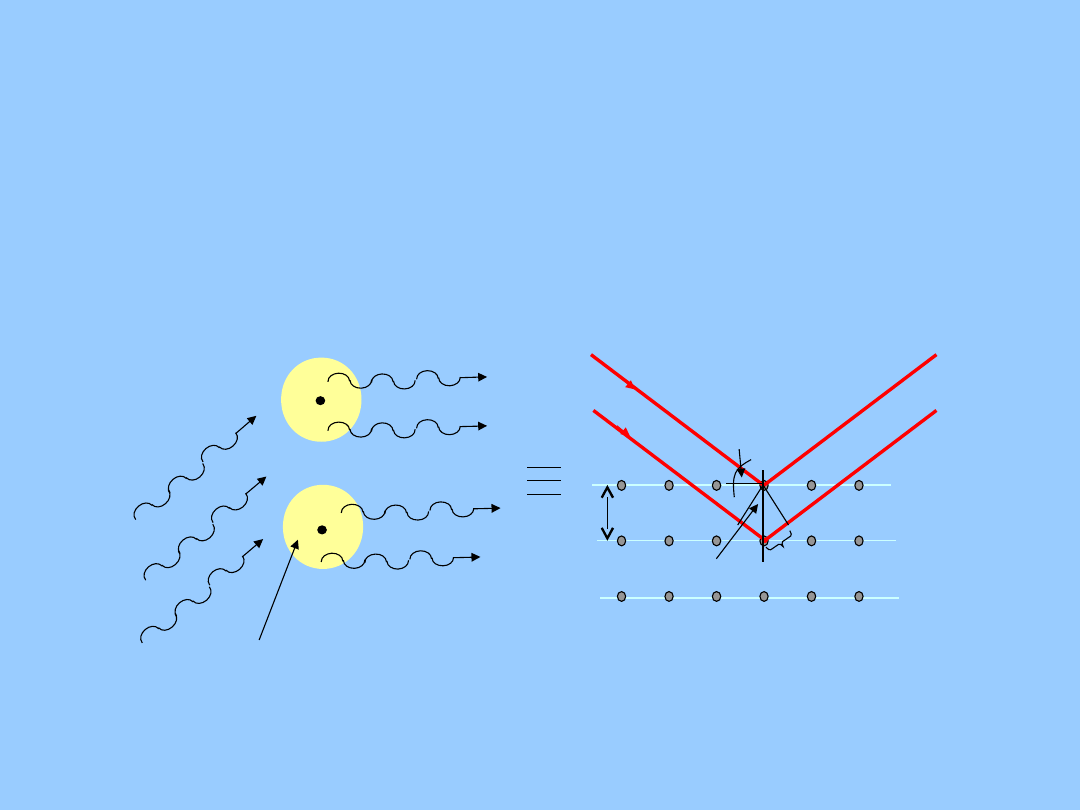
ROZPROSZENIE PROMIENI RENTGENA NA

SIECI KRYSTALICZNEJ

wiązka
padająca

d

hk

l





x

wiązka
rozproszona

elektrony
wokół jądra

wiązka
padająca

Fizyka współczesna

Promieniowanie Roentgena

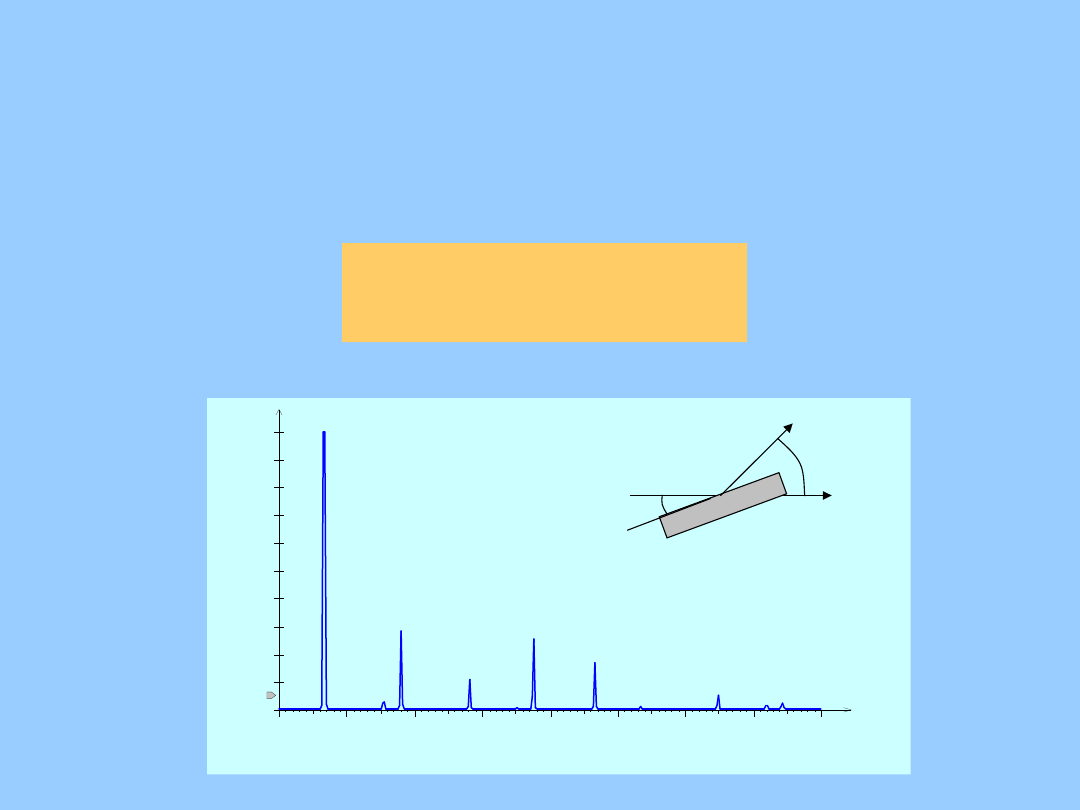
prawo Bragga

n = 2 d

hkl

sin 

Intensity (%)

 

2

40

50

60

70

80

90

100

110

120

0

10

20

30

40

50

60

70

80

90

100

o

(1.540562 Ĺ)
20°,60°]

B = 2.0 Ų

2



2,2,0

2,2,2

4,0,0

4,2,0

4,2,2

4,4,2

lampa Cu, =1.54562Ĺ



2

Fizyka współczesna

Promieniowanie Roentgena

Diagnostyka - prześwietlanie kości, płuc czy

zębów.
Rentgenoterapia - okresowe naświetlanie

promieniami X pozwala na zniszczenie chorej

tkanki. Wykorzystano w leczeniu schorzeń

skóry, a w szczególności do leczenia

nowotworów. Źródłem promieniowania są

izotopy promieniotwórcze stosowane w formie

tzw. bomb naświetleniowych - dużych próbek,

które emitując z zewnątrz promieniowanie

zabijają komórki rakowe.

Tomograf komputerowy – służy do naświetlania

chorych tkanek.

Fizyka współczesna

Promieniowanie Roentgena

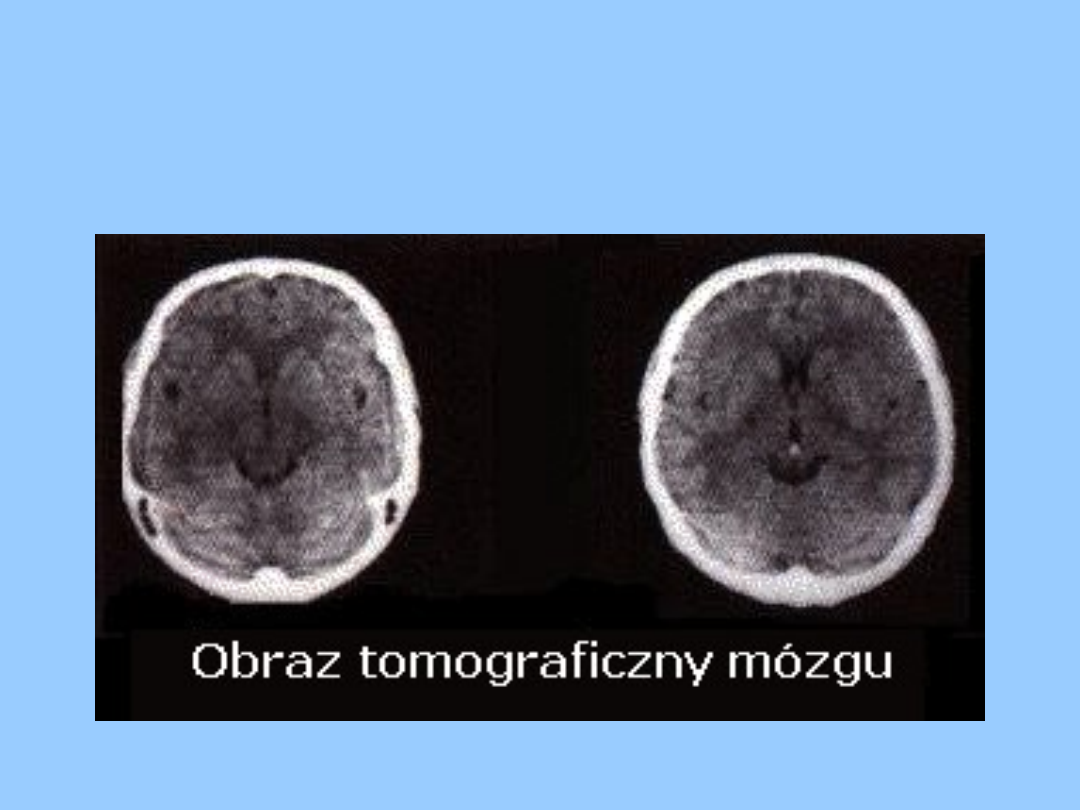
Fizyka współczesna

Promieniowanie Roentgena

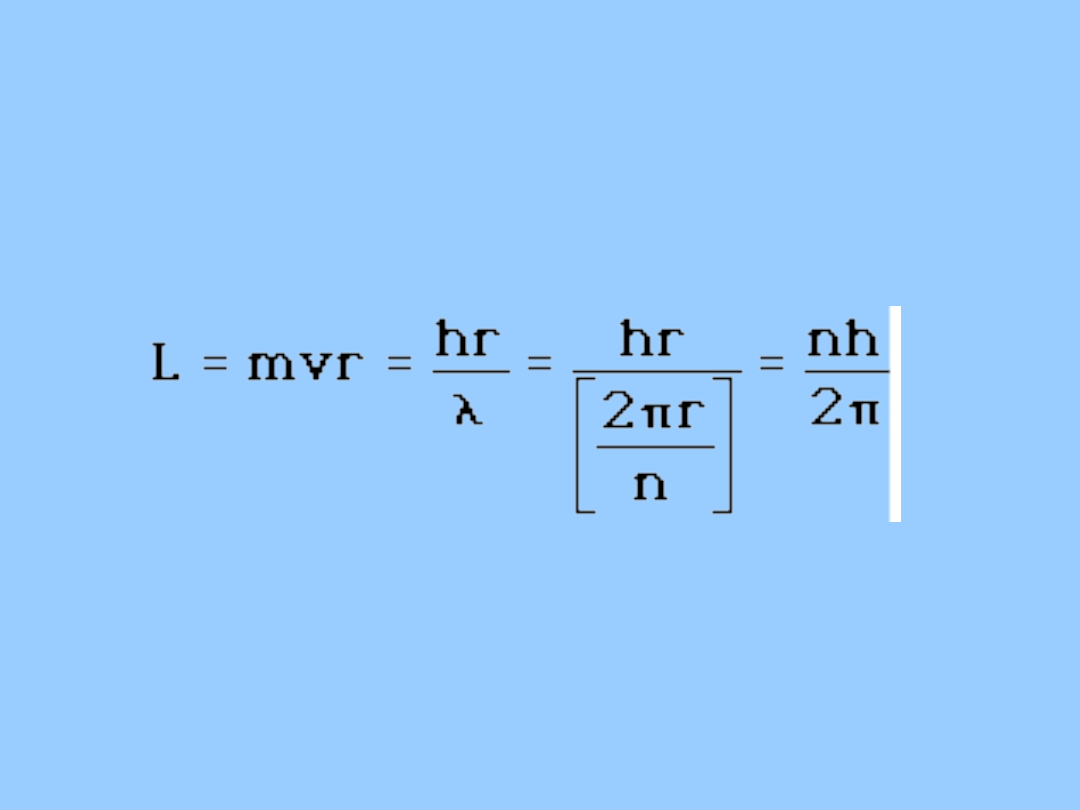
Fizyka współczesna

Model Bohra atomu wodoru

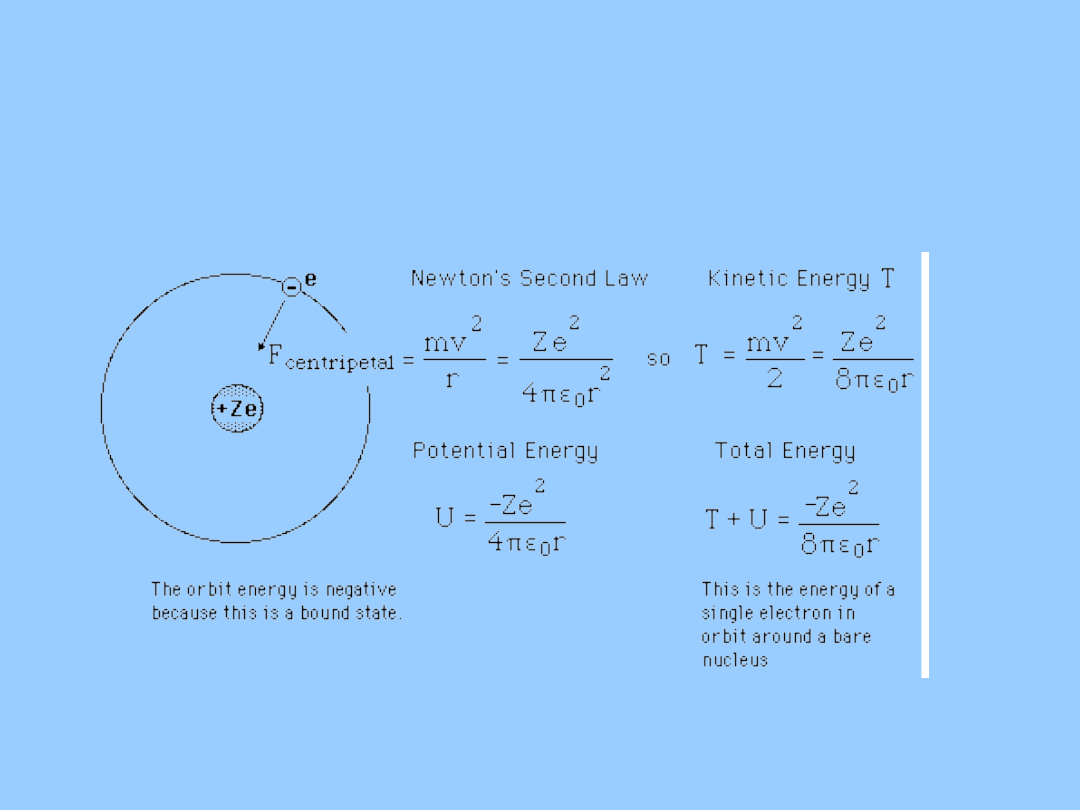
Fizyka współczesna

Model Bohra atomu wodoru

Fizyka współczesna

Model Bohra atomu wodoru

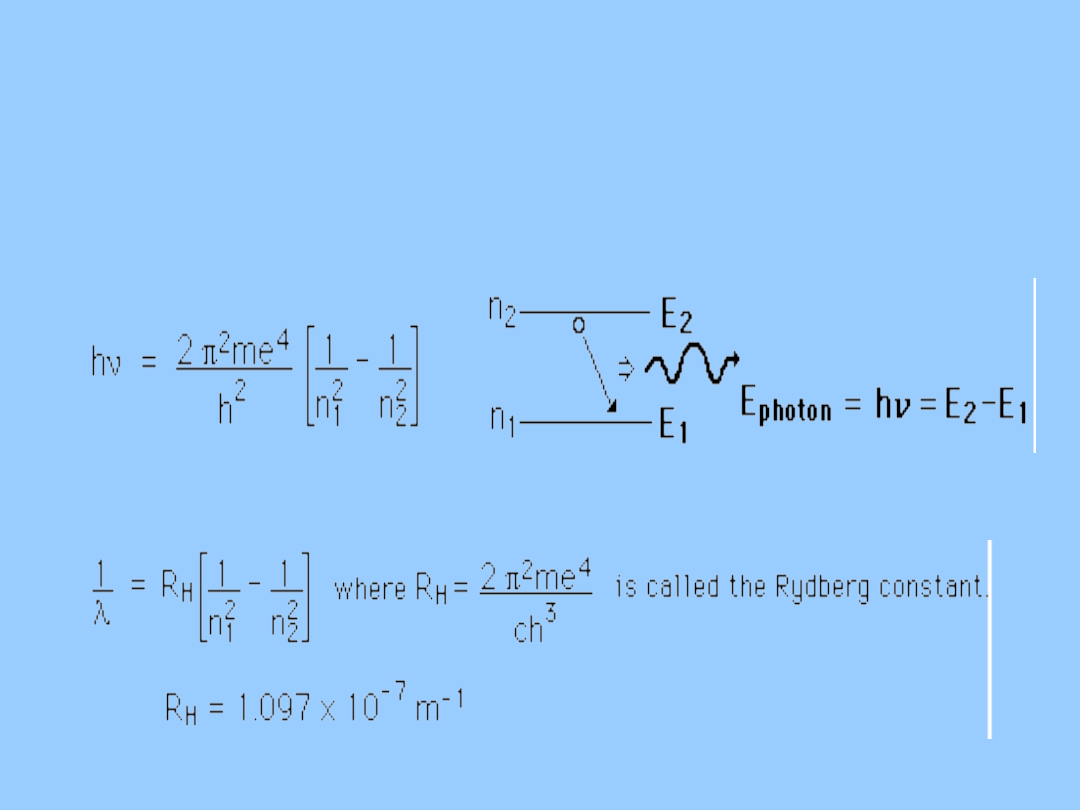
Fizyka współczesna

Model Bohra atomu wodoru

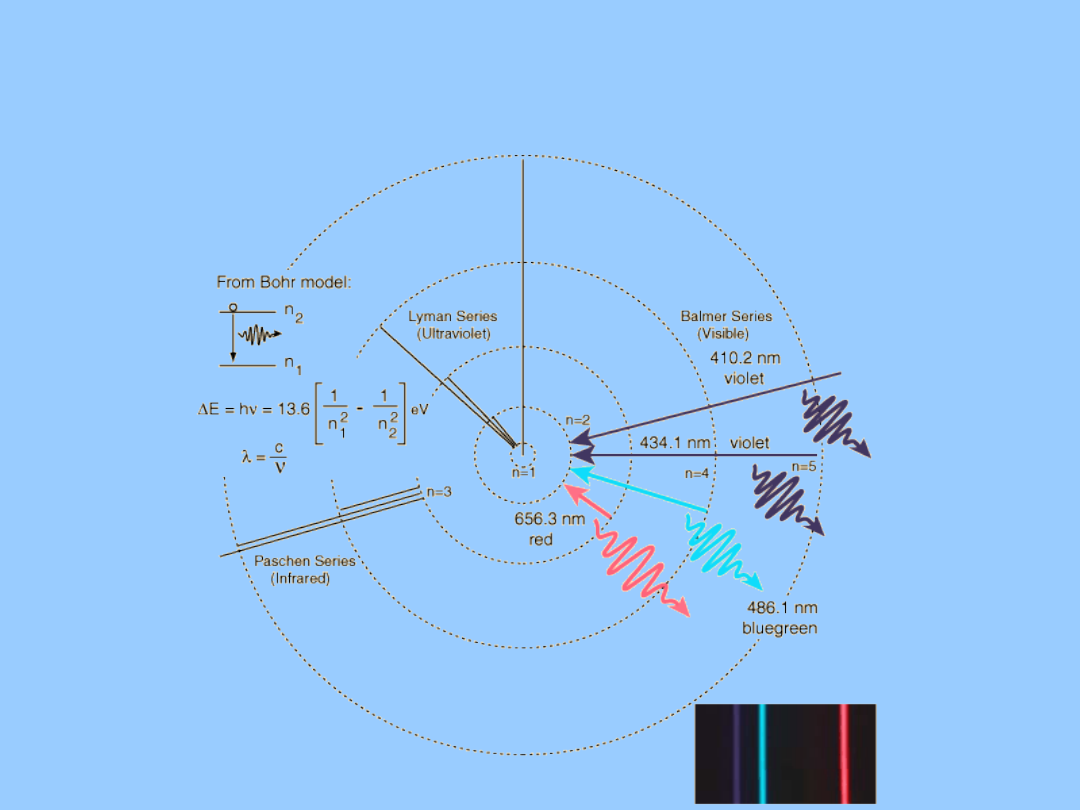
Fizyka współczesna

Model Bohra atomu wodoru

Fizyka współczesna

Model Bohra atomu wodoru

Widmo
helu

Widmo
azotu

1917 – teoretyczne podstawy maserów i laserów

opisane przez Alberta Einsteina – opis zjawiska

emisji spontanicznej i wymuszonej promieniowania

elektromagnetycznego.

1952 - Charles H. Townes zademonstrował możliwość

wyprodukowania i utrzymania większej liczby

atomów w stanach wzbudzonych niż w stanach

podstawowych. Urządzeniem produkującym i

utrzymującym był maser amoniakalny.

1960 – odkrycie przez T.H. Maimana lasera

rubinowego

w Malibu, Kalifornia.

Fizyka współczesna

Lasery

Laser

–

jest

to

skrót

od

angielskiego sformułowania

L

ight

A

mplification

by

S

timulated

E

mission of

R

adiation co oznacza

po polsku wzmocnienie światła
przez

wymuszoną

emisję

promieniowania

.

Fizyka współczesna

Lasery

Fizyka współczesna

Lasery

•

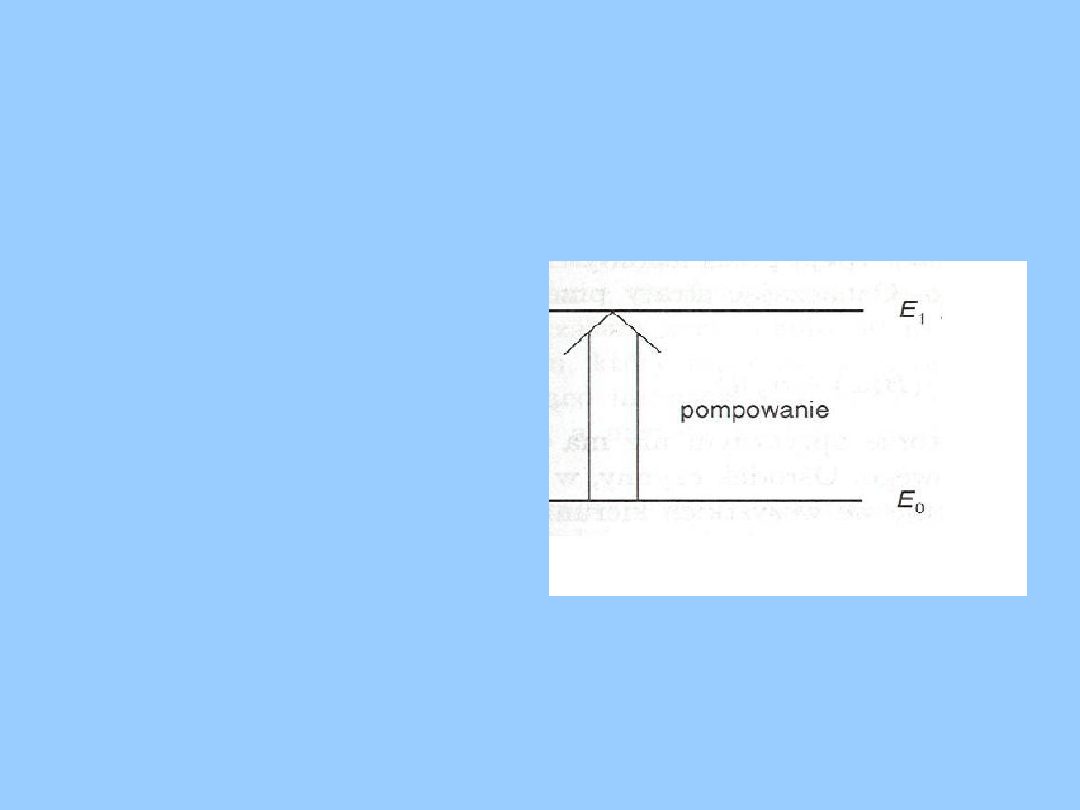
Do substancji czynnej,

którą może być ciecz, gaz

lub ciało stałe, znajdującej

się w stanie podstawowym

E

0

dostarczana jest energia

w postaci promieniowania

(proces

ten

nazywamy

pompowaniem).
•Poprzez absorpcję fotonów

elektrony zwiększają swoją

energię. Znajdują się na

poziomie energetycznym E

1

.

Fizyka współczesna

Lasery

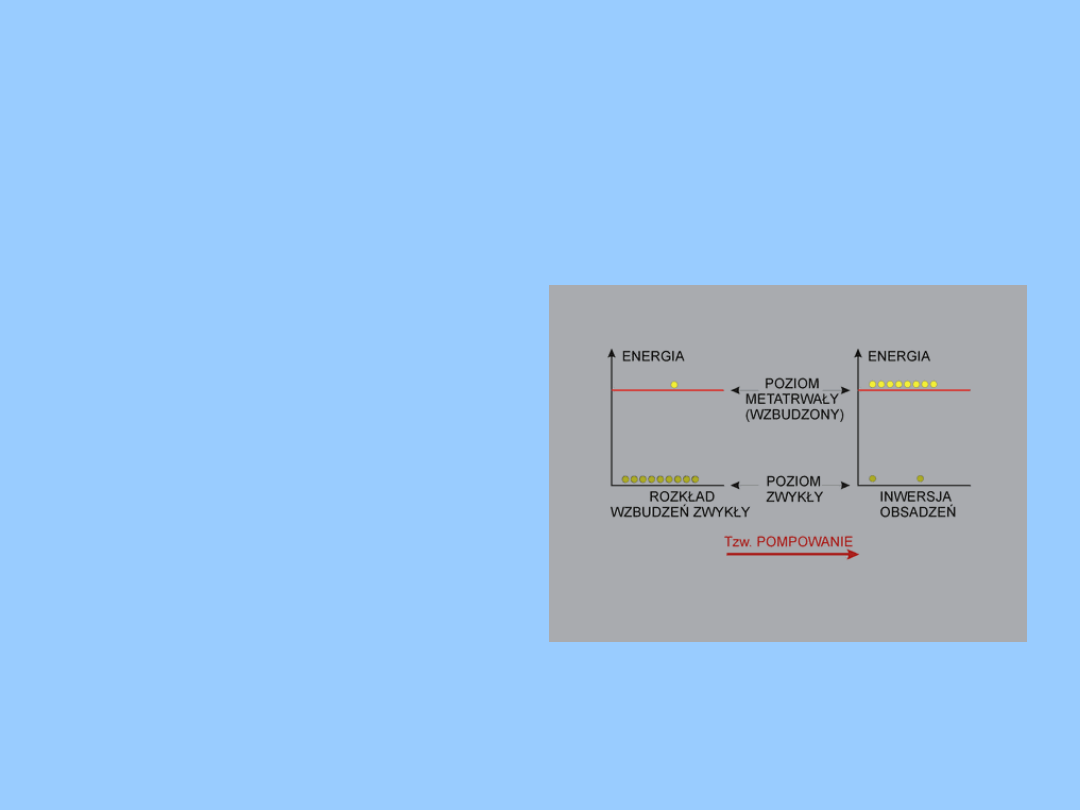
Kiedy

liczba

elektronów w stanie
wzbudzonym

(o

większej energii) jest
większa od liczby
elektronów w stanie
podstawowym mamy
do

czynienia

z

inwersją obsadzeń.

Fizyka współczesna

Lasery

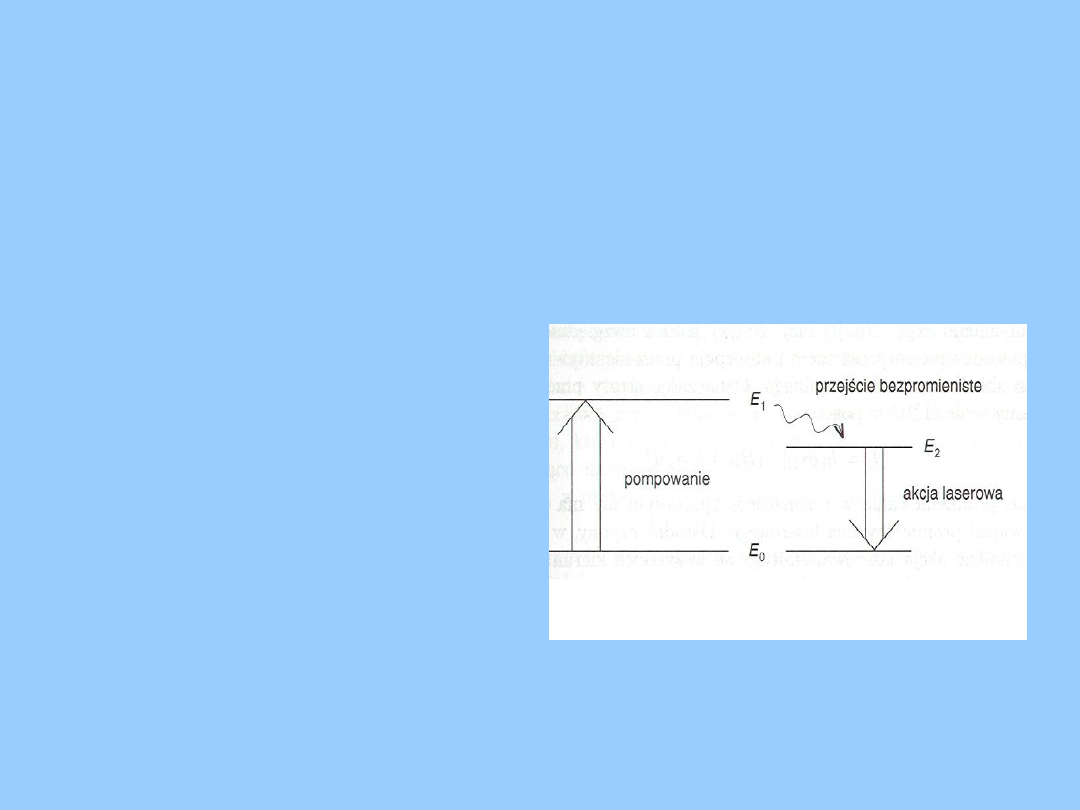
Czas

życia

elektronów w stanie

E

1

jest krótki (około

10

-9

s), wobec tego

następuje

bezpromieniste

przejście do stanu

energetycznego

E

2

(na którym długość

życia elektronów jest

rzędu mikro- a nawet

milisekund)

nazywanego stanem

metastabilnym.

Fizyka współczesna

Lasery

Emisja

wymuszona

(indukowana)

zachodzi jeżeli atom

znajduje się w stanie

wzbudzonym,

pod

wpływem padającego

na niego fotonu o

odpowiedniej,

rezonansowej energii

przechodzi na niższy

poziom energetyczny

emitując swój własny

foton.

Emitowany

foton jest spójny z

fotonem

wymuszającym.

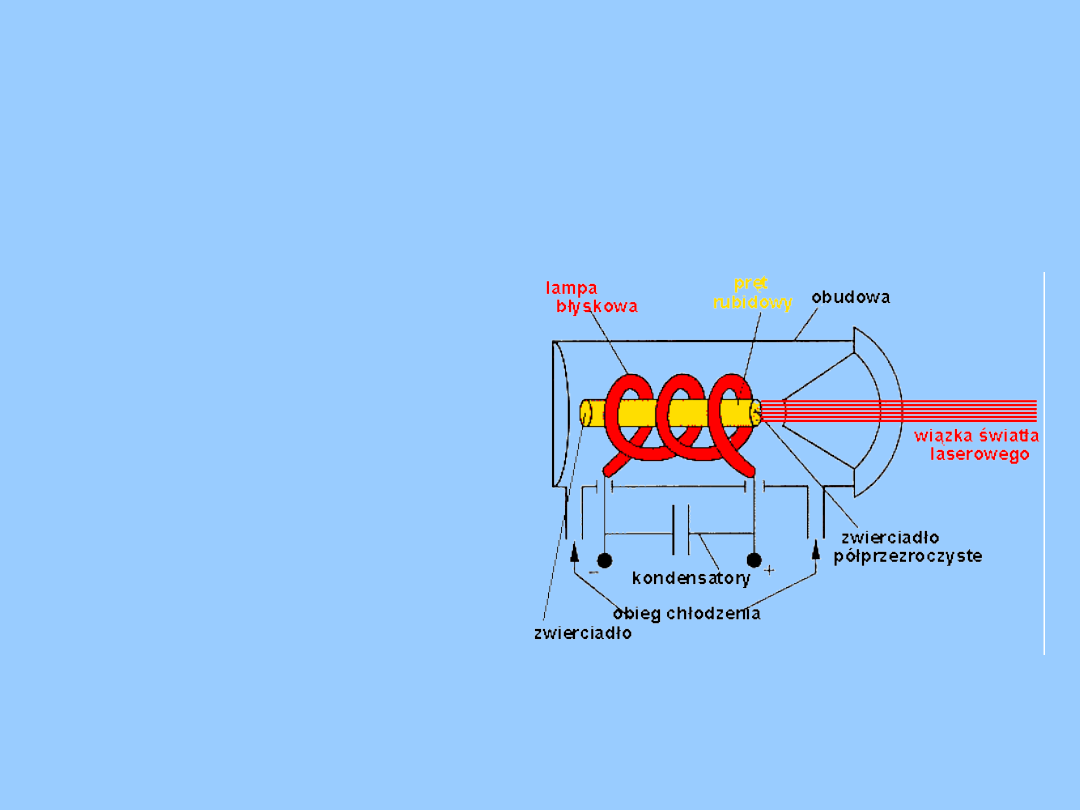
Fizyka współczesna

Lasery

Laser rubinowy –
substancją

czynną

jest kryształ korundu
Al

2

O

3

+ chrom lub

pręt

rubinowy,

pompowany
optycznie

przez

lampę

błyskową

(laser

impulsowy),

emituje

światło

czerwone,

rzadko

stosowany.

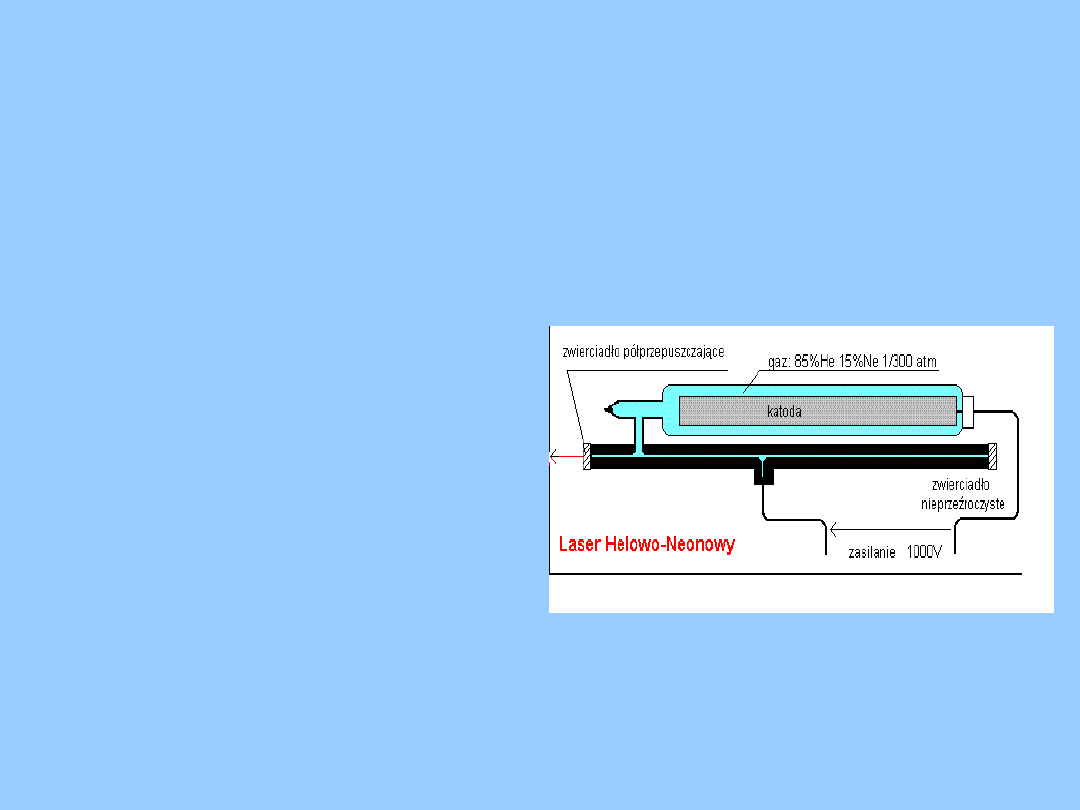
Fizyka współczesna

Lasery

Laser

gazowy

–

substancją czynną są
różne gazy np. hel i
neon,

krypton,

ksenon lub argon,
pompowane

są

elektrycznie
(wyładowania
elektryczne),
stosowany

w

badaniach

i

do

pompowania lasera
barwnikowego.

Fizyka współczesna

Lasery

Laser barwnikowy – substancją czynną

jest tzw. barwnik organiczny np.

rodamina, pompowanie za pomocą

laserów argonowych, kryptonowych

lub ksenonowych, charakteryzuje się

przestrajaną w szerokim zakresie

długością emitowanej fali świetlnej,

poprzez strojenie długości rezonatora

optycznego.

Fizyka współczesna

Lasery

Laser

półprzewodnikowy

–

ośrodkiem

czynnym jest półprzewodnik, pompowanie
jest

wykonane

przez

wstrzykiwanie

ładunków przez złącze, jego zaletami jest
niska cena produkcji, małe rozmiary co za
tym idzie mały pobór mocy, wysoka
wytrzymałość mechaniczna, zastosowanie:
- o małej mocy – wskaźniki laserowe,
drukarki,

nagrywarki

CD/DVD,

telekomunikacja
- o dużej mocy – w przemyśle do cięcia i
spawania

Fizyka współczesna

Lasery

Laser

wykorzystujemy do

odczytywania danych

lub do ich zapisu. W

CD-Romach

mamy

lasery jedynie do

odczytu.

W

nagrywarkach

występują

lasery

odczytująco-

zapisujące.

Fizyka współczesna

Lasery

Technologia Blu-ray -

nowy

format

zapisu

magnetycznego,

który

pozwala zapisać 25 GB

informacji.

W

przeciwieństwie

do

dzisiejszych nagrywarek

laser nie jest czerwony,

lecz

niebieski.

Podstawową

różnicą

pomiędzy tymi laserami

jest

długość

fali

-

czerwony

ma

650

nanometrów,

niebieski

405.

Pozwala

na

dokładniejsze

zapisywanie danych.

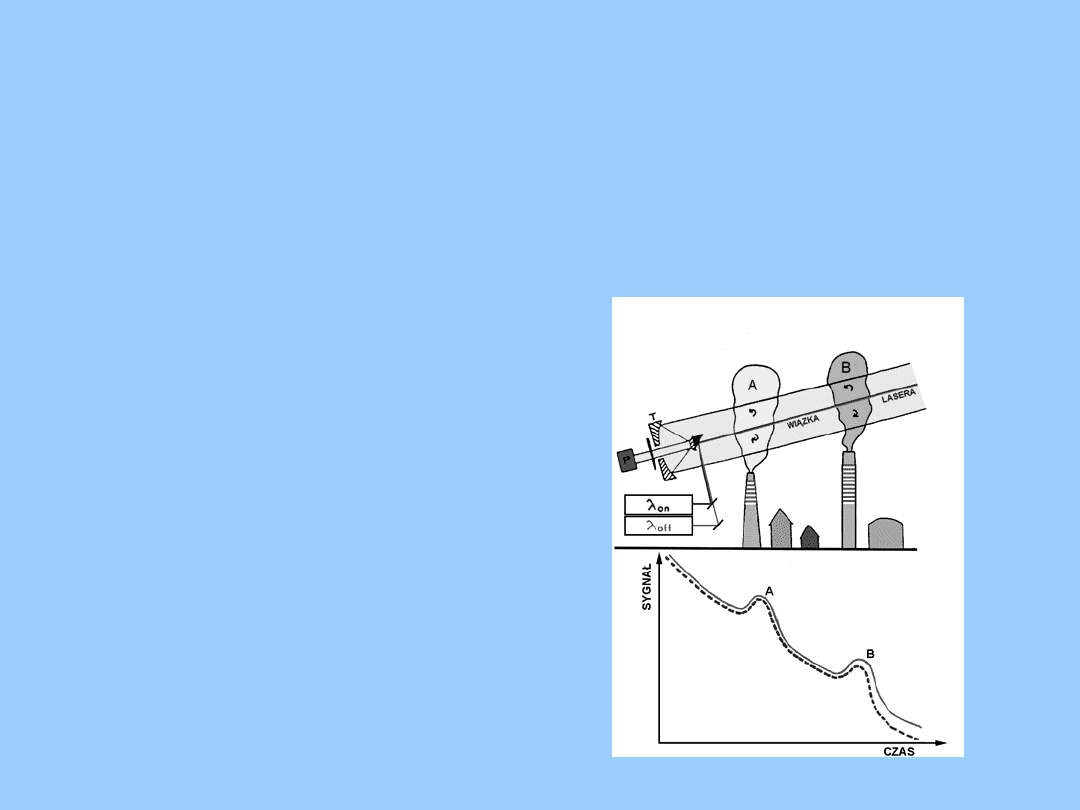
Fizyka współczesna

Lasery

LiDAR czyli Light Detection and

LiDAR czyli Light Detection and

Ranging

Ranging

Laser

impulsowy

wysyła

krótkie w czasie ‘’paczki’’

światła, które są rozpraszane

wzdłuż drogi, również do

tyłu. To rozproszone światło

jest przechwytywane przez

teleskop. Pomiar czasu od

wysłania

wiązki

i

przechwycenia

jej

przez

teleskop

pozwala

na

określenie gdzie znajduje się

element

rozpraszający

w

przestrzeni.

Fizyka współczesna

Równanie Schrödingera

Fale materii – Hipoteza de Broglie’a

Fizyka współczesna

Równanie Schrödingera

Fale materii – Hipoteza de Broglie’a

Korpuskularno-falowe charakter metrii

Tak samo jak z fotonem stowarzyszona jest pewna fala która
rządzi jego ruchem tak i cząstce materialnej przypisana jest
pewna fala materii.

Energia dowolnego obiektu fizycznego jest związana z
częstotliwością ν pewnej fali stowarzyszonej

E = hν

Pęd obiektu związany jest z długością tej fali

p = h/λ

Fizyka współczesna

Równanie Schrödingera

• Określa prawa ruchu falowego

opisującego zachowanie się cząstek
w dowolnym układzie
mikroskopowym

• Stanowi uogólnienie hipotezy de

Broglie’a

Fizyka współczesna

Równanie Schrödingera

•

Własności kwantowego równania falowego:

1.

Równanie musi być zgodne z postulatami de Broglie’a i Einsteina

i

2.

Równanie musi być zgodne ze związkiem

3.

Równanie musi być liniowe względem Ψ(x,t).

4.

Energia potencjalna V jest funkcja x oraz t. W przypadeku

szczególnym, w którym V(x,t)=V

0

tym samym

Mamy wówczas do czynienia z cząstka swobodna o stałych

λ i v

możemy przypuszczać ze w tym przypadku rozwiązanie ma postać

sinusoidalnej fali bierzącej

h

E





p

h





V

m

p

E





2

2

const

p

dx

t

x

dV

F









,

0

)

,

(

)

sin(

)

(

2

sin

)

,

(

t

kx

vt

x

t

x

















Fizyka współczesna

Równanie Schrödingera

Rozwiązanie:

Zgadujemy rozwiązanie w

następującej postaci

Jest to równanie

Schrödingera











)

,

(

2

2

2

t

x

V

m

k

)

sin(

)

cos(

)

,

(

t

kx

t

kx

t

x

















)

,

(

)

,

(

)

,

(

)

,

(

2

2

2

t

x

dt

d

i

t

x

t

x

V

t

x

dx

d

m























)

,

(

)

,

(

)

,

(

)

,

(

2

2

t

x

dt

d

t

x

t

x

V

t

x

dx

d















Fizyka współczesna

Równanie Schrödingera

• Jedynym rozwiązaniem równania

Schrodingera jest zespolona funkcja falowa

– znaczy to że funkcja falowa nie ma

żadnego fizycznego znaczenia!

• Podstawowy związek pomiędzy własnościami

funkcji falowej Ψ(x,t) a zachowaniem
związanej z nią cząstki wyraża się za
pośrednictwem gęstości
prawdopodobieństwa

P(x,t) = Ψ*(x,t)

Ψ(x,t)

Fizyka współczesna

Równanie Schrödingera

• Jeżeli w chwili t dokonamy pomiaru

mającego na celu ustalenie położenia
cząstki opisywanej funkcji falowej

Ψ(x,t)

to prawdopodobieństwo

P(x,t)dx

tego że wynik pomiaru

wykaże położenie cząstki w przedziale
pomiędzy x a x+dx wynosi

Ψ*(x,t)

Ψ(x,t)

Fizyka współczesna

Równanie Schrödingera

• Dzięki funkcji P(x,t) możemy wyznaczać wartości

średnie szukanych wielkości.











dx

t

x

xP

x

)

,

(















dx

t

x

x

t

x

x

)

,

(

)

,

(

*

dx

t

x

p

t

x

p

)

,

(

)

,

(

*















x

i

p







 

gdzi

e

Fizyka współczesna

Równanie Schrödingera



E

e

x

t

x

t

i















,

)

(

)

,

(

)

(

)

(

)

(

)

(

2

2

2

x

E

x

x

V

dx

x

d

m















iKx

iKx

Be

Ae

x







)

(



• Równanie Schrödingera niezależne od

czasu

– Jeśli Energia potencjalna nie zależy od czasu

to

• ψ(x)

która określa

zależność przestrzenna

Ψ(x,t)

jest rozwiązaniem

równania

Fizyka współczesna

Równanie Schrödingera

• Przy zmieniającym się potencjale tak wolno że

praktycznie o stałej wartości na obszarze rzędu

długości fali de Broglie’a cząstki. Z równań

Schrödingera wiążącego zmianę prędkości paczki

falowej ze zmianą potencjału.











 















m

x

V

dx

d

dt

x

d

dt

d

)

(

m

x

F

m

dt

x

d

)

(

dx

dV(x)

2

2







• Zasada Dynamiki Newtona są szczególnym

przypadkiem równań Schrödingera

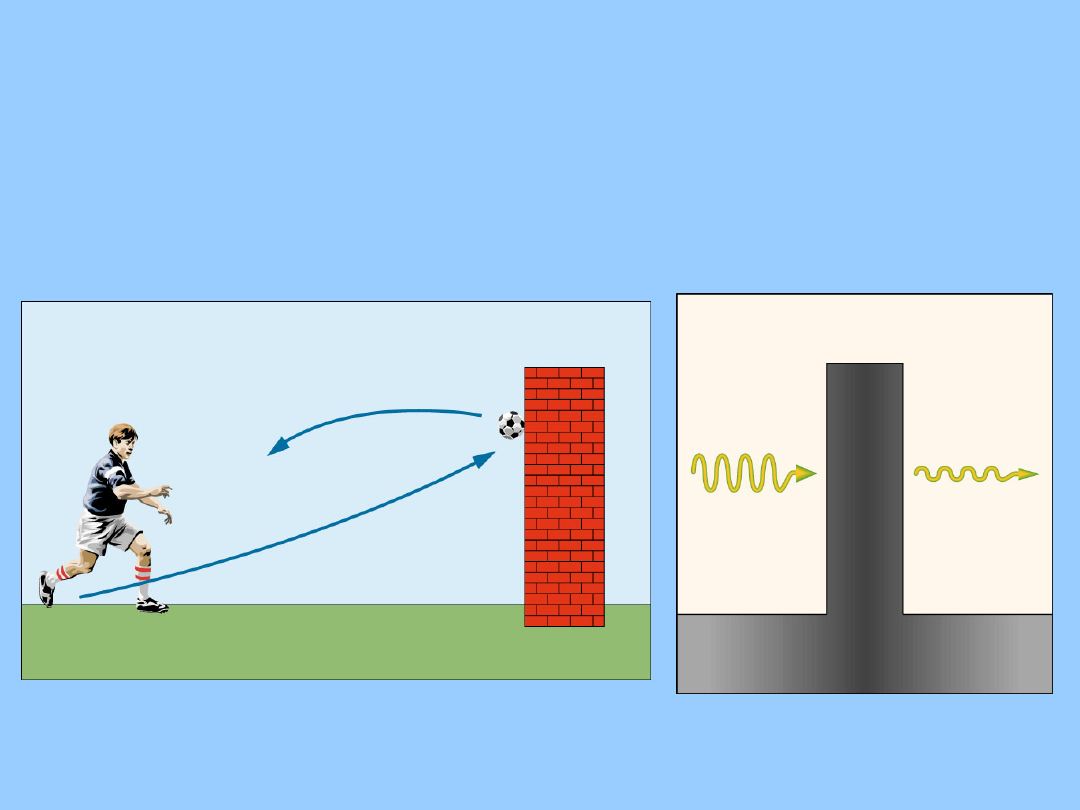
Fizyka współczesna

Równanie Schrödingera

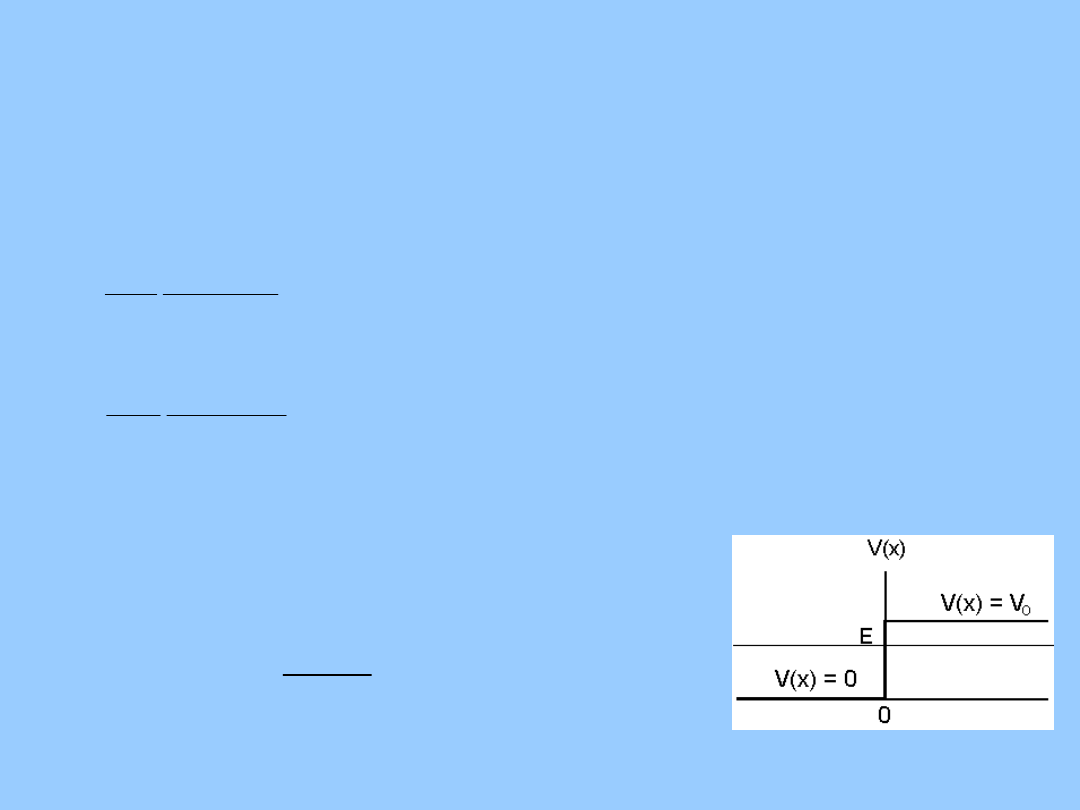
Fizyka współczesna

Równanie Schrödingera

0

),

(

)

(

2

2

2







x

x

E

dx

x

d

m







0

),

(

)

(

)

(

2

0

2

2

2









x

x

E

x

V

dx

x

d

m









x

ik

x

ik

Be

Ae

x

1

1

)

(











1

*

*





A

A

B

B

R

Dla x<0 pierwszy człon wiąże się z padaniem
cząstki na próg potencjału , a drugi z odbiciem od
niego. Prawdopodobieństwo tego że cząstka
zostanie odbita zależy od współczynnika odbicia R

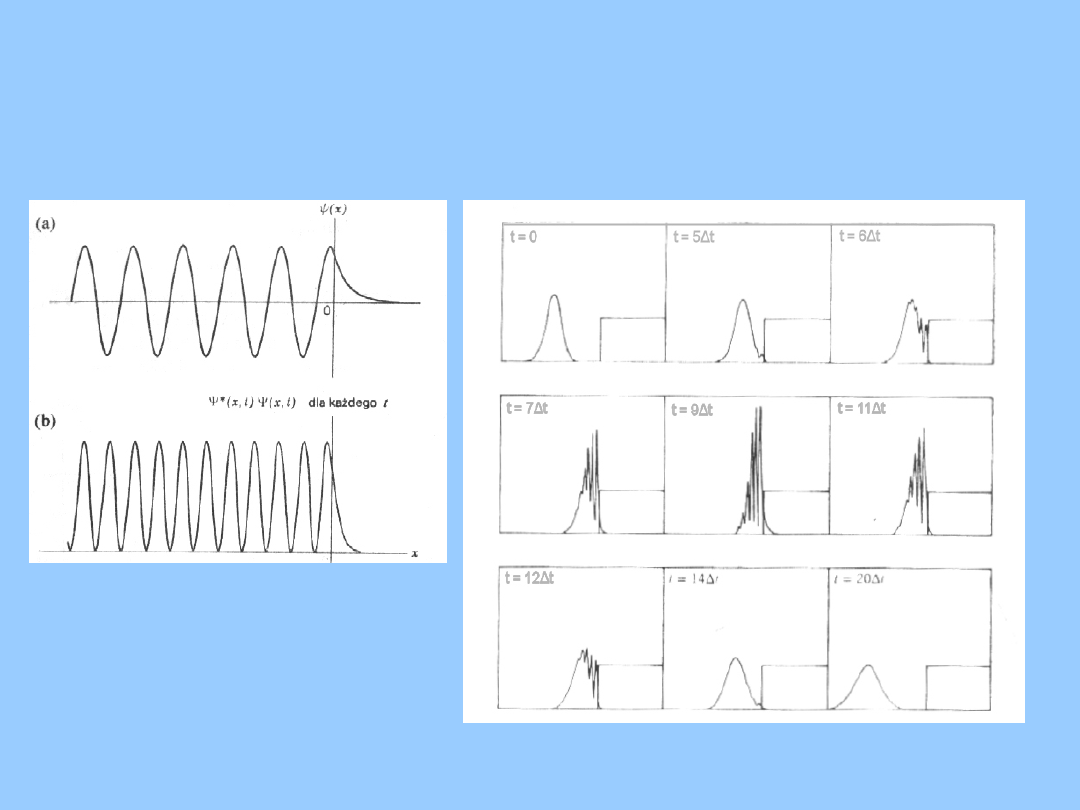
Fizyka współczesna

Równanie Schrödingera

x

k

De

D

2

2

*

*









Jednak dla x>0 gęstość
prawdopodobieństwa wynosi

Zjawisko wnikania w obszar klasycznie wzbroniony

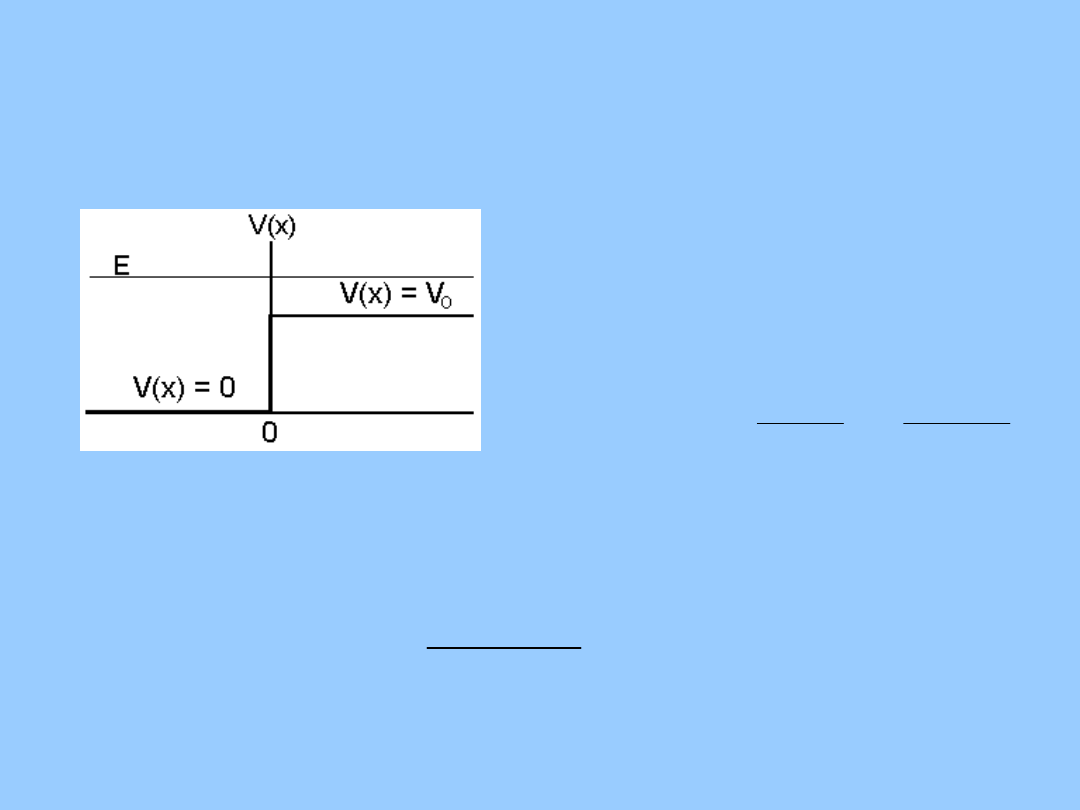
Fizyka współczesna

Równanie Schrödingera

0

,

)

(

1

1









x

Be

Ae

x

x

ik

x

ik



0

,

)

(

2

2









x

De

Ce

x

x

ik

x

ik



2

2

1

2

1

*

*





















k

k

k

k

A

A

B

B

R

R>0 czyli istnieje prawdopodobieństwo
tego że cząstka zostanie odbita,
Niezależnie od którego kierunku
nadjedzie.





2

2

1

2

1

4

1

k

k

k

k

R

T









T jest współczynnikiem
przejścia

Fizyka współczesna

Równanie Schrödingera

r

Ze

r

V

0

2

4

2

)

(









a

E

V

m

a

k

e

e

T











0

2

2

2

2

2



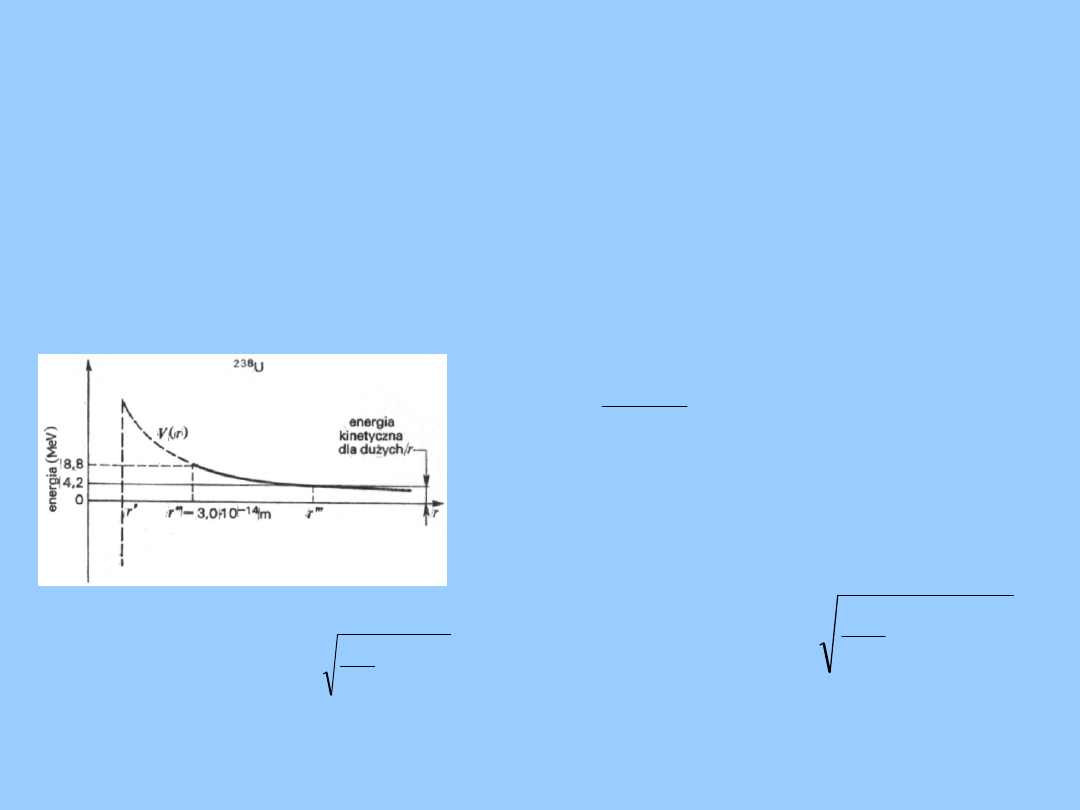
Historycznie pierwsze zastosowanie kwantowej teorii
przenikania przez barierę wiąże się z wyjaśnieniem długo
istniejącego paradoksu dotyczącego emisji cząstki

α

w procesie

promieniotwórczego rozpadu jąder

- Potencjał
kulombowski

Energia cząstki

α

emitowana w

czasie rozpadu radioaktywnego
wynosi 4,2 MeV

W roku 1928 obliczono współczynnik przejścia T

ogólniej





dr

E

r

V

m

r

r

e

T









'''

'

2

)

(

2

2



Fizyka współczesna

Równanie Schrödingera

a

x

Ge

Fe

x

x

k

x

k











0

,

)

(

2

2



0

,

)

(

1

1









x

Be

Ae

x

x

ik

x

ik



0

,

,

)

(

1

1











D

a

x

De

Ce

x

x

ik

x

ik



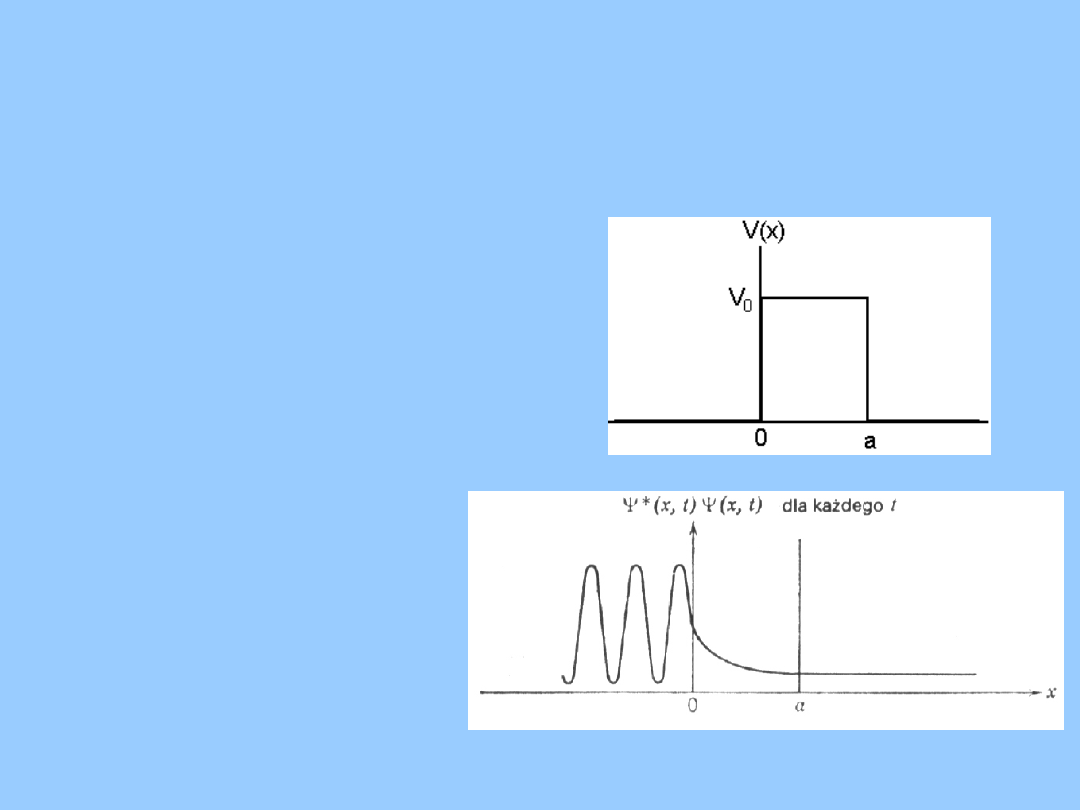
Dla E<V

0

w obszarze x>0 funkcja

falowa jest czystą falą bieżącą
wiec gęstość P(x,t) jest stała.
Natomiast dla x<0 jest prawie falą
stojącą ,amplituda fali odbitej jest
mniejsza od padającej. Dla 0<x<a
jest w zasadzie falą stojącą o
wykładniczo malejącej amplitudzie

Fizyka współczesna

Równanie Schrödingera

1

,

1

16

1

4

sinh

1

*

*

2

2

0

0

1

0

0

2

2

2









































































a

k

e

V

E

V

E

T

V

E

V

E

a

k

A

A

C

C

T

a

k

Z powyższego wzoru wynika , że cząstka o masie m i energii
całkowitej E padając na barierę o wysokości V

0

>E i

skończonej szerokości a, ma pewne prawdopodobieństwo T
przeniknięcia przez barierę i pojawienia się po jej drogiej
stronie.

Fizyka współczesna

Równanie Schrödingera

Dla E>V

0

funkcja własna jest funkcją oscylującą we

wszystkich trzech obszarach, ale w obszarze bariery
ma ona większą długość fali.

1

0

0

3

2

1

4

sin

1

















































V

E

V

E

a

k

T

Dla

k

3

a = π , 2π ,3π,…

Jest to warunek

na to że szerokość bariery a jest
całkowitą lub połówkową wielokrotnością
długością fali de Broglie’a

λ

3

=2π/k

3

cząstki w tym obszarze.

Wówczas współczynnik przejścia jest równy 1 jest to
wynikiem interferencji między odbiciem w x=0 a x=a.

(Efekt Ramsauera)

Fizyka współczesna

Scaningowy mikroskop tunelowy

Idea tunelowania, wykorzystana w skaningowym mikroskopie tunelowym, narodziła się w latach
dwudziestych naszego stulecia wraz z rozwojem mechaniki kwantowej

W 1958 roku japoński fizyk pracujący w Stanach Zjednoczonych, Leo Esaki, zaobserwował je w
silnie domieszkowanym złączu półprzewodnikowym typu p-n.Efekt ten wykorzystany został w
działaniu diody tunelowej, pozwalającej w tym czasie konstruować oscylatory i wiele innych
szeroko stosowanych układów elektronicznych.

Dwa lata później amerykański fizyk norweskiego pochodzenia, Ivar Giaever, zademonstrował
tunelowanie elektronów między dwoma paskami metalicznymi rozdzielonymi cienką przekładką
izolatora. Jako barierę tunelową wykorzystał w tym eksperymencie warstewkę tlenku aluminium
o grubości około 2 nm. Doświadcznie to potwierdziło teorie nadprzewodnictwa

W 1965 roku ten sam eksperymentator zaobserwował efekt Josephsona polegający na
tunelowaniu par elektronów między dwoma nadprzewodzącymi elektrodami

Wreszcie nadszedł 1979 rok. W połowie stycznia Gerd Binnig i Heinrich Rohrer przedstawili
pierwszy patent odsłaniający tajemnicę skaningowego mikroskopu tunelowego.

W 1982 roku opublikowano pierwsze wyniki pomiarów pokazujących ułożenie atomów na
powierzchni CaIrSn4, Au i Si(111).

Fizyka współczesna

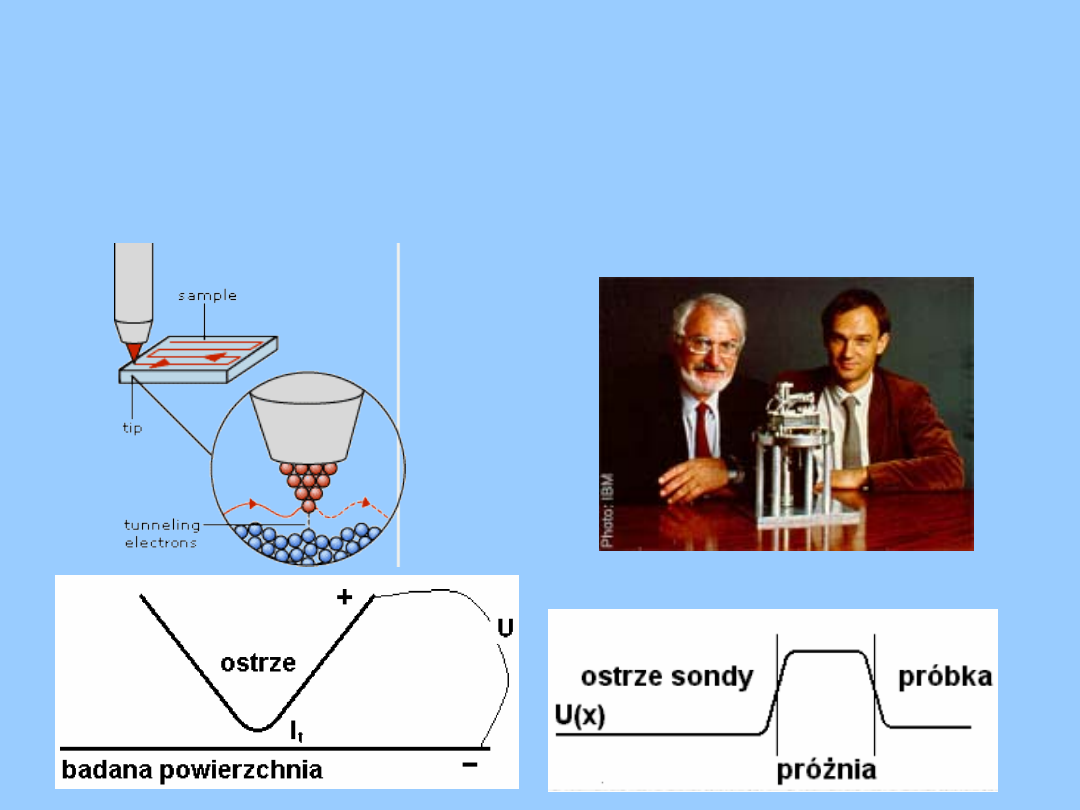
Scaningowy mikroskop tunelowy

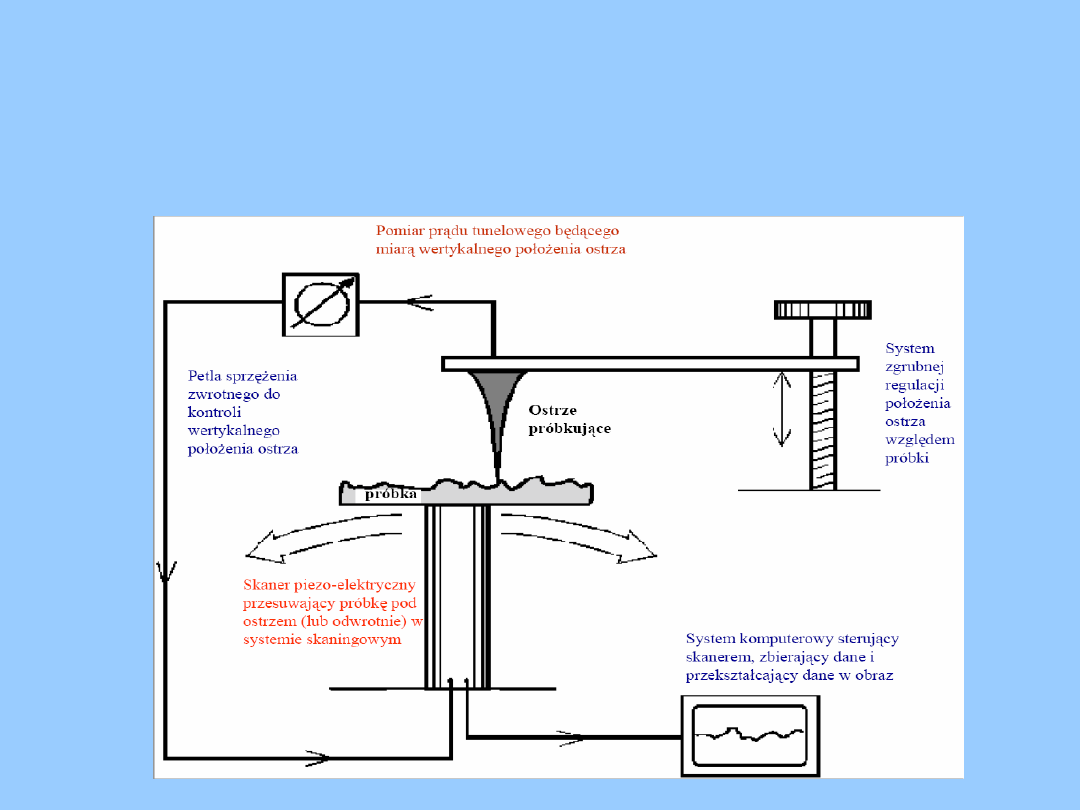
Zasada działania:

Bariera potencjału dla elektronów

Heinrich Rohrer i Gerd Binnig
The Nobel Prize in Physics, 1986

Fizyka współczesna

Scaningowy mikroskop tunelowy

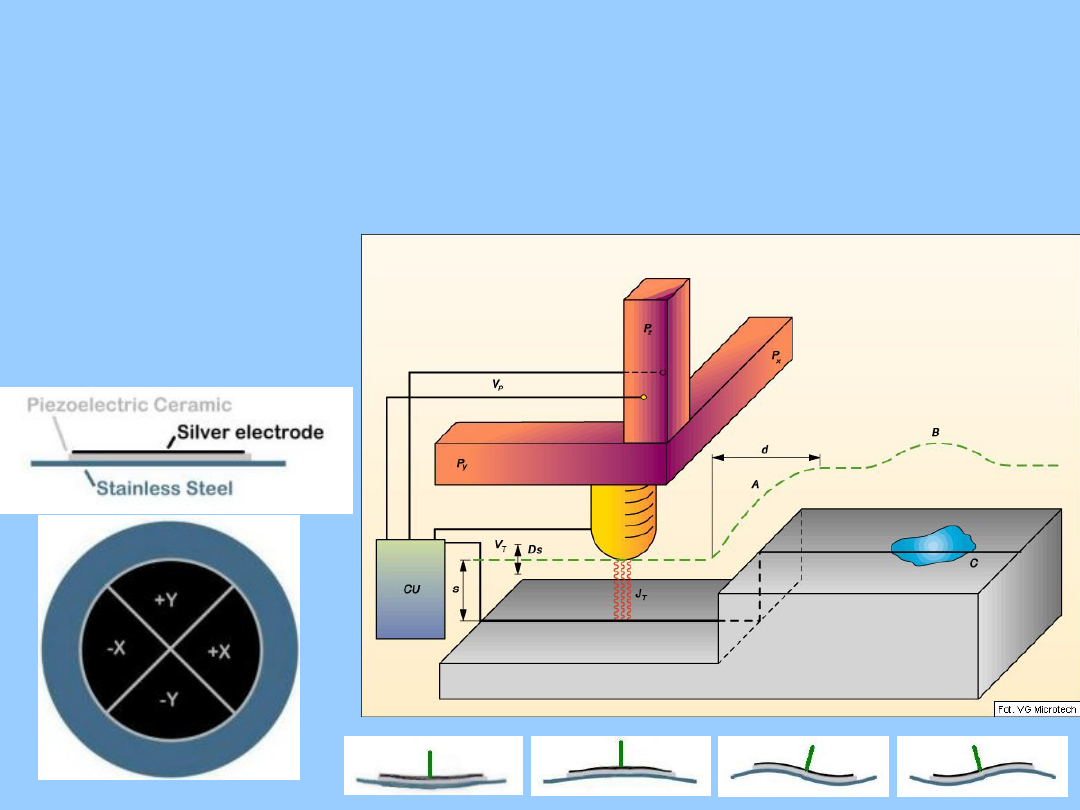
W czasie pracy igła mikroskopu znajduje się 0,5-1 nm od powierzchni badanej

próbki.

Jej precyzyjny ruch we

wszystkich trzech kierunkach

umożliwiają piezoelementy PX,

PY, PZ (materiały ceramiczne

zmieniające swe rozmiary pod

wpływem pola elektrycznego),

do których jest przymocowana.

Fizyka współczesna

Scaningowy mikroskop tunelowy

Fizyka współczesna

Scaningowy mikroskop tunelowy

Sercem przyrządu jest igła

Fizyka współczesna

Scaningowy mikroskop tunelowy

1 – uchwyt ostrza
2 – układ do próbek i układ przesuwu
3 – amortyzator tłumiący drgania

Fizyka współczesna

Scaningowy mikroskop tunelowy

Rekonstrukcja powierzchni krzemu
o orientacji (111).
Rozmiar analizowanego obszaru
wynosi 30 x 21 nm

2

. Żółte kółka są

obrazami atomów krzemu
ulokowanych w najwyższej
warstwie. Każda komórka
elementarna o kształcie rombu
zawiera 12 takich atomów

Fizyka współczesna

Scaningowy mikroskop tunelowy

Powierzchnia kryształu
NaCl. Amplituda rzeźby
powierzchni ma około
0,1nm.

Fizyka współczesna

Scaningowy mikroskop tunelowy

Mistrzowskie zdolności manipulacji pojedynczymi atomami pokazał
amerykański fizyk Don Eigler. Jego dwa spektakularne
eksperymenty, przeprowadzono w układzie ultrawysokiej próżni w
temperaturze 4 K. Wykorzystano w nich oddziaływania
występujące pomiędzy atomami igły mikroskopu i próbki (siły
elektrostatyczne i van der Waalsa).

Atomy ksenonu zostały osadzone w sposób przypadkowy przez
naparowanie na powierzchni niklu. Następnie skanowanie igły
zatrzymywano w chwili, gdy znajdowała się ona dokładnie nad
atomem ksenonu. Następnie siły oddziaływania powiększano,
zmniejszając dystans dzielący atom i igłę. W trzecim kroku
przesuwano igłę równolegle do powierzchni podłoża niklowego, a
atom ksenonu "wędrował" po niej w ślad za igłą. Gdy przesuwany
obiekt osiągał żądaną pozycję, igłę ostrożnie oddalano.

Igła jako głowica czytająca i zapisująca

Fizyka współczesna

Scaningowy mikroskop tunelowy

Efektem 18-godzinnego doświadczenia był znak firmowy
laboratorium, w którym eksperyment został wykonany. Napis IBM
składał się z 35 atomów. Rozmiar liter wynosił 5 nm!

Fizyka współczesna

Scaningowy mikroskop tunelowy

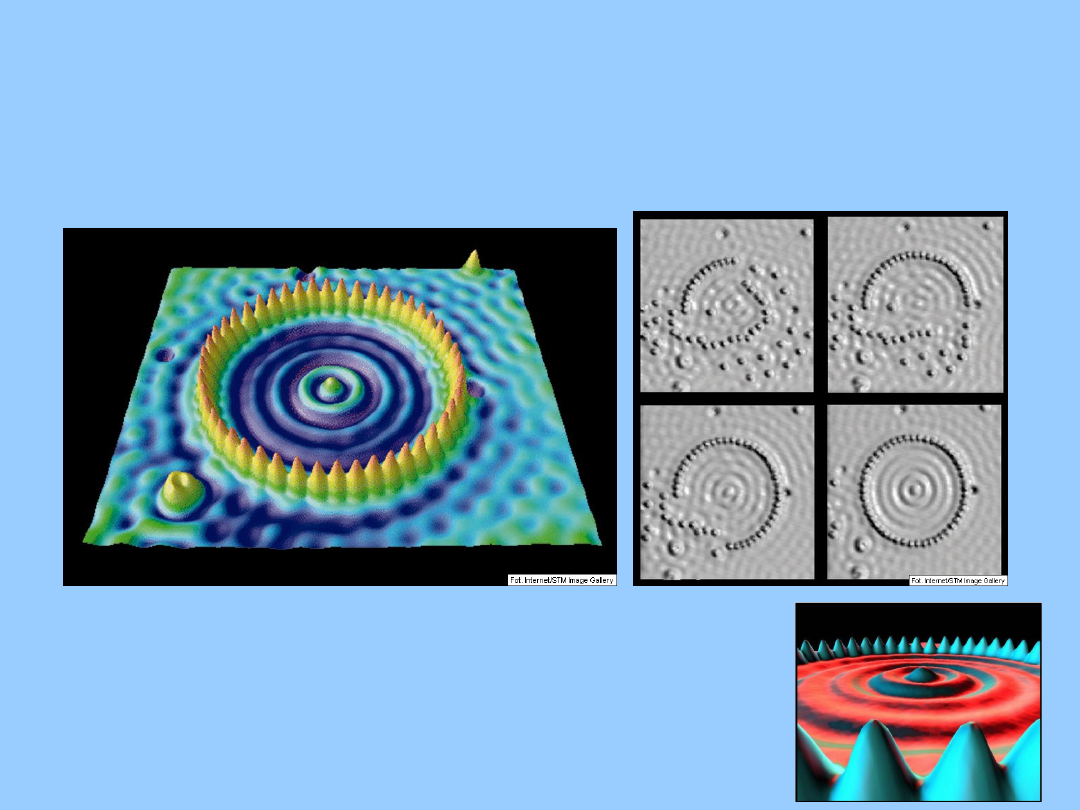
48 atomów żelaza na miedzi , fale w środku
pochodzą od interferencji falowej elektronów

Fizyka współczesna

Scaningowy mikroskop tunelowy

The original STM image
of a logic three-input
sorter. A sorter is a small
part of the CPU in a
computer.

Fizyka współczesna

Scaningowy mikroskop tunelowy

A stadium shaped
corral made by iron
atoms on a copper
surface.

Fizyka współczesna

Scaningowy mikroskop tunelowy

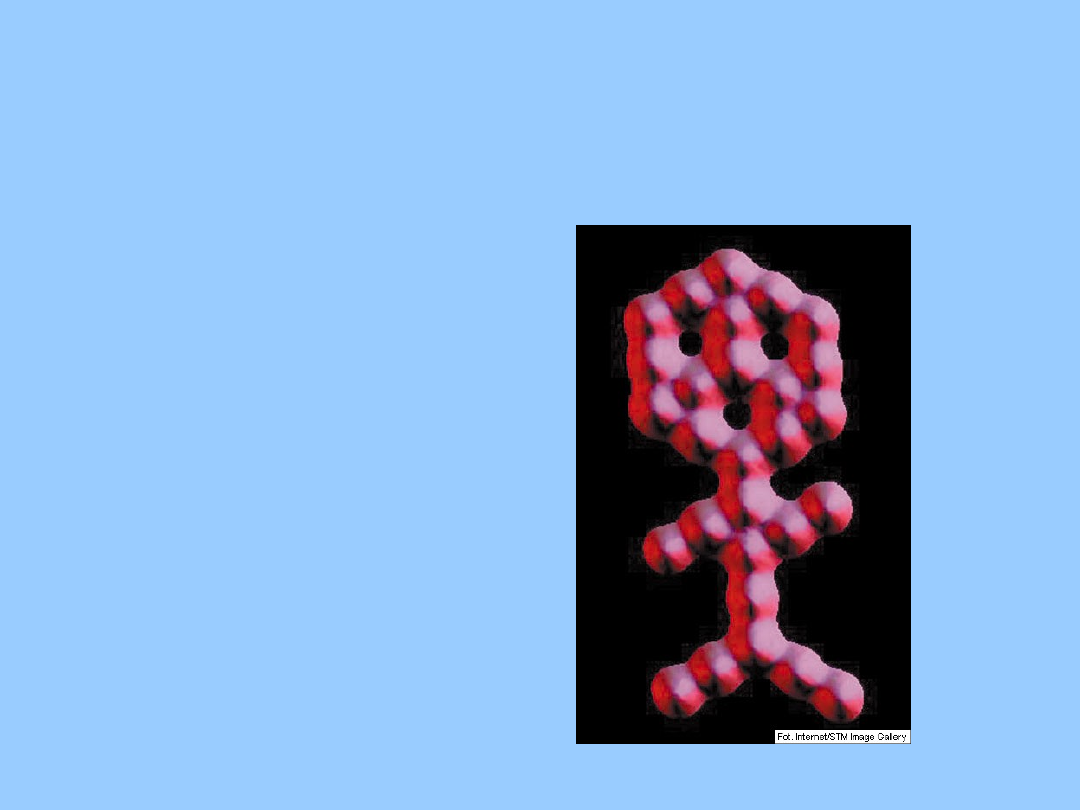
Najmniejszy człowiek świata
Postać zbudowana z
cząsteczek tlenku węgla
osadzonych na powierzchni
platyny

W przygotowaniu tego wykładu
korzystałem z prezentacji
wykonanych przez studentów IV roku
GiG oraz II roku Informatyki
Stosowanej WFiIS w ramach
prowadzonych przeze mnie zajęć
seminaryjnych z „Fizyki
Współczesnej”.

Wiesław Marek Woch.