1

Istotą procesów dyfuzyjno-cieplnych jest wymiana masy

i ciepła między stykającymi się fazami.

Intensywność tej wymiany zależy m. in. od stopnia

odchylenia stanu okłady od tzw. stanu równowagi
międzyfazowej.

Najczęściej przyjmuje się, że układ znajduje się w stanie

równowagi międzyfazowej wówczas, gdy efektywność wymiany
ciepła i masy między stykającymi się fazami jest równa zero.

Zgodnie z definicją termodynamiczną stan równowagi

osiągany jest wówczas, gdy potencjał termodynamiczny układu
jest minimalny.

2

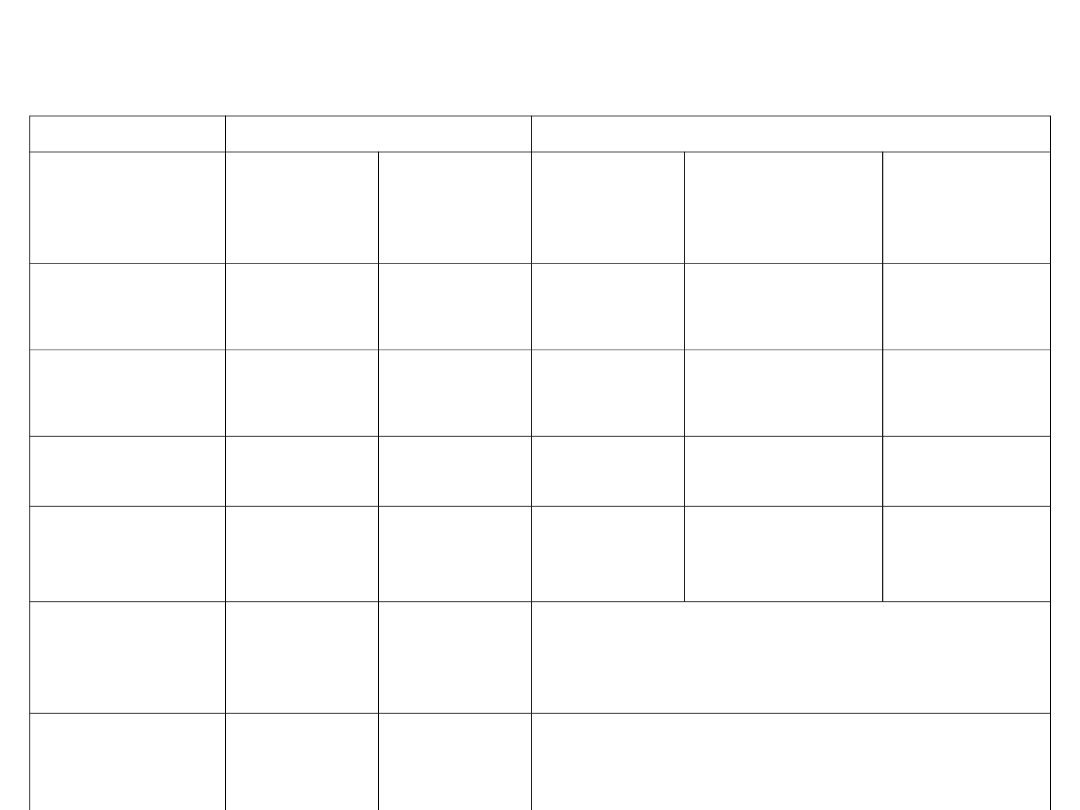
Tab. 1. Definicje stężeń

Stężenia uogólnienie: Z – faza gazowa, S – faza ciekła

Nazwa

Oznaczenie

Definicja

układ dwu-

składniko

wy

układ

wielo-

składniko

wy

układ

dwu-

składniko

wy

układ wielo-

składnikow

y

Ułamek

(udział)

masowy

x
y

x

A

y

A

m

A

/

(m

A

+m

B

)

[kg A /

kg miesz.]

m

A

/



i=A

k

m

i

Ułamek

(udział)
molowy

x

mol

y

mol

x

molA

y

molA

n

A

/

(n

A

+n

B

)

[kmol A /

kmol miesz.]

n

A

/



i=A

k

n

i

Stosunek

masowy

X

Y

X

A

Y

A

m

A

/

m

B

[kg A /

kg nie A]

m

A

/



i=B

k

m

i

, i ≠ A

Stosunek

molowy

X

mol

Y

mol

X

molA

Y

molA

n

A

/

n

B

[kmol A /

kmol nie A]

n

A

/



i=B

k

n

i

,

i ≠ A

Stężenie

masowe

(koncentracja

masowa)

c

c

A

m

A

/ V [kg A/m

3

miesz.]

Stężenie

molowe

(koncentracja

molowa)

C

C

A

n

A

/ V [kg A/m

3

miesz.]

3

! UWAGA !

OZNACZENIA NA WYKŁADACH

wykłady

ćwiczenia

x

A

x

molA

y

A

y

molA

! ułamki molowe!

4

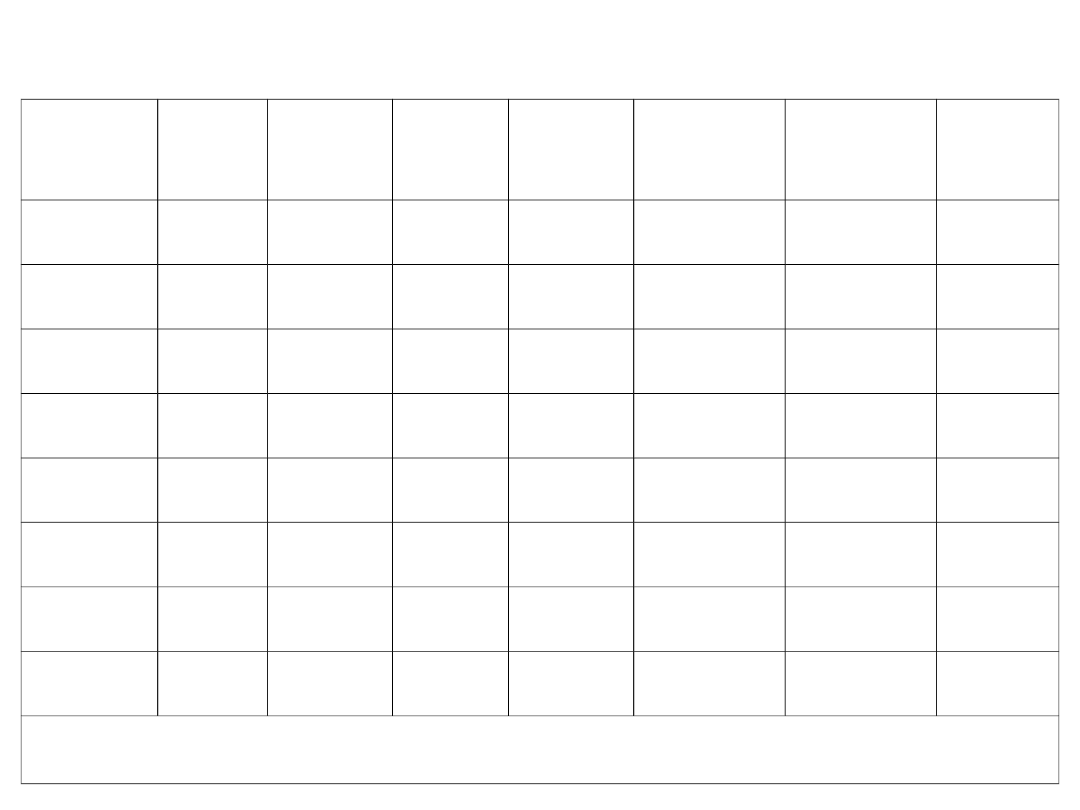
Tab. 2. Wzory do przeliczania stężeń w mieszaninach

Dane:

Szukane:

Udział

masowy

x`

A

kg/kg

Udział

molowy

x

A

kmol/kmol

Stosunek

masowy

X`

A

kg/kg

Stosunek

molowy X

A

kmol/kmol

Koncentracja

masowa

c`

A

kg/m

3

Koncentracja

molowa

c

A

kg/m

3

Ciśnienie

cząstkowe

p

A

Pa

x`

A

=m

A

/m=

(x

A

M

A

) /



i

k

(x

j

M

j

)

X`

A

/



i

k

X`

j

(X

A

M

A

) /



i

k

(X

j

M

j

)

c`

A

/



i

k

c

j

(c

A

M

A

) /



i

k

(c

j

M

j

)

(p

A

M

A

) / *



i

k

(p

j

M

j

)

x

A

=n

A

/n=

(x`

A

/M

A

) /



i

k

(x`

j

/M

j

)

(X`

A

/M

A

) /



i

k

(X`

j

/M

j

)

X

A

/



i

k

X

j

(c`

j

/M

j

) /



i

k

(c`

j

/M

j

)

c

A

/



i

k

c

j

p

A

/ *

p

X`

A

=m

A

/m

t

=

x`

A

/

x`

t

x

A

M

A

/

x

t

M

t

X

A

M

A

/

M

t

c`

A

/

c

t

c

A

M

A

/

c

t

M

t

p

A

M

A

/ *

p

t

M

t

X

A

=n

A

/n

t

=

x`

A

M

t

/

x`

t

M

A

x

A

/

x

t

X`

A

M

t

/

M

A

c`

A

M

t

/

c`

t

M

A

c

A

/

c

t

p

A

/ *

p

t

ć

A

=m

A

/V=

x`

A

/ *



i

k

(x`

j

/

j

)

(x

A

M

A

) / *



i

k

(x

j

M

j

/

j

)

X`

A

/ *



i

k

(X`

j

/

j

)

(X

A

M

A

) / *



i

k

(X

j

M

j

/

j

)

c

A

M

A

p

A

M

A

/ *

RT

c

A

=n

A

/V=

(x`

A

/M

A

) / *



i

k

(x`

j

/

j

)

x

A

/ *



i

k

(x

j

M

j

/

j

)

(X`

A

/M

A

) / *



i

k

(X`

j

/

j

)

X

A

/ *



i

k

(X

j

M

j

/

j

)

c`

A

/

M

A

p

A

/ *

RT

c

A

=n

A



m

/m=

**

(x`

A



m

) / **

M

A

(x

A



m

)

/ **



i

k

(x

j

M

j

)

(X`

A



m

) / **

M

A



i

k

X`

j

(X

A



m

) / **



i

k

X

j

M

j

p

A

=n

A

RT/V=

*

[(y`

A

RT)/M

A

]

/ 

i

k

(y`

j

/

j

)

y

A

p *

[(Y`

A

RT)/M

A

]

/ 

i

k

(Y`

j

/

j

) *

Y

A

RT / *



i

k

(Y

j

M

j

/

j

)

c`

A

RT

.

/ *

M

A

c

A

RT *

Oznaczenia: A – składnik, j – składniki bieżące, r – składnik inertny (rozpuszczalnik).

Uwagi: Wzory „*” dotyczą mieszanin idealnych; „**” dotyczą mieszanin o znanej gęstości 

m

.

Dla fazy gazowej symbole x, x`, X, X` należy zastąpić symbolami y, y`, Y, Y`.

5

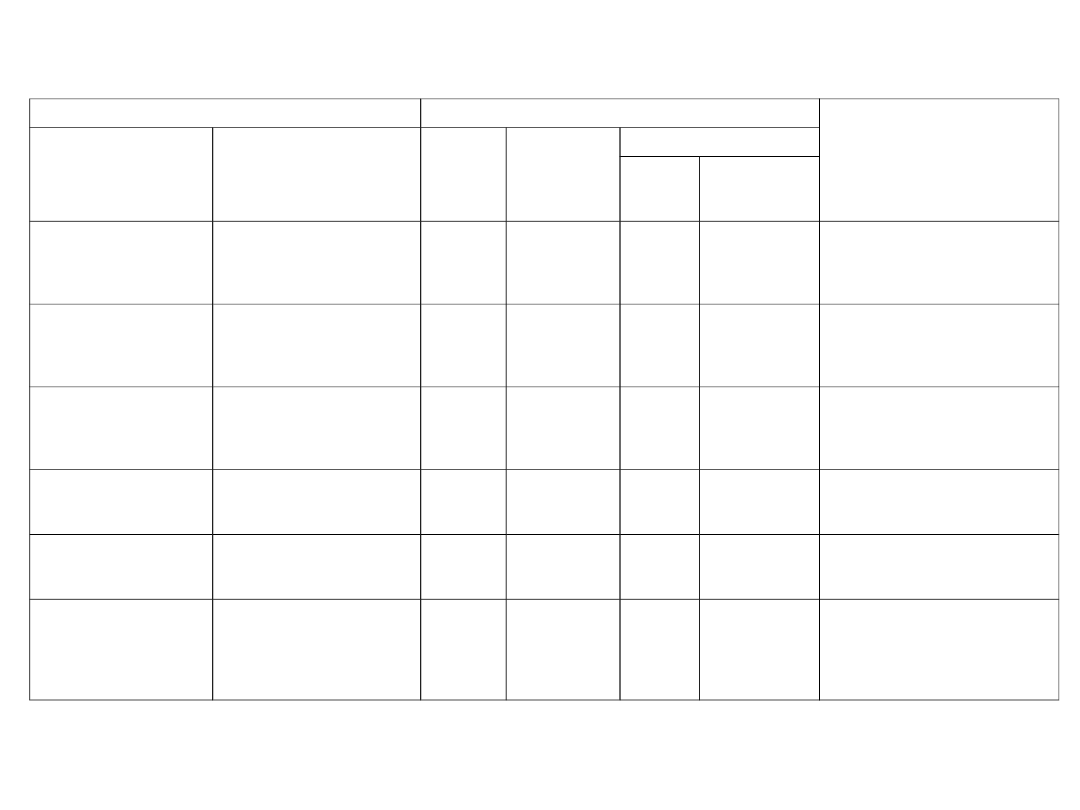
Tab. 3. Zdolność przepuszczania granicy rozdziału układów

Granica rozdziału

Możliwy przepływ

Rodzaj wymiennika w

jakim występuje

Rodzaj

Stosowane nazwy

substa

ncji

niektórych

składnikó

w

energii

wewn

ętrzne

j

ciepła

z fazy stałej zwartej

(np. metal, grafit,

szkło, ceramika)

przepona, ściana,

przegroda, wypełnienie

(w wymienniku

regeneracyjnym)

nie

nie

nie

tak

wymiennik ciepła

(powszechnie)

z fazy stałej

makroporowatej (np.

drobne otwory, albo

materiały spiekane)

ściana porowata

tak

nie

tak,

wraz z

substa

ncją

tak

możliwa w wymienniku

ciepła z odsysaniem

z fazy stałej

mikroporowatej

sorbenty, węgle

aktywowane, sita

molekularne, jonity,

anionity i kationity

nie

tak

tak, ze

składni

kami

możliwy

adsorber, wymiennik jonowy

błona

półprzepuszczalna

membrany z polimerów,

membrany o

porowatości włoskowatej

nie

tak

tak, ze

składni

kami

możliwy, ale

nie istotny

wymiennik masy, dializer

powierzchnia

międzyfazowa (np.

ciecz-gaz)

-

nie

tak

tak, ze

składni

kami

nie

wymiennik masy: absorber,

desorber, ekstraktor

powierzchnia

międzyfazowa (np.

ciecz-gaz)

-

nie

tak

tak, ze

składni

kami

tak

jednoczesny wymiennik

ciepła i masy: skruber,

kondensator par

wieloskładnikowych,

chłodnia kominowa

6

Tab. 4. Sposoby prowadzenia procesów wymiany masy

L.p.

Sposób prowadzenia procesu

Krótka

charakterystyka

Przykłady zastosowań

1

proces okresowy

obie fazy umieszczone w

wymienniku masy

ekstrakcja okresowa
ługowanie okresowe

adsorpcja okresowa

2a

proces z ciągłym

doprowadzeniem

jednej fazy

jedna z faz umieszczona

w wymienniku masy,

druga faza

doprowadzona do

wymiennika masy

destylacja okresowa

desorpcja okresowa

2b

proces z ciągłym

odprowadzeniem

jednej fazy

jedna z faz umieszczona

w wymienniku masy,

druga faza

odprowadzana w sposób

ciągły z wymiennika

masy

3

proces z ciągłym

przepływem jednej

fazy przez

wymiennik masy

jedna z faz umieszczona

w wymienniku masy,

druga faza w sposób

ciągły przepływa przez

wymiennik masy

suszenie

adsorpcja
absorpcja

desorpcja

ługowanie

4

proces przepływu

jednej fazy z

równoczesnym

powstaniem

drugiej fazy

jedna z faz w sposób

ciągły przepływa przez

wymiennik masy,

powstająca druga faza

jest usuwana z

wymiennika masy

destylacja okresowa

kondensacja

krystalizacja

5

proces ciągły

obie fazy przepływają w

sposób ciągły przez

wymiennik masy

rektyfikacja

suszenie ciągłe

absorpcja ciągła

nawilżanie powietrza

7

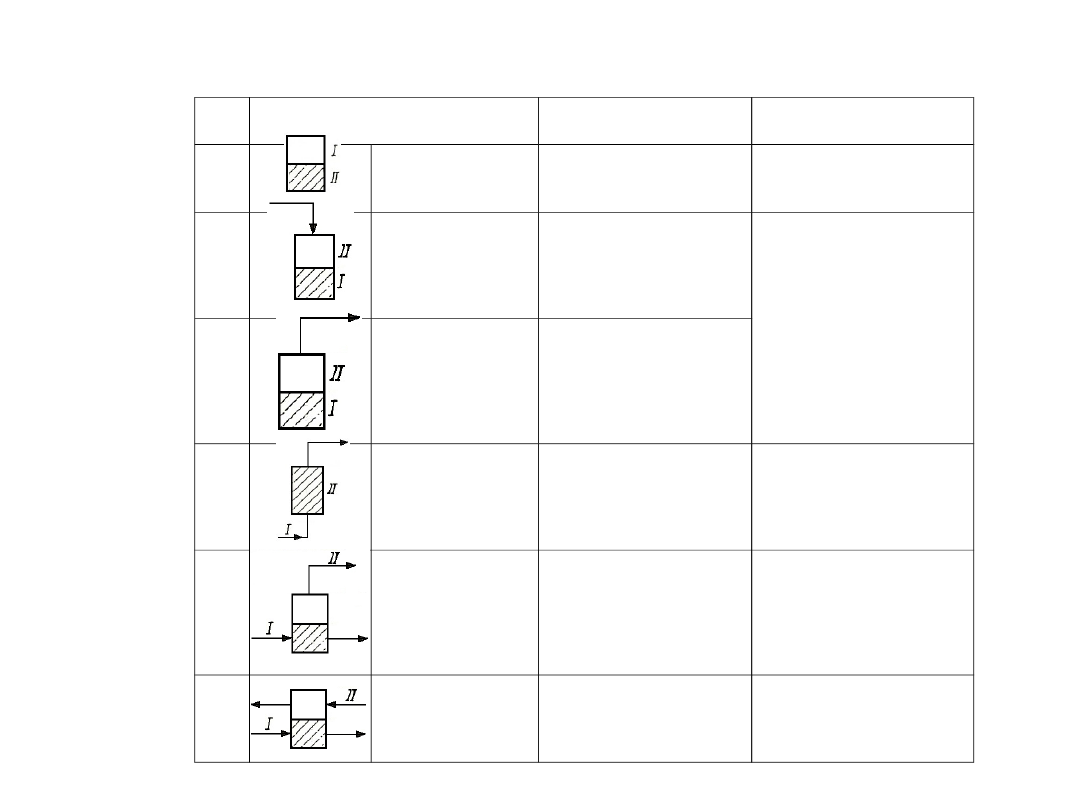
Tab. 5. Modelowa przepuszczalność granicy rozdziału utworzonej z

powierzchni międzyfazowej gaz-ciecz

Modelowa

przepuszczalność

Przepływ przez

granicę rozdziału

Warunki

temperaturowe w

obszarze

membrany

Nazwa

występującej

wymiany w

wyniku

określonej

przepuszczalnośc

i granicy

rozdziału

Przykładowy

wymiennik, w

którym

realizowany jest

proces

przepuszcza jeden

składnik w jedną

stronę, drugi w

drugą (oba

składniki

rozpuszczają się w

obu układach)

dwóch składników

przy równych i

przeciwnie

skierowanych

strumieniach

molowych

izotermiczne

wymiana masy w

warunkach dyfuzji

równomolowej

wymiennik masy,

kolumna

rektyfikacyjna

przepuszcza tylko

jeden składnik, ten

jeden składnik

rozpuszcza się w

obu układach

tylko jednego

składnika

izotermiczne

wymiana masy w

warunkach dyfuzji

przez gaz obojętny

wymiennik masy:

absorber, desorber,

adsorber

przepuszcza jeden

składnik, ze

składnikiem płynie

strumień energii

wewnętrznej, ciepło

płynie w tym

samym kierunku lub

przeciwnym

tylko jednego

składnika oraz

ciepła

nieizotermiczne

jednoczesna

wymiana ciepła i

masy

jednoczesny

wymiennik ciepła i

masy; skraplacz

mieszanin par,

chłodnia kominowa,

skruber do

chłodzenia gazu

8

{ilość substancji składnika j-ego w

układzie}

{stężenie składnika j-ego w układzie} =
------------------------------------------------------------

{ilość substancji w układzie}

{dowolnie wyrażona ilość przepływającej wielkości}

{strumień} = ------------------------------------------------------------------------

{przedział czasu}

{siła napędowa}  U

{strumień przepływający przez powierzchnię A} = ----------------------- = ------ =
---- = I

{opór} R R

9

WYMIENNIKI MASY

Sposób prowadzenia procesu:

1. ciągły;

2. okresowy.

1. W procesie ciągłym istnieje stały przepływ faz przez wymiennik 

parametry procesu są tylko funkcją miejsca.

2. W procesie periodycznym aparat pracuje szarżami, a parametry

procesu są funkcjami nie tylko miejsca, ale i czasu.

W zależności od czasu trwania rozróżnia się procesy:

- krótko trwające (t

m

< 30s);

- średni trwające (30s < t

m

< 2h);

- długo trwające (2h < t

m

< 1 doba).

10

Pod względem konstrukcyjnym aparaty do wymiany masy

powinny umożliwiać maksymalny kontakt faz oraz gwarantować
mechaniczny rozdział tych faz tak, aby możliwe było odprowadzenie ich z
aparatu w osobnych strumieniach.

Procesy wymiany masy prowadzi się bądź w jednym aparacie,

bądź też w kilku aparatach podobnego typu ustawionych obok siebie lub
jeden nad drugim. Często aparaty ustawione jeden nad drugim są
połączone jednym płaszczem i noszą nazwę KOLUMNY.

m*

p

Dopływ

m*

k

Odpły

w

Przestrzeń

bilansowa

m

Akumulacja

Dopływ = Odpływ + Akumulacja

m*

p

= m*

k

+ m

m*

jp

= m*

jk

+ m

j

(dla j = A, B, C, …, k)

m*

p

= m*

k

m*

jp

= m*

jk

(dla j = A, B, C, …, k)

Bilans energetyczny

(uproszczony)

Dla procesów ustalonych

Q*

p

± Q* = Q*

k

Q*

p

 strumień ciepła zawartego w substancjach

wchodzących do przestrzeni bilansowej;
Q*

k

 strumień ciepła zawartego w substancjach

wychodzących do przestrzeni bilansowej;
Q*  strumień ciepła dostarczony (+) lub

odprowadzony (-) z

przestrzeni bilansowej

niezależnie od substancji

wchodzących lub

wychodzących. Najczęściej są to tzw. straty ciepła
oraz efekty cieplne reakcji.

Równowaga międzyfazowa

Reguła faz Gibbsa

s = k – f +2

W układzie zawierającym czynnik jednorodny (np. wodę i parę

wodną)

s = 1 – 2 + 2 = 1

Jeden stopień swobody oznacza, że dowolnie można odebrać

temperaturę lub ciśnienie, wówczas drugi parametr jest jednoznacznie
wyznaczony za pomocą pewnej zależności funkcyjnej: p

An

= f(T) lub T

n

=f(p).

W układzie zawierającym składniki A, B, C, …, k w pełni

rozpuszczalne w fazie ciekłej i gazowej (przypadek występujący w
rektyfikacji)

s = k – 2 + 2 = k

Liczba stopni swobody równa liczbie składników oznacza, że

jeżeli proces prowadzi się przy obranym p = const, to pozostaje jeszcze
(k – 1) stopni swobody, które służą do określania składu mieszaniny.
Dowolny dobór pozostałych parametrów, np. temperatury, jest już
niemożliwy, gdyż wynika ona z założonego ciśnienia i składu.

Równowaga między fazą

ciekłą i gazową (parową)

Równowaga faz para-ciecz dla czynnika

jednorodnego

Układ dwufazowy ciecz-gaz jest bardzo ważny, gdyż

występuje często m. in. w procesach destylacji, rektyfikacji, adsorpcji i
desorpcji.

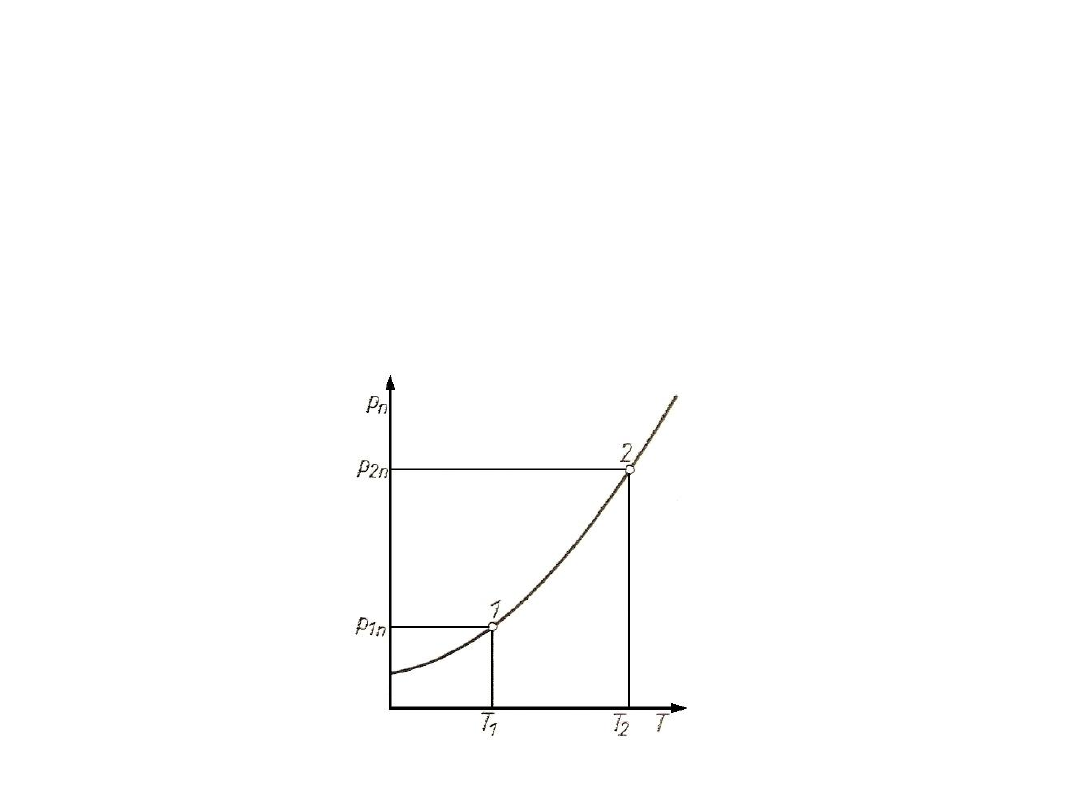
Rys. 1. Krzywa nasycenia dla czynnika jednorodnego

14

Zależność p

n

= f(T) jest opisana przez prawo Clausiusa-

Clapeyrona:

dp

n

/ dT = Ĥ / [T (`` - `)]

gdzie:

Ĥ - zmiana entalpii 1 kmola substancji przy przejściu z fazy ciekłej
do

gazowej

(ciepło parowania pod stałym ciśnieniem)

J/kmol;

``, ` -

objętość 1 kmola substancji w stanie gazowym i

ciekłym m

3

/kmol.

W praktyce bardzo popularne jest empiryczne uogólnienie

nazywane równaniem Antoine`a:

ln(p

n

) = A – [B / (T + C)]

Znajomość zależności p

n

= f(T) dla konkretnej substancji

pozwala na wyznaczenie temperatury wrzenia pod dowolnym
ciśnieniem.

Równowaga między fazą

ciekłą i gazową w mieszaninach

dwu- i wielo-składnikowych

Układy, w których znajduje się więcej niż jeden związek chemiczny

nazywane są układami wieloskładnikowymi lub mieszaninami. Jeżeli dany
układ wieloskładnikowy składa się z dwu faz – ciekłej i gazowej, to na ogół
składy tych faz są różne.

W stanie równowagi przy ustalonym ciśnieniu i ustalonej

temperaturze skład jednej z faz jest wyznaczony jednoznacznie przez skład
drugiej fazy. Można to zapisać następująco:

Z*

j

= f(S

j

)

j = A, B, …, k

lub

S*

j

= f(Z

j

)

j = A, B, …, k

gdzie: Z i S – stężenia uogólnione, gwiazdka oznacza stan równowagi.

Przebieg funkcji dla konkretnego rodzaju stężenia w ustalonej

temperaturze i pod ustalonym ciśnieniem, np. y*

j

= f(x

j

), nazywamy krzywą

równowagi. Zależnie od postaci użytych stężeń przebieg tej linii będzie różny,
ale charakter jej będzie podobny.

16

Tradycyjnie przyjęło się, że stosunek stężenia

równowagowego w fazie gazowej do odpowiadającego mu stężenia w
fazie ciekłej jest nazywany stałą równowagi i oznaczany przez K:

Z*

j

/ S

j

= K

j

j = A, B, …, k

W dalszych rozważaniach stężeń równowagowych jako

składnik przykładowy będzie brany pod uwagę składnik A.

Wartość K zależy od sposobu wyrażania stężeń w

poszczególnych fazach:

K

y,x

= y*

A

/ x

A

, K

Y,X

= Y*

A

/ X

A

, K

pc

= p*

A

/ c

Ac

itp.

Stałą równowagi w dowolnym punkcie wykresu Z*

j

= f(S

j

) da

się przedstawić następująco:

tg = Z*

A

/ S

A

= K

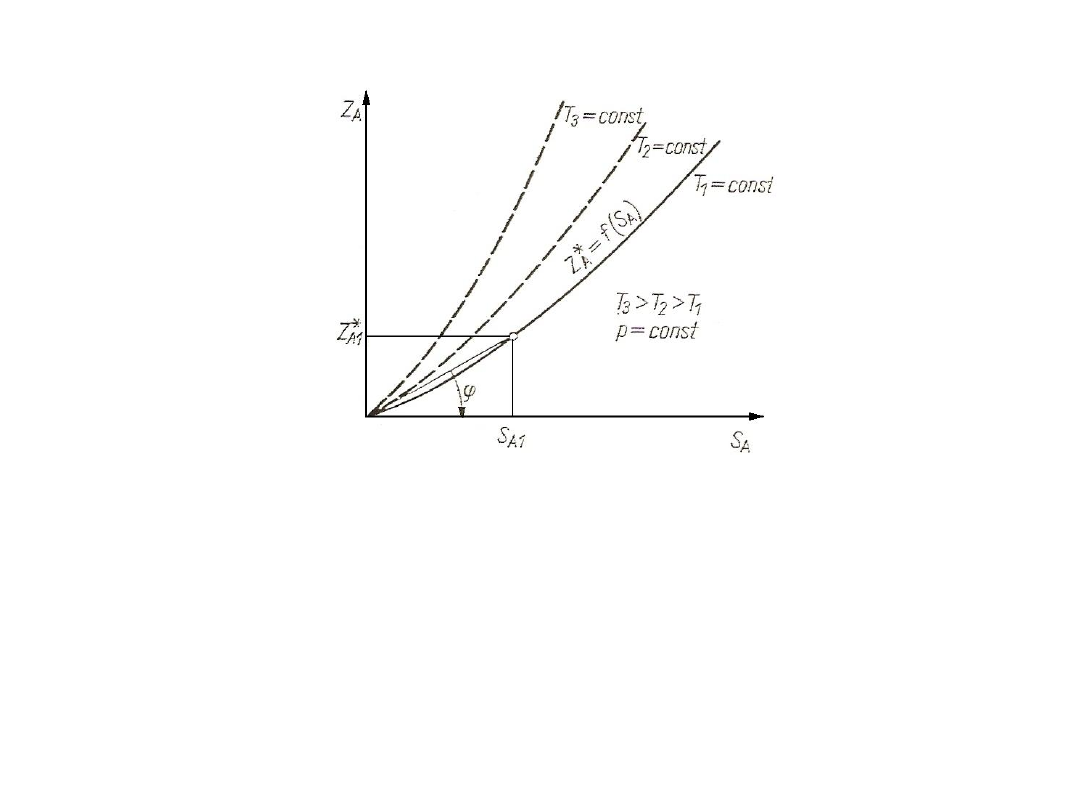
17

Gdy K = const, linia równowagi jest linią prostą. Linie równowagi dla

wyższych temperatur leżą wyżej.

Rys. 2. Linie równowagi Z*

A

= f(S

A

) dla różnych temperatur

Najogólniej można powiedzieć, że K = f(T, p, S

A

). Określenie stała

równowagi jest nieco mylące, gdyż wielkość ta jest stała tylko w bardzo
nielicznych przypadkach. Jeżeli wartość K nie zależy od stężenia, to dla
stałego ciśnienia można zapisać:

(K)

p

= f(T)

lub

(K)

p,T

= const

W 1803 r. Henry odkrył prawo, które rządzi rozpuszczalnością gazów

w cieczach i które dla T = const ma następującą postać:

p*

A

= H x

A

18

Stała Henry`ego H ma wymiar ciśnienia, a jej wartość można znaleźć w
różnych poradnikach technicznych. Jest ona szczególną postacią stałej K:

(K

p,x

)

T

= (H)

T

Prawo Henry`ego dotyczy tylko małych stężeń, niezbyt niskiej

temperatury oraz umiarkowanego ciśnienia. Jeżeli w równowadze z
cieczą znajduje się nie jeden gaz, ale mieszanina gazów, to prawo
Henry`ego obowiązuje dla każdego ze składników oddzielnie.

W ogólnym przypadku stała K ≠ const, więc linia równowagi nie

jest linią prostą, ale krzywą o zmiennym nachyleniu. Nachylenie to jest
ważnym parametrem we wzorach określających przenikanie masy. W
przypadku, gdy znane jest równanie:

Z*

A

= f(S

A

) nachylenie linii równowagi można obliczyć z definicji:

m = dZ*

A

/ dS

A

= df(S

A

) / dS

A

W przypadku, gdy linia równowagi jest dana w postaci wykresu,

dwa niezbyt odległe punkty krzywej umożliwiają określenie przybliżonej
wartości nachylenia linii równowagi w pewnym zakresie:

m = dZ*

A

/ dS

A

= Z*

A

/ S

A

= (Z*

A2

- Z*

A1

) / (S

A2

– S

A1

)

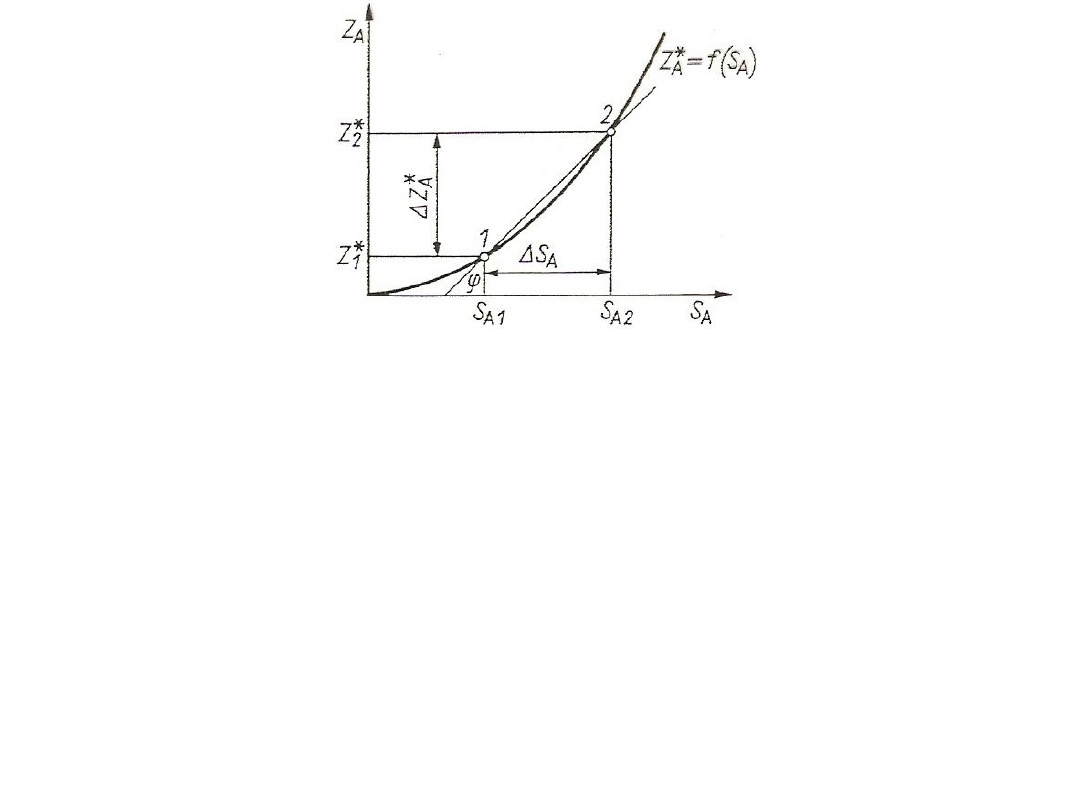
19

Rys. 3. Wyznaczanie nachylenia linii równowagi

W zakresie S

A1

≤ S

A

≤ S

A2

można krzywą równowagi aproksymować w

pewnym przybliżeniu za pomocą linii prostej:

Z*

A

= Z*

A1

+ m(S

A

– S

A1

)

W obliczeniach praktycznych jest potrzebna liczbowa wartość m tylko

w pewnych określonych punktach krzywej równowagi, np. u wlotu albo wylotu
wymiennika masy. Wyznaczenie jej graficznie lub z przyrostów skończonych
nie zawsze jest dokładne. Przybliża się wtedy krzywą równowagi funkcją
potęgową (S do potęgi r)

Z*

A

= B S

a

Po zlogarytmowaniu otrzymuje się linię prostą:

lgZ*

A

= lgB + r lgS

A

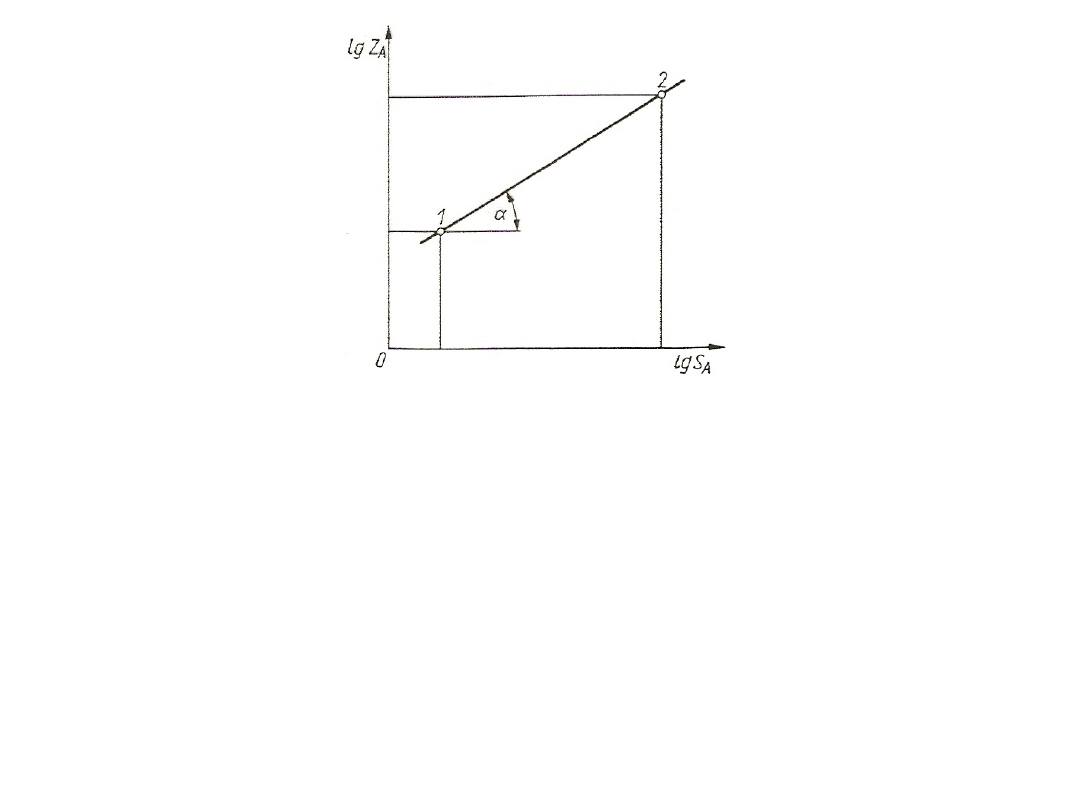
20

Rys. 4. Wyznaczanie wykładnika r krzywej równowagi

Nachylenie tej prostej określa wykładnik r:

r = tg = d(lgZ*

A

) / d(lgS

A

) = d(lnZ*

A

) / d(lnS

A

) = (dZ*

A

/ Z*

A

) (S

A

/ dS

A

) =

m / K

Tym sposobem można więc znaleźć wykładnik r na podstawie

znajomości dwu punktów dość dalekich od siebie, np. stanu na wlocie i
wylocie z wymiennika masy.

W punkcie 1: m

1

= r K

1

, a w punkcie 2: m

2

= r K

2

. Dla linii

równowagi odbiegających od funkcji potęgowych podane związki są
tylko przybliżeniem. Gdy układ stosuje się do prawa Henry`ego, wtedy
dla stężeń prężność cząstkowa – ułamek molowy r = 1 i m = K

px

= H

21

Równowaga w roztworach

(mieszaninach) idealnych

Jeżeli ciśnienie w układzie jest umiarkowane (dużo mniejsze od

ciśnień krytycznych wszystkich składników), a budowa strukturalna
składników jest podobna, to równowagę w układzie opisuje prawo
Raoulta będące szczególnym przypadkiem prawa Henry`ego.

Zgodnie z prawem Raoulta stała Henry`ego składnika A w

równaniu przyjmuje wartość prężności pary nasyconej tego składnika w
temperaturze roztworu tzn. H = p

An

, a równanie przybiera postać:

p*

A

= p

An

x

A

(forma I)

Po podzieleniu tego równania przez wartość ciśnienia w

wymienniku masy otrzymuje się:

p*

A

/ p = (p

An

/ p) x

A

i dalej:

y*

A

= K

yx

x

A

(forma II)

przy czym: - K

yx

stała równowagi w równaniu Raoulta.

22

Prawo Raoulta jest więc szczególnym przypadkiem prawa

Henry`ego dla roztworów idealnych, gdy składniki w fazie gazowej
mogą się wykraplać w temperaturze roztworu. W zasadzie zarówno
prawo Henry`ego, jak też prawo Raoulta są prawami graficznymi.
Równanie Raoulta przedstawia asymptotę do rzeczywistego
przebiegu krzywej ciśnień cząstkowych p*

A

= f(x

A

) dla x

A

 1.

Równanie Henry`ego opisuje natomiast graniczną styczną dla tej
samej krzywej, gdy x

A

 0, a więc dla gazów o bardzo małym

stężeniu składnika absorbowanego. Jak stwierdzono powyżej prawo
Raoulta obowiązuje dla mieszanin idealnych. Są to takie mieszaniny,
w których siły występujące między cząsteczkami różnych
składników i między cząsteczkami jednego (tego samego) składnika
są jednakowo wielkie. Po zmieszaniu takich składników, gdy p*

A

=

const, nie ma zmiany objętości, ani też nie powstaje dodatkowe
ciepło mieszania.

Jeżeli układ stosuje się do prawa Raoulta, to przebieg linii

równowagi można opisać równaniem analitycznym, wychodząc z
prawa Raoulta dla składników A i B:

y*

A

= (p

An

/ p) x

A

y*

B

= (p

Bn

/ p) x

B

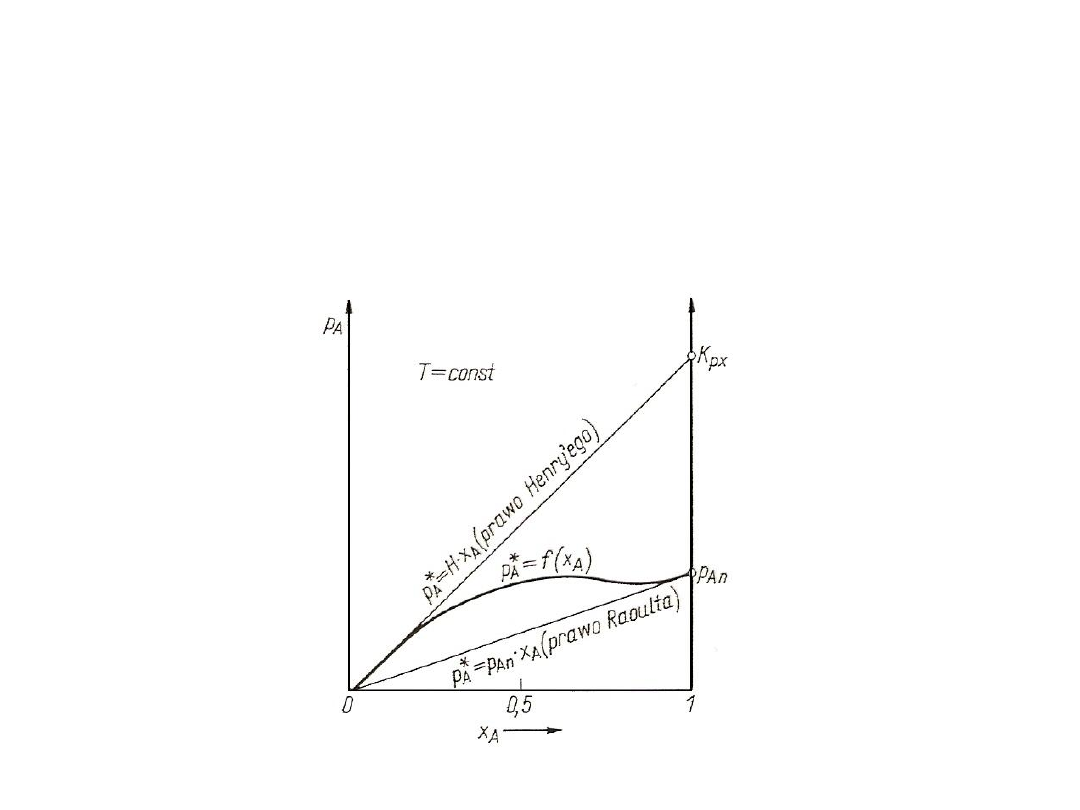
23

Rys. 5. Graficzna interpretacja prawa Raoulta i prawa Henry`ego

Przez podzielenie tych dwóch równań stronami i podstawienie:

x

B

= 1 – x

A

oraz y*

B

= 1 - y*

A

,

po przekształceniach otrzymuje się równanie linii równowagi
Fenskego:

y*

A

= ( x

A

) / [1 + x

A

( - 1)]

gdzie:  = p

An

/ p

Bn

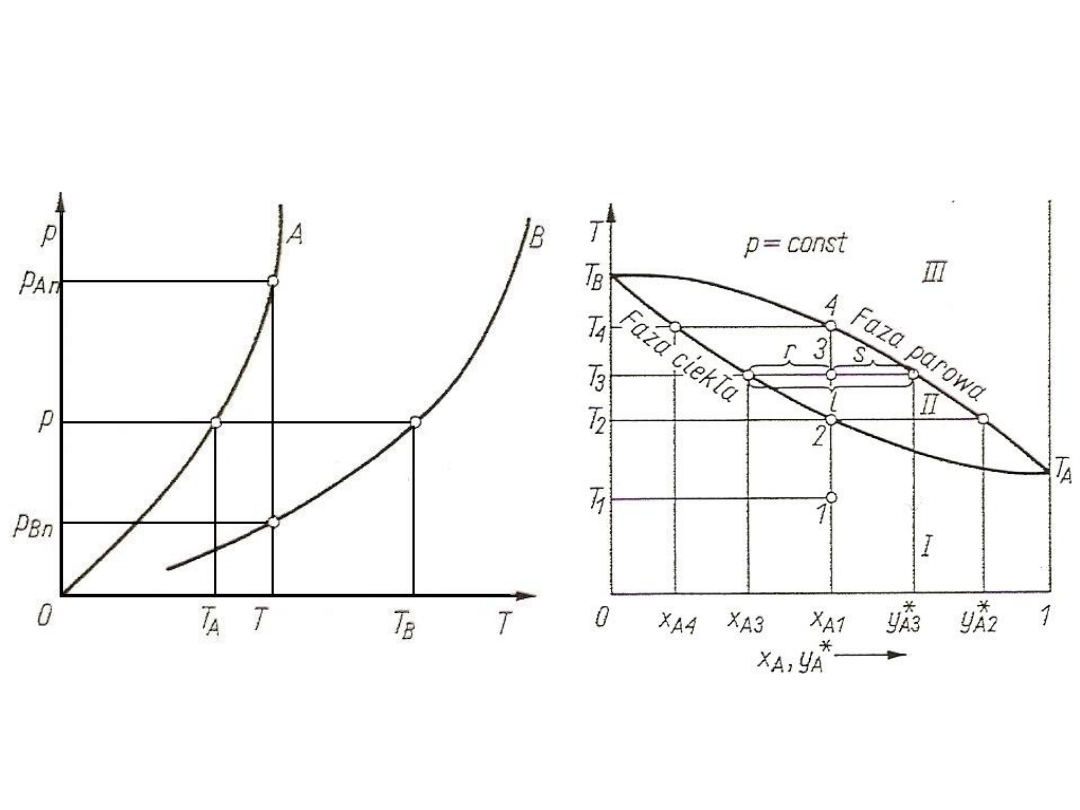
24

Rys. 7. Krzywa składu w układzie

dwuskładnikowym

Do pełnej interpretacji procesu destylacji i warunków

równowagowych w układach dwuskładnikowych są stosowane wykresy
pomocnicze:

1. Krzywa składu, którą można wyznaczyć na podstawie krzywych
prężności pary nasyconej poszczególnych składników.

Rys. 6. Krzywa prężności pary

nasyconej składników A i B

mieszaniny dwuskładnikowej

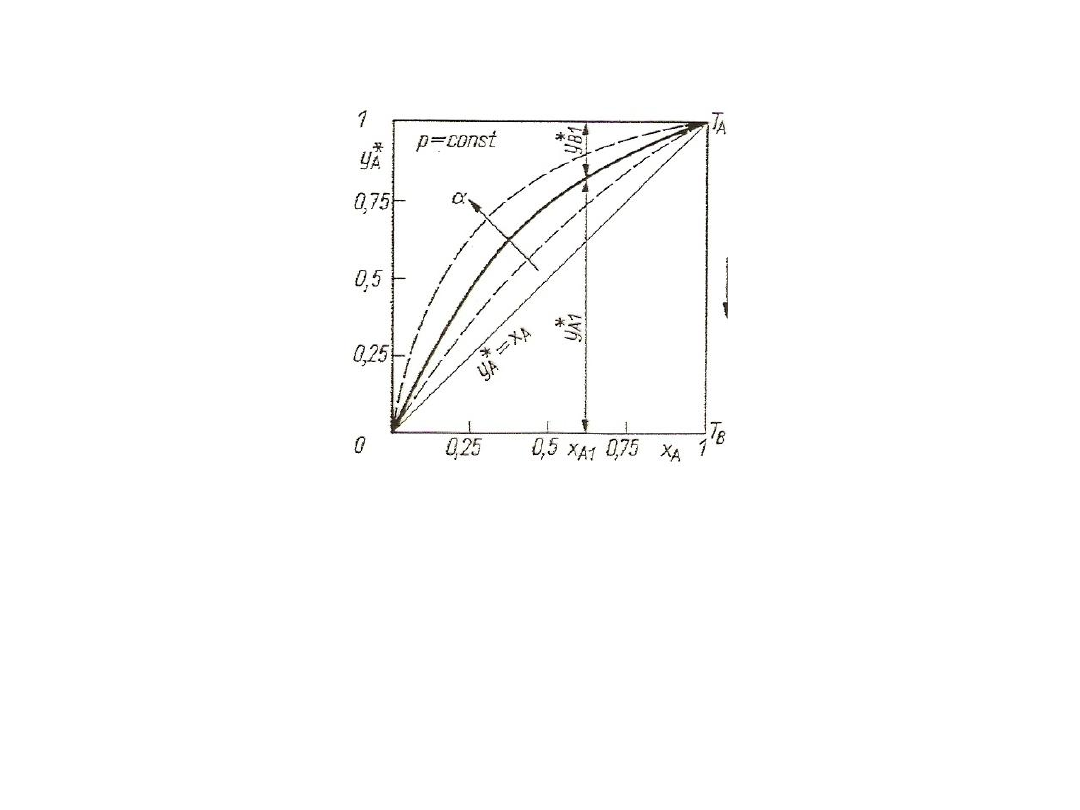
25

2. Wykresy krzywej równowagi można zbudować z wykresu składu lub z
obliczeń na podstawie równania: y*

A

= (p

An

/ p) x

A

.

Rys. 8. Krzywa równowagi w układzie dwuskładnikowym

Współczynnik względnej lotności α dla wielu mieszanin

dwuskładnikowych zależy bardzo nieznacznie od temperatury. W praktyce
oblicza się go bardzo często jako średnią geometryczną dla skrajnych
wartości temperatury w układzie. Dla bardzo małych stężeń x

A

wyrażenie

( - 1) x

A

jest dużo mniejsze od jedności, więc y*

A

= ( x

A

) . Z tego też

powodu w pobliżu x

A

≈ 0 linia równowagi jest prawie linią prostą. Z kolei

dla małych stężeń składnika B tzn. dla wartości x

A

zbliżonych do jedności,

zachodzi zależność graniczna y*

A

 (1 / ) x

A

+ ( - 1) , czyli linia

równowagi również jest prawie linią prostą.

26

Współczynnik względnej lotności jest miarą trudności rozdziału

danej mieszaniny. Współczynnik ten rośnie, gdy ciśnienie układu maleje,
a linia równowagi ma wtedy przebieg bardziej wypukły, tzn. że różnice w
składach fazy parowej i ciekłe się powiększają. Gdy  = 1, y*

A

= x

A

, znika

więc wzbogacanie fazy parowej przez odparowanie.

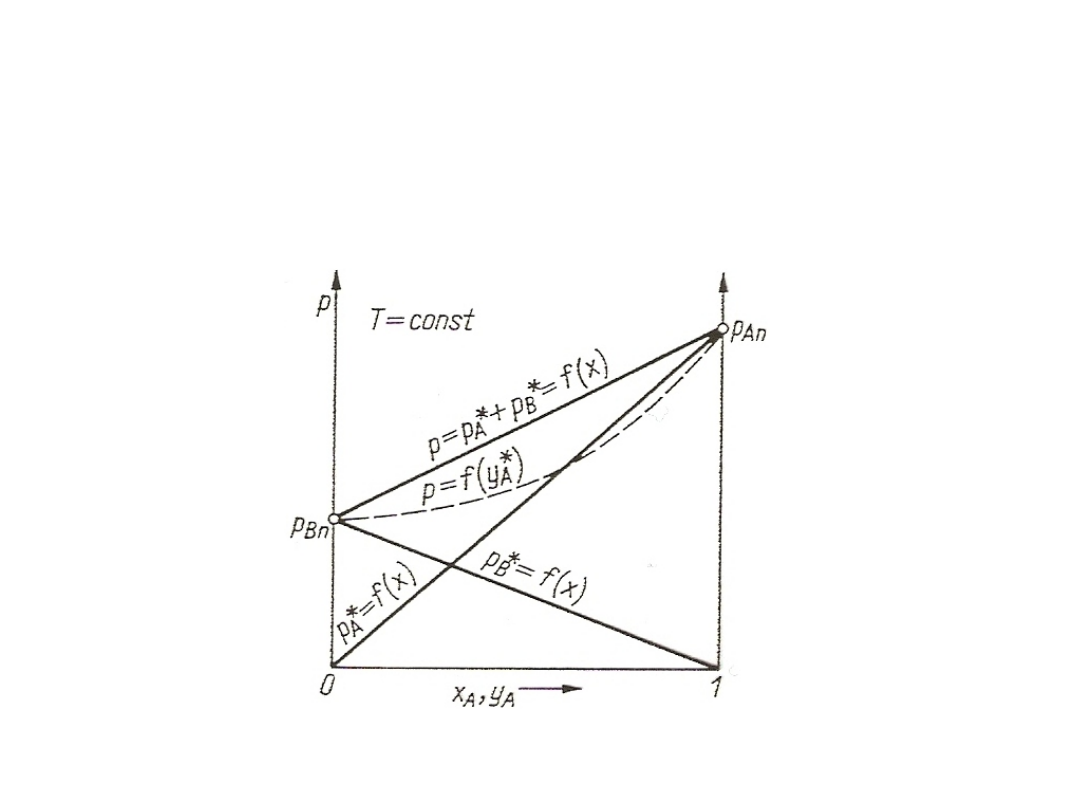
3. Wykres ciśnień cząstkowych.

Rys. 9. Zależność prężności par dla składu cieczy w stałej temperaturze dla

układu dwuskładnikowego stosującego się do prawa Raoulta

27

Zgodnie z prawem Daltona dla mieszaniny idealnej w

stałej temperaturze suma prężności cząstkowych par
składników jest równa ciśnieniu całkowitemu układu:

p = p*

A

+ p*

B

Na rysunku pokazano przebieg zmian ciśnień cząstkowych i
ciśnienia całkowitego w zależności od udziałów molowych w
fazie ciekłej w stałej temperaturze. Dodatkowo zaznaczony jest
przebieg zmian ciśnienia całkowitego p od stężenia y*

A

w fazie

gazowej.

28

Układy dwufazowe (równowaga w roztworach rzeczywistych)
składające się z fazy gazowej i ciekłej można podzielić na 4 grupy:

1. Zarówno gaz, jak i ciecz można traktować jako mieszaniny idealne.

W układach takich spełnione jest prawo Raoulta i Daltona. Sytuacja
taka dotyczy mieszaniny związków o podobnej budowie pod niskim
ciśnieniem.

2. Fazę gazową można uznać za mieszaninę idealną, natomiast gaz jest

mieszaniną rzeczywistą. Spełnione jest prawo Raoulta, prawo
Daltona nie obowiązuje. Dotyczy to mieszanin związków o podobnej
budowie pod zwiększonym ciśnieniem. Rzeczywiste zachowanie się
mieszanin gazowych tym bardziej odróżnia się od zachowania gazów
idealnych, im większe są wartości ciśnienia zredukowanego i im
niższa jest temperatura zredukowana.

3. Mieszanina gazowa jest idealna (spełnia prawo Daltona) natomiast

mieszanina ciekła jest rzeczywista – prawo Raoulta nie jest spełnione
 mieszaniny zarówno o różnej budowie pod niskim ciśnieniem.

4. Ani faza gazowa, ani ciekła nie są idealne. Związki (mieszaniny

związków) o różnej budowie pod wysokim ciśnieniem. Tu 

modyfikacji prawa Raoulta:

p*

A

= 

A

p

A

x

A

gdzie: 

A

- współczynnik aktywności.

29

Równowaga w roztworach

(mieszaninach) rzeczywistych

p*

A

= 

A

p

A

x

A



A

- współczynnik aktywności



A

= f(p

A

,x

A

)

Siły przyciągania między cząsteczkami różnych składników A i

B w cieczy:

F

AB

= (F

AA

F

BB

)

1/2

F

AA

F

BB

– siły przyciągania między cząstkami tego samego związku

(

A

> 1)

F

AB

< (F

AA

F

BB

)

1/2

 dodatnie odchylenie

(b)

(

A

< 1)

F

AB

> (F

AA

F

BB

)

1/2

 ujemne odchylenie

(a)

Mieszaniny o składzie odpowiadającym punktom ekstremalnym

 azeotropy.

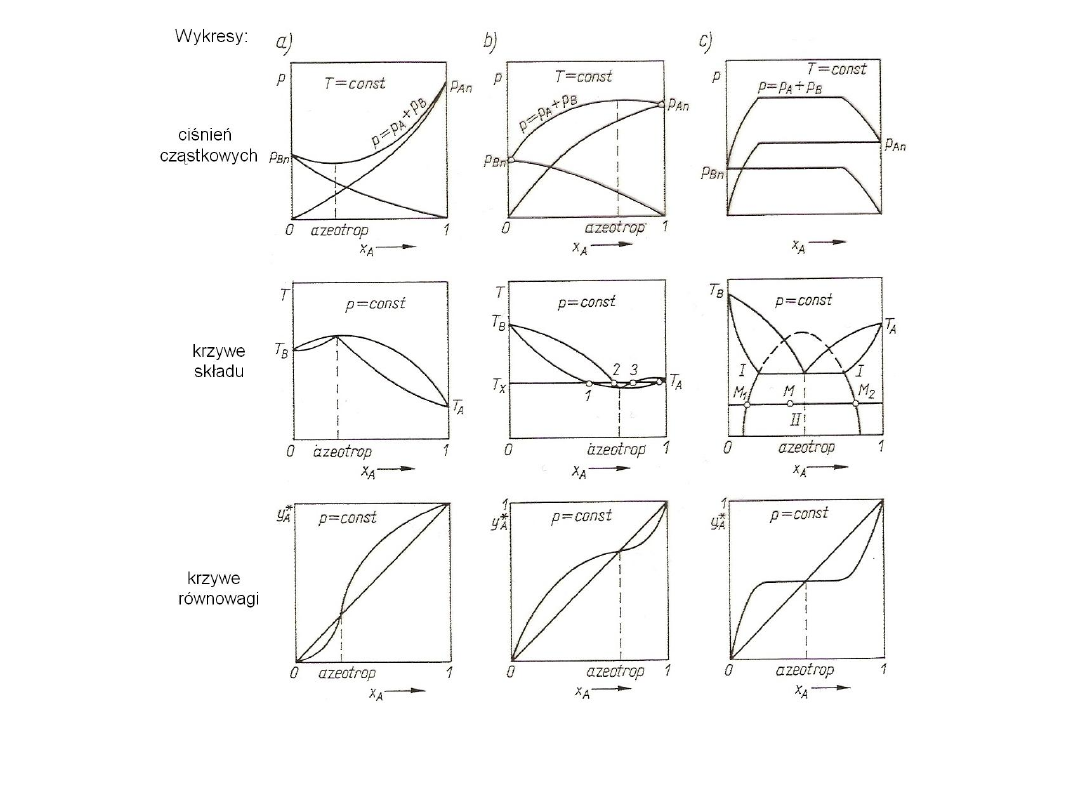
30

Rys. 10. Mieszaniny dwuskładnikowe odchylające się od prawa Raoulta:

a) 

A

<1; b) 

A

>1; c) mieszaniny o częściowej rozpuszczalności w fazie ciekłej

31

Równowaga międzyfazowa w

układzie ciecz-ciecz

Zagadnienie równowagi w układzie ciecz-ciecz występuje w

procesie ekstrakcji składnika C z cieczy A za pomocą ciekłego
rozpuszczalnika B. Strumień rozpuszczalnika B o dużej zawartości
składnika C jest nazwany ekstraktem, strumień A (zubożały w składnik
C) – rafinatem, a mieszanina składników A + C = F stanowi tzw.
surówkę ekstrakcyjną. W procesie ekstrakcji ekstrakt i rafinat tworzą
dwie fazy ciekłe, które można rozdzielić metodami mechanicznymi.
Składnik C zawarty jest w obydwu fazach. Podobnie jak dla przypadku
układu gaz-ciecz, stężenia składnika C w ekstrakcie i w rafinacie w
stanie równowagi są powiązane zależnością:

X*

CE

= f(X

CR

)

gdzie: X

CR

– stosunek molowy składnika C w rafinacie;

X*

CE

- stosunek molowy składnika C w ekstrakcie (w stanie

równowagi).

Tradycyjnie wprowadza się tutaj wielkość K zwaną

współczynnikiem podziału Nersta:

K = X*

CE

/ X

CR

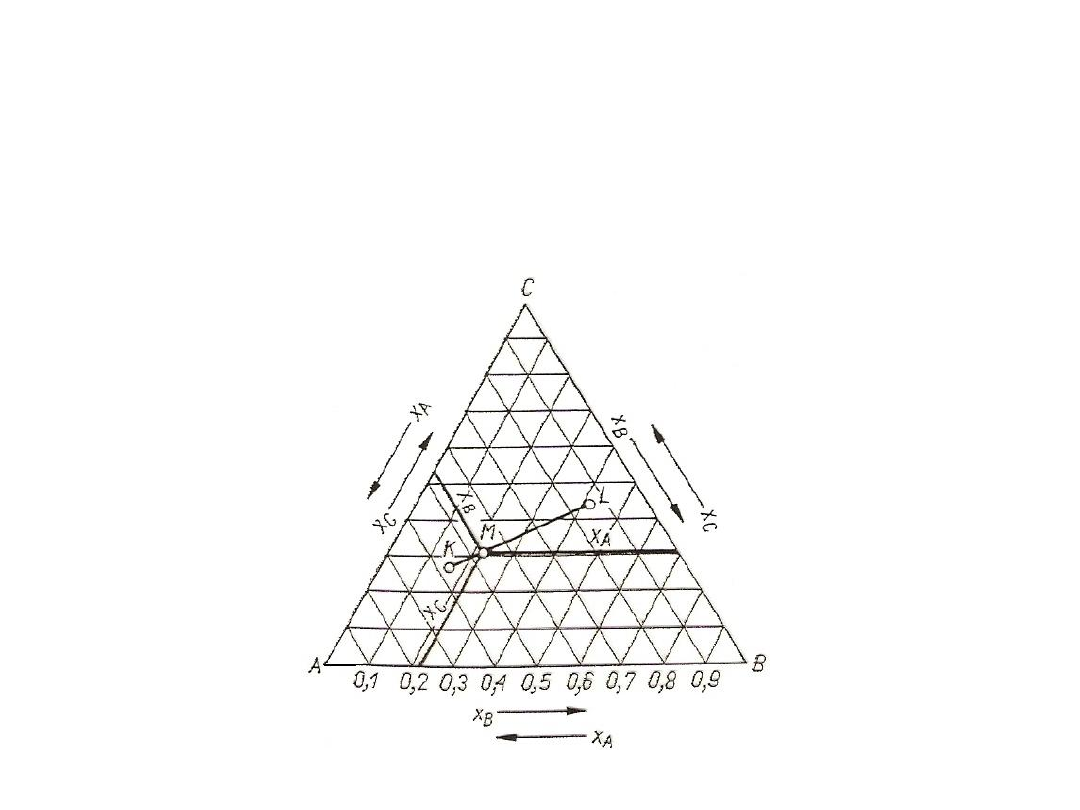
32

Wartość współczynnika K zależy od temperatury, ciśnienia oraz

składu faz pozostających w równowadze. W przypadku, gdy składniki A i
B są absolutnie w sobie nierozpuszczalne, a stężenia składnika C w
ekstrakcie i w rafinacie są niewielkie, współczynnik K jest wielkością
stałą, a zależność ta nosi nazwę prawa podziału Nersta. Jednak w
większości przypadków składniki A i B są częściowo w sobie
rozpuszczalne i sytuacje należy rozważać na wykresie trójkątnym
nazywanym też trójkątem Gibbsa.

Rys. 11. Wykres trójkątny Gibbsa dla mieszanin trójskładnikowych

33

Ilościowe parametry transportu

masy

Podstawową jednostką masy jest kilogram. Bardzo często

używaną jednostką jest kilomol. Masę wyrażoną w kilogramach oznacza
się literą m, a w kilomolach literą n i czasami nazywa się ją ilością
substancji.

Podstawową wielkością kinetyczną charakteryzującą każdy ruch

jest jego prędkość. Prędkość ruchu masy określa się przez strumień
masy lub gęstość strumienia masy.

Strumieniem przepływającej masy (substancji) składnika i,

nazywa się ilość masy (substancji) składnika i, przepływającej w
jednostce czasu przez wybraną w rozważanej przestrzeni powierzchnię
A:

m`

i

= dm

i

/ d n`

i

= dn

i

/ d

Gęstością strumienia nazywa się strumień przepływający przez

jednostkę powierzchni. Strumień jest wielkością charakterystyczną dla
wybranej powierzchni, a gęstość strumienia jest charakterystyczna dla
pewnego punktu leżącego na tej powierzchni:

J

i

= lim

A0

n`

i

/ A=dn`

i

/ dA

gdzie: n`

i

- strumień przepływający przez powierzchnię A.

34

Gęstość strumienia jest w ogólnym przypadku wielkością

wektorową, gdyż zależy od ustawienia powierzchni względem kierunku
ruchu masy. Całkowity strumień składnika i przepływający przez
wybraną powierzchnie A można wyznaczyć z zależności:

n`

i

= ∫

A

J

i

dA

Jeżeli gęstość strumienia J

i

nie zależy od położenia, a powierzchnia A

jest prostopadła do kierunku przepływu substancji, to powyższa
zależność przybiera znacznie prostszą postać:

n`

i

= J

i

A

gdzie: A – powierzchnia, przez którą przepływa substancja.

Transport masy może być ustalony lub nieustalony. Transport

ustalony jest wówczas, gdy wielkość J

i

nie zależy od czasu.

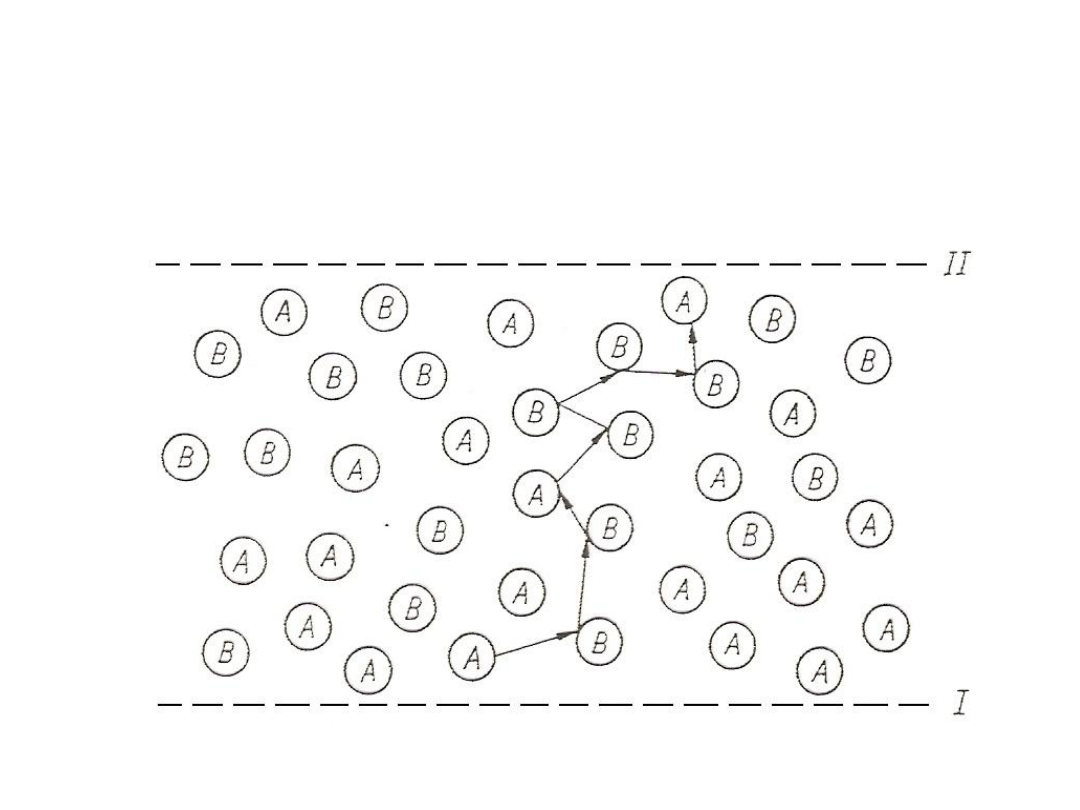
Podstawowe prawa dyfuzji

Wstępny opis dyfuzji

czącząsteczkowej

Rys. 12. Dyfuzja cząsteczkowa

36

I prawo Ficka

Dla rozważanego przypadku układu dwuskładnikowego (A, B)

prawo to ma postać:

J

A

= - D

AB

dc

A

/ dz

gdzie: D

AB

– kinematyczny współczynnik dyfuzji, m

2

/s;

z – odległość mierzona w kierunku ruchu masy, m;

„-” –

znak minus wynika z przepływu masy w

kierunku spadku

stężenia.

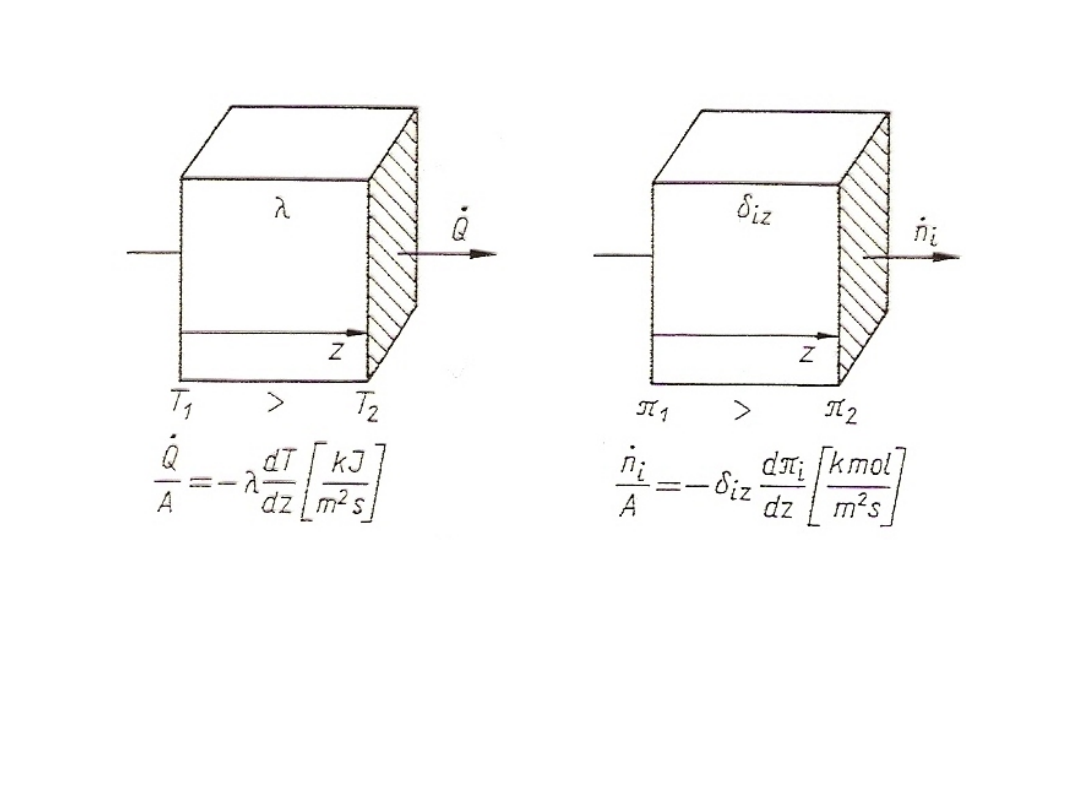
37

Rys. 13. Porównanie dyfuzji substancji z przewodzeniem ciepła

Zjawisko dyfuzji jest analogiczne do zjawiska przewodzenia

ciepła, co przedstawiono poglądowo na rysunku powyżej. Podobieństwo
praw opisujących te zjawiska wynika z tego, że są one wywołane tym
samym mechanizmem, a mianowicie chaotycznym ruchem cząstek.

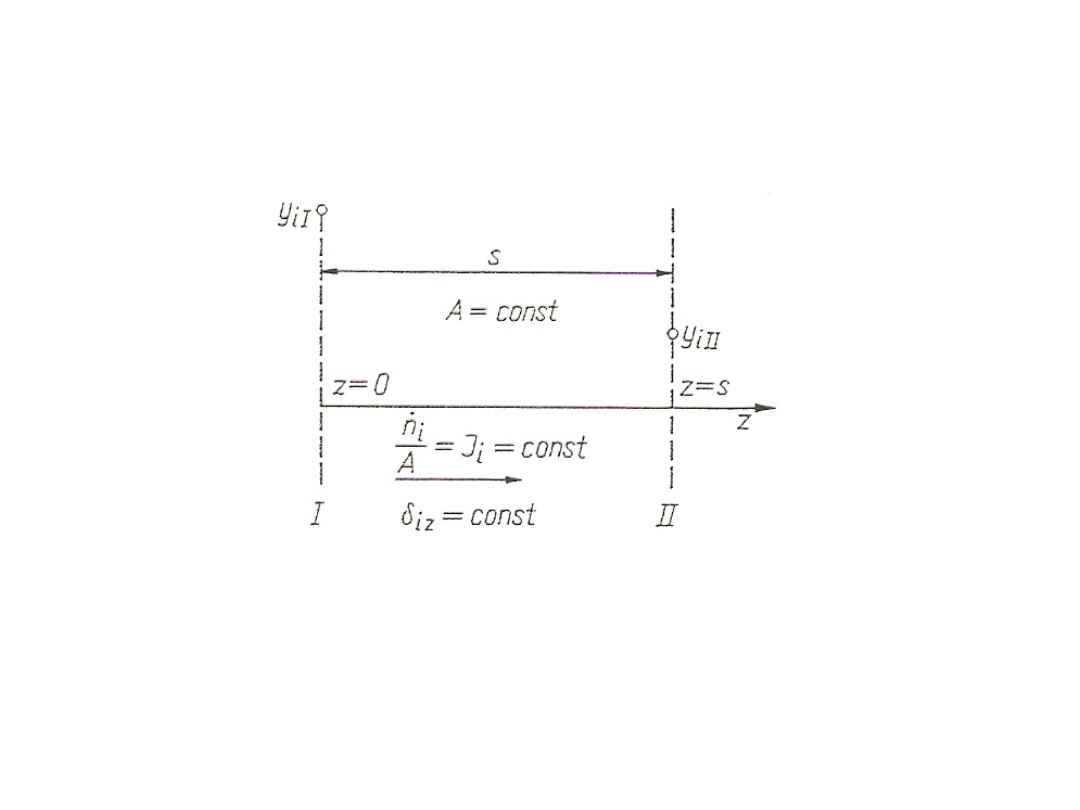
Dyfuzja ustalona

Rozważania ogólne

Rys. 14. Dyfuzja ustalona przez nieruchomą warstwę

Jeżeli zastępczy współczynnik dyfuzji i jest stały od przekroju

I do przekroju II, to:

J

i

= 

iz

/ s ∫

yiII

yiI

dy

i

/ y

fi

gdzie: s – odległość przekrojów I i II.

39

Uwzględniając definicje y

fi

:

∫

yiII

yiI

dy

i

/ y

fi

= ∫

yiII

yiI

y

iI

/ (1 + 

i

y

i

) = (1 / 

i

) ln[(1 + 

i

y

iI

) / (1 + 

i

y

iII

)]

Ostatecznie otrzymuje się wzór na gęstość strumienia składnika i

dla ustalonej dyfuzji między przekrojami I i II:

J

i

= [

iz

/ (s 

i

)] ln(y

fI

/ y

fII

)

gdzie: y

fI

i y

fII

– przeciwstężenia składnika i odpowiednio w przekrojach I i

II.

Znacznie wygodniej jest stosować inną postać wzoru po

wprowadzeniu średniej logarytmicznej:

(y

fi

)

m

= (y

fI

- y

fII

) / ln(y

fI

/ y

fII

)

stąd:

ln(y

fI

/ y

fII

) = (y

fI

- y

fII

) / (y

fi

)

m

ale:

y

fI

- y

fII

= 1 + 

i

y

iI

- 1 - 

i

y

iII

= 

i

(y

iI

- y

iII

)

Po podstawieniu:

J

i

= (

i

/ s) [(y

fI

- y

fII

) / (y

fi

)

m

]

Wzór ten jest najbardziej ogólnym wzorem określającym gęstość

strumienia dyfundującego składnika i w stanie ustalonym.

40

Podstawowe prawa dyfuzji

w fazie gazowej

Na podstawie teorii kinetycznej można dla fazy gazowej

wyprowadzić bardziej ogólne prawo dyfuzji, którego szczególnym
przypadkiem jest prawo Fica. Opierając się na tzw. założeniach
Maxwella, otrzymuje się dla składnika i w układzie k-składnikowym
następujący wzór określający gęstość strumienia masy:

J

i

= - 

iz

(d

i

/ dz)

gdzie: 

iz

- zastępczy dynamiczny współczynnik dyfuzji składnika i w

układzie

wieloskładnikowym, kmol/(ms);



iz

= (1 + 

i

y

i

) / [

(j=1, j≠i)

k

(y

i

/ 

ij

) - y

i



(j=1, j≠i)

k

(y

ji

/ 

ij

)]

gdzie: 

ij

– binarny dynamiczny współczynnik dyfuzji w układzie

dwuskładnikowym i-j;



ij

= D

ij

c

m

c

m

= 

j=1

k

c

j

= 

m

/ M

m

gdzie: D

ij

- binarny kinematyczny współczynnik dyfuzji w układzie

dwuskładnikowym i-j, m

2

/s;

41



i

- parametr określający rodzaj dyfuzji:



i

= - 

j=1

k



ji



ji

= J

j

/ J

i

(j = 1, 2, 3, …i, …k)

d

i

- różniczkowy moduł napędowy dyfuzji określony za pomocą wzoru:

d

i

= dy

i

/ y

fi

y

fi

- przeciwstężenie składnika i:

y

fi

= 1 + 

i

y

i

Według Hoblera wzory te będą słuszne również dla fazy ciekłej.

42

Szczególne przypadki

dyfuzji

Wyprowadzone uprzednio wzory są prawdziwe dla każdego

przypadku dyfuzji. W praktyce bardzo często występują znaczne
uproszczenia.

Dyfuzja ekwimolarna przeciwkierunkowa

Jest to przypadek dyfuzji gdy:



j=1

k

J

j

= 0

Warunek ten oznacza, że dyfuzyjny ruch pewnych składników

w jedną stronę musi być stowarzyszony z dyfuzyjnym ruchem
pozostałych składników w stronę przeciwną. Dla układu
dwuskładnikowego A-B oznacza to, że:

J

A

= - J

B



i

= 

j=1

k

J

j

/ J

i

= (1 / J

i

)  J

j

= 0 

y

fi

= 1

J

i

= (

i

/ s) (y

iI

- y

iII

)

Dla układu dwuskładnikowego A-B, otrzymujemy wyrażenie na

zastępczy współczynnik dyfuzji:



Az

= 1 / {(y

B

/ 

AB

) – [y

A

( -1 / 

AB

)]} = 

AB

43

Po podstawieniu otrzymanych wyników do podstawowego

równania różniczkowego dyfuzji otrzymujemy:

J

A

= - 

AB

(dy

A

/ dz)

lub:

J

A

= - D

AB

(dc

A

/ dz)

Jest to klasyczne prawo Ficka. Zatem dla dyfuzji ekwimolarnej

przeciwkierunkowej prawo Ficka jest spełnione w sposób ścisły.

Dyfuzja składnika przez jeden lub kilka składników

inertnych

Z definicji przypadek ten występuje wówczas, gdy w układzie

dyfunduje tylko składnik i, pozostałe natomiast nie ulegają dyfuzji i
dlatego nazywa się je składnikami inertnymi (obojętnymi), zatem:

J

i

≠ 0; J

j

= 0 dla

j ≠ i

Po uwzględnieniu tego warunku w definicji parametru 

i

otrzymuje się zależność:



i

= - (J

i

/ J

i

) = - 1

y

fi

= 1 - y

i

Wyrażenie określające zastępczy współczynnik dyfuzji przybiera

postać:



iz

= (1 - y

i

) / [

(j=1, j≠i)

k

(y

i

/ 

ij

)]

44

Dla układu dwuskłanikowego A-B (dyfuzja składnika A przez

inert B):



Az

= (1 – y

A

) / (y

B

/ 

AB

) = 

AB

Wyrażenie określające gęstość strumienia składnika i dla

dyfuzji przez warstwę grubości s przybiera postać:

J

i

= (

iz

/ s) ln[(1 - y

iII

) / (1 – y

iI

)]

lub

J

i

= (

iz

/ s) [(y

iI

- y

iII

) / (1 - y

i

)

m

]

lub

J

i

= (

iz

/ s) [(Y

iI

- Y

iII

) / (1 - Y

i

)

m

]

Wyrażenia (1 - y

i

)

m

i (1 - Y

i

)

m

oznaczają średnie logarytmiczne

odpowiednich wartości w przekrojach I i II.

45

Dyfuzja nieustalona

Bardzo często w rzeczywistych układach strumień

dyfundującej masy zmienia się w czasie. Taki przypadek nazywamy
dyfuzja nieustaloną, Dyfuzję nieustaloną często omawia się przy okazji
różnego rodzaju rozważań teoretycznych. Podstawowym prawem,
opisującym dyfuzje nieustaloną, jest drugie prawo Ficka, które jest
ściśle słuszne dla dyfuzji ekwimolarnej, a w przybliżeniu dla małych
stężeń składnika i. W kartezjańskim układzie współrzędnych prawo to
ma postać równania:

c

i

/  = D

iz

[(

2

c

i

/ x

2

) + (

2

c

i

/ y

2

) + (

2

c

i

/ z

2

)] = D

iz



2

c

i

W bardzo wielu przypadkach dyfuzja zachodzi tylko w jednym

kierunku. Jeżeli tym kierunkiem jest oś z, to drugie prawo Ficka ma
postać najczęściej stosowaną:

c

i

/  = D

iz

(

2

c

i

/ z

2

)

Są to równania różniczkowe cząstkowe II rzędu (typu

parabolicznego).

Transport masy przez wnikanie

Ogólna charakterystyka i podział wnikania

masy

W punkcie tym omówiono ruch jednego wyróżnionego składnika

A w układach jednofazowych wieloskładnikowych. Na wstępie zakłada
się, że w rozważanym układzie można wydzielić rdzeń, w którym
stężenia wszystkich składników są wyrównane, oraz pewną strefę
graniczną zawierającą brzeg układu. Tę część brzegu układu, która
styka się z inną fazą nazywa się powierzchnią międzyfazową lub
zwierciadłem i oznacza indeksem z.

Proces przenoszenia składnika A z rdzenia do zwierciadła lub ze

zwierciadła do rdzenia nazywa się wnikaniem masy. Składa się ono z
dwóch różnych mechanizmów – dyfuzji i konwekcji. Aby proces dyfuzji
był efektywny, konieczna jest różnica stężeń składnika A przy
zwierciadle i rdzeniu układu, czyli c

Az

≠ c

Ar

. Jeżeli c

Az

> c

Ar

, to składnik

jest przenoszony od zwierciadła do rdzenia, a jeżeli c

Az

< c

Ar

, to składnik

jest przenoszony od rdzenia do zwierciadła.

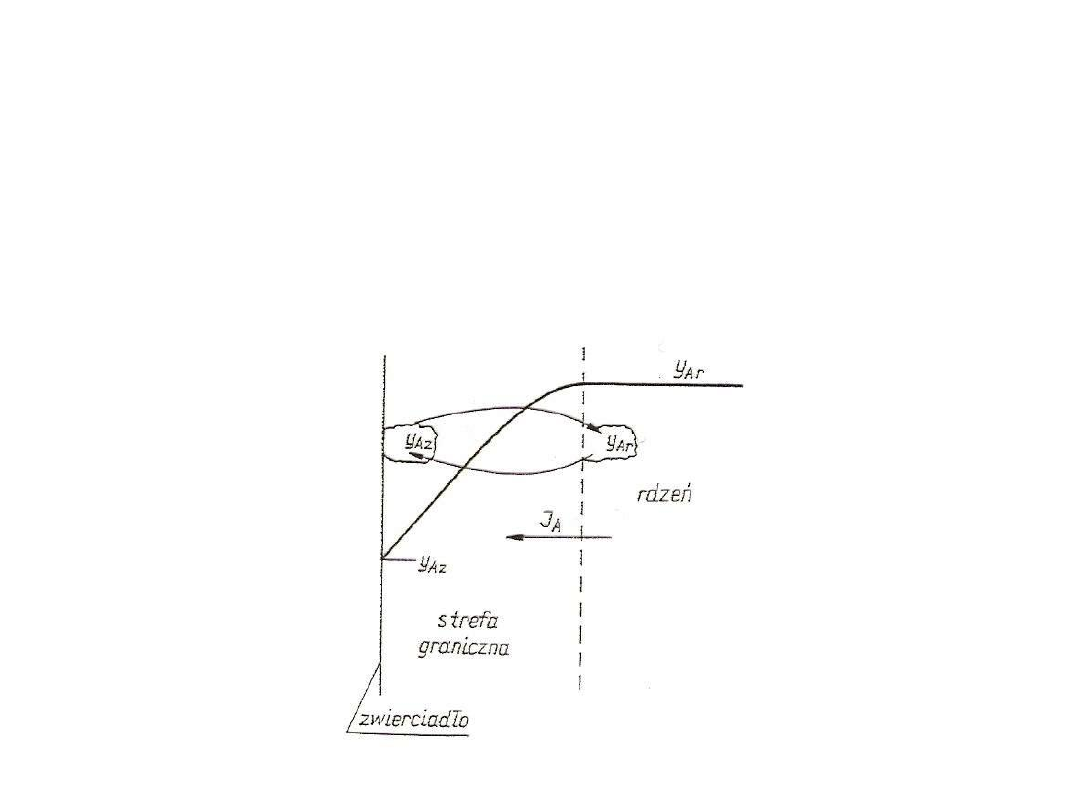
Konwekcja, czyli mechaniczne przenoszenie składnika A wraz z

innymi składnikami bądź do zwierciadła, bądź do rdzenia może
zachodzić nawet przy c

Az

= c

Ar

, jednak wówczas nie będzie ona

efektywna. Konwekcję dzieli się na wymuszoną (odbywa się na wskutek
wymuszonego ruchu w obrębie danej fazy) lub naturalną (ruch w
obrębie fazy wytwarza się samorzutnie, np. wskutek różnic gęstości w
różnych miejscach układu).

Wnikanie masy w fazach gazowej i ciekłej może się odbywać

zarówno poprzez dyfuzję, jak i konwekcję. W fazie stałej natomiast jest
możliwa tylko dyfuzja.

Rys. 15. Schemat procesu wnikania masy

48

Ilościowe określenie wnikania

masy

Ilościowo wnikanie masy składnika A określa się za pomocą

równania definicyjnego:

J

A

= 

A

(

A

)

gdzie: 

A

-

współczynnik wnikania masy, kmol/(m

2

s);



A

-

moduł napędowy wnikania masy.

Wartość współczynnika wnikania masy określa gęstość

strumienia wnikającej masy składnika A przy module napędowym (

A

)

= 1.

Moduł napędowy wnikania masy jest określony za pomocą

wzoru:



A

= (y

Ar

- y

Az

) / (y

fA

)

m

gdzie: (y

fA

)

m

-

średnia logarytmiczna z przeciwstężeń

składnika A w rdzeniu i

przy zwierciadle.

Dla dyfuzji ekwimolarnej lub dla małych stężeń składnika A

obowiązuje znacznie prostszy wzór:



A

= y

Ar

- y

Az

Dla innych przypadków dyfuzji można znaleźć odpowiednie

wyrażenia w literaturze specjalistycznej.

49

Współczynnik wnikania masy określony za pomocą wzoru

odnosi się do rzeczywistej powierzchni międzyfazowej, którą często jest
rudno wyznaczyć. Dlatego wnikanie masy jest odnoszone bądź do
jakiejś umownej powierzchni A

p

, np. do powierzchni przekroju aparatu,

bądź do jakiejś umownej objętości V

p

, np. do objętości aparatu. W

takich przypadkach rozważa się od razu cały strumień:

n`

A

= 

Ap

A

p



A

lub:

n`

A

= 

Vp

V

p



A

Współczynniki 

Ap

lub 

Vp

są ważne tylko dla aparatów

charakteryzujących się podobnymi parametrami geometrycznymi.

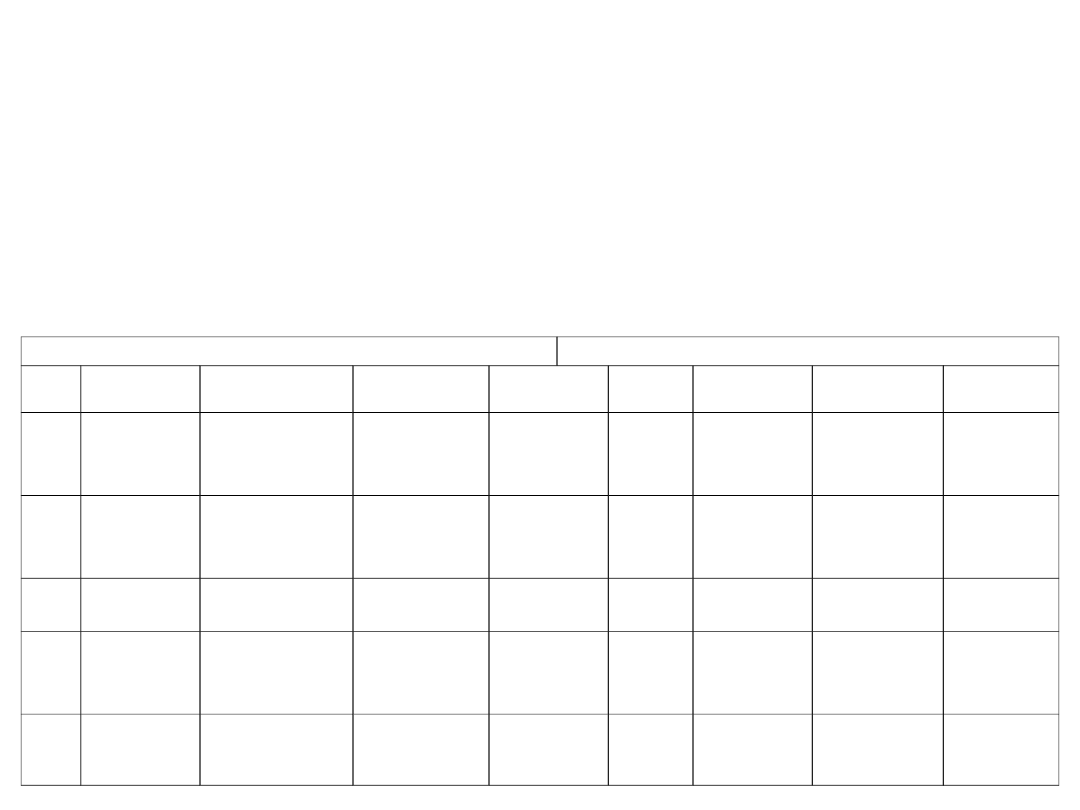
Bardzo często, zwłaszcza w ujęciach tradycyjnych, spotyka się

opis, w którym zamiast modułu napędowego 

A

używa się różnicy

stężeń. Ponieważ sposobów wyrażania stężeń jest dosyć dużo, więc jest
wiele możliwych kombinacji. Stosunkowo najczęściej używa się do tego
celu koncentracji molowej c

A

. Gęstość strumienia wnikającej masy w

takim ujęciu wyraża się wzorem:

J

A

= 

c

c

A

Indeks przy współczynniku  oznacza rodzaj stężenia użytego

do określenia siły napędowej (wyrażenia użytego zamiast modułu
napędowego 

A

).

50

Wzory określające gęstość strumienia wnikającej masy,

wyrażone za pomocą ułamków molowych lub stosunków molowych:

J

A

= 

y

y

A

J

A

= 

Y

Y

A

Tab. 6. (skrypt) k = 

Faza gazowa

Faza ciekła

Ozn.

dyfuzja

p-kierun.

dyfuzja

jednokierun.

wzór uprosz.

wymiar

Ozn.

dyfuzja

p-kierun.

dyfuzja

jednokierun.

wzór

uprosz.

k

CG

k

G

(k

G

C

G

) /

(C

BG

m)

k

G

kmol A /

[m

2

s (kmol A

/

m

3

)] = m/s

k

CL

k

L

(k

L

C

L

) /

(C

BL

m)

k

L

k

ymol

k

G

C

G

(k

G

C

G

) /

(1-y

mol

)

m

k

G

C

G

kmol A /

[m

2

s (kmol A

/

kmol A+B)]

k

xmol

k

L

C

L

(k

L

C

L

) /

(1-x

mol

)

m

k

L

C

L

k

p

k

G

/

RT

(k

G

C

G

) /

(p

B

m)

k

G

/

RT

kmol A /

(m

2

s Pa)

-

-

-

-

k

Ymol

(k

G

C

G

) /

[(1+Y

mol

)

(1+Y

mol z

)]

(k

G

C

G

) /

(1+Y

mol

)

m

k

G

C

G

kmol A /

[m

2

s (kmol A

/

kmol B)]

k

Xmol

(k

L

C

L

) /

[(1+X

mol

)

(1+X

mol z

)]

(k

L

C

L

) /

(1+X

mol

)

m

k

L

C

L

k

Y

(k

G

C

G

m*) /

[(m*+Y)

(m*+Y

z

)]

(k

G

C

G

) /

(m*+Y)

m

(k

G

C

G

) /

m*

kmol A /

[m

2

s (kg A /

kg B)]

k

X

(k

L

C

L

m*) /

[(m*+X)

(m*+X

z

)]

(k

l

C

L

) /

(m*+X)

m

(k

L

C

L

) /

m*

51

Aby dokładnie scharakteryzować proces wnikania masy,

należy przede wszystkim zbadać zależności, jakim podlega
współczynnik wnikania masy .
 - zależy od właściwości dyfuzyjnych układu, jak też od

warunków

hydrodynamicznych panujących w układzie.

Istnieje kilka teoretycznych modeli próbujących

matematycznie opisać proces wnikania masy.

We wszystkich rozważaniach zakłada się dyfuzję ekwimolarną

przeciwkierunkową lub małe stężenie składnika wnikającego oraz, że
słuszne jest zarówno pierwsze, jak i drugie prawo Ficka.

Należy zauważyć, że w tym ujęciu współczynnik wnikania 

zależy od rodzaju użytego stężenia i od rodzaju dyfuzji. Obydwie te
zależności nie będą występować jeżeli użyje się modułu napędowego


A

. Oto zależność między współczynnikami 

A

i 

c

:



A

= (y

f

)

m

c

m



c

52

Teoretyczne modele wnikania

masy

Model warstewki granicznej Lewisa-Whitmana

Model ten zakłada, że rozważany układ składa się z rdzenia, w

którym stężenia wszystkich składników są wyrównane oraz z
nieruchomej warstewki granicznej. W rdzeniu zachodzi czysta
konwekcja, a w warstewce granicznej czysta dyfuzja.

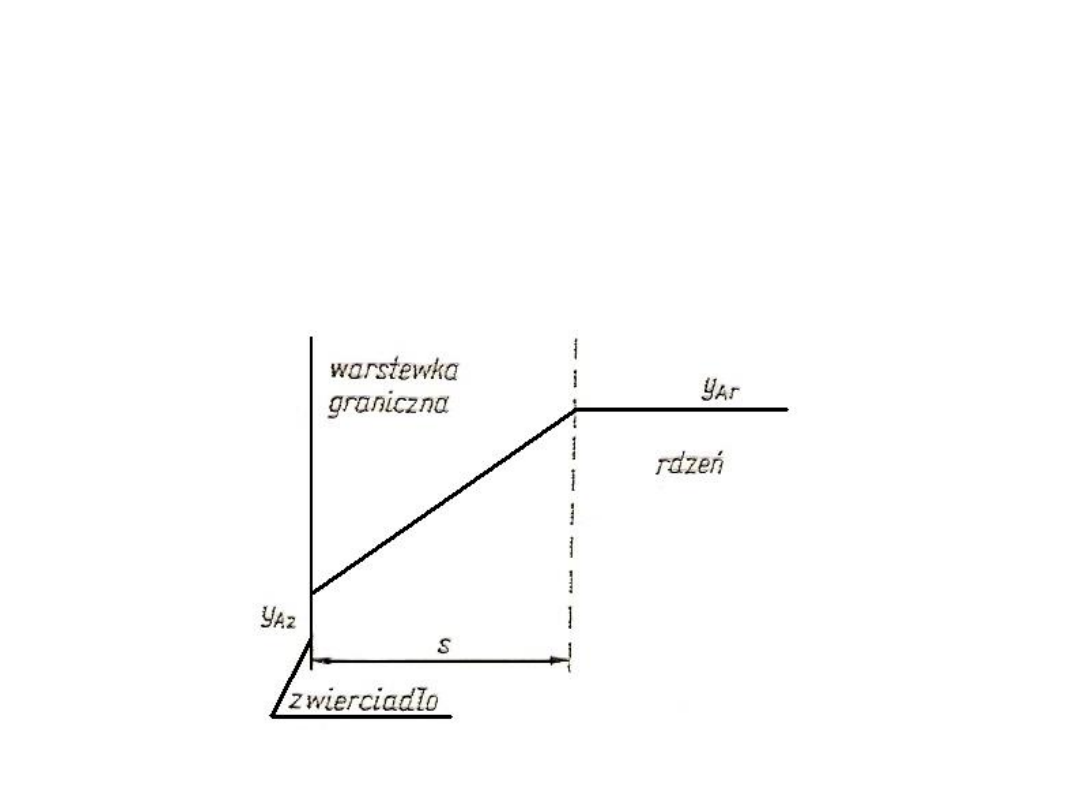
Rys. 16. Rozkład stężeń składnika A wg modelu warstwy granicznej

53

Rozkład stężeń wnikającego składnika A przedstawiono na rys.

16. Ponieważ w rdzeniu stężenia są wyrównane, efektywny ruch masy
zachodzi tylko w warstewce granicznej. Gęstość strumienia wnikającej
masy:

J

A

= (

Az

/ s) ( y

Ar

– y

Az

)

Wartość J

A

można również wyrazić wzorem określającym wnikanie

masy:

J

A

= 

A

( y

Ar

– y

Az

)

Z porównania tych wzorów wynika:



A

= (

Az

/ s) = (D

A

c

m

) / s

Do obliczenia współczynnika 

A

konieczna jest znajomość

grubości warstewki granicznej s.

54

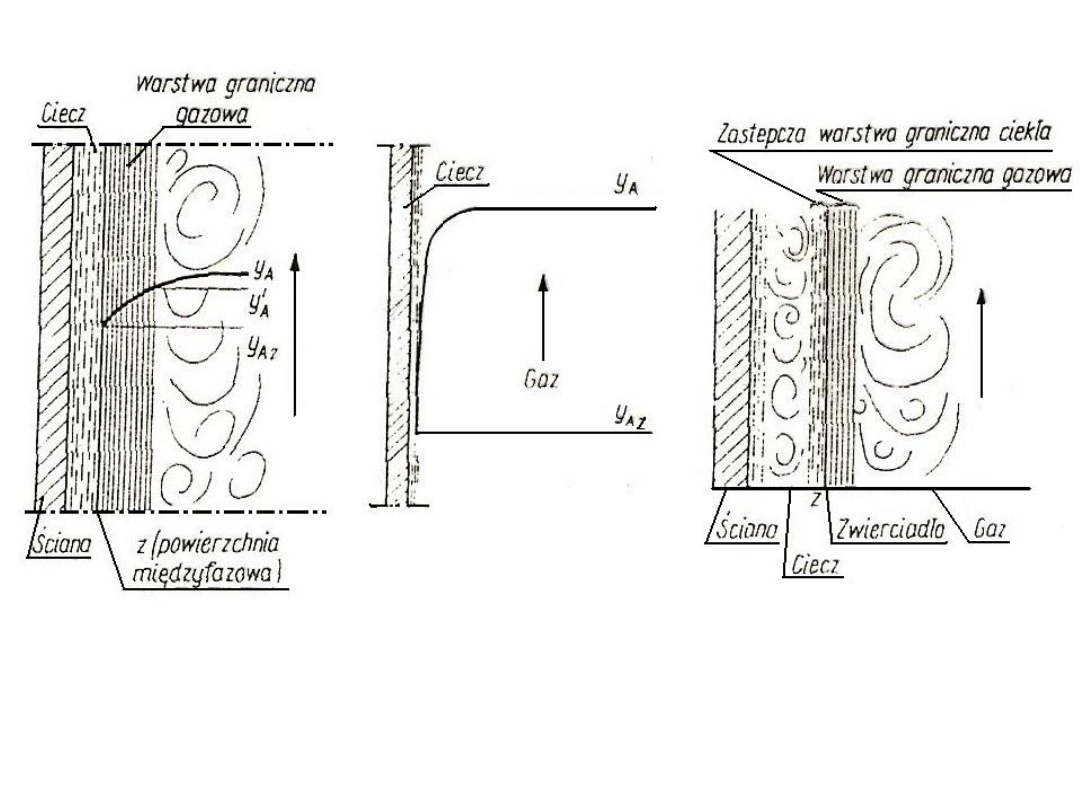
Rys. 17. Przykładowy

model wnikania masy

w fazie gazowej,

oznaczony przy

pomocy stężeń y

A

Rys. 18. Rozkład

stężeń przy wnikaniu

masy w fazie gazowej

Rys. 19. model ilustrujący

koncepcję dwóch warstw

granicznych

55

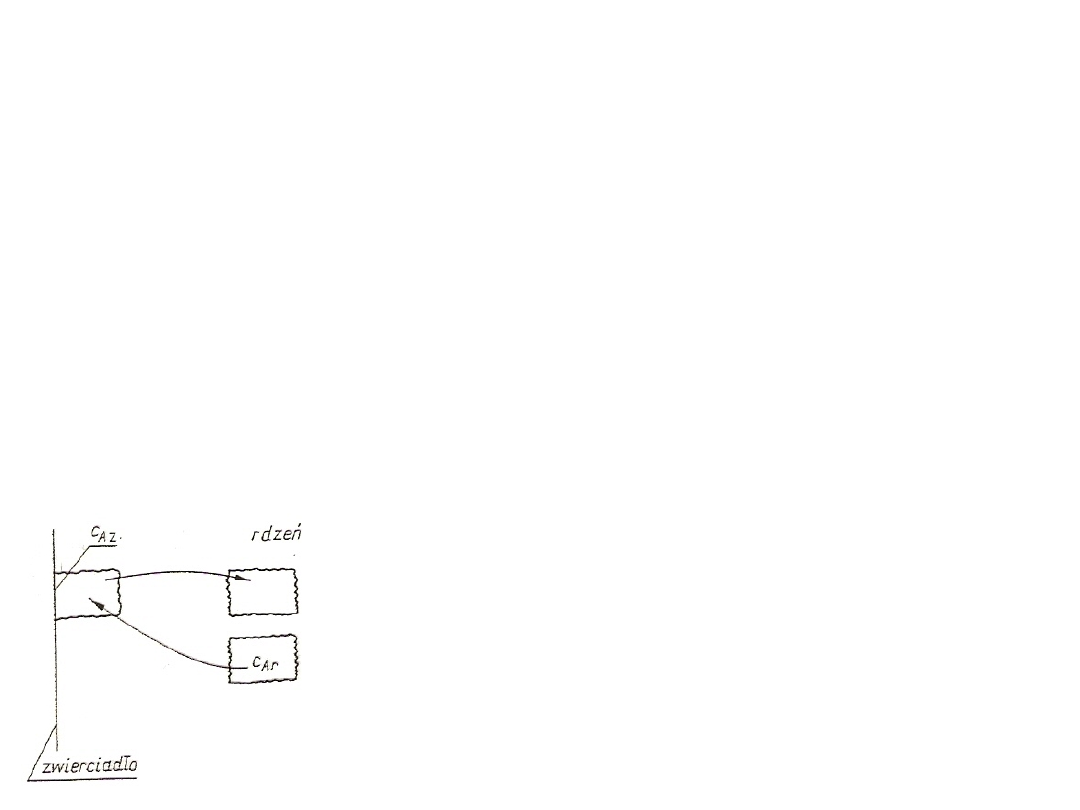
Model penetracji Hibgiego

Model ten został w zasadzie opracowany dla fazy ciekłej, jednakże
można za jego pomocą opisywać również wnikanie w fazie gazowej.
Założenia są następujące:

1. Stężenie składnika A na powierzchni międzyfazowej jest stałe i

wynosi c

Az

.

2. Stężenie składnika A w rdzeniu fazy jest wyrównane i wynosi c

Ar

.

3. Na powierzchni międzyfazowej znajdują się nieruchome elementy tej

fazy. Elementy te przebywają na powierzchni przez czas , a

następnie wskutek ruchu burzliwego zostają przenoszone do rdzenia.
Na powstałe miejsce przedostaje się inny element z rdzenia.

4. Długość elementu jest nieskończona. Stężenie składnika A w dużej

odległości od zwierciadła jest równe jego stężeniu w rdzeniu, czyli:

lim

z ∞

c

A

= c

Ar

Rys. 20. Schemat penetracyjnego wnikania

masy

56

Podczas przebywania elementu przy powierzchni odbywa się

nieustalona dyfuzja składnika A. Strumień wnikającego składnika zmienia
się w czasie. Średnia wartość tego strumienia jest równa średniej
całkowej z zawartości chwilowych względem czasu.

Na podstawie powyższych założeń przez rozwiązanie równania

dyfuzji nieustalonej uzyskuje się wzór teoretyczny na obliczanie
współczynnika wnikania masy przy znanej wartości czasu przebywania
elementów na powierzchni :



A

= 2 [D

Az

/ ()]

1/2

c

m

Model odnawiania powierzchni Danckwertsa

Jest to pewna modyfikacja modelu Higbiego. Wszystkie założenia

są w nim takie same, jak w modelu penetracji. Jedyna różnicą jest
założenie, że czas przebywania elementów na powierzchni jest losowy
(przypadkowy), natomiast stały jest parametr rozkładu czasów
przebywania p

s

zwany szybkością odnawiania powierzchni. Wynikiem

końcowym modelu jest wzór:



A

= [D

Az

p

s

]

1/2

c

m

Praktyczne zastosowanie wzoru wymaga znajomości parametru

p

s

.

Badania doświadczalne wykazują, że w układach o przepływie

zbliżonym do laminarnego wnikanie masy jest lepiej opisane przez teorię
warstewkową. W układach o większej burzliwości przepływu, bardziej
adekwatne są modele penetracyjne.

57

Sposoby wyznaczania

współczynników wnikania masy

Znajomość współczynników wnikania masy jest nieodzowna w

obliczeniach wymienników masy. Współczynniki wnikania masy mogą
być wyznaczone w sposób teoretyczny, półempiryczny i czysto
doświadczalny. Końcowe wzory określające współczynniki wnikania masy
są najczęściej przedstawiane za pomocą liczb bezwymiarowych.
Przedstawianie takie daje pewne uogólnienie wynikające z teorii
podobieństwa. najczęsciej stosuje się następujące liczby bezwymiarowe:

Liczba Sherwooda – Sh:

Sh = (

A

L) / 

Az

≈ (

C

L) / D

Az

„L” oznacza tutaj wymiar liniowy. W każdym przypadku wymiar ten
powinien być ściśle zdefiniowany.

Liczba Reynoldsa – Re:

Re = (w L ) / 

Zarówno prędkość w, jak i wymiar liniowy L są wielkościami

umownymi i powinny być ściśle zdefiniowane w każdym przypadku.
Liczba Reynoldsa charakteryzuje w pewnym sensie warunki
hydrodynamiczne panujące w układzie. Można przyjąć, że większej
wartości Re odpowiada większa burzliwość.

58

Liczba Schmidta – Sc:

Sc = v / D

Az

=  / (M

m



Az

)

Liczba Schmidta jest zależna tylko od właściwości

fizykochemicznych układu. może być zależna od temperatury poprzez
lepkość i współczynnik dyfuzji.

Liczba Fouriera – Fo:

Fo = (D

A

) / L

2

Wielkość  oznacza tutaj czas trwania procesu. Liczba Fouriera

charakteryzuje niestacjonarność procesu.

Liczba Pecleta – Pe:

Pe = (w L) / D

A

= Re · Sc

Wzory określające wnikanie masy bardzo często doprowadza się do

postaci:

Sh = f(Re, Sc, Fo, Pe, …)

Funkcja f najczęściej ma postać potęgową. Szczególnie postacie

wzorów dla różnych procesów i aparatów można znaleźć w literaturze
fachowej i naukowej.

59

Współczynnik dyfuzji

W poprzednich rozważaniach wprowadzono dwa współczynniki

dyfuzji: kinematyczny D

ij

[m

2

/s] i dynamiczny 

ij

[kmol/(m s)].

Współczynniki te są związane równaniem:



ij

= D

ij

c

m

dla fazy ciekłej:

c

m

= 

m

/ M

m

w którym c

m

oznacza całkowitą koncentrację.

Wielkość tę dla fazy gazowej pod umiarkowanym ciśnieniem

można obliczyć ze wzoru:

c

m

= p / (R T)

Współczynniki D

ij

i D

ji

oraz 

ij

i 

ji

nazywa się binarnymi

współczynnikami dyfuzji. Wychodząc z założenia Maxwella można
wykazać, że dla układów dwuskładnikowych:

D

AB

= D

BA

Binarne współczynniki dyfuzji są zatem sobie równe. Zależność

ta jest ścisła dla dwuskładnikowych układów gazowych.

60

Tab. 7.

61

Jeżeli całkowanie podstawowego równania różniczkowego

przeprowadzi się w granicach od y

iI

do pewnego y

i

, to otrzyma się

rozkład stężeń składnika i wzdłuż drogi dla tego przypadku:

y

i

= 1 – (1 – y

iII

)

z/s

(1 – y

iI

)

1-(z/s)

Przypadek dyfuzji jednego składnika przez inerty występuje

często w praktyce w procesach absorpcji lub desorpcji. Pewne
zastrzeżenie może tutaj budzić założenie, że inertne składniki nie
dyfundują. Przecież również dla nich występują gradienty stężeń w
kierunku przeciwnym, a więc powinny one dyfundować w tym kierunku.
W rzeczywistych układach absorpcyjnych i desorbcyjnych dyfuzja
składników inertnych jednak nie występuje. Dzieje się tak dlatego, że
opór w drugiej fazie jest tak duży dla tych składników, że nie mogą one
przepływać z jednej fazy do drugiej. A zatem można przyjąć, że w
warunkach ustalonych nie przepływają one (nie dyfundują) również w
obrębie jednej fazy.

W celu otrzymania rozkładu stężenia składnika i na drodze

dyfuzji całkuje się równanie w granicach od y

iI

do pewnego y

i

:

y

i

= y

iI

– (z / s) (y

iI

– y

iII

)

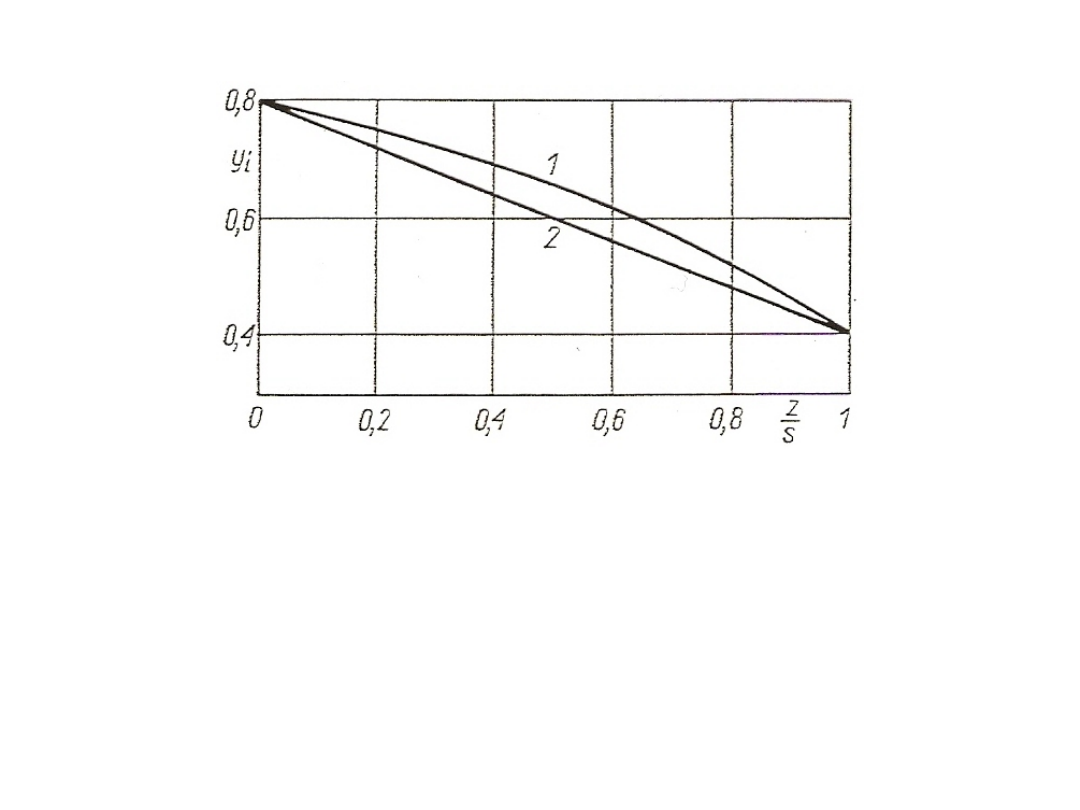
Jest to rozkład liniowy, przedstawiony graficznie na rys. 21.

62

Rys. 21. Rozkład stężeń: 1 – podczas dyfuzji przez inert;

2 – podczas dyfuzji ekwimolarnej przeciwkierunkowej

Przypadek dyfuzji ekwimolarnej występuje przede wszystkim

w procesach rektyfikacji. Otrzymane wzory można stosować również
w innych przypadkach, gdy stężenie rozważanego składnika i jest
małe. Wtedy y

i

<< 1  y

fi

≈ 1.

63

Przenikanie masy (dwie fazy) k-składników założenia:

- rozważać będziemy ruch wyróżnionego składnika A. Pozostałe

składniki mogą być obojętne lub również mogą się poruszać;

- każda faza składa się z rdzenia o wyrównanych stężeniach wszystkich

składników oraz ze strefy granicznej;

- strefy graniczne obydwu faz stykają się ze sobą wzdłuż powierzchni

międzyfazowej, którą nazywa się zwierciadłem.

Proces polegający na przenoszeniu składnika A z rdzenia jednej

fazy do rdzeni drugiej fazy nazywa się przenikaniem masy składnika
A:

Proces przenikania masy można podzielić na:

1. Proces wnikania masy od rdzenia fazy I do zwierciadła.

2. Proces przechodzenia masy przez zwierciadło.

3. Proces wnikania masy od zwierciadła do fazy II.

x – ułamki molowe w fazie I;

y - ułamki molowe w fazie II;

Ilościowo przenikanie masy jest dla danego układu określone

przez strumień składnika A przechodzący z fazy do fazy.
Podstawowym zagadnieniem w opisie przenikania masy jest więc
określenie gęstości strumienia J

A

. Rozważamy proces ustalony.

Gęstość strumienia przenikającej masy.

Współczynnik przenikania masy

W celu wyprowadzenia ogólnego wzoru określającego

przenikanie masy trzeba przyjąć następujące założenia:

1. Znane są współczynniki wnikania masy w obu fazach 

AI

i 

AII

.

2. Znana jest linia równowagi y*

A

= f(x

A

).

3. Na powierzchni międzyfazowej panuje równowaga międzyfazowa

składnika A:

y

Az

= y*(x

Az

)

Założenie to jest jednoznaczne ze stwierdzeniem, że powierzchnia
międzyfazowa nie stawia żadnego oporu dla ruchu składnika A.

4. Rodzaj dyfuzji w obu fazach jest taki sam, tzn. współczynnik ε

charakteryzujący dyfuzję jest jednakowy w obydwu fazach. Założenie
to jest słuszne dla ustalonego wnikania masy bez przebiegu reakcji
chemicznej. w przypadku wystąpienia reakcji chemicznej założenie
to może nie być słuszne.

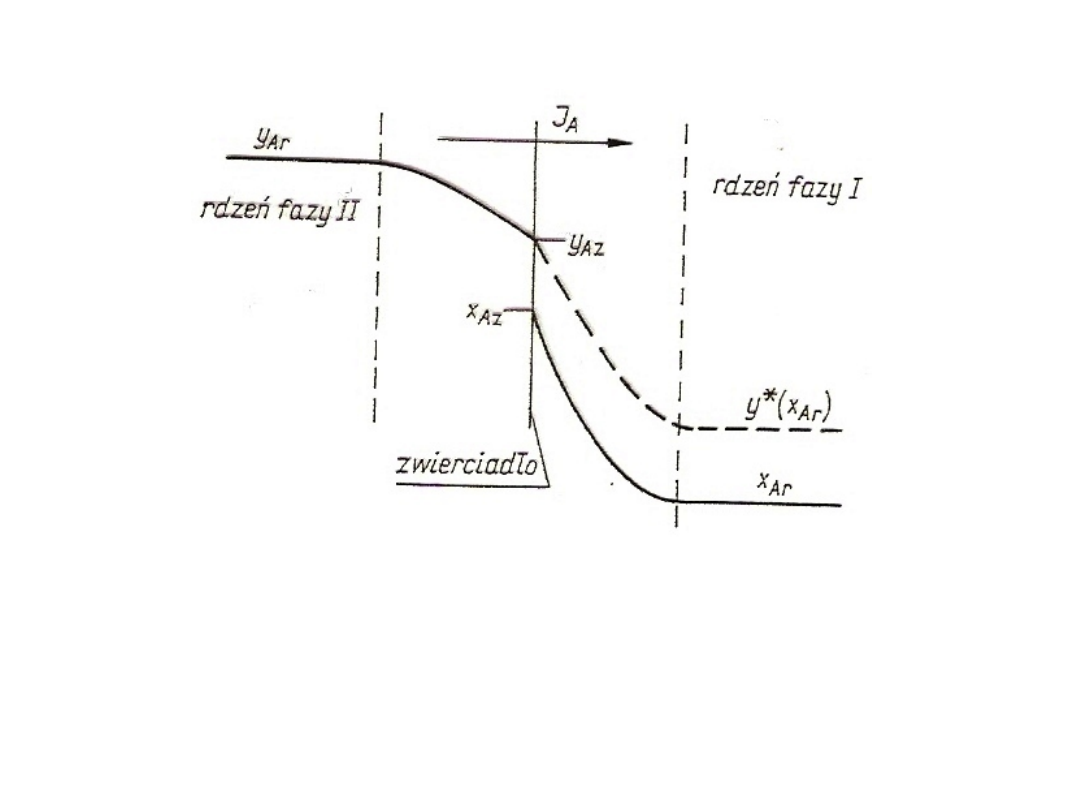
65

Rys. 22. Przykład rozkładu stężeń składnika A podczas przenikania masy

Ponieważ przenikanie jest ustalone, całkowita gęstość

strumienia masy przenikającej J

A

musi być równa gęstości strumienia

masy składnika A wnikającej od rdzenia fazy II do zwierciadła, jak
również gęstość strumienia masy składnika A wnikającej od
zwierciadła do rdzenia fazy I.

66

Gęstość strumienia masy przy wnikaniu można opisać

podstawowymi równaniami wnikania masy:

J

A

= 

AII

(

A

)

II

oraz:

J

A

= 

AI

(

A

)

I

gdzie: (

A

)

II

- moduł napędowy wnikania masy w fazie II;

(

A

)

I

-

moduł napędowy wnikania masy w fazie I;

Wielkości te można rozpisać:

(

A

)

I

= (y

Ar

– y

Az

) / (y

f

)

m

= (1 / 

A

) ln[(1 + 

A

y

Ar

) / (1 + 

A

y

Az

)]

(

A

)

II

=(x

Ar

– x

Az

) / (x

f

)

m

= (1 / 

A

) ln[(1 + 

A

x

Ar

) / (1 + 

A

x

Az

)]

zatem:

J

A

= (

AII

/ 

A

) ln[(1 + 

A

y

Ar

) / (1 + 

A

y

Az

)]

J

A

= (

AI

/ 

A

) ln[(1 + 

A

x

Ar

) / (1 + 

A

x

Az

)]

Następnie wzory te dzieli się stronami odpowiednio przez 

AII

i 

AI

:

J

A

/ 

AII

= (1 / 

A

) ln[(1 + 

A

y

Ar

) / (1 + 

A

y

Az

)] = (1 / 

A

) [ln(1 + 

A

y

Ar

) - ln(1 +



A

y

Az

)]

J

A

/ 

AI

= (1 / 

A

) ln[(1 + 

A

x

Ar

) / (1 + 

A

x

Az

)] = (1 / 

A

) [ln(1 + 

A

x

Ar

) - ln(1 +



A

x

Az

)]

J

A

= 

AII

(

A

)

II

= 

AII

(y

Ar

– y

Az

)

J

A

= 

AI

(

A

)

I

= 

AI

(x

Ar

– x

Az

)

67

Po podzieleniu powyższych równań stronami oraz odpowiednim

przekształceniu otrzymuje się równanie:

y

Az

= - (

AI

/ 

AII

) (x

Az

– x

Ar

) + y

Ar

Ze względu na x

Az

i y

Az

jet to równanie prostej przechodzącej

przez punkt (x

Ar

, y

Ar

) i mającej nachylenie (- 

AI

, 

AII

).

Na powierzchni międzyfazowej panuje równowaga, co oznacza,

że:

y

Az

= y*(x

Az

)

Zatem:

y*(x

Az

) = (- 

AI

/ 

AII

) (x

Az

– x

Ar

) + y

Ar

Punkt, którego współrzędne określają stężenia x

Az

i y

Az

, leży

zatem na przecięciu prostej z linią równowagi.

Można też pokazać graficzną interpretacje zamiennika n dla

przenikania z dyfuzją ekwimolarną przeciwkierunkową lub przy małych
stężeniach składnika A. Ze wzoru definicyjnego można otrzymać:

n = [y*(x

Az

) - y*(x

Ar

)] / (x

Az

– x

Ar

)

Jak wynika z powyższego wzoru, zamiennik n dla tego

przypadku jest równy nachyleniu linii prostej przechodzącej przez
punkty B i C.

68

Następnie w celu wyeliminowania stężeń przy zwierciadle

wprowadza się wielkość n określoną wzorem:

n = {ln[1 + 

A

y*(x

Az

)] – ln[1 + 

A

y*(x

Ar

)]} / [ln(1 + 

A

x

Az

) – ln(1 + 

A

x

Ar

)]

gdzie: - równowagowe stężenie składnika A do jego stężenia w rdzeniu
fazy I.

Obie strony równania mnoży się przez n:

(n J

A

) / 

AJ

= (1 / 

A

) {ln(1 + 

A

y

Ar

) - ln[1 + 

A

y*(x

Az

)]}

Następnie dodaje się stronami równania:

J

A

[(1 / 

AII

) + (n / 

AI

)] = (1 / 

A

) {ln(1 + 

A

y

Ar

) - ln[1 + 

A

y*(x

Az

)]}

Prawą stronę powyższej równości oznacza się przez (

A

)

0II

i

nazywa ogólnym modułem napędowym przenikania masy:

(

A

)

0II

=(1 / 

A

) {ln(1 + 

A

y

Ar

) - ln[1 + 

A

y*(x

Az

)]}

Wyrażenie określające można przedstawić w prostszej postaci,

wprowadzając średnią logarytmiczną. Można bardzo łatwo wykazać, że:

(

A

)

0II

= [y

Ar

- y*(x

Az

)] / (y

f

)

m

gdzie: (y

f

)

m

- średnia logarytmiczna z wyrażeń (1 + 

A

y

Ar

) i [1 + 

A

y*(x

Ar

)].

Moduł napędowy (

A

)

0II

można obliczyć znając stężenie

składnika A w rdzeniu obu faz.

J

A

= (

A

)

0II

/ [(1 / 

AII

) + (n / 

AI

)]

69

Bezpośrednie korzystanie ze wzoru definicyjnego, jest niemożliwe z

powodu nieznajomości wartości stężeń przy powierzchni międzyfazowej.
Dlatego trzeba go tak przekształcać, aby otrzymać wyrażenie nadające się do
bezpośredniego zastosowania:

n = {ln[1 + 

A

y*(x

Ar

)]} / ln(1 + 

A

y

Ar

)

Jeżeli występujące w tym wzorze przyrosty skończone zastąpi się

przyrostami różniczkowymi, to popełniony błąd nie będzie duży. Zatem:

n = {dln[1 + 

A

y*(x

Ar

)]} / dln(1 + 

A

y

Ar

) = { (1 + 

A

x

Ar

) / [1 + 

A

y*(x

Ar

) ] } (dy*

/ dx)

x=xAr

Wyrażenie (dy* / dx) określa nachylenie linii równowagi w układzie x-

y, które oznacza się symbolem m

y

:

(dy* / dx)

x=xAr

= m

y

Wyrażenie określające zamiennik n otrzymuje zatem postać:

n = m

y

{(1 + 

A

x

Ar

) / [1 + 

A

y*(x

Ar

)]}

Znając wartość m

y

, 

A

, x

Ar

i y*(x

Ar

) można obliczyć wartość zamiennika

n, a następnie wartość współczynnika przenikania masy k

A

.

Po wprowadzeniu współczynnika przenikania masy k

AII

otrzymuje się

podstawowe równanie przenikania masy:

J

A

= k

AII

(

A

)

0II

Równanie to jest prawdziwe w zastosowaniu do ustalonego przenikania, dla
różnych rodzajów dyfuzji, pod warunkiem, że w obydwu fazach zachodzi ten
sam rodzaj dyfuzji.

70

Jeżeli w obydwu fazach występuje dyfuzja ekwimolarna

przeciwkierunkowa lub stężenia składnika A są małe, powyższe wzory
znacznie się upraszczają. Ponieważ



A

= 0 i y

f

= 1, więc:

(

A

)

0II

= y

Ar

- y*(x

Ar

)

oraz:

n = m

y

Przypadki dyfuzji ekwimolarnej przeciwkierunkowej oraz dyfuzji w

małych stężeniach są bardzo częste, dlatego dokładnie rozważono
przenikanie masy w tych warunkach.

J

A

= (

A

)

0II

/( 1 / 

AII

) + (n / 

AI

)

Wzór ten jest nieco podobny do wzoru Ohma znanego z elektroniki.

Gęstość strumienia odpowiada natężeniu prądu, a moduł napędowy
odpowiada napięciu. Wobec tego wyrażenie w mianowniku powinno
odpowiadać oporowi przewodnika. Zgodnie z tą analogią mianownik
wyrażenia nazywa się oporem przenikania masy, a odwrotność oporu
przenikania nazywa się współczynnikiem przenikania masy i oznacza literką
k

A

. Zgodnie z tym:

1 / k

AII

= (1 / 

AII

) + (n / 

AI

)

Indeks II przy współczynniku k

A

oraz przy ogólnym module

napędowym (

A

)

0

oznacza, że za punkt odniesienia jest przyjęta faza II.

Moduł napędowy jest wyrażony za pomocą stężeń właściwych dla tej fazy.
W rozważanym przypadku stężeniami tymi są ułamki molowe y

A

.

71

Do obliczenia wartości współczynnika przenikania masy,

potrzebne są wartości współczynników wnikania 

AII

i 

AI

oraz wielkość

n, która jest nazywana zamiennikiem stężeń.

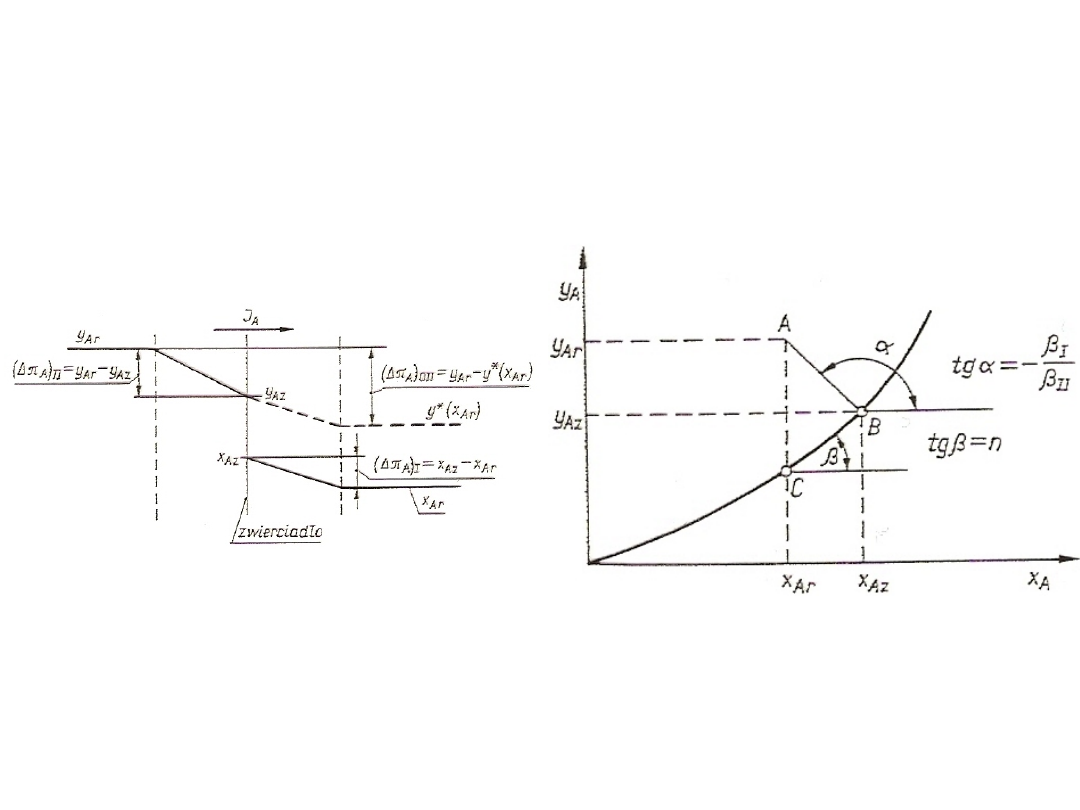
Rys. 23. Rozkład stężeń przy

przenikaniu składnika A w przypadku

dyfuzji ekwimolarnej

przeciwprądowej

Rys. 24. Wykreślna ilustracja

przenikania masy w układzie stężeń

x

A

-y

A

w przypadku dyfuzji

ekwimolarnej przeciwprądowej

72

Analogie

Wartości współczynników wnikania masy potrzebne do obliczeń

projektowych otrzymuje się najczęściej z badań eksperymentalnych.
Dzięki możliwości porównywania różnych układów wyniki uzyskane dla
jednego układu można przenieść na inny i w ten sposób częściowo
zaoszczędzić czas i koszty eksperymentu.

Jest to możliwe wówczas, gdy zachodzi analogia

MATEMATYCZNA  różne pod względem fizycznym procesy stosują się

do tych samych praw matematycznych.

Analogia taka zachodzi w przypadku transportu pędu, ciepła i

masy. Dzięki niej, ze znanych np. współczynników wnikania ciepła,
można wnioskować o wartości współczynników wnikania masy i
odwrotnie.

Należy jednak pamiętać, że tylko w niektórych przypadkach ta

analogia jest ścisła,  jest to w większości przypadków przybliżenie.

które umożliwia właściwe ukierunkowanie badań teoretycznych lub
eksperymentalnych w celu znalezienia właściwych zależności.

73

Analogie między transportem

pędu, ciepła i masy

Podstawą analogi transportu pędu, ciepła i masy jest

podobieństwo podstawowych praw opisujących te procesy, tzn. prawa
Newtona, Fouriera i Ficka, które dla jednego kierunku z mają postać:

F

S

/ (A ) = -  (dw / dz) (prawo Newtona)

Q* / (A c

P

) = - a (dT / dz)

(prawo Fouriera)

n`

A

/ A = - D

Az

(dc

A

/ dz) (prawo Ficka)

gdzie: , a i D

Az

- podstawowe współczynniki kinetyczne, m

2

/s;

Q*

- strumień ciepła, W;

n`

A

- strumień masy, kmol/s;

F

s

- siła naprężeń statycznych odpowiadająca

strumieniowi pędu, N.

74

W rozważaniach analogi często wykorzystuje się analizę

wymiarową, w której operuje się liczbami bezwymiarowymi zwanymi
liczbami podobieństwa. Definicje podstawowych liczb bezwymiarowych
wynikają ze stosunków współczynników , a i D

Az

w powyższych

wzorach – są to odpowiednio liczby Prandtla – Pr, Schmidta – Sc i
Lewisa – Le:

Pr = / a = (c

P

 ) /  = (c

P

) / 

Sc = / D

Az

= ( c

m

) / 

Az

=  / (M

m



Az

)

Le = a / D

Az

= / (c

P



Az

M

m

) = Sc / Pr

W teorii analogi transportu masy i pędu często stosuje się

Liczbę Stantona St:

St = Sh / (Re Sc)

gdzie: Sh i Re – liczby Sherwooda i Reynoldsa zdefiniowane wzorami.

Analogia transportu masy i pędu daje wyniki w przypadku

przepływu płynu przez rurociągi. Przy założeniu odpowiedniego
rozkładu prędkości w rurociągu otrzymuje się wzory nazywane
odpowiednio analogami Reynoldsa, Taylora, Karmana i Colburna.

Analogia Reynoldsa:

St =  / 8

W analogi tej zakłada się w całym przekroju ruch burzliwy i równość Sc
= 1.

75

Analogia Taylora

St = ( / 8) / [1 + 5 ( / 8)

1/2

(Sc – 1)]

Do wyprowadzenia powyższego wzoru wykorzystuje się uniwersalny
rozkład prędkości.

Analogia Karmana

W analogi tej zakłada się istnienie w rurociągu trzech stref: przepływu
laminarnego, przepływu burzliwego i przejściowej:

St = ( / 8) / {1 + 5 ( / 8)

1/2

[Sc – 1 + ln((5 Sc + 1)/6)]}

Jeżeli Sc = 1, to zarówno analogia Taylora jak i Karmana sprowadzają się
do prostej analogi Reynoldsa.

Analogia Colburna

St = ( / 8) / Sc

2/3

Po rozwinięciu liczby Stantona otrzymuje się analogię Colburna w
postaci:

Sh / (Re Sc

1/3

) = ( / 8)

Doświadczenia wykazały, że analogia Colburna daje bardzo dobre
wyniki.

Na podstawie powyższych wzorów można obliczyć współczynnik

wnikania masy korzystając ze znajomości łatwego do wyznaczenia
współczynnika oporu  występującego we wzorze Darcy`ego-

Weissbacha.

76

Dzięki analogi w procesach transportu ciepła i masy można

wyznaczyć współczynnik wnikania masy, korzystając ze wzorów
wyprowadzonych na podstawie badań wnikania ciepła.

Współczynnik przewodzenia temperatury (współczynnik

wyrównania temperatury, dyfuzji ciepła) a:

a =  / (c

P

)

[m

2

/s]

Kinematyczny współczynnik lepkości  [m

2

/s].

=

Zastępczy wymiar liniowy 

z

:



z

= [ 

2

/ (g 

2

)]

1/3

(zastępczy wymiar poprzeczny dla przepływu nieustalonego).

77

Ogólne zasady obliczania

wymienników masy

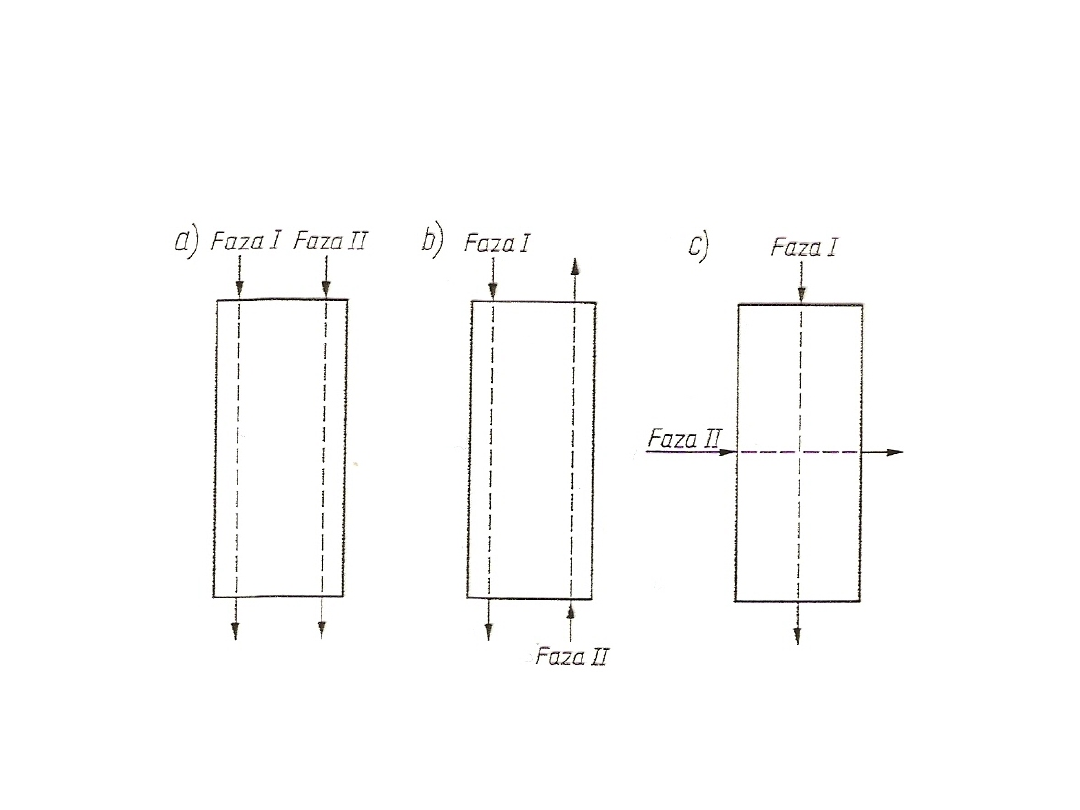
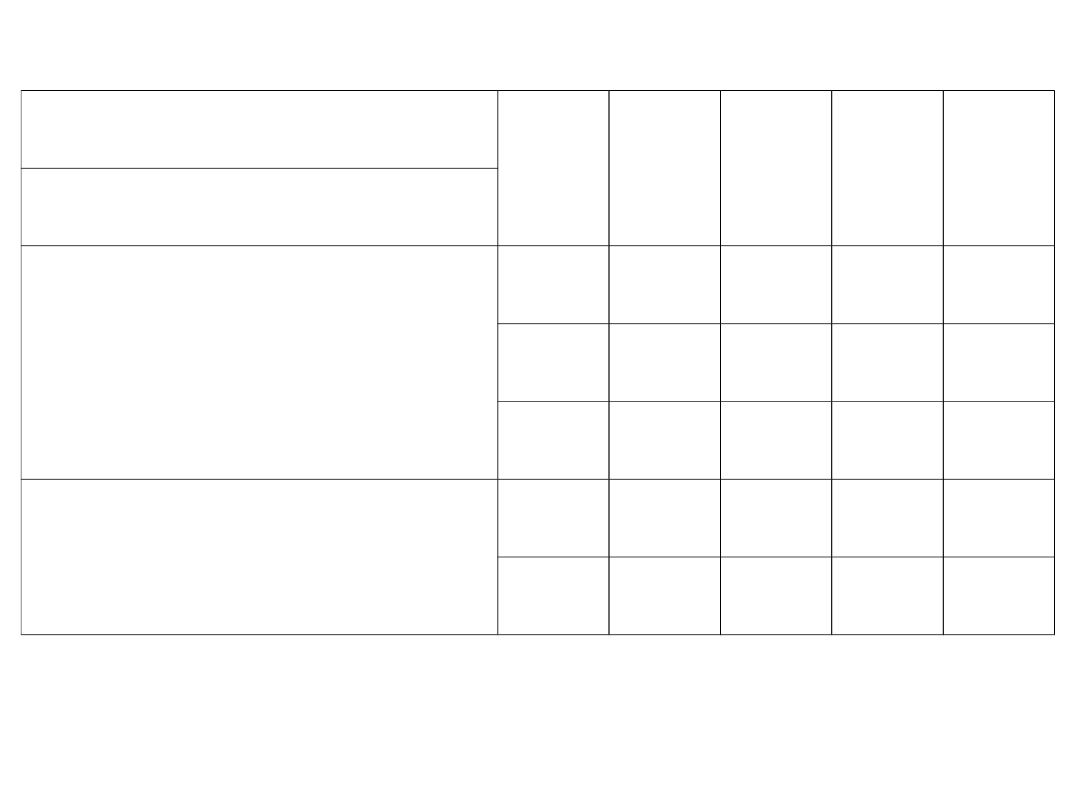
Rys. 25. Sposoby prowadzenia faz w wymiennikach masy:

a) współprąd, b) przeciwprąd, c) prąd krzyżowy

Bilanse materiałowe

ciągłych wymienników

masy

Rozważania ogólne

W obliczeniach wymienników masy bardzo ważną rolę

odgrywają bilanse materiałowe, a zwłaszcza bilans wymienianego
składnika, np. A. Zakłada się, że w wymienniku kontaktują się fazy I i II
oraz, że jest wymieniany składnika A. Aby rozważania uogólnić stosuje
się tzw. uogólnione strumienie 

I

, 

II

i 

A

oraz uogólnione stężenia S

A

i

Z

A

. Szczegółowe znaczenie tych symboli dla konkretnych procesów

zestawiono w tabeli poniżej. Indeksem r oznaczono tam strumienie
składników inertnych, czyli rozpuszczalników. Na kolejnym rysunku
przedstawiono graficzną ilustracje bilansu materiałowego w układzie
stężeń uogólnionych dla współprądu oraz przeciwprądu. Bilans ogólny
nie zależy od sposobu prowadzenia faz i zapisać można go w postaci
równania:



Ip

S

Ap

+ 

IIp

Z

Ap

= 

Ik

S

Ak

+ 

IIk

Z

Ak

Strumień wymienianego składnika A można wyrazić za pomocą

równań:



A

= 

IIp

Z

Ap

- 

IIk

Z

Ak

= 

Ik

S

Ak

-



Ip

S

Ap

79

Tab. 8. Zestawienie strumieni i stężeń uogólnionych

Na ogół strumienie przepływających faz zmieniają się wzdłuż

aparatu (kolumny). Często jednak można tak dobrać stężenia S

A

i Z

A

,

aby odpowiednie strumienie 

I

i 

II

były stałe wzdłuż całego aparatu.

Oznaczenie:



I



I



A

S

A

Z

A

Proces:

Absorpcja, desorpcja
- dyfuzja przez inert

n`

cr

n`

gr

n`

A

X

A

Y

A

m`

cr

m`

gr

m`

A

X`

A

Y`

A

V`

c

V`

g

n`

A

c

cA

c

gA

Destylacja, rektyfikacja
- dyfuzja ekwimolarna
przeciwkierunkowa

n`

c

n`

g

n`

A

x

A

y

A

m`

c

m`

g

m`

A

x`

A

y`

A

80

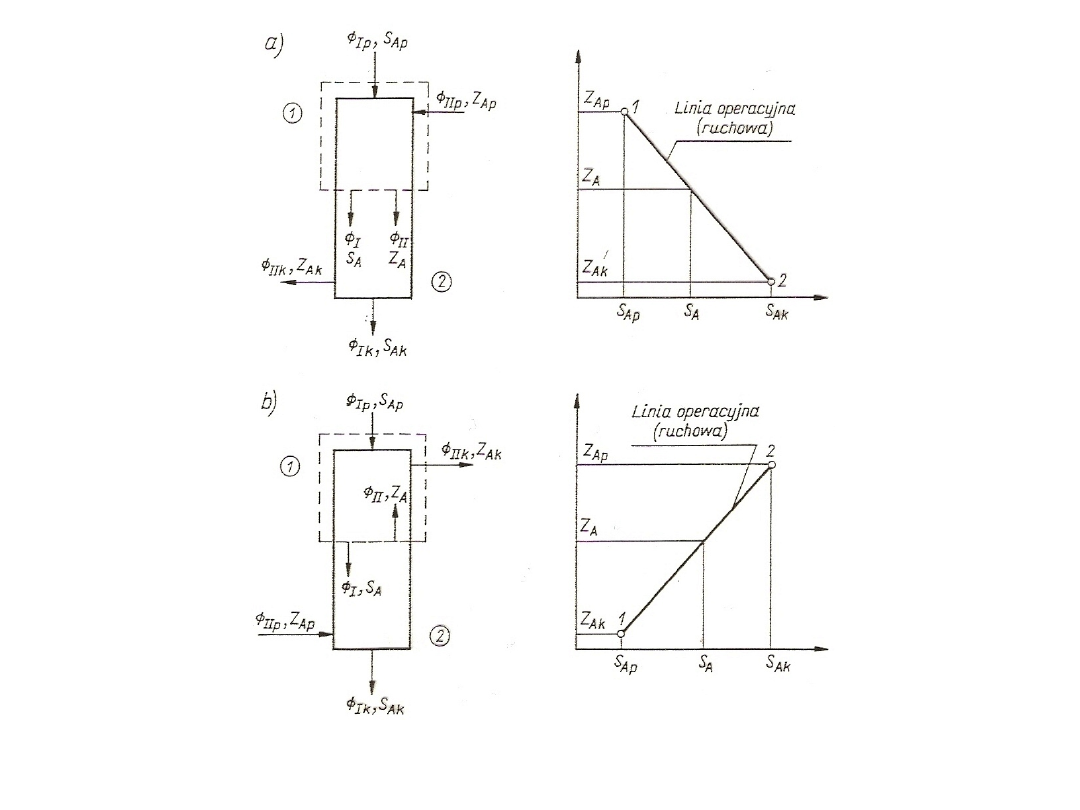
Rys. 26. Ilustracja bilansu materiałowego składnika A na wykresie stężeń

uogólnionych: a) współprąd, b) przeciwprąd

81

W dalszych rozważaniach zakłada się, że strumienie 

I

i 

II

są

stałe tzn.:



I

= 

Ip

= 

Ik



II

= 

IIp

= 

IIk

Równani na 

A

otrzymuje postać:



A

= 

II

(Z

Ap

- Z

Ak

) = 

I

(S

Ak

- S

Ap

)

Częściowe bilansowanie wymiennika (w przestrzeni oznaczonej

linią kreskowaną na rysunku) umożliwia uzależnienie od siebie stężeń
składników A w obydwu fazach w dowolnym przekroju aparatu.

Bilans wymiennika współprądowego

Bilans częściowy wymiennika współprądowego ma postać

równania:



Ip

S

Ap

+ 

IIp

Z

Ap

= 

I

S

A

+ 

II

Z

A

Po przekształceniu;

Z

A

= - (

I

/ 

II

) S

A

+ (

Ip

/ 

II

) S

Ap

+ (

IIp

/ 

II

) Z

Ap

Jest to zależność w układzie Z

A

-S

A

w określonym przekroju

wymiennika. Graficzna ilustracja tej zależności nosi nazwę linii
operacyjnej (ruchowej).

Z założenia o stałości strumieni:

Z

A

= - (

I

/ 

II

) S

A

+ (

I

/ 

II

) S

Ap

+ Z

Ap

82

Bilans wymiennika przeciwprądowego

Bilans przestrzeni zakreślonej na ostatnim rysunku:



Ip

S

Ap

+ 

II

Z

A

= 

I

S

A

+ 

IIk

Z

Ak

stąd

Z

A

= (

I

/ 

II

) S

A

+ (

IIk

/ 

II

) Z

Ak

- (

Ip

/ 

II

) S

Ap

Równanie to jest ogólną postacią równania linii operacyjnej

przeciwprądowego wymiennika masy. Z założenia o stałości strumieni:

Z

A

= (

I

/ 

II

) S

A

+ Z

Ak

- (

I

/ 

II

) S

Ap

W procesach absorpcji i desorpcji używa się stosunków

masowych i molowych i zakłada się, że stałe są strumienie inertów w
fazie ciekłej i gazowej (n`

gr

= const, n`

cr

= const).

W procesie rektyfikacji, przy założeniu ekwimolarnej wymiany

masy stałe są molowe strumienie czynników (n`

g

= const, n`

c

= const).

83

Gabaryty

Najczęściej spotykanym zagadnieniem wymienników masy jest

wyznaczenie wymaganej wielkości (wysokości) aparatu
zapewniającego założone stężenie wylotowe.

Wielkość ta zależy przede wszystkim od intensywności

wymiany masy, który z kolei określa szybkość przenikania masy.

Przenikanie masy jest możliwe wówczas, gdy stężenie

składnika A w określonym przekroju jest różne od stężenia
równowagowego. Warunki równowagowe określa się za pomocą linii
równowagi, jeśli na wykresie Z

A

-S

A

leży ona niżej niż linia operacyjna,

to w całym aparacie Z

A

> Z*

A

, co oznacza, że składnik A przenika od

fazy II do fazy I (absorpcja).

Gdy linia równowagi leży wyżej niż linia operacyjna, wówczas

Z

A

< Z*

A

i składnik A przechodzi od fazy I do fazy II (desorpcja).

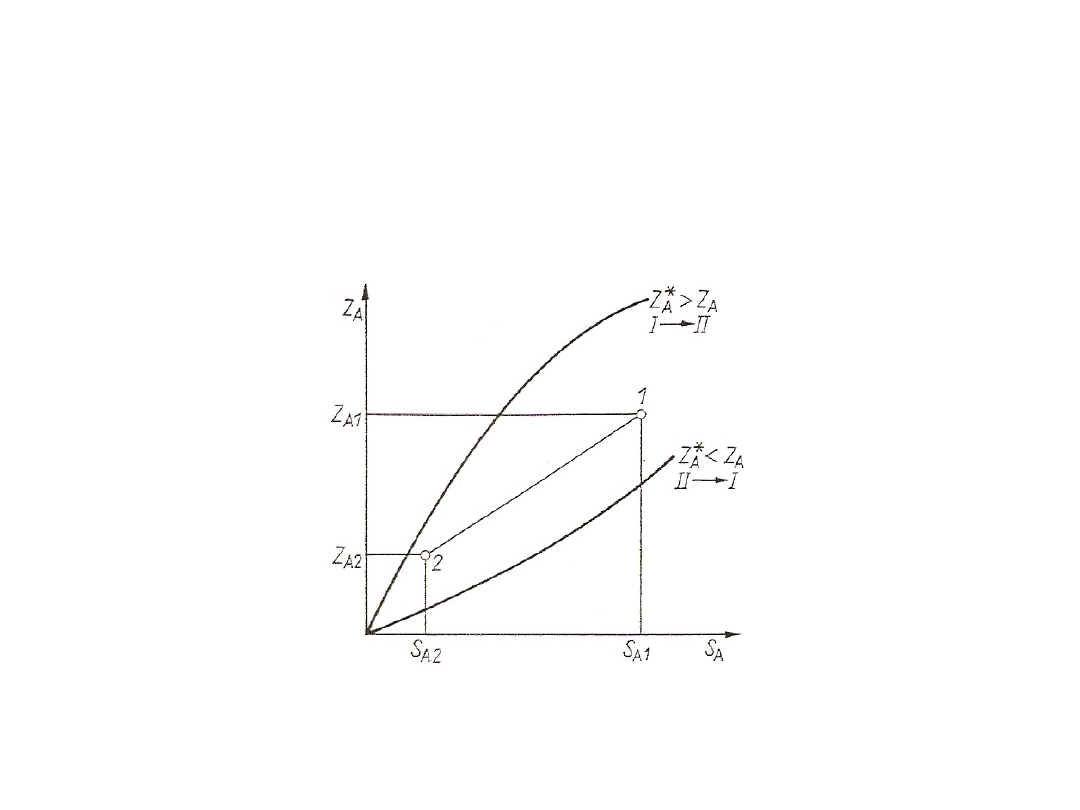
Metody obliczania

gabarytów wymienników

masy

Rozważania ogólne

Rys. 27. Wpływ wzajemnego usytuowania linii równowagi

i operacyjnej na kierunek transportu składnika A

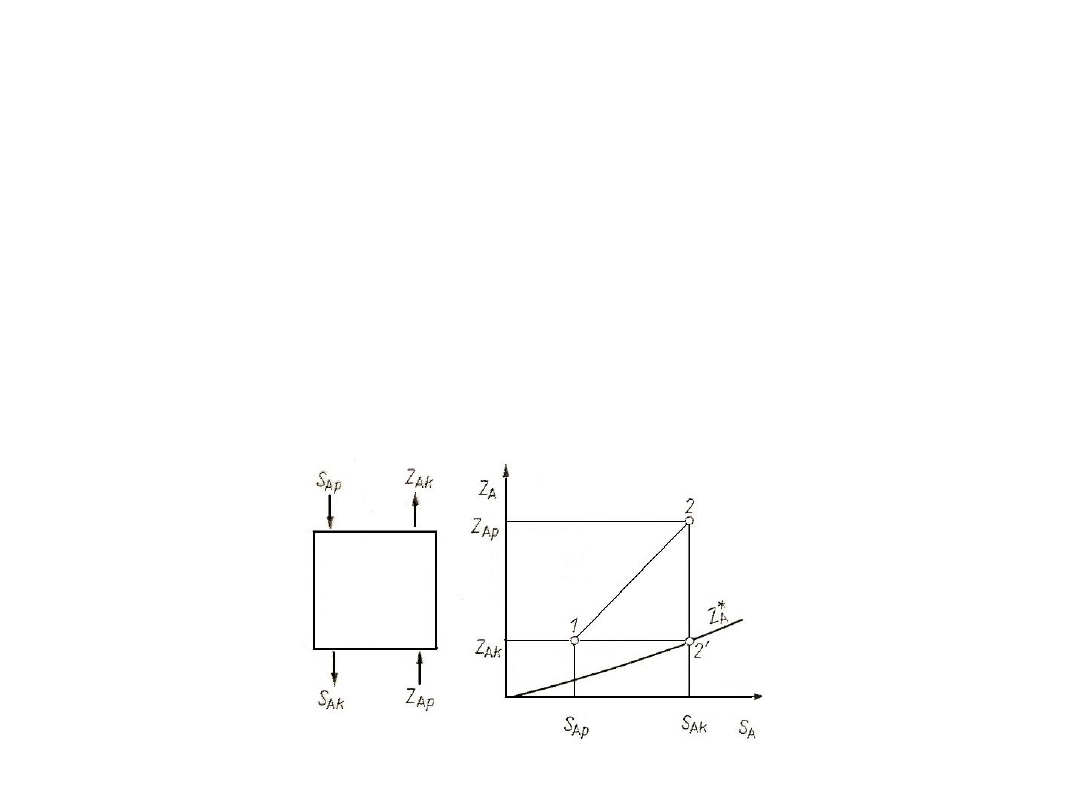
85

W praktyce najczęściej stosuje się 3 metody obliczania

wielkości wymienników masy:

- metodę stopni teoretycznych;
- metodę kinetyczną;
- metodę Colburna.

Metoda stopni teoretycznych

Na rysunku 28 przedstawiono wymiennik z zaznaczonymi

stężeniami wlotowymi i wylotowymi. Zakłada się, że dla punktu 2`
jest spełniona zależność:

Z

Ak

= Z*(S

Ak

)

Rys. 28. Metoda stopnia teoretycznego

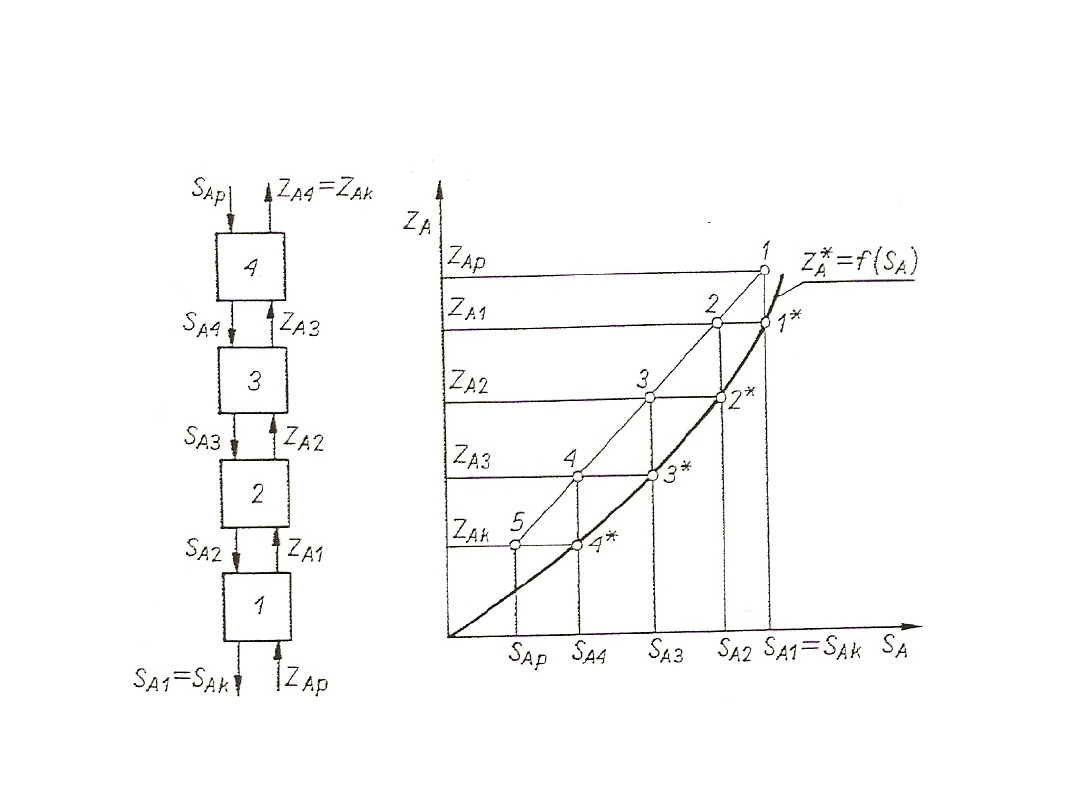
86

Z

Aj

= Z*(S

Aj

)

Rys. 29. Praca przeciwprądowej kaskady wymienników (stopni teoretycznych)

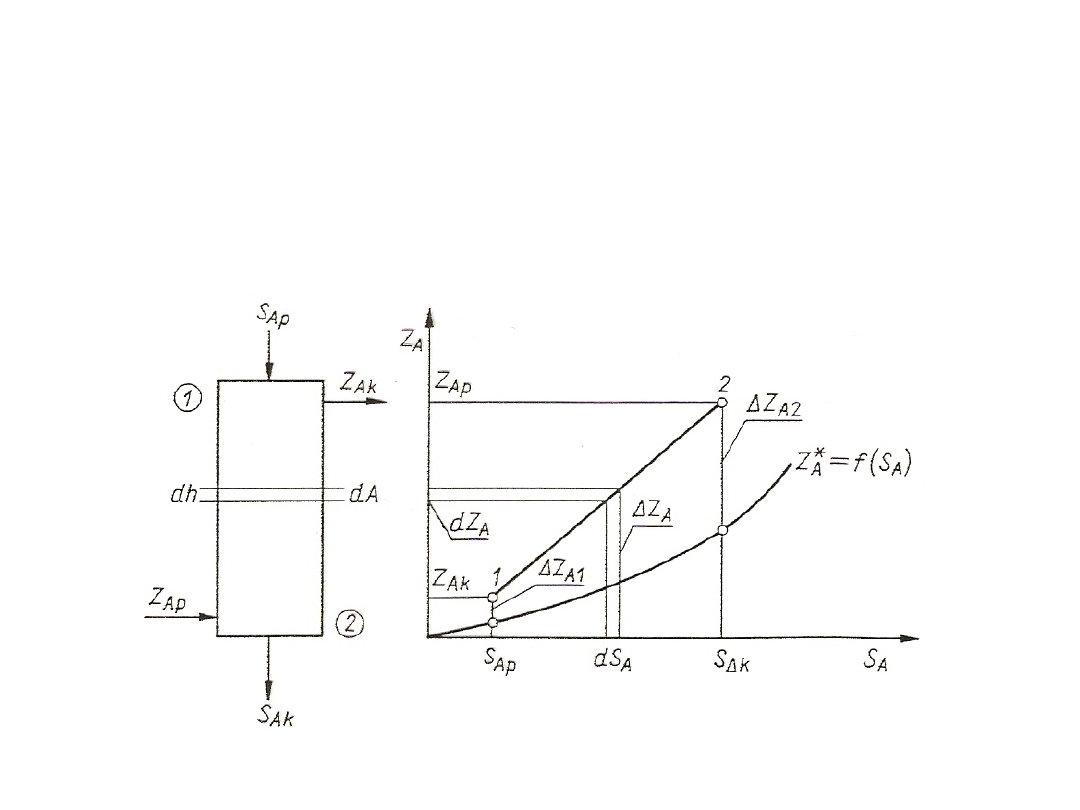
87

Metoda kinetyczna

W metodzie kinetycznej stosuje się wzór określający szybkość

przenikania masy składnika A. Podstawową jej ideą jest założenie. że
całkowity strumień wymienianego składnika A można zapisać za
pomocą wzoru:



A

= k

A

A (

A

)

m

gdzie: (

A

)

m

- średni moduł napędowy przenikania asy składnika A.

Rys. 30. Wykres pomocniczy do kinetycznej metody obliczania wymienników

masy

88

W różniczkowej warstwie wymiennika o powierzchni wymiany dA

następują przyrosty stężeń dS

A

i dZ

A

. W rozważanej warstwie zachodzi

przenikanie masy, dla którego:

J

A

= d

A

/ dA = k

AII

(

A

)

0II

Jednocześnie z bilansu warstwy:

d

A

= 

II

dZ

A

= 

I

dS

A

Połączenie tych dwóch wzorów prowadzi do zależności:

dA = (

II

dZ

A

) / [k

AII

(

A

)

0II

]

Po scałkowaniu w granicach od punktu 1 do 2 otrzymuje się:

A = ∫

1

2

(

II

dZ

A

) / [k

AII

(

A

)

0II

]

(

A

)

m

= [

II

(Z

Ap

- Z

Ak

)] / {k

A

∫

1

2

(

II

dZ

A

) / [k

AII

(

A

)

0II

]}

Przy założeniu, że w całym wymienniku 

II

= const oraz k

A

=

const = k

AII

otrzymuje się wyrażenie określające średni moduł napędowy

napędowy wymiennika masy:

(

A

)

m

= (Z

Ap

- Z

Ak

) / ∫

1

2

dZ

A

/ (

A

)

0II

89

Obliczanie całki w mianowniku w istotny sposób zależy od sposobu
wyrażania modułu napędowego przenikania masy oraz od
zależności((

A

) = f(Z

A

). Jeżeli założy się zależność liniową, to średni

moduł napędowy będzie średnią logarytmiczną z modułów na końcach
wymiennika, tzn.:

(

A

)

m

= (

A1

– 

A2

) / ln 

A2

/ 

A1

Metoda Colburna

Jest to pewna modyfikacja metody kinetycznej. W literaturze

znana jest również pod nazwą metody wysokości jednostkowej
wymiany masy HTU [Hight of Transfer Unit].

Podstawowy wzór tej metody jest następujący:

H = (h

og

) (N

og

)

lub:

H = (h

oc

) (N

oc

)

gdzie: H

- wysokość wymiennika masy, m;

h

og

i h

oc

- jednostkowa wysokość wymiany masy odniesiona do

fazy

gazowej

lub ciekłej, m;

N

og

i N

oc

- liczba jednostek wymiany masy w fazie gazowej lub

ciekłej.

90

Wysokość różniczkowej warstwy wymiennika można związać z

różniczkową powierzchnią wymiany masy dA za pomocą zależności:

dh = dA /a dA

k

gdzie: a

– tzw. jednostkowa powierzchnia wymiany masy, tzn.

powierzchnia odniesiona do objętości, m

2

/m

3

;

A

k

– przekrój poprzeczny aparatu, m

2

.

dh = (

II

dz

A

) / [a A

k

k

AII

(

A

)

0II

]

Po scałkowaniu w granicach od punktu 1 do 2:

H = ∫

ZAk

ZAp

{(

II

dz

A

) / [a A

k

k

AII

(

A

)

0II

]}

Po założeniu, że wielkość 

II

/ (a A

k

k

AII

) = const, można napisać:

H = [

II

/ (a A

k

k

AII

)] ∫

ZAk

ZAp

[ dz

A

/ (

A

)

0II

] = (h

og

) (N

og

)

gdzie:

h

og

= 

II

/ (a A

k

k

AII

)

N

og

= ∫

ZAk

ZAp

[ dz

A

/ (

A

)

0II

]

91

Rektyfikacja

Destylacja prosta umożliwia jedynie ograniczony rozdział

mieszaniny na składniki, przy czym stopień czystości produktów
(destylatu i wyczerpanej cieczy) zależy od tego, jak dalece linia
równowagi odbiega od przekątnej kwadratu stężeń x-y. Aby osiągnąć
lepszy rozdział mieszaniny, a w granicznym przypadku zupełnie
czyste składniki, należy stosować bardziej skomplikowaną metodę
rozdziału – rektyfikację. Proces ten prowadzi się najczęściej w
aparatach nazywanych kolumnami rektyfikacyjnymi.

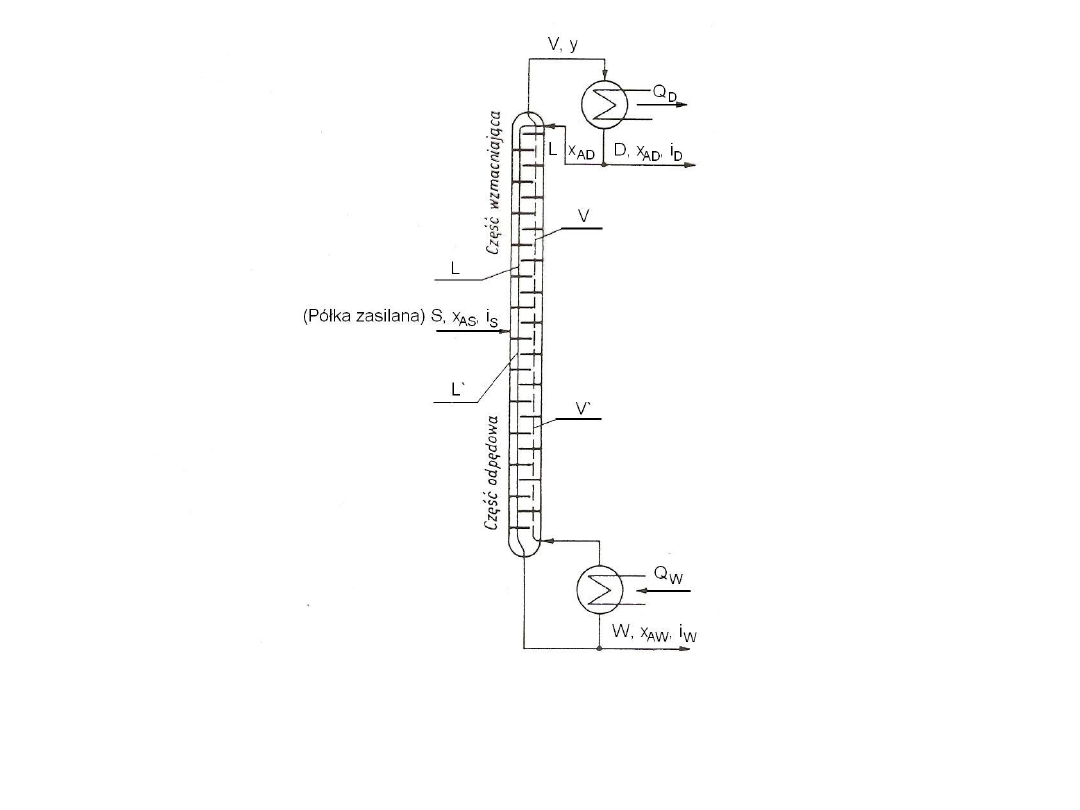
92

Rys. 31. Schemat kolumny rektyfikacyjnej do rozdzielania mieszaniny

dwuskładnikowej

CZĘŚĆ WZMACNIAJĄCA ≡ REKTYFIKACJA

CZĘŚĆ ODPĘDOWA ≡ ODPAROWUJĄCA ≡ WYCZERPUJĄCA

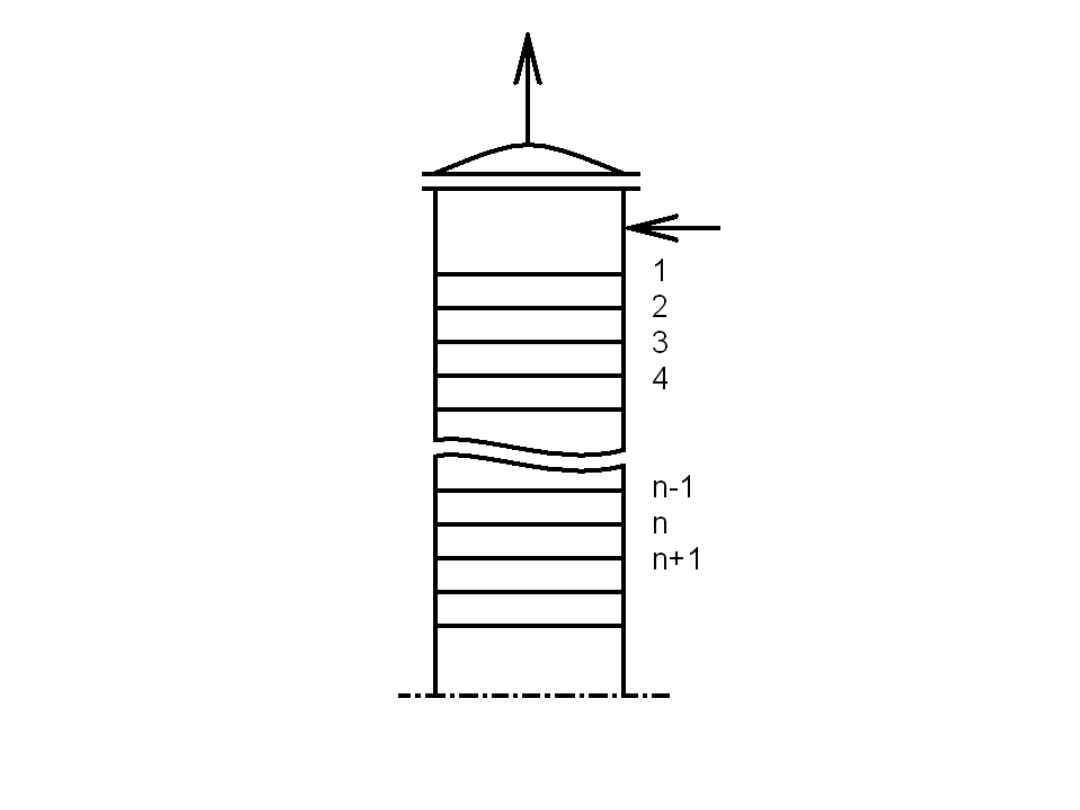
93

Rys. 32. Zasada numeracji półek w kolumnie rektyfikacyjnej

94

W praktyce najczęściej jest dany strumień surowca S oraz jego

skład wyrażony przez stężenie x

AS

. Celem rektyfikacji jest rozdział

surowca na destylat o stężeniu składnika D x

AD

i ciecz wyczerpaną o

stężeniu x

AW

. W dalszym ciągu rozważań indeks D będzie oznaczał

wielkość charakterystyczną dla destylatu, natomiast indeks W wielkość
charakterystyczną dla cieczy wyczerpanej (wypływającej z kotła
destylacyjnego).

Pierwszym zadaniem jest wyznaczenie otrzymanych w danej

instalacji strumieni destylatu i cieczy wyczerpanej. W tym celu
wykonuje się bilans molowy całej kolumny.

Bilans masowy kolumny

S = D + W

S x

AS

= D x

AD

+ W x

AW

Stąd np.:

D = (x

AS

- x

AW

) / (x

AD

- x

AW

) S

W = (x

AD

- x

AS

) / (x

AD

- x

AW

) S

Bilans cieplny kolumny

Q

W

+ S i

S

= D i

D

+ W i

W

+ Q

D

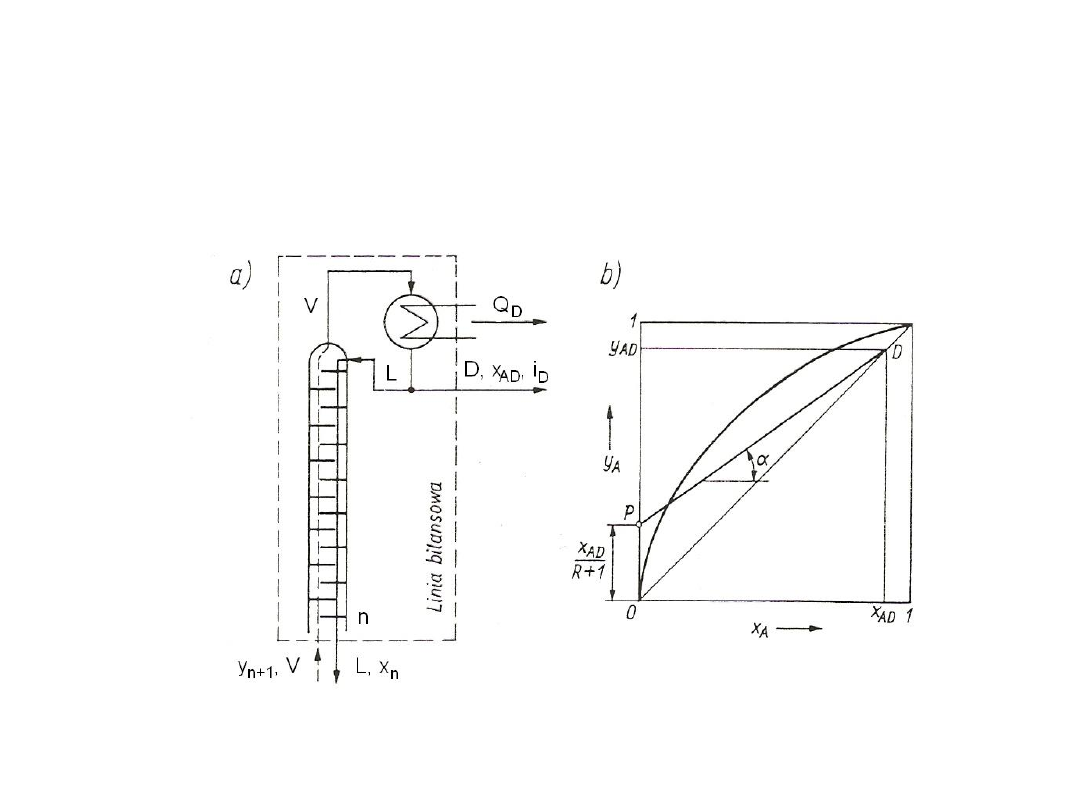
95

Bilanse masowe i linie operacyjne

dla pełnego zestawu

rektyfikacyjnego

Część wzmacniająca (górna) kolumny rektyfikacyjnej

Linią bilansową (kreskowaną) wyodrębnia się część wzmacniającą

kolumny.

Rys. 33. Część wzmacniająca kolumny rektyfikacyjnej:

a) schemat bilansowania, b) linia operacyjna

96

Bilans skraplacza

V = D + L

Założenia początkowe: kolumna pracuje z pełnym zawracaniem
destylatu  D = 0

V = L

V y

n+1

= L x

n

Równanie linii bilansowej ma więc postać:

y

A

= x

A

 linia bilansowa pokrywa się z podstawą kwadratu stężeń x-y –

część b rysunku.

97

Jak zmieniają się parametry strumienia ciekłego i parowego

wzdłuż kolumny, gdy odbiera się część destylatu D > 0.

Założenia upraszczające:

- mamy do czynienia z układem dwuskładnikowym który
charakteryzuje się jednakowymi kilomolowymi entalpiami wrzenia
czystych składników A i B oraz, że entalpia wrzącej mieszaniny cieczy
złożonej ze składników A i B nie zależy od składu i równa się entalpii 1
kilomola składnika A albo B:

i`

n+1

≈ i`

n

≈ i`

n-1

≈ … ≈ i`

- zmiany ciśnienia wzdłuż wysokości kolumny są bardzo małe 

i = const

- ciepło parowania 1 kmol składnia w Ai B oraz i kmol mieszaniny
wrzącej cieczy złożonej ze składników A i B gdzie stałe:

r

n+1

≈ r

n

≈ r

n-1

≈ … ≈ r

- kolumna pracuje adiabatycznie  ciepło wyzwolone podczas

skraplania 1 kmol mieszaniny ze strumienia pary do strumienia cieczy
powoduje odparowanie 1 kmol cieczy i powstanie 1 kmol pary bogatej
w składnik bardziej lotny  Strumienie molowe cieczy i pary podczas

przepływu przez daną część kolumny są stałe.

98

V = L + D

dla n-tej półki i składnika A

V y

n+1

= L x

n

+ D x

D



y

n+1

= (L / V) x

n

+ (D / V) x

D



y

n+1

= [L / (L + D)] x

n

+ [D / (L + D)] x

D

Wielkości x

n

, y

n+1

możemy traktować jako zmienne bieżące

(punkt o tych współrzędnych leży na linii operacyjnej), a równanie
ostatnie można napisać wtedy w postaci ogólnej:

y = [L / (L + D)] x + [D / (L + D)] x

D

Jest to równanie GLO.

Wprowadzając pojęcie powrotu (orosienia):

R = L / D

otrzymujemy:

y = [R / (R + 1)] x + [I / (R + 1)] x

D

[UWAGA: to są stężenia molowe]

Jest to najczęściej spotykane równanie linii operacyjnej (bilansowej)
GLO. Uwaga: linia operacyjna jest linią prostą tylko przy spełnieniu
wszystkich założeń upraszczających.

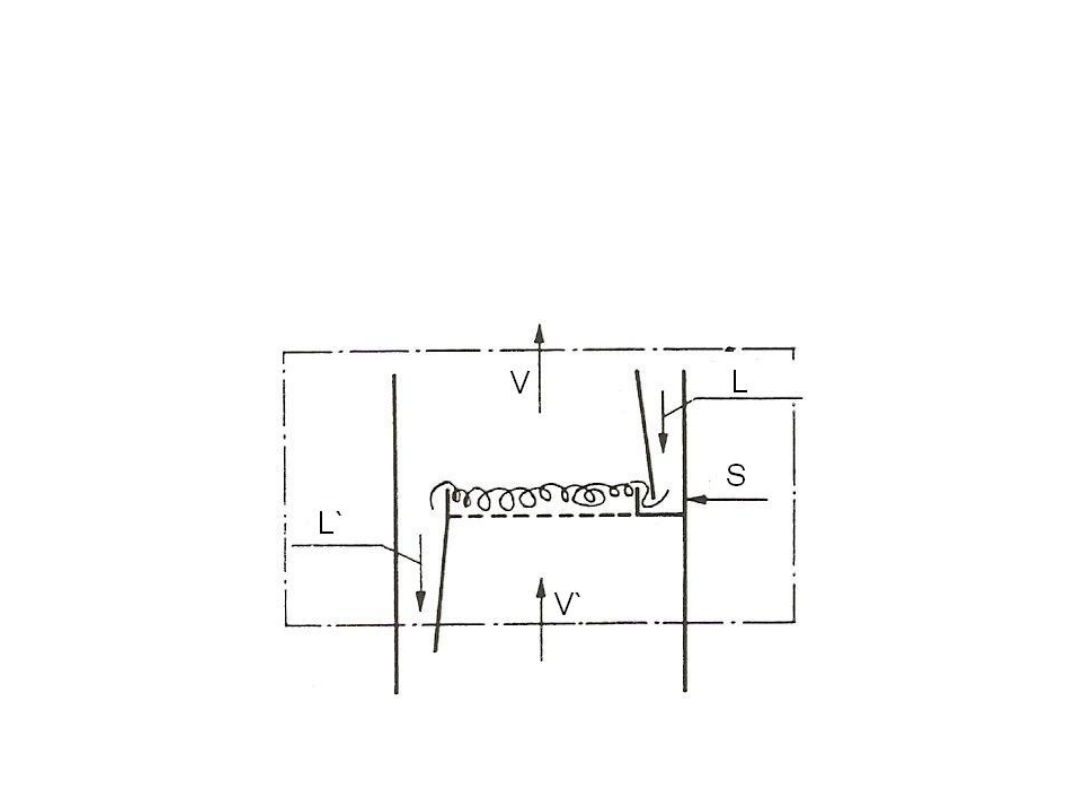
99

GLO przecina przekątną kwadratu stężeń w punkcie yAD =xAD

(D) jej nachylenie wynosi:

tg = R / (R + 1) ≤ 1

tg = 1 występuje gdy L = V, a więc dla całkowitego powrotu (R  ∞)

wówczas linia operacyjna  pokrywa się z przekątną kwadratu stężeń.

Współrzędne punktu P [0, x

D

/(R+1)].

Rys. 34. Schemat bilansowania półki zasilającej

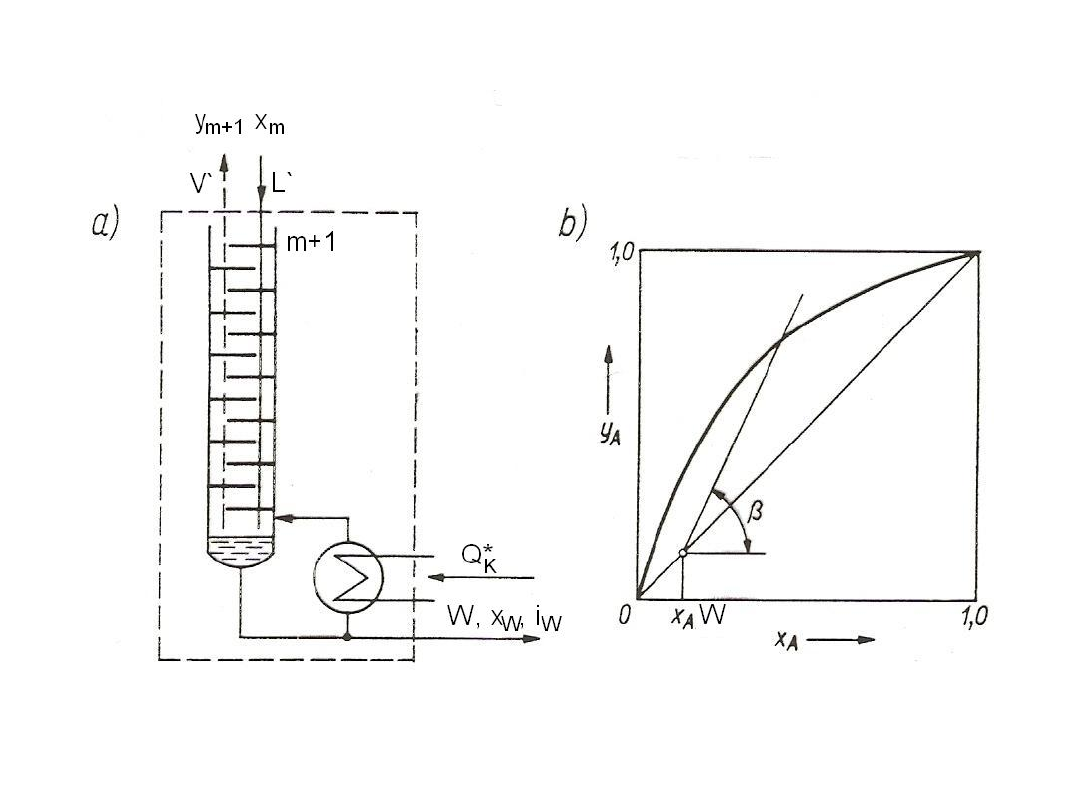
100

Część odpędowa (dolna) kolumny rektyfikacyjnej

Rys. 35. Część odpędowa kolumny rektyfikacyjnej:

a) schemat bilansowania, b) linia operacyjna

101

Bilans:

L` = V` + W

L` x

m

= V’ y

m+1

+ W x

W



y

m+1

= (L` / V’) x

m

– (W / V’) x

W

lub:

y

m+1

= [L` / (L` - W)] x

m

– [W / (L` - W)] x

W

ogólnie:

y = [L` / (L` - W)] x

– [W / (L` - W)] x

W

RDLO

Uwzględniając molowe strumienie cieczy i pary dopływające do

półki zasilanej i odpływające z niej  układamy bilans materiałowy

półki zasilanej:

L + V` + S = L` + V

Należy znaleźć związek miedzy liczbą moli cieczy płynącej w

górnej części kolumny L, a liczbą moli płynącej w dolnej części kolumny
L`.

Podobnie należy ustalić związek między molowym natężeniem

przepływu pary w górnej V i dolnej V` części kolumny.

Rozwiązanie tego zagadnienia staje się możliwe po

uwzględnieniu wpływu stanu cieplnego surówki na strumienie cieczy i
pary w obu częściach kolumny.

102

Wprowadzamy pomocniczą wielkość e, która charakteryzuje

stan cieplny surówki.

Linia operacyjna (DLO) przecina przekątną kwadratu stężeń

x-y w punkcie x

W

=y

W

=x

w

i jej nachylenie wynosi:

tg = L` / V` ≥ 1

gdy: V` = L` to tg = 1 i linia operacyjna pokrywa się z przekątną

kwadratu stężeń.

103

Definicja e

Wielkość e oznacza stosunek ilości ciepła, jaką należy dostarczyć 1

kmol surówki, aby zamienić ją w nasyconą parę suchą do kilomolowego
ciepła parowania:

e = (i`` - i

S

) / r

gdzie: i

S

- entalpia 1 kmol surówki, J/kmol;

i``

- entalpia 1 kmol pary suchej w temperaturze wrzenia

surówki, J/kmol;

r

- molowe ciepło parowania, J/kmol.

Uwzględniając definicje wielkości e mamy:

L` = L + e S



L + V` + S = L + e S + V



V` = V + S (e - 1)

Jeśli uwzględnimy te zależności w równaniach linii operacyjnych 

DLO:

y = [L` / (L` - W)] x

– [W / (L` - W)] x

W

= [(L + eS) / (L + eS - W)] x

– [W / (L +

eS - W)] x

W

 przebieg DLO zależy m. in. od stanu cieplnego surówki e.

104

Oznacza to również, że współrzędne punktu przecięcia obu linii

operacyjnych dla górnej i dolnej części kolumny zależą od wartości e.

Zauważmy, że nachylenie DLO wyniesie:

tg` = (L + eS) / (L + eS - W) = f(e)

Wyznaczenie współrzędnych punktu przecięcia obu linii

operacyjnych sprowadza się do wyznaczenia miejsca geometrycznego
punktów przecięć tych linii dla różnych stanów cieplnych surówki.

Matematycznie oznacza to rozwiązanie układu dwóch równań

linii operacyjnych dla górnej i dolnej części kolumny przy jednoczesnym
wyeliminowaniu wielkości L:

y = [L / (L + D)] x + [D / (L + D)] x

D

y = [(L + eS) / (L + eS - W)] x

– [W / (L + eS - W)] x

W

po przekształceniach mamy:

y = [e / (e -1)] x – [x

S

/ (e – 1)]

Równanie linii surowca (równanie linii e).

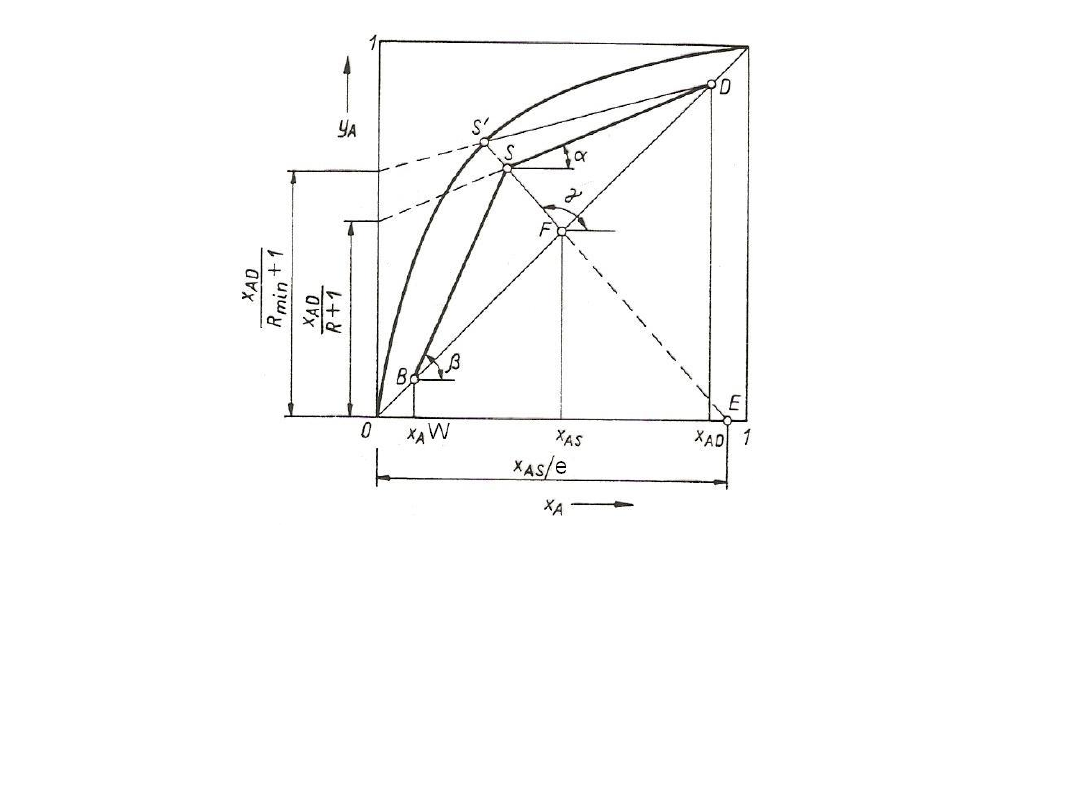
105

Rys. 36. Wykreślanie linii operacyjnych i linii surowca

Na linii surowca przecinają się obydwie linie operacyjne (punkt

S na rysunku). Dla y

A

= 0 , x

A

= x

AS

/ e jest to punkt przecięcia się

prostej surowca z osią odciętych (punkt E).

Dla x

A

= y

A

= x

AS

/ e mamy punkt przecięcia linii surowca z

przekątną kwadratu stężeń (punkt F). Znajomość położenia punktu E
umożliwia wykreślenie linii surowca jako przedłużenie odcinka EF.

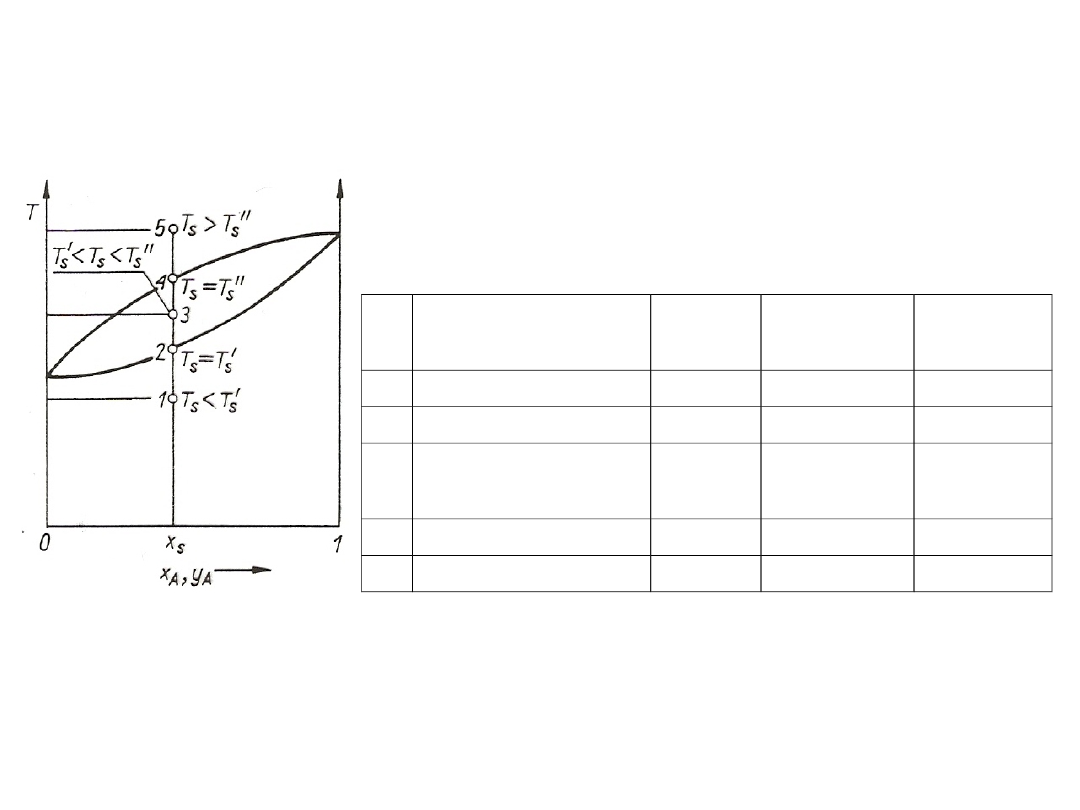
106

Różna możliwe stany surowca przedstawia rysunek poniżej. W

tablicy przedstawiono wpływ stanu surowca na parametry linii operacyjnej
surowca.

Rys. 37. Możliwe stany

surowca w rektyfikacji

mieszaniny

dwuskładnikowej

Tab. 9. Wpływ surówki na parametry linii
surowca

tg = e / (e – 1)

Lp

.

Stan surówki

Temp.

Współczynni
k kaloryczny

Nachylenie

linii

surowca

1

Ciecz przechłodzona

T

S

< T`

S

e > 1

tg > 1

2

Ciecz w stanie wrzenia

T

S

= T`

S

e =1

tg = ∞

3

Mieszanina cieczy

wrzącej

i pary nasyconej

T

S

> T`

S

T

S

< T``

S

o < e < 1

tg < 1

4

Para nasycona

T

S

= T``

S

e = 0

tg = 0

5

Para przegrzana

T

S

> T``

S

e < 0

0 < tg < 1

107

Minimalna i optymalna ilość

powrotu (orosienia) w kolumnie

Kolumna rektyfikacyjna może być rozpatrywana jak wymiennik

masy, w którym składnik bardziej lotny A przechodzi z fazy ciekłej do
fazy gazowej. Intensywność wymiany masy jest proporcjonalna do
modułu napędowego, tj. różnicy między równowagowym ułamkiem
molowym y*

A

a rzeczywistą wartością y

A

reprezentowaną przez linie

operacyjne. Intensywność wymiany masy rośnie zatem, gdy linie
operacyjne oddalają się od linii równowagi i maleje, gdy zbliżają się one
do tej linii. Z punktu widzenia wymiany masy korzystne jest więc, gdy
linie operacyjne oddalają się od linii równowagi, Położeniem granicznym
jest przekątna kwadratu stężeń x-y odpowiadająca wartości n`

D

=0, czyli

R=∞. Moduł napędowy wymiany masy jest wtedy największy. W
praktyce zwiększenie przepustowości kolumny wymaga zmniejszenia
wartości R, co powoduje zbliżenie punktu S do linii równowagi.
Graniczną wartością R jest taka wartość, dla której punkt przecięcia się
linii operacyjnych leży na krzywej równowagi – położenie S`. W punkcie
S` moduł napędowy osiąga wartość zerową, a to oznacza, że transport
masy ustaje. Wartość współczynnika orosienia osiąga wartość
minimalną R=R

min.

Wyznaczenie wartości R

min

jest ważnym etapem projektowania

kolumn rektyfikacyjnych.

108

(tg)

min.

= R

min.

/ (R

min.

+ 1) = [x

AD

– (y

AS

)

min.

] / [x

AD

– (x

AS

)

min.

]

Stąd:

R

min.

= [x

AD

– (y

AS

)

min.

] / [x

AD

– (x

AS

)

min.

]

gdzie: (x

AS

)

min

, (y

AS

)

min

- współrzędne punktu S``. Współrzędne te można

wyznaczyć

dla x=const rozwiązując układ równań:

(y

AS

)

min

= y* (x

AS

)

min

=

[

A

(x

AS

)

min

] / [1 + (x

AS

)

min

(

A

- 1)]

(y

AS

)

min

= [e / (e-1)] (x

AS

)

min

– [x

AS

/ (e-1)]

Jeżeli surowiec jest podawany w postaci cieczy wrzącej, e=1, to

oraz .

R

min.

= [1 / (-1)] { (x

AD

/ x

AS

) –  [(1 - x

AD

) / (1 - x

AS

)] }

Rzeczywista wartość stosunku orosienia R musi być większa od

wartości minimalnej. Najczęściej w praktyce stosuje się:

R = k R

min.

gdzie: k – liczba większa od jedności (najczęściej zawarta w granicach od

1,3 do 2).

Przy doborze wartości R należy kierować się względami

ekonomicznymi. Dysponując danymi dotyczącymi kosztów inwestycyjnych
(budowy kolumny, aparatów cieplnych, pomp, fundamentów, budynków
itp.) oraz kosztów eksploatacyjnych (przetłaczanie surowca, pary grzejnej,
wody chodzącej, obsługi itp.) można określić minimum kosztów
sumarycznych, przy których obrany powrót R będzie optymalny.

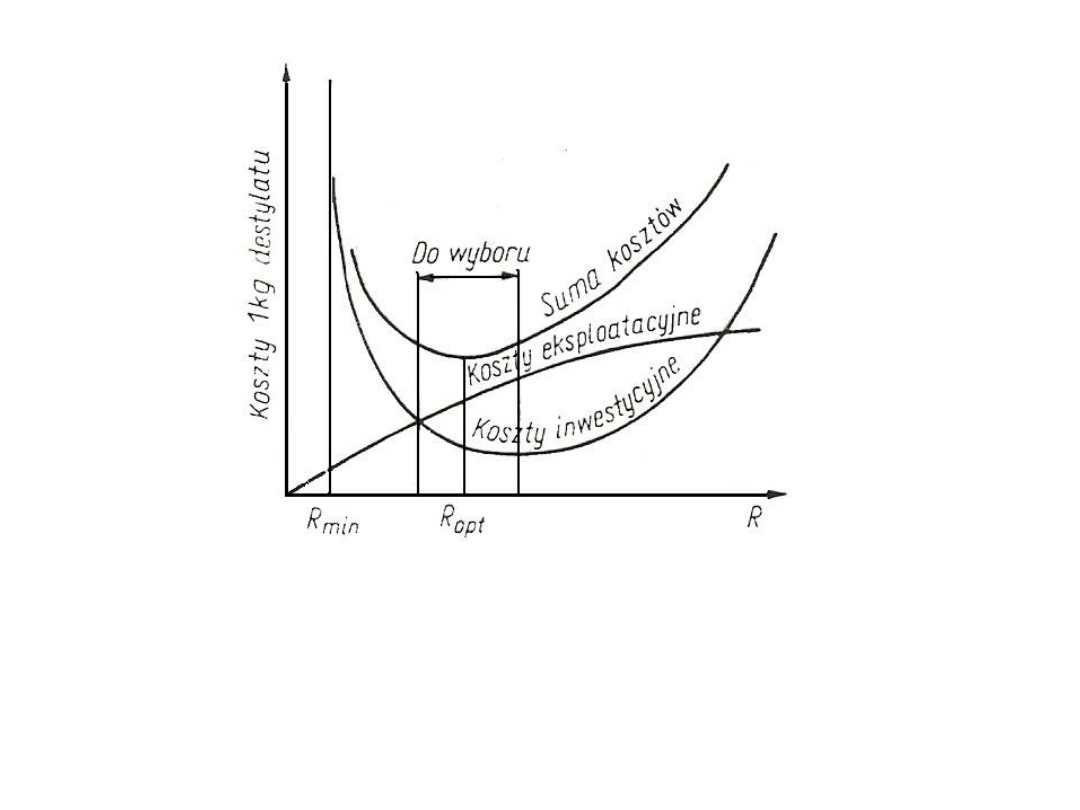
109

Rys. 38. Sposób wyboru rzeczywistego powrotu w kolumnie rektyfikacyjnej na

podstawie kosztów

Zmniejszenie wartości R powoduje zwiększenie kosztów

inwestycyjnych, gdyż zmniejszający się moduł napędowy wymiany masy
musi być zrekompensowany wielkością aparatu (wysokością kolumny).
Zwiększenie wartości R powoduje natomiast wzrost kosztów
eksploatacyjnych.

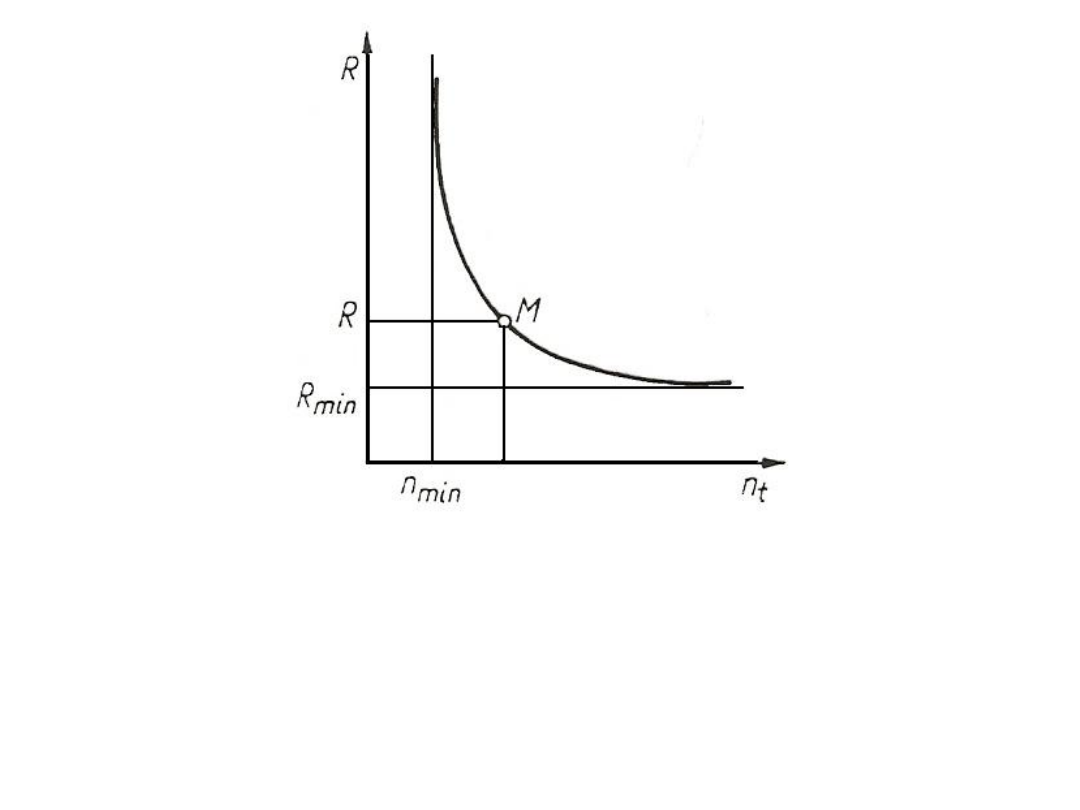
110

Rys. 39. Szacunkowy wybór rzeczywistego powrotu w kolumnie

rektyfikacyjnej

W przypadku, gdy dane ekonomiczne są niedostępne problem

przyjęcia wartości R można rozwiązać graficznie. Dla kilku dowolnie
przyjętych wartości R (w granicach nadmiaru 1 … 10) określa się
równania linii operacyjnych i wyznacza odpowiadającą danemu R
wysokość kolumny H lub konstruuje się wykres. Na wykresie szuka się
punktu M, od którego dalsze zmniejszanie wartości R powoduje
gwałtowny wzrost liczby n

t

. Tak otrzymana wartość R, odpowiadająca

punktowi M jest przyjmowana do dalszych obliczeń.

111

Metody wyznaczania wysokości

kolumn rektyfikacyjnych

Tradycyjnie stosuje się metodę stopni (półek) teoretycznych.

Graficzna wersja dla tej metody dla rektyfikacji dwuskładnikowej została
zaproponowana przez McCabe`a i Thielego i polega na zastosowaniu
tzw. konstrukcji schodkowej między linią równowagową a operacyjną.
Schodkowanie można wykonać osobno dla każdej części kolumny albo
też dl obydwu części łącznie.

Na rysunku pokazano przykładową konstrukcje McCabe`a-

Thielego dla dwuskładnikowej mieszaniny i surowca w postaci cieczy
przechłodzonej ( > 1). W graficznej metodzie wyznaczania liczby półek
teoretycznych należy uwzględnić to, że wyparka zastępuje jedną półkę
teoretyczną oznaczoną na rysunku punktem 7.

Jeżeli założy się, że współczynnik względnej lotności  jest stały,

to liczbę półek teoretycznych można wyznaczyć analitycznie metodą
Smokera, odpowiednie wzory dostępne są w literaturze specjalistycznej.

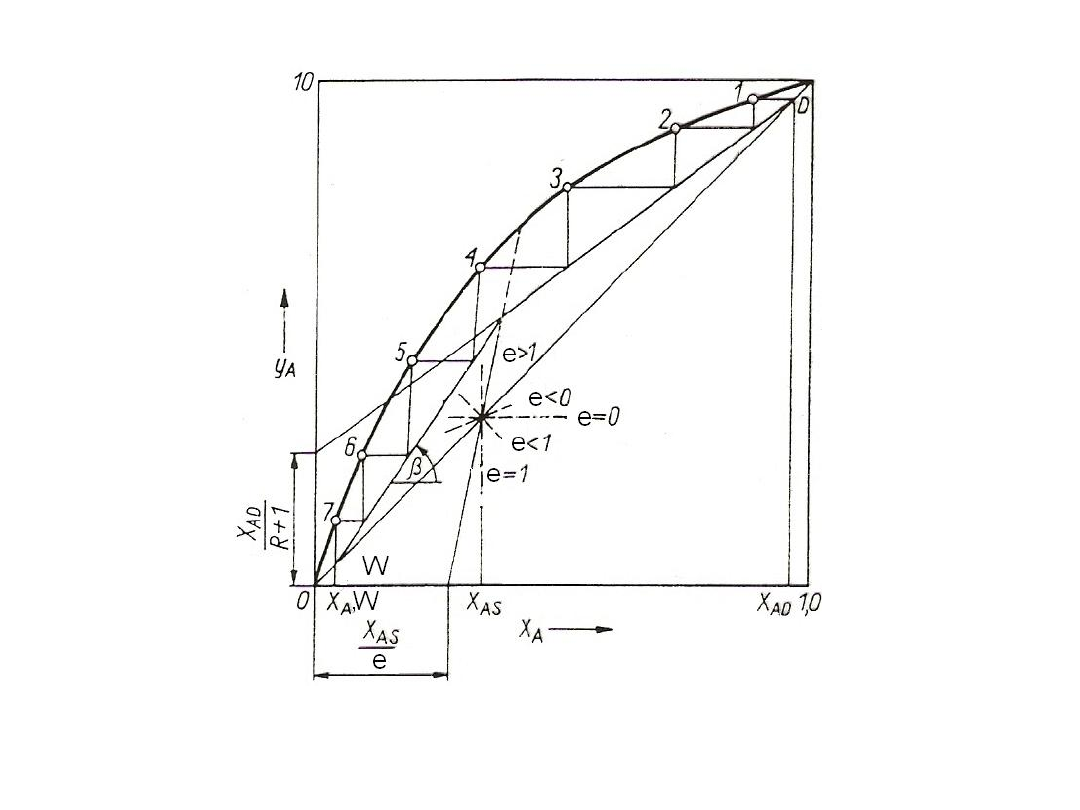
112

Rys. 40. Wyznaczanie liczby półek teoretycznych w kolumnie

rektyfikacyjnej metodą McCabe`a-Thielego

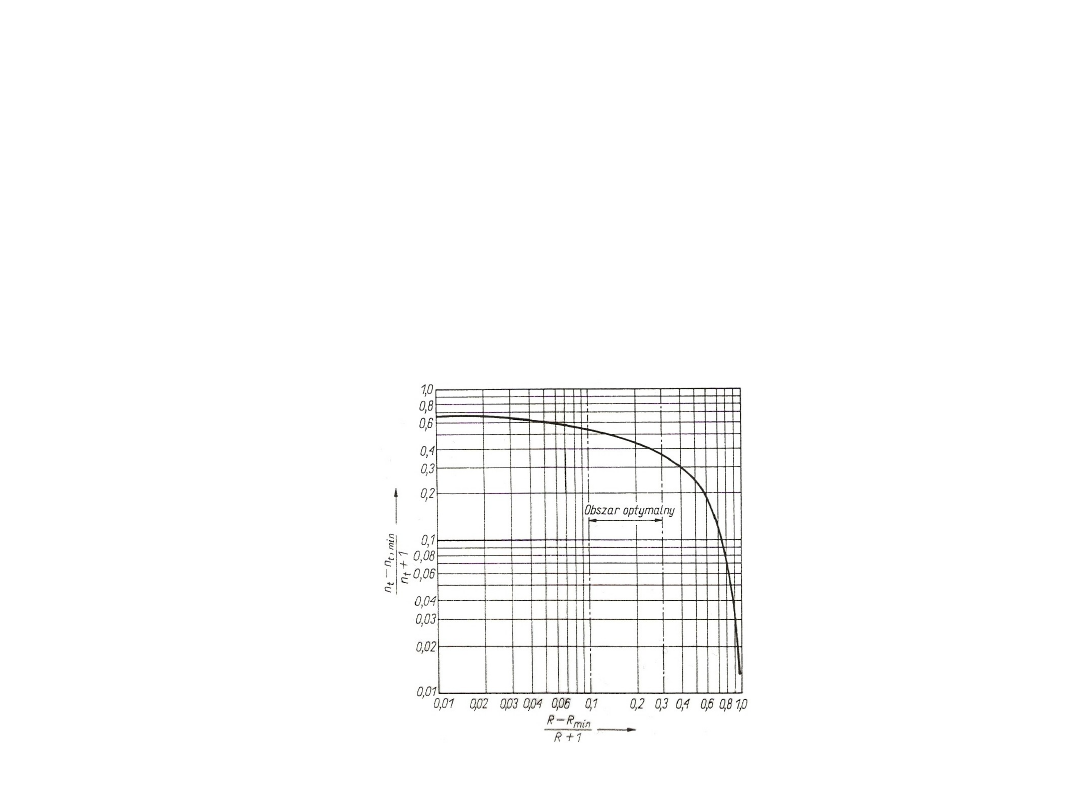
113

Do szybkiego oszacowania liczby półek teoretycznych można

zastosować metodę Gillilanda, która na podstawie rozważań Fenskiego
i Underwooda opracował zależność empiryczną między teoretyczną
liczbą półek i powrotem (orosieniem) R. Zależność tę można stosować
również dla mieszanin nieidealnych i wieloskładnikowych. W celu
wyznaczenia liczby półek teoretycznych n

t

, należy wcześniej wyznaczyć

wartość R

min.

oraz n

t, min

dla R=∞. Tę ostatnią wartość wyznacza się

albo metodą McCabe`a-Thielego przez schodkowanie między linią
równowagi, a przekątną kwadratu stężeń x-y, albo też dla A=const za

wzoru Fenskiego:

n

t, min

= {ln { [x

AD

(1 - x

AK

)] / [x

AK

(1 - x

AD

)] } / ln 

A

} - 1

Rys. 41. Wykres Gillialanda do określania liczby półek teoretycznych

114

Jak wspomniano wcześniej sposób prowadzenia procesu

wymiany masy może być: ciągły lub okresowy (periodyczny).

W procesie ciągłym istnieje stały przepływ faz przez wymiennik

masy, więc parametry procesu są funkcją tylko miejsca , a nie czasu.

W procesie periodycznym aparat pracuje szarżami, a parametry

procesu są funkcją miejsca i czasu.

Niekiedy z aparatu odbiera się w sposób ciągły tylko jedną fazę,

podczas gdy druga pozostaje w nim aż do czasu przerobienia danej
szarży.

Dla określenia pracy aparatu ważnym parametrem jest czas

potrzebny do rozdziału mieszaniny, który powinien być równy
efektywnemu czasowi przebywania substancji w aparacie.

Natomiast dla eksploatacji ciągłej definiuje się średni czas

przebywania substancji w aparacie:



m

= V / V*

gdzie: V – objętość zajęta przez mieszaninę, m

3

;

V* -

objętościowy strumień przepływu mieszaniny

m

3

/s.

115

Metoda stopni teoretycznych polega na zastosowaniu

wymiennika masy hipotetyczną kaskadą n stopni teoretycznych.
Liczbę n dla zadanych położeń linii operacyjnej i równowagowej
wyznacza się za pomocą konstrukcji schodkowej, polegającej na
przemiennym kreśleniu odcinków pionowych i poziomych, aż do
osiągnięcia wymaganych stężeń. Konstrukcje tą można wykonać
graficznie lub za pomocą obliczeń komputerowych. Numeryczna
wersja tej konstrukcji  metodą „z półki na półkę”  sprawność.

116

Sprawność ogólna kolumny

półkowej

Bardzo ważnym pojęciem określającym intensywność wymiany

masy na półkach jest pojęcie sprawności kolumny lub półki. Pojęcie
sprawności umożliwia przejście z liczby półek teoretycznych na liczbę
półek rzeczywistych, niezbędnych do zapewnienia założonych składów
produktów. Termin sprawność jest niejednoznaczny. W praktyce używa
się kilku rodzajów sprawności inaczej definiowanych i mających inne
wartości. Oto najważniejsze definicje i wzory mające zastosowanie w
praktyce.

Sprawność ogólna kolumny (sekcji) E

k

– wyraża najstarszą, a

jednocześnie najprostszą metodę wyznaczania liczby półek
rzeczywistych w kolumnie. Zgodnie z definicją:

E

k

= n

t

/ n

gdzie: n – liczba półek rzeczywistych;

n

t

- liczba półek teoretycznych.

Znajomość wartości E

k

umożliwia bezpośrednie obliczenie

liczby półek teoretycznych n:

n = n

t

/ E

k

117

W literaturze podaje się wzory lub wykresy do oszacowania

wartości E

k

. Są to zazwyczaj zależności czysto empiryczne, ważne tylko

dla określonego typu półek i określonego procesu. Na przykład dla
destylacyjnych kolumn kołpakowych sprawność ogólną kolumny można
obliczyć z korelacji O`Connela:

E

k

= 0,0906 (

c

)

-0,245

gdzie:  – współczynnik względnej lotności.

Po założeniu, że linie równowagowa i operacyjna są proste,

sprawność ogólną można obliczyć za pomocą wzoru Lewisa:

dla D ≠ 1

E

k

= { ln [1 + E

Mg

(D - 1)] } / lnD

dla D = 1

E

k

= E

Mg

gdzie:

D = m ( 

g

/ 

c

)

E

Mg

- sprawność umowna półki;



g

i 

c

-

uogólnione strumienie gazu i cieczy;

m -

nachylenie linii równowagi w uogólnionym

układzie stężeń.

118

Strumienie gazu i cieczy opuszczające półkę teoretyczną są ze

sobą w równowadze, ale na półce rzeczywistej tek nie jest. Stopień
oddalenia wartości stężeń rzeczywistych od wartości równowagowych
można wyrazić za pomocą sprawności umownie zdefiniowanej przez
Murphree`go. Definicję można sformułować używając albo stężeń w
fazie gazowej, albo w fazie ciekłej.

Jeżeli zastosuje się stężenia uogólnione S i Z, i założy, że

rozważany składnik A przechodzi od fazy ciekłej do fazy gazowej;
definicja jest następująca:

E

Mg

= [(Z

n

)

śr

– (Z

n-1

)

śr

] / [Z*

n

- (Z

n-1

)

śr

]

gdzie: Z*

n

– równowagowe stężenie składnika A do stężenia w cieczy

opuszcającej półkę, czyli:

Z*

n

= K S

n

W przypadkach, gdy wskutek silnej zmiany stężenia cieczy

wzdłuż drogi na półce, może zajść nierówność Z*

n

< (Z

n

)

śr

, wówczas E

Mg

przybiera wartości większe od jedności. Świadczy to o umownym
charakterze tej definicji i dlatego niektórzy autorzy unikają nawy
sprawność, np. w literaturze niemieckiej wielkość ta określana jest jako
stopień wzmocnienia.

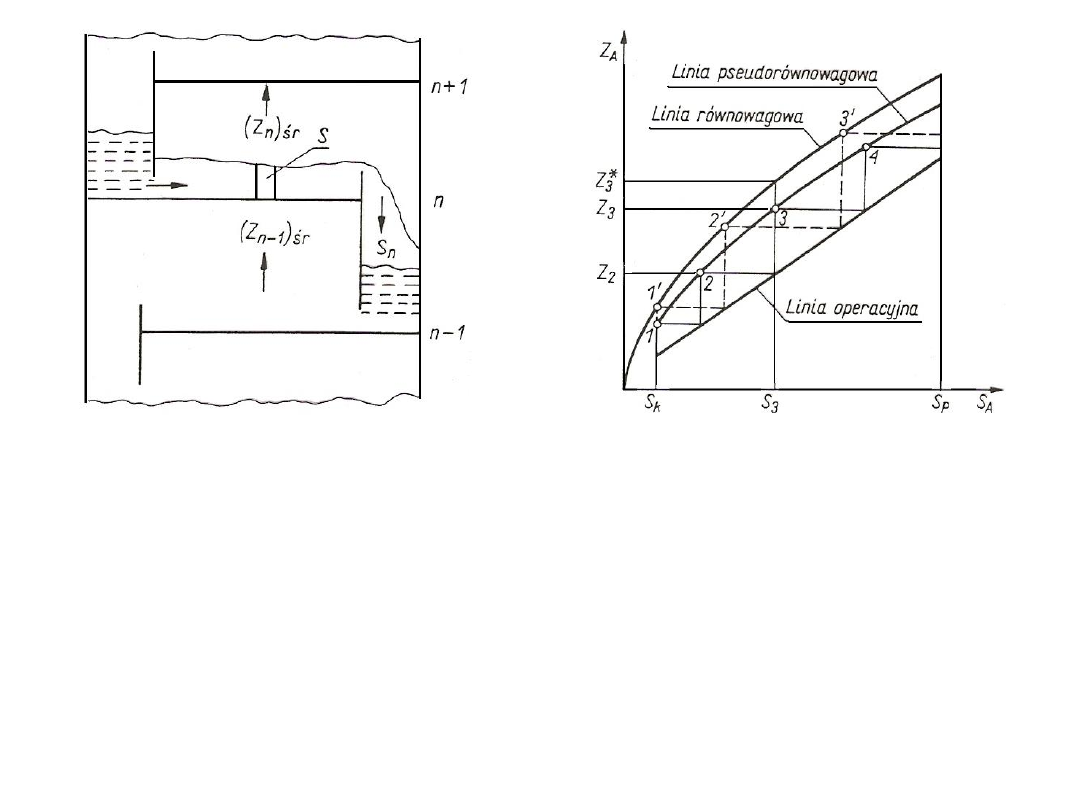
119

Rys. 42. Oznaczenia do definicji

umownej sprawności półki

Rys. 43. Zmodyfikowana metoda

McCabe-Thielego wyznaczania liczby

półek rzeczywistych

Wartość sprawności E

Mg

może być wykorzystana do wyznaczania

liczby półek rzeczywistych za pomocą zmodyfikowanej metody
graficznej McCabe-Thielego. Modyfikacja polega na tym, że pionowe
odcinki między linią operacyjną i równowagową mnoży się przez E

Mg

.

Otrzymane punkty tworzą tzw. linię pseudorównowagową. Konstrukcja
schodkowania między linią operacyjną a pseudorównowagową daje
rzeczywistą liczbę półek. Na rysunku przedstawiono przykład takiej
konstrukcji. Zaznaczono tam też stężenia faz dla półki 3.

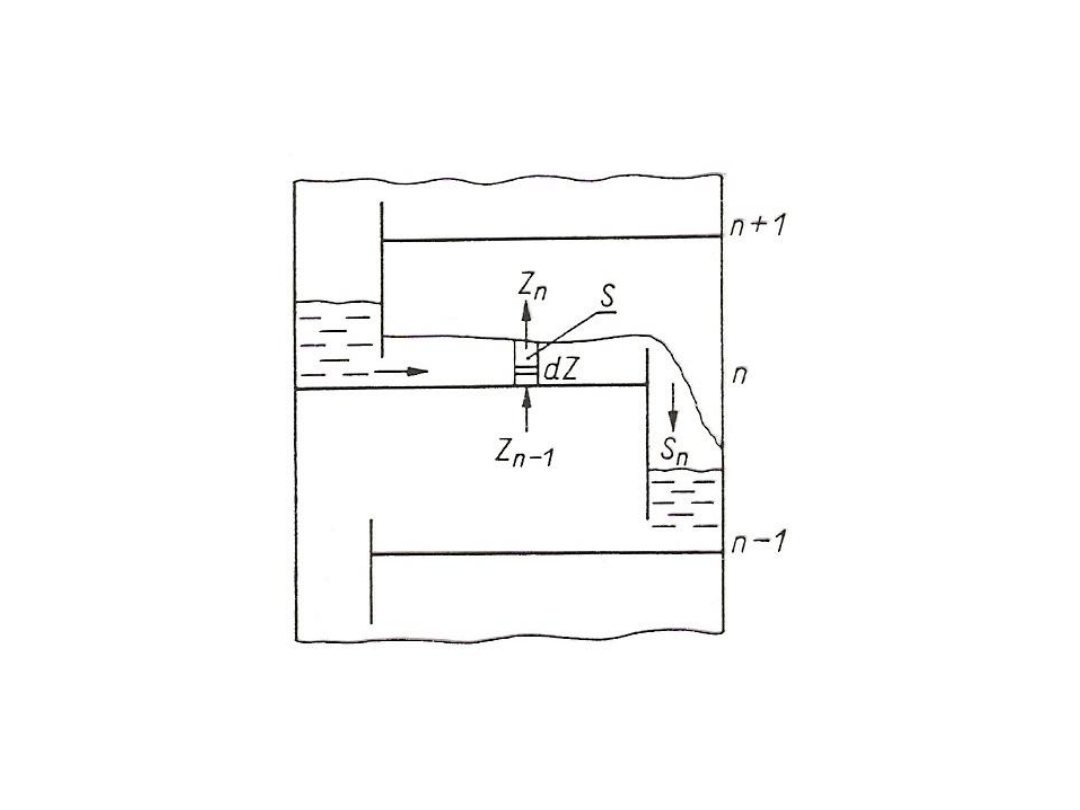
120

Sprawność lokalna półki

Rys. 44. Oznaczenia do definicji sprawności lokalnej półki

121

Pojęcie sprawności lokalnej pozwala na powiązanie

zagadnienia sprawności z teorią wymiany masy. Sprawność lokalna
jest wielkością charakterystyczną dla wybranego punktu na półce –
stąd nazwa. Oznaczenia potrzebne do definicji przedstawiono na
rysunku.

Sprawność lokalna (wyrażona przez stężenia w fazie gazowej) E

g

dla

wybranego punktu na półce wynosi:

E

g

= (Z

n

– Z

n-1

) / (Z*

n

– Z

n-1

)

gdzie: Z*

n

- równowagowe stężenie składnika A do stężenia w cieczy

w danym punkcie, w tym przypadku:

Z*

n

= K S

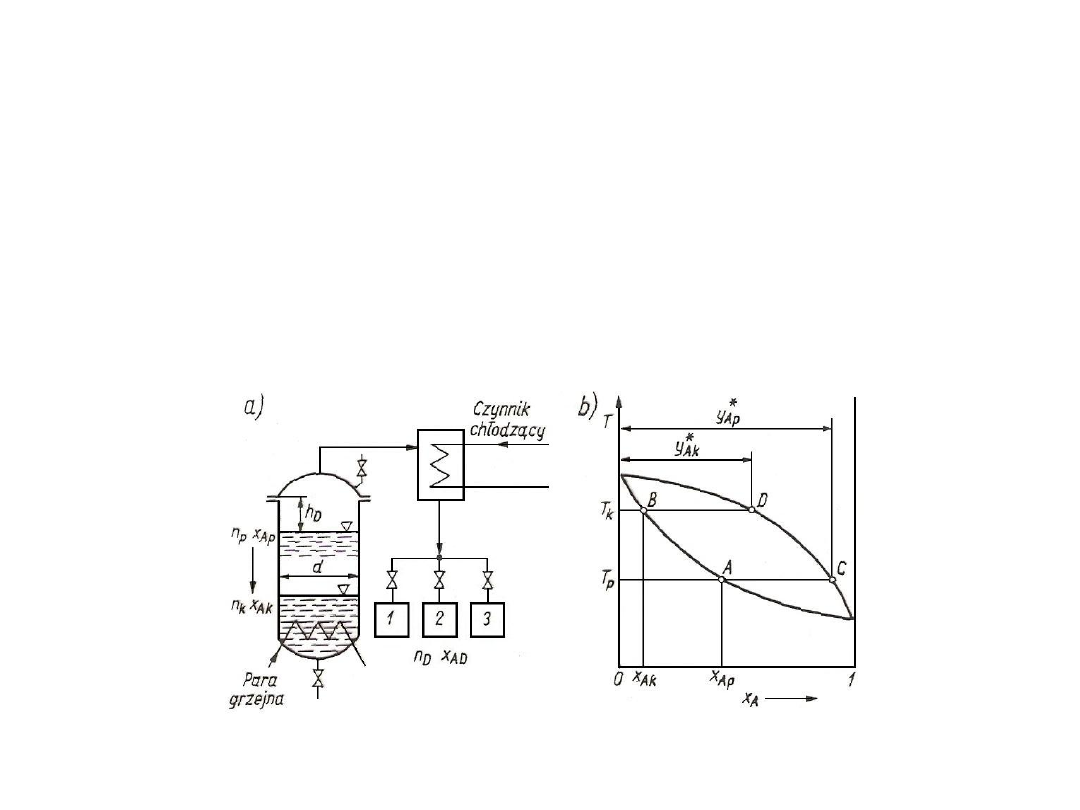
122

Destylacja prosta różniczkowa

(kotłowa)

Na rysunku przedstawiono schemat destylacji różniczkowej

periodycznej. Produkt górny (destylat) jest odbierany kolejno do oddzielnych
zbiorniczków. Otrzymuje się w ten sposób frakcje o różnym składzie składnika
lżejszego (bardziej lotnego). Przebieg takiej destylacji przedstawiono na
wykresie składu. Temperatura w kotle do prowadzenia mieszaniny do wrzenia
zmienia się od T

p

do T

k

, skład cieczy w kotle - od A do B, a skład fazy parowej

(destylatu) – od C do D. Przy założonych stężeniach na początku i na końcu
destylacji można z bilansu obliczyć ilość odparowanej cieczy.

Rys. 45. Schemat prostej destylacji różniczkowej (kotłowej):

a) schemat instalacji, b) wykres składu

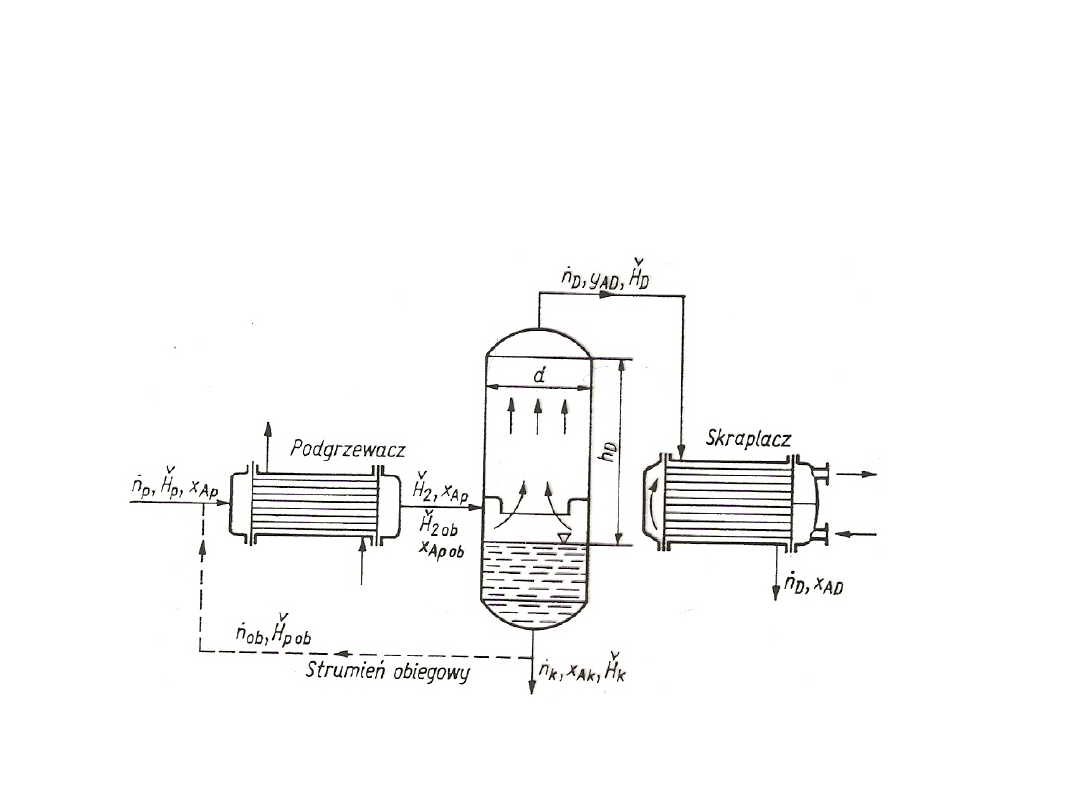
123

Rys. 46. Schemat instalacji do prostej destylacji równowagowej (rzutowej)

Destylację prostą równowagową najczęściej prowadzi się w

sposób ciągły. Jej zasada wynika ze schematu pokazanego na rysunku.
Mieszanina cieczy i pary może pochodzić ze stopnia reakcyjnego lub z
podgrzewacza, w których ciśnienie jest wyższe niż w rozdzielaczu. Taka
metoda destylacji nadaje się szczególnie do mieszanin, których krzywe
składu są od siebie bardzo odsunięte. Wtedy efekt rozdziału przy
jednokrotnym odparowaniu jest dostatecznie duży.

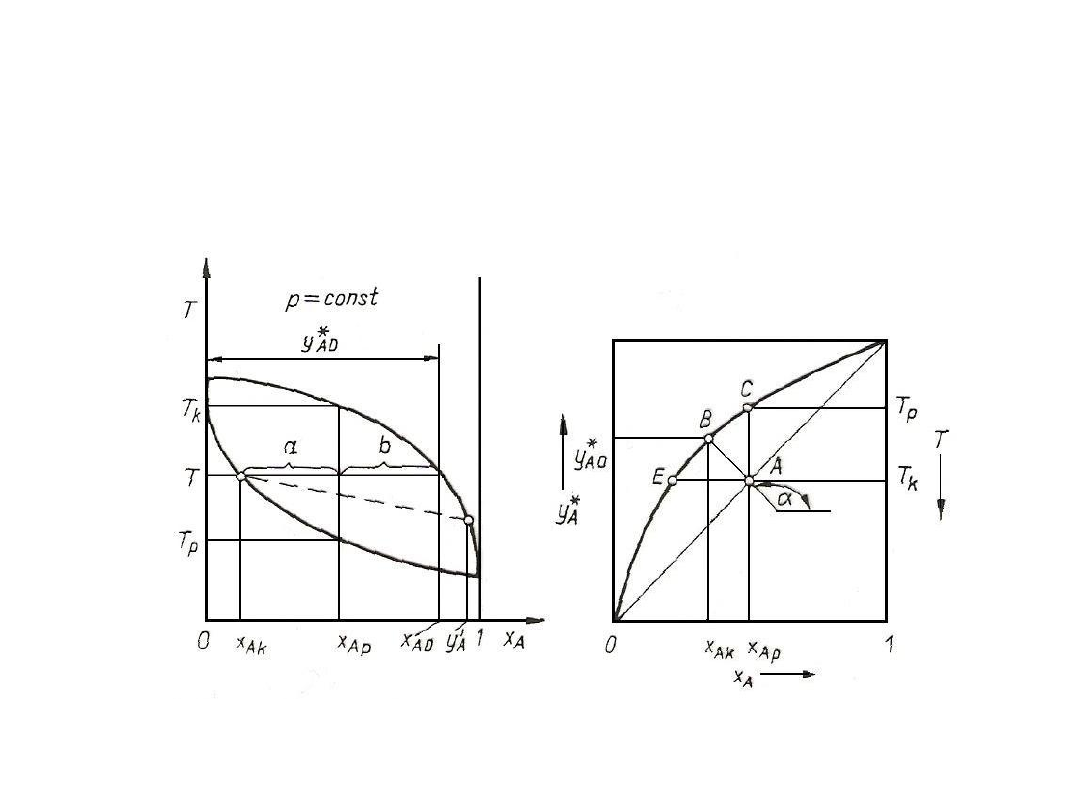
124

Rys. 47. Krzywa składu i krzywa równowagi wyjaśniające zasadę

destylacji równowagowej (rzutowej)

Jeżeli wymieszanie obu faz podczas przepływu przez instalację

nie jest pełne, to ostateczne składy obydwu faz mogą się różnić od
składów wynikających ze stanu równowagi (linia kreskowana na
rysunku). W takiej sytuacji, przy ograniczonym czasie kontaktu obu faz,
separator opuszcza para o stężeniu y`

A

> y*

AD

i rozdział jest lepszy,

ponieważ stężenia nie zdążą się wyrównać.

125

Destylacja z parą wodną

Destylacja z parą wodną służy przede wszystkim do usuwania

różnych zanieczyszczeń z mieszanin o wysokiej temperaturze wrzenia
za pomocą czynnika nie rozpuszczającego lub słabo rozpuszczającego w
fazie ciekłej. Czynnikiem tym jest najczęściej para wodna (niekiedy
stosuje się inny składnik inertny nie mieszający się z cieczą) stąd nazwa
– destylacja z parą wodną. Proces prowadzi się tak, że do cieczy w kotle
doprowadza się nasyconą lub przegrzaną parę wodną. Powoduje to
odparowanie składnika zanieczyszczającego w znacznie niższej
temperaturze. Para wodna spełnia ponadto rolę nośnika ciepła do
podgrzewania cieczy w kotle do temperatury wrzenia i dostarcza ciepła
destylacji.

Temperatury wrzenia mieszaniny można wyznaczyć graficznie.

Ciśnienie par nad mieszaniną np. dwóch składników A i B zupełnie w
sobie nierozpuszczalnych jest równe sumie ciśnień par czystych
składników:

p

An

+ p

Bn

= p

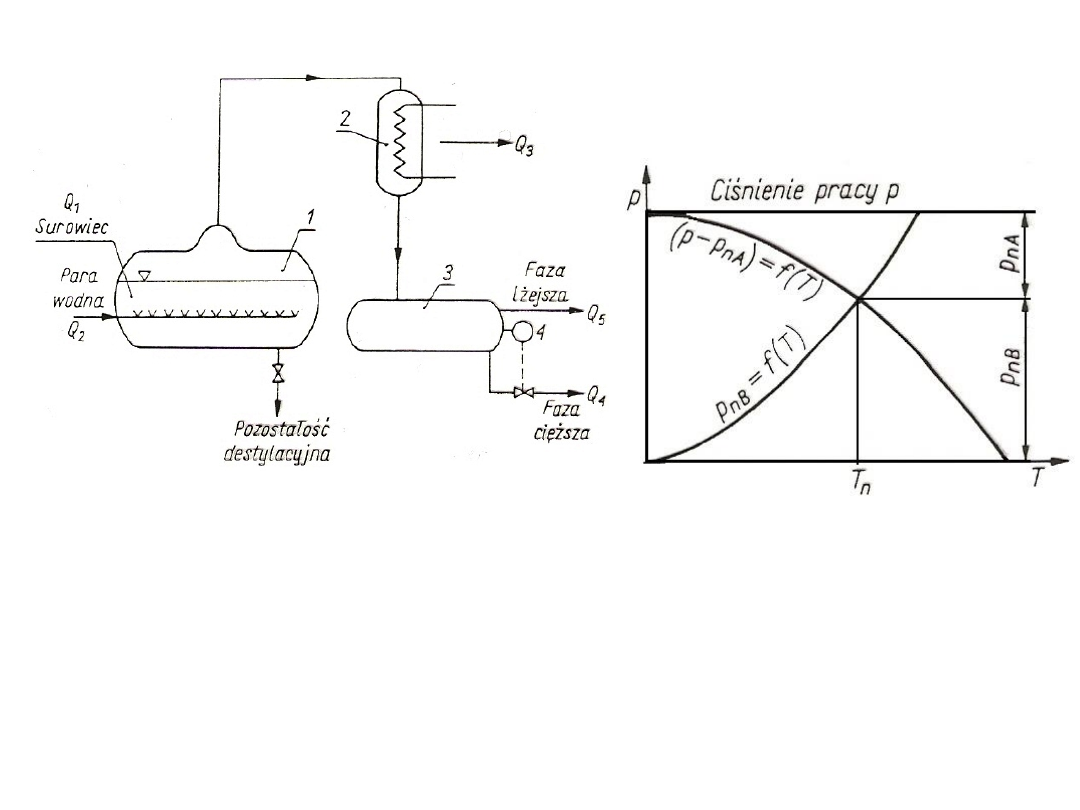
126

Rys. 50. Schemat instalacji periodycznej

do destylacji z parą wodną:

1 – kocioł, 2 –skraplacz,

3 – rozdzielacz faz, 4 – regulator poziomu

Rys. 51. Wykres wyjaśniający

destylację z parą wodną

(sposób wyznaczania

temperatury wrzenia)

127

W celu przeanalizowania procesu sporządza się bilans molowy:

ń

p

= ń

k

+ ń

D

ń

p

x

Ap

= ń

k

x

Ak

+ ń

D

x

AD

Na podstawie tych dwóch równań można napisać:

ń

k

/ ń

D

= (ń

p

– ń

D

) / ń

D

= (x

AD

– x

Ap

) / (x

Ap

– x

Ak

) = b / a = (1 – ) / 

gdzie:  = ń

D

/ ń

p

–

oznacza stopień odparowania; wielkość

odcinków a oraz b

pokazano na rysunku.

Przebieg procesu destylacji równowagowej mieszaniny

dwuskładnikowej można przedstawić na wykresie krzywej równowagi. Z
punktu A kreśli się linię prostą pod kątem , gdzie tg() = - ń

k

/ń

D

i

otrzymuje się punkt B (y*

AD

, x

Ak

) na linii równowagi.

Linia AB jest linią operacyjną charakteryzującą przebieg procesu:

- gdy  = 0 (linia AC), nie ma odparowania, jest tylko podgrzewanie

cieczy do temperatury T

p

;

- gdy  = 1 (linia AE), występuje pełne odparowanie odpowiadającego

temperaturze T

k

.

128

W dowolnym punkcie trwania procesu możemy napisać bilans

molowy składnika A:

n x

A

= (n – dn)(x

A

– dx

A

) + dn y*

A

Po wymnożeniu otrzymuje się:

n x

A

= n x

A

– dn x

A

– n (dx

A

) + dn (dx

A

) + dn y*

A

Po uproszczeniu i pominięciu iloczynu dn dx

A

:

dn (y*

A

- x

A

) = n dx

A

albo:

dn / n = dx

A

/ (y*

A

- x

A

)

Równanie całkuje się w granicach od n

p

 n

k

i x

Ap

 x

Ak

∫

np

nk

dn / n = ∫

xAk

xAp

dx

A

/ (y*

A

- x

A

) = - Ra(całka Rayleigha)

Lewą stronę równania można z łatwością scałkować otrzymując:

[ln(n)]│

np

nk

= ln(n

k

) - ln(n

p

) = - Ra  (n

k

/ n

p

) = e

- Ra

lub:

n

k

= n

p

e

- Ra

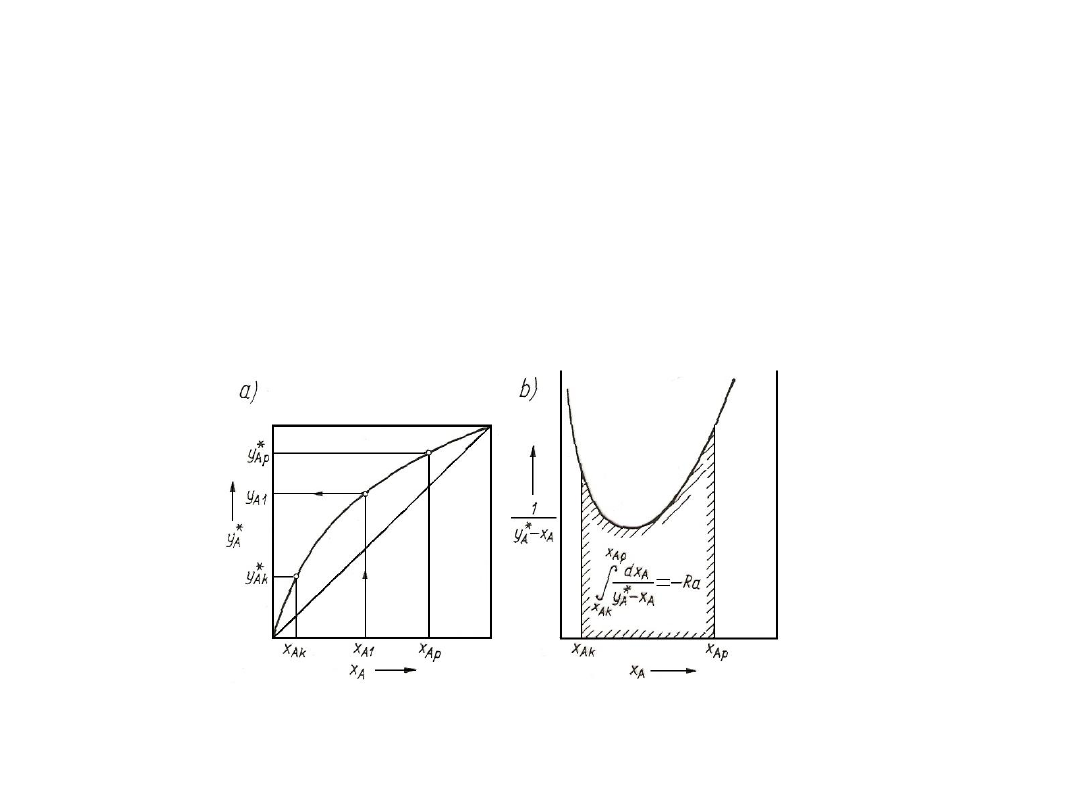
129

Ostateczne zagadnienie sprowadza się do wyznaczenia całki

Rayleigha, którą zwykle otrzymuje się graficznie przez planimetrowanie
powierzchni pod krzywą:

1 / (y*

A

– x

A

) = f(x

A

)

w zaznaczonych granicach.

W przypadku szczególnym, gdy współczynnik względnej

lotności  jest prawie wielkością stałą można do całki wstawić y*

A

z

równania Fenskiego:

y*

A

= { ( x

A

) / [1 + x

A

( – 1)] }

Rys. 52. Graficzne wyznaczenie całki Rayleigha:

a) krzywa równowagi, b) wykres pomocniczy

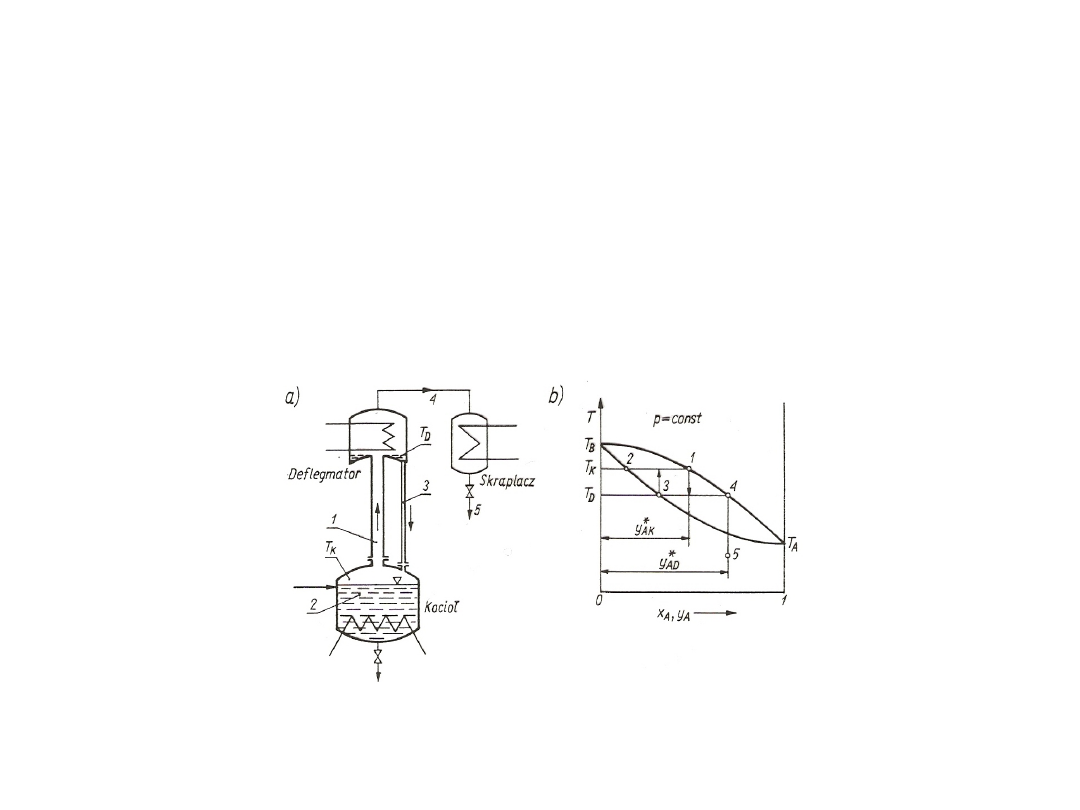
130

Rektyfikacja mieszanin

dwuskładnikowych

Destylacja z deflegmatorem – zakłada się, że poddawana

rektyfikacji mieszanina składa się z dwu składników A i B, przy czym
składnik A jest bardziej lotny.

Pośrednią instalacją między kolumną rektyfikacyjną a destylacją

prostą jest destylacja z deflegmatorem to jest z częściowym
skraplaczem.

Rys. 53. Destylacja z deflegmatorem: a) schemat,

b) wyjaśnienie działania na wykresie składu

131

Jeżeli w kotle i w deflegmatorze przy dwóch różnych temperaturach

T

K

i T

D

ustalą się stany równowagi, to stężenie składnika bardziej lotnego w

oparach z deflegmatora będzie znacznie większe niż w oparach z kotła y

AD

>y

AK

. Skropliny z deflegmatora zawraca się do kotła, ich skład odpowiada

punktowi 3 na wykresie składu, natomiast opary z kotła mają stężenie
odpowiadające punktowi 1. Pozostałość w kotle, tzn. produkt dolny ma
stężenie odpowiadające punktowi 2.

Kolumna rektyfikacyjna z częścią odpędową i wzmacniającą

Jednoczesne otrzymywanie w sposób ciągły obydwu produktów o

odpowiednim stopniu czystości można uzyskać w kolumnie zawierającej
część odpędową (dolną) i część wzmacniającą (górną) – jak to pokazana na
rysunku. Miejsce doprowadzenia surówki dzieli kolumnę na wymienione dwie
części. Jeżeli surówkę doprowadza się w postaci cieczy, dołącza się ona do
fazy ciekłej spływającej z części wzmacniającej, której skład powinien być w
przybliżeniu równy składowi surowca i wspólnie spływają przez część
odpędową wzbogacając się w składnik mniej lotny. Na dole jest odbierana
ciecz wyczerpana (produkt dolny), a górą rektyfikat (produkt górny).

Tego rodzaju instalacje rektyfikacyjne mogą mieć również wbudowany

deflegmator (częściowy skraplacz), w którym przez regulację ilości wody
chłodzącej tylko część par ulega skraplaniu, a resztę stanowi destylat parowy
przepływający do kondensatora. kondensator może być też ustawiony w dole
kolumny, co wymaga pompowania skroplin, ale oszczędza tłoczenia wody
chłodzącej. Zamknięcie hydrauliczne między kolumną deflegmatorem
uniemożliwia ucieczkę pary z pominięciem deflegmatora. Element grzejny
(wyparka) może znajdować się w korpusie kolumny u dołu, albo na zewnątrz
w postaci recyrkulatora.

132

Rektyfikacja adiabatyczna ciągła z częścią wzmacniającą

W dążeniu do jeszcze lepszego rozdziału mieszaniny wlotowej na

składniki o bardzo dużej czystości należy stosować wiele stopni rozdziału,
tzn. kolumnę rektyfikacyjną.

Zasadę działania kolumny rektyfikacyjnej wyjaśniono na wykresie

składu. Założono ustalenie się temperatury na każdym stopniu aparatu
kolumnowego i tym samym osiągnięcie kolejnych stanów równowagi. Od
stopnia do stopnia można prześledzić wzbogacenie się oparów w składnik
lżejszy A i coraz większe zubożenie w ten składnik spływającej w dół
kolumny fazy ciekłej, która jednocześnie wzbogaca się w składnik B.

Jeżeli kolumna zawiera dużo takich stopni, to istnieje możliwość
otrzymania bardzo czystych składników. Elementy zabudowy kolumny
(półki lub wypełnienia) maja za zadanie wytworzenie dużej powierzchni
styku obydwu faz i dużej turbulencji przepływu, co przyczynia się do
intensywnej wymiany ciepła i masy między strumieniami cieczy i pary.

Ze skraplacza jedynie część cieczy odbiera się jako destylat

(produkt górny), część natomiast misi być zawrócona na szczyt kolumny
jako powrót (refluks, orosienie). Ze względu na przepustowość instalacji
odbiór destylatu jako produktu górnego powinien być jak największy, a
kolumna powinna zawracać tylko minimalną jego część. O wielkości
zawracania destylatu jest mowa w dalszym toku analizy pracy kolumny.

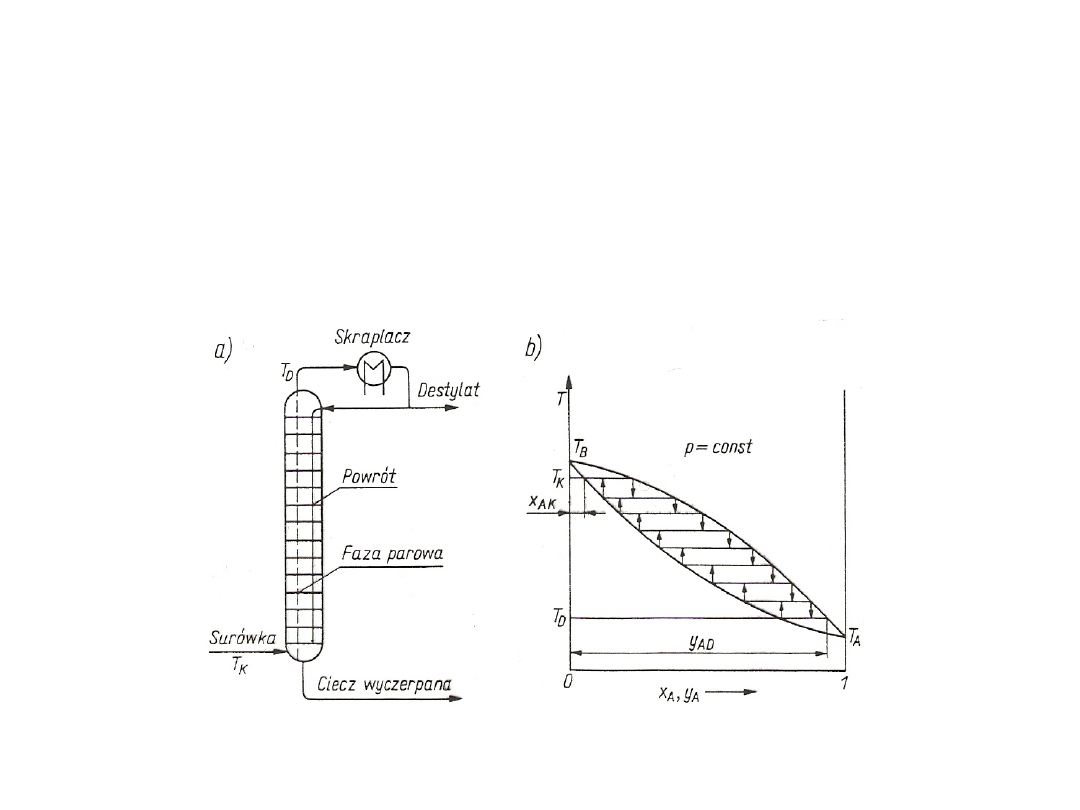
133

Przedstawiona na rysunku instalacja rektyfikacji zawiera jedynie

część wzmacniającą, leżącą powyżej miejsca doprowadzenia surówki.
Tego rodzaju kolumny są stosowane bardzo często do pracy okresowej.
Kocioł (nie pokazany na schemacie) napełnia się surowcem i prowadzi
rektyfikację, otrzymując u góry kolumny składnik bardziej lotny, a u dołu
w kotle – jako pozostałość – składnik cięższy (mniej lotny). Kolumna taka,
pracująca w sposób ciągły, dostarcza jedynie produkt górny o
wymaganej czystości, natomiast u dołu jest odprowadzany produkt
dolny – wzbogacony wprawdzie w składnik mniej lotny, ale o
niewystarczającym stopniu czystości.

Rys. 54. Rektyfikacja ciągła tylko z częścią wzmacniającą:

a) schemat, b) wyjaśnienie działania na wykresie składu

Zasady bilansowe w procesach

absorpcji i desorpcji

Rozważania ogólne

Jeżeli w danym procesie rozpuszczalnik jest obojętny

(inertny), tzn. nie bierze udziału w transporcie masy, to jego ilość w
poszczególnych fazach jest stała. Fakt ten ułatwia bilansowanie
procesu, pod warunkiem odpowiedniego doboru rodzaju strumieni i
stężeń. W przypadku procesów absorpcyjno-desorpcyjnych najczęściej
przyjmuje się strumienie molowe rozpuszczalnika tzn. ń

cr

i ń

gr

oraz

stosunki molowe składnika wymienianego tzn. X

A

i Y

A

.

UWAGA: w skrypcie masowe natężenie przepływu:

G

A

 ilość absorbowanego składnika A, kg/s;

G

i

 natężenie przepływu inertu gazowego, kg/s;

L

i

 natężenie przepływu inetru ciekłego, kg/s;

X, Y  stosunki masowe składnika A w cieczy i w gazie.

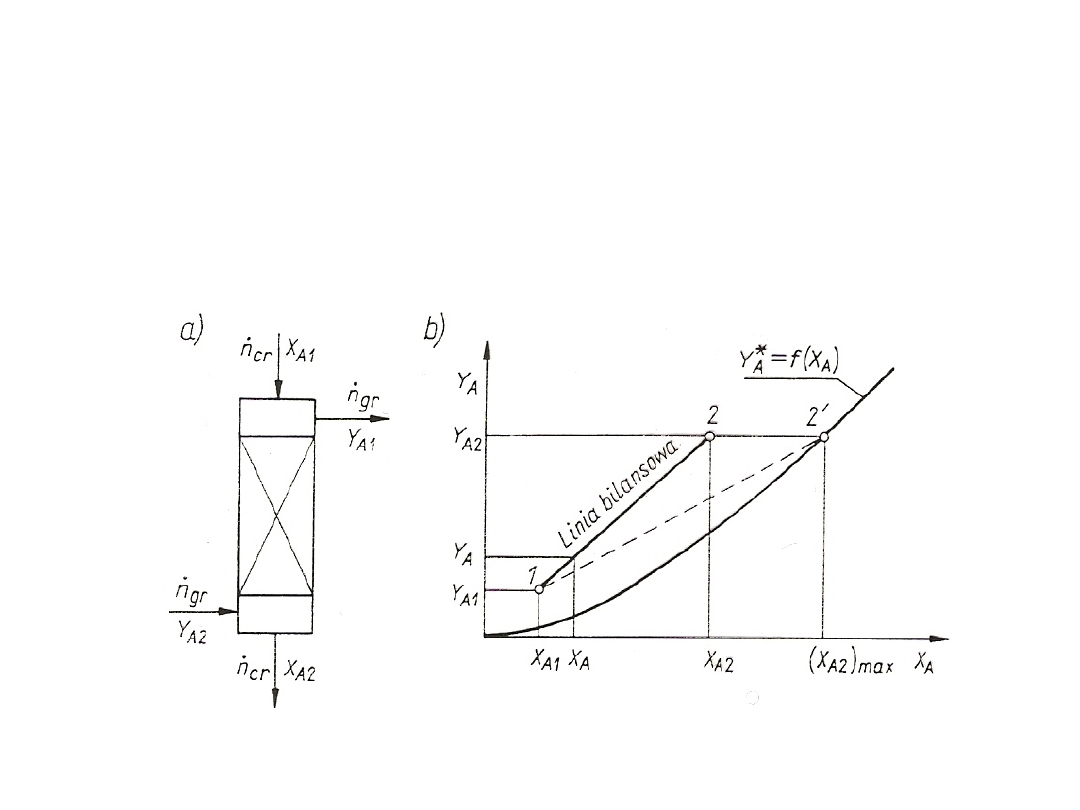
135

Bilans procesu absorpcji

W procesie absorpcji, którego celem jest usunięcie składnika A z

fazy gazowej najczęściej zadane z góry są stężenia tego składnika na
wlocie i wylocie absorbera np. Y

A2

– wlot i Y

A1

– wylot. Zazwyczaj znane

jest też stężenie składnika A w świeżej cieczy chłonnej doprowadzanej do
aparatu np. X

A1

. Przypadek ten przedstawiono na rysunku:

Rys. 55. Schemat absorpcji składnika A z fazy gazowej za pomocą cieczy

chłonnej:

a) oznaczenia strumieni i stężeń, b) wykres stężeń

136

Jeżeli znane są strumienie ń

cr

i ń

gr

, to powinno być spełnione

równanie bilansowe:

ń

A

= ń

cr

(X

A2

– X

A1

) = ń

gr

(Y

A2

– Y

A1

)

Równanie to umożliwia obliczenie strumienia absorbowanego składnika, a
także stężenia składnika A w cieczy opuszczającej absorber X

A2

. Jeżeli

podobne równanie bilansowe napisze się dla górnej części absorbera
ograniczonej przekrojem, w którym stosunki molowe w cieczy i gazie
wynoszą X

A

i Y

A

, to otrzyma się równaie linii bilansowej w postaci:

Y

A

= (ń

cr

/ ń

gr

) X

A

+ [Y

A1

- (ń

cr

/ ń

gr

) X

A1

]

Gdy wartość (ń

cr

/ ń

gr

) jest stała, wówczas jest to równanie linii prostej. Na

rysunku jest to linia prosta przechodząca przez punkty 1 i 2. Nachylenie
linii bilansowej jest określone stosunkiem (ń

cr

/ ń

gr

) . Gdy stosunek ten

maleje, wówczas przy stałym położeniu punktu 1 linia bilansowa przesuwa
się w kierunku linii równowagi. W skrajnym przypadku linia bilansowa
przecina się z linią równowagi w punkcie 2`. Wartość parametru w tym
przypadku nosi nazwę minimalnego stosunku orosienia, dla którego
stężenie składnika A w cieczy osiąga wartość maksymalną (X

A2

)

max

.

Ponieważ punkt 2` leży na linii równowagi, wartość (X

A2

)

max

odpowiada

równowagowemu stężeniu składnika A w cieczy do wartości Y

A2

, czyli:

(X

A2

)

max

= X*

A

(Y

A2

) = Y

A2

/ K

XY

Znajomość stężenia (X

A2

)

max

umożliwia obliczenie minimalnego stosunku

orosienia:

R

min.

= (ń

cr

/ ń

gr

)

min.

= (Y

A2

- Y

A1

) / [(X

A2

)

max

- X

A1

]

137

Minimalnemu stosunkowi orosienia odpowiada przerywana linia
bilansowa 1-2` na rysunku.

Stosując minimalną ilość cieczy chłonnej, podobnie jak w

procesie destylacji, można osiągnąć założony rozdział mieszaniny
jedynie przy nieskończenie dużej liczbie stopni rozdziału. Rzeczywista
wartość R musi być większa i dobiera się ją zwykle na podstawie
doświadczeń (praktyki przemysłowej) za pomocą zależności:

R = k R

min.

gdzie: k – liczna większa od jedności (najczęściej zawarta w granicach
od 1,3 do 1,6)

W procesie desorpcji najczęściej z góry zadane są stężenia

składnika A w cieczy na wlocie X

A2

, na wylocie X

A1

oraz stężenie A w

świeżym gazie Y

A1

. Bilans ogólny procesu jest identyczny jak bilans

procesu absorpcji.

Wielkością analogiczną do stosunku orosienia jest stosunek strumieni
fazy gazowej i ciekłej. Stosunek ten oznaczymy przez R

g

:

R

g

= ń

gr

/ ń

cr

Po zbilansowaniu dolnej części desorbera do pewnego przekroju

otrzymuje się równanie linii bilansowej w postaci:

Y

A

= (1 / R

g

) X

A

+ [Y

A1

– (X

A1

/ R

g

)]

138

Jeżeli R

g

=const to równanie jest równaniem linii prostej. Na rysunku jest

to prosta łącząca punkty 1 i 2. Do zrealizowania założonego rozkładu
stężeń konieczne jest, aby stosunek R

g

był większy od pewnej wartości

minimalnej (R

g

)

min

. Ponieważ linia równowagi w układach absorpcyjno-

desorpcyjnych zazwyczaj jest krzywą wklęsłą, więc przy wyznaczaniu
wartości (R

g

)

min

mogą zajść dwa przypadki. W przypadku gdy linia

równowagi jest słabo wklęsła lub wypukła, punkt 2` odpowiadający
minimalnej wartości R

g

jest punktem przecięcia linii bilansowej z linią

równowagi. Wylotowe stężenie składnika A w gazie wylotowym osiąga
wartość maksymalną (Y

A2

)

max

. Minimalną wartość (R

g

)

min

można obliczyć

ze wzoru:

(R

g

)

min

= (X

A2

– X

A1

) / [(Y

A2

)

max

– Y

A1

]

Jeżeli krzywa równowagi jest bardziej wklęsła (np. w zakresie małych
stężeń w układzie SO

2

-H

2

O) to punkt 2` odpowiadający minimalnej

wartości R

g

jest punktem styczności linii równowagowej i bilansowej.

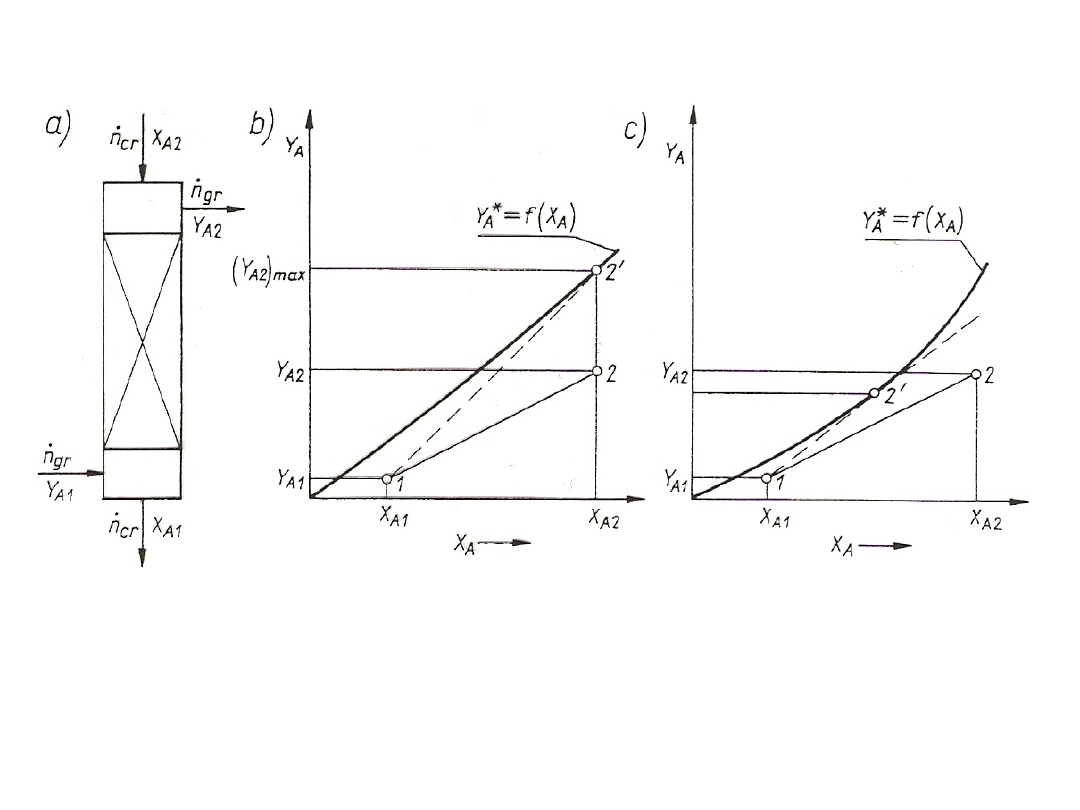
139

Rys. 56. Schemat desorpcji składnika A z cieczy za pomocą gazu:

a) oznaczenia strumieni i stężeń,

b) krzywa równowagi słabo wklęsła lub wypukła,

c) krzywa równowagi silnie wklęsła

140

Cyrkulacja cieczy chłonnej w

procesie absorpcji

Jeżeli ilość cieczy chłonnej, wynikają ca z bilansu molowego, jest

stosunkowo niewielka i nie gwarantuje właściwego zwilżania
powierzchni wypełnienia absorbera albo w czasie procesu absorpcji
wydzielają się bardzo duże ilości ciepła, to stosuje się cyrkulację cieczy
z chłodzeniem. Bilans materiałowy takiego układu jest następujący:

ń

gr

(Y

Ap

- Y

Ak

) = z ń

cr

(X

Ak

- X

Ap

)

gdzie: z – krotność cyrkulacji (stosunek ilości cieczy zraszającej do ilości
cieczy świeżej).

Ten sam bilans dla przypadku bez cyrkulacji ma postać:

ń

gr

(Y

Ap

- Y

Ak

) = ń

cr

(X

Ak

- X

Ap

)

Z porównania równań otrzymuje się krotność cyrkulacji

wyrażoną stężeniami:

z = (X

Ak

- X

Ap

) / (X

Ak

– X`

Ap

) > 1

Wymieszanie się strumieni cieczy o stężeniu i daje pewne

stężenia pośrednie:

X`

Ap

= [X

Ap

+ (z – 1) X

Ak

] / z

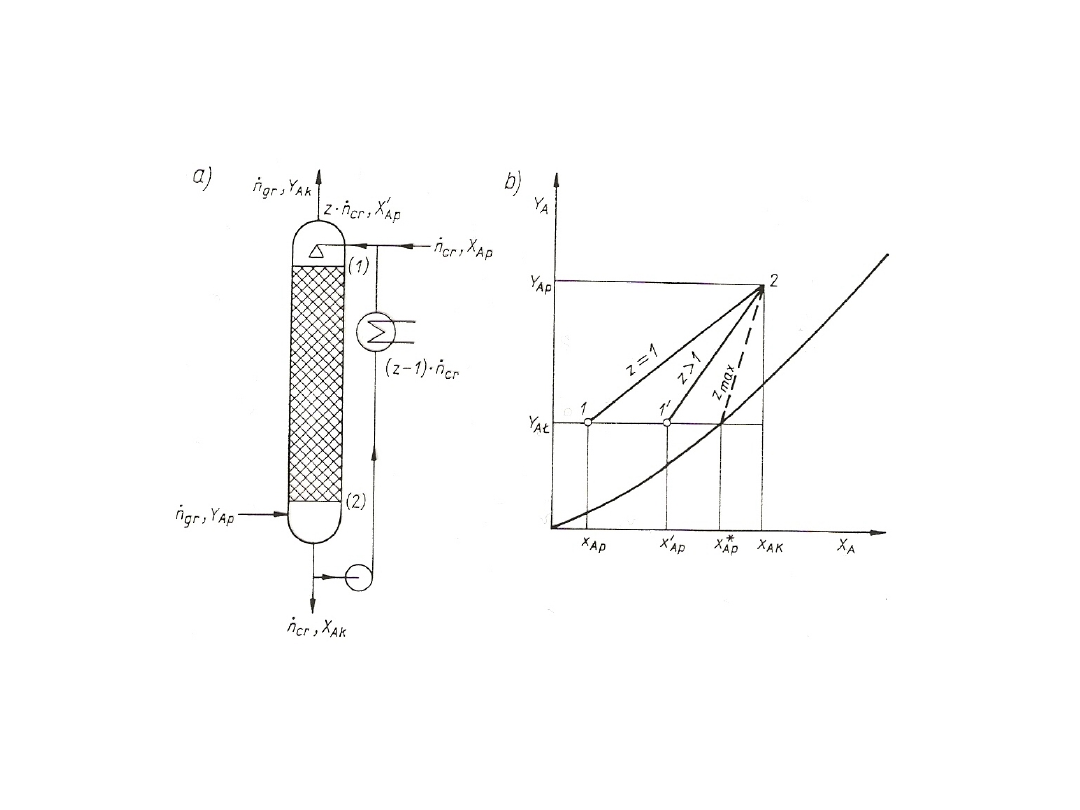
141

Rys. 57. Zależność położenia linii operacyjnej od krotności cyrkulacji:

a) schemat, b) wykres operacyjny

142

Zwiększenie strumienia cieczy cyrkulacyjnej powoduje bardziej

stromy przebieg linii bilansowej, a tym samym zmniejsza średni moduł
napędowy transportu masy. Jest to duża wada tego rozwiązania.

W przypadku gdy:

z = z

max

= (X

Ak

- X

Ap

) / (X

Ak

– X*

Ap

)

wówczas średni moduł napędowy maleje do zera, co uniemożliwia
stosowanie takiej cyrkulacji w praktyce.

Rozłożenie procesu absorpcji na kilka stopni zmniejsza ujemny

wpływ cyrkulacji na moduł napędowy. Rezultat jest tym lepszy, im więcej
stopni jest zastosowanych w procesie.

Jak widać z wykresu na rysunku przy zastosowaniu cyrkulacji

jednostopniowej linia bilansowa I przecięłaby linię równowagi, co
uniemożliwiłoby przeprowadzenie procesu. Na podstawie teoretycznych
rozważań Hoblera można stwierdzić, że zastosowanie cyrkulacji cieczy
daje duże korzyści tam, gdzie jest mało cieczy chłonnej i gdzie moduły
napędowe transportu masy są dość duże.

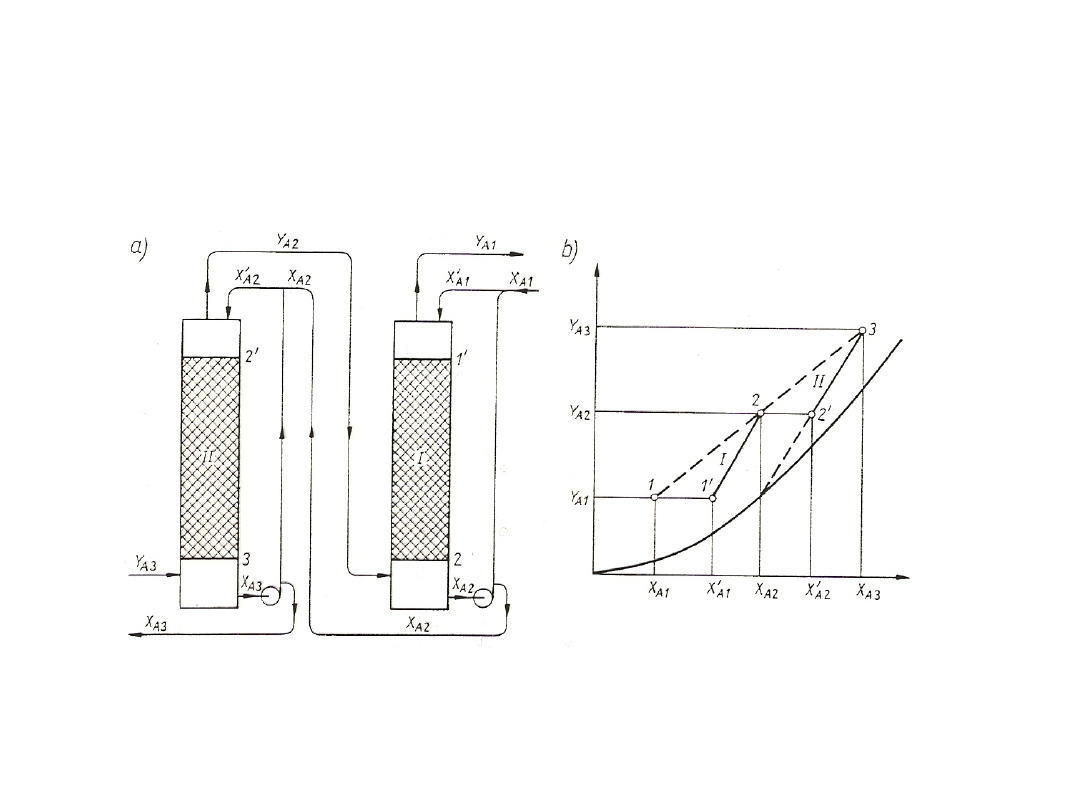
143

Rys. 58. Dwustopniowy proces absorpcji z cyrkulacją cieczy:

a) schemat, b) wykres operacyjny.

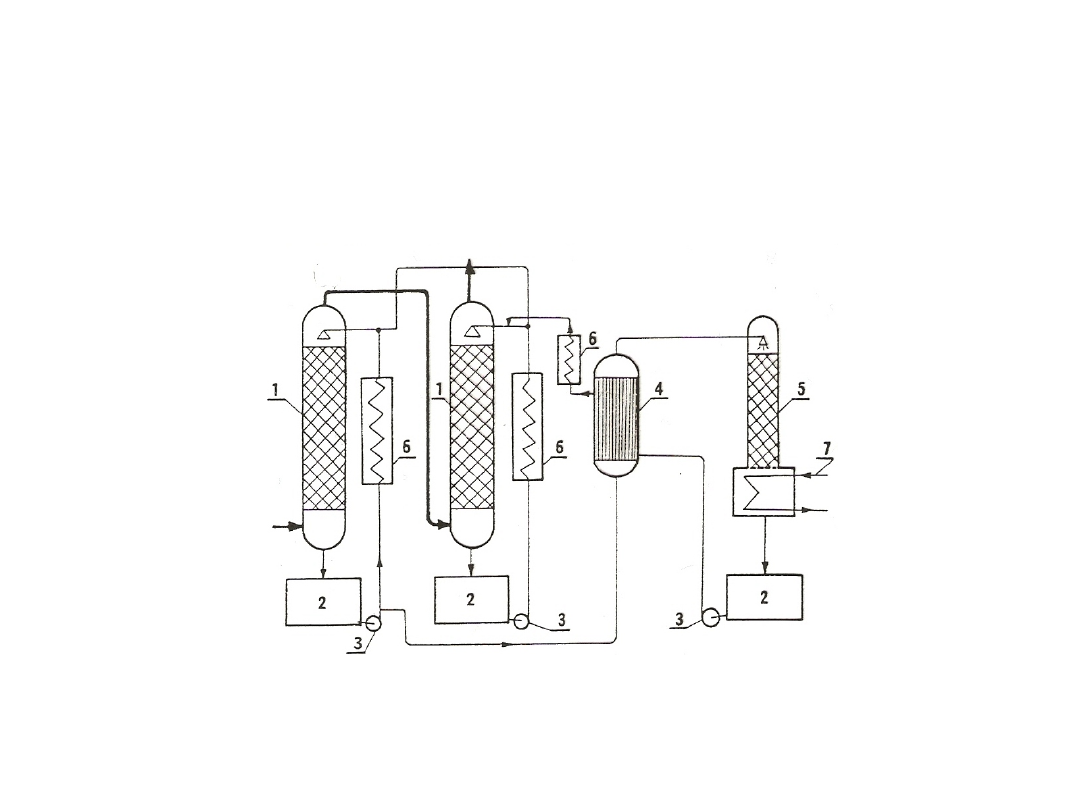
144

Korzystne warunki dla procesu absorpcji (wysokie ciśnienie i

niska temperatura) są przeciwieństwem warunków korzystnych dla
procesu desorpcji. Kierunek przebiegu procesu transportu masy zależy
każdorazowo od stanów równowagi w danych warunkach.

Na rysunku przedstawiono typowy schemat instalacji

absorpcyjno-desorpcyjnej z cyrkulacją cieczy chłonnej.

Rys. 59. Schemat instalacji absorpcyjno-desorpcyjnej z cyrkulacją cieczy:

1 – absorbery; 2 – zbiorniki, 3 – pompy, 4 – wymiennik ciepła,

5 – kolumna desorpcyjna; 6- chłodnice, 7 – para grzejna

145

Ciecz absorpcyjna (chłonna) powinna charakteryzować się:

- dużą rozpuszczalnością wymaganego składnika (korzystnym
przebiegiem linii równowagi);

- odpowiednią selektywnością, np. podczas absorpcji fizycznej
rozpuszczalność innych składników nie powinna przekraczać ilości 1/5
składnika absorbowanego;

- łatwością regeneracji (nie powinna tworzyć azeotropu z
absorbowanym składnikiem, powinna wykazywać dużą różnicę
temperatur wrzenia w stosunku do absorbowanego składnika oraz mieć
korzystny przebieg linii równowagi desorpcyjnej);

- niskim ciśnieniem par w temperaturze procesu absorpcji w celu
zmniejszenia strat cieczy chłonnej przez parowanie;

- małą lepkość;
- brak własności korodujących;
- brakiem toksyczności;
- niską ceną zakupu;
- brakiem ujemnego wpływu ewentualnego zanieczyszczenia
przerabianej mieszaniny cieczą chłonną na ilość produktów.

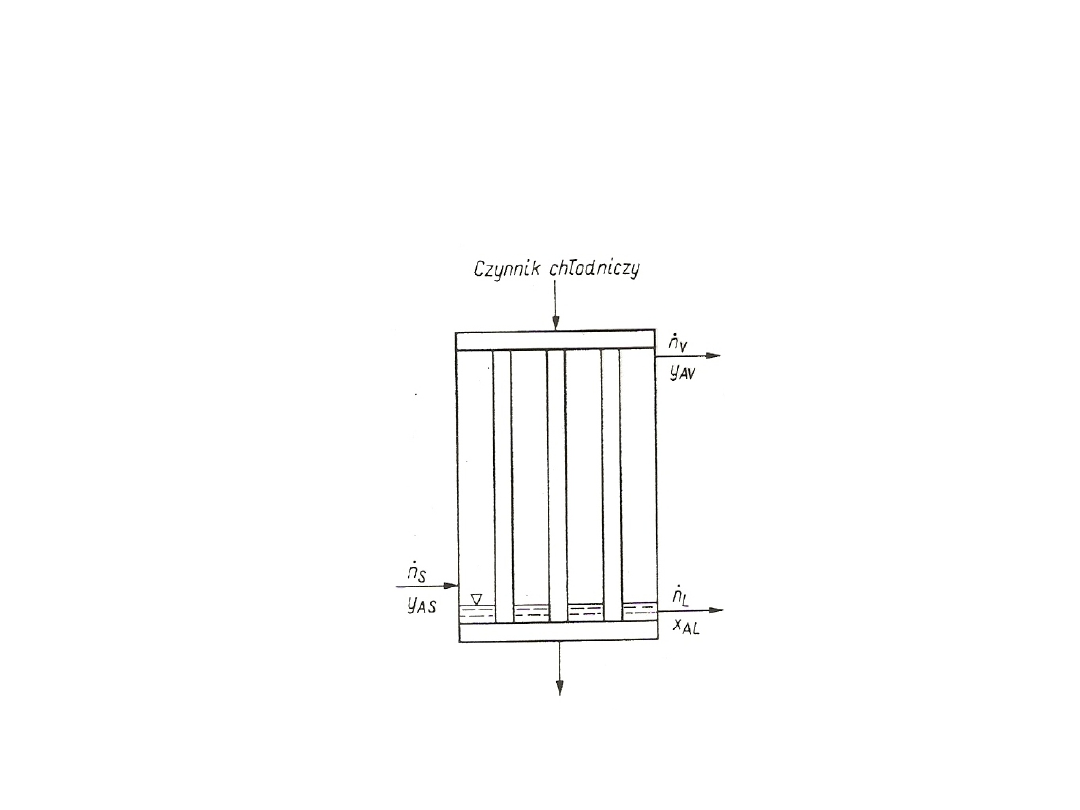
146

Kondensacja częściowa

Procesem analogicznym do destylacji różniczkowej jest

kondensacja częściowa. odbywa się ona w aparatach nazywanych
deflegmatorami. Schematycznie proces ten przedstawiono na rysunku.

Rys. 60. Schemat kondensacji częściowej w deflegmatorze

147

Deflegmator jest typowym wymiennikiem ciepła, najczęściej

rurkowym, ustawionym pionowo. Jako surowiec do deflegmatora dopływa
mieszanina par różnych składników w ilości ń

S

. Ułamek molowy bardziej

lotnego składnika A w surowcu wynosi y

AS

. Przepływająca w górę para

kondensuje się częściowo na powierzchni chłodzonej, wzbogacając się
jednocześnie w składnik A. Nie skroplona część par w ilości ń

V

jest

odbierana z górnej części aparatu. Ułamek molowy składnika A w tym
produkcie wynosi y

AV

. Kondensat spływa po powierzchni chłodzonej i

odpływa dołem aparatu w ilości ń

AL

zubożony w składnik A, którego ułamek

molowy wynosi x

AL

. Istotnym parametrem w procesie jest stosunek

kondensacji r zdefiniowany wzorem:

r = ń

L

/ ń

V

= (ń

S

– ń

V

) / ń

V

Równania bilansu molowego procesu mają postać:

ń

S

= ń

L

+ ń

V

ń

AS

y

AS

= ń

L

x

AL

+ ń

V

y

AV

x

AL

= y

AS

– [ (y

AV

– y

AS

) / r ]

Stosunek kondensacji r zależy od intensywności chłodzenia. Dla

mieszaniny dwuskładnikowej, przy założeniu że w każdym przekroju
skraplacza ciecz jest w równowadze z parą, można wyprowadzić zależność
między wartością r a ułamkami molowymi y

AS

i y

AV

:

ln (r + 1) = ∫

yAS

yAV

[ dy

A

/ (y

A

– x*

A

)]

gdzie: x*

A

- wartość równowagowa do ułamka y

A

na styku faz w dowolnym

przekroju deflegmatora

148

Zakładając, że w rozważanym zakresie stężeń współczynnik

względnej lotności  jest stały:

x*

A

= y

A

/ [  – y

A

( -1)]

r = (y

AV

/ y

AS

)

/( -1)

[(1 - y

AS

) / (1- y

AV

)]

1/( -1)

- 1

W przypadku szczególnym, gdy współczynnik względnej

lotności w zaznaczonym zakresie jest wielkością prawie stałą:

ln (n

k

/ n

p

) = - ∫

xAk

xAp

{ dx

A

/ [ ( ( x

A

) / (1 + x

A

( -1)) ) – x

A

] }

Po scałkowaniu i przyjęciu, że n

D

= n

p

– n

k

otrzymuje się:

n

D

= n

p

{ 1 – [ 1 / ( (x

Ap

/x

Ak

)

1/(-1)

( (1-x

Ak

)/(1-x

Ap

) )

1/(-1)

) ] }

149

Ogólne wskazania przy projektowaniu

instalacji do prowadzenia procesów

dyfuzyjno-cieplnych

Podczas projektowania instalacji do procesów dyfuzyjno-

cieplnych należy uwzględnić podane niżej czynności w takiej lub innej
kolejności w zależności od indywidualnych warunków:

1. Wybór najodpowiedniejszego procesu dla zadanego problemu

rozdziału mieszaniny. Oprócz właściwości rozdzielanej mieszaniny
należy uwzględnić również ekonomikę procesu, jego wpływ na
środowisko i niezawodność eksploatacji.

2. Zebranie danych fizyczno-chemicznych obydwu faz (stany

równowag).

3. Badanie procesowe mające na celu dopasowanie procesu do danego

przypadku rozdziału mieszaniny, tzn. właściwy dobór zabudowy
wnętrza aparatu i jego kształtu. Badania mogą być prowadzone w
skali laboratoryjnej, a jeśli to konieczne, to w instalacji pilotowej. Przy
przeniesieniu wyników należy uwzględnić problemy powiększania
skali.

4. Ustalenie sposobu eksploatacji aparatu i jego warunków ruchu.
5. Wykonanie obliczeń procesowych aparatu:

a) wstępne oszacowanie długości lub wysokości aparatu na
podstawie skróconych obliczeń rachunkowych lub graficznych;
b) iteracyjne powtórne przeliczenie;

150

c) uwzględnienie sprawności stopni rozdziału na podstawie badań
półtechnicznych (najlepiej) lub danych z przemysłu;
d) rozplanowanie wybranej zabudowy wnętrza aparatu zgodnie z
wynikami przeprowadzonych badań i sprawdzonych danych z
literatury.

6. Zaprojektowanie lub dobranie zgodnie z zasadami techniki

procesowej wszystkich elementów peryferyjnych, np. pomp,
wymienników ciepła, zbiorników itp..

7. Przeprowadzenie próby optymalizacji instalacji do rozdziału

mieszaniny, np. ze względu na minimum kosztów ogólnych.

8. Opracowanie schematu urządzeń kontrolno-pomiarowych i

regulujących dla całej instalacji.

9. Przedstawienie rozwiniętego schematu całej projektowanej

instalacji.

10. Przeliczenie i przedstawienie schematu pełnej sieci rurociągów

danej instalacji.

11. Przeliczenia wytrzymałościowe i konstrukcja elementów

projektowanej instalacji.

12. Ustalenie przestrzennego rozmieszczenia elementów instalacji

(plan fundamentów, izometryczny plan sieci rurociągów,
ewentualnie model instalacji w odpowiednio dobranej skali).