RACHUNEK PRAWDOPODOBIEŃSTWA

MAEW104

PROJEKT (F)

ILUSTRACJA CENTRALNEGO TWIERDZENIA
GRANICZNEGO

Projekt wykonany przez studentów I roku
ARI Politechniki Wrocławskiej:

Natalia Czop
Dawid Dąbrowski
Aneta Górniak
Andrzej Jakubiec
Piotr Walczak

09 czerwca 2008

C

ENTRALNE

T

WIERDZENIE

G

RANICZNE

(CTG Lindeberga-Lévy’ego)

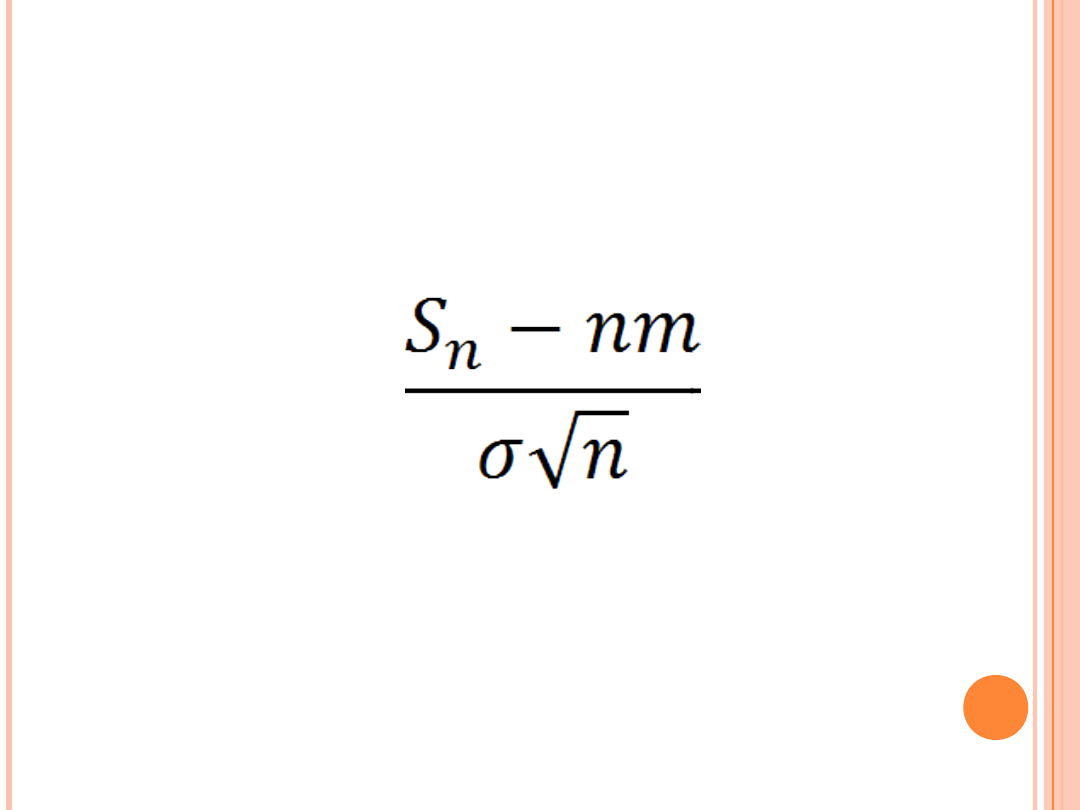
Rozważmy zmienną losową postaci:

m – wartość oczekiwana
σ – pierwiastek z wariancji

CENTRALNE TWIERDZENIE GRANICZNE

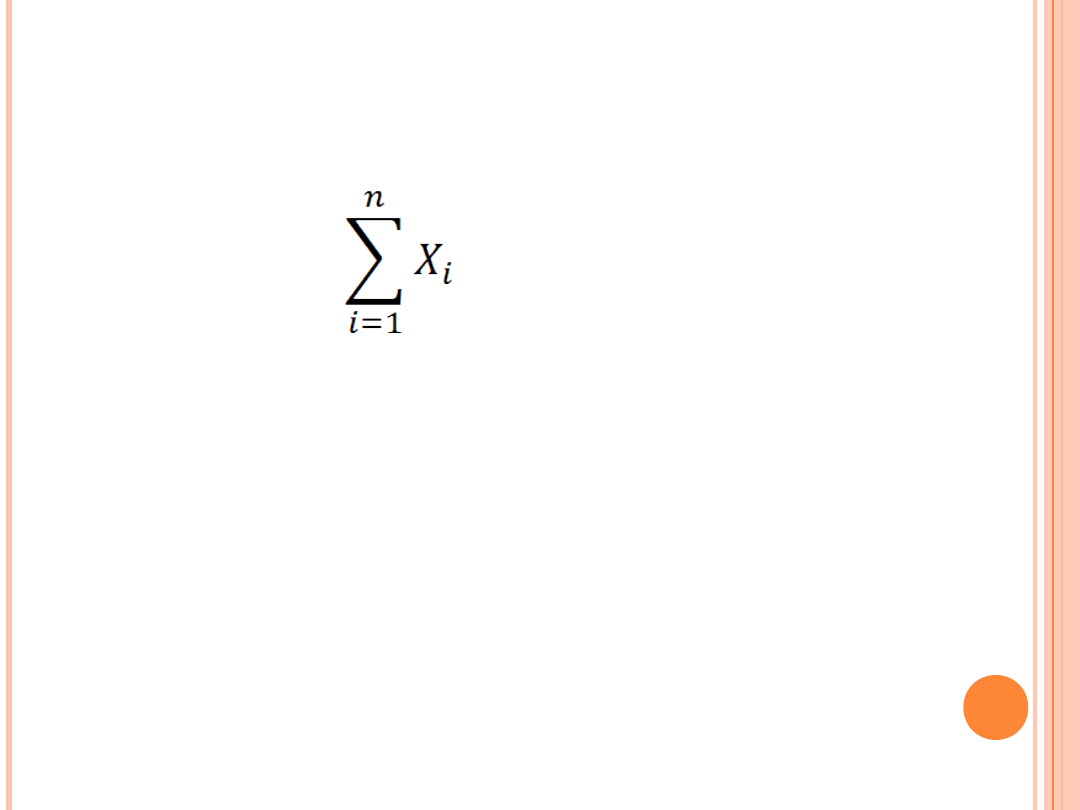
S

n

oznacza

, gdzie

X

i

są

niezależnymi zmiennymi losowymi o:

●

jednakowym rozkładzie

●

takiej samej wartości oczekiwanej

m

●

skończonej wariancji σ

2

> 0

CENTRALNE TWIERDZENIE GRANICZNE

Wtedy zmienna losowa o takiej

postaci zbiega według rozkładu do

standardowego rozkładu normalnego,

gdy

n

(liczba zmiennych losowych

tworzących daną sumę) rośnie do

nieskończoności.

CENTRALNE TWIERDZENIE GRANICZNE

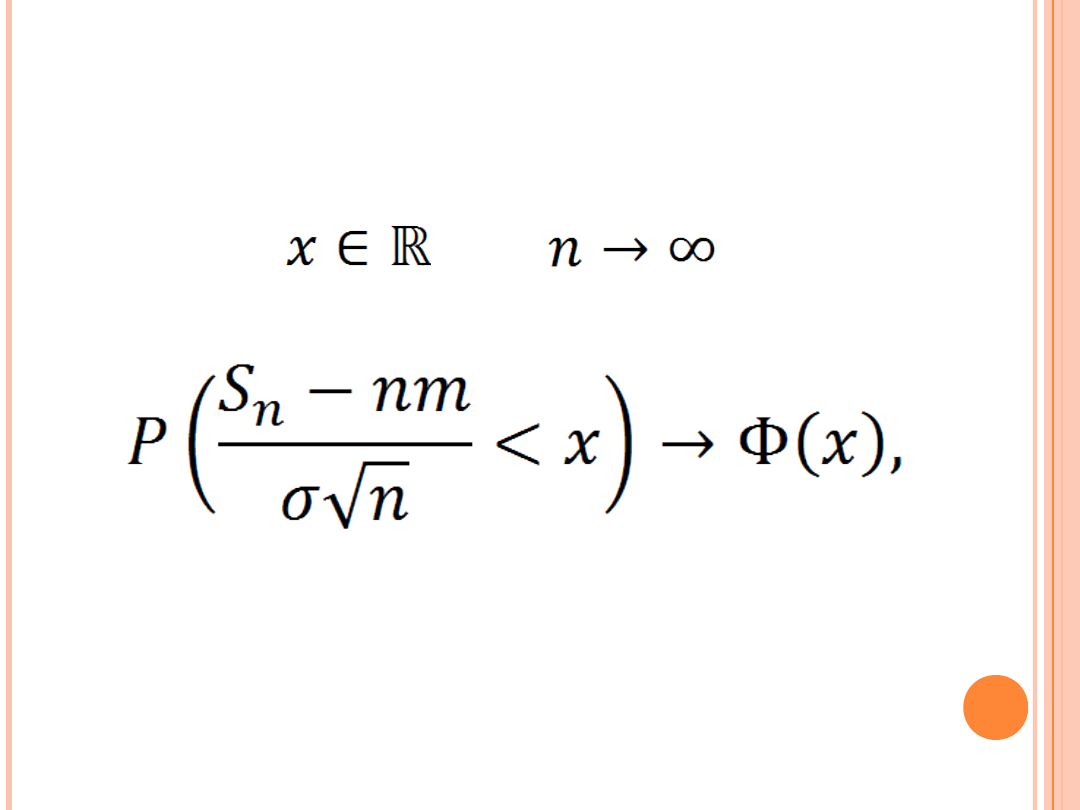
Dla każdego

przy

CENTRALNE TWIERDZENIE GRANICZNE

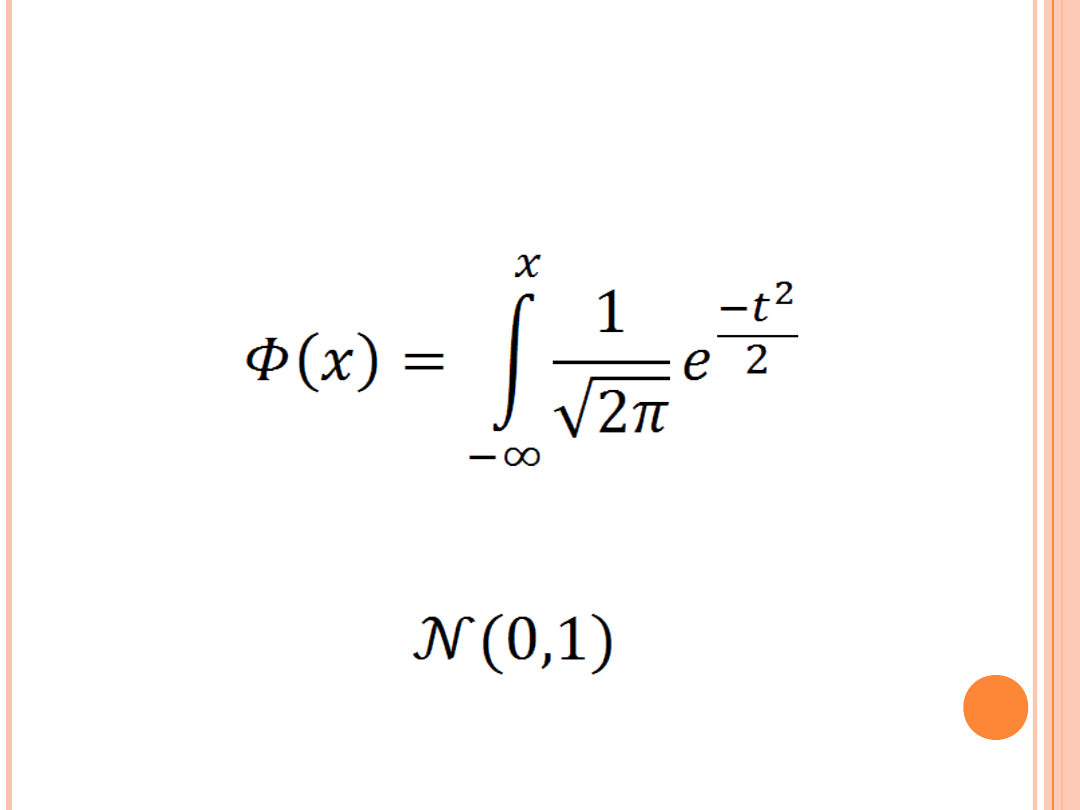
Gdzie:

to dystrybuanta standardowego rozkładu

normalnego

CENTRALNE TWIERDZENIE GRANICZNE

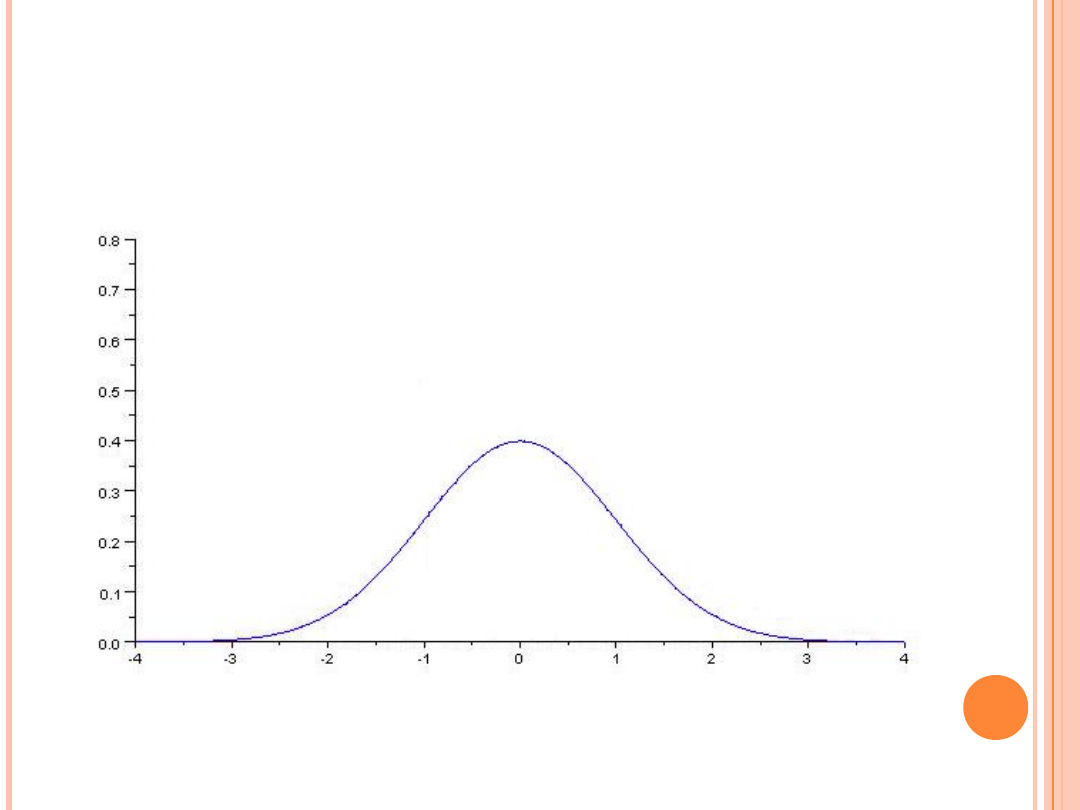
CENTRALNE TWIERDZENIE GRANICZNE

krzywa Gauss’a – funkcja gęstości prawdopodobieństwa standardowego rozkładu normalnego o

wartości oczekiwanej równej zeru i wariancji równej 1.

JAK DZIAŁA

CTG
?

X

i

o rozkładzie

Poissona



Losujemy

n

liczb o takim samym

rozkładzie



Sumę tych

n

liczb normalizujemy

(aby rozkład zbiegał do rozkładu

normalnego o parametrach

m = 0

,

σ² = 1

)



Czynność powtarzamy

N

razy

JAK DZIAŁA CTG?

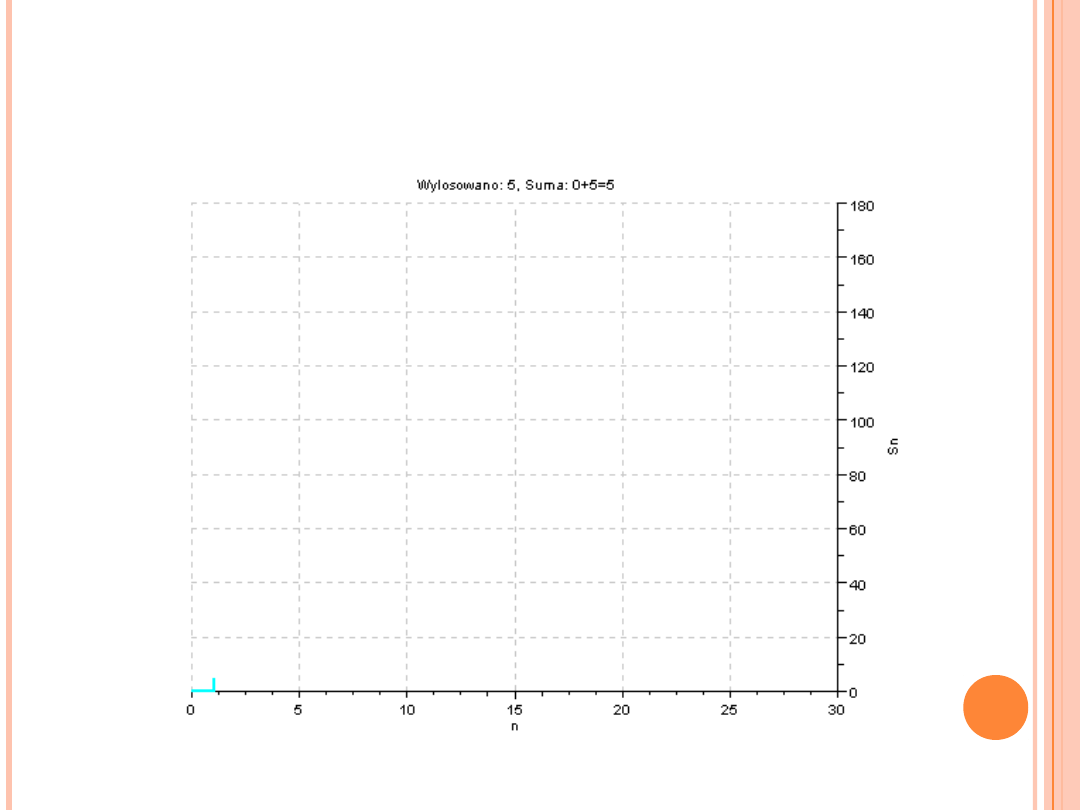
JAK DZIAŁA CTG?

(„rysowanie ścieżek” – błądzenie losowe z prawdopodobieństwem z rozkładu Poissona, λ = 5)

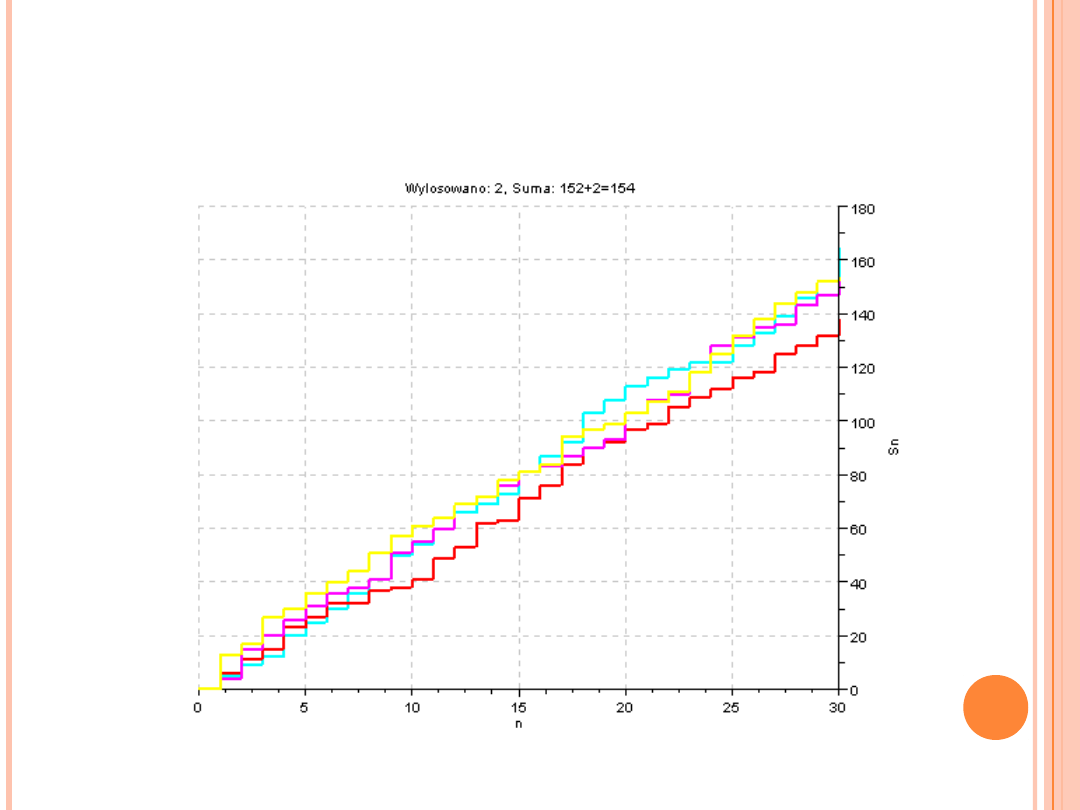
(„rysowanie ścieżek” – błądzenie losowe z prawdopodobieństwem z rozkładu Poissona, λ = 5)

JAK DZIAŁA CTG?

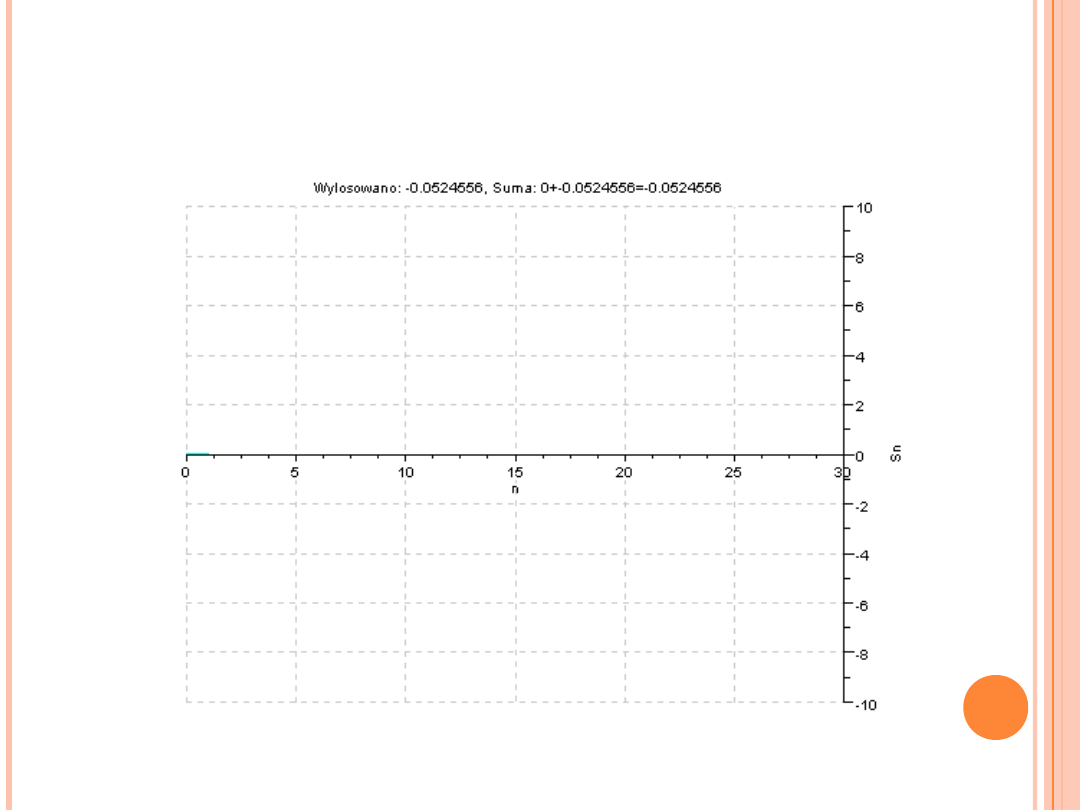
JAK DZIAŁA CTG?

(„rysowanie ścieżek” – błądzenie losowe z prawdopodobieństwem z rozkładu Laplace’a, l=0, λ

= 2)

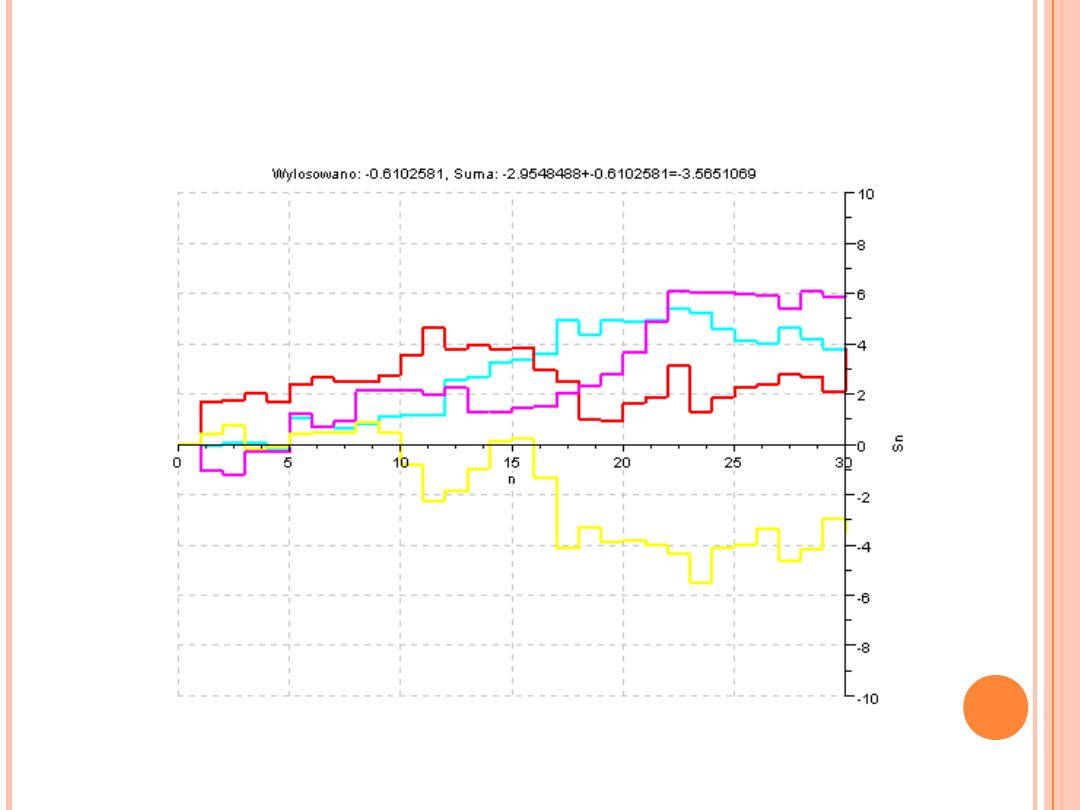
JAK DZIAŁA CTG?

(„rysowanie ścieżek” – błądzenie losowe z prawdopodobieństwem z rozkładu Laplace’a, l=0, λ

= 2)

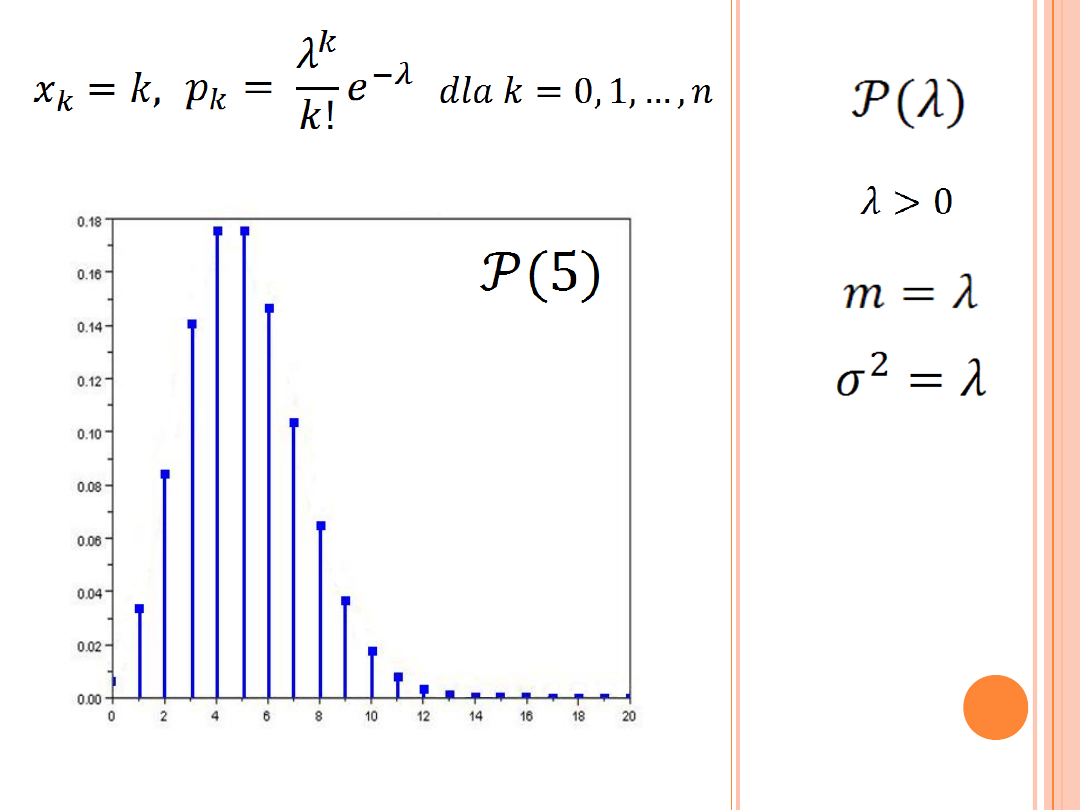
To rozkład dyskretny

przedstawiający liczbę wystąpień

zjawiska w czasie

t

, w określonej

liczbie prób, gdy wystąpienia te

są niezależne od siebie.

ROZKŁAD POISSONA

R

O

Z

K

Ł

A

D

P

O

IS

S

O

N

A

Rysujemy wykres:



Tworzymy histogram na podstawie

otrzymanych w wyniku błądzenia

losowego sum zmiennych losowych



sprawdzamy czy histogram

jest zbliżony do krzywej Gaussa.

JAK DZIAŁA CTG?

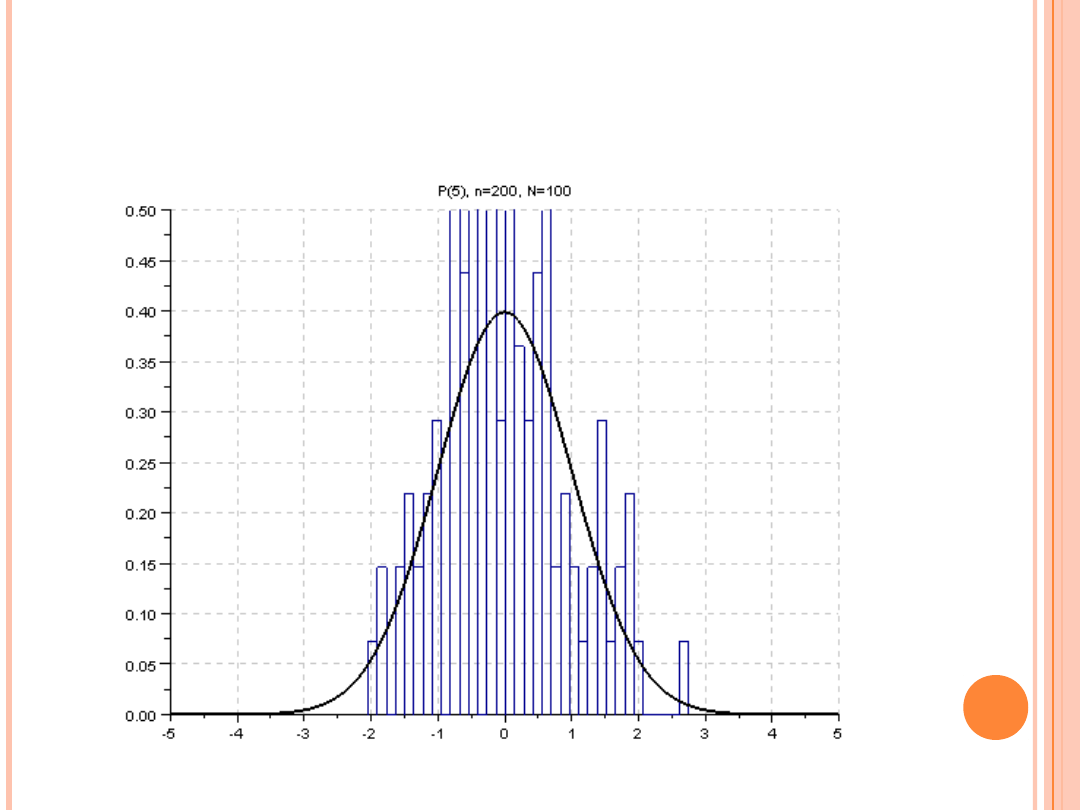
(liczba zmiennych losowych w sumie n = 200, liczba sum N = od 100 do

10 000)

JAK DZIAŁA CTG?

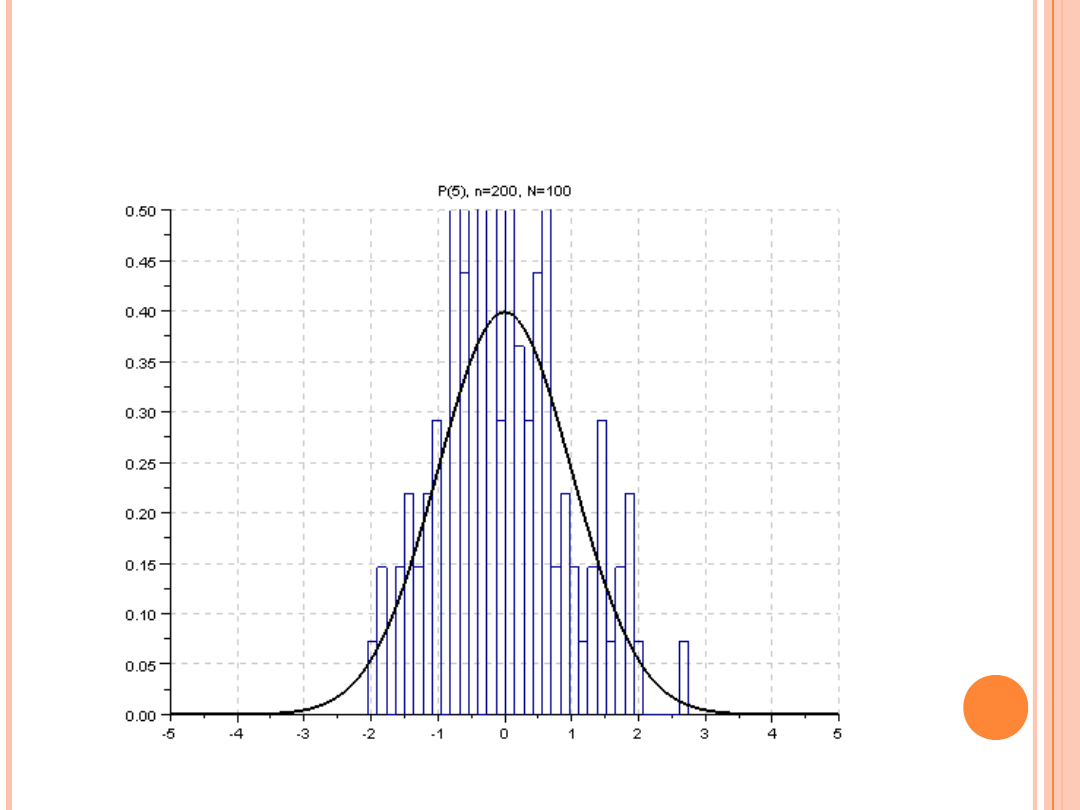
(liczba zmiennych losowych w sumie n = 200, liczba sum N = od 100 do

10 000

JAK DZIAŁA CTG?

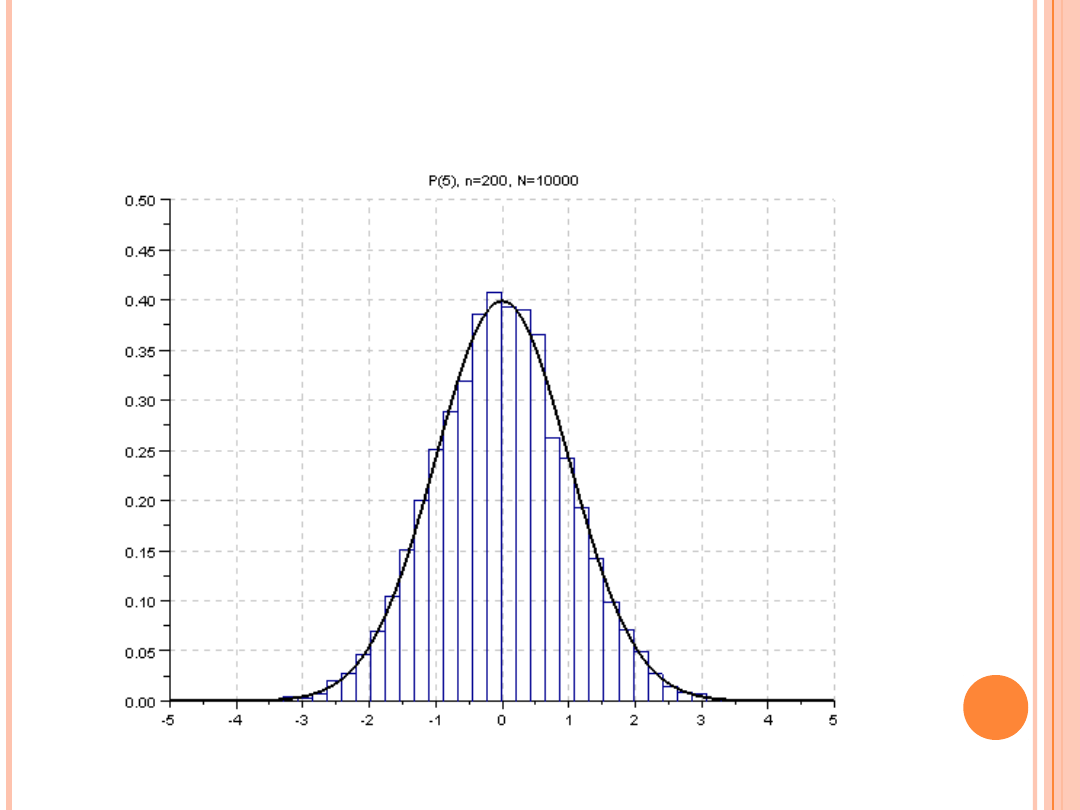
(liczba zmiennych losowych w sumie n = 200, liczba sum N = od 100 do

10 000

JAK DZIAŁA CTG?

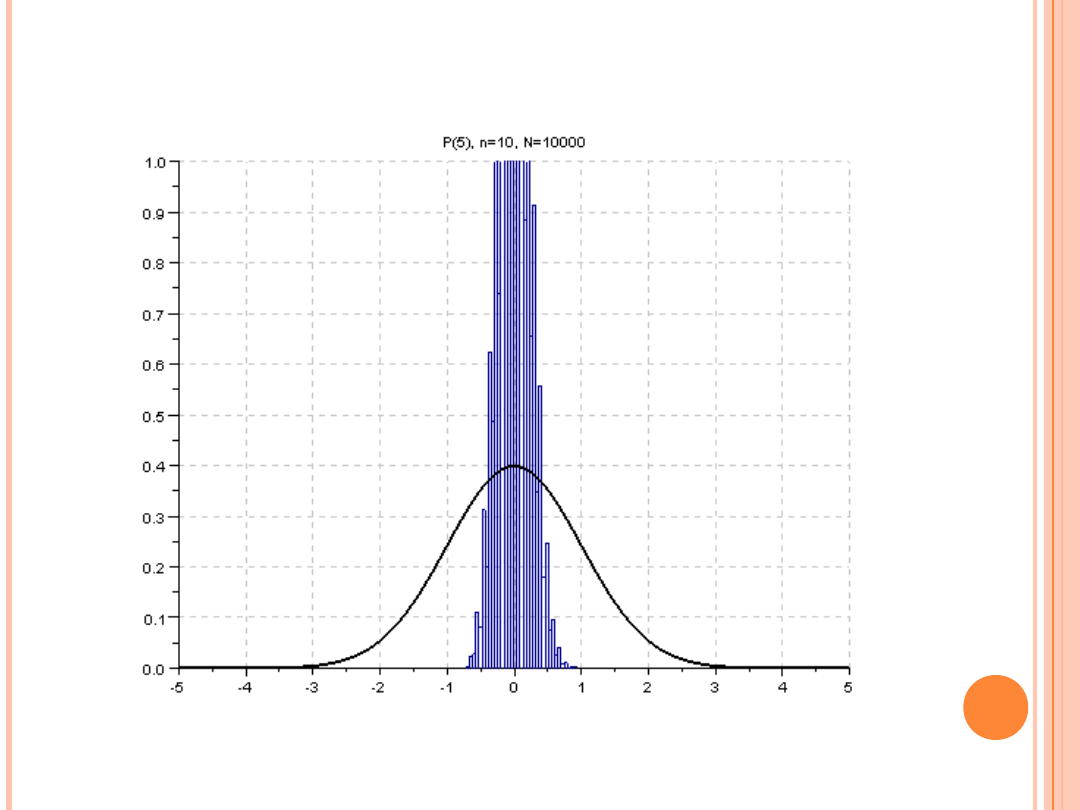
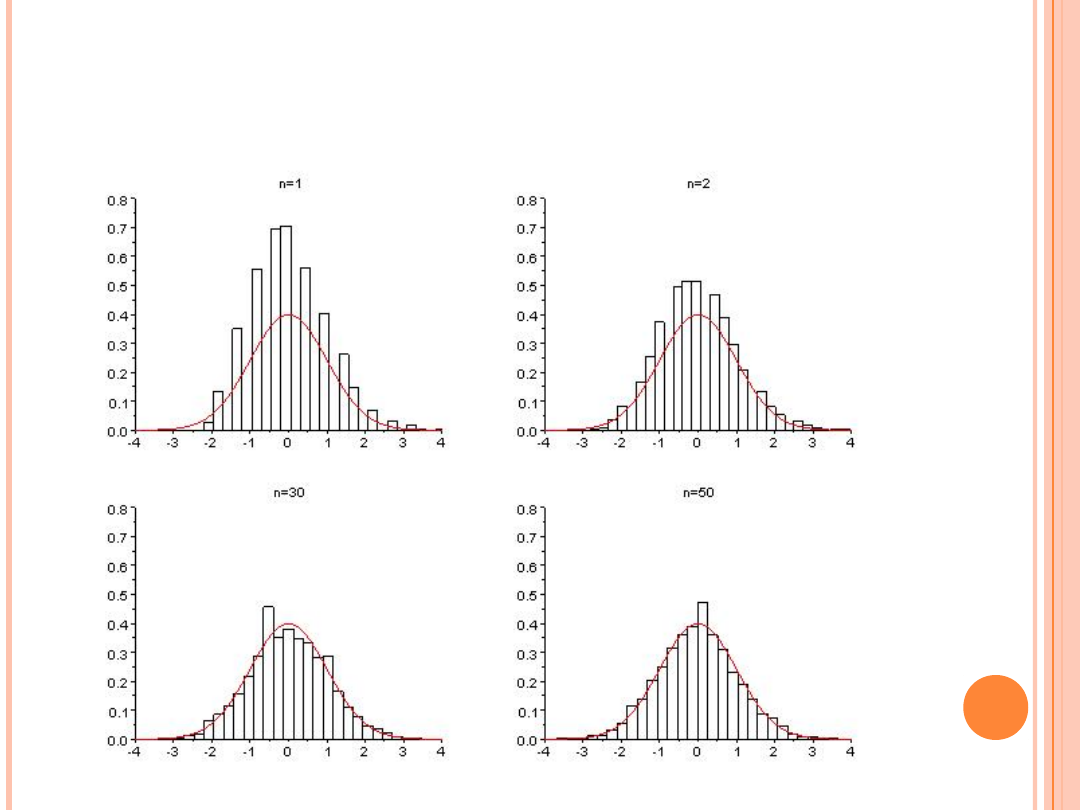
(liczba zmiennych losowych w sumie n = od 10 do 200, liczba sum N =

10 000)

JAK DZIAŁA CTG?

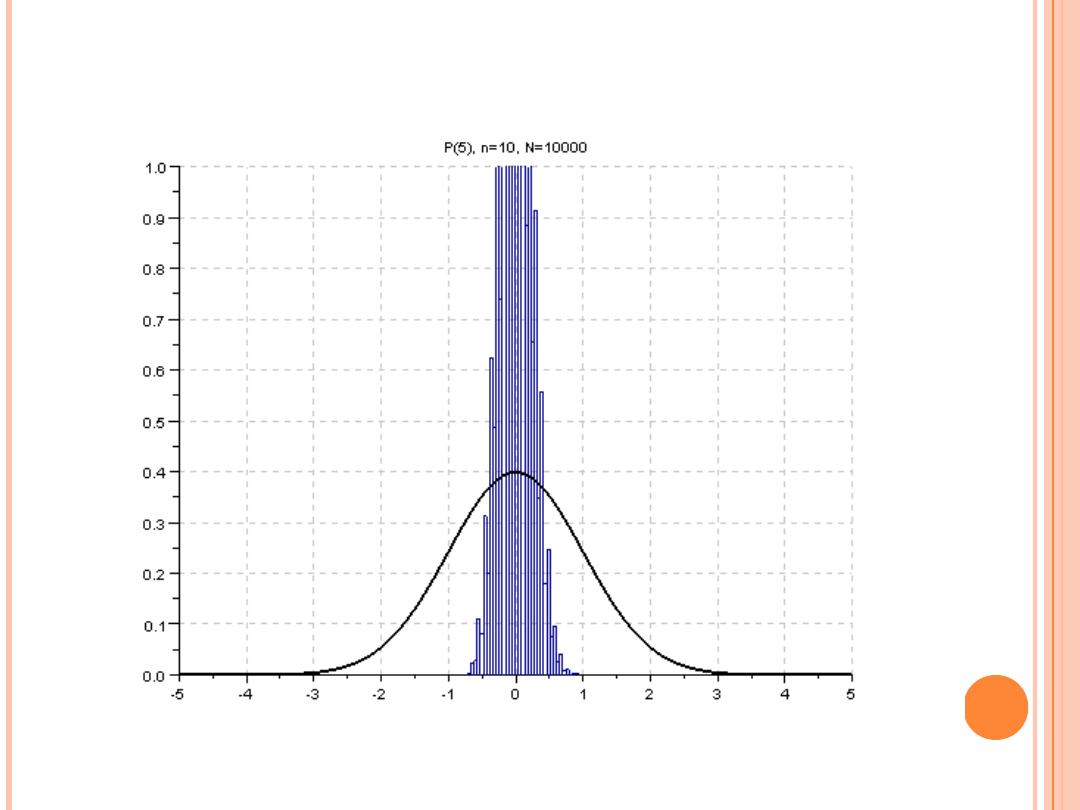
(liczba zmiennych losowych w sumie n = od 10 do 200, liczba sum N =

10 000)

JAK DZIAŁA CTG?

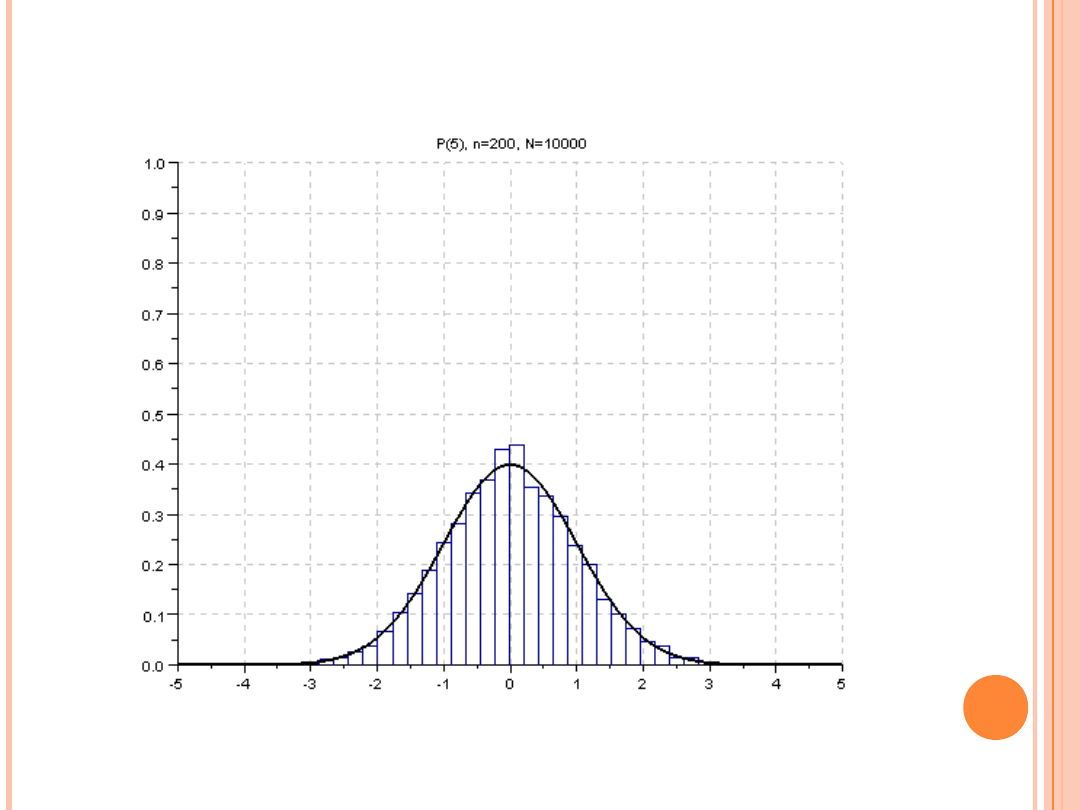
(liczba zmiennych losowych w sumie n = od 10 do 200, liczba sum N =

10 000)

JAK DZIAŁA CTG?

DOPASOWANIE KRZYWEJ GAUSSA

DO WYKRESU ROZKŁADU POISSONA

INNE
PRZYKŁADY
ROZKŁADU X

I

ROZKŁAD LAPLACE’A

(PODWÓJNIE WYKŁADNICZY)

Matematyczne zastosowania

rozkładu Laplace'a można

znaleźć w pracy Johnsona i

Kotza (Continuous univariate

distributions,1995).

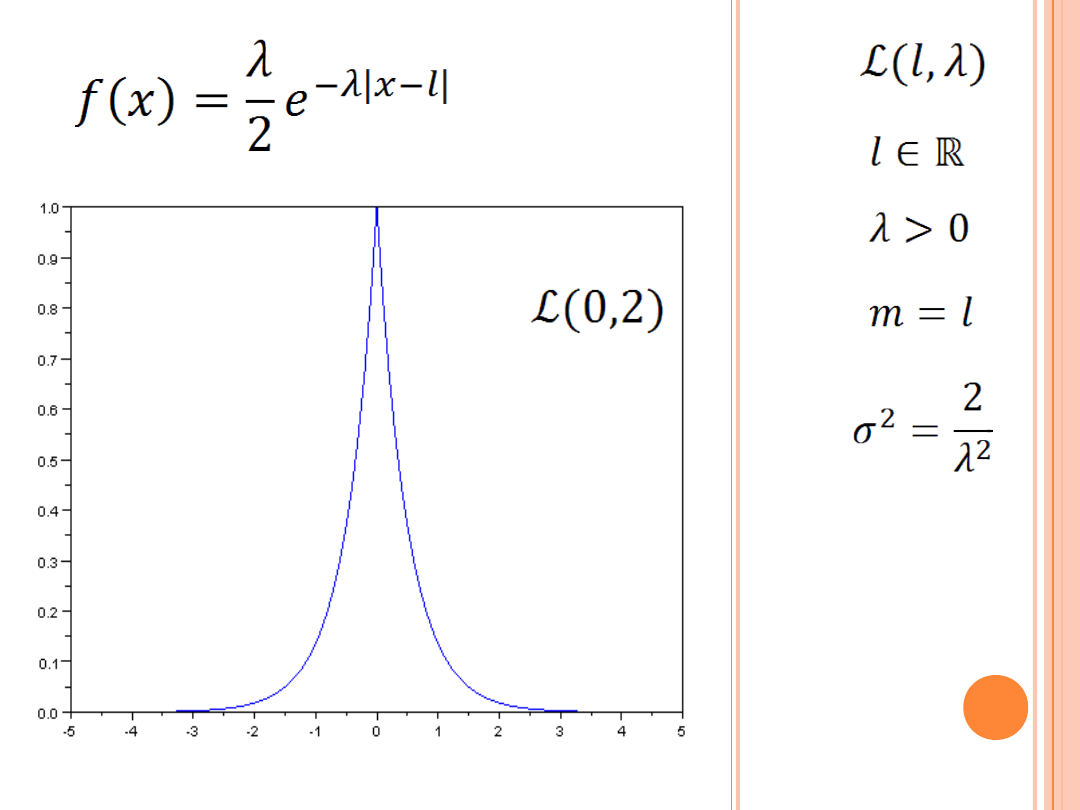
R

O

Z

K

Ł

A

D

L

A

P

L

A

C

E

’A

(

P

O

D

W

Ó

JN

IE

W

Y

K

Ł

A

D

N

IC

Z

Y

)

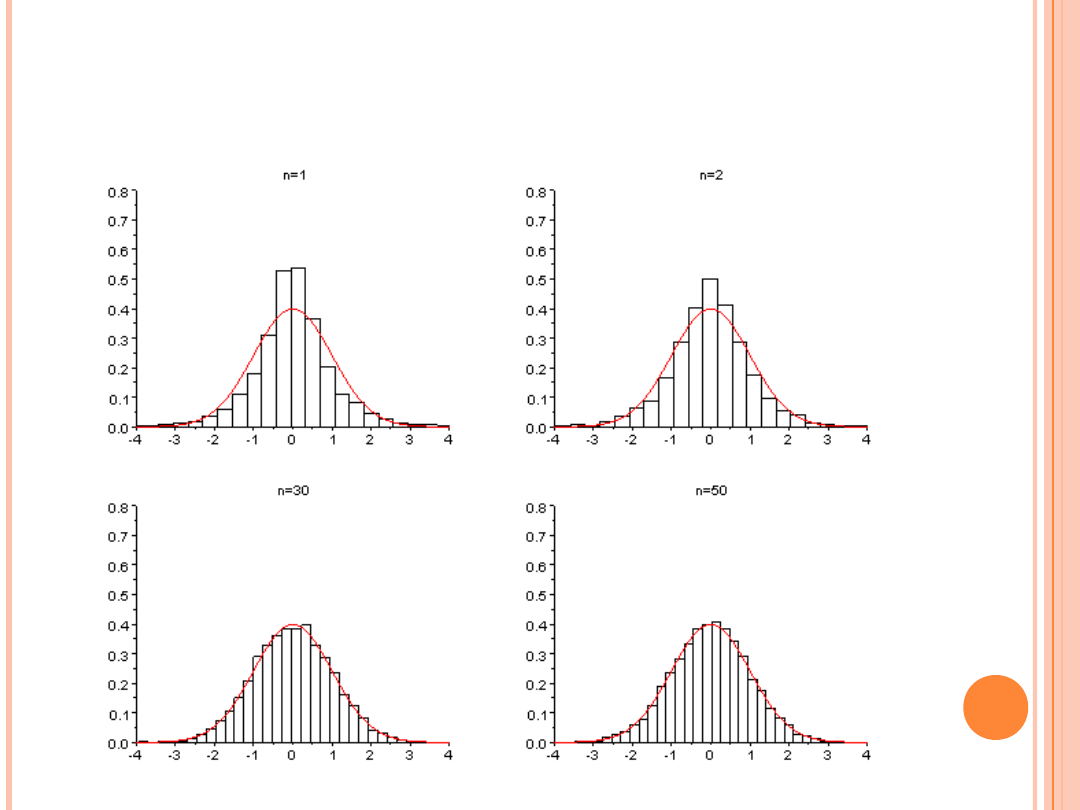
DOPASOWANIE KRZYWEJ GAUSSA

DO WYKRESU ROZKŁADU LAPLACE’A

ROZKŁAD PASCALA

(UJEMNY DWUMIANOWY)

Dyskretny rozkład prawdopodobieństwa

opisujący czas oczekiwania na l-ty sukces .

Jeśli l to liczba sukcesów, k - liczba porażek,

a p – prawdopodobieństwo sukcesu

(w badanych próbach Bernoulliego)

to rozkład Pascala opisuje jakie jest

prawdopodobieństwo wystąpienia

l sukcesów w k+l próbach.

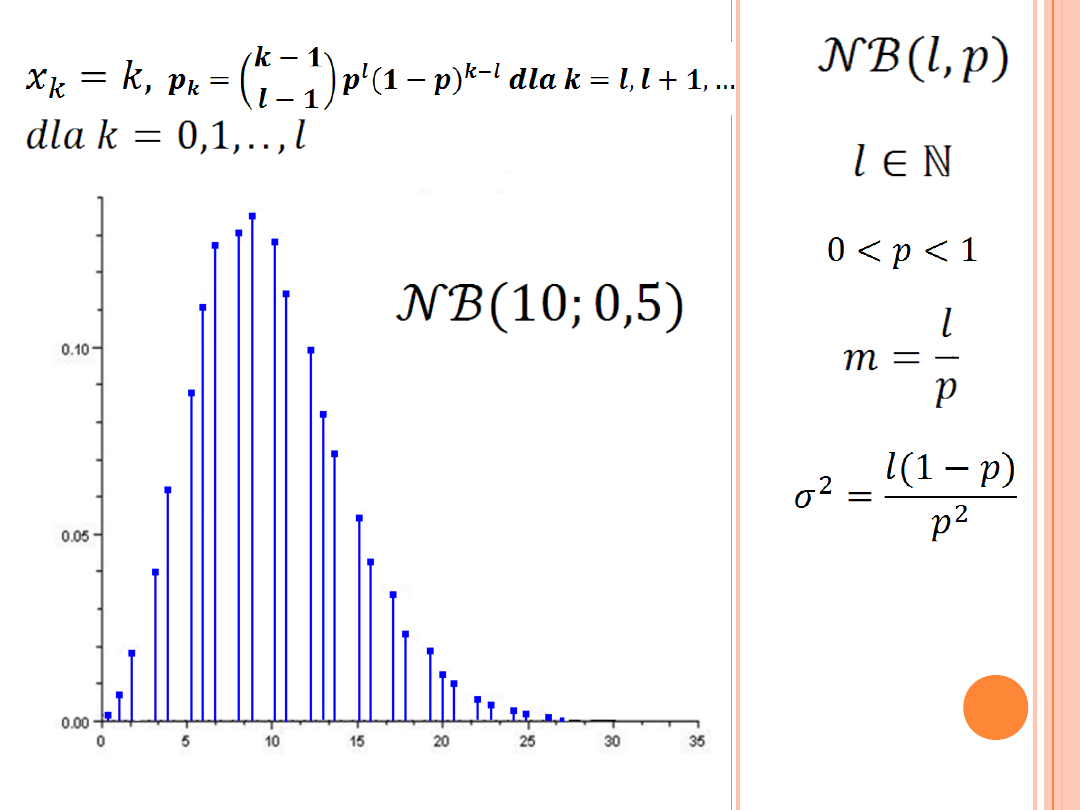
R

O

Z

K

Ł

A

D

P

A

S

C

A

L

A

(

U

JE

M

N

Y

D

W

U

M

IA

N

O

W

Y

)

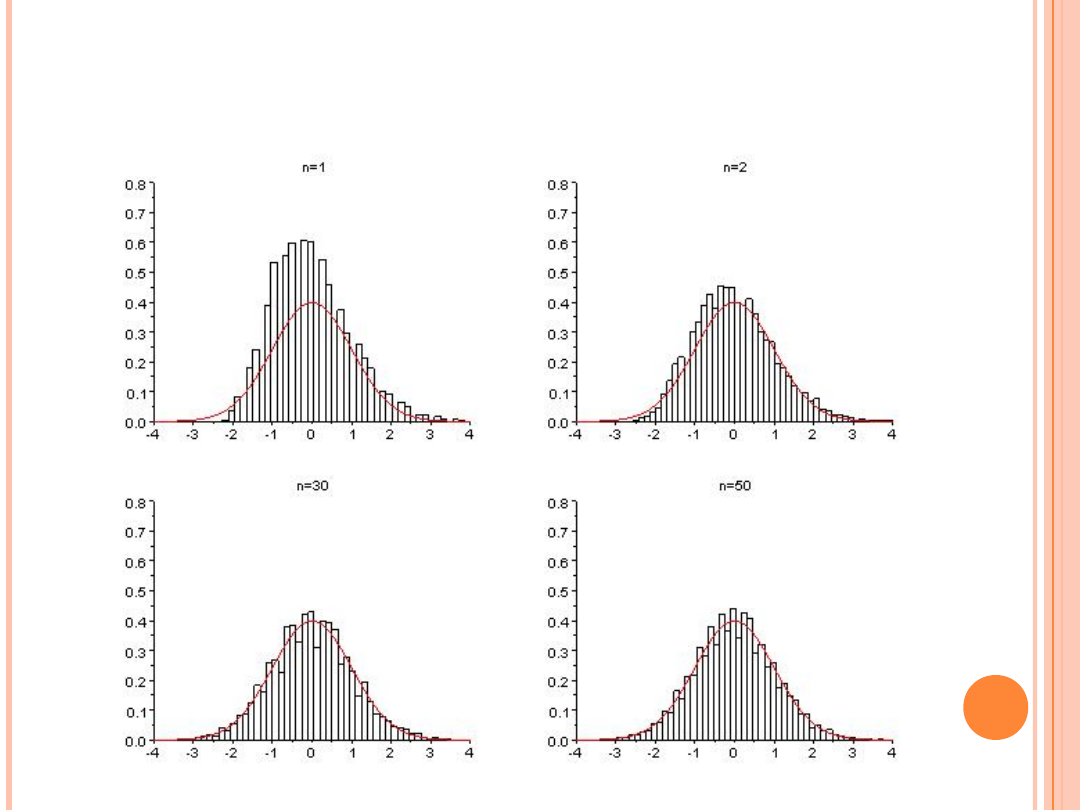
DOPASOWANIE KRZYWEJ GAUSSA

DO WYKRESU ROZKŁADU PASCALA

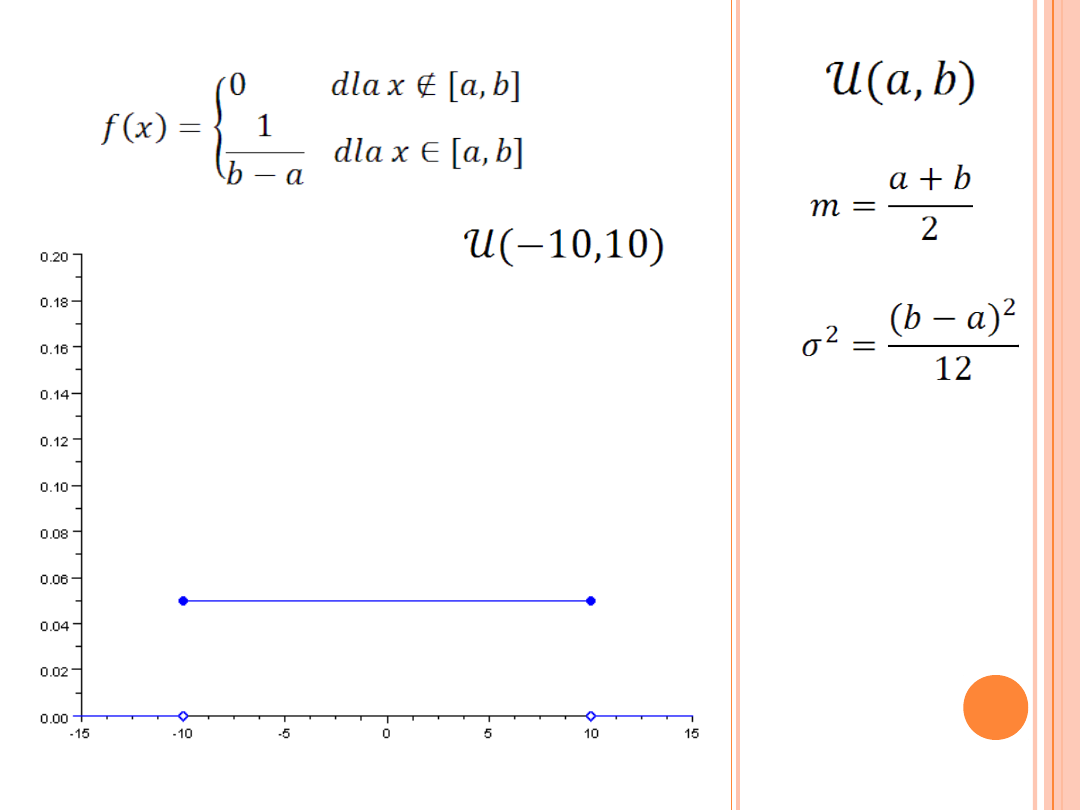
Rozkład prawdopodobieństwa,

dla którego gęstość

prawdopodobieństwa na

przedziale (a,b) jest stała i różna

od 0, a poza nim równa 0 ( gdzie b

> a )

ROZKŁAD JEDNOSTAJNY CIĄGŁY

R

O

Z

K

Ł

A

D

JE

D

N

O

S

T

A

JN

Y

C

IĄ

G

ŁY

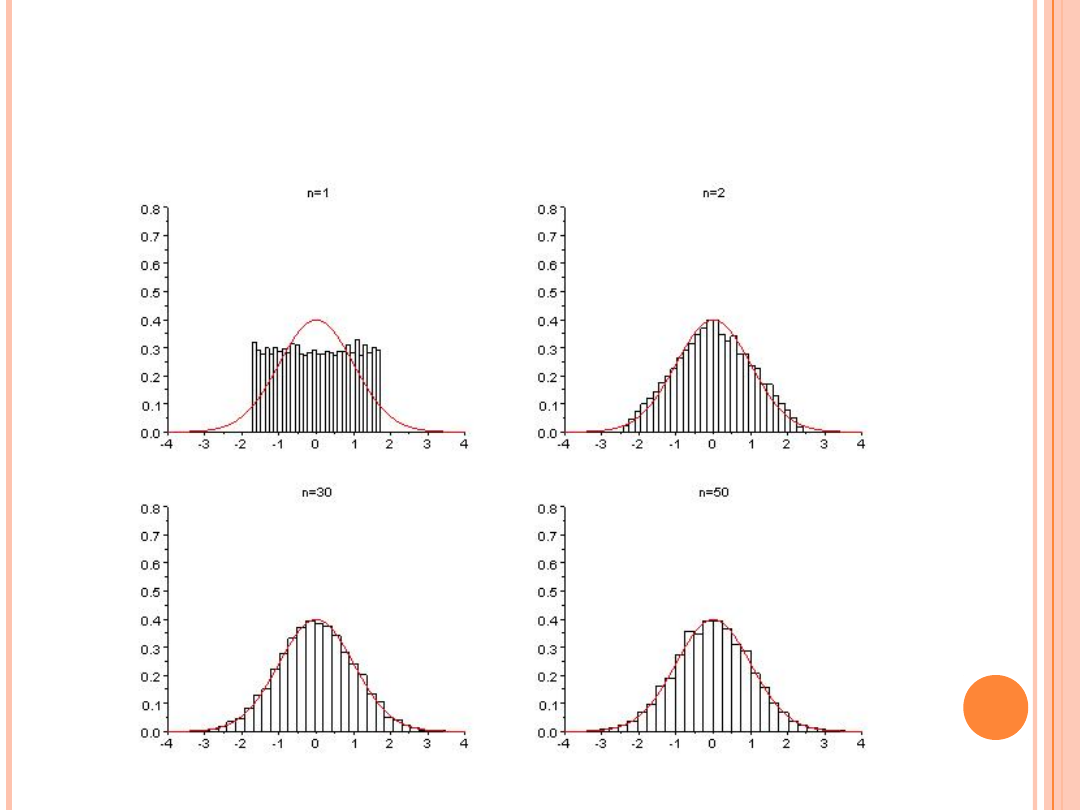
DOPASOWANIE KRZYWEJ GAUSSA

DO WYKRESU ROZKŁADU

JEDNOSTAJNEGO

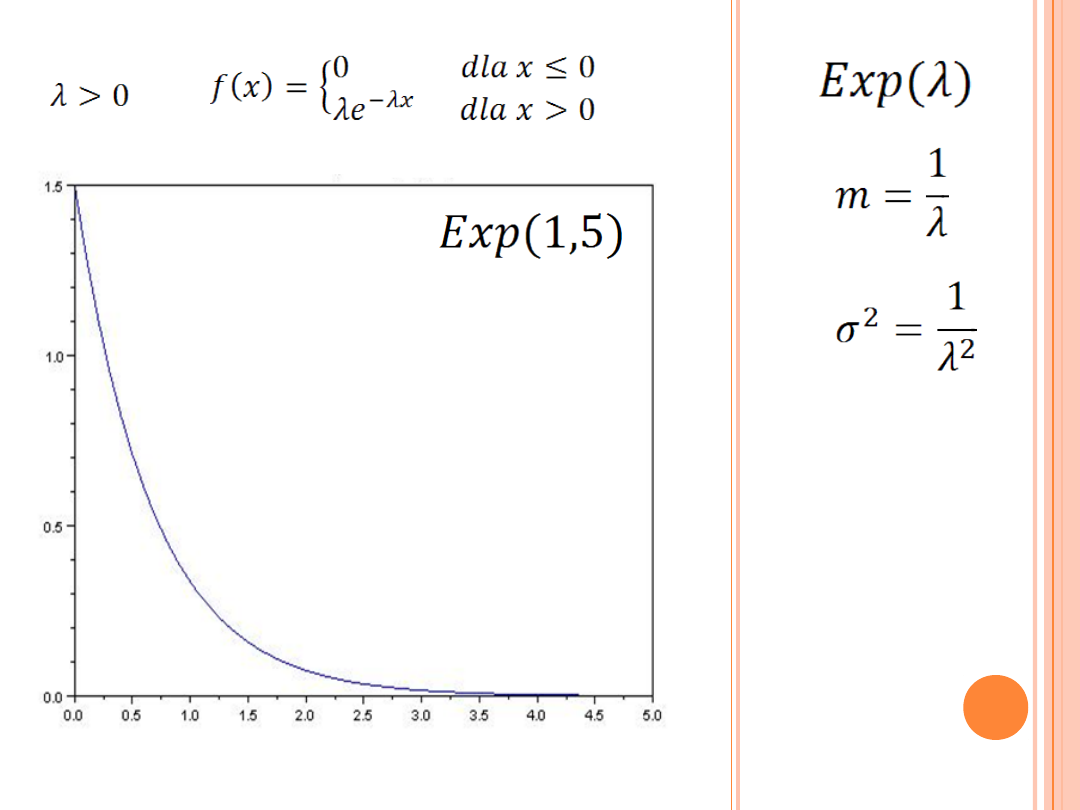
Rozkład zmiennej losowej

opisujący sytuację, w której obiekt

może przyjmować stany X i Y,

przy czym obiekt w stanie X może

ze stałym prawdopodobieństwem

przejść w stan Y w jednostce czasu.

ROZKŁAD WYKŁADNICZY

R

O

Z

K

Ł

A

D

W

Y

K

Ł

A

D

N

IC

Z

Y

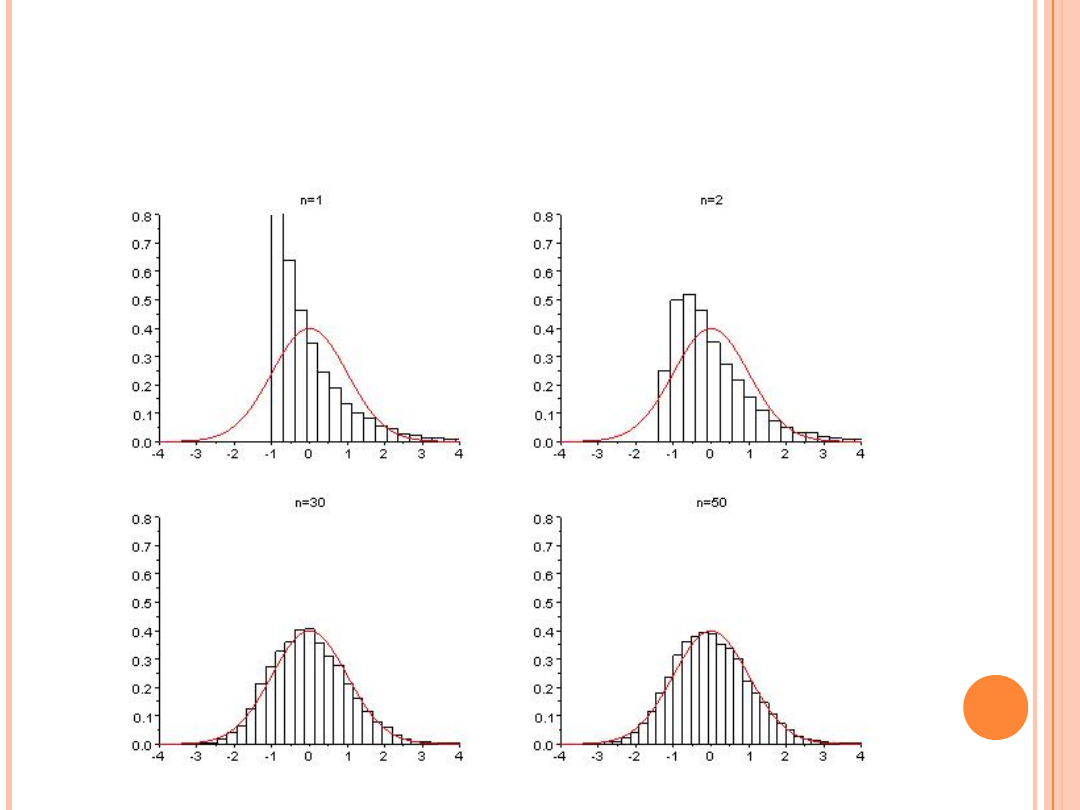
DOPASOWANIE KRZYWEJ GAUSSA

DO WYKRESU ROZKŁADU

WYKŁADNICZEGO