8. NUMERYCZNE TABLICE
WODY I PARY WODNEJ

1

8.1. Wprowadzenie
8.2. Tablice wody i pary do MathCada i Excela
8.3. Tablice wody i pary do MathCada i Excela
8.4. Tablice wody i pary – omówienie
8.5. Funkcje dla pary mokrej
8.6. Funkcje dla pary mokrej – c.d.
8.7. Instalacja tablic

8.1. Wprowadzenie

2

 Stosowane parametry wody i pary:

t – temperatura,
p – ciśnienie,
h – entalpia właściwa,
s – entropia właściwa,
v – objętość właściwa,
x – stopień suchości

 Ze względu na szeroki zakres zmienności parametrów (ciśnienia do 100 Mpa,

temperatury do 800

o

C)

obszar wody i pary dzieli się na kilka regionów (8 lub 5) i w każdym z nich
sformułowane są oddzielne
funkcje aproksymacyjne. W większości regionów parametrami wejściowymi są
temperatura i ciśnienie,
w pozostałych temperatura i objętość właściwa. Zwykle publikowany jest ograniczony
zestaw funkcji
aproksymacyjnych, np. h(t,p), s(t,p), v(t,p). W praktyce obliczeniowej czasami pożądane
są również
funkcje t(p,h) lub t(p,s) – te muszą być wyznaczone przez odwracanie.

 Badaniami własności wody i pary wodnej zajmuje się International Association for the

Properties
of Water and Steam (IAPWS)

 Pierwszym standardem były sformułowania IFC-67 (obecnie uznaje się jako przestarzałe)
 Aktualnie:

IAPWS-95 "for general and scientific use" - do obliczeń naukowych (jednofunkcyjne)
IAPWS-IF97 „industrial” – do szybkich obliczeń, z podziałem obszaru na 5 regionów
(nieciągłości)
nie ulegną zmianie przez wiele lat

http://gibbs.mech.kyushu-u.ac.jp/~akasaka/propath_man/

 http://www.iapws.org/relguide/IF97-Rev.pdf http://www.nist.gov/srd/nist10.cfm

8.2. Tablice wody i pary do MathCada i
Excela

3

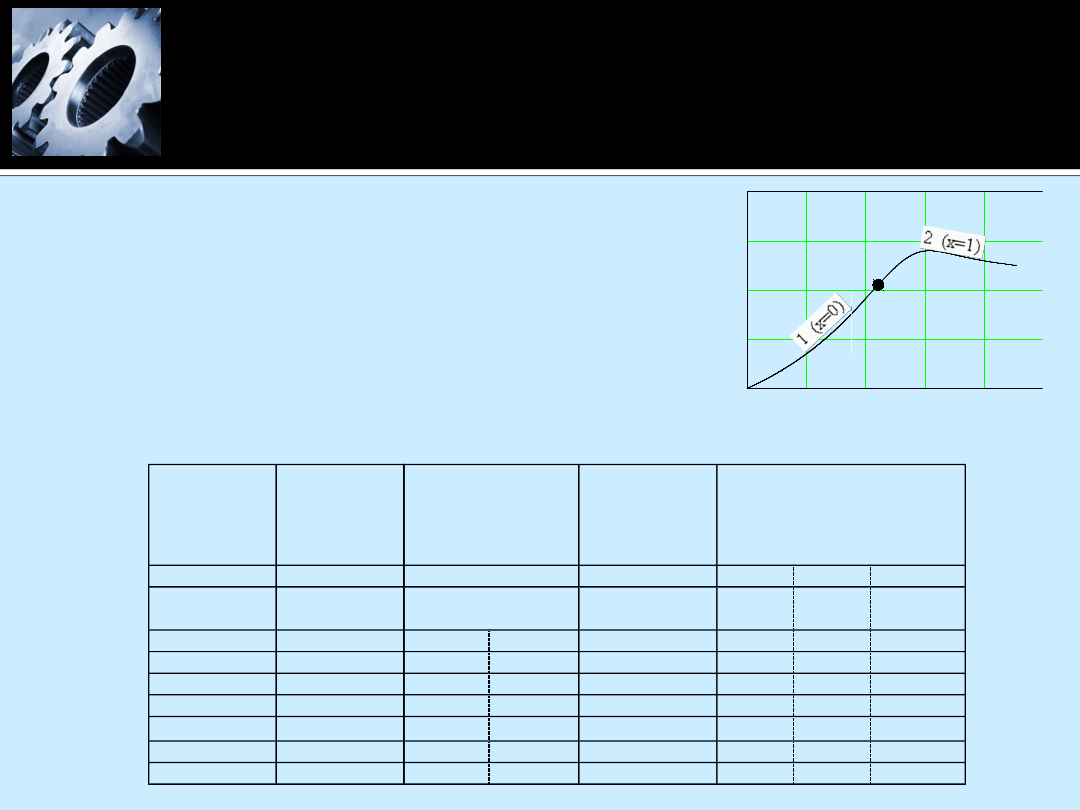
W tabeli zawarto funkcje dla wody i pary w bibliotece dla
MathCada (thmcad2008v1.dll) i Excela (ThExcel4.xla). Są
to funkcje oparte na standardzie IFC-67. Część funkcji to
oryginalne funkcje standardu, pozostałe – funkcje
odwracające.
Zakresy - (0,01-800

o

C), (0,0006 - 100 MPa),

dla pary mokrej - (0,01 - 374,12

o

C), (0,0006 - 22,115

MPa)

Wielkość
Obliczana

Jednostka

Obszar pary

mokrej

Bez

obszaru

pary

mokrej

W całym obszarze

Ciśnienie

Mpa

p(t)

 

 

 

p(t,v)

Temperatur
a

°C

t(p)

 

t(p,s)

t(p,h)

 

Entalpia wł.

kJ/kg

h’(t)

h’’(t)

h(t,p)

h(p,s)

 

h(t,v)

Entropia wł.

kJ/(kg·K)

s’(t)

s’’(t)

s(t,p)

 

s(p,h)

s(t,v)

Objętość wł. m

3

/kg

v’(t)

v’’(t)

v(t,p)

v(p,s)

v(p,h)

 

St.suchości

-

 

 

 

x(p,s)

x(p,h)

 

Ciepło wł.

kJ/(kg·K)

C

p

’(t)

C

p

’’(t)

C

p

(t,p)

 

 

 

Lepkość d.

Pa·s

’(t)

’’(t)

(t,p)

 

 

 

Przew. ciep.

W/(m·K)

’(t)

’’(t)

(t,p)

 

 

 

0

2

4

6

8

10

0

1

10

3



2

10

3



3

10

3



4 10

3



4.174

h1Sat t.x

( )

h2Sat t.x

( )

9.13

0.015

s1Sat t.x

( )

s2Sat t.x

( )

,

s [kJ/kgK]

h
[kJ/k
g]

Obszar
pary
mokrej

Tabela 1

8.3. Tablice wody i pary do MathCada i
Excela

4

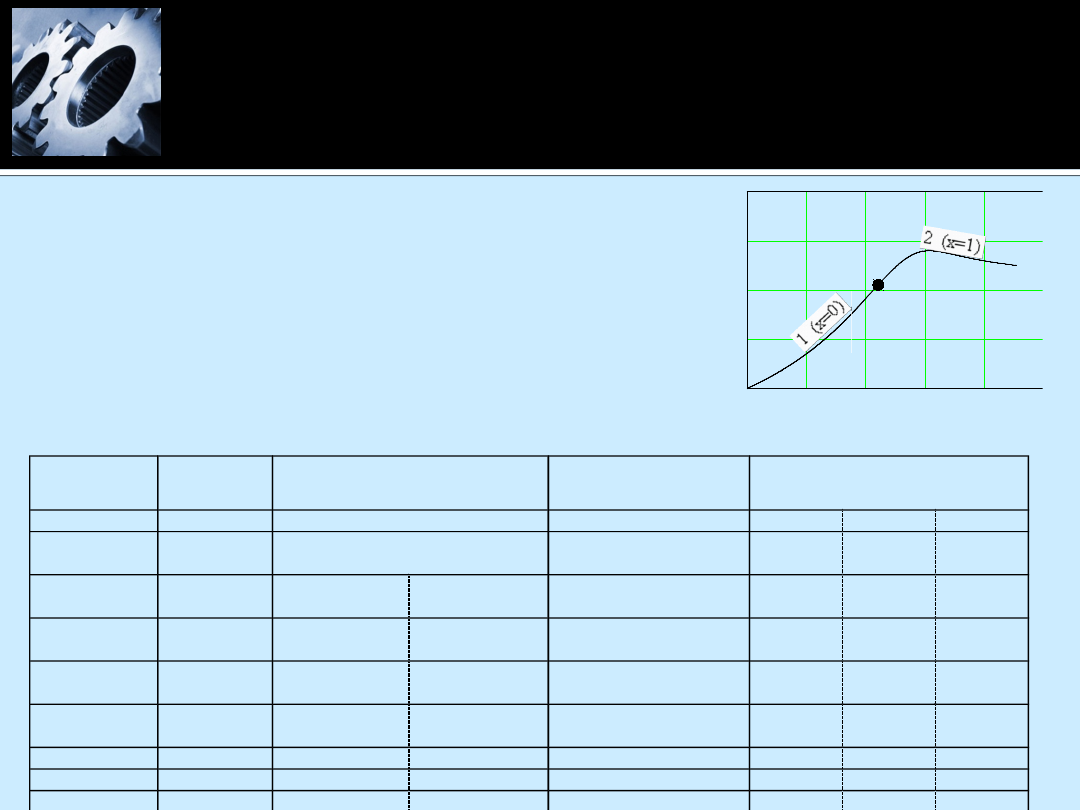
W tabeli nazwy funkcji (MathCad i Excel)
bibliotecznych:

Wielkość

Obliczana

Jednostk

a

Obszar pary mokrej

Bez obszaru

pary mokrej

W całym obszarze

Ciśnienie

Mpa

pSat(t)

 

 

 

p_tv(t,v)

Temperatur
a

°C

tSat(p)

 

t_ps(p,s)

t_ph(p,h
)

 

Entalpia wł.

kJ/kg

h1Sat(t)

h2Sat(t)

h_tp(t,p)

h_ps(p,s
)

 

h_tv(t,v)

Entropia wł.

kJ/(kg·K)

s1Sat(t)

s2Sat(t)

s_tp(t,p)

 

s_ph(p,h
)

s_tv(t,v)

Objętość wł. m

3

/kg

v1Sat(t)

v2Sat(t)

v_tp(t,p)

v_ps(p,s
)

v_ph(p,
h)

 

St.suchości

-

 

 

 

x_ps(p,s
)

x_ph(p,
h)

 

Ciepło wł.

kJ/(kg·K)

Cp1Sat(t)

Cp2Sat(t)

Cp(t,p)

 

 

 

Lepkość d.

Pa·s

Visc1Sat(t)

Visc2Sat(t)

Visc(t,p)

 

 

 

Przew. ciep.

W/(m·K)

Lambda1Sat(
t)

Lambda2Sat(
t)

Lambda(t,p)

 

 

 

0

2

4

6

8

10

0

1

10

3



2

10

3



3

10

3



4 10

3



4.174

h1Sat t.x

( )

h2Sat t.x

( )

9.13

0.015

s1Sat t.x

( )

s2Sat t.x

( )

,

s [kJ/kgK]

h
[kJ/k
g]

Obszar
pary
mokrej

Tabela 2.

Implementacja funkcji z Tabeli 1 w MathCadzie

i Excelu

8.4. Tablice wody i pary - omówienie

5

Funkcje dla wody i pary można podzielić na następujące kategorie:
1. Przeliczniki (temperatura nasycenia  ciśnienie nasycenia)
t = t(p); p = p(t)

MathCad 

t = tSat(p); p = pSat(t)

2. Funkcje na krzywych granicznych (wykres h-s)
np. h = h’(t); h = h’’(t)

MathCad 

h = h1Sat(t); h = h2Sat(t)

gdzie h’(t) entalpia wody w temp. nasycenia – krzywa graniczna 1 (x=0) na wykresie h-s
h’’(t) entalpia pary w temp. nasycenia – krzywa graniczna 2 (x=1) na wykresie h-s
3. Funkcje dwu-parametrowe obowiązujące dla wody, pary przegrzanej i pary mokrej
np. funkcje na h

h=h(p,s)

MathCad 

h = h_ps(p,s)

h=h(t,v)

MathCad 

h = h_tv(p,s)

w całym obszarze wykresu h-s krzywe (p,s) oraz (t,v) przecinają się w jednym punkcie więc
istnieją
odpowiednio jednoznaczne funkcje h(p,s) oraz h(t,v)
4. Funkcje dwu-parametrowe obowiązujące dla wody i pary przegrzanej
np. funkcje na h

h=h(t,p)

MathCad 

h = h_tp(t,p)

krzywe (t,p) przecinają się w jednym punkcie tylko dla wody i pary przegrzanej. Dla pary
mokrej
krzywe te pokrywają się i w tym obszarze nie ma jednoznacznej funkcji h(t,p). Parametry
pary mokrej
wyznaczamy przy pomocy funkcji na krzywych granicznych

8.5. Funkcje dla pary mokrej

6

W obszarze pary mokrej można stosować ogólne funkcje h(p,s) lub h(t,v) ale w praktyce dane
wejściowe
w tym regionie to (t,x) lub (p,x).
Entalpia właściwa pary mokrej dla tych danych
dane: (t,x)

h=h’(t)(1-x)+h’’(t)x

MathCad 

h = h1Sat(t)(1-x)+h2Sat(t)x

dane: (p,x)

t=t(p) h=h’(t)(1-x)+h’’(t)x

MathCad 

t=tSat(p) h = h1Sat(t)(1-x)

+h2Sat(t)x

Objętość właściwa
dane: (t,x)

v=v’(t)(1-x)+v’’(t)x

MathCad 

v = v1Sat(t)(1-x)+v2Sat(t)x

dane: (p,x)

t=t(p) v=v’(t)(1-x)+v’’(t)x

MathCad 

t=tSat(p) v = v1Sat(t)(1-x)

+v2Sat(t)x

Entropia właściwa
dane: (t,x)

s=s’(t)(1-x)+s’’(t)x

MathCad 

s = s1Sat(t)(1-x)+s2Sat(t)x

dane: (p,x)

t=t(p) s=s’(t)(1-x)+s’’(t)x

MathCad 

t=tSat(p) s = s1Sat(t)(1-x)

+s2Sat(t)x

8.6. Funkcje dla pary mokrej – c.d.

7

Należy unikać jawnego stosowania funkcji h(t,p) (

również s(t,p), v(t,p) ,…

) jeśli czynnik może być

parą mokrą – wtedy entalpię liczymy przecież z wzoru: h=h’(t)(1-x)+h’’(t)x
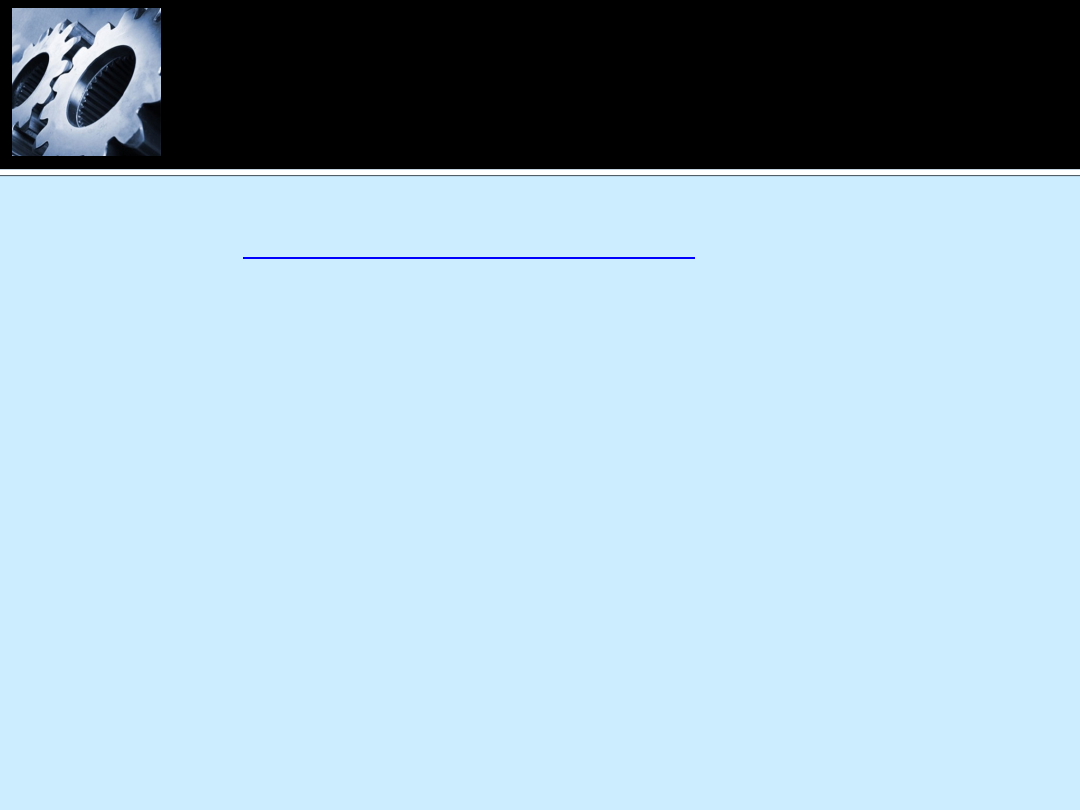
O możliwych problemach świadczy poniższy przykład:

D

1

,

t

1

,

p

1

D

2

,

t

2

, p

2

t

3

, p

3

Przykład 1

Oblicz temperaturę czynnika t

3

za schładzaczem jeśli:

D1 3 kg sek

1

-

=

t1 415 ° C

=

p1 6 MPa

=

D2 0.5 kg sek

1

-

=

t2 170 ° C

=

p2 6.2 MPa

=

p3 5.9 MPa

=

rozwiązujemy
równanie:

D1 h t1 p1

,

(

)

D2 h t2 p2

,

(

)



D1 D2



(

)

h t3 p3

,

(

)

=

t3 200°C



given

D1 h_tp t1 p1

,

(

)

D2 h_tp t2 p2

,

(

)



D1 D2



(

)

h_tp t3 p3

,

(

)

=

t3 find t3

( )

°C





find t3

( )

°C



rozwiązujemy
równanie:

D1 h t1 p1

,

(

)

D2 h t2 p2

,

(

)



D1 D2



(

)

i3

=

i3

D1 h_tp t1 p1

,

(

)

D2 h_tp t2 p2

,

(

)



D1 D2





t3 t_ph p3 i3

,

(

)

274.4°C





x3 x_ph p3 i3

,

(

)

0.917





I sposób

II sposób

Gdyby w rurociągu 3 czynnik był wodą lub parą przegrzaną I sposób byłby
skuteczny, ale …

8.7. Instalacja tablic

8

Pliki ze strony

http://fluid.itcmp.pwr.wroc.pl/~zmodl/

Instalacja w MathCadzie.

 thmcad2008v1.dll - biblioteka kilkuset funkcji (m.innymi tablice) – napisana w języku C+

+.

Należy ją umieścić w katalogu ...\MathCad\userefi.

Podczas uruchamiania MathCad przegląda ten katalog i ładuje
wszystkie

biblioteki .dll (dynamic-link library)

 user_EN.xml - plik opisujący funkcje.

Należy umieścić (nadpisać) go w katalogu ...\MathCad\doc\funcdoc
Plik nie jest bezwzględnie potrzebny, dzięki niemu funkcje są widoczne
w oknie (menu) InsertFunction Function Category

Instalacja w Excelu

 ThExcel4.xla - plik typu dodatek – napisany w VBA.

Należy go umieść w dowolnym katalogu, ale najlepiej niech to będzie:
C:\Program Files (x86)\Microsoft Office\Office12\Library (Excel 2007)
C:\Windows\Dane aplikacji\Microsoft\AddIns (Excel 97)

Trzeba go uaktywnić przy pomocy menu: …Dodatki