Inteligencja obliczeniowa

Sztuczne sieci

neuronowe

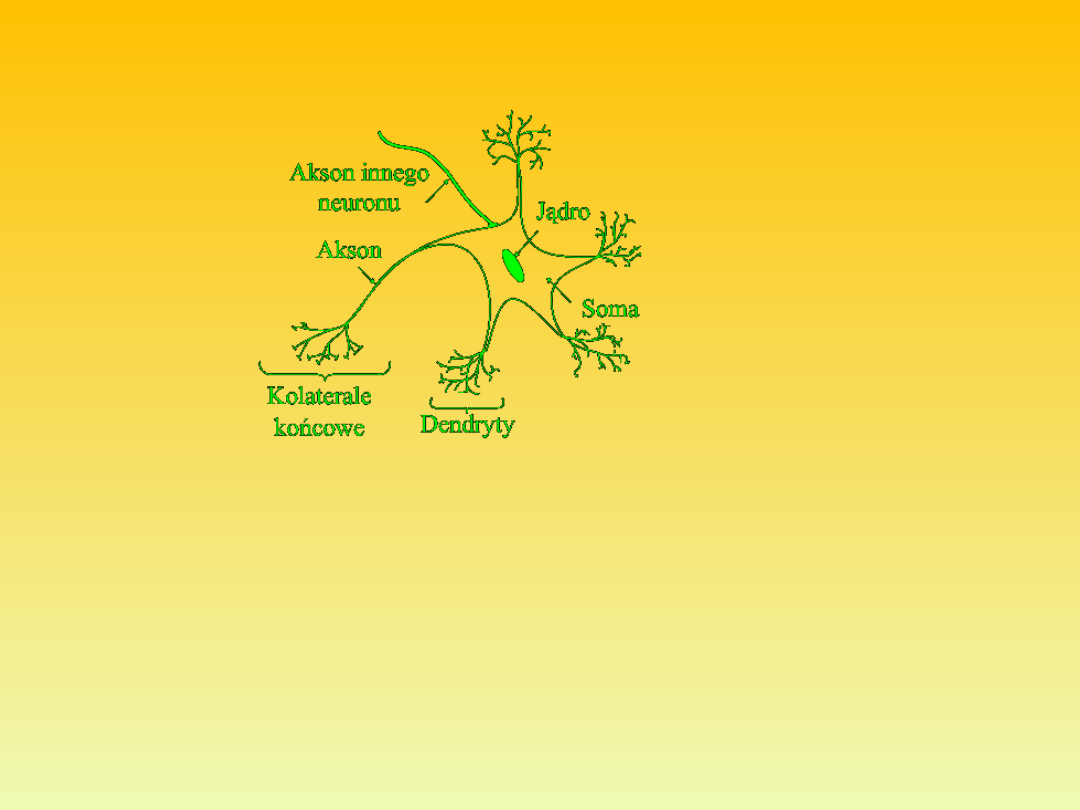
Pojedyncza komórka neuronowa – budowa [Rafał Czapaj].

Sieć neuronowa jest systemem przetwarzającym informacje w sposób
równoległy.

System ten składa się z dużej liczby neuronów, formujących (na wzór
mózgu) struktury rozpoznające obrazy.

Każdy z neuronów ma wiele wejść (synaps) i jedno wyjście (akson).

Ze względu na specyficzne cechy i niepodważalne zalety obszar

zastosowań sieci neuronowych jest rozległy i obejmuje mi.:

- Rozpoznawanie wzorców (znaków, liter, kształtów, sygnałów
mowy, sygnałów sonarowych)
- Klasyfikowanie obiektów
- Prognozowanie i ocena ryzyka ekonomicznego
- Prognozowanie zmian cen rynkowych (giełdy, waluty)
- Ocena zdolności kredytowej podmiotów
- Prognozowanie zapotrzebowania na energię elektryczną
- Diagnostyka medyczna
- Dobór pracowników
- Prognozowanie sprzedaży
- Aproksymowanie wartości funkcji

 

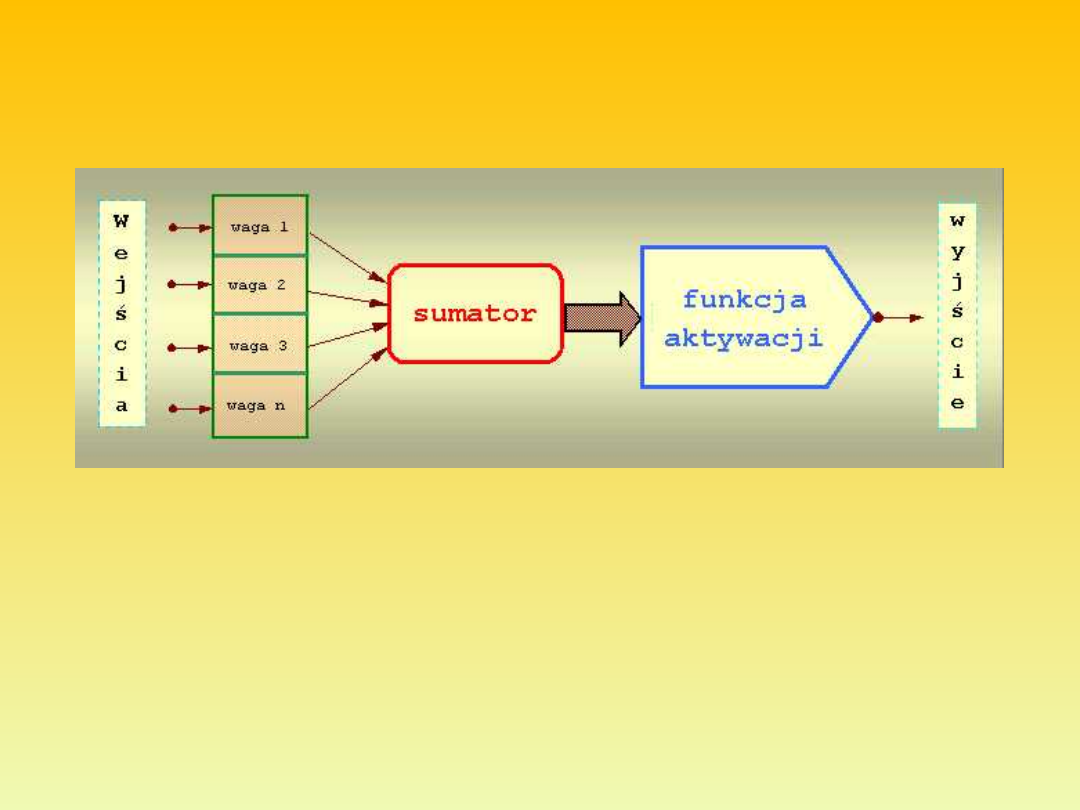
Sztuczny neuron nieliniowy

Jego schemat został opracowany przez McCullocha i Pittsa w
1943 roku i oparty został na budowie komórki nerwowej.

Jego działanie jest następujące:
Do wejść doprowadzane są sygnały dochodzące z neuronów warstwy
poprzedniej. Każdy sygnał mnożony jest przez odpowiadającą mu wartość
liczbową zwaną wagą. Wpływa ona na percepcję danego sygnału wejściowego i
jego udział w tworzeniu sygnału wyjściowego przez neuron. Waga może być
pobudzająca - dodatnia lub opóźniająca – ujemna; jeżeli nie ma połączenia
między neuronami to waga jest równa zero. Zsumowane iloczyny sygnałów i
wag stanowią argument funkcji aktywacji neuronu.
W przypadku gdy funkcja aktywacji nie występuje mamy do czynienia z
neuronem liniowym.

Wartość funkcji aktywacji jest sygnałem wyjściowym neuronu i
propagowana jest do neuronów warstwy następnej.

Wymagane cechy funkcji aktywacji to:

ciągłe przejście pomiędzy swoją wartością maksymalną a
minimalną (np. 0 - 1)

 łatwa do obliczenia i ciągła pochodna

 możliwość wprowadzenia do argumentu parametru do ustalania
kształtu krzywej
Najczęściej stosowaną jest funkcja sigmoidalna zwana też krzywą
logistyczną ( przyjmuje ona wartości pomiędzy 0 a 1 ).

Przykład 1:

Sieć wielowarstwowa

Uczenie metodą wstecznej propagacji błędów

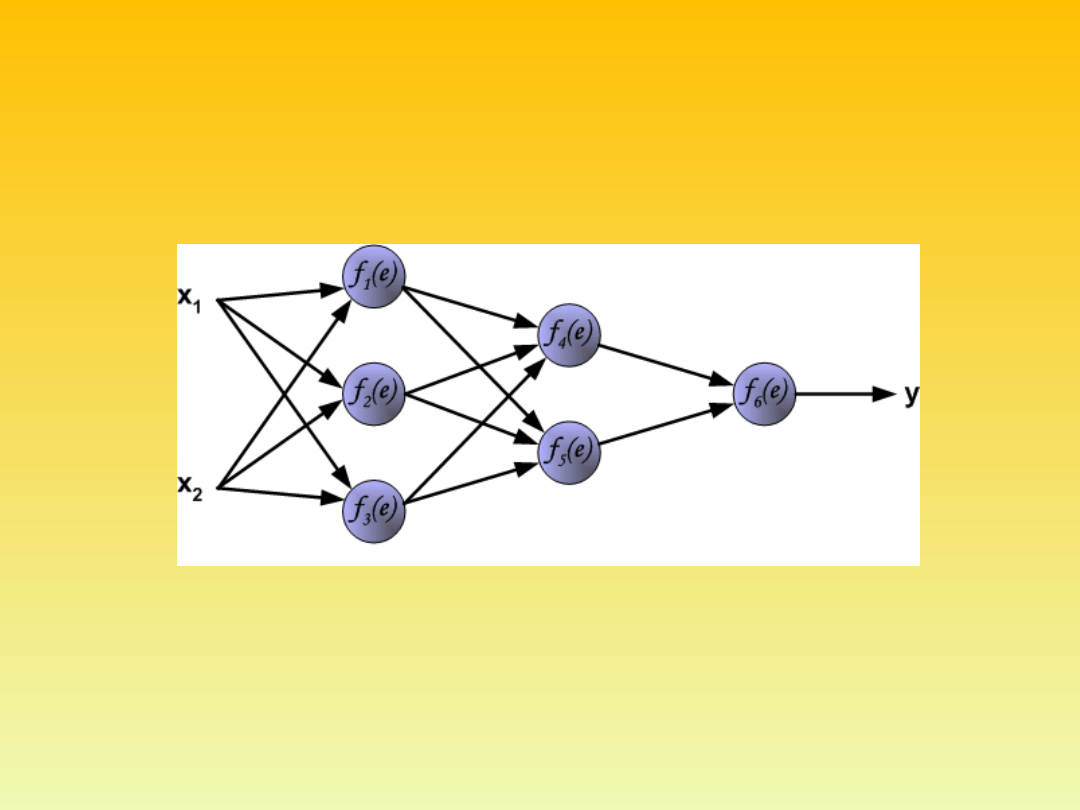
Principles of training multi-layer neural network using
backpropagation

The project describes teaching process of multi-layer neural network
employing backpropagation algorithm. To illustrate this process the
three layer neural network with two inputs and one output, which is
shown in the picture below, is used:

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

Each neuron is composed of two units. First unit adds products of
weights coefficients and input signals. The second unit realise
nonlinear function, called neuron activation function. Signal e is adder
output signal, and y = f(e) is output signal of nonlinear element. Signal
y is also output signal of neuron.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

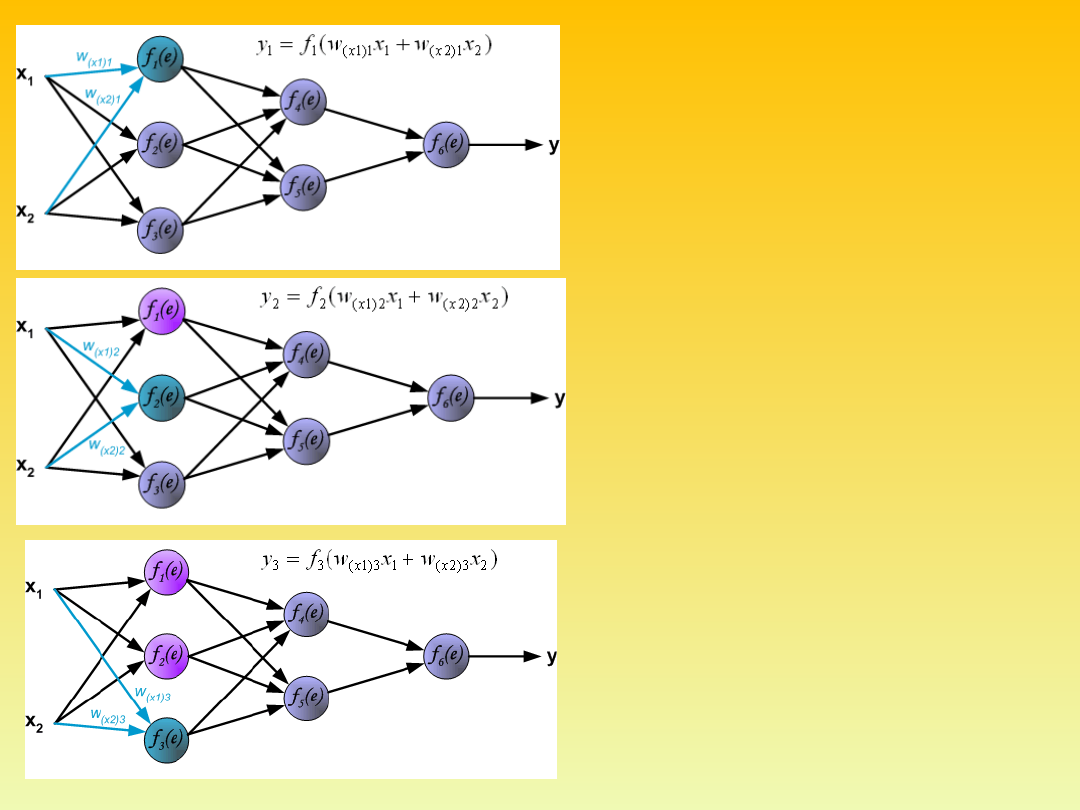
To teach the neural network we
need training data set. The training
data set consists of input signals (x

1

and x

2

) assigned with

corresponding target (desired
output) z. The network training is
an iterative process. In each
iteration weights coefficients of
nodes are modified using new data
from training data set. Modification
is calculated using algorithm
described below: Each teaching
step starts with forcing both input
signals from training set. After this
stage we can determine output
signals values for each neuron in
each network layer. Pictures below
illustrate how signal is propagating
through the network, Symbols w

(xm)n

represent weights of connections
between network input x

m

and

neuron n in input layer. Symbols y

n

represents output signal of neuron
n.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

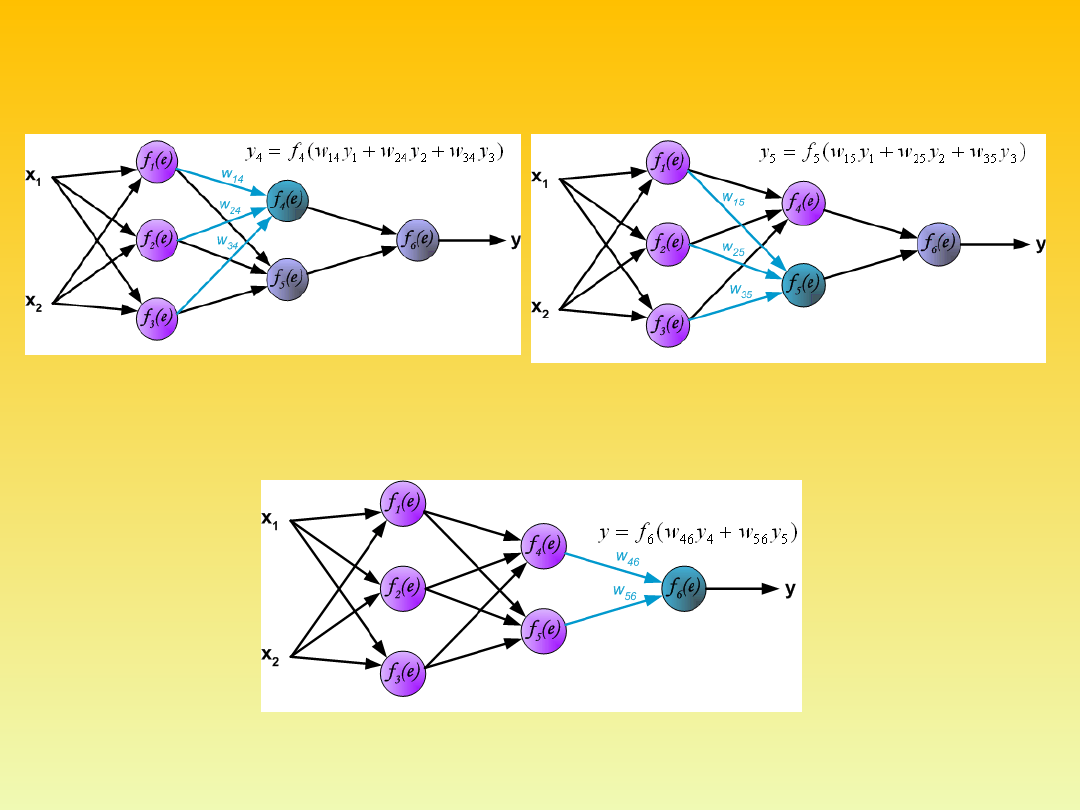
Propagation of signals through the hidden layer. Symbols w

mn

represent

weights of connections between output of neuron m and input of neuron n
in the next layer.

Propagation of signals through the output
layer.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

In the next algorithm step the output signal of the network y is compared
with the desired output value (the target), which is found in training data
set. The difference is called error signal d of output layer neuron.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

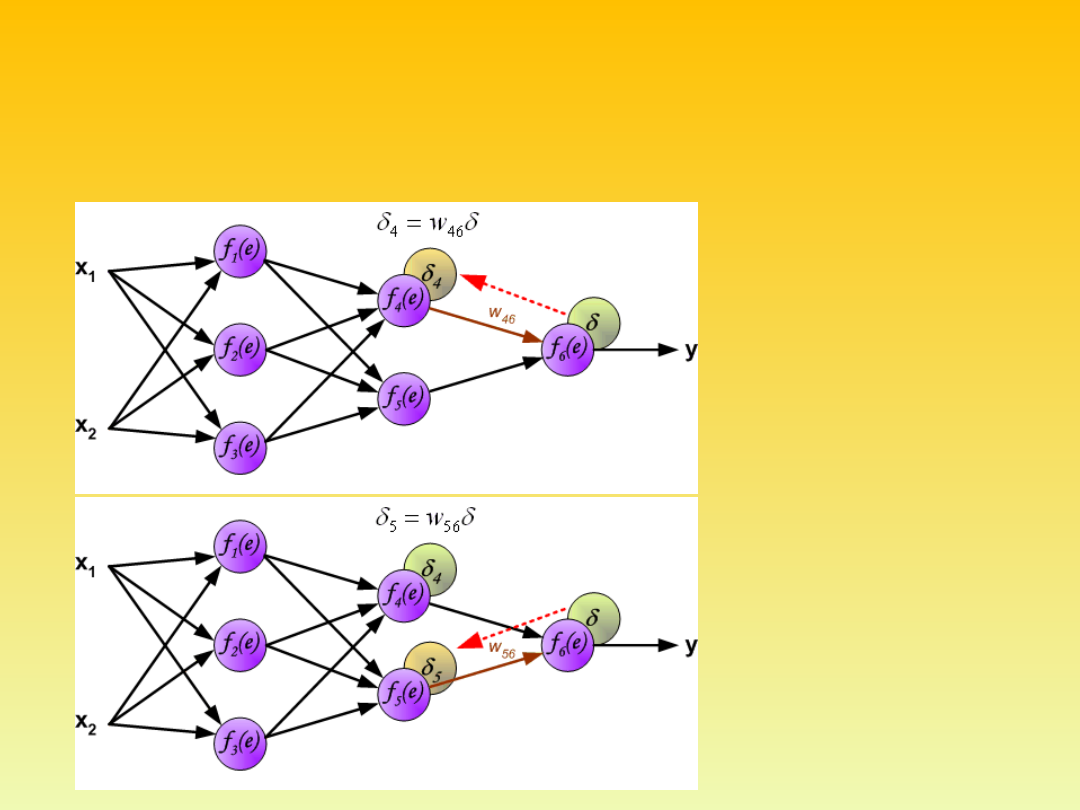
It is impossible to compute error signal for internal neurons directly,
because output values of these neurons are unknown. For many years the
effective method for training multiplayer networks has been unknown. Only
in the middle eighties the backpropagation algorithm has been worked out.
The idea is to propagate error signal d (computed in single teaching step)
back to all neurons, which output signals were input for discussed neuron.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

The weights'
coefficients w

mn

used to

propagate errors back
are equal to this used
during computing
output value. Only the
direction of data flow is
changed (signals are
propagated from
output to inputs one
after the other). This
technique is used for all
network layers. If
propagated errors
came from few neurons
they are added. The
illustration is below:

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

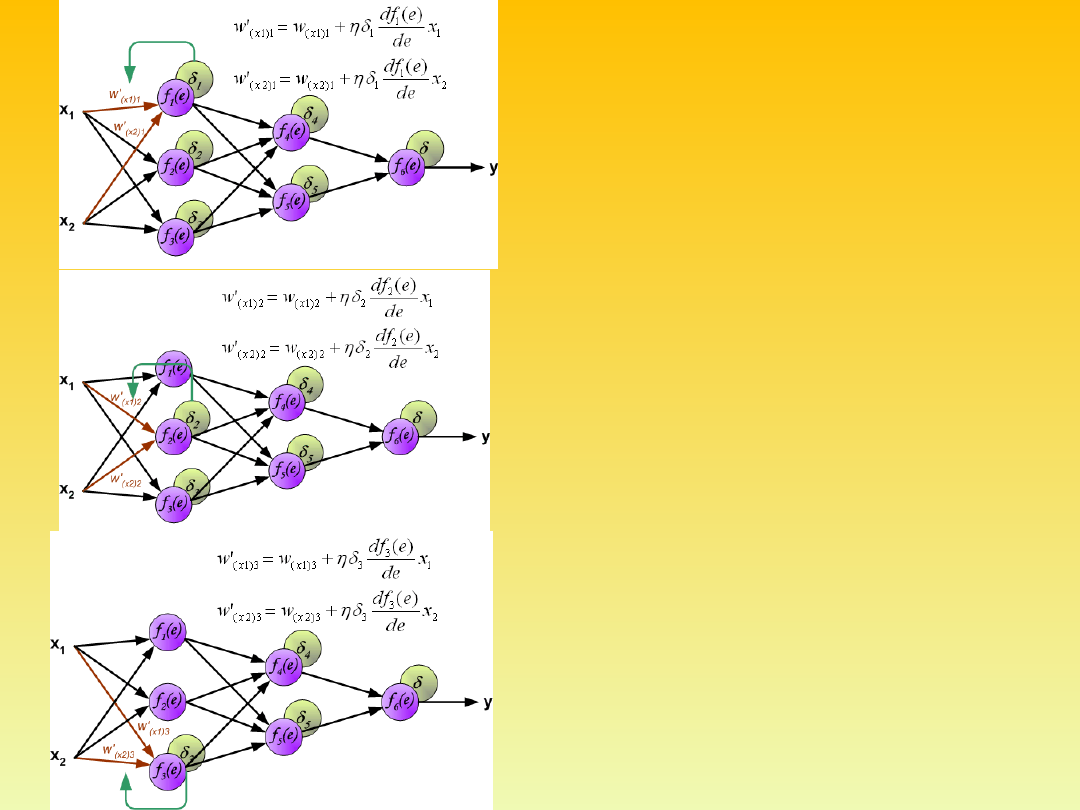
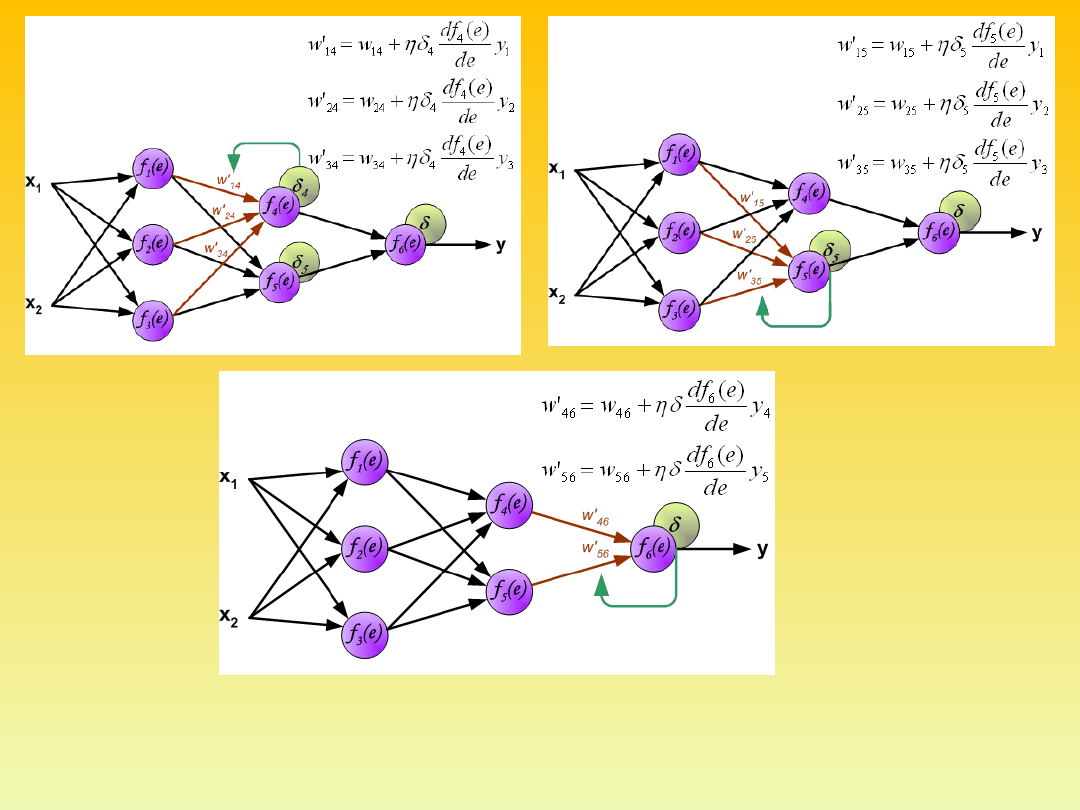
When the error signal for
each neuron is computed,
the weights coefficients of
each neuron input node
may be modified. In
formulas below df(e)/de
represents derivative of
neuron activation function
(which weights are
modified).

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

Coefficient η affects network teaching speed. There are a few
techniques to select this parameter.

•The first method is to start teaching process with large value of
the parameter. While weights coefficients are being established the
parameter is being decreased gradually.

•The second, more complicated, method starts teaching with small
parameter value. During the teaching process the parameter is
being increased when the teaching is advanced and then
decreased again in the final stage. Starting teaching process with
low parameter value enables to determine weights coefficients
signs.

mgr inż. Adam Gołda
(2005)
Katedra Elektroniki AGH

Cecha

system ekspertowy

sieć neuronowa

Uczenie na podstawie

przykładów

Nie

Tak

Samo-adaptacja

Nie

Tak

Tolerowanie błędnych

danych

Nie

Tak

Zdolność do

posługiwania się

kategoriami rozmytymi

Zazwyczaj nie

Tak

Wysiłek poniesiony na

oprogramowanie

Duży

Niewielki

Wysiłek poniesiony na

utrzymanie

Duży

Niewielki

Zdolność do

uzasadnienia

postępowania

Duża

Niewielka

Zdolność do

zapamiętywania

danych

Wysoka

Niska

Obliczenia

Proste, jednolite

Skomplikowane,

różnorodne

Logika

Zazwyczaj binarna

Rozmyta

Wnioskowanie

Według strategii

Bez strategii

Dziedzina

Specyficzna

Dowolna

Cechy systemów ekspertowych i sztucznych sieci neuronowych

[S.H.Huang, H.C.Zhang: Neural-expert hybrid approach for intelligent manufacturing’95]

Zastosowanie metody sieci neuronowych do
określania podobieństwa postaci konstrukcyjnej
części maszyn (elementarnych form).

W konkretnym przypadku zastosowania metody sieci neuronowych do
rozpoznawania bruzd walców hutniczych, macierz X ma wymiar [100 x
32]. Liczba wierszy 100 wynika z podziału obszaru rastra na 100 pól (10
x 10). Ze względu na symetrię wszystkich analizowanych obiektów,
wzięto pod uwagę tylko półprzekroje. Wszystkie analizowane rastrowe
obrazy form obrabiany przeskalowano do wspólnego, kwadratowego
rastra. Element x

ij

macierzy X zawiera znormalizowany, do wartości [0,1],

wskaźnik wypełnienia i-tego kwadratu rastra dla j-tego wykroju. 32
kolumny w macierzy X odpowiadają liczebności zbioru uczącego.

Przykład
2.

Macierz wag W posiada wymiar [7 x 100]. Liczba wierszy 7 odpowiada
liczbie grup wyodrębnionych w zbiorze uczącym. Przed procesem uczenia
macierz W jest wypełniana losowo liczbami z zakresu [0,1]. Macierz
wynikowa Y posiada więc wymiar [7 x 32]. Elementy y macierzy Y po
zakończonym procesie uczenia lub rozpoznawania zostają zaokrąglone do
wartości ze zbioru {0,1}. Element y

mn

macierzy Y zawiera 1 w przypadku

gdy obiekt n ze zbioru uczącego został przydzielony do grupy m, 0 w
przeciwnym przypadku.

Na podstawie sygnału błędu  oraz sygnału wejściowego X

j

, możliwe jest takie

skorygowanie odpowiedniego wiersza macierzy wag W

k

(k – numer klasy), żeby

neuron popełniał mniejszy błąd. Nowy wektor wag W

k

’ obliczany jest z wzoru dla

sieci liniowych

W

k

’ = W

k

+   X

j

gdzie  jest współczynnikiem liczbowym, decydującym o szybkości uczenia. Drugim
parametrem, mającym wpływ na szybkość uczenia jest dopuszczalny błąd neuronu
E

dop

.

1

10

100

1000

10000

100000

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

L

ic

zb

a

se

sj

i

u

cz

ą

cy

ch

Edop.=0.01
Edop.=0.05
Edop=0.1

Szybkość uczenia jako
funkcja  dla różnych
dopuszczalnych
błędów neuronu

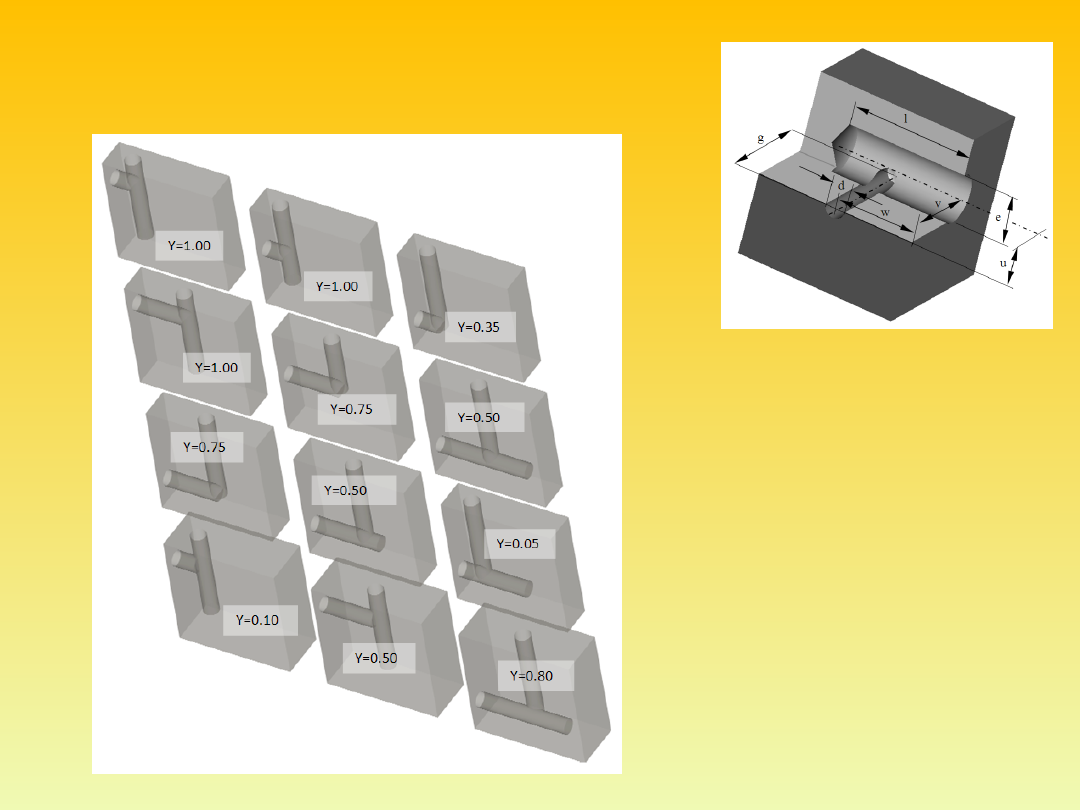
Przykład
3.

X

d

= (d, g, w, e, l, v,

u),

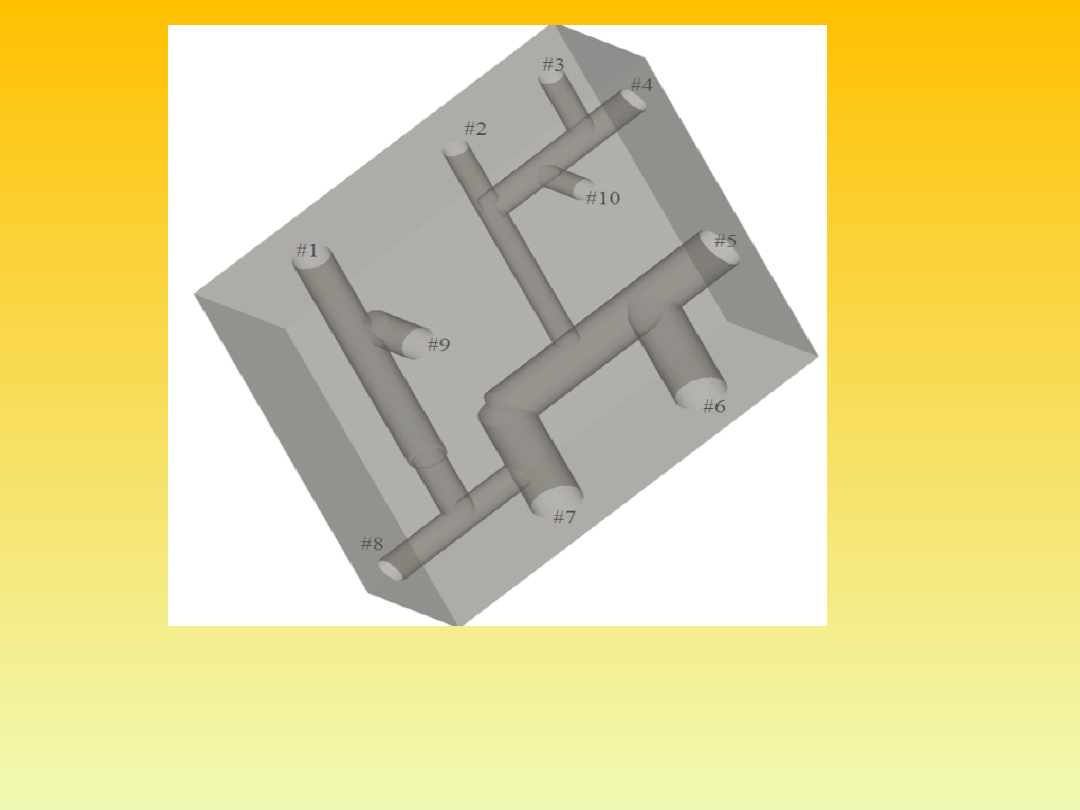
Fig. 6 A manifold hydraulic block

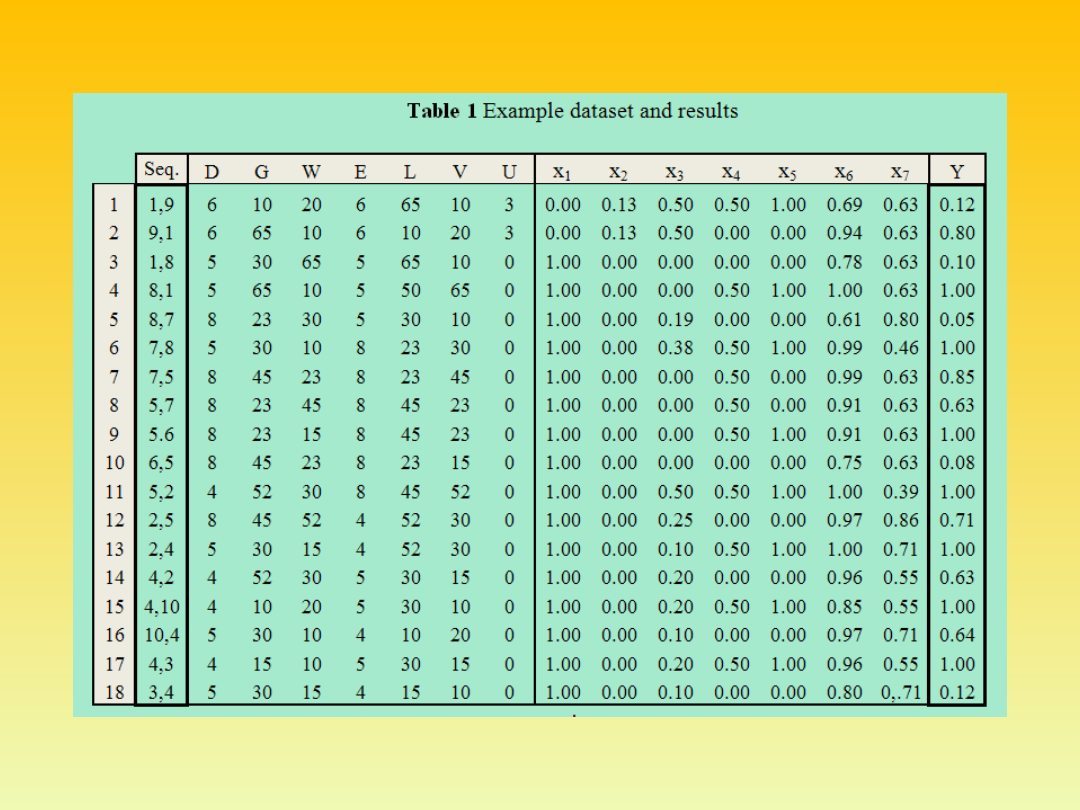
Fig. 8 (a) before
firing, (b) after firing
t

7

Fig. 7 Preliminary Petri net model

Fig. 10 The final
precedence graph

Fig. 9 The best
chromosome as result
of the GA

Neuronowy model powiązań pomiędzy układami
współrzędnych
i szybkościami kątowymi manipulatora.

Przykład 4

•The proposed technique does not require any prior knowledge of
the kinematics

•model of the system being controlled.

•Any modification in the physical set-up of the robot such as the
addition of a new tool would only require training for a new
trajectory without the need for any major system software
modification, which is a significant advantage of using neural
network approach.

•It can be applied to any general serial manipulator with
positional degrees of freedom since learning is only based on
observations of input/output relationships of the system being
controlled.

•Reasonable accuracy can be achieved along the desired path.

•The proposed approach can be adapted to any general serial
manipulator including both redundant and non-redundant
systems.