SZTUCZNE SIECI

NEURONOWE

„Inteligentne systemy w

zarządzaniu”

Teoria i praktyka

Pod redakcją Jerzego S. Zielińskiego

•

Pojęcie sieci neuronowej

•

Zadania SSN

•

Uczenie SSN

•

Klasyfikacja SSN

•

Sieci jednokierunkowe

•

Sieci rekurencyjne

•

Sieci komórkowe

•

Matematyczny model

neuronu

•

Warstwowe sieci

perceptronowe

•

Charakterystyka

warstwowych sieci

perceptronowych

•

Uczenie sieci

perceptronowej

• Modelowanie danych

treningowych

• Integralność danych
• Błędy w bazie

historycznej

• Sieci Kohonena
• Uczenie

konkurencyjne

• Sieci SOM
• Uczenie sieci SOM
• Sieci LVQ
• Uczenie sieci LVQ
• Sieć Hopfielda
• Uczenie sieci

Hopfielda

• Zastosowanie SSN

Pojęcie sieci neuronowej

Sztuczna sieć neuronowa – jest systemem wzajemnie połączonych

prostych elementów przetwarzających informacje, zwanych

neuronami, jednostkami lub węzłami.

Do połączeń między elementami są przyporządkowane

współczynniki wagowe, określające siłę powiązań i tworzące

zbiór parametrów modelu.

Cała wiedza sieci o sposobie rozwiązywania danego problemu

przechowywana jest w jej wewnętrznych odwzorowaniach ,

definiowanych przez wartości wag, i może być przywołana w

procesie reakcji na określony sygnał.
Współczynniki wagowe są przydzielone albo wyznaczone w

procesie treningowym, zmierzającym do nauczenia SSN.

W działaniu SSN można wyodrębnić dwie fazy:
• treningową
• reakcji na określony bodziec zewnętrzny

Model rozwiązywania na początku nie musi być
znany lecz jest budowany przez sieć w
procesie uczenia, na podstawie dostarczonych
tzw. danych treningowych.

Zadania SSN

SSN realizują najczęściej następujące rodzaje przetwarzania:
• przypominanie, polegające na: odzyskiwaniu (albo

interpretowaniu) zmagazynowanych w SSN informacji, obliczaniu

wyjścia dla danego wejścia;

• skojarzenie, realizowane w następujących wariantach: skojarzenie

uszkodzonego (zdeformowanego) wejścia (albo wywołania) z

najbliższym przechowywanym wzorcem, skojarzenie między parą

wzorców, diagnostyka, analiza;

• klasyfikacja, realizowana poprzez podział zbioru wejściowego na

klasy lub kategorie i skojarzenie każdego wejścia z kategorią;

• rozpoznawanie, rozumiane jako klasyfikowanie wejścia, mimo że

nie odpowiada ono żadnemu z przechowywanych wzorców;

• estymacja, czyli realizacja następujących zadań: aproksymacja,

interpolacja, filtrowanie, predykcja, prognozowanie;

• optymalizacja, w tym rozwiązywanie liniowych i nieliniowych

równań;

• sterowanie, realizowane inteligentnie bez konieczności

opracowania modelu. oparte wyłącznie na doświadczeniu.

Uczenie

SSN

Proces uczenia SSN polega na modyfikacji współczynników

wagowych połączeń jej elementów.

• Uczenie nadzorowane (z nauczycielem). Dane treningowe

zawierają zestaw sygnałów wejściowych sieci oraz

poprawnych reakcji systemu. Uczenie polega na takiej

modyfikacji wag, aby rzeczywiste wyjścia były jak najbliższe

wartościom pożądanym. Jeżeli w czasie treningu nie

prezentujemy sieci dokładnej wartości pożądanego wyjścia, a

jedynie informację, czy reaguje ona prawidłowo, to mamy do

czynienia ze specjalnym przypadkiem uczenia

nadzorowanego. tzw. uczeniem ze wzmocnieniem.

• Uczenie bez nadzoru. W procesie uczenia sieć neuronowa nie

otrzymuje żadnej informacji na temat pożądanych reakcji.

Dane treningowe obejmują jedynie zbiór sygnałów

wejściowych. Sieć ma za zadanie samodzielnie przeanalizować

zależności i korelacje w zbiorze treningowym. Tego typu sieci

nazywamy samoorganizującymi (ang. selforganising networks)

lub autoasocjacyjnymi.

Klasyfikacja SSN

Sieci jednokierunkowe.

Sieci rekurencyjne.
Sieci komórkowe.

Sieci jednokierunkowe

Ogólnie można powiedzieć, że ich struktura

stanowi acykliczny graf skierowany. Sieci

jednokierunkowe mają wyraźnie wyróżnione

neurony wejściowe (przyjmujące informacje z

zewnątrz) i wyjściowe (przesyłające przetworzoną

informację na zewnątrz). Sygnał przekazywany jest

zawsze do przodu: z warstwy wejściowej, poprzez

jednostki ukryte, do warstwy wyjściowej, bez

rekurencyjnych połączeń wstecznych. Dla

dowolnego neuronu wartości wejść nie zależą w

żaden sposób (bezpośredni czy też pośredni) od

jego stanu, czyli wartości wyjściowej. Typowym

przykładem takiej sieci są wielowarstwowe sieci

perceptronowe.

Sieci rekurencyjne

W przeciwieństwie do sieci jednokierunkowych
dopuszczamy występowanie w nich cykli. Sygnał
wyjściowy neuronu może, bezpośrednio lub za
pośrednictwem innych węzłów, być przekazywany na
jego wejście. Dynamika działania tego typu sieci jest
znacznie bardziej skomplikowana niż w przypadku sieci
jednokierunkowych. W sieci rekurencyjnej jednokrotne
pobudzenie sieci poprzez sygnał wejściowy powoduje
wielokrotną aktywację wszystkich, lub tylko części,
neuronów w procesie tzw. relaksacji sieci. Aby więc sieć
działała poprawnie, należy zapewnić dodatkowy
warunek stabilności. Pobudzona sieć, w skończonym
czasie, musi osiągać stan stabilny, w którym wartości
neuronów dla danego wejścia pozostają stałe. Dopiero
wówczas określić można wartość wyjścia. Przykładem
sieci rekurencyjnych mogą być sieci Hopfielda.

Sieci komórkowe.

W tej grupie sieci neuronowych wprowadza się
dodatkowo pojęcie sąsiedztwa węzłów.
Połączone między sobą są tylko jednostki
znajdujące się w obrębie sąsiedztwa.
Charakter tych powiązań może być różny,
zależny od konkretnego przypadku.
Przykładem tego typu sieci mogą być
neuronowe sieci komórkowe (ang. cellural
neural networks). Do tej kategorii zaliczyć
można również sieci SOM Kohonena.

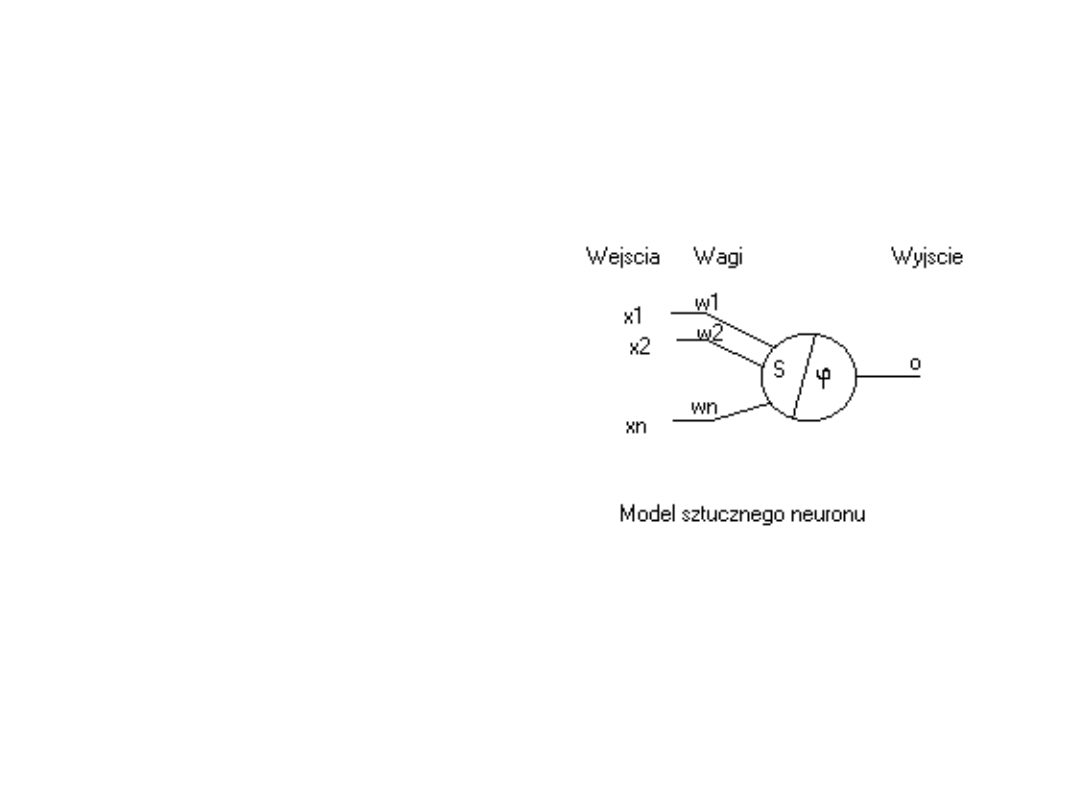
Matematyczny model neuronu

Przyjmuje się, że
sztuczny neuron jest
układem
przetwarzającym o
wielu wejściach i
jednym wyjściu.
Schemat jego
działania opiera się
na modelu
zaproponowanym w
1943 r. przez
McCullocha i Pittsa.

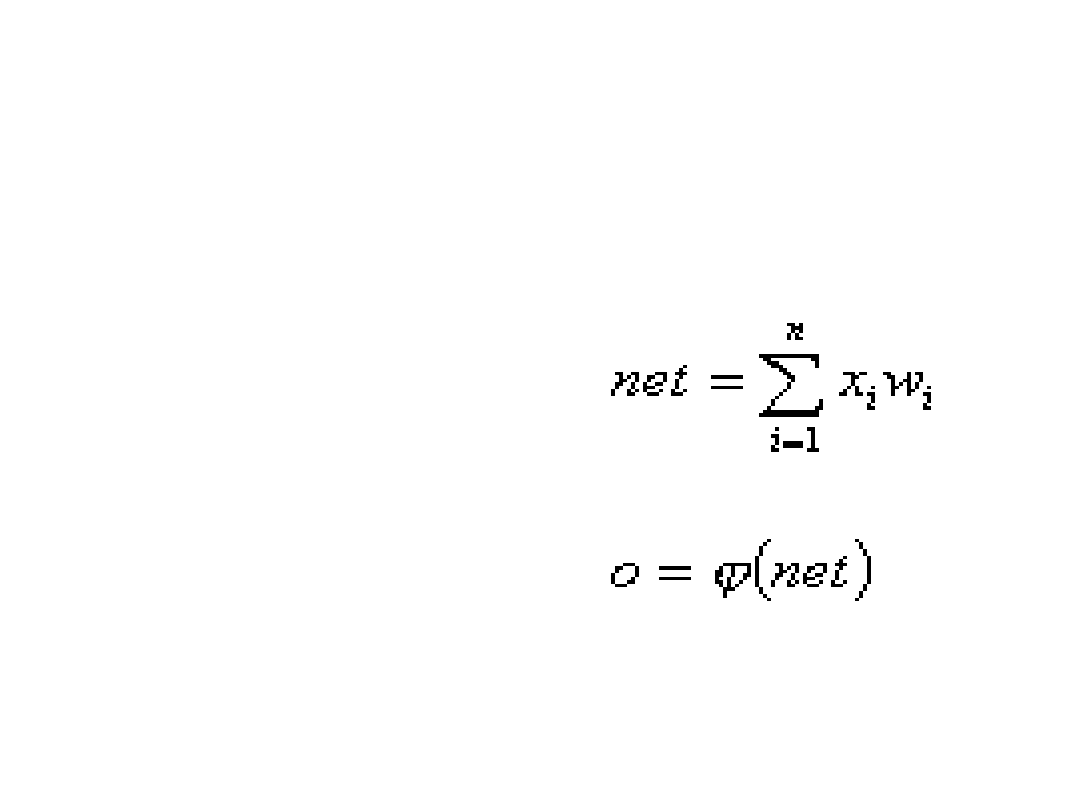
Matematyczny model neuronu

c.d.

Dzięki takiej

reprezentacji
neuronu możemy,
korzystając z
wzorów, obliczyć
m.in.:

• pobudzenie neuronu

(net)

• wartość sygnału

wyjściowego (o )

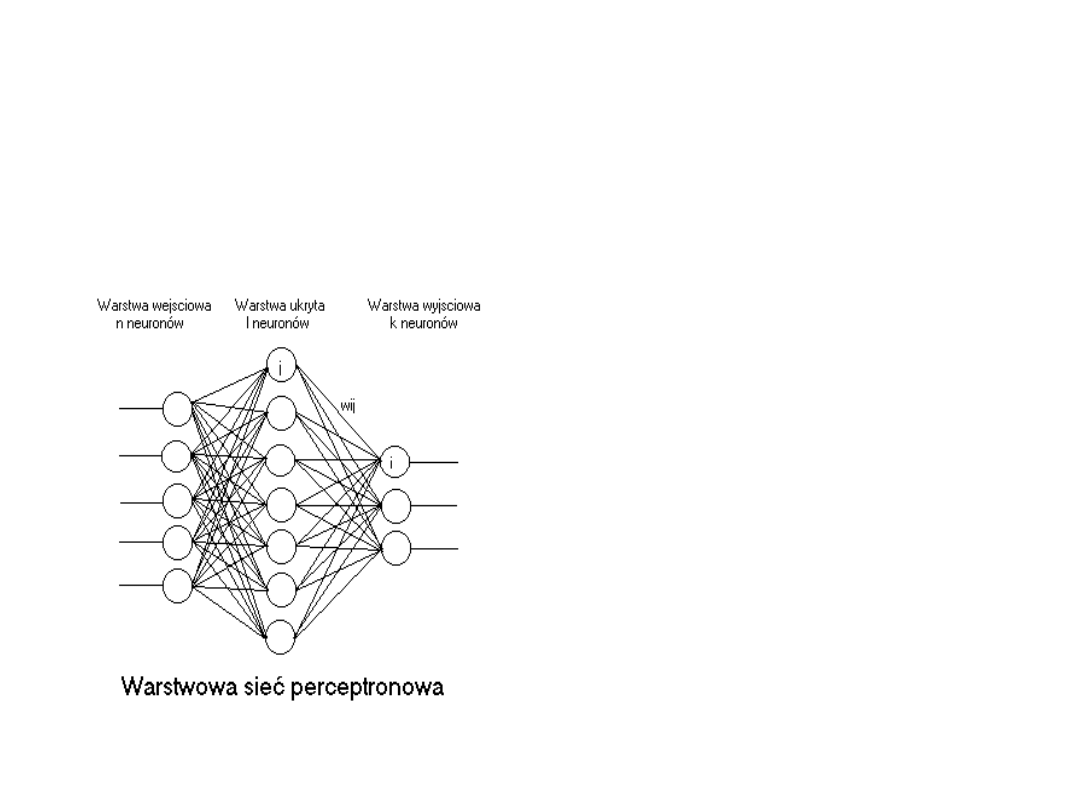
Warstwowe sieci perceptronowe

Perceptrony są

przykładem sieci

jednokierunkowych.

Neurony są

zgrupowane w co

najmniej dwu

warstwach. Pierwsza

nazywana jest warstwą

wejściową, ostatnia zaś

warstwą wyjściową.

Między nimi może

występować jedna lub

więcej warstw

ukrytych.

Charakterystyka warstwowych

sieci perceptronowych

• Sygnał może być przekazywany jedynie do przodu, a więc z

warstwy poprzedniej do następnej

• Niemożliwe jest przekazywanie sygnałów między neuronami

tej samej warstwy lub wstecz, na przykład z warstwy

wyjściowej do ukrytej.

• Warstwa wejściowa pełni jedynie funkcję organizacyjną i nie

wykonuje właściwie żadnego przetwarzania. Jej zadaniem

jest przyjmowanie sygnału wejściowego i jego dystrybucja

do neuronów kolejnej warstwy. Nie podlega ona również

adaptacji w procesie uczenia, gdyż jej neurony nie mają

wag.

• Adaptacyjny charakter mają wszystkie kolejne warstwy. Sieć

z jedną warstwą ukrytą przez niektórych specjalistów bywa

nazywana siecią trójwarstwową (od liczby warstw ogółem ),

przez innych natomiast dwuwarstwową (od liczby warstw

przetwarzających).

• Jeżeli w sieci nie ma neuronów ukrytych to nazywamy ją

perceptronem prostym. W przeciwnym przypadku mówimy o

perceptronie wielowarstwowym (MLP).

Uczenie sieci perceptronowej

Algorytm uczenia sieci perceptronowej polega
na wielokrotnym, iteracyjnym prezentowaniu
sieci serii par wektorów:

{ X

k ,

T

k

},k = 1,...,N

gdzie X

k

jest k-tym wzorcem wejściowym, T

k

odpowiadającym mu wzorcem treningowym.
Celem uczenia jest takie dostosowanie wag,
aby reakcja sieci na wejścia X

k

była jak

najbliższa wartościom pożądanym T

k.

(uczenie nadzorowane)

Modelowanie danych

treningowych

Przygotowanie danych treningowych i uczenie
sieci to najważniejszy etap budowy modelu
neuronowego. Istotny jest nie tylko proces
doboru odpowiednich zmiennych wejściowych
modelu, ale również proces wstępnego
przetworzenia danych oraz wyboru konkretnych
wektorów treningowych. Sieć neuronowa jest
narzędziem uniwersalnym i cała jej widza
zdobywana jest na podstawie analizy
przygotowanych danych uczących. Jakość
modelu jest w dużym stopniu zależna od rodzaju
i jakości danych użytych do jego treningu.

Integralność danych

Wzorce treningowe dla sieci wybierane są

najczęściej z większego zbioru danych (baza danych

historycznych). Obejmuje on zwykle periodyczne

zapisy wartości istotnych dla rozważanego modelu

zmiennych. Mogą to być na przykład ważne

współczynniki ekonometryczne, rejestry cen i

indeksów giełdowych czy też zapisy wskaźników

finansowych przedsiębiorstw. Dane tego typu

opracowywane i archiwizowane są na ogół przez

ludzi, a ponadto ze swej natury zawierają pewien

procent szumów i niepewności. Oczywiście nie

jesteśmy w stanie wykryć wszystkich

niedokładności, ale możemy wyeliminować z pary

danych przynajmniej najbardziej rażące błędy.

Błędy w bazie historycznej

• Pierwszym źródłem niedokładności może być brak albo

zduplikowanie określonych danych lub ich fragmentów. Tego typu

błędy mogą być wykryte przez dokładną inspekcję (automatyczną

albo ręczną w arkuszu kalkulacyjnym lub edytorze). W przypadku

ich stwierdzenia należy całkowicie usunąć uszkodzoną daną z

bazy i próbować ją odtworzyć, korzystając z innych źródeł, lub

interpolować za pomocą innych wartości tej samej zmiennej.

• Znacznie trudniejszym zadaniem jest wykrycie błędów w

wartościach danych. Mogą one manifestować się jako dane

wykraczające poza normalny zakres zmiennej. Można je więc

wykrywać, badając odchylenie danych od średniej wartości.

Odchylenie większe niż ±5 odchyleń standardowych wskazuje na

konieczność bliższego przyjrzenia się podejrzanej danej. Duże

odchylenie niekoniecznie jednak oznaczać musi błąd. Może być

ono spowodowane anomalią w danych. Należy je zweryfikować

przy wykorzystaniu innych, niezależnych źródeł danych. W

pewnych przypadkach możemy sprawdzić inne zmienne bazy

danych, które są zwykle blisko skorelowane z rozważaną.

Sieci Kohonena

• Wykorzystywane są głównie w procesie

klasyfikacji i grupowania danych,

• Składają się zwykle z warstwy

wejściowej oraz jednej warstwy
neuronów przetwarzających, zwanej
warstwą konkurencyjną lub Kohonena,

• Każdy neuron w warstwie

konkurencyjnej połączony jest ze
wszystkimi wejściami

Uczenie konkurencyjne

W sieciach Kohonena stosowany jest
algorytm uczenia, zwany uczeniem
konkurencyjnym lub uczeniem typu
„zwycięzca bierze wszystko”. Neurony
sieci, w odpowiedzi na sygnał wejściowy,
rywalizują ze sobą. Neuron „zwycięski”
oraz ewentualnie jego najbliższe
otoczenie podlegają procesowi uczenia,
polegającym na zbliżeniu ich wag do
wektora wejściowego.

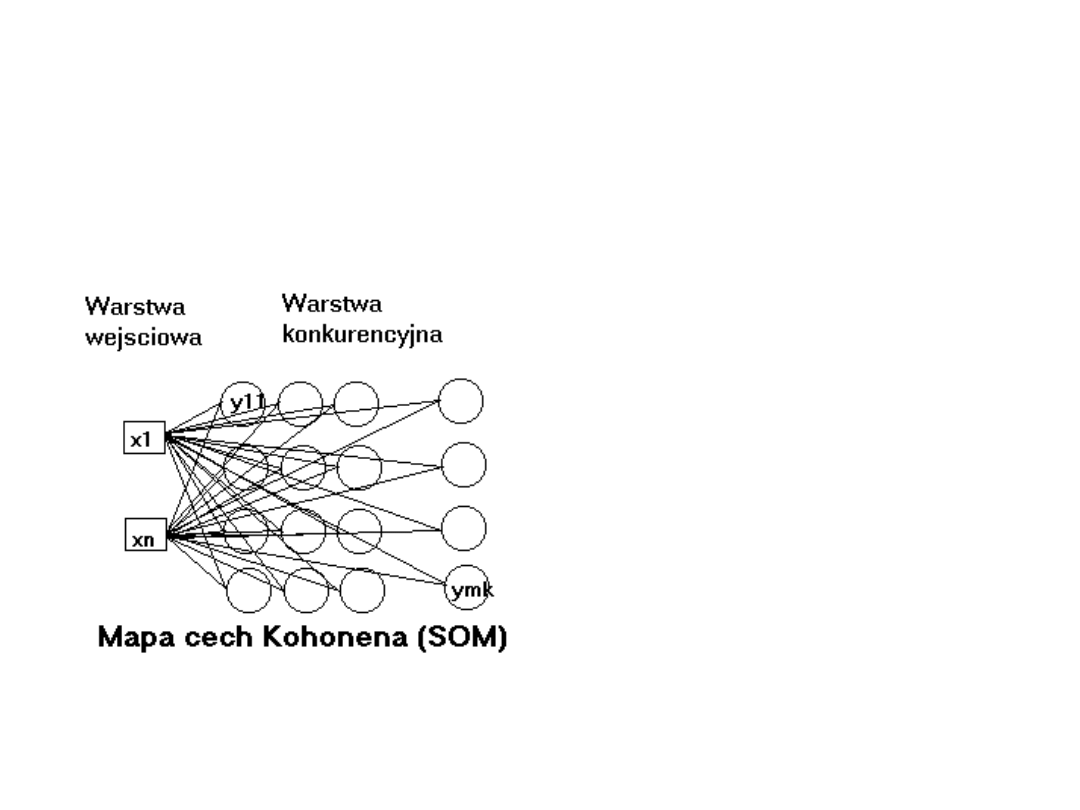
Sieci SOM

(ang. Self Organising Maps)
Architktura stworzona w

1982r. przez Kohonena.

Warstwa konkurencyjna

ma postać dwu lub

jednowymiarowej tablicy

neuronów, które

połączone są ze

wszystkimi wejściami, a

więc każdy neuron ma

tyle współczynników

wagowych, ile jest wejść

sieci.

Uczenie sieci SOM

Uczenie ma charakter nienadzorowany.
Dane treningowe nie zawierają żadnej
informacji na temat pożądanych wyjść.
Sieć ma za zadanie samodzielnie
poklasyfikować niezaetykietowane dane
jedynie na podstawie występujących w
nich korelacji. Poszczególne klasy
formowane są przez wektory wejściowe,
dla których zwycięża ten sam neuron.

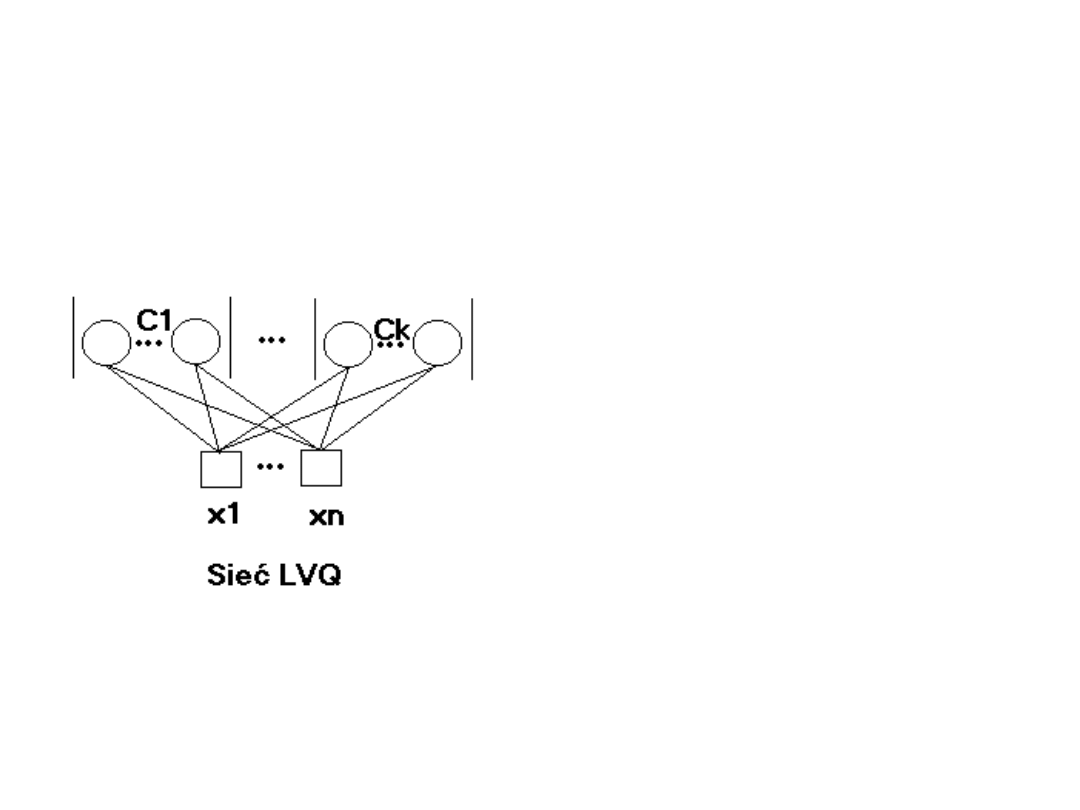
Sieci LVQ

(ang. Learning Vector

Quantization)

Poszczególnym klasom

przyporządkowany jest
jeden lub kilka
neuronów w warstwie
konkurencyjnej.

Każda jednostka

połączona jest ze
wszystkimi wejściami

.

Uczenie sieci LVQ

Sieci LVQ są przykładem nadzorowanego

uczenia konkurencyjnego. Zakładamy, ąe

liczba klas danych jest znana oraz

dysponujemy zbiorem indeksowanych

danych i jesteśmy w stanie określić klasę,

do której należą. Każdy wektor treningowy

musi być oznaczony etykietą swojej klasy.
Działanie sieci polega na znalezieniu

neuronu, którego wektor wagowy jest

najbliższy sygnałowi wejściowemu.

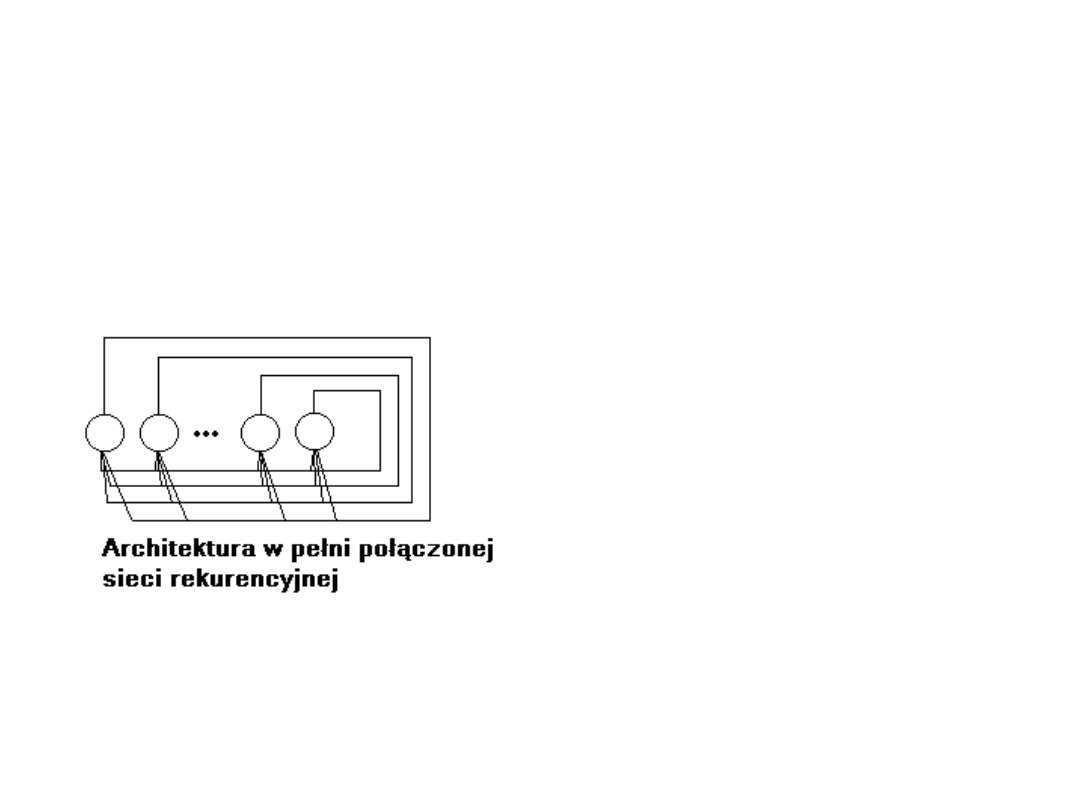
Sieć Hopfielda

• Przykład sieci

rekurencyjnych

• Każdy neuron połączony

jest z każdym

• W tym przypadku nie

wyróżnia się neuronów

wejściowych i

wyjściowych

• Przekazanie sygnału

wejściowego polega na

ustaleniu stanu

początkowego

jednostek sieci.

Uczenie sieci Hopfielda

Uczenie sieci Hopfielda jest procesem
nienadzorowanym. Polega ono na
zaprezentowaniu pewnej serii wzorców,
które są przez nią zapamiętywane.
Wystarczy jedna prezentacja serii
treningowej (ang. one shot learning).
Formuła modyfikacji wag zastosowana
przez Hopfielda jest wariantem tzw. Reguły
Hebba, będącej podstawą wielu metod
uczenia nienadzorowanego.

Zastosowania sieci neuronowych

Sieci perceptronowe:

• Prognozowanie krótkoterminowego zapotrzebowania na

energię elektryczną.
Zakład energetyczny jest spółką dystrybucyjną, pośredniczącą

między producentami energii a jej odbiorcami. Prognozowanie

sprzedaży energii ma istotne znaczenie dla wielu zagadnień

związanych z zarządzaniem tego typu przedsiębiorstwem:
1. Długoterminowe prognozowanie ekonometryczne dla celów

planowania systemu elektroenergetycznego, wielkości

produkcji i przesyłu, typu wprowadzanych urządzeń

przesyłowych oraz projektowania rozwoju.
2. Średniookresowe prognozowanie służy planowaniu zapasów

paliwowych i utrzymaniu działania systemu.
3. Krótkoterminowe prognozowanie wykorzystywane jest do

codziennych operacji zarządzania i sterowania systemem oraz

planowania harmonogramów i wielkości przesyłów mocy w

systemie.

Zastosowania sieci neuronowych

c.d.

• Prognozowanie cen na rynkach

kapitałowych.
Modelowanie krótkookresowych procesów

na rynkach kapitałowych opiera się zwykle

na technicznej analizie ruchów cenowych

poszczególnych walorów. Zakłada się, że

czynniki fundamentalne przekładają się na

wzorce cenowe występujące na rynku.

Przyszłe ceny w krótkim horyzoncie

czasowym zwykle mogą być dostatecznie

dokładnie oszacowane przy wykorzystaniu

ich wartości z bliższej lub dalszej

przeszłości. Do celów prognostycznych

wykorzystywane są więc różnego rodzaju

metody analizy szeregów czasowych.

Zastosowania sieci neuronowych

c.d.

Analiza danych z wykorzystaniem sieci

Kohonena.
Jedną z podstawowych metod ułatwiających
zrozumienie danych jest ich grupowanie.
Ogólnie mówiąc, grupowanie jest procesem
analizy skończonego zbioru wzorców w celu
wyodrębnienia występujących w nim
naturalnych kategorii. Innymi słowy, szukamy w
zebranych danych jednorodnych podzbiorów.
Elementy tego samego podzbioru powinny być
do siebie jak najbardziej podobne, zaś elementy
różnych podzbiorów - jak najbardziej odmienne.

Zastosowania sieci neuronowych

c.d.

Sieć Hopfielda jako pamięć asocjacyjna.

Sieć Hopfielda jest bardzo dobrą pamięcią

asocjacyjną. Jej szczególnie cenną właściwością
jest umiejętność rozpoznania prototypu nawet
na podstawie niewielkiego fragmentu danych.
Cecha ta może być szczególnie cenna dla
wczesnego rozpoznawania formacji cenowych
występujących na rynku. Wadą sieci Hopfielda
jest jednak duży koszt przechowywania
informacji. Oszacowania jej pojemności mówią,
że na każdy wzorzec przechowywany w pamięci
powinno przypadać niemal dziesięć neuronów.

Podsumowanie

• Sztuczne sieci neuronowe, naśladując

działanie systemów biologicznych, pozwalają
na skuteczne i efektywne rozwiązywanie
problemów, które były dotąd postrzegane
jako problemy typowo "ludzkie", takie jak:
rozpoznawanie obrazów i mowy,
rozpoznawanie trendów. Ich możliwości mogą
być również wykorzystane do rozwiązywania
zupełnie innego rodzaju problemów, jak np.:
modelowanie, kontrola systemów w czasie
rzeczywistym, filtrowanie sygnałów, redukcja
szumów, analiza obrazu, klasyfikacja.

• Wykorzystywanie ekspertów wiąże się z

pewnymi problemami. Człowiek działa często

powolnie i nie konsekwentnie. Nie wszystkie

opinie różnych osób są zbieżne, jak również

każda z osób może postrzegać problemy różnie

w czasie, zmieniając swoje oceny z dnia na

dzień. Czasami problemy, z którymi trzeba się

uporać, ilościowo przerastają możliwości

człowieka. Poza tym z zatrudnieniem eksperta

wiążą się również inne problemy polegające np.

na długim czasie przyuczania do wykonywanej

czynności lub niemożnością przekazania w

prosty sposób wiedzy nabytej innym osobom.

Sieci neuronowe nie są obarczone

wymienionymi wadami. Są bardzo szybkie,

skuteczne, nie męczą się, nie ulęgają

stresom oraz dają się łatwo powielać.