MATEMATYKA DYSKRETNA

2010/2011

 

Zakres:

1. Rachunek zdań ; Rachunek zbiorów
 
2. Rachunek predykatów ; Schematy wnioskowania
 
3.Funkcje całkowitoliczbowe ; Kombinatoryka
 
4. Rekurencje ; Postać zwarta schematu rekurencyjnego
 
5. Schemat Hornera ; Kongruencje
 
6. Grafy – definicje, klasyfikacje, reprezentacje, właściwości
 
7. Grafy – algorytmy na grafach

 

Literatura:

http://wazniak.mimuw.edu.pl/index.php?title=Strona_g%C5%82%C3%B3wna

Ross K.A., Wright C.R.B.: Matematyka dyskretna, PWN, Warszawa 1996.
Sysło M.M.: Algorytmy, WSiP, Warszawa 1997.
Lipski W.: Kombinatoryka dla programistów, WNT, Warszawa 1982.
Wilson R.J.: Wprowadzenie do teorii grafów, Warszawa 1998.
Bryant V.: Aspekty kombinatoryki, WNT, Warszawa 1997.
Ziembiński Z., Logika praktyczna, PWN, Warszawa 2000.

 

MATEMATYKA DYSKRETNA

Wymiar: 2 1 0 0 0

Wymagania: matematyka na poziomie szkoły średniej

Zaliczenie przedmiotu: Ocena z ćwiczeń audytoryjnych wystawiona na podstawie trzech
testów i aktywności na ćwiczeniach

Założenia programowe: Zapoznanie z podstawowymi obiektami i strukturami matematyki
dyskretnej, przydatnymi do wysłuchania dalszych pozostałych przedmiotów poświęconych
projektowaniu i analizie algorytmów wspomagania decyzji, a także ich dalszych
komputerowych implementacji.

Wykład:

1. Podstawy logiki i teorii mnogości. – Elementy teorii zbiorów – zbiory, alfabety,
rachunek zbiorów, funkcje. Zastosowania – maszyna Turinga. Funkcje całkowitoliczbowe:
powała i podłoga. Zastosowanie – szacowanie długości słowa maszynowego.

2. Podstawy logiki i teorii mnogości. – Logika pierwszego rzędu. Rachunek zdań. Reguły
wnioskowania (modus ponens, zasada rezolucji). Zastosowania w strukturach systemów
ekspertowych.

3. Podstawy logiki i teorii mnogości. – Dowody formalne, pojęcia poprawności i pełności
systemu logicznego. Teorie formalne.

4. Asymptotyka funkcji liczbowych. – Zastosowania – szacowanie złożoności
obliczeniowej. Problemy decyzyjne i optymalizacyjne. Problemy łatwe i trudne. Zastosowania
- zasada dziel i zwyciężaj.

5. Elementy teorii liczb – Podzielność liczb naturalnych – algorytm Euklidesa.
NWP, NWW. Operator modulo. Liczby pierwsze i rozkład liczb na czynniki pierwsze.
Zastosowania – kryptografia. Liczby doskonałe. Równanie diofantyczne.

6.Elementy kombinatoryki – Zasada gołębnika. Zasada włączania i wyłączania.
Generowanie obiektów kombinatorycznych. Permutacje, kombinacje, wariacje.
Zastosowania – szacowanie złożoność obliczeniowej.

7. Elementy kombinatoryki – Definicje, algorytmy i zależności rekurencyjne.
Rozwiązywanie zależności rekurencyjnych – przez podstawianie i za pomocą
równania charakterystycznego. Zastosowania - symbol Newtona, trójkąt Newtona.

8. Elementy kombinatoryki – Kongruencje. Zastosowania – na jaka cyfrę kończy
się liczba 5

100

? Systemy liczbowe. Schemat Hornera. Zastosowania – szybkie

potęgowanie.

9. Elementy teorii grafów – Relacje i ich reprezentacje. Grafy symetryczne i
skierowane. Charakterystyki - drogi, cykle, pętle, itd. Właściwości i klasyfikacje
grafów: drzewa, grafy dwudzielne, grafy pełne, grafy planarne, itp.

10. Elementy teorii grafów – Badanie właściwości grafów. Grafy Eulera i
Hamiltona. Izomorfizm grafów. Zastosowania – wybrane ilustracje problemów
łatwych i trudnych. Strategie zachłanne.

11 Elementy teorii grafów. Macierzowe reprezentacje grafów – macierz
incydencji, macierz stowarzyszona. Zastosowania – badanie właściwości grafów.

12 Elementy teorii grafów. Algorytmy na grafach – drzewa rozpinające. Zastosowania –
wyznaczanie
sieci instalacji elektrycznej.

13 Elementy teorii grafów. Algorytmy na grafach – zadania najkrótszych dróg. Zastosowania –
wyznaczanie najkrótszej drogi (metoda podziałów i ograniczeń).

14. Elementy teorii grafów –Grafy AND/OR. Zastosowania – planowanie działań (np. montażu).

Ćwiczenia
Ćwiczenia polegają na rozwiązywaniu zadań opracowanych do poszczególnych partii materiału z
wykładu.
Są to głównie ćwiczenia rachunkowe, ale w wielu przypadkach sprowadzają się do „giełdy” pomysłów
nowych (niestandardowych) rozwiązań oraz skojarzeń i pomysłów związanych z praktycznym
wykorzystaniem
zdobytych umiejętności.

Literatura:

Ross K.A., Wright C.R.B., Matematyka dyskretna, PWN, Warszawa 1996.

Sysło M.M., Algorytmy, WSziP, Warszawa, 1997

Lipski W., Kombinatoryka dla programistów, WNT, Warszawa, 1982

Wilson R.J., Wprowadzenie do teorii grafów, PWN, Warszawa, 1998.

Ziembiński Z., Logika praktyczna, PWN, Warszawa 2000.

Zaliczenie

:

•MAX{„Z”,”0”} , gdzie:

Ind.Akt.Studenta

•IF((#1 + #2 + #3)/3  3) THEN („Z” = 3 + Bonus); Bonus =

* 0.5

(MAX Akt.
Grupy)/4

Test (przykład)

1. Uprość wyrażenie: (p  p)  (p  p)  ?

2. Oblicz wartość formuły: (q  p)  ? , dla q = p = 1

3. Wyznacz

pierwszych

pięć

elementów

zbioru:

{5/n

|

nN}

=

{ , , , , }

4. Czy prawdą jest, że: (A \ B) \ C = A \ (B \ C)

5. Czy prawdą jest, że z faktów a i b wynika fakt g?

R1: IF b THEN h

R2: IF b i h THEN f

R3: IF a i b THEN c

R4: IF c i h THEN g

Wykład 1

1.Elementy teorii zbiorów

•rachunek zdań,

•sprzeczności i tautologie, reguły wnioskowania (reguła modus ponens),

•zastosowania w strukturach systemów ekspertowych,

•zbiory i działania na zbiorach,

•rachunek predykatów, zasada rezolucji,

Rachunek zdań

ZDANIA, SPÓJNIKI, FORMUŁY

Poniższe napisy nie są formułami

p   q


Ten napis na pewno nie jest formułą,

(p  q))

Poniższe napisy są formułami

p  (r  q)
q
p  q

p  p  p
(p  p)  p  p  (p  p)

Oznaczenia

N – zbiór liczb naturalnych (bez zera)

N

0

- zbiór liczb naturalnych z zerem

Z – zbiór liczb całkowitych

Z

+

- zbiór liczb całkowitych dodatnich

Q – zbiór liczb wymiernych

R – zbiór liczb rzeczywistych

x  A – x należy do zbioru A (x jest elementem zbioru A)

x  A – x nie należy do zbioru A

A  B – zbiór A jest podzbiorem zbioru B (zbiór A zawiera się w zbiorze B)

A  B - zbiór A nie jest podzbiorem zbioru B

A  B – iloczyn zbiorów

A  B – suma zbiorów

A \ B – różnica zbiorów

A  B – różnica symetryczna zbiorów

Ø = { } - zbiór pusty

|A|- moc zbioru A (liczba elementów zbioru A)

 - znak sumy

 - znak iloczynu

x – dla każdego x

x – istnieje x

! x – istnieje jedno x

 – ...nieprawda, że... (negacja)

 – ...lub... (alternatywa)

 – ...i... (koniunkcja)

 – ...jeżeli, to... (implikacja)

 – ...wtedy i tylko wtedy... (równoważność)

A  - A jest zdefiniowane jako...

 x  - największa liczba całkowita niewiększa niż x

 x  - najmniejsza liczba całkowita niemniejsza niż

x

SPÓJNIKI ZDANIOWE

Zapis

Nazwa

Symbol

..nieprawda, że..

negacja



...lub...

alternatywa



...i...

koniunkcja



...jeżeli...to...

implikacja



...wtedy i tylko wtedy gdy…

równoważność



HIERARCHIA
SPÓJNIKÓW

 ;  ;  ;  ; 

p



p

0

1

1

0



0

1

0

0

1

1

1

1



0

1

0

0

0

1

0

1



0

1

0

1

1

1

0

1

a  b  a  b

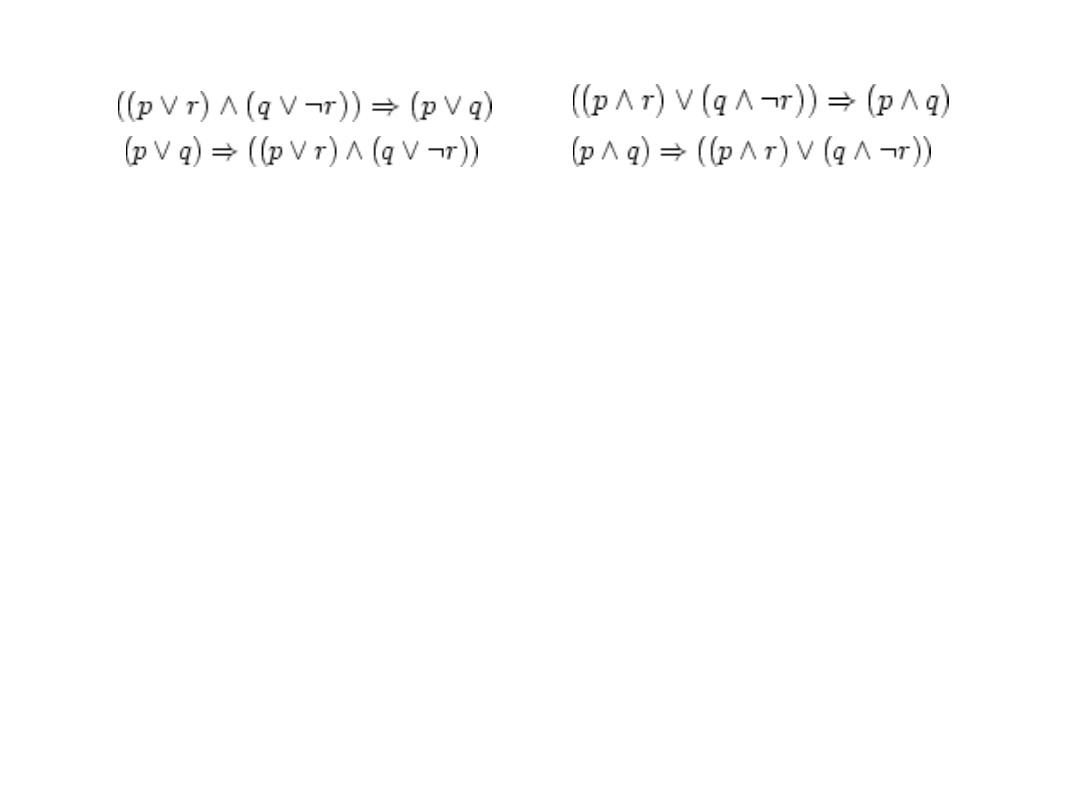
Sprawdź które z następujących formuł są
tautologiami

Sprawdź:

(a  b)  (b  c)  (c  a)  b ,

((p  q)  p)  (p 

q)

((p  q)  p)  (p  q

)

P R A W A

Przemienności

p  q  q  p

,

p  q  q p

Łączności

p  (q  r)  (p  q)  r ,

p  (q  r)  (p q)  r

Rozdzielności mnożenia względem dodawania

(p  q)  r  p  r  q  r

Rozdzielności dodawania względem mnożenia

(p  q)  r  (p  r)  (q  r)

De Morgana

 (p  q)  p  q , (p  q)  p  q

Powtórzeń

p  p  p … p  p ,

p  p  p … p  p

PRAWA (TAUTOLOGIE, SPRZECZNOŚCI)

Zdania złożone, które są zawsze prawdziwe, niezależnie od
wartości logicznych
zmiennych zdaniowych p, q nazywamy tautologiami.

p  p  1 ; (p  p)  q)  q

Zdaniem sprzecznym (sprzecznością) jest zdaniem złożonym,
które jest zawsze
fałszywe.

p  p  0 ; (p  p)  0

(p  p)  p

 p  (p p)

( p  p)  p p  ( p  p)




1
p

p  1

0 p

 p  1





p

1

p (p  p)(A  p)  (p  A)

A

0 1 0 0 1
1 1 1 1 1

((a  b)  (a  d))  (b  d)

 a  b  d

((a  (b  d))  (b  d)

p  p p … p  p

(a  (b  d))  (b  d) ,

a  b  b  d

(a  (b  d))  (b  d)

,

(p  r)  p  q

(a  b  d)  ( (b  d)  (b  d))

,

a  b  d

,

x  x 

1

(p  q)  r  (p  r)  (q  r)

(p  q ) 
r

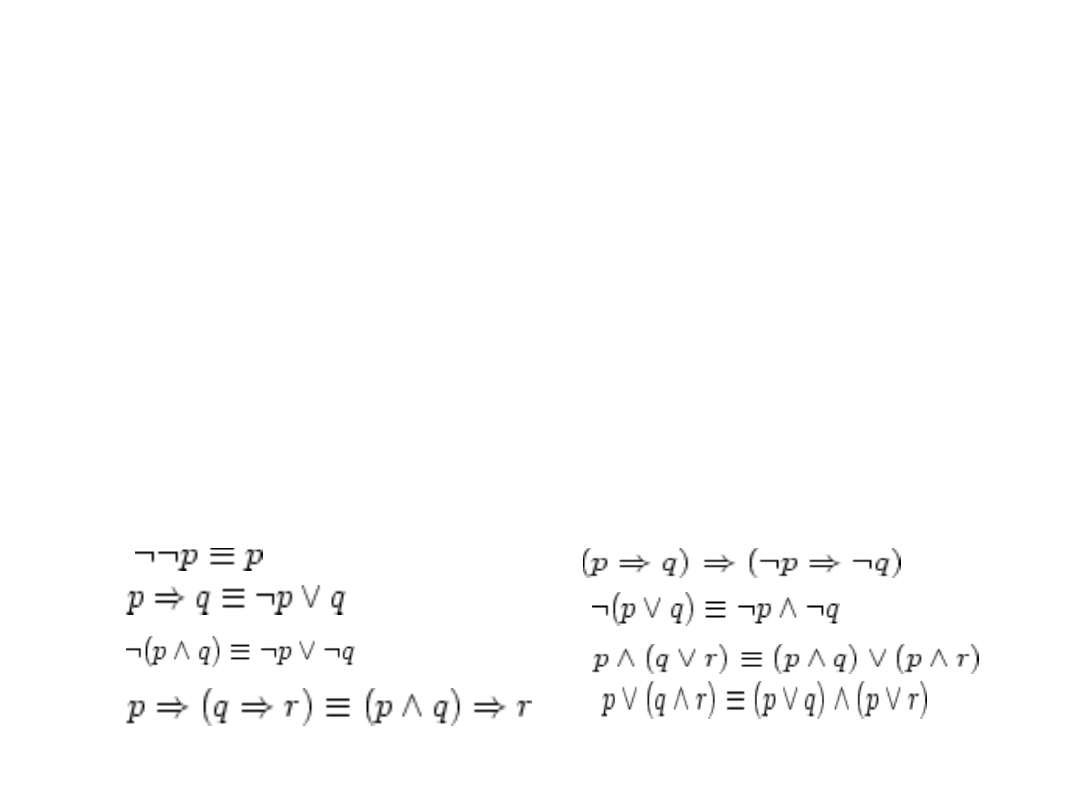
1. Podaj przykład wartościowania zmiennych tak aby poniższe formuły były

wartościowane na 0

p  (q  r)
(p  q)  r
(p  q)

2. Podaj przykład wartościowania zmiennych tak, aby poniższe formuły były

wartościowane na 1

(p  q)
(p  q)
(q  q)  (p  q)

3. Udowodnij następujące równoważności

ZBIORY

Zbiór liczb naturalnych: 1, 2, 3 , 4 , 5 , ...

N = {1, 2, 3 , 4 , 5 , ...}

Zbiór liczb wmiernych: 1/2, 2/3 , 4/4 , 5/6 , ... W = {1/2, 2/3 , 4/4,

5/6 , ...}

Zbiór liczb niewmiernych: 2, , e ,... -

 W

Zbiór liczb rzeczywistych

-

R

Zbiór liczb całkowitych

-

C

N  C  W  R ;

 W  C

;

 W  R

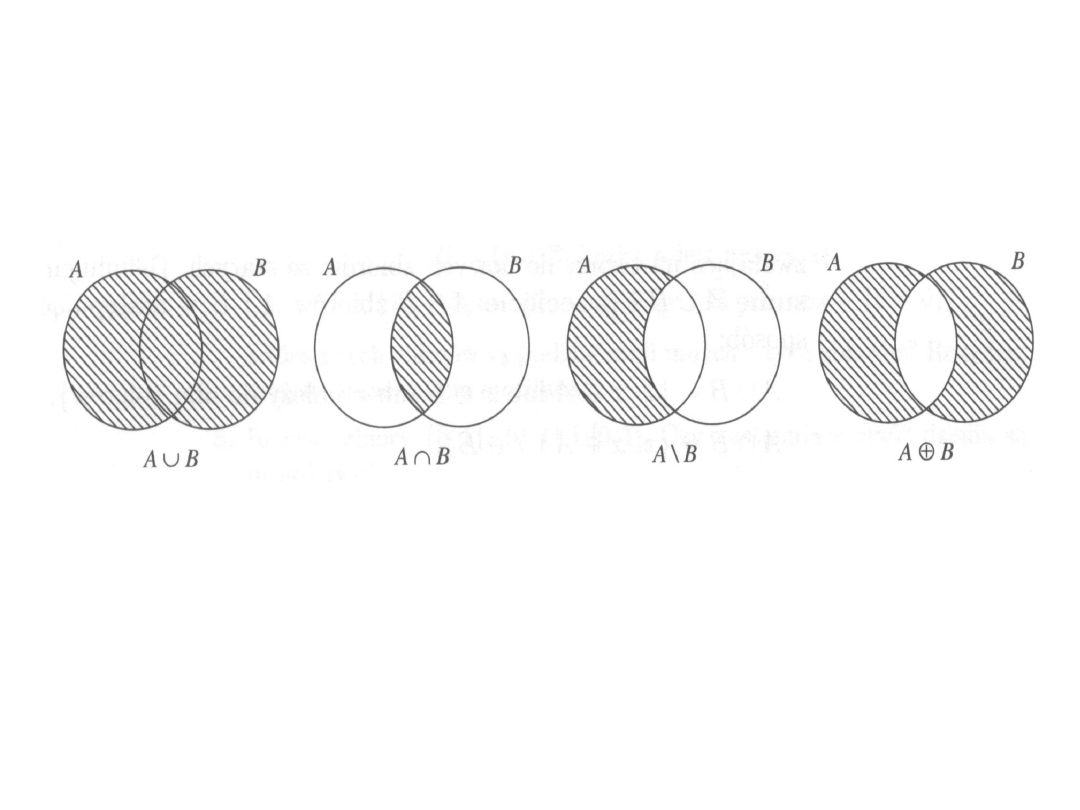
Suma

A  B = C ;

C = {c  A  c  B}

Iloczyn

A  B = C ;

C = {c  A  c  B}

Różnica

A \ B = C ;

C = {c  A  c  B}

Różnica symetryczna
A  B = C

; C = { c  A  B  c  A  B } = { c  A \ B  c

 B \ A }

Zbiór pusty

A =    a [a  A ]

Inkluzja dwóch zbiorów

( A  B )  a [ a  A  b  B ]

Zbiory liczbowe
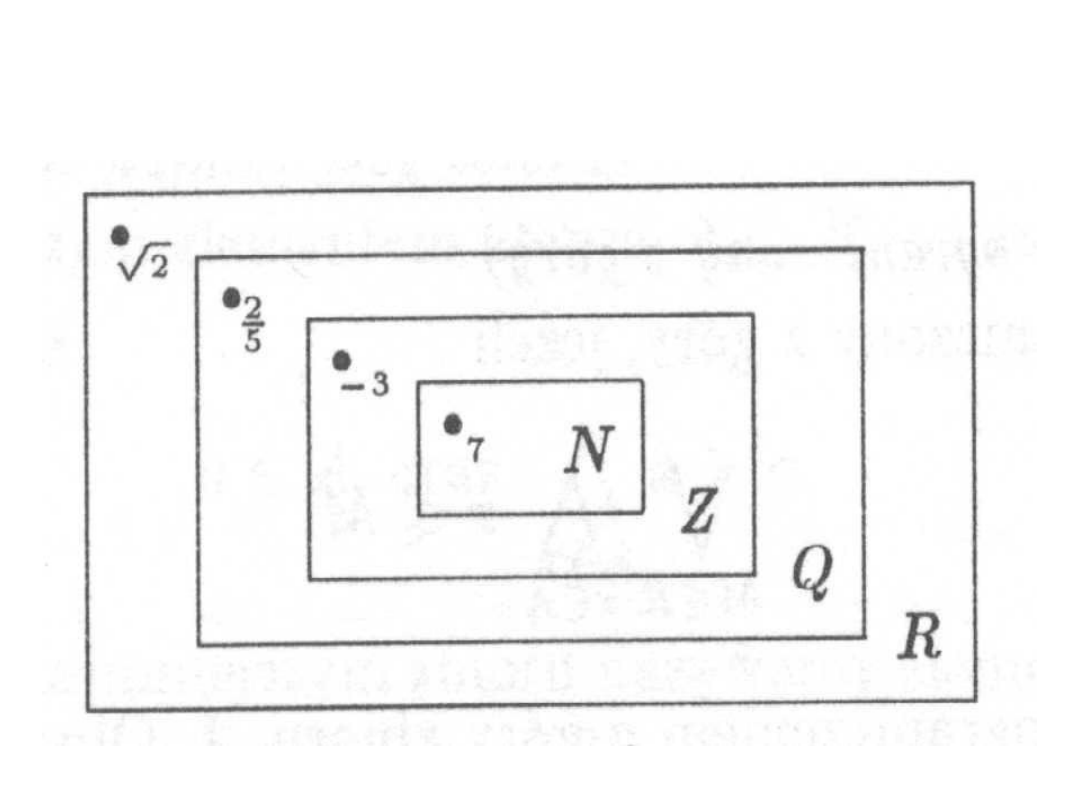
N - zbiór liczb naturalnych N ={1,2,3,4,}
Z - zbiór liczb całkowitych Z
={0,±1,±2,±3,±4,}
Q - zbiór liczb wymiernych Q=


: m Z, n Z, n 0
n
m
R – zbiór liczb rzeczywistych
Rys. 1.1 Relacje midzy zbiorami N, Z, Q, R
N Ì Z Ì Q Ì R

A

A’

1

a  A  a 1  a  A

A’ = 1 \ A

N  W

; (W  N )

;

W  W =  ;

N \ W = 

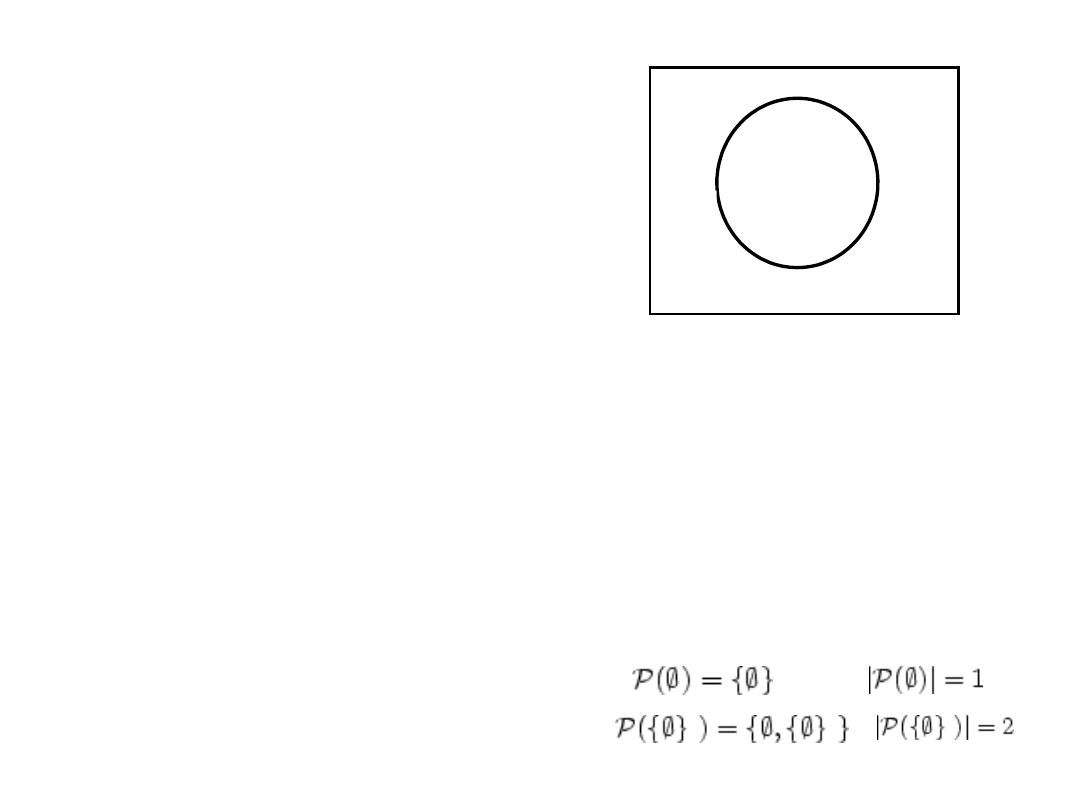
Zbiór potęgowy P(S) zbioru S – zbiór wszystkich podzbiorów

zbioru S.

S={a,b} ; P(S) = { , {a}, {b} , {a,b}}

|S| = 2 ,

|P(S)| = 2

n

|P()| = ??? ,

|P({1})| = ???

Przestrzeń (zbiór pełny) 1

Dopełnienie A’ zbioru A przestrzeni 1

{

5n | n  N} = {5, 10, 15,…}

{4n + 3 | n N} = { }

1.Wypisać po kilka elementów z następujących zbiorów:

{nN: n jest podzielna przez 5}

{2

n

: n  N }

{1/n : n=1,2,3,4}

{ x  R : x=k/n oraz k  {1,2} i n  {1,2,4,8} }

2. Jaka jest liczba elementów podanych poniżej zbiorów?

{n  N : n

2

= 2},

{x  Q: x

2

= 2}, {x  R: x

2

= 2}

{n  N: n jest liczbą pierwszą , niewiększą niż 10}

{n  N: n jest potęgą 2}

{x  Z: |x| <10}, {x  R: |x| <10}

{n  N : n jest liczbą parzystą i liczbą}

3.

Niech U={n  N: n < 20} będzie ustalonym uniwersum i niech A i B

będą jego podzbiorami takimi, że A= {2n+1: n  N i n < 6},

B =

{3n+2: n  N i n < 6}.

Wyznacz elementy zbiorów A  B, A  B, A\B, B\A,

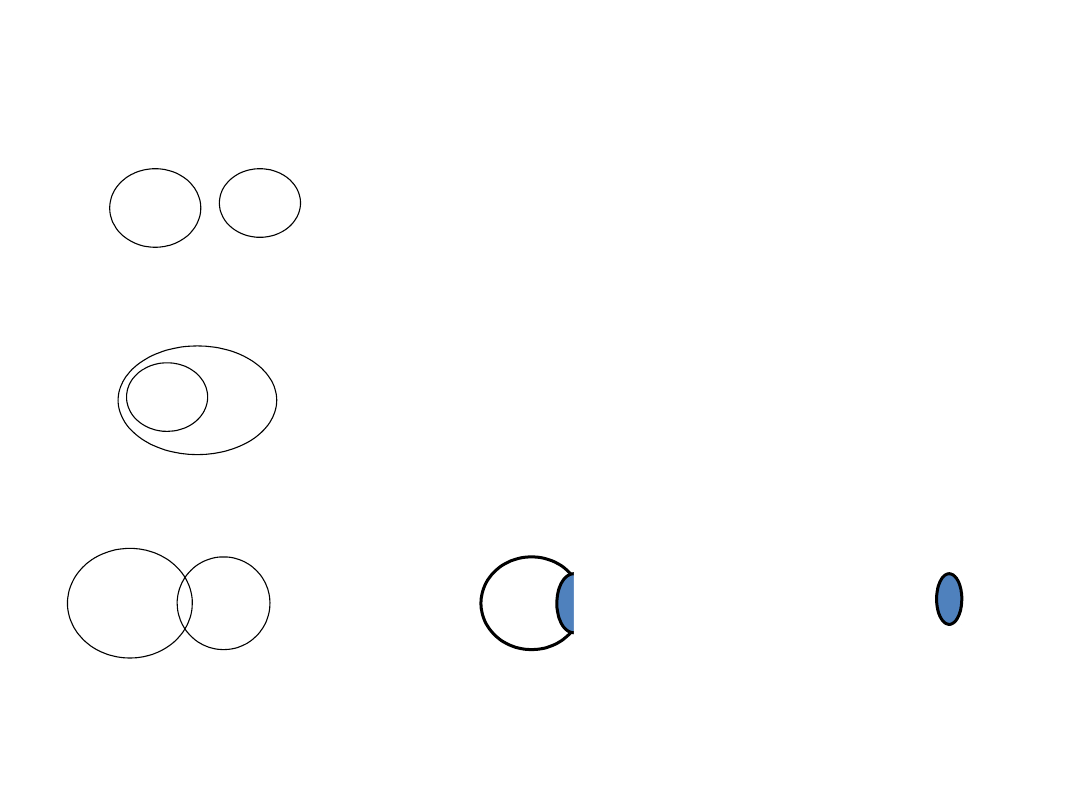
A \ B  A  B

A

B

1. A  B =


A \ B = A

, A  B = 

, A  

2. A 
B

A \ B =  , A  B = A

,   A

A \ B =

,



, A  B =

A

B

B

3. A  B  

A

Sprawdź:

A  B  A  B

A  B  A  B

Niech A = {1,2,3,4,8,16}, B = {2,4,6,8,10} , C =

{1,3,7,15}.

Wyznacz:

A \ C

B  (C  B)

A  B

(B  A)  (A  C)

A  B

`

C \ (B \ A)

B  C

A  (B  C)

Iloczyn kartezjański zbiorów ( produkt )

Dla dowolnych zbiorów A, B iloczynem kartezjańskim nazywamy
zbiór
wszystkich par uporządkowanych (a, b) takich, że a  A i b  B

A  B={(a,b) : a  A  b  B

}

Produkt dowolnej skończonej rodziny zbiorów

S

1

 S

2

 S

3

... S

n

= { (s

1

, s

2

, s

3

, ..., s

n

) : s

k

 S

k

dla k =

1, 2, 3, ..., n }

PRZYKŁAD

{a}  {b} = {(a,b)}

{3}  {a,b} = {(3,a), (3,b)}

{1,2}  {a,b} = {(1,a), (1,b), (2,a), (2,b)}

Wprowadzimy oznaczenia dla pewnych szczególnych
podzbiorów zbioru R, nazywanych przedziałami.

Dla a,b  R gdzie a < b, określamy:

{ x  R : a < x < b } = (a,b)

– przedział otwarty

{ x  R : a  x  b } = [a,b]

– przedział domknięty

{ x  R : a  x < b } = [a,b)

– przedział

prawostronnie otwarty

{ x  R : a < x  b } = (a,b]

– przedział

prawostronnie domknięty

Alfabet to skończony zbiór S , którego elementami są symbole zwane
literami
alfabetu S .

Słowem danego alfabetu S nazywamy dowolny skończony ciąg liter
tego zbioru S

Zbiór wszystkich słów zbudowanych z elementów zbioru S oznaczamy
S *.
S* jest zbiorem nieskończonym.

Dowolny podzbiór zbioru S* nazywamy językiem nad alfabetem S .

Słowo puste -  (ciąg nie zawierający liter ); analogia do
zbioru pustego.

PRZYKŁAD

Jeżeli  = { a,b }, to S *= {, a, b, aa, bb, abb, aaa, babb,

... }

Jeżeli  = { a }, to S *= {, a, aa, aaa, aaaa, ... }

Jeżeli  = { 0, 1, 2} , to *= {, 0, 1, 2, 00, 01, 02, 11, 12,

20, 21, 22, 000, ... }

Jeżeli  = { a,b } i dł(w) oznacza długość słowa w zbiorze

*, to

A = { w   *: dł(w) = 2 } = { aa, ab, bb,

ba }

Wnioskowanie

Modus ponens

a  b

a, a  b

b

Zasada rezolucji

(a  b  b  c)  (a  c)

a  b, b  c

b  c

Objawy Diagnoza
Terapia

Dowody Wyrok Kara

A i B przyprostokątne, IF A i B przyprostokątne THEN

C

2

= A

2

+ B

2

p – dzisiaj jest niedziela
q – mam wolny dzień
r – jadę na ryby

Jeżeli prawdą jest p  q , oraz jeżeli prawdą jest, że q 
r,

Zatem:

w każdą niedzielę p

bo p, p  q

q

q , q  r
r

jestem na rybach r.

C

2

= A

2

+ B

2

Fakty: a, b

Baza

wiedzy:

R1. a  c  d

R2. a  b  c

R3. b  d  g

R4. c  g  h

h?

g

d

R3

a

b

R2 c

h

R1

R4

Udowodnij że nie jesteś
wielbłądem!

R

1

: a  b  c  d

R

2

: d  c  f

R

3

: f  d  x  h

h?

Spójność: (a,L)  (c,3)  (d,H) , (~(a,H))  (c,3)  (d,H)

Niesprzeczność: (a,L)  (c,3)  (d,H) ,

(a,L)  (c,3)  (d,L)

Pochłanianie:

(a,L)  (c,3)  (d,H) , (a,L)  (b,D)  (c,3) 

(d,H)

(c,3)  (d,H) , (a,L)  (c,3)  (d,H)

Zapętlenie: (a,L)  (c,5)  (d,H) , (d,H)  (f,2) , (f,2)  (g,4) 

(c,5)

(a, L)

(d, H)

(f, 2)

(c, 5)

(g, 4)

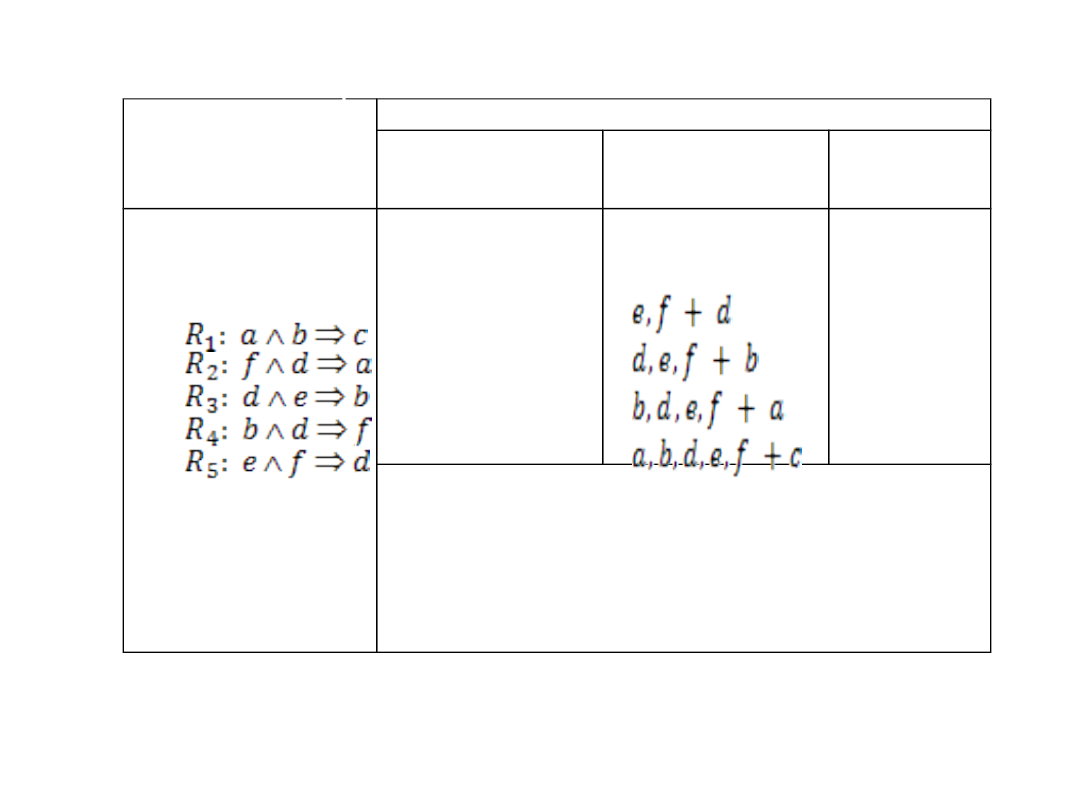
Początkowa baza

faktów: e, f

Wnioskowanie: c?

Nr kroku

Ewolucja

Bazy faktów

Reguły

Baza reguł

1

2

3

4

5

3

2

1

Baza faktów końcowa: a, b, c, d, e, f

Fakt c wynika z faktów: e, f

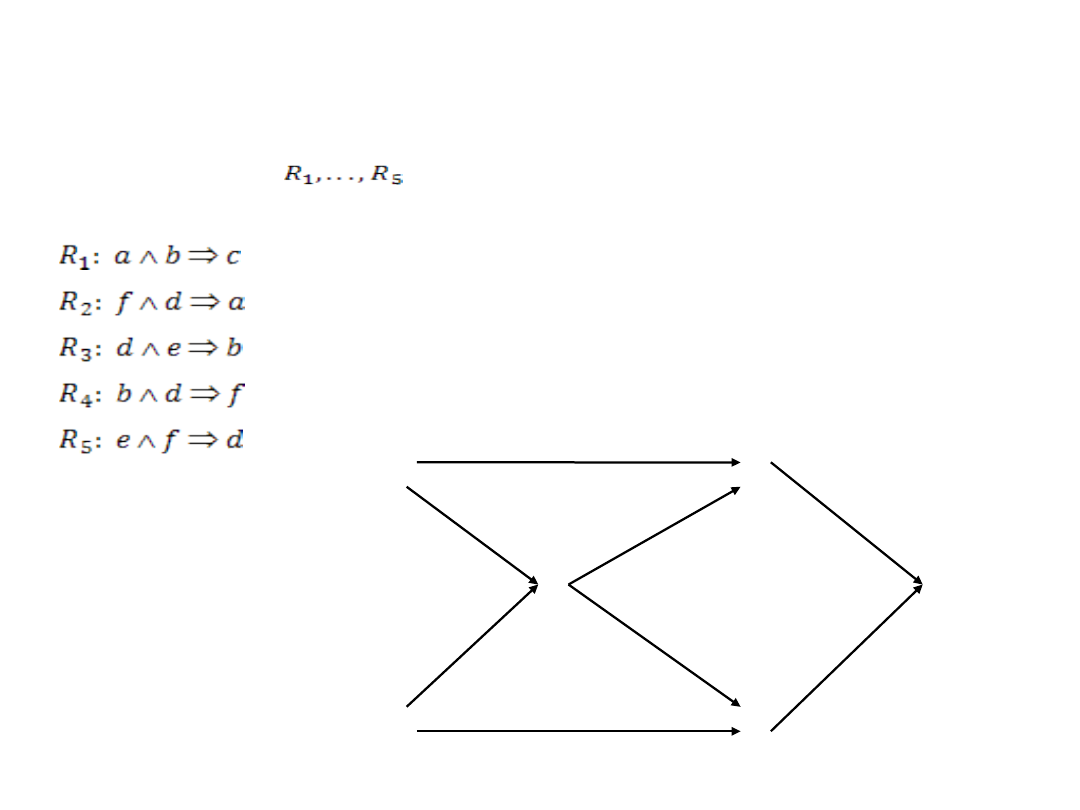
Baza faktów: BF = {e,f}

Baza reguł: BR = {

}

e

f

d

b

a

c

R

3

R

1

R

5

R

2

Przykłady

P(Janek,Zosia) = [Janek jest bratem Zosi] , P(V,x,y,z) = [V

= x*y*z]

xR [x + 0 = x] , xN [x = x*x] , xN [x < 0] , xR [x <

0] ,

x  zbiór kotów [x pije mleko] , x  zbiór szpaków [x jest

ptakiem]

x  zbiór dzieci y  zbiór rodziców [x jest dzieckiem y]

Rachunek predykatów

 jeden talerz  student

,

 student  jeden talerz

Niech P(x) = [x = x*x] która z tez jest prawdziwa:

 x  R P(x)

,

 x  R P(x)

 x {0,1} [x  x  0]

,

x {0,1} [x  x  1]

Predykaty

P(x)

P(x) = [ x = 3] , P(x) = [Q(x) U(x)] , [pije mleko] ,

[jest zielone],

P(x

1

,x

2

,...,x

n

) P(x,y,z) = [x + y = z] , P(x,y) = [x > y] , [jest

dzieckiem],

Bardziej formalnie:

Predykatem lub funkcją zdaniową nazywamy wyrażenie W(x), w którym
występuje zmienna x i które staje się zdaniem prawdziwym lub fałszywym, gdy w
miejsce x podstawimy wartość zmiennej x.

Rachunek predykatów został stworzony poprzez rozszerzenie rachunku zdań o
kwantyfikatory ogólny i szczególny: „dla każdego”  oraz „istnieje takie, że” .

Rachunek predykatów przyjmuje założenie o monotoniczności logiki. Oznacza to,
że jeżeli po przyjęciu zbioru aksjomatów wykazywana hipoteza jest poprawna
(czyli jest twierdzeniem), to po dodaniu nowego aksjomatu wynik ten nie może
ulec zmianie. Założenie to nie pozwala na uwzględnienie wyjątków powodujących,
że zbiór aksjomatów staje się zbiorem sprzecznym, co w niektórych przypadkach
ogranicza możliwość zastosowania omawianego rachunku.

Przykład

 x[jest_ptakiem(x)  potrafi_latac(x)]

jest_ptakiem(struś)

¬ potrafi_latac(struś)

Twierdzenie „dla wszystkich x, jeżeli x jest ptakiem, to x potrafi latać” jest nie do
końca poprawne ponieważ występują pewne odstępstwa od niego.
Otóż, struś jest ptakiem i nie potrafi latać. Bazę wiedzy należałoby uzupełnić o
nowy aksjomat:
¬ potrafi_latac(struś). Uwzględnianiem takich przypadków zajmuje się logika
niemonotoniczna.

Sprawdzanie prawdziwości

x P(x) - „jeden zaprzecza wszystkiemu“

x P(x) - „jeden wystarcza“

( x P(x))   x [P(x)]

Przykład

( x  R [x < x + 1]   x  R [x  x + 1]

( y Q(y))   y [Q(y)]

Przykład

( x  y [y > x])   x ( y [y > x])   x  y ( [y > x])   x 

y [y  x]]

Niech U’ = {1,2,3} , U” = {4,5,6,7} sprawdź
prawdziwość:

 X  U’  y  U” [y > x]

 x  U’  y  U” [y > x]

 X  U’  y  U” [y > x]

 x  U’  y  U” [y > x]

! xR [x*6 = 0]

 x  R  y R ! z  R [x + y = z]

 x {1,2,3} P(x)  P(1)  P(2)  P(3) ,

(x P(x)  x P(x))  (x P(x)  x Q(x))

x P(x) x P(x) x Q(x) x P(x)  x P(x)

x P(x) 

x Q(x)

0

0

0

1

1

0

0

1

1

1

0

1

0

1

0

0

1

1

1

1

1

0

0

1

0

1

1

1

0

( x P(x)   x P(x))  ( x P(x)   x Q(x))

( A  A )

 ( B  C )

( A  A )

 (B  C )

1



?????

( x P(x)   x P(x))  ( x P(x)   x Q(x))

Sprawdź

Twierdzenie o dedukcji (zasada rezolucji)

Jeżeli formuły {A1, A2,…, An} nie są sprzeczne, to formuła B jest

ich konkluzją (tzn. wynika inferencyjnie z formuł A1, A2,…, An)

wtedy i tylko wtedy, gdy formuły { A1,A2,…,An, ¬B} są

sprzeczne.

Każdy człowiek jest śmiertelny.

 x : Cz(x)  Śm(x)

Marek jest człowiekiem.

Cz(M)

Czy Marek jest śmiertelny?

Śm(M)?

 x : Cz(x)  Śm(x)

Cz(x)  Śm(x)

Cz(M)

Cz(M)

Śm(M)?

Śm(M)

Cz(x)  Śm(x) , Cz(M)

Śm(M)

Śm(M) , Śm(M)



Cz(x)  Śm(x)

, Cz(M)

Śm(M)

Śm(M)

x:=M



Zasada rezolucji

(a  b  b  c)  (a  c)

a  b, b  c

a  c

Każdy człowiek jest śmiertelny.

 x : Cz(x)  Śm(x)

Marek nie jest człowiekiem.

Cz(M)

Czy Marek jest śmiertelny?

Śm(M)?

 x : Cz(x)  Śm(x)

Cz(x)  Śm(x)

Cz(M)

Cz(M)

Śm(M)?

Śm(M)

Cz(x)  Śm(x)

,  Cz(M)

Cz(M)  Śm(M) , Śm(M)

Cz(x)  Śm(x)

,  Cz(M)

x:=M

Cz(M)  Śm(M)

Cz(M)  Śm(M) Śm(M)

Cz(M)

Cz(M)

Według kodeksu cywilnego jeżeli x jest mężem y to y jest żoną x.

Korzystając z

tego faktu oraz przyjmując, że x to Linda, a y to Bil, należy

przekonać Bila, że Linda jest jednak jego żoną, czemu on gorąco

zaprzecza. W zapisie predykatowym mamy zatem:

Żona(Linda, Bil)

¬Żona(x,y)  Mąż(y,x)

¬Mąż(Bil, Linda)

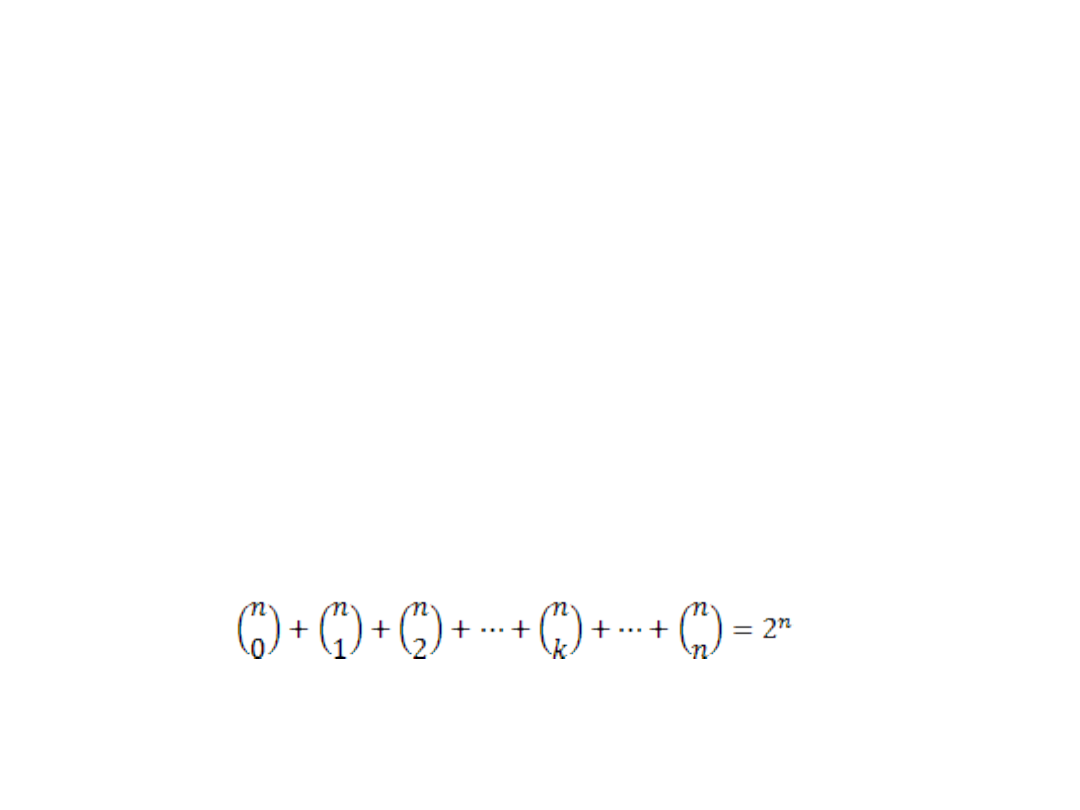
Rozważmy system ekspertowy, którego baza wiedzy zawiera m reguł,

a maksymalna liczba faktów wynosi n.

Przyjmijmy najgorszy przypadek, w którym baza wiedzy zawiera tylko

jeden fakt. Oznacza to, że należy wygenerować pozostałych n-1 faktów.
W przeszukiwaniu bazy reguł należy sprawdzać wszystkie kombinacje

faktów każdorazowo rozszerzonej bazy faktów.

Oznacza to, że każda z n reguł musi być „sprawdzona” kolejno dla

kombinacji 1 po 1, 2 po 1 i 2 po 2, 3 po 1 i 3 po 2 oraz 3 po 3, aż do

kombinacji z n-1 po 1, itd.

Tak więc sprawdzeniami objętych jest m2

1

+ m2

2

+…+m2

n-1

przypadków. Wykorzystywana jest tutaj zależność:

Niech m = 500 reguł oraz n = 101 faktów. Oznacza to konieczność

dokonania ok. 2

100

sprawdzeń.

Przyjmując, że rok ma 31 536 000 sekund, tzn. ok. 310

7

sekund,

zakładając wykorzystanie komputera umożliwiającego wykonywanie

1000 sprawdzeń na jedną nanosekundę, a zatem posiadając możliwość

dokonywania rocznie

3 10

7

10

9 

10

3

= 3 10

19

sprawdzeń,

samo sprawdzanie (wyszukiwanie) postawionej hipotezy w najgorszym

przypadku trwałoby 10

30

/(3 10

19

) 

10

11

lat.

Zauważmy bowiem, że 2

100

 10

30

,

ponieważ 2

10

 10

3

,

więc 2

10

2

10

2

10

... 2

10

 10

3

10

3

10

3

... 10

3

= 10

310

 10

30

.

10

10

x{P(x)  {y[P(y)  P(f(x,y))]  ~y[Q(x,y)  P(y)}}

Krok 1 x{~P(x)  {y[~P(y)  P((f(x,y))]  ~y[~Q(x,y) 

P(y)]}}

Krok 2 x{~P(x)  {y[~P(y)  P((f(x,y))]  y[Q(x,y) 

~P(y)]}}

Krok 3

x{~P(x)  {y[~P(y)  P((f(x,y))]  z[Q(x,z) 

~P(z)]}}

Krok 4 x{~P(x)  {y[~P(y)  P((f(x,y))]  [Q(x,z) 

~P(z)]}}

Krok 5 x y{~P(x)  {[~P(y)  P((f(x,y))]  [Q(x,z) 

~P(z)]}}

Krok 6 i 7

[~P(x)  ~P(y)  P((f(x,y))]  [~P(x)  Q((f(x,g(x))]  [~P(x) 

~P(g(x))]

A  (B  C)  (D  E)  (A  B  C)  (A  D)  (A  E)

Krok 8

~P(x) ∨ ~P(y) ∨ P((f(x,y))
~P(x) ∨ Q((f(x,g(x))
~P(x)∨ ~P(g(x))

Krok 9

~P(x

1

) ∨ ~P(y

1

) ∨ P((f(x

1

,y

1

))

~P(x

2

)∨ Q((f(x

2

,g(x

2

))

~P(x

3

)∨ ~P(g(x

3

))

Dana jest formuła postaci:

 x[P(x) ( y[P(y)  P(f(x,y))]  ¬  y[Q(x,y)  P(y)])]

1. Podczas pierwszego kroku usuniemy symbol implikacji,

wykorzystując znane przekształcenie A B  ( ¬ A)  B.

 x[ ¬ P(x)  ( y[ ¬ P(y)  P(f(x,y))]  ¬  y[ ¬ Q(x,y)  P(y)])]

2. W tym kroku przemieszczamy wszystkie zewnętrzne znaki negacji

do wewnątrz w celu przypisania ich wyłącznie formułom atomowym. W
przypadku kwantyfikatora ogólnego korzystamy z własności ¬  x[A]  
x[ ¬ A].

 x[ ¬ P(x)  ( y[ ¬ P(y)  P(f(x,y))]   y[ ¬ ( ¬ Q(x,y) 

P(y))])]

Korzystając z prawa de Morgana ¬ (A  B)  ( ¬ A)  ( ¬ B)

otrzymujemy

 x[ ¬ P(x)  ( y[ ¬ P(y)  P(f(x,y))]   y[Q(x,y)  ¬ P(y)])]

3. Eliminujemy kwantyfikator szczegółowy  poprzez wprowadzenie
odpowiednich stałych w miejsce zmiennych będących w zasięgu
kwantyfikatora.

 x[ ¬ P(x)  ( y[ ¬ P(y)  P(f(x,y))]  z[Q(x,z)  ¬ P(z)])]

Następnie usuwamy kwantyfikator szczegółowy . Powołując się na
zasadę: Jeżeli kwantyfikator szczegółowy jest w zasięgu kwantyfikatora
ogólnego to należy wprowadzić funkcję uzależnioną od zmiennej
kwantyfikatora ogólnego.
wstawiamy funkcję g(x) w miejsce zmiennej z

 x[ ¬ P(x)  ( y[ ¬ P(y)  P(f(x,y))]  (Q(x,g(x))  ¬ P(g(x)))]

4. W tym kroku przemieszczamy kwantyfikator ogólny  na zewnątrz formuły
złożonej.
 x y[ ¬ P(x)  (( ¬ P(y)  P(f(x,y)))  (Q(x,g(x))  ¬ P(g(x)))]
Korzystając z zasady: Jeżeli wszystkie zmienne są w zasięgu kwantyfikatora
to możemy z niego zrezygnować pamiętając, że każda zmienna w formule
została wyprowadzona za pomocą kwantyfikatora ogólnego.
pozbywamy się kwantyfikatorów ogólnych

¬ P(x)  (( ¬ P(y)  P(f(x,y)))  (Q(x,g(x))  ¬ P(g(x)))

5. W tym miejscu należy tak przekształcić formułę, aby funktory
koniunkcji były zewnętrzne względem funktorów alternatywy.
Korzystamy z własności A  (B  C)  (A  B)  (A  C)

{ ¬ P(x)  ¬ P(y)  P(f(x,y))}  [{ ¬ P(x)  Q(x,g(x))}  { ¬ P(x)

 ¬ P(g(x)}]

6. Z ostatniego wyrażenia po usunięciu symbolu koniunkcji otrzymujemy
postać klauzulową

i) ¬ P(x)  ¬ P(y)  P(f(x,y))

ii) ¬ P(x)  Q(x,g(x))

iii) ¬ P(x)  ¬ P(g(x)

Wykład 2

Elementy teorii liczb

•funkcje całkowitoliczbowe: powała i podłoga,

•podzielność liczb – algorytm Euklidesa,

•równanie diofantyczne,

•NWD, NWW, operator modulo,

•liczby pierwsze i rozkład liczb na czynniki, liczby doskonałe,

Ciągi - funkcje zmiennej naturalnej

a

n

= n

;

a

1

= 1 , a

2

= 2 , a

3

= 3

,

. . .

a

n

= n

2

;

a

n

= 2

n

,

a

n

= n!

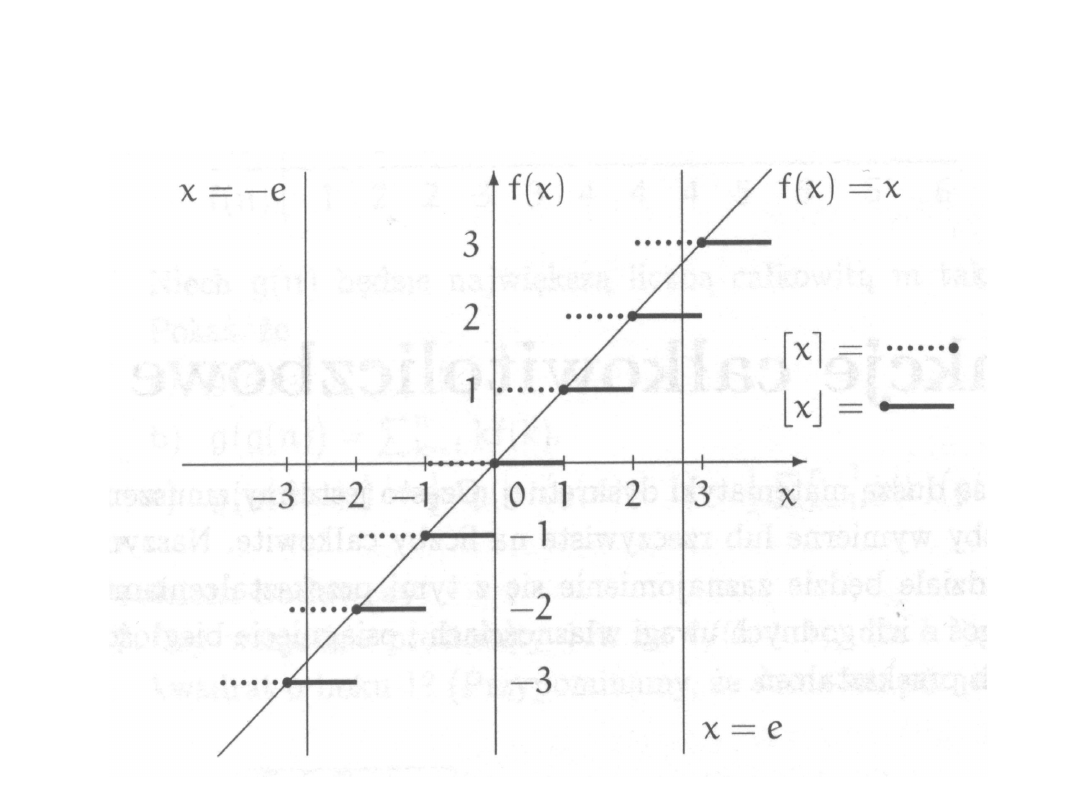
Funkcje całkowitoliczbowe

Podłoga

xR

, x = max{nC : n x}

 = 3;

- = -4

Powała

xR

, x = min{nC : n x}

 = 4;

 = -3

Funkcje całkowitoliczbowe

Podłoga

xR

, x = max{nC : n x}

 = 3;

- = -4

Powała

xR

, x = min{nC : n x}

 = 4;

 = -3

1 x = x  x = x  xC

;

x  x  x

2 x - x = 1  xR

3 - x = - x

;

x = - - x

4 x = n  n  x < n+1

5 x = n  x – 1 < n  x

6 x = n  n – 1 < x  n

7 x = n  x  n < x+1

Dane n  N

Ile potrzeba zarezerwować bitów pamięci dla zapisania n w komputerze?

(2002)

10

= 2 10

3

+ 0 10

2

+ 0 10

1

+ 2 10

0

(101001)

2

= 1 2

5

+ 0 2

4

+ 1 2

3

+ 0 2

2

+ 0 2

1

+ 1 2

0

32 8 1

2

5

= 32  41 < 64 = 2

6

Zatem liczba n zapisana na m bitach spełnia nierówność

2

m-1

 n < 2

m

2

m-1

 n < 2

m

/ log

2

x = n  n  x < n+1

m-1  log

2

n < m

log

2

n = m-1

a

zatem

m = log

2

n +1

Przykład

n = 7

;

log

2

7 = 2 (bo 2

2

= 4 a 2

3

= 8 ) zatem m = 2 + 1 =

3

Właściwość: 4 x = n  n  x <n+1

m-1  log

2

n < m

Algorytm Euklidesa

(por.: Sysło M.M., Algorytmy, WSiP, Warszawa, 1997, Sysło M.,

Piramidy, szyszki I inne konstrukcje algorytmiczne. WsiP, Warszawa, 1998.)

Liczba k jest największym wspólnym dzielnikiem m i n, tzn. NWD(m,n), jeśli

dzieli m oraz n

i jest największą liczba o tej właściwości.

Algorytm Euklidesa znajduje NWD(m,n).

NWD(n,m) = max{kN : k dzieli n  k dzieli m }

NWD(48,6) = 6 , NWD(26,15) = 1

NWD(n,m)

Niech n  m

n/m = q + r ; n = q m + r ; r = n - q m ; 0  r  m-1

NWD(n,m) = NWD(m,r)

NWD(24,12) ; 24 = 2 x 12 + 0 ; NWD(12,0)

NWD(37,35) ; 37 = 1 x 35 + 2 ; NWD(35,2) = NWD(17,1)

NWD(n,m)

Niech n  m

n/m = q + r ; n = q m + r ; r = n - q m ; 0  r  m-1

NWD(n,m) = NWD(m,r)

; NWD(37,35) ; 37 = 1 x 35 + 2

NWD(721,448)

n

= q x m + r

721 =

1 x 448 + 273

448 =

1 x 273 +

175

273 =

1 x 175 +

98

175 =

1 x 98 +

77

98 =

1 x 77 +

21

77 =

3 x 21 +

14

21 =

1 x 14 +

7

14 =

2 x 7

+ 0

NWD(721,448) = 7

NWD(35,2) ; 35 = 2 x 17 + 1 ;
NWD(17,1)

Równania diofantyczne

A

2

+ B

2

= C

2

3

2

+ 4

2

= 5

2

trójkaty pitagorejskie

A

n

+ B

n

= C

n

Przykład

Dane są naczynia o pojemności m i n. Czy korzystając z nich można

napełnić zbiornik o pojemności k ? Jeżeli tak to w jaki sposób?

Niech m, n  N , x, y  Z ;

k = x m + y n

5 x + 7 y = 3

;

15 = 4 x + 10 y ;

3 = 6 x + 18 y

NWD(7,5) = 1

NWD(10,4) = 2

NWD(18,6) =6

Rozwiązanie istnieje gdy k jest wielokrotnością NWD(m,n).

15 = 4 x + 10 y

nie ma rozwiązania, bo 2 = NWD(4,10),

3 = 5 x + 7 y

rozwiązanie istnieje, bo 1 = NWD(5,7).

Najmniejsza wspólna wielokrotność:

NWW(m,n)

NWW(m,n) = min{k: k jest podzielne przez m  k jest podzielne przez m}

NWW(12,9) = 3 bo ;

12 = 3 3 2

;

9 = 3 3

m n

12 9

NWW(12,9) = ---------------- = ------ = 36
NWD(12,9)

3

Liczby pierwsze

nN jest liczbą pierwszą jeśli n jest podzielne tylko przez 1 i n.

Liczb pierwszych jest nieskończenie wiele.

Każdą liczbę naturalną można przedstawić w postaci

H = 2

l1

3

l3

5

l5

7

l7

11

l11

13

l13

.........

l

1

, l

3

, l

5

, . .. – nieujemne liczby całkowite

Niech p

1

, p

2

, p

3

, ..., p

k

wszystkie liczby pierwsze

Euler

M = p

1

* p

2

* p

3

* ...* (p

k

+ 1) - liczba pierwsza

O

1

= 2

O

2

= 2 +1 = 3

O

3

= 2 3 +1 = 7

O

4

= 2 3 5 + 1 = 43

ale O

4

= 2 3 5 43 + 1 = 1807 = 13*139

2

k

Fermat

L

k

= 2 + 1

k = 1, 2 , 3 , 4 - liczba pierwsza

ale dla k = 5 nie jest liczbą pierwszą

n mod m , Mod(n,m) , MOD(n,m)

- reszta z dzielenia n

przez m

7 mod 3 = 1

;

1 mod 7 = 1

;

7 mod 7 = 0

n div m , Div(n,m) , DIV(n,m)

-

całkowita część

wyniku dzielenia

7 div 3 = 2 ;

1 div 7 = 0 ;

7 div 7 = 1

Liczba doskonała

Liczba doskonała jest liczbą naturalną gdy jest równa sumie

wszystkich swoich dzielników właściwych, tzn. takich które są

od niej mniejsze.

6 = 1 + 2 + 3

28 = 1 + 2 + 4 + 7 + 14

Wykład 3

Elementy kombinatoryki

• zasada gołębnika,

• zasada włączania i wyłączania,

• permutacje, kombinacje, podziały liczb,

• algorytmy generowania obiektów kombinatorycznych,

Zasada Gołębnika

(Zasada szufladkowa DIRICHLET’A)

Niech:

m obiektów oraz n pudełek

jeżeli n < m, to przynajmniej dwa obiekty są w jednym pudełku

Niech |A| - moc zbioru A ;

np. A = {a,b,c,d,e} ; |A| = 5

Jeżeli skończony zbiór S jest podzielony na k zbiorów, to co najmniej jeden z tych

zbiorów ma |S|/k lub więcej elementów.

Zastosowania:

W każdej grupie n osób są przynajmniej 2 osoby, które znają tę samą liczbę

osób.

Dany zbiór A = {

a

1

, a

2

,...,a

9

} taki, że suma jego elementów = 90.

a)  trzy takie elementy zbioru A, że ich suma  30.

b)  cztery takie elementy zbioru A, że ich suma  40.

a)

(a

1

+ a

2

+ a

3

)

+ (a

4

+ a

5

+ a

6

) + (a

7

+ a

8

+ a

9

) =

90

 < 30

 < 30

 > 30

 < 30

 = 30

 > 30

b

)

a

1

a

2

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

2

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

2

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

2

a

3

4 x 90 = 360 zatem 360/9 = 40

a

1

+ a

2

+ a

3

+ a

4

lub a

2

+ a

3

+ a

4

+ a

5

lub .......  40

Zasada włączania i wyłączania

Należy „włączyć” (dodać do siebie liczności poszczególnych zbiorów),

następnie „wyłączyć” (odjąć liczność przecięć po dwa zbiory), potem

„włączyć” (dodać liczności wszystkich przecięć po trzy zbiory), itd.

| A  B  C | = |A| + |B| + |C| - |A  B| - |A  C| - |B  C| + |A
 B  B|

Ilustracja

A = {a,b} ;

B = {1,2}

;

C = {x,y}

|A  B  C | = 6 = 2 + 2 + 2 – 0 – 0 – 0 + 0 = 6

A

B

C

Zastosowanie

Ile jest liczb między 1 a 999 nie podzielnych, ani przez 5, ani przez 7?

/
7

/
5

1, 2, ... , 999

999 - „/5” - „/7” + „/5 7” = 999 -  999/5  -  999/7  + 
999/35  =

= 999 - 199 - 142 + 28 = 686

Ile liczb naturalnych ze zbioru S = {1,2,3,...,1000} dzieli się przez

3 lub

5 lub przez obie te liczby jednocześnie?

Niech D

3

= {nS : n dzieli się przez 3}

D

5

= {nS : n dzieli się przez 5}

D

3



D

5

= {nS : n dzieli się przez 15}

D

3

= {3mS : 1 m  333}

| D

3

|

=  1000/3  = 333

D

5

= {5mS : 1 m  200}

| D

5

|

=  1000/5  = 200

| D

3



D

5

| =  1000/15  = 66

Zatem

| D

3

 D

5

| = | D

3

| + | D

5

| - | D

3



D

5

| = 333 + 200 – 66 = 467

Permutacje

- funkcje na zbiorze liczb naturalnych {a

1

,a

2

, ...,a

n

}

Liczba permutacji

P

n

= n! = n (n-1) (n-2) ...1 = 1 2 3 ...n

0! = 1

{A , B , C}

A B
C

B C A C
A B
C B C A
B A

Urzędnik zapomniał hasła do swoje aktówki. Hasło jest liczbą 7 cyfrową złożoną z

cyfr od 1 do 7. Cyfry w haśle nie powtarzają się. (Ostatnie 3 cyfry wybierane są ze

zbioru {3,4,7}) Ile możliwości w najgorszym przypadku trzeba sprawdzić aby

otworzyć zamek?

{3,4,7} - (3,4,7) , (4,7,3) , (7,4,3) , (3,7,4) , (4,3,7) , (7,3,4)

Wariacje

- bez powtórzeń

Dany zbiór A = {a

1

,a

2

, ...,a

n

}.

Wariacja – k-elementowy ciąg nie powtarzających się obiektów zbioru A.

Liczba k-elementowych wariacji zbioru A, n = |A| .

V

n

k

= n (n-1) (n-2) ... (n – k+1))

n!

n (n-1) (n-2) ...(n-k+1) (n- k) (n-k-1)..2 1

V

n

k

=

=

(n-k)!

(n-k) (n-k-1) ...2 1

= n(n-1)...(n-k+1)

A = {a,b,c}

; k = 2 ;

(a,b) , (a,c) , (b,c) , (b,a) , (c,a) , (c,b)

W urnie jest 10 kul ponumerowanych od 1 do 10. Losujemy kolejno i bez zwrotu 5

kul. Po każdym losowaniu zapisujemy jej numer. Ile jest wszystkich możliwych

wyników losowania?

V

n

k

= n (n-1) (n-2) ... (n – (k-1)) ; V

10

5

= 10 9 8 7 6

Wariacje

- z powtórzeniami

Rzucamy 10 razy monetą. Ile jest możliwych wyników tego

doświadczenia?

Liczba k- elementowych wariacji z powtórzeniami

W

n

k

= n n n n ...n = n

k

k

{O,R} , {O,R},..., {O,R}

2

n

Na ile sposobów można rozmieścić 2 kule (czarna i białą) w 3 szufladach?

I

II

III

0

b

c

0

c

b

0

c-b 0

0

0

c-b

b

c

0

c

b

0

c-b 0

0

b

0

c

c

0

b

Kombinacje

Dany zbiór A = {a

1

,a

2

, ...,a

n

}.

Kombinacja – k-elementowy podzbiór zbioru A.

Liczba k-elementowych kombinacji ze zbioru A, n = |A| .

n! n

C

n

k

= =

k!(n-k)! k

3 3!

= = 3 , {3,2,1}

, k = 2

; (1,2) , (1,3) ,

(2,3)
2 2! 1!

Łatwo zauważyć, że:

n!

V

n

k

= = k! C

n

k

(n-k)!

Na ile sposobów można wybrać 8 kart z talii 24 kart jeżeli kolejność nie

jest ważna?

Ile z tych układów 8- kartowych zawiera 2 asy.

C

20

6

C

4

2

Na ile sposobów można rozmieścić 6 osób w 3 różnych pokojach 2 osobowych?

C

2

6

C

2

4

C

2

2

Własności kombinacji

a)

n

n

=

k

n - k

b)

n

n

=

0

n

c)

n

n

=

1

n - 1

Trójkat Pascal’a

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

Dwumian Newton’a

n

n

n

n

(a + b)

n

=

a

n

+ a

n-1

b + ... + a b

n-1

+ b

n

0

1

n-1

n

n

n

(a +b)

n

=  a

n-i

b

i

i=0

i

Ciąg Fibonacciego Leonardo Fibonacci (1175 - 1250)).

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,

2584, 4181,...

F

1

= 1

;

F

2

= 1 ;

F

n

= F

n-1

+ F

n-2

dla n > 2

Pary

1 1 2 3 5 8

Okresy 1 2 3 4 5
6

M

M

M

M

M

M

M

R

R

R

R

R

R

R
R

R

R

R

M

R

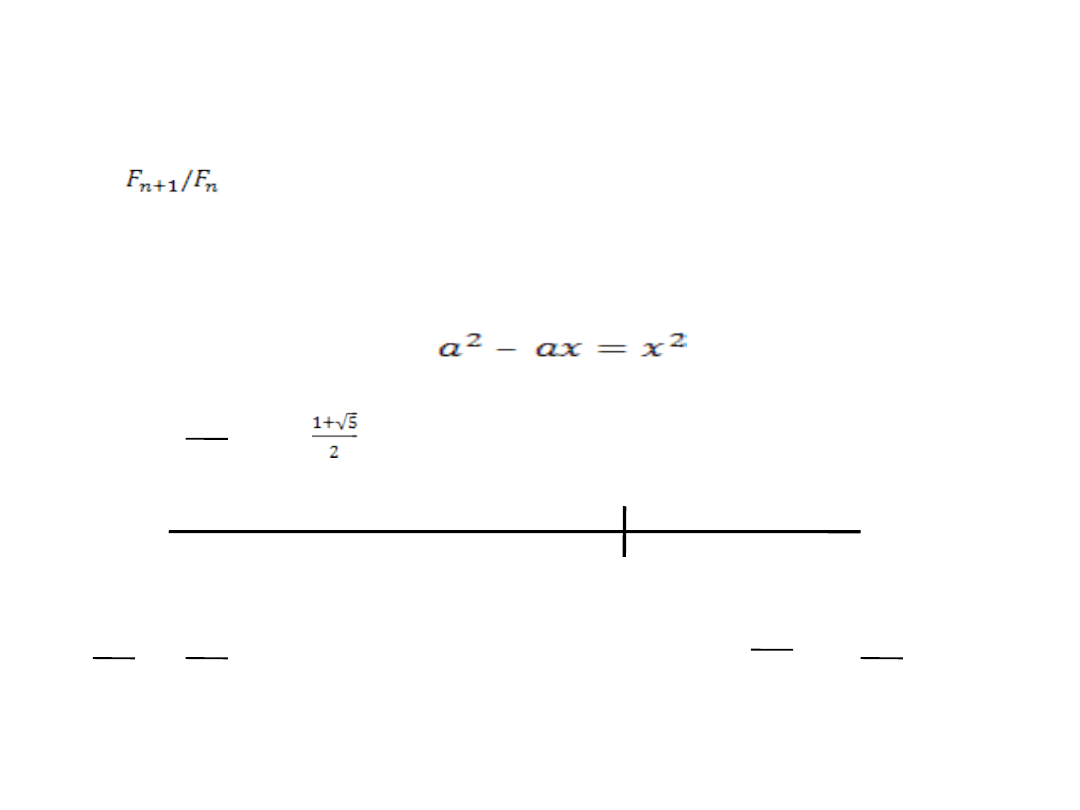
Złota

proporcja

2/1 = 2 ; 3/2 = 1.5 ; 5/3 = 1.667 ; 8/5 = 1.6 ; 13/8 = 1.625
21/13 = 1.615 ; 34/21 = 1.619 ; 55/34 = 1.618 . . .

≈ 1,618033989

współczynnik „złotych proporcji”

rozwiązanie równania:

a

x

a-x

a x

a

2

a

=

;

a

2

– a x = x

2

- - 1 = 0

x a – x

x

2

x

a
x

=

front Partenonu

F

n+1

5 + 1

 =

=

= 1,618033989.....

F

n

2

1 1 + 5

1 - 5

F

n

=

5 2

2

n

n

a

x

a –
x

Wykład 4

Elementy kombinatoryki

• algorytmy i zależności rekurencyjne,
• symbol Newtona, trójkąt Pascal’a
• rozwiązywanie zależności rekurencyjnych – przez podstawianie i za pomocą

równania charakterystycznego,

• kongruencje, schemat Hornera

(por.: Sysło M., Piramidy, szyszki i inne konstrukcje algorytmiczne. WSiP, Warszawa, 1998.

Ross K.A., Wright C.R.B., Matematyka dyskretna, PWN, Warszawa 1996.)

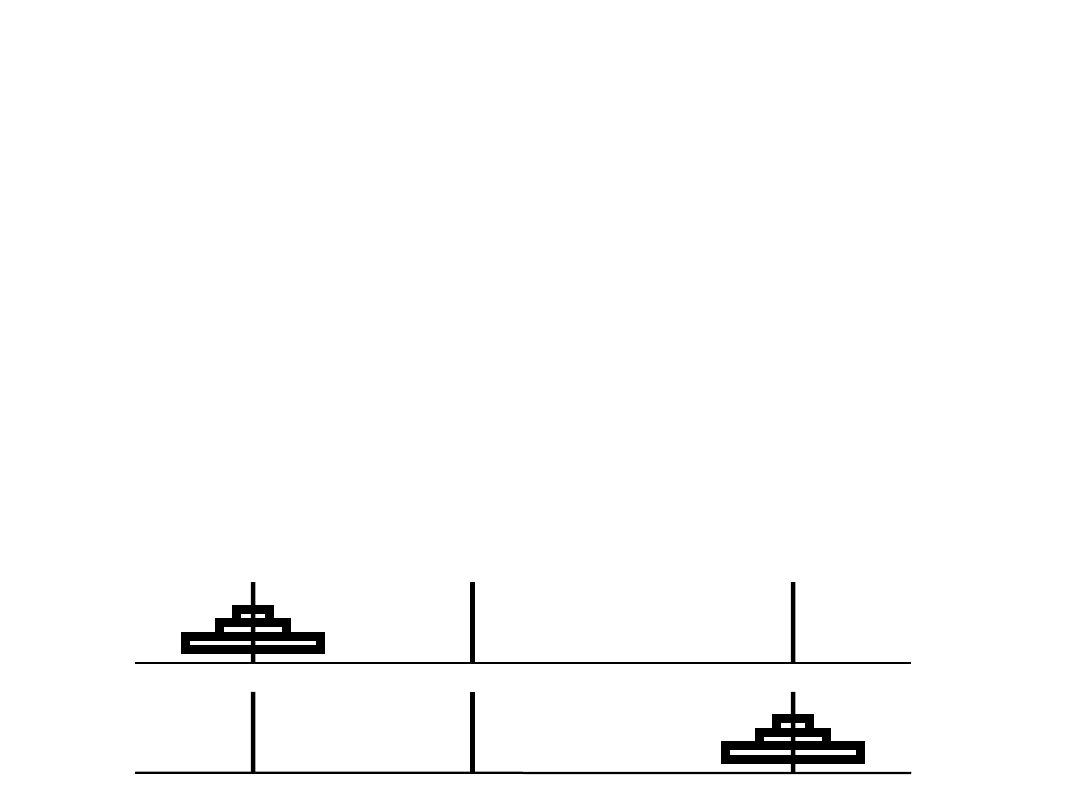
Algorytmy i zależności rekurencyjne

Wieża w Hanoi

2

n

- 1

Trzy kręgi

wymagają 7 przełożeń bo 2

3

– 1 = 7

Trzy kręgi wymagają 7 przełożeń bo 2

3

– 1 = 7

Jeden krąg - jedno przełożenie

2

1

- 1

Dwa kręgi - trzy przełożenia

2

2

- 1

Zależności rekurencyjne

1 , -3 , - 27 , -185 ,

S

n

= 6S

n-1

– 9S

n-2

, n  2 , S

o

= 1 , s

1

= -3

S

n

= 3

n

- 2n3

n

, n  N

0

Sprawdzenie:

n

S

n

= 6S

n-1

– 9S

n-2

S

n

= 3

n

- 2n3

n

0

1

3

0

- 2*0*3

0

=1

1

-3

3

1

- 2*1*3

1

= -3

2

6*(-3)– 9*1 = -27

3

2

- 2*2*3

2

= -27

3

6*(-27)– 9*(-3) = -185

3

3

- 2*3*3

3

= -185

4

. . .

. . .

Trójkat Pascal’a

n = 4

{a,b,c,d}

k = 0



1

k = 1

{a}, {b}, {c}, {d}

4

k = 2

{a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d}

6

k = 3

{a,b,c}, {a,b,d},{a,c,d}, {b,c,d}

4

k = 4

{a,b,c,d}

1

n! n

C

n

k

= =

k!(n-k)! k

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

(symbol Newton’a)

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

n

n n n

(a – b)

n

=

a

n

+ a

n-1

b + . . . + a b

n-1

+ b

n

0

1 n-1 n

n n
(a – b)

n

=



a

n-i

b

i

i=0 i

Dwumian Newton’a

Liczby Fibonacciego

1 1

2 3 5 8 13 21 34 55 89 144 ...

F

1

= 1 ;

F

2

= 1 ;

F

n

= F

n-1

+ F

n-2

dla n > 2

n n

1 1 + 5 1 - 5

F

n

=

5

2 2

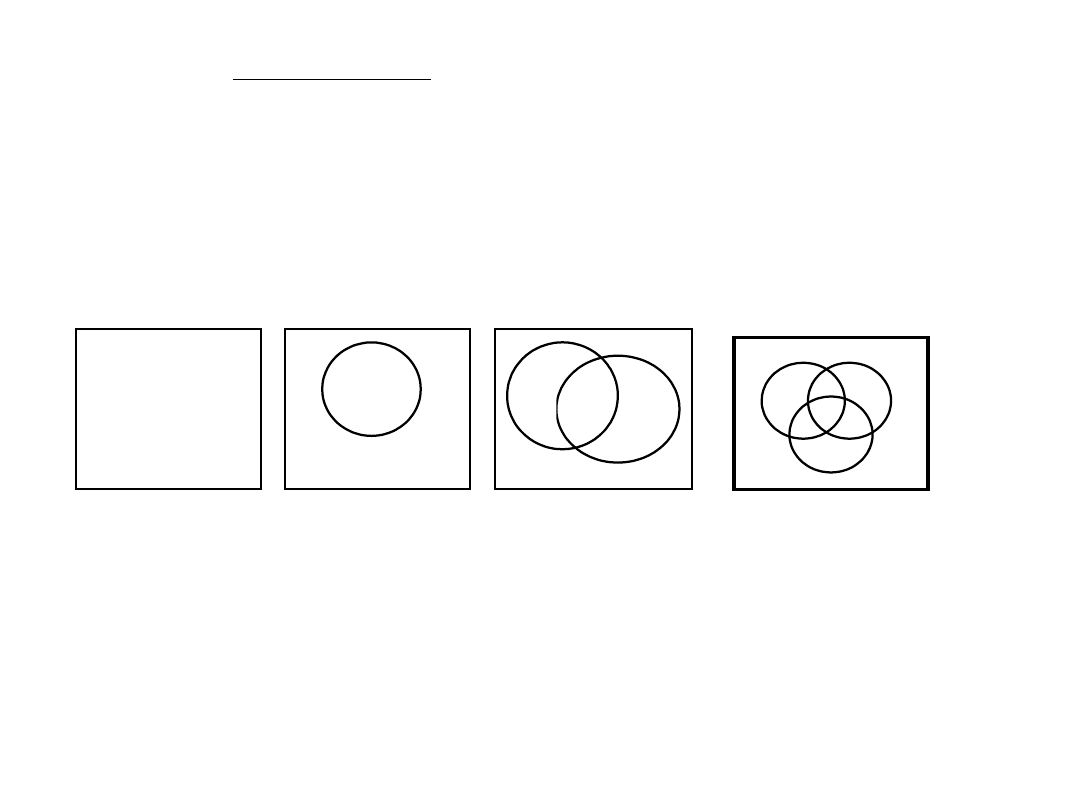
Na płaszczyźnie jest danych n okręgów.

Jaka jest maksymalna liczba obszarów, na które dzielą one

płaszczyznę?

Wyprowadź

rozwiązanie

w

postaci

odpowiedniej

zależności

rekurencyjnej.

1

2

1

2

4

3

1 = 2

0

1 + 1 = 2 = 2

1

1 + 2 + 1 = 4 = 2

2

1 + 3 + 3 + 1 = 8

= 2

3

n n
 =
2

n

i=0 i

a = b =
1

n

n

n

n

2

n

=

+ + ... +

+

0

1

n-1

n

1 + 4 + 6 + 4 + 1 = 16 = 2

4

4 n
 =
2

4

i=0 i

n

n

n

n n

2

n

=

+ + ... + + = (a +

b)

0

1

n-1

n

Zależności rekurencyjne

– wzory jawne

Metoda przez podstawianie

Przyklad

a

1

, a

2

, a

3

,...,a

i

, a

i+1

,... ;

1 , 2 , 3 , 7 ,15 . 31 .

...

a

1

=1

a

n

= 2 a

n-1

+ 1

n>1 ; a

n

=2

n

– 1

; n>1

a

n

= 2 a

n-1

+ 1 = 2(2 a

n-2

+ 1) + 1 = 2

2

a

n-2

+ 2 + 1 =

= 2

2

(2 a

n-3

+ 1) + 2 + 1 = 2

3

a

n-3

+ 2

2

+ 2

1

+ 2

0

=

. . .

= 2

k

a

n-k

+ 2

k-1

+ 2

k-2

+ ... + 2

2

+ 2

1

+ 2

0

=

= 2

n-1

+ 2

n-2

+ ... + 2

2

+ 2

1

+ 2

0

= 2

n

– 1

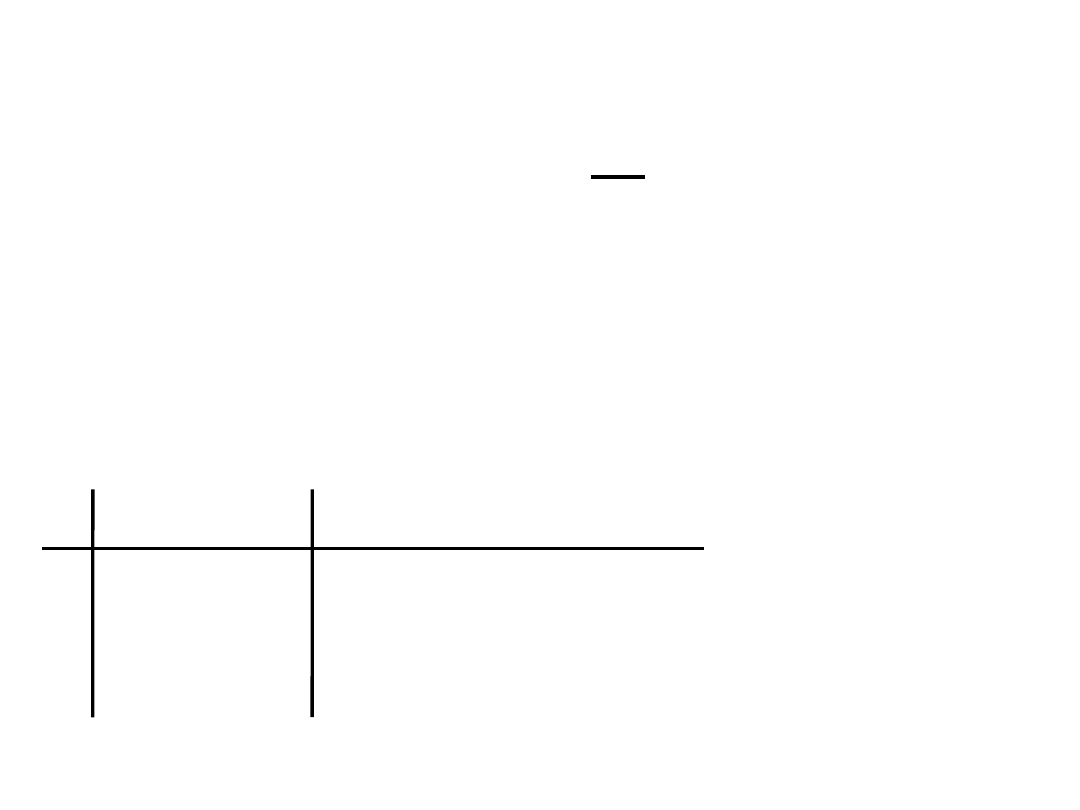
Suma wyrazów postępu geometrycznego

a

1

, a

2

, a

3

,...,a

i

, a

i+1

,... ; .q = a

i+1

/a

i

1 - q

n

S = a

1

1 - q

2

n-1

+ 2

n-2

+ ... + 2

2

+ 2

1

+ 2

0

= 2

n

– 1

a

n

+ a

n-1

+ ...+ a

3

+a

2

+ a

1

Ponieważ

q = 2

i+1

/2

i

= 2

i

a

1

= 1

zatem

S

n

= (1-2

n

)/(1-2) = - (1-2

n

) = 2

n

-1

Sprawdzenie:

n

a

n

= 2 a

n-1

+ 1

a

n

= 2

n

- 1

1

1

1

2

2*1 + 1 = 3

2

2

– 1 = 3

3

2*3 + 1 = 7

2

3

– 1 = 7

4

2*7 + 1 = 15 2

4

– 1 = 15

5

2*15 + 1 = 31

2

5

– 1 = 31

Przykład

Dana jest zależność rekurencyjna

f(n) = f(n-1) + 3

n

;

n > 1 ; f(1) = 3

Wyznacz postać analityczną

f(n) = f(n-1) + 3

n

;

n > 1 ; f(1) = 3

f(n) = f(n-1) + 3

n

= (f(n-2) + 3

n-1

) + 3

n

=

= ((f(n-3) + 3

n-2

) + 3

n-1

) + 3

n

=

= . . .=

= 3

1

+ 3

2

+ 3

3

+ 3

4

+ . . . + 3

n-1

+ 3

n

Ponieważ kolejny wyraz f(n) jest sumą postępu arytmetycznego

1 - q

n

S = a

1

1 - q

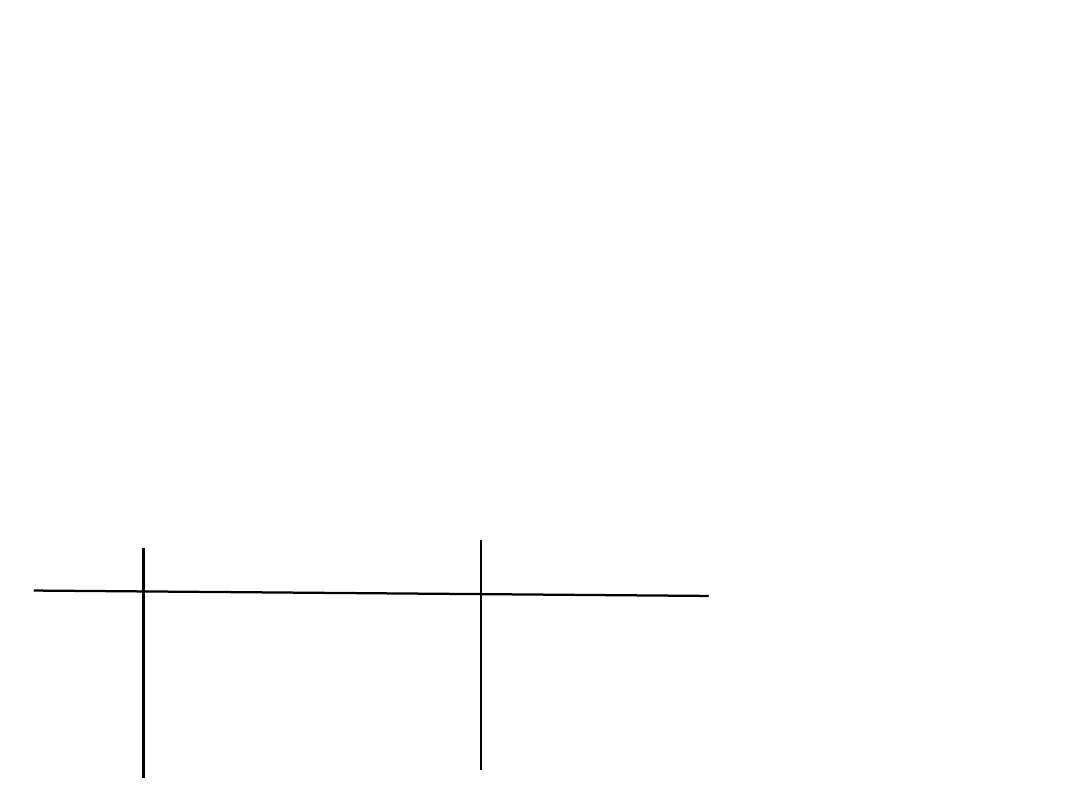
q = f(i+1)/f(i) = 3

i+1

/3

i

= 3

, a

1

= 3

Zatem

f(n) = (1- 3

n

)/(1-3)*3 = 3/2(3

n

– 1)

Sprawdzenie

n

f(n) = f(n-1) + 3

n

f(n) = 3/2(3

n

– 1)

1

3

3

2

3 + 3

2

= 12

3/2(3

2

– 1) = 3/2(8) = 12

3

12 + 3

3

= 39

3/2(3

3

– 1) = 3/2(26) = 39

4

39 + 3

4

3/2(3

4

– 1)

Metoda równania charakterystycznego

Rozważmy ciągi postaci:

s

n

= a*s

n-1

+ b*s

n-2

. a , b - stałe

Przypadek a)

a = 0 lub b = 0

;

znane są wartości s

0

i s

1

Jeżeli b = 0 to s

n

= a*s

n-1

dla n  1.

Zatem s

1

= as

0

, s

2

= as

1

= a

2

s

o

,...

Ostatecznie

s

n

= a

n

s

o

Przykład

s

n

= 3s

n-1

, gdzie s

0

= 5

;

5, 15, 45, …

ponieważ a = 3 zatem ostatecznie s

n

= 3

n

5

;5, 15,

45, …

Metoda równania charakterystycznego

Rozważmy ciągi postaci:

s

n

= a*s

n-1

+ b*s

n-2

. a , b - stałe

Jeżeli a = 0 to s

n

= b*s

n-2

dla n  2.

Zatem s

2

= bs

0

, s

4

= bs

2

= b

2

s

o

,...

Ostatecznie

s

2n

= b

n

s

o

dla

n  N

Podobnie

s

3

= bs

1

, s

5

= bs

3

= b

2

s

1

,...

Ostatecznie

s

2n+1

= b

n

s

1

dla

n  N

Przykład

s

n

= 3s

n-2

,

gdzie s

0

= 5 i s

1

= 2 ,

Ostatecznie s

2n

= 3

n

5

i

s

2n+1

= 3

n

2

Przykład

s

n

= 3s

n-2

,

gdzie s

0

= 5 i s

1

= 2 ,

Ostatecznie s

2n

= 3

n

5

i

s

2n+1

= 3

n

2

Sprawdzenie:

n

s

n

= 3s

n-2

s

2n

= 3

n

5

, s

2n+1

= 3

n

2

0

5

5

2n = 0



n = 0

1

2

2

2n+1 = 1  n = 0

2

15 15

2n = 2



n = 1

3

6

6

2n+1 = 3  n = 1

4

45 45

2n = 4



n = 2

5

18

18

2n+1 = 5  n = 2

… … … …

… …

Przypadek b)

a  0 lub b 0

; znane są wartości s

0

i s

1

Znana jest zależność

s

n

= a*s

n-1

+ b*s

n-2

; a , b - stałe

Rozważmy równanie charakterystyczne

x

2

– a*x – b = 0

F

n

= F

n-1

+ F

n-2

równanie jednorodne

x

n

= x

n-1

+ x

n-2

równanie charakterystyczne

x

n

= x

n-1

+ x

n-2

/ x

n-2

x

2

= x+ 1

F

n

= A x

1

n

+ B x

2

n

ogólna postać rozwiązania

Rozważmy równanie charakterystyczne

x

2

– a*x – b = 0

W sytuacji gdy równanie to ma dwa różne rozwiązania r

1

i r

2

wówczas

s

n

= c

1

r

1

n

+ c

2

r

2

n

Gdy s

o

i s

1

są dane wówczas przez podstawienie n = 0 i n=1 wyznaczyć

można c

1

i c

2

.

W sytuacji gdy równanie to ma tylko jedno rozwiązanie r

wówczas

s

n

= c

1

r

n

+ c

2

n r

n

Gdy s

o

i s

1

są dane wówczas przez podstawienie n = 0 i n=1 wyznaczyć

można c

1

i c

2

.

Rozważmy równanie charakterystyczne

x

2

– a*x – b = 0

Przykład

s

n

= s

n-1

+ 2 s

n-2

;

s

0

= s

1

= 3

równanie charakterystyczne ma postać x

2

– a*x – b = 0 zatem

x

2

–x – 2 = 0

 = b

2

– 4ac = 1 +8 = 9 ; x

1

= (-b + )/2a = (1 + 3)/2 = 2 . x

2

= -1

Postać poszukiwana

s

n

= c

1

r

1

n

+ c

2

r

2

n

Zatem s

n

= c

1

2

n

+ c

2

(-1)

n

Wiadomo, że s

0

= s

1

= 3

Wyznaczane są: c

1

i c

2

Dla n = 0

s

n

= c

1

2

0

+ c

2

(-1)

0

= c

1

+ c

2

= 3

Dla n = 1

s

n

= c

1

2

1

+ c

2

(-1)

1

= 2c

1

- c

2

= 3

3c

1

= 6 ,

c

1

= 2 , c

2

= 1

Ostatecznie s

n

= 2*2

n

+ (-1)

n

Sprawdzenie

n

s

n

= s

n-1

+ 2 s

n-

2

s

n

= 2*2

n

+ (-1)

n

0

3

2*2

0

+ (-1)

0

= 3

1

3

2*2

1

+ (-1)

1

= 3

2

3 + 2*3

2*2

2

+ (-1)

2

= 9

3

9 + 2*3

2*2

3

+ (-1)

3

= 15

4

15 + 2*9

2*2

4

+ (-1)

4

Przykład

s

n

= 4s

n-1

– 4s

n-2

, n  2 ;

s

0

= 1 , s

1

= 8

równanie charakterystyczne ma postać x

2

– ax – b = 0 zatem

x

2

–4x + 4 = 0

 = b

2

– 4ac = 16 - 16 = 0 ; x

1

= x

2

= 4/2 = 2

Postać poszukiwana s

n

= c

1

r

n

+ c

2

nr

n

a dokładniej

s

n

= c

1

2

n

+ c

2

n2

n

Wyznaczane są: c

1

i c

2

Dla n = 0

s

n

= c

1

2

0

+ c

2

*0*2

0

= c

1

= 1

Dla n = 1

s

n

= c

1

2

1

+ c

2

*1*2

1

= 2c

1

+ 2c

2

= 8

c

1

= 1 , c

2

= 3

Ostatecznie s

n

= 2

n

+ 3*n*2

n

Sprawdzenie

n

s

n

= 4s

n-1

– 4s

n-2

s

n

= 2

n

+ 3*n*2

n

0

1

2

0

+ 3*0*2

0

= 1

1

8

2

1

+ 3*1*2

1

= 8

2

4*8 - 4*1

2

2

+ 3*2*2

2

= 28

3

4*28 - 4*8

2

3

+ 3*3*2

3

Kongruencje

x  y (mod m)

kongruencja

;

m - moduł

6  1 (mod 5)

;

12  2 (mod 5) ;

14  4 (mod 5)

Kongruencje nie zmieniają swoich właściwości przy obustronnym

podnoszeniu do potęgi (pierwiastkowaniu) oraz przy mnożeniu i

dzieleniu przez inne kongruencje

6  1 (mod 5) / 6

36  6 (mod 5)  1 (mod 5)

6  1 (mod 5) / * (12  2 (mod 5))

72  2 (mod 5)

Zastosowania

Wyznacz największe x  3

15

podzielne przez 17

3

3

= 27  10 (mod 17)

27  10 (mod 17) / * 27  10 (mod 17)

3

6

 100 (mod 17)  15 (mod 17)

3

6

 15 (mod 17) / * 3

6

 15 (mod 17)

3

12

 225 (mod 17)  4 (mod 17)

3

12

 4 (mod 17) / *3

3

 10 (mod 17)

3

15

 40 (mod 17)  6 (mod 17)

Zatem

3

15

– 6  0 (mod 17) bo 0 (mod 17)  17 (mod 17)  34 (mod 17),

itd

x = 3

15

– 6

Na jaką cyfrę kończy się liczba 2

100

?

2

10

 4 (mod 10)

1024  4 (mod 10)

2

10

 4 (mod 10) /

2

2

20

 16 (mod 10)  6 (mod 10)

2

20

 6 (mod 10) /

2

2

40

 36 (mod 10)  6 (mod 10)

2

40

 6 (mod 10) /

2

2

80

 36 (mod 10)  6 (mod 10

2

80

 6 (mod 10) / (2

20

 6 (mod 10) )

2

100

 36 (mod 10)  6 (mod 10)

2

100

 6 (mod 10)

Zatem 2

100

kończy się cyfrą 6.

91

Schemat Hornera

Dana jest reprezentacja liczby M w systemie przy podstawie a.

Oblicz jej dziesiętną postać.

M = r

k

a

k

+ r

k-1

a

k-1

+ r

k-2

a

k-2

+ ...+ r

1

a

1

+ r

0

M = (r

k

a

k-1

+ r

k-1

a

k-2

+ r

k-2

a

k-1

+ ...+ r

1

)a

1

+ r

0

M = ((r

k

a

k-1

+ r

k-1

a

k-2

+ r

k-2

a

k-1

+ ...+ r

2

)a+ r

1

)a + r

0

M = (...((r

k

a+ r

k-1

)a

+ r

k-2

)a + ...+ r

1

)a + r

0

Przykład

M = (45)

10

= (101101)

2

= 1*2

5

+ 0*2

4

+ 1*2

3

+1*2

2

+ 0*2

1

+ 1*2

0

1*2

5

+ 0*2

4

+ 1*2

3

+1*2

2

+ 0*2

1

+ 1*2

0

= 1*2

5

+ 1*2

3

+1*2

2

+ 1*2

0

=

= 100000 + 1000 + 100 + 1 = 101101

(101101)

2

=

= ((((1*2

+ 0)2

+ 1)2

+1)2 + 0)2+

1 = ((((1*2

)2

+1)2

+1)2)2+

1 =

= (((5) 2 +1)2)2+1 =

= ((11)2)2+1 = 44 + 1 = 45

Zastosowanie

Najszybszy sposób obliczania potęgi x

n.

Niech n = 45.

Zatem x

45

= x

((((1*2 + 0)2 + 1)2 +1)2 + 0)2+ 1

= (((((x

2

)

2

x)

2

)x)

2

)

2

x

Bo x*x = x

2

;

x

2

x

2

= x

2+2

;

(x

2

)

3

= x

2*3

Sprawdzenie

x

((((1*2 + 0)2 + 1)2 +1)2 + 0)2+ 1

= (x

((((1*2 + 0)2 + 1)2 +1)2 + 0)2

)x =

= (x

(((1*2 + 0)2 + 1)2 +1)2

)

2

x =

= ((x

((1*2 + 0)2 + 1)2 +1

)

2

)

2

x =

= (((x

((1*2 + 0)2 + 1)2

)x)

2

)

2

x =

= (((((x

(1*2 + 0)2

)x)

2

)x)

2

)

2

x =

= (((((x

(1*2 + 0)

)

2

x)

2

)x)

2

)

2

x =

= (((((x

(1*2)

)

2

x)

2

)x)

2

)

2

x =

= (((((x

2

)

2

x)

2

)x)

2

)

2

x

Przykład

X

22

= X

16

X

4

X

2

bo 22 = 2

4

+ 2

2

+ 2

1

= 16 + 4 + 2

X

22

= (X

8

X

2

)

2

X

2

X

22

= ((X

2

)

4

X

2

)

2

X

2

W Y K Ł A D - 5

Elementy teorii grafów

• relacje,

• grafy (symetryczne i skierowane),

• drogi, cykle, rodzaje grafów: drzewa, dwudzielne, pełne,

• macierzowe reprezentacje grafów,

• grafy Eulera i Hamiltona, grafy płaskie

(Wilson R.J., Wprowadzenie do teorii grafów, PWN, Warszawa, 1998. Ross K.A., Wright C.R.B.,
Matematyka dyskretna, PWN, Warszawa 1996. N. Deo, Teoria grafów i jej zastosowania w
technice i informatyce. PWN, Warszawa 1980.)

Relacje

R

- relacja dwuargumentowa na zbiorze

S

x

T

R  S

x

T

Przykład
S = {1,2,3}, T = {a, b} , S x T = {(1,a), (1,b), (2,a), (2,b), (3,a),

(3,b)}

R = S x T = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b)}

1

2

3

a

b

1

2

3

Przykład

S = {1,2,3},

T = {1,2,3} ,

S x T = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3),(3,1),

(3,2), (3,3)}

R’ = {(1,2),(1,3),(2,3)}  S x T;

a R’ b  a < b

dla a S, bT

R” = {(1,1),(2,2),(3,3)}  S x T

;

a R” b  a = b dla a S, bT

R’’’ = { }  S x T

;

a R’’’ b  a mod 5 = b mod 5 = 4 mod 5

dla a S, bT

1

2

3

a

b

Niech R  S x S

(relacja R w zbiorze S )

Jest zwrotna

(x,x)  R

, x  S

Jest przeciwzwrotna

(x,x)  R

, x S

Jest symetryczna

(x,y)  R  (y,x)  R, x,y S

Jest antysymetryczna

(x,y)  R & (y,x)  R  x = y

Jest przechodnia

(x,y)  R & (y,z)  R  (x,z)  R

Przykład

R’ = {(1,2),(1,3),(2,3)}  S x T;

a R’ b  a < b

dla a S, bT

R” = {(1,1),(2,2),(3,3)}  S x T

;

a R” b  a = b dla a S, bT

Jeżeli R  S x T to R^  T x S jest relacja odwrotną

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R =

{(a,a), (b,b),

(c,c), (d,d), (a,b)}. Czy relacja ta jest zwrotna.

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,a),

(b,b),(c,c), (d,d)}. Czy relacja ta jest przechodnia

Jeżeli dana relacja jest symetryczna, zwrotnia i przechodnia, to jest relacją

równoważności, na której definiujemy klasy abstrakcji.

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,c),

(a,a)}. Czy relacja ta jest przeciwzwrotna.

Przykład

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,a),(c,c), (d,c), (c,d)}. Czy relacja ta jest symetryczna.

Przykład

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,c),

(c,d), (d,a)}. Czy relacja ta jest przeciwsymetryczna.

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b), (a,c),

(b,a)}. Czy relacja ta jest spójna.

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,a),(c,c)}. Czy relacja ta jest symetryczna.

Relacja jest spójna, jeżeli

x,y S, x ≠ y  (y,x)  R  (x,y)  R

Relacje < i ≤ są relacjami spójnymi w zbiorze liczb rzeczywistych

a

b

c

a

b

c

S = {a,b,c}

;

R’ = {(a,b),(c.b),(a,c)} ;

a

b

c

G R A F Y

Graf

G = (S, R)

Przykład

S = {a,b,c}

;

R = {(a,b),(b,a),(b,c),(c.b),(c,a),(a,c)}

G = (S, R’)

A

D

C

B

C

D

B

(1736) Leonard Euler

Problem mostów

królewieckich

Przejść przez każdy z mostów dokładnie jeden raz i powrócić do punktu
wyjściowego.

A

6

7

2

3

1 8

3 5

4

Problem sieci wodnej (W), gazowej (G) i elektrycznej (E). Są trzy domy H

1

,

H

2

i H

3

, z których każdy musi być podłączony przewodami do każdej z

trzech sieci. Czy jest możliwe dokonanie takich połączeń bez skrzyżowania

przewodów?

H

1

H

2

H

3

W

G

E

Krawędzie, łuki, wierzchołki, drogi, ścieżki, pętle, kontury, obwody,

cykle, drogi zamknięte.

Ścieżka (droga) elementarna - nie przecina samej siebie.

Graf spójny G

- jeżeli istnieje przynajmniej jedna ścieżka (droga)

miedzy każdą para wierzchołków w G.

Podgraf

G’  G = (X,R) , G’ = (X’,R’); X’  X ; R’  R

Długość drogi – liczba krawędzi drogi.

Stopień wierzchołka - liczba krawędzi z nim incydentnych.

Graf regularny – wszystkie wierzchołki sa tego samego stopnia

Charakterystyki grafu

n - liczba wierzchołków

e - liczba krawędzi

k - liczba składowych (spójności)

e 

n – k

r - rząd grafu

r = n – k

 - zerowość grafu

 = e – n + k

Przykład

Rząd grafu = liczba gałęzi w każdym dendrycie grafu

Zerowość grafu = liczba cięciw w grafie

rząd + zerowość = liczba krawędzi w grafie

Izomorfizm

Dwa grafy są izomorficzne jeśli zachodzi wzajemnie jednoznaczna

odpowiedniość między ich wierzchołkami oraz ich krawędziami przy

zachowaniu relacji incydencji.

Grafy izomorficzne muszą mieć:

• tę samą liczbę wierzchołków

• tę samą liczbę krawędzi

• równa liczbę wierzchołków o danym stopniu

Poszukiwane jest kryterium efektywnego obliczeniowo wykrywania
izomorfizmu!

I z o m o r f i z
m

N o m e n k l a t u r
a

Dwa grafy G

1

i G

2

są izomorficzne, jeżeli istnieje wzajemna

jednoznaczna odpowiedniość między wierzchołkami grafu

G

1

i wierzchołkami grafu G

2

, taka że liczba krawędzi łącząca

dwa dowolne wierzchołki w G

1

jest równa liczbie krawędzi

łączących odpowiadające im wierzchołki w G

2

.

Grafy dwudzielne, grafy pełne, drzewa

Graf dwudzielny

Graf pełny

Drzewo

Graf dwudzielny

– wierzchołki którego można pokolorować dwoma barwami.

Graf pełny

- każdy wierzchołek którego jest połączony (krawędzią lub łukiem) z

pozostałymi

wierzchołkami

Drzewo

- graf spójny bez obwodów (drzewo genealogiczne, rzeka, drzewo

decyzyjne, itp.)

Właściwości drzewa:

•między każdą parą wierzchołków istnieje tylko jedna droga

•drzewo o n wierzchołkach ma n-1 krawędzi

Drzewo binarne

- dokładnie jeden wierzchołek jest stopnia drugiego a

pozostałe stopnia

trzeciego lub pierwszego.

poziom 0

poziom 1

poziom 3

poziom 4

Właściwości drzew binarnych:

- liczba wierzchołków n w drzewie binarnym jest zawsze

nieparzysta.

- liczba krawędzi w drzewie jest równa

p = (n+1)/2,

- p – liczba wierzchołków wiszących

1/2(p + 3(n-p-1)+2) = n-1

- liczba krawędzi w

drzewie

Własności drzew (dla grafu T mającego n-wierzchołków):

• T nie zawiera cykli, ilość krawędzi = n-1
• T jest grafem spójnym, każda krawędź jest mostem.
• Każde dwa wierzchołki T połączone są dokładnie jedną drogą.
• T nie zawiera cykli, ale po dodaniu dowolnej nowej krawędzi otrzymujemy graf

z dokładnie jednym cyklem.

Grafy platońskie

A

A

A

A

B

D

C

B

D

C

B

D

C

B

D

C

Drzewa o wierzchołkach zaetykietowanych

Liczba drzew zaetykietowanych o n wierzchołkach

(n2)

wynosi

n

n-2

.

A

A

B

D

C

B

D

C

C

A

B

D

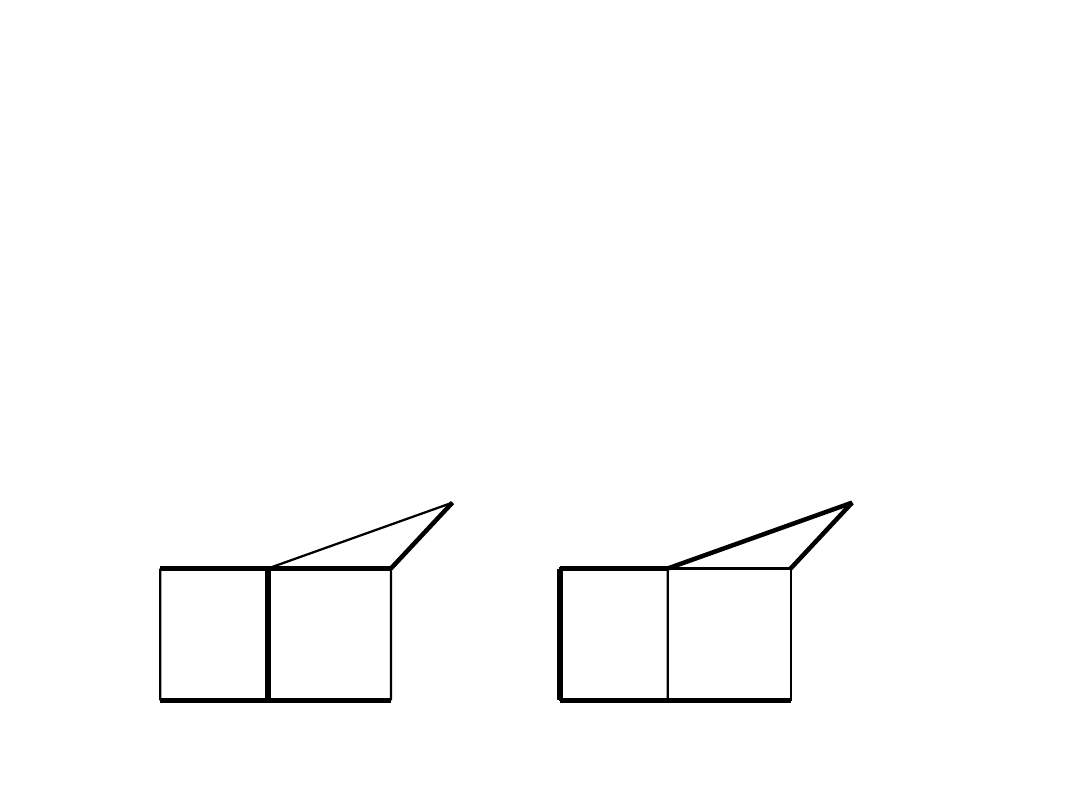
Łatwo zauważyć, że liczba drzew niezaetykietowanych o czterech
wierzchołkach wynosi 2.

Dendrytem grafu spójnego G nazywamy drzewo będące jego
podgrafem i zawierającym wszystkie wierzchołki grafu G.

Graf niespójny o k składowych ma las dendrytów składający się z k
drzew.

Każdy graf spójny ma przynajmniej jeden dendryt.

Cięciwą nazywamy krawędź grafu G która nie należy do danego
dendrytu.

Przykład

REPREZENTACJE MACIERZOWE

Macierz sąsiedztwa

A

(n x n)

,

Macierz incydencji

M

(n x m)

grafu o n wierzchołkach i m krawędziach

a

i,j

- liczba krawędzi łączących wierzchołek „i” z wierzchołkiem „j”

m

i,j

= 1 jeśli i-ty wierzchołek jest incydenty z j-tą krawędzią

3 b
4

1 a
2

c d
e

m

i,j

= 0 w przeciwnym wypadku

1 2 3

4

1

0 1

1 0

2

1 0

1 1

A =

3

1 1 0 1

4

0 1 1 0

a b

c d e

1

1 0 1 0 0

2

1 0 0 1 1

M =

3

1 1 1 0 0

4

0 1 0 0 1

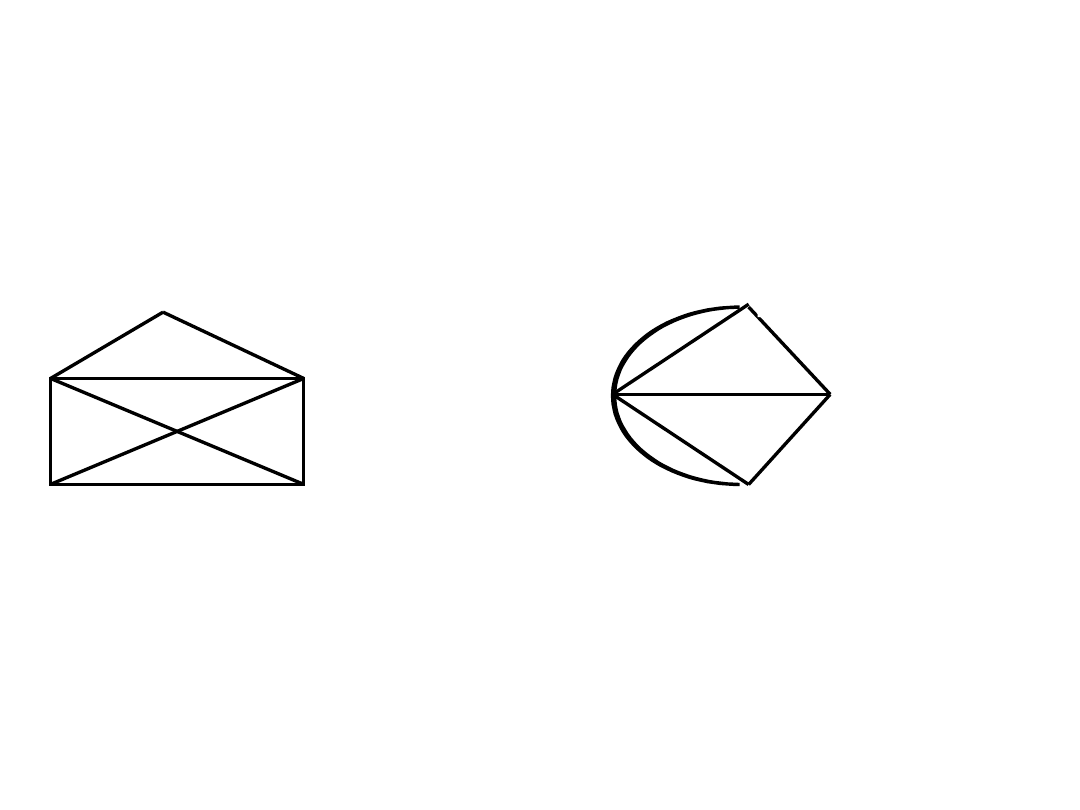
Grafy Eulera (przechodzenie przez krawędzie)

Grafem Eulera nazywamy graf składający się z drogi Eulera.

Drogą Eulera nazywamy drogę zamknięta przechodzącą dokładnie jeden raz
przez każdą krawędź z grafu G.

Graf jest grafem Eulera wtedy i tylko wtedy gdy wszystkie wierzchołki G są
stopnia parzystego.

A

D

C

B

Graf spójny mający dokładnie dwa wierzchołki
stopnia

nieparzystego, ma drogę Eulera

.

Obwód Hamiltona (przechodzenie przez wierzchołki)

Obwodem Hamiltona w grafie spójnym jest droga zamknięta. Która przechodzi

przez każdy wierzchołek grafu G dokładnie jeden raz.

Obwód Hamiltona w grafie o n wierzchołkach składa się z n
krawędzi.

Problem komiwojażera.

Całkowita liczba różnych obwodów

Hamiltona w grafie pełnym o n wierzchołkach:
(n-1)/2!

Grafy planarne

Graf planarny to graf który można narysować na płaszczyźnie bez przecięć – to

znaczy tak aby, żadne dwie krawędzie nie przecinały się na rysunku poza

wierzchołkiem z którym są incydentne.

Grafy

K

3,3

i

K

5

są nieplanarne.

Dany graf G jest planarny wtedy i tylko wtedy gdy nie zawiera

podgrafu homeomorficznego z grafem K

3,3

i K

5

.

Dany graf G jest planarny wtedy i tylko wtedy gdy jest ściągalny

do podgrafu K

3,3

lub do podgrafu K

5

.

Problem
kolorowania

Shell

Esso

Gulf

BP

Shell

lub

Gulf

Graf jest k - kolorowalny jeżeli każdemu wierzchołkowi można przypisać jeden z k

kolorów, w taki sposób że żadne dwa wierzchołki sąsiednie nie mają tego samego

koloru.

W Y K Ł A D - 6

Elementy teorii grafów
- przeszukiwanie grafów
- algorytmy na grafach (zadania najkrótszych dróg): algorytm Fleury’go,
algorytm Kruskala, algorytm
Prima, algorytm Dijkstry
(Ross K.A., Wright C.R.B., Matematyka dyskretna, PWN, Warszawa 1996.)

Problem wyznaczania najkrótszej trasy: znaleźć taka ścieżkę, prowadzącą od węzła i

do węzła j, by suma wartości przebywanych połączeń była jak najmniejsza. Wyznacz

najkrótsza ścieżkę łączącą węzły A i J.

PRZESZUKIWANIE GRAFÓW (metoda podziału i ograniczeń)

Dane są naczynia o pojemności odpowiednio 4 i 3 litra. Czy można z ich pomocą

odmierzyć pojemność 2 litrów? Wszystko to przy założeniu, że naczynia te nie są

cechowane, a możliwe działania obejmują nalewanie do pełna (bądź opróżnianie)

lub przelewanie z jednego naczynia do drugiego.

A

J

Algorytm Dijkstry

Jaka jest długość najkrótszej drogi łączącej dwa wierzchołki w danym grafie

skierowanym? Jeśli graf skierowany ma wagi, to jaka jest waga minimalna

lub maksymalna takiej drogi?)

Przykład

v

2

7

v

4

2

v

6

3 7 9

v

1

2 5 4

9

1 8

v

3

4 v

5

v

7

ALGORYTMY NA GRAFACH

Algorytm Fleury’go (wyznaczanie drogi Eulera)

Niech ES – ciąg krawędzi drogi lub cyklu Eulera, VS – ciąg wierzchołków tej

drogi lub cyklu. Niech V(G) – zbiór wierzchołków, a E(G) – zbiór krawędzi

grafu G

1. Wybierz dowolny wierzchołek v nieparzystego stopnia, jeśli taki

istnieje. W przeciwnym przypadku wybierz dowolny wierzchołek v.

Niech VS = v i niech ES = .

2. Jeśli z wierzchołka v nie wychodzi już żadna krawędź, zatrzymaj się.

3. Jeśli pozostała dokładnie jedna krawędź wychodząca z wierzchołka v ,

powiedzmy krawędź e z wierzchołka v do w, to usuń e z E(G) oraz

v z V(G) i przejdź do kroku 5.

4. Jeśli została więcej niż jedna krawędź wychodząca z wierzchołka v ,

wybierz krawędź, powiedzmy e z v do w , po usunięciu której graf

pozostanie spójny, następnie usuń e z E(G).

5. Dołącz w na końcu ciągu VS, dołącz e na końcu ciągu ES, zastąp v

wierzchołkiem w i przejdź do kroku 2.

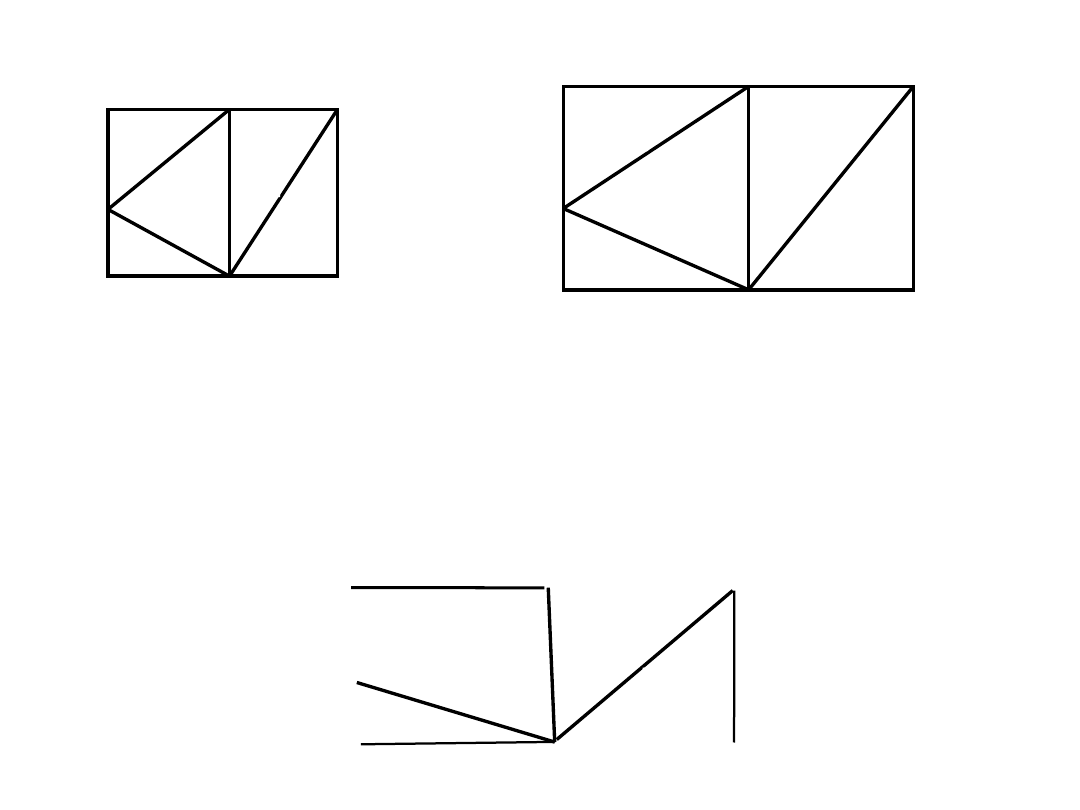
Algorytm Fleury’go (wyznaczanie drogi Eulera)

Algorytm Kruskala (minimalne drzewo spinające)

Dane: skończony graf spójny G z wagami, którego krawędzie są uporządkowane

według wzrastających wag.

Wyniki: zbiór E krawędzi minimalnego drzewa spinającego grafu G

Niech E:= .

Dla j = 1 do |E(G)|

Jeśli graf E  {e

j

} jest acykliczny, to dołącz e

j

do E.

Przykład

2

5

3

3

5

5

5

3

4

1

5

2

e

8

e

9

e

7

e

8

e

4

e

5

e

6

e

2

e

1

e

10

e

3

e

11

Wagi krawędzi W(e

i

) mają tworzyć ciąg niemalejący, tzn. W(e

i

) < W(e

j

) dla i <

j , zatem:

e

1

2

5

3

3

5

5

5

3

4

1

5

2

e

8

e

9

e

7

e

8

e

4

e

5

e

6

e

2

e

1

e

10

e

3

e

11

e

1

e

2

e

3

e

4

e

5

e

6

e

7

e

8

e

9

e

10

e

11

1 2 2 3 3 4 5 5 5 5 5

e

7

e

3

e

5

e

6

e

2

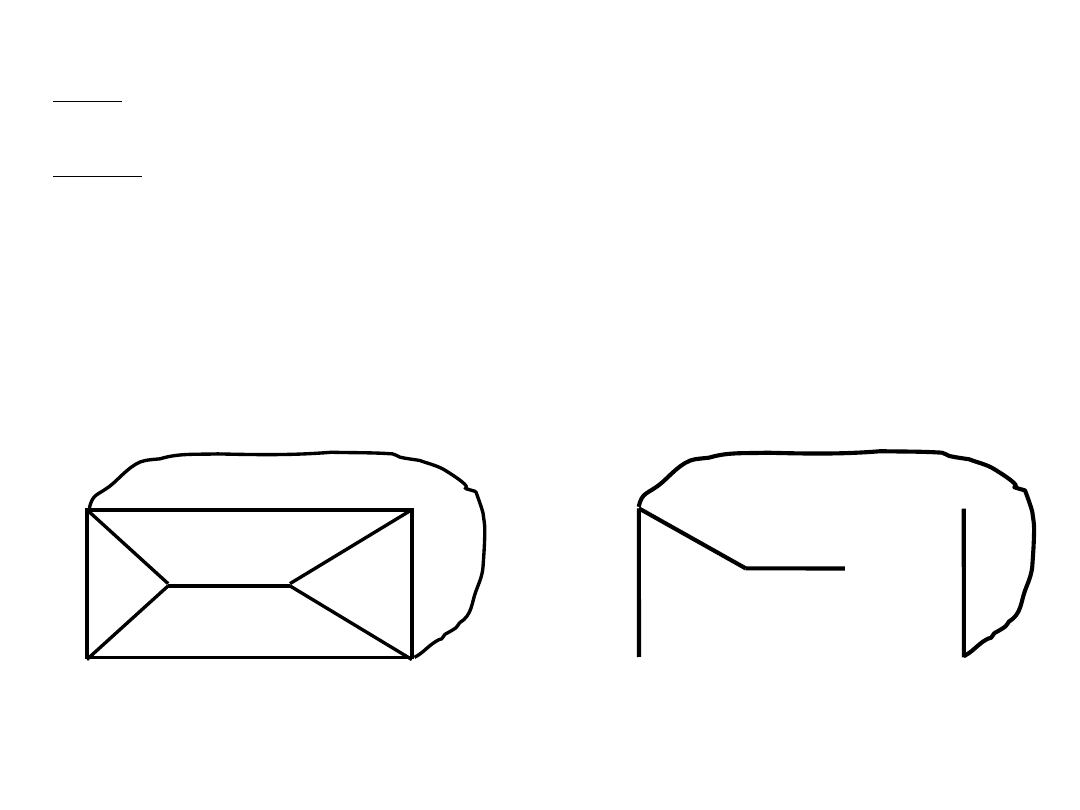
Algorytm Prima (minimalne drzewo spinające)

Dane: skończony graf spójny G z wagami (z krawędziami wypisanymi w

dowolnym porządku)

Wyniki: zbiór E krawędzi minimalnego drzewa spinającego grafu G

Niech E:= .

Wybierz w ze zbioru V(G) i niech V := {w}

Dopóki V  V(G), wykonuj

wybierz w zbiorze E(G) krawędź (u,v) o najmniejszej możliwej wadze, taką że

u  V i

v  V(G) \ V dołącz krawędź (u,v) do zbioru E i wierzchołek v do zbioru V.

2

b

3 1

d e

1

c

2

1

4

5

4

3

a

Algorytmy Prima i Kruscala są algorytmami zachłannymi, tzn.
algorytmami wybierającymi zawsze najmniejszą krawędź, która
należy dodać lub największą krawędź, którą należy odrzucić.

Przykład