Mechanika Pękania
Zadanie nr 2
Kaproń Damian
Orman Sławomir
Gr. P
Treść zadania
Współczynnik intensywności naprężeń dla elementów o skończonej
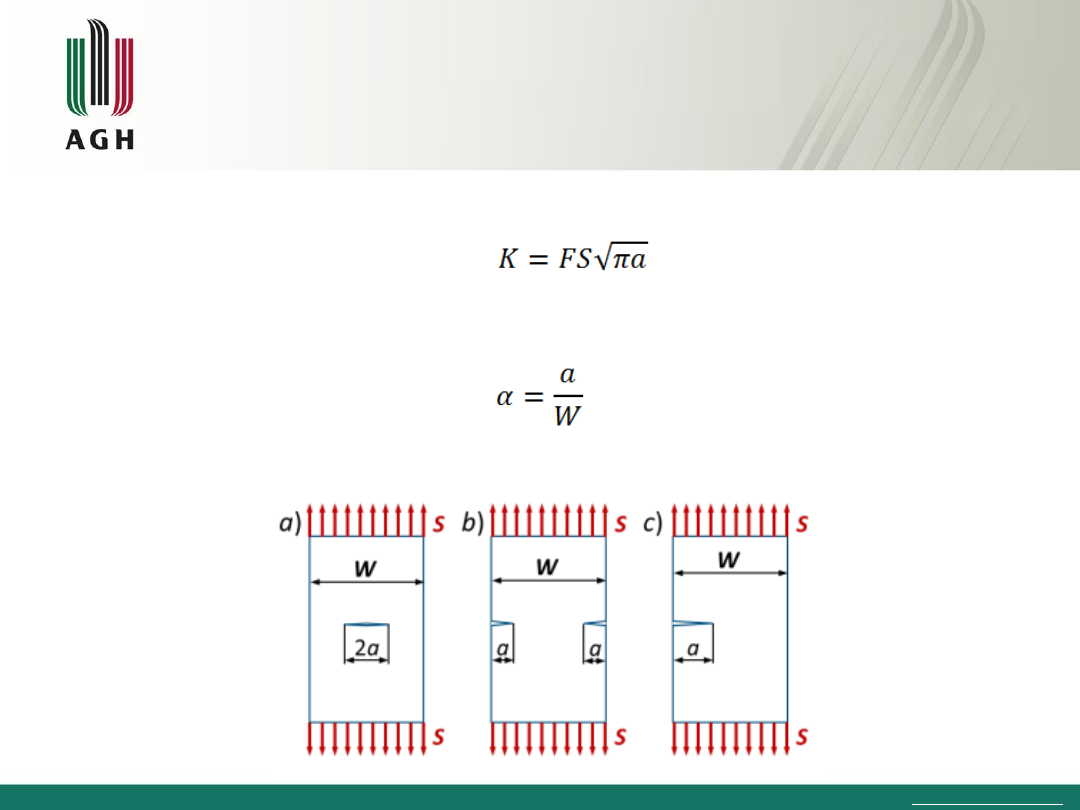
geometrii określić można jako:
Wykorzystując wzory podane na wykładzie, wykreślić na zbiorczym
wykresie zależność współczynnika korekcyjnego geometrii F w funkcji
stosunku:
dla trzech geometrii pęknięcia pokazanych na poniższych rysunkach.
Współczynnik intensywności naprężeń
K
(i)
Współczynnik intensywności naprężeń jest podstawowym
parametrem LSMP, który jednoznacznie określa stan naprężenia
przed frontem pęknięcia.
Gdzie:
i – I, II, III (sposób pękania),
jk – x,y,z (płaszczyzny pęknięcia).
Współczynnik intensywności naprężeń
K
(i)
K
(i)
zależy od:
•
geometrii,
•
sposobu obciążenia,
•
wielkości obciążenia,
•
długości pęknięcia
a
Typowa forma przedstawienia :
gdzie:
S – naprężenie w przekroju pęknięcia,
F – funkcja bezwymiarowa zależna od geometrii, sposobu obciążenia oraz
stosunku a/W,
a – długość pęknięcia,
W – wymiar geometryczny na kierunku pęknięcia np. szerokość próbki
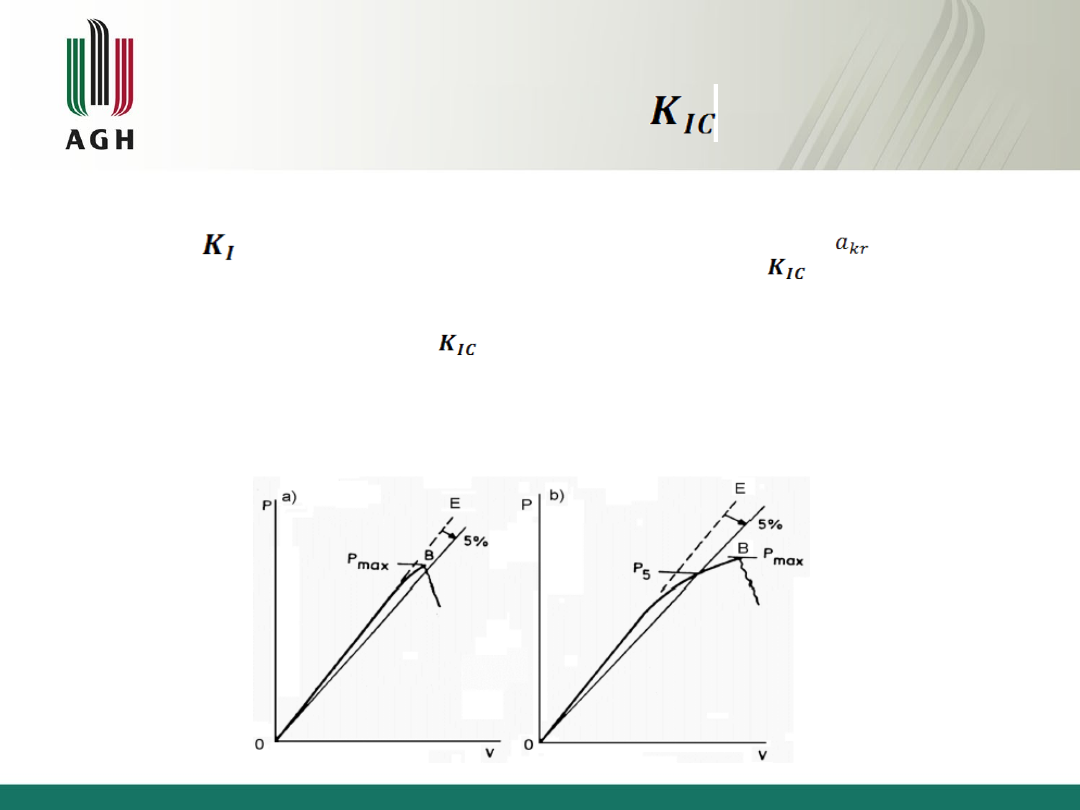
Odporność na pękanie
W określonych warunkach pomiarów współczynnik intensywności
naprężeń , przy którym pęknięcie osiąga wymiar krytyczny , jest stałą
materiałową; nosi ona nazwę odporności na pękanie,
Procedura wyznaczania :
1) Badanie zmęczeniowe przy stałej amplitudzie obciążenia, aż do wytworzenia
pęknięcia zmęczeniowego o określonej dł. a,
2) Rozciąganie statyczne
Odporność na pękanie
Po badaniu następuje obliczanie krytycznej wartości współczynnika
intensywności naprężeń:
Wyniki badań:
1. Jeżeli wartość spełnia warunek PSO to
2. Jeżeli wartość nie spełnia warunku PSO, ale spełnia warunek LSMP, to
, gdzie jest odpornością na pękanie zmierzoną w
warunkach PSN,
3. Jeżeli nie spełnia tych dwóch warunków to pomiar jest nieważny.
Warunek PSO Warunek LSMP
Współczynnik intensywności naprężeń
K
(i)
a) Próbka M(T) – dla
b) Próbka DE(T) - dla
b) Próbka SE(T) –
dla
Współczynnik korekcyjny geometrii F
a) Próbka M(T) – dla
b) Próbka DE(T) - dla
b) Próbka SE(T) – dla
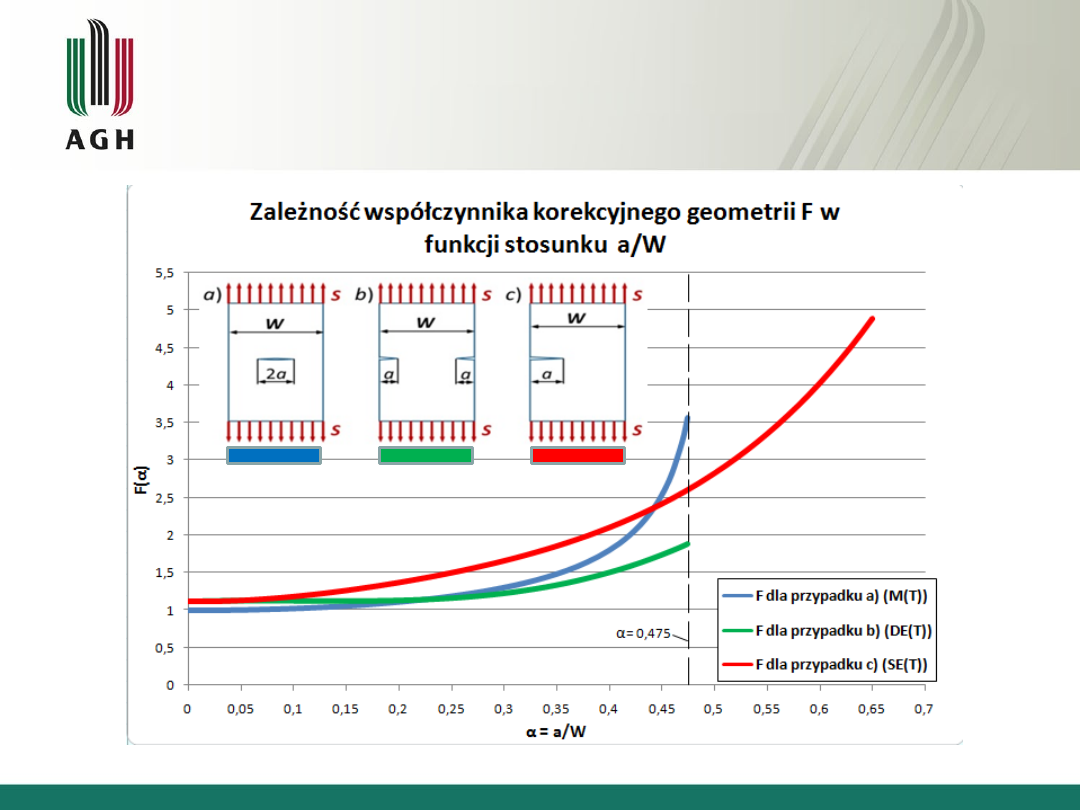
Zależność współczynnika korekcyjnego
geometrii F w funkcji stosunku a/W