Wykres momentu

zginającego

i reakcje w belce zginanej

Marek Dąbrowski

Politechnika Warszawska, Wydział

SiMR

grupa 2.1 mgr, nr indeksu 222143

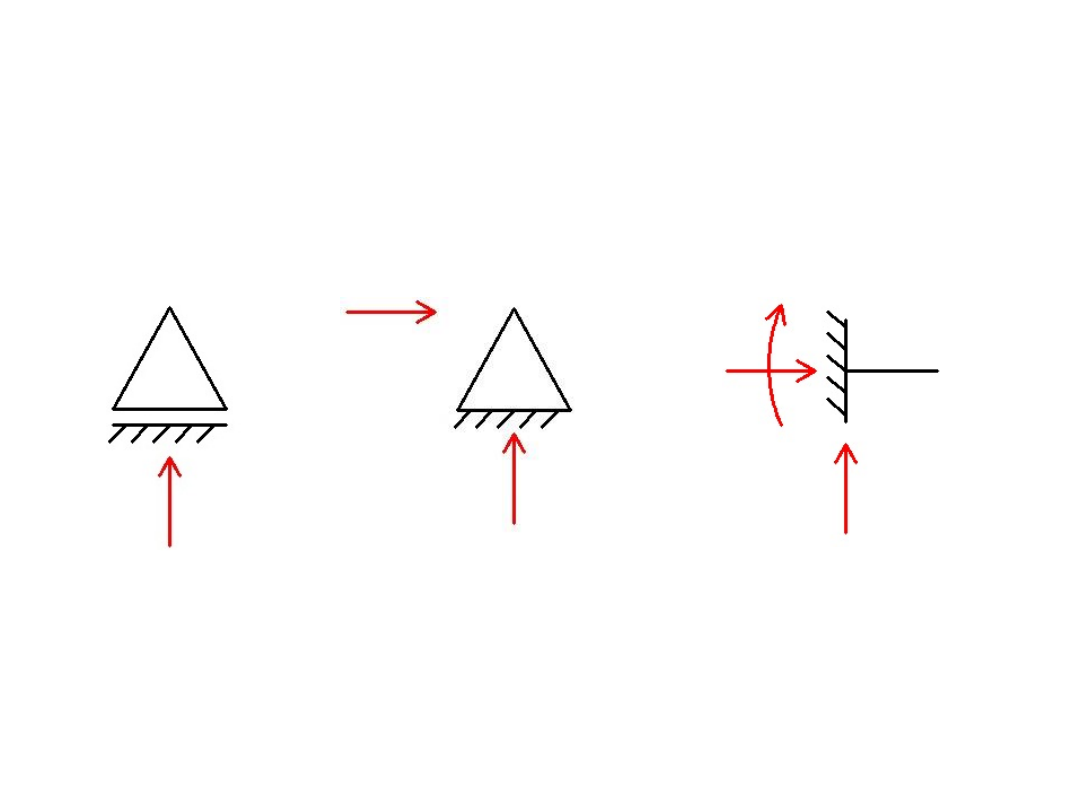
Reakcje w podporach

Podpora
przegubowo
przesuwna

Powstaje jedna
reakcja
(pionowa)

Podpora
przegubowo
nieprzesuwna

Powstają dwie
reakcje
(pionowa
i pozioma)

Utwierdzenie
stałe

Powstają trzy
reakcje
(pionowa,
pozioma i
moment)

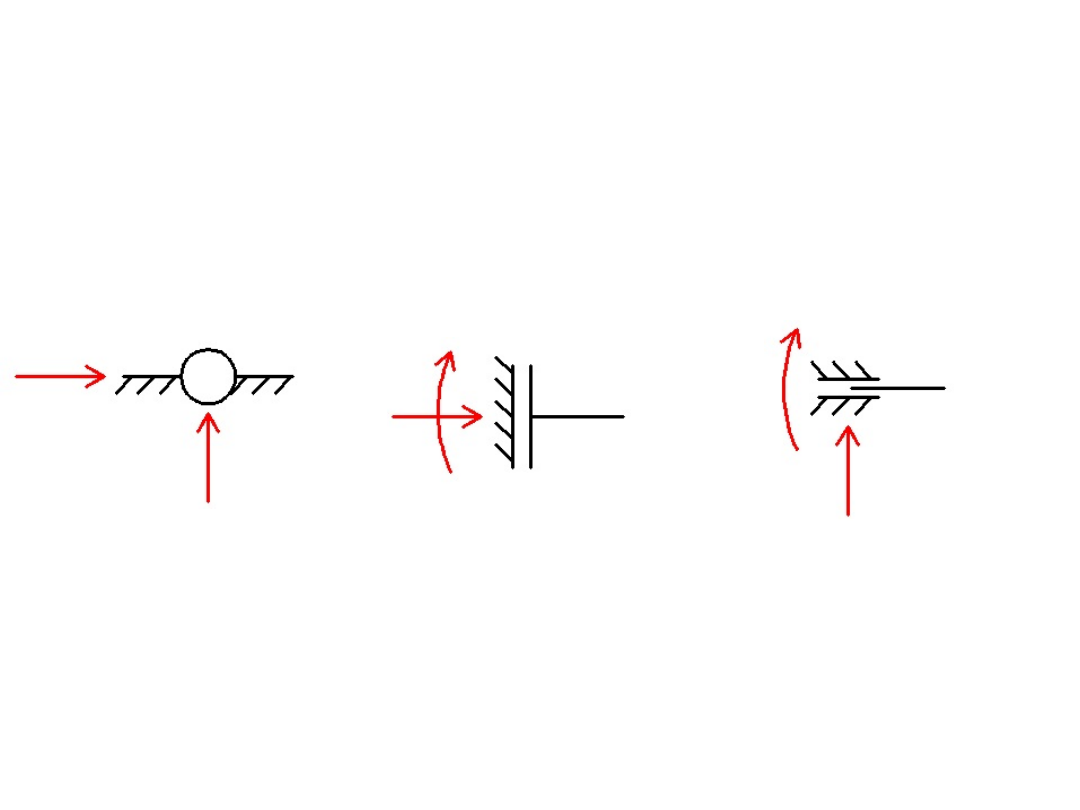
Reakcje w podporach

Przegub

Powstaje dwie
reakcje
(pionowa i
pozioma)

Łyżwa
pionowa

Powstają dwie
reakcje
(pozioma i
moment)

Łyżwa
pozioma

Powstają dwie
reakcje
(pionowa i
moment)

Wykres momentu gnącego –

tok obliczeń

1.Liczymy reakcje w podporach (z

równań statyki)

2.Dzielimy belkę na przedziały

(granice przedziałów ustalamy w
miejscu przyłożenia siły, momentu lub
reakcji oraz na początku i końcu
obciążenia ciągłego)

3. Dla każdego przedziału sporządzamy

równanie momentu gnącego

4. Podstawiamy wartości liczbowe

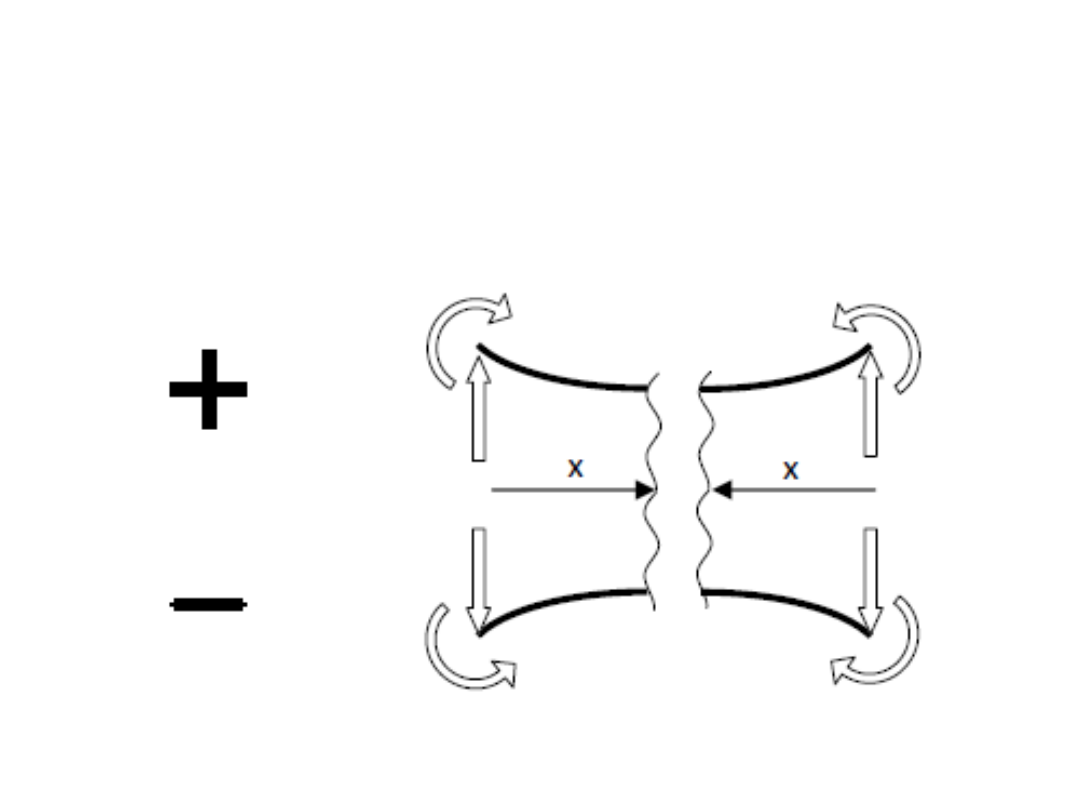
Wykres momentu gnącego –

umowa dot. znaku

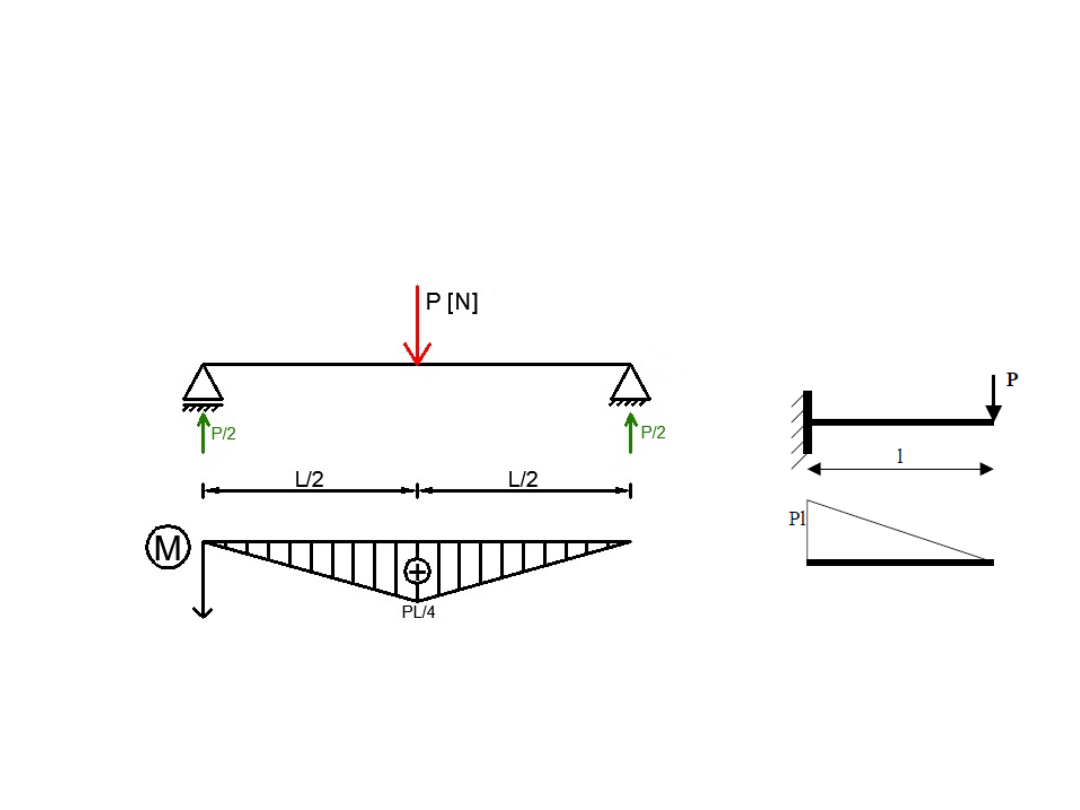
Wykres momentu

zginającego

1. Siła skupiona

- Wykres momentu jest krzywą pierwszego stopnia (prosta)

- W miejscu przyłożenia siły na wykresie występuje załamanie

Wykres momentu

zginającego

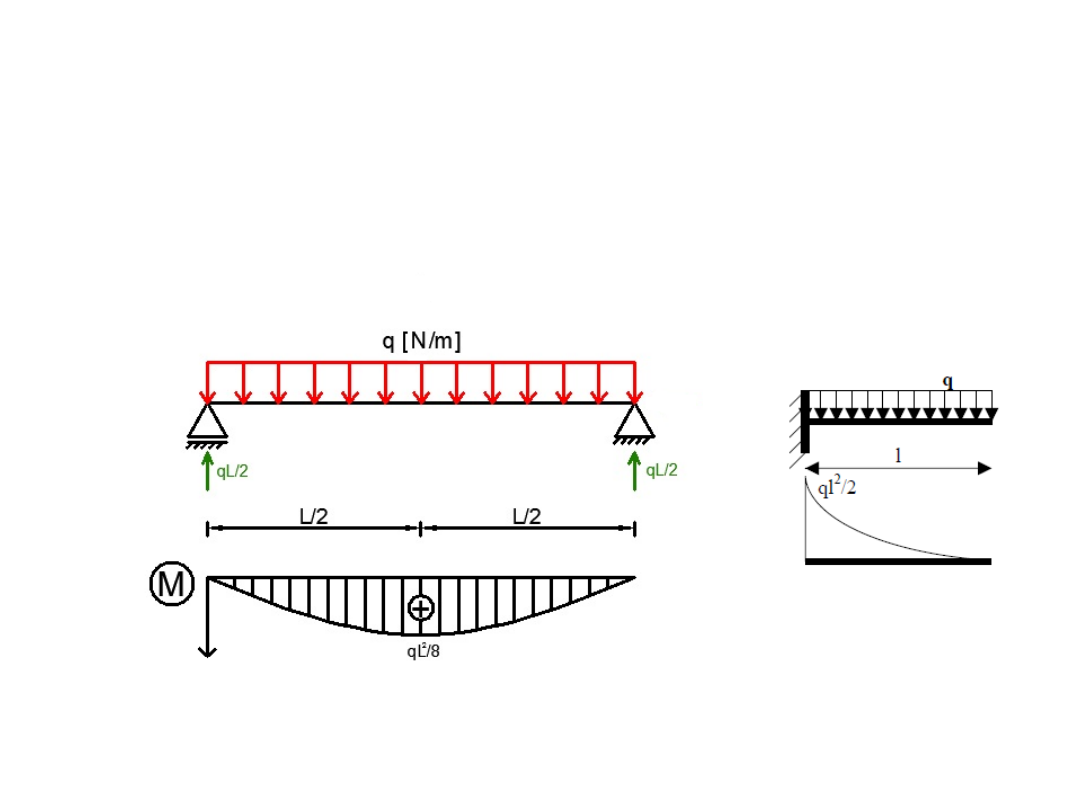
2. Obciążenie ciągłe

- Wykres momentu jest krzywą drugiego stopnia

Wykres momentu

zginającego

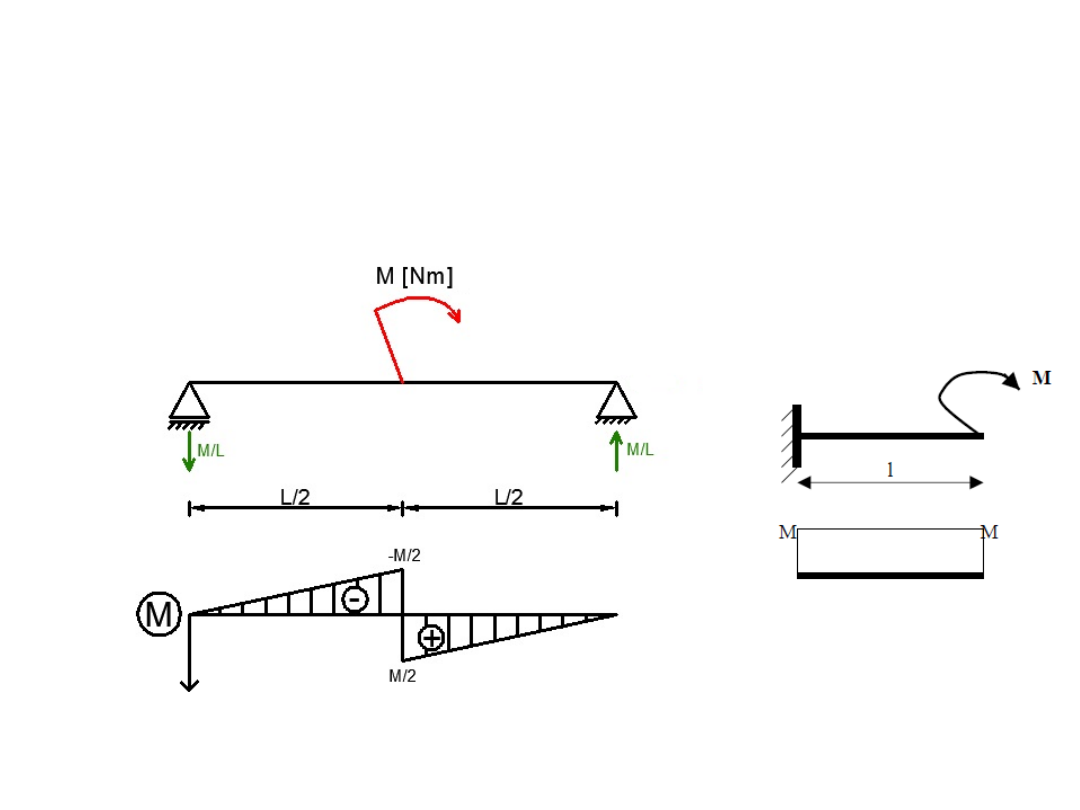
3. Moment skupiony

- W miejscu przyłożenia momentu skupionego na wykresie

występuje skok równy jego wartości

Belka statycznie

wyznaczalna

i statycznie

niewyznaczalna

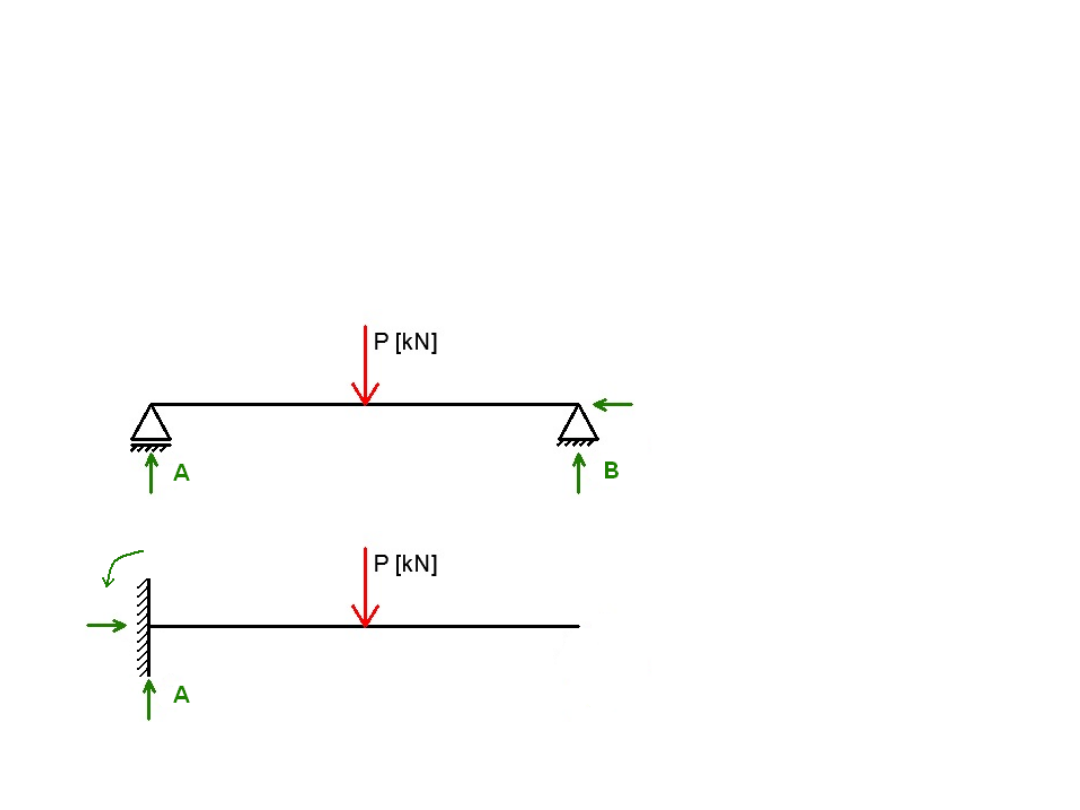
Belka statycznie

wyznaczalna

Liczba niewiadomych reakcji jest równa liczbie

równań równowagi

Równania równowagi – 3
ΣF

x

, ΣF

y

, ΣM

Niewiadome reakcje – 3
R

Ay

, R

Bx

, R

By

Równania równowagi – 3
ΣF

x

, ΣF

y

, ΣM

Niewiadome reakcje – 3
R

Ay

, R

Ax

, M

A

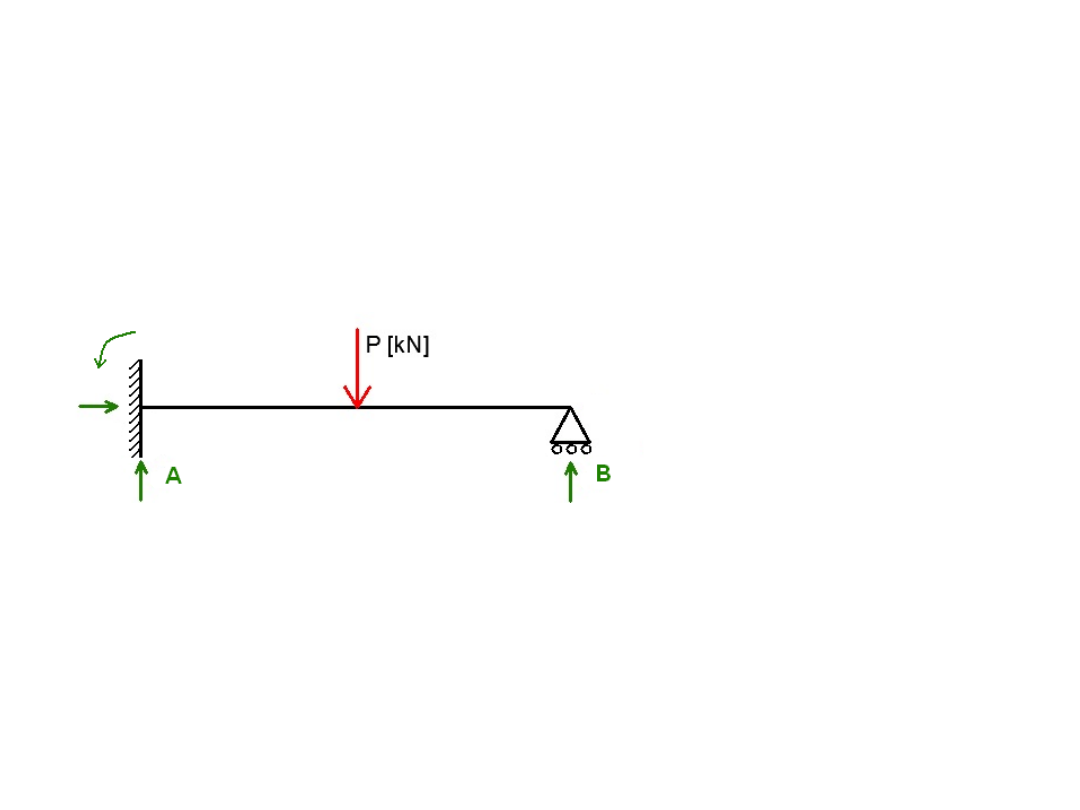
Belka statycznie

niewyznaczalna

Siły reakcji w niej występujące nie dają się wyliczyć

wyłącznie przy pomocy równań równowagi

Równania równowagi – 3
ΣF

x

, ΣF

y

, ΣM

Niewiadome reakcje – 4
M

a

, R

ay

, R

bx

, R

by

Krotność statycznie niewyznaczalnej belki:

N = l

r

– 3 (l

r

– liczba nieznanych reakcji)

(powyżej belka jednokrotnie statycznie

niewyznaczalna)

Belka statycznie

niewyznaczalna

Metody rozwiązywania takich zadań to

m.in.:

1. Metoda sił

2. Metoda przemieszczeń

3. Metoda superpozycji

4. Metoda trzech momentów

5. Metoda Menabrei

Metoda sił

Metoda polegająca na rozwiązywaniu

układu statycznie wyznaczalnego

(układ podstawowy), który powstaje

z układu niewyznaczalnego przez

wprowadzenie niewiadomych sił w

miejsce odrzuconych więzów

Metoda sił – algorytm

1. Określamy krotność statycznie

niewyznaczalnej belki

2. Usuwamy nadliczbowe więzy układu

rzeczywistego

3. Wprowadzamy siły uogólnione
(nadliczbowe niewiadome) w miejsce

usuniętych więzów

4. Układamy i rozwiązujemy równania

kanoniczne metody sił

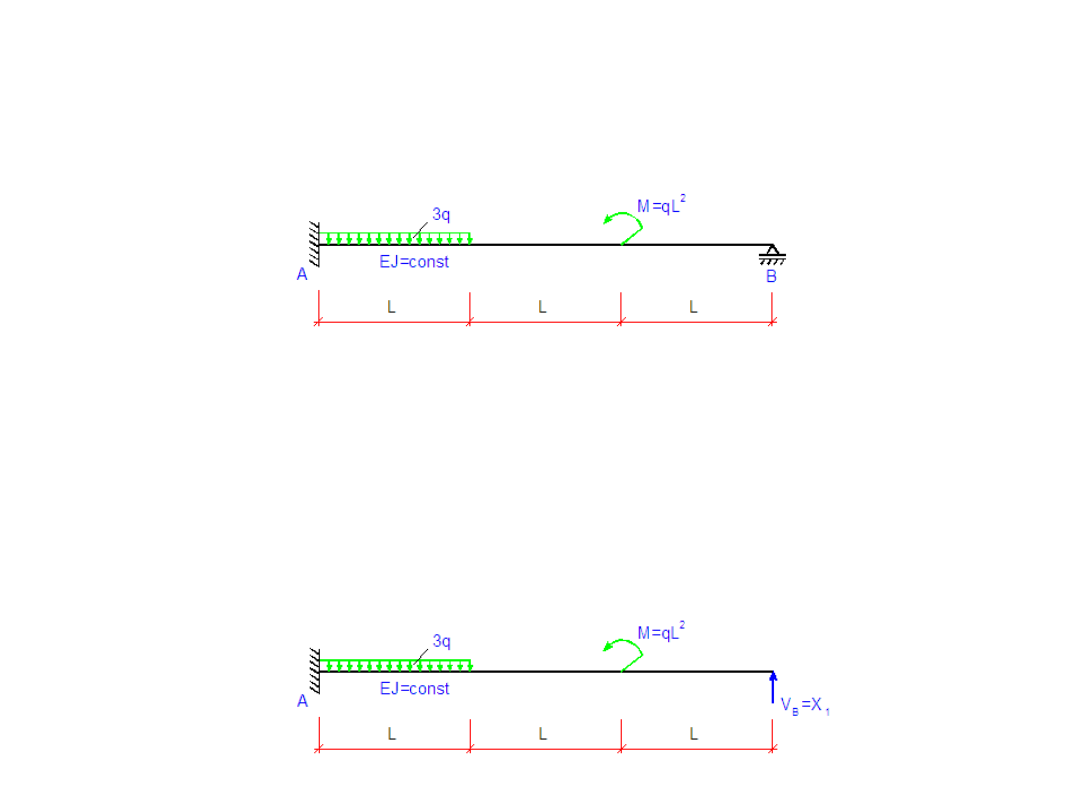
Metoda sił – przykład

Przykładowa belka jest układem

jednokrotnie statycznie

niewyznaczalnym. Usuwamy

nadliczbowy więz podporowy i

zastępujemy go siłą X

1

(układ

podstawowy)

Metoda sił – przykład

Sporządzamy wykresy momentu

gnącego dla układu podstawowego

obciążonego siłami zewnętrznymi i

siłą X

1

=1

Wykres momentu gnącego od
obciążenia zewnętrznego

Wykres momentu gnącego od
siły X

1

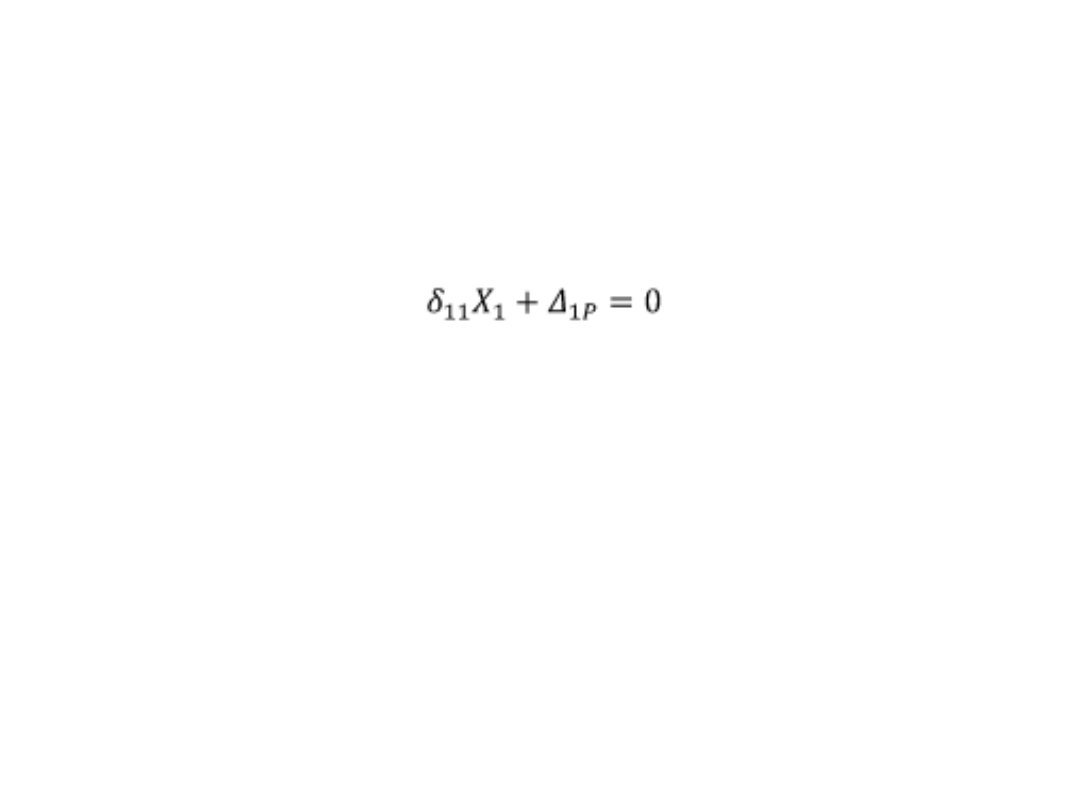
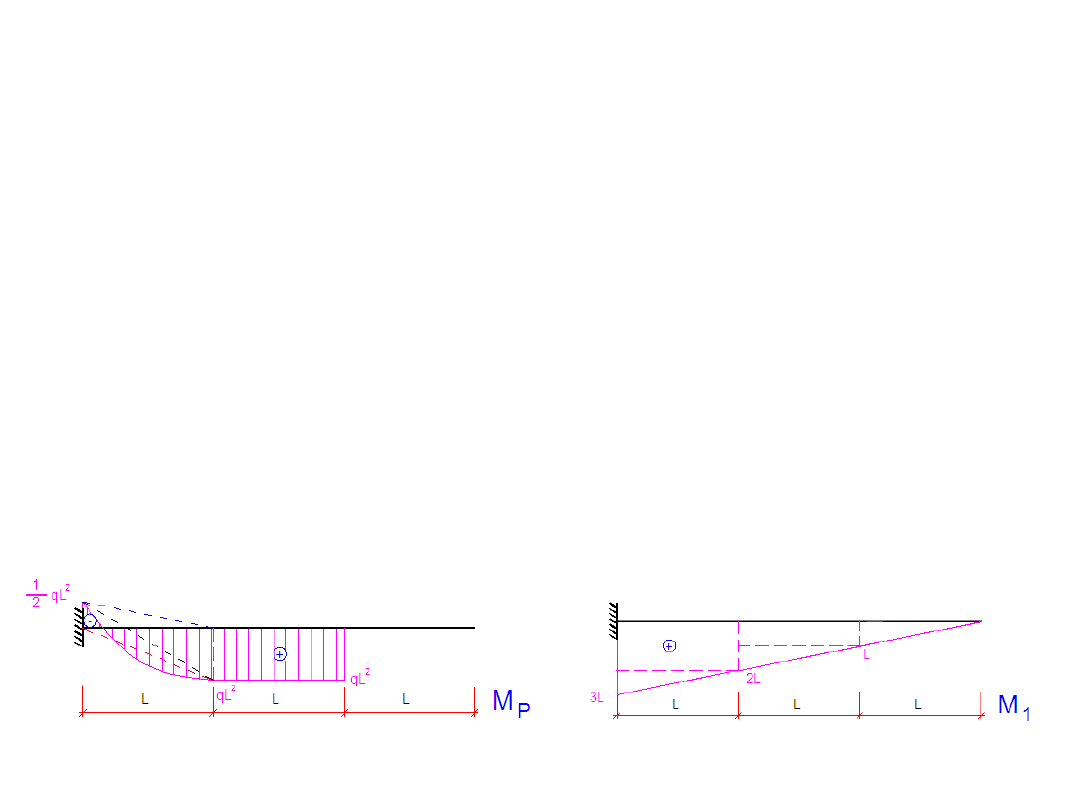
Metoda sił – przykład

Równanie kanoniczne metody sił:

gdzie: δ

11

– przesunięcie lub obrót na

kierunku działania siły o wartości X

1

pod wpływem obciążenia układu
podstawowego siłą X

1

=1

Δ

1p

– przemieszczenie układu

podstawowego wzdłuż kierunku i pod
wpływem sił zewnętrznych

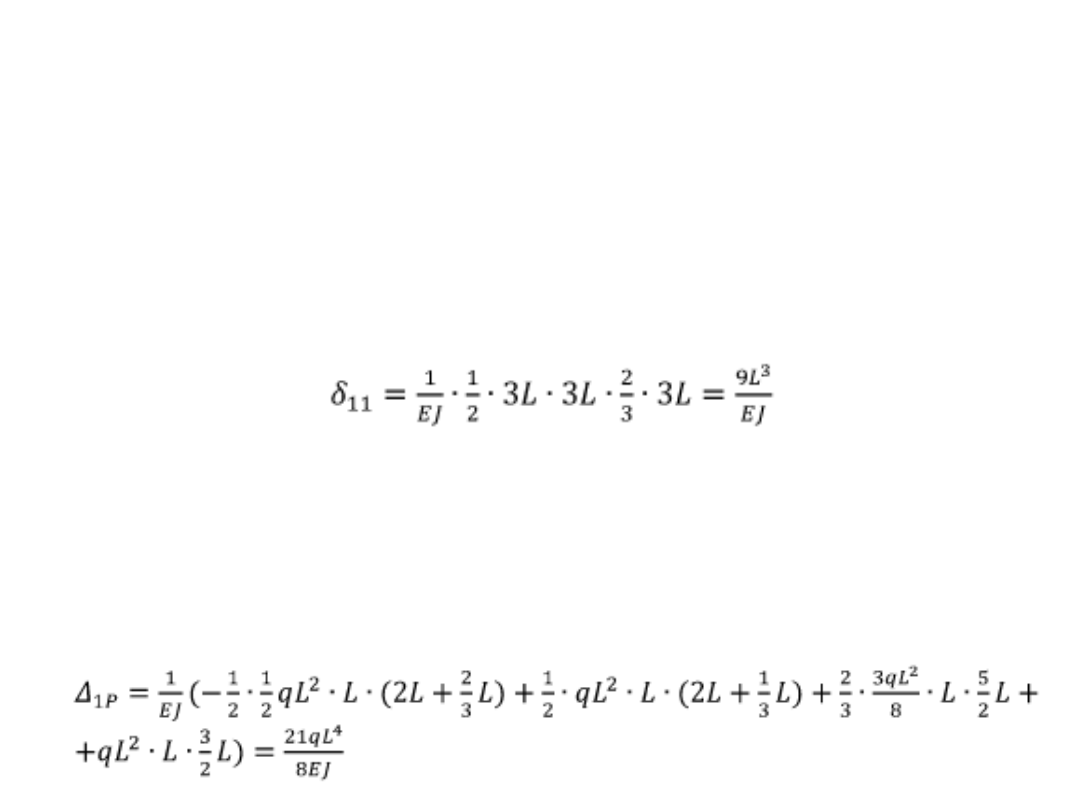
Metoda sił – przykład

Aby policzyć współczynnik δ

11

przemnażamy pole z wykresu M

1

z

wartością momentu dla środka

ciężkości tego wykresu

Aby policzyć współczynnik Δ

1p

przemnażamy pola z wykresu M

p

z

wartościami momentu na wykresie

M

1

dla środka ciężkości z wykresu M

p

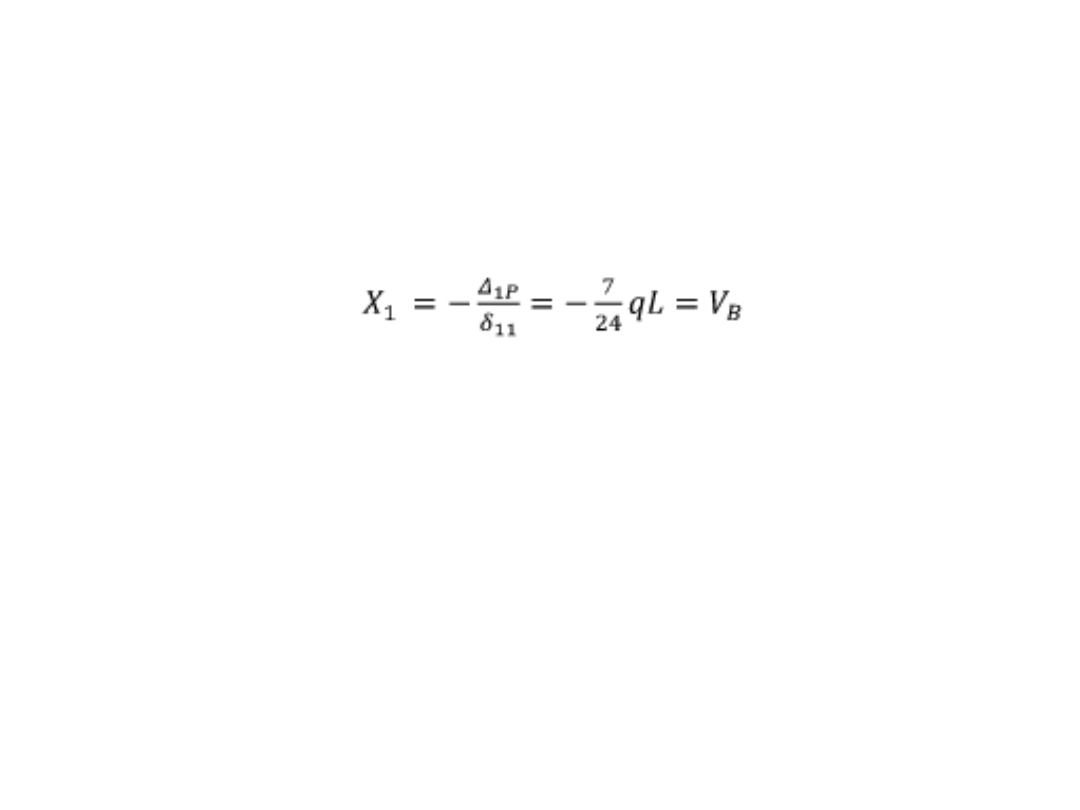
Metoda sił – przykład

Przekształcając wzór otrzymujemy:

Następnie liczymy pozostałe reakcje

korzystając z równań statyki i

działamy jak na układzie statycznie

wyznaczalnym

Dziękuję