Model liniowy Holt’a

Daria Karnicka

24 marca
2015r.

Co to właściwie jest?

Model liniowy Holt’a służy do wygładzania szeregu
czasowego, w którym wyróżniamy :

• trend (tendencję

rozwojową),

• wahania przypadkowe .

Wyróżniamy także dwa inne modele stosowane do wygładzania szeregu
czasowego ,tj.
Model Browna oraz Model Wintera (addytywny i multiplikatywny).

TREND

- (tendencja

rozwojowa) –
to długookresowa skłonność do jednokierunkowych zmian wartości
zmiennej prognozowanej, wzrostu lub spadku poziomu badanego
zjawiska w długim okresie czasu.

WAHANIA PRZYPADKOWE-

nieregularne i niecykliczne wahania, powodowane czynnikami
losowymi (np. wojna, klęska, strajki lub zmiany polityki państwa).

Przypomnienie pojęć.

Równania w modelu Holt’a.

Model ten składa się z dwóch równań rekurencyjnych:

I. Służy do wyznaczania wygładzonych wartości szeregu czasowego w

chwili t.

)

S

F

(

)

(

y

F

t

t

t

t

1

1

1





















II. Służy do wyznaczania wygładzonych wartości przyrostu trendu w
chwili t.

1

t

1

t

t

t

S

)

1

(

)

F

F

(

S





















gdzie:


α, β

∈ [0,1] - parametry wygładzania,

F

t

- odpowiada wygładzonej wartości  z prostego modelu

wygładzania wykładniczego (ocena wartości średniej na okres t ),

S

t

- wygładzony  przyrost trendu na  okres t.

W modelu Holt’a obliczamy zarówno

prognozy wygasłe

jak i

prognozy na przyszłe okresy

(tzw. rzeczywiste).

Prognozy wygasłe obliczamy wg
wzoru:

y

t

*

= F

t-1

+

S

t-1

dla t = 2, 3,…, n.

Prognozę na okres T>n wyznacza się ze
wzoru:

y

T

*

= F

n

+ (T – n)S

n

dla T = n +1, n + 2
itd.

gdzie n jest liczbą posiadanych
obserwacji.

Równania w modelu Holt’a.

Obliczanie prognoz w modelu
Holt’a.

Potrzebujemy początkowe wartości F

1

i S

1

. Na ich wyznaczenie

istnieją trzy sposoby:

F

1

=y

1

, S

1

= y

2

-y

1

F

1

=y

1

, S

1

= 0

F

1

= a

0

wyraz wolny liniowej funkcji trendu

,

S

1

=a

1

współczynnik kierunkowy liniowej funkcji trendu,

którą oszacowaliśmy na podstawie danych za pomocą metody
najmniejszych kwadratów

.

Prognoz
y.

Co z α i β?

Jak dobieramy parametry α i β?

Najczęściej przyjmuje się takie
wartości parametrów wygładzania α i
β aby wybrany błąd ex post prognoz
wygasłych służący do oceny modelu
przyjął wartość

minimalną

.

Przykład – SAS.

Zadanie.

Na podstawie danych z 15stu miesięcy dotyczących wielkości
sprzedaży w setkach sztuk w sklepie z artykułami kolekcjonerskimi
wyznaczyć prognozę na kolejny miesiąc.

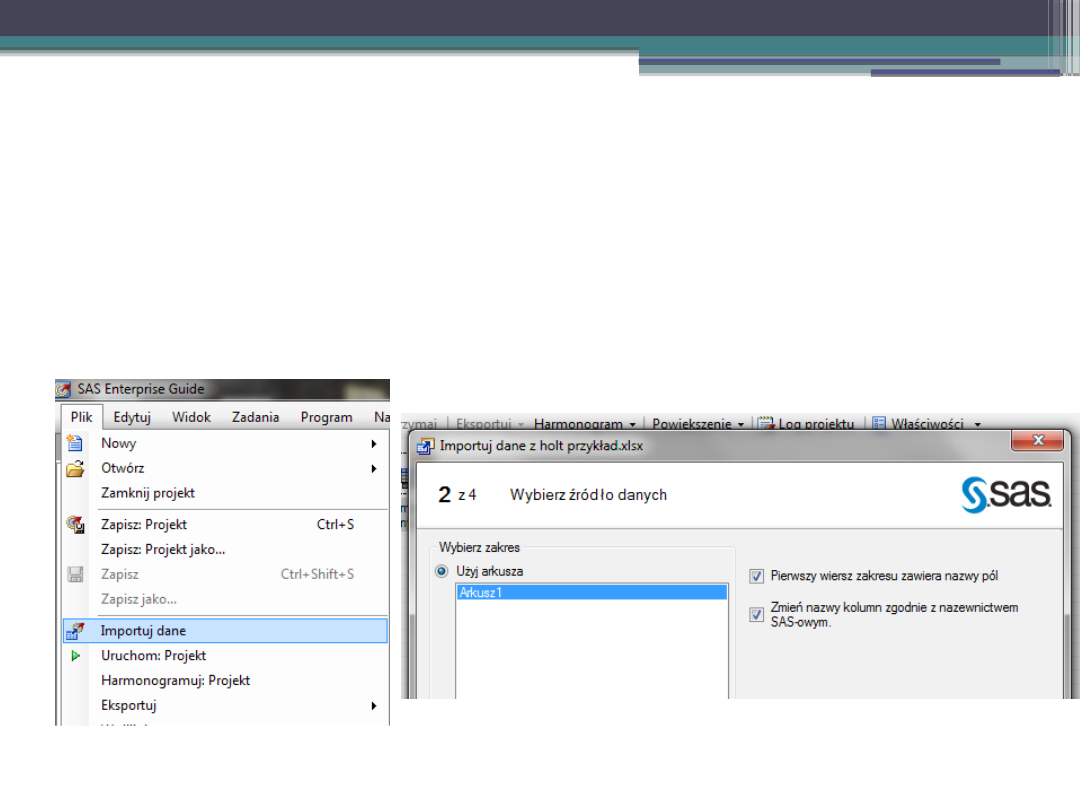
I. Import danych.

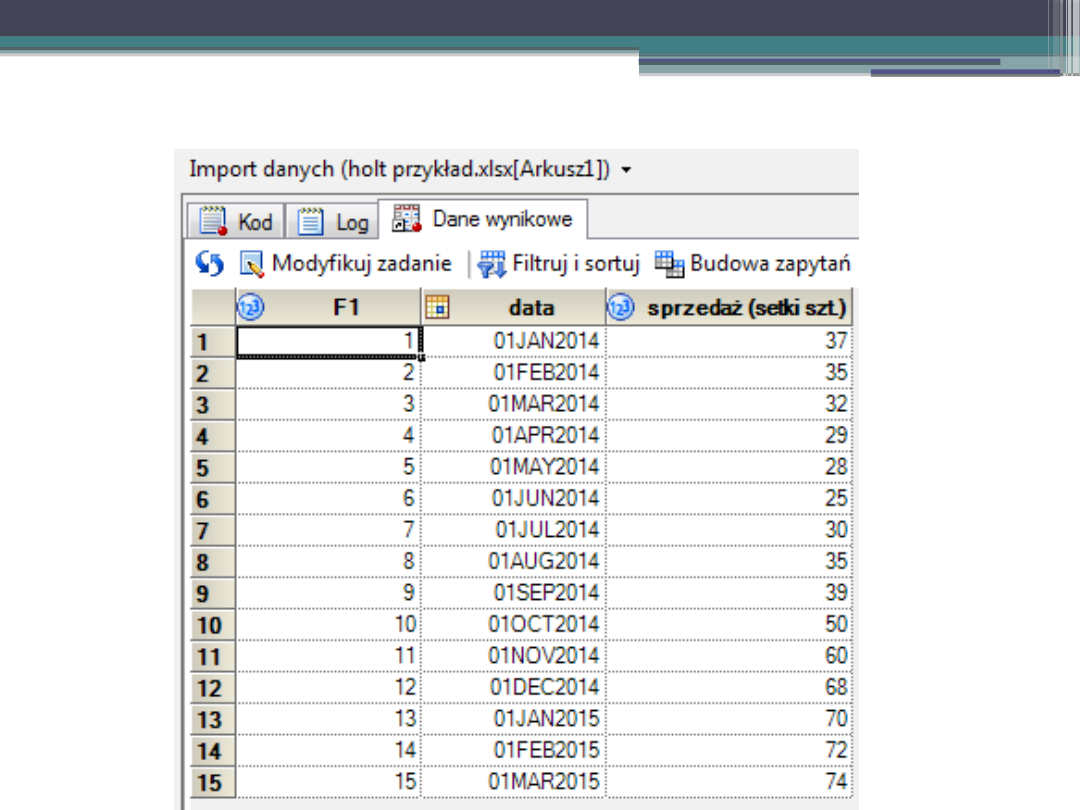
Dane: wielkość sprzedaży w setkach sztuk.

Przykład –
SAS.

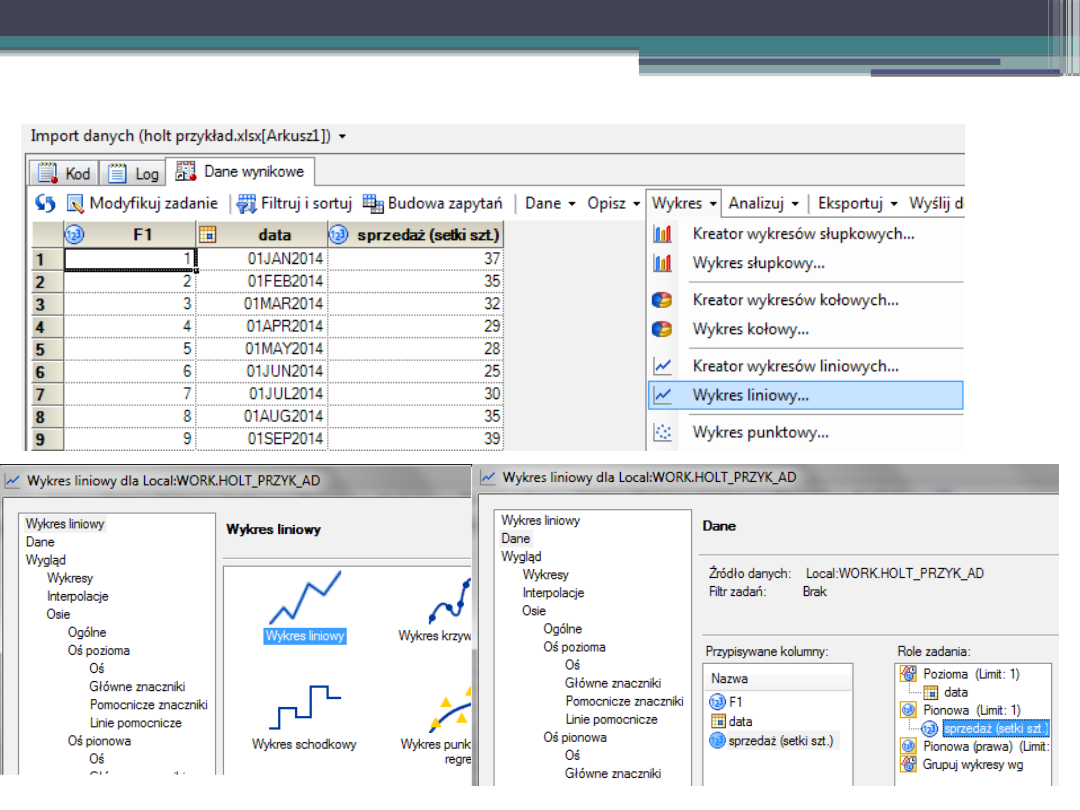
Przykład – SAS.

II. Tworzenie wykresu.

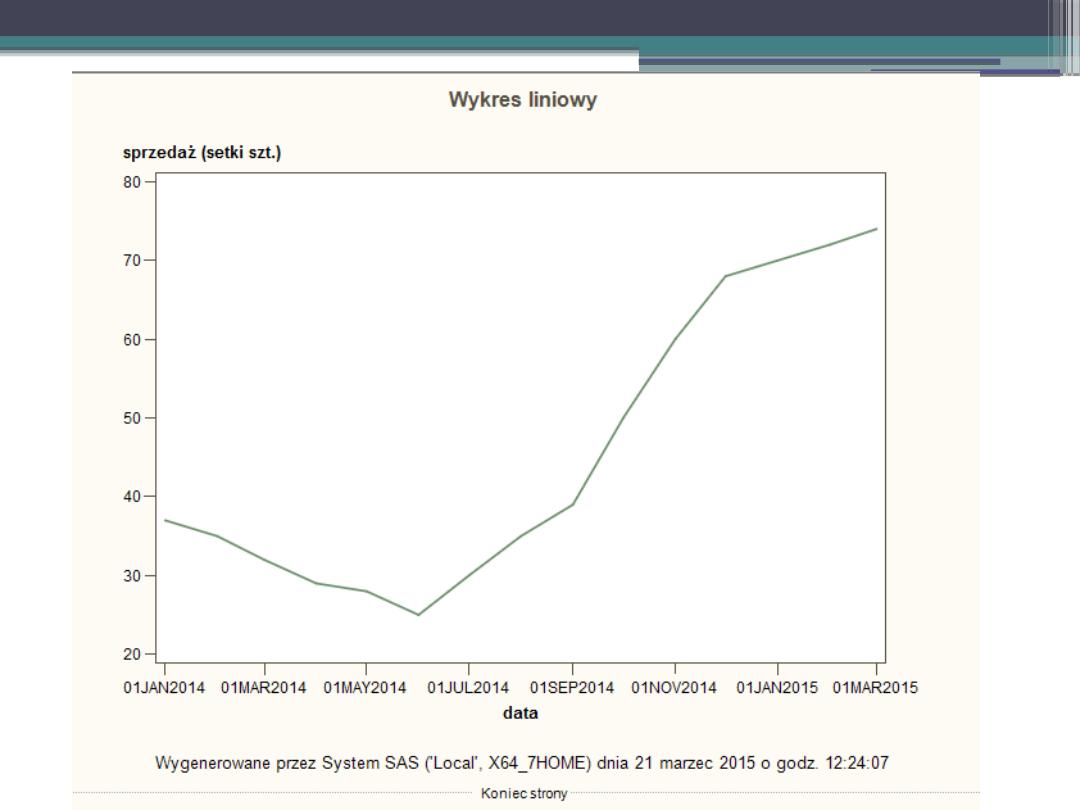
Przykład –
SAS.

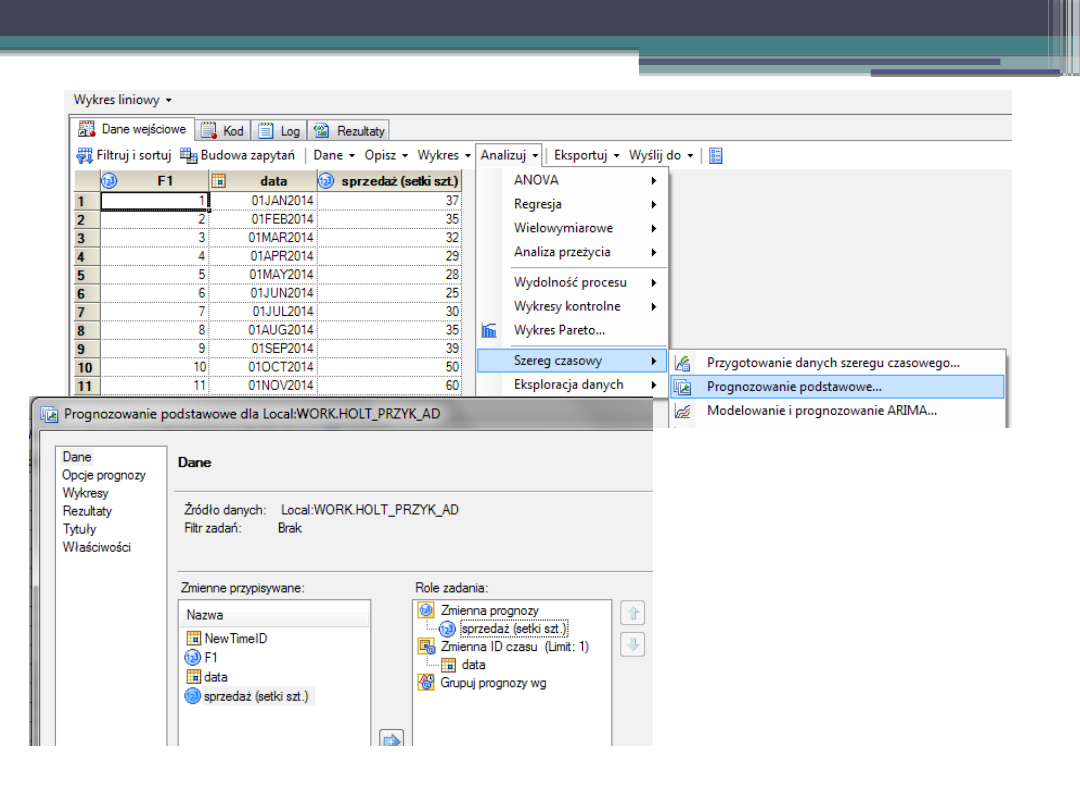
Przykład – SAS.

III. Prognozowanie.

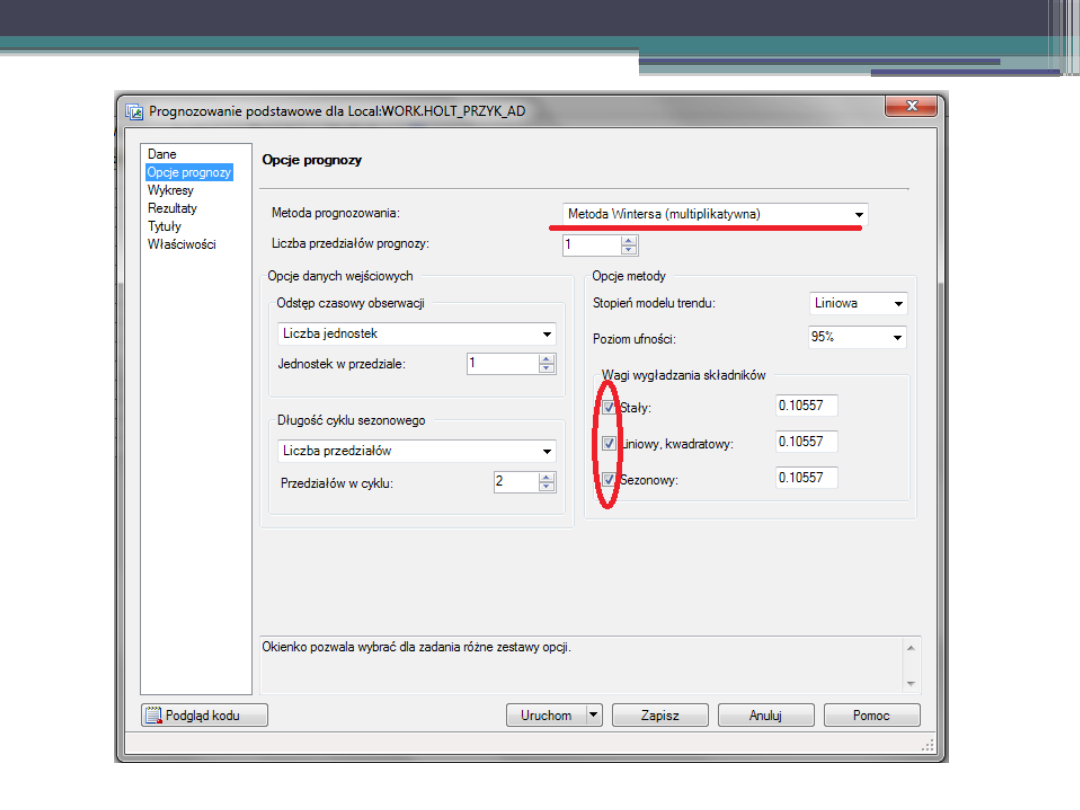
Przykład – SAS.

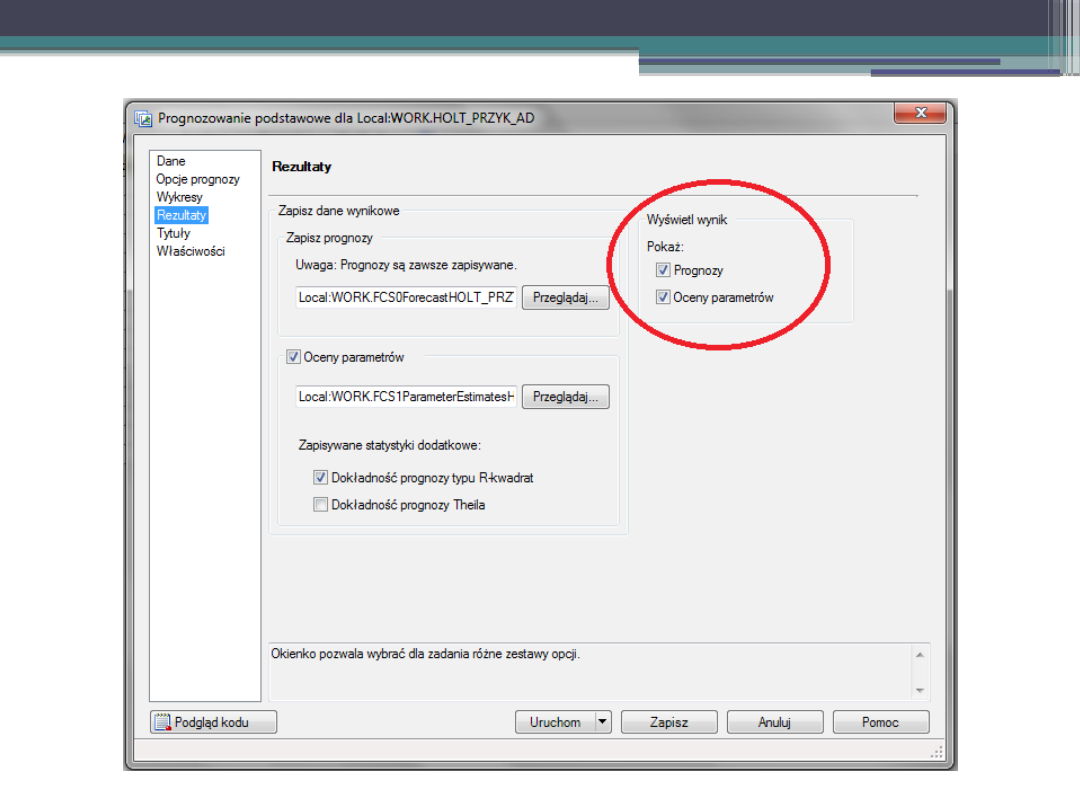
Przykład – SAS.

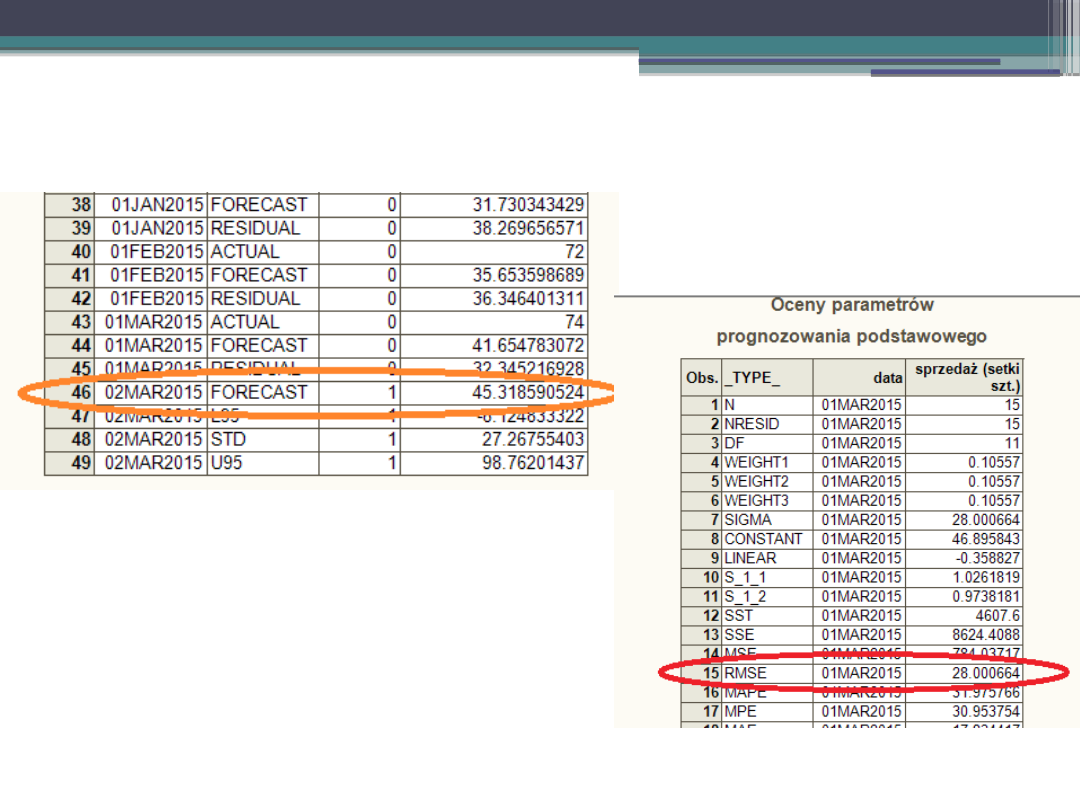
Przykład – SAS.

Prognozy otrzymane modelem Winters’a multiplikatywnym:

Mając RMSE warto policzyć także wskaźnik
W

m

.

100





M

m

Y

RMSE

W

gdzie

M

Y

to średnia zmiennej prognozowanej w okresach od t=2
do t=15.

21429

,

46



M

Y

Wówczas,

58876

,

60



m

W

Na podstawie wielkości wskaźnika W

M

możemy stwierdzić, że błąd

RMSE stanowi około 60,59% średniej wielkości sprzedaży w
miesiącach od drugiego do piętnastego.

Przykład – SAS.

Jak z modelu Winters’a zrobić model Holt’a?

1. Z kodu usuwamy „SEASONS=„
2. Sezonową wagę wygładzania ustawiamy na 0.

Pierwotny kod:

Poprawiony kod:

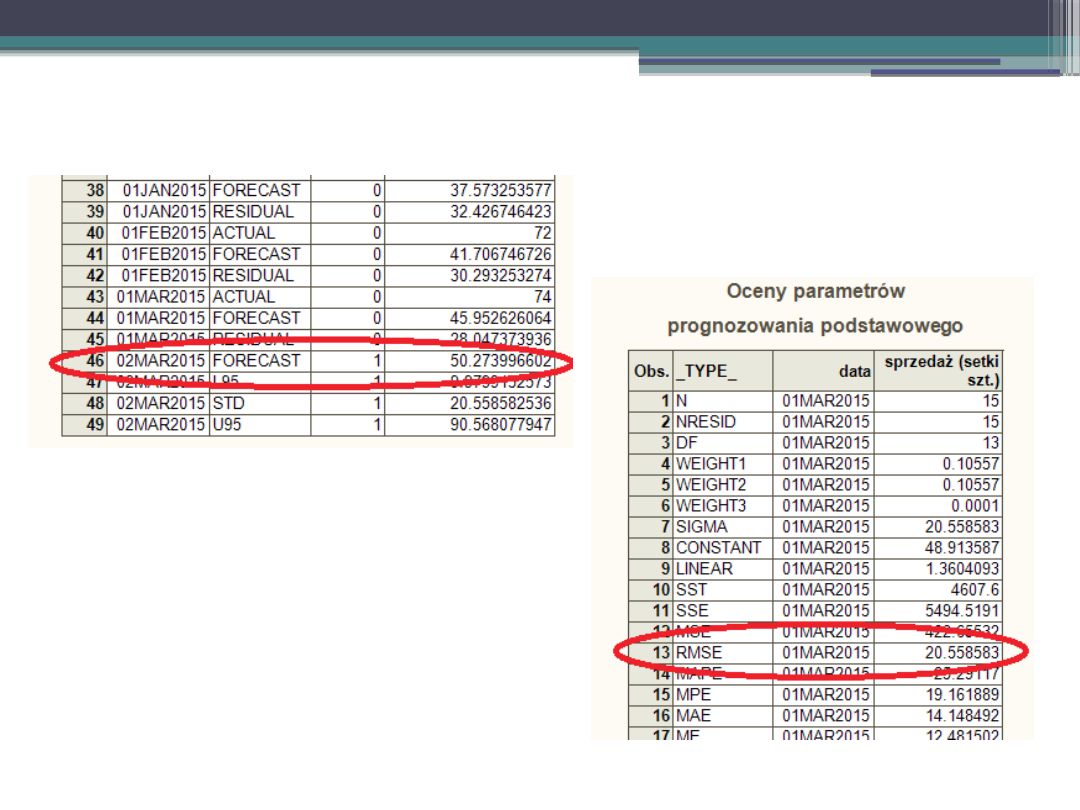
Przykład – SAS.

Prognoza i oceny parametrów po zmianie kodu.

48534

,

44



m

W

W tym przypadku W

m

wynosi:

Zatem błąd RMSE stanowi około 44,48%
średniej wielkości sprzedaży w
miesiącach od drugiego do piętnastego.

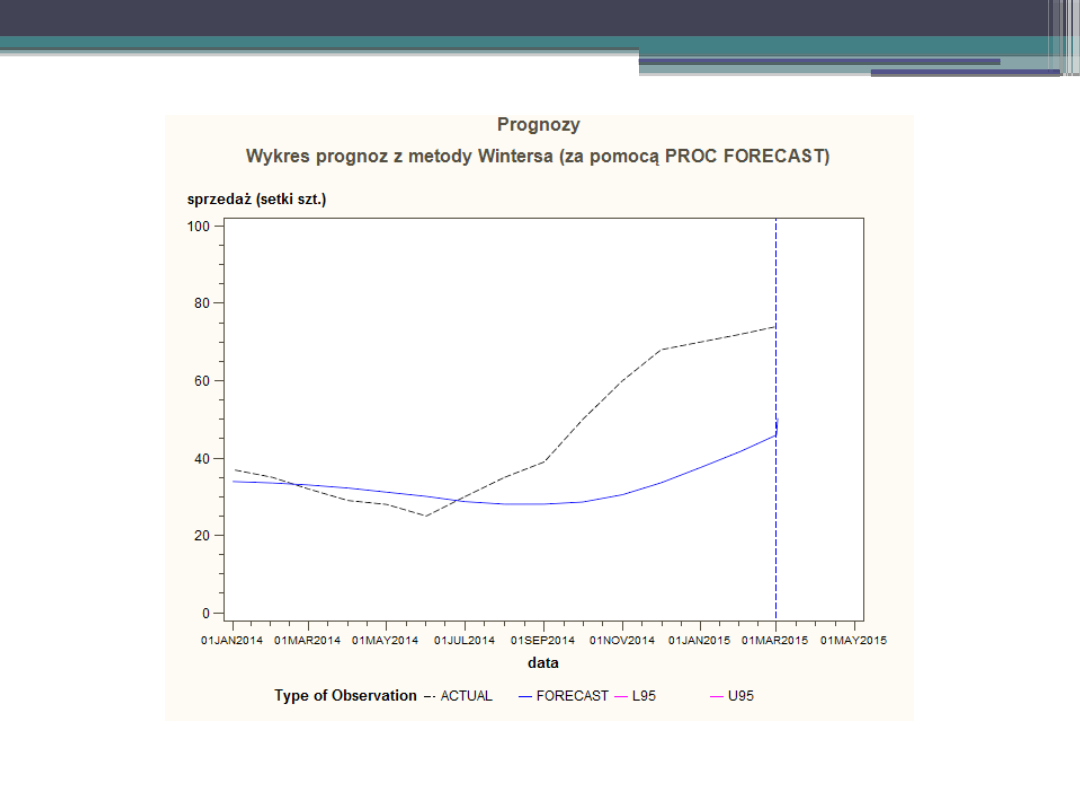
Przykład – SAS.

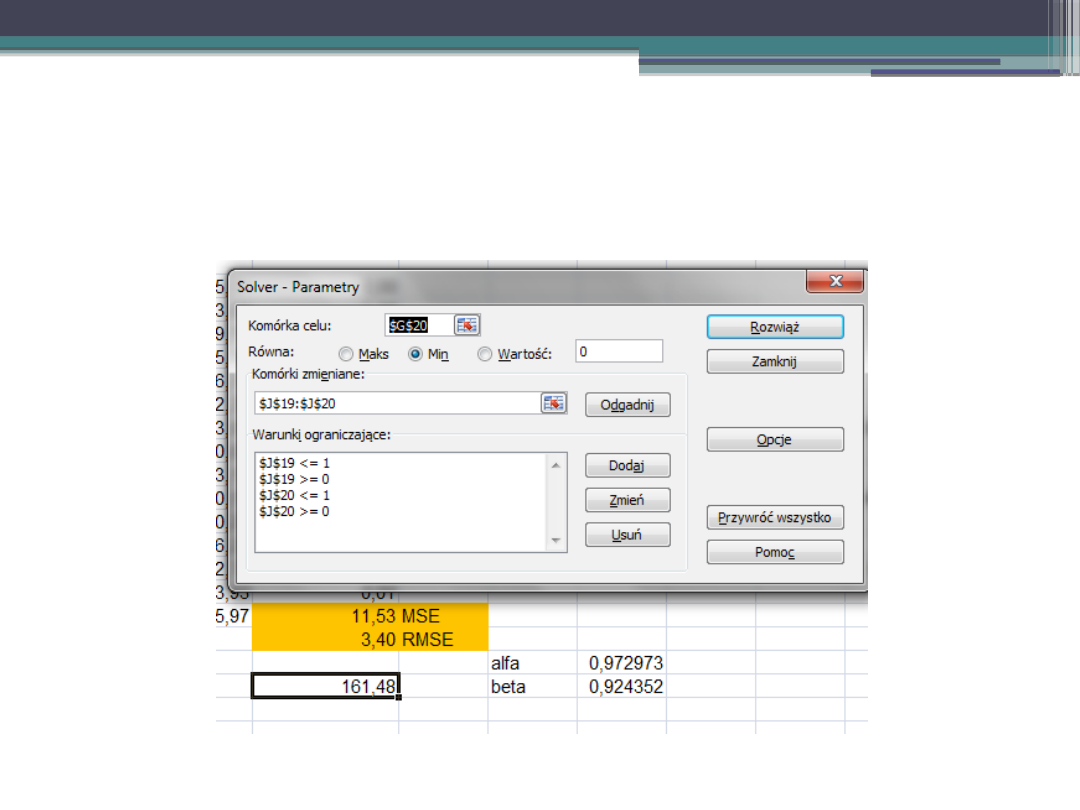
Jak widać błąd RMSE jest dość duży i nie należy używać tak
skonstruowanego modelu Holta do prognozowania. Wielkość błędu
RMSE możemy spróbować zmniejszyć zmieniając wartości α i β . Do
znalezienia wartości minimalnej RMSE użyjemy narzędzia Solver

Przykład - SAS.

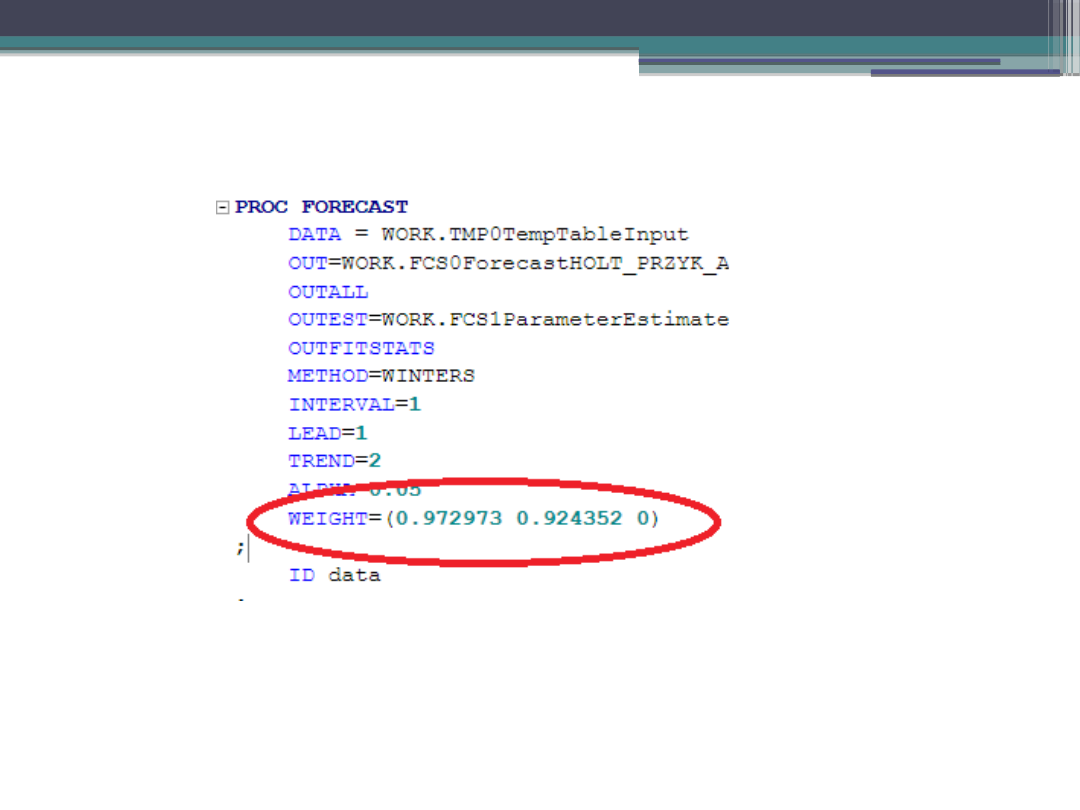
Przykład – SAS.

Zmieniamy wartości stałych wygładzania na 0,972973 oraz
0,924352.

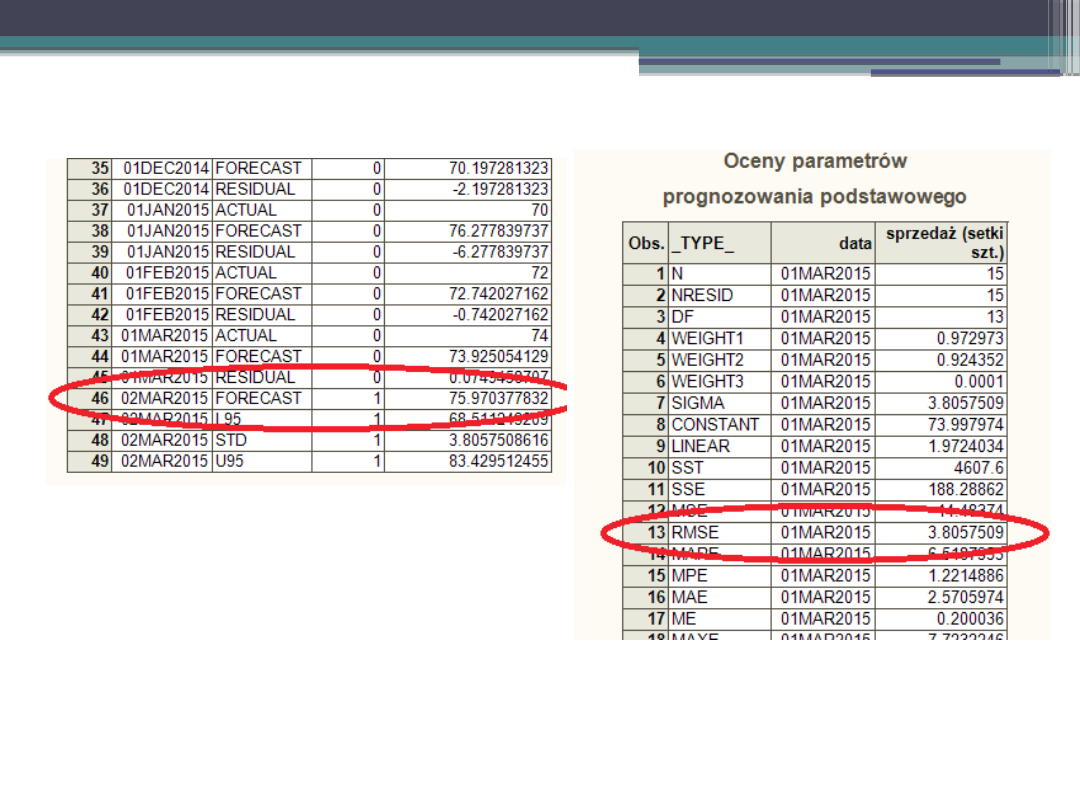
Przykład – SAS.

Prognozy i oceny parametrów po zmianie stałych wygładzania:

23501

,

8



m

W

Otrzymujemy:

Na podstawie wielkości wskaźnika W

M

możemy stwierdzić, że błąd

RMSE stanowi około 8,24% średniej wielkości sprzedaży w miesiącach
od drugiego do piętnastego. Błąd RMSE jest niewielki a więc model
Holt’a z parametrami wygładzania α=0,972973 i β=0,924352 może
zostać użyty do prognozowania.

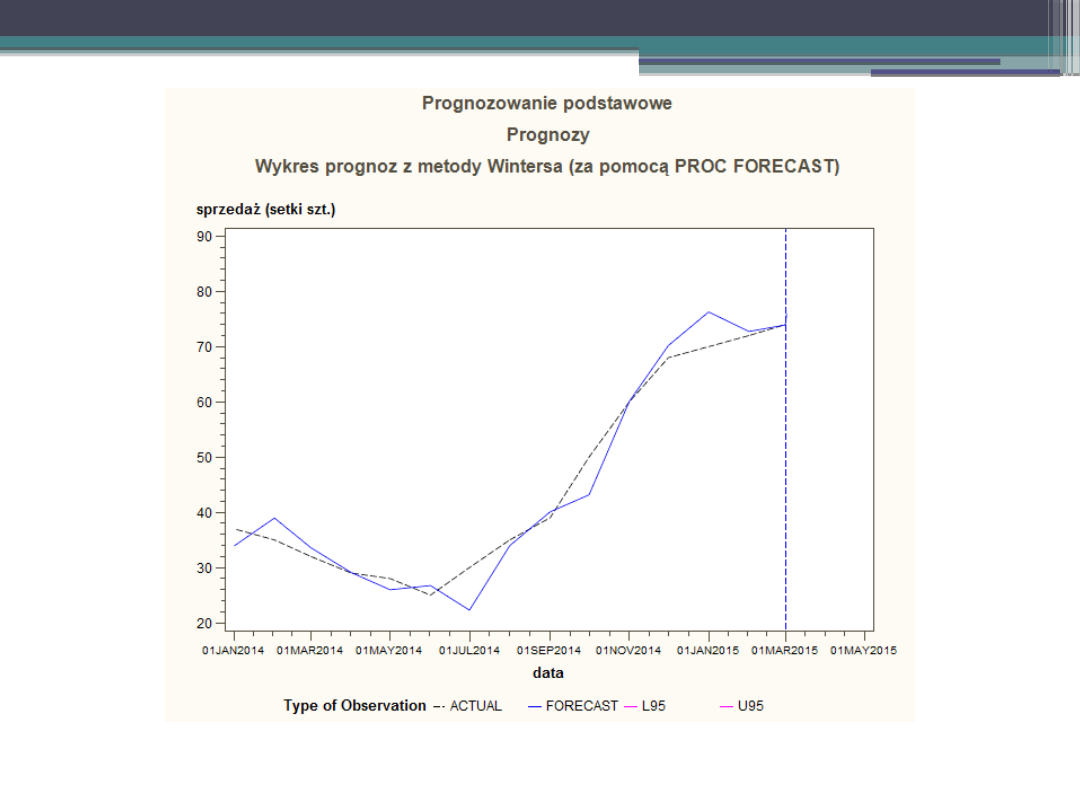
Przykład – SAS.

KONIEC

DZIĘKUJĘ ZA UWAGĘ!! 